峰峰值,峰值,平均值,有效值的关系
常见信号的有效值与峰值的关系

常见信号的有效值与峰值的关系1、何为有效值?从热等效原理定义有效值。
让交流电与直流电分别通过同一电阻,若两者在相同的时间内所消耗的电能相等(或产生的焦耳热相同),那么该直流电的数值就叫做交流电的有效值。
2、何为均方根?含义说明:从数学的角度定义AC波(交流信号)的有效电压值或电流值。
英语写为:Root Mean Square (RMS)均方根。
RMS是定义AC波有效值的一种普遍的数学方法。
RSM(Root Mean Square)在美国传统词典的定义为:The square root of the average of squares of a set of numbers.即:将N个项的平方和除以N后开平方的结果,即均方根的结果。
公式:这种数学表示为什么就是信号的有效值呢?一下是简单的高等数学分析:设信号的峰值表达式为UMAX,同时该信号的有效值为URMS,负载为R。
那么用这两种信号值计算一个周期内的做功如下:“”3、有效值与均方根的关系有效值从正真意义上定义了AC信号等效为直流信号的值,而均方根只是一般的结果表达式而已。
其作用也不大。
如果要计算任意一个周期信号的有效值还是要从热等效原理出发,利用极限求和以及定积分的知识去,求解等效的直流信号值即有效值。
4、有效值与均方根的计算4.1计算的思想对于一般信号有效值的定义:“时变量的瞬时值在给定时间间隔内的均方根值。
对于周期量,时间间隔为一个周期。
”4.2正弦波有效值推导的一般方法从定义出发计算有效值,即,交流电与直流电分别通过同一电阻,若两者在相同的时间内所消耗的电能相等(或产生的焦耳热相同),那么该直流电的数值就叫做交流电的有效值。
信号功率在时间上的积累即为信号做的功用定积分计算交流信号在负载R上一个周期内做的功。
他就等于一个直流量(有效值)在负载R 上一个周期内做的功。
“”4.3正弦波有效值推导的常用方法计算需要采用定积分运算,当信号为sinx时,计算他的有效值,应该进行如下运算:求(sinx)^2在-π~π范围内的定积分。
振动常用术语

振动常用术语1. 机械振动物体相对于平衡位置所作的往复运动称为机械振动;简称振动;例如,机器箱体的颤动、管线的抖动、叶片的摆动等都属于机械振动;振动用基本参数、即所谓“振动三要素” —振幅、频率、相位加以描述;3. 振幅振幅振幅是物体动态运动或振动的幅度;振幅是振动强度和能量水平的标志,是评判机器运转状态优劣的主要指标;峰峰值、单峰值、有效值振幅的量值可以表示为峰峰值pp、单峰值p、有效值rms或平均值ap;峰峰值是整个振动历程的最大值,即正峰与负峰之间的差值;单峰值是正峰或负峰的最大值;有效值即均方根值;只有在纯正弦波如简谐振动的情况下,单峰值等于峰峰值的1/2,有效值等于单峰值的倍,平均值等于单峰值的倍;平均值在振动测量中很少使用;它们之间的换算关系是:峰峰值=2×单峰值=2×21/2×有效值;此换算关系并无多大的实用价值,只是说明振幅在表示为峰峰值、峰值、有效值时,数值不同、相差很大;振动位移、振动速度、振动加速度振幅分别用振动位移、振动速度、振动加速度值加以描述、度量,三者相互之间可以通过微分或积分进行换算;在振动测量中,除特别注明外,习惯上,振动位移的量值为峰峰值,单位是微米μm或密耳mil;振动速度的量值为有效值,单位是毫米/秒mm/s 或英寸/秒ips;振动加速度的量值是单峰值,单位是重力加速度g或米/秒平方m/s2,1g = m/s2;可以认为,在低频范围内,振动强度与位移成正比;在中频范围内,振动强度与速度成正比;在高频范围内,振动强度与加速度成正比;因为频率低意味着振动体在单位时间内振动的次数少、过程时间长,速度、加速度的数值相对较小且变化量更小,因此振动位移能够更清晰地反映出振动强度的大小;而频率高,意味着振动次数多、过程短,速度、尤其是加速度的数值及变化量大,因此振动强度与振动加速度成正比;也可以认为,振动位移具体地反映了间隙的大小,振动速度反映了能量的大小,振动加速度反映了冲击力的大小;在实际应用中,大型旋转机械的振动用振动位移的峰峰值μm表示,用装在轴承上的非接触式电涡流位移传感器来测量转子轴颈的振动;一般转动设备的振动用振动速度的有效值mm/s表示,用手持式或装在设备壳体上靠近轴承处的磁电式速度传感器或压电式加速度传感器如今主要是加速度传感器来测量;齿轮和滚动轴承的振动用振动加速度的单峰值g表示,用加速度传感器来测量;振动烈度振动烈度是振动标准中的通用术语,是描述一台机器振动状态的特征量;在我国及国际振动标准中,几乎都规定振动烈度的度量值为振动速度的有效值;因此,可以认为振动烈度就是振动速度的有效值;所以,在对一般转动设备进行振动监测时,应测量振动速度的有效值并要求在靠近轴承位置处的水平、垂直、轴向三个方向上进行测量,取最大值,因为只有振动烈度才有振动标准可以参照大机组不完全如此,评定机器运转状态的优劣时才能做到有据可依;右图为中石化旋转机械振动标准SHS 01003-2004关于机器振动烈度的评定等级表;我国及国际其它振动标准关于机器振动烈度的评定等级也大致如此;例如,ISO 3945对转速为600~12000 r/min,功率大于300kW的大型旋转机械的标准与此完全相同;德国工程师协会VDI 2056标准与此基本相同低一格;其中,根据输出功率、机器—支承系统的刚性等将旋转机械分为如下4类:Ⅰ~小型转机,如15 kW以下的电机;Ⅱ~安装在刚性基础上的中型转机,功率在300 kW以下;Ⅲ~大型转机,机器—支承系统为刚性支承状态;Ⅳ~大型转机,机器—支承系统为挠性支承状态;当支座的固有频率大于转子轴承系统的固有频率时,为刚性支承状态;当支座的固有频率小于转子轴承系统的固有频率时,为挠性支承状态;振动烈度Xrms与振动位移Xpp、振动加速度Xp的换算关系式为:Xrms=2πf/2 21/210-3Xpp ≈10-3 Xpp f mm/sXrms=21/2/2/2πf 103Xp ≈103Xp/f mm/s式中,Xpp~振动位移峰峰值,μm;Xp~振动加速度单峰值,g;f~主振动的频率,通常取工频,Hz;频率、周期频率f是物体每秒钟内振动循环的次数,单位是赫兹 Hz;频率是振动特性的标志,是分析振动原因的重要依据;周期T是物体完成一个振动过程所需要的时间,单位是秒 s ;例如一个单摆,它的周期就是重锤从左运动到右,再从右运动回左边起点所需要的时间;频率与周期互为倒数,f=1/T;对旋转机械来说,转子每旋转一周就是完成了一个振动过程,为一个周期,或者说振动循环变化了一次;因此转速n、角速度ω都可以看作频率,称为旋转频率、转速频率、圆频率,或n、ω、f不分,都直接简称为频率,它们之间的换算关系为:f = n/60,ω=2πf=2πn/60≈,其中转速n的单位为转/分钟r/min,角速度ω的单位为弧度/秒rad/s;倍频、一倍频、二倍频、倍频、工频、基频、转频振动频率也可以用转速频率的倍数来表示;倍频就是用转速频率的倍数来表示的振动频率;如果振动频率为机器实际运行转速频率的一倍、二倍、三倍、倍、倍、…时,则称为一倍频习惯上又称为1X,或1×、二倍频2X、2×、三倍频3X、3×、倍频、×、倍频、×、…等;其中,一倍频,即实际运行转速频率又称为工频、基频、转频,倍频又称为半频;例如,某机器的实际运行转速n为6000 r/min,那么,转速频率=n/60=6000/60=100Hz,其工频为100Hz,二倍频为200Hz,半频为50Hz;通频振动、选频振动通频振动是原始的、未经傅里叶变换分解处理的、由各频率振动分量相互迭加后的总振动;其振动波形是复杂的波形;选频振动是从通频振动中所分解出来的、振动波形是单一正弦波的、某一选定频率的振动如工频、倍频、二倍频、…;故障特征频率各种不同类型的故障所引起的振动都有各自的特征频率;例如,转子不平衡的振动频率是工频,齿式联轴器带中间齿套不对中的振动频率是二倍频,油膜涡动的振动频率是倍频实际上要小一点,等等;由各频率成分的幅值大小和分布情况,从中查找出发生了异常变化的频率,再联系故障特征频率探索构成振动激振力的来源,是判别振动故障类型通常采用的诊断方法;但是反过来,某种振动频率又和多种类型的故障有关联;例如,动不平衡的特征频率是工频,但不能说工频高就是发生了动不平衡,因为某些轴承及不对中等故障的振动频率也是工频;因此,频率和振动故障的对应关系并不是唯一的;为了得到正确的诊断结论,需要对各种振动信息进行综合分析;常见的故障特征频率及相应的故障类型,简要介绍如下:①工频工频成分在所有情况下都存在,工频幅值几乎总是最大,应该在其发生异常增大的情况下才视为故障特征频率;工频所对应的故障类型相对较多;多数60%以上为不平衡故障,如转子发生机械损伤脱落断叶片、叶轮破裂等、结垢、初始不平衡,以及轴弯曲等;同时,相当数量接近40%为轴承偏心类故障,如间隙过大、轴承合金磨损、轴颈与轴承偏心、轴承座刚度差异过大等;此外,还有刚性联轴器的角度端面不对中;支座、壳体、基础的松动、变形、裂缝等支承刚度异常引起的振动或共振;运行转速接近临界转速;发电机及电动机转子偏心等;②二倍频二倍频成分在所有情况下也都存在,幅值往往低于工频的一半,常伴有呈递减状的三倍频、四倍频、…,也应该在异常增大的情况下视为故障特征频率;二倍频所对应的故障类型较为集中;绝大多数为不对中含联轴器故障,如齿式联轴器带中间短接和金属挠性膜盘、叠片联轴器的不对中、刚性联轴器的平行径向不对中,其中,既有安装偏差大所产生的冷态不对中,又有由温差产生的支座升降不均匀以及管道力所引起的热态不对中,以及联轴器损伤故障等;此外,还有概率较小的其它故障,如转动部件松动,转子刚度不对称横向裂纹,支承刚度在水平、垂直方向上相差过大等;⑤机器自身和基础或其它附着物的固有频率⑥齿轮故障的特征频率由于齿轮的轮齿在进入和脱离啮合时,载荷突变、碰撞加剧,瞬时的高频冲击振幅与周期性变化的转频振幅相互叠加而产生幅值调制;制造时的轮齿分度不均匀、即周节误差使旋转速率发生变化则产生了频率调制;齿轮振动的特征频率为:fm ± i f , i为正整数i=1,2,3,…式中,fm~啮合频率,为载波频率, fm=f1z1=f2z2,其中, f1、f2、z1、z2分别为主动轮、从动轮的转速频率及齿数;f~齿轮的转速频率,为调制频率;表现在频谱图上,是以啮合频率fm为中心、以齿轮转速频率f为间隔,不太对称地分布于fm的两侧对称度与周节误差相关,两侧称为边频带、边带;如果缺陷分布较均匀、如磨损,频谱图上的边频带则显现为窄、高、起伏大;如果发生断齿或大的局部性缺陷,边带则宽、低、平;⑦滚动轴承故障的特征频率滚动体的通过频率对于滚动轴承来说,由于轴承游隙的存在,滚动体在通过载荷方向时受力最大,反方向时最小或无;因此,每个滚动体在通过载荷方向时就会发生一次力的变化,内圈及轴颈、外圈及轴承座也同时受到一次激励,此激励频率称为滚动体的通过频率fe;显然,fe=z fc,其中,z~滚动体个数,fc~滚动体的公转频率、也是保持架的旋转频率;。
有效值,峰值,峰峰值的转换关系

有效值,峰值,峰峰值的转换关系嘿,朋友们!今天咱们来聊聊有效值、峰值和峰峰值这几个有点绕的概念,就像在迷宫里找宝藏一样,不过这宝藏可是知识的宝藏哦。
首先呢,峰值就像是山的最高峰。
想象一下,你站在山脚下,抬头看那座山,最高的那个点就是峰值啦。
比如说电压,它就像一个调皮的小怪兽,一下子能蹦到最高的那个数值,这个最高的数值就是峰值。
它总是在那耀武扬威地展示自己能达到的最厉害高度。
那峰峰值呢?这可就更有趣了。
峰峰值就像是从山谷最低点到山峰最高点的距离。
如果峰值是山顶上插着的那面旗帜,峰峰值就是从山脚下的深谷一直到那面旗帜的超级大距离。
就好像是一个超级长腿的巨人,一步从谷底跨到了山顶,这一步的跨度就是峰峰值。
它比峰值可更能显示出整个波动的“大长腿”范围呢。
现在轮到有效值出场啦。
有效值就像是这个波动世界里的实干家。
它不像峰值和峰峰值那样爱出风头。
有效值就好比是一群小动物每天出去找食物,平均下来每天找到的食物量就是有效值。
对于电压或者电流来说,有效值更能反映出它们在实际工作中的“平均实力”。
这三者之间的关系呀,就像是一个小团队。
峰值是那个最有冲劲的前锋,总是冲在最前面,大喊着“我最高”。
峰峰值呢,是那个管着前锋和后卫距离的教练,它要确保整个队伍的跨度范围。
而有效值就是队伍里默默干活,把事情稳稳当当做好的后勤人员。
从数值关系上看,峰峰值就像是峰值的双倍放大版,就像照镜子的时候,镜子里的你和你组成了一个双倍的你,峰峰值就是峰值的这种双倍效果。
而有效值和峰值之间的关系就有点像一个神秘的魔法。
有效值大概是峰值的0.707倍,就好像是峰值这个大明星被打了个折扣,变成了有效值这个低调但很实在的小助手。
在电路的大舞台上,这三个家伙各有各的角色。
峰值和峰峰值在那里表演着高难度的杂技,而有效值在后台默默支撑着整个表演的稳定运行。
如果没有有效值,就像表演没有了后勤保障,肯定会乱成一团。
如果没有峰值和峰峰值,就像表演没有了精彩的看点,变得平淡无奇。
物理因素导致的职业病:振动 2

有效值(rms ) • 平均值= 1 • 峰值
22
2
3
(一)振动卫生学评价的物理参量
2.卫生学评价参量 (1)振动频谱 振动频谱是将复杂振动的各频带测得的振 动强度(如,加速度有效值)数值按频率大小排列的图形。 常用频带:1/1倍频带(简称倍频带)、1/3倍频带两种; 频率范围:6.3~1 250Hz(倍频带),
16
(四)手臂振动病
➢ 定义:长期从事手传振动作业所引起的以手部末 梢循环障碍和/或手臂神经功能障碍为主的疾病 (也可累及手臂骨关节-肌肉的损伤)。
➢ 典型表现:振动性白指(VWF)
17
(四)手臂振动病
捣固工
铆工
油锯工
风钻工
砂轮磨光工
18
(四)手臂振动病
1.发病机制
① 手部接
触振动
局部组织 压力↑
➢ 临床表现:疲劳、冷汗、面色苍白、眩晕、恶心、 呕吐、血压下降、视物模糊,频繁呕吐可引起水、 电解质紊乱、休克。
14
(三)振动对机体的影响
1. 全身振动
➢ 内脏位移,机械性损伤; ➢ 自主神经功能紊乱; ➢ 胃肠分泌功能减弱,食欲减退,胃下垂; ➢ 腰背痛、椎间盘突出、脊柱骨关节病变; ➢ 内分泌系统调节功能紊乱,月经周期紊乱,流产
n:频带数; Ki:第i频带的计权系数;
ahi:第i频带的加速度有效值(m/s2)。
9
(一)振动卫生学评价的物理参量
2.卫生学评价参量
(3) 4小时等能量频率计权振动加速度[ahw(4)]
每日接振不足或超过4小时,按公式换算为ahw(4):
式中,T:日接振时间(小时) ahw(T):日接振T小时的手传振动频率计权加速度(m/s2)
电路基础原理交流电路中的有效值与峰值的关系

电路基础原理交流电路中的有效值与峰值的关系交流电路是我们日常生活中广泛使用的电路,它是通过交替方向变化的电流来传输能量。
在交流电路中,我们经常会遇到两个概念,即有效值和峰值。
本文将探讨有效值与峰值在交流电路中的关系及其重要性。
在交流电路中,电流和电压的大小是随时间变化的,通常呈正弦波形。
峰值是指正弦波的最大值,即波峰的高度;有效值则是指正弦波电流或电压的平均值。
有效值被广泛应用于交流电路的分析和设计中。
那么,有效值与峰值之间有何关系呢?根据数学原理,正弦波电流或电压的有效值等于峰值除以√2,即:有效值 = 峰值/ √2这个公式告诉我们,只要我们知道了正弦波的峰值,就可以轻松地计算出它的有效值。
换句话说,峰值是有效值的√2倍。
在实际应用中,我们经常使用有效值来比较大小,因为它更能反映电流或电压的实际能量传输情况。
那么,为什么有效值在交流电路中如此重要呢?这涉及到交流电路的功率传输。
功率是电流和电压的乘积,而正弦波电流和电压的峰值乘积即为它们的瞬时功率。
然而,交流电路中实际传输的功率是电流和电压的有效值乘积。
这是因为交流电路中电流和电压是连续变化的,瞬时功率会随时间变化。
而有效值则是瞬时功率的平均值,能更准确地反映电能的传输。
了解有效值与峰值之间的关系,对于交流电路的分析和设计非常重要。
在电路设计中,我们通常需要计算电流和电压的有效值,并根据需求选择合适的元器件,以确保电路能够正常运行。
例如,在家用交流电路中,我们需要选择合适的电线、插座和开关,以承受正常使用的电流和电压。
此外,了解有效值与峰值的关系也对电路的安全起着关键作用。
因为峰值电流和电压的大小直接影响电路元器件的负载能力和稳定性。
如果电流或电压超过了元器件的额定值,就可能引发短路、过载和损坏等问题。
因此,在电路设计和使用中,我们必须在合适范围内控制电流和电压的峰值,以确保电路的正常运行和安全性。
综上所述,交流电路中的有效值与峰值有密切关系,峰值是有效值的√2倍。
均值,方差,峰值,峭度,有效值,峰值因子,脉冲因子,波形因子,裕度因子九个指标-概述说明以及解释

均值,方差,峰值,峭度,有效值,峰值因子,脉冲因子,波形因子,裕度因子九个指标-概述说明以及解释1.引言1.1 概述概述部分的内容如下:引言部分旨在介绍本文所要探讨的九个指标,即均值、方差、峰值、峭度、有效值、峰值因子、脉冲因子、波形因子和裕度因子。
这些指标在统计学和信号处理领域中具有重要的应用价值,能够揭示数据或信号的不同特征和性质。
首先,均值是一项基本的统计指标,用于度量数据集的集中趋势。
它简单地表示了数据的平均值,是了解数据集整体水平的重要参考指标。
其次,方差是描述数据变化程度的指标。
它反映了数据分布的离散程度,即数据离均值的距离。
方差越大,数据的分散程度也就越大,而方差较小则说明数据的分布较为集中。
接下来,峰值是描述数据集中程度的指标。
它代表了数据集中出现的最大值,反映了数据分布的集中程度。
峰值较高表示数据集中的数值相对集中,而较低的峰值则意味着数据的分布相对分散。
峭度是描述数据分布形态的指标。
它度量了数据分布的尖锐程度和尾部厚度,反映了数据集中的峰值特征。
较高的峭度表示数据分布相对集中,而较低的峭度则意味着数据分布相对平缓。
有效值是描述周期性信号振幅的指标。
它是信号的均方根值,即信号在一个周期内的振幅的平均平方根值。
有效值能够客观地衡量信号的幅度大小,常用于衡量信号的能量。
峰值因子是描述信号峰值与有效值的比值的指标。
它表示了信号的峰值相对于有效值的倍数,能够反映信号的峰值性质与振幅特征。
脉冲因子是描述信号短时特征的指标。
它衡量了信号中脉冲的持续时间与周期的比值,能够反映信号的波形形状和脉冲特征。
波形因子是描述信号周期性特征的指标。
它表示了信号波形的变化程度,即信号峰值与有效值之间的比值。
波形因子较大表示信号波形变化幅度较大,而较小的波形因子则表示信号变化幅度较小。
最后,裕度因子是描述信号稳定性的指标。
它衡量了信号振幅的波动范围与有效值之间的比值,能够反映信号的稳定性和波动程度。
本文将详述这九个指标的定义和计算方法,并通过实例和案例分析,探讨它们在不同领域的应用与意义。
有效值与平均值

有效值与平均值
有效值:让一个交流电流和一个直流电流分别通过阻值相同的电阻,如果在相同时间内产生的热量相等,那么就把这一直流电的数值叫做这一交流电的有效值。
平均值:正弦交流电的波形是对称于横轴的,在一个周期内的平均值恒等零,所以一般所说平均值是指半个周期内的平均值。
交流电流表和交流电压表测量的值都是有效值。
在选取晶闸管额定电压、电流的时候考滤的是最大值。
最大值也称为幅值或峰值。
最大值=跟号2倍的有效值
平均值=0.637倍的最大值
对于正弦交流,有效值等于1.1倍平均值,等于0.707倍峰值.
对于任意波形(包括直流),有效值满足均方根关系.即:瞬间电压的平方在一个周期内的积分的平方根再除以时间.
如果它的峰峰值是Upp的话那么有效值就是它除以2倍根号2,如果它的幅值是Um的话就除以根号2。
AC信号的特征描述

1AC 信号的特征参数最常见的AC (Alternating Current )信号是正弦波、三角波、脉冲等几种交流信号,是我们技术工作中使用频度最高的名词,周期性变化是其共性。
本文对描述AC 信号的常用参量加以说明,以求对AC 信号的深入理解和灵活描述。
常用的AC 信号描述参数有有效值、峰值和峰峰值、平均值及dBm 等。
1 参量的特征及其定义⒈1 有效值(RMS )(root mean square )有效值是依据电流的热效应来规定的。
两个同阻值的电阻,一个通直流,一个通交流,若在同一时间内,它们产生的热量相等,则其中直流电压的数值既为另一个交流电压的有效值。
在数学上,有效值与均方根值是同义词,一个周期波形的RMS 值是通过求均方根值获得的。
RMS 值只对周期性信号才有意义。
设u (t )为交流信号,T 为其周期,则其RMS 值为:()⎰=T dt t u T U 021即在u (t )的整个周期上,将每一个点的电压值平方后再相加,再求均值,最后开方。
用这种方法求得的波形RMS 值与信号的波形形状无关,只是测定波形的幅度特性。
显然,对于正弦波与其全波整流后的波形,其有效值相同。
RMS 值是规定交流信号幅度最有用的办法,常用大写字母表示。
1.2 峰值和峰-峰值峰值是从参考电平开始计算的,即从零电平到最大电压值的差值,有正峰值和负峰值之分。
峰-峰值是从最小的负电压值到最大的正电压值之间的差值,既正峰值和负峰值之间的差值。
峰值因子(crest facter )(简C.F.)是指波形的峰值对有效值的比率。
若已知一特定交流信号,可用其相关峰值因子将峰值转化成相应的RMS 值。
1.3 平均值平均值指交流信号中不随时间变化的常数,是该信号级数展开式中的恒定分量。
交流信号的平均值等于此信号绝对值的平均值。
假如对于一个正弦波而言,在一个周期中,正半周内波形与负半周内波形相同,但方向相反,则平均幅度为零。
但我们感兴趣的值是指该电压加在一个电阻上的发热值,故正弦波的平均值指正弦波经过全波整流后的平均值。
机械振动与故障诊断基本知识

旋转机械状态监测与故障诊断讲义陈国远深圳市创为实技术发展有限公司2005年8月目录第一章状态监测的基本知识 (4)一、有关的名词和术语 (4)1. 振动的基本参量:幅值、周期(频率)和相位 (4)2. 通频振动、选频振动、工频振动 (6)3. 径向振动、水平振动、垂直振动、轴向振动 (6)4. 同步振动、异步振动 (7)5. 谐波、次谐波、亚异步、超异步 (7)6. 相对轴振动、绝对轴振动、轴承座振动 (7)7. 自由振动、受迫振动、自激振动、随机振动 (7)8. 高点和重点 (8)9. 刚度、阻尼和临界阻尼 (8)10. 共振、临界转速、固有频率 (9)11. 分数谐波共振、高次谐波共振和参数激振 (9)12. 涡动、正进动和反进动 (9)13. 同相振动和反相振动 (10)14. 轴振型和节点 (10)15. 转子挠曲 (11)16. 电气偏差、机械偏差、晃度 (11)17. 偏心和轴心位置 (11)18. 间隙电压、油膜压力 (11)二、传感器的基本知识 (12)1. 振动传感器 (12)2. 电涡流振动位移传感器的工作原理 (13)3. 电动力式振动速度传感器的工作原理 (13)⒋压电式加速度传感器的工作原理 (14)第二章状态监测常用图谱 (15)1.波德图 (15)2.极坐标图 (16)3.频谱瀑布图 (16)4.极联图 (17)5.轴心位置图 (18)6.轴心轨迹图 (18)7.振动趋势图 (19)8.波形频谱图 (20)第三章旋转机械的故障诊断 (22)1. 不平衡 (22)2. 不对中 (23)3. 轴弯曲和热弯曲 (26)4. 油膜涡动和油膜振荡 (28)5. 蒸汽激振 (30)6. 机械松动 (33)7. 转子断叶片与脱落 (33)8. 摩擦 (38)9. 轴裂纹 (40)10. 旋转失速与喘振 (40)11. 机械偏差和电气偏差 (43)第一章状态监测的基本知识一、有关的名词和术语机械振动是指物体围绕其平衡位置附近来回摆动并随时间变化的一种运动。
交流与直流电流换算公式_解释说明以及概述

交流与直流电流换算公式解释说明以及概述1. 引言1.1 概述交流电流和直流电流是电学中重要的两种电流形式。
在现代社会,无论是家庭用电、工业生产还是通讯系统,我们都离不开这两种电流。
了解交流与直流电流之间的差异以及它们的换算公式对于我们正确认识和应用电学原理具有重要意义。
1.2 文章结构本文将首先介绍交流电流和直流电流的区别与特点,包括它们的定义、特点及应用场景。
接着,我们会详细阐述交流电流和直流电流的换算公式。
在交流部分,我们将讨论峰峰值、平均值和有效值之间的关系,并给出计算方法;同时,也会介绍脉冲信号的表示方法与相应的换算公式。
在直流部分,我们将重点讲解线性负载下欧姆定律的计算方法,并探讨非线性负载情况下的换算公式及实际应用示例。
最后,在结论部分我们将总结交直流换算公式并归纳其应用范围。
1.3 目的本文旨在深入介绍交直流电流的区别、特点和应用,并详细讲解两者之间的换算公式,以帮助读者更好地理解交直流电流的本质和计算方法。
通过阅读本文,读者将能够掌握交直流电流换算公式的推导过程和实际应用场景,并能够灵活运用这些公式解决相关问题。
同时,本文也可以作为学习电学基础知识和深入研究交直流电流转换桥梁,进一步拓宽读者对于电学领域的认识和理解。
2. 交流电流和直流电流的区别与特点2.1 交流电流的定义和特点:交流电流指的是电荷在导体中来回移动,其方向和大小都会随着时间而变化。
交流电流的特点是:- 方向变化:在一个完整的周期内,交流电流会改变方向多次。
这是因为交流电源(如发电机)产生的电压具有周期性,从正值到负值再到正值。
- 幅度变化:同样,在一个周期内,交流电流的幅度也会随着时间不断变化,从最大正值到最小值再到最大负值。
此外,根据频率的不同,可以将交流电分为低频、中频和高频三类。
低频交流电常用于家庭用电和工业应用中,而高频交流电常用于通信和无线传输等领域。
2.2 直流电流的定义和特点:相比之下,直流电流(Direct Current, DC)指的是沿着一个固定方向持续不变的电荷运动。
三角波有效值和峰峰值的关系

三角波有效值和峰峰值的关系三角波是一种周期的交替波形,它的形状类似于三角形,因此得名。
在电子技术领域中,三角波非常常见,是各种信号处理电路中的基础元件。
在处理这种波形信号时,需要掌握它的有效值和峰峰值之间的关系。
首先,我们需要了解有效值的概念。
有效值指的是一个周期内波形的均方根值,也被称为“RMS”值。
在直流电路中,电压或电流的数量级都是不变的,但在交流电路中,电压和电流的数值是随着时间变化的。
因此,相较于最大值和最小值,我们更关心能量的平均值,即有效值。
峰峰值则指的是波形的最大值和最小值之间的范围。
峰峰值是指一个周期内波形上升到最高点和下降到最低点之间的距离。
对于三角波,我们可以通过以下几个步骤来计算其有效值和峰峰值之间的关系:1. 计算波峰和波谷的幅度值。
三角波的峰值等于其幅度值的绝对值,波谷等于幅度值的相反数。
2. 计算波峰、波谷和零点之间的距离。
对于一个完整的周期,三角波从波谷(或零点)到波峰(或零点)再到波谷(或零点)的距离都是相等的。
3. 计算三角波的峰峰值。
峰峰值等于波峰和波谷之间的距离的两倍。
4. 计算三角波的有效值。
由于三角波的形状相对简单,我们可以采用等效方法来计算其有效值。
用波峰值乘以0.632,再用波谷值乘以0.632,得到的两个值之和再除以2即可得到三角波的有效值。
因此,三角波有效值和峰峰值之间的关系可以用下面这个简单的公式表示:有效值 = (波峰值× 0.632 + 波谷值× 0.632) / 2峰峰值 = 波峰值 - 波谷值需要注意的是,这个公式只适用于纯三角波。
对于复合波,我们可能需要使用更为复杂的计算方法。
此外,由于三角波的峰峰值是从波峰到波谷的距离,所以我们也可以将其看成是总振幅的两倍。
因此,在三角波信号的处理中,我们还可以使用这个公式来计算三角波的总振幅。
总之,了解三角波的有效值和峰峰值之间的关系对于正确处理这种波形信号至关重要。
通过上述公式的计算,我们可以轻松地获取三角波信号的相关参数,从而在电子技术领域的各种应用中获得更好的表现。
正弦电压和电流的有效值、平均值、瞬时值及峰值
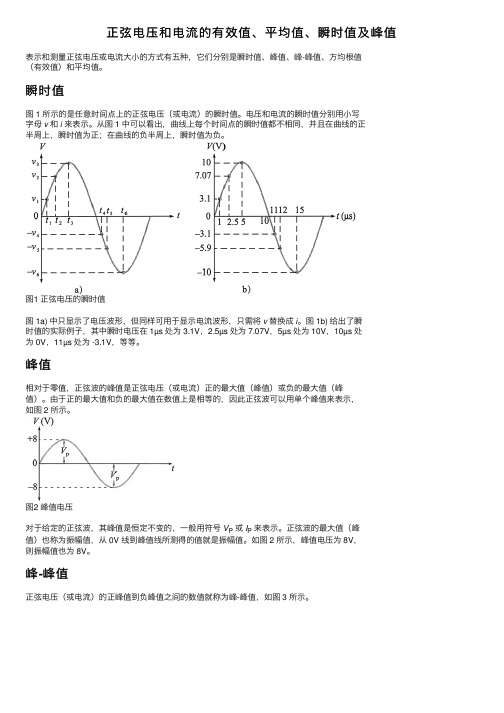
正弦电压和电流的有效值、平均值、瞬时值及峰值表⽰和测量正弦电压或电流⼤⼩的⽅式有五种,它们分别是瞬时值、峰值、峰-峰值、⽅均根值(有效值)和平均值。
瞬时值图 1 所⽰的是任意时间点上的正弦电压(或电流)的瞬时值。
电压和电流的瞬时值分别⽤⼩写字母v和i来表⽰。
从图 1 中可以看出,曲线上每个时间点的瞬时值都不相同,并且在曲线的正半周上,瞬时值为正;在曲线的负半周上,瞬时值为负。
图1 正弦电压的瞬时值图 1a) 中只显⽰了电压波形,但同样可⽤于显⽰电流波形,只需将v 替换成i。
图 1b) 给出了瞬时值的实际例⼦,其中瞬时电压在 1µs 处为 3.1V,2.5µs 处为 7.07V,5µs 处为 10V,10µs 处为 0V,11µs 处为 -3.1V,等等。
峰值相对于零值,正弦波的峰值是正弦电压(或电流)正的最⼤值(峰值)或负的最⼤值(峰值)。
由于正的最⼤值和负的最⼤值在数值上是相等的,因此正弦波可以⽤单个峰值来表⽰,如图 2 所⽰。
图2 峰值电压对于给定的正弦波,其峰值是恒定不变的,⼀般⽤符号V P或I P来表⽰。
正弦波的最⼤值(峰值)也称为振幅值,从 0V 线到峰值线所测得的值就是振幅值。
如图 2 所⽰,峰值电压为 8V,则振幅值也为 8V。
峰-峰值正弦电压(或电流)的正峰值到负峰值之间的数值就称为峰-峰值,如图 3 所⽰。
图3 峰-峰值电压峰-峰值通常是峰值的两倍,⽤公式表⽰为:⽅均根值(有效值)⽅均根(RMS)值也称为有效值,其中 RMS 是英语⽅均根⾸字母的缩写。
⼤多数交流电压表显⽰的都是电压的有效值,例如,墙壁插座引出的 120V 电压就是有效电压值。
电压的有效值是正弦电压热效应的度量值。
如图 4a) 所⽰,当把电阻器连接到交流(正弦波形)电压源上时,电阻器会以热量的形式消耗⼀部分能量。
如图 4b) 所⽰,将同样的电阻器连接到直流电压源上,调整交流电压源的电压值,可使连接在交流电压源上的电阻器产⽣和连接在直流电压源上的电阻器相等的热量。
振动分析和故障诊断

机器振动测量和评价的有关标准
ISO10816-1 专用机组宽带 振动准则
I SO10816-1:I类--发动机和机器的单独部件; II类--无专用基础的中型机器(15-75KW);专用刚性基础上300KW以下中型机器; III类--刚性基础上的大型机器; IV类--柔性基础上的大型机器。
常见机械故障
用频谱图表示
快 速 傅 里 叶 分 析 (FFT) 原 理
幅 值
时域 频域
x Ai sin(it i )
i 1
振动监测中的一些技术 细节要点
• 简 谐 振 动 位 移 , 速 度和 加 速度三者关系
振动加速度a0 振动加速度a0 振动速度V0 振动位移d0 1 a0/ (2f) a0 / (2f) ² 振动速度v0 (2f)V0 1 V0 / (2f) 振动位移d0 (2f) ² d0 (2f)d0 1
悬 臂 转 子不 平衡
轴向和 径向
1. 4
悬 臂 转 子 不 平 衡
悬 向 向 动 水 相 不 种 个
臂 引 振 可 平 位 平 都 修
转 起 动 能 方 差 衡 需 正
子 大 趋 不 向 相 和 要 面
不 的 向 稳 的 匹 力 修 内
平 衡 在 轴 向 1 转 速 频 率 于 同 相 位 , 定 。 然 而 , 相 位 差 通 常 配 ( 30 度 )。 偶 不 平 衡 两 正 。 因 此,总 加 以 修 正 重
没有观察
12075 10150
6000
800
1475
可用的频率范围为传感器固定自振频 率Fn的约50%
振动监测中的一些技术细节要点
振动传感器固定方式的影响
螺纹固定
AC信号的特征描述

1AC 信号的特征参数最常见的AC (Alternating Current )信号是正弦波、三角波、脉冲等几种交流信号,是我们技术工作中使用频度最高的名词,周期性变化是其共性。
本文对描述AC 信号的常用参量加以说明,以求对AC 信号的深入理解和灵活描述。
常用的AC 信号描述参数有有效值、峰值和峰峰值、平均值及dBm 等。
1 参量的特征及其定义⒈1 有效值(RMS )(root mean square )有效值是依据电流的热效应来规定的。
两个同阻值的电阻,一个通直流,一个通交流,若在同一时间内,它们产生的热量相等,则其中直流电压的数值既为另一个交流电压的有效值。
在数学上,有效值与均方根值是同义词,一个周期波形的RMS 值是通过求均方根值获得的。
RMS 值只对周期性信号才有意义。
设u (t )为交流信号,T 为其周期,则其RMS 值为:()⎰=T dt t u T U 021即在u (t )的整个周期上,将每一个点的电压值平方后再相加,再求均值,最后开方。
用这种方法求得的波形RMS 值与信号的波形形状无关,只是测定波形的幅度特性。
显然,对于正弦波与其全波整流后的波形,其有效值相同。
RMS 值是规定交流信号幅度最有用的办法,常用大写字母表示。
1.2 峰值和峰-峰值峰值是从参考电平开始计算的,即从零电平到最大电压值的差值,有正峰值和负峰值之分。
峰-峰值是从最小的负电压值到最大的正电压值之间的差值,既正峰值和负峰值之间的差值。
峰值因子(crest facter )(简C.F.)是指波形的峰值对有效值的比率。
若已知一特定交流信号,可用其相关峰值因子将峰值转化成相应的RMS 值。
1.3 平均值平均值指交流信号中不随时间变化的常数,是该信号级数展开式中的恒定分量。
交流信号的平均值等于此信号绝对值的平均值。
假如对于一个正弦波而言,在一个周期中,正半周内波形与负半周内波形相同,但方向相反,则平均幅度为零。
但我们感兴趣的值是指该电压加在一个电阻上的发热值,故正弦波的平均值指正弦波经过全波整流后的平均值。
交流电的峰值和有效值

交流电的峰值和有效值交流电是我们日常生活中经常接触的电能形式之一。
在电路中,交流电的峰值和有效值是非常重要的参数,它们不仅影响着电路的性能和稳定性,而且对于电力系统的工作也有着至关重要的作用。
本文将对交流电的峰值和有效值进行详细介绍,以帮助读者更好地了解这两个概念。
一、交流电的基本概念交流电,简称交流,是指电压、电流等随时间周期性变化的电信号。
在交流电中,电压和电流都是随着时间不断变化的,其变化规律是以正弦曲线为代表的。
交流电通常采用标志性的波形符号表示,波形符号上画出的线条形态即是周期性变化的电信号形状。
交流电信号的频率是指电信号在一秒钟内经历的周期数,单位为赫兹(Hz)。
二、交流电的峰值交流电的峰值(Peak Value)又称为峰峰值(Peak-to-Peak Value),是指电信号波形远离中轴线的最大值或最小值。
其中,正弦波的峰值为其绝对值的最大值,用Vm表示;负弦波的峰值为其绝对值最小值,用-Vm表示。
在交流电的波形图上,峰值就是波形振幅的绝对值,通常用Vm表示。
峰值可以用公式Vm = Vp / √2来计算,其中Vp表示交流电信号的峰峰值。
三、交流电的有效值交流电的有效值(RMS Value)又称为均方根值,是指电信号的电平使得它所带的功率与直流电源等效时的电平大小。
在交流电的波形图上,有效值是指在一定时间间隔内,电量的平均值,通常用Vrms表示。
电量的平均值可以用公式Vrms = Vp /√2来计算,其中Vp表示交流电信号的峰峰值。
四、峰值与有效值的区别通过上述介绍,我们可以得知,交流电的峰值和有效值是两个非常重要的参数。
尽管它们都是基于交流电信号的电位值测量出来的,但是它们是有区别的。
峰值通常表示电信号的最大值或最小值,而有效值则表示电信号的平均值。
在一定周期内,这两个参数的比值为√2,这也是计算它们之间的关系时所用的公式。
在电路设计中,峰值和有效值的不同特性将决定电路元件以及整个系统的效果。
峰峰值,峰值,平均值,有效值的关系

a) 电子测量的基础概念电子线路测量中,电压和电流是最基本的参量,对它们的测量是最基本的测量,其它的测量很多都以二者为基础。
电压的定义是对电路结构中的两点来定义的,只有载流子在从一点到另一点的运动过程中的电势能发生变化时,两点之间的电压差才非零。
所以电压对两点才有意义,对电压的测量一定是对两点的测量,一定是将电压表并联在电路中使用。
电流是对一个面积分得到的,单位时间内流过这个面的载流子的电荷数的度量被称为电流。
从电路拓扑的角度看,电流是对电路结构中的一点来说的,即单位时间内通过这一点的电荷数的度量被称为电流。
所以,电流对一点有意义,对电流的测量相当于观察这个点,对电流的测量一定是对一点的测量,对电流的测量一定是将电流表串联到电路中使用的。
电压有直流电压和交流电压两种。
在所关心的测量时间内,直流电压表示两端电压恒定的高低关系,就是说其中一端对另外一端总是高的,或总是低的;交流电压表示两端电压时变的高低关系,就是说两端电压的高低关系是随时间不断变化的。
当两点之间的电压保持恒定不变时,宏观上可以定义这两点之间的直流电压,只要一个值就可以完整地描述电压。
而当两点间不能保持电压恒定不变时,从宏观上对电压的描述有多种,分别描述它们不同方面的特性。
下面只考虑用得最多的周期信号的描述。
峰峰值V pp (Peak to Peak )。
峰峰值是指一个周期内信号最高值和最低值之间差的值,就是最大和最小之间的范围。
它描述了信号值的变化范围的大小。
峰值V p (Peak )。
峰值是指一个周期内信号最高值或最低值到平均值之间差的值。
一般来说,峰值对上下对称的信号才有定义。
可以看到,峰值等于峰峰值的一半。
有效值/均方根值V rms (Root Mean Square )。
是指在一个周期内对信号平方后积分,再开方平均,如公式2.1所示。
有效值的意义是:在一个周期内做功的大小等于与该值相等的直流电压所做功的大小。
dt t f T V Trms∫=02)(12.1* 设T 为信号的周期,下同。
电路原理电压的有效值 峰峰值 与平均值

电路原理中的电压有效值、峰峰值和平均值1. 电压的基本概念电压是电路中一种重要的物理量,用于描述电荷在电路中的差异程度。
它是指在两个点之间存在的电势差,常用单位是伏特(V)。
2. 电压的表示方法电压可以通过直流电和交流电来表示。
直流电的电压保持不变,而交流电的电压会随时间变化。
3. 交流电压的表示方法交流电压是指电压随时间变化的特殊类型电压。
它可以通过振幅、频率和相位来表示。
3.1 振幅振幅是交流电压在变化过程中的峰值大小,用于表示电压变化的幅度。
振幅通常用V表示,如Vmax。
3.2 频率频率是指交流电压变化的周期数,用于表示电压变化的速度。
频率通常用f表示,单位是赫兹(Hz),即每秒振动的周期数。
3.3 相位相位是指交流电压相对于某个参考点的延迟或提前。
它描述了交流电压波形在时间上的偏移。
相位通常用角度来表示,单位是度或弧度。
4. 电压的有效值有效值是交流电压幅值的大小,可以用于表示交流电压的大小。
它是指在一个周期内,正弦波电压所具有的相同功率的直流电压值。
有效值通常用Vrms表示。
公式:Vrms = Vmax / √2有效值是交流电压的一种标准表示方法,因为它可以用于计算交流电流和功率等其他参数。
5. 电压的峰峰值峰峰值是交流电压波动范围的大小,用于表示正弦波电压波动的幅度差。
它是指峰值与波谷之间的差值。
公式:Vpp = 2 * Vmax峰峰值是描述交流电压波形振幅的一种方式,它代表了一个周期内电压变化的最大范围。
6. 电压的平均值平均值是交流电压在一个周期内的平均值。
对于正弦波电压,平均值为零。
公式:Vavg = 0平均值用于描述电压在一个周期内的零点位置。
7. 总结•电压是电路中的重要物理量,用于描述电荷之间的电势差。
•交流电压是指随时间变化的电压,可以通过振幅、频率和相位来表示。
•电压的有效值是交流电压的一种标准表示方法,用于计算电流、功率等参数。
•电压的峰峰值是交流电压波动范围的大小,用于表示波动的幅度差。
音频知识(二)

28
FM广播的预加重和去加重
z 常用的预(去)加重时间常数 t=50uS 对应频率为Fs=3.18kHz t=75uS 对应频率为Fs=2.12kHz
z 接收机和发射机的加重时间常数必需一致
29
FM广播的预加重和去加重
z 举例说明(不合理的去加重时间常数):
30
问题讨论
问题讨论
31
11
各种节目源的峰值因数说明
FM广播频偏的有关解释:
¾ FM广播的国际标准调整频偏为75kHz。(对应节目信号的最大
峰值电平,即准峰值)
¾ FM广播的额定工作频偏为22.5kHz。(对应节目信号的额定工 作电平,即准平均值)
¾ FM广播调制度为
m = 22.5k ×100 = 30% 75k
¾ FM广播的峰值余量为 HR = 20 log 1 = 10.4dB 0.3
举例: ¾ DVD模式下,播放-60dBFS信号,测量线路输出的
THD+N的dB值, (THD+N)+60dB=DNR。
24
音频系统的几个重要概念
z 信噪比和动态范围示意图
信号最高准峰值电平
动态范围
信号最高准平均值电平 信噪比
噪声准峰值电平
噪声准平均值电平
25
FM广播的预加重和去加重
z 为什么要预加重
¾ 根据调频波的信噪比分析得出,调频信号的信噪比是和调制指 数成正比,即:
SNR ∝ m = Δf fA
式中∆f为频偏数值,fA为调制信号的最高频率(FM广播15kHz)。
¾ 实际FM广播中,调制信号是从30Hz-15kHz,低音和中音成 分比较强,而高音成分比较弱,使得在高音的调制频偏∆f比较 小,对应高音的调制指数变小,信噪比下降。
峰值有效值的关系(一)

峰值有效值的关系(一)
峰值有效值的关系
1. 什么是峰值和有效值?
•峰值(Peak Value)指信号在某一时刻的最大值,通常用Vp表示。
•有效值(RMS Value)指信号经过平方、积分、开平方等统计运算后得到的等效直流值,通常用Vrms表示。
2. 峰值有效值之间的关系
峰值和有效值之间存在着一定的关系,这个关系可以通过下述公式表示:
Vrms = Vp / √2
•Vrms:信号的有效值
•Vp:信号的峰值
3. 解释说明
峰值有效值之间的关系可以通过简单的推导得出。
假设信号的波形为正弦波,那么它的数学表达式为:
V(t) = Vp * sin(ωt + φ)
其中V(t)表示随时间变化的信号值,Vp为峰值,ω为角频率,t
为时间,φ为相位角。
有效值是信号经过统计处理后得到的等效直流值,可以通过下述
公式得到:
Vrms = sqrt(∫(V(t)^2 dt) / T)
其中∫(V(t)^2 dt)表示信号的功率平均值,T表示一个周期的时间。
对于正弦波,功率平均值可以写成:
∫(sin^2(ωt + φ) dt) = T / 2
带入公式后可得:
Vrms = Vp / √2
由此可见,正弦波信号的有效值等于其峰值的1/√2倍。
4. 结论
通过上述推导和解释,我们可以得出峰值和有效值之间的关系:
对于正弦波信号,有效值等于峰值的1/√2倍。
需要注意的是,此结论只适用于正弦波信号。
对于其他波形信号,峰值有效值之间的关系可能会有所不同。
峰峰值与有效值的关系

峰峰值与有效值的关系
哎呀呀,啥是峰峰值和有效值呀?这可把我这个小学生难住啦!
老师在课堂上讲的时候,我一开始那是一头雾水,就好像走进了一个黑漆漆的山洞,啥都看不见,啥都摸不着。
老师说,峰峰值就像是我们跳绳时,绳子甩到最高和最低的那个距离。
那有效值呢,又像是我们跑步时,平均下来的速度。
这可怎么理解呢?
我就想呀,峰峰值是不是就像我坐过山车,从最高处一下子冲到最低处,这两个极端之间的差距就是峰峰值嘛!那有效值呢,就好比我每天上学,有时候跑得快,有时候跑得慢,但是把这些天综合起来,平均一下每天走的路程,这是不是就是有效值呀?
我问同桌小明:“你能明白峰峰值和有效值不?”小明挠挠头说:“我也不太懂,感觉好复杂呀!”我又去问学习委员小红,她皱着眉头说:“我好像懂一些,但也不是特别清楚。
”
这可咋办呀?我回家问爸爸,爸爸耐心地跟我说:“孩子,你看咱们家里的电灯,它亮着的时候,电流和电压不是一直不变的,有高有低,峰峰值就是最高和最低的差别,有效值呢,就是能让电灯一直保持差不多亮度的那个平均的值。
”
我还是有点迷糊,又去问妈妈,妈妈笑着说:“宝贝,你想想咱们去超市买东西,峰峰值就像是最贵的东西和最便宜的东西价格差好多,有效值呢,就是咱们买东西花的平均钱数。
”
这下我好像有点明白了,峰峰值就是那个最大的差距,有效值就是平均的水平。
所以呀,我觉得峰峰值和有效值虽然有点难理解,但是只要我们多想想,多问问,总是能搞清楚的!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a) 电子测量的基础概念
电子线路测量中,电压和电流是最基本的参量,对它们的测量是最基本的测量,其它的测量很多都以二者为基础。
电压的定义是对电路结构中的两点来定义的,只有载流子在从一点到另一点的运动过程中的电势能发生变化时,两点之间的电压差才非零。
所以电压对两点才有意义,对电压的测量一定是对两点的测量,一定是将电压表并联在电路中使用。
电流是对一个面积分得到的,单位时间内流过这个面的载流子的电荷数的度量被称为电流。
从电路拓扑的角度看,电流是对电路结构中的一点来说的,即单位时间内通过这一点的电荷数的度量被称为电流。
所以,电流对一点有意义,对电流的测量相当于观察这个点,对电流的测量一定是对一点的测量,对电流的测量一定是将电流表串联到电路中使用的。
电压有直流电压和交流电压两种。
在所关心的测量时间内,直流电压表示两端电压恒定的高低关系,就是说其中一端对另外一端总是高的,或总是低的;交流电压表示两端电压时变的高低关系,就是说两端电压的高低关系是随时间不断变化的。
当两点之间的电压保持恒定不变时,宏观上可以定义这两点之间的直流电压,只要一个值就可以完整地描述电压。
而当两点间不能保持电压恒定不变时,从宏观上对电压的描述有多种,分别描述它们不同方面的特性。
下面只考虑用得最多的周期信号的描述。
峰峰值V pp (Peak to Peak )。
峰峰值是指一个周期内信号最高值和最低值之间差的值,就是最大和最小之间的范围。
它描述了信号值的变化范围的大小。
峰值V p (Peak )。
峰值是指一个周期内信号最高值或最低值到平均值之间差的值。
一般来说,峰值对上下对称的信号才有定义。
可以看到,峰值等于峰峰值的一半。
有效值/均方根值V rms (Root Mean Square )。
是指在一个周期内对信号平方后积分,再开方平均,如公式2.1所示。
有效值的意义是:在一个周期内做功的大小等于与该值相等的直流电压所做功的大小。
dt t f T V T
rms
∫=0
2)(1
2.1
* 设T 为信号的周期,下同。
平均值(Average )。
指信号在一个周期内的平均值。
用公式表示为式2.2。
avg V dt t f T V T
avg
∫=0
)(1
2.2
对于正负对称的信号来说,平均值显然为零,有时规定这时的平均值为全波整流之后的
平均值,即公式2.3的定义。
dt t f T V T
avg
∫=0
|)(|1
2.3
实际中经常会用到有效值和平均值的转换,定义一个信号的有效值与平均值之比为波形
系数,即公式2.4。
avg
rms
F V V K =
2.4
显然,信号的类型不同,波形系数也不同。
考虑最常见的正弦信号,其波形系数为:
11.12
2|)(|1)(1
2≈===
∫∫πdt t f T dt t f T V V K T T
avg rms
F 定义一个信号的峰值与有效值之比为波峰系数,即公式2.5。
rms
p p V V K =
2.5
下表给出常见波形的一些参数。
表2.0.1. 常见波形及基本参数
* 规定脉冲的周期是T ,脉冲宽度为τ
** 为简便处理和比较方便,规定所有信号的峰值都为1
在知道波形系数和波峰系数之后,对特定信号可以很容易的进行不同值之间的转换。
实际上,有些仪表就利用了转换的原理。
但从定义和上表可以看到,不同类型信号的转换的系数是不一样的,所以在使用中,应当注意。
参照以上各种电压值的定义,可以给出各种电流值的定义。
从频谱分析的角度看,无论是直流电压,还是交流电压都可以将其分解为直流分量和不同的频率分量的叠加。
如公式2.6、
2.7、2.8:
t jn n n e a a t f ω−∞
=∑+=1
0)(
2.6
t jn n n e b b t f ω−∞
=∑+=102
)(
2.7
t jn n n e c c t f ω−∞
=∑+=1
0|)(|
2.8
不同的值的定义,其实就是对信号进行不同变换之后得到的系数a n 、b n 、c n ,或其简单计算的结果。
实验之中会大量的测到各种波形的参数,下图给出波形各种参数的定义
max min
V top
V base
Rise Fall 100%
0%
图2.0.1 波形参数的定义。
