C语言-递推递归
C++函数、递推、递归ppt课件

i = 7 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(7) = 2 * (S(8) + 1) // s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
看一个简单的例子:
1 4
第九讲——函数、递推、递归
递归
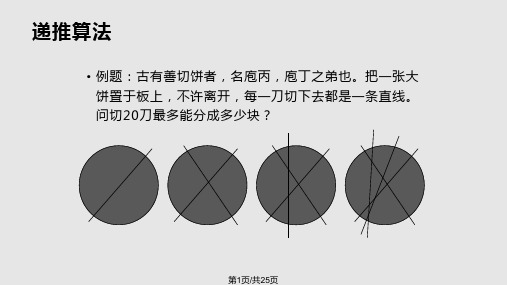
有 5 个人坐在一起,问第 5 个人多少岁? 他说比第 4 个人 大两岁。问第 4 个人岁数,他说比第 3 个人大两岁。问第 3 个人,又说比第 2 个人大两岁。问第 2 个人,说比第 1 个人 大两岁。最后问第 1 个人,他说是 10 岁。请问第 5 个人多 大?
3
第九讲——函数、递推、递归
解题思路:
假设用 S(i) 表示第 i 天没吃之前的桃子数目;
则
S(1) 即为第 1 天所摘的桃子数; S(2) = S(1) * 1/2 – 1 第 2 天没吃之前的桃子数
S(3) = S(2) * 1/2 - 1 第 3 天没吃之前的桃子数
…
…
S(9) = S(8) * 1/2 - 1 第 9 天没吃之前的桃子数
= age(2) + 2 + 2 + 2 // c = age(2) + 2
= age(1) + 2 + 2 + 2 + 2;// c = 10;
2 2
计算年龄程序
第九讲——函数、递推、递归
2 3
第九讲——函数、递推、递归
递归算例(2)
用递归方法计算 n! 算法思路:
C语言递归函数

C语言递归函数C语言是一种非常重要的编程语言,递归函数是C语言中的一个重要概念。
本文将详细介绍C语言递归函数的定义、实现以及递归函数的优缺点。
1. 递归函数的定义在C语言中,递归函数是指在函数内部调用自身的函数。
递归函数通常包含一个或多个基准情况(递归终止条件),在满足基准情况之前,递归函数会不断调用自身来解决更小规模的问题。
2. 递归函数的实现为了实现递归函数,我们需要考虑两个重要的要素:基准情况和递归关系。
2.1 基准情况在编写递归函数时,必须确定递归终止条件。
这个条件通常是问题规模足够小,可以直接得出答案的情况。
通过设置基准情况,可以避免递归函数陷入无限循环,导致程序崩溃。
2.2 递归关系递归关系指的是将原始问题拆分为更小规模的子问题,并且这些子问题与原问题的解具有相同的结构。
递归函数通过调用自身来解决子问题,将子问题的解合并为原问题的解。
递归关系的正确定义是确保递归函数能够有效地解决问题的关键。
3. 递归函数的示例下面是一个计算斐波那契数列的递归函数的示例:```c#include <stdio.h>int fibonacci(int n){if(n <= 1) // 基准情况return n;else // 递归关系return fibonacci(n-1) + fibonacci(n-2);}int main(){int n = 10;int result = fibonacci(n);printf("斐波那契数列的第%d项为%d\n", n, result); return 0;}```在以上示例中,递归函数fibonacci计算了斐波那契数列的第n项。
当n小于等于1时,即为基准情况,直接返回n。
否则,递归调用fibonacci函数计算第n-1和第n-2项,并将结果相加返回。
4. 递归函数的优缺点递归函数具有以下优点:- 可以简化代码实现,使代码更加简洁易读。
HDU2046骨牌铺方格递推C语言

HDU2046⾻牌铺⽅格递推C语⾔
题⽬:
知道应该⽤递归递推来做,但是⼀直找不到规律……拖了好久,终于决定今天做完。
苦思⽆果搜题解,发现代码只有⼏⾏…… 递推递归果然神奇啊
思路:f(1)=1,f(2)=2,f(3)=5,当有n个⽅格的时候,有两种铺法:
1)先铺好n-1个格,有f(n-1)个⽅法,再铺第n层的时候只有⼀种⽅法,所以总⽅法是1*f(n-1);
2)先铺好n-2格,有f(n-2)个⽅法,再铺后⾯两层的时候只能两个都横着铺(否则与第⼀种情况重复),所以也只有⼀种情况,总⽅法数是1*f(n-2)
再没有其他情况了。
推出f(n)=f(n-1)+f(n-2)
提交情况: 2次TLE,两次WA
AC code:
View Code
1#include <stdio.h>
2#include <stdlib.h>
3int main () {
4int n;
5int i;
6 __int64 a[60] = {0, 1, 2};
7for (i = 3; i <= 51; i++)
8 a[i] = a[i - 1] + a[i - 2];
9while (~scanf ("%d", &n))
10 printf ("%I64d\n", a[n]);
11//system ("pause");
12return0;
13}
先开始写了⼀个⼦函数递归,于是超时了,改⽤数组写,a[n]开成了int型,溢出了,于是WA了……
这种找规律的题还是要多多练习才⾏啊!。
递归和递推(end)

分析
二分查找的基本思想:首先将结点按排序,其次将查 找值与中间位置的值比较,相等,查找成功;不等,则中 间数据大于或小于查找值,无论怎样查找将在一半的 数据中查找。
例如在有序数列15 数x=19
20 26 31
40中查找
第一次:left=1 right=5 mid=3 x<a[mid]
var m:longint;
writeln(m); end;
利用实参实现!
函数与过程区别
1.声明方式不同 2.返回值的方式不同,函数必须 要对函数名进行赋值,过程则 不必。
讨论:函数与过程的选择?
例3
function fac(x:integer):longint; begin if x=1 then fac:=1 else fac:=fac(x-1)*x; end; 问:此函数合法吗? 实现什么功能?如何实现?
递归的概念
• 递归就是函数或过程自己直接或间 接调用自己! • 两个条件: 1.递归式(递归关系); 2.边界条件。 递归表达式才是解题的关键!
function fac(x:integer):longint; begin if x=1 then fac:=1 else fac:=fac(x-1)*x; end;
迭代
反向迭代
S:=__④____;
N:=0;
Repeat
N:=n+1;s:=n;
For i:=____①___do
For i:=___⑤___ do
S:=___⑥______; Writeln(s);
s:=__②___;
Until s=__③____; Writeln(n);
(2)猴子吃桃。有一群猴子摘来了一批桃子,猴王 规定每天只准吃一半加一只(即第二天吃剩下的一半 加一只,以此类推),第九天正好吃完,问猴子们摘 来了多少桃子?
c语言使用递归函数

递归函数是一种特殊的函数,它调用自身来解决问题。
在C语言中,递归函数可以通过以下方式实现:
1. 定义一个函数,该函数返回一个值,或者没有返回值(void)。
2. 在函数的函数体中,使用return语句或break语句来结束函数的执行。
3. 在函数的函数体中,调用自身,将问题的规模减小,直到问题能够直接解决为止。
下面是一个简单的递归函数示例,该函数计算一个数的阶乘:
```c
#include <stdio.h>
int factorial(int n) {
if (n == 0) {
return 1;
} else {
return n * factorial(n - 1);
}
}
int main() {
int n = 5;
int result = factorial(n);
printf("%d! = %d\n", n, result);
return 0;
}
```
在上面的代码中,factorial()函数是一个递归函数。
当n等于0时,函数返回1。
否则,函数返回n乘以factorial(n-1)的结果。
在main()函数中,我们调用factorial()函数来计算5的阶乘,并将结果打印到控制台上。
C语言与程序设计ppt-第12章递归

第12章 递 归
华中科技大学计算机学院 卢萍
华中科技大学计算机学院C语言课
2021/4/25
程组
1
本章讲授内容
递归(recursion)是一项非常重要的编 程技巧,可以使程序变得简洁和清晰,是 许多复杂算法的基础。本章介绍 递归、递归函数的概念; 递归的执行过程; 典型问题的递归函数设计; 分治法与快速排序; 回溯法; 递归在动态规划等算法中的应用。
12
【例12.3】 设计一个求解汉诺塔问题的算法。
这是一个典型的用递归方法求解的问题。要移动n个 盘子,可先考虑如何移动n 1个盘子。分解为以下3 个步骤:
(1)把A上的n-1个盘子借助C移到B。 (2)把A上剩下的盘子(即最大的那个)移到C。 (3)把B上的n-1个盘子借助A移到C。 其中,第(1)步和第(3)步又可用同样的3步继
2021/4/25
华中科技大学计算机学院C语言课程组
2
12.1 递归概述
递归是一种函数在其定义中直接或间接调用 自己的编程技巧。递归策略只需少量代码就 可描述出解题过程所需要的多次重复计算, 十分简单且易于理解。
递归调用:函数直接调用自己或通过另一函 数间接调用自己的函数调用方式
递归函数:在函数定义中含有递归调用的函 数
续分解,依次分解下去,盘子数目n每次减少1,直 至n为1结束。这显然是一个递归过程,递归结束条 件是n为1。
2021/4/25
华中科技大学计算机学院C语言课程组
13
函数move(n,a,b,c)
为了更清楚地描述算法,可以定义一个函数 move(n,a,b,c)。该函数的功能是:将n个盘 子从木桩a上借助木桩b移动到木桩c上。算法 的第(1)步和第(3)步的实现都是递归调 用,分别为move(n-1,a,c,b)和move(n1,b,a,c)。
C语言递归

C语言递归递归是一种常见的编程技术,也是C语言中的一种重要的编程方法。
递归是指函数通过自身调用来解决问题的一种方式。
在递归中,函数会重复调用自己,并且每次调用都会解决问题的一部分,直到最终问题被解决。
递归算法递归算法的核心思想是将问题分解成若干个与原问题相似的子问题,并递归地解决这些子问题。
通过最终得出每个子问题的解,再逐步合并,最终得出原问题的解。
递归算法的基本流程如下:递归的优劣递归算法具有可读性好、思路清晰、代码简洁等优点,但是在实现过程中,递归的性能有时会受到限制。
递归算法在运行时会不断地创建新的栈帧,这会占用大量的内存空间,如果递归深度过高,会导致栈溢出的问题。
递归函数中的 STACK OVERFLOW问题:在将递归算法实现时,必须注意递归的深度,否则就会出现STACK OVERFLOW问题。
递归的应用递归算法在很多算法中都有广泛的应用,例如——1.排序算法快速排序、归并排序、堆排序等排序算法中都有递归的应用。
2.搜索算法深度优先搜索和广度优先搜索等搜索算法中都有递归的应用。
3.数学计算递归算法经常用于解决复杂的数学计算问题。
实例以下是一个简单的递归函数例子,函数将返回从1到输入参数 n 的和。
以上代码中,函数 sum 通过递归的方式计算从1到 n 的和。
当 n 的值等于1时,函数返回1,否则函数返回n加上sum(n-1)的值。
```csum:55```输出结果为55,证明递归函数成功地计算出了从1到10之间的所有数字的和。
总结递归是一种非常有用的编程技术,可以帮助我们在编写程序时处理一些复杂的问题。
递归算法的核心思想是将问题分解成若干个与原问题相似的子问题,并通过递归的方式解决它们。
在递归过程中,我们必须注意避免栈溢出等问题,以确保程序能够正常运行。
C语言-递推递归

2012-3-20
12
伯努利装错信封问题
某人给不同地址不同姓名的n位朋友写信,信 某人给不同地址不同姓名的n位朋友写信, 信封都分别写好了。请问:所有信笺、 笺、信封都分别写好了。请问:所有信笺、 信封全都装错的情况有多少种? 信封全都装错的情况有多少种? 信封:A B 信封: 信笺: 信笺:a b C c D d E e F f … …
信封:A B C D E F … 信封: 信笺: 后 封也都装错 封也都装错) 信笺:b a (后n-2封也都装错
错误2: 错误 :
信封: 信封:A B C D E F … 信笺: 封也都装错) 信笺:b 非a (后n-2封也都装错 后 封也都装错
2012-3-20
装错情况 种数Sn-1
14
Sn= (n-1)(Sn-1+ Sn-2)
A B C
2012-3-2024 Nhomakorabea递归
• 当有n个盘子需要移动时,通常的方法如下: (1)把A柱上n-1个盘子借助C柱移动到B柱上。只有 这样,C柱才能为空,则A柱上的第n个盘子(最大 的那个)才能直接移动到C柱上。 (2)将A柱上的剩下的第n个盘子移动到C柱上。这个 盘子已最后到位,不需要再移动了。 (3)再将B柱上的n-1个盘子借助A柱移动到C柱。
2012-3-20 19
递归
f (1) = 1 n =1 f ( n) = f ( 2) = 1 n=2 f (n) = f (n − 2) + f (n − 1) n ≥ 3
int func(int n) /*求斐波那契数列的第n个数*/ { int result; if(n==1) result=1; else if(n==2) result=1; else result=func(n-1)+func(n-2); /*递归*/ return result; } 2012-3-20
递推和递归方法在C语言程序设计中的应用

递推和递归方法在C语言程序设计中的应用作者:张春燕沈漪来源:《软件导刊》2013年第03期摘要:递推和递归问题是计算机高级语言程序设计课程中的重点和难点问题。
以卖票问题为例,对递推和递归方法进行了探讨,并通过C程序进行了验证。
关键词:递推;递归;C程序中图分类号:TP311.5 文献标识码:A 文章编号:16727800(2013)003005701作者简介:张春燕(1982-),女,硕士,无锡科技职业学院讲师,研究方向为数据库开发、算法设计。
1 递归和递推算法递归作为一种算法在程序设计语言中广泛应用。
它是调用一个函数的过程中又出现直接或者间接地调用该函数本身。
递归是计算机科学的一个重要概念,递归的方法是程序设计中有效的方法,采用递归编写程序能使程序变得简洁和清晰。
递推算法是一种用若干步可重复的简运算(规律)来描述复杂问题的方法。
递推是序列计算机中的一种常用算法。
递推法的特点是从一个已知的事实出发,按照一定规律推出下一个事实,再从这个新的已知事实出发,再向下推出一个新的事实。
2 问题提出一场球赛开始前,售票工作正在紧张进行中,每张球票为50元,现有m+n个人排队等待购票,其中有m个人手持50元的钞票,另外n个人手持100元的钞票。
假设开始售票时售票处没有零钱,求出这m+n个人排队购票,使售票处不至出现找不开钱的局面的不同排队种数(这里正整数m、n从键盘输入)。
这个问题用一般的解决方法非常麻烦,下面用递归和递推方法解决。
3 购票问题分析这是一道组合计数问题。
令f(m,n)表示有m个人手持50元的钞票,n个人手持100元的钞票时共有的方案总数。
(1) n=0。
n=0意味着排队购票的所有人手中拿的都是50元的钞票,那么这m个人的排队总数为1,即f(m,0)=1。
(2) m (3)其它情况。
m+n个人排队购票,第m+n个人站在第m+n-1个人的后面,则第m+n个人的排队方式可由两种情况获得:①第m+n个人手持100元的钞票,则在他之前的m+n-1个人中有m个人手持50元的钞票,有n-1个人手持100元的钞票,此种情况共有f (m,n-1);②第m+n个人手持50元的钞票,则在他之前的m+n-1个人中有m-1个人手持50元的钞票,有n个人手持100元的钞票,此种情况共有f(m-1,n)。
C语言中的递归函数与应用实例

C语言中的递归函数与应用实例递归是一种重要的编程技术,它在 C 语言中被广泛应用。
递归函数指的是在函数的定义中调用自身的函数。
本文将详细介绍 C 语言中的递归函数的概念、用法以及应用实例。
一、递归函数的概念与特点递归函数是指函数在其定义中直接或间接地调用自身的函数。
递归函数具有以下重要特点:1. 自我调用:递归函数能够在函数体内调用自身。
2. 结束条件:递归函数必须包含一个或多个终止条件,以避免无限循环调用。
3. 逐层推进:递归函数通过不断调用自身并向基本情况靠近,逐层迭代解决问题。
二、递归函数的基本形式在 C 语言中,递归函数的基本形式如下:```c返回类型函数名(参数列表) {if (终止条件) {// 返回终止条件的结果} else {// 递归调用自身,并处理返回的结果}}```三、递归函数的应用实例下面是几个常见的递归函数实例,展示了递归在不同问题中的应用。
1. 计算阶乘阶乘是一个常见的数学运算,表示从 1 至某个正整数的连续乘积。
在 C 语言中,可以使用递归函数来计算阶乘,如下所示:```cint factorial(int n) {if (n == 0) {return 1;} else {return n * factorial(n - 1);}}```该递归函数通过不断将问题规模缩小,直至达到终止条件,然后逐层返回结果,最终得到阶乘的值。
2. 斐波那契数列斐波那契数列是一个常见的数列,其特点是每个数恰好是前两个数的和。
我们可以使用递归函数来生成斐波那契数列,如下所示:```cint fibonacci(int n) {if (n == 0 || n == 1) {return n;} else {return fibonacci(n - 1) + fibonacci(n - 2);}}```该递归函数通过逐层迭代调用自身,不断将问题规模缩小,最终计算得到第 n 个斐波那契数。
3. 遍历目录在文件系统中,我们经常需要遍历目录中的文件和子目录。
c语言递归调用例子

c语言递归调用例子【篇一:c语言递归调用例子】* 小编已将正确代码放在左侧任务的“不知道怎么办”里* 小编希望各位童鞋独立完成哦~*///定义一个函数,传送人员序号进去,返回该序号员工的年龄。
int getage(numpeople) //定义返回的年龄 int age; //如果是第1个人的时候,年龄为10岁 if(numpeople==1) age=10; //这是回推墙,也就是结束递归的条件。
else //还没接触到回推墙,就自我调用,谓之递归。
age = getage(numpeople-1) //年龄等于上一个人的年龄加2 return age;int main() printf( 第5个人的年龄是%d岁 , getage(5));return 0;}【篇二:c语言递归调用例子】一、基本内容:c语言中的函数可以递归调用,即:可以直接(简单递归)或间接(间接递归)地自己调自己。
要点:1、c语言函数可以递归调用。
2、可以通过直接或间接两种方式调用。
目前只讨论直接递归调用。
二、递归条件采用递归方法来解决问题,必须符合以下三个条件:1、可以把要解决的问题转化为一个新问题,而这个新的问题的解决方法仍与原来的解决方法相同,只是所处理的对象有规律地递增或递减。
说明:解决问题的方法相同,调用函数的参数每次不同(有规律的递增或递减),如果没有规律也就不能适用递归调用。
2、可以应用这个转化过程使问题得到解决。
说明:使用其他的办法比较麻烦或很难解决,而使用递归的方法可以很好地解决问题。
3、必定要有一个明确的结束递归的条件。
说明:一定要能够在适当的地方结束递归调用。
不然可能导致系统崩溃。
三、递归实例例:使用递归的方法求n!当n 1时,求n!的问题可以转化为n*(n-1)!的新问题。
比如n=5:第一部分:5*4*3*2*1 n*(n-1)!第二部分:4*3*2*1 (n-1)*(n-2)!第三部分:3*2*1 (n-2)(n-3)!第四部分:2*1 (n-3)(n-4)!第五部分:1 (n-5)! 5-5=0,得到值1,结束递归。
C语言的递归函数详解

C语⾔的递归函数详解⽬录函数递归什么是递归?递归的俩个必要条件代码引例1栈溢出(StackOverflow)合理使⽤递归代码引例3代码引例4解释要合理使⽤递归总结函数递归程序调⽤⾃⾝的编程技巧称为递归 recursion)函数⾃⼰调⽤⾃⼰就是递归你也可以理解成是⼀种嵌套结构,但递归分为俩部分,第⼀是“递”,进⼊嵌套结构。
第⼆是”归“,最终会⼀步⼀步返回。
第⼀次接触递归都会很懵,慢慢理解这个过程就明⽩了。
什么是递归?递归做为⼀种算法在程序设计语⾔中⼴泛应⽤。
⼀个过程或函数在其定义或说明中有直接或间接调⽤⾃⾝的⼀种⽅法,它通常把⼀个⼤型复杂的问题层层转化为⼀个与原问题相似的规模较⼩的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,⼤⼤地减少了程序的代码量。
递归的主要思考⽅式在于:把⼤事化⼩递归的俩个必要条件代码引例1接受⼀个整型值(⽆符号),按照顺序打印它的每⼀位。
例如:输⼊:123,输出 1 2 3参考代码:#include <stdio.h>void print(int n) {if(n>9){print(n/10);}printf("%d ", n%10);}int main(){int num = 123;print(num);return 0; }运⾏结果如下:我们要怎么理解这个函数递归的实现呢我们可以采⽤画图⽅式理解这个过程所以我们可以看到,递归必须满⾜俩个必要条件:1.存在限制条件,当满⾜这个限制条件的时候,递归便不再继续。
2.每次递归调⽤之后越来越接近这个限制条件。
题中的限制条件就是(n>9),当我们的n通过(n/10)越来越少,直⾄n=1,⽆法满⾜时,递归停⽌,并开始返回。
这⾥有⼀个重要点就是print(n/10),如果没有这个条件,换成print(n)的话,n⼀直⽆法减⼩,⼀直进⾏递归。
最后会导致栈溢出(Stack Overflow)。
C语言递归算法PPT演示课件

for (k=1;k<=10;k++)
cin>>a[k];
cin>>x;
search(x,L,R);
system("pause");
} void search(int x,int top,int bot) //二分查找递归过程
{
int mid;
if (top<=bot)
{ mid=(top+bot)/2;
an加入到k个子集中的任一个中去,共有k种加入方式,这样对
于an的每一种加入方式,都可以使集合划分为k个子集,因此
根据乘法原理,划分数共有k * S(n-1,k)个。
•16
综合上述两种情况,应用加法原理,得出n个元素的集合 {a1,a2,……,an}划分为k个子集的划分数为以下递归公 式:S(n,k)=S(n-1,k-1) + k * S(n-1,k) (n>k,k>0)。
确定n个元素a1 ,a2 ,……,an 放入k个无标号盒子中去
的划分数S(n,k)。
【输入样例】setsub.in
23 7
【输出样例】setsub.out
4382641999117305
•15
【算法分析】
先举个例子,设S={1,2,3,4},k=3,不难得出S有 6种不同的划分方案,即划分数S(4,3)=6,具体方案为:
int s(int n, int k)
//数据还有可能越界,请用高精度计算
{
if ((n < k) || (k == 0)) return 0;
//满足边界条件,退出
if ((k == 1) || (k == n)) return 1;
C语言递归函数编写方法

C语言递归函数编写方法递归是一种重要的编程技术,可以简化程序的设计和实现过程。
在C语言中,递归函数的编写方法需要遵循一定的规则和原则。
本文将介绍C语言递归函数的编写方法,并分享一些注意事项。
一、什么是递归函数递归函数是在函数体内直接或间接地调用自身的函数。
通过递归调用,可以将复杂的问题分解成更简单的子问题,从而实现问题的解决。
在编写递归函数时,需要考虑两个关键要素:递归终止条件和递归调用。
二、递归函数的编写步骤1. 确定递归函数的函数名和参数列表:根据问题的要求,确定递归函数的函数名和参数列表。
参数列表中通常包括问题的输入值和递归的状态。
2. 设计递归终止条件:递归终止条件是指在递归调用中,满足条件时停止递归调用。
需要注意的是,设置终止条件时应确保递归能够正常结束,否则可能导致无限递归。
3. 编写递归调用:在递归函数体内,根据问题的要求进行递归调用。
递归调用时,应传递适当的参数值,以便解决子问题。
4. 处理递归返回值:如果递归函数需要返回一个值,需要在递归调用结束后进行处理,并将返回值传递给上一级调用。
三、递归函数的实例为了更好地理解递归函数的编写方法,下面以求解斐波那契数列为例进行说明。
斐波那契数列是一个经典的递归问题,定义如下:F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) (n>=2)基于以上定义,可以编写一个递归函数来求解斐波那契数列。
```c#include <stdio.h>int fibonacci(int n) {if (n == 0) {return 0;} else if (n == 1) {return 1;} else {return fibonacci(n-1) + fibonacci(n-2);}}int main() {int n = 10;printf("斐波那契数列的第%d项为:%d\n", n, fibonacci(n));return 0;}```在上述代码中,递归函数fibonacci()通过递归调用自身来计算斐波那契数列的第n项。
c语言递归算法及经典递归例子代码实现

c语⾔递归算法及经典递归例⼦代码实现⼀、什么叫做递归?⼀个过程或 函数 在其定义或说明中有直接或间接调⽤⾃⾝的⼀种⽅法;递归函数就是直接或间接调⽤⾃⾝的函数,也就是⾃⾝调⽤⾃⼰;刚接触递归的同学,可能难以理解递归,难以理解的点可能很多,例如:1.函数为什么可以在⾃⼰的内部⼜调⽤⾃⼰呢?2.既然可以⾃⼰调⽤⾃⼰,那么递归运⾏过程中⼀定回有很多层相互嵌套,到底什么时候不再嵌套呢?3.递归运⾏过程中,相互嵌套的多层之间会有参数传递,多层之间是否会相互影响?递归两个要素1.递归边界2.递归的逻辑——递归"公式"递归的过程⼀定有参数的变化,并且参数的变化,和递归边界有关系.在难度较⼤的题⽬中,这两者均不容易直接得到.递归的种种问题,也许理解的同学可能可以⽤⼀句话解释清楚,但是不理解的同学再怎么说也没办法理解.下⾯通过⼏个简单的例⼦【体会】⼀下递归,先从【感性】的⾓度理解递归.1.Fibonacci数我们直到Fibonacci数的递推公式为:F(0)=F(1)=1,F(n)=F(n-1)+F(n-2) n>=2;这个明显地给出了递归边界n=0或1的时候F(n)的值,和递归逻辑F(n)=F(n-1)+F(n-2),即递推公式.所以这个递归函数不难书写#includeusing namespace std;int F(int n)//函数返回⼀个数对应的Fibonacci数{ if(n0 || n1)//递归边界return 1; return F(n-1) + F(n-2);//递归公式}int main(){ //测试int n; while(cin >> n) cout << F(n) << endl;return 0;}2.阶乘阶乘的递归公式为:代码如下:#includeusing namespace std;int F(int n){ if(n==0)//递归边界return 1;return n*F(n-1);//递归公式}int main(){ int n; cin >> n; cout << F(n) << endl;return 0;}3.数组求和给⼀个数组a[]:a[0],a[1],…,a[n-1]如何⽤递归的⽅式求和?仍然是两个问题:递归边界和递归公式.递归边界是什么?⼀时不容易想到,但是我们想到了求和,多个数的求和过程是什么,x,y,z,w⼿动求和的过程是什么?步骤如下:x+y=a,任务变为a,z,w求和a+z=b,任务变为b,w求和b+w=c得出答案思考⼀下,【得出答案】这⼀步为什么就可以得出答案呢?(废话?)是因为,⼀个数不⽤相加就能得出答案.所以,递归的边界就是只有⼀个数.所以,递归边界有了,那么递归公式呢?其实⼿动计算过程中,隐含了递归公式:其中+为求两个数的和,F为求多个数的和的递归函数.代码如下:#includeusing namespace std;int F(int a[],int start,int end){ if(start==end)//递归边界return a[start];return a[start] + F(a,start+1,end);//递归公式}int main(){ int a[] = {1,2,3,4,5}; int s=0,e=4; cout << F(a,s,e) << endl;return 0;}4.求数组元素最⼤值⼿动求最⼤值的过程是什么,遍历+⽐较,过程如下:例如,求3,2,6,7,2,4的最⼤值:先设置最⼤值max=-999999,然后将max和数组元素逐个(遍历)⽐较如果a[i]>max,则更新max的值为a[i],否则max不变,继续向后遍历,直到遍历结束.max<3,则max=3max>2,max=3不变max<6,则max=6max<7,则max=7max>2,max=7不变max>4,max=7不变遍历结束,max=7为最⼤值.和求和类似,递归的公式如下:其中max为求两个数的较⼤值函数,F为求多个数的最⼤值的递归函数.代码如下:#includeusing namespace std;#define max(a,b) (a>b?a:b)int F(int a[],int s,int e){ if(s==e) return a[s]; else if(s+1 == e)//递归边界return max(a[s],a[e]);return max(a[s],F(a,s+1,e));//递归公式}int main(){ int a[] = {5,1,4,6,2}; int s = 0,e = 4; cout << F(a,s,e) << endl;return 0;}之所以,说上⾯的⼏个例⼦是【简单例⼦】,是因为上述所有的递归都属于【单向递归】.单向递归,递归的路径就是⼀个⽅向,所以思路相对⽐较容易想到.较难的递归问题,⼀般都不是单向递归,⽽是需要使⽤【回溯】的⽅法,递归的⽅法不太容易想到.写在最后每天晚上20:00我都会开直播给⼤家免费分享C/C++学习知识和路线⽅法,C/C++交流学习群:814974917,邀请码:洋洋。
C语言递推与递归PPT课件
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
c语言函数之递归函数

c语言函数之递归函数朱有鹏1、递归函数1.1、函数的调用机制C语言函数的调用一般在X86平台是用栈的方式来支持其操作的(也就是Calling Convention),栈是先进后出的数据结构,当函数发生调用的时候,函数以入栈的方式,将函数的返回地址、参数等进行压栈,C语言默认环境下的调用规范为,参数是从右向左依次压栈(如:printf函数),这就是函数的调用机制。
同时函数每调用一次,就会进行一次压栈,其所占的空间彼此独立,调用函数和被调用函数依靠传入参数和返回值彼此联系。
如: 一个main()函数调用函数sub(int a, int b)的简单的内存图形是:入栈int aInt bsub()返回地址main参数main()返回地址栈1.2、递归函数(1)什么是递归函数?通过简单的了解函数的调用机制,在程序设计中经常会用递归函数解决问题,此方法清晰易于理解。
那么什么是递归函数呢?递归函数的本质就是函数直接或间接调用其函数本身。
直接调用函数调用本身示例:求n的阶乘?factorial()函数直接调用其本身。
间接调用是函数调用其它函数,其它函数又调用其本身函数示例:func_1()函数中调用了func_2() 函数,func_2()函数又调用了func_1() 这样的方式就是间接递归,此示例,本身就是个错误,各位不要急后面一一道来(没有注意收敛性)。
(2)递归的调用的原理比如下例:#include<stdio.h>void recursion(int n) {printf("递归前:n = %d.\n", n); if (n > 1) {recursion(n-1);} else {printf("结束递归,n = %d.\n", n); }printf("递归后:n = %d.\n", n); }int main(void){void recursion(3);}执行结果为:递归前:n = 3.递归前:n = 2.递归前:n = 1.结束递归,n = 1.递归后:n = 1.递归后:n = 2.递归后:n = 3.函数的执行顺序,如图所示:解析:当程序执行时,通过主函数执行到void recursion(3);时,以n=3进入recursion函数中。
C语言递归课件

1.1将A上1个盘子从A移到C; 1.2将A上1个盘子从A移到B; 1.3将C上1个盘子从C移到B。 第3步可以分解为: 3.1将B上1个盘子从B移到A上; 3.2将B上1个盘子从B移到C上; 3.3将A上1个盘子从A移到C上。
将以上综合起来,可得到移动3个盘子的步骤为 A→C,A→B,C→B,A→C,B→A,B→ C,A→C。
在调用f1函数过程中要调用f2函数,而在调用 f2函数过程中又要调用f1函数,这两种递归调 用都是无终止的自身调用。显然,程序中不 应出现这种无终止的递归调用,而只应出现 有限次数的、有终止的递归调用,这可以用if 语句来控制,只有在某一条件成立时才继续 执行递归调用,否则就不再继续。
例7.7 有5个人坐在一起,问第5个人多少岁? 他说比第4个人大2岁。问第4个人岁数,他说 比第3个人大2岁。问第3个人,又说比第2个 人大2岁。问第2个人,说比第1个人大2岁。 最后问第1个人,他说是10岁。请问第5个人 多大。显然,这是一个递归问题。要求第5个 人的年龄,就必须先知道第4个人的年龄,而 第4个人的年龄也不知道,要求第4个人的年 龄必须先知道第3个人的年龄,而第3个人的 年龄又取决于第2个人的年龄,第2个人的年 龄取决于第1个人的年龄。而且每一个人的年 龄都比其前1个人的年龄大2。
#include<stdio.h> //利用递归完成求n的m次方 float f(int n,int m) { float y; if (m==0) y=1; else if (m>0) y=f(n,m-1)*n; else y=f(n,m+1)/n; return y; } void main() { int n=2; int m=-3; printf("请输入n和m的值:"); scanf("%d%d",&n,&m); printf("n的m次方为:%f",f(n,m)); }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 3
走上第2级台阶,从平地起步, 2步和 步和“ 走上第2级台阶,从平地起步,有“一步1级”走2步和“一步 级台阶 一步1级 2级”走1步这两种走法,u2=2; 步这两种走法, 级 步这两种走法 ; 走上第3级台阶,或者从台阶 一步 一步1级 步上来, 走上第 级台阶,或者从台阶2“一步 级”走1步上来,或者从 级台阶 步上来 台阶1“一步 级”走1步上来,u3=u2+u1=2+1=3; 台阶 一步2级 步上来, ; 一步 步上来 走上第n级台阶,只能从第 级 一步1级 步上来, 走上第 级台阶,只能从第n-1级“一步 级”走1步上来,或者 级台阶 步上来 从第n-2级台阶 一步2级 级台阶“ 步上来, 从第 级台阶“一步 级”走1步上来,un=un-1+un-2 (n>2); 步上来 ;
2012-3-20
11
骨牌铺放
2(n-1) 2(n-2)
1、如果用一个骨牌直接覆盖最左边一列,则剩下的2(n-1)个方格有 、如果用一个骨牌直接覆盖最左边一列,则剩下的 个方格有f(n-1) 个方格有 种铺法; 种铺法; 2、如果用两个骨牌横向覆盖,则剩下的2(n-2)个方格有 、如果用两个骨牌横向覆盖,则剩下的 个方格有f(n-2)种铺法; 种铺法; 个方格有 种铺法 3、第1列没有其他铺法,因此,f(n)=f(n-1)+f(n-2); 、 列没有其他铺法, 列没有其他铺法 因此, ;
第n个月 1 2 3 4 5 6 7 …
2012-3-20 6
大兔对数 0 0 1 1 2 3 5
中兔对数 0 1 0 1 1 2 3
小兔对数 1 0 1 1 2 3 5
总对数
1 1 2 3 5 8 13
Fibnacci 数列
1 f n= 1 f +f n−2 n −1 n =1 n=2 n≥3
A B C
2012-3-20
24
递归
• 当有n个盘子需要移动时,通常的方法如下: (1)把A柱上n-1个盘子借助C柱移动到B柱上。只有 这样,C柱才能为空,则A柱上的第n个盘子(最大 的那个)才能直接移动到C柱上。 (2)将A柱上的剩下的第n个盘子移动到C柱上。这个 盘子已最后到位,不需要再移动了。 (3)再将B柱上的n-1个盘子借助A柱移动到C柱。
/*借助 ,把n-1个盘子从 移动到 借助C, 个盘子从A移动到 借助 个盘子从 移动到B*/ /*把第 个盘子从 移动到 把第n个盘子从 移动到C*/ 把第 个盘子从A移动到
/*借助 ,再把 个盘子从 移动到 借助A,再把n-1个盘子从 移动到C*/ 个盘子从B移动到 借助
scanf("%d",&n); /*盘子个数 盘子个数*/ 盘子个数 hanoi(n,'A','B','C');
//找不到为-1,找到则为0~n-1的数值
特点:用所给关 特点: 键字与线性表中 各元素的关键字 逐个比较, 逐个比较,直到 成功或失败为止。 成功或失败为止。 特点:从前到后, 特点:从前到后, 或从后到前。 或从后到前。
A
B
C
21
递归
• (1)假如只有一个盘子的话,可以直接将 盘子从A柱移动到C柱,即A C。
A
B
C
2012-3-20
22
递归
• • • • (2)假如有两个盘子,则: A B A C B C
A
B
C
2012-3-20
23
递归
• (3)假如有三个盘子,则情况开始复杂,移动 顺序为: • A C • A B • C B • A C • B A • B C • A C
显然可以得到如下公式: 显然可以得到如下公式:
化简后的公式: F(n)=10+(n-1)*2
2012-3-20 5
斐波那契级数-递推的经典问题
• 一对新生小兔,一个月后长成中兔,从第三个月开始长成大 一对新生小兔,一个月后长成中兔, 兔并每个月生一对小兔。按此规律,一年后共有多少对兔子。 兔并每个月生一对小兔。按此规律,一年后共有多少对兔子
班长
fact(2) =2*fact(1)
设计递归程序的重点 是给下级安排工作
班委
fact(1) =1*fact(0)
同学
fact(0) =1
2012-3-20 18
递归
int SearchBin(int *r,int k,int low,int high) //递归 递归 { if(row>high) return 0; //failed mid=(low+high)/2; if(k==r[mid]) return mid; //success else if(k>r[mid]) return SearchBin(*r,k,mid+1,high); else return SearchBin(*r,k,low,mid-1); } }
n=0 1 n!= n(n − 1)! n ≥ 1
printf("%d!=%d\n",5,fact(5));
2012-3-20
17
递归
院长
fact(5) =5*fact(4)
主任
n=0 1 n!= n(n − 1)! n ≥ 1
教师
fact(4) =4*fact(3)
fact(3) =3*fact(2)
2012-3-20
A
B
C
25
递归
void hanoi(int n,char A,char B,char C)
移动到C*/ 移动到 /*借助 ,把n个盘子从 借助B, 个盘子从A 借助 个盘子从
{ if(n==1) move(A,C); else { hanoi(n-1,A,C,B); move(A,C); hanoi(n-1,B,A,C); } }
2012-3-20 3
递推
• 有5人坐在一起,当问第5个人多少岁,他说 比第4个人大2岁,问第4个人多少岁,他说比 第3个人大2岁,依此下去,问第一个人多少 岁,他说他10岁,最后求第5个人多少岁? • 如果所坐的不是5人而是n人,写出第 n个人的年龄表达式。
10
2012-3-20
…….
x
x+2
4
分析思路: 分析思路:
S1=0, S2=1, 封信, 只1封信,不会装错 2封信, 2封信,互相装错 封信
S3=2(S2+S1)=2, 3封信,a->B,b->C,c->A或a->C,c->B,b->A 封信, >B,b->C,c->A或 >C,c->B,bS4=3(S3+S2)=9
2012-3-20
2012-3-20 19
递归
f (1) = 1 n =1 f ( n) = f ( 2) = 1 n=2 f (n) = f (n − 2) + f (n − 1) n ≥ 3
int func(int n) /*求斐波那契数列的第n个数*/ { int result; if(n==1) result=1; else if(n==2) result=1; else result=func(n-1)+func(n-2); /*递归*/ return result; } 2012-3-20
20
递归
• Hanoi(汉诺塔)问题:三根柱子A、B、C,其中A柱 上有64个大小不等的圆盘,并且大的在下,小的在上。 要求把这64个圆盘从A柱移动到C柱上,每次只能移 动一个圆盘,移动时可以借助B来进行,但在任何时 候,任何柱上的圆盘都必须保持大盘在下,小盘在上。 求移动的过程。
2012-3-20
第二讲
基础算法
计算机科学与技术 陈叶芳
2012-3-20 1
目录
• 递推 • 递归 • 排序与检索
2012-3-20
2
递推
• 指一个序列 1,u2,u3,…,un-1,un,后面的 指一个序列u 每一项都能按公式由前面的一项或连 续的几项推算出来, 续的几项推算出来,或者前面的每一 项都能按公式由后面的一项或连续的 几项推算出来。前者叫“顺推” 几项推算出来。前者叫“顺推”,后 者叫“逆推” 者叫“逆推”。 • 递推关系可用它前面1项表示的叫一阶 递推关系可用它前面 项表示的叫一阶 递推数列,可用它前面2项表示的叫二 递推数列,可用它前面 项表示的叫二 阶递推数列。 阶递推数列。
2012-3-20
A
B
C26
排序与检索
• 查找表:用于查找的数据集合,由同一类型数据元 素构成.
2012-3-20
27
排序与查找
列表:同一类型的数据元素(或记录)构成的集合。 列表 可利用任何数据结构实现。 关键字 :数据元素的某个数据项的值。 查找:根据给定的关键字,在特定列表中确定与与之 查找 相同的数据元素,并返回该数据元素在列表中的位置。
即:1、1、2、3、5、8、13、21、34…
关键: 关键:确定问题的递归特性 关键: 关键:分析出递归公式 关键: 关键:分析出初始条件
2012-3-20 7
例-巧妙推算走楼梯
• 楼梯有 级台阶,如果一步走1级或 级,试 楼梯有n级台阶,如果一步走 级或 级或2级 级台阶 n 共有多少种不同的走法? 问:共有多少种不同的走法?
2012-3-20 8
例-巧妙推算走楼梯
初始条件: 初始条件:u1=1;u2=2; ; 1、2、3、5、8、13、21、34、55 、 、 、 、 、 、 、 、
1 2 3 n
