浙教版-数学-七年级上册-《代数式的值》典型例题1
代数式的值 浙教版七年级上册练习题(含答案)

4.3代数式的值一、选择题1.已知|x|=3,|y|=2,且xy>0,则x−y的值等于()A. 5或−5B. 1或−1C. 5或1D. −5或−12.若|a|=8,|b|=5,且ab<0,那么a−b的值为()A. 3或13B. 13或−13C. 8或−8D. −3或−133.已知m是√15的整数部分,n是√10的小数部分,则m2−n的值是()A. 6−√10B. 6C. 12−√10D. 134.已知|2m+n+1|+(3y+1)2=0,则3y+2m+n的值是()A. 1B. 0C. −2D. 25.已知代数式x−5y的值是100,则代数式−2x+10y+5的值是()A. 205B. −200C. −195D. 2006.已知a+b=12,则代数式2a+2b−3的值是()A. 2B. −2C. −4D. −3127.若a,b互为相反数,c,d互为倒数,则代数式(a+b−1)(cd+1)的值是()A. 1B. 0C. −1D. −28.已知a2+3a=1,则代数式2a2+6a−1的值为()A. 0B. 1C. 2D. 39.已知a+b=4,则代数式1+a2+b2的值为()A. 3B. 1C. 0D. −110.若x2−3x−5=0,则6x−2x2+5的值为()A. 0B. 5C. −5D. −10二、填空题11.如果m−n=3,那么2m−2n−3的值是______.12.在一次智力竞赛中,主持人问了这样的一道题目:“a是最小的正整数,b是最大的负整数的相反数,c是绝对值最小的有理数,请问:a、b、c三数之和为多少?”你能回答主持人的问题吗?其和应为______.13.若|x−5|+(y+1)2=0,则xy的值是_______14.有理数2,+7.5,−0.03,−300%,0,中,非负整数有a个,负数有b个,正分数有c个,则a−b+c=__________.三、解答题15.已知a,b互为相反数,m,n互为倒数,c的绝对值为2,求代数式a+b+mn−c的值.16.某班为了开展乒乓球比赛活动,准备购买一些乒乓球和乒乓球拍,通过去商店了解情况,甲乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价48元,乒乓球每盒定价12元,经商谈,甲乙两家商店给出了如下优惠措施:甲店每买一副乒乓球拍赠送一盒乒乓球,乙店全部按定价的9折优惠.现该班急需乒乓球拍5副,乒乓球x盒(不少于5盒).(1)请用含x的代数式分别表示去甲、乙两店购买所需的费用;(2)当需要购买40盒乒乓球时,通过计算,说明此时去哪家商店购买较为合算;(3)当需要购买40盒乒乓球时,你能给出一种更为省钱的方法吗?试写出你的购买方法和所需费用.17.分别用a,b,c,d表示有理数,a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,d是数轴上到原点距离为5的点表示的数,求|3a−b+2c−d|的倒数.答案和解析1.【答案】B【解析】解:∵|x|=3,|y|=2,∴x=±3,y=±2.又xy>0,∴x=3,y=2或x=−3,y=−2.∴x−y=±1.故选:B.绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.有理数的乘法法则:同号得正,异号得负.本题考查了代数式求值、绝对值的性质:互为相反数的绝对值相等.能够根据两个数的乘积的符号判断两个数的符号的关系.2.【答案】B【解析】【分析】本题主要考查的是绝对值,有理数的乘法,有理数的减法,代数式求值的有关知识,先根据ab<0可以得到a,b异号,然后求出a,b,再代入代数式求值即可.【解答】解:∵ab<0,∴a,b异号,∵|a|=8,|b|=5,∴a=8,b=−5或a=−8,b=5,∴a−b=8−(−5)=13或a−b=−8−5=−13.故选B.3.【答案】C【解析】略4.【答案】C【解析】【分析】本题主要考查了绝对值,完全平方的非负性,令2m+n+1=0,3y+1=0,运用整体代入可以求出2m+n=−1,3y=−1的值代入即可求出结果.【解答】解:∵|2m+n+1|+(3y+1)2=0∴2m+n+1=0,3y+1=0∴2m+n=−1,3y=−1∴3y+2m+n=−2.故选C.5.【答案】C【解析】【分析】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.原式前两项提取−2变形后,把已知x−5y=100代入计算即可求出值.【解答】解:∵x−5y=100,∴原式=−2(x−5y)+5=−200+5=−195故选C.6.【答案】B【解析】【分析】本题主要考查的是代数式求值,运用了整体代入法的有关知识,将给出的代数式进行变形,然后整体代入求值即可.【解答】解:∵a+b=12,∴原式=2(a+b)−3=2×12−3=1−3=−2,故选B.7.【答案】D【解析】【分析】本题主要考查的是代数式求值,相反数,倒数的有关知识,先利用相反数,倒数的定义得到a+b=0,cd=1,然后代入代数式求值即可.解:∵a,b互为相反数,c,d互为倒数,∴a+b=0,cd=1,∴原式=(−1)×(1+1)=−2,故选D.8.【答案】B【解析】【分析】此题主要考查了代数式求值,正确将原式变形是解题关键.直接利用已知将原式变形,然后整体代入计算即可求出答案.【解答】解:∵a2+3a=1,∴2a2+6a=2(a2+3a)=2∴2a2+6a−1=2−1=1.故选B.9.【答案】A【解析】解:当a+b=4时,原式=1+12(a+b)=1+12×4=1+2=3,故选:A.将a+b的值代入原式=1+12(a+b)计算可得.本题主要考查代数式求值,解题的关键是得出待求代数式与已知等式间的特点,利用整体代入的办法进行计算.10.【答案】C【解析】本题考查了代数式求值,整体代入法,关键是由x2−3x−5=0,得x2−3x=5把x2−3x看作一个整体,代入计算的值即可.【解答】解:6x−2x2+5,=−2x2+6x+5=−2(x2−3x)+5=−2×5+5=−5.故选C.11.【答案】3【解析】解:∵m−n=3,∴原式=2(m−n)−3=2×3−3=6−3=3.故答案为:3.原式前两项提取公因式变形后,把已知等式代入计算即可求出值.此题考查了代数式求值,利用了整体代入的思想,熟练掌握运算法则是解本题的关键.12.【答案】2【解析】解:∵a是最小的正整数,b是最大的负整数的相反数,c是绝对值最小的有理数,∴a=1,b=1,c=0,∴a+b+c=1+1+0=2.故答案是2.先根据已知条件求出a、b、c的值,再代入代数式求值即可.解题的关键是先求出a、b、c的值,然后再求代数式的值.13.【答案】−514.【答案】2【解析】【分析】本题考查了有理数的分类,解题的关键是分类的标准要不重不漏的找到符合条件的a,b,c的值.根据有理数的分类标准把给出的非负整数有a个,负数有b个,正分数有c 个,,即可求出a−b+c的值.【解答】解:有理数2,+7.5,−0.03,−300%,0中,非负整数有3个,负数有2个,正分数有1个,则a−b+c=3−2+1=2.故答案为2.15.【答案】解:∵a,b互为相反数,m,n互为倒数,c的绝对值为2,∴a+b=0,mn=1,c=±2,当c=2时,a+b+mn−c=0+1−2=−1;当c=−2时,a+b+mn−c=0+1−(−2)=0+1+2=3;由上可得,代数式a+b+mn−c的值是−1或3.【解析】本题考查的是相反数定义,倒数定义和绝对值的性质以及代数式的值,根据a,b互为相反数,m,n互为倒数,c的绝对值为2,可以求得a+b,mn、c的值,从而可以求得所求式子的值.16.【答案】解:(1)甲店购买需付款48×5+(x−5)×12=(12x+180)元;乙店购买需付款48×90%×5+12×90%×x=(10.8x+216)元;(2)当x=40时,甲店需12×40+180=660元;乙店需10.8×40+216=648元;所以乙店购买合算;(3)先甲店购买5副球拍,送5盒乒乓球240元,另外35盒乒乓球再乙店购买需378元,共需618元.【解析】(1)按照对应的方案的计算方法分别列出代数式即可;(2)把x=40代入求得的代数式求得数值,进一步比较得出答案即可;(3)根据两种方案的优惠方式,可得出先甲店购买5副球拍,送5盒乒乓球,另外35盒乒乓球再乙店购买即可.此题考查列代数式,理解两种方案的优惠方案,得出运算的方法是解决问题的关键.17.【答案】解:∵a是最小的正整数,∴a=1,∵b是最大的负整数,∴b=−1,∵c是绝对值最小的有理数,∴c=0,∵d是数轴上到原点距离为5的点表示的数,∴d=±5,∴|3a−b+2c−d|=|3+1+0−5|=1或|3a−b+2c−d|=|3+1+0+5|=9∴|3a−b+2c−d|的倒数为1或19【解析】本题主要考查了有理数的加减混合运算,有理数、绝对值,数轴及倒数,熟练掌握各自的定义是解决本题的关键.根据最小的正整数为1,最大的负整数为−1,绝对值最小的有理数为0,以及数轴上到原点距离的定义,确定出a,b,c,d的值,即可求出|3a−b+2c−d|的值,再求出其倒数即可.。
2019年秋浙教版七年级数学上册习题课件:4.3 代数式的值(共23张PPT)

解:(1)书的厚度为:(88-86.5)÷(6 -3)=0.5(cm);课桌的高度为:86.5 -3×0.5=85(cm).故答案为:0.5; 85; (2)∵x本书的高度为0.5x,课桌的高 度为85,
(3)当x=55-18=37时,85+0.5x= 103.5 cm.故余下的数学课本高出地面 的距离是103.5 cm.
摄氏温度是 20 ℃.
7.若x的相反数是3,|y|=5,则-x8-或2y
=
.
8.当 x=-2,y=3 时,求下列代数式的值.
(1)x2-yx;
解:5.5;
(2)2(xx-+yy)-3(x-y).
解:14.6.
9.如图,一张长3x的正方形纸片,剪去 两个一样的小直角三角形和一个长方形. 设剪去的小长方形的长和宽分别为x, y,剪去的两个小直角三角形直角边的 长也分别为x,y. (1)用含有x,y的式子表示图中阴影部
(2)当m=50时,甲方案:16×50= 800(元),乙方案:15×50+105= 855(元),∵800<855,∴甲方案优 惠;
(3)当m=400时,甲方案:16×400= 6400(元),乙方案:15×400+105=
13.人在运动时的心跳速度通常和人的 年龄有关.如果用A表示一个人的年龄, 用B表示正常情况下此人在运动时所 能承受的每分钟心跳的最高次数,则 B=0.8(220-A). (1)正常情况下,一个15岁的少年在运
5.当 a=2,b=13时,下列求代数式的值错误的一 项是( D ) A.a(a+b)=2×(2+13)=423 B.a2+b=22+13=413 C.a+ab=2+2×13=223 D.(a+b)(a-b)=(2+13)×(2-13)=313
6.已知摄氏温度 Tc(℃)与华氏温度 TF( )之间的转 换关系是:Tc=59×(TF-32).若华氏温度 68 ,则
2019秋浙教版七年级数学上册习题课件:4.3 代数式的值 (共22张PPT)

18.如图 4-3-3,某长方形广场的四个角都有一块半径相同的四 分之一圆的草地,若圆的半径为 r(m),长方形长为 a(m),宽为 b(m).
图 4-3-3 (1)分别用代数式表示草地和空地的面积; (2)若长方形长为 300 m,宽为 200 m,圆形的半径为 10 m,求广场 空地的面积(计算结果保留到整数). 解:(1)草地面积为 4×14πr2=πr2(m2), 空地面积为(ab-πr2)m2; (2)当 a=300 m,b=200 m,r=10 m 时, ab-πr2=300×200-100π≈59 686(m2). 答:广场空地的面积约为 59 686 m2.
4.3 代数式的值
1.[2018·贵阳]当 x=-1 时,代数式 3x+1 的值是
A.-1
B.-2
C.-4
D.4
(B)
【解析】 将 x=-1 代入代数式 3x+1 计算,即 3×(-1)+1 =-3+1=-2.
2.[2017·重庆]若 x=-13,y=4,则代数式 3x+y-3 的值为( B )
解:(1)当 a=3,b=-1 时,原式=2×4=8; (2)当 a=3,b=-1 时,原式=9-6+1=4.
11.求下列代数式的值. (1)已知 a=1,b=2,c=3,求a2+abb2c+c2的值; (2)在求匀变速直线运动运动距离的公式 s=v0t+12at2 中,已知 v0= 8 m/s,t=20 s,a=10 m/s2,求 s.
( D)
4.若 x 是 2 的相反数,|y|=3,则 x-y 的值是
A.-5
B.1
C.-1 或 5
D.1 或-5
七年级数学上册4.3代数式的值典型例题素材1浙教版(new)

要求:
(1)用代数式表示出第二个月的产值。
(2)当m=20 ,a=5时第二月的产值.
例题解析
例1 解:(1)当a=4, b=12时,
a2- +2=42- +2=16-3+2=15
(2)当a= ,b= 时,
= = = .
点评:(1)求代数式的值的解题步骤是:
1)第二个月的产值为(m+m·a%)万元;
2)当m=20, a=5时
m+m·a%=20+20×5%=21(万元)
小结:若每月的增产率不变,下一个月的产值就等于本月产值+本月产值×增产率。请试着写出第三个月的产值,并计算当m=20,a=5时产值.
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.
例3 解:当a-=2时
(a- )2- +6+a=(a- )2+(a- )+6
=22+2+6
=12.
分析:本例仿例3,把 看一个整体,把所给代数式进行变形。
例4解:当 =2时
代数式的值- 2022-2023学年七年级上册数学同步培优题库(浙教版)(解析卷)

专题4.3 代数式的值模块一:知识清单代数式的值:用具体数值代替代数式中的字母,就可以得到代数式的值。
注意:求代数式的值的步骤:(1)代入数值; (2)计算结果.整体思想是一种重要的数学思想,它抓住了数学问题的本质,是直接思维和逻辑思维的和谐统一。
有些数学问题在解题过程中,如果按照常规解法运算较繁,而且容易出错;如果我们从整体的高度观察、分析问题的整体形式、整体结构、整体与局部之间的关系、联想相关的知识,就能寻求捷径,从而准确、合理地解题。
模块二:同步培优题库全卷共24题 测试时间:80分钟 试卷满分:100分一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022•浙江七年级期末)若x ﹣2y =3,则2(x ﹣2y )﹣x +2y ﹣5的值是( ) A .﹣2B .2C .4D .﹣4【分析】直接利用合并同类项法则计算,再把已知数据代入得出答案. 【解答】解:∵x ﹣2y =3,∴2(x ﹣2y )﹣x +2y ﹣5=2(x ﹣2y )﹣(x ﹣2y )﹣5=x ﹣2y ﹣5=3﹣5=﹣2.故选:A .2.(2022•丹阳市期末)若代数式x 2的值和代数式2x +y ﹣1的值相等,则代数式9﹣2(y +2x )+2x 2的值是( ) A .7B .4C .1D .不能确定【分析】由题意可得2x +y =1+x 2,代入所求的式子即可解决问题.【解答】解:∵代数式x 2的值和代数式2x +y ﹣1的值相等,∴x 2=2x +y ﹣1;∴2x +y =1+x 2; ∴9﹣2(y +2x )+2x 2=9﹣2(1+x 2)+2x 2=9﹣2﹣2x 2+2x 2=9﹣2=7.故选:A .3.(2022·江苏苏州草桥中学九年级一模)已知25x y -=,那么代数式836x y -+的值是( ) A .7- B .0C .23D .3【答案】A【分析】将8-3x +6y 变形为8-3(x -2y ),然后代入数值进行计算即可. 【详解】解:∵x -2y =5,∴8-3x +6y =8-3(x -2y )=8-3×5=-7;故选A . 【点睛】本题主要考查的是求代数式的值,将x -2y =5整体代入是解题的关键.4.(2022•浙江七年级期末)当x =2时,整式ax 3+bx ﹣1的值等于﹣100,那么当x =﹣2时,整式ax 3+bx ﹣1的值为( )A .100B .﹣100C .98D .﹣98【分析】将x =2代入整式,使其值为﹣100,列出关系式,把x =﹣2代入整式,变形后将得出的关系式代入计算即可求出值.【解答】解:∵当x =2时,整式ax 3+bx ﹣1的值为﹣100,∴8a +2b ﹣1=﹣100,即8a +2b =﹣99, 则当x =﹣2时,原式=﹣8a ﹣2b ﹣1=99﹣1=98.故选:C . 5.(2022·江苏·七年级期末)已知2018,2020a b b c +=+=,则4()a c -=( )A .8B .8-C .16D .16-【答案】C【分析】已知两等式相减求出a -c 的值,代入原式计算即可得到结果. 【详解】解:∵2018,2020a b b c +=+=,∴()()201820202a c a b b c -=+-+=-=-,∴()44()216a c -=-=,故选C .【点睛】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.6. (2021绵阳市七年级期末) 已知a ﹣2b =﹣5,b ﹣c =﹣2,3c +d =6,求(a +3c )﹣(2b +c )+(b +d )的值.【分析】原式去括号整理后,把已知等式代入计算即可求出值. 【解答】解:∵a ﹣2b =﹣5,b ﹣c =﹣2,3c +d =6∴原式=a +3c ﹣2b ﹣c +b +d =(a ﹣2b )+(b ﹣c )+(3c +d )=﹣5﹣2+6=﹣1. 7.(2022·浙江七年级期中)已知2510a a ,则,1a a+的值为( ) A .3 B .5C .7D .9【答案】B【分析】方程a 2-5a +1=0,两边除以a ,即可解决问题; 【详解】解:∵a 2-5a +1=0,两边除以a 得到,a -5+1a =0,∴a +1a=5,故选:B . 【点睛】本题考查代数式求值等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型. 8.(2022·宁夏回族自治区初一期末)按如图所示的运算程序,能使输出的结果为12的是( )A .3,3x y ==B .4,2x y =-=-C .2,4x y ==D .4,2x y ==【答案】C【分析】由题可知,代入x 、y 值前需先判断y 的正负,再进行运算方式选择,据此逐项进行计算即可得.【解析】A 选项0y ≥,故将x 、y 代入22x y +,输出结果为15,不符合题意;B 选项0y ≤,故将x 、y 代入22x y -,输出结果为20,不符合题意;C 选项0y ≥,故将x 、y 代入22x y +,输出结果为12,符合题意;D 选项0y ≥,故将x 、y 代入22x y +,输出结果为20,不符合题意,故选C.【点睛】本题主要考查程序型代数式求值,解题的关键是根据运算程序,先进行y 的正负判断,选择对应运算方式,然后再进行计算.9.(2022·河北省初一期中)5a b -=,那么13756()3a b a b ++-+等于( ) A .7- B .10C .9-D .8-【答案】D【解析】原式=3a +7+5b ﹣6a ﹣2b =3b ﹣3a +7=﹣3(a ﹣b )+7=﹣8.故选D .点睛:将整式的加减与代数式变形相结合解题是中考中经常考查的知识点.先把此代数式变形为a ﹣b 的形式,代入数值即可.10.(2022·河南七年级期末)当x 分别取值12019,12018,12017,⋯,12,1,2,⋯,2017,2018,2019时,计算代数式22122x x -+的值,将所得结果相加,其和等于( )A .1B .20192C .1009D .0【答案】D【分析】先把x=n 和1x=n代入代数式,并对代数式化简求值,得到它们的和为0,然后把x=1代入代数式求出代数式的值,再把所得的结果相加求出所有结果的和.【详解】解:设22x -1f (x)=2x +2,将x=n 和1x=n 代入代数式,222222221()-11n -1n -11-n n f (n)f ()===01n 2n +22n +22n +22()+2n+++, ∴111f()+f()+f()+f(2)+f(2018)+f(2019)=020*******…+?+,则原式=221-1f (1)==02+2,故选:D .【点睛】本题考查的是代数式的求值,本题的x 的取值较多,并且除x=1外,其它的数都是成对的且互为倒数,把互为倒数的两个数代入代数式得到它们的和为0,原式即为x=1代入代数式后的值. 二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在横线上)11.(2022·云南曲靖市·九年级二模)已知32021x -=,则()()23202131x x ---+的值为__________. 【答案】1【分析】把32021x -=直接代入即可解答.【详解】解:∵32021x -=,∴()()223202131=2021202120211x x ---+-⨯+, ∴()()23202131=1x x ---+.故答案为1.【点睛】本题主要考查了代数式求值,利用整体思想是解题关键.12.(2022·江苏九年级一模)若2320a a --=,则2726a a +-=______. 【答案】3【分析】知道2320a a --=,可以得到232a a -=,变形得到()223a a --,最后用整体法代入即可.【详解】∵2320a a --=,∴232a a -=,则2726a a +-()2237a a =--+227=-⨯+47=-+3=,故答案为:3. 【点睛】此题考查的是代数式求值,掌握整体法是解题的关键.13.(2022·浙江杭州市·七年级期末)当2020x =-时,代数式531ax bx +-的值为3,则当2020x =时,代数式532ax bx ++值为_______. 【答案】-2【分析】把x =-2020代入代数式ax 5+bx 3-1使其值为3,可得到-20205a -20203b =4,再将x =-2020代入ax 5+bx 3+2后,进行适当的变形,整体代入计算即可. 【详解】解:当x =-2020时,代数式ax 5+bx 3-1的值为3, 即-a ×20205-20203b -1=3,也就是:-20205a -20203b =4, ∴当x =2020时,ax 5+bx 3+2=20205a +20203b +2=-(-20205a -20203b )+2=-4+2=-2,故答案为:-2. 【点睛】本题考查代数式求值,代入是常用的方法,将代数式进行适当的变形是解决问题的关键.14.(2021•常州期末)已知(x ﹣1)2021=a 0+a 1x 1+a 2x 2+a 3x 3+…+a 2021x 2021,则a 1+a 2+…+a 2021= .【分析】令x =1代入求值可得a 0+a 1+a 2+a 3+…+a 2021=0,令x =0可得a 0=﹣1,易得结果. 【解答】解:当x =1时,a 0+a 1+a 2+a 3+…+a 2021=(1﹣1)2021=0; 当x =0时,a 0=(0﹣1)2021=﹣1,a 1+a 2+a 3+…+a 2021=0﹣(﹣1)=1,故答案为:1.15.(2022·射洪县七年级月考)已知:3a b -=,2c d +=,则()()221b c a d +--+的值为______. 【答案】-5【分析】原式去括号整理后,将已知等式代入计算即可求出值.【详解】解:∵a -b =3,c +d =2,∴原式=2b -2a +c +d -1=-2(a -b )+(c +d )-1=-6+2-1=-5.故答案为:-5. 【点睛】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.16.(2022·山东七年级期末)如果代数式4y 2﹣2y +5的值为1,那么代数式2y 2﹣y +1的值为 ___. 【答案】1-【分析】先根据已知代数式的值可得22y y -的值,再将其作为整体代入求值即可得.【详解】解:由题意得:24512y y +=-,整理得:222y y -=-,则221211y y +=-+=--,故答案为:1-.【点睛】本题考查了代数式求值,熟练掌握整体思想是解题关键.17.(2022·北京北理工附中七年级期末)历史上数学家欧拉最先把关于x 的多项式用记号()f x 来表示,把x 等于某数a 时的多项式的值用()f a 来表示.例如,对于多项式42()5f x mx nx x =+++,当2x =时,多项式的值为(2)1647f m n =++,若(2)10f =,则()2f -的值为_________.【答案】6【分析】由(2)10f =得1643m n +=,把它整体代入()21643f m n -=++求值. 【详解】解:∵(2)10f =,∴164710m n ++=,即1643m n +=, ∴()216425336f m n -=+-+=+=.故答案是:6.【点睛】本题考查代数式求值,解题的关键是掌握整体代入的思想求值.18.(2022·福建泉州·七年级期末)“整体思想”是数学中的一种重要的思想方法,它在数学运算、推理中有广泛的应用.如:已知2m n +=-,3=-mn ,则()()22234m n mn +-=--⨯-=.利用上述思想方法计算:已知22m n -=,1mn =-.则()()2m n mn n ---=______. 【答案】3【分析】先将原式去括号、合并同类项,然后利用整体代入法求值即可. 【详解】解:∵22m n -=,1mn =- ∴()()2m n mn n --- =22+m n mn n -- =2m n mn -- =2-(-1) =3故答案为:3.【点睛】此题考查的是整式的化简求值,掌握去括号法则、合并同类项法则和整体代入法是解题关键. 三、解答题(本大题共6小题,共46分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(2021•大兴区期末)已知:m 2+mn =30,mn ﹣n 2=﹣10,求下列代数式的值: (1)m 2+2mn ﹣n 2;(2)m 2+n 2﹣7.【分析】(1)把m 2+mn =30,mn ﹣n 2=﹣10两个算式左右两边分别相加,求出m 2+2mn ﹣n 2的值是多少即可.(2)把m 2+mn =30,mn ﹣n 2=﹣10两个算式左右两边分别相减,求出m 2+n 2﹣7的值是多少即可.【解答】解:(1)∵m 2+mn =30,mn ﹣n 2=﹣10, ∴m 2+2mn ﹣n 2=(m 2+mn )+(mn ﹣n 2)=30+(﹣10)=20(2)∵m 2+mn =30,mn ﹣n 2=﹣10,∴m 2+n 2﹣7=(m 2+mn )﹣(mn ﹣n 2)﹣7=30﹣(﹣10)﹣7=3320.(2021春•三明期末)已知a ﹣3b =2,m +2n =4,求代数式2a ﹣6b ﹣m ﹣2n 的值. 【分析】先将原式分为两组后,进行变形,再将已知的a ﹣3b =2,m +2n =4,整体代入即可. 【解答】解:∵a ﹣3b =2,m +2n =4,∴2a ﹣6b ﹣m ﹣2n =2(a ﹣3b )﹣(m +2n )=2×2﹣4=0.21.(2022·河南周口·七年级期末)阅读材料:“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛,如我们把()3a b +看成是一个整体,则()()()()()()332353325363a b a b a b a b a b +-+++=-++=+.尝试应用:(1)把()22a b -看成一个整体,合并()()()222225262a b a b a b ---+-的结果是____________.(2)已知2320x y +-=,求2392016x y ++的值;(3)已知21a b -=,23b c -=-,6c d -=,求()()()22a c b c b d ---+-的值. 【答案】(1)()232a b -(2)2022(3)4【分析】(1)利用合并同类项进行计算即可;(2)把2392016x y ++的前两项提公因式3,再代入求值即可; (3)利用已知条件求出a c -,2b d -的值,再代入计算即可. (1)()()()222225262a b a b a b ---+- ()()22562a b =-+- ()232a b =-故答案为:()232a b -. (2)∵2320x y +-=, ∴232x y +=, ∴2392016x y ++ ()2332016x y =++322016=⨯+2022=;(3)∵21a b -=①,23b c -=-②,6c d -=③, ∴①+②得:2a c -=-,②+③得:23b d -=, ∴()()()22a c b c b d ---+-()233=---+ 4=【点睛】此题主要考查了整式的加减--化简求值,解题的关键是掌握整体思想,注意去括号时符号的变化.22.(2022·浙江义乌七年级月考)阅读以下的师生对话,并完成相应的问题.老师:同学们,已知3ab =,我们怎么求代数式()2a ab b +的值呢?小聪:我们只要找到乘积恰好为3的两个数,如1a =,3b =,再代入求值即可.老师:小聪用的是特殊值法,该方法很多时候确实能较快地得岀答案.但是,如果用不同的特殊值,我们没法确定答案是否一致.所以,我们需要一般的方法.小慧:我们不妨把()2a ab b +计算出来,再看看计算结果与已知条件之间有什么关系.老师:很好,努力寻找目标式与已知式之间的联系,再运用整体思想,也许我们能更好地解决该问题,并理解该问题的本质.同学们赶紧试试吧!(1)请用小聪的特殊值法求出代数式()2a ab b +的值.(2)请用小慧的方法解决该问题. 【答案】(1)12;(2)见解析【分析】(1)将a =1,b =3代入计算即可;(2)将原式括号展开,再利用积的乘方得到()2a ab b +=()2ab ab +,最后代入计算.【详解】解:(1)当a =1,b =3时,()2a ab b +=()21133⨯⨯+=12; (2)∵3ab =,∴()2a ab b +=22a b ab +=()2ab ab +=233+=12【点睛】本题考查了代数式求值,积的乘方,解题的关键是读懂材料,理解两位同学的方法,并掌握整式的混合运算法则.23.(2021.河北省初一期末)已知代数式533ax bx x c +++,当0x =时,该代数式的值为-1. (1)求c 的值.(2)已知当1x =时,该代数式的值为-1,求a b c ++的值. (3)已知当3x =时,该代数式的值为9,试求当3x =-时该代数式的值. (4)在第(3)小题已知条件下,若有35a b =成立,试比较+a b 与c 的大小. 【答案】(1)1c =-;(2)-4;(3) 8;(4)a b c +>【分析】(1)将x=0代入代数式求出c 的值即可;(2)将x=1代入代数式即可求出a+b+c 的值; (3)将x=3代入代数式求出35a+33b 的值,再将x=-3代入代数式,变形后将35a+33b 的值代入计算即可求出值;(4)由35a+33b 的值,变形得到27a+3b=-2,将5a=3b 代入求出a 的值,进而求出b 的值,确定出a+b 的值,与c 的值比较大小即可.【解析】(1)当x=0时,533ax bx x c +++=-1,则有c=﹣1; (2)把x=1代入代数式,得到a+b+3+c=﹣1,∴a+b+c=﹣4;(3)把x=3代入代数式,得到35a+33b+9+c=﹣10,即35a+33b=﹣10+1﹣9=﹣18, 当x=﹣3时,原式=﹣35a ﹣33b ﹣9﹣1=﹣(35a+33b )﹣9﹣1=18﹣9﹣1=8; (4)由(3)题得35a+33b=﹣18,即27a+3b=﹣2, 又∵3a=5b ,∴27a+3×35a=﹣2,∴a=﹣572,则b=35a=﹣124,∴a+b=﹣572﹣124=﹣19>﹣1,∴a+b >c .【点睛】此题考查了代数式求值,利用了整体代入的思想,熟练掌握运算法则是解本题的关键. 24.(2022·山西七年级期末)观察下列表格中两个代数式及其相应的值,回答问题:(初步感知)(1)根据表中信息可知:a =______;b =______;(归纳规律)(2)表中25x -+的值的变化规律是:x 的值每增加1,25x -+的值就都减少2.类似地,27x -的值的变化规律是:______;(问题解决)(3)请从A ,B 两题中任选一题作答.我选择______题. A .根据表格反应的变化规律,当x ______时,25x -+的值大于27x -的值.B .请直接写出一个含x 的代数式,要求x 的值每增加1,代数式的值就都减小5,且当0x =时,代数式的值为-7.【答案】(1)1;-3;(2)x 的值每增加1,2x -7的值就增加2;(3)A :<3;B :-5x -7【分析】(1)直接将x =2代入代数式计算可得;(2)类似-2x +5的变化规律可得2x -7的变化规律; (3)A :令-2x +5=2x -7,解得x 的值,再结合表格中数据变化可得;B :设代数式为mx +n ,根据变化规律得到m ,再将数值代入得到n ,可得结果. 【详解】解:(1)当x =2时,a =-2×2+5=1; 当x =2时,b =2×2-7=-3; (2)x 的值每增加1,2x -7的值就增加2; (3)A :当-2x +5=2x -7时,解得:x =3,∵随着x 的增加,2x -7增大,-2x +5减小;反之,随着x 的减小,2x -7减小,-2x +5增大; ∴当x <3时,-2x +5>2x -7;B :设代数式为mx +n ,根据规律可知:当x 的值每增加1,代数式的值减少5时,x 的系数m =-5, 又∵当x =0时,代数式的值为-7,即-5×0+n =-7,解得:n =-7,故代数式为-5x -7. 【点睛】本题考查了代数式的有关问题,属于规律性问题和一元一次方程的应用,认真理解题意,利用代数式的有关知识解决问题.。
浙教版七年级上册数学习题课件:4.3代数式的值(共25张PPT)

废料最少,则正整数x,y应分别为( )
A.x=1,y=3
B.x=C4,y=1
C.x=3,y=2
D.x=2,y=3
10.为确保信息安全,信息需要加密传输,发送方将明文加
密为密文传输给接收方,接收方收到密文后解密还原为明
文.已知某种加密规则为:明文a,b对应的密文是a-2b,
2a+b.例如明文1,2对应的密文是-3,4.那么明文3,1对
17.【2018·长春绿园区期末】如图,在一块长为a,宽为2b 的长方形铁皮中,以2b为直径分别剪掉两个半圆. (1)求剩下铁皮的面积;(用含a,b的式子表示)
解:剩下铁皮的面积为 a·2b-12π22b2×2=2ab-πb2.
(2)当a=4,b=1时,求剩下铁皮的面积约是多少?(π取 3.14)
解(2):3a原2-式2=ab+(a24+b22. ab)+(b2-2ab)=-2+6=4.
解:原式=3(a2+2ab)+4(b2-2ab)=-6+24=18.
16.公安人员在破案时常常根据案发现场作案人留下的脚印 推断犯人的身高,如果用a(单位:cm)表示脚印长度, b(单位:cm)表示身高,则b=7a-3.07. (1)某人脚印长度为24.5 cm,则他的身高约为多少?
售价c/元
4+0.2 8+0.4 12+0.6 16+0.8 20+1
携带物品质量 m/千克 0≤m≤20
20<m≤100
m>100
部分每千克2元
收费标准
不收费 100元 超过100千 克的
(1)用含x的代数式表示售价c; 解:c=4x+0.2x=4.2x. (2)若小明想买3.5千克这种货物,请帮他算一算需付给商 店多少钱;
B.互为倒数
C.符号相反
【复习必备】2019七年级数学上册 第4章 代数式 4.3 代数式的值同步练习 (新版)浙教版

4.3 代数式的值知识点1 求代数式的值1.当x =1时,代数式4-3x 的值是( )A .1B .2C .3D .42.2017·重庆若x =-13,y =4,则代数式3x +y -3的值为( ) A .-6 B .0 C .2 D .63.当a 分别为2和-2时,代数式a 2+1的两个值( )A .互为相反数B .互为倒数C .异号D .相等4.当x =-2时,代数式6x +51-x的值是________. 5. 三角形的面积公式是S =12ab (其中a 表示三角形的一条边长,b 表示这条边上的高),当a =5 cm ,b =4 cm 时,三角形的面积S 是________cm 2.6.当x =-2,y =3时,求下列代数式的值:(1)5x +y 2; (2)2(x +y )+xy -1.知识点2 求代数式的值的实际应用7.由于生产成本和人力成本的增加,经物价主管部门批准,某厂商对某种食用油的销售单价进行调整.该种食用油今天比昨天的单价上涨了20%.(1)如果昨天该种食用油的单价为a 元/升,用代数式表示今天该种食用油的单价;(2)当a =42时,求今天该种食用油的单价.8.若m +n =3,则2(m +n )-6的值为( )A .12B .6C .3D .09.若x =y =-1,a ,b 互为倒数,则12(x +y )+3ab 的值是( ) A .2 B .3 C .4 D .3.510.如图4-3-1是一个数值转换器,若输入的a 的值为2,则输出的值为( )图4-3-1A .2B .0C .1D .-111. 定义一种新运算a b =a 2-ab ,则4(-3)=________.12.2017·慈溪月考历史上,数学家欧拉最先把关于x 的多项式用符号f (x )来表示,把x 等于某数a 时的多项式的值用f (a )来表示.例如x =-1时,多项式f (x )=x 2+3x -5的值记为f (-1),那么f (-1)等于________.13.已知|a -2|+|b +1|=0,求5a 2b -2ab 2+3ab 的值.14.新学期,两摞规格相同的数学课本整齐地叠放在课桌上,请根据图4-3-2中所给出的数据信息,解答下列问题:(1)每本书的厚度为________cm,课桌的高度为________cm;(2)当同样规格的数学课本数为x(本)时,请写出将它们叠放在课桌上时,桌面上的课本高出地面的高度为________(用含x的代数式表示);(3)桌面上有55本与(1)中规格相同的数学课本,它们整齐叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的高度.图4-3-21.A2.B [解析] 把字母x ,y 的值代入要求的代数式,然后按代数式指明的运算顺序进行计算.把x =-13,y =4代入3x +y -3,得3×⎝ ⎛⎭⎪⎫-13+4-3=-1+4-3=0.故选B. 3.D [解析] 当a =2时,a 2+1=22+1=5;当a =-2时,a 2+1=(-2)2+1=5.∴当a =2与a =-2时,代数式a 2+1的值相等.故选D.4.-73 [解析] 因为x =-2,所以6x +51-x =-12+51+2=-73. 5.10 6.(1)-1 (2)-57.[解析] 今天的单价是昨天单价的(1+20%).解:(1)(1+20%)a 元/升.(2)当a =42时,(1+20%)a =1.2×42=50.4,所以今天该种食用油的单价为50.4元/升.8. D [解析] 当m +n =3时,原式=2×3-6=0.9. A10.B11.28[解析] 4(-3)=42-4×(-3)=16+12=28.12.-7 [解析] 根据题意,得f (-1)=1-3-5=-7.13.解:因为|a -2|+|b +1|=0,|a -2|≥0,|b +1|≥0,所以|a -2|=0,|b +1|=0,所以a =2,b =-1.当a =2,b =-1时,原式=5×22×(-1)-2×2×(-1)2+3×2×(-1)=-20-4-6=-30.14.解:(1)每本书的厚度为(88-86.5)÷(6-3)=0.5(cm);课桌的高度为86.5-3×0.5=85(cm).故答案为0.5,85.(2)因为x本书的高度为0.5x cm,课桌的高度为85 cm,所以这些课本高出地面的高度为(85+0.5x)cm.故答案为(85+0.5x)cm.(3)当x=55-18=37时,85+0.5x=103.5.故余下的数学课本高出地面的高度为103.5 cm.。
4.2+代数式的值+课件+--2024-2025学年浙教版(2024)七年级数学+上册

6a-2b+5=2(3a-b)+5=2×2+5=9.
变式2 已知3a-b=2,求代数式 -6a+2b +5的值.
-2(3a-b)
解:当3a-b=2时,
-6a+2b+5=-2(3a-b)+5=(-2)×2+5=1.
小结:用整体代入法求代数式的值,往往先通过观察
发现所求代数式的系数和已知代数式的系数的关系,
=
=6.
小结:1.直接用数值代替代数式里的字母,计算代数式的值
的方法叫做直接代入法.
2.要按照代数式指明的运算顺序进行计算.
3.当字母用数值替代时,要补上乘号.
=-0.12.
3.例题应用,理解概念
( −)
变式:当n分别取下列值时,求代数式
的值.
(1)n=-2.
(2)n= .
小明求解过程如下:
哥哥今年18岁.即当m=15时,代数式m+3的值为18.
由此可以看到,对代数式m+3中的字母m代入合理的
数值,就可以求出代数式m+3的值.
2.提炼概念,初步感知
像这样,用数值代替代数式里的字母,计算后所得的结果,
叫做代数式的值.
我们可将上述过程看作一个计算程序:
代数式
m+3
输入m具
体数值
求解m+3的值
2.若3a-b=2,则代数式12a-4b+5的值为
解: 当3a-b=2时,
12a-4b+5=4(3a-b)+5=4×2+5=13.
.
.
5.巩固练习,掌握新知
3.如图,某窗框上半部分为半圆形,下半部分为长方形,已知
长方形的长为a米,宽为b米. (图中虚线部分不需要安装材料)
七年级数学上册 4.3 代数式的值典型例题素材2 (新版)浙教版
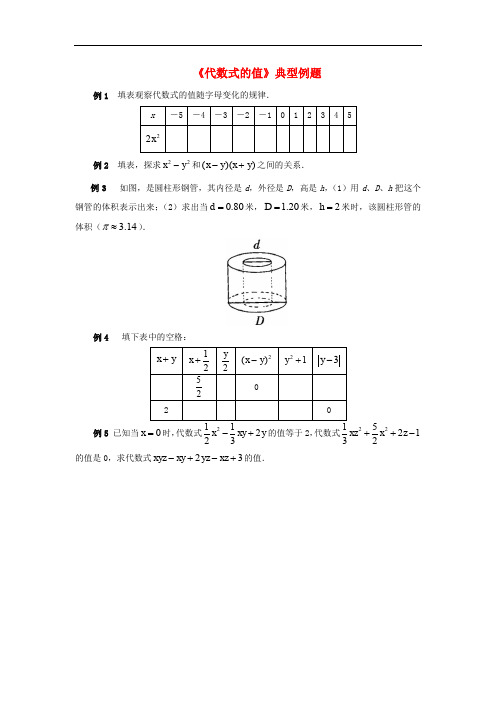
《代数式的值》典型例题例1 填表观察代数式的值随字母变化的规律.例2 填表,探求22y x -和))((y x y x +-之间的关系.例3 如图,是圆柱形钢管,其内径是d ,外径是D ,高是h ,(1)用d 、D 、h 把这个钢管的体积表示出来;(2)求出当80.0=d 米,20.1=D 米,2=h 米时,该圆柱形管的体积(14.3≈π).例4 填下表中的空格:例5 已知当0=x 时,代数式y xy x 2322+-的值等于2,代数式1225322-++z x xz 的值是0,求代数式32+-+-xz yz xy xyz 的值.参考答案例1 分析:先把x 取的值分别代入22x 中,求出22x 的值,再通过观察,探索代数式的值随x 值变化的变化规律.解:填表如下:通过观察表格可以发现,当0<x 时,随着x 值的逐渐增大,22x 的值逐渐减小;当0>x 时,随着x 的逐渐增大,22x 的值也逐渐增大.说明:要注意比较字母取值之间的变化,同时也要比较代数式值的变化,才能找出规律.例2 分析:把y x ,的值分别代入两个代数式中就可求出代数式的值,再比较两个代数式的值,就可以发现两个代数式之间的关系.解:填表如下经过观察我们可以发现,当这两个代数式中字母取值相同时,代数式的值相等. 说明:我们这种观察,推测只能是一种猜想,有时并不是都正确,还需进行推理论证,当然))((22y x y x y x +-=-,在我们后面的学习中是可以证明的.例3 分析:钢管的体积等于以D 为底面直径的圆柱体的体积,减去以d 为底面直径的圆柱体的体积.解:(1)这个钢管的体积可以表示为:h dh D 22)2()2(ππ-(2)当80.0=d 米,20.1=D 米,2=h 米时,这个钢管的体积是h d h D22)2()2(ππ-)(256.12)280.0(14.32)220.1(14.3322米≈⨯⨯-⨯⨯≈说明:(1)已知给出的是内径、外径,指的都是直径,不要误认为是半径;(2)由于π取的是近似值,所以结果应是近似值.例4 分析:对于第2行,应先从2521=+x 求得2=x ,再代入0)(2=-y x ,得2=y ,从而其他空格可填。
浙教版七年级上册数学第4章 4.3代数式的值 基础知识、课后巩固练习(包含答案)

4.3 代数式的值学习指要知识要点1.代数式的值:一般地,用数值代替代数式里的字母,计算后所得的结果叫做代数式的值2.利用代数式求值推断代数式所反映的规律3.解释代数式的值的实际意义重要提示1.求代数式的值是由一般的式子到特殊的数的问题,代数式里的字母取值要使代数式有意义如:代数式中要保证分母x-2≠0,即x不能取22.求代数式的值的步骤:(1)代人:代入时要注意:①如果代数式中省略乘号,代入后必须添上乘号.②如果字母给出的值是负数或分数,并作乘方或乘法运算,代入时都必须添上括号.③代人数值时,要“对号入座”,谨防混淆.④当题目按常规方法不能求解时,要充分利用“整体思想”将某一代数式作为一个整体,用“整体代入法”求解,解答此类问题的关键是确定合适的整体.(2)计算:计算时要注意运算顺序,同时考虑运用运算律简化运算.课后巩固之夯实基础一、选择题1.(2018·湖州长兴县期中)当x =-1时,代数式3x +1的值是( ) A .-1B .-2C .4D .-42.当x =-1时,下列代数式:①1-x ,②1-x 2,③-12x ,④1+x 3中,值为零的有( )A .1个B .2个C .3个D .4个3.(2018·杭州萧山区戴村片期中)当a =3,b =-1时,代数式0.5(a -2b)的值是( ) A .1B .0.5C .-2.5D .2.54.(2018·温州龙港镇期中)若2x -y =-3,则代数式1-4x +2y 的值等于( ) A .7B .-5C .5D .-45.若x =y =-1,a ,b 互为倒数,则代数式12(x +y)+3ab 的值是( )A .2B .3C .4D .3.56.下列代数式中,值一定为正数的是( ) A .(x +2)2 B .|x +1| C .(-x)2+2D .1-x 27.(2017·杭州大江东期中)如图K -23-1是一个数值运算程序,当输入x 的值为-2时,输出的结果为( )图K -23-1A .3B .8C .64D .638.图K-23-2中的图形都是由若干个灰色和白色的正方形按一定规律组成的,图①中有2个灰色正方形,图②中有5个灰色正方形,图③中有8个灰色正方形,图④中有11个灰色正方形……按此规律,图⑩中灰色正方形的个数是()图K-23-2A.32 B.29 C.28 D.26二、填空题9.当a=1,b=2时,代数式a2-ab的值是________.10.同一时刻北京的时间为7:00时,悉尼的时间是9:00.若北京时间用a表示,则悉尼时间为________,当北京时间为23:00时,悉尼时间为__________.11.(2017·湖州长兴县期末)已知实数x,y满足|x-4|+y+11=0,则代数式x-y 的值为________.12.(2018·绍兴嵊州期末)若a-b=2,则代数式5-2a+2b的值是________.13.某市出租车收费标准为起步价10元,3千米后每千米加收2元,那么乘坐出租车x(x>3)千米的收费y(元)的计算公式是y=__________,如果某人乘坐出租车5千米,那么应收费______元.14.(2018·杭州开发区期末)如图K-23-3是一种数值转换机的运算程序.若第一次输入的数为7,则第2018次输出的数是________;若第一次输入的数为x,使第2次输出的数也是x,则x=__________.图K-23-3三、解答题15.(2018·湖州长兴县期中)当a=2,b=-1时,求下列代数式的值:(1)2a+5b;(2)a2-2ab+b2.16.(2018·宁波余姚期末)已知2x-y=5,求-2(y-2x)2+3y-6x的值.17.若将一个棱长为8 cm的立方体的体积减小V cm3,而保持立方体形状不变,则棱长应减小多少厘米?若V=504,则棱长应减小多少厘米?18.(2018·衢州期中)“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图K-23-4所示,一张边长为20 cm的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形的长和宽分别为x cm,y cm,剪去的两个小直角三角形的两直角边长也分别为x cm,y cm.(1)用含有x,y的代数式表示图中“囧”字图案(阴影部分)的面积;(2)当x=8,y=6时,求此时“囧”字图案(阴影部分)的面积.图K-23-419.(2018·湖州长兴县期中)某农户承包果树若干亩,收获水果总产量为20000千克,此水果可以在果园直接销售,也可以运去市场销售.已知在果园直接销售每千克售a元;在市场上每千克售b元,农户将水果运到市场销售平均每天售出1000千克,且在运到市场的过程中,需每天开支400元.(1)分别用含a,b的代数式表示两种方式销售水果的收入;(2)若a=4,b=4.5,且两种销售水果的方式都在规定的时间内售完全部水果,请你通过计算说明选择哪种销售方式较好.课后巩固之能力提升20.探索发现(2018·温州龙港镇期中)填写下表,观察下列两个代数式的值的变化情况:用代入检验的方法说明哪个代数式的值先超过100.21.新学期,两摞规格相同的数学课本整齐地叠放在课桌上,请根据图K-23-5(示意图)中所给出的数据信息,解答下列问题:(1)每本课本的厚度为________cm,课桌的高度为________cm;(2)若将x本同样规格的数学课本整齐地叠放在课桌上,则桌面上的课本距地面的高度为________cm(用含x的代数式表示);(3)桌面上有55本与(1)中规格相同的数学课本,它们整齐地叠放成一摞,若18名同学每人从中取走1本,则余下的数学课本距地面的高度是多少?图K-23-5详解详析1.[答案] B2.[答案] B3.[答案] D4.[答案] A5.[答案] A6.[答案] C7.[解析] D当x=-2时,输出(-2)2-1=3,再把x=3代入x2-1中,得x2-1=32-1=8,再把x=8代入x2-1中,得x2-1=82-1=63.∵63>50,∴输出的结果是63.故选D.8.[解析] B因为图①中有2个灰色正方形,2=3-1=3×1-1,图②中有5个灰色正方形,5=6-1=3×2-1,图③中有8个灰色正方形,8=9-1=3×3-1(3n -1)个灰色正方形,所以图⑩中灰色正方形的个数是3×10-1=29.故选B.9.[答案] -1[解析] a2-ab=12-1×2=-1.10.[答案] a+2次日1:00[解析] 悉尼与北京的时间差为2小时,所以当北京时间为a时,悉尼时间为a+2,当a=23时,a+2=25,即次日1:00.11.[答案] 15[解析] 因为|x-4|+y+11=0,所以x-4=0,y+11=0,所以x=4,y=-11,所以x-y=15.12.[答案] 113.[答案] 10+2(x -3) 14 14.[答案] 2 6或0或3 15.[答案] (1)-1 (2)9 16.[答案] -6517.解:棱长应减小⎝⎛⎭⎫8-383-V cm. 当V =504时, 棱长应减小8-383-504=6(cm).18.[解析] (1)直接利用正方形面积-2×三角形面积-长方形面积即可得出答案;(2)利用(1)中所求,将x ,y 的值代入,得出答案.解:(1)“囧”字图案阴影部分的面积=20×20-12xy×2-xy =(400-2xy)cm 2.(2)当x =8,y =6时,原式=400-2×8×6=304.故当x =8,y =6时,“囧”字图案(阴影部分)的面积为304 cm 2. 19.解:(1)在果园直接销售收入为20000a 元; 将这批水果运到市场上销售收入为(20000b -8000)元. (2)当a =4时,在果园直接销售收入为20000×4=80000(元);当b =4.5时,将这批水果运到市场上销售收入为20000×4.5-8000=82000(元). 因为82000>80000,所以选择运到市场上销售较好. [素养提升] 20.解:填表如下:因为当x =15时,12x 2=2252>100,6x -8=82,所以12x 2的值先超过100.21解:(1)每本课本的厚度为(88-86.5)÷(6-3)=0.5(cm); 课桌的高度为86.5-3×0.5=85(cm).故答案为0.5,85. (2)因为x 本课本的高度为0.5x cm ,课桌的高度为85 cm , 所以这些课本距地面的高度为(85+0.5x )cm. 故答案为(85+0.5x ).(3)当x =55-18=37时,85+0.5x =103.5. 故余下的数学课本距地面的高度为103.5 cm.。
【浙教版】2018年七上数学第4章代数式4.3代数式的值同步测试卷.docx

【浙教版】 2018 年七上数学同步检测试题4.3代数式的值 ( 见 A 本 29 页 )A 练就好基础 基础达标1.当 x = 1 时,代数式 4-3x 的值是 ( A)A . 1B . 2C . 3D .412.若 x =- 3, y =4,则代数式 3x + y -3 的值为 ( B )A .- 6B . 0C . 2D .63.当 x = 3, y = 2 时,代数式 2x - y的值是 ( A)34A. 3 B . 2C . 0D .34.当 a = 3, b = 2 时,代数式 a 2+ 2ab + b 2 的值是 ( D )A . 5B . 13C . 21D .255.当 a =- 2,b = 3 时, a 2- 2b + 3 的值为 (B)A .- 7B . 1C . 4D .66.若 x 是 5 的相反数, |y|= 6,则 x - y 的值是 (D ) A .- 11 B . 11C .- 1 或 11D . 1 或- 117.如图是一数值转换机的示意图,若输入的 x 值为 32,则输出的结果为 (D )第 7 题图A . 50B . 80C . 110D .130【解析】当 x = 32 时, 5(x - 2)= 5× (32- 2)= 50<90,3 3当 x = 50 时,53(x - 2)=53× (50- 2)= 80<90,55当 x = 80 时, 3(x - 2)= 3× (80- 2)= 130> 90,即输入的 x 值为 32,则输出的结果为130.故选 D.a8.某人做零件 a 只,原计划每天做80 只,需要 __80__天完成,实际每天多做7 只,因此实际需要 __aa - a87__天完成,实际比原计划提前__80 87__天完成,若 a = 6960,则实际比原计划提前 __7__天完成.9.某汽车行驶时油箱中余油量Q(千克 )与行驶时间 t(小时 )的关系如下表:行驶时间 t(小时 )余油量 Q(千克 )1 36- 62 36- 123 36- 18 436- 24 536- 30(1)写出用时间 t 表示余油量 Q 的代数式: __36 - 6t__.3时,则余油量 Q 的值为 __27__ .(2)当 t =2(3)根据所列代数式回答,汽车行驶之前油箱中有油多少千克? 解: (3)3610.当 x = 3, y =- 2 时,求下列代数式的值.①x 2- y 2; ② x + y ;x - y③ x 2- 2xy + y 2;④ 1+ 1.x y 解:当 x = 3, y =- 2 时, ① x 2- y 2= 9- 4= 5;②x + y =3- 2= 1;x- y 3+ 2 5 ③ x 2- 2xy + y 2= 9+ 12+ 4=25;1 1 1 1 1④ += - =- .xy32611.探索代数式 22与代数式 (a +b)( a -b) 的关系. a - b (1)当 a = 5, b = 2 时分别计算两个代数式的值. (2)当 a = 7, b =- 13 时分别计算两个代数式的值. (3)你发现了什么规律? (4)利用你发现的规律计算: 8892-1112.解: (1)当 a =5, b = 2 时,22a -b = 25-4= 21,(2)当 a = 7, b =- 13 时,22a -b = 49-169=- 120, (a + b)(a - b)=- 6×20=- 120. (3)a 2 -b 2=( a + b)( a - b). (4)889 2- 1112= 778 000.12.如图,一张长 3x 的正方形纸片,剪去两个一样的小直角三角形和一个长方形.设剪去的小长方形的长和宽分别为x , y ,剪去的两个小直角三角形直角边的长也分别为x , y.(1)用含有 x ,y 的式子表示图中阴影部分的面积. (2)当 x = 8, y = 2 时,求此阴影部分的面积.第 12 题图1解: (1)3x ·3x - xy -2xy × 2 = 9x 2- 2xy.(2)当 x = 8, y = 2 时,9x 2- 2xy= 9× 82- 2× 8× 2 = 576- 32= 544.B 更上一层楼能力提升a c -1 3 13.定义一种新运算法则是=ad - bC ,则2=__- 10__.bd414.如图所示, 将面积为 a 2 的小正方形和面积为b 2 的大正方形放在同一水平面上(b > a>0) .(1)用 a 、 b 表示阴影部分的面积.(2)计算当 a =3, b = 4 时,阴影部分的面积.第 14 题图解: (1)阴影部分的面积为 1 b 2+ 1 a(a + b).2 2(2)当 a = 3,b = 4 时, 1 b 2+1 a(a + b)= 1× 16+ 1× 3×(3+ 4)= 37,则阴影部分的面积为2 22 2 237 2.15.在某地,人们发现在一定温度下, 某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀 1 min 叫的次数 n 除以 7,然后再加上3,就可以近似地得到该地当时的温度(℃ ).(1)用代数式表示该地当时的温度.(2)当蟋蟀 1 min 叫的次数为100 时,该地当时的温度约为多少(精确到个位 )?解: (1)根据题意可知该地当时的温度为n+ 3 ℃ .7n 100(2)当 n = 100 时, 7+ 3= 7 + 3≈ 17(℃ ).答:该地当时的温度约为 17 ℃ . C 开拓新思路拓展创新16.有一种放铅笔的V 形槽,如图所示,第一层放 1 支,第二层放2 支,依次每层增放 1 支,只要数一数顶层的支数 n 就可用公式算出槽内铅笔的支数.(1)根据图示你能推出这个公式吗? (2)你还有没有其他方法推出这个公式? (3)利用公式分别计算当n = 6, n = 11 时,槽内铅笔的支数.第16解: (1)由意和可知:笔数 1+ 2+⋯+ n=n(n+1).2(2)可以看作上底1,下底n,高 n 的梯形,照梯形的面公式算.(3)当 n= 6 ,槽内笔的数当 n=11 ,槽内笔的数6×( 6+1)= 21(支 );211×( 11+ 1)= 66(支 ).2。
【最新整理版】浙教版数学七年级上册4.3《代数式的值》ppt练习课件.ppt

【解析】 (1)(8a+3b)元. (2)当 a=8,b=12 时,8a+3b=8×8+3×12=100(元). (3)100÷8=12.5≈12,即用 100 元最多能买 12 支钢笔. 100÷3=3313≈33,即用 100 元最多能买 33 本笔记本. 【答案】 (1)(8a+3b)元 (2) 100 元 (3) 12 支,33 本
【答案】 (1)-3 (2) 49
2.用整体代入法求代数式的值
【典例 2】 已知 x2+5x+8 的值是 2,求代数式 3x2+15x+8 的值.
【点拨】 (1)本题主要考查求代数式的值的方法.
(2)注意 x2+5x 与 3x2+15x 的关系,采用整体代入法. 【解析】 由已知条件知 x2+5x+8=2,∴x2+5x=-6. 当 x2+5x=-6 时,3x2+15x+8=3(x2+5x)+8=3×(-6)+8 =-10. 即代数式 3x2+15x+8 的值为-10. 【答案】 -10
添上括号;②计算. (2)代入求值时,注意书写格式,特别是不要漏掉“当……时” 等文字.
【解析】 (1)当 x=-12,y=4 时,原式=-122+42- (-2)当21×a4==414,+b1=6+-213=时1,814原. 式=14×44-3---1313 3=161+33217= 413137.
因此原来每 500 g 0.5 元的山东大白菜要涨到每 500 g :0.5+0.275
=0.775(元).
【答案】
3000+y (1)1000(15-x)
元
(2) 0.775 元
名师指津
1. 求代数式的值的步骤为:(1)代入:当……时,代数 式中的字母用数代入;(2)计算.
2. 一般地,代数式的值随字母的取值变化而变化. 3. 注意整体思想在求代数式的值中的应用.
新浙教版七年级上册数学第四章代数式知识点典型例题
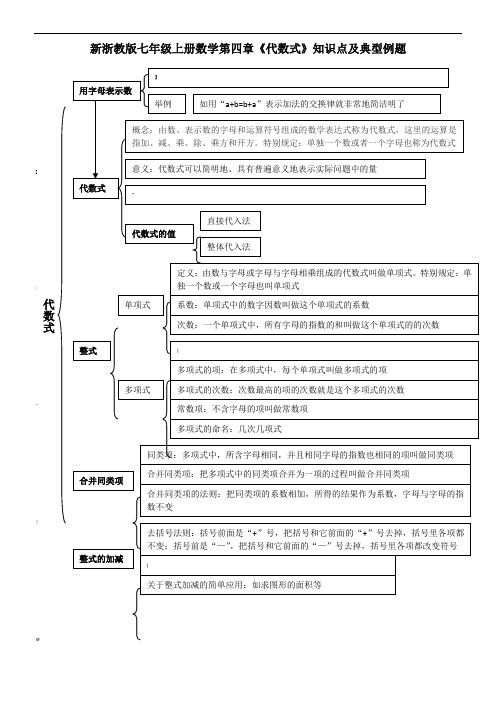
新浙教版七年级上册数学第四章《代数式》知识点及典型例题@关于代数式分类的拓展考点一、关于代数式的书写是否正确的问题考点二、关于去括号的问题;考点三、关于代数式中考概念的题目考点四、关于代数式求值的问题,主要有先化简再直接代入、整体代入、稍作变形后再代入(把整式的加减也归入这一类)考点五、用代数式表示实际生活中的问题考点六、用代数式表示图形的长度及面积问题考点七、用代数式求关于规律性的题目将考点与相应习题联系起来考点一、关于代数式的书写是否正确的问题^1、下列代数式书写规范的是()A.512ab2B.ab÷c C.a-cbD.m·32、下列代数式书写规范的是()A.a÷3 B.8×a C.5a D.21 2 a考点二、关于去括号的问题1、下列运算正确的是()A.-3(x-1)=-3x-1 B.-3(x-1)=-3x+1 C.-3(x-1)=-3x-3 D.-3(x-1)=-3x+3 2、下列去括号中错误的是(),A.2x2-(x-3y)= 2x2-x+3y B.13x2+(3y2-2xy)=13x2-2xy +3y2C.a2-4(-a+1)= a2-4a-4 D.- (b-2a)-(-a2+b2)= - b+2a+a2-b23、下列去括号,错误的有()个①x2+(2x-1)= x2+2x-1,②a2-(2a-1)= a2-2a-1,③m-2(n-1)=m-2n-2,④a-2(b-c)=a-2b+cA. 0B. 1C. 2D. 34、去括号:-[-(1-a)-(1-b)]=考点三、关于代数式中与概念有直接关系的题目1、单项式中-27πa2b的系数和次数分别是(),A.-27,4 B.27,4 C.-27π,3 D.27π,32.下列代数式中,不是整式的是()A. 13a2+12a+1 B. a2+1bC. m+12D.2006x+y3.下列说法正确的是()⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧)(被开方数含有字母无理式分式多项式单项式整式有理式代数式A. x 2-3x 的项是x 2,3xB.3a b +是单项式 C. 12,πa ,a 2+1都是整式 D. 3a 2bc-2是二次二项式 4、若m ,n 为自然数,则多项式x m -y n -2m+n 的次数是( )A. mB. nC. m+nD. m ,n 中较大的数 5、下列各项式子中,是同类项的有( )组 。
浙教版七年级数学上册《代数式的值》件

3、求代数式的值可以解决许多实际问题; 4、相同的代数式可以看作一个字母——整体代换.
1、代a2数 b2的 式值 (D )
A大于0;
B大于2;
C等于0;
D大于或等于0
2、 x23的值 ( C )
A大于3;
B等于3;
C大于或等于3; D小于3
x
……(2)如果随意
给出一个正整数,记为x,那么利用这个正整数,我们都可以
根据代数式(1)或(2)求出一个对应值。
我们约定一个规则:若正整数x为奇数,我们就根据(1)式求 对应值;若正整数x为偶数,我们就根据 (2)式求对应值。 例如根据这种规则,若取正整数x为18(偶数),则由(2)式 求得对应值为9;而正整数9(奇数),由(1)式求得对应值 为28;同样,正整数28(偶数)对应14……。我们感兴趣的是
,从某一个正整数出发,不断地这样对应下去,会是一个什么 样的结果呢?也许这是一个非常吸引人的数学游戏。
通过这节课的学习,
你有什么收获同大家一起分享吗?
1、求代数式的值的步骤: 2、求代数式的值的注意事项: (1)代入数值前应先指明字母的取值,把“当……时”写出来 ;
(2)代数式中省略了乘号时,代入数值以后必须添上乘号;
(2)数字与数字相乘,要写“×”号,因此, 如
果原代数式中有乘法运算,当其中的字母用 数字在替代时,要恢复“×”号。
实际应用
例3. 圆柱的体积等于底面积乘高. 若用h表示圆 柱的高,r表示底面半径(如下图),V表示圆
柱的体积.
(1)请用字母 h, r,V写出圆柱的体积公式.
(2)求底面半径为50cm,高为20cm的圆柱的 体积.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《代数式的值》典型例题
例1 求下列代数式的值:
(1) a2- +2 其中a=4, b=12,
(2) 其中a= , b= .
例2当a=-1,b=2,c=3时,求下列各代数式的值。
(1)(2)(a2+b2-c2)2(3)
例3已知a-=2,求代数(a-)2-+6+a的值。
例4当=2时,求代数式的值。
例5某车间第一个月产值为m万元,平均每月增产率为a% 要求:
(1)用代数式表示出第二个月的产值。
(2)当m=20 ,a=5时第二月的产值。
例题解析
例1 解:(1)当a=4, b=12时,
a2- +2=42- +2=16-3+2=15
(2)当a= ,b= 时,
= = = 。
点评:(1)求代数式的值的解题步骤是:
①指出代数式中的字母所取的值;②抄写原代数式;
③把字母的值代入代数式中;④按规定的运算顺序进行计算。
(2)代数式的值是由代数式里字母所取的数的大小来确定的,代数式里的字母可取不同的值,但这些值必须使代数式和它所表示的实际数量有意义。
(1)题中的a不能取0,因为当a取0时,的分母为零,代数式无意义。
(2)题中a+b不能为0。
分析:求代数式在a=-1,b=2,c=3时的值,就是把代数式中的字a、b、c,分别用-1,2,3代替,按原来的运算顺序进行运算即可。
例2 解:
(1)
(2)(a2+b2-c2)2=2=2=16
(3)
分析:本例中代数式(a-)2-+6+a是含字母a的代数式,若已给出a 的值,用a的值代换代数式中的字母a,即可进行运算,但现在没给a的值,又
无法求出a的值。
只知:a-=2,所以我们应把a-作为一个整体,把代数式(a-)2-+6+a进行变形,使代数式中的字母以a-的形成出现,再用2代替a-即可求值。
例3 解:当a-=2时
(a-)2-+6+a=(a-)2+(a-)+6
=22+2+6
=12.
分析:本例仿例3,把看一个整体,把所给代数式进行变形。
例4 解:当=2时
=2×2+3×=5
分析:平均每月增产率为a%,即第二月的产值比第一个月的产值增加
m×a%,所以第二月的产值为m+m·a%.
例5解:
1)第二个月的产值为(m+m·a%)万元;
2)当m=20,a=5时
m+m·a%=20+20×5%=21(万元)
小结:若每月的增产率不变,下一个月的产值就等于本月产值+本月产值×增产率。
请试着写出第三个月的产值,并计算当m=20,a=5时产值。
