2017襄阳20中10月份考试试题
2017年襄阳中考语文试题及答案

2017年襄阳市初中毕业生学业水平考试语文试题一、积累与运用(20分)1.下面句子中两个错别字,请改正后用正楷字将整个句子抄写在米字格中。
(2分)传家风耳儒目染,诵经典固本筑魂。
2.根据语境,给下面一段话中加点的字注音。
(2分)源远流长,底蕴()深厚、异彩纷呈的中华文化,为中华民族培育者思想的花朵,驱动者,精神的帆樯,引领着前进的航向,是我们自信的强大依托与丰沛()源泉。
3.下列句子中加点成语使用正确的一项是()(2分)A.临近毕业,同学们都依依不舍,大家约定在新学校里萍水相逢。
B.天舟一号与天宫二号成功对接,在我国航天发展史上留下了刻骨铭心的一笔。
C.全市中小学生积极响应团中央号召,纷纷各自为阵参加“清明网上祭英烈”活动。
D.傍晚时分,漫步江边,汉江两岸的彩灯点亮了襄阳的夜空,令人心旷神怡。
4.下列句子没有语病的一项是()(2分)A.“一带一路”这个战略构想,举世瞩目,影响深远,实现它是中华民族兴衰的关键。
B.4月19日,庞公大桥江心主墩开始钻孔,此桥建成将大大缓解我市交通拥堵的现状。
C.《襄阳古城墙保护条例》将对古城墙的依法保护和科学管理发挥重要的作用。
D.由于对志愿者精神理解不深,使的部分志愿者还不能主动投入到全国文明城创建活动中。
5.将下列句子组成语意连贯的一段话,语序排列正确的一项是()(2分)①全民阅读率的上升,显然是一件好事。
②因此,全民阅读质量的真正提升之路还很漫长。
③但有必要思考的是:现在齐升的到底是整体式阅读还是碎片式阅读,到底是深阅读,还是浅阅读?④或者把问题进一步简化为:到底是高质量的阅读还是低质量的阅读?⑤在这些方面,并没有准确的数字区分,但就我们眼中所见而言,高质量阅读,可能并不尽如人意。
A.②④①③⑤B.①③④⑤②C.②④⑤③①D.①④⑤③②6.名著之所以“著名”,不仅因文字,更因情怀。
《傅雷家书》是一部书信集,凝聚着傅雷先生对、对儿子深厚的爱;《昆虫记》在真实记录和描写昆虫生活的同时,还渗透着法布尔对的思考。
湖北省襄阳市2017年中考数学真题及答案

湖北省襄阳市2017年中考数学真题试题
一、选择题(本大题共10个小题,每小题3分,共30分)
1.﹣5的倒数是( ) A. 15 B. 15
- C.5 D.﹣5 2.下列各数中,为无理数的是( )
C.
13 3.如图,BD ∥AC ,BE 平分∠ABD ,交AC 于点E .若∠A =50°,则∠1的度数为( )
A.65° B.60° C.55° D.50° 4.下列运算正确的是( )
A.32a a -= B. ()325a a = C. 235a a a = D.632a a a ÷=
5.下列调查中,调查方式选择合理的是( )
A.为了解襄阳市初中每天锻炼所用时间,选择全面调查
B.为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查
C.为了解神舟飞船设备零件的质量情况,选择抽样调查
D.为了解一批节能灯的使用寿命,选择抽样调查 6.如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )
A. B. C. D.
7.下列图形中,既是中心对称图又是轴对称图形的是( )。
湖北省襄阳市2017年中考数学真题试题(含解析)

湖北省襄阳市2017年中考数学真题试题一、选择题(本大题共10个小题,每小题3分,共30分)1.﹣5的倒数是( )A . 15B . 15- C .5 D .﹣5 【答案】B .【解析】试题分析:﹣5的倒数是15-,故选B . 考点:倒数.2.下列各数中,为无理数的是( )A .B .C .13D 【答案】D .考点:无理数.3.如图,BD ∥AC ,BE 平分∠ABD ,交AC 于点E .若∠A =50°,则∠1的度数为( )A .65°B .60°C .55°D .50°【答案】A .【解析】试题分析:∵BD ∥AC ,∠A =50°,∴∠ABD =130°,又∵BE 平分∠ABD ,∴∠1=12∠ABD =65°,故选A .考点:平行线的性质.4.下列运算正确的是( )A .32a a -=B . ()325aa = C . 235a a a = D .632a a a ÷=【答案】C .【解析】 试题分析:A .3a ﹣a =2a ,故此选项错误;B .()326aa =,故此选项错误; C .235a a a =,正确; D .633a a a ÷=,故此选项错误;故选C .考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.5.下列调查中,调查方式选择合理的是( )A .为了解襄阳市初中每天锻炼所用时间,选择全面调查B .为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查C .为了解神舟飞船设备零件的质量情况,选择抽样调查D .为了解一批节能灯的使用寿命,选择抽样调查【答案】D .考点:全面调查与抽样调查.6.如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )A .B .C .D .【答案】A .【解析】试题分析:从上边看第一列是一个小正方形,第二列是两个小正方形,第三列是一个小正方形,故选A . 考点:简单组合体的三视图.7.下列图形中,既是中心对称图又是轴对称图形的是( )A .B .C .D .【答案】C .考点:中心对称图形;轴对称图形.8.将抛物线()2241y x =--先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A . 221y x =+B .223y x =-C . ()2281y x =-+D .()2283y x =-- 【答案】A .【解析】试题分析:抛物线()2241y x =--先向左平移4个单位长度,得到的抛物线解析式为()22441y x =-+-,即221y x =-,再向上平移2个单位长度得到的抛物线解析式为2212y x =-+,即221y x =+;故选A .考点:二次函数图象与几何变换.9.如图,在△ABC 中,∠ACB =90°,∠A =30°,BC =4,以点C 为圆心,CB 长为半径作弧,交AB 于点D ;再分别以点B 和点D 为圆心,大于12BD 的长为半径作弧,两弧相交于点E ,作射线CE 交AB 于点F,则AF的长为()A.5 B.6 C.7 D.8【答案】B.考点:作图—基本作图;含30度角的直角三角形.10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若()221+=,大正方形的面积为13,则小正方形的面积为()a bA.3 B.4 C.5 D.6【答案】C.【解析】试题分析:如图所示,∵()221a b+=,∴22++=21,∵大正方形的面积为13,2ab=21﹣13=8,2a ab b∴小正方形的面积为13﹣8=5.故选C.考点:勾股定理的证明.二、填空题(本大题共6个小题,每小题3分,共18分)11.某天襄阳某镇观赏桃花的游客近16000人,数据16000用科学记数法表示为.【答案】1.6×104.【解析】试题分析:将16000用科学记数法表示为:1.6×104.故答案为:1.6×104.考点:科学记数法—表示较大的数.12.分式方程233x x=-的解是.【答案】=9.考点:解分式方程.13.不等式组211841x xx x->+⎧⎨+≥-⎩的解集为.【答案】2<≤3.【解析】试题分析:211841x xx x->+⎧⎨+≥-⎩①②,解不等式①,得>2.解不等式②,得≤3,故不等式组的解集为2<≤3.故答案为:2<≤3.考点:解一元一次不等式组.14.同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是.【答案】38.【解析】试题分析:画树状图得得:由树状图可知所有可能情况有8种,其中两枚正面向上,一枚正面向下的情况数为3种,所以两枚正面向上,一枚正面向下的概率=38.考点:列表法与树状图法.15.在半径为1的⊙O中,弦AB、AC的长分别为1,则∠BAC的度数为.【答案】15°或105°.考点:垂径定理;解直角三角形;分类讨论.16.如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE 折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为.【答案】258.考点:翻折变换(折叠问题);勾股定理;综合题.三、解答题(本大题共9个小题,共72分)17.先化简,再求值:2111x y x y xy y ⎛⎫+÷⎪+-+⎝⎭,其中52x =,52y =. 【答案】2xy x y -,12. 【解析】试题分析:先根据分式的混合运算顺序和法则化简原式,再将、y 的值代入求解可得.试题解析:原式=1[]()()()()()x y x y x y x y x y x y y x y -++÷+-+-+=2()()()x y x y x y x y ⋅++- =2xy x y - 当52x =,52y =时,原式2(52)(55252+-+=24=12. 考点:分式的化简求值.18.中华文化,远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是部,中位数是部,扇形统计图中“1部”所在扇形的圆心角为度.(2)请将条形统计图补充完整;(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部阅读,则他们选中同一名著的概率为.【答案】(1)1,2,126;(2)作图见解析;(3)14.试题解析:(1)调查的总人数为:10÷25%=40,∴1部对应的人数为40﹣2﹣10﹣8﹣6=14,∴本次调查所得数据的众数是1部,∵2+14+10=26>21,2+14<20,∴中位数为2部,扇形统计图中“1部”所在扇形的圆心角为:1440×360°=126°;故答案为:1,2,126;(2)条形统计图如图所示:(3)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,画树状图可得:共有16种等可能的结果,其中选中同一名著的有4种,故P(两人选中同一名著)=416=14.故答案为:14.考点:列表法与树状图法;全面调查与抽样调查;扇形统计图;条形统计图;中位数;众数.19.受益于国家支持新能汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)求该企业从2014年到2016年利润的年平均增长率;(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?【答案】(1)20%;(2)能超过.试题解析:(1)设这两年该企业年利润平均增长率为.根据题意得2(1+)2=2.88,解得 1 =0.2=20%,2 =﹣2.2 (不合题意,舍去).答:这两年该企业年利润平均增长率为20%.(2)如果2017年仍保持相同的年平均增长率,那么2017年该企业年利润为:2.88(1+20%)=3.456,3.456>3.4答:该企业2017年的利润能超过3.4亿元.考点:一元二次方程的应用;增长率问题.20.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;(2)若∠ADB=30°,BD=6,求AD的长.【答案】(1)证明见解析;(2)【解析】试题分析:(1)由平行线的性质和角平分线定义得出∠ABD =∠ADB ,证出AB =AD ,同理:AB =BC ,得出AD =BC ,证出四边形ABCD 是平行四边形,即可得出结论;(2)由菱形的性质得出AC ⊥BD ,OD =OB =12BD =3,再由三角函数即可得出AD 的长.考点:菱形的判定与性质.21.如图,直线直线1y ax b =+与双曲线2k y x=交于A 、B 两点,与轴交于点C ,点A 的纵坐标为6,点B 的坐标为(﹣3,﹣2).(1)求直线和双曲线的解析式;(2)求点C 的坐标,并结合图象直接写出10y <时的取值范围.【答案】(1)124y x =+,26y x =;(2)<﹣2.【解析】试题分析:(1)由点B的坐标求出=6,得出双曲线的解析式.求出A的坐标为(1,6),由点A和B的坐标以及待定系数法即可求出直线的解析式;考点:反比例函数与一次函数的交点问题.22.如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD 的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;(2)若DE=1,BC=2,求劣弧BC的长l.【答案】(1)证明见解析;(2)23.【解析】试题分析:(1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;(2)连接OD,DC,根据角平分线的定义得到∠DAC=∠OAC,根据三角函数的定义得到∠ECD=30°,得到∠OCD=60°,得到∠BOC=∠COD=60°,OC=2,于是得到结论.试题解析:(1)证明:连接OC,∵OA=OC,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∵∠AEC =90°,∴∠OCF =∠AEC =90°,∴EF 是⊙O 的切线;(2)连接OD ,DC ,∵∠DAC =12∠DOC ,∠OAC =12∠BOC ,∴∠DAC =∠OAC ,∵ED =1,DC =2,∴sin ∠ECD =12DE DC =,∴∠ECD =30°,∴∠OCD =60°,∵OC =OD ,∴△DOC 是等边三角形,∴∠BOC =∠COD =60°,OC =2,∴l =602180π⨯ =23π.考点:切线的判定与性质;弧长的计算.23.为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m 2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为(m 2),种草所需费用1y (元)与(m 2)的函数关系式为()()11206006001000k x x y k x b x ≤<⎧⎪=⎨+≤≤⎪⎩,其图象如图所示:栽花所需费用2y (元)与(m 2)的函数关系式为220.012030000y x x =--+(0≤≤1000).(1)请直接写出1k 、2k 和b 的值;(2)设这块1000m 2空地的绿化总费用为W (元),请利用W 与的函数关系式,求出绿化总费用W 的最大值;(3)若种草部分的面积不少于700m 2,栽花部分的面积不少于100m 2,请求出绿化总费用W 的最小值.【答案】(1)130k =,220k =,b =6000;(2)32500;(3)27900.【解析】试题分析:(1)将=600、y=18000代入y1=1可得1;将=600、y=18000和=1000、y=26000代入y1=2+b可得、b.2(2)当0≤<600时,W=30+(﹣0.012﹣20+30000)=﹣0.012+10+30000,∵﹣0.01<0,W=﹣0.01(﹣500)2+32500,∴当=500时,W取得最大值为32500元;当600≤≤1000时,W=20+6000+(﹣0.012﹣20+30000)=﹣0.012+36000,∵﹣0.01<0,∴当600≤≤1000时,W随的增大而减小,∴当=600时,W取最大值为32400,∵32400<32500,∴W取最大值为32500元;(3)由题意得:1000﹣≥100,解得:≤900,由≥700,则700≤≤900,∵当700≤≤900时,W随的增大而减小,∴当=900时,W取得最小值27900元.考点:二次函数的应用;最值问题;二次函数的最值;分段函数;综合题.24.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)如图1,若CE=CF,求证:DE=DF;(2)如图2,在∠EDF绕点D旋转的过程中:①探究三条线段AB,CE,CF之间的数量关系,并说明理由;②若CE=4,CF=2,求DN的长.【答案】(1)证明见解析;(2)①AB 2=4CE •CF ;②2103. 【解析】 试题分析:(1)根据等腰直角三角形的性质得到∠BCD =∠ACD =45°,∠BCE =∠ACF =90°,于是得到∠DCE =∠DCF =135°,根据全等三角形的性质即可的结论;试题解析:(1)证明:∵∠ACB =90°,AC =BC ,AD =BD ,∴∠BCD =∠ACD =45°,∠BCE =∠ACF =90°,∴∠DCE =∠DCF =135°,在△DCE 与△DCF 中,∵CE =CF ,∠DCE =∠DCF ,CD =CD ,∴△DCE ≌△DCF ,∴DE =DF ;(2)解:①∵∠DCF =∠DCE =135°,∴∠CDF +∠F =180°﹣135°=45°,∵∠CDF +∠CDE =45°,∴∠F =∠CDE ,∴△CDF ∽△CED ,∴CD CF CE CD =,即CD 2=CE •CF ,∵∠ACB =90°,AC =BC ,AD =BD ,∴CD =12AB ,∴AB 2=4CE •CF ; ②如图,过D 作DG ⊥BC 于G ,则∠DGN =∠ECN =90°,CG =DG ,当CE =4,CF =2时,由CD 2=CE •CF 得CD =22Rt △DCG 中,CG =DG =CD •sin ∠DCG =22sin45°=2,∵∠ECN =∠DGN ,∠ENC =∠DNG ,∴△CEN ∽△GDN ,∴CN CE GN DG = =2,∴GN =13CG =23,∴DN 22GN DG +222()23+=2103.考点:几何变换综合题;探究型;和差倍分;综合题.25.如图,矩形OABC 的两边在坐标轴上,点A 的坐标为(10,0),抛物线24y ax bx =++过点B ,C 两点,且与轴的一个交点为D (﹣2,0),点P 是线段CB 上的动点,设CP =t (0<t <10).(1)请直接写出B 、C 两点的坐标及抛物线的解析式;(2)过点P 作PE ⊥BC ,交抛物线于点E ,连接BE ,当t 为何值时,∠PBE =∠OCD ?(3)点Q 是轴上的动点,过点P 作PM ∥BQ ,交CQ 于点M ,作PN ∥CQ ,交BQ 于点N ,当四边形PMQN 为正方形时,请求出t 的值.【答案】(1)B (10,4),C (0,4),215463y x x =-++;(2)3;(3)t 的值为103或203.试题解析:(1)在24y ax bx =++中,令=0可得y =4,∴C (0,4),∵四边形OABC 为矩形,且A (10,0),∴B (10,4),把B 、D 坐标代入抛物线解析式可得:10010444240a b a b ++=⎧⎨-+=⎩,解得:1653a b ⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线解析式为215463y x x =-++;(3)当四边形PMQN 为正方形时,则∠PMC =∠PNB =∠CQB =90°,PM =PN ,∴∠CQO +∠AQB =90°,∵∠CQO +∠OCQ =90°,∴∠OCQ =∠AQB ,∴Rt △COQ ∽Rt △QAB ,∴CO OQ AQ AB=,即OQ •AQ =CO •AB ,设OQ =m ,则AQ =10﹣m ,∴m (10﹣m )=4×4,解得m =2或m =8;①当m =2时,CQ =BQ sin ∠BCQ =BQ BC=5,sin∠CBQ =CQ CB PM =PC •sin ∠PCQ t ,PN =PB •sin ∠CBQ 10﹣t )t (10﹣t ),解得t =103; ②当m =8时,同理可求得t =203,∴当四边形PMQN 为正方形时,t 的值为103或203. 考点:二次函数综合题;分类讨论;动点型;压轴题.。
湖北省襄阳市2017年中考数学试题(扫描版,含答案)

知己知彼,百战不殆。
《孙子兵法·谋攻》
樱落学校
曾泽平
大地二中
张清
泉
【素材积累】
1、2019年,文野31岁那年,买房后第二年,完成了人生中最重要的一次转变。
这一年,他摘心里对自己的定位,从穷人变成了有钱人。
一些人哪怕有钱了,心里也永远甩不脱穷的影子。
2、10月19 日下战书,草埠湖镇核心学校组织全镇小学老师收看了江苏省泰安市洋思中学校长秦培元摘宜昌所作的教训呈文录象。
秦校长的讲演时光长达两个多小时,题为《打造高效课堂实现减负增效全面提高学生素质》。
【素材积累】
每个人对未来都有所希望和计划,立志是成功的起点,有了壮志和不懈的努力,就能向成功迈进。
1、立志多在少年,但宋朝文学家苏洵27岁开始发愤,立志就读,昼夜不息,结果大器晚成,终于成为唐宋八大家之一。
2、我国明代画家王冕,少年放牛时,立志要把荷花佳景惟妙惟肖地画出来。
他不分昼夜地绘画,立志不移,后来成为当时著名的画家。
3、越王勾践被吴国军队打败,忍受奇耻大辱,给吴王夫差当奴仆。
三年后,他被释放回国,立志洗雪国耻。
他卧薪尝胆,发愤图强,终于打败了吴国。
4、有志者事竟成,百二秦关终归楚;苦心人天不负,三千越甲可吞吴。
——蒲松龄。
湖北省襄阳市2017届九年级10月月考数学试卷

s tO s tO stOs tOyxC AO九年级数学月考试题一、选择题(每题3分,共30分)1.把方程(x -5)(x +5)+(2x -1)2=0化为一元二次方程的一样形式是( ). A .5x 2-4x -4=0 B .x 2-5=0 C .5x2-2x +1=0D .5x 2-4x +6=02.已知关于x 的一元二次方程(m -2)x 2+3x +m 2-4=0有一个根为0,那么m 的值是( ).A .2B .-2C .±2D .43.关于x 的一元二次方程x 2-k =0有实数根,那么( ). A .k <0 B .k >0 C .k ≥0 D .k ≤0 4.用配方式解以下方程,配方正确的选项是( ).A .3x 2-6x =9可化为(x -1)2=4B . x 2-4x =0可化为(x +2)2=4C .x 2+8x +9=0可化为(x +4)2=25D .2y 2-4y -1=0可化为2(y +1)2=35.在同一坐标系中,一次函数y =ax +2与二次函数y =x 2+a 的图象可能是( ).A .B .C .D .6.设x 1,x 2是方程x 2+3x -3=0的两个实数根,那么x 1x 2+x 2x 1的值为( )A .5B .-5C .1D .-17.已知一个三角形的两边长是方程x 2-8x +15=0的两根,那么第三边y 的取值范围是( ).A .y <8B .3<y <5C .2<y <8D .无法确信8.二次函数y =2x 2,y =-2x 2,y =x 2的图象的一起点是( )A .都是关于x 轴对称,抛物线开口向上B .都是关于y 轴对称,抛物线开口向下C .都是关于原点对称,抛物线的极点都是原点D .都是关于y 轴对称,抛物线的极点都是原点9.已知二次函数y =ax 2,以下说法正确的选项是( )A .当a >0,x ≠0时,y 总取负值B .当a <0,x <0时,y 随x 的增大而减小C .当a <0时,函数图象有最低点,y 有最小值D .当a >0,x >0时,图象在第一象限10.柿子从树上落下所通过的路程s 与下落时刻t 知足S =gt 2(g =9.8),那么此函数的图象大致是( ).A .B .C .D .二、填空题(每题3分,共18分)11.关于x 的一元二次方程ax 2+bx +c =0知足a +c =b ,那么此方程必有一根为 . 12.假设关于x 的方程(k -1)x 2-4x -5=0有实数根,那么k 的取值范围是 . 13.若(a 2+b 2-1)2=16,那么a 2+b 2= .14.将抛物线y =ax 2+bx +c 沿x 轴向左平移2个单位,再沿y 轴向上平移3个单位,取得的抛物线的函数解析式为y =x 2-2x +1,那么a 、b 、c 别离等于 、 、 .15.二次函数y =x 2-2x -1的图象在x 轴上截得的线段长为 .16.抛物线y =ax 2+bx +c 上部份点的横坐标x ,纵坐标y 的对应值如右表:从而可知以下说法中正确的选项是 .(填写序号)①抛物线与x 轴的一个交点为(3,0);②函数y =ax 2+bx +c 的最大值为6;③抛物线的对称轴是x =;④在对称轴左侧,y 随x 增大而增大.三、解答题(本大题共9个小题,共72分)解许诺写出必要的文字说明,证明进程或演算步骤. 17.(4分)解方程x (2x -5)=4x -10.18.(6分)已知点A (1,-k 2+2)在有最高点的抛物线y =kx 2上,求常数k 的值.19.(6分)先化简代数式x 2-1x 2+2x ÷x -1x,再选择方程x 2+2x -3=0的一个根计算该代数式的值.20. (6分)二次函数y =12(x +h )2的图象如下图,已知OA =OC ,试求该抛物线的解析式.21. (9分)在直角坐标系中,△AOB 的位置如下图.已知∠AOB =90°,AO =BO ,点A 的坐标为(-3,1).(1)求点B 的坐标;(2)求过A 、O 、B 三点的抛物线的解析式;(3)设点B 关于抛物线的对称轴l 的x … -2 -1 0 1 2 …y … 0 46 6 资源库4 …对称点为B 1,求△AB 1B 的面积. y x BAO22. (8分)已知:方程4x 2+4ax +2b -c =0有两个相等的实数根,a 、b 、c 为△ABC 的三边且知足 3a -2c =b .(1)求证:△ABC 是等边三角形.(2)若a 、b 为方程x 2-2kx -(2k -3)=0二根,求k 的值.23. (9分)我校社团“念书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查,2021年全校有1000名学生,2021年全校学生人数比2021年增加10%,2021年全校学生人数比2021年增加100人.(1)求2021年全校学生人数;(2)2021年全校学生人均阅读量比2021年多1本,阅读总量比2021年增加1700本(注:阅读总量=人均阅读量×人数). ①求2021年全校学生人均阅读量;②2021年念书社人均阅读量是全校学生人均阅读量的倍,若是2021年、2021年这两年念书社人均阅读量都比前一年增加一个相同的百分数a ,2021年全校学生人均阅读量比2021年增加的百分数也是a ,那么2021年念书社全数80名成员的阅读总量将达到全校学生阅读总量的25%,求a 的值.资源库24.(12分)如图,二次函数y =ax 2的图象与一次函数y =x +b 的图象相交于A (-2,2)、B 两点,从点A 和点B 别离引平行于y 轴的直线与x 轴别离交于C ,D 两点,点P (t ,0)为线段CD 上的动点,过点P 且平行于y轴的直线与抛物线和直线别离交于R ,S .(1)求一次函数和二次函数的解析式,并求出点B 的坐标;(2)当SR =2RP 时,计算线段SR 的长;(3)假设线段BD 上有一动点Q 且其纵坐标为t +3,问是不是存在t 的值,使S △BRQ =15.假设存在,求t 的值;假设不存在,说明理由.xyRSDCB A OP Q25. (12分)如图1,正方形ABCD的边长为1,E为AB边上一动点,BE的长为x,连接DE,过B点作BF∥DE 交CD于点F,以CF为边作正方形CFMN,且点N在BC边的延长线上.(1)求证:四边形BEDF为平行四边形;(2)连接DN、EN,且EN与BF交于点G.请判定△EDN的形状,并说明理由;(3)如图2,连接DE、DM、EM,求当x为何值时,△EDM的面积取得最小值,并求△EDM的面积最小值.(第25题图1)E(第25题图2)。
湖北省襄阳市2017年中考数学真题试题(含答案)

2017年襄阳市初中毕业生学业水平考试数学试题一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.-5的倒数是( )A . 15B . 15- C . 5 D . -5 2.下列各数中,为无理数的是( )A .B ..13D 3. 如图,//,BD AC BE 平分ABD ∠,交AC 于点E .若050A ∠=,则1∠的度数为( )A . 65°B . 60°C .55°D . 50°4. 下列运算正确的是( )A .32a a -=B . ()325a a = C. 235a a a = D .632a a a ÷= 5. 下列调查中,调查方式选择合理的是( )A .为了解襄阳市初中生每天锻炼所用的时间,选择全面调查B .为了解襄阳电视台《襄阳新闻》栏目的收视率,选择全面调查C. 为了解神舟飞船设备零件的质量情况,选择抽样调查D .为了解一批节能灯的使用寿命,选择抽样调查6. 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )A .B . C. D .7.下列图形中,既是中心对称图形又是轴对称图形的是( )A .B . C. D . 8. 将抛物线()2241y x =--先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A . 221y x =+B .223y x =- C. ()2281y x =-+ D .()2283y x =--9. 如图,在ABC ∆中,0090,30,4ACB A BC ∠=∠==.以点C 为圆心,CB 长为半径作弧,交AB 于点D ;再分别以点B 和点D 为圆心,大于12BD 的长为半径作弧,两弧相交于点E ;作射线CE 交AB 于点F .则AF 的长为( )A . 5B . 6 C. 7 D .810. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a ,较短直角边长为b ,若()221a b +=,大正方形的面积为13,则小正方形的面积为( )A . 3B . 4 C. 5 D .6二、填空题(本大题共6个小题,每小题3分,共18分,将答案填在答题纸上)11.某天到襄阳某镇观赏桃花的游客近16000人,数据16000用科学计数法表示为___________.12.分式方程233x x=-的解是____________. 13.不等式组211841x x x x ->+⎧⎨+≥-⎩的解集为 .14.同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是 .15.在半径为1的O 中,弦,AB AC 的长分别为1,则BAC ∠的度数为 .16.如图,在ABC ∆中,090ACB ∠=,点,D E 分别在,AC BC 上,且CDE B ∠=∠,将CDE∆沿DE 折叠,点C 恰好落在AB 边上的点F 处,若8,10AC AB ==,则CD 的长为 .三、解答题 (本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤.)17.先化简,再求值:2111x y x y xy y⎛⎫+÷ ⎪+-+⎝⎭,其中2,2x y ==. 18.中华文化,源远流长.在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是____________部,中位数是___________部;扇形统计图中“1部”所在扇形的圆心角为____________度;(2)请将条形统计图补充完整;(3)没有读过四大名著的两名学生准备从四大古典名著中各自随机选择一部来阅读,则他们选中同一名著的概率为______________.19.受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高.据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)求该企业从2014年到2016年利润的年平均增长率;(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?20.如图,//AE BF ,AC 平均BAE ∠,且交BF 于点,C BD 平分ABF ∠,且交AE 于点D ,连接CD .(1)求证:四边形ABCD 是菱形;(2)若030,6ADB BD ∠==,求AD 的长.21. 如图,直线1y ax b =+与双曲线2k y x=交于,A B 两点,与x 轴交于点C ,点A 的纵坐标为6,点B 的坐标为()3,2--.(1)求直线和双曲线的解析式;(2)求点C 的坐标,并结合图象直接写出10y <时x 的取值范围.22.如图,AB 为O 的直径,,C D 为O 上两点,BAC DAC ∠=∠,过点C 作直线EF AD ⊥,交AD 的延长线于点E ,连接BC.(1)求证:EF 是O 的切线;(2)若1,2DE BC ==,求劣弧BC 的长l .23. 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为21000m 的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为()2x m,种草所需费用1y (元)与()2x m 的函数关系式为()()112,0600,6001000k x x y k x b x ≤<⎧⎪=⎨+≤≤⎪⎩,其图象如图所示;栽花所需费用2y (元)与()2x m 的函数关系式()220.01203000001000y x x x =--+≤≤.(1)请直接写出12,k k 和b 的值;(2)设这块21000m 空地的绿化总费用为W (元),请利用W 与x 的函数关系式,求出绿化总费用W 的最大值;(3)若种草部分的面积不少于2700m ,栽花部分的面积不少于2100m ,请求出绿化总费用W 的最小值.24.如图,在ABC ∆中,090ACB ∠=,CD 是中线,AC BC =.一个以点D 为顶点的45°角绕点D 旋转,使角的两边分别与,AC BC 的延长线相交,交点分别为点,E F ,DF 与AC 交于点M ,DE 与BC 交于点N .(1)如图1,若CE CF =,求证:DE DF =;(2)如图2,在EDF ∠绕点D 旋转的过程中:①探究三条线段,,AB CE CF 之间的数量关系,并说明理由;②若4,2CE CF ==,求DN 的长.25.如图,矩形OABC 的两边在坐标轴上,点A 的坐标为()10,0,抛物线24y ax bx =++过,B C 两点,且与x 轴的一个交点为()2,0D -,点P 是线段CB 上的动点,设()010CP t t =<<.(1)请直接写出,B C 两点的坐标及抛物线的解析式;(2)过点P 作PE BC ⊥,交抛物线于点E ,连接BE ,当t 为何值时,PBE OCD ∠=∠?(3)点Q 是x 轴上的动点,过点P 作//PM BQ ,交CQ 于点M ,作//PN CQ ,交BQ 于点N .当四边形PMQN 为正方形时,请求出t 的值.。
2017-2018学年度湖北省襄阳市二十中九年级十月考试数学试题
2017-2018学年度湖北省襄阳市二十中九年级十月考试数学试题一、选择题(每小题3分,共36分)1.下列方程是一元二次方程的是()A .20ax bx c ++=B .C .215x x+= D .)1)(12(22-+=+x x x x 2.若x =3是关于x 的方程230x bx a --=的一个根,则a +b 的值为( )A .3B .C .9D .3.关于x 的一元二次方程220x x k -+=有两个相等的实数根,则k 的值为( )A .1-B .1C .2-D .24.若12x x ,是一元二次方程26-80x x -=的两个根,则12x x +的值是( ).A .6B .6-C .8-D .85.抛物线y=2x 2-5x+3与坐标轴的交点共有( )A .1个B .2个C . 3个D . 4个6.二次函数y=(x-1)2-2的顶点坐标是()A .(-1,-2)B .(-1,2)C .(1,2)D .(1,-2)7.参加一次商品交易会的每两家公司都签订了一份合同,所有公司共签订了45份合同,则参加这次商品交易会的公司共有( ).A.11家B.10家C. 9家D.8家8.一次函数y ax b =+与二次函数2y ax bx c =++在同一坐标系中的图象大致是( )9..如图,抛物线y =ax 2+bx +c (a ≠0)与x 轴一个交点为(-2,0),对称轴为直线x =1,则y <0时x 的范围是( )A .x >4或x <-2B .-2<x <4C .-2<x <3D .0<x <310.已知抛物线2y ax bx c =++(a <0)的对称轴是2x =-,且抛物线经过A (13,y -)、B (23,y )两点,则1y 与2y 的大小关系是( )A .1y >2yB .1y <2yC .1y =2yD .无法确定11.将抛物线22-=x y 向左平移3个单位长度,再向上平移2个单位长度,所得的抛物线的解析式为()A .()23+=x yB .()23-=x yC .()122++=x yD .()122+-=x y12.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列5个结论:①abc >0;②24b ac ->0;③0>+-c b a ;④+30c a >;⑤a +b ≥m (am +b ),其中正确..信息的个数有( ) A .2 B .3 C .4 D .513.如果二次三项式2216x bx -+是一个完全平方式,那么b 的值是14.若二次函数22(1)1y m x x m =--+-的图象经过原点,则m 的值为 ________.15.已知抛物线22(3)12y x k x =-++的顶点在y 轴上,则k =16.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,若方程20ax bx c k ++-=有两个不相等的实数根,则k 的取值范围是17.要为一副长29cm ,宽22cm 的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一。
湖北省襄阳市2017年中考数学试题(附答案)

2017年襄阳市初中毕业生学业水平考试数学试题一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.-5的倒数是( )A . 15B . 15- C . 5 D . -5 2.下列各数中,为无理数的是( )A .B .C .13D 3. 如图,//,BD AC BE 平分ABD ∠,交AC 于点E .若050A ∠=,则1∠的度数为( )A . 65°B . 60°C .55°D . 50°4. 下列运算正确的是( )A .32a a -=B . ()325a a = C. 235a a a = D .632a a a ÷=5. 下列调查中,调查方式选择合理的是( )A .为了解襄阳市初中生每天锻炼所用的时间,选择全面调查B .为了解襄阳电视台《襄阳新闻》栏目的收视率,选择全面调查C. 为了解神舟飞船设备零件的质量情况,选择抽样调查D .为了解一批节能灯的使用寿命,选择抽样调查6. 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )A .B . C. D .7.下列图形中,既是中心对称图形又是轴对称图形的是( )A .B . C.D .8. 将抛物线()2241y x =--先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A . 221y x =+B .223y x =- C. ()2281y x =-+D .()2283y x =--9. 如图,在ABC ∆中,0090,30,4ACB A BC ∠=∠==.以点C 为圆心,CB 长为半径作弧,交AB 于点D ;再分别以点B 和点D 为圆心,大于12BD 的长为半径作弧,两弧相交于点E ;作射线CE 交AB 于点F .则AF 的长为( )A . 5B . 6 C. 7 D .810. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a ,较短直角边长为b ,若()221a b +=,大正方形的面积为13,则小正方形的面积为( )A . 3B . 4 C. 5 D .6二、填空题(本大题共6个小题,每小题3分,共18分,将答案填在答题纸上)11.某天到襄阳某镇观赏桃花的游客近16000人,数据16000用科学计数法表示为___________.12.分式方程233x x=-的解是____________. 13.不等式组211841x x x x ->+⎧⎨+≥-⎩的解集为 .14.同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是 .15.在半径为1的O 中,弦,AB AC 的长分别为1则BAC ∠的度数为 .16.如图,在ABC ∆中,090ACB ∠=,点,D E 分别在,AC BC 上,且CDE B ∠=∠,将CDE ∆沿DE 折叠,点C 恰好落在AB 边上的点F 处,若8,10AC AB ==,则CD 的长为 .三、解答题 (本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤.)17.先化简,再求值:2111x y x y xy y ⎛⎫+÷ ⎪+-+⎝⎭,其中2,2x y =. 18.中华文化,源远流长.在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是____________部,中位数是___________部;扇形统计图中“1部”所在扇形的圆心角为____________度;(2)请将条形统计图补充完整;(3)没有读过四大名著的两名学生准备从四大古典名著中各自随机选择一部来阅读,则他们选中同一名著的概率为______________.19.受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高.据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)求该企业从2014年到2016年利润的年平均增长率;(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?20.如图,//AE BF ,AC 平均BAE ∠,且交BF 于点,C BD 平分ABF ∠,且交AE 于点D ,连接CD .(1)求证:四边形ABCD 是菱形;(2)若030,6ADB BD ∠==,求AD 的长.21. 如图,直线1y ax b =+与双曲线2k y x=交于,A B 两点,与x 轴交于点C ,点A 的纵坐标为6,点B 的坐标为()3,2--.(1)求直线和双曲线的解析式;(2)求点C 的坐标,并结合图象直接写出10y <时x 的取值范围.22.如图,AB 为O 的直径,,C D 为O 上两点,BAC DAC ∠=∠,过点C 作直线EF AD ⊥,交AD 的延长线于点E ,连接BC .(1)求证:EF 是O 的切线;(2)若1,2DE BC ==,求劣弧BC 的长l .23. 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为21000m 的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为()2x m ,种草所需费用1y (元)与()2x m 的函数关系式为()()112,0600,6001000k x x y k x b x ≤<⎧⎪=⎨+≤≤⎪⎩,其图象如图所示;栽花所需费用2y (元)与()2x m 的函数关系式()220.01203000001000y x x x =--+≤≤.(1)请直接写出12,k k 和b 的值;(2)设这块21000m 空地的绿化总费用为W (元),请利用W 与x 的函数关系式,求出绿化总费用W 的最大值;(3)若种草部分的面积不少于2700m ,栽花部分的面积不少于2100m ,请求出绿化总费用W 的最小值.24.如图,在ABC ∆中,090ACB ∠=,CD 是中线,AC BC =.一个以点D 为顶点的45°角绕点D 旋转,使角的两边分别与,AC BC 的延长线相交,交点分别为点,E F ,DF 与AC 交于点M ,DE 与BC 交于点N .(1)如图1,若CE CF =,求证:DE DF =;(2)如图2,在EDF ∠绕点D 旋转的过程中:①探究三条线段,,AB CE CF 之间的数量关系,并说明理由;②若4,2CE CF ==,求DN 的长.25.如图,矩形OABC 的两边在坐标轴上,点A 的坐标为()10,0,抛物线24y ax bx =++过,B C 两点,且与x 轴的一个交点为()2,0D -,点P 是线段CB 上的动点,设()010CP t t =<<.(1)请直接写出,B C 两点的坐标及抛物线的解析式;(2)过点P 作PE BC ⊥,交抛物线于点E ,连接BE ,当t 为何值时,PBE OCD ∠=∠?(3)点Q 是x 轴上的动点,过点P 作//PM BQ ,交CQ 于点M ,作//PN CQ ,交BQ 于点N .当四边形PMQN 为正方形时,请求出t 的值.。
湖北省襄阳市襄州区A片区2024-2025学年八年级上学期10月月考语文试题(含答案)

八年级10月考语文试题(时间150分钟,满分120分)一、积累与运用(20分)班级开展“读新闻·学语文”学习活动,小文和小习特邀你参加。
2.下面是小习整理的有关“闻”字的【资料卡片】,请你在(1)(2)处分别补充一个含有“闻”字的词语。
(2分)【资料卡片】“闻”的含义含“闻”字的词语听见(1) 听见的事情;消息(2) 有名望的闻人3.小习发现很多新闻标题都对仗工整,请你试着将“解码”和“探索”还原到新闻标题中。
(2分) 化石信息 演化奥秘4.根据语境,补写出古代诗文名句。
(8分)斑斓的色彩遇到经典诗文,便有了别样的意境意趣。
白居易《钱塘湖春行》“最爱湖东行不足,① ”道出对西湖美景的喜爱之情;《庭中有奇树》“庭中有奇树,② ”表达的是一人独赏春日佳景,顿生思念之情;曹操《龟虽寿》“③ ,志在千里”告诉我们有远大抱负的人到了晚年,奋发进取的雄心不会止息;王维《使至塞上》“④ ,⑤ ”以瑰丽的笔墨描绘了塞外奇特雄浑的风光;崔颢《黄鹤楼》“晴川历历汉阳树 ⑥ ”是崔颢登楼所观江上美景;陶弘景《答谢中书书》“晓雾将歇,⑦ 。
夕日欲颓,⑧ ”在清爽宜人的山川画卷上平添了绚烂辉煌的一笔。
5.人无信不立,同桌小明缩印了历史知识点,打算期中考试的时候作弊。
请你劝说他。
(3分)6.小文梳理了新闻中常见的问题,列举了其中的三类,请你从每类中选择一处修改。
(3分)(1)容易读错的字 A.悄(qiāo)然 B.镌(juàn)刻(2)容易写错的词 A.锐不可挡 B.震聋发聩(3)容易说错的话A.感谢各位老师和同学莅临指导和积极参与,我们下期再会。
B.“文化中国行”专栏组织编辑记者奔赴各地,聚集中华优秀传统文化传承发展,呈现中华文化的历史底1.如图是小文发现的甲骨文中新闻的“闻”字的写法(由一个坐着的人和“耳”构成),请你据此猜想我们祖先“闻”的生活画面,用一句话说说 (2分)蕴。
二、阅读与鉴赏(45分)(一)阅读下面古诗,完成7~8题。
2017湖北襄阳试题答案解析

2017年湖北省湖北襄阳市中考生物试卷参考答案与试题解析一、选择题(共6小题,每小题1分,满分6分)17.(1分)(2017•湖北襄阳)敏敏同学用普通光学显微镜观察人血的永久涂片,视野中观察到了清晰的红细胞,但没有发现白细胞,她再采用下列哪一项操作最有可能找到白细胞?()A.换用高倍物镜B.换用凹面反光镜C.移动永久涂片D.调节细准焦螺旋C 解析:血细胞中红细胞的数目最多;白细胞的体积最大,数目最少,只有移动装片才最有可能观察到白细胞。
18.(1分)(2017•湖北襄阳)父母生育了我们,呵护我们健康成长,我们要常怀感恩之心。
下列叙述错误的是()A.精子和卵细胞都是生殖细胞B.精子与卵细胞在卵巢内形成受精卵C.胎盘是胎儿与母体交换物质的器官D.分娩时常常伴随着剧烈的阵痛B 解析:卵细胞与精子在输卵管内相遇形成受精卵,受精卵的形成是新生命诞生的起点,B的叙述错误。
19.(1分)(2017•湖北襄阳)“民以食为天”,人的生活离不开营养物质。
下列叙述中错误的是()A.胃是人体消化和吸收的主要器官B.青少年应养成不挑食的习惯C.老年人缺钙易患骨质疏松症D.购买食品时要关注生产日期和保质期A 解析:胃是消化道最膨大的部分,能暂时储存食物,并能分泌胃液初步消化蛋白质,A 的叙述错误。
20.(1分)(2017•湖北襄阳)十二生肖是中国的传统文化之一,其中“龙”的创造充满了想象力。
据说“龙”的体表覆盖角质的鳞片,有四肢和牙齿,卵外有坚韧的卵壳,能在水中和陆地生活。
下列动物中与上述特征相似度最高的是()A.鱼B.两栖动物C.爬行动物D.哺乳动物C 解析:爬行动物的体表覆盖角质鳞片或甲,用肺呼吸,有四肢和牙齿,卵外有坚韧的卵壳保护,因此与题干中的描述相似度最高的是爬行动物。
21.(1分)(2017•湖北襄阳)下列关于预防艾滋病和血吸虫病的叙述中错误的是()A.艾滋病和血吸虫病都是传染病B.血吸虫寄生在人和动物(如钉螺)体内C.HIV主要侵犯并瓦解人体的免疫系统D.艾滋病病毒和血吸虫都具有细胞结构D 解析:艾滋病病毒无细胞结构,由蛋白质外壳和内部的遗传物质构成,D的叙述错误。
2017年湖北省襄阳市中考语文试卷及试卷解析

2017年湖北省襄阳市中考语文试卷一、积累与运用(20分)1.(2分)下面句子中两个错别字,请改正后用正楷字将整个句子抄写在米字格中。
传家风耳儒目染,诵经典固本筑魂。
2.(2分)根据语境,给下面一段话中加点的字注音。
源远流长,底蕴.深厚、异彩纷呈的中华文化,为中华民族培育者思想的花朵,驱动者,精神的帆樯,引领着前进的航向,是我们自信的强大依托与丰沛.源泉。
3.(2分)下列句子中加点成语使用正确的一项是()A.临近毕业,同学们都依依不舍,大家约定在新学校里萍水相逢....。
.B.天舟一号与天宫二号成功对接,在我国航天发展史上留下了刻骨铭心....的一笔。
C.全市中小学生积极响应团中央号召,纷纷各自为政....参加“清明网上祭英烈”活动。
D.傍晚时分,漫步江边,汉江两岸的彩灯点亮了襄阳的夜空,令人心旷神怡。
......4.(2分)下列句子没有语病的一项是()A.“一带一路”这个战略构想,举世瞩目,影响深远,实现它是中华民族兴衰的关键。
B.4月19日,庞公大桥江心主墩开始钻孔,此桥建成将大大缓解我市交通拥堵的现状。
C.《襄阳古城墙保护条例》将对古城墙的依法保护和科学管理发挥重要的作用。
D.由于对志愿者精神理解不深,使的部分志愿者还不能主动投入到全国文明城创建活动中。
5.(2分)将下列句子组成语意连贯的一段话,语序排列正确的一项是()①全民阅读率的上升,显然是一件好事。
②因此,全民阅读质量的真正提升之路还很漫长。
③但有必要思考的是:现在齐升的到底是整体式阅读还是碎片式阅读,到底是深阅读,还是浅阅读?④或者把问题进一步简化为:到底是高质量的阅读还是低质量的阅读?⑤在这些方面,并没有准确的数字区分,但就我们眼中所见而言,高质量阅读,可能并不尽如人意。
A.②④①③⑤B.①③④⑤②C.②④⑤③①D.①④⑤③②6.(2分)名著之所以“著名”,不仅因文字,更因情怀。
《傅雷家书》是一部书信集,凝聚着傅雷先生对、对儿子深厚的爱;《昆虫记》在真实记录和描写昆虫生活的同时,还渗透着法布尔对的思考。
湖北省襄阳市2017届高三10月月考数学(文)试题 Word版含答案

第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.设集合{}1,2,3,4U =,集合{}2|540A x N x x =∈-+<,则C A 等于( )A .{}1,2 B .{}1,4 C .{}2,4 D .{}1,3,42.已知角θ的终边经过点()(),30Px x <且cos x =,则x 等于( )A .1-B .13-C .3-D .3-3. 0cos80cos130sin100sin130-等于( )A B .12 C .12- D .4.已知函数()2111x f x x ++=+,则曲线()y f x =在()()1,1f 处切线 的斜率为( ) A .1 B .-1 C .2 D .-25.为得到函数sin 2y x =-的图像,可将函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象( ) A .向左平移3π个单位 B .向左平移6π个单位 C .向右平移3π个单位 D .向右平移23π个单位5.“2a =”是“函数()4f x ax =-在区间()2,+∞上的单调递增”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 7. sin 3,sin1.5,cos8.5的大小关系为( )A .sin1.5sin 3cos8.5<<B .cos8.5sin 3sin1.5<<C .sin1.5cos8.5sin 3<<D .cos8.5sin1.5sin 3<<8.已知命题:p 对任意()480,,log log x x x ∈+∞<,命题:q 存在“x R ∈,使得tan 13x x =-”,则下面命题为真命题的是( )A .p q ∧B .()()p q ⌝∧⌝ C .()p q ∧⌝ D .()p q ⌝∧8.奇函数()f x 满足()10f =,且()f x 在()0,+∞上是单调递减,则()()210x f x f x -<--的解集为( ) A .()1,1- B .()(),11,-∞-+∞ C .(),1-∞- D .()1,+∞10.若函数()()22f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象关于直线12x π=对称,且当1212172,,,123x x x x ππ⎛⎫∈--≠ ⎪⎝⎭时,()()12f x f x =,则()12f x x +等于( )A B .2 C .2 D .411.设函数()()()21ln 31f x g x ax x ==-+,若对任意[)10,x ∈+∞,都存在2x R ∈,使得()()12f x g x =,则实数a 的最大值为( )A .94 B .2 C .92D .4 12.若函数()()()()()1cos sin cos sin 3sin cos 412f x x x x x a x x a x =-++-+-在,02π⎡⎤-⎢⎥⎣⎦上单调递增,则实数a 的取值范围为( ) A .1,17⎡⎤⎢⎥⎣⎦ B .11,7⎡⎤-⎢⎥⎣⎦ C .[)1,1,7⎛⎤-∞-+∞ ⎥⎝⎦ D .[)1,+∞ 第Ⅱ卷二、填空题(本大题共4小题,每小题5分,满分20分,将答案填在答题纸上)13.命题“若1x ≥,则2421x x -+≥-”的否命题为____________. 14.已知集合(){}(){}222,y |,,1,,|,,41A x x y R xy B x y x y R y x =∈+==∈=-,则A B的元素个数是____________.15.已知tan 23πα⎛⎫+= ⎪⎝⎭,则42sin cos 335cos sin 66ππααππαα⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭____________.16.设函数()()()3,132,1x a x f x x a x a x π⎧-<⎪=⎨--≥⎪⎩,若()f x 恰有2个零点,则实数a 的取值范围是_____________.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分) 已知集合{}|2131A x a x a =-<<+,集合{}|14B x x =-<<.(1)若A B ⊆,求实数a 的取值范围;(2)是否存在实数a ,使A B =?若存在,求出a 的值;若不存在,说明理由. 18.(本小题满分12分) 设0,3πα⎛⎫∈ ⎪⎝⎭αα=. (1)求cos 6πα⎛⎫+⎪⎝⎭的值; (2)求cos 212πα⎛⎫+⎪⎝⎭的值. 19.(本小题满分12分)设:p 实数a 满足不等式39,:aq ≤函数()()32331932a f x x x x -=++无极值点. (1)若“p q ∧”为假命题,“p q ∨”为真命题,求实数a 的取值范围; (2)已知“p q ∧”为真命题,并记为r ,且211:2022t a m a m m ⎛⎫⎛⎫-+++> ⎪ ⎪⎝⎭⎝⎭,若r 是t ⌝的必要不充分条件,求正整数m 的值. 20.(本小题满分12分) 已知函数()23cos 2f x x =++.(1)当,63x ππ⎡⎤∈-⎢⎥⎣⎦时,求函数()y f x =的值域;(2)已知0ω>,函数()212x g x f ωπ⎛⎫=+⎪⎝⎭,若函数()g x 在区间2,36ππ⎡⎤-⎢⎥⎣⎦上是增函数,求ω的最大值.21.(本小题满分12分) 已知函数()()2741201x x f x a a a --=->≠且.(1)当2a =时,求不等式()0f x <的解集; (2)当[]0,1x ∈时,()0f x <恒成立,求实数a 的取值范围.22.(本小题满分12分) 已知函数()()1ln 0,f x a x a a R x=+≠∈. (1)若1a =,求()f x 的极值和单调区间;(2)若在区间(]0,e 上至少存在一点0x ,使得()00f x <成立,求实数a 的取值范围.参考答案一、选择题13.若1x <,则2421x x -+<-;14.3;15.-3;16.[)11,3,32⎡⎫+∞⎪⎢⎣⎭三、解答题17.解:(1)因为A B ⊆,所以集合A 可以分为A =∅或A ≠∅两种情况来讨论;.......... 1分当A =∅时,21312a a a -≥+⇒≤-....................2分 当A ≠∅时,得211314012131a a a a a -≥-⎧⎪+≤⇒≤≤⎨⎪-<+⎩....................... 5分 综上,(][],20,1a ∈-∞- ................................ 6分(2)若存在实数a ,使A B =,则必有21103141a a a a -=-=⎧⎧⇒⎨⎨+==⎩⎩,无解. 故不存在实数a ,使A B =..................... 10分(2)由(1)可得221cos 22cos 121364ππαα⎛⎫⎛⎫+=+-=⨯-= ⎪ ⎪⎝⎭⎝⎭⎝⎭.................8分 ∵0,3a π⎛⎫∈ ⎪⎝⎭,∴2,33a πππ⎛⎫+∈ ⎪⎝⎭,∴sin 23πα⎛⎫+=⎪⎝⎭.................10分∴cos 2cos 2cos 2cos sin 2sin 123434348πππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=+-=+++=⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.................................... 12分19.解:由39a≤,得2a ≤,即:2p a ≤................ 1分∵函数()f x 无极值点,∴()0f x '≥恒成立,得()293490a ∆=--⨯≤,解得15a ≤≤,即:15q a ≤≤..................................3分 (1)∵“p q ∧”为假命题,“p q ∨”为真命题,∴p 与q 只有一个命题是真命题. 若p 为真命题,q 为假命题,则2115a a a a ≤⎧⇒<⎨<>⎩或;..................... 5分 若q 为真命题,p 为假命题,则22515a a a >⎧⇒<≤⎨≤≤⎩.............. 6分于是,实数a 的取值范围为{}|125a a a <<≤或..................... 7分(2)∵“p q ∧”为真命题,∴21215a a a ≤⎧⇒≤≤⎨≤≤⎩.............. 8分又2112022a m a m m ⎛⎫⎛⎫-+++> ⎪ ⎪⎝⎭⎝⎭, ∴()102a m a m ⎡⎤⎛⎫--+> ⎪⎢⎥⎝⎭⎣⎦, ∴a m <或12a m >+,...................10分 即:t a m <或12a m >+,从而1:2t m a m ⌝≤≤+, ∵r 是t ⌝的必要不充分条件,即t ⌝是r 的充分不必要条件,∴1122m m ≥⎧⎪⎨+≤⎪⎩,解得312m ≤≤,∵*m N ∈,∴1m =..................12分20.解:(1)∵()1cos 232sin 222226x f x x x π+⎛⎫=++=++ ⎪⎝⎭............. 2分 ∵,63x ππ⎡⎤∈-⎢⎥⎣⎦,∴52,666x πππ⎡⎤+∈-⎢⎥⎣⎦,∴1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭,............. 4分 ∴函数()y f x =的值域为3,32⎡⎤⎢⎥⎣⎦,....................... 5分(2)()sin 22123x g x f x ωππω⎛⎫⎛⎫=+=++ ⎪ ⎪⎝⎭⎝⎭,......................... 6分 当22,,,3633363x x πππωππωππω⎡⎤⎡⎤∈-+∈-++⎢⎥⎢⎥⎣⎦⎣⎦,......................8分 ∵()g x 在2,36ππ⎡⎤-⎢⎥⎣⎦上是增函数,0ω>. ∴2,2,2,336322k k k Z ωππωππππππ⎡⎤⎡⎤-++⊆-++∈⎢⎥⎢⎥⎣⎦⎣⎦...................10分即223322632k k ωππππωππππ⎧-+≥-+⎪⎪⎨⎪-≤+⎪⎩,化简得534112k k ωω⎧≤-⎪⎨⎪≤+⎩, ∵0ω>,∴15,1212k k Z -<<∈,∴0k =,解得1ω≤,因此ω的最大值为1............12分21.解:(1)由于1222a -==,于是不等式()0f x <即为()14127222x x ---<............. 2分所以()127412x x -=--,解得158x <...................4分 即原不等式的解集为15,8⎛⎫-∞ ⎪⎝⎭.........................6分 (2)由()()22414227lg 241lga x lg lg 0128x x a a x x a --<⇒-<-⇒+< ........ 7分 设()24lg lg 128af x x a =+,则()f x 为一次函数或常数函数,由[]0,1x ∈时, ()0f x <恒成立得:()()24241lg lg 010lg 03211281283200401280128lg 0128a f a a a a f a a a ⎧+<⎧⎪<⎧⎧<>⎪⎪⎪⇒⇒⇒⇒<<⎨⎨⎨⎨<<<⎪⎩⎩⎪⎪<<<⎩⎪⎩, 又0a >且1a ≠,∴()1,1284a ⎛⎫∈ ⎪ ⎪⎝⎭..........................12分22.解:(1)当()221111,x a f x x x x-'==-+=, 令()0f x '=得1x =,又()f x 的定义域为()0,+∞,由()0f x '<得01x <<,由()0f x '>得1x >,所以1x =时,()f x 有极小值为1.()f x 的单调递增区间为()1,+∞,单调递减区间为()0,1....................5分(2)()2211a ax f x x x x -'=-+=,且0a ≠,令()0f x '=,得到1x a=,若在区间(]0,e 上存在一点0x ,使得()00f x <成立,即()f x 在区间(]0,e 上的最小值小于0.当10x a=<,即0a <时,()0f x '<恒成立,即()f x 在区间(]0,e 上单调递减, 故()f x 在区间(]0,e 上的最小值为()11ln f e a e a ee=+=+,由10a e +<,得1a e -,即1,a e ⎛⎫∈-∞- ⎪⎝⎭.......................8分 当10x a=>,即0a >时, ①若1e a<,则()0f x '<对(]0,x e ∈成立,所以()f x 在区间(]0,e 上单调递减, 则()f x 在区间(]0,e 上的最小值为()11ln 0f e a x a ee=+=+>,显然,()f x 在区间(]0,e 上的最小值小于0不成立.②若10e a <<,即1a e>时,则有所以()f x 在区间(]0,e 上的最小值为11ln f a a a a ⎛⎫=+ ⎪⎝⎭,由()11ln 1ln 0f a a a a a a ⎛⎫=+=-<⎪⎝⎭,得1ln 0a -<,解得a e >,即(),a e ∈+∞, 综上,由①②可知:()1,,a e e ⎛⎫∈-∞-+∞ ⎪⎝⎭符合题意.....................12分。
2017年湖北省襄阳市中考数学真题及答案

2017年湖北省襄阳市中考数学真题及答案一、选择题(本大题共10个小题,每小题3分,共30分)1.﹣5的倒数是()A.B.﹣ C.5 D.﹣52.下列各数中,为无理数的是()A.B.C.D.3.如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为()A.65° B.60° C.55° D.50°4.下列运算正确的是()A.3a﹣a=2 B.(a2)3=a5C.a2•a3=a5D.a6÷a3=a25.下列调查中,调查方式选择合理的是()A.为了解襄阳市初中每天锻炼所用时间,选择全面调查B.为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查C.为了解神舟飞船设备零件的质量情况,选择抽样调查D.为了解一批节能灯的使用寿命,选择抽样调查6.如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是()A.B.C.D.7.下列图形中,既是中心对称图又是轴对称图形的是()A. B.C.D.8.将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为()A.y=2x2+1 B.y=2x2﹣3 C.y=2(x﹣8)2+1 D.y=2(x﹣8)2﹣39.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为()A.5 B.6 C.7 D.810.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为()A.3 B.4 C.5 D.6二、填空题(本大题共6个小题,每小题3分,共18分)11.某天襄阳某镇观赏桃花的游客近16000人,数据16000用科学记数法表示为.12.分式方程的解是.13.不等式组的解集为.14.同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是.15.在半径为1的⊙O中,弦AB、AC的长分别为1和,则∠BAC的度数为.16.如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C 恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为.三、解答题(本大题共9个小题,共72分)17.先化简,再求值:( +)÷,其中x=+2,y=﹣2.18.中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是部,中位数是部,扇形统计图中“1部”所在扇形的圆心角为度.(2)请将条形统计图补充完整;(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为.19.受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)求该企业从2014年到2016年利润的年平均增长率;(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?20.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;(2)若∠ADB=30°,BD=6,求AD的长.21.如图,直线y1=ax+b与双曲线y2=交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).(1)求直线和双曲线的解析式;(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.22.如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;(2)若DE=1,BC=2,求劣弧的长l.23.为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000).(1)请直接写出k1、k2和b的值;(2)设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.24.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)如图1,若CE=CF,求证:DE=DF;(2)如图2,在∠EDF绕点D旋转的过程中:①探究三条线段AB,CE,CF之间的数量关系,并说明理由;②若CE=4,CF=2,求DN的长.25.如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.2017年湖北省襄阳市中考数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分)1.﹣5的倒数是()A.B.﹣ C.5 D.﹣5【考点】17:倒数.【分析】根据乘积为1的两个数互为倒数,可得一个数的倒数.【解答】解:﹣5的倒数是﹣,故选:B.2.下列各数中,为无理数的是()A.B.C.D.【考点】26:无理数.【分析】根据无理数、有理数的定义即可判定选择项.【解答】解:,,是有理数,是无理数,故选:D.3.如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为()A.65° B.60° C.55° D.50°【考点】JA:平行线的性质.【分析】根据平行线的性质,得到∠ABD=130°,再根据BE平分∠ABD,即可得到∠1的度数.【解答】解:∵BD∥AC,∠A=50°,∴∠ABD=130°,又∵BE平分∠ABD,∴∠1=∠ABD=65°,故选:A.4.下列运算正确的是()A.3a﹣a=2 B.(a2)3=a5C.a2•a3=a5D.a6÷a3=a2【考点】48:同底数幂的除法;35:合并同类项;46:同底数幂的乘法;47:幂的乘方与积的乘方.【分析】分别利用幂的乘方运算法则、同底数幂的乘除法运算法则分别化简求出答案.【解答】解:A、3a﹣a=2a,故此选项错误;B、(a2)3=a6,故此选项错误;C、a2•a3=a5,正确;D、a6÷a3=a3,故此选项错误;故选:C.5.下列调查中,调查方式选择合理的是()A.为了解襄阳市初中每天锻炼所用时间,选择全面调查B.为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查C.为了解神舟飞船设备零件的质量情况,选择抽样调查D.为了解一批节能灯的使用寿命,选择抽样调查【考点】V2:全面调查与抽样调查.【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.【解答】解:A、为了解襄阳市初中每天锻炼所用时间,选择抽样调查,故A不符合题意;B、为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择抽样调查,故B不符合题意;C、为了解神舟飞船设备零件的质量情况,选普查,故C不符合题意;D、为了解一批节能灯的使用寿命,选择抽样调查,故D符合题意;故选:D.6.如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是()A.B.C.D.【考点】U2:简单组合体的三视图.【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:从上边看第一列是一个小正方形,第二列是两个小正方形,第三列是一个小正方形,故选:A.7.下列图形中,既是中心对称图又是轴对称图形的是()A. B.C.D.【考点】R5:中心对称图形;P3:轴对称图形.【分析】根据中心对称图形和轴对称图形对各选项分析判断即可得解.【解答】解:A、是轴对称图形,不是中心对称图形,故本选项错误;B、是中心对称图,不是轴对称图形,故本选项错误;C、既是中心对称图又是轴对称图形,故本选项正确;D、是轴对称图形,不是中心对称图形,故本选项错误.故选C.8.将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为()A.y=2x2+1 B.y=2x2﹣3 C.y=2(x﹣8)2+1 D.y=2(x﹣8)2﹣3【考点】H6:二次函数图象与几何变换.【分析】根据平移的规律即可得到平移后函数解析式.【解答】解:抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,得到的抛物线解析式为y=2(x﹣4+4)2﹣1,即y=2x2﹣1,再向上平移2个单位长度得到的抛物线解析式为y=2x2﹣1+2,即y=2x2+1;故选A.9.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为()A.5 B.6 C.7 D.8【考点】N2:作图—基本作图;KO:含30度角的直角三角形.【分析】连接CD,根据在△ABC中,∠ACB=90°,∠A=30°,BC=4可知AB=2BC=8,再由作法可知BC=CD=4,CE是线段BD的垂直平分线,故CD是斜边AB的中线,据此可得出BD的长,进而可得出结论.【解答】解:连接CD,∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,∴AB=2BC=8.∵作法可知BC=CD=4,CE是线段BD的垂直平分线,∴CD是斜边AB的中线,∴BD=AD=4,∴BF=DF=2,∴AF=AD+DF=4+2=6.故选B.10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为()A.3 B.4 C.5 D.6【考点】KR:勾股定理的证明.【分析】观察图形可知,小正方形的面积=大正方形的面积﹣4个直角三角形的面积,利用已知(a+b)2=21,大正方形的面积为13,可以得出直角三角形的面积,进而求出答案.【解答】解:∵如图所示:∵(a+b)2=21,∴a2+2ab+b2=21,∵大正方形的面积为13,2ab=21﹣13=8,∴小正方形的面积为13﹣8=5.故选:C.二、填空题(本大题共6个小题,每小题3分,共18分)11.某天襄阳某镇观赏桃花的游客近16000人,数据16000用科学记数法表示为 1.6×104.【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将16000用科学记数法表示为:1.6×104.故答案为:1.6×104.12.分式方程的解是x=9 .【考点】B3:解分式方程.【分析】观察可得最简公分母是x(x﹣3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:方程的两边同乘x(x﹣3),得3x﹣9=2x,解得x=9.检验:把x=9代入x(x﹣3)=54≠0.∴原方程的解为:x=9.故答案为:x=9.13.不等式组的解集为2<x≤3 .【考点】CB:解一元一次不等式组.【分析】分别求出求出各不等式的解集,再求出其公共解集即可.【解答】解:,解不等式①,得x>2.解不等式②,得x≤3,故不等式组的解集为2<x≤3.故答案为2<x≤3.14.同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是.【考点】X6:列表法与树状图法.【分析】根据题意,通过列树状图的方法可以写出所有可能性,从而可以得到两枚正面向上,一枚正面向下的概率.【解答】解:画树状图得得:由树状图可知所有可能情况有8种,其中两枚正面向上,一枚正面向下的情况数为3种,所以两枚正面向上,一枚正面向下的概率=.15.在半径为1的⊙O中,弦AB、AC的长分别为1和,则∠BAC的度数为15°或105°.【考点】M2:垂径定理;T7:解直角三角形.【分析】根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.【解答】解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.∵OE⊥AC,OD⊥AB,∴AE=AC=,AD=AB=,∴sin∠AOE==,sin∠AOD==,∴∠AOE=45°,∠AOD=30°,∴∠BAO=60°,∠CAO=90°﹣45°=45°,∴∠BAC=45°+60°=105°,或∠BAC′=60°﹣45°=15°.∴∠BAC=15°或105°.故答案是:15°或105°.16.如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C 恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为.【考点】PB:翻折变换(折叠问题);KQ:勾股定理.【分析】根据D,C,E,F四点共圆,可得∠CDE=∠CFE=∠B,再根据CE=FE,可得∠CFE=∠FCE,进而根据∠B=∠FCE,得出CF=BF,同理可得CF=AF,由此可得F是AB的中点,求得CF=AB=5,再判定△CDF∽△CFA,得到CF2=CD×CA,进而得出CD的长.【解答】解:由折叠可得,∠DCE=∠DFE=90°,∴D,C,E,F四点共圆,∴∠CDE=∠CFE=∠B,又∵CE=FE,∴∠CFE=∠FCE,∴∠B=∠FCE,∴CF=BF,同理可得,CF=AF,∴AF=BF,即F是AB的中点,∴Rt△ABC中,CF=AB=5,由D,C,E,F四点共圆,可得∠DFC=∠DEC,由∠CDE=∠B,可得∠DEC=∠A,∴∠DFC=∠A,又∵∠DCF=∠FCA,∴△CDF∽△CFA,∴CF2=CD×CA,即52=CD×8,∴CD=,故答案为:.三、解答题(本大题共9个小题,共72分)17.先化简,再求值:( +)÷,其中x=+2,y=﹣2.【考点】6D:分式的化简求值.【分析】先根据分式的混合运算顺序和法则化简原式,再将x、y的值代入求解可得.【解答】解:原式=[+]÷=•y(x+y)=,当x=+2,y=﹣2时,原式===.18.中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查所得数据的众数是 1 部,中位数是 2 部,扇形统计图中“1部”所在扇形的圆心角为126 度.(2)请将条形统计图补充完整;(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为.【考点】X6:列表法与树状图法;V2:全面调查与抽样调查;VB:扇形统计图;VC:条形统计图;W4:中位数;W5:众数.【分析】(1)先根据调查的总人数,求得1部对应的人数,进而得到本次调查所得数据的众数以及中位数,根据扇形圆心角的度数=部分占总体的百分比×360°,即可得到“1部”所在扇形的圆心角;(2)根据1部对应的人数为40﹣2﹣10﹣8﹣6=14,即可将条形统计图补充完整;(3)根据树状图所得的结果,判断他们选中同一名著的概率.【解答】解:(1)调查的总人数为:10÷25%=40,∴1部对应的人数为40﹣2﹣10﹣8﹣6=14,∴本次调查所得数据的众数是1部,∵2+14+10=26>21,2+14<20,∴中位数为2部,扇形统计图中“1部”所在扇形的圆心角为:×360°=126°;故答案为:1,2,126;(2)条形统计图如图所示,(3)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,画树状图可得:共有16种等可能的结果,其中选中同一名著的有4种,故P(两人选中同一名著)==.故答案为:.19.受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)求该企业从2014年到2016年利润的年平均增长率;(2)若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?【考点】AD:一元二次方程的应用.【分析】(1)设这两年该企业年利润平均增长率为x.根据题意2013年创造利润250(1+x)万元人民币,2014年创造利润250(1+x)2 万元人民币.根据题意得方程求解;(2)根据该企业从2014年到2016年利润的年平均增长率来解答.【解答】解:(1)设这两年该企业年利润平均增长率为x.根据题意得2(1+x)2=2.88,解得 x1 =0.2=20%,x2 =﹣2.2 (不合题意,舍去).答:这两年该企业年利润平均增长率为20%.(2)如果2017年仍保持相同的年平均增长率,那么2017年该企业年利润为:2.88(1+20%)=3.456,3.456>3.4答:该企业2017年的利润能超过3.4亿元.20.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;(2)若∠ADB=30°,BD=6,求AD的长.【考点】LA:菱形的判定与性质.【分析】(1)由平行线的性质和角平分线定义得出∠ABD=∠ADB,证出AB=AD,同理:AB=BC,得出AD=BC,证出四边形ABCD是平行四边形,即可得出结论;(2)由菱形的性质得出AC⊥BD,OD=OB=BD=3,再由三角函数即可得出AD的长.【解答】(1)证明:∵AE∥BF,∴∠ADB=∠CBD,又∵BD平分∠ABF,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AB=AD,同理:AB=BC,∴AD=BC,∴四边形ABCD是平行四边形,又∵AB=AD,∴四边形ABCD是菱形;(2)解:∵四边形ABCD是菱形,BD=6,∴AC⊥BD,OD=OB=BD=3,∵∠ADB=30°,∴cos∠ADB==,∴AD==2.21.如图,直线y1=ax+b与双曲线y2=交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).(1)求直线和双曲线的解析式;(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.【考点】G8:反比例函数与一次函数的交点问题.【分析】(1)由点B的坐标求出k=6,得出双曲线的解析式为y2=.求出A的坐标为(1,6),由点A和B 的坐标以及待定系数法即可求出直线的解析式为直线y1=2x+4;(2)求出点C的坐标为(﹣2,0),即可得出当y1<0时x的取值范围.【解答】解:(1)∵点B(﹣3,﹣2)在双曲线y2=上,∴,∴k=6,∴双曲线的解析式为y2=.把y=6代入y2=得:x=1,∴A的坐标为(1,6),∵直线y1=ax+b经过A、B两点,∴,解得:,∴直线的解析式为直线y1=2x+4;(2)由直线y1=0得,x=﹣2,∴点C的坐标为(﹣2,0),当y1<0时x的取值范围是x<﹣2.22.如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;(2)若DE=1,BC=2,求劣弧的长l.【考点】ME:切线的判定与性质;MN:弧长的计算.【分析】(1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;(2)连接OD,DC,根据角平分线的定义得到∠DAC=∠OAC,根据三角函数的定义得到∠ECD=30°,得到∠OCD=60°,得到∠BOC=∠COD=60°,OC=2,于是得到结论.【解答】(1)证明:连接OC,∵OA=OC,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∵∠AEC=90°,∴∠OCF=∠AEC=90°,∴EF是⊙O的切线;(2)连接OD,DC,∵∠DAC=DOC,∠OAC=BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l==π.23.为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000).(1)请直接写出k1、k2和b的值;(2)设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.【考点】HE:二次函数的应用.【分析】(1)将x=600、y=18000代入y1=k1x可得k1;将x=600、y=18000和x=1000、y=26000代入y1=k2x+b 可得k2、b.(2)分0≤x<600和600≤x≤1000两种情况,根据“绿化总费用=种草所需总费用+种花所需总费用”结合二次函数的性质可得答案;(3)根据种草部分的面积不少于700m2,栽花部分的面积不少于100m2求得x的范围,依据二次函数的性质可得.【解答】解:(1)将x=600、y=18000代入y1=k1x,得:18000=600k1,解得:k1=30;将x=600、y=18000和x=1000、y=26000代入,得:,解得:;(2)当0≤x<600时,W=30x+(﹣0.01x2﹣20x+30000)=﹣0.01x2+10x+30000,∵﹣0.01<0,W=﹣0.01(x﹣500)2+32500,∴当x=500时,W取得最大值为32500元;当600≤x≤1000时,W=20x+6000+(﹣0.01x2﹣20x+30000)=﹣0.01x2+36000,∵﹣0.01<0,∴当600≤x≤1000时,W随x的增大而减小,∴当x=600时,W取最大值为32400,∵32400<32500,∴W取最大值为32500元;(3)由题意得:1000﹣x≥100,解得:x≤900,由x≥700,则700≤x≤900,∵当700≤x≤900时,W随x的增大而减小,∴当x=900时,W取得最小值27900元.24.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)如图1,若CE=CF,求证:DE=DF;(2)如图2,在∠EDF绕点D旋转的过程中:①探究三条线段AB,CE,CF之间的数量关系,并说明理由;②若CE=4,CF=2,求DN的长.【考点】RB:几何变换综合题.【分析】(1)根据等腰直角三角形的性质得到∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,于是得到∠DCE=∠DCF=135°,根据全等三角形的性质即可的结论;(2)①证得△CDF∽△CED,根据相似三角形的性质得到,即CD2=CE•CF,根据等腰直角三角形的性质得到CD=AB,于是得到AB2=4CE•CF;②如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,求得CD=2,推出△CEN∽△GDN,根据相似三角形的性质得到=2,根据勾股定理即可得到结论.【解答】(1)证明:∵∠ACB=90°,AC=BC,AD=BD,∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,∴∠DCE=∠DCF=135°,在△DCE与△DCF中,,∴△DCE≌△DCF,∴DE=DF;(2)解:①∵∠DCF=∠DCE=135°,∴∠CDF+∠F=180°﹣135°=45°,∵∠CDF+∠CDE=45°,∴∠F=∠CDE,∴△CDF∽△CED,∴,即CD2=CE•CF,∵∠ACB=90°,AC=BC,AD=BD,∴CD=AB,∴AB2=4CE•CF;②如图,过D作DG⊥BC于G,则∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,由CD2=CE•CF得CD=2,∴在Rt△DCG中,CG=DG=CD•sin∠DCG=2×sin45°=2,∵∠ECN=∠DGN,∠ENC=∠DNG,∴△CEN∽△GDN,∴=2,∴GN=CG=,∴DN===.25.如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.【考点】HF:二次函数综合题.【分析】(1)由抛物线的解析式可求得C点坐标,由矩形的性质可求得B点坐标,由B、D的坐标,利用待定系数法可求得抛物线解析式;(2)可设P(t,4),则可表示出E点坐标,从而可表示出PB、PE的长,由条件可证得△PBE∽△OCD,利用相似三角形的性质可得到关于t的方程,可求得t的值;(3)当四边形PMQN为正方形时,则可证得△COQ∽△QAB,利用相似三角形的性质可求得CQ的长,在Rt △BCQ中可求得BQ、CQ,则可用t分别表示出PM和PN,可得到关于t的方程,可求得t的值.【解答】解:(1)在y=ax2+bx+4中,令x=0可得y=4,∴C(0,4),∵四边形OABC为矩形,且A(10,0),∴B(10,4),把B、D坐标代入抛物线解析式可得,解得,∴抛物线解析式为y=﹣x2+x+4;(2)由题意可设P(t,4),则E(t,﹣ t2+t+4),∴PB=10﹣t,PE=﹣t2+t+4﹣4=﹣t2+t,∵∠BPE=∠COD=90°,∠PBE=∠OCD,∴△PBE∽△OCD,∴=,即BP•OD=CO•PE,∴2(10﹣t)=4(﹣t2+t),解得t=3或t=10(不合题意,舍去),∴当t=3时,∠PBE=∠OCD;(3)当四边形PMQN为正方形时,则∠PMC=∠PNB=∠CQB=90°,PM=PN,∴∠CQO+∠AQB=90°,∵∠CQO+∠OCQ=90°,∴∠OCQ=∠AQB,∴Rt△COQ∽Rt△QAB,∴=,即OQ•AQ=CO•AB,设OQ=m,则AQ=10﹣m,∴m(10﹣m)=4×4,解得m=2或m=8,①当m=2时,CQ==2,BQ==4,∴sin∠BCQ==,sin∠CBQ==,∴PM=PC•sin∠PCQ=t,PN=PB•sin∠CBQ=(10﹣t),∴t=(10﹣t),解得t=,②当m=8时,同理可求得t=,∴当四边形PMQN为正方形时,t的值为或.。
2017-2018-7年级上-10月月考-实验中学 (2)

襄阳市实验中学2017-2018学年度七年级10月月考数学试卷姓名:班级:老师:分数:一、选择题:(每小题2分,共20分)1.―2的相反数是()A .2B.―2C.12D12-2.―5的绝对值是()A.5B.―5C. 15D.15-3.116,2008,2,0,24-3.25,+1,-中,正整数和负分数共有()A.3个B.4个C.5个D.6个4.有理数a、b在数轴上的位置如图所示,则a+b的值()A.大于0B.小于0C.小于a D.大于b5.若字母a表示任意一个数,则-a表示的数是()A.正数B.负数C.0D.以上情况都有可能6.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg、(25±0.2)kg、(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差()A.0.8kg B.0.6kg C.0.5kg D.0.4kg7.某地今年1月1日至4日每天的最高气温与最低气温如下表:A.1月1日B.1月2日C.1月3日D.1月4日8.下列说法错误的是A.有理数是指整数、分数、正有理数、零、负有理数这五类数B.一个有理数不是整数就是分数C.正有理数分为正整数和正分数10.绝对值不小于1,而大于4的所有的正整数的和是( )A.0B.7C.6D. 5二、填空题:(每小题2分,共16分)11.3122-+= 。
12.34⎛⎫-- ⎪⎝⎭____()0.75-+-⎡⎤⎣⎦ (填“>”“<”“=”)。
13.25x -= ,则x = _______。
14.若m,n 互为相反数,则1m n -+= ___________。
15.若a 是最小的正整数,b 是最大的负整数,c 是绝对值最小的有理数,则a +b+c= 。
16.已知1302a b ++-= ,则a +b=________ 17.数轴上A 点表示+7,B ,C 两点所表示的数是相反数,且B 点与A 点的距离为2,则C 点对应的数是____18.小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的个数有_____.三、计算题(每题4分)19.(1)()()389715-+++-+- (2)()0.9(4.4)(8.1)(5.6)-+++-++(3)()113+0.25+5844⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭(-3)+ (4)()112 2.511222-+-++-四、解答题(共48分)20.把下列各数分别填在相应集合中:(8分)11,0.20,3,325,789,0.618,20175--- 负数集合:{ …};分数集合:{ …};负分数集合:{ …};整数集合:{ …}。
湖北省襄阳八年级物理上学期10月月考试卷(含解析) 新人教版

2016-2017学年湖北省襄阳八年级(上)月考物理试卷(10月份)一、选择题1.小华在钢水管的一头敲一下,小珍在另一头却听到三下声音,这三下声音依次是由下述物质传播的()A.钢、空气、水 B.钢、水、空气 C.水、空气、钢 D.空气、水、钢2.在城市高架道路的某些路段两侧设有3~4米高的透明板墙,安装这些板墙是为了()A.保护车辆安全行驶B.阻止车辆排放的废气外泄C.体现高架道路设计的美观D.阻挡车辆产生的噪声,减小噪声污染3.医生用听诊器能够清楚的听到病人胸腔内的声音,是因为听诊器可以()A.提高声音的音调B.提高振幅C.增强音色 D.减少声音的分散,提高响度4.我们学过的许多成语包含了声现象,如:①隔墙有耳、②掩耳盗铃、③低声细语、④悦耳动听、⑤震耳欲聋.这些成语中描述同一声音特征的是()A.①② B.②⑤ C.③④ D.③⑤5.小轿车在笔直的高速公路上行驶,通过前一半路程的平均速度为30m/s,通过后一半路程的平均速度为20m/s,则小轿车通过全程的平均速度是()A.50m/s B.25m/s C.24m/s D.10m/s6.一列队伍长50米,行进速度为2.5米/秒,经过一座全长100米的桥,从队伍的第一个人踏上桥到队伍最后一个人离开桥,总共需用()A.20s B.40s C.50s D.60s7.甲乙两物体做匀速直线运动,如果甲乙速度之比为4:3,通过的路程之比为5:2,则所用时间之比为()A.10:3 B.3:10 C.15:8 D.8:158.下列数据中,最符合实际情况的是()A.人的正常体温为39℃B.初中生掷实心球的距离约为30mC.小红上学时步行的速度约是1.1m/sD.正常成年人得鞋子的长度为50cm9.下列物体的运动可近似看作匀速直线运动的是()A.正在进站的火车B.离开脚后在草地上滚动的足球C.站在商城自动扶梯上顾客的运动D.绕地球匀速转动的“北斗”卫星10.诗句“不疑行船动,唯看远树来”中“远树来”所选择的参照物是()A.山峰 B.远树 C.河岸 D.行船11.甲物体的速度比乙物体的速度大,下列说法错误的是()A.甲比乙通过的路程长B.甲比乙运动的快C.通过相同的路程,甲比乙用的时间短D.相同的时间内,甲比已通过的路程长12.一个做直线运动的物体,如果它在每1min内通过的路程都相等,那么这个物体所做的运动()A.一定是匀速直线运动B.一定是变速直线运动C.可能是匀速直线运动,可能是变速直线运动D.既不是匀速直线运动,也不是变速直线运动13.观察图中的烟和小旗,关于甲(左车)乙(右车)两车的相对于房子的运动情况,下列说法中正确的是()A.甲、乙两车一定向左运动B.甲、乙两车一定向右运动C.甲车可能静止,乙车向左运动D.甲车可能运动,乙车向右运动14.短跑运动员在某次百米赛跑中共用时10秒;测得第5秒末的速度为9.0m/s,第10秒末到达终点时的速度为10.2m/s,则下列说法正确的是()A.在前5秒内运动员的平均速度为4.5 m/sB.在后5秒内运动员的平均速度为9.6m/sC.在本次百米赛跑中运动员的平均速度为10.0 m/sD.在本次百米赛跑中运动员的平均速度为9.1 m/s15.要想改变锣的音调,可采用的方法是()A.改变敲锣时用力的大小 B.改变敲锣的快慢C.换用其他大小不同的锣来敲 D.换用其他的锤来敲16.如果自行车轮胎内的气过多,轮胎在阳光照射下,轮胎温度升高或在重压时会破裂并发出很大的响声,这是由于()A.引起空气急剧振动而发出的声音B.轮胎这种材料破裂时发出的声音C.轮胎内空气受重压而发出的声音D.轮胎内空气在温度升高时发出的声音17.如图记录了甲、乙两辆汽车在平直公路上行驶时,在某段时间内的运动过程.关于甲、乙两车的运动情况,说法错误的是()A.前10s内甲车运动的路程大于乙车运动的路程B.乙车到达600m处所用时间大于甲车达此处所用时间C.乙车在做匀速直线运动D.甲、乙两车在40s内的平均速度相同18.一只小鸟从枇杷树上飞到地面,啄食掉落在地上的熟枇杷,吃了一会儿,路边传来吆喝声,小鸟立即飞回树上它出发时的位置,如图所示,能够大致描述小鸟运动情况的是()A. B.C.D.19.冬天乌苏里江的气温达到﹣50℃时,河面结冰,但冰面下水却在流动,冰面下冰与水接触的温度为()A.﹣50℃B.低于0℃C.高于0℃D.等于0℃20.雅安地震时,解放军及时赶到灾区进行救援.被埋者也要积极采取措施配合,方法之一是不断敲击周围坚硬物体,其目的是()A.将周围物体砸开B.利用声传递能量C.利用声传递信息D.消除寂寞二、非选择题21.我国古书《套买曜》上记载有:“人在舟中闭牖(门窗)而坐,舟行而人不觉”,其中“舟行”是以为参照物,“人不觉”是以为参照物.这是的生动描述.22.如图所示,所测木块的长度是cm23.小明利用最小分度值为1mm的刻度尺测量一个物体的长度,三次测量的数据分别为2.35cm、2.36cm、2.36cm,则测量结果应记为.24.海洋动物质量越大,其叫声越是有力而低沉,即响度较(大/小),音调较(高/低).甲、乙两曲线为科考船声纳系统收录的500kg的海豚和50t的蓝鲸叫声的波形图,其中,(甲/乙)是蓝鲸发出的.25.吹奏笛子时,笛子发出的声音是由引起的;锣发声的时候,用手按住锣面,锣声就消失了,这是因为.26.表演二胡时不断用手指控制琴弦长度,这样做的目的是为了改变声音的.击鼓时,击鼓的力量越大,鼓皮的越大,声音就越响亮.27.“掩耳盗铃”是大家非常熟悉的故事,从物理学角度分析盗贼所犯的错误是:既没有阻止声音的,又没有阻止声音的,只是阻止声音进入自己的耳朵.28.进行百米赛跑时,若终点计时员在听到枪声后才开始计时,这样做会使运动员的成绩记(填“少“或”多“),如果计时员的秒表上此时记录的是11s,则他的实际成绩应该是s.(声音在空气中的速度取340m/s,结果保留一位小数)29.甲乙两车同时由东向西行驶,甲、乙两车运动的s﹣t图象分别如图(a)(b)所示.以甲为参照物,乙是向行驶(选填“东”或“西”);甲、乙各运动8米,所用时间相差秒.30.课外活动中,小明和同学们一起,利用太阳能驱动玩具车并记录相关数据.实验后,根据实验数据绘制图象如图所示.由此可知:甲车全程的平均速度是m/s;前20s内,乙车比甲车多运动了m.31.在如图所示的十字路口处,有一辆长10m、宽2.2m的客车,客车正以10m/s速度正常匀速行驶在马路中间,当它与班马线的中点B相距60m时,马路边上的小王同学正好在斑马线中间A点出发沿AB穿过马路,A、B间的距离为8m.问:(1)若车刚穿过时人再穿过,小王同学运动的速度不超过多少时,能够安全过马路?(2)若人刚穿过时车再过线,小王同学运动的速度至少为多少时,能够安全过马路?32.甲、乙两支温度计,玻璃泡里装等量的水银,甲温度计的玻璃管的内径比乙粗,若两支温度计的分度值相同,则的刻度更密一些.用它们测同一液体的温度,则测得更准确些.33.没有甩过的体温计的读数是37.7℃,用两支这样的体温计给两个病人测体温.如果病人的体温分别是37.5℃和38.4℃,则两支体温计的读数将分别是℃和℃.三、实验题34.如图所示,在“测量平均速度”的实验中,提供的实验器材有:木板(长120.0cm底端有金属挡板)、小车(长15.0cm)、秒表、木块.(1)该实验的原理是(2)实验时应保持斜面的倾角较小,这是为了减小测量(选填“路程”或“时间”)时造成的误差.(3)斜面倾角不变时,小车由静止释放,小车通过的路程较长,其平均速度越(选填“大”或“小”);小车由静止释放,通过相同路程,斜面的倾角越大,小车运动的平均速度越(选填“大”或“小”).(4)一次实验中,小华测得小车从静止开始运动两个车长的距离所用时间为1.2s则小车的平均速度为m/s.35.如图所示.两支温度计的分度值分别是:甲图℃.乙图℃;两支温度计的示数分别是:甲图℃.乙图℃.36.如图所示,用三支相同温度计测量水温,(1)造成读数偏高的温度计是,造成读数偏高的原因是;(2)造成读数偏低的温度计是,造成读数偏低的原因是.37.如图所示是探究声现象时常用的装置(1)图甲中所示的实验现象说明;(2)图甲中乒乓球在实验中的作用是;(3)图甲本实验物理研究方法是;(4)如图乙所示,把正在发声的闹钟放在玻璃罩内,闹钟和罩的底座之间垫上软的泡沫塑料,逐渐抽出罩内的空气,闹钟的声音会逐渐变小,.38.子弹在离人17m处以680m/s的速度离开枪口,若声音在空气中的速度为340m/s,当人听到枪声时,子弹己前进了多少?39.某班同学在用皮尺和秒表测平均速度时,四位计时员记录了王军同学跑步通过10m、20m、30m、40m处的时刻,并记录在表中.根据上面数据,计算出王军同学在各段的平均速度:(1)从起点到10m处的平均速度为多少?(2)从20m处到40m处的平均速度为多少?40.(列车运行时刻表对于合理安排旅行非常重要,学生应该学会使用.下表是由青岛开往北京的T26次列车的运行时刻表.通过分析此运行时刻表,请你计算:(1)T26次列车从济南到北京的运行距离为多少?(2)T26次列车从济南到北京的运行时间为多少?(3)该次列车从济南到北京的平均速度大约是多少?41.一辆汽车以20m/s的速度驶向一座山崖,在某一时刻鸣笛,4秒后听到回声,则鸣笛处离山崖的距离是多远?2016-2017学年湖北省襄阳二十中八年级(上)月考物理试卷(10月份)参考答案与试题解析一、选择题1.小华在钢水管的一头敲一下,小珍在另一头却听到三下声音,这三下声音依次是由下述物质传播的()A.钢、空气、水 B.钢、水、空气 C.水、空气、钢 D.空气、水、钢【考点】声音在不同介质中的传播速度.【分析】解决此类问题的关键是知道声音在不同的介质中的传播速度不同,在固体中传播速度最快,在液体中次之,最慢的是在气体中传播.【解答】解:在一根较长的装满水的钢管一端敲击一下,在钢管的另一端可以听到3次声音,第一次是在通过钢管传来的,第二次是通过水传来的,第三次是通过空气传来的;故选B.2.在城市高架道路的某些路段两侧设有3~4米高的透明板墙,安装这些板墙是为了()A.保护车辆安全行驶B.阻止车辆排放的废气外泄C.体现高架道路设计的美观D.阻挡车辆产生的噪声,减小噪声污染【考点】防治噪声的途径.【分析】防治噪声的途径有三条:防止噪声产生,阻断噪声的传播,防止噪声进入人耳.【解答】解:道路两侧设有3米至4米高的透明板墙是用来反射道路上的过往车辆所发出的噪声,其作用相当于一个隔音板,在噪声的传播过程中减弱噪声.道路两侧设置的是透明板墙,就是通过阻断噪声的传播,以减弱噪声对道路两旁住宅和办公楼的噪声污染,它并不能保护车辆安全行驶,也不能阻止车辆排放的废气外泄和体现高架道路设计的美观.故选D.3.医生用听诊器能够清楚的听到病人胸腔内的声音,是因为听诊器可以()A.提高声音的音调B.提高振幅C.增强音色 D.减少声音的分散,提高响度【考点】响度.【分析】响度和物体振幅有关,振幅越大,响度越大.响度还和距离发声体的远近有关,距离越远,响度越小.【解答】解:医生如果不用听诊器,无法清楚地听到病人胸腔内的声音,是因为声音在空气中传播时分散了,响度变小了.听诊器可以减少声音的分散,提高响度.故选D.4.我们学过的许多成语包含了声现象,如:①隔墙有耳、②掩耳盗铃、③低声细语、④悦耳动听、⑤震耳欲聋.这些成语中描述同一声音特征的是()A.①② B.②⑤ C.③④ D.③⑤【考点】音调、响度与音色的区分.【分析】对每个成语从声学角度分别分析,明确各自包含的声学规律,然后确定相同的一组.【解答】解:①隔墙有耳说明固体可以传播声音;②掩耳盗铃指在人耳处减弱噪声;③低声细语指声音的响度小;④悦耳动听指声音的音色好;⑤震耳欲聋指声音的响度大.故选D.5.小轿车在笔直的高速公路上行驶,通过前一半路程的平均速度为30m/s,通过后一半路程的平均速度为20m/s,则小轿车通过全程的平均速度是()A.50m/s B.25m/s C.24m/s D.10m/s【考点】变速运动与平均速度;速度的计算.【分析】设总路程为s,算出前一半路程用的时间t1,后一半路程用的时间t2,则总时间为t=t1+t2,用公式v=计算出平均速度.【解答】解:设总路程为s,则前、后一半路程均为,前一半路程用的时间:t1==,后一半路程所用的时间:t2==,物体全程时间:t=t1+t2,全程平均速度:v======24m/s.故选C.6.一列队伍长50米,行进速度为2.5米/秒,经过一座全长100米的桥,从队伍的第一个人踏上桥到队伍最后一个人离开桥,总共需用()A.20s B.40s C.50s D.60s【考点】速度公式及其应用.【分析】当队伍全部通过大桥时,队伍经过的距离为队伍的长度与大桥长度之和,行进速度已知,根据速度公式的导出公式求所需的时间.【解答】解:从队伍的第一个人踏上桥到队伍最后一个人离开桥,队伍一共行走的路程为s=s队+s桥=50m+100m=150m,∵v=,∴当队伍全部穿过大桥所需要的时间为t===60s.故选D.7.甲乙两物体做匀速直线运动,如果甲乙速度之比为4:3,通过的路程之比为5:2,则所用时间之比为()A.10:3 B.3:10 C.15:8 D.8:15【考点】速度公式及其应用.【分析】已知速度的比和路程的比,求时间之比;利用速度公式变形t=计算即可.【解答】解:由v=得t=;==×=×=15:8.故选C.8.下列数据中,最符合实际情况的是()A.人的正常体温为39℃B.初中生掷实心球的距离约为30mC.小红上学时步行的速度约是1.1m/sD.正常成年人得鞋子的长度为50cm【考点】温度;长度的估测;速度与物体运动.【分析】此题考查对生活中常见物理量的估测,结合对生活的了解和对物理单位的认识,找出符合实际的选项.【解答】解:A、正常情况下,人的体温在37℃左右,变化幅度很小.故A不符合实际;B、初中生掷实心球的距离一般在10m左右.故B不符合实际;C、中学生正常步行的速度在4km/h=4×m/s≈1.1m/s左右.故C符合实际;D、中学生的步幅在50cm左右,成年人鞋子的长度大约是此数值的一半,在25cm左右.故D不符合实际.故选C.9.下列物体的运动可近似看作匀速直线运动的是()A.正在进站的火车B.离开脚后在草地上滚动的足球C.站在商城自动扶梯上顾客的运动D.绕地球匀速转动的“北斗”卫星【考点】匀速直线运动.【分析】匀速直线运动的速度和方向都保持不变,处于平衡状态,受平衡力作用.【解答】解:A、正在进站的火车速度越来越慢,不是匀速直线运动,故A错误;B、离开脚后在草地上滚动的足球速度越来越慢,不是匀速直线运动,故B错误;C、站在商城自动扶梯上顾客的运动速度和方向保持不变,是匀速直线运动,故C正确;D、绕地球匀速转动的“北斗”卫星方向在不断改变,不是匀速直线运动,故D错误.故选C.10.诗句“不疑行船动,唯看远树来”中“远树来”所选择的参照物是()A.山峰 B.远树 C.河岸 D.行船【考点】参照物及其选择.【分析】由题意可知,本题研究的是树的运动状态,“远树来”说明树处于相对运动状态,那么它与所选参照物之间的位置应该发生了变化.【解答】解:以行船为参照物,行船处于相对静止状态,远处的树和行船之间的位置不断发生变化,树是运动的,所以会感到“远树来”.故选D.11.甲物体的速度比乙物体的速度大,下列说法错误的是()A.甲比乙通过的路程长B.甲比乙运动的快C.通过相同的路程,甲比乙用的时间短D.相同的时间内,甲比已通过的路程长【考点】速度公式及其应用.【分析】速度是来表示物体运动快慢的物理量,速度与路程和时间有关,可利用控制变量法分析速度与任何一个量的关系.【解答】解:A、速度与通过的路程和所用的时间有关,只有通过的路程,不确定时间的长短,故A错误;B、根据速度的含义可知,速度越大物体运动越快,故B正确;C、通过相同的路程,速度大的用的时间短,所以甲比乙用的时间短;故C正确;D、相同的时间内,速度大的通过的路程长,所以甲比乙通过的路程长;过D正确.故选A.12.一个做直线运动的物体,如果它在每1min内通过的路程都相等,那么这个物体所做的运动()A.一定是匀速直线运动B.一定是变速直线运动C.可能是匀速直线运动,可能是变速直线运动D.既不是匀速直线运动,也不是变速直线运动【考点】匀速直线运动;变速运动与平均速度.【分析】物体沿着直线快慢不变的运动,叫做匀速直线运动.判断一个物体的运动是匀速直线运动还是变速直线运动,关键就在于分析物体的速度是否变化.【解答】解:题目中给出物体每1min内通过的路程是相等的,我们可以看出相等的时间内路程相等,很多同学直接通过速度的计算公式v=认为速度也是相等的;这种判断方法是不对的,计算出的速度是1min内的平均速度,可以先快后慢、先慢后快等很多种情况;因此1min内通过相等的路程,可以是匀速的,也可以是变速的;故选C.13.观察图中的烟和小旗,关于甲(左车)乙(右车)两车的相对于房子的运动情况,下列说法中正确的是()A.甲、乙两车一定向左运动B.甲、乙两车一定向右运动C.甲车可能静止,乙车向左运动D.甲车可能运动,乙车向右运动【考点】运动和静止的相对性.【分析】研究物体的运动情况时,首先要选取一个物体作为标准,这个被选作标准的物体叫做参照物.研究对象的运动情况是怎样的,就看它与参照物的相对位置是否变化.由此来突破此题.【解答】解:由图中的信息可以判断出:因为房子的烟向左飘,所以风是向左吹;所以甲车运动状态有三种可能 1、向右运动; 2、静止;3、向左运动,但运动速度小于风速;因为乙车旗向右飘,所以乙车只能向左运动,且速度要大于风的速度.综上分析可知,只有C正确,ABD错误;故选C.14.短跑运动员在某次百米赛跑中共用时10秒;测得第5秒末的速度为9.0m/s,第10秒末到达终点时的速度为10.2m/s,则下列说法正确的是()A.在前5秒内运动员的平均速度为4.5 m/sB.在后5秒内运动员的平均速度为9.6m/sC.在本次百米赛跑中运动员的平均速度为10.0 m/sD.在本次百米赛跑中运动员的平均速度为9.1 m/s【考点】变速运动与平均速度.【分析】正确理解平均速度的定义,平均速度等于总路程除以总时间.百米竞赛的位移就是100m,10s到达终点,时间就为10s.【解答】解:A、因为运动员不是匀速运动,故测得第5秒末的速度为9.0m/s,不能确定在前5秒内运动员的平均速度是多少,故A错误;B、在后5秒内运动员的路程不知,所以不能求得在后5秒内运动员的平均速度,故B错误;CD、在本次百米赛跑中运动员的平均速度v===10m/s,故C正确;D错误.故选C.15.要想改变锣的音调,可采用的方法是()A.改变敲锣时用力的大小 B.改变敲锣的快慢C.换用其他大小不同的锣来敲 D.换用其他的锤来敲【考点】频率及音调的关系.【分析】音调指声音的高低,由发声体振动的频率决定.据此判断.【解答】解:A、改变敲击锣面力的大小,可改变锣面的振幅,能改变响度,但不能改变音调,故A错误;B、改变敲锣的快慢,声音发出的时间间隔会改变,但不会改变锣振动的频率,故B错误;C、不同大小的锣面其固有的频率不同,换用其他的锣面来敲可以改变振动频率,从而改变音调,故C正确;D、换用敲击锣面的锤子敲锣,对锣面振动的频率不会有影响,也不能改变音调,故D错误.故选C.16.如果自行车轮胎内的气过多,轮胎在阳光照射下,轮胎温度升高或在重压时会破裂并发出很大的响声,这是由于()A.引起空气急剧振动而发出的声音B.轮胎这种材料破裂时发出的声音C.轮胎内空气受重压而发出的声音D.轮胎内空气在温度升高时发出的声音【考点】声音的产生.【分析】声音是由物体的振动产生的.【解答】解:由于轮胎破裂时引起空气急剧振动而发出的声音;破裂、重压和温度升高都不会发出声音,故BCD都是错误的;故选A.17.如图记录了甲、乙两辆汽车在平直公路上行驶时,在某段时间内的运动过程.关于甲、乙两车的运动情况,说法错误的是()A.前10s内甲车运动的路程大于乙车运动的路程B.乙车到达600m处所用时间大于甲车达此处所用时间C.乙车在做匀速直线运动D.甲、乙两车在40s内的平均速度相同【考点】速度公式及其应用.【分析】(1)分析前10s内甲车和乙车运动的路程即可得出结论;(2)分析小车到达600m处所用的时间即可得出结论;(3)乙车在相等时间内通过路程的关系得出乙车的运动状态;(4)根据甲、乙两车在40s内通过的路程利用速度公式v=比较平均速度.【解答】解:A、由图知,前10s内甲车和乙车运动的路程分别为300m、200m,则甲车运动的路程大于乙车运动的路程,故A正确;B、由图知,甲车到达600m处所用的时间为20s,乙车到达600m处所用的时间大于20s,所以乙车到达600m处所用时间大于甲车达此处所用时间,故B正确;C、由图知,在相同的时间内乙小车通过的路程在变大,说明小车在做变速运动;故C错误;从20s时到40s所用的时间为:t=40s﹣20s=20s从20s时到40s通过的路程为:s=1200m﹣450m=750mD、甲、乙两车在40s内通过的路程s=1200m,则根据v=可知甲、乙两车的平均速度相同,故D正确.故选C.18.一只小鸟从枇杷树上飞到地面,啄食掉落在地上的熟枇杷,吃了一会儿,路边传来吆喝声,小鸟立即飞回树上它出发时的位置,如图所示,能够大致描述小鸟运动情况的是()A. B.C.D.【考点】速度与物体运动.【分析】位移﹣时间图象描述物体的位移随时间变化的规律;由题意可知小鸟相对树位移的变化.【解答】解:距离﹣时间图象描述物体的距离随时间变化的规律;由题意可知小鸟离地面的距离先减小,然后静止在地面;然后再远离地面,离地面的距离在增大,故只有A正确;故选:A.19.冬天乌苏里江的气温达到﹣50℃时,河面结冰,但冰面下水却在流动,冰面下冰与水接触的温度为()A.﹣50℃B.低于0℃C.高于0℃D.等于0℃【考点】温度.【分析】冰水混合物的温度是0℃.水与冰的交界处,水和冰的温度是相同的,等于冰水混合物的温度.【解答】解:冰下和水的交界处,有冰有水,其温度等于冰水混合物的温度0℃.故选D.20.雅安地震时,解放军及时赶到灾区进行救援.被埋者也要积极采取措施配合,方法之一是不断敲击周围坚硬物体,其目的是()A.将周围物体砸开B.利用声传递能量C.利用声传递信息D.消除寂寞【考点】声与信息.【分析】声音既能够传递信息,又能够传递能量.【解答】解:在地震中遇难,被埋在地震废墟下时,不要大声呼喊,要保存体力,不断敲击周围坚硬物体,发出声音,通过声音传递信息,被搜救人员发现.故选C.二、非选择题21.我国古书《套买曜》上记载有:“人在舟中闭牖(门窗)而坐,舟行而人不觉”,其中“舟行”是以河岸为参照物,“人不觉”是以人为参照物.这是运动和静止的相对性的生动描述.【考点】运动和静止的相对性.【分析】物体的运动和静止,都是被研究的物体相对参照物来讲的,这是物体运动和静止的相对性.舟运动,一定选择一个和舟之间发生位置改变的物体为参照物.人不觉说明人是静止的,一定选择一个和人之间没有发生位置改变的物体为参照物.【解答】解:舟行,舟和河岸之间发生了位置的改变,以河岸为参照物,舟是运动的.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年度二十中九年级十月考试数学试题
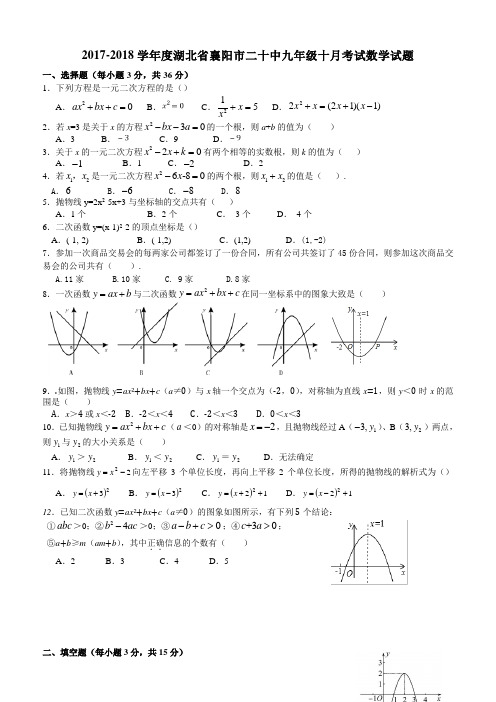
一、选择题(每小题3分,共36分)
1.下列方程是一元二次方程的是( )
A .20ax bx c ++=
B .
C .215x x +=
D .
)1)(12(22-+=+x x x x 2.若x=3是关于x 的方程230x bx a --=的一个根,则a+b 的值为( )
A .3
B .12
C .9
D .6
3.关于x 的一元二次方程220x x k -+=有两个相等的实数根,则k 的值为( )
A .1-
B .1
C .2-
D .2
4.若12x x ,是一元二次方程26-80x x -=的两个根,则12x x +的值是( ).
A .6
B .6-
C .8-
D .8
5.抛物线y=2x2-5x+3与坐标轴的交点共有( )
A .1个
B .2个
C . 3个
D . 4个
6.二次函数y=(x-1)2-2的顶点坐标是( )
A .(-1,-2)
B .(-1,2)
C .(1,2)
D .(1,-2)
7.参加一次商品交易会的每两家公司都签订了一份合同,所有公司共签订了45份合同,则参加这次商品交易会的公司共有( ).
A.11家
B.10家
C. 9家
D.8家
8.一次函数y ax b =+与二次函数
2y ax bx c =++在同一坐标系中的图象大致是( )
9..如图,抛物线y=ax2+bx+c (a ≠0)与x 轴一个交点为(-2,0),对称
轴为直线x=1,则y <0时x 的范围是( )
A .x >4或x <-2
B .-2<x <4
C .-2<x <3
D .0<x <3
10.已知抛物线
2y ax bx c =++(a <0)的对称轴是2x =-,且抛物线 经过A (
13,y -)、B (23,y )两点,则1y 与2y 的大小关系是( ) A .1y >2y B .1y <2y C .1y =2y D .无法确定
11.将抛物线22-=x y 向左平移3个单位长度,再向上平移2个单位长度,所得的抛物线
的解析式为() A .()23+=x y B .()23-=x y C .()122++=x y D .()122+-=x y
12.已知二次函数y=ax2+bx+c (a ≠0)的图象如图所示,有下列5个结论:
①abc >0;②24b ac ->0;③0>+-c b a ;④+30c a >;
⑤a+b ≥m (am+b ),其中正确信息的个数有( )
A .2
B .3
C .4
D .5
二、填空题(每小题3分,共15分)
13.如果二次三项式2216x bx -+是一个完全平方式,那么b 的值是
14.若二次函数
22(1)1y m x x m =--+-的图象经过原点,则m 的值为 ________. 15.已知抛物线
22(3)12y x k x =-++的顶点在y 轴上,则k = 16.已知二次函数
2(0)y ax bx c a =++≠的图象如图所示,若方程 20ax bx c k ++-=有两个不相等的实数根,则k 的取值范围是
17.要为一副长29cm ,宽22cm 的照片配一个镜框,要求镜框的四条边宽
度相等,且镜框所占面积为照片面积的四分之一。
设镜框边的宽度为x cm ,
所列方程为
三、解答题:(共69分)
18.解方程:(每小题3分,共12分)
(1)20x x +=
(2)23650x x +-= (用配方法)
(3)2310x x +-=(用公式法) (4)22(21)(3)x x -=-
19.(6分)如图,小明同学投掷铅球的出手点C 距地面1米,出手后的运动路线是抛物线,出手后4秒到达最大高度3米,求小明这次投掷从出手到落地的时间?
20.(6分)一幅长20cm 、宽12cm 的图案,如图有一横两竖的彩条,横、竖彩条的宽度比
为3:2.若图案中三条彩条所占面积是图案面积的2
5,求横、竖彩条的宽
度.
21.(7分)如图,直线11y x =-和抛物线22y x bx c =++都经过
点A (1,0),B (3,2)
(1)求抛物线的解析式;
(2)直接回答当13x <<时,2y 的取值范围是什么?
(3)直接回答,当x 为何值时,不等式2x bx c ++>1x -?
22.(7分)已知关于x 的一元二次方程x2+(k-5)x+1-k=0,其中k 为常数.
(1)求证:无论k 为何值,方程总有两个不相等实数根;
(2)已知函数y=x 2+(k-5)x+1-k 的图象与x 轴有两个交点,且这两个交点都交在x 轴的正半轴,
求k 的取值范围;
23.(8分)如图,抛物线
254y x x =-+-与x 轴交于点A 和点B ,与y 轴交于点C 。
(1)在抛物线的对称轴上找一点D ,使DA+DC 最短,求出D 点坐标;
(2)P 是y 轴正半轴上一点,且△PAB 是以AB 为腰的等腰三角形,试
求P 点坐标。
24.(11分)某商品的进价为每件40元,售价为每件50元时,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x 元(x 为正整数),每个月的销售利润为y 元
(1)求y 与x 的函数关系式并直接写出自变量x 的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?
25.(12分)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A 和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC 交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线n与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,直接写出满足条件。
