西安交大传热学上机实验报告
传热综合实验实验报告

传热综合实验一、实验目的:1、 掌握传热系数K 、传热膜系数α1的测定方法,加深对其概念和影响因素的理解;2、 掌握用最小二乘法确定关联式me AR Nu =中常熟A 、指数m 的值;3、 通过对普通套管换热器和强化套管换热器的比较,了解工程上强化传热的措施;4、 掌握孔板流量计的原理;5、 掌握测温热电偶的使用方法。
二、实验原理(一)无量纲准则数对流传热准数关联式是无量纲准则数之间的方程,主要是有关Nu 、Re 、Pr 等数据组的关系。
雷诺准数μρdu =Re努赛尔特准数λαdNu =普兰特准数λμP C =Pr式中:d ——换热器内管内劲,m ;α——空气传热膜系数,W ·m -2·℃; ρ——空气密度,kg ·m -3;λ——空气的传热系数,W ·m -1·℃;p C ——空气定压比热,J ·kg -1·℃;μ——空气的动力粘度,Pa ·S 。
实验中用改变空气的流量来改变准数Re 之值。
根据定性温度计算对应的Pr 准数值。
同时由牛顿冷却定律,求出不同流速下的传热膜系数α值,进而算得Nu 准数值。
(二)对流传热准数关联式对于流体在圆形直管中作强制湍流时的对流传热系数的准数关联式可以表示成:nm C Nu Pr Re =系数C 、指数m 和n 则需由实验加以确定。
通过实验测得不同流速下孔板流量计的压差,空气的进、出口温度和换热器的壁温,根据所测的数据,经过差物性数据和计算,可求出不同流量下的Nu 和Re ,然后用线性回归方法(最小二乘法)确定关联式me AR Nu =中常数A 、m 的值。
(三)线性回归用图解法对多变量方程进行关联时,要对不同变量Re 和vPr 分别回归。
为了便于掌握这类方程的关联方法,可去n=0.4。
这样就简化成单变量方程。
两边取对数,得到直线方程Re lg lg Prlg4.0m C Nu+= 在双对数坐标系中作图,找出直线斜率,即为方程的指数m 。
西安交通大学传热学大作业

《传热学》上机大作业二维导热物体温度场的数值模拟学校:西安交通大学姓名:张晓璐学号:10031133班级:能动A06一.问题(4-23)有一个用砖砌成的长方形截面的冷空气通道,形状和截面尺寸如下图所示,假设在垂直纸面方向冷空气和砖墙的温度变化很小,差别可以近似的予以忽略。
在下列两种情况下计算:砖墙横截面上的温度分布;垂直于纸面方向上的每米长度上通过墙砖上的导热量。
第一种情况:内外壁分别维持在10C ︒和30C ︒第二种情况:内外壁与流体发生对流传热,且有C t f ︒=101,)/(2021k m W h ⋅=,C t f ︒=302,)/(422k m W h ⋅=,K m W ⋅=/53.0λ二.问题分析 1.控制方程02222=∂∂+∂∂ytx t 2.边界条件所研究物体关于横轴和纵轴对称,所以只研究四分之一即可,如下图:对上图所示各边界:边界1:由对称性可知:此边界绝热,0=w q 。
边界2:情况一:第一类边界条件C t w ︒=10情况二:第三类边界条件)()(11f w w w t t h ntq -=∂∂-=λ 边界3:情况一:第一类边界条件C t w ︒=30情况二:第三类边界条件)()(22f w w w t t h ntq -=∂∂-=λ 三:区域离散化及公式推导如下图所示,用一系列和坐标抽平行的相互间隔cm 10的网格线将所示区域离散化,每个交点可以看做节点,该节点的温度近似看做节点所在区域的平均温度。
利用热平衡法列出各个节点温度的代数方程。
第一种情况: 内部角点:11~8,15~611~2,5~2)(411,1,,1,1,====++++=+-+-n m n m t t t t t n m n m n m n m n m 平直边界1:11~8),2(415~2),2(411,161,16,15,161,11,12,1,=++==++=+-+-n t t t t m t t t t n n n nm m m m平直边界2:7,16~7,107~1,6,10,,======n m t n m t n m n m平直边界3:12,16~2,30;12~1,1,30,,======n m t n m t n m n m第二种情况: 内部角点:11~8,15~611~2,5~2)(411,1,,1,1,====++++=+-+-n m n m t t t t t n m n m n m n m n m 平直边界1:11~8),2(415~2),2(411,161,16,15,161,11,12,1,=++==++=+-+-n t t t t m t t t t n n n nm m m m平直边界2:7,16~7206~1,61.0,10,)2(222111111,1,,1,======∆=∆︒=+∆∆+++=-+-n m h n m m y x C t xh t xh t t t t f f n m n m n m n m λλ平直边界3:12,16~2411~1,11.0,30,)2(222222221,1,,1,======∆=∆︒=+∆∆+++=-+-n m h n m m y x C t xh t xh t t t t f f n m n m n m n m λλ内角点:20,10,)3(22)(2111116,67,78,67,57,6=︒=+∆∆++++=h C t xh t xh t t t t t f f λλ外角点:4,30,)1(222222211,112,212,1=︒=+∆∆++=h C t xh t x h t t t f f λλ4,30,2222222,11,21,1=︒=+∆∆++=h C t xh t xh t t t f f λλ4,30,22222212,1511,1612,16=︒=+∆∆++=h C t xh t xh t t t f f λλ20,10,2111112,61,51,6=︒=+∆∆++=h C t xh t xh t t t f f λλ20,10,2111118,167,157,16=︒=+∆∆++=h C t xh t xh t t t f f λλ四.编程计算各节点温度和冷量损失(冷量推导在后面)(用fortran编程)由以上区域离散化分析可以得到几十个方程,要求解这些方程无疑是非常繁琐的,所以采用迭代法,用计算机编程求解这些方程的解,就可以得到各点温度的数值。
西安交通大学传热学上机实验报告

φ1 − φ2 E= (φ1 + φ2)2
三、计算过程
用 MATLAB 编写计算程序,取网格步长 ∆x = ∆y = 0.1m 。 1、第一类边界条件 (1)运行程序 1(见附录 1) ,得到等温边界条件下计算墙角温度分布图:
图 4 等温边界条件下计算等温线分布(左图中每两条线间隔为三摄氏度) 运行程序 2(见附录 2) ,得到等温边界条件下实测墙角温度分布图:
s1=0; for i=2:11 s1=s1+(30-T(i,2))*0.53; end for j=2:15 s1=s1+(30-T(11,j))*0.53; end s1=s1+(30-T(1,2))*0.53/2+(30-T(11,16))*0.53/2
%墙角外侧换热量
s2=0; for i=2:6 s2=s2+T(i,5)*0.53; end for j=7:15 s2=s2+T(8,j)*0.53; end s2=s2+T(1,5)*0.53/2+T(8,16)*0.53/2+T(7,5)*0.53/2+T(8,6)*0.53/2 %墙角内侧换热量 s=2*(s1+s2) %单位长度墙壁的总换热量 e=abs(s1-s2)/((s1+s2)/2)
图3
内节点和绝热边界
图 3 所示的内节点和绝热边界节点方程如下: 内节点:
⎡(t −t )∆x (t −t )∆x (t −t )∆y (t −t )∆y⎤ ΦN +ΦS +ΦE +ΦW = λ⋅1⋅ ⎢ i, j+1 i, j + i, j−1 i, j + i+1, j i, j + i−1, j i, j ⎥ = 0 ∆y ∆y ∆x ∆x ⎣ ⎦
传热学课程上机实习

传热学计算机实习指导书本指导书是为配合本科生传热学课中计算机应用方面的教学而编写的。
应用计算机解决工程实际问题,是现代工程技术人员所必备的技能。
在传热学课程中引入计算机实习的目的,是使学生初步掌握用计算机求解传热问题的技能,从而提高学生应用计算机解决工程实际问题的能力。
大量的传热问题能够用计算机求解。
研究如何用计算机求解传热问题的专门知识数值传热学(或称计算传热学)已经发展成了传热学的一个分支学科。
传热学课中所涉及的只是数值传热学的初步知识。
因此,本次计算机实习也仅仅是作为数值传热学的入门。
本指导书给出了三个练习题及相应的算法。
这三个练习题分别涉及了一维稳态导热、二维稳态导热和一维非稳态导热。
要求学生在掌握问题的数值计算方法的基础上,独立编写计算机程序并用所编的程序计算出这三个练习题的数值结果。
1 练习题一:一维稳态导热的数值计算1.1 物理问题图1示出了一个等截面直肋,处于温度t ∞=80℃的流体中。
肋表面与流休之间的对流换热系数为h=45W/m 2.℃,肋基处温度t w =300℃,肋端绝热。
肋片由铝合金制成,其导热系数为λ=110W/m ℃,肋片厚度为δ=0.01m ,高度为H=0.1m 。
试计算肋内的温度分布及肋的总换热量。
1. 2数学描述及其解析解引入无量纲过余温度∞∞--=t t t t w θ,则以无量纲温度θ描述的肋片导热微分方程及其边界条件为:0,1,00222=∂∂====-xH x x m dxd θθθθ (1-2)(1-1)(1-3)其中Ahpm λ=(其中符号含义与教科书杨世铭陶文铨编著《传热学》相同,以下同)。
上述数学模型的解析解为:()()[]()()()m H th t t mhpm H ch H x m ch t t t t w w ∞∞∞-=-⋅-=-φ (1-4)按式(1-4)计算得到的在肋内各点的温度由表1给出。
1. 3数值离散1.3.1区域离散在对方程(1-1)~(1-3)进行数值离散之前,应首先进行计算区域的离散。
西安交大传热学上机实验报告

传热学上机实验报告二维导热物体温度场的数值模拟学院:化工学院姓名:沈佳磊学号:2110307016班级:装备11一、物理问题有一个用砖砌成的长方形截面的冷空气空道,其截面尺寸如下图所示,假设在垂直于纸面方向上冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:(1)砖墙横截面上的温度分布;(2)垂直于纸面方向的每米长度上通过砖墙的导热量。
外矩形长为3.0m,宽为2.2m;内矩形长为2.0m,宽为1.2m。
第一种情况:内外壁分别均匀地维持在0℃及30℃;第二种情况:内外表面均为第三类边界条件,且已知:外壁:30℃,h1=10W/m2·℃,内壁:10℃,h2= 4 W/m2·℃砖墙的导热系数λ=0.53 W/m·℃由于对称性,仅研究1/4部分即可。
二、数学描写 对于二维稳态导热问题,描写物体温度分布的微分方程为拉普拉斯方程 22220t t x x ∂∂+=∂∂这是描写实验情景的控制方程。
三、方程离散用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为确定温度值的空间位置,即节点。
每一个节点都可以看成是以它为中心的一个小区域的代表。
由于对称性,仅研究1/4部分即可。
依照实验时得点划分网格。
建立节点物理量的代数方程对于内部节点,由∆x=∆y ,有,1,1,,1,11()4m n m n m n m n m n t t t t t +-+-=+++由于本实验为恒壁温,不涉及对流,故内角点,边界点代数方程与该式相同。
设立迭代初场,求解代数方程组图中,除边界上各节点温度为已知且不变外,其余各节点均需建立类似3中的离散方程,构成一个封闭的代数方程组。
以t ₀=0°C 为场的初始温度,代入方程组迭代,直至相邻两次内外传热值之差小于0.01,认为已达到迭代收敛。
四、编程及结果program mainimplicit nonereal ,dimension(1:16,1:12)::treal ,dimension(1:16,1:12)::t1real q,q1,q2,q3,q4,q5,q6,q7,q8,q9,q10,q11,ainteger m,n,zlogical::converged=.false.z=1t=0a=0.53do n=1,12t(1,n)=30end dodo m=2,16t(m,12)=30end dodo n=1,7t(6,n)=0end dodo m=7,16t(m,7)=0end dodo while(.not.converged.and.z<10000)t1=tdo m=2,5do n=1,11if( n==1 )thent(m,n)=0.25*(t(m-1,n)+t(m+1,n)+2*t(m,n+1))elset(m,n)=0.25*(t(m-1,n)+t(m+1,n)+t(m,n-1)+t(m,n+1)) end ifend doend dodo n=8,11do m=6,16if (m==16) thent(m,n)=0.25*(t(m,n-1)+t(m,n+1)+2*t(m-1,n))elset(m,n)=0.25*(t(m-1,n)+t(m+1,n)+t(m,n-1)+t(m,n+1))end ifend doend doz=z+1do m=1,16do n=1,12if(abs(t(m,n)-t1(m,n))>0.000001) thenconverged=.false.exitelseconverged=.true.end ifend doend doend dowrite(*,'(16f5.1)',advance='no')((t(m,n),m=1,16),n=12,7,-1) write(*,*)write(*,'(6f5.1)',advance='no')((t(m,n),m=1,6),n=6,1,-1) do n=2,11q1=(t(1,n)-t(2,n))*a+q1 end dodo m=2,15q2=(t(m,12)-t(m,11))*a+q2 end doq3=(t(1,1)-t(2,1))*a*0.5q4=(t(16,12)-t(16,11))*a*0.5 q10=q1+q2+q3+q4write(*,*)do n=2,6q5=(t(5,n)-t(6,n))*a+q5 end dodo m=7,15q6=(t(m,8)-t(m,7))*a+q6 end doq7=(t(5,1)-t(6,1))*a*0.5q8=(t(16,8)-t(16,7))*a*0.5 q9=(t(5,7)-t(6,7))*a*2q11=q5+q6+q7+q8+q9q=(q10+q11)*0.5*4print*,"外表面导量=",q10,"内表面导热量",q11,"每米高砖墙导热量",qend结果截图:五、结果讨论将以上结果用matlab画图工具绘制出如下图像:将上述结果与实验结果对比,结论基本一致。
传热实验报告
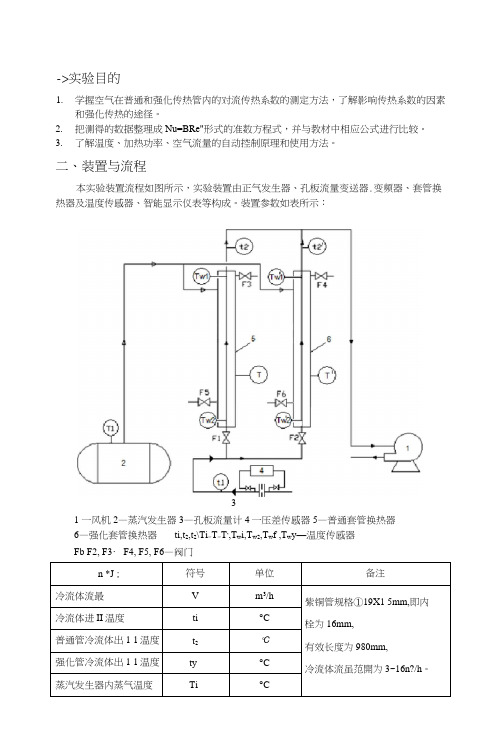
->实验目的1.学握空气在普通和强化传热管内的对流传热系数的测定方法,了解影响传热系数的因素和强化传热的途径。
2.把测得的数据整理成Nu=BRe"形式的准数方程式,并与教材中相应公式进行比较。
3.了解温度、加热功率、空气流量的自动控制原理和使用方法。
二、装置与流程本实验装置流程如图所示,实验装置由正气发生器、孔板流量变送器.变频器、套管换热器及温度传感器、智能显示仪表等构成。
装置参数如表所示:31 一风机2—蒸汽发生器3—孔板流量计4一压差传感器5—普通套管换热器6—强化套管换热器ti,t2,t2\Ti>T>T,,T w i,T w2,T w f ,T w y—温度传感器Fb F2, F3・ F4, F5, F6—阀门普通热流体进II端壁温T w i°C普通热流体出11端壁温T W2°C普通管外蒸气温度T°C加强热流体进11端壁温T w f°C加强热流体出丨|端壁温几2‘°C加强管外蒸/(温度T,°C空气一水蒸气换热流程:來自蒸汽发生器的水蒸气进入套管换热器,与被风机抽进的空气进行热交换,冷凝水经排出阀排入盛水装置。
空气经孔板流最计进入套管换热器的内管(紫铜管),流量通过变频器调节电机转速达到自动控制,热交换后从风机出II排出。
注意:本实验中,普通和强化实验通过管路上的切换阀门进行切换。
三、基本原理在工业生产过程中,人量情况2采用间壁式换热方式进行换热。
所谓间壁式换热,就是冷、热两种流体之间有一固体壁面,两流体分别在固体璧面的两侧流动,两流体不直接接触,通过固体壁面(传热元件)进行热臺交换。
本装置主要研究汽一气综合换热,包括普通管和加强管。
其中,水蒸汽和空气通过紫铜管间接换热,空气走紫铜管内,水蒸汽走紫铜管外,采用逆流换热。
所谓加强管,是在紫铜管内加了弹簧,堀人了绝对粗糙度,进而堀大了空气流动的湍流程度,使换热效果更明显。
传热学实验报告

传热学实验报告班级:安全工程(单)0901班姓名:***学号:01第一节稳态平板法测定绝热材料导热系数实验一、实验目的1.巩固和深化稳定导热过程的基本理论,学习用平板法测定绝热材料导热系数的试验方法和技能。
2.测定试验材料的导热系数。
3.确定试验材料导热系数与温度的关系。
二、实验原理导热系数是表征材料导热能力的物理量。
对于不同的材料,导热系数是各不相同的,对同一材料,导热系数还会随着温度、压力、湿度、物质的结构和重度等因素而变异。
各种材料的导热系数都用试验方法来测定,如果要分别考虑不同因素的影响,就需要针对各种因素加以试验,往往不能只在一种实验设备上进行。
稳态平板法是一种应用一维稳态导热过程的基本原理来测定材料导热系数的方法,可以用来进行导热系数的测定试验,测定材料的导热系数及其和温度的关系。
实验设备是根据在一维稳态情况下通过平板的到热量Q 和平板两面的温差t ∆成正比,和平板的厚度h 成反比,以及和导热系数λ成反比的关系来设计的。
我们知道,通过薄壁平板(壁厚小于十分之一壁长和壁宽)的稳定导热量为:S t hQ *∆*=λ(1)其中:Q 为传到平板的热量,w ;λ为导热系数,w/m ℃;h 为平板厚度,m ; t ∆为平板两面温差,℃; S 为平板表面积;m 2;测试时,如果将平板两面温差t ∆、平板厚度h 、垂直热流力向的导热面积S 和通过平板的热流量Q 测定后,就可以根据下式得出导热系数:St hQ *∆*=λ (2) 其中:d u T -T t =∆,T u 为平板上测温度,T d 为平板下侧温度,℃;这里,公式2所得出的导热系数是在当时的平均温度下材料的导热系数值,此平均温度为:()d u T T 21t +=(3) 在不同的温度和温差条件下测出相应的λ值,然后按λ值标在λ-t 坐标图内,就可以得出()t f =λ的关系曲线。
三、实验装置及测试仪器稳态平板法测定绝热材料的导热系数的电器连接图和实验装置如图1和图2所示。
西安交通大学数学建模上机实验报告
问题一某大型制药厂销售部门为了找出某种注射药品销量与价钱之间的关系,通过市场调查搜集了过去30个销售周期的销量及销售价钱的数据,如表.按照这些数据至少成立两个数学模型, 作出图形,比较误差。
问题分析:该问题是通过已知的过去30个销售周期的销量及销售价钱的 数据,来寻觅一个最能反映该药销量与价钱之间的函数曲 线。
在数学上归结为最佳曲线拟合问题。
大体思想:曲线拟合问题的提法:已知一组二维数据,即平面上的n 个点),x i i y ( i=1,2,3.....n ,i x 互不相同,寻求一个函数)(f y x =,使)(x f 在某中准则下与所有数据点最为接近,即曲线拟合得最好。
最小二乘法是解决曲线拟合最常常利用的方式.大体思路:1122 ()()()()m m f x a r x a r x a r x =+++令其中rk(x) 是事前选定的一组函数,ak 是待定系数(k=1,2,…,m,m <n), 拟合准则是使n 个点(xi,yi) (i=1,2…,n),与y=f(xi)的距离 的平方和最小,称最小二乘法准则。
一、系数的肯定22111 (,,)[()]n nm ii i i i J a a f x y δ====-∑∑记求m a a ,,1 使得使J 达到最小.0 (1,,)kJ k m a ∂==∂ 取得关于 m a a ,,1 的线性方程组:11111()[()]0 ()[()]0nmi k k i i i k n mm i k k i i i k r x a r x y r x a r x y ====⎧-=⎪⎪⎪⎨⎪⎪-=⎪⎩∑∑∑∑ 1 ,,().m a a f x 解出,即得散点图: 程序: x=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; y=[,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]; plot(x,y,'r.')通过观察,结合实际情形。
传热综合实验报告

传热综合实验报告传热综合实验报告引言:传热是物质内部或不同物质之间热能传递的过程。
在工程领域中,传热的研究对于提高能源利用效率、改善工艺流程等方面具有重要意义。
本实验旨在通过实际操作,探究传热的基本原理和实际应用。
实验目的:1. 了解传热的基本概念和原理;2. 掌握传热实验的基本操作方法;3. 分析传热实验结果,探讨传热机制。
实验步骤:1. 实验前准备:准备实验所需材料和仪器设备,包括热导率测量仪、传热模型等;2. 实验一:热导率测量。
通过热导率测量仪测量不同材料的热导率,包括金属、塑料等;3. 实验二:传热模型实验。
选择一个传热模型,如平板散热器,将其加热并记录温度变化;4. 实验三:传热管实验。
将传热管加热并测量不同位置的温度,分析传热过程。
实验结果与分析:1. 热导率测量结果表明,不同材料的热导率存在较大差异。
金属材料的热导率较高,而塑料等非金属材料的热导率较低。
这与金属的晶体结构和电子传导机制有关;2. 传热模型实验结果显示,随着加热时间的增加,模型表面的温度逐渐升高,表明传热过程中热能从高温区传递到低温区;3. 传热管实验结果表明,在传热管的两端,温度差异较大,而在中间位置,温度差异较小。
这说明传热管的传热效果在两端较好,而在中间位置传热效果较差。
实验讨论:1. 通过热导率测量实验,我们了解了不同材料的热导率特性。
这对于材料选择和工程设计中的热传导问题具有指导意义;2. 传热模型实验结果表明,传热是一个由高温区向低温区传递热能的过程。
这与热力学第二定律相符合;3. 传热管实验结果提示我们,在传热过程中,传热效果会受到材料、管道长度等因素的影响。
因此,在实际工程应用中,需要考虑传热效果的优化。
结论:通过本次传热综合实验,我们对传热的基本原理和实际应用有了更深入的了解。
热导率测量结果表明不同材料的热导率存在差异,传热模型实验结果显示了传热的基本过程,传热管实验结果提示了传热效果受到多种因素影响。
西安交通大学传热学上机报告材料-墙角导热数值分析报告

实用文档传热大作业二维导热物体温度场的数值模拟:璇班级:能动A02学号:10031096一.物理问题有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如下图所示,假设在垂直于纸面方向上用冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:(1)砖墙横截面上的温度分布;(2)垂直于纸面方向的每米长度上通过砖墙的导热量。
第一种情况:外壁分别均与地维持在0℃及30℃;第二种情况:外壁均为第三类边界条件,且已知:t ∞1=30℃,ℎ1=10wm2∙℃t ∞2=10℃,ℎ2=4wm2∙℃砖墙的导热系数λ=0.53 Wm∙℃二.数学描写由对称的界面必是绝热面,可取左上方的四分之一墙角为研究对象,该问题为二维、稳态、无热源的导热问题,其控制方程和边界条件如下:ðt2ðx2+ðt2ðy2=0边界条件(情况一) t(x,0)=30 0≤x≤1.5t(0,y)=30 0≤y≤1.1t(0.5,y)=0 0.5≤y≤1.1t(x,0.5)=0 0.5≤x≤1.5ðt(1.5,y)=0 0≤y≤0.5ðy∂t(x,1.1)=0 0≤x≤0.5ℎ(t−t f1) x=0,0≤y≤1.11=ℎ(t−t f2) x=0.5,0.5≤y≤1.12ℎ(t−t f1) y=0,0≤x≤1.51ℎ(t−t f2) y=0,0.5≤x≤21.50 0≤y≤0.5=0 0≤x≤0.5∂x三.网格划分网格划分与传热学实验指导书中“二维导热物体温度场的电模拟实验”一致,如下图所示:四.方程离散对于节点,离散方程t[i][j]=0.25*(t[i+1][j]+t[i-1][j]+t[i][j+1]+t[i][j-1])对于边界节点,则应对一、二两种情况分开讨论:情况一:绝热平直边界点:t[15][j]=0.25*(2*t[14][j]+t[15][j-1]+t[15][j+1])1≤j≤4t[i][11]=0.25*(2*t[i][10]+t[i-1][11]+t[i+1][11]) 1≤i≤4外等温边界点:t[i][j]=30等温边界点:t[i][j]=0情况二:(Bi1,Bi2为网格Bi数,Bi1=ℎ1∆xλ Bi2=ℎ2∆xλ)绝热平直边界点:t[15][j]=0.25*(2*t[14][j]+t[15][j-1]+t[15][j+1])1≤j≤4t[i][11]=0.25*(2*t[i][10]+t[i-1][11]+t[i+1][11]) 1≤i≤4外侧对流平直边界:t[i][0]=(2*t[i][1]+t[i+1][0]+t[i-1][0]+2*Bi1*tf1)/(2*Bi1+4) 1≤i≤14t[0][j]=(2*t[1][j]+t[0][j+1]+t[0][j-1]+2*Bi1*tf1)/(2*Bi1+4) 1≤j≤10侧对流平直边界:t[i][5]=(2*t[i][4]+t[i+1][5]+t[i-1][5]+2*Bi2*tf2)/(2*Bi2+4) 6≤i≤14t[5][j]=(2*t[4][j]+t[5][j+1]+t[5][j-1]+2*Bi2*tf2)/(2*Bi2+4) 6≤j≤10特殊点:a点t[15][0]=(t[14][0]+t[15][1]+tf1*Bi1)/(Bi1+2)b点t[15][5]=(t[14][5]+t[15][4]+tf2*Bi2)/(Bi2+2)c点t[5][5]=(2*t[4][5]+2*t[5][4]+t[5][6]+t[6][5]+3*Bi2*tf2)/(2*Bi2+6) d点t[5][11]=(t[5][10]+t[4][11]+tf2*Bi2)/(Bi2+2)e点t[0][11]=(t[0][10]+t[1][11]+tf1*Bi1)/(Bi1+2)f点t[0][0]=(t[0][1]+t[1][0]+tf1*Bi1*2)/(2*Bi1+2)五.编程思路及流程图编程思路为设定两个二维数组t[i][j]、ta[i][j]分别表示本次迭代和上次迭代各节点的温度值,iter表示迭代进行的次数,daore_in、daore_out分别表示外边界的散热量。
物体的传热实验报告(3篇)

第1篇一、实验目的1. 理解和掌握热传导、对流和辐射三种传热方式的基本原理。
2. 通过实验验证不同材料、不同条件下物体的传热效率。
3. 分析影响物体传热效率的因素,如材料的热导率、物体的形状、环境温度等。
二、实验原理物体的传热主要有三种方式:热传导、对流和辐射。
1. 热传导:热量通过物体内部的微观粒子(如原子、分子)的振动和碰撞传递。
其传热速率与物体的热导率、温度梯度、物体的截面积和传热距离有关。
2. 对流:热量通过流体(如液体、气体)的流动传递。
其传热速率与流体的流速、温度差、流体的热导率、物体的形状和截面积有关。
3. 辐射:热量通过电磁波的形式传递。
其传热速率与物体的温度、表面积、辐射系数、物体表面的发射率、周围环境的辐射强度和距离的平方有关。
三、实验材料与仪器1. 实验材料:金属棒、铜棒、铝棒、塑料棒、水、酒精、盐、温度计、计时器、支架、加热器等。
2. 实验仪器:电热板、热电偶、数字温度计、数据采集器、计算机等。
四、实验步骤1. 热传导实验:- 将金属棒、铜棒、铝棒和塑料棒分别置于支架上。
- 在一端加热金属棒,另一端用温度计测量温度。
- 记录不同材料的温度变化,计算热传导速率。
2. 对流实验:- 将水加热至一定温度,倒入烧杯中。
- 在水中放入金属棒,用温度计测量棒上不同位置的温度。
- 记录温度变化,计算对流速率。
3. 辐射实验:- 将电热板置于支架上,调整温度。
- 在一定距离处放置温度计,测量温度。
- 记录不同温度下的温度变化,计算辐射速率。
五、实验结果与分析1. 热传导实验:- 金属棒的热传导速率高于塑料棒,说明金属的热导率较高。
- 铜棒的热传导速率高于铝棒,说明铜的热导率较高。
2. 对流实验:- 水的对流速率较快,说明水的流动性较好。
- 金属棒在不同位置的温度变化较大,说明对流在金属棒上起主要作用。
3. 辐射实验:- 电热板温度越高,辐射速率越快。
- 辐射速率与距离的平方成反比。
六、实验结论1. 物体的传热方式主要有热传导、对流和辐射三种。
传热实验实验报告【范本模板】
姓名院 专业 班 年 月 日实验内容 指导教师 一、 实验名称:传热实验二、实验目的:1.熟悉套管换热器的结构;2。
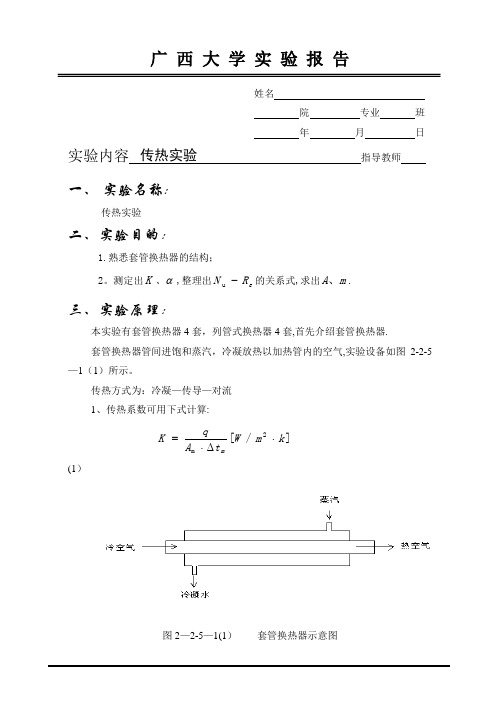
测定出K 、α,整理出e R N -u 的关系式,求出m A 、.三、实验原理:本实验有套管换热器4套,列管式换热器4套,首先介绍套管换热器.套管换热器管间进饱和蒸汽,冷凝放热以加热管内的空气,实验设备如图2-2-5—1(1)所示。
传热方式为:冷凝—传导—对流 1、传热系数可用下式计算: ]/[2m k m W t A q K m⋅∆⋅=(1)图2—2-5—1(1) 套管换热器示意图传热实验姓名院 专业 班 年 月 日实验内容 指导教师式中:q-—传热速率[W] A-—传热面积[m 2] △t m —传热平均温差[K ]○,1传热速率q 用下式计算:])[(12W t t C V q p S -=ρ (2) 式中:3600/h S V V =-—空气流量[m 3/s]V h —-空气流量[m 3/h]ρ——空气密度[kg/m 3],以下式计算:]/)[273(4645.031m kg t R p Pa ++=ρ (3)Pa ——大气压[mmHg]Rp ——空气流量计前表压[mmHg] t 1——空气进换热器前的温度[℃]Cp-—空气比热[K kg J ⋅/],查表或用下式计算:]/[04.01009K kg J t C m p ⋅+= (4) t m =(t 1+t 2)/2—-空气进出换热器温度的平均值(℃) t 2-—空气出口温度[℃]②传热平均面积A m :][2m L d A m m π= (5)式中:d m =传热管平均直径[m ]L —传热管有效长度[m ]③传热平均温度差△t m 用逆流对数平均温差计算:姓名院 专业 班 年 月 日实验内容 指导教师T ←——T t 1——→t 2 )(),(2211t T t t T t -=∆-=∆2121ln t t t t t m ∆∆∆-∆=∆ (6) 式中:T ——蒸汽温度[℃]2、传热膜系数(给热系数)及其关联式空气在圆形直管内作强制湍流时的传热膜系数可用下面准数关联式表示:nr m e P AR Nu = (7)式中:N u ——努塞尔特准数R e -—雷诺准数 P r ——普兰特准数A ——系数,经验值为0。
数值传热_传热学上机实验_墙角稳态导热问题数值模拟

图一
二、 计算原理
本次上机模拟实验选等温边界条件。墙角是中心对称的,所以取其 1/4 研究, 方便计算机计算。上机模拟选取网格划分方法同实际实验,可根据热平衡法列 出节点方程,各方向导入单元体的热量之和为零。该边界条件下共有四类节点,
Hale Waihona Puke 内节点、内边界点、外边界点和绝热边界点。
图二
四种节点的节点方程简化如下:
eps=1; temp=A[i][j]; A[i][j]=(A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4; eps=A[i][j]-temp;
} eps=1; temp=A[0][j]; A[0][j]=(A[0][j-1]+A[0][j+1]+2*A[1][j])/4; eps=A[i][15]-temp; } //计算墙体外表面导热量 q_out=0; for(i=1;i<11;i++) q_out=q_out+A[i][0]-A[i][1]; for(j=1;j<15;j++) q_out=q_out+A[11][j]-A[10][j]; q_out=q_out+(A[0][0]-A[0][1]+A[11][15]-A[10][15])/2; q_out=q_out*0.53; //计算墙体内表面导热量 q_in=0; for(i=1;i<7;i++) q_in=q_in+A[i][4]-A[i][5]; for(j=5;j<15;j++) q_in=q_in+A[7][j]-A[6][j]; q_in=q_in+(A[0][4]-A[0][5]+A[7][15]-A[6][15])/2; q_in=q_in*0.53; //计算平均导热量和相对误差 q=(q_in+q_out)/2; eps=abs(q_in-q_out); } //输出结果 for(i=11;i>5;i--) { for(j=0;j<16;j++) out<<setw(8)<<setprecision(2)<<A[i][j]<<" "; out<<endl; } for(i=5;i>=0;i--) { for(j=0;j<6;j++) out<<setw(8)<<setprecision(2)<<A[i][j]<<" "; out<<endl; } out<<"墙体内表面导热量q_in="<<q_in<<"\n"; out<<"墙体外表面导热量q_out="<<q_out<<"\n"; out<<"墙体平均导热量q="<<q<<"\n"; return 0; }
西安交通大学传热学大作业---二维温度场热电比拟实验

西安交通大学传热学大作业一、物理问题有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如下图1-1所示,假设在垂直于纸面方向上用冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:砖墙横截面上的温度分布;垂直于纸面方向的每米长度上通过砖墙的导热量。
第一种情况:内外壁分别均匀维持在0℃及30℃;第二种情况:内外壁均为第三类边界条件,且已知:K m W K m W h C t K m W h C t ∙=∙=︒=∙=︒=∞∞/53.0砖墙导热系数/20,10/4,30222211λ二、数学描写由对称的界面必是绝热面,可取左上方的四分之一墙角为研究对象,该问题为二维、稳态、无内热源的导热问题。
控制方程:02222=∂∂+∂∂y tx t边界条件:① 给出了边界上的温度,属于第一类边界条件:由对称性知边界1绝热: 0=w q ; 边界2、3为等温边界:t w2=0℃,t w3=30℃② 给出了边界上的边界上物体与周围流体间的表面传热系数h 及周围流体的温度t f ,属于第三类边界条件 由对称性知边界1绝热: 0=w q ;边界2为对流边界,)()(2f w w w t t h n tq -=∂∂-=λ; 边界3为对流边界,)()(3f w w w t t h n t q -=∂∂-=λ。
1-1图2-1图三、数学模型网格划分:将长方形截面离散成31×23个点,用有限个离散点的值的集合来代替整个截面上温度的分布,通过求解按傅里叶导热定律、牛顿冷却公式及热平衡法建立的代数方程,来获得整个长方形截面的温度分布,进而求出其通过壁面的冷量损失。
步长为0.1m ,记为△x=△y=0.1m 。
采用热平衡法,利用傅里叶导热定律和能量守恒定律,按照以导入元体(m,n )方向的热流量为正,列写每个节点代表的元体的代数方程。
第一种情况:()()()()()()()()()()⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧+++==︒==︒==︒==︒==︒==︒==︒==︒=+-+-代表内部点,,点4126~6,1018,26~6,106,18~6,10,2618~6,10,631~1,3023,31~1,301,23~1,30,3123~1,30,11,1,,1,1,n m t t t t t n C m t n C m t n C n t n C n t n C m t n C m t n C n t n C n t n m n m n m n m n m 第二种情况对于外部角点(1,1)、(1,23)、(31,1)、(31,,23)有:()()02222,1,,22,,1,22=∆∆-+-∆+∆∆-+-∆±±x y t t t t x h y x t t t t yh n m n m n m f n m n m n m f λλ 得到:()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++=++=++=++=22,3123,3023,312,311,301,3122,123,223,12,11,21,11865331400186533140018653314001865331400t t t t t t t t t t t t 同理可得:对于内部角点(6,6)(6,18)(26,6)(26,18) ,有()()()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++++=++++=++++=++++=7,2618,2518,2719,2618,267,266,256,275,266,2618,717,619,618,518,67,66,75,66,56,671853359533592000718533595335920007185335953359200071853359533592000t t t t t t t t t t t t t t t t t t t t对于外部边界节点有()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++==+++==+++==+++=+-+-+-+-20~2,29253146537360020~2,29253146537360022~2,29253146537360022~229253146537360023,123,122,23,1,11,12,1,1,311,31,30311,11,1,21m t t t t m t t t t n t t t t n t t t t m m m m m m m m n n n n n n n n ,,, 对于内部边界节点有()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++==+++==+++==+++=+-+-+-+-25~7,6125330653153100025~7,6125330653153100017~7,6125330653153100017~7,6125330653153100018,118,119,18,6,16,15,6,1,261,26,27261,61,6,56n t t t t n t t t t n t t t t n t t t t m m m m m m m m n n n n n n n n ,, 对于内部节点有()1,1,,1,1,41+-+-+++=n m n m n m n m n m t t t t t传热问题的有限差分解法中主要采用迭代法。
传热学实验报告.docx

传热学实验报告班级:安全工程(单) 0901班姓名:***学号: 01第一节稳态平板法测定绝热材料导热系数实验一、实验目的1.巩固和深化稳定导热过程的基本理论,学习用平板法测定绝热材料导热系数的试验方法和技能。
2.测定试验材料的导热系数。
3.确定试验材料导热系数与温度的关系。
二、实验原理导热系数是表征材料导热能力的物理量。
对于不同的材料,导热系数是各不相同的,对同一材料,导热系数还会随着温度、压力、湿度、物质的结构和重度等因素而变异。
各种材料的导热系数都用试验方法来测定,如果要分别考虑不同因素的影响,就需要针对各种因素加以试验,往往不能只在一种实验设备上进行。
稳态平板法是一种应用一维稳态导热过程的基本原理来测定材料导热系数的方法,可以用来进行导热系数的测定试验,测定材料的导热系数及其和温度的关系。
实验设备是根据在一维稳态情况下通过平板的到热量Q 和平板两面的温差t 成正比,和平板的厚度h 成反比,以及和导热系数成反比的关系来设计的。
我们知道,通过薄壁平板(壁厚小于十分之一壁长和壁宽)的稳定导热量为:Q t S(1)h其中: Q 为传到平板的热量,w ;为导热系数, w/m ℃;h 为平板厚度, m;t 为平板两面温差,℃;S 为平板表面积;m2;测试时,如果将平板两面温差t 、平板厚度h 、垂直热流力向的导热面积S 和通过平板的热流量Q 测定后,就可以根据下式得出导热系数:Q h( 2)t S其中:t T u - T d,T u为平板上测温度,T d为平板下侧温度,℃;这里,公式 2 所得出的导热系数是在当时的平均温度下材料的导热系数值,此平均温度为:t 1T d( 3)T u2在不同的温度和温差条件下测出相应的值,然后按值标在- t坐标图内,就可以得出 f t 的关系曲线。
三、实验装置及测试仪器稳态平板法测定绝热材料的导热系数的电器连接图和实验装置如图1和图 2所示。
被试验材料做成两块方形薄壁平板试件,面积为300*300[mm2],实际导热计算面积 S为 200*200[mm 2] ,平板厚度 h[mm] 。
西安交通大学数值传热学大作业

图 3 边界条件展示图
x 方向上的 1-1 和 2-2 所代表的如上图所示。其中 ABCD 为一个计算区域。
6
数值传热学论文
其中平均速度由下式来确定。
TP TP Tb ( x)= T ( x,y )u ( x,y )dy / u ( x,y )dy
控制方程用有限容积法离散,采用幂指数法来离散对流扩散项。计算中用到 了 SIMPLER 算法[5]。考虑到对百叶窗翅片区域的处理,所以在迭代计算过程中, 该区域中的速度为零。除此之外,扩散系数在流体区域中取值为 1,在孤立的固 态区域取很大的值(20×1025) 。网格节点通过手动划分,根据给定的 x 方向的网 格数自动根据角度来计算 y 方向的网格数目。 本文计算中取的网格系统的节点为 70×70。 进行了 1000 次外迭代,速度和温度的参差小于 10^3。翅片与流体间的传热 和 Nusselt 数有关,平均 Nusselt 数通过垂直壁的表面数字综合确定,表达如下
Abstract: In order to investigate the periodic fully developed heat transfer on a louver fin unit with a certain angle to the flow direction, SIMPLER algorithm was adopted based on the Reylonds conservation equations of the steady-state constant property laminar flow and a fin with a constant temperature condition. The heat transfer coefficient and resistance factor was obtained under the angle of louver finsθ =25°, the Reynold number ranges from 10 to 500. The numerical results show that as the Reynold number increases, the average Nusselt number increases and the resistance coefficient decreases. Key words: Fin; Fully periodical flow; Numerical Simulation, SIMPLER algorithm
传热学上机实验

传热学上机实验报告一·上机题目一尺寸为240*400平方毫米的薄矩形板,已知各边界表面的条件为:左侧边界面为绝热;右侧边界面为第三类边界条件:h=40/(㎡·k),t f =25℃;上顶面边界为第一类边界条件,已知界面温度为200℃;下底面边界为第二类边界条件,已知热流密度q w =1500W/㎡。
已知薄板材料的导热系数λ=45W/(m ·k ),∆x =∆y =40"mm"划分网格,试计算该薄板的稳态温度分布。
分析:由题意得,该矩形板被划分为7行11列,对各节点进行编号,如下图:012345678910 1 2 3 4 5 6下面列出特殊节点的方程式:(i 代表行,j 代表列) (0,0):200℃;(0,3):1,1,,1,240i j i j i j i j t t t t +-+++-=;(0,6):1,,1,20w i ji j i j q xt t t λ-+⨯∆+-+=;(5,6):1,,1,1,2240wi ji j i j i j x q t t t t λ--+∆⨯+++-=; (10,6):,,11,,()20w f i j i j i j i j q xh y t t t t t λλ--⨯∆⨯∆-+-++=;(10,3):,11,1,,22(2)20i j i j i j i j f h x h xt t t t t λλ--+⨯∆⨯∆++-++=;(10,0):200℃; (5,0):200℃; (5,3):,1,11,,,40i j i j i j i i j i j t t t t t +-+-+++-=。
C++编程如下: #include<stdio.h > #include<math.h > int main(){int K=100,i,j,IT,m=0,c=6,d=10;float TTB=200.0,TRB=25.0,H=40.0,Q=1500.0,G=45.0;float EPS,X=1.0,e=0.04,f=0.04;float a[7][11],b[7][11];for(i=0;i<7;i++)for(j=0;j<11;j++)a[i][j]=100.0;while(X>0.01){m++;for(i=0;i<=c;i++){for(j=0;j<=d;j++){b[i][j]=a[i][j];if(i==0&&0<=j&&j<=d)a[0][j]=200;elseif(0<i&&i<c&&j==0)a[i][j]=(a[i+1][j]+a[i-1][j]+2*a[i][j+1])/4.0;elseif(i==c&&j==0)a[i][j]=(a[i-1][j]+a[i][j+1]+Q*e/G)/2.0;elseif(i==c&&0<j&&j<d)a[i][j]=(2*a[i-1][j]+a[i][j-1]+a[i][j+1]+2*Q*e/G)/4.0;elseif(i==c&&j==d)a[i][j]=(a[i][j-1]+a[i-1][j]+Q*e/G+H*f*TRB/G)/(2+H*f/G);elseif(0<i&&i<c&&j==d)a[i][j]=(2*a[i][j-1]+a[i-1][j]+a[i+1][j]+2*H*e*TRB/G)/(4+2*H*e/G);elsea[i][j]=(a[i][j+1]+a[i][j-1]+a[i-1][j]+a[i+1][j])/4.0;}}X=0.0;for(i=0;i<=c;i++){for(j=0;j<=d;j++){EPS=fabs(b[i][j]-a[i][j]);if(EPS>X)X=EPS;}}if(m>1000)break;}if(m >1000){printf("不收敛");} else{printf("\n 收敛\n\n 循环次数:%d\n\n",m); for(i=0;i<7;i++) { for(j=0;j<11;j++){printf("%7.2lf",a[i][j]);} printf("\n");}}getchar(); }三·实验结果通过编译运行该程序,可得到如下结果:收敛 循环次数:172200.00200.00200.00200.00200.00200.00200.00200.00200.00200.00200.00 200.21200.18200.07199.87199.58199.15198.56197.71196.44194.42190.74 200.50200.43200.22199.85199.29198.49197.37195.83193.65190.52185.89 200.94200.85200.55200.03199.25198.15196.63194.59191.83188.13183.21 201.60201.48201.12200.49199.55198.23196.44194.07190.97186.98181.95 202.51202.38201.98201.28200.24198.79196.84194.29191.01186.88181.80 203.70203.57203.16202.44201.36199.87197.87195.26191.92187.74182.63四、思考题1、2400240mm ⨯的薄矩形板,长和宽各为多少?解:长为240mm ,宽为400mm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传热学上机实验报告
二维导热物体温度场的数值模拟
学院:化工学院
姓名:沈佳磊
学号:2110307016
班级:装备11
一、物理问题
有一个用砖砌成的长方形截面的冷空气空道,其截面尺寸如下图所示,假设在垂直于纸面方向上冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算:
(1)砖墙横截面上的温度分布;
(2)垂直于纸面方向的每米长度上通过砖墙的导热量。
外矩形长为3.0m,宽为2.2m;内矩形长为2.0m,宽为1.2m。
第一种情况:内外壁分别均匀地维持在0℃及30℃;
第二种情况:内外表面均为第三类边界条件,且已知:
外壁:30℃,h1=10W/m2·℃,
内壁:10℃,h2= 4 W/m2·℃
砖墙的导热系数λ=0.53 W/m·℃
由于对称性,仅研究1/4部分即可。
二、数学描写 对于二维稳态导热问题,描写物体温度分布的微分方程为拉普拉斯方程
22220t t x x ∂∂+=∂∂
这是描写实验情景的控制方程。
三、方程离散
用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为确定温度值的空间位置,即节点。
每一个节点都可以看成是以它为中心的一个小区域的代表。
由于对称性,仅研究1/4部分即可。
依照实验时得点划分网格。
建立节点物理量的代数方程
对于内部节点,由∆x=∆y ,有
,1,1,,1,11()4m n m n m n m n m n t t t t t +-+-=+++
由于本实验为恒壁温,不涉及对流,故内角点,边界点代数方程与该式相同。
设立迭代初场,求解代数方程组
图中,除边界上各节点温度为已知且不变外,其余各节点均需建立类似3中的离散方程,构成一个封闭的代数方程组。
以t ₀=0°C 为场的初始温度,代入方程组迭代,直至相邻两次内外传热值之差小于0.01,认为已达到迭代收敛。
四、编程及结果
program main
implicit none
real ,dimension(1:16,1:12)::t
real ,dimension(1:16,1:12)::t1
real q,q1,q2,q3,q4,q5,q6,q7,q8,q9,q10,q11,a integer m,n,z
logical::converged=.false.
z=1
t=0
a=0.53
do n=1,12
t(1,n)=30
end do
do m=2,16
t(m,12)=30
end do
do n=1,7
t(6,n)=0
end do
do m=7,16
t(m,7)=0
end do
do while(.not.converged.and.z<10000)
t1=t
do m=2,5
do n=1,11
if( n==1 )then
t(m,n)=0.25*(t(m-1,n)+t(m+1,n)+2*t(m,n+1))
else
t(m,n)=0.25*(t(m-1,n)+t(m+1,n)+t(m,n-1)+t(m,n+1)) end if
end do
end do
do n=8,11
do m=6,16
if (m==16) then
t(m,n)=0.25*(t(m,n-1)+t(m,n+1)+2*t(m-1,n)) else
t(m,n)=0.25*(t(m-1,n)+t(m+1,n)+t(m,n-1)+t(m,n+1)) end if
end do
end do
z=z+1
do m=1,16
do n=1,12
if(abs(t(m,n)-t1(m,n))>0.000001) then
converged=.false.
exit
else
converged=.true.
end if
end do
end do
end do
write(*,'(16f5.1)',advance='no')((t(m,n),m=1,16),n=12,7,-1) write(*,*)
write(*,'(6f5.1)',advance='no')((t(m,n),m=1,6),n=6,1,-1)
do n=2,11
q1=(t(1,n)-t(2,n))*a+q1
end do
do m=2,15
q2=(t(m,12)-t(m,11))*a+q2
end do
q3=(t(1,1)-t(2,1))*a*0.5
q4=(t(16,12)-t(16,11))*a*0.5
q10=q1+q2+q3+q4
write(*,*)
do n=2,6
q5=(t(5,n)-t(6,n))*a+q5
end do
do m=7,15
q6=(t(m,8)-t(m,7))*a+q6
end do
q7=(t(5,1)-t(6,1))*a*0.5
q8=(t(16,8)-t(16,7))*a*0.5
q9=(t(5,7)-t(6,7))*a*2
q11=q5+q6+q7+q8+q9
q=(q10+q11)*0.5*4
print*,"外表面导量=",q10,"内表面导热量",q11,"每米高砖墙导热量",q
end
结果截图:
将以上结果用matlab画图工具绘制出如下图像:
将上述结果与实验结果对比,结论基本一致。
通过本次数值模拟实验,进一步熟悉了二维稳态导热物体温度场的分布特点,对用数值模拟方法求解传热学问题的过程有了更加深刻、直观的认识,并体会到了数值模拟在求解物理问题上的方便性,也熟悉了相关软件的基本使用方法。
Welcome !!!
欢迎您的下载,
资料仅供参考!
精选资料,欢迎下载。
