(完整版)matlabR2012a课后习题答案第三章
MATLAB答案

double Cs2 = sym
Cs3 =
sym Cs4 = sym
2. 在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是自由符号变量。
for k=1:m %m 决定循环次数
sa(k)=(aa+2*pi*(k-1))*n/m; %
计算各根的相角
end
result=(ma^(2/3)).*exp(j*sa) % result =
计ቤተ መጻሕፍቲ ባይዱ各根
-2.0000 + 3.4641i 4.0000 - 0.0000i -2.0000 - 3.4641i
( 2)
〖解答〗( 1)否;( 2)否。
123 7. 想要在 MATLAB中产生二维数组 S 456 ,下面哪些指令能实现目的?
789
(1) S=[1,2,3;4,5,6;7,8;9]
(2) S=[1 2 3;4 5 6;7 8 9]
(3) S=[1 , 2,3;4,5, 6;7,8, 9] % 整个指令在中文状态下输入
MATLAB R2012a 课后习题答案全解
第一章 基础准备及入门
习题 1 及解答
1. 数字 1.5e2 , 1.5e3 中的哪个与 1500 相同吗? 〖解答〗 1.5e3
2. 请指出如下 5 个变量名中,哪些是合法的?
abcd-2 xyz_3 3chan a 变量 ABCDefgh
〖解答〗 2、 5 是合法的。
3. 在 MATLAB环境中,比 1 大的最小数是多少?
〖解答〗 1+eps
4. 设 a = -8 , 运行以下三条指令,问运行结果相同吗?为什么?
w1=a^(2/3)
w2=(a^2)^(1/3)
信号与系统_MATLAB_实验_课后习题答案
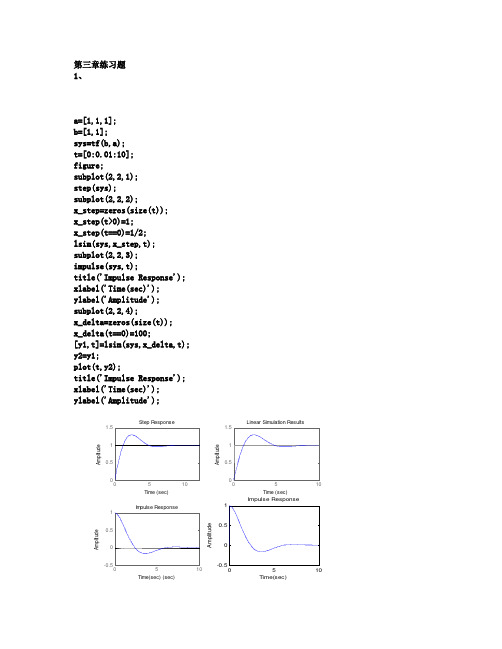
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下:t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下:function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同(b)Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数:Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统:Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统:Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。
matlab课后习题答案(附图)

matlab课后习题答案(附图)习题2.1画出下列常见曲线的图形y (1)⽴⽅抛物线3x命令:syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令:clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令:>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令:>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令:>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令:>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令:clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令:cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令:>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值(1)nnn n3→命令:>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3(2))121(lim n n n n ++-+∞→命令:>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0(3)x x x 2cot lim 0→命令:syms x ;>> limit(x*cot(2*x),x,0) ans = 1/2 (4))(coslimcm xx ∞→命令:syms x m ; limit((cos(m/x))^x,x,inf) ans = 1(5))111(lim 1--→exx x命令:syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) (6))(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分,并⽤diff 验证:(1)+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1)dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2)xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552(4)>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752(5) >> clear >> syms x1判断下列级数的收敛性,若收敛,求出其收敛值。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/306ff29b690203d8ce2f0066f5335a8102d266cb.png)
(完整版)MATLAB)课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值,然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤,其中t =0:0.5:2.5 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建⽴⼀个字符串向量,删除其中的⼤写字母。
解:(1) 结果:(2). 建⽴⼀个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵,试通过数值计算验证2 2E R RS A O S +??=。
解: M ⽂件如下;5. 下⾯是⼀个线性⽅程组:1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。
(2) 将⽅程右边向量元素b 3改为0.53再求解,并⽐较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M ⽂件如下:123d4e56g9实验三选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
解:M ⽂件如下:2. 输⼊⼀个百分制成绩,要求输出成绩等级A、B、C、D、E。
matlab课后习题及答案详解

matlab课后习题及答案详解第1章练习题1.安装matlab时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?在安装matlab时,安装内容由选择组件窗口中个复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即matlab选项)必须安装。
第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可。
2.matlab操作方式桌面存有几个窗口?如何并使某个窗口瓦解桌面沦为单一制窗口?又如何将瓦解过来的窗口再次置放至桌面上?与其他计算机语言相比较,matlab语言注重的特点就是什么?matlab系统由那些部分共同组成?在matlab操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的close按钮,一个是可以使窗口成为独立窗口的undock按钮,点击undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择dock……菜单项就可以将独立的窗口重新防止的桌面上。
matlab具备功能强大、使用方便、输出简便、库函数多样、开放性弱等特点。
matlab系统主要由开发环境、matlab数学函数库、matlab语言、图形功能和应用程序接口五个部分组成。
3.如何设置当前目录和搜寻路径,在当前目录上的文件和在搜寻路径上的文件存有什么区别?命令历史窗口除了可以观测前面键入的命令外,除了什么用途?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的setpath菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
命令历史窗口除了用作查阅以前键入的命令外,还可以轻易执行命令历史窗口中选取的内容、将选取的内容拷贝到剪贴板中、将选取内容轻易拷贝到m文件中。
MATLAB教程2012a第3章习题解答张志涌(可编辑修改word版)

F2a=b.^A F2 =
0.99095 -0.66337 F2a =
0.5 0.125
%标量底矩阵指数的求幂 %标量底数组指数的求幂
-0.44225 0.32759
0.25 0.0625
(3)
F3a=A.^C
F3a =
1
4
3
2
%数组底数组指数的求幂
F3=A^C
%矩阵底矩阵指数的求幂运算不存在
〖解答〗
A=magic(3), B=[1,2,1;3,4,3;5,6,7]%创建阵列
A=
8
1
6
3
5
7
4
9
2
B=
1
2
1
3
4
3
5
6
7
(1)
C1amb=A*B
C1bma=B*A C1amb =
41 56 53 53 68 67 41 56 45 C1bma = 18 20 22 48 50 52 86 98 86
后根据计算结果回答以下问题:
(提示:根据对计算结果的目测回答问题)
〖目的〗 数组运算和矩阵运算的不同。 如何判断两个双精度数组是否相等。 norm 指令的应用。
〖解答〗
A=[1, 2; 3, 4],b=0.5,C=[4, 2; 1, 0.5]
A=
1
2
3
4
b=
0.5
C=
4
2
1
0.5
%创建数据
(1)
第 3 章 数值阵列及其运算
习题 3 及解答
1 在 MATLAB 中,先运行指令 A=magic(3), B=[1,2,1;3,4,3;5,6,7]
matlab第三章课后部分答案

matlab第三章课后部分答案习题三3-2 从键盘输入一个三位整数,将它反向输出。
如输入639,输出为936程序如下:m=input('请输入一个三位整数:');m1=fix(m/100);%求m的百位整数m2=rem(fix(m/10),10);%求m的十位数字m3=rem(m,10);%求m的个位数字m=m3*100+m2*10+m1%反向输出m3-3 输入一个百分制成绩,要求输出成绩等级A,B,C,D,E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
程序如下:(1)if语句c=input('请输入成绩:');if c>=90&c<=100disp('A 成绩合理');elseif c>=80&c<=89disp('B 成绩合理');elseif c>=70&c<=79disp('C 成绩合理');elseif c>=60&c<=69disp('D 成绩合理');elseif c<60disp('E 成绩合理');elsedisp('成绩错误');end(2)switch语句c=input('请输入成绩:');switch fix(c)case num2cell(90:100)disp('A 成绩合理');case num2cell(80:89)disp('B 成绩合理');case num2cell(70:79)disp('C 成绩合理');case num2cell(60:69)disp('D 成绩合理');case num2cell(0:59)disp('E 成绩合理');otherwisedisp('成绩错误');end3-4 建立5*6矩阵,要求输出矩阵第N行元素。
(完整版)matlabR2012a课后习题答案第三章

第3章数值数组及其运算习题3及解答1要求在闭区间[0,2 ]上产生具有10个等距采样点的一维数组。
试用两种不同的指令实现。
〖目的〗数值计算中产生自变量采样点的两个常用指令的异同。
〖解答〗%方法一t1=li nspace(0,2*pi,10)%方法二t2=0:2*pi/9:2*pi %要注意采样间距的选择,如这里的2*pi/9.t1 =Colu mns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888Colu mns 8 through 104.88695.58516.2832t2 =Colu mns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888Colu mns 8 through 104.88695.58516.28322 由指令rng('default'),A=rand(3,5)生成二维数组A,试求该数组中所有大于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
〖目的〗数组下标的不同描述:全下标和单下标。
sub2ind, int2str, disp 的使用。
随机发生器的状态控制:保证随机数的可复现性。
〖解答〗rng('default')A=ra nd(3,5)[ri,cj]=fi nd(A>0.5);id=sub2 in d(size(A),ri,cj);ri=ri';cj=cj';disp('')disp(' 大于0.5的元素的全下标')disp([' 行号',i nt2str(ri)])disp([' 列号',i nt2str(cj)])disp('')disp(' 大于0.5的元素的单下标')disp(id')A =0.8147 0.9134 0.2785 0.9649 0.95720.9058 0.6324 0.5469 0.1576 0.48540.1270 0.0975 0.9575 0.9706 0.8003大于0.5 的元素的全下标行号 1 2 1 2 2 3 1 3 1 3列号 1 1 2 2 3 3 4 4 5 5大于0.5 的元素的单下标1 2 4 5 8 9 10 12 13 153 采用默认全局随机流,写出产生长度为1000的“等概率双位(即取-1,+1)取值的随机码”程序指令,并给出-1码的数目。
matlab课后答案完整版

matlab课后答案完整版ones表⽰1矩阵zeros表⽰0矩阵ones(4)表⽰4x4的1矩阵zeros(4)表⽰4x4的0矩阵zeros(4,5)表⽰4x5的矩阵eye(10,10)表⽰10x10的单位矩阵rand(4,5)表⽰4x5的伴随矩阵det(a)表⽰计算a的⾏列式inv(a)表⽰计算a的逆矩阵Jordan(a)表⽰求a矩阵的约当标准块rank(a)表⽰求矩阵a的秩[v,d]=eig(a)对⾓矩阵b=a’表⽰求a矩阵的转置矩阵sqrt表⽰求平⽅根exp表⽰⾃然指数函数log⾃然对数函数abs绝对值第⼀章⼀、5(1)b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12]; >> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112(2)a=50:1:100⼆、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =-0.09012、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)y =0.7218 1.0474-0.2180 1.15624、a*b表⽰a矩阵和b矩阵相乘a.*b表⽰a矩阵和b矩阵单个元素相乘A(m,n)表⽰取a矩阵第m⾏,第n列A(m,:)表⽰取a矩阵第m⾏的全部元素A(:,n)表⽰取a矩阵的第n列全部元素A./B表⽰a矩阵除以b矩阵的对应元素,B.\A等价于A./BA.^B表⽰两个矩阵对应元素进⾏乘⽅运算A.^2表⽰a中的每个元素的平⽅A^2表⽰A*A例:x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量(如y=2).底数也可以是标量(如x=2)5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =0.8660 + 0.5000id=c+a*b/(a+b)d =1.6353 + 1.8462i第⼆章⼆、4、(1)y=0;k=0;>> while y<3k=k+1;>> display([k-1,y-1/(2*k-1)])ans =56.0000 2.9944第三章⼆1(1) x=0:pi/10:2*pi; >> y=x-x.^3/6; >> plot(x,y)1234567-40-35-30-25-20-15-10-505(2)x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)012345670.20.40.60.811.21.41.6(3)x=-8:0.01:8; y=sqrt((64-x.^2)/2);plot(x,y)-8-6-4-2024680123456(4)t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t);-25-20-15-10-50510152025-30-20-10102030例3.4x=0:pi/100:2*pi; y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x); plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} '); >> xlabel('variable x'); >> ylabel('variable y'); >> text(1.5,0.5,'曲线y1=e^(-0.5x)'); >> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}'); >> legend('y1','y2')1234567-0.4-0.20.20.40.60.81x from 0 to 2πvariable xv a r i a b l e y曲线y1=e (-0.5x)曲线y2=cos(4πx)e -0.5xy1y22、(1)y1=2*x-0.5;t=linspace(0,pi,100); x=sin(3*t).*cos(t); y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2); >> t1=t(k) t1 =0 0.7933 1.04722.0944>> z=sin(3.*(t1)).*cos(t1) z =0 0.4841 0.0000 0.0000 -0.0000>> plot(t,x,t,y,'k:',t1,z,'bp');0.511.522.533.5-1-0.8-0.6-0.4-0.200.20.40.60.81(2)subplot(1,2,1); >> scatter(x1,y1,10); >> title('y=2x-0.5'); >> subplot(1,2,2); >> scatter(x,y,10)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.63、subplot(1,2,1); x=0:0.01:pi; y=sin(1./x); plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])1234-1-0.8-0.6-0.4-0.200.20.40.60.81204060801000.10.20.30.44、t=0:pi:2*pi; y=1./(1+exp(-t));subplot(2,2,1);%图形窗⼝的分割bar(t,'group'); %绘制柱形图(分组) subplot(2,2,2);barh(t,'stack');%绘制柱形图(堆积) subplot(2,2,3);loglog(t,y); %函数使⽤全对数坐标,x,y 均采⽤常⽤对数刻度 subplot(2,2,4); semilogy(t,y); %函数使⽤半对数坐标,y 轴为常⽤对数刻度,x 轴仍为线性刻度1230246802468123100.5100.710-0.01810-0.0010246810-0.310-0.210-0.15、(1)theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); (2)x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x)); polar(x,r);3021060240902701203001503301806、(1)t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t); >> y=exp((-t)/20).*sin(t); >> z=t; >> plot3(x,y,z);-1-0.50.51-1-0.50.5102468(2)t=0:0.01:1; x=t;>> y=t.^2; >> z=t.^3;>> plot3(x,y,z);0.20.40.60.800.20.40.60.817、x=-30:0.1:0; >> y=0:0.1:30;>> [x,y]=meshgrid(x,y); >>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2);>> meshc(x,y,z);绘制曲⾯图和等⾼线-30-20-10102030-4-202468、x=linspace(-3,3,100); >> y=linspace(-3,3,100); >> [x y]=meshgrid(x,y); %可以将向量转化为矩阵 >> fxy=-5./(1+x.^2+y.^2); >> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN; >>surf(x,y,fxy) %绘制三维曲⾯图-4-224-4-224-4-3-2-19、u=linspace(1,10,100); v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;-40-20-1010200100200300400第五章⼆1、a=rand(1,30000);mean(a) %求平均数 ans =0.5010 >>b=std(a) %求标准差 b =0.2882 >> c=max(a) c =0.9999 >> d=min(a) d =3.5706e-005size(find(a>0.5))/size(a) %求⼤于0.5的随机数个数占总数的百分⽐ans =0.50322、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500]; >> ww=interp1(h,w,hh,'spline')ww =6.4903 3.5226 2.3845 3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.') 123456789100.511.522.55、(1)、(2) p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.4656 0.6128 + 1.6278i 0.6128 - 1.6278i 1.2400-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a)%以矩阵a 为⾃变量 y2 =391 2084 3273 502 2693 4207 720 3775 5892 6、(1)z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根 z =-0.4903 第⼋章⼆、2t=0:pi/20:2*pi; x=sin(t); y=cos(t); x1=sin(7*t); y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2); set(gca,'xtick',-1:0.1:1); title('篮筐')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.91 -1-0.8-0.6-0.4-0.200.20.40.60.81篮筐3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2; h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3);text(5,2.4,'y=exp(-0.2*x).*cos(x)+2');02468101214161.41.61.822.22.42.62.83y=exp(-0.2*x).*cos(x)+24、t=-pi:pi/100:pi; x=cos(t); y=sin(t); z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);-4-3-2-101234-4-3-2-101234字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串(空格也算)ans =WELCOME TO BEIJING >> length(k)统计⼩写字母的个数ans = 14 例:已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0; >> n=100; >> for i=1:100; y=y+(-1)^(i-1)/i; end>> disp(y)0.6882绘制⼆维曲线图x=0:pi/100:2*pi; >> y1=0.2*exp(-0.5*x).*cos(4*pi*x); >> y2=1.5*exp(-0.5*x).*cos(pi*x); >> plotyy(x,y1,x,y2); 7-0.20.20123456-202绘制三维图像例:x=sint+tcost y=cost-tsint z=tt=0:pi/10:10*pi; x=sin(t)+t.*cos(t); y=cos(t)-t.*sin(t); z=t; plot3(x,y,z); axis([-30 30 -30 30 0 35]); 坐标轴的最⼤值与最⼩值title('line in 3-D space'); 图形的题⽬ >> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加⽹格线 -30-20-10102030-20205101520253035xline in 3-D spaceyz三维例]2/,0[],,0[,cos sin 22ππ∈∈+=y x y x z [x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]); 012340.511.5-1.5-1-0.500.511.5例3.16t=0:pi/20:2*pi; subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲⾯图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维⽹格图-11-10100.20.40.60.81-55-505-10-5510多项式求导例:f(x)=1/x^2+5 p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注:c=conv(a,b) 表⽰a 多项式与b 多项式乘积[p,r]=deconv(a,b) 表⽰a 多项式与b 多项式相除其中p 为商向量 r 为余数向量p=polyder(p) 表⽰求p 的导数 p=poleder(p,q) 表⽰求p 乘以q 的导数[p,q]=poleder(p,q) 表⽰p 除以q 的导数多项式求根例:f(x)=2x^4-12x^3+3x^2+5 p=[2,-12,3,0,5]; >> x=roots(p); >> p=[2,-12,3,0,5]; x=roots(p) 求⽅程f(x)=0的根 x =5.7246 0.8997 -0.3122 + 0.6229i -0.3122 - 0.6229i>> g=poly(x) 已知多项式的根求多项式 g =1.0000 -6.0000 1.5000 -0.00002.5000符号求导例7.3x=a(t-tsint)y=b(1-cost) 求y 对x 的⼀阶导数 syms x y a b t;>> f21=a*(t-sin(t)); >> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y 对x 的⼀阶导数ans =b*sin(t)/a/(1-cos(t))注:diff(f1,x,2) 表⽰f1对x 的⼆阶导数diff (f3,x )表⽰z 对x 的偏导 diff (f3,y )表⽰z 对y 的偏导求不定积分int(f) 求f 的不定积分 f1=int(f,a,b) 求f 在a ,b 之间的定积分eval (f1)计算积分值符号求极限例7.2 syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h 趋向于0ans =cos(x)例2f=sym('(1+t/x)^x');limit(f,inf) f趋向于⽆穷ans =exp(t)例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正⽆穷ans =1/2⼤⼩写ch='Welcome to Beijing';subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a');>> char(ch)ans =welcome to beijing>> length(k)ans =2。
MATLAB教程R2012a课后习题答案

习题
〖解答〗
1.5e3
abcd-2xyz_33chana变量ABCDefgh
〖解答〗
2、5是合法的。
〖解答〗
1+eps
w1=a^(2/3)
w2=(a^2)^(1/3)
w3=(a^(1/3))^2
〖解答〗
(1)不同。具体如下
w1=a^(2/3)%仅求出主根
w2=(a^2)^(1/3)%求出(-8)^2的主根
(2)x=pi/3
x=pi/3;a=x,b=sym(x),c=sym(x,'d'),d=sym('pi/3'),
a =
1.0472
b =
pi/3
c =
1.047197551196597631317786181171
d =
pi/3
v1=vpa(abs(a-d)),v2=vpa(abs(b-d)),v3=vpa(abs(c-d))
y2 =
piecewise([b <> 0, (a*a^k)/(a - b) - (b*b^k)/(a - b)])
d =
1/(a11*a22*a33 - a11*a23*a32 - a12*a21*a33 + a12*a23*a31 + a13*a21*a32 - a13*a22*a31)
〖目的〗
symsum, subs的应用。
从实例中,感受指令所给出的关于 符号解的含义。
〖解答〗
symsx k
f=x^(k);
d0_=limit(d,t,0,'left') %求dy/dt|t=0-
dpi_2=limit(d,t,pi/2) %求dy/dt|t=pi/2
matlab程序设计第三章课后习题答案资料

m a t l a b程序设计第三章课后习题答案1. p138 第6题在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。
>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)');>> plot(double(s.x),double(s.y),'*');截图:p366 第4题绘制极坐标曲线,并分析对曲线形状的影响。
function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0:0.01:2*pi;a=input('请输入a的值:');b=input('请输入b的值:');n=input('请输入n的值:');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1,b=1,n=1的极坐标图形为基础来分析a、b、n的影响。
对a的值进行改变:对比发现a只影响半径值的整倍变化对b的值进行改变:对比发现b的值使这个圆转换了一定的角度对n的值进行改变:对比发现当n>=2时有如下规律1、当n为整数时,图形变为2n个花瓣状的图形2、当n为奇数时,图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值,对比发现图形变为2n个花瓣状,并且还旋转了一定角度1 绘制sin(x)曲线,通过句柄修改曲线的颜色,要求:a)生成曲线的同时,获取句柄,再修改颜色;>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =174.0101>> set(h,'color','r');截图如下:b)先生成曲线,然后再获取句柄,再完成颜色修改。
Matlab第三章习题答案

Matlab第三章习题答案第三章3.5计算多项式乘法()()222254x x x x ++++>> a=[1 2 2];>> b=[1 5 4];>> c=conv(a,b)c =1 7 16 18 8poly2sym(c)ans =x^4 + 7*x^3 + 16*x^2 + 18*x + 83.6计算多项式的除法()()3231368/4x x x x ++++ >> a=[3 13 6 8];>> b=[1 4];>> [q r]=deconv(a,b)q =3 1 2r =0 0 0 0>> poly2sym(q)ans =3*x^2 + x + 23.8求多项式4324121459x x x x --++的微分和积分(1)微分:>> a=[4 -12 -14 5 9];>> b=polyder(a)b =16 -36 -28 5>> poly2sym(b)ans =16*x^3 - 36*x^2 - 28*x + 5(2)积分:polyint(a)ans =0.8000 -3.0000 -4.6667 2.5000 9.00000 >> poly2sym(ans)ans =(4*x^5)/5 - 3*x^4 - (14*x^3)/3 + (5*x^2)/2 + 9*x3.9求代数⽅程32349x x x +-+=0的解。
>> [x]=solve('x^3+3*x^2-4*x+9')x =- 7/(3*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 -1/108*108^(1/2)*4703^(1/2))^(1/3) - 17/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 - (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 - 1 7/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 + (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 – 1 3.10求线性⽅程组223430x xy y x x ?++=??-+=??的解 eqn1='x^2+x*y+y=3';>> eqn2='x^2-4*x+3=0';[x,y]=solve(eqn1,eqn2)x =13y =1-3/23.11求微分⽅程64dy y x dx=+的通解。
2012年MATLAB第三章-2.3.3

Ti (C ) 19.1
25.0 30.1 36.0
Ri ( ) 76.30 77.80 79.25 80.80
82.35 83.90 85.10
列表如下
正规方程组为
245.3 a0 565.5 7 245.3 9325.83 a 20029.445 1
27.0 26.8
建立y与t的关系 y=f(t)
先画出散点图
从图可看出y与t近似直线 y=a+bt
注意:因图不是严格的直线,所以a,b怎样选择都不可能使直
线 通过所有点 问题: 怎样选择a,b使得直线与实际情况近可能的接近。
由给定的点可写出如下方程组 a= 27.0
a+b=26.8
a+2b=26.5 …
求血药浓度随时间的变化规律c(t).
10
2
c(t ) c0 e
10
1
kt
c, k为待定系数
0 2 4 6 8
10
0
半对数坐标系(semilogy)下的图形
拟合问题实例3
已知某大学生工作以后6年的工资,预测他10年后的工资 x y 0 1 1 1.6 2 2.1 3 2.4 4 3.2 5 3.4
解方程组得
a0 70.572, a1 0.921
故得R与T的拟合直线为 R=70.572+0.921T
R=70.572+0.921T
利用上述关系式,可以预测不同温度时铜导线 的电阻值。例如由R=0 得T= 242.5 ,即预测温度
T 242.5C 时,铜导线无电租。
例2 已知实验数据如下表
x x 1 1 9 27 16 64 25 125 36 216 49 343 64 512 81 729 100 1000 381 3017
matlab r2012a习题答案

matlab r2012a习题答案Matlab R2012a习题答案Matlab是一种强大的数学软件,广泛应用于科学计算和工程领域。
对于初学者来说,掌握Matlab的使用技巧是非常重要的。
本文将提供Matlab R2012a版本的一些习题答案,帮助读者更好地理解和应用Matlab。
1. 习题一:编写一个Matlab程序,计算并输出1到100之间所有奇数的和。
解答:```sum = 0;for i = 1:2:100sum = sum + i;enddisp(sum);```该程序使用for循环遍历1到100之间的奇数,并将其累加到变量sum中。
最后使用disp函数输出结果。
2. 习题二:编写一个Matlab程序,求解一个二次方程的根。
解答:```a = input('请输入二次方程的系数a:');b = input('请输入二次方程的系数b:');c = input('请输入二次方程的系数c:');delta = b^2 - 4*a*c;if delta > 0x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);disp(['方程的两个实根分别为:', num2str(x1), '和', num2str(x2)]);elseif delta == 0x = -b/(2*a);disp(['方程有一个实根:', num2str(x)]);elsedisp('方程无实根');end```该程序通过用户输入二次方程的系数a、b和c,计算并输出方程的根。
使用if-else语句来处理不同的情况,包括判别式delta的值大于0、等于0和小于0的情况。
3. 习题三:编写一个Matlab程序,生成一个5×5的随机矩阵,并计算矩阵的行列式。
matlab课后习题参考答案

Matlab课后习题部分参考答案习题二2.student=struct('name',{'zhang','wang','li'},'age',{18,21,[] },'email',{['zh ang@','zhang@'],'',''})5、a=[1 0 0;1 1 0;0 0 1];b=[2 3 4;5 6 7;8 9 10];c=[a b]d=[a;b]c =1 0 023 41 1 0 5 6 70 0 1 8 9 10d =1 0 01 1 00 0 12 3 45 6 78 9 1010、reshape(c,2,9)1 0 1 0 1 5 3 9 71 0 0 02 8 6 4 10 reshape(d,2,9)ans =1 0 5 0 0 6 0 1 71 2 8 1 3 9 0 4 10 (注意:重新排列矩阵,是将原来的矩阵按列排序)11、a.’12、a+b a.*ba\b (即inv(a)*b,考试时,要求能自己手算出a的逆)ans =2 3 43 3 38 9 1013、c=4*ones(3);a>=cb>=c14.strcat('The picture is ','very good')a=['The picture is ','very good']18.double('very good')1.norm(A),det(A),rank(A)2.b=[1 1 1 1 1];c=b';a=[17,24,1,8,50;23,5,7,14,49;4,6,13,20,43;10,12,19,21,62;11,18,25,2,56]; x=a\c习题四1、a=14*rand(1,10)-5;for i=1:9max=i;for j=i+1:10if a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;enda将上述脚本保存为script41.m2、function y=function42(n)3*randn(1,n)+3;for i=1:n-1max=i;for j=i+1:nif a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;endy=a;将上述函数保存为function42.m 3、r=input(‘please input 1/2: ’);if r= =1script41;elsen=input(‘please input the length: ’);y=funtion42(n);end4.function f=function1(x,y)if y==1f=sin(x);elseif y==2f=cos(x);elsef=sin(x).*cos(x);end在命令窗口调用函数f=function1(1,3) 5.function result=function3(x,n)result=0;for i=1:nresult=result+sin(x.*i)+(-1).^i.*cos(i.*x); endfunction result=function4(n,t)result=0;A=[1 2 3;0 1 2;0 0 1];for i=1:nresult=result+A*i.*exp(A*i.*t);end习题五3.x1=-2:0.01:2;x2=-2:0.01:2;y1=x1.*sin(x2);y2=x2.*cos(x1);plot3(x1,x2,y 1,'-d',x1,x2,y2,'-d')14、x=8*rand(1,100)-2;y=reshape(x,10,10);save mydata.mat yclearclcload mydatak=y>ones(10);totel=0;for i=1:100if k(i)==1totel=totel+1;endend15、x=rand(5); %生成5*5均匀分布的随机矩阵(该处只作举例,未按题目要求)fid=fopen(‘text.txt’,’w’);count=fwrite(fid,x,’int32’); closestatus=fclose(fid);清除内存,关闭所有窗口fid=fopen(‘text.txt’,’r’);x=fread(fid,[5,5],’int32’); closestatus=fclose(fid); inv(x)16.随便生成一个矩阵,x1=-1:0.2:0.8;x2=-1:0.2:0.8;y1=x1.*sin(x2);y2=x2.*cos(x1);a=reshape([y1;y2],10,10);fid=fopen('table.txt','w'); fprintf (fid,‘%f’,a); fclose(fid) ;清除内存,关闭所有窗口a=fscanf('table.txt','%f') ; exp(a) ;fclose(fid) ;习题六1.c=ploy2str(A);B=[2,0,0,1,3,5];2.x=1:10;B=ployval(A,x);。
MATLAB矩阵处理_习题答案

第3章 MATLAB矩阵处理习题3一、选择题1.产生对角线上全为1,其余为0的2行3列矩阵的命令是()。
CA.ones(2,3) B.ones(3,2) C.eye(2,3) D.eye(3,2)2.建立3阶单位矩阵A的命令是()。
AA.A=eye(3) B.A=eye(3,1) C.A=eye(1,3) D.A=ones(3)3.产生和A同样大小的幺矩阵的命令是()。
BA.eye(size(A)) B.ones(size(A))C.size(eye(A)) D.size(ones(A))4.建立5×6随机矩阵A,其元素为[100,200]范围内的随机整数,相应的命令是()。
DA.A=fix(100+200*rand(5,6)) B.A=fix(200+100*rand(5,6))C.A= fix(100+300*rand(5,6)) D.A=fix(100+101*rand(5,6))5.产生均值为1、方差为的500个正态分布的随机数,相应的命令是()。
A。
A.1+sqrt*randn(25,20) B.1+*randn(500)C.+randn(500) D.+randn(25,20)6.从矩阵A提取主对角线元素,并以这些元素构成对角阵B,相应的命令是()。
BA.B=diag(A) B.B=diag(diag(A))C.B=diag(triu(A)) D.B=diag(tril(A))7.在MATLAB中定义A=randn(5,4,3,2),则下列关于A的操作中正确的是()。
DA.y=eig(A) B.y=reshape(A,[4 3 6 7])C.y=cond(A) D.y=sin(A)8.在命令行窗口中分别输入下列命令,对应输出结果正确的是()。
CA.命令x=[-2:2]',结果x=[-2 -1 0 1 2]B.命令x=zeros(1,2);x>0,结果ans=1C.命令y=diag(eye(3),1)',结果y=[0 0]D.命令5-10*rand(1,2),结果ans=[ ]9.将矩阵A对角线元素加30的命令是()。
(完整版)matlab经典习题及解答

(完整版)matlab经典习题及解答第1章 MATLAB 概论1.1 与其他计算机语⾔相⽐较,MATLAB 语⾔突出的特点是什么?MATLAB 具有功能强⼤、使⽤⽅便、输⼊简捷、库函数丰富、开放性强等特点。
1.2 MATLAB 系统由那些部分组成?MATLAB 系统主要由开发环境、MATLAB 数学函数库、MATLAB 语⾔、图形功能和应⽤程序接⼝五个部分组成。
1.4 MATLAB 操作桌⾯有⼏个窗⼝?如何使某个窗⼝脱离桌⾯成为独⽴窗⼝?⼜如何将脱离出去的窗⼝重新放置到桌⾯上?在MATLAB 操作桌⾯上有五个窗⼝,在每个窗⼝的右上⾓有两个⼩按钮,⼀个是关闭窗⼝的Close 按钮,⼀个是可以使窗⼝成为独⽴窗⼝的Undock 按钮,点击Undock 按钮就可以使该窗⼝脱离桌⾯成为独⽴窗⼝,在独⽴窗⼝的view 菜单中选择Dock ……菜单项就可以将独⽴的窗⼝重新防⽌的桌⾯上。
1.5 如何启动M ⽂件编辑/调试器?在操作桌⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M ⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊edit 命令时也可以启动M ⽂件编辑/调试器。
1.6 存储在⼯作空间中的数组能编辑吗?如何操作?存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
1.7 命令历史窗⼝除了可以观察前⾯键⼊的命令外,还有什么⽤途?命令历史窗⼝除了⽤于查询以前键⼊的命令外,还可以直接执⾏命令历史窗⼝中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M ⽂件中。
1.8 如何设置当前⽬录和搜索路径,在当前⽬录上的⽂件和在搜索路径上的⽂件有什么区别?当前⽬录可以在当前⽬录浏览器窗⼝左上⽅的输⼊栏中设置,搜索路径可以通过选择操作桌⾯的file 菜单中的Set Path 菜单项来完成。
在没有特别说明的情况下,只有当前⽬录和搜索路径上的函数和⽂件能够被MATLAB 运⾏和调⽤,如果在当前⽬录上有与搜索路径上相同⽂件名的⽂件时则优先执⾏当前⽬录上的⽂件,如果没有特别说明,数据⽂件将存储在当前⽬录上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章数值数组及其运算习题3及解答1 要求在闭区间]2,0[ 上产生具有10个等距采样点的一维数组。
试用两种不同的指令实现。
〖目的〗●数值计算中产生自变量采样点的两个常用指令的异同。
〖解答〗%方法一t1=linspace(0,2*pi,10)%方法二t2=0:2*pi/9:2*pi %要注意采样间距的选择,如这里的2*pi/9.t1 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.2832t2 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.28322 由指令rng('default'),A=rand(3,5)生成二维数组A,试求该数组中所有大于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
〖目的〗●数组下标的不同描述:全下标和单下标。
●sub2ind, int2str, disp的使用。
●随机发生器的状态控制:保证随机数的可复现性。
〖解答〗rng('default')A=rand(3,5)[ri,cj]=find(A>0.5);id=sub2ind(size(A),ri,cj);ri=ri';cj=cj';disp(' ')disp('大于0.5的元素的全下标')disp(['行号 ',int2str(ri)])disp(['列号 ',int2str(cj)])disp(' ')disp('大于0.5的元素的单下标')disp(id')A =0.8147 0.9134 0.2785 0.9649 0.9572 0.9058 0.6324 0.5469 0.1576 0.4854 0.1270 0.0975 0.9575 0.9706 0.8003大于0.5的元素的全下标行号 1 2 1 2 2 3 1 3 1 3 列号 1 1 2 2 3 3 4 4 5 5大于0.5的元素的单下标1 2 4 5 8 9 10 12 13 153 采用默认全局随机流,写出产生长度为1000的“等概率双位(即取-1,+1)取值的随机码”程序指令,并给出 -1码的数目。
〖目的〗● 两种基本随机发生器的使用。
● 关系运算产生逻辑数组——可用于数组的元素的标识和寻访。
● 逻辑数组的应用。
● 如何判断两个整数数组是否相等。
〖解答〗(1)运用均匀随机数解题法——解法1rng default %为以下结果重现而设;产生默认随机流。
详见第4.3.2节A=rand(1,1000); a=2*(A>0.5)-1; Na=sum(a==-1) Na =512(2)运用正态随机数解题法——解法2randn('state',123) B=randn(1,1000); b=2*(B>0)-1; Nb=sum(b==-1) Nb = 462(3)直接发生法——解法3c=randsrc(1,1000,[-1,1]); Nc=sum(c==-1) Nc =4824 已知矩阵⎥⎦⎤⎢⎣⎡=4321A ,运行指令B1=A.^(0.5), B2=A^(0.5), 可以观察到不同运算方法所得结果不同。
(1)请分别写出根据B1, B2恢复原矩阵A 的程序。
(2)用指令检验所得的两个恢复矩阵是否相等。
〖目的〗● 数组运算和矩阵运算的不同。
● 如何判断两个双精度数组是否相等。
●norm指令的应用。
〖解答〗A=[1,2;3,4];B1=A.^0.5B2=A^0.5A1=B1.*B1;A2=B2*B2;norm(A1-A2,'fro') % 求误差矩阵的F-范数,当接近eps量级时,就认为实际相等B1 =1.0000 1.41421.73212.0000B2 =0.5537 + 0.4644i 0.8070 - 0.2124i1.2104 - 0.3186i 1.7641 + 0.1458ians =8.4961e-016t5.0-6 先运行clear,format long,rng('default'),A=rand(3,3),然后根据A写出两个矩阵:一个对角阵B,其相应元素由A的对角元素构成;另一个矩阵C,其对角元素全为0,而其余元素与对应的A阵元素相同。
〖目的〗●常用指令diag的使用场合。
〖解答〗clear,format longrng('default')A=rand(3,3)B=diag(diag(A))C=A-BA =0.814723686393179 0.913375856139019 0.2784982188670480.905791937075619 0.632359246225410 0.5468815192049840.126986816293506 0.097540404999410 0.957506835434298B =0.814723686393179 0 00 0.632359246225410 00 0 0.957506835434298C =0 0.913375856139019 0.2784982188670480.905791937075619 0 0.5468815192049840.126986816293506 0.097540404999410 07 先运行指令x=-3*pi:pi/15:3*pi; y=x; [X,Y]=meshgrid(x,y);warning off; Z=sin(X).*sin(Y)./X./Y; 产生矩阵Z。
(1)请问矩阵Z中有多少个“非数”数据?(2)用指令surf(X,Y,Z); shading interp观察所绘的图形。
(3)请写出绘制相应的“无裂缝”图形的全部指令。
〖目的〗●初步感受三维曲面的绘制方法。
●非数NaN的产生,非数的检测,和对图形的影响。
●sum的应用。
●eps如何克服“被零除”的尴尬。
〖解答〗x=-3*pi:pi/15:3*pi;y=x;[X,Y]=meshgrid(x,y);warning offZ=sin(X).*sin(Y)./X./Y;NumOfNaN=sum(sum(isnan(Z))) %计算“非数”数目subplot(1,2,1),surf(X,Y,Z),shading interp,title('有缝图')%产生无缝图XX=X+(X==0)*eps;YY=Y+(Y==0)*eps;ZZ=sin(XX).*sin(YY)./XX./YY;subplot(1,2,2),surf(XX,YY,ZZ),shading interp,title('无缝图') NumOfNaN =1818 下面有一段程序,企图用来解决如下计算任务:有矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=k k k k k k k k 10229221911 A ,当k 依次取10, 9, 8, 7, 6, 5, 4, 3, 2, 1时,计算矩阵k A “各列元素的和”,并把此求和结果存放为矩阵Sa的第k 行。
例如3=k 时,A 阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡306329522841 ,此时它各列元素 的和是一个)101(⨯行数组[]87156 ,并把它保存为Sa 的第3行。
问题:该段程序的计算结果对吗?假如计算结果不正确,请指出错误发生的根源,并改正之。
〖目的〗● 正确理解sum 的工作机理。
● reshape 的应用。
〖解答〗(1)企图用以下程序完成题目要求。
for k=10:-1:1 A=reshape(1:10*k,k,10); Sa(k,:)=sum(A); end Sa Sa =55 55 55 55 55 55 55 55 55 55 3 7 11 15 19 23 27 31 35 39 6 15 24 33 42 51 60 69 78 87 10 26 42 58 74 90 106 122 138 154 15 40 65 90 115 140 165 190 215 240 21 57 93 129 165 201 237 273 309 345 28 77 126 175 224 273 322 371 420 469 36 100 164 228 292 356 420 484 548 612 45 126 207 288 369 450 531 612 693 774 55 155 255 355 455 555 655 755 855 955(2)正确性分析 除k=1外,计算所得Sa 所有行的结果都正确。
但k=1时,]10,,2,1[1 =A ,Sa 的第1A相同。
行应该与1上述程序的错误是对sum理解不正确。
sum对二维数组,求和按列施行;而对一维数组,不管行数组或列数组,总是求那数组所有元素的和。
正确的程序应该写成for k=10:-1:1A=reshape(1:10*k,k,10);Sa(k,:)=sum(A);if k==1Sa(k,:)=A;endendSaSa =1 2 3 4 5 6 7 8 9 103 7 11 15 19 23 27 31 35 396 15 24 33 42 51 60 69 78 8710 26 42 58 74 90 106 122 138 15415 40 65 90 115 140 165 190 215 24021 57 93 129 165 201 237 273 309 34528 77 126 175 224 273 322 371 420 46936 100 164 228 292 356 420 484 548 61245 126 207 288 369 450 531 612 693 77455 155 255 355 455 555 655 755 855 955。
