数学基础常用函数
高中数学基础之函数及其表示

1.一种优先意识 函数定义域是研究函数的基础依据,对函数的研究,必须坚持定义域优先的 原则. 2.两个关注点 (1)分段函数是一个函数. (2)分段函数的定义域、值域是各段定义域、值域的并集.
核心考点突破
考点一 函数的概念
【例1】 (1)下列对应是从集合A到B的函数是( A ) A.A=N,B=N,f:x→y=(x-1)2 B.A=N,B=R,f:x→y=± x C.A=N,B=Q,f:x→y=x-1 1 D.A={衡中高三·一班的同学},B=[0,150],f:每个同学与其高考数学的分 数相对应
为相等函数.
3.函数的表示法 表示函数的常用方法有 解析法 、图象法和 列表法 .
4.分段函数 (1)若函数在其定义域的不同子集上,因 对应关系 不同而分别用几个不同的
式子来表示,这种函数称为分段函数. (2)分段函数的定义域等于各段函数的定义域的 并集 ,其值域等于各段函数
的值域的 并集 ,分段函数虽由几个部分组成,但它表示的是一个函数.
角度3:待定系数法求函数解析式 【例2-3】 已知f(x)是一次函数,且满足3f(x+1)- 2f(x-1)=2x+17,则f(x)=__2_x_+__7__.
[思路引导] 设f(x)=ax+b(a≠0)→代入已知条件→解出a、b→得f(x).
[解析] 设f(x)=ax+b(a≠0),则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a -2b=ax+5a+b,
角度2:分段函数与不等式问题
【例3-2】 (1)已知函数f(x)= 1)≤1的解集是_(_-__∞__,__-__1_+___2_]_.
-x+1,x<0, x-1,x≥0,
则不等式x+(x+1)f(x+
(2)设函数f(x)= _a_≤___2___.
十个常用数学函数公式

十个常用数学函数公式数学函数是数学领域中常用的工具,用于描述和分析数学中的关系和规律。
下面是十个常用的数学函数及其公式:1.线性函数线性函数是最简单和最常见的函数形式之一、它的一般形式为y =mx + b,其中m是斜率,b是y轴截距。
线性函数表示了两个变量之间的直接比例关系。
2.二次函数二次函数是指一元二次方程y = ax² + bx + c所表示的函数。
其中a、b、c是常数,且a ≠ 0。
二次函数通常表示一个开口向上或者向下的抛物线。
3.指数函数指数函数是以一个固定底数为底的函数形式,表示为y=a^x。
其中a是底数,x是指数。
指数函数常用于描述指数增长和指数衰减。
4.对数函数对数函数是指数函数的反函数。
对数函数的一般形式为y = logₐ(x),表示找到a的多少次幂等于x。
对数函数常用于解决指数问题,如计算复利和对数衰减。
5.三角函数三角函数包括正弦函数、余弦函数和正切函数,它们是最基本的周期性函数。
正弦函数的一般形式为y = Asin(Bx + C) + D,其中A是振幅,B是频率,C是相移,D是垂直位移。
三角函数在几何、物理、工程和计算机图形等领域中得到广泛应用。
6.反三角函数反三角函数是三角函数的反函数。
常见的反三角函数包括反正弦函数、反余弦函数和反正切函数。
它们的函数形式和三角函数相反,可表示为y = sin⁻¹(x)、y = cos⁻¹(x)和y = tan⁻¹(x)。
7.指数增长和指数衰减函数指数增长和指数衰减函数描述了随着时间的推移,变量值按照指数规律增加或减少。
指数增长函数的一般形式为y = abˣ,其中a是初始值,b是增长因子。
指数衰减函数的一般形式为y = abˣ,其中a是初始值,b是衰减因子。
8.正态分布函数正态分布函数描述了连续随机变量的分布情况。
它的一般形式为y=e^(-(x-μ)²/2σ²)/(σ√(2π)),其中μ是均值,σ是标准差。
初中数学函数知识点汇总

初中数学函数知识点汇总(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如演讲稿、总结报告、合同协议、方案大全、工作计划、学习计划、条据书信、致辞讲话、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of classic sample essays, such as speech drafts, summary reports, contract agreements, project plans, work plans, study plans, letter letters, speeches, teaching materials, essays, other sample essays, etc. Want to know the format and writing of different sample essays, so stay tuned!初中数学函数知识点汇总函数作为数学基础知识点之一,学习好并且掌握函数是我们学习好数学的基础,下面是本店铺给大家带来的初中数学函数知识点汇总,希望能够帮助到大家!初中数学函数知识点汇总1、正比例函数及性质一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.注:正比例函数一般形式 y=kx (k不为零) ① k不为零② x 指数为1 ③ b取零当k>0时,直线y=kx经过三、一象限,从左向右上升,即随x 的增大y也增大;当k (1) 解析式:y=kx(k是常数,k≠0)(2) 必过点:(0,0)、(1,k)(3) 走向:k>0时,图像经过一、三象限;k (4) 增减性:k>0,y随x的增大而增大;k (5) 倾斜度:|k|越大,越接近y轴;|k|越小,越接近x轴2、一次函数及性质一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.注:一次函数一般形式 y=kx b (k不为零) ① k不为零②x指数为1 ③ b取任意实数一次函数y=kx b的图象是经过(0,b)和(-k/b,0)两点的一条直线,我们称它为直线y=kx b,它可以看作由直线y=kx平移|b|个单位长度得到.(当b>0时,向上平移;当b (1)解析式:y=kx b(k、b 是常数,k0)(2)必过点:(0,b)和(-k/b,0)(3)走向:k>0,图象经过第一、三象限;k b>0,图象经过第一、二象限;b (4)增减性:k>0,y随x的增大而增大;k (5)倾斜度:|k|越大,图象越接近于y轴;|k|越小,图象越接近于x轴.(6)图像的平移:当b>0时,将直线y=kx的图象向上平移b个单位;当b 初中数学一次函数知识点汇总3、一次函数y=kx+b的图象的画法.根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b),(-k/b,0).即横坐标或纵坐标为0的点。
高三数学高考基础知识复习:基本函数

高考数学基础知识复习:基本函数1知识清单:1.一元一次函数:)0(≠+=a b ax y ,当0>a 时,是增函数;当0<a 时,是减函数;2.一元二次函数:一般式:)0(2≠++=a c bx ax y ;对称轴方程是2b x a =-;顶点为24(,)24b ac b a a--;两点式:))((21x x x x a y --=;对称轴方程是;与x 轴的交点为; 顶点式:h k x a y +-=2)(;对称轴方程是;顶点为; ⑴一元二次函数的单调性:当0>a 时:为增函数;为减函数; 当0<a 时:为增函数;为减函数;⑵二次函数求最值问题:首先要采用配方法,化为h k x a y +-=2)(的形式, (Ⅰ)、若顶点的横坐标在给定的区间上,则当0>a 时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;当0<a 时:在顶点处取得最大值,最小值在距离对称轴较远的端点处取得;(Ⅱ)若顶点的横坐标不在给定的区间上,则当0>a 时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;当0<a 时:最大值在距离对称轴较近的端点处取得,最小值在距离对称轴较远的端点处取得; ⑶二次方程实数根的分布问题: 设实系数一元二次方程0)(2=++=c bx ax x f 的两根为21,x x ;则:另外:①二次方程f (x )=0的一根小于p ,另一根大于q (p <q )⇔()0()0a f p a f q ⋅<⎧⎨⋅<⎩。
②二次方程f (x )=0在区间(p ,q )内只有一根⇔f (p )·f (q )<0,或⎩⎨⎧>⋅=0)(0)(q f a p f (检验)或⎩⎨⎧>⋅=0)(0)(p f a q f (检验)。
③若在闭区间],[n m 讨论方程0)(=x f 有实数解的情况,可先利用在开区间),(n m 上实根分布的情况,得出结果,在令n x =和m x =检查端点的情况。
高中数学常见函数图像

高中数学常见函数图像高中数学是学生学习数学的一个重要阶段,其中函数图像是高中数学中的重要内容之一。
本文将介绍一些高中数学中常见的函数图像,包括正弦函数、余弦函数、指数函数和对数函数等。
首先,正弦函数和余弦函数是三角函数中的两个重要函数,它们的图像都是周期性的。
正弦函数的图像在区间[0,2π]上是一个完整的周期,最大值为1,最小值为-1。
余弦函数的图像也是一个完整的周期,最大值为1,最小值为-1。
余弦函数的图像相对于正弦函数来说是“平移”了一段时间。
其次,指数函数是指数运算的一种形式,其表达式为y=a^x,其中a 为大于0且不等于1的常数。
指数函数的图像在区间[0,∞)上是一个单调递增的曲线,当a大于1时,图像呈现出“陡峭”的趋势,当0小于a小于1时,图像呈现出“平缓”的趋势。
最后,对数函数是一种特殊的函数,其表达式为y=log(x),其中x 大于0且不等于1。
对数函数的图像在区间(0,∞)上是一个单调递增的曲线,呈现出“平缓”的趋势。
综上所述,高中数学中常见的函数图像包括正弦函数、余弦函数、指数函数和对数函数等。
这些函数的图像都具有不同的特点和性质,需要学生在学习过程中深入理解和掌握。
这些函数图像的应用也非常广泛,涉及到物理学、工程学、计算机科学等多个领域。
因此,学生应该在学习过程中注重实践和应用,加深对函数图像的理解和掌握。
高中数学函数的图像高中数学是许多学生感到困难的科目之一,而函数的学习更是其中的难点。
函数的图像是理解函数的重要工具,因此掌握函数的图像对于高中数学的学习非常重要。
函数的概念是指在一定的自变量取值范围内,对应于每个自变量的函数值都有唯一确定的数值。
函数的表示方法有很多种,其中图像法是最直观的方法之一。
函数的图像是在直角坐标系中表示函数关系的一种曲线。
在绘制函数的图像时,我们需要先确定自变量的取值范围,然后根据函数的表达式计算出对应的函数值。
将自变量和对应的函数值在直角坐标系中标记出来,然后连接这些点就可以得到函数的图像。
十个常用数学函数公式

十个常用数学函数公式一、一次函数的表达式与性质一次函数,也称为线性函数,其表达式为y=ax+b,其中a和b是常数,a不等于0。
其中,a称为斜率,决定了函数的斜率的大小和正负方向;b称为截距,决定了函数与y轴的交点位置。
一次函数的图像是一条直线,具有直线的特性,如对称性和平移性等。
二、二次函数的表达式与性质二次函数,其表达式为y=ax^2+bx+c,其中a、b和c是常数,a 不等于0。
二次函数的图像是一个抛物线,具有开口方向、顶点坐标和对称轴等性质。
通过二次函数的图像,可以判断该函数的最大值或最小值,以及抛物线的开口方向。
三、指数函数的表达式与性质指数函数,其表达式为y=a^x,其中a是常数,且a大于0且不等于1。
指数函数的图像是一个逐渐增长或逐渐减小的曲线,具有指数增长和指数衰减的特性。
指数函数的图像在x轴上有一水平渐近线,且图像通过点(0, 1)。
四、对数函数的表达式与性质对数函数,其表达式为y=loga(x),其中a是常数,且a大于0且不等于1。
对数函数的图像是一条逐渐增长或逐渐减小的曲线,具有对数增长和对数衰减的特性。
对数函数的图像在y轴上有一垂直渐近线,且图像通过点(1, 0)。
五、三角函数的表达式与性质三角函数包括正弦函数、余弦函数和正切函数等。
正弦函数的表达式为y=sin(x),余弦函数的表达式为y=cos(x),正切函数的表达式为y=tan(x)。
三角函数的图像是周期性的曲线,具有周期、幅值和相位等特性。
三角函数的图像在特定区间内可以取得最大值和最小值。
六、双曲函数的表达式与性质双曲函数包括双曲正弦函数、双曲余弦函数和双曲正切函数等。
双曲正弦函数的表达式为y=sinh(x),双曲余弦函数的表达式为y=cosh(x),双曲正切函数的表达式为y=tanh(x)。
双曲函数的图像是一条渐近于直线的曲线,具有对称性和渐进线等特性。
七、多项式函数的表达式与性质多项式函数,其表达式为y=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0,其中a_n、a_{n-1}、...、a_1和a_0是常数,n 是非负整数。
常用三角函数计算公式

常用三角函数计算公式在数学中,三角函数是一类基础的数学函数,它们与三角形的边长关系密切相关。
常用的三角函数有正弦函数、余弦函数和正切函数。
下面是一些常用的三角函数计算公式。
1. 正弦函数(sin):正弦函数表示一个角的正弦值与其对边与斜边之比。
在单位圆上,一个角对应于圆周上的一个弧,弧的长度即为角的大小。
常用的正弦函数公式如下:- sin(θ + π) = -sin(θ) (正弦函数的周期性)- sin(θ + 2π) = sin(θ)- sin(π/2 - θ) = cos(θ) (正弦函数的补角关系)- sin(θ + π/2) = cos(θ)- sin(π/2 + θ) = cos(θ)- sin(π - θ) = sin(θ) (正弦函数的对称性)- sin(2θ) = 2sin(θ)cos(θ) (正弦函数的倍角公式)2. 余弦函数(cos):余弦函数表示一个角的余弦值与其邻边与斜边之比。
在单位圆上,余弦值等于角对应的点的横坐标。
常用的余弦函数公式如下:- cos(θ + π) = -cos(θ) (余弦函数的周期性)- cos(θ + 2π) = cos(θ)- cos(π/2 - θ) = sin(θ) (余弦函数的补角关系)- cos(θ + π/2) = -sin(θ)- cos(π/2 + θ) = -sin(θ)- cos(π - θ) = -cos(θ) (余弦函数的对称性)- cos(2θ) = cos²(θ) - sin²(θ) (余弦函数的倍角公式)3. 正切函数(tan):正切函数表示一个角的正切值与其对边与邻边之比。
在单位圆上,正切值等于角对应的点的纵坐标与横坐标之比。
常用的正切函数公式如下:- tan(θ) = sin(θ) / cos(θ) (正切函数与正弦、余弦的关系)- tan(θ + π) = tan(θ) (正切函数的周期性)- tan(θ + 2π) = tan(θ)- tan(π/2 - θ) = 1/tan(θ) (正切函数的补角关系)- tan(π/2 + θ) = -1/tan(θ)- tan(π - θ) = -tan(θ) (正切函数的对称性)- tan(2θ) = 2tan(θ) / (1 - tan²(θ)) (正切函数的倍角公式)除了上述的基本公式外,三角函数还有很多推导公式和恒等式,用于推导和证明其他数学问题。
高中数学函数基础知识

高中数学函数基础知识高中数学中,函数是一个非常重要的概念,贯穿于整个数学学科的各个领域中。
掌握函数基础知识,对于高中学生来说是至关重要的。
本文将系统地介绍高中数学函数的基础知识,帮助学生更好地理解和掌握这一概念。
1. 函数的定义函数是一种特殊的关系,即对每一个定义域中的元素,有且只有一个对应的值。
通俗地讲,函数就是一种“输入-输出”的关系,每个输入对应唯一的输出。
数学上用符号f(x) 来表示函数,其中x 表示自变量,f(x) 表示因变量。
形式化地定义,若对于每个 x∈X,存在唯一的 y∈Y,使得对于每个 x,都有唯一的 y 与之对应,则称 f 为定义在 X 上的函数,其中 X 为定义域,Y 为值域。
2. 函数的图象与性质函数的图象是函数 f(x) 在直角坐标系中的几何表示。
通过绘制函数的图象,我们可以直观地看出函数的性质,如单调性、奇偶性、周期性等。
对于一元函数 f(x),其图象通常是一条曲线或者曲线段。
通过观察函数的图象,我们可以更深入地理解函数的性质。
3. 函数的表示方法函数可以通过各种形式进行表示,常见的表示方法包括解析式表示、列表法、集合法等。
其中,解析式表示是最常见的形式,如 f(x) = x²表示一个函数关系。
此外,函数还可以通过函数图像、函数表格等形式进行表示,以便更加清晰地展示函数的性质。
4. 基本函数在高中数学中,常见的基本函数包括线性函数、二次函数、指数函数、对数函数、三角函数等。
这些基本函数在数学中起着重要的作用,通过熟练掌握这些基本函数的性质和图象,可以更好地理解和运用函数的相关知识。
5. 函数的运算函数之间可以进行各种运算,如加法、减法、乘法、除法、复合运算等。
通过函数的运算,可以得到新的函数,对于复杂的函数关系可以通过适当的运算进行简化和分解,便于进行进一步的分析和求解。
6. 函数的应用函数在现实生活中有着广泛的应用,如描述物体的运动规律、经济学中的供求关系、生物学中的生长模型等。
6类基本初等函数以及三角函数(考研数学基础)
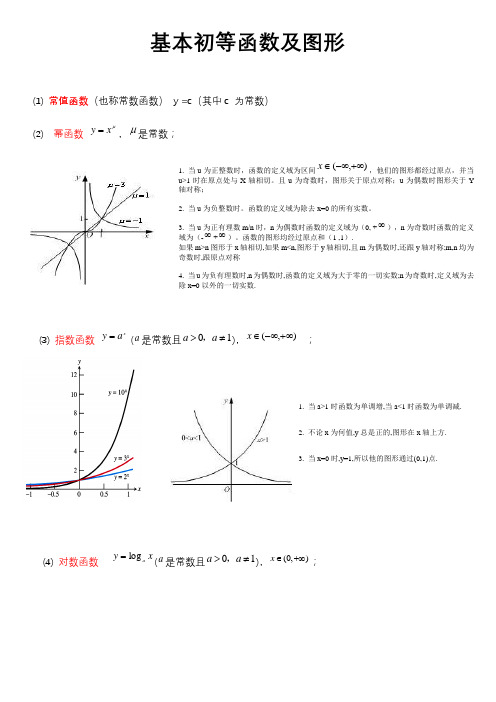
基本初等函数及图形(1) 常值函数(也称常数函数) y =c (其中c 为常数)(2) 幂函数 μx y =,μ是常数;(3) 指数函数 xa y = (a 是常数且01a a >≠,),),(+∞-∞∈x ;(4) 对数函数x y a log =(a是常数且01a a >≠,),(0,)x ∈+∞;1. 当u 为正整数时,函数的定义域为区间),(+∞-∞∈x ,他们的图形都经过原点,并当u>1时在原点处与X 轴相切。
且u 为奇数时,图形关于原点对称;u 为偶数时图形关于Y 轴对称;2. 当u 为负整数时。
函数的定义域为除去x=0的所有实数。
3. 当u 为正有理数m/n 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞+∞)。
函数的图形均经过原点和(1 ,1).如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n 均为奇数时,跟原点对称4. 当u 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数.1. 当a>1时函数为单调增,当a<1时函数为单调减.2. 不论x 为何值,y 总是正的,图形在x 轴上方.3. 当x=0时,y=1,所以他的图形通过(0,1)点.(5) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;1. 他的图形为于y 轴的右方.并通过点(1,0)2. 当a>1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1, +∞),y 值为正,图形位于x 轴上方.在定义域是单调增函数. a<1在实用中很少用到/(6)反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .小结:(a 为任意实数)(正弦函数)正弦函数是奇函数且三角公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦:r y =αsin 余弦:r x=αcos 正切:xy=αtan 余切:y x =αcot正割:xr=αsec 余割:y r =αcsc注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
十个常用数学函数公式

十个常用数学函数公式数学函数是描述数值之间关系的一种工具,可以帮助我们理解和解决各种数学问题。
在数学中,有许多常用的数学函数公式,下面是十个常见的数学函数公式:1.平方函数公式:f(某)=某^2,其中某是任意实数。
该函数的图像是一个平滑的开口向上的抛物线。
2.立方函数公式:f(某)=某^3,其中某是任意实数。
该函数的图像是一个平滑的开口向上的抛物线。
3.开方函数公式:f(某)=√某,其中某是非负实数。
该函数的图像是一个从原点出发的逐渐上升的曲线。
4. 正弦函数公式:f(某) = sin(某),其中某是弧度。
该函数的图像是一个周期性的波动曲线,取值范围在-1到1之间。
5. 余弦函数公式:f(某) = cos(某),其中某是弧度。
该函数的图像也是一个周期性的波动曲线,取值范围在-1到1之间,但与正弦函数相位差。
6. 正切函数公式:f(某) = tan(某),其中某是弧度。
该函数的图像是一个周期性的波动曲线,取值范围在负无穷到正无穷之间。
7.指数函数公式:f(某)=a^某,其中a是大于0且不等于1的常数,某是任意实数。
该函数的图像是一个逐渐上升或下降的曲线。
8. 对数函数公式:f(某) = log_a(某),其中a是大于0且不等于1的常数,某是大于0的实数。
该函数的图像是一个逐渐上升或下降的曲线,是指数函数的反函数。
9.绝对值函数公式:f(某)=,某,其中某是任意实数。
该函数的图像是以原点为对称轴的V形曲线,取值范围在0到正无穷之间。
10.阶乘函数公式:f(某)=某!,其中某是非负整数。
该函数表示某的阶乘,即从1到某的所有正整数的乘积。
这些常用数学函数公式在各个数学领域中都有广泛的应用,如代数、几何、微积分等。
它们的图像和性质对于建立数学模型、解决实际问题以及深入理解数学概念都起到了重要的作用。
数学基础-三角函数

同时我们定义正角三角形中:正割:sec
A
斜边 A的邻边
c b
,
余割:csc
A
斜边 A的对边
c a
tan cot 1 sin csc 1 cos sec 1
tan sin / cos cot cos / sin
sin2 cos2 1 tan2 1 sec2 1 cot2 csc2
例题 3:计算 tan 60 sin2 45 2 cos30 的值.
解: tan 60 sin2 45 2 cos 30
3
2 2
2
2
31 22
练习 3:计算 2 cos 30 2 sin 45 tan 60 的值.
例题 4:已知角 的终边经过 p(4,3) ,求 sin,cos, tan,cot,sec,csc 的值.
图1
公元前 600 年左右古希腊学者泰勒斯利用相似三角形的原理测出金字塔的高,成为西方
三角测量的肇始。他首先步测金字塔底座的边,确定它的尺寸。接着关注金字塔的高度,步
测从金字塔的一条边到它投下的阴影顶点处的距离,估计出从金字塔基座中心到阴影顶端的
长度为 310 步。而他知道自己的身高为 3 步,测得他的影子长度为 5 步。利用现有的信息,
因此 sin 370
cos 370
tan 370
53o 的直角三角形三边比为
还要记住,随着 增大, sin
sin 00
, sin 900
因此 sin 530
cos 530
tan 530
(填增大或减小), cos
(填增大或减小)。
cos 00
, cos 900
2. sin330°=
初中高中数学七大函数的性质 图像

初中高中数学七大函数的性质图像1.一次函数(包括正比例函数)最简单最常见的函数,在平面直角坐标系上的图象为直线。
定义域(下面没有说明的话,都是在无特殊要求情况下的定义域):R值域:R奇偶性:无周期性:无平面直角坐标系解析式(下简称解析式):①ax+by+c=0[一般式]②y=kx+b[斜截式](k为直线斜率,b为直线纵截距,正比例函数b=0)③y-y1=k(x-x1)[点斜式](k为直线斜率,(x1,y1)为该直线所过的一个点)④(y-y1)/(y2-y1)=(x-x1)/(x2-x1)[两点式]((x1,y1)与(x2,y2)为直线上的两点)⑤x/a-y/b=0[截距式](a、b分别为直线在x、y轴上的截距)解析式表达局限性:①所需条件较多(3个);②、③不能表达没有斜率的直线(平行于x轴的直线);④参数较多,计算过于烦琐;⑤不能表达平行于坐标轴的直线和过圆点的直线。
倾斜角:x轴到直线的角(直线与x轴正方向所成的角)称为直线的倾斜角。
设一直线的倾斜角为a,则该直线的斜率k=tg(a)。
2.二次函数:题目中常见的函数,在平面直角坐标系上的图象是一条对称轴与y轴平行的抛物线。
定义域:R值域:(对应解析式,且只讨论a大于0的情况,a小于0的情况请读者自行推断)①[(4ac-b^2)/4a,正无穷);②[t,正无穷)奇偶性:偶函数周期性:无解析式:①y=ax^2+bx+c[一般式]⑴a≠0⑵a>0,则抛物线开口朝上;a<0,则抛物线开口朝下;⑶极值点:(-b/2a,(4ac-b^2)/4a);⑷Δ=b^2-4ac,Δ>0,图象与x轴交于两点:([-b+√Δ]/2a,0)和([-b+√Δ]/2a,0);Δ=0,图象与x轴交于一点:(-b/2a,0);Δ<0,图象与x轴无交点;②y=a(x-h)^2+t[配方式]此时,对应极值点为(h,t),其中h=-b/2a,t=(4ac-b^2)/4a);3.反比例函数在平面直角坐标系上的图象为双曲线。
五大基本初等函数

五大基本初等函数五大基本初等函数是数学中的重要概念,用于阐明计算机科学中的方程和数学关系。
熟悉了五大基本初等函数,可以更好地理解和分析复杂的数学概念,如几何形状的性质,三角函数的解析和复数的运算和表示等。
以下是五大基本初等函数:1. 指数函数指数函数是指其函数图像呈指数状,是数学上最简单也是最常用的函数,在很多领域都有广泛应用,比如利息计算,复利计算,对数函数中出现概述等。
指数函数是由一个有意义的变量间的关系而构成的,通常用数学表示为y=a^x(其中a为任意正值),其函数图形曲线具有经典的指数曲线特点,曲线的斜率随自变量x的取值变大而变大,变化趋势是上升的。
2. 对数函数对数函数是建立在指数函数基础上的一种反函数,通常用数学表示为y=logaX(a为任意正值),它和指数函数正好相反,而且它是一种以底数为任意正数的单调变换,它的函数图像是一条函数线段,随变量x 的取值变大,函数的值也在增大,但是斜率却有在、趋向-∞的趋势,因此从该函数的性质可以看出它又是一种指数函数的相反函数。
3. 线性函数线性函数是数学中的重要函数,通常用数学表示为y=kax+b(其中a,k为任意实数),比较常见的有一元一次函数和一元二次函数,线性函数的函数图像是一条直线段,它体现了因变量和自变量之间线性的变化特征,线性函数的斜率和截距也是它的重要特征,它可以直观地表示出变量之间的函数关系,但是有些非线性的问题却无法通过线性函数来完美地描述。
4. 幂函数幂函数是类似指数函数的一种特殊函数,通常用数学表示为y= aX^k (其中a,k为任意实数),它具有指数函数强调的指数状特征,但是有所不同,它不仅包括k=1时的指数函数,还包含k>1和k<1时的函数,而函数非线性曲线一般为鹰眼状,斜率具有变大或变小的特点,它有良好的平稳特征,可以用于描述不同数量的衰减或增长的函数关系。
5. 双曲函数双曲函数是一类特殊的曲线函数,具有指数函数和对数函数的结合。
高中数学函数知识点归纳

高中数学函数知识点归纳高中数学函数知识点归纳(上)函数是高中数学中一个非常重要的知识点,是数学中的基础概念之一。
函数的研究和应用贯穿于高中数学的整个教学过程。
下面将对高中数学中函数的知识点进行系统的归纳总结。
一、函数的定义及其表达方式1. 函数的定义函数是指在两个集合之间有规律地对应元素的关系。
一般地,设A、B是两个非空集合,则f是从A到B的函数,如果对于任意的a∈A,有且只有一个b∈B与之对应,即f(a)=b,称b是a的像,a是b的原像,记作f:A→B。
2. 函数的表达方式(1)显式表达式:y=f(x),y是关于x的函数,f(x)是y的表达式。
(2)参数方程:x=f(t),y=g(t),t是参数,x和y均为t的函数。
(3)极坐标方程:r=f(θ),θ是极角,r是极径。
二、函数的性质及其应用1. 奇偶性设f(x)是定义在R上的函数,如果对于任意x有f(-x)=-f(x),则称f(x)是奇函数。
如果对于任意x有f(-x)=f(x),则称f(x)是偶函数。
如果函数既不是奇函数也不是偶函数,则称其为一般函数。
奇偶性可以通过图像的对称性来判断。
2. 周期性设f(x)是定义在R上的函数,如果存在一个正数T,使得对于任意x有f(x+T)=f(x),则称f(x)是周期函数,T称为函数的周期。
周期性可以通过函数的图像来判断。
3. 单调性设f(x)是定义在[a,b]上的函数,如果对于任意的x1<x2有f(x1)≤f(x2),则称f(x)在[a,b]上是单调不降的;如果对于任意的x1<x2有f(x1)≥f(x2),则称f(x)在[a,b]上是单调不增的;如果存在x1<x2,使得f(x1)<f(x2),则称f(x)在[a,b]上是单调递增的;如果存在x1<x2,使得f(x1)>f(x2),则称f(x)在[a,b]上是单调递减的。
4. 函数的极限当自变量趋近于某一值的时候,函数值也会趋近于某一值,这种趋近可以用极限来描述。
函数概念与基本初等函数高中数学知识点总结

函数概念与基本初等函数高中数学知识点总结函数是数学中一种重要的概念,它描述了一种特定的关系,将一个集合的元素映射到另一个集合的元素。
函数在高中数学中占据了重要的地位,是数学学习的基础。
在这篇文章中,我们将总结函数的概念以及一些基本的初等函数的知识点。
一、函数的概念函数是一种特定的关系,它将一个集合的元素映射到另一个集合的元素。
通常用字母f表示函数,例如f(x)。
其中x是函数的自变量,f(x)是函数的值或因变量。
函数的定义域是自变量可能取值的集合,值域是函数可能取值的集合。
函数可以用图像、表格或公式来表示。
函数有一些重要的特点:1.单值性:对于定义域中的每个自变量值,函数只能有一个对应的值。
2.定义域:函数的自变量可能取值的集合。
3.值域:函数的值可能取值的集合。
4.对称性:函数可能具有一些对称性质,例如奇函数和偶函数。
5.增减性:函数可能随着自变量的增大或减小而增加或减少。
初等函数是一类经过常见运算(加法、减法、乘法、除法、乘方、开方等)和函数复合(如求和、求积、复合函数等)得到的函数。
下面是一些常见的初等函数及其特点和知识点:1.幂函数:幂函数的表达式是y=x^m,其中m是实数。
幂函数的图像可能是一条直线、二次曲线、指数曲线等。
幂函数的正负性、单调性和奇偶性与指数m的关系密切。
2.指数函数:指数函数的表达式是y=a^x,其中a是大于0且不等于1的实数。
指数函数的图像是一个递增的曲线。
指数函数的性质包括连续性、正负性、单调性和极限等。
3.对数函数:对数函数的表达式是 y = log_a(x),其中 a 是大于 0 且不等于 1 的实数。
对数函数是指数函数的反函数,其图像是对数曲线。
对数函数的性质包括连续性、正负性、单调性和极限等。
4.三角函数:三角函数包括正弦函数、余弦函数、正切函数等。
它们的图像是周期性的波浪曲线。
三角函数的性质包括周期性、奇偶性、单调性和求导等。
5.反三角函数:反三角函数是指正弦函数、余弦函数、正切函数的反函数,用sin^(-1)(x)、cos^(-1)(x)、tan^(-1)(x) 表示。
十个常用数学函数公式

十个常用数学函数公式1. 线性函数:y = mx + c,其中 m 是斜率,c 是 y 轴截距。
2.幂函数:y=x^n,其中n是常数。
3.指数函数:y=a^x,其中a是底数,x是指数。
4. 对数函数:y = log_a x,其中 a 是底数,x 是对数。
5. 三角函数:sin(x), cos(x), tan(x),常用来描述角度和周期性。
6. 反三角函数:arcsin(x), arccos(x), arctan(x),常用来求解角度。
7. 椭圆函数:y = a cos(bx) 或 y = a sin(bx),常用来描述周期性。
8.高斯函数:y=e^(-x^2),常用在概率分布和统计学中。
9.函数逼近:泰勒级数,用一系列多项式逼近函数的方法。
10.分段函数:根据不同的条件,给出不同的函数表达式,常用于物理和工程问题的建模。
这些常用数学函数公式在科学、工程、数学和计算机科学等领域中起着重要的作用。
它们有着广泛的应用,以下是一些实际应用的示例:1.线性函数可用于描述物体的速度、加速度与时间的关系。
在工程中,线性函数也可以用来进行线性回归分析,预测未来的趋势。
2.幂函数在物理学中常用来描述力、质量和距离之间的关系。
例如,牛顿万有引力定律中的F=G(m1m2/r^2),其中F是引力,m1、m2是质量,r是距离。
3.指数函数常见于自然增长和衰减的过程。
例如,放射性衰变中的核素数量随时间的变化常用指数函数来表示。
4.对数函数在应用中常用于描述复杂度和增长率。
例如,在算法分析中,对数函数可以描述一些算法的运行时间。
5.三角函数在几何学、物理学和工程学中广泛应用。
例如,通过正弦函数和余弦函数可以描述物体的周期性运动。
6.反三角函数可用于计算角度,例如在三角学和几何学中。
在导航和图像处理中,反三角函数也常用于确定对象在图像中的位置。
7.椭圆函数在电子工程和天体物理学中使用广泛。
例如,通过椭圆函数可以描述地球的形状和轨道。
常见数学函数

2.1 基本数学函数2.1.1 三角函数与双曲函数函数 sin 、sinh功能 正弦函数与双曲正弦函数格式 Y = sin(X) %计算参量X (可以是向量、矩阵,元素可以是复数)中每一个角度分量的正弦值Y ,所有分量的角度单位为弧度。
Y = sinh(X) %计算参量X 的双曲正弦值Y 注意:sin(pi)并不是零,而是与浮点精度有关的无穷小量eps ,因为pi 仅仅是精确值π浮点近似的表示值而已;对于复数Z= x+iy ,函数的定义为:sin(x+iy) = sin(x)*cos(y) +i*cos(x)*sin(y),2e e )z sin(iziz --=,2e e )z sin(z z --=例2-1x = -pi:0.01:pi; plot(x,sin(x))x = -5:0.01:5; plot(x,sinh(x))图形结果为图2-1。
图2-1 正弦函数与双曲正弦函数图函数 asin 、asinh功能 反正弦函数与反双曲正弦函数格式 Y = asin(X) %返回参量X (可以是向量、矩阵)中每一个元素的反正弦函数值Y 。
若X 中有的分量处于[-1,1]之间,则Y = asin(X)对应的分量处于[-π/2,π/2]之间,若X 中有分量在区间[-1,1]之外,则Y= asin(X)对应的分量为复数。
Y = asinh(X) %返回参量X 中每一个元素的反双曲正弦函数值Y 说明 反正弦函数与反双曲正弦函数的定义为:)z 1z i l n(i z s i n a 2-+⋅⋅-=,)z 1z ln(z sinh a 2++=例2-2x = -1:.01:1; plot(x,asin(x)) x = -5:.01:5; plot(x,asinh(x))图形结果为图2-2。
图2-2 反正弦函数与反双曲正弦函数图函数 cos 、cosh功能 余弦函数与双曲余弦函数格式 Y = cos(X) %计算参量X (可以是向量、矩阵,元素可以是复数)中每一个角度分量的余弦值Y ,所有角度分量的单位为弧度。
数学基础常用函数

求 f(-x/2+p/4)
§0-1 常用函数—变型(练习)
f(x)={ cos(x), |x|p/2 0 其它 求 f (-x/2+p/4)
-p/2 f(x) x
0
p/2
解: f(-x/2+p/4)= f[- (x- p/2)/2],包含折叠、扩展、平移 先折叠, 偶函数折叠后不变 再扩展, 最后平移
§0-1 常用函数 (续)
六、高斯函数 Gaussian Function Gaus(x) = exp(-px2) Gaus(0) = 1 S=1 是非常平滑的函数,即 各阶导数均连续.
二维情形:
Gaus(x)Gaus(y)=exp[- p(x2+y2)] 可代表单模激光束的光强分布
Gaus(x)
第一部分 数学基础
§0-1 常用函数 —变型
f(x)
x
f(x- x0) x0 x
f(x/a) x
f(-x) x
bf(x) -f(x) x x
平移
(原点移至x0)
比例缩放
折叠
取反
与f(x)关于x轴 镜像对称
倍乘
y方向幅度变 化
a>1, 在x方向展宽a倍 与f(x)关于y轴 a<1, 在x方向压缩a倍 镜像对称
sin2(px) (px)2
sinc (x) sinc2(x) 1
数互为傅里叶变换 • 物理上,单一矩形脉冲 rect(t)的频谱是sinc函数; 单缝的夫琅和费衍射花 样是sinc函数
-1
0
1
x
二维sinc函数: sinc(x)sinc(y)
sinc2(0)=1, S = 1 与sinc(x)相比,曲线形状不同, 但曲线下面积相同,为什么?
高中数学 14种函数图像和性质知识解析 新人教A版必修1

高中数学 14种函数图像和性质知识解析新人教A版必修1高中不得不掌握的函数图像与常用性质高中常用函数有14种,它们是:1.正比例函数;2.反比例函数;3.根式函数;4一次函数;5.二次函数;6双勾函数.;7..双抛函数;8.指数函数;9对数函数;10.三角函数;11分段函数.;12.绝对值函数;13.超越函数;14.抽象函数。
而函数的性质常见的有:1.定义域;2.值域;3.单调性;4.奇偶性;5.周期性;6.对称性;7.有界性;8.反函数;9.连续性.高中都是从函数解析式入手画出函数图像,再利用函数图像研究其性质,下面我们就函数的图像和性质做归纳总结。
1.正比例函数解析式图像定义域:值域:单调性:奇偶性:反函数:2.反比例函数解析式图像性质定义域:值域:单调性:奇偶性:反函数:对称性:定义域:值域:单调性:对称性:3根式函数解析式图像定义域:值域:单调性:奇偶性:反函数:4一次函数解析式图像定义域:值域:1 性质性质性质用心爱心专心单调性:反函数:5二次函数解析式图像定义域:值域:单调性:对称性:定义域:值域:单调性:对称性:6.双勾函数解析式图像定义域:值域:单调性:奇偶性:对称性:定义域:值域:单调性:奇偶性:对称性:7.双抛函数解析式图像定义域:值域:单调性:奇偶性:对称性:定义域:性质性质性质用心爱心专心值域:单调性:奇偶性:对称性:8.指数函数解析式图像定义域:值域:单调性:9.对数函数解析式图像定义域:值域:单调性:10.三角函数解析式图像单调性:周期性:奇偶性:有界性:对称性:定义域:值域:单调性:周期性:奇偶性:有界性:对称性:定义域:值域:单调性:周期性:奇偶性:有界性:对称性:定义域:值域:单调性:周期性:奇偶性:有界性:对称性:11.分段函数分段函数是在其定义域的不同子集上,分别用几个不同的式子来表示对应关系的函数,它是一类较特殊的函数。
其图像的画法是按定义域的划分分别作图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§0-1 常用函数 (续)
三.矩形函数 Rectangle Function
定义
re(x c) t 1, 0,
x其 1 2,标 它准 :re(型 x c- a tx0) 1 0 ,,
x-x01 a2 其它
原型特点: rect(0)=1, 矩形宽度=1,矩形面积=1, 偶函数
rect(x) 1
七、圆域函数 Circular Function
定义: circ(r) = cir(cx2y2)1,
0,
x2y2 1 其它
circ函数是不可分离变量的二元函数
描述无穷大不透明屏上半径为1的圆孔的透过率
1y
0
x
a 0
circ
x2 y 2
a
§0-1 常用函数 (续)
八、复指数函数 Complex exponential function
再扩展, 最后平移
x
-p/2
0 p/2
注意:曲线下面积:
S f(x)dx -
在缩放前后的变化
§0-1 常用函数
注意:1.函数在时域和空域各代表什么物理对象 2. 一维向二维扩展,各代表什么物理对象
一. 阶跃函数 Step Function
1 , x>0 定义: Step(x)={ 1/2, x=0
x- x 0 1 a 其它
tri(x) 1 -1 0 1 x
1 -a+x0
x x0 a+x0
底宽: 2 最大值:tri(0)=1 曲线下面积: S=1
底宽:2|a|, 面积: S= |a|
又写成:L(x)
要关注它和矩形函数的关系
§0-1 常用函数 (续)
五、sinc函数
原 :s型 i(x n ) s cip x n ), (标:s 准 i(x n - x 型 0 c )
§0-1 常用函数—变型(例)
例:
f(x)={
x, 0
0<x<1 其它
f(x) 0 1x
求 f(-2x+4)
解: f(-2x+4)= f[-2(x-2)],包含折叠、压缩、平移
先折叠
再压缩
最后平移
f(-x)
f(-2x)
f[-2(x-2)]
-1 0
x
-1/2 0 x
0 3/2 x
练习:f(x)={cos(x),
§0-1 常用函数 (续)
六、高斯函数 Gaussian Function
Gaus(x) = exp(-px2)
Gaus(0) = 1
S=1 是非常平滑的函数,即
各阶导数均连续.
Gaus(x)
x
0
二维情形: Gaus(x)Gaus(y)=exp[- p(x2+y2)] 可代表单模激光束的光强分布
§0-1 常用函数 (续)
课堂练习(要求写在作业本上)
0-1. 已知函数
U(x)=Aexp(j2pf0x)
求下列函数,并作出函数的图形 (1) | U(x) |2 (2) U(x) + U*(x) (3) | U(x) + U*(x) |2 0-2. 已知函数 f(x)=rect(x+2)+rect(x-2) 求下列函数,并作出函数的图形. (1) f(x-1) (2) f(x)sgn(x)
x -1/2 0 1/2
快门; 单缝, 矩孔,区域限定
y
x0
0
a
x
rect(x-x0 ) a
y
a x0, y0 b
0
x
a
rec (xt-x0)rec (yt-y0)
a
b
§0-1 常用函数 (续)
四、三角形函数 Triangle Function
原 :t型 ( rx )i 1 0 - ,x,其 x 1 ,标 它 :准 t( rx- ia x 0 型 ) 1 0 - ,x- a x 0,
课堂练习(要求写在作业本上)
0-3. 画出下列函数的图形 (1) f(x)recxt-recxt
4 2
(2) g(x)2trix-trix()
2
(3)
h(x)2trix-2trix() 2
(4) p(x)trix()stex)p(
0, x<0
Step(x) 1
0
x
0
x
代表:开关, 无穷大半平面屏
§0-1 常用函数 (续)
二. 符号函数 Signum
{ 1 , x>0
定义: Sgn(x)= 0, x=0
-1, x<0
原型
Sgn(x) 1
与 Step函数的关系: Sgn(x)=2 Step (x)-1
0 -1
x
代表“p”相移器、反相器
p x
a
sinc(x) 1
-1 1
特点:
0ቤተ መጻሕፍቲ ባይዱ
x
最大值:sinc(0)=1;lim
sinc(x)=0
曲线下面积: S=1,偶x函数
0点位置:x=n (n=1, 2, 3…)等间隔
两个一级0点之间的主瓣宽度=2
1
a+x0
x
x0 -a+x0
§0-1 常用函数
五.sinc函数(续)
Sinc函数的重要性:
附: sinc2函数 sinc2(x)=[sinc(x)]2
• 数学上,sinc函数和rect函 数互为傅里叶变换
sin2(px)
• 物理上,单一矩形脉冲
(px)2
rect(t)的频谱是sinc函数; 单缝的夫琅和费衍射花
sinc2(x)
sinc (x) 1
样是sinc函数
0
-1 1
x
二维sinc函数: sinc(x)sinc(y)
sinc2(0)=1, S = 1 与sinc(x)相比,曲线形状不同, 但曲线下面积相同,为什么?
0
|x|p/2 其它
求 f(-x/2+p/4)
§0-1 常用函数—变型(练习)
f(x)={
cos(x), 0
|x|p/2 其它
求 f (-x/2+p/4) -p/2
f(x)
x
0
p/2
解: f(-x/2+p/4)= f[- (x- p/2)/2],包含折叠、扩展、平移
先折叠, 偶函数折叠后不变
f(-x)
Aexp(jq)=Acosq +jAsinq
w = 2pn
A
q
0
对于简谐振动,q = 2pn t
q:振子的位相角
推广到二维:
Aexp[j 2p (fxx+fyy)]
注意
以上定义的函数,其宗量均无量纲. 在处理 实际问题时,要根据所取的单位采用适当的 缩放因子.
例: 以 rect(x) 代表单缝. 若x单位为cm, 则 rect(x) 代表宽度为1cm 的单缝.若x单位 为mm,则 rect(x/10) 代表宽度为1cm 的单缝.
