高考数学选择试题分类汇编 直线与圆
高考数学-圆和直线位置关系练习题

2
2
.
10. 已知圆 C: x y 2 x ay 3 0 (a 为实数)上任意一点关于直线 l:x-y+2 =0 对称的点都在圆 C 上,则 a= 三、解答题 11. 已知圆 C : x y 2 x 4 y 4 0 , 问是否存在斜率为 1 的直线 l , 使直线 l 被圆 C 截得的弦为 AB ,且以 AB 为直径的圆经过原点,若存在,写出直线 l 的方程,若不存在, 请说明理由. 12. 在平面直角坐标系 xOy 中,二次函数 f ( x ) x 2 x b ( x R )与两坐标轴有
2 2
7. 圆 x y 1 与直线 y kx 2 没有 公共点的充要条件是 ( .. A. k ( 2, 2) C. k ( 3, 3) 二、填空题
B. k (, 2) ( 2, ) D. k (, 3) ( 3, )
8. 经 过 圆 x 2 x y 0 的 圆 心 C , 且 与 直 线 x y 0 , 垂 直 的 直 线 方 程 是 ________________. 9. 直线 l 与圆 Cx2+y2+2x-4y+a=0(a<3)相交于 A,B 两点,弦 AB 的中点为 M (0,1) ,则直线 l 的方程为
2 2
D. x 2 y 5
3.由点 P (1,3) 引圆 x y 9 的切线的长是 ( A. 2 A. 2 ( ) A. 相离 B. 相交 C. 内切 B.
19
B. 1
2 2
C. 1
4. 三直线 ax 2 y 8 0,4 x 3 y 10,2 x y 10 相交于一点,则 a 的值是( D. 1
5. 已知两圆的方程是 x y 1 和 x y 6 x 8 y 9 0 ,那么两圆的位置关系是 D. 外切 ( ) B. 必要而不充分条件 D. 既不充分也不必要条件 )
高考数学分类汇编直线方程与圆的方程

2012年高考数学分类汇编 直线方程与圆的方程一、选择题1 .(2012年高考(陕西理))已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则 ( )A .l 与C 相交B .l 与C 相切C .l 与C 相离D .以上三个选项均有可能2 .(2012年高考(天津理))设m ,n R ∈,若直线(1)+(1)2=0m x n y ++-与圆22(1)+(y 1)=1x --相切,则+m n 的取值范围是( )A .[1B .(,1[1+3,+)-∞-∞C .[2-D .(,2[2+22,+)-∞-∞3 .(2012年高考(重庆文))设A,B 为直线y x =与圆221x y += 的两个交点,则||AB =( )A .1BCD .24 .(2012年高考(陕西文))已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则 ( )A .l 与C 相交B .l 与C 相切 C .l 与C 相离D .以上三个选项均有可能5 .(2012年高考(山东文))圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为( )A .内切B .相交C .外切D .相离6 .(2012年高考(辽宁文))将圆x 2+y 2-2x-4y+1=0平分的直线是 ( )A .x+y-1=0B .x+y+3=0C .x-y+1=0D .x-y+3=07 .(2012年高考(湖北文))过点(1,1)P 的直线,将圆形区域{}22(,)|4x y xy +≤分两部分,使得这两部分的面积之差最大,则该直线的方程为 ( )A .20x y +-=B .10y -=C .0x y -=D .340x y +-=8 .(2012年高考(广东文))(解析几何)在平面直角坐标系xOy 中,直线3450x y +-=与圆224x y +=相交于A 、B 两点,则弦AB 的长等于( )A .B .CD .19 .(2012年高考(福建文))直线20x +-=与圆224x y +=相交于,A B 两点,则弦AB的长度等于 ( )A .B .CD .110 .(2012年高考(大纲文))正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC上,13AB BF ==动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为 ( )A .8B .6C .4D .311.(2012年高考(安徽文))若直线10x y -+=与圆22()2x a y -+=有公共点,则实数a 取值范围是 ( )A .[3,1]--B .[1,3]-C .[3,1]-D .(,3][1,)-∞-+∞12 .(2012年高考(重庆理))对任意的实数k,直线y=kx+1与圆222=+y x 的位置关系一定是( ) A .相离 B .相切 C .相交但直线不过圆心D .相交且直线过圆心二、填空题13.(2012年高考(浙江文))定义:曲线C 上的点到直线l 的距离的最小值称为曲线C 到直线l的距离,已知曲线C 1:y=x 2+a 到直线l:y=x 的距离等于曲线C 2:x 2+(y+4)2=2到直线l:y=x 的距离,则实数a=_______.14.(2012年高考(天津文))设,m n R ∈,若直线:10l mx ny +-=与x 轴相交于点A ,与y 轴相交于B ,且l 与圆224x y +=相交所得弦的长为2,O 为坐标原点,则AOB ∆面积的最小值为_________.15.(2012年高考(上海文))若)1,2(=是直线l 的一个方向向量,则l 的倾斜角的大小为__________(结果用反三角函数值表示). 16.(2012年高考(山东文))如图,在平面直角坐标系xOy 中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P 的位置在(0,0),圆在x 轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,OP 的坐标为____.17.(2012年高考(江西文))过直线0x y +-=上点P 作圆221x y +=的两条切线,若两条切线的夹角是60︒,则点P 的坐标是__________。
高考数学试题分类汇编——直线与圆

高考数学试题分类汇编直线与圆一. 选择题:1.(全国一10)若直线1x ya b+=与圆221x y +=有公共点,则( D )A .221a b +≤B .221a b +≥C .22111a b+≤D .2211a b+≥12.(全国二3)原点到直线052=-+y x 的距离为( D ) A .1B .3C .2D .53.(全国二6)设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值为( D ) A .2-B .4-C .6-D .8-4.(安徽卷10)若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( D )A .[3,3]B .(3,3)C .33[33-D .33(,)33-5.(安徽卷11) 若A 为不等式组002x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域,则当a 从-2连续变化到1时,动直线x y a += 扫过A 中的那部分区域的面积为 ( C )A .34B .1C .74D .56.(北京卷6)若实数x y ,满足1000x y x y x ⎧-+⎪+⎨⎪⎩,,,≥≥≤则2z x y =+的最小值是( A )A .0B .12C .1D .27.(福建卷2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的C A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件8.(福建卷10)若实数x 、y 满足10,0,2,x y x x -+≤⎧⎪⎨⎪≤⎩则y x 的取值范围是DA.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞)9.(广东卷6)经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是( C )A 、10x y ++=B 、10x y +-=C 、10x y -+=D 、10x y --=10.(海南卷10)点P (x ,y )在直线4x + 3y = 0上,且满足-14≤x -y ≤7,则点P 到坐标原点距离的取值范围是( B )A. [0,5]B. [0,10]C. [5,10]D. [5,15]11.(湖北卷5)在平面直角坐标系xOy 中,满足不等式组,1x y x ⎧≤⎪⎨⎪⎩的点(,)x y 的集合用阴影表示为下列图中的C12.(湖南卷3.已条变量y x ,满足⎪⎩⎪⎨⎧≤-≤≥,0,2,1y x y x 则y x +的最小值是( C )A .4 B.3 C.2 D.113.(辽宁卷3)圆221x y +=与直线2y kx =+没有..公共点的充要条件是( B ) A .(22)k ∈-,B . (33)k ∈-,C .(2)(2)k ∈--+∞,,∞D .(3)(3)k ∈--+∞,,∞ 14.(辽宁卷9)已知变量x y ,满足约束条件1031010y x y x y x +-⎧⎪--⎨⎪-+⎩≤,≤,≥,则2z x y =+的最大值为( B ) A .4B .2C .1D .4-15.(山东卷11)若圆C 的半径为1,圆心在第一象限,且与直线430x y -=和x 轴相切,则该圆的标准方程是( B )A .227(3)13x y ⎛⎫-+-= ⎪⎝⎭B .22(2)(1)1x y -+-=C .22(1)(3)1x y -+-=D .223(1)12x y ⎛⎫-+-= ⎪⎝⎭16.(陕西卷5)直线30x y m -+=与圆22220x y x +--=相切,则实数m 等于( A )A 3或3-B .3-33C .33-3D .3-3317.(四川卷6)直线3y x =绕原点逆时针旋转090,再向右平移1个单位,所得到的直线为( A )(A)1133y x =-+ (B)113y x =-+(C)33y x =- (D)113y x =+18.(天津卷2)设变量x y ,满足约束条件012 1.x y x y x y -⎧⎪+⎨⎪+⎩≥,≤,≥则目标函数5z x y =+的最大值为( D ) A .2B .3C .4D .519.(浙江卷10)若0,0≥≥b a ,且当⎪⎩⎪⎨⎧≤+≥≥1,0,0y x y x 时,恒有1≤+by ax ,则以a ,b 为坐标点(,)P a b 所形成的平面区域的面积等于C (A )12 (B )4π (C )1 (D )2π 20.(重庆卷3)曲线C :cos 1.sin 1x y θθ=-⎧⎨=+⎩(θ为参数)的普通方程为C(A)1)1()1(22=++-y x(B)1)1()1(22=+++y x(C) 1)1()1(22=-+-y x(D)1)1()1(22=-++y x二. 填空题:1.(全国一13)若x y ,满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤则2z x y =-的最大值为 .92.(福建卷14)若直线3x+4y +m =0与圆x 2+y 2-2x +4y +4=0没有公共点,则实数m 的取值范围是 . (,0)(10,)-∞⋃+∞3.(广东卷12)若变量x ,y 满足240,250,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩则z =3x +2y 的最大 值是________。
高考数学真题分类汇编 9.3 直线与圆、圆与圆的位置关系 理 (1)

§9.3 直线与圆、圆与圆的位置关系考点直线与圆、圆与圆的位置关系1(2014江西,9,5分)在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为( )A.πB.πC.(6-2)πD.π答案 A2.(2014课标Ⅱ,16,5分)设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是.答案[-1,1]3.(2014江苏,9,5分)在平面直角坐标系xOy中,直线x+2y-3=0被圆(x-2)2+(y+1)2=4截得的弦长为.答案4.(2014湖北,12,5分)直线l1:y=x+a和l2:y=x+b将单位圆C:x2+y2=1分成长度相等的四段弧,则a2+b2= .答案 25.(2014重庆,13,5分)已知直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=4相交于A,B两点,且△ABC为等边三角形,则实数a= .答案4±6.(2014江苏,18,16分)如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=.(1)求新桥BC的长;(2)当OM多长时,圆形保护区的面积最大?解析解法一:(1)如图,以O为坐标原点,OC所在直线为x轴,建立平面直角坐标系xOy.由条件知A(0,60),C(170,0),直线BC的斜率k BC=-tan∠BCO=-.因为AB⊥BC,所以直线AB的斜率k AB=.设点B的坐标为(a,b),则k BC==-,k AB==.解得a=80,b=120.所以BC==150.因此新桥BC的长是150 m.(2)设保护区的边界圆M的半径为r m,OM=d m(0≤d≤60).由条件知,直线BC的方程为y=-(x-170),即4x+3y-680=0.由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,即r==. 因为O和A到圆M上任意一点的距离均不少于80 m,所以即解得10≤d≤35.故当d=10时,r=最大,即圆面积最大.所以当OM=10 m时,圆形保护区的面积最大.解法二:(1)如图,延长OA,CB交于点F.因为tan∠FCO=,所以sin∠FCO=,cos∠FCO=.因为OA=60,OC=170,所以OF=OCtan∠FCO=,CF==,从而AF=OF-OA=.因为OA⊥OC,所以cos∠AFB=sin∠FCO=.又因为AB⊥BC,所以BF=AFcos∠AFB=,从而BC=CF-BF=150.因此新桥BC的长是150 m.(2)设保护区的边界圆M与BC的切点为D,连结MD,则MD⊥BC,且MD是圆M的半径,并设MD=r m,OM=d m(0≤d≤60).因为OA⊥OC,所以sin∠CFO=cos∠FCO.故由(1)知sin∠CFO====,所以r=.因为O和A到圆M上任意一点的距离均不少于80 m,所以即解得10≤d≤35.故当d=10时,r=最大,即圆面积最大.所以当OM=10 m时,圆形保护区的面积最大.。
高考数学真题题型分类解析专题专题07 直线与圆

高考数学真题题型分类解析高考数学真题题型分类解析 专题07直线与圆直线与圆命题解读考向考查统计1.高考对直线的考查,重点是直线的倾斜角与斜率、直线方程的求法、两条直线的位置关系、距离公式、对称问题等。
2.高考对圆的考查,重点是圆的标准方程与一般方程的求法,除了待定系数法外,要特别要重视利用几何性质求解圆的方程。
同时,除了直线与圆、圆与圆的位置关系的判断,还特别要重视直线与圆相交所得弦长及相切所得切线的问题。
3.其他就是直线、圆与其他知识点的交汇。
直线与圆的位置关系2023·新高考Ⅰ卷,62022·新高考Ⅱ卷,152023·新高考Ⅱ卷,152024·新高考Ⅱ卷,10(多选题的一个选项中考查)圆与圆的位置关系2022·新高考Ⅰ卷,14直线的斜率2022·新高考Ⅱ卷,3命题分析2024年高考新高考Ⅰ卷未直接考查直线与圆的相关知识点,Ⅱ卷在多选题的一个选项中考到了直线与圆相切的问题,其实在压轴题中也有直线斜率的影子,后续专题再呈现。
其实直线与圆直接考查的话,难度一般是较易的,一般计算不出错即可。
在一些上难度的题型中,往往有直线斜率的一些影子。
直线与圆考查应关注:直线、圆的方程及位置关系,直线方程的求解、直线过定点问题的求解、含参直线方程中参数取值范围求解、直线与圆的位置关系中涉及的弦长与切线方程的求解。
以常规题型、常规解法为主要方向,常结合基本不等式、函数、三角形面积等知识考查最值问题。
预计2025年高考还是主要考查直线与圆的位置关系。
试题精讲一、多选题1.(2024新高考Ⅱ卷·10)抛物线C :24y x =的准线为l ,P 为C 上的动点,过P 作22:(4)1A x y +−=⊙的一条切线,Q 为切点,过P 作l 的垂线,垂足为B ,则( )A .l 与A 相切B .当P ,A ,B 三点共线时,||PQ =C .当||2PB =时,PA AB ⊥D .满足||||PA PB =的点P 有且仅有2个一、单选题1.(2023新高考Ⅰ卷·6)过点()0,2−与圆22410x y x +−−=相切的两条直线的夹角为α,则sin α=( )A .1B2.(2022新高考Ⅱ卷·3)图1是中国称为步,垂直距离称为举,图2是某古1111,,,OD DC CB BA 是相等的步,相邻桁的成公差为0.1的等差数列,且直线A .0.75B .0.8C .0.85D .0.93.(2022新高考Ⅰ卷·14)写出与圆是中国古代建筑中的举架结构,,,,AA BB CC DD ′′′′是桁是某古代建筑屋顶截面的示意图.其中111,DD CC 邻桁的举步之比分别为1111111,0.5,DD CC BB k OD DC CB ==OA 的斜率为0.725,则3k =( )与圆221x y +=和22(3)(4)16x y −+−=都相切的一条直是桁,相邻桁的水平距离1,,BB AA 是举,1231,AAk k BA ==.已知123,,k k k 一条直线的方程.由图像可知由图像可知,,共有三条直线符合条件又由方程22(3)(4)16x y −+−=和x 即为过两圆公共切点的切线方程即为过两圆公共切点的切线方程,,又易知两圆圆心所在直线OC 的方程为直线OC 与直线10x +=的交点为条件条件,方程为(当切线为l时,因为14 3OOk=,所以O到l的距离||19116td==+,解得当切线为m时,设直线方程为kx由题意211344pkk p=+++=,解得kp.(新高考卷)设点有公共点,则a的取值范围是.5.(2023新高考Ⅱ卷·15)已知直线:10l x my −+=与2:14C x y −+= 交于A ,B 两点,写出满足“ABC面积为85”的m 的一个值.一、直线的倾斜角和斜率1、直线的倾斜角若直线l 与x 轴相交,则以x 轴正方向为始边,绕交点逆时针旋转直至与l 重合所成的角称为直线l 的倾斜角,通常用,,, αβγ表示(1)若直线与x 轴平行(或重合),则倾斜角为0 (2)倾斜角的取值范围[0),∈απ 2、直线的斜率设直线的倾斜角为α,则α的正切值称为直线的斜率,记为tan =k α (1)当2=πα时,斜率不存在;所以竖直线是不存在斜率的(2)倾斜角α与斜率k 的关系当0=k 时,直线平行于轴或与轴重合;当0>k 时,直线的倾斜角为锐角,倾斜角随k 的增大而增大; 当0<k 时,直线的倾斜角为钝角,倾斜角随k 的增大而增大; 3、过两点的直线斜率公式已知直线上任意两点,11(),A x y ,22(),B x y 则2121−=−y y k x x (1)直线的斜率是确定的,与所取的点无关.(2)若12=x x ,则直线AB 的斜率不存在,此时直线的倾斜角为90° 4、三点共线两直线,AB AC 的斜率相等→、、A B C 三点共线;反过来,、、A B C 三点共线,则直线,AB AC 的斜率相等(斜率存在时)或斜率都不存在.二、直线的方程1、直线方程的五种形式在已知曲线类型的前提下,求曲线(或直线)方程的思路通常有两种:(1)直接法:寻找决定曲线方程的要素,然后直接写出方程,例如在直线中,若用直接法则需找到两个点,或者一点一斜率(2)间接法:若题目条件与所求要素联系不紧密,则考虑先利用待定系数法设出曲线方程,然后再利用条件解出参数的值(通常条件的个数与所求参数的个数一致) 3、线段中点坐标公式若点12,P P 的坐标分别为1122()(),,,x y x y 且线段12PP 的中点M 的坐标为(),x y ,则121222+= + = x x x y y y ,此公式为线段12PP 的中点坐标公式. 4、两直线的夹角公式若直线11y k x b =+与直线22y k x b =+的夹角为α,则2112tan 1k k k k α−=+.三、两直线平行与垂直的判定两条直线平行与垂直的判定以表格形式出现,如表所示. 两直线方程平行垂直11112222:0:0++=++=l A x B y C l A x By C1221122100且−=−≠A B A B B C B C12120+=A A B B111222::=+=+l y k x b l y k x b (斜率存在)11,22::==l x x l x x (斜率不存在)1212,=≠k k b b 或 1212,,==≠x x x x x x121=−i k k 或12与k k 中有一个为0,另一个不存在.四、三种距离1、两点间的距离平面上两点111222(,),(,)P x y P x y 的距离公式为12||=P P. 特别地,原点O (0,0)与任一点P (x ,y )的距离||=OP 2、点到直线的距离点000(,)P x y 到直线:0++=l Ax By C 的距离=d 特别地,若直线为l :x =m ,则点000(,)P x y 到l 的距离0||=−d m x ;若直线为l :y =n ,则点000(,)P x y 到l 的距离0||=−d n y 3、两条平行线间的距离已知12,l l 是两条平行线,求12,l l 间距离的方法:(1)转化为其中一条直线上的特殊点到另一条直线的距离.(2)设1122:0,:0++=++=l Ax By C l Ax By C ,则1l 与2l 之间的距离=d注:两平行直线方程中,x ,y 前面对应系数要相等. 4、双根式双根式()=±f x 型函数求解,首先想到两点间的距离,或者利用单调性求解.五、圆1、圆的四种方程(1)圆的标准方程:222()()−+−=x a y b r ,圆心坐标为(a ,b ),半径为(0)>r r(2)圆的一般方程:22220(40)++++=+−>x y Dx Ey F D E F ,圆心坐标为,22−− D E ,半径r(3)圆的直径式方程:若1122(,),(,)A x y B x y ,则以线段AB 为直径的圆的方程是1212()()()()0−−+−−=x x x x y y y y2、点与圆的位置关系判断(1)点00(,)P x y 与圆222()()−+−=x a y b r 的位置关系: ①222()()−+−>⇔x a y b r 点P 在圆外; ②222()()−+−=⇔x a y b r 点P 在圆上; ③222()()−+−<⇔x a y b r 点P 在圆内.(2)点00(,)P x y 与圆220++++=x y Dx Ey F 的位置关系:①2200000++++>⇔x y Dx Ey F 点P 在圆外; ②2200000++++=⇔x y Dx Ey F 点P 在圆上; ③2200000++++<⇔x y Dx Ey F 点P 在圆内.六、直线与圆的位置关系1、直线与圆的位置关系判断(1)几何法(圆心到直线的距离和半径关系)圆心(,)a b 到直线0Ax By C ++=的距离,则d =:d r <⇔直线与圆相交,交于两点,P Q ,||PQ =d r =⇔直线与圆相切; d r >⇔直线与圆相离(2)代数方法(几何问题转化为代数问题即交点个数问题转化为方程根个数)由2220()()Ax By C x a y b r++= −+−= , 消元得到一元二次方程20p x q x t ++=,20p x q x t ++=判别式为∆,则:0∆>⇔直线与圆相交; 0∆=⇔直线与圆相切; 0∆<⇔直线与圆相离.七、两圆位置关系的判断用两圆的圆心距与两圆半径的和差大小关系确定,具体是:设两圆12,O O 的半径分别是,R r ,(不妨设R r >),且两圆的圆心距为d ,则:d R r <+⇔两圆相交; d R r =+⇔两圆外切; R r d R r −<<+⇔两圆相离 d R r =−⇔两圆内切;0d R r ≤<−⇔两圆内含(0d =时两圆为同心圆)设两个圆的半径分别为R r ,,R r >,圆心距为d ,则两圆的位置关系可用下表来表示: 位置关系 相离 外切 相交 内切 内含几何特征 d R r >+d R r =+R r d R r −<<+d R r =−d R r <−代数特征 无实数解 一组实数解 两组实数解 一组实数解 无实数解 公切线条数 4321【直线与圆常用结论直线与圆常用结论】】一、直线1、点关于点对称点关于点对称的本质是中点坐标公式:设点11(),P x y 关于点00(),Q x y 的对称点为22(),′P x y ,则根据中点坐标公式,有12012022+=+ = x x x y y y 可得对称点22(),′P x y 的坐标为0101(22),−−x x y y 2、点关于直线对称点11(),P x y 关于直线:0++=l Ax By C 对称的点为22(),′P x y ,连接′PP ,交l 于M 点,则l 垂直平分′PP ,所以′⊥PP l ,且M 为′PP 中点,又因为M 在直线l 上,故可得12121022′⋅=− ++++= l PP k k x x y y AB C ,解出22(),x y 即可.3、直线关于点对称法一:在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点坐标,再由两点式求出直线方程;法二:求出一个对称点,再利用两对称直线平行,由点斜式得到所求直线方程. 4、直线关于直线对称求直线1:0++=l ax by c ,关于直线2:0++=l dx ey f (两直线不平行)的对称直线3l 第一步:联立12,l l 算出交点00(),P x y第二步:在1l 上任找一点(非交点)11(),Q x y ,利用点关于直线对称的秒杀公式算出对称点22(),′Q x y 第三步:利用两点式写出3l 方程 5、常见的一些特殊的对称点(),x y 关于x 轴的对称点为(),−x y ,关于y 轴的对称点为(),−x y .点(),x y 关于直线=y x 的对称点为(),y x ,关于直线=−y x 的对称点为(),−−y x . 点(),x y 关于直线=x a 的对称点为(2),−a x y ,关于直线=y b 的对称点为(2),−x b y . 点(),x y 关于点(),a b 的对称点为(22),−−a x b y .点(),x y 关于直线+=x y k 的对称点为(),−−k y k x ,关于直线−x y =k 的对称点为(),+−k y x k . 6、过定点直线系过已知点00(),P x y 的直线系方程00()−=−y y k x x (k 为参数). 7、斜率为定值直线系斜率为k 的直线系方程=+y kx b (b 是参数). 8、平行直线系与已知直线0++=Ax By C 平行的直线系方程0++=Ax By λ(λ为参数). 9、垂直直线系与已知直线0++=Ax By C 垂直的直线系方程0−+=Bx Ay λ(λ为参数). 10、过两直线交点的直线系过直线1111:0++=l A x B y C 与2222:0++=l A x B y C 的交点的直线系方程:111222()0+++++=A x B y C A x B y C λ(λ为参数).二、圆1、圆的参数方程①222(0)+=>x y r r 的参数方程为cos sin = =x r y r θθ(θ为参数);②222()()(0)−+−=>x a y b r r 的参数方程为cos sin =+ =+x a r y b r θθ(θ为参数).注意:对于圆的最值问题,往往可以利用圆的参数方程将动点的坐标设为(cos ,sin )++a r b r θθ(θ为参数,,()a b 为圆心,r 为半径),以减少变量的个数,建立三角函数式,从而把代数问题转化为三角问题,然后利用正弦型或余弦型函数的有界性求解最值. 2、关于圆的切线的几个重要结论(1)过圆222x y r +=上一点00(,)P x y 的圆的切线方程为200x x y y r +=. (2)过圆222()()x a y b r −+−=上一点00(,)P x y 的圆的切线方程为200()()()()x a x a y b y b r −−+−−=(3)过圆220x y D x E y F ++++=上一点00(,)P x y 的圆的切线方程为0000022x x y y x x y y D E F ++++⋅+⋅+= (4)求过圆222x y r +=外一点00(,)P x y 的圆的切线方程时,应注意理解: ①所求切线一定有两条;②设直线方程之前,应对所求直线的斜率是否存在加以讨论.设切线方程为00()y y k x x −=−,利用圆心到切线的距离等于半径,列出关于k 的方程,求出k 值.若求出的k 值有两个,则说明斜率不存在的情形不符合题意;若求出的k 值只有一个,则说明斜率不存在的情形符合题意.一、单选题1.(2024·江西新余·二模)已知直线0x ay −=交圆C:2220x y y +−−=于M ,N 两点,则“MCN △为正三角形”是“0a =”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.(2024·陕西西安·三模)若过点0,1P 可作圆22240x y x y a +−−+=的两条切线,则a 的取值范围是( ) A .()3,+∞B .()1,3−C .()3,5D .()5,+∞【答案答案】】C【分析分析】】根据点在圆外即可求解.【详解详解】】圆22240x y x y a +−−+=,即圆()()22125x y a −+−=−,则50a −>,解得5a <.的距离的最大值为( ) A .1B .2C .3D .44.(2024·四川成都·三模)已知直线1:10l x ay −+= 与:11C x a y −+−= 相交于 A B , 两点,若ABC 是直角三角形,则实数 a 的值为( )A .1 或 1−B 或C .17− 或 1−D .17− 或5.(2024·湖南邵阳·三模)已知直线l :1x y +=,过直线l 上的任意一点P 作圆O 的切线PA ,PB ,切点分别为A ,B ,则APB ∠的最大值为( ) A .3π4B .2π3C .π2D .π6当OP 最小时最小时,,则sin APO ∠又因为OP 的最小值即为圆心此时2sin ,2APO APO ∠=∠故选故选::C . 6.(2024·重庆·二模)已知圆:O 若92PA PB ⋅= ,则OP =( ) A B .3C .设,APO BPO OP α∠=∠=则23sin ,cos x xxαα==cos cos212sin APB ∠α==−3,x y P +=是圆O 外一点,过点P 作圆O 的两条切线7.(2024·北京·三模)已知圆()2:11C x y +−=和两点()()(),0,,00A t B t t −>,若圆C 上存在点P ,使得0PA PB ⋅=,则t 的取值范围为( )A .(]0,1B .[]1,3C .[]2,3D .[]3,4故选故选::B A .()2,6B .()3,5C .()()2,35,6∪D .()()2,36,+∞∪9.(2024·北京·三模)已知直线,圆:16O x y +=,下列说法错误..的是()A .对任意实数a ,直线l 与圆O 有两个不同的公共点;B .当且仅当12a =−时,直线l 被圆O 所截弦长为C .对任意实数a ,圆O 不关于直线l 对称;D .存在实数a ,使得直线l 与圆O 相切.10.(2024·江西鹰潭·三模)已知m ∈R ,直线1:20l mx y m ++=与2:40l x my m −+=的交点P 在圆C :()()()222340x y r r −+−=>上,则r 的最大值是( )A ....【答案答案】】D【分析分析】】根据两直线方程可知两直线分别过定点且垂直根据两直线方程可知两直线分别过定点且垂直,,可求得P 点轨迹方程点轨迹方程,,再由圆与圆的位置关系找出圆心距与两圆半径之间的关系可得结果.二、多选题11.(2024·湖南长沙·三模)已知圆 ()22:24C x y ++=,直线 ()():1210l m x y m m ++−+=∈R ,则( )A .直线 l 恒过定点 ()1,1−B .当0m =时,圆C 上恰有三个点到直线l 的距离等于 1 C .直线l 与圆C 可能相切D .若圆C 与圆 22280x y x y a +−++=恰有三条公切线,则8a =12.(2024·山西临汾·三模)已知,E F 是以为半径的圆上任意两点,且满足,P是EF 的中点,若存在关于()3,0对称的,A B 两点,满足0PA PB ⋅=,则线段AB 长度的可能值为( )A .3B .4C .5D .613.(2024·河南郑州·三模)已知直线:10l ax by ++=(,a b 不同时为0),圆22:20C x y x +−=,则( )A .当221b a −=时,直线l 与圆C 相切B .当2a b +=−时,直线l 与圆C .当1,1a b ==−时,与圆C 外切D .当1,1a b ==−时,直线l 与坐标C 不可能相交外切且与直线l 相切的动圆圆心的轨迹是一条抛物线与坐标轴相交于,A B 两点,则圆C 上存在点P 抛物线满足0PA PB ⋅=14.(2024·山东青岛·三模)已知动点M N , 分别在圆()()221:121C x y −+−= 和 ()()222:343C x y −+−=上,动点P 在 x 轴上,则( )A .圆2C 的半径为3B .圆1C 和圆2C 相离C .PM PN +的最小值为D.过点P 做圆1C15.(2024·浙江温州·二模)已知圆1与圆2相交于122C AB C AB S S =△△,则实数a 的值可以是( )A .10B .2C .223D .14316.(2024·浙江绍兴·三模)已知M ,N 为圆224x y +=上的两个动点,点1,1P −,且PM PN ⊥,则()A .max2PM =B .maxMN=C .PMN 外接圆圆心的轨迹方程为22113222x y++−=D .PMN 重心的轨迹方程为22551666x y++−=对于C 中,设PMN 的外接圆的圆心则有22(1)(1)4(x y ++−=−即22113()()222x y ++−=,对于D 中,设PMN 的重心为点由C 项知PMN 的外接圆的圆心点三、填空题17.(2024·广东汕头·三模)已知圆(i )则圆C 的标准方程为;(ii )若直线AB 关于y a =对称的直线知圆C 经过()2,0A ,()0,2B ,()2,4C 三点, 的直线与圆C 有公共点,则a 的取值范围是.18.(2024·天津和平·三模)已知圆C 以点1,1为圆心,且与直线相切,则满足以上条件的圆C 的半径最大时,圆C 的标准方程为.19.(2024·内蒙古呼和浩特·二模)点1,P a −关于直线0x y −=的对称点在圆22(2)(4)13x y −+−=内,则实数a 的取值范围是.因为(),1Q a −在圆22(2)(4)13x y −+−=的内部的内部,,所以22(2)(14)13a −−+−<,解得40a -<<,即实数a 的取值范围是()4,0−. 故答案为故答案为::()4,0−.20.(2024·湖南·二模)已知直线l 是圆22:1O x y +=的切线,点()2,1A −和点()0,3B 到l 的距离相等,则直线l 的方程可以是.(写出一个满足条件的即可)。
高考数学真题练习——直线与圆的位置关系

直线与圆的位置关系一.选择题(共16小题)1.(2015•重庆)已知直线10x ay +-=是圆22:4210C x y x y +--+=的对称轴,过点(4,)A a -作圆C 的一条切线,切点为B ,则||(AB = )A .2B .6C .D .2.(2014•全国)若直线21y x =+与圆222(3)(2)x y r -+-=相切,则2(r = )A .8B .5C .D3.(2014•福建)已知直线l 过圆22(3)4x y +-=的圆心,且与直线10x y ++=垂直,则l 的方程是( ) A .20x y +-=B .20x y -+=C .30x y +-=D .30x y -+=4.(2014•北京)已知圆22:(3)(4)1C x y -+-=和两点(,0)A m -,(B m ,0)(0)m >,若圆C 上存在点P ,使得90APB ∠=︒,则m 的最大值为( )A .7B .6C .5D .45.(2014•安徽)过点(P 1)-的直线l 与圆221x y +=有公共点,则直线l 的倾斜角的取值范围是( ) A .(0,]6πB .(0,]3πC .[0,]6πD .[0,]3π6.(2014•浙江)已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4,则实数a 的值是( ) A .2-B .4-C .6-D .8-7.(2014•江西)在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线240x y +-=相切,则圆C 面积的最小值为( )A .45πB .34πC .(6π-D .54π8.(2013•重庆)设P 是圆22(3)(1)4x y -++=上的动点,Q 是直线3x =-上的动点,则||PQ 的最小值为( ) A .6B .4C .3D .29.(2013•陕西)已知点(,)M a b 在圆22:1O x y +=外,则直线1ax by +=与圆O 的位置关系是( ) A .相切B .相交C .相离D .不确定10.(2013•江西)过点引直线l 与曲线y =A ,B 两点,O 为坐标原点,当ABO ∆的面积取得最大值时,直线l 的斜率等于( )A B .C . D . 11.(2013•天津)已知过点(2,2)P 的直线与圆22(1)5x y -+=相切,且与直线10ax y -+=垂直,则(a = ) A .12-B .1C .2D .1212.(2013•安徽)直线250x y +-=被圆22240x y x y +--=截得的弦长为( )A .1B .2C .4 D.13.(2012•天津)设m ,n R ∈,若直线(1)(1)20m x n y +++-=与圆22(1)(1)1x y -+-=相切,则m n +的取值范围是( )A.[11+ B .(-∞,1[13+,)+∞C.[2-2+D .(-∞,2[222-+,)+∞14.(2012•重庆)对任意的实数k ,直线1y kx =+与圆222x y +=的位置关系一定是( ) A .相离B .相切C .相交但直线不过圆心D .相交且直线过圆心15.(2012•陕西)已知圆22:40C x y x +-=,l 为过点(3,0)P 的直线,则( ) A .l 与C 相交 B .l 与C 相切C .l 与C 相离D .以上三个选项均有可能16.(2012•安徽)若直线10x y -+=与圆22()2x a y -+=有公共点,则实数a 取值范围是( ) A .[3-,1]-B .[1-,3]C .[3-,1]D .(-∞,3][1-,)+∞二.填空题(共10小题)17.(2018•天津)已知圆2220x y x +-=的圆心为C,直线13x y ⎧=-⎪⎪⎨⎪=-⎪⎩,(t 为参数)与该圆相交于A ,B 两点,则ABC ∆的面积为 .18.(2017•全国)直线20x -=被圆2220x y x +-=截得的线段长为 .19.(2017•上海)若P 、Q 是圆222440x y x y +-++=上的动点,则||PQ 的最大值为 .20.(2016•上海)在平面直角坐标系xOy 中,点A ,B 是圆22650x y x +-+=上的两个动点,且满足||AB =则||OA OB +的最小值为 .21.(2014•湖北)直线1:l y x a =+和2:l y x b =+将单位圆22:1C x y +=分成长度相等的四段弧,则22a b += . 22.(2014•上海)已知曲线:C x =,直线:6l x =,若对于点(,0)A m ,存在C 上的点P 和l 上的Q 使得0AP AQ +=,则m 的取值范围为 .23.(2014•江苏)在平面直角坐标系xOy 中,直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为 . 24.(2013•湖北)已知圆22:5O x y +=,直线:cos sin 1(0)2l x y πθθθ+=<<.设圆O 上到直线l 的距离等于1的点的个数为k ,则k = .25.(2013•浙江)直线23y x =+被圆22680x y x y +--=所截得的弦长等于 . 26.(2013•山东)过点(3,1)作圆22(2)(2)4x y -+-=的弦,其中最短的弦长为 . 三.解答题(共4小题)27.(2017•上海)某景区欲建造两条圆形观景步道1M 、2M (宽度忽略不计),如图所示,已知AB AC ⊥,60AB AC AD ===(单位:米),要求圆1M 与AB 、AD 分别相切于点B 、D ,圆2M 与AC 、AD 分别相切于点C 、D ;(1)若60BAD ∠=︒,求圆1M 、2M 的半径(结果精确到0.1米)(2)若观景步道1M 与2M 的造价分别为每米0.8千元与每米0.9千元,如何设计圆1M 、2M 的大小,使总造价最低?最低总造价是多少?(结果精确到0.1千元)28.(2015•陕西)如图,AB 切O 于点B ,直线AO 交O 于D ,E 两点,BC DE ⊥,垂足为C . (Ⅰ)证明:CBD DBA ∠=∠;(Ⅱ)若3AD DC =,BC =,求O 的直径.29.(2013•江苏)在平面直角坐标系xOy 中,点(0,3)A ,直线:24l y x =-,设圆C 的半径为1,圆心在l 上. (1)若圆心C 也在直线3y x =-上,过点A 作圆C 的切线,求切线方程; (2)若圆C 上存在点M ,使||2||MA MO =,求圆心C 的横坐标的取值范围.30.(2013•四川)已知圆C 的方程为22(4)4x y +-=,点O 是坐标原点.直线:l y kx =与圆C 交于M ,N 两点. (Ⅰ)求k 的取值范围;(Ⅱ)设(,)Q m n 是线段MN 上的点,且222211||||||OQ OM ON =+.请将n 表示为m 的函数.直线与圆的位置关系参考答案与试题解析一.选择题(共16小题)1.(2015•重庆)已知直线10x ay +-=是圆22:4210C x y x y +--+=的对称轴,过点(4,)A a -作圆C 的一条切线,切点为B ,则||(AB = )A .2B .6C .D .【解答】解:圆22:4210C x y x y +--+=,即22(2)(1)4x y -+-=, 表示以(2,1)C 为圆心、半径等于2的圆.由题意可得,直线:10l x ay +-=经过圆C 的圆心(2,1), 故有210a +-=,1a ∴=-,点(4,1)A --.(AC ==2CB R ==,∴切线的长||6AB ===.故选:B .2.(2014•全国)若直线21y x =+与圆222(3)(2)x y r -+-=相切,则2(r = )A .8B .5C .D【解答】解:直线21y x =+与圆222(3)(2)x y r -+-=相切,∴圆心(3,2)C 到直线的距离d r ===,25r ∴=.故选:B .3.(2014•福建)已知直线l 过圆22(3)4x y +-=的圆心,且与直线10x y ++=垂直,则l 的方程是( ) A .20x y +-=B .20x y -+=C .30x y +-=D .30x y -+=【解答】解:由题意可得所求直线l 经过点(0,3),斜率为1, 故l 的方程是30y x -=-,即30x y -+=, 故选:D .4.(2014•北京)已知圆22:(3)(4)1C x y -+-=和两点(,0)A m -,(B m ,0)(0)m >,若圆C 上存在点P ,使得90APB ∠=︒,则m 的最大值为( )A .7B .6C .5D .4【解答】解:圆22:(3)(4)1C x y -+-=的圆心(3,4)C ,半径为1, 圆心C 到(0,0)O 的距离为5,∴圆C 上的点到点O 的距离的最大值为6.再由90APB ∠=︒可得,以AB 为直径的圆和圆C 有交点,可得12PO AB m ==,故有6m , 故选:B .5.(2014•安徽)过点(P 1)-的直线l 与圆221x y +=有公共点,则直线l 的倾斜角的取值范围是( )A .(0,]6πB .(0,]3πC .[0,]6πD .[0,]3π【解答】解:由题意可得点(P 1)-在圆221x y +=的外部,故要求的直线的斜率一定存在,设为k ,则直线方程为1(y k x +=,即10kx y -+-=.1,即22311k k -++,解得03k ,故直线l 的倾斜角的取值范围是[0,]3π,故选:D .6.(2014•浙江)已知圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4,则实数a 的值是( ) A .2-B .4-C .6-D .8-【解答】解:圆22220x y x y a ++-+= 即22(1)(1)2x y a ++-=-,故弦心距d =再由弦长公式可得224a -=+,4a ∴=-, 故选:B .7.(2014•江西)在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线240x y +-=相切,则圆C 面积的最小值为( )A .45πB .34πC .(6π-D .54π【解答】解:如图,设AB 的中点为C ,坐标原点为O ,圆半径为r ,由已知得||||OC CE r ==,过点O 作直线240x y +-=的垂直线段OF , 交AB 于D ,交直线240x y +-=于F ,则当D 恰为OF 中点时,圆C 的半径最小,即面积最小 此时圆的直径为(0,0)O 到直线240x y +-=的距离为:d ==此时12r d ==∴圆C 的面积的最小值为:245min S ππ=⨯=. 故选:A .8.(2013•重庆)设P 是圆22(3)(1)4x y -++=上的动点,Q 是直线3x =-上的动点,则||PQ 的最小值为( ) A .6B .4C .3D .2【解答】解:过圆心A 作AQ ⊥直线3x =-, 与圆交于点P ,此时||PQ 最小, 由圆的方程得到(3,1)A -,半径2r =, 则||||624PQ AQ r =-=-=. 故选:B .9.(2013•陕西)已知点(,)M a b 在圆22:1O x y +=外,则直线1ax by +=与圆O 的位置关系是( ) A .相切B .相交C .相离D .不确定【解答】解:(,)M a b 在圆221x y +=外, 221a b ∴+>,∴圆(0,0)O 到直线1ax by +=的距离1d r <=,则直线与圆的位置关系是相交. 故选:B .10.(2013•江西)过点引直线l 与曲线y =A ,B 两点,O 为坐标原点,当ABO ∆的面积取得最大值时,直线l 的斜率等于( )A B .C . D .【解答】解:由y =221(0)x y y +=.所以曲线y =x 轴上方的部分(含与x 轴的交点), 设直线l 的斜率为k ,要保证直线l 与曲线有两个交点,且直线不与x 轴重合,则10k -<<,直线l 的方程为0(y k x -=-,即0kx y -=.则原点O 到l 的距离d =,l则2211ABO k S k ∆-==+==令211t k =+,则ABO S ∆=34t =,即21314k =+时,ABOS ∆有最大值为12.此时由21314k =+,解得k = 故选:D .11.(2013•天津)已知过点(2,2)P 的直线与圆22(1)5x y -+=相切,且与直线10ax y -+=垂直,则(a = ) A .12-B .1C .2D .12【解答】解:因为点(2,2)P 满足圆22(1)5x y -+=的方程,所以P 在圆上, 又过点(2,2)P 的直线与圆22(1)5x y -+=相切,且与直线10ax y -+=垂直, 所以切点与圆心连线与直线10ax y -+=平行, 所以直线10ax y -+=的斜率为:20221a -==-. 故选:C .12.(2013•安徽)直线250x y +-=被圆22240x y x y +--=截得的弦长为( )A .1B .2C .4D .【解答】解:由22240x y x y +--=,得22(1)(2)5x y -+-=,所以圆的圆心坐标是(1,2)C ,半径r =圆心C 到直线250x y +-+=的距离为1d ===.所以直线直线250x y +-=被圆22240x y x y +--=截得的弦长为4. 故选:C .13.(2012•天津)设m ,n R ∈,若直线(1)(1)20m x n y +++-=与圆22(1)(1)1x y -+-=相切,则m n +的取值范围是( )A .[11+B .(-∞,1[13+,)+∞C .[2-2+D .(-∞,2[222-+,)+∞【解答】解:由圆的方程22(1)(1)1x y -+-=,得到圆心坐标为(1,1),半径1r =, 直线(1)(1)20m x n y +++-=与圆相切,∴圆心到直线的距离1d ==,整理得:21()2m n m n mn +++=, 设m n x +=,则有214x x +,即2440x x --,2440x x --=的解为:12x =+22x =-∴不等式变形得:(220x x ---+,解得:222x +或222x -,则m n +的取值范围为(-∞,2[222-+,)+∞. 故选:D .14.(2012•重庆)对任意的实数k ,直线1y kx =+与圆222x y +=的位置关系一定是( ) A .相离B .相切C .相交但直线不过圆心D .相交且直线过圆心【解答】解:对任意的实数k ,直线1y kx =+恒过点(0,1),且斜率存在 (0,1)在圆222x y +=内∴对任意的实数k ,直线1y kx =+与圆222x y +=的位置关系一定是相交但直线不过圆心故选:C .15.(2012•陕西)已知圆22:40C x y x +-=,l 为过点(3,0)P 的直线,则( ) A .l 与C 相交 B .l 与C 相切C .l 与C 相离D .以上三个选项均有可能【解答】解:将圆的方程化为标准方程得:22(2)4x y -+=,∴圆心(2,0)C ,半径2r =,又(3,0)P与圆心的距离12d r ==<=,∴点P 在圆C 内,又直线l 过P 点,则直线l 与圆C 相交. 故选:A .16.(2012•安徽)若直线10x y -+=与圆22()2x a y -+=有公共点,则实数a 取值范围是( ) A .[3-,1]-B .[1-,3]C .[3-,1]D .(-∞,3][1-,)+∞【解答】解:直线10x y -+=与圆22()2x a y -+=有公共点∴圆心到直线10x y -+=2|1|2a ∴+31a ∴-故选:C .二.填空题(共10小题)17.(2018•天津)已知圆2220x y x +-=的圆心为C,直线13x y ⎧=-⎪⎪⎨⎪=-⎪⎩,(t 为参数)与该圆相交于A ,B 两点,则ABC ∆的面积为12. 【解答】解:圆2220x y x +-=化为标准方程是22(1)1x y -+=,圆心为(1,0)C ,半径1r =;直线13x y ⎧=-⎪⎪⎨⎪=-⎪⎩化为普通方程是20x y +-=,则圆心C到该直线的距离为d ==弦长||22AB =⨯=, ABC ∴∆的面积为111||2222S AB d ==⨯=. 故答案为:12. 18.(2017•全国)直线20x -=被圆2220x y x +-=【解答】解:圆2220x y x +-=化为22(1)1x y -+=,设直线20x --=与圆22(1)1x y -+=的交点为A 、B ,圆心为(1,0)O , 线段AB 的中点为D ,半径为1r =则由圆的几何性质可知,OD AB ⊥,且1||2OD ==,||1OA r ==,||2||AB AD ∴===19.(2017•上海)若P 、Q 是圆222440x y x y +-++=上的动点,则||PQ 的最大值为 2 . 【解答】解:圆222440x y x y +-++=,可化为22(1)(2)1x y -++=,P 、Q 是圆222440x y x y +-++=上的动点,||PQ ∴的最大值为2,故答案为2.20.(2016•上海)在平面直角坐标系xOy 中,点A ,B 是圆22650x y x +-+=上的两个动点,且满足||AB =则||OA OB +的最小值为 4 .【解答】解:设1(A x ,1)y ,2(B x ,2)y ,AB 中点(,)M x y ''. 122x x x +'=,122y y y +'=, ∴12(OA OB x x +=+,12)2y y OM +=,圆22:650C x y x +-+=,22(3)4x y ∴-+=,圆心(3,0)C ,半径2CA =.点A ,B 在圆C 上,AB = 2221()2CA CM AB ∴-=,即1CM =.点M 在以C 为圆心,半径1r =的圆上.312OM OC r ∴-=-=.||2OM ∴,∴||4OA OB +,∴||OA OB +的最小值为4.故答案为:4.21.(2014•湖北)直线1:l y x a =+和2:l y x b =+将单位圆22:1C x y +=分成长度相等的四段弧,则22a b += 2 . 【解答】解:由题意可得,圆心(0,0)到两条直线的距离相等,且每段弧长都是圆周的14,∴cos 452==︒=,222a b ∴+=, 故答案为:2.22.(2014•上海)已知曲线:C x =,直线:6l x =,若对于点(,0)A m ,存在C 上的点P 和l 上的Q 使得0AP AQ +=,则m 的取值范围为 [2,3] .【解答】解:曲线:C x =,是以原点为圆心,2 为半径的圆,并且[2P x ∈-,0], 对于点(,0)A m ,存在C 上的点P 和l 上的Q 使得0AP AQ +=, 说明A 是PQ 的中点,Q 的横坐标6x =, 6[22Px m +∴=∈,3]. 故答案为:[2,3].23.(2014•江苏)在平面直角坐标系xOy 中,直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为 . 【解答】解:圆22(2)(1)4x y -++=的圆心为(2,1)C -,半径2r =, 点C 到直线直线230x y +-=的距离d ,∴根据垂径定理,得直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为==. 24.(2013•湖北)已知圆22:5O x y +=,直线:cos sin 1(0)2l x y πθθθ+=<<.设圆O 上到直线l 的距离等于1的点的个数为k ,则k = 4 .【解答】解:由圆的方程得到圆心(0,0)O ,半径r =圆心O 到直线l 的距离1d ==,且11r d d -=->=,∴圆O 上到直线l 的距离等于1的点的个数为4,即4k =.故答案为:425.(2013•浙江)直线23y x =+被圆22680x y x y +--=所截得的弦长等于 【解答】解:圆22680x y x y +--=的圆心坐标(3,4),半径为5,=因为圆心距,半径,半弦长满足勾股定理,所以直线23y x =+被圆22680x y x y +--=所截得的弦长为:2=故答案为:26.(2013•山东)过点(3,1)作圆22(2)(2)4x y -+-=的弦,其中最短的弦长为 【解答】解:根据题意得:圆心(2,2),半径2r =,2,(3,1)∴在圆内,圆心到此点的距离d ,2r =,∴最短的弦长为=故答案为:三.解答题(共4小题)27.(2017•上海)某景区欲建造两条圆形观景步道1M 、2M (宽度忽略不计),如图所示,已知AB AC ⊥,60AB AC AD ===(单位:米),要求圆1M 与AB 、AD 分别相切于点B 、D ,圆2M 与AC 、AD 分别相切于点C 、D ;(1)若60BAD ∠=︒,求圆1M 、2M 的半径(结果精确到0.1米)(2)若观景步道1M 与2M 的造价分别为每米0.8千元与每米0.9千元,如何设计圆1M 、2M 的大小,使总造价最低?最低总造价是多少?(结果精确到0.1千元)【解答】解:(1)1M 半径60tan3034.6=︒≈,2M 半径60tan1516.1=︒≈; (2)设2BAD α∠=,则总造价0.8260tan 0.9260tan(45)y παπα=+︒-, 设1tan x α+=,则1812(817)84y x x ππ=+-,当且仅当32x =,1tan 2α=时,取等号,1M ∴半径30,2M 半径20,造价263.8千元.28.(2015•陕西)如图,AB 切O 于点B ,直线AO 交O 于D ,E 两点,BC DE ⊥,垂足为C . (Ⅰ)证明:CBD DBA ∠=∠;(Ⅱ)若3AD DC =,BC =,求O 的直径.【解答】证明:(Ⅰ)DE 是O 的直径, 则90BED EDB ∠+∠=︒, BC DE ⊥,90CBD EDB ∴∠+∠=︒,即CBD BED ∠=∠,AB 切O 于点B ,DBA BED ∴∠=∠,即CBD DBA ∠=∠;(Ⅱ)由(Ⅰ)知BD 平分CBA ∠, 则3BA ADBC CD ==, 2BC =AB ∴=4AC =,则3AD =,由切割线定理得2AB AD AE =,即26AB AE AD==,故3DE AE AD =-=, 即可O 的直径为3.29.(2013•江苏)在平面直角坐标系xOy 中,点(0,3)A ,直线:24l y x =-,设圆C 的半径为1,圆心在l 上. (1)若圆心C 也在直线3y x =-上,过点A 作圆C 的切线,求切线方程; (2)若圆C 上存在点M ,使||2||MA MO =,求圆心C 的横坐标的取值范围.【解答】解:(1)由题设,圆心C 在3y x =-上,也在直线24y x =-上,设切点的横坐标为a , 243a a -=-,1a ∴=,(1,2)C ∴-.22:(1)(2)1C x y ∴-++=,由题,当斜率存在时,过A 点切线方程可设为3y kx =+,即30kx y -+=1=,解得:125k =-,⋯(4分)又当斜率不存在时,也与圆相切,∴所求切线为0x =或1235y x =-+, 即0x =或125150x y +-=;(2)设点(,)M x y ,由||2||MA MO =,化简得:22(1)4x y ++=,∴点M 的轨迹为以(0,1)-为圆心,2为半径的圆,可记为圆D ,又点M 在圆C 上,∴圆C 与圆D 的关系为相交或相切,1||3CD ∴,其中||CD221(23)3a a ∴+-,解得:1205a. 30.(2013•四川)已知圆C 的方程为22(4)4x y +-=,点O 是坐标原点.直线:l y kx =与圆C 交于M ,N 两点. (Ⅰ)求k 的取值范围;(Ⅱ)设(,)Q m n 是线段MN 上的点,且222211||||||OQ OM ON =+.请将n 表示为m 的函数. 【解答】解:(Ⅰ)将y kx =代入22(4)4x y +-=中,得:22(1)8120(*)k x kx +-+=,根据题意得:△22(8)4(1)120k k =--+⨯>,即23k >, 则k 的取值范围为(-∞,⋃,)+∞;(Ⅱ)由M 、N 、Q 在直线l 上,可设M 、N 坐标分别为1(x ,1)kx ,2(x ,2)kx ,2221||(1)OM k x ∴=+,2222||(1)ON k x =+,22222||(1)OQ m n k m =+=+,代入222211||||||OQ OM ON =+得:22222212211(1)(1)(1)k m k x k x =++++, 即21212222221212()2211x x x x m x x x x +-=+=, 由(*)得到12281kx x k +=+,122121x x k =+, 代入得:222222824()211144(1)k kk m k -++=+,即223653m k =-, 点Q 在直线y kx =上,n km ∴=,即n k m =,代入223653m k =-,化简得225336n m -=, 由223653m k =-及23k >,得到203m <<,即(m ∈0)(0⋃, 根据题意得点Q 在圆内,即0n >,n ∴=则n 与m的函数关系式为(n m =∈0)(0⋃.。
2011-2020年高考数学真题分类汇编 专题25 直线与圆(教师版含解析)
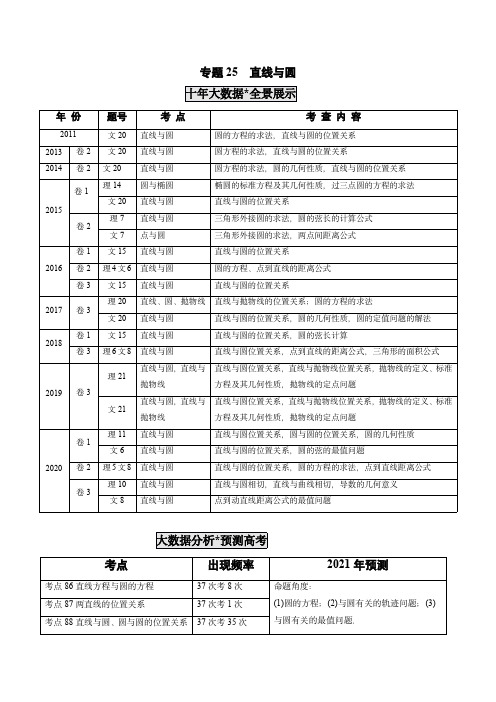
专题25直线与圆年份题号考点考查内容2011文20直线与圆圆的方程的求法,直线与圆的位置关系2013卷2文20直线与圆圆方程的求法,直线与圆的位置关系2014卷2文20直线与圆圆方程的求法,圆的几何性质,直线与圆的位置关系2015卷1理14圆与椭圆椭圆的标准方程及其几何性质,过三点圆的方程的求法文20直线与圆直线与圆的位置关系卷2理7直线与圆三角形外接圆的求法,圆的弦长的计算公式文7点与圆三角形外接圆的求法,两点间距离公式2016卷1文15直线与圆直线与圆的位置关系卷2理4文6直线与圆圆的方程、点到直线的距离公式卷3文15直线与圆直线与圆的位置关系2017卷3理20直线、圆、抛物线直线与抛物线的位置关系;圆的方程的求法文20直线与圆直线与圆的位置关系,圆的几何性质,圆的定值问题的解法2018卷1文15直线与圆直线与圆的位置关系,圆的弦长计算卷3理6文8直线与圆直线与圆位置关系,点到直线的距离公式,三角形的面积公式2019卷3理21直线与圆,直线与抛物线直线与圆位置关系,直线与抛物线位置关系,抛物线的定义、标准方程及其几何性质,抛物线的定点问题文21直线与圆,直线与抛物线直线与圆位置关系,直线与抛物线位置关系,抛物线的定义、标准方程及其几何性质,抛物线的定点问题2020卷1理11直线与圆直线与圆位置关系,圆与圆的位置关系,圆的几何性质文6直线与圆直线与圆的位置关系,圆的弦的最值问题卷2理5文8直线与圆直线与圆的位置关系,圆的方程的求法,点到直线距离公式卷3理10直线与圆直线与圆相切,直线与曲线相切,导数的几何意义文8直线与圆点到动直线距离公式的最值问题考点出现频率2021年预测考点86直线方程与圆的方程37次考8次命题角度:(1)圆的方程;(2)与圆有关的轨迹问题;(3)与圆有关的最值问题.考点87两直线的位置关系37次考1次考点88直线与圆、圆与圆的位置关系37次考35次考点86直线方程与圆的方程1.(2020全国Ⅲ文6)在平面内,,A B 是两个定点,C 是动点.若1AC BC,则点C 的轨迹为()A .圆B .椭圆C .抛物线D .直线【答案】A【思路导引】首先建立平面直角坐标系,然后结合数量积的定义求解其轨迹方程即可.【解析】设 20AB a a ,以AB 中点为坐标原点建立如图所示的平面直角坐标系,则: ,0,,0A a B a ,设 ,C x y ,可得: ,,,AC x a y BC x a y,从而: 2AC BC x a x a y,结合题意可得: 21x a x a y ,整理可得:2221x y a ,即点C 的轨迹是以AB 为半径的圆.故选:A .2.(2020全国Ⅲ文8)点(0,﹣1)到直线 1y k x 距离的最大值为()A .1B .C .D .2【答案】B【解析】由(1)y k x 可知直线过定点(1,0)P ,设(0,1)A ,当直线(1)y k x 与AP 垂直时,点A 到直线(1)y k x 距离最大,即为||AP3.(2015北京文)圆心为(1,1)且过原点的圆的方程是A .22(1)(1)1x y B .22(1)(1)1x y C .22(1)(1)2x y D .22(1)(1)2x y【答案】D 【解析】由题意可得圆的半径为r22112x y .4.【2018·天津文】在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________.【答案】2220x y x 【解析】设圆的方程为220x y Dx Ey F ,圆经过三点(0,0),(1,1),(2,0),则01104020F D E F D F ,解得200D E F,则圆的方程为2220x y x .5.【2017·天津文】设抛物线24y x 的焦点为F ,准线为l .已知点C 在l 上,以C 为圆心的圆与y 轴的正半轴相切于点A .若120FAC ,则圆的方程为___________.【答案】22(1)(1x y 【解析】由题可设圆心坐标为(1,)C m ,则(0,)A m ,焦点(1,0)F ,(1,0),(1,)AC AF m,1cos 2AC AF CAF AC AF,解得m ,由于圆C 与y轴得正半轴相切,则m所求圆的圆心为( ,半径为1,所求圆的方程为22(1)(1x y .6.【2016·浙江文数】已知a R ,方程222(2)4850a x a y x y a 表示圆,则圆心坐标是_____,半径是______.【答案】(2,4) ;5.【解析】由题意22a a ,12a 或,1a 时方程为224850x y x y ,即22(2)(4)25x y ,圆心为(2,4) ,半径为5,2a 时方程为224448100x y x y ,2215((1)24x y 不表示圆.7.【2016·天津文数】已知圆C 的圆心在x 轴的正半轴上,点M 在圆C 上,且圆心到直线20x y的距离为5,则圆C 的方程为__________.【答案】22(2)9.x y 【解析】设(,0)(0)C a a2,35a r,故圆C 的方程为22(2)9.x y 8.(2011辽宁文)已知圆C 经过A(5,1),B(1,3)两点,圆心在x 轴上,则C 的方程为.【答案】22(2)10x y 【解析】以题意设圆C 的方程为222()x a y r ,把所给的两点坐标代入方程得2222(5)1(1)9a r a r,解得2210a r ,所以圆C :22(2)10x y .考点87两直线的位置关系9.【2016·上海文科】已知平行直线012:,012:21 y x l y x l ,则21,l l 的距离_______________.【答案】5【解析】利用两平行线间距离公式得d 510.(2011浙江文)若直线250x y 与直线260x my 互相垂直,则实数m =.【答案】1【解析】当0m 时,两直线不垂直,故0m .因为直线250x y 与直线260x my 的斜率分别为12和2m ,由12(12m,故1m .考点88点与圆、直线与圆、圆与圆的位置关系11.(2020·新课标Ⅰ文)已知圆2260x y x ,过点(1,2)的直线被该圆所截得的弦的长度的最小值为()A .1B .2C .3D .4【答案】B【解析】圆2260x y x 化为22(3)9x y ,所以圆心C 坐标为(3,0)C ,半径为3,设(1,2)P ,当过点P 的直线和直线CP 垂直时,圆心到过点P 的直线的距离最大,所求的弦长最短,根据弦长公式最小值为2 .12.(2020·新课标Ⅱ文理5)若过点 2,1的圆与两坐标轴都相切,则圆心到直线032 y x 的距离为()A .55B .552C .553D .554【答案】B【思路导引】由题意可知圆心在第一象限,设圆心的坐标为 ,,0a a a ,可得圆的半径为a ,写出圆的标准方程,利用点 2,1在圆上,求得实数a 的值,利用点到直线的距离公式可求出圆心到直线230x y 的距离.【解析】由于圆上的点 2,1在第一象限,若圆心不在第一象限,则圆与至少与一条坐标轴相交,不合乎题意,∴圆心必在第一象限,设圆心的坐标为,a a ,则圆的半径为a ,圆的标准方程为222x a y a a .由题意可得 22221a a a ,可得2650a a ,解得1a 或5a ,∴圆心的坐标为 1,1或 5,5,圆心到直线230x y的距离均为5d ,∴圆心到直线230x y.故选B .13.(2020全国Ⅰ理11】已知⊙22:2220M x y x y ,直线:220l x y ,P 为l 上的动点,过点P 作⊙M 的切线,PA PB ,切点为,A B ,当PM AB 最小时,直线AB 的方程为()A .210x yB .210x y C .210x y D .210x y 【答案】D【思路导引】由题意可判断直线与圆相离,根据圆的知识可知,四点,,,A P B M 共圆,且AB MP ,根据22PAM PM AB S PA △可知,当直线MP l 时,PM AB 最小,求出以MP 为直径的圆的方程,根据圆系的知识即可求出直线AB 的方程.【解析】圆的方程可化为 22114x y ,点M 到直线l的距离为2d ,∴直线l 与圆相离.依圆的知识可知,四点,,,A P B M 四点共圆,且AB MP ,∴12222PAM PM AB S PA AM PA △,而PA ,当直线MP l时,min MP,min 1PA ,此时PM AB 最小.∴ 1:112MP y x 即1122y x ,由1122220y x x y解得,10x y.∴以MP 为直径的圆的方程为 1110x x y y ,即2210x y y ,两圆的方程相减可得:210x y ,即为直线AB 的方程,故选D .14.(2020·北京卷)已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为()A .4B .5C .6D .7【答案】A【解析】设圆心 ,C x y ,则1 ,化简得 22341x y ,所以圆心C 的轨迹是以(3,4)M 为圆心,1为半径的圆,所以||1||OC OM 5 ,所以||514OC ,当且仅当C 在线段OM 上时取得等号,故选A .15.(2019北京文8)如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB 是锐角,大小为β.图中阴影区域的面积的最大值为(A)4β+4cosβ(B)4β+4sinβ(C)2β+2cosβ(D)2β+2sinβ【答案】B【解析】由题意和题图可知,当P 为优弧 AB 的中点时,阴影部分的面积取最大值,如图所示,设圆心为O ,2AOB , 1222BOP AOP.此时阴影部分面积211222222AOP BOP AOB S S S S △△扇形 sin 44sin .故选B .16.【2018·全国Ⅲ文】直线20x y 分别与x 轴,y 轴交于A ,B 两点,点P 在圆22(2)2x y 上,则ABP △面积的取值范围是A . 26,B . 48,C .D . 【答案】A【解析】∵直线20x y 分别与x 轴,y 轴交于A ,B 两点, 2,0,0,2A B ,则AB .∵点P 在圆22(2)2x y 上, 圆心为(2,0),则圆心到直线的距离1d故点P 到直线20x y 的距离2d 的范围为,则 2212,62ABP S AB d△.故答案为A .17.【2018高考全国2理2】已知集合22,3,,A x y xy x yZ Z ,则A 中元素的个数为()A .9B .8C .5D .4【答案】A【解析】试题分析:根据枚举法,确定圆及其内部整点个数.试题解析:2223,3x y x ∵,又,1,0,1x x Z .当1x 时,1,0,1y ;当0x 时,1,0,1y ;当1x 时,1,0,1y ;所以共有9个,选A .【考点】本题考查集合与元素关系,点与圆位置关系,考查学生对概念理解与识别.18.【2018高考全国3理6】直线20x y 分别与x 轴y 交于,A B 两点,点P 在圆 2222x y 上,则ABP △面积的取值范围是()A . 26,B .48,C .D . 【答案】A【解析】∵直线20x y 分别与x 轴,y 轴交于,A B 两点, 2,0,0,2A B ,则AB∵点P 在圆 2222x y 上, 圆心为 2,0,则圆心到直线距离1d,故点P 到直线20x y 的距离2d 的范围为,则 2212,62ABP S AB d△,故选A .19.【2018高考北京理7】在平面直角坐标系中,记d 为点 cos ,sin P 到直线20x my 的距离.当,m 变化时,d 的最大值为()A .1B .2C .3D .4【答案】C【解析】试题分析:P 为单位圆上一点,而直线20x my 过点 2,0A ,则根据几何意义得d 的最大值为1OA .试题解析:22cos sin 1P ∵,为单位圆上一点,而直线20x my 过点 2,0A ,所以d 的最大值为1213OA ,选C .【名师点睛】与圆有关的最值问题主要表现在求几何图形的长度、面积的最值,求点到直线的距离的最值,求相关参数的最值等方面.解决此类问题的主要思路是利用圆的几何性质将问题转化.20.(2017新课标Ⅲ理)在矩形ABCD 中,1AB ,2AD ,动点P 在以点C 为圆心且与BD 相切的圆上.若AP AB AD,则 的最大值为A .3B.CD .2【答案】A 【解析】如图建立直角坐标系,x则(0,1)A ,(0,0)B ,(2,1)D ,(,)Px y 所以圆的方程为224(2)5x y,所以(,1)AP x y ,(0,1)AB ,(2,0)AD,由AP AB AD ,得21x y ,所以 =12x y ,设12x z y,即102xy z ,点(,)P x y 在圆上,所以圆心到直线102xy z 的距离小于半径,,解得13z≤≤,所以z的最大值为3,即的最大值为3,选A.21.【2016·山东文数】已知圆M:2220(0)x y ay a+-=>截直线0x y+=所得线段的长度是M与圆N:22(1)1x y+-=(-1)的位置关系是()(A)内切(B)相交(C)外切(D)相离【答案】B【解析】由2220x y ay(0a )得 222x y a a(0a ),所以圆M的圆心为0,a,半径为1r a ,因为圆M截直线0x y所得线段的长度是,解得2a ,圆N的圆心为 1,1,半径为21r ,所以MN ,123r r ,121r r ,因为1212r r MN r r,所以圆M与圆N相交,故选B.22.【2016·北京文数】圆22(1)2x y的圆心到直线3y x 的距离为()A.1B.2CD.2【答案】C【解析】圆心坐标为(1,0),由点到直线的距离公式可知d ,故选C.23.【2016·新课标2文数】圆x2+y2−2x−8y+13=0的圆心到直线ax+y−1=0的距离为1,则a=()(A)−43(B)−34(D)2【答案】A【解析】由2228130x y x y配方得22(1)(4)4x y,所以圆心为(1,4),因为圆2228130x y x y的圆心到直线10ax y的距离为11 ,解得43a ,故选A.24.(2015安徽文)直线34x y b与圆222210x y x y相切,则b的值是A .-2或12B .2或-12C .-2或-12D .2或12【答案】D【解析】圆的标准方程为22(1)(1)1x y ,圆心(1,1)到直线34x y b 的距离|7|15b ,所以2b 或12b .25.(2015新课标2文)已知三点)0,1(A ,)3,0(B ,)3,2(C ,则ABC 外接圆的圆心到原点的距离为A .35B .321C .352D .34【答案】B 【解析】由题意可得,2AB BC AC ===,∴ΔABC 为等边三角形,故ΔABC 的外接圆圆心时ΔABC 的中心,又等边ΔABC (1,3,故ΔABC 外接圆的圆心到原点的距离为3=.26.(2015山东理)一条光线从点(2,3) 射出,经y 轴反射后与圆22(3)(2)1x y 相切,则反射光线所在直线的斜率为A .53 或35B .32或23C .54或45D .43或34【答案】D 【解析】(2,3) 关于y 轴对称点的坐标为(2,3) ,设反射光线所在直线为3(2)y k x ,即230k x y k ,则1d ,|55|k 43k 或34.27.(2015广东理)平行于直线210x y 且与圆225x y 相切的直线的方程是A .250x y 或250x yB .20x y 或20x yC .250x y 或250x y D .20x y 或20x y【答案】A 【解析】设所求直线的方程为20x y c (1) c,所以c ,故所求直线的方程为250x y 或250x y .28.(2015新课标2理)过三点(1,3)A ,(4,2)B ,(1,7)C 的圆交于y 轴于M 、N 两点,则MN =A .26B .8C .46D .10【答案】C 【解析】设过,,A B C 三点的圆的方程为220x y Dx Ey F ,则3100422007500D E F D E F D E F,解得2,4,20D E F ,所求圆的方程为2224200x y x y ,令0x =,得24200y y ,设1(0,)M y ,2(0,)N y ,则124y y ,1220y y ,所以12||||MN y y29.(2015重庆理)已知直线l :10()x ay a R 是圆C :224210x y x y 的对称轴,过点(4,)A a 作圆C 的一条切线,切点为B ,则AB =A .2B.C .6D.【答案】C 【解析】圆C 标准方程为22(2)(1)4x y ,圆心为(2,1)C ,半径为2r ,因此2110a ,1a ,即(4,1)A,6AB .选C .30.(2014新课标2文理)设点0(,1)M x ,若在圆22:=1O x y 上存在点N ,使得°45OMN ,则0x 的取值范围是A .1,1B .1122,C. D.22,【答案】A 【解析】当点M 的坐标为(1,1)时,圆上存在点(1,0)N ,使得45OMN,所以01x 符合题意,排除B 、D ;当点M的坐标为时,OM M 作圆O 的一条切线MN ,连接ON ,则在Rt OMN中,sin 32OMN,则45OMN ,故此时在圆O 上不存在点N ,使得°45OMN,即0x C ,故选A .31.(2014福建文)已知直线l 过圆 2234x y 的圆心,且与直线10x y 垂直,则l 的方程是A .20x yB .20x yC .30x yD .30x y 【答案】D 【解析】直线l 过点(0,3),斜率为1,所以直线l 的方程为30x y .32.(2014北京文)已知圆 22:341C x y 和两点 ,0A m , ,00B m m ,若圆C 上存在点P ,使得90APB ,则m 的最大值为A .7B .6C .5D .4【答案】B 【解析】因为圆C 的圆心为(3,4),半径为1,||5OC ,所以以原点为圆心、以m 为半径与圆C 有公共点的最大圆的半径为6,所以m 的最大值为6,故选B .33.(2014湖南文)若圆221:1C x y 与圆222:680C x y x y m 外切,则mA .21B .19C .9D .11【答案】C 【解析】由题意得12(0,0),(3,4)C C ,121,r r 1212||15C C r r ,所以9m .34.(2014安徽文)过点P )(1,3 的直线l 与圆122y x 有公共点,则直线l 的倾斜角的取值范围是A .]6,(B .3,(C .60[ ,D .]30[ ,【答案】D 【解析】设直线l 的倾斜角为 ,由题意可知min max 0,263.35.(2014浙江文)已知圆22220x y x y a 截直线20x y 所得弦的长度为4,则实数a 的值是A .-2B .-4C .-6D .-8【答案】B 【解析】圆的标准方程为22(1)(1)2x y a ,则圆心(1,1)C ,半径r 满足22r a ,则圆心C 到直线20x y 的距离d2422r a ,故4a .36.(2014四川文)设m R ,过定点A 的动直线0x my 和过定点B 的动直线30mx y m 交于点(,)P x y ,则||||PA PB 的取值范围是A .B .C .D .【答案】B 【解析】易知直线0x my 过定点(0,0)A ,直线30mx y m 过定点(1,3)B ,且两条直线相互垂直,故点P 在以AB 为直径的圆上运动,故||||||cos ||sin PA PB AB PAB AB PAB 102sin()4PAB[10,25] .故选B .37.(2014江西文)在平面直角坐标系中,,A B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线240x y 相切,则圆C 面积的最小值为A .45B .34C .(625)D .54【答案】A 【解析】由题意可知以线段AB 为直径的圆C 过原点O ,要使圆C 的面积最小,只需圆C 的半径或直径最小.又圆C 与直线240x y 相切,所以由平面几何知识,知圆的直径的最小值为点0到直线240x y 的距离,此时25r5r,圆C 的面积的最小值为245S r.38.(2014福建理)已知直线l 过圆 2234x y 的圆心,且与直线10x y 垂直,则l 的方程是A .20x y B .20x y C .30x y D .30x y 【答案】D 【解析】直线l 过点(0,3),斜率为1,所以直线l 的方程为30x y .39.(2014北京理)已知圆 22:341C x y 和两点 ,0A m , ,00B m m ,若圆C 上存在点P ,使得90APB ,则m 的最大值为A .7B .6C .5D .4【答案】B 【解析】因为圆C 的圆心为(3,4),半径为1,||5OC ,所以以原点为圆心、以m 为半径与圆C 有公共点的最大圆的半径为6,所以m 的最大值为6,故选B .40.(2014湖南理)若圆221:1C x y 与圆222:680C x y x y m 外切,则m A .21B .19C .9D .11【答案】C 【解析】由题意得12(0,0),(3,4)C C ,121,25r r m1212||1255C C r r m ,所以9m .41.(2014安徽理)过点P )(13 的直线l 与圆122y x 有公共点,则直线l 的倾斜角的取值范围是A .]6,(B .3,(C .60[ ,D .]30[ ,【答案】D 【解析】设直线l 的倾斜角为 ,由题意可知min max 0,263.42.(2014浙江理)已知圆22220x y x y a 截直线20x y 所得弦的长度为4,则实数a 的值是A .-2B .-4C .-6D .-8【答案】B 【解析】圆的标准方程为22(1)(1)2x y a ,则圆心(1,1)C ,半径r 满足22r a ,则圆心C 到直线20x y 的距离d 所以2422r a ,故4a .43.(2014四川理)设m R ,过定点A 的动直线0x my 和过定点B 的动直线30mx y m 交于点(,)P x y ,则||||PA PB 的取值范围是A .B .C .D .【答案】B 【解析】易知直线0x my 过定点(0,0)A ,直线30mx y m 过定点(1,3)B ,且两条直线相互垂直,故点P 在以AB 为直径的圆上运动,故||||||cos ||sin PA PB AB PAB AB PAB 4PAB.故选B .44.(2014江西理)在平面直角坐标系中,,A B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线240x y 相切,则圆C 面积的最小值为A .45B .34C .(6D .54【答案】A 【解析】由题意可知以线段AB 为直径的圆C 过原点O ,要使圆C 的面积最小,只需圆C 的半径或直径最小.又圆C 与直线240x y 相切,所以由平面几何知识,知圆的直径的最小值为点O 到直线240x y 的距离,此时2rr,圆C 的面积的最小值为245S r.45.(2013山东文)过点(3,1)作圆 2211x y 的两条切线,切点分别为A ,B ,则直线AB 的方程为()A .230x y B .230x y C .430x y D .430x y 【答案】A 【解析】根据平面几何知识,直线AB 一定与点(3,1),(1,0)的连线垂直,这两点连线的斜率为12,故直线AB 的斜率一定是–2,只有选项A 中直线的斜率为–2.46.(2013重庆文)已知圆 221:231C x y ,圆 222:349C x y ,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN 的最小值为A .524B .171C .622D .17【答案】A 【解析】圆C 1,C 2的圆心分别为C 1,C 2,由题意知|PM|≥|PC 1|-1,|PN|≥|PC 2|-3,∴|PM|+|PN|≥|PC 1|+|PC 2|-4,故所求值为|PC 1|+|PC 2|-4的最小值.又C 1关于x 轴对称的点为C 3(2,-3),所以|PC 1|+|PC 2|-4的最小值为|C 3C 2|-4=2223344524 ,故选A .47.(2013安徽文)直线2550x y 被圆22240x y x y 截得的弦长为A .1B .2C .4D .46【答案】C 【解析】圆心(1,2),圆心到直线的距离1+4-5+5=15d,半径5r ,所以最后弦长为222(5)14 .48.(2013新课标2文)已知点 1,0A ; 1,0B ; 0,1C ,直线y ax b (0)a 将△ABC 分割为面积相等的两部分,则b 的取值范围是A .(0,1)B .211,22C .211,23D .11,32【答案】B 【解析】(1)当y ax b 过 1,0A 与BC 的中点D 时,符合要求,此13b ,(2)当y ax b 位于②位置时1,0b A a,11,11b a b D a a,令1112A BD S 得212b a b,∵0a ,∴12b (3)当y ax b 位于③位置时21,11b b a A a a,21,11b a b D a a,令2212A CD S,即 111112112b b b a a ,化简得22241a b b ,∵0a ,∴22410b b,解得1122b.综上:21122b,故选B .49.(2013陕西文)已知点M(a ,b)在圆221:O x y 外,则直线ax +by =1与圆O 的位置关系是A .相切B .相交C .相离D .不确定【答案】B 【解析】点M(a ,b)在圆.112222b a y x 外111)00(.22ba d by ax O 距离到直线,圆=圆的半径,故直线与圆相交,故选B .50.(2013天津文)已知过点P(2,2)的直线与圆225(1)x y 相切,且与直线10ax y 垂直,则aA .12B .1C .2D .12【答案】C 【解析】设直线斜率为k ,则直线方程为2(2)yk x ,即220kx y k ,圆心(1,0)到12k.因为直线与直线10ax y 垂直,所以112k a,即2a ,选C .51.(2013广东文)垂直于直线1y x 且与圆221x y 相切于第一象限的直线方程是A.0x y B .10x y C .10x y D .0x y 【答案】A【解析】∵圆心到直线的距离等于1r ,排除B 、C ;相切于第一象限排除D ,选A .直接法可设所求的直线方程为: 0y x k k ,再利用圆心到直线的距离等于1r ,求得k.52.(2013新课标2文)设抛物线2:4C y x 的焦点为F ,直线l 过F 且与C 交于A ,B 两点.若||3||AF BF ,则l 的方程为A .1y x 或1y x B .3(1)3y x或3(1)3y xC .1)y x 或1)y x D .(1)2y x或(1)2y x 【答案】C 【解析】抛物线24y x 的焦点坐标为(1,0),准线方程为1x ,设11(,)A x y ,22(,)B x y ,则因为|AF|=3|BF|,所以1213(1)x x ,所以1232x x ,因为1||y =32||y ,1x =92x ,所以1x =3,2x =13,当1x =3时,2112y ,所以此时1y ,若1y ,则123(3,(,33A B ,此时AB k ,此时直线方程为1)y x .若1y ,则1(3,(,)33A B ,此时AB k ,此时直线方程为1)y x .所以l 的方程是1)y x或1)y x ,选C .53.(2013山东理)过点(3,1)作圆 2211x y 的两条切线,切点分别为A ,B ,则直线AB 的方程为A .230x y B .230x y C .430x y D .430x y 【答案】A 【解析】根据平面几何知识,直线AB 一定与点(3,1),(1,0)的连线垂直,这两点连线的斜率为12,故直线AB 的斜率一定是2 ,只有选项A 中直线的斜率为2 .54.(2013重庆理)已知圆 221:231C x y ,圆 222:349C x y ,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN 的最小值为A .4B 1C .6D .【答案】A 【解析】圆C 1,C 2的圆心分别为C 1,C 2,由题意知|PM|≥|PC 1|-1,|PN|≥|PC 2|-3,∴|PM|+|PN|≥|PC 1|+|PC 2|-4,故所求值为|PC 1|+|PC 2|-4的最小值.又C 1关于x 轴对称的点为C 3(2,-3),所以|PC 1|+|PC 2|-4的最小值为|C 3C 2|-444 ,故选A .55.(2013安徽理)直线250x y 被圆22240x y x y 截得的弦长为A .1B .2C .4D .【答案】C 【解析】圆心(1,2),圆心到直线的距离d,半径r ,所以最后弦长为4 .56.(2013新课标2理)已知点 1,0A ; 1,0B ; 0,1C ,直线y ax b (0)a 将△ABC 分割为面积相等的两部分,则b 的取值范围是A .(0,1)B .11,22C .11,23D .11,32【答案】B 【解析】(1)当y ax b 过 1,0A 与BC 的中点D 时,符合要求,此13b ,(2)当y ax b 位于②位置时1,0b A a,11,11b a b D a a,令1112A BD S 得212b a b,∵0a ,∴12b .(3)当y ax b 位于③位置时21,11b b a A a a,21,11b a b D a a,令2212A CD S,即 111112112b b b a a ,化简得22241a b b ,∵0a ,∴22410b b ,解得221122b综上:1122b,故选B .57.(2013陕西理)已知点(,)M a b 在圆221:O x y 外,则直线1ax by 与圆O 的位置关系是A .相切B .相交C .相离D .不确定【答案】B 【解析】点M(a,b)在圆221x y 外,∴221a b .圆(0,0)O 到直线1ax by 距离1d=圆的半径,故直线与圆相交.所以选B .58.(2013天津理)已知过点P(2,2)的直线与圆225(1)x y 相切,且与直线10ax y 垂直,则aA .12B .1C .2D .12【答案】C 【解析】设直线斜率为k ,则直线方程为2(2)yk x ,即220kx y k ,圆心(1,0)到12k.因为直线与直线10ax y 垂直,所以112k a,即2a ,选C .59.(2013广东理)垂直于直线1y x 且与圆221x y 相切于第一象限的直线方程是A.0x y B .10x y C .10x y D .0x y【答案】A【解析】∵圆心到直线的距离等于1r ,排除B 、C ;相切于第一象限排除D ,选A .直接法可设所求的直线方程为: 0y x k k ,再利用圆心到直线的距离等于1r ,求得k.60.(2013新课标2理)设抛物线2:4C y x 的焦点为F ,直线l 过F 且与C 交于A ,B 两点.若||3||AF BF ,则l 的方程为A .1y x 或1y xB .(1)3y x或(1)3y xC .1)y x 或1)y x D .(1)2y x或(1)2y x 【答案】C 【解析】抛物线24y x 的焦点坐标为(1,0),准线方程为1x ,设11(,)A x y ,22(,)B x y ,则因为|AF|=3|BF|,所以1213(1)x x ,所以1232x x ,因为1||y =32||y ,1x =92x ,所以1x =3,2x =13,当1x =3时,2112y ,所以此时1y ,若1y ,则1(3,(,33A B ,此时AB k ,此时直线方程为1)y x .若1y ,则123(3,(,)33A B ,此时AB k ,此时直线方程为1)y x .所以l 的方程是1)y x或1)y x ,选C .61.(2012浙江文)设a R ,则“1a ”是“直线1l :210ax y 与直线2l :(1)40x a y 平行”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A 【解析】“直线1l :210ax y 与直线2l :(1)40x a y 平行”的充要条件是(1)2a a ,解得,1a 或2a ,所以是充分不必要条件.62.(2012天津文)设m ,n R ,若直线(1)+(1)2=0m x n y 与圆22(1)+(y 1)=1x 相切,则+m n 的取值范围是A .[1B .(,1)C .[2D .(,2)【答案】D 【解析】∵直线(1)+(1)2=0m x n y 与圆22(1)+(y 1)=1x 相切,∴圆心(1,1)到直线的距离为d ,所以21()2m n mn m n ,设=t m n ,则21+14t t ,解得(,2)t .63.(2012湖北文)过点(1,1)P 的直线,将圆形区域 22(,)|4x y x y 分为两部分,使得这两部分的面积之差最大,则该直线的方程为A .20x y B .10y C .0x y D .340x y 【答案】A 【解析】要使直线将圆形区域分成两部分的面积之差最大,必须使过点P 的圆的弦长达到最小,所以需该直线与直线OP 垂直即可.又已知点(1,1)P ,则1OP k ,故所求直线的斜率为–1.又所求直线过点(1,1)P ,故由点斜式得,所求直线的方程为 11y x ,即20 x y .故选A .64.(2012天津文)在平面直角坐标系xOy 中,直线3450x y 与圆224x y 相交于,A B 两点,则弦AB 的长等于()()A()B ()C ()D【答案】B 【解析】圆224x y 的圆心(0,0)O 到直线3450x y 的距离515d,弦AB 的长AB .65.(2012浙江理)设a R ,则“1a ”是“直线1l :210ax y 与直线2l :(1)40x a y 平行”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A 【解析】“直线1l :210ax y 与直线2l :(1)40x a y 平行”的充要条件是(1)2a a ,解得,1a 或2a ,所以是充分不必要条件.66.(2012天津理)设m ,n R ,若直线(1)+(1)2=0m x n y 与圆22(1)+(y 1)=1x 相切,则+m n 的取值范围是A .[1B .(,1)C .[2D .(,2)【答案】D 【解析】∵直线(1)+(1)2=0m x n y 与圆22(1)+(y 1)=1x 相切,∴圆心(1,1)到直线的距离为d ,所以21()2m n mn m n ,设=t m n ,则21+14t t ,解得(,2)t .67.(2012湖北理)过点(1,1)P 的直线,将圆形区域 22(,)|4x y x y 分为两部分,使得这两部分的面积之差最大,则该直线的方程为A .20x y B .10y C .0x y D .340x y 【答案】A 【解析】要使直线将圆形区域分成两部分的面积之差最大,必须使过点P 的圆的弦长达到最小,所以需该直线与直线OP 垂直即可.又已知点(1,1)P ,则1OP k ,故所求直线的斜率为 1.又所求直线过点(1,1)P ,故由点斜式得,所求直线的方程为11y x ,即20 x y .故选A .68.(2012天津理)在平面直角坐标系xOy 中,直线3450x y 与圆224x y 相交于,A B 两点,则弦AB 的长等于A .B .CD .【答案】B 【解析】圆224x y 的圆心(0,0)O 到直线3450x y 的距离515d弦AB 的长AB .69.(2011北京文)已知点A(0,2),B(2,0).若点C 在函数y x 的图像上,则使得ΔABC 的面积为2的点C 的个数为A .4B .3C .2D .1【答案】A 【解析】设点2(,)C t t ,直线AB 的方程是20x y ,||AB 由于ABC 的面积为2,则这个三角形中AB 边上的高h 满足方程122,即h ,22|2|2t t ,解得有4个实根,故这样的点C 有4个.70.(2011江西文)若曲线1C :2220x y x 与曲线2C :()0y y mx m 有四个不同的交点,则实数m 的取值范围是A .(3,3文)B .(3,0) (0,3)C .[3 ,3]D .( ,3) (3,+ )【答案】B 【解析】221:(1)1C x y ,2C 表示两条直线即x 轴和直线l :(1)y m x ,显然x 轴与1C 有两个交点,由题意l 与2C 相交,所以1C 的圆心到l 的距离1d r,解得33(,)33m,又当0m 时,直线l 与x 轴重合,此时只有两个交点,不符合题意.故选B .71.(2011北京理)已知点A(0,2),B(2,0).若点C 在函数y =x 的图像上,则使得ΔABC 的面积为2的点C 的个数为A .4B .3C .2D .1【答案】A 【解析】设点2(,)C t t ,直线AB 的方程是20x y ,||AB 由于ABC 的面积为2,则这个三角形中AB 边上的高h 满足方程122,即h ,22|2|2t t ,解得有4个实根,故这样的点C 有4个.72.(2011江西理)若曲线1C :2220x y x 与曲线2C :()0y y mx m 有四个不同的交点,则实数m 的取值范围是A .(33,33)B .(33,0) (0,33)C .[3 ,3]D .( ,3) (3,+ )【答案】B 【解析】221:(1)1C x y ,2C 表示两条直线即x 轴和直线l :(1)y m x ,显然x 轴与1C 有两个交点,由题意l 与2C 相交,所以1C 的圆心到l的距离1d r,解得(,33m,又当0m 时,直线l 与x 轴重合,此时只有两个交点,不符合题意.故选B .73.【2020年高考天津卷12】已知直线80x 和圆222(0)x y r r 相交于,A B 两点.若||6AB ,则r 的值为_________.【答案】5【解析】因为圆心 0,0到直线80x的距离4d,由l6 ,解得=5r .74.【2020年高考浙江卷15】设直线:(0)l y kx b k ,圆221:1C x y ,222:(4)1C x y ,若直线l与1C ,2C 都相切,则k ;b.【答案】33;233【解析】由题意可知直线l 是圆1C 和圆2C 的公切线,∵0k ,为如图所示的切线,由对称性可知直线l 必过点 2,0,即20k b ①1,②由①②解得:3k,3b,故答案为:3;3.75.【2020年高考江苏卷14】在平面直角坐标系xOy 中,已知3,0)2P ,A B 、是圆C :221(362x y上的两个动点,满足PA PB ,则PAB 面积的最大值是________.【答案】【解析】如图,作PC 所在直径EF ,交AB 于点D ,则:∵PA PB ,6CA CB R ,∴PC AB ,EF 为垂径.要使面积PAB S 最大,则P D 、位于C 两侧,并设CD x ,计算可知1PC ,故1PD x ,2AB BD ,故1(12PAB AB PD S x,令6cos x ,(1(16cos )6sin 6sin 18sin 2PAB S x ,02q,记函数()6sin 18sin 2f ,则2()6cos 36cos26(12cos cos 6)f ,令2()6(12cos cos 6)0f ,解得2cos 3 (3cos 04舍去)显然,当20cos 3时,()0f ,()f 单调递减;当2cos 13时,()0f ,()f 单调递增;结合cos 在(0,2 递减,故2cos3 时()f 最大,此时sin 3,故max 552()636333f,即PAB 面积的最大值是.(注:实际上可设BCD ,利用直角BCD 可更快速计算得出该面积表达式)76.【2019·浙江卷】已知圆C 的圆心坐标是(0,)m ,半径长是r .若直线230x y 与圆C 相切于点(2,1)A ,则m =___________,r =___________.【答案】2【解析】由题意可知11:1(2)22ACk AC y x,把(0,)m代入直线AC的方程得2m,此时||r AC77.【2018·全国I文】直线1y x 与圆22230x y y交于A B,两点,则AB ________.【答案】【解析】根据题意,圆的方程可化为 2214x y,所以圆的圆心为0,1 ,且半径是2,根据点到直线的距离公式可以求得d ,结合圆中的特殊三角形,可知AB,故答案为.78.【2018·江苏卷】在平面直角坐标系xOy中,A为直线:2l y x上在第一象限内的点,(5,0)B,以AB 为直径的圆C与直线l交于另一点D.若0AB CD,则点A的横坐标为________.【答案】3【解析】设,2(0)A a a a ,则由圆心C为AB中点得5,,2aC a易得:520C x x a y y a,与2y x联立解得点D的横坐标1,Dx 所以 1,2D.所以55,2,1,22aAB a a CD a,由0AB CD得2551220,230,32aa a a a a a或1a ,因为0a ,所以 3.a79.【2018高考上海12】已知实数1212x x y y,,,满足:22221122121211,1,2x y x y x x y y,则的最大值为.【解析】试题分析:由已知可得点1122,,,A x yB x y在单位圆221x y 上.又由121212x x y y,容易想到向量的数量积,从而得AOB的大小.而容易想到点11,A x y到直线10x y 的距离,因此问题转化为圆上两点 1122,,,A x y B x y 到直线10x y 距离和的最大值问题,再三角换元,进而应用三角函数来求最大值.试题解析:由已知可得两点 1122,,,A x y B x y 在单位圆221x y 上.121211,cos ,223OA OB x x y y AOB AOB OA OB∵ .设 cos ,sin ,cos ,sin 33A B,则 .已知点 1122,,,A x y B x y 在直线10x ysin 1cos sin 13311sin 1cos sin sin cos 1222233cos sin 22222cos 4sin 412当且仅当122即12.80.(2017江苏理)在平面直角坐标系xOy 中,(12,0)A ,(0,6)B ,点P 在圆O :2250x y 上,若20PA PB≤,则点P 的横坐标的取值范围是.【答案】[ 【解析】设(,)P x y ,由20PA PB≤,得250x y ≤,x如图由250x y ≤可知,P 在 MN 上,由2225050x y x y,解得(1,7)M ,(5,5)N ,所以P 点横坐标的取值范围为[ .81.【2016·四川文科】在平面直角坐标系中,当P(x ,y)不是原点时,定义P 的“伴随点”为'2222(,)y xP x y x y;当P 是原点时,定义P 的“伴随点”为它自身,现有下列命题:①若点A 的“伴随点”是点'A ,则点'A 的“伴随点”是点A .②单元圆上的“伴随点”还在单位圆上.③若两点关于x 轴对称,则他们的“伴随点”关于y 轴对称④若三点在同一条直线上,则他们的“伴随点”一定共线.其中的真命题是.【答案】②③【解析】对于①,若令(1,1)P ,则其伴随点为11(,)22P ,而11(,)22P 的伴随点为(1,1) ,而不是P ,故①错误;对于②,令单位圆上点的坐标为(cos ,sin )P x x ,则其伴随点为(sin ,cos )P x x ,仍在单位圆上,故②正确;对于③,设曲线(,)0f x y 关于x 轴对称,则(,)0f x y 与曲线(,)0f x y 表示同一曲线,其伴随曲线分别为2222(,)0y x f x y x y 与2222(,)0y xf x y x y ,它们也表示同一曲线,又因为伴随曲线2222(,)0y x f x y x y 与2222(,)0y xf x y x y关于y 轴对称,所以③正确;对于④,取直线y kx b 上一点P(x ,y),则其伴随点2222(,)y xx y x y ,消参后轨迹是圆,故④错误.所以真命题为②③.82.[2016·新课标Ⅲ文数]已知直线l :60x 与圆2212x y 交于,A B 两点,过,A B 分别作l 的垂线与x 轴交于,C D 两点,则||CD _____________.【答案】4【解析】由60x ,得6x,代入圆的方程,并整理,得260y ,解得12y y 120,3x x ,所以||AB .又直线l 的倾斜角为30 ,由平面几何知识知在梯形ABDC 中,||||4cos30AB CD.83.【2016·新课标1文数】设直线y=x+2a 与圆C :x 2+y 2-2ay-2=0相交于A ,B 两点,若퐴 =23,则圆C 的面积为.【答案】4【解析】圆22:220C x y ay ,即222:()2C x y a a ,圆心为(0,)C a ,由||AB 圆心C 到直线2y x a,所以得222()22a ,则22,a 所以圆的面积为2π(2)4πa .84.(2015重庆文)若点(1,2)P 在以坐标原点为圆心的圆上,则该圆在点P 处的切线方程为________.【答案】250x y 【解析】由点(1,2)P 在以坐标原点为圆心的圆上知此圆的方程为:225x y ,所以该圆在点P 处的切线方程为125x y 即250x y .85.(2015湖南文)若直线3450x y 与圆 2220x y r r 相交于,A B 两点,且120o AOB (O为坐标原点),则r =_____.【答案】2【解析】如图直线3450x y 与圆2220x y r r (>)交于,A B 两点,O 为坐标原点,且120o AOB ,则圆心(0,0)到直线3450x y 的距离为2r 2r,∴2r =.86.(2015湖北文)如图,已知圆C 与x 轴相切于点(1,0)T ,与y 轴正半轴交于两点,A B (B 在A 的上方),。
高考数学复习-直线与圆练习试题、参考答案

高考数学复习-直线与圆练习试题第Ⅰ卷 (选择题 共40分)一、选择题(10×4′=40′)1.直线l 与直线y =1、x-y -7=0分别交于P 、Q 两点,线段PQ 的中点为(1,-1),则直线l 的斜率为( )A.23 B.32 C.-32D.-232.点P 在直线2x +y +10=0上,P A 、PB 与圆422=+y x 分别相切于A 、B 两点,则四边形P AOB 面积的最小值为 ( )A.24B.16C.8D.43.已知直线1l :y =x ,2l :ax -y =0,其中a 为实数,当这两直线的夹角θ∈(0,12π)时,a 的取值范围为 ( )A.(0,1)B.(33,3) C.(33,1)∪(1,3) D.(1,3) 4.设a 、b 、k 、p 分别表示同一直线的横截距、纵截距、斜率和原点到直线的距离,则有( ) A.)1(2222k p k a += B.k =abC.b a 11+=pD.a =-kb5.已知直线x +3y -7=0,kx-y -2=0和x 轴、y 轴围成四边形有外接圆,则实数k 等于 ( ) A.-3 B.3 C.-6 D.66.若圆222r y x =+(r >0)上恰有相异两点到直线4x -3y +25=0的距离等于1,则r 的取值范围是( ) A.[4,6] B.[4,6) C.(4,6] D.(4,6)7.直线1l :0=++c by ax ,2l :0=++p ny mx ,则bnam=-1是1l ⊥2l 的 ( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分又不必要条件8.过圆422=+y x 外一点P(4,-1)引圆的两条切线,则经过两切点的直线方程为 ( ) A.4x -y -4=0 B.4x +y -4=0 C.4x +y +4=0 D.4x -y +4=09.倾斜角为60°,且过原点的直线被圆222)()(r b y a x =-+-(r >0)截得弦长恰好等于圆的半径,则a 、b 、r 满足的条件是 ( )A.)3(|3|3a b b a r ≠-=B.)3(|3|23a b b a r ≠-=C.)3(|3|3a b b a r ≠+=D.)3(|3|23a b b a r ≠-=10.直线y =kx +1与圆0922=--++y kx y x 的两个交点关于y 轴对称,则k 为 ( )A.-1B.0C.1D.任何实数第Ⅱ卷 (非选择题 共60分)二、填空题(4×3′=12′)11.若点P (a ,b )与点Q (b +1,a -1)关于直线l 对称,则直线l 的方程是 .12.已知圆16)1()2(22=-+-y x 的一条直径通过直线x -2y -3=0被圆截弦的中点,则该直径所在直线的方程为 .13.关于x 的方程kx +1=21x -有且只有一个实根,则实数k 的取值范围是 . 14.经过点P (-2,4),且以两圆0622=-+x y x 和422=+y x 的公共弦为一条弦的圆的方程是 .三、解答题(6×8′=48′)15.若直线1l :x+y+a =0,2l :x+ay +1=0,3l :ax+y +1=0能围成三角形,求a 的取值范围.16.已知点P 是直线l 上的一点,将直线l 绕点P 逆时针方向旋转α(0<α<2π)所得直线1l 的方程为3x -y -4=0,若继续绕点P 逆时针方向旋转α-π2,则得2l 的方程为x +2y +1=0,试求直线l 的方程.17.设P 是圆M :1)5()5(22=-+-y x 上的动点,它关于A (9,0)的对称点为Q ,把P 绕原点依逆时针方向旋转90°到点S ,求|SQ |的最值.18.已知点A (3,0),点P 在圆122=+y x 的上半圆周上,∠AOP 的平分线交P A 于Q ,求点Q 的轨迹方程.19.如图,已知⊙A :425)2(22=++y x ,⊙B :41)2(22=+-y x ,动圆P 与⊙A 、⊙B 都外切. (1)求动圆圆心P 的轨迹方程,并说明轨迹是什么曲线;(2)若直线y=kx +1与(1)中的曲线有两个不同的交点1P 、2P ,求k 的取值范围; (3)若直线l 垂直平分(2)中的弦21P P ,求l 在y 轴上的截距b 的取值范围.20.已知圆C :044222=-+-+y x y x ,是否存在斜率为1的直线l ,使得l 被圆C 截得弦AB 为直径的圆过原点?若存在,求出l 的方程;若不存在,说明理由.参考答案1.C 方法1 设直线l 为y=kx+b ,分别与y =1,x-y -7=0联立解得P (-b k ,1),Q (k b -+17,kb k -+17).由PQ 中点为(1,-1),∴217=-++-k b b k ,且1+kb k -+17=-2,∴k =-32,故选C. 方法2 设P (a ,1),Q (b +7,b ),因PQ 的中点为(1,-1),∴⎪⎪⎩⎪⎪⎨⎧-=+=++121127b b a ,解得⎩⎨⎧-=-=32b a ,故P 为(-2,1),Q 为(4,-3),∴3224131-=+--==PQ k k ,故选C. 2.C 如图,PAOB S =22||||2||2||||21232AO PO PA OA PA PAO -==⋅⋅=⋅∆=24||2-PO . 要求PAOB S 的最小值,只需求|PO |的最小值即可.5212|10002|||22min =+++⨯=PO ,∴8)(min =PAOB S ,故选C.3.C 如图,设直线y=ax 的倾斜角为α, 则α≠4π,∴|α-4π|<12π, ∴6π<α<3π,且α≠4π.a =tan α∈(33,1)∪(1,3).4.A 应用点到直线的距离公式,选A.5.B 如图,设围成四边形为OABC ,因OABC 有外接圆,且∠AOC =90°,故∠ABC =90°. ∴两条直线x +3y -7=0,kx -y -2=0互相垂直,(-31)·k =-1,即k =3,故选B.说明 运用圆的几何性质是解决圆的问题的有效途径.6.D 如图,设l :4x -3y +25=0,与l 平行且距离等于1的直线为4x -3y +b =0. ∴2015|25|=⇒=-b b 或b =30.第2题图解第3题图解第5题图解1l :4x -3y +20=0,2l :4x -3y +30=0.圆心(0,0)到1l 和2l 的距离分别为5201=d =4,5302=d =6. 故满足条件的r 取值范围(4,6).实际上,圆222r y x =+没有点到直线4x -3y +25=0的距离等于1, 则0<r <4,若圆上只有一点到直线4x -3y +25=0的距离等于1,则r =4,类似可求出圆上有三点、四点到直线的距离等于1 的r 的取值范围.7.A 由1-=bnam,可得1l ⊥2l ,∴选A. 8.A 方法1 设切点为A 、B ,则AB ⊥OP , ∵410401-=---=OP k ,∴4=AB k .故排除B 、C. 又由图可知,AB 在y 轴的截距为负,故排除D,所以选A.方法2 设A (1x ,1y ),B (2x ,2y ), 由AP ⊥OA 可得AP k ·OA k =-1, 即1411111-=⋅-+x y x y .∴04112121=+-+y x y x ,又42121=+y x , ∴04411=++-y x .同理可得04422=++-y x ,∴AB 直线为-4x +y +4=0,即4x -y -4=0.方法3 设A (1x ,1y ),B (2x ,2y ),则切线P A 为411=+y y x x ,422=+y y x x . ∴4411=-y x ,4422=-y x ,∴A 、B 在直线4x -y -4=0上.另:此题可推广到一般结论,若P (0x ,0y )为圆222r y x =+ (r >0)外一点,过P 引圆的两条切线,则经过两切点的直线方程为200r y y x x =+.9.A 直线方程为x y 3=,则圆心(a ,b )到直线3x -y =0的距离为d =2|3|b a -,又因截得弦长恰好等于圆的半径,故d =23r ,∴|3a -b |=3r ,故选A. 10.B 方法1 将y =kx +1代入922=-++y kx y x 中有092)1(22=-++kx x k . 设交点为 A (1x ,1y ),B (2x ,2y ),∵A 、B 关于y 轴对称,∴021=+x x , ∴k =0.故选B.方法2 因直线与圆的两个交点A (1x ,1y ),B (2x ,2y )关于y 轴对称 ∴021=+x x ,21y y =,故圆心在y 轴上,∴k =0,故选B.11.x-y -1=0 P 、Q 关于直线l 对称,故1k k PQ ⋅=-1且PQ 中点在l 上, ∴11111=---+-=-=aa bb k k PQ,又PQ 中点为(21++b a ,21-+a b ),第6题图解第8题图解∴l 的方程为y -21-+a b =x -21++b a ,即x-y -1=0.此题也可将a ,b 赋特殊值去求直线l .12.2x +y -3=0 由圆的几何意义知该直径与直线x -2y -3=0垂直.故该直径方程为y +1=-2(x -2),即2x +y -3=0.13.{k |k >1或k =0或k <-1} 画出函数y =kx +1、y =21x -的图象,两曲线相切及只有一个交点时如图所示.14.08622=-++x y x 设圆的方程为0)4(62222=-+λ+-+y x x y x 经过P (-2,4), ∴0]44)2[()2(64)2(2222=-+-λ+--+-, ∴λ=-2,∴所求的圆的方程为08622=-++x y x .15.解 由1l 、2l 相交,需1·a -1·1≠0,得a ≠1,此时解方程组⎩⎨⎧=++=++010ay x a y x ,可解得⎩⎨⎧=-=11y x 即1l 、2l 的交点为(-1-a ,1),由1l 、3l 相交,需1·1-1·a ≠0,∴a ≠1,由2l ,3l 相交,需1·1-a ·a ≠0,∴a ≠±1,又(-1-a ,1)∉3l , ∴a ·(-1-a )+1+1≠0,得a ≠1且a ≠-2,综上所述,a ∈R 且a ≠±1且a ≠-2,能保证三交点(-1-a ,1),(1,-1-a )、(-1-a ,-1+a +2a )互不重合,所以所求a 的范围为a ∈(-∞,-2)∪(-2,-1)∪(-1,1)∪(1,+∞).16.解 由已知条件知P 为直线3x -y -4=0和直线x +2y +1=0的交点,联立两直线方程得⎩⎨⎧=++=--012043y x y x ,∴⎩⎨⎧-==11y x .∴P 点为(1,-1). 又l 与2l 垂直,故l 的方程为y +1=2(x -1),即l 的方程为2x -y -3=0. 17.解 设P (x ,y ),则Q (18-x ,-y ),记P 点对应的复数为x +y i, 则S 点对应的复数为:(x +y i )·i=-y +x i,即S (-y ,x ),∴|SQ |=xy y x xy y x y x x y y x 22363618)()18(2222222+++-+-++=--++- =2222)9()9(2818118182++-⋅=+++-+⋅y x y x y x其中22)9()9(++-y x 可以看作是点P 到定点B (9,-9)的距离,其最大值为|MB |+r =253+1,最小值为|MB |-r =253-1,则|SQ |的最大值为2106+2,|SQ |的最小值为2106-2.第13题图解18.解 方法1 如图,设P (0x ,0y )(0y >0),Q (x ,y ). ∵OQ 为∠AOP 的平分线,∴31||||==OA OP QA PQ , ∴Q 分P A 的比为31.∴⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+⨯+=+=+⨯+=000043311031)1(43311313y y y x x x 即⎪⎪⎩⎪⎪⎨⎧=-=y y x x 3413400.又因12020=+y x ,且0y >0,∴1916)43(91622=+-y x . ∴Q 的轨迹方程为169)43(22=+-y x (y >0). 方法2 设∠AOP =α,α∈(0,π),则P (cos α,sin α),∠AOQ =2α, 则OQ 直线方程为y =x ·tan2α=kx ① 3cos sin -αα=PA k ,∴直线P A 方程为y =3cos sin -αα(x -3) ②由Q 满足①②且k =tan2α. 由②得y =12)3()3(311122222+--=-⋅-+-+k x k x k k k k.消去k 有y =12)3(22+--x y x x y,∴02322=-+x y x ,由图知y >0. 故所求Q 点轨迹方程为02322=-+x y x (y >0). 说明 上述两种方程为求轨迹的基本方法、相关点及参数法. 19.解 (1)如图,设⊙P 的圆心P (x ,y ),半径为R , 由题设,有|P A |=R +25,|PB |=R +21,∴|P A |-|PB |=2. ∴⊙P 的圆心轨迹是实轴长为2,焦点在x 轴上,且焦距长 为4的双曲线的右支,其方程为1322=-y x (x >0).第18题图解第19题图解(2)由方程组⎪⎩⎪⎨⎧>=-+=)0(13122x y x kx y ,有042)3(22=---kx x k (x >0). ①因为直线与双曲线有两个不同交点,∴⎪⎪⎩⎪⎪⎨⎧≠->⋅>+>∆030022121k x x x x .从而,有⎪⎪⎩⎪⎪⎨⎧><-<3034222k k kk ⇒⎪⎩⎪⎨⎧>-<<<-<<<-3330322k k k k k 或或. ∴-2<k <-3. (3)设21P P 的中点为M (M x 、M y ),则M x =22132k kx x -=+. 又M 在y=kx +1上,∴M y =k M x +1=233k-.∴M (23k k-,233k -).∴21P P 的垂直平分线l 的方程为:y-M y =-k 1(x -M x ),即y -233k -=-k 1(x -23kk -). 令x =0,得截距b =234k-,k ∈(-2,-3),又-2<k <-3,∴-1<3-2k <0.∴b <-4.20.解 假设存在这样的直线,设直线l 方程为y=x+b .方法1 将y=x+b 代入圆的方程有0222)1(22=+-+++b b x b x .由题设知OA ⊥OB ,设A (1x ,1y ),B (2x ,2y ),∴1x 2x +1y 2y =0.又1y 2y =(1x +b )(2x +b )=1x 2x +b (1x +2x )+2b ,∴21x 2x +b (1x +2x )+2b =0. 又∵1x +2x =-(b +1),1x 2x =2b -2+22b ,∴2(22b +2b -2)-b (b +1)+ 2b =0.∴b =1或b =-4.此时Δ=0)22(4)1(2>--+b b , ∴存在这样的直线l :y=x +1或y=x -4满足题设.方法2 设过圆C 与l 的交点的圆系D 为.0)(44222=+-λ+-+-+b y x y x y x 即04)4()2(22=-λ+λ-+-λ++b y x y x . 圆心为(-22-λ,-24λ-),在直线y=x+b 上,∴-24λ-=-22-λ+b ,即λ=3+b . ①又圆D 过原点,∴b λ-4=0. ② 由①②得,0432=-+b b ,即b =1或b =-4.此时圆D 的方程存在.故存在直线y=x +1或y=x -4.。
【题库大全】2005-2012年高考数学(理)试题分项 专题09 直线与圆

求坐标原点到 距离的比值.
(2012年高考辽宁卷理科20)(本小题满分12分)
如图,椭圆 ,动圆 .点 分别为 的左、右顶点, 与 相交于 四点
(1)求直线 与直线 交点 的轨迹方程;
(2)设动圆 与 相交于 四点,其中 , .若矩形 与矩形 的面积相等,证明: 为定值
2011年高考数学选择试题分类汇编——直线与圆
一、选择题:
1.(2011年高考江西卷理科9)若曲线 : 与曲线 : 有四个不同的交点,则实数m的取值范围是
A.( , ) B.( ,0)∪(0, )
c.[ , ] D.( , )∪( ,+ )
解析:选B,由题意,AC为直径,设圆心为F,则 ,圆的标准方程为 ,故 ,由此,易得: ,又 ,所以直线BD的方程为 ,F到BD的距离为 ,由此得, 所以四边形ABCD的面积为
解析:方法一、圆心为(0,0),半径为2
圆心到直线 的
距离为d=
故
得|AB|=2
答案:2
(2010广东理数)12.已知圆心在x轴上,半径为 的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是
12. .设圆心为 ,则 ,解得 .
(2010山东理数)
(2010湖南理数)
2.(2010江苏卷)9、在平面直角坐标系xOy中,已知圆 上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是______▲____
的弧长为[ B]
A B C D
2008年高考数学试题分类汇编——直线与圆
一.选择题:
1,(2008上海卷15)如图,在平面直角坐标系中, 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点 、点 满足 且 ,则称P优于 .如果 中的点 满足:不存在 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧(D)
三年高考高考数学试题分项版 专题08直线与圆 理(含解

第八章 直线与圆一、选择题1. 【2015高考广东,理5】平行于直线012=++y x 且与圆522=+y x 相切的直线的方程是( )A .052=+-y x 或052=--y x B. 052=++y x 或052=-+y x C. 052=+-y x 或052=--y x D. 052=++y x 或052=-+y x 【答案】D .【名师点睛】本题主要考查直线与圆的位置关系,利用点到直线距离求直线的方程及转化与化归思想的应用和运算求解能力,根据题意可设所求直线方程为20x y c ++=,然后可用代数方法即联立直线与圆的方程有且只有一解求得,也可以利用几何法转化为圆心与直线的距离等于半径求得,属于容易题.2. 【 2013湖南8】在等腰三角形ABC 中,=4AB AC =,点P 是边AB 上异于,A B 的一点,光线从点P 出发,经,BC CA 发射后又回到原点P (如图1).若光线QR 经过ABC ∆的中心,则AP 等于( ) A .2 B .1 C .83 D .43【答案】 D【解析】 使用解析法。
).34,34(32).2,2(),0,(O O ABC D BC x P ∴∆处,在中线的的重心的中点设Θ))1(3)12(4,)1(3)2(4()),1(34,0(34)34(,++++-⇒+-=k k k k Q k R x k y k RQ 则其方程为的斜率为设直线,0)1)(12(1,0,)1(3)2(4)12(4,3)1(4=--⇒=⋅=++-++=-=k k k k k k k x k k k k k QP RP QP RP 由题知⎪⎪⎩⎪⎪⎨⎧==⎩⎨⎧==⇒3421(01x k x k ,舍) 选D【考点定位】直线与方程【名师点睛】本题考查直线与点的对称问题,涉及直线方程的求解以及光的反射原理的应用,解决问题的关键是根据光的反射原理正确计算对称点坐标,利用对称性得到直线斜率之间的关系解决问题即可.3. 【2013山东,理9】过点(3,1)作圆(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为( ).A .2x +y -3=0B .2x -y -3=0C .4x -y -3=0D .4x +y -3=0 【答案】:A【名师点睛】本题考查直线与圆的位置关系、直线方程.此类问题的基本解法有 “几何法”和 “代数法”,涉及切线问题,往往利用圆心到直线的距离等于圆的半径建方程求解. 本题是一道能力题,在考查查直线与圆的位置关系、直线方程等基础知识的同时,考查考生的计算能力、逻辑思维能力及数形结合思想.是一道常见题型,故考生易于正确解答. 4. 【2015高考山东,理9】一条光线从点()2,3--射出,经y 轴反射后与圆()()22321x y ++-=错误!未找到引用源。
高考数学试题分类详解直线与圆

高考数学试题分类详解直线与圆一、选择题1、.与直线20x y +-=和曲线221212540x y x y +--+=都相切的半径最小的圆的标准方程是. 【答案】:.22(2)(2)2x y -+-=【分析】:曲线化为22(6)(6)18x y -+-=,其圆心到直线20x y +-=的距离为6625 2.2d +-==所求的最小圆的圆心在直线y x =上,其到直线的距离为2,圆心坐标为(2,2).标准方程为22(2)(2)2x y -+-=。
2、(某某文5)若圆04222=--+y x y x 的圆心到直线0=+-a y x 的距离为22,则a 的值为(A)-2或2(B)2321或 (C)2或0 (D)-2或0解析:若圆04222=--+y x y x 的圆心(1,2)到直线0=+-a y x 的距离为22,∴|12|222a -+=,∴a =2或0,选C 。
3、(某某文13)圆01222=--+x y x 关于直线032=+-y x 对称的圆的方程是( ) A.21)2()3(22=-++y x B.21)2()3(22=++-y x C.2)2()3(22=-++y xD.2)2()3(22=++-y x【答案】C【解析】圆2222210(1)2x y x x y +--=⇒-+=,圆心(1,0),半径2,关于直线032=+-y x 对称的圆半径不变,排除A 、B ,两圆圆心连线段的中点在直线032=+-y x 上,C 中圆2)2()3(22=-++y x 的圆心为(-3,2),验证适合,故选C 。
4、(某某理10)已知直线1x ya b+=(a b ,是非零常数)与圆22100x y +=有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( ) A .60条 B .66条 C .72条 D .78条 答案:选A解析:可知直线的横、纵截距都不为零,即与坐标轴不垂直,不过坐标原点,而圆22100x y +=上的整数点共有12个,分别为()()()6,8,6,8,8,6±-±±,()()()8,6,10,0,0,10-±±±,前8个点中,过任意一点的圆的切线满足,有8条;12个点中过任意两点,构成21266C =条直线,其中有4条直线垂直x 轴,有4条直线垂直y 轴,还有6条过原点(圆上点的对称性),故满足题设的直线有52条。
2023年高考数学试题分类解析【第十章 直线与圆】附答案解析

2023年高考数学试题分类解析【第十章直线与圆】第三节直线与圆的位置关系1.(2023全国甲卷理科8,文科9)已知双曲线()222210,0x y a b a b-=>>,其中一条渐近线与圆()()22231x y -+-=交于,A B 两点,则AB =()A.15【解析】由e =,则222222215c a b b a a a +==+=,解得2b a =.所以双曲线的一条渐近线为2y x =,则圆心()2,3到渐近线的距离d ==,所以弦长5AB ===.故选D.2.(2023全国乙卷理科22,文科22)在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为2sin 42ρθθππ⎛⎫= ⎪⎝⎭ ,曲线22cos :2sin x C y αα=⎧⎨=⎩(α为参数,2απ<<π).(1)写出1C 的直角坐标方程;(2)若直线y x m =+既与1C 没有公共点,也与2C 没有公共点,求m 的取值范围.【分析】(1)根据极坐标与直角坐标之间的转化运算求解,注意,x y 的取值范围;(2)根据曲线12,C C 的方程,结合图形通过平移直线y x m =+分析相应的临界位置,结合点到直线的距离公式运算求解即可.【解析】(1)因为2sin ρθ=,即22sin ρρθ=,可得222x y y +=,整理得()2211x y +-=,表示以()0,1为圆心,半径为1的圆,又因为cos 2sin cos sin 2x ρθθθθ===,2sin 2sin 1cos 2y ρθθθ===-,且42θππ ,则2θππ2 ,则[]sin 20,1x θ=∈,[]1cos 21,2y θ=-∈,故()[][]221:11,0,1,1,2C x y x y +-=∈∈.(2)因为22cos :2sin x C y αα=⎧⎨=⎩(α为参数,2απ<<π),整理得224x y +=,表示圆心为()0,0O ,半径为2,且位于第二象限的圆弧,如图所示,若直线y x m =+过()1,1,则11m =+,解得0m =;若直线y x m =+,即0x y m -+=与2C相切,则20m =>⎩,解得m =若直线y x m =+与12,C C均没有公共点,则m >0m <,即实数m 的取值范围为()(),0-∞+∞.4.(2023新高考I 卷6)过点()0,2-与圆22410x y x +--=相切的两条直线的夹角为α,则sin α=()A.1B.154C.104 D.64【解析】()222241025x y x x y +--=⇒-+=,所以圆心为()2,0B ,记()0,2A -,设切点为,M N ,如图所示.因为AB =BM =,故AM =cos cos2AM MAB AB α=∠==,sin 2α=,sin 2sin cos 2224ααα==⨯.故选B.5.(2023新高考II 卷15)已知直线10x my -+=与圆()22:14C x y -+=交于,A B 两点,写出满足“85ABC S =△”的m 的一个值______.【解析】由题意可知,直线恒过点()1,0A -,此点同时为圆C 与x 轴负半轴的交点.又圆心()1,0C ,则2AC =,所以1825ABC B B S AC y y =⨯⨯==△,解得85B y =±,115B x =或15B x =-.所以满足条件的点B 可以为12341181181818,,,,,,,55555555B B B B ⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,代入直线方程得2m =或2m =-或12m =或12m =-.。
平面解析几何(选择题、填空题)(解析版)-三年(2022–2024)高考数学真题分类汇编(全国通用)

专题05平面解析几何(选择题、填空题)考点三年考情(2022-2024)命题趋势考点1:直线方程与圆的方程2022年全国II卷、2022年全国甲卷(文)2022年全国乙卷(理)近三年高考对解析几何小题的考查比较稳定,考查内容、频率、题型难度均变化不大,备考时应熟练以下方向:(1)要重视直线方程的求法、两条直线的位置关系以及点到直线的距离公式这三个考点.(2)要重视直线与圆相交所得弦长及相切所得切线的问题.(3)要重视椭圆、双曲线、抛物线定义的运用、标准方程的求法以及简单几何性质,尤其是对离心率的求解,更是高考的热点问题,因方法多,试题灵活,在各种题型中均有体现.考点2:直线与圆的位置关系2024年北京卷、2022年全国甲卷(理)2022年天津卷、2022年北京卷2023年全国Ⅰ卷、2024年北京卷考点3:圆与圆的位置关系2022年全国I卷考点4:轨迹方程及标准方程2023年北京卷、2023年天津卷2024年全国Ⅱ卷、2022年天津卷2022年全国甲卷(文)考点5:椭圆的几何性质2022年全国I卷2023年全国甲卷(理)2023年全国甲卷(文)考点6:双曲线的几何性质2022年北京卷2023年全国乙卷(理)考点7:抛物线的几何性质2024年北京卷、2024年天津卷2023年全国乙卷(理)2023年天津卷、2023年全国Ⅱ卷2024年全国Ⅱ卷、2022年全国I卷考点8:弦长问题2022年全国乙卷(理)2023年全国甲卷(理)考点9:离心率问题2024年全国Ⅰ卷、2022年全国甲卷(文)2023年全国Ⅰ卷、2022年浙江卷2022年全国乙卷(理)2024年全国甲卷(理)2023年全国Ⅰ卷、2022年全国甲卷(理)考点10:焦半径、焦点弦问题2022年全国II卷、2023年北京卷考点11:范围与最值问题2022年全国II卷2024年全国甲卷(文)2023年全国乙卷(文)考点12:面积问题2024年天津卷、2023年全国Ⅱ卷2023年全国Ⅱ卷考点13:新定义问题2024年全国Ⅰ卷考点1:直线方程与圆的方程1.(2022年新高考全国II 卷数学真题)已知直线l 与椭圆22163x y +=在第一象限交于A ,B 两点,l 与x 轴,y 轴分别交于M ,N 两点,且||||,||23MA NB MN ==l 的方程为.【答案】2220x -=【解析】[方法一]:弦中点问题:点差法令AB 的中点为E ,设()11,A x y ,()22,B x y ,利用点差法得到12OE AB k k ⋅=-,设直线:AB y kx m =+,0k <,0m >,求出M 、N 的坐标,再根据MN 求出k 、m ,即可得解;令AB 的中点为E ,因为MA NB =,所以ME NE =,设()11,A x y ,()22,B x y ,则2211163x y +=,2222631x y +=,所以2222121206633x x y y -+-=,即()()()()12121212063x x x x y y y y -++-+=所以()()()()1212121212y y y y x x x x +-=--+,即12OE AB k k ⋅=-,设直线:AB y kx m =+,0k <,0m >,令0x =得y m =,令0y =得m x k =-,即,0m M k ⎛⎫- ⎪⎝⎭,()0,N m ,所以,22m m E k ⎛⎫- ⎪⎝⎭,即1222mk m k⨯=--,解得22k =或22k =(舍去),又23MN =,即()22223MN m m=+=2m =或2m =-(舍去),所以直线2:22AB y x =-+,即2220x -=;故答案为:2220x -=[方法二]:直线与圆锥曲线相交的常规方法由题意知,点E 既为线段AB 的中点又是线段MN 的中点,设()11,A x y ,()22,B x y ,设直线:AB y kx m =+,0k <,0m >,则,0m M k ⎛⎫- ⎪⎝⎭,()0,N m ,,22m m E k ⎛⎫- ⎪⎝⎭,因为3MN =3OE =联立直线AB 与椭圆方程得22163y kx m x y =+⎧⎪⎨+=⎪⎩消掉y 得222(12)4260k x mkx m +++-=其中2221224=4-4(12)260,12mkmk k m x x k ∆+-+=-+()()>,∴AB 中点E 的横坐标2212E mk x k =-+,又,22m m E k ⎛⎫- ⎪⎝⎭,∴22=122E mk x k m k =-+-∵0k <,0m >,∴22k 又22+322O m m k E -=()(),解得m=2所以直线2:22AB y x =-+,即2220x -=2.(2022年高考全国甲卷数学(文)真题)设点M 在直线210x y +-=上,点(3,0)和(0,1)均在M 上,则M 的方程为.【答案】22(1)(1)5x y -++=【解析】[方法一]:三点共圆∵点M 在直线210x y +-=上,∴设点M 为(,12)-a a ,又因为点(3,0)和(0,1)均在M 上,点M 到两点的距离相等且为半径,2222(3)(12)(2)-+-+-a a a a R ,222694415-++-+=a a a a a ,解得1a =,∴(1,1)M -,5R =M 的方程为22(1)(1)5x y -++=.故答案为:22(1)(1)5x y -++=[方法二]:圆的几何性质由题可知,M 是以(3,0)和(0,1)为端点的线段垂直平分线y=3x-4与直线210x y +-=的交点(1,-1).5R =M 的方程为22(1)(1)5x y -++=.故答案为:22(1)(1)5x y -++=3.(2022年高考全国乙卷数学(理)真题)过四点(0,0),(4,0),(1,1),(4,2)-中的三点的一个圆的方程为.【答案】()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭.【解析】[方法一]:圆的一般方程依题意设圆的方程为220x y Dx Ey F ++++=,(1)若过()0,0,()4,0,()1,1-,则01640110F D F D E F =⎧⎪++=⎨⎪+-++=⎩,解得046F D E =⎧⎪=-⎨⎪=-⎩,所以圆的方程为22460x y x y +--=,即()()222313x y -+-=;(2)若过()0,0,()4,0,()4,2,则01640164420F D F D E F =⎧⎪++=⎨⎪++++=⎩,解得042F D E =⎧⎪=-⎨⎪=-⎩,所以圆的方程为22420x y x y +--=,即()()22215x y -+-=;(3)若过()0,0,()4,2,()1,1-,则0110164420F D E F D E F =⎧⎪+-++=⎨⎪++++=⎩,解得083143F D E ⎧⎪=⎪⎪=-⎨⎪⎪=-⎪⎩,所以圆的方程为22814033x y x y +--=,即224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭;(4)若过()1,1-,()4,0,()4,2,则1101640164420D E F D F D E F +-++=⎧⎪++=⎨⎪++++=⎩,解得1651652F D E ⎧=-⎪⎪⎪=-⎨⎪=-⎪⎪⎩,所以圆的方程为2216162055x y x y +---=,即()2281691525x y ⎛⎫-+-= ⎪⎝⎭;故答案为:()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭.[方法二]:【最优解】圆的标准方程(三点中的两条中垂线的交点为圆心)设()()()()0,04,01,14,2A B C D -点,,,(1)若圆过、、A B C 三点,圆心在直线2x =,设圆心坐标为(2,)a ,则()2224913,413a a a r a +=+-⇒=+=22(2)(3)13x y -+-=;(2)若圆过A B D 、、三点,设圆心坐标为(2,)a ,则22244(2)1,45a a a r a +=+-⇒==+=的方程为22(2)(1)5x y -+-=;(3)若圆过A C D 、、三点,则线段AC 的中垂线方程为1y x =+,线段AD 的中垂线方程为25y x =-+,联立得4765,333x y r ==⇒=,所以圆的方程为224765()()339x y -+-=;(4)若圆过B C D 、、三点,则线段BD 的中垂线方程为1y =,线段BC 中垂线方程为57y x =-,联立得813,155x y r ==⇒=,所以圆的方程为()228169()1525x -y +-=.故答案为:()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭.【整体点评】方法一;利用圆过三个点,设圆的一般方程,解三元一次方程组,思想简单,运算稍繁;方法二;利用圆的几何性质,先求出圆心再求半径,运算稍简洁,是该题的最优解.考点2:直线与圆的位置关系4.(2024年北京高考数学真题)若直线()3y k x =-与双曲线2214xy -=只有一个公共点,则k 的一个取值为.【答案】12(或12-,答案不唯一)【解析】联立()22143x y y k x ⎧-=⎪⎨⎪=-⎩,化简并整理得:()222214243640k x k x k -+--=,由题意得2140k -=或()()()2222Δ244364140k k k =++-=,解得12k =±或无解,即12k =±,经检验,符合题意.故答案为:12(或12-,答案不唯一).5.(2022年高考全国甲卷数学(理)真题)若双曲线2221(0)x y m m-=>的渐近线与圆22430x y y +-+=相切,则m =.33【解析】双曲线()22210x y m m-=>的渐近线为y x m =±,即0x my ±=,不妨取0x my +=,圆22430x y y +-+=,即()2221x y +-=,所以圆心为()0,2,半径1r =,依题意圆心()0,2到渐近线0x my +=的距离2211m d m==+,解得33m =或33m =.336.(2022年新高考天津数学高考真题)若直线()00x y m m -+=>与圆()()22113x y -+-=相交所得的弦长为m ,则m =.【答案】2【解析】圆()()22113x y -+-=的圆心坐标为()1,13圆心到直线()00x y m m -+=>1122m-+由勾股定理可得22322m ⎛⎫+= ⎪⎝⎭,因为0m >,解得2m =.故答案为:2.7.(2022年新高考北京数学高考真题)若直线210x y +-=是圆22()1x a y -+=的一条对称轴,则=a ()A .12B .12-C .1D .1-【答案】A【解析】由题可知圆心为(),0a ,因为直线是圆的对称轴,所以圆心在直线上,即2010a +-=,解得12a =.故选:A .8.(2023年新课标全国Ⅰ卷数学真题)过点()0,2-与圆22410x y x +--=相切的两条直线的夹角为α,则sin α=()A .1B .154C .104D .64【答案】B【解析】方法一:因为22410x y x +--=,即()2225x y -+=,可得圆心()2,0C ,半径5r =,过点()0,2P -作圆C 的切线,切点为,A B ,因为()22222PC =+-223PA PC r =-可得51036sin ,cos 442222APC APC ∠=∠==,则10615sin sin 22sin cos 2444APB APC APC APC ∠=∠=∠∠=⨯⨯=,22226101cos cos 2cos sin 0444APB APC APC APC ⎛⎫⎫∠=∠=∠-∠=-=-< ⎪⎪ ⎪⎪⎝⎭⎝⎭,即APB ∠为钝角,所以()15sin sin πsin 4APB APB =-∠=∠=α法二:圆22410x y x +--=的圆心()2,0C ,半径5r =,过点()0,2P -作圆C 的切线,切点为,A B ,连接AB ,可得()22222PC =+-223PA PB PC r ==-=,因为22222cos 2cos PA PB PA PB APB CA CB CA CB ACB +-⋅∠=+-⋅∠且πACB APB ∠=-∠,则()336cos 5510cos πAPB APB +-∠=+--∠,即3cos 55cos APB APB -∠=+∠,解得1cos 04APB ∠=-<,即APB ∠为钝角,则()1cos cos πcos 4APB APB =-∠=-∠=α,且α为锐角,所以215sin 1cos 4αα=-=;方法三:圆22410x y x +--=的圆心()2,0C ,半径5r 若切线斜率不存在,则切线方程为0x =,则圆心到切点的距离2d r =>,不合题意;若切线斜率存在,设切线方程为2y kx =-,即20kx y --=,22251k k -=+2810k k ++=,且644600∆=-=>设两切线斜率分别为12,k k ,则12128,1k k k k +=-=,可得()21212124215k k k k k k -+-=所以1212tan 151k k k k -==+αsin 15cos αα=,可得cos 15=α,则2222sin sin cos sin 115+=+=αααα,且()0,πα∈,则sin 0α>,解得15sin 4α=.故选:B.9.(2024年北京高考数学真题)圆22260x y x y +-+=的圆心到直线20x y -+=的距离为()A 2B .2C .3D .32【答案】D【解析】由题意得22260x y x y +-+=,即()()221310x y -++=,则其圆心坐标为()1,3-,则圆心到直线20x y -+=()()221323211--+=+-故选:D.考点3:圆与圆的位置关系10.(2022年新高考全国I 卷数学真题)写出与圆221x y +=和22(3)(4)16x y -+-=都相切的一条直线的方程.【答案】3544y x =-+或7252424y x =-或=1x -【解析】[方法一]:显然直线的斜率不为0,不妨设直线方程为0x by c ++=,2||11c b =+24.1b=+故221c b =+①,|34||4|.b c c ++=于是344b c c ++=或344b c c ++=-,再结合①解得01b c =⎧⎨=⎩或247257b c ⎧=-⎪⎪⎨⎪=-⎪⎩或4353b c ⎧=⎪⎪⎨⎪=-⎪⎩,所以直线方程有三条,分别为10x +=,724250x y --=,3450.x y +-=(填一条即可)[方法二]:设圆221x y +=的圆心(0,0)O ,半径为11r =,圆22(3)(4)16x y -+-=的圆心(3,4)C ,半径24r =,则12||5OC r r ==+,因此两圆外切,由图像可知,共有三条直线符合条件,显然10x +=符合题意;又由方程22(3)(4)16x y -+-=和221x y +=相减可得方程3450x y +-=,即为过两圆公共切点的切线方程,又易知两圆圆心所在直线OC 的方程为430x y -=,直线OC 与直线10x +=的交点为4(1,)3--,设过该点的直线为4(1)3y k x +=+24311k k -=+,解得724k =,从而该切线的方程为724250.(x y --=填一条即可)[方法三]:圆221x y +=的圆心为()0,0O ,半径为1,圆22(3)(4)16x y -+-=的圆心1O 为(3,4),半径为4,22345+=,等于两圆半径之和,故两圆外切,如图,当切线为l 时,因为143OO k =,所以34l k =-,设方程为3(0)4y x t t =-+>O 到l 的距离19116d ==+,解得54t =,所以l 的方程为3544y x =-+,当切线为m 时,设直线方程为0kx y p ++=,其中0p >,0k <,由题意22113441p k k p k ⎧=⎪+⎪⎨++⎪=⎪+⎩,解得7242524k p ⎧=-⎪⎪⎨⎪=⎪⎩,7252424y x =-当切线为n 时,易知切线方程为=1x -,故答案为:3544y x =-+或7252424y x =-或=1x -.考点4:轨迹方程及标准方程11.(2023年北京高考数学真题)已知双曲线C 的焦点为(2,0)-和(2,0)2,则C 的方程为.【答案】22122x y -=【解析】令双曲线C 的实半轴、虚半轴长分别为,a b ,显然双曲线C 的中心为原点,焦点在x 轴上,其半焦距2c =,由双曲线C 22ca=2a =222b c a =-=所以双曲线C 的方程为22122x y -=.故答案为:22122x y -=12.(2023年天津高考数学真题)已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12F F 、.过2F 向一条渐近线作垂线,垂足为P .若22PF =,直线1PF 的斜率为24,则双曲线的方程为()A .22184x y -=B .22148x y -=C .22142x y -=D .22124x y -=【答案】D【解析】如图,因为()2,0F c ,不妨设渐近线方程为by x a=,即0bx ay -=,所以222bc bcPF b ca b ==+,所以2b =.设2POF θ∠=,则2tan PF b bOP OP aθ===,所以OP a =,所以2OF c =.因为1122P ab c y =⋅,所以P ab y c =,所以tan P P P aby b c x x a θ===,所以2P a x c =,所以2,a ab P c c ⎛⎫ ⎪⎝⎭,因为()1,0F c -,所以122222222424PF ab ab a a ck a a c a a a c c=====+++++,)2224a a +=,解得2a =所以双曲线的方程为22124x y -=故选:D13.(2022年新高考天津数学高考真题)已知抛物线21245,,y F F =分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,抛物线的准线过双曲线的左焦点1F ,与双曲线的渐近线交于点A ,若124F F A π∠=,则双曲线的标准方程为()A .22110x y -=B .22116y x -=C .2214y x -=D .2214x y -=【答案】C【解析】抛物线245y =的准线方程为5x =-5c =,则()15,0F 、)25,0F ,不妨设点A 为第二象限内的点,联立b y x a x c⎧=-⎪⎨⎪=-⎩,可得x c bc y a =-⎧⎪⎨=⎪⎩,即点,bc A c a ⎫⎛- ⎪⎝⎭,因为112AF F F ⊥且124F F A π∠=,则12F F A △为等腰直角三角形,且112AF F F =,即2=bc c a,可得2ba =,所以,22225ba c c ab ⎧=⎪⎪⎪⎨⎪=+⎪⎪⎩,解得125a b c ⎧=⎪=⎨⎪=⎩,因此,双曲线的标准方程为2214y x -=.故选:C.14.(2022年高考全国甲卷数学(文)真题)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为13,12,A A 分别为C 的左、右顶点,B 为C 的上顶点.若121BA BA ⋅=-,则C 的方程为()A .2211816x y +=B .22198x y +=C .22132x y +=D .2212x y +=【答案】B【解析】因为离心率22113c b e a a ==-,解得2289b a =,2289=b a ,12,A A 分别为C 的左右顶点,则()()12,0,,0A a A a -,B 为上顶点,所以(0,)B b .所以12(,),(,)=--=- BA a b BA a b ,因为121BA BA ⋅=-所以221-+=-a b ,将2289=b a 代入,解得229,8a b ==,故椭圆的方程为22198x y +=.故选:B.15.(2024年新课标全国Ⅱ卷数学真题)已知曲线C :2216x y +=(0y >),从C 上任意一点P 向x 轴作垂线段PP ',P '为垂足,则线段PP '的中点M 的轨迹方程为()A .221164x y +=(0y >)B .221168x y +=(0y >)C .221164y x +=(0y >)D .221168y x +=(0y >)【答案】A【解析】设点(,)M x y ,则0(,),(,0)P x y P x ',因为M 为PP '的中点,所以02y y =,即(,2)P x y ,又P 在圆2216(0)x y y +=>上,所以22416(0)x y y +=>,即221(0)164x y y +=>,即点M 的轨迹方程为221(0)164x y y +=>.故选:A考点5:椭圆的几何性质16.(2022年新高考全国I 卷数学真题)已知椭圆2222:1(0)x y C a b a b+=>>,C 的上顶点为A ,两个焦点为1F ,2F ,离心率为12.过1F 且垂直于2AF 的直线与C 交于D ,E 两点,||6DE =,则ADE V 的周长是.【答案】13【解析】∵椭圆的离心率为12c e a ==,∴2a c =,∴22223b a c c =-=,∴椭圆的方程为222222213412043x y x y c c c+=+-=,即,不妨设左焦点为1F ,右焦点为2F ,如图所示,∵222AF a OF c a c ===,,,∴23AF O π∠=,∴12AF F △为正三角形,∵过1F 且垂直于2AF 的直线与C 交于D ,E 两点,DE 为线段2AF 的垂直平分线,∴直线DE 的斜率为333直线DE 的方程:3x c =-,代入椭圆方程22234120x y c +-=,整理化简得到:22136390y cy c --=,判别式()2222634139616c c c ∆=+⨯⨯=⨯⨯,∴()212Δ13226461313cDE y =+-==⨯⨯⨯=,∴138c =,得1324a c ==,∵DE 为线段2AF 的垂直平分线,根据对称性,22AD DF AE EF ==,,∴ADE V 的周长等于2F DE △的周长,利用椭圆的定义得到2F DE △周长为222211*********DF EF DE DF EF DF EF DF DF EF EF a a a ++=+++=+++=+==.故答案为:13.17.(2023年高考全国甲卷数学(理)真题)设O 为坐标原点,12,F F 为椭圆22:196x y C +=的两个焦点,点P 在C 上,123cos 5F PF ∠=,则||OP =()A .135B .302C .145D .352【答案】B【解析】方法一:设12π2,02F PF θθ∠=<<,所以122212tan tan 2PF F F PF S b b θ∠== ,由22212222cos sin 1tan 3cos cos 2cos +sin 1tan 5F PF θθθθθθθ--∠====+,解得:1tan 2θ=,由椭圆方程可知,222229,6,3a b c a b ===-=,所以,1212111236222PF F p p S F F y y =⨯⨯=⨯=⨯ ,解得:23p y =,即2399162p x ⎛⎫=⨯-= ⎪⎝⎭,因此22930322p p OP x y =++故选:B .方法二:因为1226PF PF a +==①,222121212122PF PF PF PF F PF F F +-∠=,即2212126125PF PF PF PF +-=②,联立①②,解得:22121215,212PF PF PF PF =+=,而()1212PO PF PF =+ ,所以1212OP PO PF PF ==+ ,即22121122111315302212222522PO PF PF PF PF PF PF =++⋅+=+⨯⨯= .故选:B .方法三:因为1226PF PF a +==①,222121212122cos PF PF PF PF F PF F F +-∠=,即2212126125PF PF PF PF +-=②,联立①②,解得:221221PF PF +=,由中线定理可知,()()222212122242OP F F PF PF +=+=,易知1223F F=302OP =.故选:B .18.(2023年高考全国甲卷数学(文)真题)设12,F F 为椭圆22:15x C y +=的两个焦点,点P 在C 上,若120PF PF ⋅=,则12PF PF ⋅=()A .1B .2C .4D .5【答案】B【解析】方法一:因为120PF PF ⋅= ,所以1290FPF ∠=,从而122121tan 4512FP F S b PF PF ===⨯⋅,所以122PF PF ⋅=.故选:B.方法二:因为120PF PF ⋅= ,所以1290FPF ∠= ,由椭圆方程可知,25142c c =-=⇒=,所以22221212416PF PF F F +===,又1225PF PF a +==22121212216220PF PF PF PF PF PF ++=+=,所以122PF PF ⋅=.故选:B.考点6:双曲线的几何性质19.(2022年新高考北京数学高考真题)已知双曲线221x y m +=的渐近线方程为33y x =±,则m =.【答案】3-【解析】对于双曲线221x y m+=,所以0m <,即双曲线的标准方程为221x y m -=-,则1a =,b m =-221x y m +=的渐近线方程为33y =±,所以33a b =33m =-,解得3m =-;故答案为:3-20.(2023年高考全国乙卷数学(理)真题)设A ,B 为双曲线2219y x -=上两点,下列四个点中,可为线段AB 中点的是()A .()1,1B .()1,2-C .()1,3D .()1,4--【答案】D【解析】设()()1122,,,A x y B x y ,则AB 的中点1212,22x x y y M ++⎛⎫⎪⎝⎭,可得1212121212122,2ABy y y y y y k k x x x x x x +-+===+-+,因为,A B 在双曲线上,则221122221919y x y x ⎧-=⎪⎪⎨⎪-=⎪⎩,两式相减得()2222121209y y x x ---=,所以221222129AB y y k k x x -⋅==-.对于选项A :可得1,9AB k k ==,则:98AB y x =-,联立方程229819y x y x =-⎧⎪⎨-=⎪⎩,消去y 得272272730x x -⨯+=,此时()2272472732880∆=-⨯-⨯⨯=-<,所以直线AB 与双曲线没有交点,故A 错误;对于选项B :可得92,2AB k k =-=-,则95:22AB y x =--,联立方程22952219y x y x ⎧=--⎪⎪⎨⎪-=⎪⎩,消去y 得245245610x x +⨯+=,此时()224544561445160∆=⨯-⨯⨯=-⨯⨯<,所以直线AB 与双曲线没有交点,故B 错误;对于选项C :可得3,3AB k k ==,则:3AB y x=由双曲线方程可得1,3a b ==,则:3AB y x =为双曲线的渐近线,所以直线AB 与双曲线没有交点,故C 错误;对于选项D :94,4AB k k ==,则97:44AB y x =-,联立方程22974419y x y x ⎧=-⎪⎪⎨⎪-=⎪⎩,消去y 得2631261930x x +-=,此时21264631930∆=+⨯⨯>,故直线AB 与双曲线有交两个交点,故D 正确;故选:D.考点7:抛物线的几何性质21.(2024年北京高考数学真题)抛物线216y x =的焦点坐标为.【答案】()4,0【解析】由题意抛物线的标准方程为216y x =,所以其焦点坐标为()4,0.故答案为:()4,0.22.(2024年天津高考数学真题)圆22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合,A 为两曲线的交点,则原点到直线AF 的距离为.【答案】45/0.8【解析】圆22(1)25-+=x y 的圆心为()1,0F ,故12p=即2p =,由()2221254x y y x ⎧-+=⎪⎨=⎪⎩可得22240x x +-=,故4x =或6x =-(舍),故()4,4A ±,故直线()4:13AF y x =±-即4340x y --=或4340x y +-=,故原点到直线AF 的距离为4455d ==,故答案为:4523.(2023年高考全国乙卷数学(理)真题)已知点(5A 在抛物线C :22y px =上,则A 到C 的准线的距离为.【答案】94【解析】由题意可得:2521p =⨯,则25p =,抛物线的方程为25y x =,准线方程为54x =-,点A 到C 的准线的距离为59144⎛⎫--= ⎪⎝⎭.故答案为:94.24.(2023年天津高考数学真题)已知过原点O 的一条直线l 与圆22:(2)3C x y ++=相切,且l 与抛物线22(0)y px p =>交于点,O P 两点,若8OP =,则p =.【答案】6【解析】易知圆()2223x y ++=和曲线22y px =关于x 轴对称,不妨设切线方程为y kx =,0k >,2231k k =+3k =232y y px ⎧=⎪⎨=⎪⎩解得:00x y =⎧⎨=⎩或23233p x p y ⎧=⎪⎪⎨⎪=⎪⎩,所以2222348333p p p OP ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,解得:6p =.当3k =-故答案为:6.25.(多选题)(2024年新课标全国Ⅱ卷数学真题)抛物线C :24y x =的准线为l ,P 为C 上的动点,过P 作22:(4)1A x y +-=⊙的一条切线,Q 为切点,过P 作l 的垂线,垂足为B ,则()A .l 与A 相切B .当P ,A ,B 三点共线时,||15PQ =C .当||2PB =时,PA AB⊥D .满足||||PA PB =的点P 有且仅有2个【答案】ABD【解析】A 选项,抛物线24y x =的准线为=1x -,A 的圆心(0,4)到直线=1x -的距离显然是1,等于圆的半径,故准线l 和A 相切,A 选项正确;B 选项,,,P A B 三点共线时,即PA l ⊥,则P 的纵坐标4P y =,由24P P y x =,得到4P x =,故(4,4)P ,此时切线长22224115PQ PA r =-=-=,B 选项正确;C 选项,当2PB =时,1P x =,此时244P P y x ==,故(1,2)P 或(1,2)P -,当(1,2)P 时,(0,4),(1,2)A B -,42201PA k -==--,4220(1)AB k -==--,不满足1PA AB k k =-;当(1,2)P -时,(0,4),(1,2)A B -,4(2)601PA k --==--,4(2)60(1)AB k --==--,不满足1PA AB k k =-;于是PA AB ⊥不成立,C 选项错误;D 选项,方法一:利用抛物线定义转化根据抛物线的定义,PB PF =,这里(1,0)F ,于是PA PB =时P 点的存在性问题转化成PA PF =时P 点的存在性问题,(0,4),(1,0)A F ,AF 中点1,22⎛⎫ ⎪⎝⎭,AF 中垂线的斜率为114AF k -=,于是AF 的中垂线方程为:2158x y +=,与抛物线24y x =联立可得216300y y -+=,2164301360∆=-⨯=>,即AF 的中垂线和抛物线有两个交点,即存在两个P 点,使得PA PF =,D 选项正确.方法二:(设点直接求解)设2,4t P t ⎛⎫⎪⎝⎭,由PB l ⊥可得()1,B t -,又(0,4)A ,又PA PB =,422(4)1164t t t +-=+,整理得216300t t -+=,2164301360∆=-⨯=>,则关于t 的方程有两个解,即存在两个这样的P 点,D 选项正确.故选:ABD26.(多选题)(2022年新高考全国I 卷数学真题)已知O 为坐标原点,点(1,1)A 在抛物线2:2(0)C x py p =>上,过点(0,1)B -的直线交C 于P ,Q 两点,则()A .C 的准线为1y =-B .直线AB 与C 相切C .2|OP OQ OA ⋅>D .2||||||BP BQ BA ⋅>【答案】BCD【解析】将点A 的代入抛物线方程得12p =,所以抛物线方程为2x y =,故准线方程为14y =-,A 错误;1(1)210AB k --==-,所以直线AB 的方程为21y x =-,联立221y x x y=-⎧⎨=⎩,可得2210x x -+=,解得1x =,故B 正确;设过B 的直线为l ,若直线l 与y 轴重合,则直线l 与抛物线C 只有一个交点,所以,直线l 的斜率存在,设其方程为1y kx =-,1122(,),(,)P x y Q x y ,联立21y kx x y=-⎧⎨=⎩,得210x kx -+=,所以21212Δ401k x x k x x ⎧=->⎪+=⎨⎪=⎩,所以2k >或2k <-,21212()1y y x x ==,又2221111||OP x y y y =+=+,2222222||OQ x y y y =+=+所以2121212||||(1)(1)||2||OP OQ y y y y kx kx k OA ⋅=++=⨯=>=,故C 正确;因为21||1||BP k x =+,22||1|BQ k x =+,所以2212||||(1)||15BP BQ k x x k ⋅=+=+>,而2||5BA =,故D 正确.故选:BCD27.(多选题)(2023年新课标全国Ⅱ卷数学真题)设O 为坐标原点,直线)31y x =--过抛物线()2:20C y px p =>的焦点,且与C 交于M ,N 两点,l 为C 的准线,则().A .2p =B .83MN =C .以MN 为直径的圆与l 相切D .OMN 为等腰三角形【答案】AC【解析】A 选项:直线)31y x =-过点()1,0,所以抛物线()2:20C y px p =>的焦点()1,0F ,所以1,2,242pp p ===,则A 选项正确,且抛物线C 的方程为24y x =.B 选项:设()()1122,,,M x y N x y ,由)2314y x y x⎧=--⎪⎨=⎪⎩消去y 并化简得()()231033310x x x x -+=--=,解得1213,3x x ==,所以121163233MN x x p =++=++=,B 选项错误.C 选项:设MN 的中点为A ,,,M N A 到直线l 的距离分别为12,,d d d ,因为()()12111222d d d MF NF MN =+=+=,即A 到直线l 的距离等于MN 的一半,所以以MN 为直径的圆与直线l 相切,C 选项正确.D 选项:直线)31y x =-330x y +=,O 330y +的距离为3d =所以三角形OMN 的面积为1163432323⨯=由上述分析可知)1212333123,3133y y ⎫=--=-=--=⎪⎭所以()22221231332321,333OM ON ⎛⎫⎛⎫=+-==+= ⎪ ⎪ ⎪⎝⎭⎝⎭,所以三角形OMN 不是等腰三角形,D 选项错误.故选:AC.考点8:弦长问题28.(2022年高考全国乙卷数学(理)真题)设F 为抛物线2:4C y x =的焦点,点A 在C 上,点(3,0)B ,若AF BF =,则AB =()A .2B .22C .3D .32【答案】B【解析】由题意得,()1,0F ,则2AF BF ==,即点A 到准线=1x -的距离为2,所以点A 的横坐标为121-+=,不妨设点A 在x 轴上方,代入得,()1,2A ,所以()()22310222AB =-+-=.故选:B29.(2023年高考全国甲卷数学(理)真题)已知双曲线2222:1(0,0)x y C a b a b-=>>5C 的一条渐近线与圆22(2)(3)1x y -+-=交于A ,B 两点,则||AB =()A .55B .255C .355D .455【答案】D【解析】由5e =222222215c a b b a a a+==+=,解得2ba=,所以双曲线的一条渐近线为2y x =,则圆心(2,3)到渐近线的距离25521d ==+,所以弦长22145||22155AB r d =-=-=.故选:D考点9:离心率问题30.(2024年新课标全国Ⅰ卷数学真题)设双曲线2222:1(0,0)x y C a b a b -=>>的左右焦点分别为12F F 、,过2F 作平行于y 轴的直线交C 于A ,B 两点,若1||13,||10F A AB ==,则C 的离心率为.【答案】32【解析】由题可知2,,A B F 三点横坐标相等,设A 在第一象限,将x c =代入22221x ya b -=得2b y a =±,即22,,,b b A c B c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,故2210b AB a ==,225bAF a ==,又122AF AF a -=,得1222513AF AF a a =+=+=,解得4a =,代入25b a=得220b =,故22236,c a b =+=,即6c =,所以6342c e a ===.故答案为:3231.(2022年高考全国甲卷数学(文)真题)记双曲线2222:1(0,0)x y C a b a b-=>>的离心率为e ,写出满足条件“直线2y x =与C 无公共点”的e 的一个值.【答案】2(满足15e <皆可)【解析】2222:1(0,0)x y C a b a b -=>>,所以C 的渐近线方程为b y x a =±,结合渐近线的特点,只需02b a <≤,即224b a≤,可满足条件“直线2y x =与C 无公共点”所以221145=++c b e a a又因为1e >,所以15e <≤故答案为:2(满足15e <皆可)32.(2023年新课标全国Ⅰ卷数学真题)已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为12,F F .点A 在C 上,点B 在y 轴上,11222,3F A F B F A F B ⊥=- ,则C 的离心率为.355/355【解析】方法一:依题意,设22AF m =,则2113,22BF m BF AF a m ===+,在1Rt ABF 中,2229(22)25m a m m ++=,则(3)()0a m a m +-=,故a m =或3a m =-(舍去),所以124,2AF a AF a ==,213BF BF a ==,则5AB a =,故11244cos 55AF a F AF ABa ∠===,所以在12AF F △中,2221216444cos 2425a a c F AF a a +-∠==⨯⨯,整理得2259c a =,故355c e a =方法二:依题意,得12(,0),(,0)F c F c -,令()00),,(0,A x y B t ,因为2223F A F B =-,所以()()002,,3x c y c t -=--,则00235,3x c y t ==-,又11F A F B ⊥ ,所以()1182,,33F A F B c t c t ⎛⎫⋅=-⋅ ⎪⎝⎭ 2282033c t =-=,则224t c =,又点A 在C 上,则2222254991c t a b-=,整理得2222254199c t a b -=,则22222516199c c a b -=,所以22222225169c b c a a b -=,即()()2222222225169c c a a c a c a --=-,整理得4224255090c a c a -+=,则()()22225950c a c a --=,解得2259c a =或225c a =,又1e >,所以355e =或55e =(舍去),故355e =故答案为:355.33.(2022年新高考浙江数学高考真题)已知双曲线22221(0,0)x y a b a b -=>>的左焦点为F ,过F 且斜率为4b a的直线交双曲线于点()11,A x y ,交双曲线的渐近线于点()22,B x y 且120x x <<.若||3||FB FA =,则双曲线的离心率是.【答案】364【解析】过F 且斜率为4b a 的直线:()4b AB y x c a=+,渐近线2:b l y x a =,联立()4b y x c a b y xa ⎧=+⎪⎪⎨⎪=⎪⎩,得,33c bc B a ⎛⎫ ⎪⎝⎭,由||3||FB FA =,得5,,99c bc A a ⎛⎫- ⎪⎝⎭而点A 在双曲线上,于是2222222518181c b c a a b -=,解得:228124c a =,所以离心率36e 4=.36434.(多选题)(2022年高考全国乙卷数学(理)真题)双曲线C 的两个焦点为12,F F ,以C 的实轴为直径的圆记为D ,过1F 作D 的切线与C 交于M ,N 两点,且123cos 5F NF ∠=,则C 的离心率为()A 52B .32C 132D .172【答案】AC【解析】[方法一]:几何法,双曲线定义的应用情况一M 、N 在双曲线的同一支,依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为B ,所以1OB F N ⊥,因为123cos 05F NF ∠=>,所以N 在双曲线的左支,OB a =,1OF c =,1FB b =,设12F NF α∠=,由即3cos 5α=,则4sin 5α=,235NA NF 22a a ==,21NF NF 2a-=532222a a b a ⎛⎫--= ⎪⎝⎭,52b e 2a =∴=,选A 情况二若M 、N 在双曲线的两支,因为123cos 05F NF ∠=>,所以N 在双曲线的右支,所以OB a =,1OF c =,1FB b =,设12F NF α∠=,由123cos 5F NF ∠=,即3cos 5α=,则4sin 5α=,235NA NF 22a a ==,12NF NF 2a -=352222a b a a +-=,所以23b a =,即32b a =,所以双曲线的离心率221312c b e a a =+=选C[方法二]:答案回代法5A e 2=选项特值双曲线())22121,F 5,0,F 5,04x y -=∴,过1F 且与圆相切的一条直线为(y 2x 5=+,两交点都在左支,62N 5,555⎛∴ ⎝,2112NF 5,NF 1,FF 5∴===,则123cos 5F NF ∠=,13C e 2=选项特值双曲线())2212x y 1,F 13,0,F 13,049-=∴-,过1F 且与圆相切的一条直线为(2y x 133=+, 两交点在左右两支,N 在右支,1418N 13,131313∴,2112NF 5,NF 9,FF 213∴===,则123cos 5F NF ∠=,[方法三]:依题意不妨设双曲线焦点在x 轴,设过1F 作圆D 的切线切点为G ,若,M N 分别在左右支,因为1OG NF ⊥,且123cos 05F NF ∠=>,所以N 在双曲线的右支,又OG a =,1OF c =,1GF b =,设12F NF α∠=,21F F N β∠=,在12F NF △中,有()212sin sin sin NF NF cβαβα==+,故()122sin sin sin NF NF cαββα-=+-即()sin sin sin a c αββα=+-,所以sin cos cos sin sin sin a cαβαββα=+-,而3cos 5α=,sin a c β=,cos bcβ=,故4sin 5α=,代入整理得到23b a =,即32b a =,所以双曲线的离心率221312c b e a a =+=若,M N 均在左支上,同理有()212sin NF NF c βαβα==+,其中β为钝角,故cos bcβ=-,故()212sin sin sin NF NF cβαβα-=-+即sin sin cos cos sin sin a c βαβαβα=--,代入3cos 5α=,sin a c β=,4sin 5α=,整理得到:1424a b a =+,故2a b =,故2512b e a ⎛⎫=+= ⎪⎝⎭,故选:AC.35.(2024年高考全国甲卷数学(理)真题)已知双曲线的两个焦点分别为()()0,4,0,4-,点()6,4-在该双曲线上,则该双曲线的离心率为()A .4B .3C .2D 2【答案】C【解析】由题意,设()10,4F -、()20,4F 、()6,4P -,则1228F F c ==,()22164410PF =++=,()2226446PF +-=,则1221064a PF PF =-=-=,则28224c e a ===.故选:C.36.(2023年新课标全国Ⅰ卷数学真题)设椭圆2222122:1(1),:14x x C y a C y a +=>+=的离心率分别为12,e e .若213e e =,则=a ()A 233B 2C 3D 6【答案】A【解析】由213e e =,得22213e e =,因此2241134a a --=⨯,而1a >,所以233a =.故选:A37.(2022年高考全国甲卷数学(理)真题)椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ,点P ,Q 均在C上,且关于y 轴对称.若直线,AP AQ 的斜率之积为14,则C 的离心率为()A .32B .22C .12D .13【答案】A【解析】[方法一]:设而不求设()11,P x y ,则()11,Q x y -则由14AP AQk k ⋅=得:21112211114AP AQ y y y k k x a x a x a ⋅=⋅==+-+-+,由2211221x y a b +=,得()2221212b a x y a-=,所以()2221222114b a x ax a -=-+,即2214b a =,所以椭圆C 的离心率22312c b e a a ==- A.[方法二]:第三定义设右端点为B ,连接PB ,由椭圆的对称性知:PB AQ k k =-故()14AP AQ PA PB k k k k ⋅=⋅-=-,由椭圆第三定义得:22PA PBb k k a⋅=-,故2214b a =所以椭圆C 的离心率22312c b e a a ==- A.考点10:焦半径、焦点弦问题38.(多选题)(2022年新高考全国II 卷数学真题)已知O 为坐标原点,过抛物线2:2(0)C y px p =>焦点F 的直线与C 交于A ,B 两点,其中A 在第一象限,点(,0)M p ,若||||AF AM =,则()A .直线AB 的斜率为26B .||||OB OF =C .||4||AB OF >D .180OAM OBM ∠+∠<︒【答案】ACD【解析】对于A ,易得(,0)2p F ,由AF AM =可得点A 在FM 的垂直平分线上,则A 点横坐标为3224ppp +=,代入抛物线可得2233242p y p p =⋅=,则36()42p A ,则直线AB 的斜率为6226342p p =-,A 正确;对于B ,由斜率为26可得直线AB 的方程为226p x y =+,联立抛物线方程得2206y py p -=,设11(,)B x y ,则16626p y p +=,则163y =-,代入抛物线得2162p p x ⎛=⋅ ⎝⎭,解得13p x =,则6(,)33p pB ,则22673332p p p p OB OF ⎛⎫⎛⎫=+-≠= ⎪ ⎪ ⎪⎝⎭⎝⎭,B 错误;对于C ,由抛物线定义知:325244312p p pAB p p OF =++=>=,C 正确;对于D ,23663663()(,)0423343234p p p p p p p p OA OB ⎛⎫⋅=⋅-=⋅+⋅-=-< ⎪ ⎪⎝⎭,则AOB ∠为钝角,又26262665()(,)0423343236p p p p p MA MB ⎛⎫⎛⎫⋅=-⋅--=-⋅-+⋅-=-< ⎪ ⎪ ⎪⎝⎭⎝⎭,则AMB ∠为钝角,又360AOB AMB OAM OBM ∠+∠+∠+∠= ,则180OAM OBM ∠+∠< ,D 正确.故选:ACD.39.(2023年北京高考数学真题)已知抛物线2:8C y x =的焦点为F ,点M 在C 上.若M 到直线3x =-的距离为5,则||MF =()A .7B .6C .5D .4【答案】D【解析】因为抛物线2:8C y x =的焦点()2,0F ,准线方程为2x =-,点M 在C 上,所以M 到准线2x =-的距离为MF ,又M 到直线3x =-的距离为5,所以15MF +=,故4MF =.故选:D.考点11:范围与最值问题40.(2022年新高考全国II 卷数学真题)设点(2,3),(0,)A B a -,若直线AB 关于y a =对称的直线与圆22(3)(2)1x y +++=有公共点,则a 的取值范围是.【答案】13,32⎡⎤⎢⎥⎣⎦【解析】()2,3A -关于y a =对称的点的坐标为()2,23A a '--,()0,B a 在直线y a =上,所以A B '所在直线即为直线l ,所以直线l 为32a y x a -=+-,即()3220a x y a -+-=;圆()()22:321C x y +++=,圆心()3,2C --,半径1r =,依题意圆心到直线l 的距离()()223342132a ad a ----=≤-+,即()()2225532a a -≤-+,解得1332a ≤≤,即13,32a ⎡⎤∈⎢⎥⎣⎦;故答案为:13,32⎡⎤⎢⎥⎣⎦41.(2024年高考全国甲卷数学(文)真题)已知直线20ax y a ++-=与圆2241=0C x y y ++-:交于,A B 两点,则AB 的最小值为()A .2B .3C .4D .6【答案】C 【解析】因为直线20ax y a ++-=,即()120a x y -++=,令10x -=,则x 1,y 2==-,所以直线过定点()1,2-,设()1,2P -,将圆2241=0C x y y ++-:化为标准式为()2225x y ++=,所以圆心()0,2C -,半径5r =,1PC =当PC AB ⊥时,AB 的最小,此时222514AB r PC =-⨯-.故选:C42.(2023年高考全国乙卷数学(文)真题)已知实数,x y 满足224240x y x y +---=,则x y -的最大值是()A .3212B .4C .132+D .7【答案】C【解析】法一:令x y k -=,则x k y =+,代入原式化简得()22226440y k y k k +-+--=,因为存在实数y ,则0∆≥,即()()222642440k k k --⨯--≥,化简得22170k k --≤,解得132132k -≤≤+故x y -的最大值是321,法二:224240x y x y +---=,整理得()()22219x y -+-=,令3cos 2x θ=+,3sin 1y θ=+,其中[]0,2πθ∈,则π3cos 3sin 132cos 14x y θθθ⎛⎫-=-+=++ ⎪⎝⎭,[]0,2θπ∈ ,所以ππ9π,444θ⎡⎤+∈⎢⎥⎣⎦,则π2π4θ+=,即74πθ=时,x y -取得最大值321,法三:由224240x y x y +---=可得22(2)(1)9x y -+-=,设x y k -=,则圆心到直线x y k -=的距离|21|32k d =≤,解得132132k -≤≤+故选:C.考点12:面积问题43.(2024年天津高考数学真题)双曲线22221()00a x y a bb >-=>,的左、右焦点分别为12.F F P 、是双曲线右支上一点,且直线2PF 的斜率为2.12PF F △是面积为8的直角三角形,则双曲线的方程为()A .22182y x -=B .22184x y -=C .22128x y -=D .22148x y -=【答案】C【解析】如下图:由题可知,点P 必落在第四象限,1290F PF ∠=︒,设2PF m =,211122,PF F PF F θθ∠=∠=,由21tan 2PF k θ==,求得1sin 5θ=因为1290F PF ∠=︒,所以121PF PF k k ⋅=-,求得112PF k =-,即21tan 2θ=,2sin 5θ=121212::sin :sin :sin 902:1:5PF PF F F θθ=︒=则由2PF m =得1122,25PF m F F c m ===,由1212112822PF F S PF PF m m =⋅=⋅= 得22m =则211222,42,2210,10PF PF F F c c =====由双曲线第一定义可得:1222PF PF a -==222,8a b c a ==-所以双曲线的方程为22128x y -=.故选:C44.(2023年新课标全国Ⅱ卷数学真题)已知直线:10l x my -+=与()22:14C x y -+= 交于A ,B 两点,写出满足“ABC 面积为85”的m 的一个值.【答案】2(112,2,,22--中任意一个皆可以)【解析】设点C 到直线AB 的距离为d ,由弦长公式得224AB d =-,。
高考数学试题分类汇编--直线与圆

高考数学选择试题分类汇编——直线与圆(江西理数)8.直线3y kx =+与圆()()22324x y -+-=相交于M,N 两点,若23MN ≥则k 的取值范围是 A. B. C. D.【答案】A【解析】考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.解法1:圆心的坐标为(3.,2),且圆与y 轴相切.当|MN |3=时,由点到直线距离公式,解得3[,0]4-; 解法2:数形结合,如图由垂径定理得夹在两直线之间即可, 不取+∞,排除B ,考虑区间不对称,排除C ,利用斜率估值,选A(安徽文数)(4)过点(1,0)且与直线x-2y-2=0平行的直线方程是(A )x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 (D )x+2y-1=04.A【解析】设直线方程为20x y c -+=,又经过(1,0),故1c =-,所求方程为210x y --=.【方法技巧】因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为20x y c -+=,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.(重庆文数)(8)若直线y x b =-与曲线2cos ,sin x y θθ=+⎧⎨=⎩([0,2)θπ∈)有两个不同的公共点,则实数b 的取值范围为(A )(22,1) (B )[22,22]-+(C )(,22)(22,)-∞-++∞ (D )(22,22)+解析:2cos ,sin x y θθ=+⎧⎨=⎩化为普通方程22(2)1x y -+=,表示圆, 304⎡⎤-⎢⎥⎣⎦,[]304⎡⎤-∞-+∞⎢⎥⎣⎦,,3333⎡-⎢⎣⎦,203⎡⎤-⎢⎥⎣⎦,21,2b-<解得2222b <<法2:利用数形结合进行分析得22,22AC b b =-=同理分析,可知2222b <<+(重庆理数)(8) 直线32x +D 的圆33,13x y θθ⎧=⎪⎨=+⎪⎩())0,2θπ⎡∈⎣交与A 、B 两点,则直线AD 与BD 的倾斜角之和为A. 76πB. 54π C.43π D. 53π 解析:数形结合301-=∠α βπ-+=∠ 302由圆的性质可知21∠=∠βπα-+=-∴ 3030故=+βα43π (广东文数)(全国卷1理数)(11)已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为两切点,那么PA PB •的最小值为(A) 4-+ (B)3- (C) 4-+3-+1. (安徽理数)9、动点(),A x y 在圆221x y +=上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、|
!_
一个人总要走陌生的路,看陌生的风景,听陌生的歌,然后在某个不经意的瞬间,你会发现,原本费尽心机想要忘记的事情真的就这么忘记了..
2010年高考数学选择试题分类汇编——直线与圆
(2010江西理数)8.直线3y kx =+与圆()()22
324x y -+-=相交于M ,N 两点,若23MN ≥,则k 的取值范围是
A. 304⎡⎤-⎢⎥⎣⎦,
B. []304⎡⎤-∞-+∞⎢⎥⎣⎦U ,,
C. 3333⎡⎤-⎢⎥⎣⎦,
D. 203⎡⎤-⎢⎥⎣⎦,
【答案】A
【解析】考查直线与圆的位置关系、点到直线距离公式,重点考察
数形结合的运用.
解法1:圆心的坐标为(3.,2),且圆与y 轴相切.当|MN |23=时,
由点到直线距离公式,解得3[,0]4
-; 解法2:数形结合,如图由垂径定理得夹在两直线之间即可,不取
+∞,排除B ,考虑区间不对称,排除C ,利用斜率估值,选A
(2010安徽文数)(4)过点(1,0)且与直线x-2y-2=0平行的直线方程是
(A )x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 (D )x+2y-1=0
4.A
【解析】设直线方程为20x y c -+=,又经过(1,0),故1c =-,所求方程为210x y --=.
【方法技巧】因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为20x y c -+=,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
(2010重庆文数)(8)若直线y x b =-与曲线2cos ,sin x y θθ=+⎧⎨
=⎩
([0,2)θπ∈)有两个不同的公共点,则实数b 的取值范围为
(A )(22,1)- (B )[22,22]-+
(C )(,22)(22,)-∞-++∞U (D )(22,22)-+ 解析:2cos ,sin x y θθ
=+⎧⎨=⎩化为普通方程22(2)1x y -+=,表示圆,
因为直线与圆有两个不同的交点,所以21,2b
-<解得2222b -<<+法2:利用数形
结合进行分析得22,22AC b b =-=∴=-
同理分析,可知2222b -<<+
(2010重庆理数)(8) 直线y=323x +与圆心为D 的圆33cos ,13sin x y θθ
⎧=+⎪⎨=+⎪⎩())0,2θπ⎡∈⎣交与A 、B 两点,则直线AD 与BD 的倾斜角之和为 A. 76π B. 54π C. 43π D. 53
π 解析:数形结合
ο301-=∠αβπ-+=∠ο302
由圆的性质可知21∠=∠
βπα-+=-∴οο3030
故=
+βα43
π (2010广东文数)
(2010全国卷1理数)(11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么PA PB
•
u u u v u u u v
的最小值为
(A) 42
-+ (B)32
-+ (C) 422
-+ (D)322
-+
1.(2010安徽理数)9、动点(),
A x y在圆221
x y
+=上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。
已知时间0
t=时,点A的坐标是
13
(,)
2
,则当012
t
≤≤时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是
A、[]0,1
B、[]
1,7C、D、[]
0,1和[]
7,12
9.D
【解析】画出图形,设动点A与x轴正方向夹角为α,则0
t=时
3
π
α=,每秒钟旋转
6
π
,在[]
0,1
t∈上[,]
32
ππ
α∈,在[]
7,12上
37
[,]
23
ππ
α∈,动点A的纵坐标y关于t都是单调递增的。
【方法技巧】由动点(),
A x y在圆221
x y
+=上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在[0,12]变化时,点A的纵坐标y关于t(单位:秒)的函数的单调性的变化,从而得单调递增区间.
[]
7,12。
