第10章 结构动力学
第十章结构动力学

度 法
m m11
yቤተ መጻሕፍቲ ባይዱ(t) 2 y(t) 0
Fm=y(1t) m 11
l EI
二阶线性齐次常微分方程
y(t) 11 F y(t) 11[my(t)]
11
1 k11
柔 度 法
其通解为
y(t) c1 cost c2 sin t
由初始条件 y(0) y0 y(0) y0
第二,结构在动荷载作用下,产生抵抗结构加速度的 惯性力。动力计算必须考虑惯性力。
4、结构动力计算中体系的自由度
自由度的定义
确定体系中所有质量位置所需的独立几何参数,称 作体系的动力自由度数。
自由度的简化
实际结构都是无限自由度体系,这不仅导致分析困难, 而且从工程角度也没必要。常用简化方法有:
结构动力学的研究内容 结构动力学是研究工程结构的动力特性及其在动荷载
作用下的动力反应分析原理和方法的一门理论和技术学科。
结构动力学的任务 讨论结构在动力荷载作用下反应的分析的方法。
寻找结构固有动力特性、动力荷载和结构反应三者间 的相互关系,即结构在动力荷载作用下的反应规律,为结 构动力可靠性设计、保证结构的经济与安全以及结构健康 诊断提供科学依据。
或者
y
ky
F P(t)
y 2 y FP (t)
m
上式就是单自由度体系强迫振动的微分方程
1、简谐振动作用时的强迫振动
运动方程及其解
F(t)
F(t) F sin t
l
F --荷载幅值 --荷载频率
运动方程
my(t) k11y(t) F sin t
或
y(t) 2 y(t) F sin t m
结构动力学:Chapter_10(结构动力学)

= =
C1 sin ωt + C1ω cosωt
C2 cos
− C2ω
ωt
sin
ωt
得:⎧⎪C2 = y0
⎨ ⎪⎩C1
=
y0
ω
于是:
y=
y0
ω
sin ωt +
y0
cos ωt
进一步可确定式 y = C sin(ωt + φ) 中的C和φ
⎧ ⎪C = ⎪
C12 +C22 =
y02
+(
y0
ω
)2
⎨
⎪⎪⎩φ
第10章 结构动力学
本章内容的基本要求
本章课程的任务是使学生了解和掌握结构的动力特性和动力响应 的计算分析方法 ,具体为:
(1)掌握结构动力分析的基本方法,掌握单自由度及两自由度体 系的自由振动及其在简谐荷载作用下的强迫振动的计算方法 ;
(2)了解阻尼的作用,了解频率的近似计算方法。
1/109
10-1 动力计算概述
φ
C2
C1
y
2π
ω
Cφ
C
φ
ωt
31/109
3、几个术语
(1)周期:振动一次所需的时间。
(2)工程频率
T = 2π ω
单位时间内的振动次数(与周期互为倒数)。
f=1= ω T 2π
(3)频率(圆频率)
旋转向量的角速度,即体系在2π秒内的振动 次数。自由振动时的圆频率称为“自振频率”。
32/109
自振频率是体系本身的固有属性,与体系的 刚度、质量有关,与激发振动的外部因素无关。
P(t)
固端弯矩 M = PL
自由端位移 w = Pδ1 δ1: 单位荷载下的位移
第10章 结构动力学

例. 计算图示体系的自振频率。
m1 m
A l /2 l B EI= k C
解:单自由度体系,
1 m2 m 3
D l /2
以表示位移参数的幅值,
各质点上所受的力为:
A1
. .
m1
B
k
C
m2
.A .
2
l I1 m1 2 A1 m 2 2 1 2 2 3 I 2 m2 A2 m l 3 2 1 m 2 l 2
动力荷载
FI my
k 弹簧刚度系数
FI FD FS Fp (t ) my(t ) cy(t ) ky(t ) Fp (t )
第10章 结构动力学
重力影响
k c
Fs k st
FD cy Fs ky
m W
m
W
Fp(t) y(t) 静位移
st
V
l /2
l /2
1
A,E,I
E,I
E,A
l3 ml 3 48 EI T 2 3 48 EI ml 48 EI
H
1 m H
l
V
1 m V
第10章 结构动力学
例3.计算图示刚架的频率和周期。
1
m EI1= I
6 EI h2 6 EI h2
k
12 EI h3
Fp (t ) k y y 4m 2m
第10章 结构动力学
1 k 2 m
例2
A l/2 l/2
B l/2 l/2
FI my
C m y
F 1
1 1 l 2 l 1 l l 2 l l3 11 ( l ) EI 2 2 3 2 2 2 2 3 2 8EI l3 y (my) 11 (my) 8EI
第10章结构动力学

由此可知,体系的自由振动由两部分组成:一部分由初位移 y 0 引
0 引起,变现为正弦规律 起,表现为余弦规律;另一部分由初速度 y
[图10-13(a)、(b)],两者叠加为简谐振动[图10-13(c)]。
目录
上页
下页
图10-13
令
y0 A sin
(d)
目录
则有
0 y
A cos
下页
图10-8 简支梁的广义位移
3. 有限单元法 有限元法是将实际结构离散成有限个单元,对每个单元给定插
目录
值函数,然后叠加单元在各个相应结点的贡献建立系统求解方程。 有限单元法根据基本未知量选取的不同,分为位移有限元法、应力
有限元法和混合有限元法。其中,位移有限元方法应用最广。
上页
在确定结构震动自由度时,应注意不能根据结构有几个集中 质量就判定它有几个自由度,而应该由确定集中质量位置所需的独
小,如图10-2。例如打桩机的桩锤对桩的冲击、各种爆炸荷载等。
目录
上页
下页
图10-2 冲击荷载
(3)突加荷载。在一瞬间施加于结构上并继续留在结构上的荷载, 如图10-3。例如吊重物的起重机突然启动时施加于钢丝绳的荷载就 是这种突加荷载。
目录
上页
下页
图10-3 突加荷载
(4)快速移动荷载。例如高速通过桥梁的列车、汽车等。
普通高等学校土木工程专业精编系列规划教材
结构力学
主编 丁克伟
目录
上页
10 结构动力学
下页
目录
目录
上页
10.1 结构动力学计算基本概念 10.2 自由度结构自由振动 10.3 简谐荷载作用下的单自由度体系受迫振动 10.4 一般荷载作用下的单自由度体系受迫振动
第10章 结构动力学基础1

(1)重力 W 为静力荷载
(2)弹性恢复力 S(t) k[ y jw y(t)] 与位移成正比,方向与位移指向相
反的。在k质为点刚上度R所(系t加)数的,c力其y• (意t) 义是使质点沿位移方向产生的单位位移时所需
(3)阻尼力
•• 与质点的速度成正比,方向与速度相反。c为
粘滞阻尼系I (数t) 。 m y(t)
my(t) cy(t) ky(t) 0
当动力位移由质点的静力平衡位置算起时,可不考虑质点的重力。
(二)柔度法:取振动体系为研究对象。
I (t) R(t)
FP 1
m y(t)
δ(柔度 系数)
按动静法,体系的动力位移可看为是由于惯性力和阻尼力静力作 用所引起的可得方程:
y(t) [I(t) R(t)]
10.1 一般概念
一、结构的动力荷载及分类
动力荷载:是指荷载的大小、方向、位置随时间迅速变化的 荷载;它使结构质量产生不容忽视的加速度,使结构发生明 显的振动,即在平衡位置附近往返运动。
静力荷载:是指荷载的大小、方向、位置不随时间变化的荷 载;同时考虑其对结构的影响来看,如果荷载变化极其缓慢, 使结构质量产生的加速度可以忽略不计时,仍属于静力荷载
T
T
T
(二)自振周期与频率
自振频率(圆频率)
自振周期
T 2
k 1 g g m m W st
T 2π m 2π mδ 2π Wδ 2π Δst
动静法 根据达朗贝尔(d’Alembert)原理,设想将惯性力I(t)加
于振动体系的质点上,则任一瞬时体系中的实际各力与惯 性力处于平衡状态。
三、 动力计算简图和动力自由度
动力计算中要引入惯性力,因此计算简图要考虑质量的 分布。
第10章动力学分析介绍

第10章动力学分析介绍在实际工程结构的设计工作中,动力学设计和分析是必不可少的一部分。
几乎现代的所有工程结构都面临着动力问题。
在航空航天、船舶、汽车等行业,动力学问题更加突出,在这些行业中将会接触大量的旋转结构例如:轴、轮盘等等结构。
这些结构一般来说在整个机械中佔有及其重要的地位,它们的损坏大部分都是由于共振引起较大振动应力而引起的。
同时由于处于旋转状态,它们所受外界激振力比较複杂,更要求对这些关键部件进行完整的动力设计和分析。
通常动力分析的工作主要有系统的动力特性分析(即求解结构的固有频率和振型),和系统在受到一定载荷时的动力响应分析两部分构成。
根据系统的特性可分为线性动力分析和非线性动力分析两类。
根据载荷随时间变化的关係可以分为稳态动力分析和瞬态动力分析。
谐响应分析是用于确定线性结构在承受随时间按正弦(简谐)规律变化的载荷时稳态响应的一种技术。
可以用瞬态动力学分析确定结构在静载荷,瞬态载荷,和简谐载荷的随意组合作用下的随时间变化的位移,应变,应力及力。
而谱分析主要用于确定结构对随机载荷或随时间变化载荷的动力响应情况。
提供了强大的动力分析工具,可以很方便地进行各类动力分析问题:模态分析、谐响应分析、瞬态动力分析和谱分析。
动力学分析根据载荷形式的不同和所有求解的内容的不同我们可以将其分为:模态分析、谐响应分析、瞬态动力分析和谱分析。
下面将逐个给予介绍。
模态分析在动力学分析过程中是必不可少的一个步骤。
在谐响应分析、瞬态动力分析动分析过程中均要求先进行模态分析才能进行其他步骤。
模态分析用于确定设计机构或机器部件的振动特性(固有频率和振型),即结构的固有频率和振型,它们是承受动态载荷结构设计中的重要引数。
同时,也可以作为其他动力学分析问题的起点,例如瞬态动力学分析、谐响应分析和谱分析。
其中模态分析也是进行谱分析或模态叠加法谱响应分析或瞬态动力学分析所必需的前期分析过程。
ansys的模态分析可以对有预应力的结构进行模态分析和迴圈对称结构模态分析。
【结构动力学】第10章 多自由度体系2020

0
0
N
其中,ωn— 第n阶自振频率,{φ}n—第 n阶振型。
[Φ]和[Ω]也分别称为振型矩阵和谱矩阵。
13
5 DOF with uniform mass and stiffness
5 DOF Base Isolated 14
15
5 DOF with uniform mass and stiffness
k22 2m22 k2N 2m2n 0
k N1 2mN1 k N 2 2mN 2 k NN 2mNN
10
对于N个自由度的稳定结构体系,频率方程是关于ω2的 N次方程,
a N ( 2 ) N a N 1 ( 2 ) N 1 a1 2 a 0 0
由此可以解得N个正实根(ω12<ω22<ω32…<ωN2)。 ωn(n=1, 2, …, N)即为体系的自振频率。其中量值最小的 频率ω1叫基本频率(相应的周期T1=2π/ω1叫基本周期)。 从以上分析可知,多自由度体系只能按一些特定的频 率即按自振频率做自由振动。按某一自振频率振动时,结 构将保持一固定的形状,称为自振振型,或简称振型。
上述齐次方程组有非零解条件为:系数行列式为零
A [I ] 0
N×N矩阵[A]一般将有N个特征值,对应N个特征向量
6
§10-2 多自由度体系的自由振动
多自由度体系无阻尼自由振动的方程为:
M u K u 0
其中:[M]、[K]为N×N阶的质量和刚度矩阵 {u}和{ü}是N阶位移和加速度向量 {0}是N阶零向量
11
把相应的自振频率ωn代入运动方程的特征方程得到振型
K n 2 M n 0
{φ}n={φ1n, φ2n , …, φNn }T—体系的第n阶振型 。 ➢ 由于特征方程的齐次性(线性方程组是线性相关的),振型向量 是不定的,只有人为给定向量中的某一值,例如令φ1n=1,才能确 定其余的值。 ➢ 实际求解时就是令振型向量中的某一分量取定值后才能求解。 虽然令不同的分量等于不同的量,得到的振型在量值上会不一样, 但其比例关系是不变的。
第10章 结构动力学

5.与其它课程之间的关系
结构动力学以和数学为基础。 要求熟练掌握已学过的知识和数学知识(微分方程的求解)。 结构动力学作为结构抗震、抗风设计计算的基础。
2014-1-10
第10章
10.2体系的动力自由度
1.动力自由度的定义
动力问题的基本特征是需要考虑惯性力,根据达朗贝尔(D‘Alembert Jean Le Rond)原理,惯性力与质量和加速度有关,这就要求分析质量分布和质量位 移,所以,动力学一般将质量位移作为基本未知量。 确定体系中全部质量位置所需要的独立几何参数数目,成为体系的动力自由 度。
4 ( x) sin
2014-1-10
…
广义坐标法是一种数学简化方法
第10章
10.2体系的动力自由度
有限单元法:
可以看作是分区的广义坐标法,其要点与静力问题一样,是先把结构划分 成适当数量的区域(称为单元),然后对每一单元施行广义坐标法。详见 有限单元法参考资料,这里不再赘述。 一般地说,有限元法是最灵活有效的离散化方法,它提供了既方便又可靠 的理想化模型,并特别适合于用电子计算机进行分析,是目前最为流行的 方法,已有不少专用的或通用的程序可供结构动力学分析之用。 有限单元法也是一种数学简化方法
2014-1-10
第10章
10.1 概述
2.动力荷载及其分类
动力荷载分类方法有很多种,常见的是按动力作用随时间的变化规律来分。 周期性荷载:其特点是在多次循环中荷载相继呈现相同的时间历程。如旋 转机械装置因质量偏心而引起的离心力。 周期性荷载又可分为简谐荷载和非简谐周期荷载,所有非简谐周期荷载均 可借助Fourier级数分解成一系列简谐荷载之和。 冲击和突加载荷: 其特点是荷载的大小在极短的时间内有较大的变化。冲 击波或爆炸是冲击载荷的典型来源;吊车制动力对厂房的水平作用是典型 的突加荷载。 随机载荷:其时间历程不能用确定的时间函数而只能用统计信息描述。风 荷载和荷载均属此类。对于随机荷载,需要根据大量的统计资料制定出相 应的荷载时间历程(荷载谱)。 前两种荷载属于确定性荷载,可以从运动方程解出位移的时间历程并进一 步求出应力的时间历程。 随机荷载属于非确定性荷载,只能求出位移响应的统计信息而不能得到确 定的时间历程,因而~92层之间有一颗巨 大的‘金色大球’,由实 心钢板堆焊而成,直径约 5.4米,重达680吨,价值 400W美元。其实质是调质 阻尼器TMD(Tuned Mass Damper),作用是减轻飓 风、地震给大楼带来的震 动。
结构动力学-课件(全10章+总结)(刘晶波,杜修力主编.机械工业出版社出版)

质量块mg 无质量弹簧k
(a) 弹簧-质点
2ust
动力反应
u
(b) 静力和动力反应
静力问题和动力问题位移反应的区别
1.4 结构离散化方法
离散化:把无限自由度问题转化为有限自由 度的过程
三种常用的离散化方法: 1、集中质量法、 2、广义坐标法、 3、有限元法。
F (t) = Asinωt F (t) = Acosωt F (t) = Asin(ωt − φ)
可以是机器转动引起的不平衡力等。
p(t)
t
(a) 简谐荷载
1.2 动力荷载的类型
(2)非简谐周期荷载
荷载随时间作周期性变化,是时间t的周期函数,但不
能简单地用简谐函数来表示。 例如:平稳情况下波浪对堤坝的动水压力;轮船螺旋 桨产生的推力等。
n =1
nπx
L
sin(.)— 形函数(形状函数),给定函数,满足边界条件;
bn(t)— 广义坐标,一组待定参数,对动力问题是作为时间的函数。
∑ u( x, t )
=
N n =1
bn
(t)
sin
nπx
L
2、广义坐标法
悬臂梁:
x
(b) 悬臂梁
用幂级数展开:
∞
∑ u(x) = b0 + b1x + b2 x2 + L = bn xn n=0
结构动力学和静力学的本质区别:考虑惯性力的影响
结构产生动力反应的内因(本质因素):惯性力
惯性力的产生是由结构的质量引起的,对结构中质量位 置及其运动的描述是结构动力分析中的关键,这导致 了结构动力学和结构静力学中对结构体系自由度定义 的不同。
结构动力学-第十章-随机振动激励响应关系

ch
0 0
0
kh(t)dt
0
0
(t)dt
0
或: m h(0 ) h(0 ) c h(0 ) h(0 ) kh( )(0 0 ) 1
即: mh(0) ch(0) 1 (1)
积分两次:
0
dt
t mhdt
0
dt
t chdt
0
dt
t
kh(t)dt
0
t
dt (t)dt
t
x(t) h(t )y( )d y(t) * h(t)
卷积积分
此式也可以由上页的(*)式推出:
y(t)
y( )
t
t
此式也可以由上页的(*)式推出:
x(t) 1
2
H
(
)
y(t)eit dteit d
1
2
H
(
)
y( )ei d eit d
1
2
y( )
H
(
)e
当t 0时, (t)=0,故有
mh ch kh 0 或 h 2nh n2h 0
其通解为: h(t) en t ( A cosd t B sin d t)
积分常数A和B由初始条件确定
则: mh ch kh (t) (*)
对(*)式两边从0-到0+积分两次
积分一次:mh 0 0
2
或: 1 e-itdt 2 ()
故: 1
2
() 或:1
2 ()
同样: 1 ei0 t
2
( 0 )
1 ei0 t
2
( 0 )
(3)脉冲响应函数
实际上,在第四章瞬态振动一章已经求过h(t)。 求h(t)的步骤如下: ①建立系统运动微分方程
第十章 结构动力学解答

为:
72������������
9
���̅���������̈ + ������4 ������ = 2������2 ������������(������)
10.6 求如图所示体系的自振频率。
m
EI1 EI1 m
l/2
l/2
EI
l/2 l/2
l
图 10-6
解:此体系为单自由度体系 (1) 将上图所示的体系转化为下图 10-6-1 所示的体系:
(4) 对位移项系数比较得:
4 ������̈ + 5������ ������1������ = 0
ω
=
√4������1 5������
=
√12������������ 5������������3
10.7 单 自 由 体 系 上 作 用 简 谐 动 荷 载 , 力 的 幅 值 F0 500N , 先 后 以 1 10rad / s 和2 17.32rad / s 两种频率分别作用,测得各相应的位移幅值和相 位角为 A1 4.995105 m , 1 2.55 ; A2 9.823105 m , 2 10.8 。试求该 体系的质量 m、刚度 k、自振频率 和阻尼比 。
将������1、������������、������������代入(c=0),得:
������������̈ + ������������ = ������������(������) 4) 求系数 k。在质点处作用单位力所得弯矩图如下图 10-4-5
3
16 ������
1
5 32 ������
3) 将������11、������1������带入,则体系运动方程为
在线测试题试题库及解答(第十章)结构动力学

在线测试题试题库及解答第十章结构动力学基础一、单项选择题1、结构的主振型与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案 A2、结构的自振频率与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案 A3、单自由度体系在简谐荷载作用下,下列哪种情况内力与位移的动力系数相同?A、均布荷载作用B、荷载作用在质点上与质点运动方向垂直C、荷载不作用在质点上D、惯性力与运动方向共线标准答案 D4、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案 D5、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案 D6、当简谐荷载作用于有阻尼的单自由度体系质点上时,若荷载频率远远大于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、重力C、阻尼力D、惯性力标准答案 D7、设ω为结构的自振频率,θ为荷载频率,β为动力系数下列论述正确的是A、ω越大β也越大B、θ/ω越大β也越大C、θ越大β也越大D、θ/ω越接近1,β绝对值越大标准答案 D8、如果体系的阻尼增大,下列论述错误的是A、自由振动的振幅衰减速度加快B、自振周期减小C、动力系数减小D、位移和简谐荷载的相位差变大标准答案 B9、无阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力C、惯性力与弹性力的合力D、没有力标准答案 D10、有阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力与弹性力的合力C、惯性力D、阻尼力标准答案 D11、当简谐荷载作用于无阻尼的单自由度体系质点上时,若荷载频率远远小于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、阻尼力C、惯性力D、重力标准答案 A12、一单自由度振动体系,其阻尼比为ξ,动力系数β,共振时下列结果正确的是A、ξ=0.05,β=10B、ξ=0.1,β=15C、ξ=0.15,β=20D、ξ=0.2,β=25标准答案 A13、一单自由度振动体系,由初始位移0.685cm,初始速度为零产生自由振动,振动一个周期后最大位移为0.50cm,体系的阻尼比为A、ξ=0.05B、ξ=0.10C、ξ=0.15D、ξ=0.20标准答案 A14、在低阻尼体系中不能忽略阻尼对什么的影响?A、频率B、主振型C、周期D、振幅标准答案 D15、单自由度体系受简谐荷载作用,ω为体系自振频率,θ为荷载频率,动位移 y(t)与荷载 P(t) 的关系是A、当θ/ω>1时,y(t)与P(t)同向,当θ/ω<1时,y(t)与P(t)反向。
结构力学:第十章结构动力学2
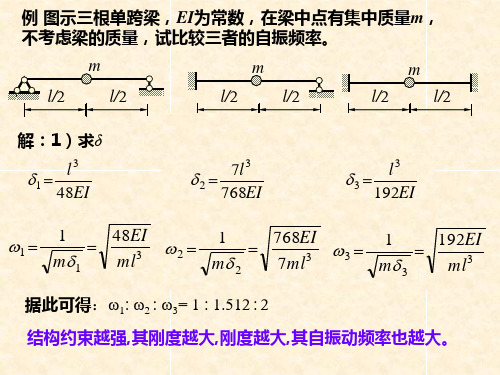
ae-ξωt t
低阻尼y- t曲线
t
无阻尼y- t曲线
②阻尼对振幅的影响.
振幅ae- ξω t 随时间衰减,相邻两个振幅的比
yk1 eT 常数 yk
振幅按等比级数递减.
经过一个周期后,相邻两振幅yk和yk+1的比值的对数为:
ln yk lneT T 2 称为振幅的对数递减率.
yk1
r
如 0.2 则 r 1, 1 r ln yk 1 ln yk
令
k m
,
c 2m ( 阻尼比)
y 2 y 2 y 0(15.16)
k m y
cy ky
c y
my
设解为:y(t) Celt 特征方程为:l2 2l 2 0
1)ξ<1(低阻尼)情况
l ( ± 2 1)
l ir 其中 r 1 2
y et C1 cosrt C2 sinrt
低阻尼体系的自振圆频率
平稳阶段:后来只按荷载频率振动的阶段。(由于阻尼的存在)
平稳阶段:
y
yst
1
1
3)ξ>1 强阻尼:不出现振动,实际问题不常见。
§10-3 单自由度体系的受迫振动
受迫振动(强迫振动):结构在动力荷载作用下的振动。
弹性力-ky、惯性力 my
和荷载P(t)之间的平衡方程为:
y(t)
k
m
m
P(t ) P(t )
myky P(t)(a)
y 2 y P(t) (15.24)
m
一、简谐荷载:
77613m86l El3I2l
5l3 )
32
71l 3
7m68E3I
192EI ml3
第10章 结构动力学
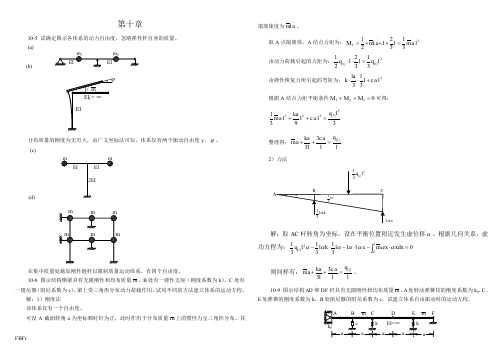
FBFr
M(t)
.. 1 ml 2
解:
k
(2)画出 M p 和 M 1 图(在 B 点处作用一附加约束)
R1 p
3 2
M t
ca
.
2k a 3ma
..
3 ka 2
3EI l
Mp
m 3 .. l M t 24
取 DF 隔离体,
M
F
0:
k11
.. 2a 3 R 2a mx 2 dx ka 2 0 2 . 3 2 R 2ma ka 4
3 l 32
1
13 l 64
(e)忽略水平位移 m
M1图
M2图
M图
3a
1 3 1 2 3 3 1 3 2 3 16 2 13 0.014974l 3 l l l l l l l EI 32 2 3 32 32 2 19 3 32 19 3 64 EI 1 EI EI 8.172 3 m 0.014974ml ml 3
ka 3c a qt 则同样有: m a 。 3l l l
..
.
10-9 图示结构 AD 和 DF 杆具有无限刚性和均布质量 m , A 处转动弹簧铰的刚度系数为 k θ, C、 E 处弹簧的刚度系数为 k ,B 处阻尼器的阻尼系数为 c,试建立体系自由振动时的运动方程。 A kθ B c a a m C k a D EI=∞ a E k a m F
水平支杆中力为3013ei3013ei3013ei2eiei常数3013ei13ei13ei1213ei13eieaeaea27eamfma13641300149743232323219eiei81720014974eieimlml1015设已测得某单自由度结构在振动10周后振幅由1188mm减小至0060mm试求该结构的阻尼比ln201016设有阻尼比02的单自由度结构受简谐荷载sin作用且有若阻尼比降低至002试问要使动位移幅值不变简谐荷载的幅值应调整到多大
10结构动力学概论

当 FP (t)为简谐荷载时,其解的形式为
第十章 结构动力学简介
y(t)
y0
cos ωt
ν0 ω
sin ωt
F
θ sin ωt
F
sin θt
m(ω2 θ 2 ) ω
m(ω2 θ 2 )
前两项为初始条件引起的自由振动;第三项为荷载(干扰力)引起的自由振 动,称为伴生自由振动。实际上,由于阻尼的存在,自由振动部分都很快 衰减掉。自由振动消失前的振动阶段称为过渡阶段。第四项为按荷载频率 进行的振动,此阶段为振动的平稳阶段,称为纯受迫振动或稳态振动。
2、平衡方程的建立
平衡方程的建立有两种方法:一是刚度法;一是柔度法。
my
y k
k
m
刚度法:根据达兰贝尔原理,沿位移正向,在质点上加上惯性力,列动态平 衡方程
ky my
k y ——总是与位移方向相反,指向平衡位置
平m衡y 方—程—与加速m度y方向相k反y 0
第十章 结构动力学简介
柔度法:在惯性力作用下,质点的位移等于实际位移
结构力学
STRUCTURAL MECHANICS
第十章 结构动力学简介
§10-1 概述
一、动力计算的内容
动力计算的内容:研究结构在动荷载作用下的动力反应的计算原理和方法。 涉及到内外两方面的因素: 1)确定动力荷载(外部因素,即干扰力); 2)确定结构的动力特性(内部因素,如结构的自振频率、周期、振型和 阻尼等等),类似静力学中的I、S等; 计算动位移及其幅值;计算动内力及其幅值。
纯受迫振动解的讨论请同学们课下自学完成!
第十章 结构动力学简介
三、阻尼对振动的影响
§10-3 单自由度体系的振动分析
