离散数学图论习题课共48页文档
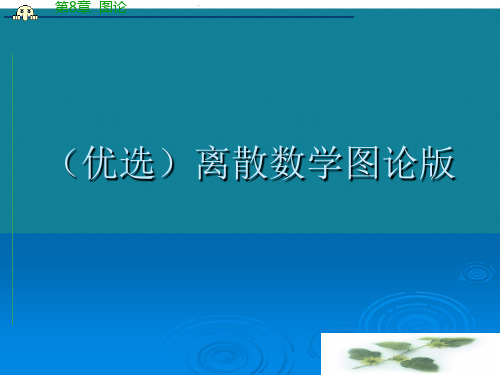
(优选)离散数学图论版
G3=(G1∪G2)-(G1∩G2),记为G3=G1 G2。
除以上4种运算外,还有以下两种操作:
E={e1,e2}={(v1,v2),(ห้องสมุดไป่ตู้2,v3)};
f(v1)=5,f(v2)=8,f(v3)=11;
g(e1)=4.6,g(e2)=7.5
8.1.2 结点的次数
定义8.1―4在有向图中,对于任何结点v,以v为始点的 边的条数称为结点v的引出次数(或出度),记为deg+(v); 以v为终点的边的条数称为结点v的引入次数(或入度), 记为deg-(v);结点v的引出次数和引入次数之和称为 结点v的次数(或度数),记作deg(v)。在无向图中,结点 v的次数是与结点v相关联的边的条数,也记为deg(v)。
i 1
i 1
定理8.1―2在图中,次数为奇数的结点必为偶数个。
证 设次数为偶数的结点有n1个,记为(i=1,2,…,n1)。 次数为奇数的结点有n2个,记为(i=1,2,…,n2)。
由上一定理得
n
n1
n2
2m deg(i ) deg(Ei ) deg(Oi )
i 1
i 1
i 1
因为次数为偶数的各结点次数之和为偶数。所以
孤立结点的次数为零。
定理8.1―1 设G是一个(n,m)图,它的结点集合为
V={v1,v2,…,vn},则 n
deg(i ) 2m
i 1
证 因为每一条边提供两个次数,而所有各结点次数
之和为m条边所提供,所以上式成立。
离散数学习题课图论

2021/6/28
6 of 220
练习2(续)
D的邻接矩阵的前4次幂.
1 2 0 0
A 0
0
1
0
1 0 0 1
0
0
1
0
1 2 2 0
A 2 1
0
0
1
1 2 1 0
1
0
0
1
3 2 2 2
A3
1
2
1
0
2 2 2 1
1
2
1
0
Hale Waihona Puke 5 6 4 2A4
2
2
2
1
4 4 3 2
2
2
2
1
2021/6/28
8 of 220
练习2(续)
(5) v1到v1长度为1,2,3,4的回路数分别为 1,1,3,5. 其中长度为1的是初级的(环);长度 为2的是复杂的;长度为3的中有1条是复杂 的,2条是初级的;长度为4的有1条是复杂 的,有4条是非初级的简单回路. (6) 长度为4的通路(不含回路)为33条. (7) 长度为4的回路为11条. (8) 长度4的通路88条,其中22条为回路. (9) 44的全1矩阵.
9阶无向图G中,每个顶点的度数不是5就 是6. 证明G中至少有5个6度顶点或至少有 6个5度顶点.
方法一:穷举法
设G中有x个5度顶点,则必有(9x)个6度顶点, 由握手定理推论可知,(x,9x)只有5种可能: (0,9), (2,7), (4,5), (6,3), (8,1)它们都满足要求.
方法二:反证法
〔1 n 6〕 熟练掌握求最优树的方法
2021/6/28
12 of 220
习题1
离散数学图论

无向图G有16条边,3个4度顶点,4个3度顶点,其余顶 点度数均小于3,问G的阶数n为几? 解 设除3度与4度顶点外,还有x个顶点v1, v2, …, vx, 则 d(vi) 2,i =1, 2, …, x, 应用握手定理,得不等式 32=2m= Σd(vi)3*4+4*3+2x 得 x 4, 阶数 n 4+3+4=11.
14
1
实例
有向图D如图所示,求D的邻接矩阵 A与 A2, A3, A4. 问D 中长度 为1, 2, 3, 4的通路各有多少条?其中回路分别有多少条?
2
实例求解
1 2 A 1 1 1 4 3 3 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 0 1 0 0 0 1 0 A
8
例题
已知无向树T中有1个3度顶点,2个2度顶点,其余顶点全是树 叶,试求树叶数. 解 设有x片树叶,于是 n = 1+2+x = 3+x, 先依树的性质m=n1, 再根据握手定理: 2m = 2(n1) = 2(2+x) = 13+22+x, 解出x = 3,故T有3片树叶.
9
例题
已知无向树T有5片树叶,2度与3度顶点各1个,其余顶 点的度数均为4,求T的阶数n. 解 设T的阶数为n, 则边数为n1,4度顶点的个数为n7. 由握手定理得 2m = 2(n1) = 51+21+31+4(n7) 解出n = 8,4度顶点为1个.
2
1 3 2 2
0 0 0 0 0 0 0 0
0 0 1 0 0 0 1
A
3
1 5 4 A 4 4
离散数学——图论部分习题课

之和为24,而图G中其余点的度数小于3,即图G中其余点的
度数只可能是2或1(由于图G是连通图,所以无零度点). 由此可知,图G中至少有11个顶点: 3个4度点,4个3度点和 4个2度点; 至多有15个顶点: 3个4度点,4个3度点和8个1
度点.
7. 设G1,G2,G3,G4均是4阶3条边的无向简单图,
n ( n 1) 2
即m=n(n-1)/4, 而m为正整数,所以要么n=4k或n=4k+1, 所以不存在3个顶点和6个顶点的自补图.
9. 设有向简单D的度数列为2,2,3,3,入度列为 0,0,2,3,试求D的出度列。 解:设有向简单图D的度数列为2,2,3,3, 对应的顶点分别为v1,v2,v3,v4,
(1)1,1,2,3,5 (3)1,3,1,3,2 答案(2) (2)1,2,3,4,5 (4)1,2,3,4,6
Байду номын сангаас
)
则它们之间至少有几个是同构的? 解: 4阶3条边非同构的无向简单图共有3个,因此 G1,G2,G3,G4中至少有2个是同构的。
8. 是否存在3个顶点和6个顶点的自补图? 解: 由于顶点为n的无向完全图的边数为
n ( n 1) 2
.
设G的自补图为G’,则G与G’的边数相等. 设它们的边数各为m,于是有m+m=
本章重点
一、掌握有关图的基本概念:
邻接 关联 有向图
平行边 多重图
无向图
n阶图
底图
连通图
自回路(环) 简单图
二、掌握图中顶点的度数,握手定理及其推论 定理:设图G是具有n个顶点、m条边的无向图, 其中点集V={v1, v2,… vn }, 则
deg(
i 1
离散数学习题解答第6部分(图论)
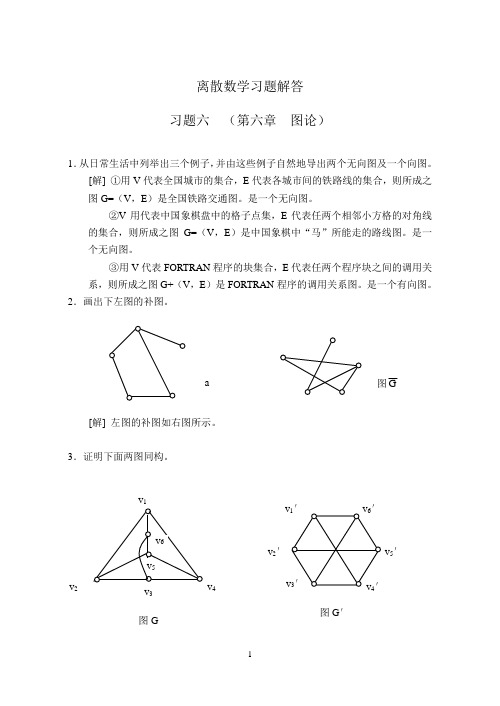
离散数学习题解答 习题六 (第六章 图论)1.从日常生活中列举出三个例子,并由这些例子自然地导出两个无向图及一个向图。
[解] ①用V 代表全国城市的集合,E 代表各城市间的铁路线的集合,则所成之图G=(V ,E )是全国铁路交通图。
是一个无向图。
②V 用代表中国象棋盘中的格子点集,E 代表任两个相邻小方格的对角线的集合,则所成之图G=(V ,E )是中国象棋中“马”所能走的路线图。
是一个无向图。
③用V 代表FORTRAN 程序的块集合,E 代表任两个程序块之间的调用关系,则所成之图G+(V ,E )是FORTRAN 程序的调用关系图。
是一个有向图。
2.画出下左图的补图。
[解] 左图的补图如右图所示。
3.证明下面两图同构。
a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1,v 2)=(v 1′,v 2′) ϕ (v 2)=v 2′ ϕ (v 2,v 3)=(v 2′,v 3′) ϕ (v 3)=v 3′ ϕ (v 3,v 4)=(v 3′,v 4′) ϕ (v 4)=v 4′ ϕ (v 4,v 5)=(v 4′,v 5) ϕ (v 5)=v 5′ ϕ (v 5,v 6)=(v 5′,v 6′) ϕ (v 6)=v 6′ϕ (v 6,v 1)=(v 6′,v 1′) ϕ (v 1,v 4)=(v 1′,v 4′) ϕ (v 2,v 5)=(v 2′,v 5′) ϕ (v 3,v 6)=(v 3′,v 6′)显然使下式成立:ψ (v i ,v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。
4.证明(a ),(b )中的两个图都是不同构的。
图G 中有一个长度为4的圈v 1v 2v 6v 5v 1,其各顶点的度均为3点,而在图G ′中却没有这样的圈,因为它中的四个度为3的顶点v 1',v 5',v 7',v 3'不成长度的4的圈。
第7章 图论 [离散数学离散数学(第四版)清华出版社]
![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://img.taocdn.com/s3/m/58b7923143323968011c9244.png)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
21
例:
a j i h c g d
1(a)
无 向 图
b
f
e
2(b)
7(j) 8(g) 9(d) 10(i)
6(e)
3(c) 4(h)
5(f)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
22
例:
1(b)
有向图
第四部分:图论(授课教师:向胜军)
6
[定义] 相邻和关联
在无向图G中,若e=(a, b)∈E,则称a与 b彼此相邻(adjacent),或边e关联 (incident) 或联结(connect) a, b。a, b称为边e的端点或 结束顶点(endpoint)。 在有向图D中,若e=<a, b>∈E,即箭头 由a到b,称a邻接到b,或a关联或联结b。a 称为e的始点(initial vertex),b称为e的终点 (terminal/end vertex)。
证明思路:将图中顶点的度分类,再利用定理1。
6/27/2013 6:02 PM 第四部分:图论(授课教师:向胜军) 9
[定理3] 设有向图D=<V, E>有n个顶点,m 条边,则G中所有顶点的入度之和等于所 有顶点的出度之和,也等于m。
即:
d ( v i ) d ( v i ) m.
i 1 i 1
n
n
证明思路:利用数学归纳法。
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
10
一些特殊的简单图:
(1) 无向完全图Kn(Complete Graphs)
离散数学图论

例:把下面的m叉树改写为二叉树。
14
第七章 图论
信 息 科 学 与 工 程 学 院
练习:把下面的有序树改写为二叉树。
。 。 。。 。 。。 。 。 。 知识点提示:
。 。。
。 。 。
。
课下自学
此方法可推广至有序森林到二叉树的转换。 此方法具有可逆性。
15
第七章 图论
信 息 科 学 与 工 程 学 院
给定一棵2叉树T,设它有t片树叶。设v为T的一个分枝点, 则v至少有一个儿子,最多有两个儿子。若v有两个儿 子,在由v引出的两条边上,左边的标上0,右边的标 上1;若v有一个儿子,在由v引出的边上可标上0,也
可标上1。设vi为T的任一片树叶,从树根到vi的通路
上各边的标号组成的0,1串组成的符号串放在vi处,t 片树叶处的t个符号串组成的集合为一个二元前缀码。
定义7-8.5
在根树中, 科 一个结点的通路长度为从树根到此结点的通路中的边 学 数。 与 分枝点的通路长度称为内部通路长度。 树叶的通路长度称为外部通路长度。
工 程 学 院
。 。 。 。。 A 。 。 。。
18
第七章 图论
信 息 科
定理7-8.2
若完全二叉树有n个分枝点,且内部通路长度总和为L,外 部通路长度总和为E,则 E=L+2n。 证明:
学 与 工 程 学 院
对分枝点数目n进行归纳证明。
。
当n=1时,如右图所示,
L=0, E=2,
。
。
显然, E=L+2n成立。
19
第七章 图论
信 息 科 学
定理7-8.2 若完全二叉树有n个分枝点,且内部通路长度总 和为L,外部通路长度总和为E,则 E=L+2n。 证明:
全版离散数学 练习题及答案.ppt

课件
例3 对任意两个集合A, B,试证 A (A B) A B
证明 对于任意的x
x A (A B)
x {x x A x ( A B)} x {x x A (x A B)} x {x x A (x A x B)} x {x x A (x A x B)} x {x x A x B}
课件
例10 求图的最小生成树
A 1B34 Nhomakorabea5
2 E
6
1A 2
B
E
4
6
C7 D
C
D
课件
例11
• 无向树T有7片树叶, 3个3度顶点,其余的 都是4度顶点,则T有几个4度顶点?
• 解:设T有x个4度顶点 顶点度数之和: 7+3*3+4x 由树的性质可得总边数: 7+3+x-1 由握手原理可得: 7+3*3+4x=2(7+3+x-1)
求g f
g f { 1,b , 2,b , 3,b }
课件
例12 求复合函数
X {1,2,3}, Y {p, q}, Z {a,b} f { 1, p , 2, p , 3, q } g { p,b , q,b }
求g f
g f { 1,b , 2,b , 3,b }
课件
例: 求幺元、零元、逆元
x A B 因为 x 是任意的,所以有
x ((x A (A B)) (x A B)) 的真值为T,
因此 A ( A B)课件 A B
例4 判断关系的性质
R1 { a, a , a,b , b,b , c,c }
a
1 1 0
M R 1 0 1 0
0 0 1
《离散数学》图论 (上)

无向图与有向图
v2
e1
e2
e3
v3
e4
v1
e5 (e1)={( v42, v24 )}
v4
(e2)={( v32, v23 )} (e3)={( v3, v4 )}
(e4)=({ v43, v34 )}
(e5)=({ v4,}v4 )
13
无向图与有向图
A B C
D E F
14
无向图与有向图
第八章 图论
第八章 图论
§8.1 基本概念
§8.1.1 无向图、有向图和握手定理 §8.1.2 图的同构与子图 §8.1.3 道路、回路与连通性 §8.1.4 图的矩阵表示
§8.2 欧拉图 §8.3 哈密尔顿图 §8.4 平面图 §8.5 顶点支配、独立与覆盖
2
无向图与有向图
3
无向图与有向图
一个无向图(undirected graph, 或graph) G 指一个三元组 (V, E, ),其中
vV
vV
24
特殊的图
假设 G=(V, E, ) 为无向图,若 G 中所有 顶点都是孤立顶点,则称 G 为零图(null graph)或离散图(discrete graph);若 |V|=n,|E|=0,则称 G 为 n 阶零图 所有顶点的度数均相等的无向图称为正 则图(regular graph),所有顶点的度数 均为 k 的正则图称为k度正则图,也记作 k-正则图 注:零图是零度正则图
19
握手定理
定理(图论基本定理/握手定理)
假设 G=(V, E, ) 为无向图,则deg(v) 2 E , vV
即所有顶点度数之和等于边数的两倍。
推论
在任何无向图中,奇数度的顶点数必是偶 数。
离散数学-图论-习题公开课获奖课件百校联赛一等奖课件

e1 e2 e3 e4 e5 e6 e7 e8 e9 A100001010 B011000100 C000110010 D1 1 0 0 0 0 0 0 1 E000011100 F001100001
311页(2)构造一种欧拉图,其结点数v和边数e满足下述条件
a)v,e旳奇偶性一样。 b) v,e旳奇偶性相反。 假如不可能,阐明原因。
练习 321页(1)
(a) v*=5,e*=8,r*=5
(b) v*=7,e*=13,r*=12
(c) v*=5,e*=6,r*=3
(d) v*=7,e*=12,r*=7
321页(4)证明:若图G是自对偶旳,则e=2v-2。
证明: 若图G是自对偶旳,则v=v*,e=e*,即 r*=v=v*=r,e=e* 则由欧拉定理v-e+r=2 得v-e+v=2,即e=2v-2。 若图G是自对偶旳,则e=2v-2。
1 0 1 10
A=
1 0 0 00
1 0 1 00
0 0 0 00 i=4时,因为A[4,2]=1,将第四行
用Warshall算法求可
加到第2行,A不变。
达性矩阵。
i=5时,因为A旳第5列全为0,所
i=1时,因为A旳第一行 以A不变。
0 0 0 00
全为0,所以A不变。
i=2时,因为A旳第2列 全为0,所以A不变。
无向图G具有一条欧拉回 路,当且仅当G是连通旳,而且 全部结点度数全为偶数。下面旳 图中全部结点度数全为偶数,所
以都是欧拉图。
ห้องสมุดไป่ตู้v=3,e=3
v=5,e=5
v=4,e=4 v=4,e=6
v=7,e=8
v=6,e=7
311页(6)
(图论)离散数学习题参考答案2
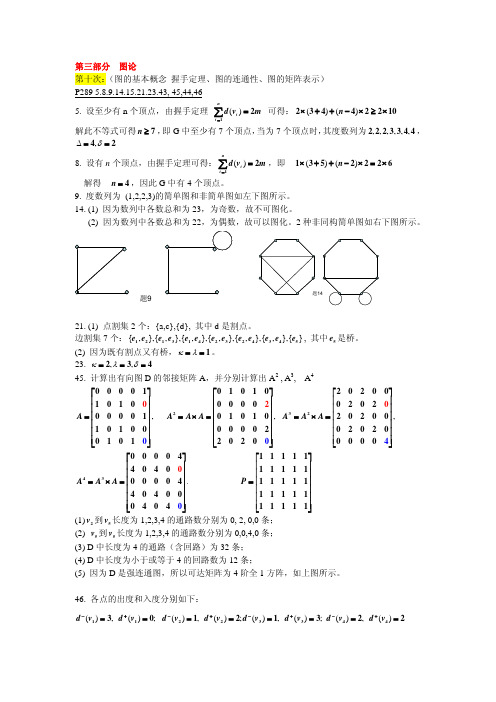
解此不等式可得 n ≥ 7 , 即 G 中至少有 7 个顶点, 当为 7 个顶点时, 其度数列为 2, 2, 2, 3, 3, 4, 4 , Δ = 4, δ = 2 8. 设有 n 个顶点,由握手定理可得: ∑ d (vi ) = 2m ,即
i =1 n
1 × (3 + 5) + (n − 2) × 2 = 2 × 6
d − (v1 ) = 3, d + (v1 ) = 0; d − (v2 ) = 1, d + (v2 ) = 2; d − (v3 ) = 1, d + (v3 ) = 3; d − (v4 ) = 2, d + (v4 ) = 2
第十一次: (欧拉图与哈密顿图)P305 1.2.11.21 (无向树及其性质)P318 2.24(a), 25(b) 1. (a),(c) 是欧拉图,因为它们均连通且都无奇度顶点; (b),(d)都不是欧拉图;因为(b) 不连通,(d) 既不连通又有奇度顶点;要使(b),(d)变为欧拉图 均至少加两条边,使其连通并且无奇度顶点。如下图所示。
(1) v2 到 v5 长度为 1,2,3,4 的通路数分别为 0, 2, 0,0 条; (2) v5 到 v5 长度为 1,2,3,4 的通路数分别为 0,0,4,0 条; (3) D 中长度为 4 的通路(含回路)为 32 条; (4) D 中长度为小于或等于 4 的回路数为 12 条; (5) 因为 D 是强连通图,所以可达矩阵为 4 阶全 1 方阵,如上图所示。 46. 各点的出度和入度分别如下:
(v2,12)** (v5, 7)*
根据上表的最后一行,从 v1 到其余各点的最短路径和距离如下: v1v2, d(v1,v2)=6 v1v2v6, d(v1,v6)=12 v1v3, d(v1,v3)=3 v1v3v4v5v7, d(v1,v7)=7 v1v3v4, d(v1,v4)=5 v1v3v4v5v7v8, d(v1,v8)=10 v1v3v4v5, d(v1,v5)=6
离散数学图论部分14章习题课

离散数学(图论部分)1-4章习题课1. 证明:在10个人中,或有3人互相认识,或有4人互不认识。
证:设x为10人中之任意某人,则在余下9人中:(1) x至少认识其中4人,或(2) x至多认识其中3人(即至少不认识其中6人),两者必居其一。
(1) 若此x认识的4人互不相识,命题得证;否则,互相认识的2人加上x构成互相认识的3人,命题得证。
(2) 若此x不认识的6人中有3人互相认识,命题得证;否则,由Ramsey(3,3)=6知,此6人中至少有3人互不认识,此3人加上x为互不认识的4人,命题得证。
2. 设(a) V={a,b,c,d},A={<a,b>,<a,c>,<b,c>,<b,d>,<c,d>}(b) V={a,b,c,d,e},E={(a,b),(a,c),(b,c),(d,e)}画出上述图的图解。
解:略。
3. 试找出K3的全部子图,并指出哪些是生成子图。
解:K3共有17个子图。
其他略。
4. 证明:在至少有2人的团体中,总存在2个人,他们在这个团体中恰有相同数目的朋友。
解:在n个人的团体中,各人可能有的朋友数目为0, 1, 2, 3, …, n-1,共n个数,但其中0和n-1 不能共存,故n个人事实上可能的朋友数目只有n-1个。
由鸽巢原理,命题得证。
5.某次宴会上许多人互相握手。
证明:必有偶数个人握了奇数次手。
证:以人为顶点,握手关系为邻接关系构造一个无向图。
由图的性质,奇数度的顶点必为偶数个,即握了奇数次手的人数必为偶数。
6. 证明:Ramsey(3,4)=9。
(提示:题1的推广)证:在9个人中,不可能每个人都恰好认识其他的3个人(即图的9个顶点不可能每个顶点的度都为3,否则违反图的奇数度的顶点必为偶数个的性质)。
设x不会恰好认识其他的3个人(即deg(x)≠3),则在余下8人中::(1) x至少认识其中4人,或(2) x至多认识其中2人(即至少不认识其中6人),两者必居其一。
离散数学——图论

2023/5/24
42
§8.3欧拉图
❖ 欧拉图产生的背景就是前面的七桥问题。
❖ 定义:图G的回路,若它通过G中的每条边一 次,这样的回路称为欧拉回路。具有欧拉回 路的图称为欧拉图。
❖ 定义欧拉通路:通过图G中每条边一次的通 路(非回路)称为欧拉通路。
2023/5/24
27
正则图
❖ 所有结点均有相同次数d的图称为d次正则图。 ❖ 如4阶的完全图是3次正则图,是对角线相连
的四边形。 ❖ 试画出两个2次正则图。
2023/5/24
28
两图同构需满足的条件
❖ 若两个图同构,必须满足下列条件: (1)结点个数相同 (2)边数相同 (3)次数相同的结点个数相同
❖ 例子
2023/5/24
❖ 1847年德国的克希霍夫(G.R.Kirchoff)将树的概念 和理论应用于工程技术的电网络方程组的研究。
❖ 1857年英国的凯莱(A.Cayley)也独立地提出了树的 概念,并应用于有机化合物的分子结构的研究中。
2023/5/24
4
❖ 1936年匈牙利的数学家哥尼格(D.Konig) 发 表了第一部集图论二百年研究成果于一书的 图论专著《有限图与无限图理论》,这是现 代图论发展的里程碑,标志着图论作为一门 独立学科。
2023/5/24
37
连通性
❖ 定义:无向图,若它的任何两结点间均是可达的, 则称图G是连通图;否则为非连通图。
❖ 定义:有向图,如果忽略图的方向后得到的无向图 是连通的,则称此有向图为连通图。否则为非连通 图。
2023/5/24
38
有向连通图
❖ 定义:设G为有向连通图, ❖ 强连通:G中任何两点都是可达的。 ❖ 单向连通:G中任何两结点间,至少存在一个方向
离散数学 第七章 图论 习题课

零图与平凡图;简单图与多重图; 完全图;子图,生成子图,补图;图的同构。 2、运用。 (1) 灵活运用握手定理及其推论, (2) 判断两个图是否同构, (3) 画出满足某些条件的子图,补图等。
第五页,共48页。
二、通路、回路、图的连通性
1、基本概念 路,回路,迹, 通路,圈 无向图和有向图中结点之间的可达关系;连通 图,连通分支,连通分支数W(G) 点割集,割点,点连通度k(G) 边割集,割边(桥),边连通度λ(G) 短程线,距离 有向图连通的分类,强连通,单侧连通,弱连 通, 强分图,单侧分图,弱分图
简单图
(2) E (a,b), (b, e), (e,b), (a, e), (d, e) 多重图
(3) E (a,b), (b, e), (e, d ), (c, c)
不是
第九页,共48页。
下列各序列中,可以构成无向简单图的度数序列的
有哪些?
(1) (2,2,2,2,2)
可以
(2)(1,1,2,2,3)
,故无向图的结点数为奇数,则所对应的n阶完全 图中每个结点的度数为n-1即为偶数, 利用奇数+奇数=偶数,偶数+偶数=偶数,所以, 在G中结点度数为奇数的结点,在其补图中的度数 也应为奇数,故G和其补图的奇数结点个数也是相 同的。
第二十五页,共48页。
P286
1、在无向图G中,从结点u到结点v有一条长度为偶数 的通路,从结点u到结点v又有一条长度为奇数的通路 ,则在G中必有一条长度为奇数的回路。
正确答案是:C。 对割边、边割集的概念理解到位。 定义 设无向图G=<V, E>为连通图,若有边集E1E
,使图G删除了E1的所有边后,所得的子图是不连通 图,而删除了E1的任何真子集后,所得的子图是连 通图,则称E1是G的一个边割集.若某个边构成一个 边割集,则称该边为割边(或桥) 如果答案A正确,即删除边(a, d)后,得到的图是不连 通图,但事实上它还是连通的。因此答案A是错误的。
离散数学图论部分经典试题及答案
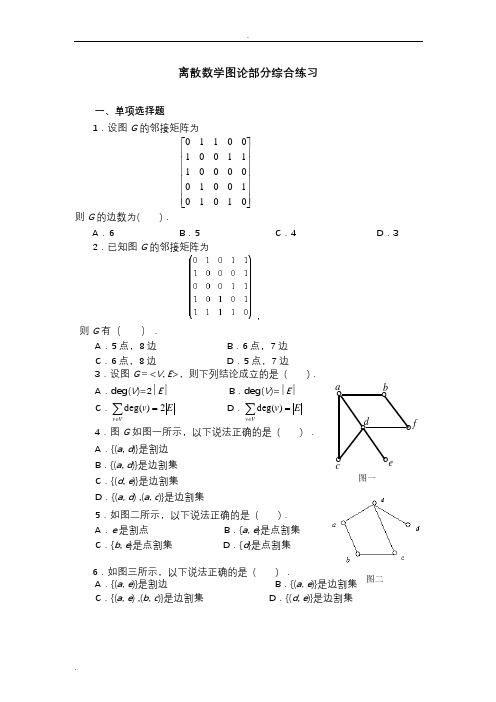
离散数学图论部分综合练习一、单项选择题1.设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010*******11100100110则G 的边数为( ).A .6B .5C .4D .32.已知图G 的邻接矩阵为,则G 有( ).A .5点,8边B .6点,7边C .6点,8边D .5点,7边3.设图G =<V , E >,则下列结论成立的是 ( ).A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v Vv 2)deg(=∑∈ D .E v Vv =∑∈)deg(4.图G 如图一所示,以下说法正确的是 ( ) . A .{(a , d )}是割边 B .{(a , d )}是边割集 C .{(d , e )}是边割集 D .{(a, d ) ,(a, c )}是边割集5.如图二所示,以下说法正确的是 ( ). A .e 是割点 B .{a, e }是点割集 C .{b , e }是点割集 D .{d }是点割集6.如图三所示,以下说法正确的是 ( ) .A .{(a, e )}是割边B .{(a, e)}是边割集 C .{(a, e ) ,(b, c )}是边割集 D .{(d , e )}是边割集οο ο ο οca b edο f图一图二图三7.设有向图(a )、(b )、(c )与(d )如图四所示,则下列结论成立的是 ( ).图四A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的 应该填写:D8.设完全图K n 有n 个结点(n ≥2),m 条边,当( )时,K n 中存在欧拉回路.A .m 为奇数B .n 为偶数C .n 为奇数D .m 为偶数 9.设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ).A .e -v +2B .v +e -2C .e -v -2D .e +v +2 10.无向图G 存在欧拉通路,当且仅当( ). A .G 中所有结点的度数全为偶数 B .G 中至多有两个奇数度结点 C .G 连通且所有结点的度数全为偶数 D .G 连通且至多有两个奇数度结点11.设G 是有n 个结点,m 条边的连通图,必须删去G 的( )条边,才能确定G 的一棵生成树.A .1m n -+B .m n -C .1m n ++D .1n m -+ 12.无向简单图G 是棵树,当且仅当( ).A .G 连通且边数比结点数少1B .G 连通且结点数比边数少1C .G 的边数比结点数少1D .G 中没有回路.二、填空题1.已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 . 2.设给定图G (如图四所示),则图G 的点割ο οο οc a b f集是 .3.若图G=<V , E>中具有一条汉密尔顿回路, 则对于结点集V 的每个非空子集S ,在G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点数|S|与W 满足的关系式为 .4.无向图G 存在欧拉回路,当且仅当G 连通 且 .5.设有向图D 为欧拉图,则图D 中每个结点的入度 . 应该填写:等于出度6.设完全图K n 有n 个结点(n 2),m 条边,当 时,K n 中存在欧拉回路.7.设G 是连通平面图,v , e , r 分别表示G 的结点数,边数和面数,则v ,e 和r 满足的关系式 .8.设连通平面图G 的结点数为5,边数为6,则面数为 . 9.结点数v 与边数e 满足 关系的无向连通图就是树.10.设图G 是有6个结点的连通图,结点的总度数为18,则可从G 中删去 条边后使之变成树.11.已知一棵无向树T 中有8个结点,4度,3度,2度的分支点各一个,T 的树叶数为 .12.设G =<V , E >是有6个结点,8条边的连通图,则从G 中删去 条边,可以确定图G 的一棵生成树.13.给定一个序列集合{000,001,01,10,0},若去掉其中的元素 ,则该序列集合构成前缀码.三、判断说明题 1.如图六所示的图G 存在一条欧拉回路.2.给定两个图G 1,G 2(如图七所示):(1)试判断它们是否为欧拉图、汉密尔顿图?并说明理由. (2)若是欧拉图,请写出一条欧拉回路.v 123 图六图七3.判别图G (如图八所示)是不是平面图, 并说明理由.4.设G 是一个有6个结点14条边的连 通图,则G 为平面图.四、计算题1.设图G =<V ,E >,其中V ={a 1, a 2, a 3, a 4, a 5},E ={<a 1, a 2>,<a 2, a 4>,<a 3, a 1>,<a 4, a 5>,<a 5, a 2>}(1)试给出G 的图形表示; (2)求G 的邻接矩阵;(3)判断图G 是强连通图、单侧连通图还是弱连通图?2.设图G =<V ,E >,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1, v 2),(v 1, v 3),(v 2, v 3),(v 2, v 4),(v 3, v 4),(v 3, v 5),(v 4, v 5) },试(1)画出G 的图形表示; (2)写出其邻接矩阵;(2)求出每个结点的度数; (4)画出图G 的补图的图形.3.设G =<V ,E >,V ={ v 1,v 2,v 3,v 4,v 5},E ={ (v 1,v 3),(v 2,v 3),(v 2,v 4),(v 3,v 4),(v 3,v 5),(v 4,v 5) },试(1)给出G 的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出其补图的图形.4.图G =<V , E >,其中V ={ a , b , c , d , e },E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (c , d ), (d , e ) },对应边的权值依次为2、1、2、3、6、1、4及5,试(1)画出G 的图形; (2)写出G 的邻接矩阵;(3)求出G 权最小的生成树及其权值.5.用Dijkstra 算法求右图中A 点到其它各点的最短路径。
离散数学教学图论【共58张PPT】

一 、图的基本概念
• 邻接和关联 • 无向图和有向图 • 零图和平凡图 • 简单图 • 完全图(无向完全图和有向完全图) • 有环图
一 、图的基本概念
• 有限图和无限图 设图G为< V,E,Ψ>
(l)当V和E为有限集时,称G为有限图,否则称G为无限图。 (2)当ΨG为单射时,称G为单图;当ΨG为非单射时,称G为重图,又称满足
二、生成树
1、生成树定义:
若无向图的一个生成子图T是树,则称T 为G的生 成树,T中的边称为树枝,E(G)-E(T)称为树T 的补,其中的每一边称为树T 的弦。
在任何图中,结点v的度(degree)d(v)是v所关联边的数目。
第三节 生成树、最短路径和关键路径 由结点a和它所有的后代导的子图,称为T的子树.
∴ T连通且具有m=n-1的图
{e5,e4,e8} , {e7,e6,e5,e2,e4} 第四节 欧拉图和哈密顿图
第四节 特殊图(欧拉图和哈密顿图等)
第五节 树、二叉树和哈夫曼树
离散数学教学图论
(优选 欧拉图和哈密顿图
(3)2=>3 ∴W(T)≤W(T1) ∴W(ei+1)≥W(f) 二. 哈密顿图的由来—周游世界问题:
第二节 图的矩阵表示 第四节 欧拉图和哈密顿图
证明:若G中一个边割集和一生成 树无公共边,则表示该边割集所分离的结点不在生成树中,这导致与生成树的定义矛盾。 哈密顿图的由来—周游世界问题: c)对新图向下旋转45度。 ei之后将取f而不是ei+1
为该顶点的度,列之和一定为2. • 有向图的关联矩阵 ----- 以节点数为行,边数为列.节点与边无关系,为0,有关系,则起点为1,
终点为-1;列之和一定为0,每行绝对值之和等于该节点的度数;其 中1的个数为该节点的出度,-1的个数为对应节点的入度;所有元 素的和为0,1的个数等于-1的个数,都等于边数m.
离散数学图论

如图G1是非连通图, G2是连通图。
G1
G2
21
连通分支:设无向图G=<V, E>,V关于顶点之间的 连通关系 的商集 V/ ={V1,V2,…,Vk},Vi为等价 类,称导出子图G[Vi] (i=1,2,…,k) 为G的连通分 支, 其个数记作p(G)=k。
如: p(G1)=2, p(G2)=1 G是连通图 p(G)=1 n阶零图的连通分支数最多, p(Nn)=n
有圈的长度2。
• 复杂通路和复杂回路: 中的边重复出现。
20
14.3 图的连通性
(23)无向图的连通性 设无向图G=<V, E>,u, vV, u与v连通:u与v之间存在通路. 记作uv. 规定uu。 连通关系: ={<u,v>| u,vV且uv}是等价关系。 连通图:平凡图, 任意两点都连通的图。
注意:图的数学定义与图形表示,在同构的意义 下是一一对应的。
7
(5)几个特殊的图
通常用G表示无向图, D表示有向图, 也常用G泛指 无向图和有向图, 用ek表示无向边或有向边. V(G), E(G) —表示图G的顶点集, 边集.
|V(G)|, |E(G)| —表示图G的顶点数集(阶)和边数.
n 阶图、有限图、零图、平凡图、空图、基图
(6)顶点和边的关联
关联、关联次数、环、孤立点
(7)相邻
vi
vj
点相邻、边相邻
(vi,vj)
ek el
8
(8)邻接
vi
邻接到、邻接于
(9)邻域和关联集
设无向图G, vV(G)
v的邻域、 v的闭邻域、 v的关联集
设有向图D, vV(D)
v的后继元集
离散数学--第七章-图论---习题课

(1)设n阶图G中有m条边,证明:δ(G)≤2m/n≤△(G) (2)n阶非连通的简单图的边数最多可为多少?最少呢?
(1)证明中关键步骤是握手定理:
2m=∑deg(vi) δ(G)≤deg(vi)≤△(G),于是得 nδ(G)≤2m≤n△(G)
⇒ δ(G)≤2m/n≤△(G) 易知2m/n为G的平均度数,因而它大于或等于
证明 :
设从结点u到结点v长度为偶数的通路是 ue1u1e2u2…e2kv,
长度为奇数的通路是ue11u11e12u12…e12h-1v, 那么路ue1u1e2u2…e2kve12h-1…u12e12u11e11u就是一条回
路,它的边数=2k+(2h-1)=2(h+k)-1,是奇数,故 这条回路的长度是奇数。
(k为正整数)。 解:
1)设图G 是自补图,G 有 e 条边,G 对应的完全图的 边数为 A。G 的补图 G’的边数应为 A 一 e。因为 G~G’, 故边数相等,e=A 一 e,A=2e,因此 G 对 应的完全图的边数 A 为偶数。
2)由 1)可知,自补图对应的完全图的边数为偶数。n 个结点的完全图 Kn 的边数为n(n-1)/2 , 所以 n(n-1)/2=2m ,即n(n-1)=4m,因而 n为4的倍数,即n=4k, 或n-1为4的倍数,即n=4k+1,
平面图的判断 欧拉公式
平面图的对偶图
无向树及其性质 根树及其应用
地图着色与平 面图着色
一、无向图与有向图
1、基本概念。
有向图与无向图的定义;有向边,无向边,平行边, 环, 孤立结点
关联与邻接(相邻); 结点的度数;结点的度, 结点的出度, 结点的入
度, 图的最大度Δ(G),最小度δ(G),
