电偶极子电势电场matlab模拟
用matlab数值分析报告电偶极子地等电势图和电场线图

合肥学院创新课程设计报告题目:用matlab分析电偶极子的等电势图和电场线系别:电子信息与电气工程系专业:通信工程专业班级: 14姓名:导师:成绩:2013 年《通信技术综合创新课程设计》任务书目录电偶极子的等电势图和电场 (5)一电偶极子原理以及相关知识 (5)1.1 电偶极子定义 (5)1.2 电偶极子原理 (6)二演示程序 (9)2.1电偶极子电势在matlab中的模拟 (9)2.2电偶极子电场在matlab中的模拟 (11)三结束语 (13)四参考文献 (13)电偶极子的等电势图和电场一电偶极子原理以及相关知识1.1 电偶极子定义一个实体,它在距离充分大于本身几何尺寸的一切点处产生的电场强度都和一对等值异号的分开的点电荷所产生的电场强度相同。
电偶极子(electric dipole)是两个相距很近的等量异号点电荷组成的系统。
电偶极子的特征用电偶极距P=lq描述,其中l是两点电荷之间的距离,l和P的方向规定由-q指向+q。
电偶极子在外电场中受力矩作用而旋转,使其电偶极矩转向外电场方向。
电偶极矩就是电偶极子在单位外电场下可能受到的最大力矩,故简称电矩。
如果外电场不均匀,除受力矩外,电偶极子还要受到平移作用。
电偶极子产生的电场是构成它的正、负点电荷产生的电场之和。
1.2 电偶极子原理两个点电荷q和-q间的距离为L。
此电偶极子在场点P 处产生的电位等于两个点电荷在该点的电位之和,即(1)图(1)表示中心位于坐标系原点上的一个电偶极子,它的轴线与Z轴重合,其中与分别是q和-q到P 点的距离。
图1 电偶极子一般情况下,我们关心的是电偶极子产生的远区场,即负偶极子到场点的距离r 远远大于偶极子长度L的情形,此时可以的到电偶极子的远区表达式(2)可见电偶极子的远区电位与成正比,与的平方成反比,并且和场点位置矢量与轴的夹角有关。
为了便于描述电偶极子,引入一个矢量P,摸P=q L,方向由-q指向q,称之为此电偶极子的电矩矢量,简称为偶极矩,记作P=q L (3)此时(2)式又可以写成(4)电偶极子的远区电场强度可由(4)式求梯度得到。
基于MATLAB的大学物理可视化研究
物理学是一门严格的、精密的基础学科,涵盖了从微观到宇观的整个自然界的经典物理模型。
要求学习者具有较强的抽象思维能力,相对来说这是一门比较难学的课程[1]。
但它的基本概念、基本理论与实验方法向其他学科的渗透,总是能促成该学科或技术领域发生革命性变化或里程碑式的进步;因此,物理是学好各自然科学和工程技术科学的基础,传统的物理课堂要对理想物理模型进行严格的分析、建立精确的数学模型并求出精确的解析解,学生普遍反映内容理论性太强,概念抽象,计算过程复杂,得到的结果难以理解。
抽象的模型、缜密的分析,严格的建模、计算,一个解析的字母表达式结果确实很难吸引学生的学习兴趣。
MATLAB代表了当今世界科学计算软件的最先进水平[2],它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,已经在很多专业学科有广泛的应用。
利用MATLAB将物理模型的最终解通过数值模拟做可视化展示,可以让学生看到更直观、明晰区域分布,大大提高学生的学习兴趣,是传统学科与先进计算技术的完美结合。
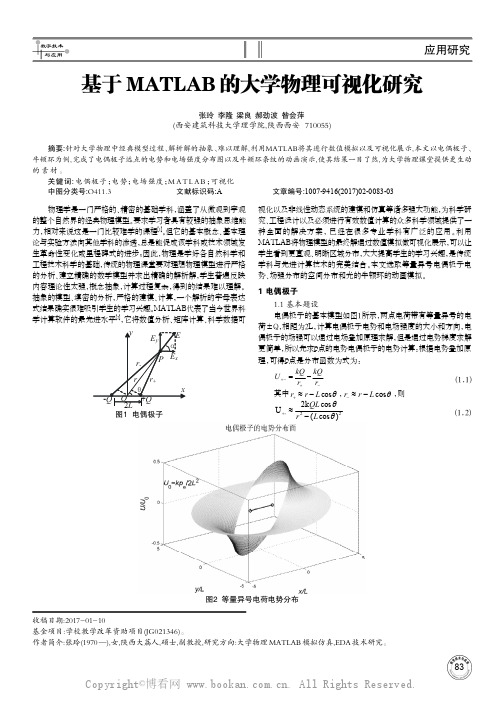
本文选取等量异号电偶极子电势、场强分布的空间分布和光的牛顿环的动画模拟。
1 电偶极子1.1 基本题设电偶极子的基本模型如图1所示,两点电荷带有等量异号的电荷±Q,相距为2L,计算电偶极子电势和电场强度的大小和方向,电偶极子的场强可以通过电场叠加原理求解,但是通过电势梯度求解更简单,所以先求p点的电势电偶极子的电势计算:根据电势叠加原理,可得p点是分布函数为式为:-+-+-=r kQ r kQ U (1.1)其中θcos L r r -≈+,θcos L r r -≈-,则22-)cos (cos k 2U θθL r QL -≈+ (1.2)基于MATLAB 的大学物理可视化研究张玲 李隆 梁良 郝劲波 昝会萍(西安建筑科技大学理学院,陕西西安 710055)摘要:针对大学物理中经典模型过程、解析解的抽象、难以理解,利用MATLAB将其进行数值模拟以及可视化展示,本文以电偶极子、牛顿环为例,完成了电偶极子远点的电势和电场强度分布图以及牛顿环条纹的动画演示,使其结果一目了然,为大学物理课堂提供更生动的素材。
电偶极子电势电场matlab模拟

电偶极子电势电场matlab模拟1. 引言电偶极子是电磁学中重要的概念,它描述了由两个等量异号电荷构成的系统,这两个电荷的距离相对较小,而总电荷为零。
在电偶极子中,电荷的等量但异号的性质决定了它在外界产生的电场和电势特性。
为了直观地了解电偶极子的电势和电场分布情况,我们可以使用MATLAB进行模拟。
2. 电势的计算电势是描述电荷对其他电荷的影响的物理量,它与电荷的分布和距离有关。
对于电偶极子,我们可以通过其定义的两个电荷的位置和电量来计算电势。
电偶极子的电势公式如下:V = k * p * (1 / r1 - 1 / r2)其中,V表示电势,k是比例常数(库仑常数),p是电偶极矩的大小,r1和r2分别表示电点距离两个电荷的距离。
在MATLAB中,我们可以使用上述公式编写一个函数来计算给定电偶极矩和位置的电势。
function V = calculate_potential(p, r1, r2)k = 9 * 10^9; % 常量 k,库仑常数V = k * p * (1 / r1 - 1 / r2);end3. 电场的计算电场是描述电荷对其他电荷施加力的物理量,它与电荷的分布和距离有关。
对于电偶极子,我们可以通过求解电势梯度来计算电场。
电势梯度公式如下:E = -grad(V)其中,E表示电场,grad表示梯度运算符,V表示电势。
在MATLAB中,我们可以使用symbolic toolbox来计算电势的梯度,并得到电场的方程。
syms x y zV = k * p * (1 / sqrt((x - x1)^2 + (y - y1)^2 + (z - z1)^2) - 1 / sqrt ((x - x2)^2 + (y - y2)^2 + (z - z2)^2));Ex = -diff(V, x);Ey= -diff(V, y);Ez = -diff(V, z);得到了电场的分量后,我们可以绘制3D图形来直观地显示电场的分布情况。
讲稿版利用Matlab模拟点电荷电场的分布

利用MATLAB 模拟点电荷电势的分布一、目的1.熟悉单个点电荷及一对点电荷的电势分布情况;2.学会使用MATLAB 进行数值计算,并绘出相应的图形;二、原理根据库仑定律:在真空中,两个静止点电荷之间的作用力与这两个电荷的电量乘积成正比,与它们之间距离的平方成反比,作用力的方向在两个电荷的连线上,两电荷同号为斥力,异号为吸引力,它们之间的力F 满足:R RQ Q k F 221=(式1) 由电场强度E 的定义可知:R RkQ E 2=(式2) 对于点电荷,根据场论基础中的定义,有势场E 的势函数为R kQ U =(式3) 在MATLAB 中,由以上公式算出各点的电势U ,可以用MATLAB 自带的库函数绘出相应的电势分布情况。
三、MATLAB 基本语法(一)标识符与数标识符是标志变量名、常量名、函数名和文件名的字符串的总称。
(二)矩阵及其元素的赋值赋值就是把数赋予代表常量或变量的标识符。
MATLAB 中的变量或常量都代表矩阵,标量应看作1×1价的矩阵。
赋值语句的一般形式为变量=表达式(或数)列如,输入语句a=[1 2 3;4 5 6;7 8 9]则显示结果为a=1 2 34 5 67 8 9输入 x=[1 2 3 4 5 6 7 8 9]结果为x= 1 2 3 4 5 6 7 8 9可以看出,矩阵的值放在方括号中,同一行中各元素之间以逗号或空格分开,不同行的元素以分号隔开。
语句的结尾可用回车或逗号“,”,此时会立即显示运算结果;如果不希望显示结果,就以分号“;”结尾再回车,此时运算仍然执行,只是不作显示。
变量的元素用圆括号“()”中的数字(也称为下标)来注明,一维矩阵(也称数组)中的元素用一个下标表示,二维矩阵可有两个下标数,以逗号分开。
在MATLAB中可以单独给元素赋值,例如,a(2,3)=6,x(2)=2等。
(三)元素群运算把n×m矩阵中的每个元素当作对象,成群地执行某种运算,称为元素群运算。
基于Matlab模拟点电荷电场线和等势线

基于Matlab模拟点电荷电场线和等势线1. 引言1.1 背景介绍电场理论是物理学中的重要概念,描述了在空间中存在的电荷所产生的相互作用力。
点电荷模型是电场研究中常用的简化模型,通过模拟点电荷的分布和运动,可以很好地描述电场的特性。
在现实生活中,我们经常会遇到点电荷电场的问题,比如电荷在空间中的分布及其对周围环境的影响。
基于Matlab的数值模拟方法可以帮助我们更好地理解电场的特性。
通过模拟点电荷的分布情况,我们可以绘制出电场线和等势线,从而直观地展示电场的分布情况和强度。
这不仅有助于理论研究,还可以在工程实践中提供重要参考。
通过基于Matlab的点电荷电场线和等势线模拟,我们可以更深入地探讨电场的性质,为相关领域的研究和应用提供支持和指导。
【字数:205】1.2 研究意义电场是物理学中非常重要的概念之一,它描述了空间中各点所受电荷作用力的性质。
而点电荷则是电荷密度在空间中极小的模型,通过研究点电荷的电场线和等势线的分布情况,可以帮助我们更好地理解电场的性质和规律。
基于Matlab进行点电荷电场线和等势线的模拟,不仅可以直观地展示电场和电势在空间中的分布情况,还可以通过调整参数来研究不同条件下电场和电势的变化规律。
研究点电荷电场线和等势线的分布对于学术研究和工程应用具有重要意义。
在学术研究方面,通过对电场线和等势线的模拟分析,可以深入探讨电场的特性和规律,进一步推动电磁学理论的发展。
在工程应用方面,电场线和等势线的模拟可以帮助工程师设计和优化电子元件、电路和传感器等设备,从而提高其性能和稳定性。
深入研究基于Matlab模拟点电荷电场线和等势线的方法和应用具有重要的理论和实际意义。
1.3 研究目的研究目的是在Matlab环境下通过模拟点电荷的电场线和等势线,深入探讨电荷在空间中产生的电场分布情况,以及不同点电荷配置对电场线和等势线的影响。
通过研究电场线和等势线的形态和分布规律,可以更好地理解电荷之间的作用关系,为进一步研究静电场提供依据。
用matlab数值分析报告电偶极子地等电势图和电场线图

合肥学院创新课程设计报告题目:用matlab分析电偶极子的等电势图和电场线系别:电子信息与电气工程系专业:通信工程专业班级: 14姓名:导师:成绩:2013 年《通信技术综合创新课程设计》任务书目录电偶极子的等电势图和电场 (5)一电偶极子原理以及相关知识 (5)1.1 电偶极子定义 (5)1.2 电偶极子原理 (6)二演示程序 (9)2.1电偶极子电势在matlab中的模拟 (9)2.2电偶极子电场在matlab中的模拟 (11)三结束语 (13)四参考文献 (13)电偶极子的等电势图和电场一电偶极子原理以及相关知识1.1 电偶极子定义一个实体,它在距离充分大于本身几何尺寸的一切点处产生的电场强度都和一对等值异号的分开的点电荷所产生的电场强度相同。
电偶极子(electric dipole)是两个相距很近的等量异号点电荷组成的系统。
电偶极子的特征用电偶极距P=lq描述,其中l是两点电荷之间的距离,l和P的方向规定由-q指向+q。
电偶极子在外电场中受力矩作用而旋转,使其电偶极矩转向外电场方向。
电偶极矩就是电偶极子在单位外电场下可能受到的最大力矩,故简称电矩。
如果外电场不均匀,除受力矩外,电偶极子还要受到平移作用。
电偶极子产生的电场是构成它的正、负点电荷产生的电场之和。
1.2 电偶极子原理两个点电荷q和-q间的距离为L。
此电偶极子在场点P 处产生的电位等于两个点电荷在该点的电位之和,即(1)图(1)表示中心位于坐标系原点上的一个电偶极子,它的轴线与Z轴重合,其中与分别是q和-q到P 点的距离。
图1 电偶极子一般情况下,我们关心的是电偶极子产生的远区场,即负偶极子到场点的距离r 远远大于偶极子长度L的情形,此时可以的到电偶极子的远区表达式(2)可见电偶极子的远区电位与成正比,与的平方成反比,并且和场点位置矢量与轴的夹角有关。
为了便于描述电偶极子,引入一个矢量P,摸P=q L,方向由-q指向q,称之为此电偶极子的电矩矢量,简称为偶极矩,记作P=q L (3)此时(2)式又可以写成(4)电偶极子的远区电场强度可由(4)式求梯度得到。
利用Matlab模拟点电荷的电场分布

实验一利用Matlab模拟点电荷的电场分布一、实验目的:1.熟悉点电荷的电场分布情况;2.学会使用Matlab绘图二、实验原理MATLAB输入命令的方式有两种,一种就是在命令窗口中直接输入简单的语句,这种方式适应于命令比较简单、且处理的问题没有普遍应用性、差错处理比较简单的场合。
但是在进行大量重复性的计算时,或者语句结构比较复杂需要进行流程控制时,这种方式就不够灵活。
出现了另一种输入命令的工作方式:M 文件的编程工作方式。
M文件是一个简单的文本文件,语法比一般的高级语言都简单,程序容易调试,交互性强;而且可以像一般文本文件那样在任何文本编辑器中进行编辑、存储、修改和读取(输入时用英文)。
这里用由MATLAB语句构成的程序文件(称作m文件,其扩展名为.m)进行编程设计。
MATLAB提供一个方便实用的M文件编辑器,利用它,用户可以完成程序的创建、编辑、调试、存储和运行等工作。
在MATLAB命令窗口中输入“edit”并回车,或者新建一个m-file文件,调出如下图所示的M文件编辑器(编辑窗口)。
MATLAB的一些通用和专用的函数文件说明:函数名称函数功能input m语言输入语句figure创建图形对象refresh刷新图形plot直角坐标系中绘图title标注图形名称xlabel X轴参量标注ylabel Y轴参量标注text在图形上标注文字注释grid在图形上加坐标网格subplot将图形窗口分为若干子图mesh3D网格图function m语言的函数文件sum求各列元素的和cross为两个矢量的矢量积(叉积)dot为两个矢量的数量积(点积)imag显示复数的虚部真空中点电荷的场强大小是:2r kqE =(式1) 其中k=9109⨯为静电力恒量,14k πε=,1910/036F m επ-=⨯,q 为点电荷的电量,r 为点电荷到场点P (x,y)的距离。
电场呈球对称分布。
取点电荷为正电荷,电力线是以电荷为起点的射线簇。
matlab电偶极子电场强度

电偶极子是指两个等量异种电荷分别位于坐标原点处的一对点电荷,它们之间的连接线称为电偶极子轴。
对于一个电偶极子,其电场强度在远场条件下可以由公式计算得到,该公式由Maxwell方程组推导得出。
一、电偶极子电场强度计算的基本原理电偶极子在空间中产生的电场是通过两个点电荷产生的电场叠加而成的,其中一个点电荷产生的电场由于另一个点电荷的作用会发生偏转,这种电场的叠加效应使得电偶极子在空间中产生了一个由正极向负极方向的电场。
二、电偶极子电场强度的计算公式电偶极子的电场强度可以通过以下公式来计算:\[ E = \frac{1}{4 \pi \varepsilon_0} \times (\frac{\bold {p}}{r^3} -\frac{3(\bold{p} \cdot \bold{r})\bold{r}}{r^5}) \]其中,E为电场强度,\( \varepsilon_0 \)为真空介电常数,p为电偶极子矩量,r为观察点到电偶极子的距离,其方向指向观察点。
该公式通过叠加电偶极子两个点电荷产生的电场得到,是对远场电场的精确描述。
三、matlab中的电偶极子电场强度计算在matlab中,可以借助向量和矩阵的计算功能来对电偶极子的电场强度进行计算。
可以将电偶极子的坐标表示为一个矩阵,然后求解每个观察点到电偶极子的距离向量,进而利用上述公式计算出每个观察点的电场强度。
在matlab中,通过简洁的代码和函数封装,可以高效地完成电偶极子电场强度的计算和可视化。
四、实际应用中的电偶极子电场强度计算电偶极子电场强度的计算在实际中有许多重要的应用,比如在天体物理学中,可以利用电偶极子模型来描述电离气体星的电场分布;在生物物理学中,可以利用电偶极子模型来模拟细胞膜的离子传输过程。
利用电偶极子电场强度计算模型,可以帮助科研人员更好地理解和解释实验现象,指导实验设计和数据分析。
五、总结电偶极子电场强度的计算是电磁学领域中的重要问题,在理论和实际应用中都有着重要的价值。
matlab点电荷的电势和电场解析式

matlab点电荷的电势和电场解析式
一、引言
在电磁学中,点电荷的电势和电场分析是基础内容。
Matlab作为一种数学计算工具,可以方便地帮助我们求解这些问题。
本文将介绍如何利用Matlab求解点电荷的电势和电场,以及它们之间的关系。
二、Matlab中点电荷电势的解析式
1.点电荷电势公式
点电荷电势公式为:
φ= k * Q / r
其中,φ表示电势,k为库仑常数,Q为电荷量,r为距离点电荷的距离。
2.Matlab代码实现
```Matlab
clear;
phi = 1/4 * pi * epsilon_0 * Q / r;
```
三、Matlab中点电荷电场的解析式
1.点电荷电场公式
点电荷电场公式为:
E = k * Q / r^2
其中,E表示电场强度,k为库仑常数,Q为电荷量,r为距离点电荷的距离。
2.Matlab代码实现
```Matlab
clear;
E = k * Q / (r.^2);
```
四、点电荷电势和电场的关系
电势是描述电场在空间中的分布情况,而电场强度则表示单位正电荷所受到的力。
点电荷的电势和电场强度之间的关系为:
φ= - gradient(E)
即电势是电场强度的负梯度。
五、结论
通过Matlab编程,我们可以方便地求解点电荷的电势和电场。
掌握这些解析式,有助于我们在实际问题中分析电场分布和电势变化,为后续的电磁学学习打下基础。
用matlab数值分析电偶极子的等电势图和电场线图(已运行可行)

等势线 பைடு நூலகம்.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-0.5
0
0.5
电场线 0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8 -0.5
0
0.5
subplot(1,2,1) contour(x,y,phi,CV);%画电势图 hold on %在原图像上作图 plot([-h:0.01:h],0,'r-');%作出 x 轴 hold off%取消保持图像 axis([-h h -h h]);title('等势线');
subplot(1,2,2) quiver(x,y,Ex,Ey,'k');%用箭头作出电场线图 hold on %在原图像上作图 plot([-h:0.01:h],0,'r-');%作出 x 轴 hold off%取消保持图像 axis([-h h -h h]);title('电场线');
以下是你的课程论文题目: 用数值计算的方法研究三维空间中电偶极子的电场以及电势的分布。
Matlab 程序:
k=1;q=1;d=0.01;h=0.8; [x,y]=meshgrid([-h:0.1:h]);%建立二维网格 r2=sqrt((x-d/2).^2+y.^2+0.001);r1=sqrt((x+d/2).^2+y.^2+0.001); phi=k*q*(1./r2-1./r1);%电势计算公式 [Ex,Ey]=gradient(-phi);%求电势 phi 对 x 和 y 的梯度 AE=sqrt(Ex.^2+Ey.^2);Ex=Ex./ AE; Ey=Ey./ AE;% 场强归一化,使箭头等长 CV=linspace(min(min(phi)),max(max(phi)),49);%产生 49 个电位值
基于Matlab模拟点电荷电场线和等势线

基于Matlab模拟点电荷电场线和等势线电场线和等势线是理解电场分布的一个重要工具。
在Matlab中,我们可以使用特定的函数和工具箱来模拟和绘制电场线和等势线。
要模拟电场线和等势线,首先需要定义电场中的点电荷和电荷的分布。
对于一个点电荷,在Matlab中可以使用"charge()"函数定义其位置和大小。
例如,我们可以定义一个正电荷位于(0,0)处,并设置其电荷量为1:charge([0 0],1)对于分布在空间中的多个电荷,可以使用矢量或矩阵来存储其位置和大小。
例如,我们定义了三个电荷,分别位于(-1,0)、(1,0)和(0,1),且其电荷量依次为1、2、3:pos=[-1 0;1 0;0 1];charge=[1 2 3];charge(pos,charge)定义好电荷后,就可以计算电场线和等势线的分布。
在Matlab中,可以使用"streamline()"函数和"contour()"函数来分别计算和绘制电场线和等势线。
[X,Y]=meshgrid(-2:.2:2,-2:.2:2); %定义网格点Ex=@(x,y)x./((x+1).^2+y^2).^(1/2)-x./((x-1).^2+y^2).^(1/2); %定义库仑电场x方向分量Ey=@(x,y)y./((x+1).^2+y^2).^(1/2)-y./((x-1).^2+y^2).^(1/2); %定义库仑电场y方向分量startx=[0]; %定义起始点x坐标starty=[0]; %定义起始点y坐标streamline(X,Y,Ex,Ey,startx,starty);对于等势线的绘制,可以使用"contour()"函数。
该函数需要定义等势线函数(在这里,我们使用库仑势能定义等势线)和不同等势线对应的值。
例如,我们定义一个库仑势能,由两个位于(-1,0)和(1,0)的单位电荷产生:V=@(x,y)1./((x+1).^2+y^2).^(1/2)+1./((x-1).^2+y^2).^(1/2); %定义库仑势能 contour(X,Y,V([-5:.5:5; -5:.5:5])) %绘制等高线此外,我们还可以使用"quiver()"函数来绘制电场的矢量图,以更直观地展示电场的分布情况。
5用matlab解决电磁学中的电场问题.

用MATLAB解决电磁学中电场问题摘要:二十一世纪以来,随着计算机技术的进一步提高以及电脑在国内的普遍使用,在很多教学领域运用计算机软件来辅助教学已经非常普遍,然而用电脑软件处理仿真电学及电磁学中电场及电势的研究却并不常见。
在进行电场及电势问题的研究时,电场虽然是确实存在的,但是由于其抽象而不易被理解,而且即使在实验室中,我们也很难实现其理想化模型。
这样就使得教师在教学过程中不能生动且直观的描述出来,学生在学习过程中也将很难理解和接受。
本文利用计算机数学软件MATLAB模拟仿真真空中自由电荷,电偶极子,带电细棒,尖端导体等附近静电场电场线及等势线分布图型,从而使其更加形象,生动,直观,更加便于学生学习,理解和接受,同时使的教师教学更加方便,快捷。
关键字:MATLAB软件,静电场,尖端导体,尖端效应,电场强度,电势。
目录1 引言 (1)2用MATLAB处理静电场中的电场线和等势线的问题 (1)2.1用MATLAB模拟仿真真空中点电荷的电场线和等势线分布 (1)2.2用MATLAB模拟仿真真空两个点电荷的电场线及等势线分布 (3)2.2.1用MATLAB模拟真空中两个同种点电荷的电场线及等势线分布 (3)2.2.2用MATLAB模拟真空中两个同号但不等量点电荷的电场线和电势分布..5 2.2.3用MATLAB模拟电偶极子的电场线及等势线分布 (6)3用MATLAB模拟均匀带电细棒的电和分布情况 (8)4用MATLAB模拟两个无限长导线的电位和电场分布 (9)5尖端导体附近的电场及电势特点及其应用 (11)5.1电场函数 (11)6总结 (13)7参考文献 (14)1引言:二十一世纪以来,随着计算机技术的进一步提高以及电脑在国内的普遍使用,在很多教学领域运用计算机软件来辅助教学已经非常普遍,然而用电脑软件处理仿真电学及电磁学中电场及电势的研究却并不常见。
我们在研究电磁学中的电场问题时,通常将自由电荷看作一个理想化的模型。
MATLAB静电场电场电势

问题引入
静电场中的电场线,等势线,等势面等图形是一种 抽象的模型,在现实世界不具可视化的空间场的物 体。所以,形象的模拟出以上问题的图形,对于更 进一步学习与研究电场知识有很大的意义。 静电场的问题学习与理解起来具有一定的特殊性: 它既有理论数值的计算,又有图形图像的辅助处理 与理解。例如:形象的模拟出电场线,等势线,等 势面,这能在教学中解决教师的授课难题,又能解 决学生的理解上的困难。 近年来,一直有人在不断的探索这方面的问题,并 且取得一定的成绩。但还存在一定的缺陷,而 Matlab恰好解决了这些问题!这使得这些抽象问题 能有一门精确的工具软件来处理完成。这正是 Matlab在图像方面问题处理的应用。
第20页/共21页
2021/3/31
感谢您的欣赏!
第21页/共21页
第6页/共21页
2 1.5
1 0.5
0 -0.5
-1 -1.5
-2 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
第7页/共21页
结论: 可以清楚的看出同号电荷 相互排斥的现象,各电荷 的等势线呈圈状围在电荷 周围,且越靠近电荷电场 线分布越密集
第8页/共21页
问题二:等量异种电荷的电势,电场的分布
0
0.5
1
1.5
2
第13页/共21页
问题三 :带电粒子在电磁场中的运动
投稿 电偶极子和电四极子电场的计算机模拟

电偶极子和电四极子电场的计算机模拟王明美1(合肥师范学院电子信息工程学院,安徽,合肥,230601)摘要:使用MATLAB 对由电偶极子和电四极子的电场强度和电势进行数值计算,给出其分布,并绘制出相应电场线和等势线的图形。
关键词:电学系统,电场线,等势面,MATLAB 绘图MATLAB 在大学物理中具有广泛的应用[1]-[7],本文使用MATLAB 对电偶极子和电四极子电场进行模拟,图像比较清晰,程序相对简单且适于推广。
1.电偶极子的电场和电势对于两个点电荷系统,设两个点电荷相距为a ,所带电量分别为1q 和2q 。
由电场强度的叠加原理可知:22221211r r e r q k e r q k E += (1) 有势场E 的势函数为 2211r kq r kq U += (2) 而 gradU E -= (3)为了便于数值计算,电势可化为*0U U =, (4)其中,x* = x/a ,y* = y/a ,U0 = kQ1/a ,q* = q 2/q 1。
U 0是q 1在原点产生的电势,21/q q q =*是电荷比。
场强可表示为*0(/)x U U U E x a x a ∂∂=-=-∂∂,即*0*x U E E x ∂=-∂, (5) 其中,E 0 = U 0/a ,U * = U/U 0。
同理可得*0*y U E E y ∂=-∂, (6)电场强度可通过约化电势计算。
电场线可根据电场强度绘制。
电场线从正电荷发出,当电场线的起点离电荷很近时,可认为起点绕电荷是均匀分布的。
1王明美(1956-),女,江苏省南京市人,合肥师范学院电子信息工程学院副教授,主要从事普通物理、近代物理和计算物理的教学和研究[基金项目] 基于稀疏随机采样技术的天线近远场快速测试算法研究,国家自然科学基金,基金号:51207041;合肥师范学院质量工程项目教学示范课程“大学物理”(2011jxsf05)在MATLAB中,仍然可以由以上公式算出各点的电势U,电场强度E后,再用MATLAB的库函数绘制出相应的电场线和等势线的分布情况。
课程设计用MATLAB模拟偶极子的电场分布

燕山大学课程设计说明书题用MATLAB模拟偶极子的电场分布学院(系):年级专业:学号:学生姓名:指导教师:教师职称:燕山大学课程设计(论文)任务书说明:此表一式四份,学生、指导教师、基层教学单位、系部各一份。
年月日燕山大学课程设计评审意见表指导教师评语:成绩:指导教师:年月日答辩小组评语:成绩:组长:年月日课程设计总成绩:答辩小组成员签字:用MATLAB 模拟偶极子的电场分布Simulateing the electric field distribution of dipole with MATLAB摘要:分析偶极子产生的电场,对于研究介质的极化;介质中的场以及电磁波的辐射等具有重要作用。
关于电偶极子的电场分布,本文介绍了电偶极子在空间任意一点激发的电场的计算公式,并用MATLAB 模拟出电偶极子的场分布图形,同时给出了图形以供参考关键词: 电偶极子,电场强度, 电势,梯度Abstract :The analysis dipole produces field,regarding research mediumpolarization;In the medium field as well as the electromagnetic waveradiation and so o n has the vital role ;About the electric dipole electric fielddistribution,this article introduce s the electric dipole in the spatial randomstimulation electric fieldformula,and simulate s the electric dipole withMATLABthefielddistribution graph, simultaneou sly gives some graphs tosupply the reference.Keywords : Electric dipole, electric -field intensity, electric potential, gradient,一.设计目的用MATLAB 实现模拟电偶极子周围场分布,以实现物理模型的可视化。
电偶极子电势电场matlab模拟

汇报型介绍
MATLAB模拟方法
电偶极子电势电场 模拟
模拟结果的可视化
模拟结果的物理意 义和实际应用
添加章节标题
电偶极子模型介绍
电偶极子是由两个相距一定距离的 等量异号点电荷组成的系统
电偶极子的电势呈二次函数关系, 且在无穷远处为零
电势分布规律:在电 偶极子附近,电势变 化剧烈,远离电偶极 子后,电势变化逐渐 趋缓
MATLAB模拟方法
M AT L A B 是 一 种 用于数值计算 的编程语言和
开发环境
它提供了大量 的内置函数和 工具箱,可用 于各种科学计 算和工程领域
M AT L A B 具 有 强 大的可视化功 能,可以绘制 各种图形和图
网格划分:将计 算区域划分为一 系列小的网格, 每个网格中心设 置一个节点
有限差分法:利 用差分近似代替 微分,将微分方 程转化为差分方 程进行求解
迭代法:通过迭 代的方式逐步逼 近真实解,直到 满足一定的精度 要求
电场分布:在电 偶极子周围,电 场线呈辐射状, 电场强度随着距 离的增加而减小
电势分布:在电 偶极子周围,电 势呈椭圆形分布, 随着距离的增加, 电势变化逐渐趋 缓
离散化:将连 续问题离散化, 将连续的物理 量转化为离散
的数值
迭代法:通过 不断迭代求解 方程组,得到
数值解
矩阵运算:利 用矩阵运算进 行数值计算, 如线性代数、
微积分等
插值和拟合: 通过插值和拟 合方法,对数 据进行处理和 拟合,得到更 精确的数值解
电偶极子电势电场 模拟
电偶极子的定义:由两个等量异号电荷组成的系统
特点:MATLAB的可视化工具箱具有多种可视化工具,如散点图、线图、曲面图、等高线图等,可以满足各种数 据可视化需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用matlab 绘制电偶极子在3维空间电势、电场的分布 电偶极子(electric dipole )是两个相距很近的等量异号点电荷组成的系统,具体模型如图1所示,两点电荷+q 和-q 相距为d ,且r >>d 。
本文主要对电偶极子在空间中产生的电势,电场分布进行计算机模拟。
图1 电偶极子 1 电偶极子的电势、电场计算
应用叠加原理,得场中任意点P 的点位为
012114q φπεr r ⎛⎫=- ⎪⎝⎭
应用关系式=-E φ∇,可以求得位于原点的电偶极子在离它r 远处产生的电场强度。
2 电偶极子电势、电场分布在matlab 中的模拟
电势分布模拟,源程序如下:
q=1;
d=2;
e0=8.854187817*10.^-12;
x=-3:0.1:3;
y=-3:0.1:3;
[x,y]=meshgrid(x,y);
z=q.*(1./sqrt((y-1).^2+x.^2)-1./sqrt((y+1).^2+x.^2))./(4*pi*e0);
mesh(x,y,z);
运行结果如下:
电场分布,源程序如下:
q=1;
d=2;
e0=8.854187817*10.^-12;
x=-3:0.1:3;
y=-3:0.1:3;
[x,y]=meshgrid(x,y);
z=q.*(1./sqrt((y-1).^2+x.^2+0.01)-1./sqrt((y+1).^2+x.^2+0.01))./(4*pi*e0); contour(x,y,z);
[px,py]=gradient(z);
hold on
streamslice(x,y,px,py,'k')
运行结果如下:。
