匈牙利算法
最大化指派问题匈牙利算法

最大化指派问题匈牙利算法匈牙利算法,也称为Kuhn-Munkres算法,是用于解决最大化指派问题(Maximum Bipartite Matching Problem)的经典算法。
最大化指派问题是在一个二分图中,找到一个匹配(即边的集合),使得匹配的边权重之和最大。
下面我将从多个角度全面地介绍匈牙利算法。
1. 算法原理:匈牙利算法基于增广路径的思想,通过不断寻找增广路径来逐步扩展匹配集合,直到无法找到增广路径为止。
算法的基本步骤如下:初始化,将所有顶点的标记值设为0,将匹配集合初始化为空。
寻找增广路径,从未匹配的顶点开始,依次尝试匹配与其相邻的未匹配顶点。
如果找到增广路径,则更新匹配集合;如果无法找到增广路径,则进行下一步。
修改标记值,如果无法找到增广路径,则通过修改标记值的方式,使得下次寻找增广路径时能够扩大匹配集合。
重复步骤2和步骤3,直到无法找到增广路径为止。
2. 算法优势:匈牙利算法具有以下优势:时间复杂度较低,匈牙利算法的时间复杂度为O(V^3),其中V是顶点的数量。
相比于其他解决最大化指派问题的算法,如线性规划算法,匈牙利算法具有更低的时间复杂度。
可以处理大规模问题,由于时间复杂度较低,匈牙利算法可以处理大规模的最大化指派问题,而不会因为问题规模的增加而导致计算时间大幅增加。
3. 算法应用:匈牙利算法在实际中有广泛的应用,例如:任务分配,在人力资源管理中,可以使用匈牙利算法将任务分配给员工,使得任务与员工之间的匹配最优。
项目分配,在项目管理中,可以使用匈牙利算法将项目分配给团队成员,以最大程度地提高团队成员与项目之间的匹配度。
资源调度,在物流调度中,可以使用匈牙利算法将货物分配给合适的运输车辆,使得货物与运输车辆之间的匹配最优。
4. 算法扩展:匈牙利算法也可以扩展到解决带权的最大化指派问题,即在二分图的边上赋予权重。
在这种情况下,匈牙利算法会寻找一个最优的匹配,使得匹配边的权重之和最大。
运筹学匈牙利法

运筹学匈牙利法运筹学匈牙利法(Hungarian Algorithm),也叫匈牙利算法,是解决二部图最大(小)权完美匹配(也称作二分图最大权匹配、二分图最小点覆盖)问题的经典算法,是由匈牙利数学家Kuhn和Harold W. Kuhn发明的,属于贪心算法的一种。
问题描述在一个二分图中,每个节点分别属于两个特定集合。
找到一种匹配,使得所有内部的节点对都有连边,并且找到一种匹配方案,使得该方案的边权和最大。
应用场景匈牙利算法的应用场景较为广泛,比如在生产调度、货车调度、学生对导师的指定、电影的推荐等领域内,都有广泛的应用。
算法流程匈牙利算法的伪代码描述如下:进行循环ɑ、选择一点未匹配的点a作为起点,它在二分图的左边β、找出a所有未匹配的点作为下一层节点ɣ、对下一层的每个节点,如果它在右边未匹配,直接匹配ɛ、如果遇到一个已经匹配的节点,进入下一圈,考虑和它匹配的情况δ、对已经匹配的点,将它已经匹配的点拿出来,作为下一层节点,标记这个点作为已被搜索过ε、将这个点作为当前层的虚拟点,没人配它,看能否为它找到和它匹配的点ζ、如果能匹配到它的伴侣,令它们成对被匹配最后输出最大权匹配。
算法优缺点优点:相比于暴力求解二分图最大权匹配来说,匈牙利算法具有优秀的解决效率和高效的时间复杂度,可以在多项式时间(O(n^3))内解决二分图最大权匹配问题。
缺点:当二分图较大时,匈牙利算法还是有很大的计算复杂度,复杂度不佳,算法有效性差。
此时就需要改进算法或者使用其他算法。
总结匈牙利算法是一个常见的解决二分图最大权匹配问题的算法,由于其简洁、易用、效率优秀等特性,广泛应用于学术和实际问题中。
匈牙利算法虽然在处理较大规模问题时效率不佳,但仍然是一种值得掌握的经典算法。
匈牙利算法离散数学

匈牙利算法离散数学
匈牙利算法是一种用于解决二分图最大匹配问题的算法,属于离散数学中图论的内容。
在二分图中,顶点集被分为左右两个部分,边连接两个部分的顶点。
最大匹配问题就是要找到一种最大的匹配方案,使得尽可能多的顶点能够被匹配。
匈牙利算法的基本思想是通过寻找增广路径来不断增加匹配的顶点数。
增广路径是指从左边的未匹配顶点出发,交替经过未匹配边和已匹配边,最终到达右边的未匹配顶点的路径。
通过不断寻找增广路径,并将路径上的边进行匹配和取消匹配,最终可以得到一个最大匹配。
具体实现时,匈牙利算法采用了深度优先搜索的方式来寻找增广路径。
首先从左边的每个未匹配顶点出发,依次进行深度优先搜索,尝试与右边的未匹配顶点进行匹配。
如果找到了增广路径,则将路径上的边进行匹配和取消匹配,继续寻找下一个增广路径。
如果无法找到增广路径,则返回当前匹配的顶点数,即为最大匹配数。
匈牙利算法的时间复杂度为O(VE),其中V是顶点数,E是边数。
通
过优化算法,如路径压缩和交替路径优化,可以进一步提高算法的效率。
匈牙利算法在实际应用中有广泛的应用,比如在求解任务分配问题、
婚姻匹配问题等方面都可以使用。
其应用领域还包括网络流问题、图像处理、人工智能等。
总之,匈牙利算法是离散数学中图论领域一个重要的算法,用于解决二分图最大匹配问题。
其基本思想是通过寻找增广路径来不断增加匹配的顶点数,从而得到一个最大匹配。
通过优化算法,可以提高算法的效率。
该算法在实际应用中有广泛的应用。
匈牙利算法
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,并推动了后来的原始对偶方法。
美国数学家哈罗德·库恩于1955年提出该算法。
此算法之所以被称作匈牙利算法,是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法。
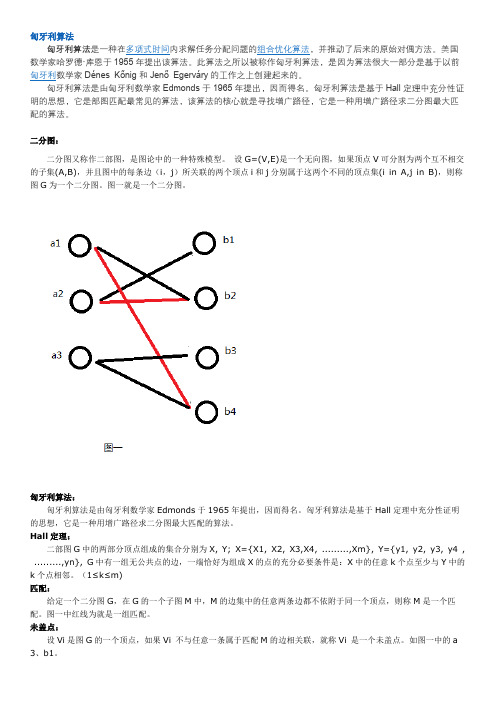
二分图:二分图又称作二部图,是图论中的一种特殊模型。
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
图一就是一个二分图。
匈牙利算法:匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想,它是一种用增广路径求二分图最大匹配的算法。
Hall定理:二部图G中的两部分顶点组成的集合分别为X, Y; X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn}, G中有一组无公共点的边,一端恰好为组成X的点的充分必要条件是:X中的任意k个点至少与Y中的k个点相邻。
(1≤k≤m)匹配:给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
图一中红线为就是一组匹配。
未盖点:设Vi是图G的一个顶点,如果Vi 不与任意一条属于匹配M的边相关联,就称Vi 是一个未盖点。
如图一中的a 3、b1。
设P是图G的一条路,如果P的任意两条相邻的边一定是一条属于M而另一条不属于M,就称P是一条交错路。
匈牙利算法

匈牙利算法是一种组合优化算法,用于解决多项式时间内的任务分配问题,并推广了后来的原始对偶方法。
美国数学家Harold Kuhn在1955年提出了该算法。
之所以将该算法称为匈牙利算法,是因为该算法的很大一部分是基于匈牙利数学家DénesKőnig和JenőEgerv áry的先前工作。
匈牙利算法是一种组合优化算法,用于解决多项式时间内的任务分配问题,并推广了后来的原始对偶方法。
美国数学家Harold Kuhn在1955年提出了该算法。
之所以将该算法称为匈牙利算法,是因为该算法的很大一部分是基于匈牙利数学家DénesKőnig和JenőEgerv áry的先前工作。
众所周知,匈牙利是一个国家的名称,与算法的发明者有关。
匈牙利算法的发明者埃德蒙兹(Edmonds)于1965年提出了匈牙利算法。
我不知道为什么匈牙利算法的发明者是匈牙利算法,而且我从未见过其他以国家命名的算法。
是因为匈牙利人提出的算法太少了吗?
匈牙利算法的核心原理非常简单,即找到增强路径以实现最大匹配。
我们将匈牙利算法与Gale-Shapley算法的原理进行了比较,您发现了什么?实际上,这两种算法的核心原理是相同的。
在GS算法中,我们首先开始追求男孩,并尽可能地进行匹配。
然后,单身男孩一次又一次地认罪,如果有更好的比赛,以前的比赛将被打破。
在稳定婚
姻的问题中,我们定义了匹配的质量,而在本地二分匹配的问题中,匹配既不是好事也不是坏事。
如果我们抛开匹配的好坏,而把高品质男生抓住劣等男生的过程当作匹配调整的过程,那么这两种算法的核心几乎是相同的。
匈牙利算法——精选推荐

匈⽛利算法0 - 相关概念0.1 - 匈⽛利算法 匈⽛利算法是由匈⽛利数学家Edmonds于1965年提出,因⽽得名。
匈⽛利算法是基于Hall定理中充分性证明的思想,它是⼆部图匹配最常见的算法,该算法的核⼼就是寻找增⼴路径,它是⼀种⽤增⼴路径求⼆分图最⼤匹配的算法。
0.2 - ⼆分图 若图G的结点集合V(G)可以分成两个⾮空⼦集V1和V2,并且图G的任意边xy关联的两个结点x和y分别属于这两个⼦集,则G是⼆分图。
1 - 基本思想1. 找到当前结点a可以匹配的对象A,若该对象A已被匹配,则转⼊第3步,否则转⼊第2步2. 将该对象A的匹配对象记为当前对象a,转⼊第6步3. 寻找该对象A已经匹配的对象b,寻求其b是否可以匹配另外的对象B,如果可以,转⼊第4步,否则,转⼊第5步4. 将匹配对象b更新为另⼀个对象B,将对象A的匹配对象更新为a,转⼊第6步5. 结点a寻求下⼀个可以匹配的对象,如果存在,则转⼊第1步,否则说明当前结点a没有可以匹配的对象,转⼊第6步6. 转⼊下⼀结点再转⼊第1步2 - 样例解析 上⾯的基本思想看完肯定⼀头雾⽔(很⼤程度是受限于我的表达能⼒),下⾯通过来就匈⽛利算法做⼀个详细的样例解析。
2.1 - 题⽬⼤意 农场主John有N头奶⽜和M个畜栏,每⼀头奶⽜需要在特定的畜栏才能产奶。
第⼀⾏给出N和M,接下来N⾏每⾏代表对应编号的奶⽜,每⾏的第⼀个数值T表⽰该奶⽜可以在多少个畜栏产奶,⽽后的T个数值为对应畜栏的编号,最后输出⼀⾏,表⽰最多可以让多少头奶⽜产奶。
2.1 - 输⼊样例5522532342153125122.2 - 匈⽛利算法解题思路2.2.1 - 构造⼆分图 根据输⼊样例构造如下⼆分图,蓝⾊结点表⽰奶⽜,黄⾊结点表⽰畜栏,连线表⽰对应奶⽜能在对应畜栏产奶。
2.2.2 - 模拟算法流程为结点1(奶⽜)分配畜栏,分配畜栏2(如图(a)加粗红边所⽰)为结点2(奶⽜)分配畜栏,由于畜栏2已经被分配给结点1(奶⽜),所以寻求结点1(奶⽜)是否能够分配别的畜栏,以把畜栏2腾给结点2(奶⽜)。
数学建模匈牙利算法

数学建模匈牙利算法
【最新版】
目录
一、匈牙利算法的概念与基本原理
二、匈牙利算法的应用实例
三、匈牙利算法的优缺点
正文
一、匈牙利算法的概念与基本原理
匈牙利算法(Hungarian algorithm)是一种求解二分图最大匹配问题的算法,由匈牙利数学家 Mátyásovszky 于 1937 年首次提出。
该算法的基本思想是:通过不断循环寻找图中的偶数长度路径,并将路径中的顶点依次匹配,直到找不到这样的路径为止。
此时,图中的所有顶点都已匹配,即得到了二分图的最大匹配。
二、匈牙利算法的应用实例
匈牙利算法广泛应用于任务分配、资源调度、数据融合等领域。
下面举一个简单的例子来说明匈牙利算法的应用。
假设有 5 个工人和 8 个任务,每个工人完成不同任务的效率不同。
我们需要为每个任务分配一个工人,使得总效率最大。
可以用一个二分图来表示这个问题,其中顶点分为两类:工人和任务。
边表示任务与工人之间的效率关系。
匈牙利算法可以用来求解这个问题,找到最优的任务分配方案。
三、匈牙利算法的优缺点
匈牙利算法的优点是简单、高效,可以解决二分图的最大匹配问题。
然而,它也存在一些缺点:
1.匈牙利算法只能解决无向图的匹配问题,对于有向图,需要将其转
换为无向图才能使用匈牙利算法。
2.当图中存在环时,匈牙利算法无法找到最大匹配。
这时需要使用其他算法,如 Euclidean algorithm(欧几里得算法)来解决。
3.匈牙利算法在实际应用中可能存在数值稳定性问题,即在计算过程中可能出现精度误差。
匈牙利算法求解原理的应用

匈牙利算法求解原理的应用什么是匈牙利算法匈牙利算法是一种用于解决二分图最大匹配问题的算法。
所谓二分图,就是一个节点集合可以分为两个不相交的子集,而且每个子集内的节点之间不存在边。
在二分图中,最大匹配问题就是寻找最大的边集合,使得每个节点都和边集合中的某条边相邻接。
匈牙利算法的原理是通过增广路径的方法来求解最大匹配问题。
其中增广路径是指在匹配图中的一条未被匹配的边交替经过未被匹配的节点,最终到达另一个未被匹配的节点的路径。
匈牙利算法的应用匈牙利算法有许多实际应用场景。
以下列举了一些典型的应用案例:1.婚姻匹配问题:假设有n个男人和n个女人,每个人都有一个倾向表,表明他们对各种婚姻选择的偏好程度。
那么如何进行匹配,使得每个人都得到一个满意度最高的选择,同时保证没有不合适的匹配?这就可以使用匈牙利算法进行求解。
2.任务分配问题:假设有m个任务和n个工人,每个任务对于每个工人都有不同的技能要求和报酬。
如何将任务分配给工人,使得任务总报酬最大化,并满足每个任务的要求?这也可以使用匈牙利算法进行求解。
3.运输问题:在某个地区有n个供应点和n个需求点,以及不同供应点到需求点之间的运输成本。
那么如何选择合适的运输方案,使得总运输成本最小?同样可以使用匈牙利算法进行求解。
4.社交网络匹配问题:在一个社交网络中,每个人都有一定的朋友圈和交往偏好。
如何将这些人进行匹配,使得每个人都能够找到最适合的交往对象?匈牙利算法也可以应用于这种情况。
匈牙利算法的实现步骤下面是匈牙利算法的具体实现步骤:1.在匹配图中选择一个未匹配的顶点作为起始点,并为其标记为已访问。
2.对于当前顶点的每一个邻接顶点,如果该邻接顶点未被匹配,则找到一条增广路径。
如果该邻接顶点已被匹配,但可以通过其他路径找到一条增广路径,则将该邻接顶点的匹配权转移到当前顶点的匹配边上。
3.继续选择下一个未匹配的顶点,重复步骤2,直到无法找到增广路径为止。
4.返回当前匹配图的最大匹配。
匈牙利算法

匈牙利算法是一种组合优化算法,可以在多项式时间内解决任务分配问题,并在以后推广原始的对偶方法。
美国数学家哈罗德·库恩(Harold Kuhn)在1955年提出了该算法。
该算法之所以称为匈牙利算法,是因为它很大程度上是基于前匈牙利数学家Denes K nig和Jen Egervary的工作。
假设它是无向图。
如果顶点集V可以分为两个不相交的子集,则在该子集中选择具有最大边数的子集称为图的最大匹配问题。
如果存在匹配项和匹配项数,则该匹配项称为完美匹配项,也称为完全匹配项。
称为完美匹配时的特殊。
在介绍匈牙利算法之前,只有几个概念,M是G的匹配项。
如果,则边缘已经在匹配的M上。
M交错的路径:P是G的路径。
如果P中的边是属于M的边和不属于M而是属于G的边交替,则称P为M交错的路。
如:路径,。
M饱和点:例如,如果V与M中的边关联,则V为m饱和点;否则,V为非M饱和点。
例如,它们都属于M饱和点,而其他所有点都属于非M饱和点。
M扩展路径:P是M交错的路径。
如果P的起点和终点均为非M饱和点,则P称为m增强路径。
例如(不要与流网络中的增强路径混淆)。
寻找最多匹配项的一种明显算法是找到所有匹配项,然后保留最多匹配项。
但是该算法的时间复杂度是边数的指数函数。
因此,我们需要找到一种更有效的算法。
下面介绍使用增强路径查找最大匹配的方法(称为匈牙利算法,由匈牙利数学家爱德蒙兹(Edmonds)于1965年提出)。
增强轨道(也称为增强轨道或交错轨道)的定义:如果P是连接图G中两个不匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配)在P上交替,则称P为扩充路径相对于M从增强路径的定义可以得出以下三个结论:(1)到P的路径数必须是奇数,并且第一个边缘和最后一个边缘都不属于M。
(2)通过将M和P取反可以获得更大的匹配度。
(3)当且仅当没有M的增加路径时,M是G的最大匹配。
算法简介:(1)令M为空(2)通过异或运算找到增强路径P并获得更大的匹配项而不是M(3)重复(2),直到找不到扩展路径。
匈牙利算法基本原理

匈牙利算法基本原理匈牙利算法是解决二分图最大匹配问题的一种经典算法。
该算法由匈牙利数学家Egerváry Jenő于1930年代初发现,后来由匈牙利的两位数学家Dénes Kőnig和Jenő Egerváry进行深入研究和推广,因此得名为匈牙利算法。
二分图是指图的所有顶点可以被分为两个不相交的集合,并且图的所有边连接两个集合中的顶点。
最大匹配问题是在二分图中寻找最大的边集合,使得任意两条边的顶点不相交。
1.初始化:首先,我们需要给定一个二分图,以及两个空的顶点集合U和V,分别用来存储左侧和右侧顶点的匹配状态,初始时,所有顶点均未匹配。
2.寻找增广路径:从左侧的一个未匹配顶点开始,按照深度优先(DFS)的方式,递归地寻找可能的增广路径(即一条由未匹配顶点和已匹配顶点交替组成的路径,路径的首尾顶点未匹配)。
如果找到了增广路径,则将路径上的顶点进行匹配或取消匹配。
如果无法找到增广路径,则转到第3步。
3.寻找增广轨:如果在第2步中无法找到增广路径,则可以说明当前的匹配是最大匹配,因此算法结束。
否则,我们需要进行增广轨的寻找。
-将所有的顶点标记为未访问状态。
-从左侧的任意一个未匹配顶点开始,按照广度优先(BFS)的方式,寻找增广轨。
如果找到了增广轨,则将轨上的顶点进行匹配或取消匹配,并结束算法。
否则,继续遍历直到左侧所有未匹配顶点都被访问过。
总结起来,匈牙利算法是一种解决二分图最大匹配问题的经典算法,通过交替路径的增广来不断更新匹配状态,直到达到最大匹配。
它可以通过深度优先和广度优先的方式来寻找增广路径和增广轨,时间复杂度为O(V*E)。
匈牙利算法在实际问题中有着广泛的应用和研究。
匈牙利算法

匈牙利算法:匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,并推动了后来的原始对偶方法。
美国数学家哈罗德·库恩于1955年提出该算法。
此算法之所以被称作匈牙利算法,是因为算法很大一部分是基于以前匈牙利数学家DénesKőnig和JenőEgerváry 的工作之上创建起来的。
设G=(V,E)是一个无向图。
如顶点集V可分割为两个互不相交的子集V1,V2,选择这样的子集中边数最大的子集称为图的最大匹配问题(maximalmatchingproblem)。
果一个匹配中,|V1|≤|V2|且匹配数|M|=|V1|,则称此匹配为完全匹配,也称作完备匹配。
特别的当|V1|=|V2|称为完美匹配。
作用:解决指派问题。
所谓的指派问题就比如:甲乙丙三个人去做ABC 三件事情。
每个人做每件事情所花的时间可能不一样。
每个人只能安排一件事情,问怎样安排才能使三个人所工作的时间之和最小?扩展成n个人n件事也可以,但要求是:事情数和人数一样多每人只能做一件事这样的问题就称作指派问题匈牙利算法就是解决这样的问题的。
步骤概括:每行减去此行最小数判断是否达到算法目标,如未达到算法目标,继续下一步。
否则结束。
横纵交替,从行开始。
找出所有还没有选中0的行(具体见步骤实例),在此行后面打钩;把此行中有0的列全打钩。
在打钩的列中,如果有零,又在有0的行打钩,如此交替,直到不能再打钩。
在没有打钩的行和打钩的列上划线,会得到发现所有的0已经被划去,如果没有划去,请检查前面的步骤。
此时剩下的所有元素中,找到最小值,就记为min吧。
在第4步画线的行减去min(此时原来的0变成-min),再在画线的列加上min(此时矩阵中没有了负数)。
回到第2步。
匈牙利算法

匈牙利算法是一种用于在多项式时间内解决任务分配问题的组合优化算法,它推广了后来的原始对偶方法。
美国数学家哈罗德·库恩(Harold Kuhn)于1955年提出了该算法。
该算法之所以称为匈牙利算法,是因为该算法的很大一部分是基于前匈牙利数学家DéNESKőnig和Jenőegerváry的工作。
概念在介绍匈牙利算法之前,我想介绍一些概念。
接下来的M是G 的匹配项。
如果是,则边缘已经在匹配的M上。
M交织路径:P是G的路径。
如果P中的边缘是属于m的边缘,而不属于m但属于G的边缘是交替的,则p是M交织的路径。
例如:路径。
M饱和点:例如,如果V与M中的边相关联,则称V为m饱和,否则V为非m饱和。
如果它们全部属于m饱和点,则其他点都属于非m饱和点。
M扩展路径:P是m隔行扫描路径。
如果P的起点和终点均为非m饱和点,则p称为m增强路径。
例如(不要与流网络中的扩展路径混淆)。
寻找最大匹配数的一种显而易见的算法是先找到所有匹配项,然后保留匹配数最大的匹配项。
但是该算法的时间复杂度是边数的指数函数。
因此,我们需要找到一种更有效的算法。
本文介绍了一种使用扩展路径查找最大匹配的方法(称为匈牙利算法,由匈牙利的Edmonds于1965年提出)。
增强导轨(也称为增强导轨或交错导轨)的定义如果P是连接图G中两个不匹配顶点的路径,并且属于m和不属于m的边缘(即,匹配边缘和待匹配边缘)在P上交替,则p称为相对于M.从增强路径的定义可以得出三个结论(1)P的路径数必须为奇数,并且第一个边缘和最后一个边缘都不属于M。
(2)通过将m和P取反可以获得更大的匹配度。
(3)当且仅当没有M的增强路径时,M是G的最大匹配。
算法概述:(1)将M设置为null(2)通过XOR操作找到扩展路径P并获得更大的匹配项而不是m(3)重复(2),直到找不到增强路径。
匈牙利算法简介

匈牙利算法匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。
匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法。
设G=(V,E)是一个无向图。
如顶点集V可分割为两个互不相交的子集V1,V2之并,并且图中每条边依附的两个顶点都分属于这两个不同的子集。
则称图G 为二分图。
二分图也可记为G=(V1,V2,E)。
给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
选择这样的子集中边数最大的子集称为图的最大匹配问题(maximal matching problem)如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备,完美匹配。
编辑本段算法描述求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的。
但是这个算法的时间复杂度为边数的指数级函数。
因此,需要寻求一种更加高效的算法。
下面介绍用增广路求最大匹配的方法(称作匈牙利算法,匈牙利数学家Edmonds于1965年提出)。
增广路的定义(也称增广轨或交错轨):若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
由增广路的定义可以推出下述三个结论:1-P的路径个数必定为奇数,第一条边和最后一条边都不属于M。
2-将M和P进行取反操作可以得到一个更大的匹配M’。
3-M为G的最大匹配当且仅当不存在M的增广路径。
算法轮廓:(1)置M为空(2)找出一条增广路径P,通过异或操作获得更大的匹配M’代替M(3)重复(2)操作直到找不出增广路径为止编辑本段时间空间复杂度时间复杂度邻接矩阵:最坏为O(n^3) 邻接表:O(mn)空间复杂度邻接矩阵:O(n^2) 邻接表:O(m+n)邻接表-C++#include <iostream>#include <cstring>using namespace std;//定义链表struct link{int data; //存放数据link* next; //指向下一个节点link(int=0);};link::link(int n){data=n;next=NULL;}int n1,n2,m,ans=0;int result[101]; //记录n1中的点匹配的点的编号//?????????????????????????????????pass 一一对应保存结果bool state [101]; //记录n1中的每个点是否被搜索过link *head [101]; //记录n2中的点的邻接节点link *last [101]; //邻接表的终止位置记录//判断能否找到从节点n开始的增广路bool find(const int n){link* t=head[n];while (t!=NULL) //n仍有未查找的邻接节点时{if (!(state[t->data])) //如果邻接点t->data未被查找过{state[t->data]=true; //标记t->data为已经被找过if ((result[t->data]==0) || //如果t->data不属于前一个匹配M(find(result[t->data]))) //如果t->data匹配到的节点可以寻找到增广路????????????????????pass{result[t->data]=n; //那么可以更新匹配M',其中n1中的点t->data匹配n return true; //返回匹配成功的标志}}t=t->next; //继续查找下一个n的邻接节点}return false;}int main(){int t1=0, t2=0;cin>>n1>>n2>>m;for (int i=0; i<m; i++){cin>>t1>>t2;if (last[t1]==NULL)last[t1]=head[t1]=new link(t2);elselast[t1]=last[t1]->next=new link(t2);}for (int i=1; i<=n1; i++){memset(state, 0, sizeof(state));if (find(i)) ans++;}cout<<ans<<endl;return 0;}邻接矩阵——C++第一个节点的flag不就一直是零了吗#include<iostream>#include<cstring>using namespace std;int map[105][105];int visit[105],flag[105];int n,m;bool dfs(int a){for(int i=1;i<=n;i++){if(map[a][i] && !visit[i]){visit[i]=1;//设置visit标识保证不出现1匹配2的情况?还是为了省事,这个节点如果可以增广,下面就把它增广了,不能的话,以后也就别费劲,把它忽略吧。
匈牙利算法 描述

匈牙利算法描述匈牙利算法是图论中一种用于解决二分图匹配问题的算法。
它首次由匈牙利数学家Denzel匈牙利在1955年发表,因而得名。
匈牙利算法属于图匹配算法的范畴,在实际应用中有着很强的效率和准确性。
本文将介绍匈牙利算法的原理、实现方法和应用领域等相关内容。
一、匈牙利算法原理匈牙利算法是解决二分图最大匹配问题的经典算法之一。
在二分图中,匈牙利算法的目标是寻找图中的最大匹配,即尽可能多地找到满足匹配条件的边,也就是找到尽可能多的配对节点。
在匈牙利算法中,主要使用了增广路的概念,通过不断地寻找增广路,来不断地扩展匹配。
具体而言,匈牙利算法的核心思想是利用增广路径寻找最大匹配。
在每一次匹配的过程中,首先选择一个未匹配的节点,然后通过交替路径寻找增广路径,直到无法找到增广路径为止。
当无法找到增广路径时,说明找到了最大匹配。
增广路径指的是一条由未匹配的节点和匹配节点交替构成的路径,其中未匹配节点为起点和终点。
通过不断地寻找增广路径,可以逐步扩展匹配。
在匈牙利算法中,为了记录节点的匹配状态和寻找增广路径,通常使用匈牙利标号和匈牙利交错路的方式。
匈牙利标号是为每个节点标记一个代表节点匹配状态的值,而匈牙利交错路则是一种用于寻找增广路径的方法。
借助这些工具,匈牙利算法可以高效地解决最大匹配问题。
二、匈牙利算法实现方法匈牙利算法的实现方法较为复杂,需要结合图论和图匹配的相关知识。
在实际应用中,匈牙利算法通常通过编程实现,以解决特定的二分图匹配问题。
下面简要介绍匈牙利算法的一般实现方法。
1. 初始化匈牙利标号:首先对图中的所有未匹配节点进行初始化标号,即给它们赋予一个初始的匈牙利标号。
2. 寻找增广路径:选择一个未匹配的节点作为起点,通过交替路径和增广路的方法寻找增广路径。
在寻找增广路径的过程中,要根据节点的匈牙利标号来选择下一个节点,从而找到满足匹配条件的路径。
3. 匹配节点:如果成功找到一条增广路径,就可以将路径中的节点进行匹配,即将原来未匹配的节点与匹配节点进行匹配。
匈牙利算法 描述

匈牙利算法描述
摘要:
1.匈牙利算法简介
2.匈牙利算法的应用背景
3.匈牙利算法的基本思想
4.匈牙利算法的实现步骤
5.匈牙利算法的优缺点分析
6.结论
正文:
匈牙利算法是一种解决匈牙利问题的图论算法,也被称为Munkres算法。
它主要用于解决最大匹配问题和最小生成树问题。
匈牙利算法在运筹学、计算机科学、通信网络等领域具有广泛的应用背景。
匈牙利算法的基本思想是:通过不断地寻找增广路径来寻找最大匹配。
增广路径是指一条从已匹配顶点出发,到达未匹配顶点的路径。
算法的基本流程如下:
1.初始化未匹配顶点和已匹配顶点集合。
2.遍历所有未匹配顶点,找到一条增广路径。
3.将增广路径上的所有顶点标记为已匹配。
4.重复步骤2和3,直到找不到增广路径为止。
匈牙利算法的实现步骤如下:
1.初始化一个长度与顶点数相同的数组,用于记录每个顶点所在的连通分
量。
2.遍历所有边,对于每条边,如果两个顶点不在同一连通分量,则将它们合并到同一个连通分量中。
3.遍历所有顶点,如果一个顶点所在的连通分量只有一个顶点,则将其标记为已匹配。
4.重复步骤3,直到找不到未匹配顶点为止。
匈牙利算法的优缺点分析:
优点:
1.匈牙利算法的时间复杂度为O(nm),其中n和m分别为顶点数和边数。
2.匈牙利算法可以保证找到最大匹配。
缺点:
1.匈牙利算法需要额外的存储空间来记录顶点所在的连通分量。
2.匈牙利算法不能保证找到最优解,因为可能存在多个最大匹配。
匈牙利算法 描述

匈牙利算法描述匈牙利算法是一种用于解决二分图最大匹配问题的算法,它由匈牙利数学家DénesKőnig和JenőEgerváry于1930年代开发而成。
该算法的主要用途是在给定一个二分图后,找出其最大的匹配,即找到最大的匹配顶点对,使得图中的边连接了尽可能多的顶点。
匈牙利算法在组合优化、网络流、计算几何等领域都有广泛的应用。
一、匈牙利算法原理匈牙利算法的基本原理是通过不断增广现有的匹配来逐步找到最大匹配。
在算法执行的过程中,它会不断尝试改进当前的匹配,找到更多的匹配边,直到无法再增广为止。
匈牙利算法是通过交替路径来实现增广匹配的。
在每一轮中,它会选择一个未匹配的起始顶点,并试图在图中找到一条交替路径,这条路径的定义是一种交替的交错顶点序列,其中相邻的两个顶点分别属于两条不相交的边。
找到这样的交替路径后,就可以通过将原匹配中的所选路径上的所有边的匹配状态进行交换,来增大当前的匹配数,如此不断重复直到无法再找到增广路径为止。
在匈牙利算法的执行过程中,需要着重考虑如何找到一条增广路径,以及如何有效地交换匹配。
通过合适的优化策略,匈牙利算法可以在较短的时间内找到最大匹配。
二、匈牙利算法步骤实际应用匈牙利算法时,通常会按照以下步骤来执行:1. 初始化:首先将所有顶点标记为未访问状态,并设置所有匹配为未知。
然后从第一个顶点开始,尝试寻找从该顶点出发的增广路径。
2. 寻找增广路径:从未匹配的顶点开始,逐一尝试寻找增广路径。
如果找到了增广路径,则将原来的匹配进行交换;如果找不到增广路径,则执行第4步。
3. 重标记:如果无法找到增广路径,需要对当前的标记状态进行调整,重新寻找增广路径。
4. 完成匹配:当无法再找到增广路径时,当前的匹配即为最大匹配,算法结束。
在实际的算法实现中,还可以通过一些优化措施来提高匈牙利算法的效率,例如路径压缩、节点标记等。
这些优化措施可以进一步提高算法的运行效率,使得匈牙利算法可以应用到更大规模的问题中。
匈牙利算法

匈牙利算法--过程图解以下算法可把G中任一匹配M扩充为最大匹配,此算法是Edmonds于1965年提出的,被称为匈牙利算法,其步骤如下:(1)首先用(*)标记X中所有的非M-顶点,然后交替进行步骤(2),(3)。
(2)选取一个刚标记(用(*)或在步骤(3)中用(y i)标记)过的X中顶点,例如顶点x i,然后用(x i)去标记Y中顶点y,如果x i与y为同一非匹配边的两端点,且在本步骤中y尚未被标记过。
重复步骤(2),直至对刚标记过的X中顶点全部完成一遍上述过程。
(3)选取一个刚标记(在步骤(2)中用(x i)标记)过的Y中结点,例如y i,用(y i)去标记X中结点x,如果y i与x为同一匹配边的两端点,且在本步骤中x尚未被标记过。
重复步骤(3),直至对刚标记过的Y中结点全部完成一遍上述过程。
(2),(3)交替执行,直到下述情况之一出现为止:(Ⅰ)标记到一个Y中顶点y,它不是M-顶点。
这时从y出发循标记回溯,直到(*)标记的X中顶点x,我们求得一条交替链。
设其长度为2k+1,显然其中k条是匹配边,k+1条是非匹配边。
(Ⅱ)步骤(2)或(3)找不到可标记结点,而又不是情况(Ⅰ)。
(4)当(2),(3)步骤中断于情况(Ⅰ),则将交替链中非匹配边改为匹配边,原匹配边改为非匹配边(从而得到一个比原匹配多一条边的新匹配),回到步骤(1),同时消除一切现有标记。
(5)对一切可能,(2)和(3)步骤均中断于情况(Ⅱ),或步骤(1)无可标记结点,算法终止(算法找不到交替链)。
我们不打算证明算法的正确性,只用一个例子跟踪一下算法的执行,来直观地说明这一点。
例9.3用匈牙利算法求图9.3的一个最大匹配。
(1)置M = Æ,对x1-x6标记(*)。
(2)找到交替链(x1, y1)(由标记(x1),(*)回溯得),置M = {(x1, y1)}。
(3)找到交替链(x2, y2)(由标记(x2),(*)回溯得),置M = {(x1, y1), (x2, y2),}。
匈牙利算法原理

匈牙利算法原理
匈牙利算法是一种用于解决二分图最大匹配问题的算法。
在二分图中,将图中的节点分为两个集合,分别为左侧节点集合和右侧节点集合,且左侧节点集合中的节点与右侧节点集合中的节点之间不存在边,只有左侧节点集合中的节点与右侧节点集合中的节点之间存在边。
二分图最大匹配问题就是找到一种最优的匹配方式,使得左侧节点集合中的每个节点都与右侧节点集合中的一个节点匹配。
匈牙利算法的基本思想是:从左侧节点集合中的每个节点开始,依次寻找与其匹配的右侧节点,如果找到了一个右侧节点,就将该右侧节点与左侧节点匹配,并继续寻找下一个左侧节点的匹配。
如果找不到一个右侧节点与该左侧节点匹配,就回溯到上一个左侧节点,并尝试匹配其他右侧节点,直到找到一个能够匹配的右侧节点或者所有的右侧节点都已经尝试过。
匈牙利算法的实现过程可以分为以下几个步骤:
1. 初始化:将所有的左侧节点都标记为未匹配状态。
2. 从左侧节点集合中的每个未匹配节点开始,依次进行匹配。
3. 对于每个未匹配节点,寻找与其相连的所有右侧节点,并尝试将其与该左侧节点匹配。
4. 如果找到了一个未匹配的右侧节点,就将该右侧节点与该左侧节点匹配,并将该左侧节点标记为已匹配状态。
5. 如果找不到一个未匹配的右侧节点与该左侧节点匹配,就回溯到上一个左侧节点,并尝试匹配其他右侧节点。
6. 如果所有的左侧节点都已经匹配完成,就得到了一个最大匹配。
7. 如果还存在未匹配的左侧节点,就说明无法找到一个最大匹配。
匈牙利算法的时间复杂度为O(n^3),其中n为节点的数量。
虽然时间复杂度比较高,但是匈牙利算法在实际应用中表现良好,可以处理大规模的二分图最大匹配问题。
匈牙利算法 描述

匈牙利算法描述
匈牙利算法(Hungarian algorithm)是一种用于解决指派问题的优化算法。
指派问题即在给定若干个任务和执行者之间,找到最佳的任务分配方案,使总体成本最小或总体效益最大。
匈牙利算法的基本思想是通过构建一个初始的匹配矩阵,然后通过一系列的步骤来逐步优化任务分配。
下面是匈牙利算法的主要步骤:
1.构建初始匹配矩阵:根据给定的任务和执行者之间的成本
或效益,构建一个初始的n × n 的匹配矩阵,其中n 表示
任务或执行者的数量。
2.执行最小化匹配:在初始匹配矩阵中,通过找到每一行和
每一列的最小值,并减去该最小值,使得每行和每列都至
少有一个零元素。
3.进行任务分配:在完成步骤2后,判断匹配矩阵中是否存
在完美匹配(即每一行和每一列都有且只有一个零元素)。
如果存在完美匹配,则结束算法,任务分配完成。
如果不
存在完美匹配,则进入下一步。
4.寻找零元素覆盖:在匹配矩阵中查找未被选择的零元素,
并尝试通过最少线覆盖来覆盖所有的零元素,以找到可能
的任务分配方案。
5.更新匹配矩阵:在覆盖了所有的零元素后,根据覆盖线的
位置来对匹配矩阵进行更新和调整,以准备下一次迭代。
6.重复步骤2至步骤5,直到找到合适的任务分配方案或达
到停止条件。
通过上述步骤,匈牙利算法能够找到最佳的任务分配方案,使得总体成本最小或总体效益最大。
该算法的时间复杂度为O(n^4),其中n 表示任务或执行者的数量。
匈牙利算法在实际应用中广泛用于任务分配、资源调度、运输优化等问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匈牙利算法(Edmonds算法)步聚:(1)首先用(*)标记X中所有的非M顶点,然后交替进行步骤(2),(3)。
(2)选取一个刚标记(用(*)或在步骤(3)中用(y i)标记)过的X中顶点,例如顶点x,如果x i与y为同一非匹配边的两端点,且在本步骤中y尚未被标记过,则用(x i)i去标记Y中顶点y。
重复步骤(2),直至对刚标记过的X中顶点全部完成一遍上述过程。
(3)选取一个刚标记(在步骤(2)中用(x i)标记)过的Y中结点,例如y i,如果y i与x为同一匹配边的两端点,且在本步骤中x尚未被标记过,则用(y i)去标记X中结点x。
重复步骤(3),直至对刚标记过的Y中结点全部完成一遍上述过程。
(2),(3)交替执行,直到下述情况之一出现为止:(I)标记到一个Y中顶点y,它不是M顶点。
这时从y出发循标记回溯,直到(*)标记的X中顶点x,我们求得一条交替链。
设其长度为2k+1,显然其中k条是匹配边,k+1条是非匹配边。
(II)步骤(2)或(3)找不到可标记结点,而又不是情况(I)。
(4)当(2),(3)步骤中断于情况(I),则将交替链中非匹配边改为匹配边,原匹配边改为非匹配边(从而得到一个比原匹配多一条边的新匹配),回到步骤(1),同时消除一切现有标记。
(5)对一切可能,(2)和(3)步骤均中断于情况(II),或步骤(1)无可标记结点,算法终止(算法找不到交替链).以上算法说穿了,就是从二分图中找出一条路径来,让路径的起点和终点都是还没有匹配过的点,并且路径经过的连线是一条没被匹配、一条已经匹配过交替出现。
找到这样的路径后,显然路径里没被匹配的连线比已经匹配了的连线多一条,于是修改匹配图,把路径里所有匹配过的连线去掉匹配关系,把没有匹配的连线变成匹配的,这样匹配数就比原来多1个。
不断执行上述操作,直到找不到这样的路径为止。
下面给出此算法的一个例子:(1)置M = 空,对x1-x6标记(*)。
(2)找到交替链(x1, y1)(由标记(x1),(*)回溯得),置M = {(x1, y1)}。
(3)找到交替链(x2, y2)(由标记(x2),(*)回溯得),置M = {(x1, y1), (x2, y2),}。
(4)找到交替链(x3, y1, x1, y4)(如图9.4所示。
图中虚线表示非匹配边,细实线表示交替链中非匹配边,粗实线表示匹配边),因而得M = {(x2, y2), (x3, y1),(x1, y4)}。
(5)找到交替链(x4, y3)(由标记(x4),(*)回溯得),置M = {(x2, y2), (x3, y1), (x1, y4), (x4, y3)}。
(6)找到交替链(x5, y4, x1, y1, x3, y7)(如图9.5所示,图中各种线段的意义同上),因而得M = {(x2, y2), (x4, y3),(x5, y4), (x1, y1), (x3, y 7)}下面是几个练习题:http://172.28.138.8:8080/acmhome/problemdetail.do?&method=showdetail&id=13871387 Guardian of Decency题目给出一些boy和girl,有一些规则他们在一些条件下可能恋爱,求最多有多少人,他们之间不会恋爱,根据这样的规则构建一个二分图:boy和girl分两边,分别作为左右结点,根据规则如果满足可能恋爱的条件就连接,否则不连接,求出最大匹配,N-max_number_of_couples即为要求的结果。
实现代码:#include<iostream>#include<string>#include<cmath>using namespace std;typedef struct{char sex;string str;int height;string sports;}People;People p[505];int n;int px[505],py[505];int map[505][505];int flag[505];int check(int i,int j){if(abs(p[i].height-p[j].height)<=40&&p[i].sex!=p[j].sex&&p[i]pare(p[j].str)==0&&p[ i]pare(p[j].sports)!=0)return 1;return 0;}int Path(int i){int j;px[i]=1;for(j=1;j<=n;j++){if(map[i][j]&&!py[j]){py[j]=1;if(flag[j]==-1||Path(flag[j])){flag[j]=i;return 1;}}}return 0;}void Max_Match(){int i;int Max=0;memset(flag,-1,sizeof(flag));for(i=1;i<=n;i++)px[i]=0;for(i=1;i<=n;i++){memset(py,0,sizeof(py));if(!px[i])Max+=Path(i);}cout<<n-Max/2<<endl;}int main(){int i,j,k;int m;cin>>m;while(m--){cin>>n;for(i=1;i<=n;i++){cin>>p[i].height>>p[i].sex>>p[i].str>>p[i].sports;}memset(map,0,sizeof(map));for(i=1;i<=n;i++)for(j=1;j<=n;j++)if(check(i,j))map[i][j]=1;Max_Match();}return 0;}2730Gopher IIhttp://172.28.138.8:8080/acmhome/problemdetail.do?&method=showdetail&id=2730该题给出m个动物的地点,n个洞,还有速度和时间(其实就是给了距离),问m个动物最多能有几个在规定的时间里一规定的速度躲到洞里逃生,。
典型的二分图匹配的问题,动物的位置为左边的结点,洞为右边的结点,如果他们的距离小于等于时间×速度,我们就认为他们是连接的,否则认为不连接,我们只要计算最大二分图匹配数,就是可以逃生的动物数,用总数减去匹配数就是不能逃生的,即为所求。
实现代码:#include<iostream>#include<math.h>usingnamespace std;#define Max 101typedefstruct{double x,y;}Node;int map[Max][Max];bool mark[Max];int nx,ny;int cx[Max],cy[Max];Node G[Max],H[Max];int Find_Path(int u){int i;for(i=0;i<ny;i++){if(map[u][i]&&!mark[i]){mark[i]=true;if(cy[i]==-1||Find_Path(cy[i])){cy[i]=u;cx[u]=i;return 1;}}}return 0;}int Max_Match()int res=0;int i,j;for(i=0;i<nx;i++)cx[i]=-1;for(i=0;i<ny;i++)cy[i]=-1;for(i=0;i<nx;i++){if(cx[i]==-1){for(j=0;j<ny;j++)mark[j]=false;res+=Find_Path(i);}}return res;}int main(){int i,j;int s,v;while(cin>>nx>>ny>>s>>v){for(i=0;i<nx;i++)cin>>G[i].x>>G[i].y;for(i=0;i<ny;i++)cin>>H[i].x>>H[i].y;for(i=0;i<nx;i++)for(j=0;j<ny;j++){if(sqrt((((G[i].x-H[j].x)*(G[i].x-H[j].x))+((G[i].y-H[j].y)*(G[i].y-H[j].y))))/v<s)map[i][j]=1;else map[i][j]=0;}cout<<nx-Max_Match()<<endl;}return 0;}1990 Asteroidshttp://172.28.138.8:8080/acmhome/problemdetail.do?&method=showdetail&id=1990题目给出一个矩阵,上面有敌人,每个子弹可以打出一横行或者一竖行,问最少用多少子弹消灭都有敌人,如:X.X.X..X.x表示敌人,显然用两个子弹就可以解决所有敌人。
下面介绍一下二分图的最小点覆盖数:假如选了一个点就相当于覆盖了以它为端点的所有边,你需要选择最少的点来覆盖所有的边。
König定理是一个二分图中很重要的定理,它的意思是,一个二分图中的最大匹配数等于这个图中的最小点覆盖数。
这样,我们可以构建一个这样的二分图,左右边的结点数分别是矩阵的行和列,然后有敌人的地方就连接上(例如第一行第一列有敌人,就连接左边的1和右边的1),这样,二分图中的每条边就代表一个敌人,我们找到最少的n个点,这n个点能覆盖二分图中的所有边,即是最小点覆盖数,根据König定理,一个二分图中的最大匹配数等于这个图中的最小点覆盖数,所以只要求这样一个二分图的最大二分匹配即可。
实现代码:#include<stdio.h>#include <string.h>#define MAXN 505int uN,vN;bool g[MAXN][MAXN];int xM[MAXN],yM[MAXN];bool chk[MAXN];bool SearchPath(int u){int v;for(v=1;v<=vN;v++)if(g[u][v]&&!chk[v]){chk[v]=true;if(yM[v]==-1||SearchPath(yM[v])){yM[v]=u;xM[u]=v;return true;}}return false;}int MaxMatch(){int u,ret=0;memset(xM,-1,sizeof(xM));memset(yM,-1,sizeof(yM));for(u=1;u<=vN;u++)if(xM[u]==-1){memset(chk,false,sizeof(chk));if(SearchPath(u))ret++;}return ret;}int main(){int i,j,x,y;while(scanf("%d %d",&vN,&uN)!=EOF){for(i=1;i<=vN;i++)for(j=1;j<=vN;j++)g[i][j]=0;for(i=0;i<uN;i++){scanf("%d %d",&x,&y);g[x][y]=1;}printf("%d\n",MaxMatch());}return 0;}1671Girls and Boyshttp://172.28.138.8:8080/acmhome/problemdetail.do?&method=showdetail&id=1671题目给出一些boy和girl,有一些人有罗曼史,比如A和B有罗曼史,那么B和A就有罗曼史,求最多有多少人,他们之间没有罗曼史,根据这样的规则构建一个二分图:boy和girl分两边,分别作为左右结点,根据规则如果有罗曼史就连接,否则不连接,求出最大匹配,N-m ax_num ber_of_couples/2即为要求的结果,因为比如A和B有罗曼史,那么B和A就有罗曼史,所以重复算了一次(在这种情况下A和B去掉一个即可)。
