地球椭球体参数列表
地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念

地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念地球椭球体(Ellipsoid)众所周知我们的地球表面是一个凸凹不平的表面,而对于地球测量而言,地表是一个无法用数学公式表达的曲面,这样的曲面不能作为测量和制图的基准面。
假想一个扁率极小的椭圆,绕大地球体短轴旋转所形成的规则椭球体称之为地球椭球体。
地球椭球体表面是一个规则的数学表面,可以用数学公式表达,所以在测量和制图中就用它替代地球的自然表面。
因此就有了地球椭球体的概念。
地球椭球体有长半径和短半径之分,长半径(a)即赤道半径,短半径(b)即极半径。
f=(a-b)/a为椭球体的扁率,表示椭球体的扁平程度。
由此可见,地球椭球体的形状和大小取决于a、b、f 。
因此,a、b、f被称为地球椭球体的三要素。
对地球椭球体而言,其围绕旋转的轴叫地轴。
地轴的北端称为地球的北极,南端称为南极;过地心与地轴垂直的平面与椭球面的交线是一个圆,这就是地球的赤道;过英国格林威治天文台旧址和地轴的平面与椭球面的交线称为本初子午线。
以地球的北极、南极、赤道和本初子午线等作为基本要素,即可构成地球椭球面的地理坐标系统(A geographic coordinate system (GCS) uses a three dimensional spherical surface to define locations on the earth. A GCS includes an angular unit of measure, a prime meridian,and a datum (based on a spheroid).)。
可以看出地理坐标系统是球面坐标系统,以经度/维度(通常以十进制度或度分秒(DMS)的形式)来表示地面点位的位置。
地理坐标系统以本初子午线为基准(向东,向西各分了1800)之东为东经其值为正,之西为西经其值为负;以赤道为基准(向南、向北各分了900)之北为北纬其值为正,之南为南纬其值为负。
cgcs2000坐标系椭球参数 -回复

cgcs2000坐标系椭球参数-回复CGCS2000(China Geodetic Coordinate System 2000),是中国国家测绘局于2003年发布的新一代国家大地坐标系。
这个椭球参数主要用于地理空间数据的测量和位置表示,广泛应用于国土资源调查、交通运输、地质、测绘和地理信息等领域。
本文将深入探讨CGCS2000坐标系椭球参数。
首先,我们需要了解什么是椭球参数。
在地球上,由于地球自转所引起的形状变化,地球并不是一个完全规则的球体。
而是类似一个稍微扁平的椭球。
为了描述地球的形状,人们引入了椭球参数,用以测量和计算地球上的距离、角度和面积。
CGCS2000坐标系使用的椭球参数被称为中国2000大地坐标系统椭球参数(CGCS2000 elliptical parameters)。
它主要包括长半轴(Semi-Major Axis)和扁率(Flattening)。
长半轴是一个椭球的主轴,它与地球的赤道直径相等,用于表示地球的大小。
在CGCS2000坐标系中,长半轴的数值约为6378137米(单位是米),这个数值有助于我们计算地球上的距离和面积。
扁率则是用来描述地球椭球的压缩程度。
扁率为零表示地球是完全的球体,而扁率为1表示地球是一个无限长的椭球。
CGCS2000坐标系的扁率数值为1/298.257222101(无单位)。
这个数值告诉我们地球的扁率程度,它对于进行地理空间数据的测量和计算非常重要。
CGCS2000坐标系的椭球参数是通过大量的地球测量学观测数据和数学模型计算得出的。
其目的是提供一个更准确的地球表面描述,使各种应用程序能够在不同的地理空间数据之间进行精确的测量和计算。
CGCS2000坐标系椭球参数的设立使得中国的测绘和地理信息行业能够更好地与国际接轨。
它为我国参与国际地理空间数据交换和地质测绘工作提供了坚实的基础。
它还有助于提高地理信息数据的一致性和可靠性,减少数据转换和投影时引入的误差。
02.自定义坐标系和投影变换

1. 概述1.1 地理投影的基本原理常用到的地图坐标系有2种,即地理坐标系和投影坐标系。
地理坐标系是以经纬度为单位的地球坐标系统,地理坐标系中有2个重要部分,即地球椭球体(spheroid)和大地基准面(datum)。
由于地球表面的不规则性,它不能用数学公式来表达,也就无法实施运算,所以必须找一个形状和大小都很接近地球的椭球体来代替地球,这个椭球体被称为地球椭球体,我国常用的椭球体如下表所示。
表:我国常用椭球体椭球体名称年代长半轴(米)短半轴(米)扁率WGS84 1984 6378137.0 6356752.3 1:298.257克拉索夫斯基(Krasovsky)1940 6378245.0 6356863.0 1:298.3Xian_1980 1975 6378140.0 6356755.3 1:298.257CGCS2000(CRS80) 2008 6378137.0 6356752.3 1:298.257我国规定1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万比例尺地形图,均采用高斯克吕格投影。
1:2.5万至1:50万比例尺地形图采用经差6度分带,1:1万和1:2.5万比例尺地形图采用经差3度分带。
1.2 国内坐标系介绍大地坐标,在地面上建立一系列相连接的三角形,量取一段精确的距离作为起算边,在这个边的两端点,采用天文观测的方法确定其点位(经度、纬度和方位角),用精密测角仪器测定各三角形的角值,根据起算边的边长和点位,就可以推算出其他各点的坐标。
这样推算出的坐标,称为大地坐标。
我国1954年在北京设立了大地坐标原点,由此计算出来的各大地控制点的坐标,称为1954年北京坐标系。
为了适应大地测量的发展,我国于1978年采用国际大地测量协会推荐的Xian_1980地球椭球体建立了我国新的大地坐标系,并在1986年宣布在陕西省泾阳县设立了新的大地坐标原点,由此计算出来的各大地控制点坐标,称为1980年大地坐标系。
GIS中坐标系定义及大地坐标系

GIS中坐标系定义及大地坐标系发布日期:2012-02-04 浏览次数:2核心提示:GIS中的坐标系定义由基准面和地图投影两组参数确定,而基准面的定义则由特定椭球体及其对应的转换参数确定。
1、椭球体GIS中的坐标系定义由基准面和地图投影两组参数确定,而基准面的定义则由特定椭球体及其对应的转换参数确定。
基准面是利用特定椭球体对特定地区地球表面的逼近,因此每个国家或地区均有各自的基准面。
基准面是在椭球体基础上建立的,椭球体可以对应多个基准面,而基准面只能对应一个椭球体。
椭球体的几何定义:O是椭球中心,NS为旋转轴,a为长半轴,b为短半轴。
子午圈:包含旋转轴的平面与椭球面相截所得的椭圆。
纬圈:垂直于旋转轴的平面与椭球面相截所得的圆,也叫平行圈。
赤道:通过椭球中心的平行圈。
基本几何参数:椭圆的扁率椭圆的第一偏心率椭圆的第二偏心率其中a、b称为长度元素;扁率α反映了椭球体的扁平程度。
偏心率e和e’是子午椭圆的焦点离开中心的距离与椭圆半径之比,它们也反映椭球体的扁平程度,偏心率愈大,椭球愈扁。
套用不同的椭球体,同一个地点会测量到不同的经纬度。
下面是几种常见的椭球体及参数列表。
几种常见的椭球体参数值克拉索夫斯基椭球体1975年国际椭球体WGS-84椭球体a6 378 245.000 000 000 0(m)6 378 140.000 000 000 0(m)6 378 137.000 000 000 0(m)b 6 356 863.018 773 047 3(m)6 356 755.288 157 528 7(m)6 356 752.314 2(m)c 6 399 698.901 782 711 0(m)6 399 596.651 988 010 5(m)6 399 593.625 8(m)α1/298.3 1/298.257 1/298.257 223 563e20.006 693 421 622 966 0.006 694 384 999 588 0.006 694 379 901 3e’20.006 738 525 414 683 0.006 739 501 819 473 0.006 739 496 742 272、地图投影地球是一个球体,球面上的位置,是以经纬度来表示,我们把它称为“球面坐标系統”或“地理坐标系統”。
地球椭球体参数列表

基本参 数编辑
2000国家大 地坐标系是全 球地心坐标系 在我国的具体 体现,其原点 为包括海洋和 大气的整个地 球的质量中心 。Z轴指向 BIH1984.0定 义的协议极地 方向(BIH国 际时间局), X轴指向 BIH1984.0定 义的零子午面 与协议赤道的 交点,Y轴按 右手坐标系确 定。2000国 家大地坐标系 采用的地球椭 球参数如下: 长半轴 a=6378137m 扁率 f=1/298.2572 22101 地心引力常数 GM=3.98600 4418× 1014m3s-2 自转角速度 ω=7.292l15× 10-5ra0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 GRS80 WGS72 Australian Krassovsky 1948(1954年北京坐系) International1924 Hayford 1909 Clarke1880 Clarke1866 Clarke1866(modifiedforMichigan) Airy1930 Bessel1841 Everest1830 Sphere Airy1930(modifiedforIreland1965) Bessel1841(modifiedforSchwarzeck) Clarke1880(modifiedforArc1950) Clarke1880(modifiedforMerchich) Everest1830(modifiedforKertau) Fischer1960 Fischer1960(modifiedforSouthAsia) Fischer1968 GRS67 Helmert1906 椭球体名称 长轴半径 6378137 6378135 6378160 6378245 6378388 6378388 6378249.145 6378206.4 6378450.047 6377563.396 6377397.155 6377276.345 6370997 6377340.189 6377483.865 6378249.145 6378249.2 6377304.063 6378166 6378155 6378150 6378160 6378200 扁率的倒数 298.2572221 298.26 298.25 298.3 297 297 293.465 294.9786982 294.9786982 299.3249646 299.1528128 300.8017 0 299.3249646 299.1528128 293.4663076 293.46598 300.8017 298.3 298.3 298.3 298.2471674 298.3
(整理)地球椭球的基本几何参数及相互关系

§7.1地球椭球的基本几何参数及相互关系7.1.1地球椭球的基本几何参数地球椭球参考椭球 具有一定的几何参数、定位及定向的用以代表某一地区大地水准面的地球椭球叫做参考椭球。
地面上一切观测元素都应归算到参考椭球面上,并在该面上进行计算,它是大地测量计算的基准面,同时又是研究地球形状和地图投影的参考面。
有关元素O 为椭球中心;NS 为旋转轴;a 为长半轴;b 为短半轴;子午圈(或径圈或子午椭圆);平行圈(或纬圈);赤道。
旋转椭球的形状和大小是由子午椭圆的五个基本几何参数(元素)来决定的,即:椭圆的长半轴: a椭圆的短半轴: b椭圆的扁率: α=-a b a (7-1)椭圆的第一偏心率: ab a e 22-= (7-2) 椭圆的第二偏心率: b b a e 22 -=' (7-3)其中:a 、b 称为长度元素;扁率α反映了椭球体的扁平程度,如α=0时,椭球变为球体;α=1时,则为平面。
e 和e /是子午椭圆的焦点离开中心的距离与椭圆半径之比,它们也反映了椭球体的扁平程度,偏心率越大,椭球愈扁。
五个参数中,若知道其中的两个参数就可决定椭球的形状和大小,但其中至少应已知一个长度元素(如a 或b ),人们习惯于用a 和α表示椭球的形状和大小,便于级数展开。
引入下列符号:ba c 2= tgB t =B e 222cos '=η (7-4)式中B 为大地纬度,c 为极曲率半径(极点处的子午线曲率半径), 两个常用的辅助函数,W 第一基本纬度函数,V 第二基本纬度函数,B e V B e W 2222cos 1sin 1'+=-= (7-5)传统大地测量利用天文大地测量和重力测量资料推求地球椭球的几何参数,自1738年(法国)布格推算出第一个椭球参数以来,200多年间各国大地测量工作者根据某一国或某一地区的资料,求出了数目繁多,数值各异的椭球参数。
由于卫星大地测量的发展,使推求总地球椭球体参数成为可能,自1970年以后的椭球参数都采用了卫星大地测量资料。
地球椭球体

任一水准面 大地水准面
17
3.2地球椭球体基本要素 3.2.3高程
A hAB
H´A
任意水准面
HA HB
H´B
大地水准面 铅垂线
18
坐标参考系统—高程系统
1956黄海高程系, 72.2893米 1950-1956年平 均海水面为0米
青岛验潮站
以1952-1979年 青岛验潮站测定 的平均海水面作 为高程基准面 观象山
地图是地球空间的缩小。把地图上所表示 的空间尺度称作比例尺。 当制图区域比较小时,由于地图投影的变 形较小,地图上各方向长度缩小的比例近 似相等。地图比例尺是指图上长度与相应 地面之间的长度比例,即d/D=1/M。 比例尺赋予地图可量测计算的性质,为地 图使用பைடு நூலகம்提供了明确的空间尺度概念。
3.2地球椭球体基本要素 3.2.2地图比例尺 1. 2. 数字比例尺 可以写成比的形式,如 1:10 000; 可以写出分式形式,如1/10000。 文字比例尺 一万分之一、五万分之一; 图上1厘米等于实地1千米。
3.2地球椭球体基本要素 3.2.2地图比例尺 3. 图解比例尺 直线比例尺:以直线线段形式标明图上线 段长度所对应的地面距离。
3.2地球椭球体基本要素 3.2.3高程 1987年国家测绘局公布 :启用《1985国家高程 基准》取代《黄海平均 海水面》,其比《黄海 平均海水面》上升29毫 米。(72.260m) 。
青 水 岛 准 观 原 象 点 山
4
3.2地球椭球体基本要素 3.2.1地球椭球体 中国在1952年以前采用海福特椭球体 (Hereford ellipsoid) ,从1953—1980年 采用克拉索夫斯基椭球体(Krasovsky )。 随着人造地球卫星的发射,有了更精密的 测算地球形体的仪器。1975年第16届国际 大地测量及地球物理联合会上通过国际大 地测量协会第一号决议中公布的地球椭球 体称为GRS(1975),中国自1980年开始采 用GRS(1975)新参考椭球体系。
2000椭球参数扁率

2000椭球参数扁率
摘要:
一、椭球参数介绍
1.椭球形状的重要性
2.2000 椭球参数的定义
二、扁率的概念
1.扁率的定义
2.扁率与地球形状的关系
三、2000 椭球扁率参数
1.2000 椭球扁率的数值
2.2000 椭球扁率的特点
四、椭球扁率的应用
1.地球测量与地图制图
2.地球物理勘探与导航定位
正文:
一、椭球参数介绍
地球是一个近似的椭球体,其形状参数包括长半轴、短半轴和扁率。
这些参数对于地球的形状描述、地球表面的测量和地图制图等有着重要的意义。
在2000 年,我国采用了新的椭球参数,被称为2000 椭球参数。
二、扁率的概念
扁率是椭球形状的一个重要参数,它反映了地球椭球扁平的程度。
扁率的
定义是地球椭球的长半轴与短半轴之差与长半轴的比值,通常用f 表示。
扁率越大,地球椭球越扁平;扁率越小,地球椭球越接近于球形。
三、2000 椭球扁率参数
2000椭球参数的扁率f为1/298.257222,这个数值是经过精确测量和计算得出的。
与之前的椭球参数相比,2000椭球参数的扁率更加精确,能够更好地反映地球的形状。
四、椭球扁率的应用
椭球扁率参数的应用十分广泛,主要包括地球测量、地图制图、地球物理勘探和导航定位等领域。
在地球测量和地图制图领域,椭球扁率参数是确定地球表面几何形状和尺寸的基础数据;在地球物理勘探和导航定位领域,椭球扁率参数直接影响到勘探精度和定位精度。
第四章坐标系统与地图投影-中国科学院测量与地球物理研究所

空间参照系统和地图投影导读:正如上一章所描述的,一个要素要进行定位,必须嵌入到一个空间参照系中,因为GIS所描述是位于地球表面的信息,所以根据地球椭球体建立的地理坐标(经纬网)可以作为所有要素的参照系统。
因为地球是一个不规则的球体,为了能够将其表面的内容显示在平面的显示器或纸面上,必须进行坐标变换。
本章讲述了地球椭球体参数、常见的投影类型。
考虑到目前使用的1:100万以上地形图都是采用高斯——克吕格投影,本章最后又对该种投影类型和相关的地形图分幅标准做了简单介绍。
1.地球椭球体基本要素1.1地球椭球体1.1.1地球的形状为了从数学上定义地球,必须建立一个地球表面的几何模型。
这个模型由地球的形状决定的。
它是一个较为接近地球形状的几何模型,即椭球体,是由一个椭圆绕着其短轴旋转而成。
地球自然表面是一个起伏不平、十分不规则的表面,有高山、丘陵和平原,又有江河湖海。
地球表面约有71%的面积为海洋所占用,29%的面积是大陆与岛屿。
陆地上最高点与海洋中最深处相差近20公里。
这个高低不平的表面无法用数学公式表达,也无法进行运算。
所以在量测与制图时,必须找一个规则的曲面来代替地球的自然表面。
当海洋静止时,它的自由水面必定与该面上各点的重力方向(铅垂线方向)成正交,我们把这个面叫做水准面。
但水准面有无数多个,其中有一个与静止的平均海水面相重合。
可以设想这个静止的平均海水面穿过大陆和岛屿形成一个闭合的曲面,这就是大地水准面(图4-1)。
图4-1:大地水准面大地水准面所包围的形体,叫大地球体。
由于地球体内部质量分布的不均匀,引起重力方向的变化,导致处处和重力方向成正交的大地水准面成为一个不规则的,仍然是不能用数学表达的曲面。
大地水准面形状虽然十分复杂,但从整体来看,起伏是微小的。
它是一个很接近于绕自转轴(短轴)旋转的椭球体。
所以在测量和制图中就用旋转椭球来代替大地球体,这个旋转球体通常称地球椭球体,简称椭球体。
1.1.2地球的大小关于地球椭球体的大小,由于采用不同的资料推算,椭球体的元素值是不同的。
地形图的坐标表示方式

1、地形图坐标系:我国的地形图采用高斯-克吕格平面直角坐标系。
在该坐标系中,横轴:赤道,用Y表示;赤道以南为负,以北为正;纵轴:中央经线,用X表示;中央经线以东为正,以西为负。
坐标原点:中央经线与赤道的交点,用O表示。
我国位于北半球,故纵坐标均为正值,但为避免中央经度线以西为负值的情况,将坐标纵轴西移500公里。
2、北京54坐标系:1954年我国在北京设立了大地坐标原点,采用克拉索夫斯基椭球体,依此计算出来的各大地控制点的坐标,称为北京54坐标系。
3、GS84坐标系:即世界通用的经纬度坐标系。
4、6度带、3度带、中央经线。
我国采用6度分带和3度分带:1∶2.5万及1∶5万的地形图采用6度分带投影,即经差为6度,从零度子午线开始,自西向东每个经差6度为一投影带,全球共分60个带,用1,2,3,4,5,……表示.即东经0~6度为第一带,其中央经线的经度为东经3度,东经6~12度为第二带,其中央经线的经度为9度。
1∶1万的地形图采用3度分带,从东经1.5度的经线开始,每隔3度为一带,用1,2,3,……表示,全球共划分120个投影带,即东经1.5~4.5度为第1带,其中央经线的经度为东经3度,东经4.5~7.5度为第2带,其中央经线的经度为东经6度.地形图上公里网横坐标前2位就是带号,例如:河北省1:5万地形图上的横坐标为20345486,其中20即为带号,345486为横坐标值。
在分层设色地形图中,绿色表示的地形是A高原B平原C山地D盆地一.什么是地图地图是按一定的数学法则和综合法则,以形象-符号表达制图物体(现象)的地理分布、组合和相互联系及其在时间中的变化的空间模型,它是地理信息的载体,又是信息传递的通道。
二.地图制图学及其理论基础地图制图学属地球科学中的一门学科。
主要是研究地图的实质(性质、内容及其表示方法)发展、制图理论和技术方法的的一门科学。
它的任务是获取各种类型的、高速优质的地图。
是制作地图的科学。
GIS学习笔记——地图投影与GPS参数计算要点
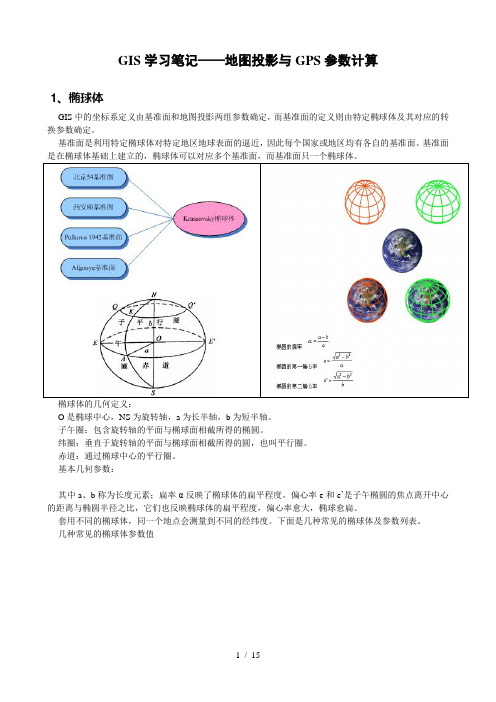
GIS学习笔记——地图投影与GPS参数计算1、椭球体GIS中的坐标系定义由基准面和地图投影两组参数确定,而基准面的定义则由特定椭球体及其对应的转换参数确定。
基准面是利用特定椭球体对特定地区地球表面的逼近,因此每个国家或地区均有各自的基准面。
基准面椭球体的几何定义:O是椭球中心,NS为旋转轴,a为长半轴,b为短半轴。
子午圈:包含旋转轴的平面与椭球面相截所得的椭圆。
纬圈:垂直于旋转轴的平面与椭球面相截所得的圆,也叫平行圈。
赤道:通过椭球中心的平行圈。
基本几何参数:其中a、b称为长度元素;扁率α反映了椭球体的扁平程度。
偏心率e和e’是子午椭圆的焦点离开中心的距离与椭圆半径之比,它们也反映椭球体的扁平程度,偏心率愈大,椭球愈扁。
套用不同的椭球体,同一个地点会测量到不同的经纬度。
下面是几种常见的椭球体及参数列表。
几种常见的椭球体参数值2、地图投影地球是一个球体,球面上的位置,是以经纬度来表示,我们把它称为“球面坐标系統”或“地理坐标系統”。
在球面上计算角度距离十分麻烦,而且地图是印刷在平面纸张上,要将球面上的物体画到紙上,就必须展平,这种将球面转化为平面的过程,称为“投影”。
经由投影的过程,把球面坐标换算为平面直角坐标,便于印刷与计算角度与距离。
由于球面無法百分之百展为平面而不变形,所以除了地球仪外,所有地图都有某些程度的变形,有些可保持面积不变,有些可保持方位不变,视其用途而定。
目前国际间普遍采用的一种投影,是即横轴墨卡托投影(Transverse Mecator Projection),又称为高斯-克吕格投影(Gauss-Kruger Projection),在小范围内保持形状不变,对于各种应用较为方便。
我们可以想象成将一个圆柱体橫躺,套在地球外面,再将地表投影到这个圆柱上,然后将圆柱体展开成平面。
圆柱与地球沿南北经线方向相切,我们将这条切线称为“中央经线”。
在中央经线上,投影面与地球完全密合,因此图形没有变形;由中央经线往東西两侧延伸,地表图形会被逐渐放大,变形也会越来越严重。
大地测量坐标系有哪些参数

大地测量坐标系有哪些参数大地测量是地球科学中的一项重要技术,它用于测量地球上不同地点的位置,并建立起一套准确的坐标系统。
在大地测量中,我们使用了一些参数来描述和定义地球的形状和大小。
下面将介绍大地测量中常用的几个参数。
1.椭球体参数在大地测量中,常常使用椭球体来代表地球的形状。
椭球体可以通过长半轴(a)和短半轴(b)来描述,在实际应用中我们常用椭球的扁率(f)来表示。
扁率是一个无单位的数值,定义为f = (a - b) / a,它描述了地球椭球体的偏率程度。
2.偏心率和第一偏心率偏心率(e)是椭球体参数中的一个重要指标,它表征了地球椭球体的扁平程度。
偏心率的计算公式为e = sqrt((a^2 - b^2) / a^2),其中sqrt表示开方运算。
它的数值范围是0到1之间。
第一偏心率(e1)是一个与偏心率相关的参数,它的计算公式为e1 =sqrt((a^2 - b^2) / b^2)。
与偏心率类似,第一偏心率的数值范围也是0到1之间。
3.地球的扁率和倾角地球的扁率是指地球赤道半径和极半径之间的比值。
它可以通过椭球体的扁率来计算,即扁率 = (a - b) / a。
扁率的数值越大,说明地球的赤道更加扁平。
地球的倾角是指地球自转轴与黄道面的夹角。
地球的倾角约为23.5度,这导致了地球的季节变化和极昼极夜的出现。
4.基准面参数大地测量中使用的基准面是一个近似于平均海平面的参考面。
基准面参数包括基准椭球体的参数和重力参数。
基准椭球体的参数主要包括长半轴、短半轴和扁率。
常用的国际基准椭球体有WGS84和CGCS2000等。
重力参数指的是地球重力场的相关参数,包括重力常数和重力梯度等。
重力参数的测定对于利用重力进行大地测量和地质勘探具有重要意义。
总结起来,大地测量坐标系中常用的参数包括椭球体参数、偏心率和第一偏心率、地球的扁率和倾角,以及基准面参数。
这些参数的使用和计算对于地球测量的精度和准确性有着重要的影响,是进行坐标测量和定位的基础。
我国三大坐标系讲解

我国三大常用坐标系区别(北京54、西安80和WGS-84)我国三大常用坐标系区别(北京54、西安80和WGS-84)1、北京54坐标系(BJZ54)北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。
1954年北京坐标系的历史:新中国成立以后,我国大地测量进入了全面发展时期,再全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。
由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。
因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。
它的原点不在北京而是在前苏联的普尔科沃。
北京54坐标系,属三心坐标系,长轴6378245m,短轴6356863,扁率1/298.3;2、西安80坐标系1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。
为此有了1980年国家大地坐标系。
1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据,即IAG 75地球椭球体。
该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇,位于西安市西北方向约60公里,故称1980年西安坐标系,又简称西安大地原点。
基准面采用青岛大港验潮站1952-1979年确定的黄海平均海水面(即1985国家高程基准)。
西安80坐标系,属三心坐标系,长轴6378140m,短轴6356755,扁率1/298.257221013、WGS-84坐标系WGS-84坐标系(World Geodetic System)是一种国际上采用的地心坐标系。
坐标原点为地球质心,其地心空间直角坐标系的Z轴指向国际时间局(BIH)1984.0定义的协议地极(CTP)方向,X轴指向BIH1984.0的协议子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系。
椭球参数

WGS-84坐标系(World Geodetic System一1984 Coordinate System)一种国际上采用的地心坐标系。
坐标原点为地球质心,其地心空间直角坐标系的Z轴指向BIH (国际时间)1984.O定义的协议地球极(CTP)方向,X轴指向BIH 1984.0的零子午面和CTP赤道的交点,Y轴与Z轴、X轴垂直构成右手坐标系,称为1984年世界大地坐标系统。
GPS广播星历是以WGS-84坐标系为根据的编辑本段WGS-84的定义:原点是地球的质心,空间直角坐标系的Z轴指向BIH(1984.0)定义的地极(CTP)方向,即国际协议原点CIO,它由IAU和IUGG共同推荐。
X轴指向BIH定义的零度子午面和CTP赤道的交点,Y轴和Z,X轴构成右手坐标系。
WGS-84椭球采用国际大地测量与地球物理联合会第17届大会测量常数推荐值,采用的两个常用基本几何参数。
WGS-84是修正NSWC9Z-2参考系的原点和尺度变化,并旋转其参考子午面与BIH定义的零度子午面一致而得到的一个新参考系,WGS-84坐标系的原点在地球质心,Z轴指向BIH1984.0定义的协定地球极(CTP)方向,X轴指向BIH1984.0的零度子午面和CTP赤道的交点,Y轴和Z、X轴构成右手坐标系。
它是一个地固坐标系。
编辑本段WGS-84椭球及其有关常数:介绍WGS-84采用的椭球是国际大地测量与地球物理联合会第17届大会大地测量常数推荐值,其四个基本参数公式长半径:a=6378137±2(m);地球引力和地球质量的乘积:GM=3986005×108m3s-2±0.6×108m3s-2;正常化二阶带谐系数:C20=-484.16685×10-6±1.3×10-9;地球重力场二阶带球谐系数:J2=108263×10-8地球自转角速度:ω=7292115×10-11rads-1±0.150×10-11rads-1 扁率f=0.003352810664北京54坐标系(BJZ54)北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系,其坐标详细定义可参见参考文献[朱华统 1990]。
地球椭球的基本几何参数及相互关系

地球椭球的基本几何参数及相互关系§7.1地球椭球的基本几何参数及相互关系7.1.1地球椭球的基本几何参数地球椭球参考椭球 具有一定的几何参数、定位及定向的用以代表某一地区大地水准面的地球椭球叫做参考椭球。
地面上一切观测元素都应归算到参考椭球面上,并在该面上进行计算,它是大地测量计算的基准面,同时又是研究地球形状和地图投影的参考面。
有关元素O 为椭球中心;NS 为旋转轴;a 为长半轴;b 为短半轴;子午圈(或径圈或子午椭圆);平行圈(或纬圈);赤道。
旋转椭球的形状和大小是由子午椭圆的五个基本几何参数(元素)来决定的,即:椭圆的长半轴: a椭圆的短半轴: b椭圆的扁率: α=-a b a (7-1)椭圆的第一偏心率: ab a e 22-= (7-2) 椭圆的第二偏心率: b b a e 22 -=' (7-3)其中:a 、b 称为长度元素;扁率α反映了椭球体的扁平程度,如α=0时,椭球变为球体;α=1时,则为平面。
e 和e /是子午椭圆的焦点离开中心的距离与椭圆半径之比,它们也反映了椭球体的扁平程度,偏心率越大,椭球愈扁。
五个参数中,若知道其中的两个参数就可决定椭球的形状和大小,但其中至少应已知一个长度元素(如a 或b ),人们习惯于用a 和α表示椭球的形状和大小,便于级数展开。
引入下列符号:ba c 2= tgB t =B e 222cos '=η (7-4)式中B 为大地纬度,c 为极曲率半径(极点处的子午线曲率半径), 两个常用的辅助函数,W 第一基本纬度函数,V 第二基本纬度函数, B e V Be W 2222cos 1sin 1'+=-= (7-5)传统大地测量利用天文大地测量和重力测量资料推求地球椭球的几何参数,自1738年(法国)布格推算出第一个椭球参数以来,200多年间各国大地测量工作者根据某一国或某一地区的资料,求出了数目繁多,数值各异的椭球参数。
不同类型地图使用的投影与坐标系

一、地球模型地球是一个近似椭球体,测绘时用椭球模型逼近,这个模型叫做参考椭球,如下图:赤道是一个半径为a的近似圆,任一圈经线是一个半径为b的近似圆。
a称为椭球的长轴半径,b称为椭球的短轴半径。
a≈6378.137千米,b≈6356.752千米。
(实际上,a也不是恒定的,最长处和最短处相差72米,b的最长处和最短处相差42米,算很小了)地球参考椭球基本参数:长轴:a短轴:b扁率:α=(a-b) / a第一偏心率:e=√(a2-b2) / a第二偏心率:e'=√(a2-b2) / b这几个参数定了,参考椭球的数学模型就定了。
什么是大地坐标系?大地坐标系是大地测量中以参考椭球面为基准面建立起来的坐标系。
地面点的位置用大地经度、大地纬度和大地高度表示:(L, B, H)。
空间直角坐标系是以参考椭球中心为原点,以原点到0度经线与赤道交点的射线为x 轴,原点到90度经线与赤道交点的射线为y轴,以地球旋转轴向北为z轴:(x, y, z)共同点:显然,这两种坐标系都必须基于一个参考椭球。
不同点:大地坐标系以面为基准,所以还需要确定一个标准海平面。
而空间直角坐标系则以一个点为基准,所以还需要确定一个中心点。
只要确定了椭球基本参数,则大地坐标系和空间直角坐标系就相对确定了,只是两种不同的表达而矣,这两个坐标系的点是一一对应的。
二、北京54,西安80,WGS84网上的解释大都互相复制,语焉不详,隔靴搔痒,说不清楚本质区别。
为什么在同一点三者算出来的经纬度不同?难道只是不认同对方的测量精度吗?为什么WGS84选地球质心作原点,而西安80选地表上的一个点作原点?中国选的大地原点有什么作用?为什么选在泾阳县永乐镇?既然作为原点,为什么经纬度不是0?下面是我个人的理解。
首先,三者采用了不同的参考椭球建立模型,即长短轴扁率这组参数是不同的。
北京54:长轴6378245m,短轴6356863,扁率1/298.2997381西安80:长轴6378140m,短轴6356755,扁率1/298.25722101WGS84:长轴6378137.000m,短轴6356752.314,扁率1/298.257223563,第一偏心率0.0818********,第二偏心率0.082095040121这些参数不同,决定了椭球模型的几何中心是不同的。
测绘技术中的地球形状参数与大地测量方法

测绘技术中的地球形状参数与大地测量方法在现代科技日益发达的今天,测绘技术在人们的生活中扮演着至关重要的角色。
测绘技术通过测量和记录地球上各个地点的准确位置和地形,为各行各业提供了宝贵的空间数据。
而为了准确地进行测绘工作,我们需要了解地球的形状参数和大地测量方法。
地球作为人类赖以生存的家园,其形状早已超越了普通的圆球模型。
根据地球上不同经纬度处的曲率半径以及地球自身的自转引起的离心力,地球可以近似看作一个稍微扁平的椭圆体,这个椭圆体被称为“地球椭球体”。
地球椭球体的形状可以通过一些参数来描述,最常用的是“椭球体标准参数”,其中包括椭球体长半轴a、短半轴b、扁率f和第一偏心率e。
椭球体的长半轴a是指通过地球两个地理极点的向量的长度,而短半轴b则是经过赤道和两个地理极点中点的向量的长度。
扁率f是指椭球体的扁平程度,可以通过公式f = (a - b)/a来计算。
第一偏心率e是用来描述椭圆体与其切平面的倾斜程度的参数,可以通过公式e = √(a^2 - b^2)/a来计算。
了解地球的形状参数有利于正确理解和处理测量数据。
在实际测绘工作中,我们常常需要利用大地测量方法来测量地球表面上的各点位置和地形。
大地测量是指利用测量仪器进行地球上点位位置和高程的测量的方法。
而要实现准确的大地测量,我们需要考虑到地球的形状以及大地测量中常用的方法。
在大地测量中,最常见的方法之一就是三角测量法。
三角测量法通过测量地球上的三角形,再利用三角形的边长和角度信息,求解未知位置的坐标。
三角测量法的原理是基于数学中的三角关系,通过测量不同位置处的角度和边长,可以计算出目标点的坐标。
除了三角测量法,大地测量中还常用的方法包括电磁测量法、全球定位系统(GPS)测量法和测角法等。
电磁测量法利用电磁波在空气中传播的速度和方向的差异,测量出目标点的位置和高程。
全球定位系统则是通过卫星定位技术,通过接收多颗卫星信号,计算出接收器的位置坐标。
测角法是利用测量仪器测量目标点与参考点之间的水平角或垂直角,进而计算目标点的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
序号 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 GRS80 WGS72 Australian Krassovsky 1948(1954年北京坐系) International1924 Hayford 1909 Clarke1880 Clarke1866 Clarke1866(modifiedforMichigan) Airy1930 Bessel1841 Everest1830 Sphere Airy1930(modifiedforIreland1965) Bessel1841(modifiedforSchwarzeck) Clarke1880(modifiedforArc1950) Clarke1880(modifiedforMerchich) Everest1830(modifiedforKertau) Fischer1960 Fischer1960(modifiedforSouthAsia) Fischer1968 GRS67 Helmert1906 椭球体名称 长轴半径 6378137 6378135 6378160 6378245 6378388 6378388 6378249.145 6378206.4 6378450.047 6377563.396 6377397.155 6377276.345 6370997 6377340.189 6377483.865 6378249.145 6378249.2 6377304.063 6378166 6378155 6378150 6378160 6378200 扁率的倒数 298.2572221 298.26 298.25 298.3 297 297 293.465 294.9786982 294.9786982 299.3249646 299.1528128 300.8017 0 299.3249646 299.1528128 293.4663076 293.46598 300.8017 298.3 298.3 298.3 298.2471674 298.3
地球椭球体参数列表
序号 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 Hough SouthAmerican WarOffice WGS60 WGS66 WGS84 IAG 75(1980年西安坐标系) Clarke1880(modifiedforIGN) MERIT83 NewInternational1967 Walbeck Bessel1841(modifiedforNGO1948) Clarke1858 Clarke1880(modifiedforJamaica) Clarke1880(modifiedforPalestine) Everest1830(modifiedforTimbalai) Everest1830(modifiedforKalianpur) Indonesian NWL9D NWL10D OSU86F OSU91A Plessis1817 Struve1860 椭球体名称 长轴半径 6378270 6378160 6378300.583 6378165 6378145 6378137 6378140 6378249.2 6378137 6378157.5 6376896 6377492.018 6378293.639 6378249.136 6378300.79 6377298.556 6377301.243 6378160 6378145 6378135 6378136.2 6378136.3 6376523 6378297 扁率的倒数 297 298.25 296 298.3 298.25 298.2572236 298.257222 293.4660213 298.257 298.25 302.78 299.15281 294.26068 293.46631 293.46623 300.8017 300.80174 298.247 298.25 298.26 298.25722 298.25722 308.64 294.73
基本参 数编辑
2000国家大 地坐标系是全 球地心坐标系 在我国的具体 体现,其原点 为包括海洋和 大气的整个地 球的质量中心 。Z轴指向 BIH1984.0定 义的协议极地 方向(BIH国 际时间局), X轴指向 BIH1984.0定 义的零子午面 与协议赤道的 交点,ቤተ መጻሕፍቲ ባይዱ轴按 右手坐标系确 定。2000国 家大地坐标系 采用的地球椭 球参数如下: 长半轴 a=6378137m 扁率 f=1/298.2572 22101 地心引力常数 GM=3.98600 4418× 1014m3s-2 自转角速度 ω=7.292l15× 10-5rad s-1
