电机转动惯量的计算
减速机与伺服电机的惯量计算

减速机与伺服电机的惯量计算减速机和伺服电机是我们经常使用的工业机械设备,在很多行业中都有广泛应用。
在设计和选型这两种设备时,我们需要考虑到它们的惯量。
下面将从以下几个方面来介绍减速机和伺服电机的惯量计算方法。
一、减速机的惯量计算减速机是将电机的高速低扭转换为低速高扭输出的装置。
在计算减速机惯量时,需要知道减速机的转动惯量,通过公式可以计算出来。
1.计算传动部分的惯量传动部分包括传动齿轮,连轴器等机构的惯量。
通常采用质量乘以半径的平方公式计算,并将结果转换为转动惯量。
例如,如果连轴器的质量为0.5千克,半径为5厘米,则其转动惯量为0.000625 kg·m²。
2.计算减速器齿轮的惯量减速器的内部齿轮也会给减速器带来一定的转动惯量。
可以将其转动惯量计算为齿轮的质量乘以半径的平方,然后除以齿轮的速比平方。
例如,如果齿轮质量为1千克,半径为10厘米,速比为40,则可以得到其转动惯量为0.025 kg·m²。
3.计算输出轴的惯量输出轴的转动惯量可以通过将其质量乘以半径的平方来计算,跟传动部分的公式类似。
例如,如果输出轴的质量为10千克,半径为15厘米,则其转动惯量为3.375 kg·m²。
二、伺服电机的惯量计算伺服电机是一种控制精度高,运转稳定的电机设备。
在伺服电机的设计和工作中,惯量也是一个非常重要的参数。
惯量越小,转速和位置就更容易控制。
下面介绍如何计算伺服电机的转动惯量。
1.计算电机惯量电机的转动惯量可以通过将电机的质量乘以半径的平方计算得出。
例如,电机质量为2千克,半径为10厘米,则其转动惯量为0.02 kg·m²。
2.计算驱动部分惯量驱动部分通常包括齿轮、皮带等传动装置,以及电机轴端的编码器等。
驱动部分的转动惯量可通过上述公式计算得出。
3.计算工作部件惯量工作部件通常指电机所带动的轴,例如平移轴、倾斜轴等。
其转动惯量也可通过使用公式来计算。
电机阻尼系数和转动惯量

电机阻尼系数和转动惯量电机阻尼系数和转动惯量是电机运动过程中的两个重要参数,对于电机的运动特性和性能具有重要影响。
本文将从理论和实际应用两个方面,分别介绍电机阻尼系数和转动惯量的概念、计算方法以及它们对电机运动的影响。
一、电机阻尼系数电机阻尼系数是描述电机转动过程中阻力大小的一个参数,它表示了电机受到的阻力对转动运动的阻碍程度。
阻尼系数越大,表示电机所受阻力越大,转动过程越缓慢;阻尼系数越小,表示电机所受阻力越小,转动过程越迅速。
计算电机阻尼系数的方法有多种,常见的有通过实验测量和理论计算两种方式。
实验测量方法是将电机转动一定角度,并记录转动过程中所受到的阻力大小,然后通过计算得到阻尼系数。
理论计算方法则是根据电机的结构参数和运动方程,通过数学模型计算得到阻尼系数。
电机阻尼系数对电机运动有着重要影响。
当阻尼系数较大时,电机的转动速度较慢,响应时间较长,适用于一些对转动速度要求不高的应用;当阻尼系数较小时,电机的转动速度较快,响应时间较短,适用于一些对转动速度要求较高的应用。
二、转动惯量转动惯量是描述物体抵抗转动的惯性大小的一个参数,它表示了物体在转动过程中惯性的大小。
转动惯量越大,表示物体越难以改变其转动状态;转动惯量越小,表示物体越容易改变其转动状态。
计算转动惯量的方法也有多种,常见的有几何形状法和质量分布法两种。
几何形状法是根据物体的几何形状和尺寸,通过数学公式计算得到转动惯量。
质量分布法则是根据物体的质量分布情况,将物体分成若干小部分,然后分别计算每个小部分的转动惯量,最后将它们相加得到总的转动惯量。
转动惯量对电机运动同样具有重要影响。
当转动惯量较大时,电机转动时需要克服较大的惯性阻力,响应时间较长,适用于一些对转动速度要求不高的应用;当转动惯量较小时,电机转动时惯性阻力较小,响应时间较短,适用于一些对转动速度要求较高的应用。
总结起来,电机阻尼系数和转动惯量是电机运动过程中的两个重要参数。
电机转动惯量计算公式

电机转动惯量计算公式
电机转动惯量是指电机在相同转速下所需的力矩大小,它是电机的一项重要参数。
电机转动惯量的大小取决于电机的物理结构,它可以通过一个特定的公式来计算。
电机转动惯量的计算公式如下:
J = (1/2)mvr2
其中,J是电机转动惯量,单位是千克·米2/秒2;m是转子的质量,单位是千克;v是转子的半径,单位是米;r是转速,单位是转/秒。
电机转动惯量的大小与转子的质量、半径和转速有关,当转子的质量、半径和转速增大时,电机转动惯量也会增大;当转子的质量、半径和转速减小时,电机转动惯量也会减小。
此外,电机转动惯量还受到电机物理结构的影响,比如电机的转子形状、磁芯材料以及绕组的结构都会影响电机转动惯量的大小。
电机转动惯量的计算公式可以帮助设计人员更好地了解电机的特性,帮助他们设计出更加合适的电机。
电机转动惯量的计算公式也可以帮助维修人员预测电机的表现,诊断电机的故障。
总的来说,电机转动惯量的计算公式是一个重要的工具,可以帮助设计人员更好地了解电机的特性,也可以帮助维修人员预测电机的
表现,诊断电机的故障。
伺服电机的选型和转动惯量的计算

伺服电机的选型和转动惯量的计算伺服电机是一种采用反馈控制系统的电机,常用于需要精确控制转动位置、速度和力矩的应用中。
选型和转动惯量的计算是为了确保电机能够满足系统的性能要求。
在进行伺服电机的选型时,需要考虑以下几个方面:1.负载特性:了解所需控制的负载类型,包括负载的惯性矩、负载对电机的回复要求等。
这些参数将对电机的性能和选型产生重要影响。
2.控制要求:了解所需控制的性能指标,包括位置精度、速度范围、加速度、力矩等。
这些参数将对电机的动态响应和控制能力产生重要影响。
3.环境条件:了解电机将运行的环境条件,包括温度、湿度、腐蚀性等。
这些条件将对电机的耐久性和可靠性产生重要影响。
4.使用寿命:了解电机的使用寿命要求,考虑使用寿命与成本之间的平衡。
基于以上要求,在伺服电机的选型中,我们可以通过以下几个步骤进行:步骤一:确定负载特性首先,需要对负载进行分析和测量,得到负载的特性参数,包括负载的惯性矩、负载对电机的回复要求等。
可以使用力矩传感器或测量设备来测量负载的特性。
步骤二:确定控制要求根据实际应用需求,确定所需的控制要求,包括位置精度、速度范围、加速度、力矩等。
可以根据系统的动态特性和控制性能要求,计算出所需的电机性能参数。
步骤三:选型电机根据负载特性和控制要求,选择适当的伺服电机。
可以根据电机供应商提供的产品目录、技术规格和性能曲线,进行比较和选择。
步骤四:计算转动惯量转动惯量是描述绕轴旋转运动的物体对转动的惯性程度的物理量。
对于伺服电机系统,转动惯量对于控制系统的动态响应和稳定性非常重要。
计算转动惯量的方法可以有多种,以下是其中一种常见的计算方法:1.将负载模型化为旋转惯性将负载视为固定于电机轴上的旋转质点,假设负载的转动惯量为J_l。
2.估算负载的转动惯量根据负载的形状和结构,可以使用以下公式估算负载的转动惯量:J_l=m*l^2其中,m为负载的质量,l为负载的一个特定距离。
3.计算电机和驱动部分的转动惯量电机和驱动部分的转动惯量可通过电机制造商提供的数据手册和技术规格进行查找。
电机转动惯量的计算

电机转动惯量的计算电机转动惯量是指电机在旋转过程中抵抗改变角速度的能力,通常用转动惯量(J)来表示。
具体来说,转动惯量是指一个物体在旋转轴上的转动质量特性,可以通过计算来得到。
在电机中,转动惯量的计算是非常重要的,它常常用来预测转矩与加速度之间的关系,以及转速与输出功率之间的关系,因此对于电机的设计和控制都至关重要。
计算电机转动惯量的方法有多种,下面将介绍几种常见的计算方法。
1.刚体模型计算法刚体模型计算法是基于刚体理论的一种计算方法,其基本思想是将电机模型化为一个刚体,利用刚体转动惯量的计算公式进行计算。
对于简单的电机结构,如均匀圆柱形电机,可以直接使用公式进行计算。
对于圆柱形电机来说,其转动惯量公式为:J=(1/2)*m*r^2其中,J为转动惯量,m为电机的质量,r为电机的半径。
对于一些复杂结构的电机,可以将其分解为若干个简单的部分,然后分别计算每个部分的转动惯量,再将其相加得到整体的转动惯量。
2.数值计算法数值计算法是一种利用数值方法进行转动惯量计算的方法,它将电机模型离散化,然后通过数值积分的方法来计算转动惯量。
最常用的数值计算方法是有限元法(FEM)和有限差分法(FDM)。
有限元法是一种基于划分离散单元的数值计算方法,它将电机模型划分为若干个小单元,然后对每个小单元进行转动惯量的计算,最后将各个小单元的转动惯量进行求和得到整体的转动惯量。
有限差分法是一种基于差分逼近的数值计算方法,它将电机模型进行网格化,然后通过差分逼近的方法来计算转动惯量。
具体而言,有限差分法利用差分逼近的思想,将微分方程离散化为代数方程组,然后通过求解代数方程组来计算转动惯量。
数值计算法的优点是可以处理复杂的电机结构,并且具有较高的计算精度,但是计算过程相对复杂,需要使用专门的计算软件进行计算。
3.经验值法经验值法是一种通过电机的实际运行数据来估计转动惯量的方法,它基于大量的实验数据和经验公式,通过与实际测量数据进行对比来估计转动惯量。
常用机构的转动惯量与扭矩的计算
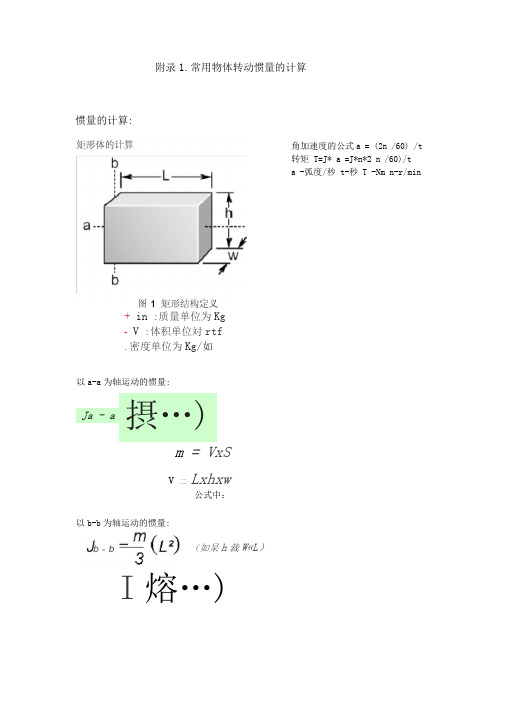
附录1.常用物体转动惯量的计算角加速度的公式a = (2n /60) /t 转矩 T=J* a =J*n*2 n /60)/t a -弧度/秒 t-秒 T -Nm n-r/min+ in :质量单位为Kg + V :体积单位対rtf .密度单位为Kg/如以a-a 为轴运动的惯量:m = VxSV 二 Lxhxw公式中:以b-b 为轴运动的惯量:I 熔…)惯量的计算:Ja - a摂…)(如杲h 裁W«L)圆柱体的惯量m = Vx3Di ~2 J 中严虽兰2 8空心柱体惯量TTD12"T"xL图2圆柱体定义图3空心柱体定义V^2-D'K L4图4-1摆臂1结构定义J = m.R3J = m R2 + mi ri2图5曲柄连杆结构定义J N :电或1S 量 J L :负载惯量J LOH :负载惯量折茸到电机侧前慣量 M L :负载转矩J R :减速机折算到输入的15量R :减速比H K :喩速机效率R=6JW = X Bf = ff X 0)L&L 3L■根爵能量守恒定律:图6带减速机结构定义Jx 丁二 J M + J R Z ,■总惆J M :电机愦童Ji :负戦惯量 M:负载力矩Jp M :电机側苻轮噴量 □PM :丐机恻帝轮直径M TM :电机侧带轮肯数J PI :负敎侧带轮惯量D PL ;负载带轮直JpLs Dp|_.6/w = R <&L 3M = Rx C JI )LA/TX Dpi./V™ D PM■ SfMSiJ 电机绘N TIL;煲载带轮齿数q:减谨机效率:皮带原量mB图7齿形带传动结构Ju :电机惯量J L:负载惯量M L :负载理矩J GM:电机侧齿轮憤量N TM :电机侧齿轮齿数J GL :负载齿轮惯量N IL:负载齿输齿数n:诚速机效率R- - 9'w - R^6L O>J0=R^O)L/Vw■总惯量:■折算到电机惯量:■折算到电机力矩:图8齿轮组传动结构J M:电机惯量Jc :连接轴惯量M L :负载质量X L:负载位置VL:负载速度mi:滑台质量FP:做功力Fg :重力Ffr:摩擦力Js :丝杠惯量p :丝杠嫌距(mm/rev)c:丝杠角廈n:丝杠效率P:摩擦系数g:重力加遽度■总惯量I折算到电机的力矩Jrr2CC门X5/”-AIr*B”sPJ>*I--.^fj--JJILT1mffJJ十4■I「-一--图9丝杠传动结构N TPI, PC PI =T?D I =Nrp^pA X L V LC7M 二------- 3皿—--------C PI Q P/J M:电机惯量m L :负载质量X L;负载位置V L:负载速度m B:传送带质量FP:作用力Fg :重力Ffr :摩擦力Jp x :瞬惯量6:辗轴直径N TPI:主眾齿数p :传送带导程(mm/tooth)C PI:主報闾也Q:倾角n:传送带效率p:摩擦系数g :引力系数图io传送带结构折算到电机的惯量F严血+ 加 >*fr —■ I irj t i /ijs IX g X Li X COo£3f MrJ G , N TG 5 P G C G - TT D G - N TG P G 9M =X L cZ V LGU M=——C GJ M :电机惯量 m L :负载质量 X L :负载位置 V L :负载速度F P :作用力F g :重力Ffr :摩擦力J G :齿轮惯量 D G :齿轮直径N TG :齿轮齿数P G :齿轮尊程(mm/tooth) C G :齿轮周长 a :轴运动角度 q:齿轮传动效率 M:摩擦系数 g:引力参数J w 二X 十人十J …图11齿轮齿条结构定义 总惯量:■折算到电机的悄量:■折算到电机的力矩:仁 U C \pLM IL卫 + 厂^ + i/r jLJGLJ1'-j]E = (m + mjxgxs 旧&■十m^jxgy/Jxcosa1,确认您的负载额定扭矩要小于减速机额定输出扭矩,2,伺服电机额定扭矩*减速比要大于负载额定扭矩。
电机转动惯量计算公式

电机转动惯量计算公式
电机转动惯量是电机的一个重要参数,它代表电机的转动惯量大小,影响着电机的转速、加速度和动力,因此,电机转动惯量的计算是电机设计和制造过程中必不可少的一步。
电机转动惯量的计算公式如下:
惯量J = m*r^2
其中,m为电机的质量,r为电机的转动半径。
电机转动惯量的计算公式比较简单,但实际计算过程中仍需要注意以下几点:
1. 计算电机转动惯量时,必须使用正确的电机质量m和转动半径r,以确保计算结果的准确性。
2. 电机质量m包括电机本身的质量和附件的质量,因此,在计算电机转动惯量时,一定不要忽略附件的质量。
3. 电机转动半径r是电机外缘到转轴的距离,因此,在计算电机转动惯量时,需要准确测量电机外缘到转轴的距离。
4. 电机转动惯量的计算结果受到电机本身的结构和工艺条件的影响,因此,在计算电机转动惯量时,需要根据电机的实际结构和工艺条
件进行修正。
总之,电机转动惯量的计算是电机设计和制造过程中不可或缺的一部分,正确使用电机转动惯量计算公式,是电机质量和性能的重要保证。
伺服电机的选型和转动惯量的计算

伺服电机的选型和转动惯量的计算引言:伺服电机是一种能够实现精确定位和速度控制的电动机。
在自动化控制系统中,伺服电机广泛应用于机械装置的定位与运动控制,如机床、工业机械手臂、机器人等。
为了确保控制系统的性能和稳定性,正确选型和计算转动惯量是非常重要的。
一、伺服电机选型1.负载特性分析:首先需要对负载特性进行分析,包括负载的质量、摩擦系数、惯性矩等。
这些参数影响到伺服电机的选择,如电机的额定转矩等。
在分析负载特性时需要考虑静态特性和动态特性。
2.运行速度要求:根据系统的运行速度要求,选择电机的额定转速。
如果要求快速响应,需要选择具有较高转速的电机;如果要求大转矩输出,需要选择具有较大额定转矩的电机。
3.控制方式:根据系统的控制方式,选择合适的伺服电机。
常见的控制方式有位置控制、速度控制和力控制。
不同的控制方式对电机的性能要求也不同。
4.转矩和转速曲线:了解电机的转矩和转速曲线,可以帮助选择合适的伺服电机。
转矩曲线决定了电机能够产生的最大转矩,转速曲线决定了电机能够输出的最大转速。
5.电机功率:根据负载特性和运行速度要求,计算出所需的电机功率。
一般情况下,应选择稍大于所需功率的电机,以保证系统的可靠性和安全性。
6.品牌和价格:最后根据伺服电机的品牌和价格进行选择。
国际知名品牌的产品质量较高,但价格也较高。
可以根据实际需求和预算进行选择。
转动惯量是描述物体抗拒改变转动状态的特性。
在伺服电机的选型和控制系统设计中,转动惯量是一个重要的参数。
计算转动惯量的一般公式为:J=m*r^2其中,J是转动惯量,m是物体的质量,r是物体相对转轴的距离。
如果物体是一个均匀的圆盘或圆柱体,根据其几何形状可以通过以下公式计算转动惯量:J=1/2*m*r^2其中,m是物体的质量,r是物体的半径。
如果物体是由多个部分组成,可以通过将各部分的转动惯量相加得到整体的转动惯量。
在实际应用中,还需要考虑其他因素对转动惯量的影响,如内部零件的分布、负载的摩擦系数等。
电机选型计算公式总结
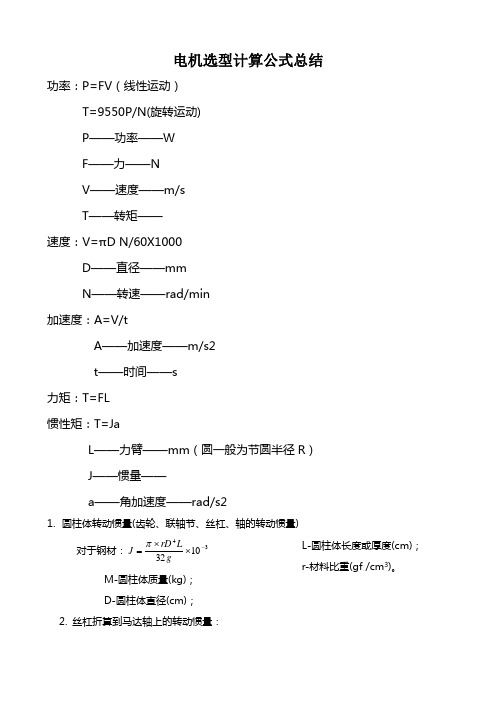
电机选型计算公式总结功率:P=FV (线性运动)T=9550P/N(旋转运动)P ——功率——WF ——力——NV ——速度——m/sT ——转矩——速度:V=πD N/60X1000D ——直径——mmN ——转速——rad/min加速度:A=V/tA ——加速度——m/s2t ——时间——s力矩:T=FL惯性矩:T=JaL ——力臂——mm (圆一般为节圆半径R ) J ——惯量——a ——角加速度——rad/s21. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)对于钢材:341032-⨯⨯=g LrD J π M-圆柱体质量(kg);D-圆柱体直径(cm);L-圆柱体长度或厚度(cm);r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·c m·s 2) J si-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w 2s 2⎪⎭⎫ ⎝⎛=π (kgf·角加速度a=2πn/60t v -工作台移动速度(cm/min);n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2;s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:J 1-齿轮z 1及其轴的转动惯量;J 2-齿轮z 2的转动惯量(kgf ·cm ·s 2);J s -丝杠转动惯量(kgf ·cm ·s 2);s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2g w R J = (kgf ·c m·s 2) R-w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量J 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf ·c m·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
电机转动惯量的计算

为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。下面给出一些
(绕定轴转动时)的刚体动力学公式
角加速度与合外力矩的关系:
角加速度与合外力矩 式中M为合外力矩,B为角加速度。可以看出这个式子与牛顿第二定
律是对应的。角动量:
角动量
刚体的定轴转动动能:
转动动能
注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动
能。
只用E=(1/2)mvA2不好分析转动刚体的问题,是因为其中不包含刚 体的任何转动信息,里面的速度v只代表刚体的质心运动情况。由这 一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体
对于细圆环
当回转轴通过中心与环面垂直时,J=mRA2当回转轴通过边缘与环
面垂直时,J=2mRA2 R为其半径
对于薄圆盘
当回转轴通过中心与盘面垂直时,J=(1/2)mRA2当回转轴通过
边缘与盘面垂直时,j=(3/2)mRA2R为其半径
对于空心圆柱当回转轴为对称轴时,J=(1/2)m[(R1)A2+(R2)A2];R1和R2
表达式:lz=Ix+Iy式中lx,ly,lz分别代表刚体对x,y,z三轴的转动惯量.对于非平面
薄板状的刚体,亦有如下垂直轴定理成立[2]:
垂直轴定理
利用垂直轴定理可对一些刚体对一特定轴的转动惯量进行较简便的
计算•
刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该 轴所形成的转动惯量。由此折算所得的质点到转轴的距离,称为刚
体绕该轴的回转半径K,其公式为 匸MK八2,式中M为刚体质量;I为转动惯量
伺服电机的转动惯量计算公式

伺服电机的转动惯量计算公式英文回答:The formula for calculating the moment of inertia of a servo motor is as follows:I = (m r^2) + I0。
Where:I is the moment of inertia of the servo motor.m is the mass of the rotor.r is the distance from the axis of rotation to the center of mass of the rotor.I0 is the moment of inertia of the rotor about its own axis.To calculate the moment of inertia, you need to know the mass of the rotor and its distribution. The mass can be determined by weighing the rotor, and the distribution can be determined by measuring the distance from the axis of rotation to the center of mass. The moment of inertia of the rotor about its own axis can be obtained from the manufacturer's specifications or by performing tests.Let's consider an example to illustrate the calculation of the moment of inertia of a servo motor. Suppose we havea servo motor with a rotor mass of 0.5 kg and a radius of0.1 meters. The moment of inertia about its own axis is given as 0.02 kgm^2.Using the formula mentioned above, we can calculate the moment of inertia as follows:I = (0.5 0.1^2) + 0.02。
转动惯量计算折算公式
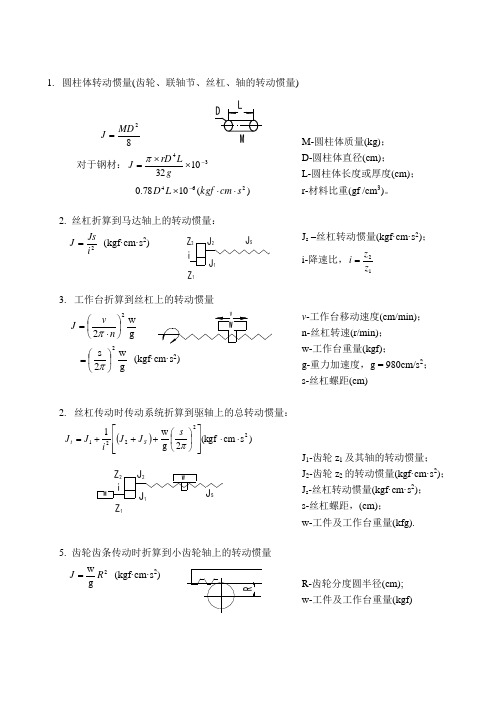
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2iJs J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
电机轴转动惯量

电机轴转动惯量电机轴转动惯量是描述电机转动惯性的物理量,它在电机设计和运行中起着重要的作用。
本文将从电机轴转动惯量的定义、计算方法以及其在实际应用中的意义等方面进行探讨。
电机轴转动惯量是指电机轴对转动运动的惯性阻力。
它反映了电机转动过程中质量分布对转动惯性的影响。
电机轴转动惯量的计算需要考虑电机的几何形状和质量分布情况。
一般来说,电机轴转动惯量越大,电机转动越不容易改变其转速。
计算电机轴转动惯量的方法有多种,其中一种常用的方法是通过积分计算。
具体而言,可以将电机轴分成无数个微小的质量元,然后对每个质量元的质量和距离轴心的距离进行积分求和。
这样就可以得到电机轴转动惯量的数值。
电机轴转动惯量在电机设计和运行中具有重要的意义。
首先,它可以用来评估电机的转动性能。
转动惯量越大,电机的转速变化越慢,转动平稳性越好。
其次,电机轴转动惯量还与电机的加速度和制动过程有关。
在电机启动和停止时,转动惯量的大小会影响电机的响应速度和能耗。
因此,在电机设计中,需要根据具体应用需求来选择合适的电机轴转动惯量。
电机轴转动惯量还与电机的动态特性和控制系统设计密切相关。
在电机控制系统中,转动惯量是一个重要的参数,它影响着电机的响应速度和稳定性。
合理选择电机轴转动惯量可以提高电机的控制性能,使其更好地适应不同的工作条件和控制要求。
电机轴转动惯量是描述电机转动惯性的重要物理量。
它的计算方法多样,可以通过积分等方式进行求解。
电机轴转动惯量的大小对电机的转动性能、响应速度和控制系统设计等方面都有着重要的影响。
因此,在电机设计和运行中,合理选择和控制电机轴转动惯量是十分关键的。
负载折算到电机轴的转动惯量计算公式

负载折算到电机轴的转动惯量计算公式负载折算到电机轴的转动惯量是指将负载的转动惯量转化为电机轴的转动惯量。
在机械系统中,负载的转动惯量会影响到电机的运行效果和控制精度。
因此,对于一些需要高精度控制的系统,准确计算负载折算到电机轴的转动惯量是非常重要的。
在计算负载折算到电机轴的转动惯量时,可以使用以下公式:Jm = Jl * (N^2)其中,Jm表示负载折算到电机轴的转动惯量,Jl表示负载的转动惯量,N表示减速器的传动比。
减速器是机械系统中常用的传动装置,通过降低输入轴的转速,增加输出轴的转矩,从而实现对负载的控制。
在减速器中,由于传动比的存在,负载的转动惯量会被折算到电机轴上,从而影响到电机的运行。
通过上述公式,我们可以看出,负载折算到电机轴的转动惯量与负载的转动惯量成正比。
传动比N越大,负载折算到电机轴的转动惯量就会越大,这意味着负载对电机的影响会更加显著。
负载折算到电机轴的转动惯量的计算对于电机系统的设计和控制具有重要意义。
通过准确计算负载折算到电机轴的转动惯量,可以更好地评估电机的性能和控制效果,从而选择合适的减速器和电机型号。
在实际应用中,负载折算到电机轴的转动惯量的计算需要考虑负载的转动惯量、减速器的传动比等因素。
在选择减速器时,需要根据负载的特点和要求,合理选择传动比,以便实现对负载的精确控制。
除了传动比,负载的转动惯量本身也是一个重要的参数。
在实际应用中,负载的转动惯量可以通过实验测量或计算得到。
通过准确测量和计算负载的转动惯量,可以更好地评估负载对电机的影响,从而更好地设计和控制机械系统。
负载折算到电机轴的转动惯量是机械系统中一个重要的参数。
通过准确计算负载折算到电机轴的转动惯量,可以更好地评估负载对电机的影响,从而选择合适的减速器和电机型号,实现对负载的精确控制。
在实际应用中,需要考虑负载的转动惯量、减速器的传动比等因素,以便得到准确的计算结果。
提升机构电机惯量计算公式

提升机构电机惯量计算公式引言。
在工程领域中,电机的惯量是一个非常重要的参数,它决定了电机的动态响应和运动特性。
在提升机构中,电机的惯量计算更是至关重要,因为它直接影响到提升机构的稳定性和运行效率。
因此,本文将介绍提升机构电机惯量的计算公式,以帮助工程师们更好地设计和优化提升机构。
电机惯量的定义。
电机的惯量是指电机在运动过程中克服自身惯性产生的阻力所需要的能量。
它是电机转动惯量和线性惯量的总和,通常用符号J表示。
电机的惯量与电机的质量分布和几何形状有关,通常可以通过数学公式进行计算。
提升机构电机惯量的计算公式。
在提升机构中,电机的惯量计算需要考虑提升重物的质量和提升高度,以及电机自身的质量和转动部件的惯量。
根据这些因素,可以得到提升机构电机惯量的计算公式如下:J = Jm + Jl + Jw。
其中,Jm表示电机自身的转动惯量,Jl表示传动装置的转动惯量,Jw表示提升重物的转动惯量。
电机自身的转动惯量可以通过电机的质量和几何形状来计算,通常可以采用以下公式进行计算:Jm = k1 m r^2。
其中,m表示电机的质量,r表示电机的半径,k1为一个与电机形状相关的常数。
传动装置的转动惯量可以通过传动装置的质量和转动部件的惯量来计算,通常可以采用以下公式进行计算:Jl = k2 ml rl^2。
其中,ml表示传动装置的质量,rl表示传动装置的半径,k2为一个与传动装置形状相关的常数。
提升重物的转动惯量可以通过重物的质量和提升高度来计算,通常可以采用以下公式进行计算:Jw = k3 mw h^2。
其中,mw表示提升重物的质量,h表示提升高度,k3为一个与提升重物形状和位置相关的常数。
综合以上三个部分的转动惯量,即可得到提升机构电机的总转动惯量J。
通过这个公式,工程师们可以更好地了解提升机构电机的惯量特性,从而进行合理的设计和优化。
应用举例。
为了更好地说明提升机构电机惯量计算公式的应用,我们可以通过一个具体的实例来进行说明。
转动惯量和启动电机功率的计算

已知刚体的转动惯量怎么求转矩转动惯量和转矩没有关系的。
转动惯量单位kgm^2,简单的说和旋转物的密度和形状有关;转矩单位Nm,是施加力的大小和力臂的乘积,与被施力物体无关。
如果说互相之间的联系,从能量的角度可找到相关的东西转动惯量和动能的关系:E=(1/2)Jw^2,J是旋转惯量,w是旋转角速度;转矩与做功的关系:A=(1/2)Mwt,M是转矩,w是旋转角速度,t是力矩施加时间。
当转动动能E=转矩做功A时,由以上公式可以得出:M=Kw/t 这个公式是在理想状态下得到的,限制条件:对一静止物质施加一个恒定转矩M,物质由角速度0经过时间t后加速到角速度w转矩M=J(转动惯量)Xβ(角加速度)大家好,最近一个项目要选择电机。
根据圆盘负载的转动惯量公式J=Mr^2/2J负载转动惯量单位kgm^2,M圆盘质量,单位kg,r圆盘半径单位m。
计算得转动惯量为0.288kgm^2.(质量10kg,半径0.24m).根据转矩公式T=Jw J 转动惯量单位kgm^2,w角加速度单位rad/s^2.可得转矩。
而直线加速度与角加速度的转换公式为w=V/r V线加速度,r半径。
那转矩公式可转变为T=Jw=J*V/r 电机960rpm/mim 时线加速度为960*0.48*3.14/60=24.1m/s^2。
转矩T=J*V/R=0.288kgm^2*24.11m/s^2/0.24m=28.9Nm最后通过公式T=9550*P/N ,电机为6极,可得P=2.9kW.不知以上的公式计算是否正确,我认为没有错,可拖动这样一个负载9公斤的铝盘需要那么大的电机吗。
唉,不是这样的。
转动惯量大不怕,问题是你是不是需要转速0-100%用这么大的加速度。
如果你不需要这么快的加速度,比如说想把转速从0慢慢提升到100%转速,那电机所需的动转矩就可以很小了。
电机的功率也降下来了。
关键是你想把电机(铝盘)的转速从0-100%变化,需用多少时间?有了这个要求,再去根据铝盘的转动惯量计算起动转矩,选取电机功率和额定转速(选择电机的极数)就OK了。
转子转动惯量

转子转动惯量
【实用版】
目录
1.转子转动惯量的定义
2.转子转动惯量的计算方法
3.转子转动惯量的应用
4.转子转动惯量对电机性能的影响
正文
一、转子转动惯量的定义
转子转动惯量,是指电机转子在旋转过程中,由于转子本身的结构和材料等因素导致的旋转惯量。
它反映了转子旋转过程中的惯性大小,是电机转动过程中的一个重要参数。
二、转子转动惯量的计算方法
转子转动惯量的计算方法通常是通过计算转子的质量矩来获得的。
质量矩是物体的质量和质心到某一点的距离的乘积。
对于电机转子来说,其质量矩可以通过以下公式计算:
质量矩 = 转子质量× (转子半径^2) / 2
然后,将质量矩乘以转子旋转的角速度,就可以得到转子的转动惯量。
三、转子转动惯量的应用
转子转动惯量在电机的设计和运行中都有重要的应用。
在设计阶段,设计师需要考虑转子的转动惯量,以确保电机的启动和停止过程能够顺利进行。
在运行阶段,转子的转动惯量会影响电机的转速和力矩等参数,因此需要对其进行监测和调整。
四、转子转动惯量对电机性能的影响
转子转动惯量对电机的启动和停止性能有重要影响。
如果转子的转动惯量过大,电机的启动和停止过程将会变得困难,可能会导致电机的损坏。
相反,如果转子的转动惯量过小,电机的转速可能会过高,导致电机的效率降低。
750瓦 电机允许转动惯量 -回复

750瓦电机允许转动惯量-回复电机允许转动惯量是指在电机运行过程中,电机所能承受的转动惯量大小。
在电机的设计和使用中,了解电机允许转动惯量的概念和计算方法非常重要。
本文将围绕“750瓦电机允许转动惯量”这一主题展开,一步一步回答相关问题。
首先,我们需要了解电机的基本知识。
电机是一种将电能转换成机械能的装置,其结构包括定子和转子。
当电流通过定子绕组时,会在磁场中产生磁力,进而驱动转子转动。
而电机的转动惯量则是表示电机对转动的抵抗程度的物理量,类似于物体对运动状态变化的惯性。
在实际应用中,电机的转动惯量需要满足一定的条件,以保证电机的正常运行。
转动惯量过大或过小,都可能导致电机的运行不稳定,甚至损坏电机。
因此,合理计算和控制电机的转动惯量对于电机的设计和使用非常关键。
那么如何计算750瓦电机允许的转动惯量呢?第一步,我们要确定电机的额定功率和转速。
根据题目中给出的信息,电机的额定功率为750瓦。
转速则需要根据具体的电机参数确定,一般标注在电机的技术资料中。
第二步,我们需要了解电机的转动惯量计算公式。
电机的转动惯量可以由转子的质量和转动半径来计算。
常用的计算公式有两种:1. 对于同心转子电机,可以使用以下公式计算转动惯量:转动惯量(kg·m²)= 0.5 × (转子质量(kg)× 转动半径(m))²2. 对于分散转子电机,可以使用以下公式计算转动惯量:转动惯量(kg·m²)= 0.5 × [(转子质量(kg)× 转动半径(m))² + (薄壁转子半径²(m²)× 转子质量(kg))]根据题目中提供的信息,“750瓦电机允许转动惯量”,没有具体说明电机的类型和参数,我们暂且假设电机为同心转子电机,通过上述第二个公式计算转动惯量。
第三步,我们需要确定转子的质量和转动半径。
这些参数通常可以通过电机的技术资料或实际测量获得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电机转动惯量的计算
对于细杆
当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3其中m是杆的质量,L是杆的长度。
对于圆柱体
当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环
当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径
对于薄圆盘
当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径
对于空心圆柱
当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳
当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体
当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径
对于立方体
当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:
角加速度与合外力矩
式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:
角动量
刚体的定轴转动动能:
转动动能
注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
其量值取决于物体的形状、质量分布及转轴的位置。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
形状规则的匀质刚体,其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。
转动惯量的表达式为I=∑mi*ri^2,若刚体的质量是连续分布的,则转动惯量的计算公式可写成I=∫r^2dm=∫r^2ρdV(式中mi表示刚体的某个质元的质量,ri表示该质元到转轴的垂直距离,ρ表示该处的密度,求和号(或积分号)遍及整个刚体。
)转动惯量的量纲为L^2M,在SI单位制中,它的单位是kg·m^2。
var cpro_psid ="u2572954"; var cpro_pswidth =966; var cpro_psheight =120;
平行轴定理
平行轴定理:设刚体质量为m,绕通过质心转轴的转动惯量为Ic,将此轴朝任何方向平行移动一个距离d,则绕新轴的转动惯量I为:
I=Ic+md^2
这个定理称为平行轴定理。
一个物体以角速度ω绕固定轴z轴的转动同样可以视为以同样的角速度绕平行于z轴且通过质心的固定轴的转动。
也就是说,绕z轴的转动等同于绕过质心的平行轴的转动与质心的转动的叠加
垂直轴定理
垂直轴定理:一个平面刚体薄板对于垂直它的平面的轴的转动惯量,等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。
垂直轴定理
表达式:Iz=Ix+Iy
式中Ix,Iy,Iz分别代表刚体对x,y,z三轴的转动惯量.对于非平面薄板状的刚体,亦有如下垂直轴定理成立[2]:
垂直轴定理
利用垂直轴定理可对一些刚体对一特定轴的转动惯量进行较简便的计算.
刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离,称为刚体绕该轴的回转半径κ,其公式为I=Mκ^2,式中M为刚体质量;I 为转动惯量。
