c语言求基本关联矩阵
c语言中的矩阵

c语言中的矩阵
【最新版】
目录
1.矩阵的定义与表示
2.矩阵的运算
3.矩阵的应用
正文
矩阵在 C 语言中是一种重要的数据结构,它主要用于表示线性方程组和线性变换。
矩阵由行和列的元素组成,这些元素可以是数字、字符或者其他数据类型。
C 语言中,矩阵可以通过数组来表示,数组的每个元素又是一个数组,从而形成一个多维数组。
这种表示方法使得矩阵的元素可以通过行列下标来访问。
矩阵的运算主要包括加法、减法、乘法和转置等。
矩阵的加法和减法要求两个矩阵的行数和列数都相等,否则无法进行运算。
矩阵的乘法要求两个矩阵的列数和行数分别相等,乘积矩阵的行数和列数分别等于两个矩阵的行数和列数之和。
矩阵的转置是将矩阵的行和列互换,得到一个新的矩阵。
在 C 语言中,矩阵的运算通常通过循环实现,可以利用数组的下标访问矩阵的元素,从而完成矩阵运算。
矩阵在 C 语言中有广泛的应用,主要包括线性方程组求解、矩阵乘法、特征值计算等。
线性方程组求解是 C 语言中矩阵运算的一个经典应用,可以通过高斯消元法、LU 分解等方法求解线性方程组。
矩阵乘法在图像处理、信号处理等领域有广泛应用,可以将一个矩阵表示为另一个矩阵的线性组合。
特征值计算是用于求解矩阵特征值和特征向量的方法,可以应用于信号处理、图像处理等领域。
总之,矩阵在 C 语言中是一种重要的数据结构,它可以用于表示线性方程组和线性变换,并支持加法、减法、乘法和转置等运算。
矩阵在多
个领域有广泛应用,如线性方程组求解、矩阵乘法、特征值计算等。
C语言矩阵的运算

C语言课程设计题目矩阵的运算西安科技大学二0 一一年十一月一、设计目的1. 综合C语言相关知识制作简单的应用程序2. 灵活对程序代码进行利用,修改和编写;3. 熟练将C语言所学知识和其它知识相结合二、功能描述编写一个矩阵运算程序,能够进行矩阵加、减、乘、转置,求矩阵的最大值,最小值,对角线元素的和等三、流程图四、源程序#define M 3#define N 3#define P 2#include<stdio.h>void main(){int i,j,k,d,m=0,l=0,max,min,a[M][N],b[M][N],c[N][P];printf("输入a矩阵:\n");for(i=0;i<M;i++)for(j=0;j<N;j++)scanf("%d",&a[i][j]);printf("输入b矩阵:\n");for(i=0;i<M;i++)for(j=0;j<N;j++)scanf("%d",&b[i][j]);printf("输入c矩阵:\n");for(i=0;i<N;i++)for(j=0;j<P;j++)scanf("%d",&c[i][j]); printf("a矩阵:\n");for(i=0;i<M;i++){{for(j=0;j<N;j++)printf("%4d",a[i][j]);}printf("\n");}printf("b矩阵:\n");for(i=0;i<M;i++){{for(j=0;j<N;j++)printf("%4d",b[i][j]);}printf("\n");}printf("c矩阵:\n");for(i=0;i<N;i++){{for(j=0;j<P;j++)printf("%4d",c[i][j]);}printf("\n");}printf("a,b矩阵之和:\n");for(i=0;i<M;i++){{for(j=0;j<N;j++)printf("%4d",a[i][j]+b[i][j]);}printf("\n");}printf("a,b矩阵之差:\n");for(i=0;i<M;i++){{for(j=0;j<N;j++)printf("%4d",a[i][j]+b[i][j]);}printf("\n");}printf("a,c矩阵之积:\n");for(i=0;i<M;i++){{for(j=0;j<P;j++){for(d=0,k=0;k<N;k++)d+=a[i][k]*c[k][j];printf("%4d",d);}}printf("\n");}printf("a矩阵的转置:\n");for(j=0;j<N;j++){{for(i=0;i<M;i++)printf("%4d",a[i][j]);}printf("\n");}printf("a矩阵的最大值:\n"); max=a[0][0];for(i=0;i<M;i++)for(j=0;j<N;j++)if (max<a[i][j])max=a[i][j];printf("%4d\n",max); printf("a矩阵的最小值:\n"); min=a[0][0];for(i=0;i<M;i++)for(j=0;j<N;j++)if (min>a[i][j])min=a[i][j];printf("%4d\n",min);printf("a矩阵的主对角线之和:\n");for(i=0;i<M;i++)m+=a[i][i];printf("%d\n",m);}五、运行界面六、心得体会课程设计是培养学生综合运用所学知识,发现,提出,分析和解决实际问题,锻炼实践能力的重要环节,是对学生实际工作能力的具体训练和考察过程。
矩阵运算——C语言实现

#include "stdafx.h"#include <stdlib.h>//结构体typedef struct{double ** mat;int row;int col;}Matrix;void InitialMatrix(Matrix *T, int row,int col); //只分配空间不初始化;void InitialMatrixZero(Matrix *T,int row, int col); //初始化为0void InitialMatrixRand(Matrix *T,int row, int col); //初始化为50以内随机正整数void InputMatrix(Matrix *T); //键盘输入矩阵void DestroyMatrix(Matrix *T); // 释放矩阵空间void PrintfMatrix(Matrix *T); //矩阵输出int AddMatrix(Matrix *A,Matrix *B,Matrix *C); // 矩阵加int MinusMatrix(Matrix *A,Matrix *B,Matrix *C); // 矩阵减int MultiMatrix(Matrix *A,Matrix *B,Matrix *C); //矩阵乘法double MeanMatrix(Matrix *T); //矩阵元素均值int SubMatrix(Matrix *T1,Matrix *T2,int BeginRow,int BeginCol,int EndRow,int EndCol); //求T1的子矩阵T2;测试程序参考界面如下所示:矩阵函数测试,请选择功能,输入对应的数字:***************************************************1:输入一个矩阵,求矩阵均值;2:产生一个随机数矩阵,求矩阵均值;3:输入两个个矩阵,求矩阵和;4:输入两个个矩阵,求矩阵差;5:输入两个个矩阵,求矩阵积;6:产生两个个随机数矩阵,求矩阵和;7:产生两个个随机数矩阵,求矩阵差;8:产生两个个随机数矩阵,求矩阵积;9:求矩阵的子阵,如矩阵的2-4行,1-3列的子阵;0:结束!#include <stdio.h>#include <stdlib.h>//结构体typedef struct {double **mat;int row;int col;} Matrix;//函数声明void InitialMatrix(Matrix *T, int row, int col);void InitialMatrixZero(Matrix *T, int row, int col);void InitialMatrixRand(Matrix *T, int row, int col);void InputMatrix(Matrix *T);void DestroyMatrix(Matrix *T); // 释放矩阵空间void PrintfMatrix(Matrix *T); //矩阵输出int AddMatrix(Matrix *A, Matrix *B, Matrix *C); // 矩阵加int MinusMatrix(Matrix *A, Matrix *B, Matrix *C); // 矩阵减int MultiMatrix(Matrix *A, Matrix *B, Matrix *C); //矩阵乘法double MeanMatrix(Matrix *T); //矩阵元素均值//int SubMatrix(Matrix *T1, Matrix *T2, int BeginRow, int BeginCol, int EndRow, int EndCol); //求T1的子矩阵T2;void NMatrix(void);//求逆矩阵//主函数int main(){int inputevent;//int i, j;int row, col;Matrix T;Matrix A;Matrix B;Matrix C;printf(" 矩阵函数测试,请选择功能,输入对应的数字:\n");printf(" ***************************************************\n\n"); printf("1:输入一个矩阵,求矩阵均值;\n");printf("2:产生一个随机数矩阵,求矩阵均值;\n");printf("3:输入两个个矩阵,求矩阵和;\n");printf("4:输入两个个矩阵,求矩阵差;\n");printf("5:输入两个矩阵,求矩阵积;");printf("\n6:产生两个随机数矩阵,求矩阵和;\n");printf("7:产生两个随机数矩阵,求矩阵差;\n");printf("8:产生两个随机数矩阵,求矩阵积;\n");printf("9:求矩阵的子阵,如矩阵的2-4行D,1-3列的子阵;\n");printf("10:输入一个方阵,求其逆矩阵\n");printf("0:结束!\n");printf("\n\n选择:");scanf("%d", &inputevent);while (inputevent != 0){if (inputevent == 1) {printf("您要输入的矩阵的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&T, row, col);InitialMatrixZero(&T, T.row, T.col);InputMatrix(&T);printf("\n矩阵的平均值为:\n%lf\n\n", MeanMatrix(&T));DestroyMatrix(&T);}if (inputevent == 2) {printf("输入您要产生的矩阵的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&T, row, col);InitialMatrixRand(&T, row, col);MeanMatrix(&T);PrintfMatrix(&T);printf("\n矩阵的平均值为:\n%lf\n\n", MeanMatrix(&T));DestroyMatrix(&T);}if (inputevent == 3) {printf("您要输入的矩阵A的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixZero(&A, A.row, A.col);InputMatrix(&A);printf("您要输入的矩阵B的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixZero(&B, B.row, B.col);InputMatrix(&B);InitialMatrix(&C, B.row, B.col);InitialMatrixZero(&C, C.row, C.col);if (AddMatrix(&A, &B, &C) == 1) {printf("\n\n矩阵的和为:A*B\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 4) {printf("您要输入的矩阵A的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixZero(&A, A.row, A.col);InputMatrix(&A);printf("您要输入的矩阵B的行数和列数e.g:5,6:");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixZero(&B, B.row, B.col);InputMatrix(&B);InitialMatrix(&C, B.row, B.col);InitialMatrixZero(&C, C.row, C.col);if (MinusMatrix(&A, &B, &C) == 1) {printf("\n矩阵的差为:A-B=\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 5) {int able;printf("您要输入的矩阵A的行数和列数e.g: 5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixZero(&A, A.row, A.col);InputMatrix(&A);printf("您要输入的矩阵B的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixZero(&B, B.row, B.col);InputMatrix(&B);InitialMatrix(&C, A.row, B.col);InitialMatrixZero(&C, C.row, C.col);able = MultiMatrix(&A, &B, &C);if (able == 1) {printf("\n积为:A*B\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 6) {printf("您要产生的矩阵A的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixRand(&A, row, col);printf("A为:\n\n");PrintfMatrix(&A);printf("您要产生的矩阵B的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixRand(&B, row, col);printf("B为:\n\n");PrintfMatrix(&B);InitialMatrix(&C, A.row, A.col);InitialMatrixZero(&C, C.row, C.col);if (AddMatrix(&A, &B, &C) == 1) {printf("\n矩阵的和为:A+B=\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 7) {printf("您要产生的矩阵A的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixRand(&A, row, col);printf("您要产生的矩阵B的行数和列数e.g:5,6: ");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixRand(&B, row, col);InitialMatrix(&C, A.row, A.col);InitialMatrixZero(&C, C.row, C.col);if (MinusMatrix(&A, &B, &C) == 1) {printf("\n矩阵的差为:A-B=\n\n");PrintfMatrix(&C);}else printf("\n\n无法计算!\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 8) {printf("您要产生的矩阵A的行数和列数e.g:5,6: \n");scanf("%d,%d", &row, &col);InitialMatrix(&A, row, col);InitialMatrixRand(&A, row, col);printf("A为:\n\n");PrintfMatrix(&A);printf("您要产生的矩阵B的行数和列数e.g:5,6: \n");scanf("%d,%d", &row, &col);InitialMatrix(&B, row, col);InitialMatrixRand(&B, row, col);printf("B为:\n\n");PrintfMatrix(&B);InitialMatrix(&C, A.row, A.col);InitialMatrixZero(&C, C.row, C.col);if (MultiMatrix(&A, &B, &C) == 1) {printf("\n积为:A*B=\n\n");PrintfMatrix(&C);;}else printf("\n\n无法计算;\n\n");DestroyMatrix(&A);DestroyMatrix(&B);DestroyMatrix(&C);}if (inputevent == 9) printf("对不起,该函数尚在完善中\n\n");if (inputevent == 10) NMatrix();if (inputevent == 0)break;printf(" 矩阵函数测试,请选择功能,输入对应的数字:\n");printf(" ***************************************************\n\n"); printf("1:输入一个矩阵,求矩阵均值;\n");printf("2:产生一个随机数矩阵,求矩阵均值;\n");printf("3:输入两个个矩阵,求矩阵和;\n");printf("4:输入两个个矩阵,求矩阵差;\n");printf("5:输入两个矩阵,求矩阵积;");printf("\n6:产生两个随机数矩阵,求矩阵和;\n");printf("7:产生两个随机数矩阵,求矩阵差;\n");printf("8:产生两个随机数矩阵,求矩阵积;\n");printf("9:求矩阵的子阵,如矩阵的2-4行D,1-3列的子阵;\n");printf("10:输入一个方阵,求其逆矩阵\n");printf("0:结束!\n");printf("\n\n选择:");scanf("%d", &inputevent);}return 0;}//其他函数void InitialMatrix(Matrix *T, int row, int col){//printf("分配内存中......\n");int i;int succ = 1;//T=(Matrix *)malloc(sizeof(Matrix));T->row = row;T->col = col;T->mat = (double **)malloc(T->row * sizeof(double *));if (T->mat == NULL) {succ = 0;}else {for (i = 0; i < T->row; i++) {T->mat[i] = (double *)malloc(T->col * sizeof(double));if (T->mat[i] == NULL) {succ = 0;break;}}//if(succ==1)// printf("内存分配成功|;?\n");//else printf("内存分配失败;\n");}}void InitialMatrixZero(Matrix *T, int row, int col) { //printf("矩阵初始化为零中......\n");int i, j;for (i = 0; i < row; i++)for (j = 0; j < col; j++)T->mat[i][j] = 0;//printf("矩阵初始化为零矩阵成功;\n"); }void InitialMatrixRand(Matrix *T, int row, int col) { int i, j;for (i = 0; i < row; i++)for (j = 0; j < col; j++)(*T).mat[i][j] = rand() % 50;}void InputMatrix(Matrix *T) {printf("输入矩阵:\n");int i, j;for (i = 0; i < (*T).row; i++)for (j = 0; j < (*T).col; j++)scanf("%lf", &(*T).mat[i][j]);}void DestroyMatrix(Matrix *T){int i;for (i = 0; i < (*T).row; i++)free((*T).mat[i]);}void PrintfMatrix(Matrix *T){int i, j;for (i = 0; i < (*T).row; i++){for (j = 0; j < (*T).col; j++)printf("%lf ", (*T).mat[i][j]);printf("\n");}}int AddMatrix(Matrix *A, Matrix *B, Matrix *C){int i, j;if ((*A).row == (*B).row && (*A).col == (*B).col){for (i = 0; i < (*A).row; i++)for (j = 0; j < (*A).col; j++)(*C).mat[i][j] = (*A).mat[i][j] + (*B).mat[i][j];for (i = 0; i < (*A).row; i++)for (j = 0; j < (*A).col; j++)return 1;}else {printf("这两个矩阵不能相加!\n");return 0;}}int MinusMatrix(Matrix *A, Matrix *B, Matrix *C){int i, j;if ((*A).row == (*B).row && (*A).col == (*B).col){for (i = 0; i < (*A).row; i++)for (j = 0; j < (*A).col; j++)(*C).mat[i][j] = (*A).mat[i][j] - (*B).mat[i][j];return 1;}elseprintf("这两个矩阵不能相减!\n");return 0;}int MultiMatrix(Matrix *A, Matrix *B, Matrix *C){int i=0, j=0;int k = 0;if ((*A).col == (*B).row){for (i = 0; i < (*A).row; i++) {for (j = 0; j < (*B).col; j++)for(k=0;k <(A->col);k++)(*C).mat[i][j] += (*A).mat[i][k] * (*B).mat[k][j];}return 1;}elseprintf("这两个矩阵不能相乘!\n");return 0;}double MeanMatrix(Matrix *T) //矩阵元素均值{double mean;double sum = 0;int i, j;for (i = 0; i < (*T).row; i++)for (j = 0; j < (*T).col; j++)sum += (*T).mat[i][j];mean = sum / ((*T).row*(*T).col);return mean;}void NMatrix(void){#define M 20#define N 20int i,j,m,n;float y=1.0;float a[M][2 * M];float b[N][2 * N];float t, x;int k, T;printf("输入方阵的维数:\n"); //请输入方阵,即行和列相等的矩阵。
c语言课程设计矩阵运算

c语言课程设计矩阵运算一、教学目标本节课的教学目标是使学生掌握C语言实现矩阵运算的基本方法,包括矩阵的创建、矩阵的加减法、矩阵的转置以及矩阵的乘法。
知识目标要求学生理解矩阵运算的数学原理,能够运用C语言实现矩阵的基本运算;技能目标要求学生熟练使用C语言进行矩阵运算的编程实践;情感态度价值观目标则是培养学生的逻辑思维能力,提高学生对计算机编程的兴趣。
二、教学内容本节课的教学内容主要包括矩阵运算的数学原理介绍、C语言实现矩阵运算的编程实践和代码调试。
教学大纲安排如下:1.引入矩阵的概念和矩阵运算的基本定义。
2.讲解矩阵的创建、矩阵的加减法、矩阵的转置以及矩阵的乘法的数学原理。
3.引导学生运用C语言实现矩阵的基本运算。
4.通过编程实践和代码调试,使学生熟练掌握C语言实现矩阵运算的方法。
三、教学方法本节课采用讲授法、讨论法和实验法相结合的教学方法。
首先,通过讲授法向学生讲解矩阵运算的数学原理和C语言实现方法;其次,通过讨论法引导学生相互交流和讨论,提高他们对矩阵运算的理解;最后,通过实验法让学生动手实践,调试代码,提高他们的编程能力。
四、教学资源本节课的教学资源主要包括教材、参考书、多媒体资料和实验设备。
教材和参考书用于为学生提供理论知识和编程技巧;多媒体资料用于辅助讲解和演示矩阵运算的原理和实现方法;实验设备则是学生进行编程实践和代码调试的必要工具。
五、教学评估本节课的教学评估主要包括平时表现、作业和考试三个部分。
平时表现主要评估学生在课堂上的参与程度、提问和回答问题的积极性等;作业则是对学生掌握矩阵运算能力的考察,要求学生独立完成并提交;考试则是对学生综合运用C语言实现矩阵运算能力的评估,包括理论知识和编程实践。
评估方式应客观、公正,能够全面反映学生的学习成果。
六、教学安排本节课的教学安排如下:总共安排4个课时,第1课时介绍矩阵运算的数学原理,第2课时讲解C语言实现矩阵运算的方法,第3课时进行编程实践和代码调试,第4课时进行教学评估。
C语言实现矩阵计算

C语言实现矩阵计算C语言是一种广泛使用的编程语言,也是实现矩阵计算的一种常用工具。
在C语言中,我们可以使用数组来表示矩阵,并通过循环结构和算术运算符来实现矩阵计算的各种功能。
首先,我们需要实现矩阵的输入和输出功能。
在C语言中,我们可以使用二维数组来表示矩阵。
下面是一个示例代码,用来输入和显示一个矩阵:```c#include <stdio.h>//定义最大矩阵的大小#define MAX_SIZE 100//函数用于输入一个矩阵void inputMatrix(int matrix[MAX_SIZE][MAX_SIZE], int rows, int cols)printf("请输入矩阵元素:\n");for (int i = 0; i < rows; i++)for (int j = 0; j < cols; j++)scanf("%d", &matrix[i][j]);}}//函数用于显示一个矩阵void displayMatrix(int matrix[MAX_SIZE][MAX_SIZE], int rows, int cols)printf("矩阵元素为:\n");for (int i = 0; i < rows; i++)for (int j = 0; j < cols; j++)printf("%d ", matrix[i][j]);}printf("\n");}```上述代码定义了两个函数:`inputMatrix`用于输入一个矩阵,`displayMatrix`用于显示一个矩阵。
我们可以通过调用这两个函数来输入和显示矩阵。
接下来,我们可以实现矩阵的加法、减法和乘法等功能。
以下是一个示例代码,用于实现矩阵的加法:```c//函数用于计算两个矩阵的加法void addMatrix(int matrix1[MAX_SIZE][MAX_SIZE], intmatrix2[MAX_SIZE][MAX_SIZE], int result[MAX_SIZE][MAX_SIZE], int rows, int cols)for (int i = 0; i < rows; i++)for (int j = 0; j < cols; j++)result[i][j] = matrix1[i][j] + matrix2[i][j];}}```上述代码中,我们定义了一个`addMatrix`函数,该函数接受两个输入矩阵和一个结果矩阵,将两个输入矩阵的对应元素相加,并将结果存储在结果矩阵中。
矩阵运算c语言

矩阵运算c语言矩阵运算C语言矩阵运算是现代数学和工程中的重要工具,它广泛应用于信号处理、计算机视觉、机器学习等领域。
而在计算机科学的领域中,矩阵运算也被广泛使用,而C语言也是最流行的语言之一。
在这篇文章中,我们将讨论矩阵运算在C语言中的不同类型。
算法是计算机科学的核心,而在矩阵中的运算也是如此。
最基本的矩阵运算是矩阵的加法和乘法。
为了在C语言中实现这些基本操作,我们需要将矩阵表示为一个二维数组。
矩阵加法是将两个矩阵相加,需要将它们的相应元素相加,并将结果存储在新的矩阵中。
这个过程可以很容易地在C语言中实现,下面是其中一个例子:```cvoid add_matrix(int A[][COL], int B[][COL], int result[][COL], int row, int col){for (int i = 0; i < row; i++){for (int j = 0; j < col; j++){result[i][j] = A[i][j] + B[i][j];}}}```矩阵乘法的实现更加复杂,因为它涉及到更多的细节。
在C语言中,矩阵乘法可以使用三层循环来实现,其中一层循环用于遍历结果矩阵的所有元素,另外两个循环用于计算每个结果元素的值。
下面是其中一个例子:```cvoid multiply_matrix(int A[][COL], int B[][COL], int result[][COL], int rowA, int colA, int rowB, int colB){for (int i = 0; i < rowA; i++){for (int j = 0; j < colB; j++){int sum = 0;for (int k = 0; k < colA; k++){sum += A[i][k] * B[k][j];}result[i][j] = sum;}}}```另外,还有一些高级的矩阵运算,如矩阵求逆、矩阵转置、矩阵行列式等。
C语言的多维数据结构与矩阵运算

多维数据结构的基本概念什么是多维数据结构多维数据结构是指在编程中使用的一种数据类型,它可以存储多个维度的数据。
通常用来表示表格、矩阵、图像等具有多个行和列的数据。
C语言提供了多种实现多维数据结构的方式,包括数组、结构体和指针等。
多维数组的定义和使用定义一个二维数组在C语言中,我们可以使用数组来表示多维数据结构。
下面是一个定义和初始化二维数组的例子:int matrix[3][3] = {{1, 2, 3},{4, 5, 6},{7, 8, 9}};访问二维数组的元素要访问二维数组的某个元素,可以使用两个索引值来指定元素的位置。
例如,要访问矩阵中的第一个元素,可以使用以下代码:int num = matrix[0][0];多维数组的遍历可以使用嵌套的循环来遍历多维数组的所有元素。
例如,以下代码演示了如何遍历一个二维数组并打印每个元素的值:for (int i = 0; i < 3; i++) {for (int j = 0; j < 3; j++) {printf("%d ", matrix[i][j]);}printf("\n");}多维结构体的定义和使用定义一个多维结构体除了数组,C语言还提供了结构体这种数据类型来实现多维数据结构。
结构体可以包含多个成员变量,每个成员变量可以是不同的数据类型。
下面是一个定义和使用多维结构体的例子:struct Point {int x;int y;};struct Matrix {struct Point points[3][3];};struct Matrix matrix = {{{ {1, 2}, {3, 4}, {5, 6} },{ {7, 8}, {9, 10}, {11, 12} },{ {13, 14}, {15, 16}, {17, 18} }}};访问多维结构体的成员变量要访问多维结构体的成员变量,可以使用.运算符来指定成员变量的位置。
c语言矩阵算法

c语言矩阵算法摘要:1.矩阵算法概述2.C 语言与矩阵算法的关系3.C 语言矩阵算法的实现4.常见C 语言矩阵算法举例5.总结正文:1.矩阵算法概述矩阵算法是一种数学算法,它主要处理矩阵数据结构。
矩阵在数学、物理、工程等领域具有广泛的应用,因此矩阵算法的研究具有重要意义。
矩阵算法包括矩阵的加法、减法、乘法、求逆、求秩等基本操作,以及一些高级操作,如矩阵分解、特征值计算等。
2.C 语言与矩阵算法的关系C 语言是一种广泛应用的编程语言,其性能优越、执行效率高,适合实现复杂的矩阵算法。
C 语言提供了丰富的运算符和函数库,可以方便地处理矩阵数据。
同时,C 语言具有较高的可移植性,可以在不同的硬件平台和操作系统上运行,为矩阵算法的实现提供了便利。
3.C 语言矩阵算法的实现在C 语言中实现矩阵算法,首先需要定义矩阵的数据结构。
一般采用二维数组来表示矩阵,同时需要为矩阵分配足够的内存空间。
接下来,可以实现矩阵的基本操作,如加法、减法、乘法等。
对于一些高级操作,如矩阵分解、特征值计算等,可以利用C 语言的函数库或自行编写算法。
4.常见C 语言矩阵算法举例以下是一些常见的C 语言矩阵算法举例:(1)矩阵加法:假设有两个矩阵A 和B,它们的行数和列数相等,可以实现矩阵的加法操作。
```cvoid matrix_add(double *a, double *b, double *c, int m, int n) { for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {c[i * n + j] = a[i * n + j] + b[i * n + j];}}}```(2)矩阵乘法:实现矩阵乘法需要满足矩阵A 的列数等于矩阵B 的行数。
```cvoid matrix_multiply(double *a, double *b, double *c, int m, int n, int p) {for (int i = 0; i < m; i++) {for (int j = 0; j < p; j++) {double sum = 0;for (int k = 0; k < n; k++) {sum += a[i * n + k] * b[k * p + j];}c[i * p + j] = sum;}}}```5.总结C 语言矩阵算法是研究矩阵数据的一种数学方法,它在工程、物理等领域具有广泛的应用。
用c++实现矩阵的基本操作

用c++实现矩阵的基本操作全文共四篇示例,供读者参考第一篇示例:矩阵是数学中一个非常重要的概念,它在科学计算、工程领域以及计算机编程中都有着广泛的应用。
通过使用矩阵,我们可以方便地表示和处理大量的数据,并进行各种数学运算。
在本文中,我们将通过使用C++语言来实现矩阵的基本操作,包括矩阵的创建、加法、减法、乘法、转置等操作。
让我们来看看如何在C++中表示矩阵。
一般来说,我们可以使用二维数组来表示一个矩阵。
一个3x3的矩阵可以用如下的代码来表示:```cppint matrix[3][3] = {{1, 2, 3},{4, 5, 6},{7, 8, 9}};```matrix是一个3x3的矩阵,我们可以通过matrix[i][j]来访问矩阵中的元素,其中i表示行数,j表示列数。
接下来,让我们来实现矩阵的加法、减法和乘法操作。
在矩阵的加法和减法操作中,我们只需要将相应位置的元素相加或相减即可。
以下是一个简单的示例代码:```cppconst int ROW = 3;const int COL = 3;// 矩阵加法int C[ROW][COL];for (int i = 0; i < ROW; i++) {for (int j = 0; j < COL; j++) {C[i][j] = A[i][j] + B[i][j];}}在矩阵的乘法操作中,我们需要注意矩阵相乘的规则,即如果一个矩阵是m x n的,另一个矩阵是n x p的,则它们的乘积矩阵是一个m x p的矩阵。
以下是一个简单的示例代码:接下来,让我们来实现矩阵的转置操作。
矩阵的转置是指将矩阵的行和列互换的操作。
以下代码展示了如何在C++中实现矩阵的转置操作:以上代码中,我们首先创建了一个3x4的矩阵A,然后通过两层循环将矩阵A转置后存储在矩阵B中。
第二篇示例:矩阵是线性代数中的重要概念,它由行和列组成,可以用来表示一系列数据或者向量。
c语言求方阵的行列式、伴随矩阵算法

c语⾔求⽅阵的⾏列式、伴随矩阵算法#include<stdio.h>#include<math.h>#define N 100 //N⽐输⼊的阶数⼤即可int main(){ int n,a[N][N],b[N][N],i,j;int row_col_times(int b[N][N],int n);void adgujate_matrix(int s[N][N],int n);printf("请输⼊⽅阵阶数:\n");scanf("%d",&n);printf("请输⼊%d阶的⽅阵(⽤空格隔开)\n",n);for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%d",&a[i][j]);printf("您输⼊的%d阶⽅阵是:\n");for(i=0;i<n;i++){for(j=0;j<n;j++){printf("%3d",a[i][j]);b[i][j]=a[i][j];}//右对齐输出矩阵printf("\n");}printf("该矩阵的伴随矩阵是;:\n");adgujate_matrix(b,n);//调⽤伴随矩阵函数printf("该矩阵的⾏列式为: %d\n",row_col_times(a,n));//调⽤⾏列式乘积函数return 0;}int row_col_times(int b[N][N],int n){ int change_col(int c[N][N],int n,int i);int product(int d[N][N],int n,int p);int i,j,k,p=0;for(i=0;i<n-1;i++)//i为阶数{if(b[i][i]==0)//当对⾓线元素为零时调换列{ p=p+change_col(b,n,i);}for(j=i+1;j<n;j++)//j指列{b[k][j]=b[k][j]*b[i][i]-b[k][i]*b[i][j];//最重要的操作 }}return product(b,n,p);}int change_col(int c[N][N],int n,int i){ int temp,j,k,flag=0;for(k=i;k<n;k++)//k指列{ if(c[i][k]!=0){for(j=i;j<n;j++)//j指⾏{temp=c[j][i];c[j][i]=c[j][k];c[j][k]=temp;//调换列}flag++;//列调换符号记录break;}}return flag;//返回调换符号记录数}int product(int d[N][N],int n,int p){ int product=1,i;for(i=0;i<n;i++)product=product*d[i][i];//对⾓线乘积for(i=0;i<n-1;i++)product=product/pow(d[i][i],n-i-1);//除回来product=product*pow(-1,p);//乘上列调换符号 return product;}void adgujate_matrix(int s[N][N],int n){int b[n][n],c[N][N],f[n][n];int i,j,k,l,a,e,g=1;for(j=0;j<n;j++)for(i=0;i<n;i++)f[i][j]=s[i][j];//赋值防⽌改变原矩阵for(j=0;j<n;j++)//依次找元素{for(i=0;i<n;i++){for(k=0;k<n;k++)for(l=j;l<n-1;l++){s[k][l]=s[k][l+1];//右边往左挪}for(k=i;k<n-1;k++)for(l=0;l<n;l++){s[k][l]=s[k+1][l];//下边往上挪}for(k=0;k<n-1;k++)for(l=0;l<n-1;l++){c[k][l]=s[k][l];}if((i+j)%2==1)g=-1;printf("%3d",row_col_times(c,n-1)*g); for(a=0;a<n;a++)for(e=0;e<n;e++)s[a][e]=f[a][e];g=1;}printf("\n");}。
矩阵运算——C语言实现

矩阵运算——C语言实现矩阵运算是线性代数中非常重要的一部分,它涉及到矩阵的加法、减法、乘法、转置等操作。
在C语言中,我们可以使用二维数组来表示和操作矩阵。
首先,我们需要定义一个表示矩阵的结构体,可以包含矩阵的行数、列数以及矩阵的元素值。
代码如下:```ctypedef structint rows; // 行数int cols; // 列数double **data; // 矩阵元素} Matrix;```在此结构体中,我们使用一个二维指针来表示矩阵的元素,其中每个指针指向一个一维数组,表示矩阵的一行。
接下来,我们可以实现一些常用的矩阵运算函数,比如矩阵的创建、销毁、加法、减法、乘法等。
1.矩阵的创建和销毁函数如下所示:```cMatrix *createMatrix(int rows, int cols)Matrix *matrix = (Matrix *)malloc(sizeof(Matrix));matrix->rows = rows;matrix->cols = cols;matrix->data = (double **)malloc(rows * sizeof(double *));for (int i = 0; i < rows; ++i)matrix->data[i] = (double *)malloc(cols * sizeof(double));}return matrix;void destroyMatrix(Matrix *matrix)for (int i = 0; i < matrix->rows; ++i)free(matrix->data[i]);}free(matrix->data);free(matrix);```这里我们使用了动态内存分配,先分配一维数组的内存,再分配二维数组的内存。
2.矩阵的加法和减法函数如下所示:```cMatrix *addMatrix(Matrix *matrix1, Matrix *matrix2)if (matrix1->rows != matrix2->rows , matrix1->cols != matrix2->cols)return NULL;}Matrix *result = createMatrix(matrix1->rows, matrix1->cols);for (int i = 0; i < matrix1->rows; ++i)for (int j = 0; j < matrix1->cols; ++j)result->data[i][j] = matrix1->data[i][j] + matrix2->data[i][j];}}return result;Matrix *subtractMatrix(Matrix *matrix1, Matrix *matrix2)if (matrix1->rows != matrix2->rows , matrix1->cols != matrix2->cols)return NULL;}Matrix *result = createMatrix(matrix1->rows, matrix1->cols);for (int i = 0; i < matrix1->rows; ++i)result->data[i][j] = matrix1->data[i][j] - matrix2->data[i][j];}}return result;```这里我们首先判断两个矩阵是否具有相同的行数和列数,如果不相同则无法进行加法或减法运算。
c语言矩阵定义

c语言矩阵定义C语言矩阵定义在C语言中,矩阵是一种常见的数据结构,用于存储和处理二维数据。
矩阵可以看作是一个由行和列组成的表格,其中每个元素都有自己的位置。
在矩阵中,我们可以进行各种运算和操作,比如矩阵的加法、减法、乘法等。
在C语言中,我们可以使用二维数组来表示矩阵。
二维数组是一种特殊的数组,它由多个一维数组组成,每个一维数组表示矩阵的一行。
通过使用二维数组,我们可以方便地对矩阵进行操作。
定义一个矩阵可以通过以下方式:```c#define ROWS 3#define COLS 3int matrix[ROWS][COLS];```在上述代码中,我们定义了一个名为matrix的二维数组,它有3行3列。
通过使用宏定义,我们可以方便地修改矩阵的大小。
矩阵的元素可以通过下标访问,下标从0开始。
例如,要访问矩阵中的第i行第j列的元素,可以使用`matrix[i][j]`的方式。
为了方便操作矩阵,我们可以编写一些函数来实现各种矩阵运算。
下面是几个常见的矩阵运算函数的示例:1. 矩阵的加法```cvoid matrix_add(int a[ROWS][COLS], int b[ROWS][COLS], int result[ROWS][COLS]) {for (int i = 0; i < ROWS; i++) {for (int j = 0; j < COLS; j++) {result[i][j] = a[i][j] + b[i][j];}}}```上述函数实现了两个矩阵的加法,将计算结果存储在result矩阵中。
2. 矩阵的乘法```cvoid matrix_multiply(int a[ROWS][COLS], int b[COLS][ROWS], int result[ROWS][ROWS]) {for (int i = 0; i < ROWS; i++) {for (int j = 0; j < ROWS; j++) {result[i][j] = 0;for (int k = 0; k < COLS; k++) {result[i][j] += a[i][k] * b[k][j];}}}}```上述函数实现了两个矩阵的乘法,将计算结果存储在result矩阵中。
C矩阵基本运算代码

C#矩阵的运算代码#region 矩阵运算/// <summary>/// 矩阵对应行列式的值/// </summary>/// <param ></param>/// <returns></returns>private double MatrixValue(double[,] MatrixList){int Level = MatrixList.GetLength(1);double[,] dMatrix = new double[Level, Level];for (int i = 0; i < Level; i++){for (int j = 0; j < Level; j++){dMatrix[i, j] = MatrixList[i, j];}}int sign = 1;for (int i = 0, j = 0; i < Level && j < Level; i++, j++){//判断改行dMatrix[i, j]是否为0,若是,则寻找i后的行(m,m>i,切dMatrix[m, j]!=0)进行交换if (dMatrix[i, j] == 0){if (i == Level - 1){return 0;}int m = i + 1;//获取一个dMatrix[m, j]不为为0的行for (; dMatrix[m, j] == 0; m++){if (m == Level - 1){return 0;}}//判断是否达到矩阵的最大行,若是,则返回0//把i行和m行调换double temp;for (int n = j; n < Level; n++){temp = dMatrix[i, n];dMatrix[i, n] = dMatrix[m, n];dMatrix[m, n] = temp;}sign *= (-1);}//把当前行以后的行所对应的列变成0double tmp;for (int s = Level - 1; s > i; s--){tmp = dMatrix[s, j];//j行后面的所有行for (int t = j; t < Level; t++){dMatrix[s, t] -= dMatrix[i, t] * (tmp / dMatrix[i, j]);}}}double result = 1;for (int i = 0; i < Level; i++){if (dMatrix[i, i] != 0){result *= dMatrix[i, i];}else{return 0;}}return sign * result;}/// <summary>/// 矩阵减法/// </summary>/// <param ></param>/// <param ></param>/// <param ></param>/// <param ></param>private double[] SubMatrix(double[] A1, double[] A2) {//判断矩阵的长短是否一致int a1 = A1.GetLength(0);int a2 = A2.GetLength(0);if (a1 != a2){return null;}//矩阵相减double[] B = new double[a1];for (int i = 0; i < a1; i++){B[i] = A1[i] - A2[i];}return B;}/// <summary>/// 矩阵乘法/// </summary>/// <param ></param>/// <param ></param>/// <returns></returns>private double[,] MultiplyMatrix(double[,] firstMatrix, double[,] secondMatrix){double[,] resultMatrix = new double[firstMatrix.GetLength(0), secondMatrix.GetLength(1)]; //判断相乘矩阵是否合法,即第一个矩阵的列要等于第二个矩阵的行if (firstMatrix.GetLength(1) != secondMatrix.GetLength(0)){return null;}//求结果矩阵for (int rowIndex = 0; rowIndex < firstMatrix.GetLength(0); rowIndex++){for (int colIndex = 0; colIndex < secondMatrix.GetLength(1); colIndex++){//初始化结果矩阵的元素resultMatrix[rowIndex, colIndex] = 0;for (int i = 0; i < firstMatrix.GetLength(1); i++){//求结果矩阵的元素值resultMatrix[rowIndex, colIndex] += firstMatrix[rowIndex, i] * secondMatrix[i, colIndex];}}}return resultMatrix;}/// <summary>/// 求逆矩阵/// </summary>/// <param ></param>/// <returns></returns>private double[,] Athwart(double[,] dMatrix){//获取矩阵的行数int Level = dMatrix.GetLength(1);double[,] dReverseMatrix = new double[Level, 2 * Level]; //初始化矩阵Level×(2*Level)for (int i = 0; i < Level; i++){for (int j = 0; j < 2 * Level; j++){if (j < Level){dReverseMatrix[i, j] = dMatrix[i, j];}else{if (j - Level == i){dReverseMatrix[i, j] = 1;}else{dReverseMatrix[i, j] = 0;}}}}for (int i = 0, j = 0; i < Level && j < Level; i++, j++){if (dReverseMatrix[i, j] == 0){if (i == Level - 1){return null;}int m = i + 1;for (; dMatrix[m, j] == 0; m++){if (m == Level - 1){return null;}if (m == Level){return null;}else{//把i行和m行相加for (int n = j; n < 2 * Level; n++){dReverseMatrix[i, n] += dReverseMatrix[m, n];}}}double temp = dReverseMatrix[i, j];if (temp != 1){//把i行数据,变成以1开始的一行数据for (int n = j; n < 2 * Level; n++){if (dReverseMatrix[i, n] != 0){dReverseMatrix[i, n] /= temp;}}}//把i行后的所有行的j列变成0for (int s = Level - 1; s > i; s--){temp = dReverseMatrix[s, j];for (int t = j; t < 2 * Level; t++){dReverseMatrix[s, t] -= (dReverseMatrix[i, t] * temp);}}}//把矩阵Level×(2*Level)前Level×Level转变为单位矩阵for (int i = Level - 2; i >= 0; i--){for (int j = i + 1; j < Level; j++){if (dReverseMatrix[i, j] != 0)double tmp = dReverseMatrix[i, j];for (int n = j; n < 2 * Level; n++){dReverseMatrix[i, n] -= (tmp * dReverseMatrix[j, n]); }}}}//返回逆矩阵double[,] dReturn = new double[Level, Level];for (int i = 0; i < Level; i++){for (int j = 0; j < Level; j++){dReturn[i, j] = dReverseMatrix[i, j + Level];}}return dReturn;}#endregion第二份:1using System;2using System.IO;3using System.Diagnostics;456namespace Adjust7{8///<summary>9///Matrix 的摘要说明。
矩阵问题(c语言)讲解
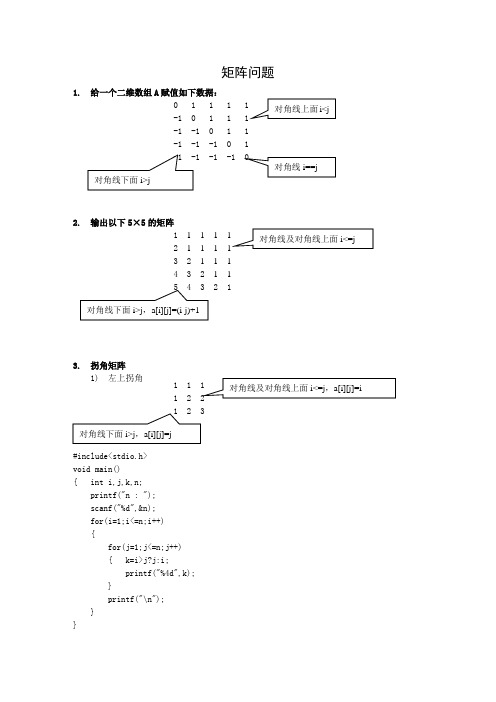
int m=a; if(m>b) m=b; if(m>c) m=c; if(m>d) m=d; return m; } main() { int i,j,k,n,mi,ma; printf("n : "); scanf("%d",&n); for(i=1;i<=n;i++) { for(j=1;j<=n;j++)
a[1]=1;
for(i=1;i<=n;i++)
{for(j=i;j>=1;j--)
a[j]=a[j]+a[j-1];
for(j=1;j<=i;j++)
printf("%4d",a[j]);
printf("\n");
}
}
9. 直角三角阵
1) 形式 1
1 3 6 10 15
2 5 9 14
4 8 13
4. 回形矩阵
11111 12221 12321 12221 11111
方法 1:四个拐角矩阵拼合而成。 方法 1 改进:减少判断条件。 #include<stdio.h> main() { int i,j,k,n,mi,ma;
printf("n : "); scanf("%d",&n); for(i=1;i<=n;i++) { mi=i<=n+1-i?i:n+1-i;+1
C语言矩阵操作范文

C语言矩阵操作范文在C语言中,矩阵操作是一项非常常见且重要的任务。
矩阵是一个二维数组,由行和列组成。
矩阵操作通常包括矩阵的创建、初始化、遍历、计算以及转置等。
下面将详细介绍一些常见的矩阵操作。
1.矩阵的创建和初始化:在C语言中,可以通过使用二维数组来创建和初始化一个矩阵。
例如,我们可以使用以下语句创建一个3x3的矩阵并进行初始化:```cint matrix[3][3] = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };```这将创建一个3x3的矩阵,并将其初始化为数字1到92.矩阵的遍历:要遍历矩阵中的每个元素,可以使用两个嵌套的循环结构,一个用于遍历行,另一个用于遍历列。
例如,以下代码将遍历并打印一个3x3的矩阵:```cint i, j;for(i = 0; i < 3; i++)for(j = 0; j < 3; j++)printf("%d ", matrix[i][j]); // 打印当前元素}printf("\n"); // 换行```这将产生下面的输出:```c123456789```3.矩阵的转置:矩阵的转置是指将矩阵的行和列交换。
例如,给定以下矩阵:```cint matrix[3][3] = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };```我们可以通过以下代码来实现矩阵的转置:```cint i, j;int transpose[3][3];for(i = 0; i < 3; i++)transpose[j][i] = matrix[i][j];}```转置后的矩阵将是:```c147258369```4.矩阵的相加和相乘:在C语言中,可以通过嵌套循环来对两个矩阵的对应元素进行相加或相乘。
例如,以下代码将两个3x3的矩阵相加并将结果存储在另一个矩阵中:```cint matrix1[3][3] = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };int matrix2[3][3] = { {9, 8, 7}, {6, 5, 4}, {3, 2, 1} };int result[3][3];int i, j;for(j = 0; j < 3; j++)result[i][j] = matrix1[i][j] + matrix2[i][j];}```相加后的矩阵将是:```c101010101010101010```同样地,两个矩阵的相乘也可以通过类似的方法实现。
用C语言实现矩阵运算之欧阳家百创编

//任务二:矩阵的基本运算欧阳家百(2021.03.07)#include<stdio.h>#include<stdlib.h>#define R1 4//矩阵MA行数,可以按具体情况修改#define C1 4//矩阵MA列数,可以按具体情况修改#define R2 4//矩阵MB行数,可以按具体情况修改#define C2 4//矩阵MB列数,可以按具体情况修改void Scalar(float MA[][C1]);void Transposition(float MA[][C1]);void Add(float MA[][C1],float MB[][C2]);void Subtraction(float MA[][C1],float MB[][C2]); void Multiplication(float MA[][C1],float MB[][C2]); void main(){float MA[R1][C1],MB[R2][C2];int c;while(1){printf("功能如下:\n");printf("数乘矩阵 1\n");printf("矩阵转换 2\n");printf("矩阵相加 3\n");printf("矩阵相减 4\n");printf("矩阵乘法 5\n");printf("结束 0\n");printf("请选定您需要的操作:\n");scanf("%d",&c);switch(c){case 1:Scalar(MA);break;case 2:Transposition(MA);break;case 3:if((R1==R2)&&(C1==C2))Add(MA,MB);elseprintf("矩阵MA与矩阵MB不能相减!\n");break;case 4:if((R1==R2)&&(C1==C2))Subtraction(MA,MB);elseprintf("矩阵MA与矩阵MB不能相加!\n");break;case 5:if(C1==R2)Multiplication(MA,MB);elseprintf("矩阵MA与矩阵MB不能相乘!\n");break;case 0:printf("结束!\n");exit(0);break;default:printf("对不起,您的输入不合法!\n");break;}}}void Scalar(float MA[][C1])//矩阵数乘函数{int i,j,k;printf("请输入乘数:\n");scanf("%d",&k);printf("请输入%d*%d矩阵MA(每行以回车结束):\n",R1,C1);for(i=0;i<R1;i++){for(j=0;j<C1;j++){scanf("%f",&MA[i][j]);}}printf("%d乘矩阵MA结果为:\n",k);for(i=0;i<R1;i++){for(j=0;j<C1;j++){printf("%6.2f ",k*MA[i][j]);}printf("\n");}}void Transposition(float MA[][C1])//矩阵转置函数{int i,j;float MD[C1][R1]={0};printf("请输入%d*%d矩阵MA(每行以回车结束):\n",R1,C1);for(i=0;i<R1;i++){for(j=0;j<C1;j++){scanf("%f",&MA[i][j]);}}for(i=0;i<R1;i++)//将矩阵MA的第n行的值赋给矩阵MD的第n列{for(j=0;j<C1;j++){MD[j][i]=MA[i][j];}}printf("矩阵MA转置后的结果为:\n");for(i=0;i<C1;i++){for(j=0;j<R1;j++){printf("%6.2f ",MD[i][j]);}printf("\n");}}void Add(float MA[][C1],float MB[][C2])//矩阵加法函数{int i,j;float ME[R1][C1]={0};printf("请输入%d*%d矩阵MA(每行以回车结束):\n",R1,C1);for(i=0;i<R1;i++){for(j=0;j<C1;j++){scanf("%f",&MA[i][j]);}}printf("请输入%d*%d矩阵MB(每行以回车结束):\n",R2,C2);for(i=0;i<R2;i++){for(j=0;j<C2;j++){scanf("%f",&MB[i][j]);}}for(i=0;i<R1;i++){for(j=0;j<C1;j++){ME[i][j]=MA[i][j]+MB[i][j];}}for(i=0;i<R1;i++){for(j=0;j<C1;j++){printf("%6.2f ",ME[i][j]);}printf("\n");}}void Subtraction(float MA[][C1],float MB[][C2])//矩阵减法函数{int i,j;float MF[R1][C1]={0};printf("请输入%d*%d矩阵MA(每行以回车结束):\n",R1,C1);for(i=0;i<R1;i++){for(j=0;j<C1;j++){scanf("%f",&MA[i][j]);}}printf("请输入%d*%d矩阵MB(每行以回车结束):\n",R2,C2);for(i=0;i<R2;i++){for(j=0;j<C2;j++){scanf("%f",&MB[i][j]);}}for(i=0;i<R1;i++){for(j=0;j<C1;j++){MF[i][j]=MA[i][j]-MB[i][j];}}for(i=0;i<R1;i++){for(j=0;j<C1;j++){printf("%6.2f ",MF[i][j]);}printf("\n");}}void Multiplication(float MA[][C1],float MB[][C2])//矩阵相乘函数{int i,j,k;float MG[R1][C2]={0};printf("请输入%d*%d矩阵MA(每行以回车结束):\n",R1,C1);for(i=0;i<R1;i++){for(j=0;j<C1;j++){scanf("%f",&MA[i][j]);}}printf("请输入%d*%d矩阵MB(每行以回车结束):\n",R2,C2);for(i=0;i<R2;i++){for(j=0;j<C2;j++){scanf("%f",&MB[i][j]);}}for(i=0;i<R1;i++){for(j=0;j<C2;j++){for(k=0;k<C1;k++){MG[i][j]=MG[i][j]+MA[i][k]*MB[k][j];}}}for(i=0;i<R1;i++){for(j=0;j<C2;j++){printf("%6.2f ",MG[i][j]);}printf("\n");}}。
c语言求基本关联矩阵

矿井通风网络论程序作业学院:矿业学院专业:安全工程姓名:雷斌学号:28年级:2012 级任课教师:袁梅2015年5 月 6 日这是个5,7图,以树T={e2,e4,e6,e7}在前余树弦在后的顺序,求B1,C f , S f下面是我所写程序,(是用C语言写的)#include <stdio.h>#include <stdlib.h>#include <conio.h>#include <math.h>int m,n;double **a,**b11,**b12,**zb11,**zb12,**nzb12,**c12,*C,*AA,*B,**sf,**s11,**cf,**B1; double *Q,*Z;void Create_Omr(int m,int n);//创建原始矩阵变量函数void Free_mr();int brinv(double *a,int n);void brmul(double a[], double b[],int m,int n,int k,double c[]); void main(){int i,j,M,k;int t=0;printf("输入m ");scanf("%d",&m);printf("输入n ");scanf("%d",&n);M=m-1;Create_Omr(m,n);//调用创建动态数组函数printf("输入起点Q[n]");for (i=0;i<n;i++)scanf("%lf",&Q[i]);printf("输入终点Z[n]");for (i=0;i<n;i++)scanf("%lf",&Z[i]);printf("<开始计算各个矩阵>\n");for (i=0;i<m;i++)for (j=0;j<n;j++)a[i][j]=0.0;//初始化a的值全部置0for(j=0;j<n;j++) //求关联矩阵的过程{ i=(int)Q[j]-1;a[i][j]=1;}for(j=0;j<n;j++){ i=(int)Z[j]-1;a[i][j]=-1;}printf("输出关联矩阵B\n");for(i=0;i<m;i++){for(j=0;j<n;j++)printf("%3d",(int)a[i][j]);printf("\n");}printf("输入基本关联矩阵B");scanf("%d",&k);for(i=0;i<m-1;i++)/////求基本关联矩阵Bk {if(i==(k-1)){ for(j=0;j<n;j++)B1[i][j]=a[k][j];t++;}elsefor(j=0;j<n;j++)B1[i][j]=a[i+t][j];}printf("输出基本关联矩阵B%d\n",k);for(i=0;i<m-1;i++){for(j=0;j<n;j++)printf("%3d",(int)B1[i][j]);printf("\n");}for(i=0;i<m-1;i++)//求B11for(j=0;j<n-m+1;j++)b11[i][j]=B1[i][j];for(i=0;i<m-1;i++)//求B12for(j=n-m+1;j<n;j++)b12[i][j-n+m-1]=B1[i][j];for(i=0;i<m-1;i++)//求-ZB11for(j=0;j<n-m+1;j++)zb11[j][i]=-(int)b11[i][j];for(i=0;i<m-1;i++)//求ZB12for(j=0;j<m-1;j++)zb12[j][i]=b12[i][j];/*从这里开始把二维数组接入一位数组,(因为动态二维数组分配的内存空间不是连续的,所以用一个一维数组记录他的数据好传给逆矩阵的调用函数)*/for (i=0; i<m-1; i++)for(j=0;j<m-1;j++){AA[i*(m-1)+j]=zb12[i][j];//这里必须给AA 和B赋值我把zb12赋值给它们不然是随机数B[i*(m-1)+j]=zb12[i][j];}i=brinv(AA,M);//求逆矩阵调用函数k=0;for(i=0;i<m-1;i++)//把所求得逆矩阵,从新变成二维数组,方便C12的计算for(j=0;j<m-1;j++){nzb12[i][j]=AA[k];k++;}for (i=0;i<n-m+1;i++)//这里必须给c12赋0,不然求不出c12for (j=0;j<m-1;j++)c12[i][j]=0.0;for (i=0;i<n-m+1;i++)//求c12的过程,用循环语句来计算矩阵的乘法{for (j=0;j<m-1;j++){for (k=0;k<m-1;k++){c12[i][j]=c12[i][j]+zb11[i][k]*nzb12[k][j];//矩阵的乘法}}for(i=0;i<n-m+1;i++)/*求cf矩阵的过程*/ for(j=0;j<n-m+1;j++)if(i==j)cf[i][j]=1.0;elsecf[i][j]=0.0;for(i=0;i<n-m+1;i++)for(j=0;j<m-1;j++)cf[i][j+n-m+1]=c12[i][j];printf("独立回路矩阵cf:\n");//输出cf矩阵for(i=0;i<n-m+1;i++){for(j=0;j<n;j++)printf("%3d",(int)cf[i][j]);printf("\n");}for(i=0;i<n-m+1;i++)//求s11矩阵的过程for(j=0;j<m-1;j++)s11[j][i]=-c12[i][j];for(i=0;i<m-1;i++)////求sf矩阵的过程sf[i][i+n-m+1]=1;for(i=0;i<m-1;i++)for(j=0;j<n-m+1;j++)sf[i][j]=s11[i][j];printf("独立割集矩阵sf:\n");for(i=0;i<m-1;i++)//输出sf矩阵{for(j=0;j<n;j++)printf("%3d",(int)sf[i][j]);printf("\n");}void Create_Omr(int m,int n)//创建各个矩阵{ int i;printf("你输的是一个%d,%d图\n",m,n);a=(double **)malloc(m*sizeof(double));b11=(double **)malloc((m-1)*sizeof(double));b12=(double **)malloc((m-1)*sizeof(double));zb11=(double **)malloc((n-m+1)*sizeof(double));zb12=(double **)malloc((m-1)*sizeof(double));C=(double *)malloc((m-1)*(m-1)*sizeof(double));B=(double *)malloc((m-1)*(m-1)*sizeof(double));AA=(double *)malloc((m-1)*(m-1)*sizeof(double));cf=(double **)malloc((n-m+1)*sizeof(double));sf=(double **)malloc((m-1)*sizeof(double));s11=(double **)malloc((m-1)*sizeof(double));B1=(double **)malloc((m-1)*sizeof(double));nzb12=(double **)malloc((m-1)*sizeof(double));c12=(double **)malloc((n-m+1)*sizeof(double));Q=(double *)malloc(n*sizeof(double));Z=(double *)malloc(n*sizeof(double));for(i = 0; i < m; i++)a[i] = (double *)malloc(n * sizeof(double));//动态分配矩阵列数组for(i = 0; i < m-1; i++)b11[i] = (double *)malloc((n-m+1) * sizeof(double));//动态分配矩阵列数组for (i=0;i<m-1;i++){b12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组zb12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组nzb12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组s11[i]= (double *)malloc((n-m+1) * sizeof(double));//动态分配矩阵列数组sf[i]=(double *)malloc(n * sizeof(double));//动态分配矩阵列数组B1[i]=(double *)malloc(n * sizeof(double));//动态分配矩阵列数组}for (i=0;i<n-m+1;i++){zb11[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组c12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组cf[i]=(double *)malloc(n * sizeof(double));//动态分配矩阵列数组}}int brinv(double *a, int n)//求逆矩阵的函数{ int *is,*js,i,j,k,l,u,v;double d,p;is=malloc(n*sizeof(double));js=malloc(n*sizeof(double));for (k=0; k<=n-1; k++){ d=0.0;for (i=k; i<=n-1; i++)for (j=k; j<=n-1; j++){ l=i*n+j; p=fabs(a[l]);if (p>d) { d=p; is[k]=i; js[k]=j;}}if (d+1.0==1.0){ free(is); free(js); printf("err**not inv\n");return(0);}if (is[k]!=k)for (j=0; j<=n-1; j++){ u=k*n+j; v=is[k]*n+j;p=a[u]; a[u]=a[v]; a[v]=p;}if (js[k]!=k)for (i=0; i<=n-1; i++){ u=i*n+k; v=i*n+js[k];p=a[u]; a[u]=a[v]; a[v]=p;}l=k*n+k;a[l]=1.0/a[l];for (j=0; j<=n-1; j++)if (j!=k){ u=k*n+j; a[u]=a[u]*a[l];}for (i=0; i<=n-1; i++)if (i!=k)for (j=0; j<=n-1; j++)if (j!=k){ u=i*n+j;a[u]=a[u]-a[i*n+k]*a[k*n+j];}for (i=0; i<=n-1; i++)if (i!=k){ u=i*n+k; a[u]=-a[u]*a[l];}}for (k=n-1; k>=0; k--){ if (js[k]!=k)for (j=0; j<=n-1; j++){ u=k*n+j; v=js[k]*n+j;p=a[u]; a[u]=a[v]; a[v]=p;}if (is[k]!=k)for (i=0; i<=n-1; i++){ u=i*n+k; v=i*n+is[k];p=a[u]; a[u]=a[v]; a[v]=p;}}free(is); free(js);return(1);}///注意,用malloc动态分配数组,本应该释放的,但为了程序短一点,所以就不释放了。
C++实现关系与关系矩阵的代码详解

C++实现关系与关系矩阵的代码详解⽬录ADT集合关系关系矩阵功能实现关系的矩阵表⽰关系的性质判断关系的合成参考:ADT集合template<class Type> //集合的元素类型class Set{ //集合ADTint size; //基数vector<Type> p;public:Set():size(0){}Set(int s):size(s){p.resize(s); //重置⼤⼩}int getSize()const{ return size; }void push(Type e){ //添加元素size++;p.push_back(e);void set(int pos,Type e){ //设置元素值p[pos]=e;Type operator[](int i){ return p[i]; } //下标读取int findElem(Type e){ //返回指定元素的下标for(int i=0;i<size;i++){if(p[i]==e) return i;}return -1;};关系template<class Type>class Relation{Set<Type> dom; //定义域Set<Type> ran; //值域public:Relation():dom(),ran(){} //⽆规模的初始化Relation(int r_,int c_):dom(r_),ran(c_){} //有规模的初始化int getR()const { return dom.getSize(); } //返回⾏,基类私有成员只可调⽤基类⾮私有函数获得int getC()const { return ran.getSize(); } //返回列Set<Type> getDom()const { return dom; } //返回定义域Set<Type> getRan()const { return ran; } //返回值域void pushDom(Type e){ dom.push(e); } //给定义域添加元素void pushRan(Type e){ ran.push(e); } //给值域添加元素int findDom(Type e){ //寻找定义域中元素的位置return dom.findElem(e);}int findRan(Type e){ //寻找值域中元素的位置return ran.findElem(e);};关系矩阵template<class Type>class RMatrix:public Relation<Type>{vector< vector<short> > m; //⼆维矩阵⽤vector实现,注意不能使⽤bool类型,它有很⾼的特殊性 public:RMatrix(int r_,int c_):Relation<Type>(r_,c_){for(int i=0;i<r_;i++){vector<short> v(c_,0);m.push_back(v); //推⼊r_个长度为c_的vector数组构成⼀个r*c的⼆维数组}}RMatrix():Relation<Type>(){ //不输⼊矩阵⼤⼩时for(int i=0;i<MAX_NUM;i++){vector<short> v(MAX_NUM,0);m.push_back(v);}}RMatrix(const RMatrix<Type> &M){ //复制构造函数// printf("here!");Set<Type> Dom=M.getDom(),Ran=M.getRan();int k1=Dom.getSize(),k2=Ran.getSize();for(int i=0;i<k1;i++){Relation<Type>::pushDom(Dom[i]);}for(int i=0;i<k2;i++){Relation<Type>::pushRan(Ran[i]);}m.resize(k1);for(int i=0;i<k1;i++){m[i].resize(0);for(int j=0;j<k2;j++){m[i].push_back(M[i][j]);// printf("%d",m[i][j]);}}}void updateSize(){ //根据定义域和值域的基数设置矩阵规模int row=Relation<Type>::getDom().getSize(); //在⼦类中调⽤基类函数需要制定基类int col=Relation<Type>::getRan().getSize();// printf("row=%d,col=%d",row,col);m.resize(row);for(int i=0;i<row;i++){m[i].resize(0);for(int j=0;j<col;j++){m[i].push_back(short(0));// printf("%d",m[i][j]);}}return;}vector<short> operator[](int p1)const { return m[p1]; } //可以直接双括号使⽤!void set(int p1,int p2,short e){ //设置矩阵值m[p1][p2]=e;}void push(vector<short> v){ //添加矩阵的⾏m.push_back(v);}/* 将两个关系矩阵合成,括号内的在右 */RMatrix<Type> matrixSynthesis(const RMatrix<Type> &M1)const {RMatrix<Type> M; //此处的M是临时变量,必定被销毁,⽆法作为引⽤被返回 (<!-1)Set<Type> d=Relation<Type>::getDom(),r=M1.getRan(); //矩阵合成的⾏列关系差点弄错!int k1=d.getSize(),k2=r.getSize(),k3=M1.getR();for(int i=0;i<k1;i++){M.pushDom(d[i]);}for(int i=0;i<k2;i++){M.pushRan(r[i]);}M.updateSize();for(int i=0;i<k1;i++){for(int j=0;j<k2;j++){bool f=0;for(int p=0;p<k3;p++){if(m[i][p] && M1[p][j]) f=1;}if(f) M.set(i,j,f);}}return M;}void randomRelation(){ //随机⽣成⼀段关系,需要放在updatesize之后// printf("time=%d\n",time(0)); //伪随机的实现需要新添加两个⽂件头srand(time(0)); //初始化随机数int r=Relation<Type>::getR(),c=Relation<Type>::getC();for(int i=0;i<r;i++){for(int j=0;j<c;j++){m[i][j]=rand()%2; //⽣成0或1}}return ;}bool isSelf()const { //⾃反性检测int r=Relation<Type>::getR();for(int i=0;i<r;i++){if(!m[i][i]) return 0;}return 1;}bool antiSelf()const { //反⾃反性检测int r=Relation<Type>::getR();for(int i=0;i<r;i++){if(m[i][i]) return 0;}return 1;}bool isSymmetric()const { //对称性int r=Relation<Type>::getR();for(int i=0;i<r;i++){for(int j=i+1;j<r;j++){if(m[i][j]!=m[j][i]) return 0;}}return 1;}bool antiSymmetric()const { //反对称性,注意都为0不违反反对称性!int r=Relation<Type>::getR();for(int i=0;i<r;i++){for(int j=i+1;j<r;j++){if(m[i][j] && m[i][j]==m[j][i]) return 0;}}return 1;}bool isPassing()const { //传递性RMatrix<Type> M_=matrixSynthesis(*this); //const函数只能调⽤const函数 <!-2int r=Relation<Type>::getR();for(int i=0;i<r;i++){for(int j=0;j<r;j++){if(m[i][j]==0 && M_[i][j]==1) return 0;}}return 1;}};<!-1 处若是给函数返回值加上引⽤会报⼀个警告,调⽤函数后集合ADT处会出现⼀个内存错误,这是因为M此处是临时变量,是⼀定被销毁的,所以作为引⽤被返回当然就出了问题,⽽此处不⽤引⽤是完全可⾏的。
[C语言]矩阵运算
![[C语言]矩阵运算](https://img.taocdn.com/s3/m/b55e60fdf80f76c66137ee06eff9aef8941e48c8.png)
[C语⾔]矩阵运算最近要做⼀个MFC的上位机,⽤到CSP滤波算法,这玩意⼉在MATLAB ⾥相当简单就能实现但C⾥⾯实现起来太蛋疼,写了⼀个晚上才把这个算法⽤到的矩阵运算部分的函数写的差不多,为了避免以后再重复造轮⼦,现在这⾥写⼀下备份⼀下吧。
1.矩阵乘法//矩阵乘法/********参数表*******@Parameter x: m⾏k列矩阵(⽤⼀维数组表⽰)@Parameter y: k⾏n列矩阵(⽤⼀维数组表⽰)@Parameter m,k,n: 矩阵⾏列参数@Parameter z: m⾏n列输出矩阵(⽤⼀维数组表⽰)***********************/void MulMatrixDD(double *x,double *y, int m,int k,int n, double *z){for(int nm=0; nm<m; nm++)for(int nn=0; nn<n; nn++)for(int nk=0; nk<k; nk++)z[nm*n+nn] += x[nm*k+nk]*y[nk*n+nn];}因为输⼊的x,y可能是不同的类型(short, double)所以我只简单的复制了⼏个函数来表⽰,⽐如输⼊如果是x如果是short型,y是double型这个函数就不好⽤了。
如果有什么更好的通⽤⽅法可以跟我交流下2.⽅阵转置//⽅阵转置/********参数表*******@Parameter x: m⾏m列矩阵(⽤⼀维数组表⽰)@Parameter m: 矩阵⾏列数***********************/void TransSquareD(double *x, int m){double temp;for(int nm=0; nm<m; nm++){ //对原矩阵第nm⾏for(int nn=0; nn<nm; nn++){ //对原矩阵第nn列temp = x[nm*m+nn]; //z矩阵第nn⾏第nm列x[nm*m+nn] = x[nn*m+nm];x[nn*m+nm] = temp;}}}3.⾮⽅阵转置//⾮⽅阵转置/********参数表*******@Parameter x: m⾏n列矩阵(⽤⼀维数组表⽰)@Parameter m,n: 矩阵⾏列数@Parameter z: n⾏m列矩阵(⽤⼀维数组表⽰)***********************/void TransMatrixD(double *x, int m, int n, double *z){for(int nm=0; nm<m; nm++) //对原矩阵第nm⾏for(int nn=0; nn<n; nn++) //对原矩阵第nn列z[nn*m+nm] = x[nm*n+nn]; //z矩阵第nn⾏第nm列}void TransMatrixS(short *x, int m, int n, double *z){for(int nm=0; nm<m; nm++) //对原矩阵第nm⾏for(int nn=0; nn<n; nn++) //对原矩阵第nn列z[nn*m+nm] = (double)x[nm*n+nn]; //z矩阵第nn⾏第nm列}4.协⽅差矩阵//协⽅差矩阵函数/********参数表*******@Parameter X[m_cov][n_cov]: m_cov⾏n_cov列矩阵(⽤⼆维数组表⽰)***********************/void CovMat(short X[m_cov][n_cov]){for(int i=0; i<m_cov; i++)for(int j=0; j<m_cov; j++)CovMatrix[i][j] = cov(*(X+i),*(X+j));}//协⽅差函数double cov(short *x, short *y){double sumx = 0;double sumy = 0;double sum = 0;int kk = 0;for(kk = 0; kk<n_cov; kk++){sumx += x[kk];sumy += y[kk];}sumx /= n_cov;sumy /= n_cov;for(kk = 0; kk<n_cov; kk++){sum += (x[kk]-sumx)*(y[kk]-sumy);}sum /= (n_cov-1);return sum;}5.求矩阵特征值和特征向量这个短时间⾃⼰造轮⼦太⿇烦了,,参考csdn上⼀篇博客:https:///zhouxuguang236/article/details/40212143 改了⼀下/********参数表******** @brief 求实对称矩阵的特征值及特征向量的雅克⽐法* 利⽤雅格⽐(Jacobi)⽅法求实对称矩阵的全部特征值及特征向量@Parameter pMatrix 长度为n*n的数组,存放实对称矩阵@Parameter nDim 矩阵的阶数@Parameter pdblVects 长度为n*n的数组,返回特征向量(按列存储)@Parameter dbEps 精度要求@Parameter nJt 整型变量,控制最⼤迭代次数@Parameter pdbEigenValues 特征值数组***********************/void JacbiCor(double * pMatrix,int nDim, double *pdblVects, double *pdbEigenValues, double dbEps,int nJt){int i,j;for(i = 0; i < nDim; i ++){pdblVects[i*nDim+i] = 1.0f;for(int j = 0; j < nDim; j ++){if(i != j)pdblVects[i*nDim+j]=0.0f;}}int nCount = 0; //迭代次数while(1){//在pMatrix的⾮对⾓线上找到最⼤元素double dbMax = pMatrix[1];int nRow = 0;int nCol = 1;for (i = 0; i < nDim; i ++) //⾏{for (j = 0; j < nDim; j ++) //列{double d = fabs(pMatrix[i*nDim+j]);if((i!=j) && (d> dbMax)){dbMax = d;nRow = i;nCol = j;}}}if(dbMax < dbEps) //精度符合要求break;if(nCount > nJt) //迭代次数超过限制break;nCount++;double dbApp = pMatrix[nRow*nDim+nRow];double dbApq = pMatrix[nRow*nDim+nCol];double dbAqq = pMatrix[nCol*nDim+nCol];//计算旋转⾓度double dbAngle = 0.5*atan2(-2*dbApq,dbAqq-dbApp);double dbSinTheta = sin(dbAngle);double dbCosTheta = cos(dbAngle);double dbSin2Theta = sin(2*dbAngle);double dbCos2Theta = cos(2*dbAngle);pMatrix[nRow*nDim+nRow] = dbApp*dbCosTheta*dbCosTheta +dbAqq*dbSinTheta*dbSinTheta + 2*dbApq*dbCosTheta*dbSinTheta;pMatrix[nCol*nDim+nCol] = dbApp*dbSinTheta*dbSinTheta +dbAqq*dbCosTheta*dbCosTheta - 2*dbApq*dbCosTheta*dbSinTheta;pMatrix[nRow*nDim+nCol] = 0.5*(dbAqq-dbApp)*dbSin2Theta + dbApq*dbCos2Theta; pMatrix[nCol*nDim+nRow] = pMatrix[nRow*nDim+nCol];for(i = 0; i < nDim; i ++){if((i!=nCol) && (i!=nRow)){int u = i*nDim + nRow; //pint w = i*nDim + nCol; //qdbMax = pMatrix[u];pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta;pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta;}}for (j = 0; j < nDim; j ++){if((j!=nCol) && (j!=nRow)){int u = nRow*nDim + j; //pint w = nCol*nDim + j; //qdbMax = pMatrix[u];pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta;pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta;}}//计算特征向量for(i = 0; i < nDim; i ++){int u = i*nDim + nRow; //pint w = i*nDim + nCol; //qdbMax = pdblVects[u];pdblVects[u] = pdblVects[w]*dbSinTheta + dbMax*dbCosTheta;pdblVects[w] = pdblVects[w]*dbCosTheta - dbMax*dbSinTheta;}}for(i = 0; i < nDim; i ++){pdbEigenValues[i] = pMatrix[i*nDim+i];}//设定正负号for(i = 0; i < nDim; i ++){double dSumVec = 0;for(j = 0; j < nDim; j ++)dSumVec += pdblVects[j * nDim + i];if(dSumVec<0){for(j = 0;j < nDim; j ++)pdblVects[j * nDim + i] *= -1;}}}⼆维数组转⼀维数组:const short m_cov = 3;const short n_cov = 3;short X[m_cov][n_cov] = {0};short *XFlat;/************X测试************/X[0][0] = 7;X[0][1] = 1;X[0][2] = 8;X[1][0] = 4;X[1][1] = 5;X[1][2] = 8;X[2][0] = 10;X[2][1] = 4;X[2][2] = 2; /*****************************/XFlat = (short *)X;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿井通风网络论程序作业学院:矿业学院专业:安全工程姓名:雷斌学号:********** 年级:2012 级任课教师:袁梅2015年5 月 6 日这是个5,7图,以树T={e2,e4,e6,e7}在前余树弦在后的顺序,求B1,C f , S f下面是我所写程序,(是用C语言写的)#include <stdio.h>#include <stdlib.h>#include <conio.h>#include <math.h>int m,n;double **a,**b11,**b12,**zb11,**zb12,**nzb12,**c12,*C,*AA,*B,**sf,**s11,**cf,**B1; double *Q,*Z;void Create_Omr(int m,int n);//创建原始矩阵变量函数void Free_mr();int brinv(double *a,int n);void brmul(double a[], double b[],int m,int n,int k,double c[]);void main(){int i,j,M,k;int t=0;printf("输入m ");scanf("%d",&m);printf("输入n ");scanf("%d",&n);M=m-1;Create_Omr(m,n);//调用创建动态数组函数printf("输入起点Q[n]");for (i=0;i<n;i++)scanf("%lf",&Q[i]);printf("输入终点Z[n]");for (i=0;i<n;i++)scanf("%lf",&Z[i]);printf("<开始计算各个矩阵>\n");for (i=0;i<m;i++)for (j=0;j<n;j++)a[i][j]=0.0;//初始化a的值全部置0for(j=0;j<n;j++) //求关联矩阵的过程{ i=(int)Q[j]-1;a[i][j]=1;}for(j=0;j<n;j++){ i=(int)Z[j]-1;a[i][j]=-1;}printf("输出关联矩阵B\n");for(i=0;i<m;i++){for(j=0;j<n;j++)printf("%3d",(int)a[i][j]);printf("\n");}printf("输入基本关联矩阵B");scanf("%d",&k);for(i=0;i<m-1;i++)/////求基本关联矩阵Bk{if(i==(k-1)){ for(j=0;j<n;j++)B1[i][j]=a[k][j];t++;}elsefor(j=0;j<n;j++)B1[i][j]=a[i+t][j];}printf("输出基本关联矩阵B%d\n",k);for(i=0;i<m-1;i++){for(j=0;j<n;j++)printf("%3d",(int)B1[i][j]);printf("\n");}for(i=0;i<m-1;i++)//求B11for(j=0;j<n-m+1;j++)b11[i][j]=B1[i][j];for(i=0;i<m-1;i++)//求B12for(j=n-m+1;j<n;j++)b12[i][j-n+m-1]=B1[i][j];for(i=0;i<m-1;i++)//求-ZB11for(j=0;j<n-m+1;j++)zb11[j][i]=-(int)b11[i][j];for(i=0;i<m-1;i++)//求ZB12for(j=0;j<m-1;j++)zb12[j][i]=b12[i][j];/*从这里开始把二维数组接入一位数组,(因为动态二维数组分配的内存空间不是连续的,所以用一个一维数组记录他的数据好传给逆矩阵的调用函数)*/for (i=0; i<m-1; i++)for(j=0;j<m-1;j++){AA[i*(m-1)+j]=zb12[i][j];//这里必须给AA 和B赋值我把zb12赋值给它们不然是随机数B[i*(m-1)+j]=zb12[i][j];}i=brinv(AA,M);//求逆矩阵调用函数k=0;for(i=0;i<m-1;i++)//把所求得逆矩阵,从新变成二维数组,方便C12的计算for(j=0;j<m-1;j++){nzb12[i][j]=AA[k];k++;}for (i=0;i<n-m+1;i++)//这里必须给c12赋0,不然求不出c12for (j=0;j<m-1;j++)c12[i][j]=0.0;for (i=0;i<n-m+1;i++)//求c12的过程,用循环语句来计算矩阵的乘法{for (j=0;j<m-1;j++){for (k=0;k<m-1;k++){c12[i][j]=c12[i][j]+zb11[i][k]*nzb12[k][j];//矩阵的乘法}}}for(i=0;i<n-m+1;i++)/*求cf矩阵的过程*/for(j=0;j<n-m+1;j++)if(i==j)cf[i][j]=1.0;elsecf[i][j]=0.0;for(i=0;i<n-m+1;i++)for(j=0;j<m-1;j++)cf[i][j+n-m+1]=c12[i][j];printf("独立回路矩阵cf:\n");//输出cf矩阵for(i=0;i<n-m+1;i++){for(j=0;j<n;j++)printf("%3d",(int)cf[i][j]);printf("\n");}for(i=0;i<n-m+1;i++)//求s11矩阵的过程for(j=0;j<m-1;j++)s11[j][i]=-c12[i][j];for(i=0;i<m-1;i++)////求sf矩阵的过程sf[i][i+n-m+1]=1;for(i=0;i<m-1;i++)for(j=0;j<n-m+1;j++)sf[i][j]=s11[i][j];printf("独立割集矩阵sf:\n");for(i=0;i<m-1;i++)//输出sf矩阵{for(j=0;j<n;j++)printf("%3d",(int)sf[i][j]);printf("\n");}}void Create_Omr(int m,int n)//创建各个矩阵{ int i;printf("你输的是一个%d,%d图\n",m,n);a=(double **)malloc(m*sizeof(double));b11=(double **)malloc((m-1)*sizeof(double));b12=(double **)malloc((m-1)*sizeof(double));zb11=(double **)malloc((n-m+1)*sizeof(double));zb12=(double **)malloc((m-1)*sizeof(double));C=(double *)malloc((m-1)*(m-1)*sizeof(double));B=(double *)malloc((m-1)*(m-1)*sizeof(double));AA=(double *)malloc((m-1)*(m-1)*sizeof(double));cf=(double **)malloc((n-m+1)*sizeof(double));sf=(double **)malloc((m-1)*sizeof(double));s11=(double **)malloc((m-1)*sizeof(double));B1=(double **)malloc((m-1)*sizeof(double));nzb12=(double **)malloc((m-1)*sizeof(double));c12=(double **)malloc((n-m+1)*sizeof(double));Q=(double *)malloc(n*sizeof(double));Z=(double *)malloc(n*sizeof(double));for(i = 0; i < m; i++)a[i] = (double *)malloc(n * sizeof(double));//动态分配矩阵列数组for(i = 0; i < m-1; i++)b11[i] = (double *)malloc((n-m+1) * sizeof(double));//动态分配矩阵列数组for (i=0;i<m-1;i++){b12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组zb12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组nzb12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组s11[i]= (double *)malloc((n-m+1) * sizeof(double));//动态分配矩阵列数组sf[i]=(double *)malloc(n * sizeof(double));//动态分配矩阵列数组B1[i]=(double *)malloc(n * sizeof(double));//动态分配矩阵列数组}for (i=0;i<n-m+1;i++){zb11[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组c12[i]=(double *)malloc((m-1) * sizeof(double));//动态分配矩阵列数组cf[i]=(double *)malloc(n * sizeof(double));//动态分配矩阵列数组}}int brinv(double *a, int n)//求逆矩阵的函数{ int *is,*js,i,j,k,l,u,v;double d,p;is=malloc(n*sizeof(double));js=malloc(n*sizeof(double));for (k=0; k<=n-1; k++){ d=0.0;for (i=k; i<=n-1; i++)for (j=k; j<=n-1; j++){ l=i*n+j; p=fabs(a[l]);if (p>d) { d=p; is[k]=i; js[k]=j;}}if (d+1.0==1.0){ free(is); free(js); printf("err**not inv\n");return(0);}if (is[k]!=k)for (j=0; j<=n-1; j++){ u=k*n+j; v=is[k]*n+j;p=a[u]; a[u]=a[v]; a[v]=p;}if (js[k]!=k)for (i=0; i<=n-1; i++){ u=i*n+k; v=i*n+js[k];p=a[u]; a[u]=a[v]; a[v]=p;}l=k*n+k;a[l]=1.0/a[l];for (j=0; j<=n-1; j++)if (j!=k){ u=k*n+j; a[u]=a[u]*a[l];}for (i=0; i<=n-1; i++)if (i!=k)for (j=0; j<=n-1; j++)if (j!=k){ u=i*n+j;a[u]=a[u]-a[i*n+k]*a[k*n+j];}for (i=0; i<=n-1; i++)if (i!=k){ u=i*n+k; a[u]=-a[u]*a[l];}}for (k=n-1; k>=0; k--){ if (js[k]!=k)for (j=0; j<=n-1; j++){ u=k*n+j; v=js[k]*n+j;p=a[u]; a[u]=a[v]; a[v]=p;}if (is[k]!=k)for (i=0; i<=n-1; i++){ u=i*n+k; v=i*n+is[k];p=a[u]; a[u]=a[v]; a[v]=p;}}free(is); free(js);return(1);}///注意,用malloc动态分配数组,本应该释放的,但为了程序短一点,所以就不释放了。
