机器人学导论chapter4
机器人学 完整版

机器人学第一章绪论1. 1 机器人发展史1.1.1 早期的自动机早在1770年,美国科学家就发明了一种报时鸟,一到整点,这只鸟的翅膀、头便开始运动,同时发出叫声。
图1-1为报时鸟的机械结构图,它的主弹簧驱动齿轮转动,使活塞压缩空气而发出叫声,同时齿轮转动时带动凸轮转动,从而驱动翅膀、头运动。
图1-1 报时鸟简图机器人(Robot)一词由一位名叫Karal Capak的捷克斯洛伐克剧作家首先使用。
在捷克语中,Robot这个词是指一个赋役的奴隶。
在1921年Capak写了一出戏剧,名叫《洛桑万能机器人公司》(Rossnm’s Universal Robots).在这出剧中,机器人是洛桑和他儿子研制的类人的生物,用来作为人类的奴仆。
随后,一名叫Isaac Asimov的科学幻想小说家使用了机器人学(Robotics)这个词来描述与机器人有关的科学。
他还提出了“机器人”的三个原则,值得今天的机器人设计者和使用者的注意。
这三个原则的原语如下:(1)A robot must not harm a human being or through inaction ,allow one tocome harm(2) A robot must always obey human beings unless that is conflict with thefirst law.(3)A robot must protect itself from harm unless that is conflict with the firstor second laws.1.1.2近似与机器人相关的装置1.操作机(Manipulators)它是目前仍然大量使用的、由机械控制的操作机。
它的各个关节由机械直接控制。
它具有和人类手臂相似的功能,可在空间抓放物体或进行其他操作。
2.远程操作手(Teleoperators)远程操作手又称主从操作手,它是在操作机之后发展起来的。
(人工智能)人工智能机器人学导论

(人工智能)人工智能机器人学导论人工智能机器人学导论1简介:1作者简介2机器人控制器和程序设计3简介:3机器人制作入门篇6简介:6作者简介6机器人智能控制工程8简介:8人工智能机器人学导论作者:Ricky文章来源:本站原创更新时间:2006年05月03日打印此文浏览数:2370 SlidesforSecondEdition(Beta)Chapter1:WhatareRobots?.pptslidesandthepdfversion(goodaquicklook) Chapter2:Telesystems.thepdfversionChapter3:BiologicalFoundationsoftheReactiveParadigm.pptslidesandpdfversion Chapter5:TheReactiveParadigmChapter6:SelectingandCombiningBehaviorsChapter7:CommonSensorsandSensingTechniquesChapter8:DesigningaBehavior-BasedImplementationChapter9:Multi-AgentsChapter10:NavigationandtheHybridParadigmChapter11:TopologicalPathPlanningChapter12:MetricPathPlanningChapter13:LocalizationandMappingChapter14:AffectiveRobotsChapter15:Human-RobotInteractionChapter16:WhatCanRobotDoandWhatWillTheyBeAbletoDo?简介:本书系统地介绍了人工智能机器人于感知、导航、路径规划、不确定导航等领域的主要内容。
全书共分俩大部分。
机器人学导论717622504

机器人学导论学院:工程机械学院专业:机械工程*名:**学号:**********任课教师:***成绩:目录一、问题重述 (4)1.1、问题重述 (4)1.2 目标任务 (4)二、问题分析 (5)三、模型的假设 (6)四、符号说明 (6)五、模型建立与求解 (7)5.1运动学模型建立与求解 (7)5.1.1机器人运动方程的建立 (7)5.1.2 利用逆运动学方法求解 (10)5.2、问题1—1的模型 (11)5.2.1搜索算法流程图 (12)5.2.2、模型求解 (15)5.3、问题1—2、3的模型 (18)5.3.1、问题1的②、③ (18)5.3.2、问题2的② (20)5.3.3、问题2的③ (22)5.4、问题3 (25)七、模型的评价 (25)7.1.模型的优点 (25)7.2.模型的缺点 (25)参考文献 (26)摘要本文探讨了六自由度机械臂从一点到另一点沿任意轨迹移动路径、一点到另一点沿着给定轨迹移动路径、以及无碰撞路径规划问题,并讨论了设计参数对机械臂灵活性和使用范围的影响,同时给出了建议。
问题一:(1)首先确定初始坐标均为零时机械臂姿态,建立多级坐标系,利用空间解析几何的变换基本原理及相对坐标系的齐次坐标变换的矩阵解析方法,来建立机器人的运动系统的多级变换方程。
通过逆运动学解法和构建规划,来求优化指令(2)假定机械臂初始姿态为Φ0,曲线离散化,每个离散点作为末端位置,通过得到的相邻两点的姿态,利用(1)中算法计算所有相邻两点间的增量指令,将满足精度要求的指令序列记录下来。
(3)通过将障碍物理想化为球体,将躲避问题就转化成保证机械手臂上的点与障碍球球心距离始终大于r的问题。
进而通过迭代法和指令检验法,剔除不符合要求的指令,从而实现避障的目的问题二:将问题二中的实例应用到问题一中的相对应的算法中。
问题三:灵活性与适用范围相互制约,只能根据权重求得较优连杆长度。
关键词:多级坐标变换逆运动学解法遗传搜索算法优化一、问题重述1.1、问题重述某型号机器人(图示和简化图略)一共有6个自由度,分别由六个旋转轴(关节)实现,使机器人的末端可以灵活地在三维空间中运动。
机器人学导论 chapter4

Inverse ManipulatorKinematicsAlgebraic solution by reduction to polynomialOutline2 Introduction IntroductionIntroductionThe Inverse kinematic is the basis of robot trajectory planning and control.5IntroductionExample :6Algebraic solution by reduction to polynomialOutline7SolvabilitySolvabilityFor the 6 DOF Puma 560 manipulator,we have:How to find the 6 joint variablesHere we might have 12 equations to solve for 6 independent variables. Constraints should be utilized.6 equations for 6 unknown variables9SolvabilityDifficulty: these 6 equations are nonlinear and transcendental equations.obtain the solution.whereSolvability11SolvabilitySolvabilityThe dexterous workspace is only one point(the origin). The There is no dexterous workspace. The reachable SolvabilityFor most industry robots, there is limitation for the joint variable range, thus the workspace is reduced.Only one attainable orientationIf a manipulator has less than 6 DOF, it can’t attain general goal position and orientation in 3D space.Workspace also depends on the tool-frame transformation.Solvability15There might be multiple solution in solving kinematic equations.Two possible solution for the same position and orientation.How to choose possible solution?Solvability” solution.The number of solutions depends on the number of and the allowable ranges of motion of the joints, also, it can be a function of other link parameters (link length, link twist, link offset, joint angle).Solvability2. Multiple solutions17The PUMA 560 can reach certain goals with 8different solutions.+Due to the limits of joints range, some of these 8 solutions could be inaccessible.SolvabilitySolvabilityAlgebraic solution by reduction to polynomial Outline20Manipulator Subspace21workspace is a portion of an n‐DOF subspacesubspace : planeworkspace : a subset of the plane{workspace} ⊂{subspace} ⊂{space}Manipulator Subspaceof a manipulator?Giving an expression for a manipulator’s wrist frame {w}to be free to take on all possible values.Manipulator SubspaceThe subspace of is given by:233R planar manipulatorAs are allowed to take on arbitrary values, the subspace is generatedNOTE : Link lengths and joints limits restrict the workspace of the manipulator to be a subset of this subspace.Algebraic solution by reduction to polynomial Outline24Algebraic vs. GeometricGiven the transformation matrix, solved for25Algebraic vs. GeometricD-H TableAlgebraic vs. GeometricThe transformation matrix can be computed viaand we haveAlgebraic vs. GeometricSpecification of the goal points can be accomplished by specifying three parameters: ..The transformation is assumed to have the following structurewhereThe above four nonlinear equations are used to solve for (unknown)Algebraic vs. GeometricThe parameters is How to solve for according thefollowing equations:Algebraic vs. Geometric1.Algebraic solution 30The is the only unknown parameter.Algebraic vs. GeometricStep1.In the solution algorithm, the above constraintshould be checked to determine whether a solution exist or not. If the constrain is not Algebraic vs. Geometric1.Algebraic solution Here, the choice of signs in the solution of corresponds to Algebraic vs. Geometric33Based on the solution of , we can get:whereAlgebraic vs. Geometricwe haveAlgebraic vs. GeometricNote:If a choice of sign is made in the solution of ,it will affect and thus affectStep5. Based on the fact that The solution of can be obtained.Algebraic vs. Geometric36solved for by using the tools of plane geometry.can utilize plane geometry directly to find a solution.Algebraic vs. Geometricconsidering the solid triangle, the “” can be applied to solve for as:37PossibleconfigurationThe other possible solution can be obtained by settingAlgebraic vs. Geometric2. Geometric solutionTo solve for , we find the express for angleand .38and can be solved via:then can be solved as:Algebraic vs. Geometric39the solution of can Algebraic solution by reduction to polynomial Outline40Algebraic solution by reduction to polynomialexpression in terms of a single variable.This is a very important geometric substitution used often in solving kinematic equations. These substitution convert transcendental equations into polynomial equations in Algebraic solution by reduction to polynomialGiven a transcendental equation try to solve for42Solutions:(when )Algebraic solution by reduction to polynomial Outline43Inverse manipulator kinematicsThe Unimation Puma 560 Industry Robot44Inverse manipulator kinematicsReview : D-H table45Inverse manipulator kinematicsReview : Transformation of each link.46Inverse manipulator kinematicsReview : Transformation of all link47whereInverse manipulator kinematics: Given the goal point and orientation specified by:(Known: Numerical value)Solve forInverse manipulator kinematics Separating out 1 unknown parameter How to solve ?Inverse manipulator kinematics2. Inverting to be obtain50 whereInverse manipulator kinematicsCheck the (2,4) elements on both sides ,we have Inverse manipulator kinematicsIntroduce the trigonometric(三角恒等变换) substitutions:52whereThen it can be obtained that:Inverse manipulator kinematics3. The left side of the following equation is known53Inverse manipulator kinematicsTaking square of the above two equations, and adding the results together, it can be obtained thatInverse manipulator kinematicsThe above equation depends only on , then similar steps can be followed to solve for as:4. Consider the following equationhave been solved, but is unknownInverse manipulator kinematics56Eq.(3.11) in Chapter3Check elements (1,4) and (2,4) on both sides, we haveInverse manipulator kinematics 57Inverse manipulator kinematics585. Now the left side of the following equation is knownEq.(3.11) in Chapter3Check the elements (1,3) and (3,3), it can be obtained thatInverse manipulator kinematics ca can be solved as:Case2.,The manipulator is in a singular configurationas axis 4 and 6 line up and cause the same motion of the last link of the robot. Thus is chosen arbitrarily.Inverse manipulator kinematics606. Consider the following equation again:andCheck the elements (1,3) and (3,3), it can be obtained thatInverse manipulator kinematics 61Hence, we can solve for as7. Applying the same method one more time, we havewhereCheck the elements (3,1) and (1,1), it can be obtained thatInverse manipulator kinematics62Thus we can solve for aswe can obtain eight sets of possible solutions, some of them will be discarded due to the joint angle limitsInverse manipulator kinematics63Summary1、原则:等号两端的矩阵中对应元素相等,列出相关方)、从含变量少的左边开始,如,向右递推,直到)、选择等号左边或右边矩阵中等于常数或仅含有一个变量的元素,列出相应元素对应的方程或方程组。
机器人学导论第4章1PPT课件

即在易使工具与环境脱离接触或产生很大作用 力的方向采用柔顺控制。其方法是:假想在此方向, 末端刚度很低,对其采用力控制。
§4.2 力和力矩分析
4.2.1 力和力矩的平衡 这一节推导表示机械手静力学特性的基本方
程。我们首先考虑在开环运动链上的一个单独连 接的自由实体的图形。图4-1表示作用在连杆i上 的力和力矩。连杆i通过关节i+1与连杆i-1和连杆
第4章 力分析及柔顺控制
学习内容: 1 动力学分析 2 静力学分析 3 坐标系间力和力矩的变换 4 柔顺控制
学习重点: 1 动力学方程的简化 2 柔顺坐标系
为了使物体加速必须对其施加力,使旋转物体 产生角加速度必须对其施加力矩,所施加力、力 矩大小为:
Fma TI
为使机器人连杆加速,驱动器必须有足够大 的力、力矩驱动机器人连杆和关节,以使他们能 以期望的加速度和速度运动。为此,必须计算每 个驱动器所需的驱动力。设计者可根据这些方程 并考虑机器人外部载荷计算出驱动器可能承受的 最大载荷,并进而设计出能够提供足够力及力矩 的驱动器。
N i 1 , i N i , i 1 ( r i 1 , i r i , c i ) f i 1 , i ( r i , c i ) ( f i , i 1 ) 0i 1 , n ,(4
这里ri-1,i是从Oi-1到Oi的3×1位置矢量,而 ri,ci表示从Oi到Ci的位置矢量。力fi-1,i和力矩Ni1,i是相邻连杆i和i-1之间的耦合力和力矩。
Fmxkx
用牛顿方程:
Fma
பைடு நூலகம்
d (mx) mx dt
Fkxma Fm akx
机械手和环境之间的接触将在接触处产生相互 作用的力和力矩。每个机械手的关节运动都是由各 自的执行装置驱动的。相应的关节输入力矩,经手 臂的连杆传送到抓具,并在抓具处引起对环境的力 和力矩。
机器人学导论
机器人的动力学模型
牛顿-欧拉方程
拉格朗日方程
凯恩方法
雅可比矩阵
机器人的运动规划与控制
运动学:研究机器人末端执行器的位置和姿态信息 动力学:研究机器人末端执行器的力和力矩信息 运动规划:根据任务要求,规划机器人的运动轨迹 控制:通过控制器对机器人进行实时控制,实现运动规划
机器人的感知与感
05
知融合
01
添加章节标题
02
机器人学概述
机器人的定义与分类
机器人的定义: 机器人是一种能 够自动执行任务 的机器系统,具 有感知、决策、
执行等能力
机器人的分类: 根据应用领域、 结构形式、智能 化程度等不同, 机器人可分为多 种类型,如工业 机器人、服务机 器人、特种机器
人等
机器人学的研究领域
机器人设计:研究机器人的结构、 运动学和动力学
机器人的感知技术
添加项标题
视觉感知技术:通 过摄像头获取环境 信息,识别物体、 场景等,实现机器 人视觉导航、物体 识别等功能。
添加项标题
听觉感知技术:通 过麦克风获取声音 信息,识别语音、 音乐等,实现机器 人语音交互、音乐 识别等功能。
添加项标题
触觉感知技术:通过 触觉传感器获取接触 信息,识别物体的形 状、大小、硬度等, 实现机器人触觉导航、 物体抓取等功能。
执行器作用:根据控制信号执行相应的动作,如移动、转动等
机器人的感知系统
传感器类型:视觉、听觉、触觉等 传感器工作原理:图像处理、语音识别、触觉反馈等 传感器在机器人中的应用:导航、目标识别、物体抓取等 感知系统对机器人性能的影响:精度、稳定性、安全性等
机器人的运动学与
04
动力学
机器人的运动学方程
机器人学导论--ppt课件可编辑全文

关节变量
ppt课件
2
1.2 描述:位置、姿态和坐标系
位置描述
一旦建立坐标系,就能用一
个3*1的位置矢量对世界坐标 系中的任何点进行定位。因 为在世界坐标系中经常还要 定义许多坐标系,因此在位 置矢量上附加一信息,标明 是在哪一坐标系中被定义的。
例如:AP表示矢量P在A坐标系中的表示。
BP 表示矢量P在B坐标系中的表示。
c os90
c os120 c os30 c os90
XB XA
X
B
YA
X B Z A
c os90 c os90 cos0
]
YB X A YB YA YB Z A
ZB XA
ZB
YA
ZB Z A
ppt课件
5
坐标系的变换
完整描述上图中操作手位姿所需的信息为位置和姿态。机器人学中
在从多重解中选择解时,应根据具体情况,在避免碰撞的前 提下通常按“最短行程”准则来选择。同时还应当兼顾“多 移动小关节,少移动大关节”的原则。
ppt课件
23
4 PUMA560机器人运动学反解-反变换法
❖ 由于z4 , z5, z6 交于一点W,点W在基础坐标系中的位置仅与 1,2,3
有关。据此,可先解出 1,2,3 ,再分离出 4 ,5,6 ,并逐
PUMA560变换矩阵
ppt课件
21
将各个连杆变换矩阵相乘便得到PUMA560手臂变换矩阵
06T 01T (1)21T (2 )23T (3 )34T (4 )45T (5 )56T (6 )
什么是机器人运动学正解? 什么是机器人运动学反解?
ppt课件
22
操作臂运动学反解的方法可以分为两类:封闭解和数值解、 在进行反解时总是力求得到封闭解。因为封闭解的计算速度 快,效率高,便于实时控制。而数值法不具有些特点为。 操作臂的运动学反解封闭解可通过两种途径得到:代数解和 几何解。 一般而言,非零连杆参数越多,到达某一目标的方式也越多, 即运动学反解的数目也越多。
机器人学导论,第三章第四章

0 l3 0 l4 1 0 0 1
0 1 1 0 3 HT 0 0 0 0
0 0 1 0
0 0 0 1
四、写出运动方程(求出
0 H
0 H
T
)
T T T T T
0 1 1 2 2 3 3 H
0 1 0 0 1 0 0 0
中间连杆 分两种情况: 首、末连杆
3.4、连杆参数和连杆坐标系(续)
首、末连杆
与基座0固接的坐标系为 {0};
基座固定不动 {0}作为机器人操作的绝对 坐标系。 原则上坐标系 {0}可以任意规定(不受连 杆参数、关节变量影响 )。
为方便起见,对 {0}规定如下: 当第一个关节变量为零 时, {0}、 {1}重合({0}为{1}的原位状态)。
3.4、连杆参数和连杆坐标系(续)
三、连杆坐标系
连杆的描述 连杆连接的描述 连杆之间位姿的描述
采用方法: 在每个连杆固接一个坐 标系,用坐标系之间的 描述表示。 例如:
与基座固接的坐标系为 {0}; 与连杆1固接的坐标系为 {1}; 与连杆i固接的坐标系为 {i};
下一步讨论:坐标系 {i}的原点、轴的方向的确 定方法。
因此,有:
i 1 i
相对于动 坐标系而 言,遵循 “从左到 右”的原 则。
T RX ( i 1 ) DX ( ai 1 ) RZ ( i ) DZ ( di )
3.5 连杆变换和运动学方程(续) i 1 iT RX ( i 1 ) DX ( ai 1 ) RZ ( i ) DZ ( di )
求
0 H
T
一、建立D-H坐标系
Z3
Z2 X3 Z1 X2
机器人学-第四讲

k x (oz a y ) / 2sin k y (ax nz ) / 2sin k z (n y ox ) / 2sin
8
三、齐次变换通式
设想 K 为坐标系{A} 上过P的任意单位矢量
K kx i k y j kz k P Px i Py j Pz k
用连杆坐标系规定连杆参数
αi-1=从zi-1到zi沿xi-1旋转的角度 ai-1 =从zi-1到zi沿xi-1测量的距离
di=从xi-1到xi沿zi测量的距离
θi=从xi-1到xi沿zi旋转的角度
Z(i - 1) Y(i -1) a(i - 1 ) di Yi Zi Xi ai
X(i -1) ( i - 1)
二次转动
首先绕X轴转 角,然后绕新的Y轴 物体的方位为:
R =R( X , ) R Y ,
角,则
如果两次转动是绕固定系的轴线,则物体的方 位为
R =R Y , R( X , )
表示姿态角,并不表示运动角,即非描述运动过程
1
3.9 旋转变换通式
前面讨论了旋转矩阵的三种特殊情况,即绕x, y和z轴的 旋转矩阵,现在讨论绕过原点的任意轴K旋转θ角的变换 A 矩阵。 B R R(k , ) 表示坐标系B相对参考系A方位
(i-1) 0 -90
a(i-1) a0 a1
di 0 d2
i 1 2
Z0 Z1
Y2
X2 X0 Y0 X1
d2
Y1
a0
a1
cosθ 1 sinθ 1 0 1T 0 0
sinθ 1 cosθ 1 0 0
0 a0 0 0 1 0 0 1
机器人课件chapter4

在Kismet学习排序活动时,人类向机器人展示一些常见 的标准(颜色),以及不同的对象应该放的位置。机器人 通过语言描述来表达自己的理解,并向目标位置点头。人 类向机器人展示搜索活动的例子,机器人通过链接名称和 对象来演示它的理解。通过搜索活动来学习Blah与blah, 新的视角产生新的感知目标,并尝试构建这个感知目标来 了解人类的感知过程。机器感知对于特定领域可以是健壮 的,但不像人类的感知方法那样具有适应性,它将传统的 机器感知和机器学习与机会主义发展策略相结合——主动 感知运动的“劳累”。如果一个机器人从事一项已知的活 动,就有足够的限制来识别该活动中的新元素。同样,如 果已知元素参与了一些不熟悉的活动,跟踪这些元素可以 帮助确定该活动的特征。潜在地,感知发展就是这样循环 的。
Text A
Perception and Perspective in Robotics Paul Fitzpatrick MIT Computer Science and Artificial Intelligence Laboratory Humanoid Robotics Group Goal To build robots that can interact with novel objects and participate in novel activities Challenge Machine perception can be robust for a specific domain such as face detection, but unlike human perception it is not currently adaptable in the face of change (new objects, changed circumstances) Approach Integrate conventional machine perception and machine learning with strategies for opportunistic development
机器人学导论

编程语言应用:机器人 操作系统、算法开发、
人机交互等
机器人的控制策略
01 控制策略类型:基于模型的控制、基于规则的控制、基于学习的控制等 02 控制策略选择:根据机器人应用场景、性能要求、技术成熟度等综合考虑 03 控制策略优化:参数调整、算法改进、系统集成等
05
机器人学的研究方法与创新
机器人学的研究方法
理论研究:数学建模、算法设计、性能分析等 实验研究:仿真实验、实验室测试、实际应用等 计算研究:计算机模拟、计算性能评估、计算优化等
机器人学的创新方向
01 技术创新:新型传感器、高性能驱动系统、先进控制算法等 02 应用创新:新兴应用领域、跨界融合、产业升级等 03 制度创新:政策支持、产学研合作、人才培养等
产业升级:传统产业的智能化改造、 新兴产业的培育与发展
技术创新:新型传感器、 高性能驱动系统、先进
控制算法等
市场需求:家庭、医疗、 教育、军事等领域的机
器人应用需求
机器人学对社会的影响
经济影响:提 高生产效率、 降低生产成本、 促进产业升级
01
社会影响:改 变生活方式、 提高生活质量、 促进社会进步
机器人学的关键技术
关键技术一:传感器技术
• 传感器的设计与制造 • 传感器的集成与融合 • 传感器的性能评估与优化
关键技术二:控制技术
• 控制算法的设计与实现 • 控制系统的稳定性与可靠性 • 控制系统的性能评估与优化
关键技术三:人工智能技术
• 机器学习与深度学习 • 自然语言处理与计算机视觉 • 智能决策与规划
机器人学的未来发展趋势
机器人技术的普及与推广:家庭机器 人、教育机器人、医疗机器人等
机器人技术的深度融合: 人工智能、物联网、大
机器人学基础 第4章 机器人动力学

2 2
g
4.1 Dynamics of a Rigid Body
12
4.1.1 Kinetic and Potential Energy of a Rigid Body
y
Total Kinetic and Potential Energy of a 2-links manipulator are
Lagrangian Function L of a 2-links manipulator:
LKP
y x
T1 d1 θ1 (x1, y1) g m1
T2 d2 θ2 m2 (x2, y2)
1 1 2 (m1 m2 )d12 12 m2 d 2 ( 12 2 1 2 22 ) 2 2
4.1 Dynamics of a Rigid Body
10
4.1.1 Kinetic and Potential Energy of a Rigid Body Kinetic and Potential Energy of a 2-links manipulator
1 2 , Py m gh , h d cos K1 m1v1 , v1 d11 1 1 1 1 1 1 2
4.1 Dynamics of a Rigid Body
11
4.1.1 Kinetic and Potential Energy of a Rigid Body
y
Kinetic Energy K2 and Potential Energy P2
of link 2
1 2 K 2 m2 v2 , P2 mgy2 2
4.1 Dynamics of a Rigid Body
学年第一学期第四讲机器人导论
可移动度/ Degree of Mobility
为了避免侧滑,R( )I 需要满足以下约束:
C1f R( )I 0 C1s (s )R( )I 0
C1 (
s
)
C1 f
C1s (
s
)
从数学上讲 R( )I 属于投影矩阵 C1(s ) 的零空间 C1(s ) 的零空间 N 是有满足一下约束的向量 n 组成
机器人的底盘运动学由一组独立的约束组成
rankC1(s )
C,1(s ) 越大, 移动受到的约束越多
从数学上来讲
m dim NC1(s ) 3 rankC1(s )
无标准轮情形 rank
所有方向都受到约束
Cr1a(nks)C1(
0
s
)
3
例如
单轮: 仅有一个固定的标准轮
差动: 两个固定标准轮
沿同一轴部署
3.3.2
机器人的机动性/Robot Maneuverability
机动程度
M m s
具有同样 M 未必是相同的 例如: 差动机器人和三轮机器人
3.3.3
具有 M 2 的机器人,其 ICR 总是被约束在一条直线上 具有 M 3 的机器人,其 ICR 可不受约束的配置在平面上的任意点
同步驱动的案例
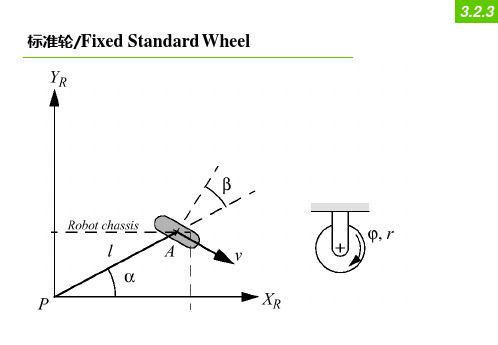
标准轮/Fixed Standard Wheel
3.2.3
转向标准轮/Steered Standard Wheel
ot Kinematic Constraints
给定具有 M 个轮子的机器人
每个轮子施加零个或多个机器人运动约束
只有固定或转向标准轮会产生约束
机器人学第四章

串联机器人运动方程
◆机器人运动学研究的是机器人各连杆间的 位移关系、速度关系和加速度关系。本章 只讨论位移关系,即研究的是机器人手部 相对于机座的位置和姿态。 ◆串联机器人是一开式运动链,它是由一系 列连杆通过转动关节或移动关节串联而成 的。关节由驱动器驱动,关节的相对运动 导致连杆的运动,使手爪到达一定的位姿。
c1 0 s1 s 0 c1 1 A1 0 1 0 0 0 0 0 0 0 1 c2 s A2 2 0 0 s2 c2 0 0 0 a 2 c2 0 a2 s2 1 d2 0 1
最后求得手部坐标系在参考坐标系中的位姿为:
nx n T y nz 0 sx sy sz 0 ax ay az 0 px py pz 1
式中, nx c1c23 (c4c5c6 s4 s6 ) s23s5c6 s1 ( s4c5c6 c4 s6 ),
n y s1c23 (c4c5c6 s4 s6 ) s23s5c6 c1 ( s4c5c6 c4 s6 ), nz s23 (c4c5c6 s4 s6 ) c23s5c6 , sx c1c23 (c4c5 s6 s4c6 ) s23s5 s6 s1 ( s4c5 s6 c4c6 ), sz s23 (c4c5 s6 s4 s6 ) c23s5c6 ,
4.1 机器人的连杆坐标系
4.1.1 连杆编号
串联机器人是一开式运动链,因此从机 器人机座开始至手爪依次对每一个连杆 从小到大编号,即连杆1、连杆2…连杆n 等。每一个关节也依次从小到大编号为 关节1、关节2 … …关节n等,机座编号 为连杆0。图4.2所示为PUMA560机器人的 连杆及关节编号。
机器人学导论第4章操作臂逆运动学

r13 r23 r33 0
px py pz 1
r11 c1 c23 c 4c5c6 s 4s 5 s 23s 5c5 s1 s 4c5c6 c 4s 6 r31 s 23 c 4c5c6 s 4s 6 c23s 5c6
当一个操作臂少于6自由度时,它在三维空间内不能达到全部位姿。显然,图4-1中的平 面操作臂不能伸出平面,因此凡是Z坐标不为0的目标点均不可达。在很多实际情况中, 具有四个或五个自由度的操作臂能够超出平面操作,但显然不能达到全部目标点。必须 研究这种操作臂以便弄清楚它的工作空间。通常这种机器人的工作空间是一个子空间, 这个空间是由特定的机器人的工作空间确定的。一个值得研究的问题是,对于少于6个 自由度的操作臂来说,给定一个确定的一般目标坐标系,什么是最近的可达目标坐标系?
4.4 代数解法与几何解法
代数解法:以第三章所介绍三连杆平面操作臂为例,其坐标和连杆参数如下
按第三章的方法,应用这些连杆参数可以求得这个机械臂的运动学方程:
c123 s 123 B 0 T T W 3 0 0
s123 c123 0 0
0 0 1 0
l1c1 l2c12 l1s1 l2 s12 0 1
s s123
4 9
4 10
4 11
2 x2 y 2 =l12 l2 2l1l2c2
4 12
解得
2 x 2 y 2 l12 l2 c2 2l1l2
S2的表达式为
2 s2 1 c2
最后利用2幅角反正切公式计算θ2,得
2 A tan2( s2 , c2 )
标即为 xk 1 。
y
机器人学导论

1 a tan 2( py px ) a tan 2( d2
) 有两个可能
px2
p
2 y
d
2 2
的解。
反解的多解性
5 PUMA560运动学反解-Pieper方法
❖ 对于6自由度的机器人而言,运动学反解非常复杂, 一般没有封闭解。只有在某些特殊情况下才可能得到封闭 解。不过,大多数工业机器人都满足封闭解的两个充分条 件之一(Pieper准则)
s in 1
0
c os 1
0
0 0 1 0
0
0 0 1
cos 2 sin 2 0 L1
21T
sin 2
0
cos 2
0
0 1
0
0
0
0
0
1
cos 3 sin 3 0 L2
23T
sin 3
0
cos 3
0
0 1
首先将BP 变换到一个中间坐标系,这个坐标系和{A}的
姿态相同、原点和{B}的原点重合,可由左乘矩阵
A B
R
得到。
然后用矢量加法将原点平移,得到:AP
BARB
P
PA BORG
可以写成:
定义一个4*4的矩阵算子并使用了4*1位置矢量,这样 可写成:
A B
RB
P
1
PA BORG
4
-90°
a3
d4
θ4(0°)
5
90°
0
0
θ5(0°)
6
-90°
0
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 4Planar KinematicsKinematics is Geometry of Motion . It is one of the most fundamental disciplines in robotics, providing tools for describing the structure and behavior of robot mechanisms. In this chapter, we will discuss how the motion of a robot mechanism is described, how it responds to actuator movements, and how the individual actuators should be coordinated to obtain desired motion at the robot end-effecter. These are questions central to the design and control of robot mechanisms. To begin with, we will restrict ourselves to a class of robot mechanisms that work within a plane, i.e. Planar Kinematics . Planar kinematics is much more tractable mathematically,compared to general three-dimensional kinematics. Nonetheless, most of the robot mechanisms of practical importance can be treated as planar mechanisms, or can be reduced to planar problems. General three-dimensional kinematics, on the other hand, needs special mathematical tools, which will be discussed in later chapters.4.1 Planar Kinematics of Serial Link MechanismsExample 4.1 Consider the three degree-of-freedom planar robot arm shown in Figure 4.1.1. The arm consists of one fixed link and three movable links that move within the plane. All the links are connected by revolute joints whose joint axes are all perpendicular to the plane of the links. There is no closed-loop kinematic chain; hence, it is a serial link mechanism.Figure 4.1.1 Three dof planar robot with three revolute jointsTo describe this robot arm, a few geometric parameters are needed. First, the length of each link is defined to be the distance between adjacent joint axes. Let points O, A, and B be the locations of the three joint axes, respectively, and point E be a point fixed to the end-effecter. Then the link lengths are E B B A A O ===321,,A A A . Let us assume that Actuator 1 drivinglink 1 is fixed to the base link (link 0), generating angle 1θ, while Actuator 2 driving link 2 is fixed to the tip of Link 1, creating angle 2θ between the two links, and Actuator 3 driving Link 3 is fixed to the tip of Link 2, creating angle 3θ, as shown in the figure. Since this robot arm performs tasks by moving its end-effecter at point E, we are concerned with the location of the end-effecter. To describe its location, we use a coordinate system, O-xy, fixed to the base link with the origin at the first joint, and describe the end-effecter position with coordinates e and e . We can relate the end-effecter coordinates to the joint angles determined by the three actuators by using the link lengths and joint angles defined above:x y)cos()cos(cos 321321211θθθθθθ+++++=A A A e x (4.1.1) )sin()sin(sin 321321211θθθθθθ+++++=A A A e y (4.1.2)This three dof robot arm can locate its end-effecter at a desired orientation as well as at a desiredposition. The orientation of the end-effecter can be described as the angle the centerline of the end-effecter measured from the positive x coordinate axis. This end-effecter orientation e φ is related to the actuator displacements as321θθθφ++=e(4.1.3)viewed from the fixed coordinate system in relation to the actuator displacements. In general, a set of algebraic equations relating the position and orientation of a robot end-effecter, or any significant part of the robot, to actuator or active joint displacements, is called Kinematic Equations, or more specifically, Forward Kinematic Equations in the robotics literature.Exercise 4.1 Shown below in Figure 4.1.2 is a planar robot arm with two revolute joints and one prismatic joint. Using the geometric parameters and joint displacements, obtain the kinematic equations relating the end-effecter position and orientation to the joint displacements.Figure 4.1.2 Three dof robot with two revolute joints and one prismatic jointNow that the above Example and Exercise problems have illustrated kinematic equations, let us obtain a formal expression for kinematic equations. As mentioned in the previous chapter, two types of joints, prismatic and revolute joints, constitute robot mechanisms in most cases. The displacement of the i-th joint is described by distance d i if it is a prismatic joint, and by angle i θ for a revolute joint. For formal expression, let us use a generic notation: q i . Namely, joint displacement q i represents either distance d i or angle i θdepending on the type of joint.i {i i d q θ= (4.1.4)Prismatic joint Revolute jointWe collectively represent all the joint displacements involved in a robot mechanism with a column vector: , where n is the number of joints. Kinematic equations relate these joint displacements to the position and orientation of the end-effecter. Let uscollectively denote the end-effecter position and orientation by vector p. For planar mechanisms, the end-effecter location is described by three variables:[T n q q q q "21=]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=e e e y x p φ(4.1.5)Using these notations, we represent kinematic equations as a vector function relating p to q :113,),(nx x q p q f p ℜ∈ℜ∈= (4.1.6)For a serial link mechanism, all the joints are usually active joints driven by individual actuators. Except for some special cases, these actuators uniquely determine the end-effecter position and orientation as well as the configuration of the entire robot mechanism. If there is a link whose location is not fully determined by the actuator displacements, such a robot mechanism is said to be under-actuated . Unless a robot mechanism is under-actuated, the collection of the joint displacements, i.e. the vector q, uniquely determines the entire robot configuration. For a serial link mechanism, these joints are independent, having no geometric constraint other than their stroke limits. Therefore, these joint displacements are generalized coordinates that locate the robot mechanism uniquely and completely. Formally, the number of generalized coordinates is called degrees of freedom. Vector q is called joint coordinates, when they form a complete and independent set of generalized coordinates.4.2 Inverse Kinematics of Planar MechanismsThe vector kinematic equation derived in the previous section provides the functionalrelationship between the joint displacements and the resultant end-effecter position andorientation. By substituting values of joint displacements into the right-hand side of the kinematic equation, one can immediately find the corresponding end-effecter position and orientation. The problem of finding the end-effecter position and orientation for a given set of joint displacements is referred to as the direct kinematics problem. This is simply to evaluate the right-hand side of the kinematic equation for known joint displacements. In this section, we discuss the problem of moving the end-effecter of a manipulator arm to a specified position and orientation. We need to find the joint displacements that lead the end-effecter to the specified position and orientation. This is the inverse of the previous problem, and is thus referred to as the inverse kinematics problem. The kinematic equation must be solved for joint displacements, given the end-effecterposition and orientation. Once the kinematic equation is solved, the desired end-effecter motion can be achieved by moving each joint to the determined value.In the direct kinematics problem, the end-effecter location is determined uniquely for anygiven set of joint displacements. On the other hand, the inverse kinematics is more complex in the sense that multiple solutions may exist for the same end-effecter location. Also, solutions may not always exist for a particular range of end-effecter locations and arm structures. Furthermore, since the kinematic equation is comprised of nonlinear simultaneous equations with many trigonometric functions, it is not always possible to derive a closed-form solution, which is the explicit inverse function of the kinematic equation. When the kinematic equation cannot besolved analytically, numerical methods are used in order to derive the desired joint displacements.Example 4.2 Consider the three dof planar arm shown in Figure 4.1.1 again. To solve itsinverse kinematics problem, the kinematic structure is redrawn in Figure 4.2.1. The problem is to find three joint angles 321,,θθθ that lead the end effecter to a desired position and orientation, e e e y x φ,,. We take a two-step approach. First, we find the position of the wrist, point B, from e e e y x φ,,. Then we find 21,θθ from the wrist position. Angle 3θ can be determined immediately from the wrist position.Figure 4.2.1 Skeleton structure of the robot arm of Example 4.1Let w and w be the coordinates of the wrist. As shown in Figure 4.2.1, point B is atdistance 3 from the given end-effecter position E. Moving in the opposite direction to the end effecter orientation x y A e φ, the wrist coordinates are given byee w e e w y y x x φφsin cos 33A A −=−= (4.2.1)Note that the right hand sides of the above equations are functions of e e e y x φ,, alone. From these wrist coordinates, we can determine the angle α shown in the figure.1wwx y 1tan −=α (4.2.2)Next, let us consider the triangle OAB and define angles γβ,, as shown in the figure. Thistriangle is formed by the wrist B , the elbow A , and the shoulder O. Applying the law of cosines to the elbow angle β yields2212221cos 2r =−+βA A A A(4.2.3)where , the squared distance between O and B. Solving this for angle 222ww y x r +=β yields 21222221122cos A A A A ww y x −−+−=−=−πβπθ(4.2.4)Similarly,221212cos 2A A A =−+γr r(4.2.5)Solving this for γyields2212221221112cos tan ww w w w w y x y x x y +−++−=−=−−A A A γαθ (4.2.6)From the above 21,θθwe can obtain213θθφθ−−=e(4.2.7)Eqs. (4), (6), and (7) provide a set of joint angles that locates the end-effecter at thedesired position and orientation. It is interesting to note that there is another way of reaching the same end-effecter position and orientation, i.e. another solution to the inverse kinematics problem. Figure 4.2.2 shows two configurations of the arm leading to the same end-effecter location: the elbow down configuration and the elbow up configuration. The former corresponds to the solution obtained above. The latter, having the elbow position at point A’, is symmetric to the former configuration with respect to line OB , as shown in the figure. Therefore, the two solutions are related asγθθθθφθθθγθθ22''''2'232132211−+=−−=−=+=e (4.2.8)Inverse kinematics problems often possess multiple solutions, like the above example,since they are nonlinear. Specifying end-effecter position and orientation does not uniquely determine the whole configuration of the system. This implies that vector p, the collective position and orientation of the end-effecter, cannot be used as generalized coordinates. The existence of multiple solutions, however, provides the robot with an extra degree offlexibility. Consider a robot working in a crowded environment. If multiple configurations exist for the same end-effecter location, the robot can take a configuration having no interference with1Unless noted specifically we assume that the arc tangent function takes an angle in a proper quadrant consistent with the signs of the two operands.the environment. Due to physical limitations, however, the solutions to the inverse kinematics problem do not necessarily provide feasible configurations. We must check whether each solution satisfies the constraint of movable range, i.e. stroke limit of each joint.11Elbow-Up ConfigurationFigure 4.2.2 Multiple solutions to the inverse kinematics problem of Example 4.24.3 Kinematics of Parallel Link MechanismsExample 4.3 Consider the five-bar-link planar robot arm shown in Figure 4.3.1.22112211sin sin cos cos θθθθA A A A +=+=e e y x (4.3.1)Note that Joint 2 is a passive joint. Hence, angle 2θis a dependent variable. Using 2θ, however, we can obtain the coordinates of point A:25112511sin sin cos cos θθθθA A A A +=+=A A y x (4.3.2)Point A must be reached via the branch comprising Links 3 and 4. Therefore,44334433sin sin cos cos θθθθA A A A +=+=A A y x(4.3.3)Equating these two sets of equations yields two constraint equations:4433251144332511sin sin sin sin cos cos cos cos θθθθθθθθA A A A A A A A +=++=+ (4.3.4)Note that there are four variables and two constraint equations. Therefore, two of the variables, such as 31,θθ, are independent. It should also be noted that multiple solutions exist for these constraint equations.xLink 0Figure 4.3.1 Five-bar-link mechanismAlthough the forward kinematic equations are difficult to write out explicitly, the inverse kinematic equations can be obtained for this parallel link mechanism. The problem is to find 31,θθ that lead the endpoint to a desired position: . We will take the following procedure:e e y x ,Step 1 Given , find e e y x ,21,θθby solving the two-link inverse kinematics problem. Step 2 Given 21,θθ, obtain . This is a forward kinematics problem. A A y x ,Step 3 Given , find A A y x ,43,θθ by solving another two-link inverse kinematics problem.Example 4.4 Obtain the joint angles of the dog’s legs, given the body position and orientation.Figure 4.3.2 A doggy robot with two legs on the groundThe inverse kinematics problem:Step 1 GivenB B B y x φ,,, find and A A y x ,C C y x , Step 2 Given , findA A y x ,21,θθ Step 3 Given , find C C y x ,43,θθ4.4 Redundant mechanismsA manipulator arm must have at least six degrees of freedom in order to locate its end-effecter at an arbitrary point with an arbitrary orientation in space. Manipulator arms with less than 6 degrees of freedom are not able to perform such arbitrary positioning. On the other hand, if a manipulator arm has more than 6 degrees of freedom, there exist an infinite number of solutions to the kinematic equation. Consider for example the human arm, which has seven degrees of freedom, excluding the joints at the fingers. Even if the hand is fixed on a table, one can change the elbow position continuously without changing the hand location. This implies that there exist an infinite set of joint displacements that lead the hand to the same location. Manipulator arms with more than six degrees of freedom are referred to as redundant manipulators. We will discuss redundant manipulators in detail in the following chapter.。
