初中数学第17章反比例函数单元测试题(含答案)

合集下载

反比例函数单元测试题及答案

第17章反比例函数综合检测题一、选择题（每小题3分，共30分） 1、反比例函数y ＝xn 5+图象经过点（2，3），则n 的值是（）． A 、－2 B 、－1 C 、0 D 、12、若反比例函数y ＝xk（k ≠0）的图象经过点（－1，2），则这个函数的图象一定经过点（）．A 、（2，－1）B 、（－21，2） C 、（－2，－1） D 、（21，2） 3、(08双柏县)已知甲、乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（）4、若y 与x 成正比例，x 与z成反比例，则y 与z 之间的关系是（）．A 、成正比例B 、成反比例C 、不成正比例也不成反比例D 、无法确定 5、一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝xk满足（）． A 、当x ＞0时，y ＞0 B 、在每个象限内，y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限6、如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线PQ 交双曲线y ＝x1于点Q ，连结OQ ，点P 沿x 轴正方向运动时， Rt △QOP 的面积（）．A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定 7、在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变． ρ与V 在一定范围内满足ρ＝Vm，它的图象如图所示，则该气体的质量m 为（）．A 、1.4kgB 、5kgC 、6.4kgD 、7kg8、若A （－3，y 1），B （－2，y 2），C （－1，y 3）三点都在函数y ＝－x1的图象上，则y 1，y 2，y 3的大小关系是（）．A 、y 1＞y 2＞y 3B 、y 1＜y 2＜y 3C 、y 1＝y 2＝y 3D 、y 1＜y 3＜y 2 9、已知反比例函数y ＝xm21-的图象上有A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜x 2＜0时，y 1＜y 2，则m 的取值范围是（）．A ．B ．C ．．A 、m ＜0B 、m ＞0C 、m ＜21 D 、m ＞21 10、如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是（）．A 、x ＜－1B 、x ＞2C 、－1＜x ＜0或x ＞2D 、x ＜－1或0＜x ＜2 二、填空题（每小题3分，共30分）11.某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12、已知反比例函数xky =的图象分布在第二、四象限，则在一次函数b kx y +=中，y 随x 的增大而（填“增大”或“减小”或“不变”）．13、若反比例函数y ＝xb 3-和一次函数y ＝3x ＋b 的图象有两个交点，且有一个交点的纵坐标为6，则b ＝． 14、反比例函数y ＝（m ＋2）xm2－10的图象分布在第二、四象限内，则m 的值为．15、有一面积为S 的梯形，其上底是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是．16、如图，点M 是反比例函数y ＝xa（a ≠0）的图象上一点，过M 点作x 轴、y 轴的平行线，若S 阴影＝5，则此反比例函数解析式为．17、使函数y ＝（2m 2－7m －9）xm2－9m ＋19是反比例函数，且图象在每个象限内y 随x 的增大而减小，则可列方程（不等式组）为．18、过双曲线y ＝xk（k ≠0）上任意一点引x 轴和y 轴的垂线，所得长方形的面积为______．19. 如图，直线y ＝kx(k ＞0)与双曲线xy 4=交于A （x 1，y 1）， B （x 2，y 2）两点，则2x 1y 2－7x 2y 1＝___________．20、如图，长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上，点B 的坐标为B （－320，5），D 是AB 边上的一点，将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是．三、解答题（共60分） 21、（8分）如图，P 是反比例函数图象上的一点，且点P 到x 轴的距离为3，到y 轴的距离为2，求这个反比例函数的解析式．22、（9分）请你举出一个生活中能用反比例函数关系描述的实例，写出其函数表达式，并画出函数图象．举例：函数表达式：23、（10分）如图，已知A （x 1，y 1），B （x 2，y 2）是双曲线y ＝xk在第一象限内的分支上的两点，连结OA 、OB ．（1）试说明y 1＜OA ＜y 1＋1y k ；（2）过B 作BC ⊥x 轴于C ，当m ＝4时，求△BOC 的面积．24、（10分）如图，已知反比例函数y ＝－x8与一次函数 y ＝kx ＋b 的图象交于A 、B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求：（1）一次函数的解析式；（2）△AOB 的面积．25、（11分）如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝xk的图象交于M 、N 两点．（1）求反比例函数与一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．26、（12分）如图，已知反比例函数y ＝xk的图象与一次函数y ＝a x ＋b 的图象交于M （2，m ）和N （－1，－4）两点．（1）求这两个函数的解析式；（2）求△MON 的面积；（3）请判断点P （4，1）是否在这个反比例函数的图象上，并说明理由．参考答案:一、选择题1、D ；2、A ；3、C ；4、B ；5、D ；6、C7、D ；8、B ；9、D ； 10、D ．二、填空题 11、y ＝x 1000； 12、减小； 13、5 ； 14、－3 ；15、y ＝xs23 ； 16、y＝－x 5； 17、⎩⎨⎧---=+-0972119922＞m m m m ； 18、|k|； 19、 20； 20、y ＝－x 12．三、解答题 21、y ＝－x6． 22、举例：要编织一块面积为2米2的矩形地毯，地毯的长x （米）与宽y （米）之间的函数关系式为y ＝2（x ＞0）．（只要是生活中符合反比例函数关系的实例均可）画函数图象如右图所示． 23、（1）过点A 作AD ⊥x 轴于D ，则OD ＝x 1，AD ＝y 1，因为点A （x 1，y 1）在双曲线y ＝xk上，故x 1＝1y k ，又在Rt △OAD 中，AD ＜OA ＜AD ＋OD ，所以y 1＜OA ＜y 1＋1y k ；（2）△BOC 的面积为2．24、（1）由已知易得A （－2，4），B （4，－2），代入y ＝kx ＋b 中，求得y ＝－x ＋2；（2）当y ＝0时，x ＝2，则y ＝－x ＋2与x 轴的交点M （2，0），即|OM|＝2，于是S △AOB＝S △AOM ＋S △BOM ＝21|OM|·|y A |＋21|OM|·|y B |＝21×2×4＋21×2×2＝6．25、（1）将N （－1，－4）代入y ＝xk ，得k ＝4．∴反比例函数的解析式为y ＝x 4．将M（2，m ）代入y ＝x 4，得m ＝2．将M （2，2），N （－1，－4）代入y ＝ax ＋b ，得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y ＝2x －2．（2）由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值．26、解（1）由已知，得－4＝1-k ，k ＝4，∴y ＝x 4．又∵图象过M （2，m ）点，∴m ＝24＝2，∵y ＝a x ＋b 图象经过M 、N 两点，∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y ＝2x －2．（2）如图，对于y ＝2x －2，y ＝0时，x ＝1，∴A （1，0），OA ＝1，∴S △MON ＝S △MOA ＋S △NOA ＝21OA ·MC ＋21OA ·ND ＝21×1×2＋21×1×4＝3．（3）将点P （4，1）的坐标代入y ＝x4，知两边相等，∴P 点在反比例函数图象上．。

八年级数学下17章反比例函数单元测试题

第17章《反比例函数》测试题一、选择题：1.下列函数中，不属于y 与x 反比例函数的是（） A.1xy = B.11y x =+ C.1y x -=- D.13y x= 2.有以下判断：①圆面积公式2S r π=中，面积S 与半径r 成正比例；②运动的时间与速度成反比例；③当电压不变时，电流强度和电阻成反比例；④圆柱体的体积公式213V r h π=中，当体积V 不变时，圆柱的高h 与底面半径r 的平方成反比例，其中错误的有（）A.1个B.2个C.3个D.4个3.若y 与x 成反比例，x 与z 成正比例，则y 是z 的（） A. 正比例函数 B. 反比例函数 C. 一次函数 D. 不能确定4.如图，A 为反比例函数ky x=图象上一点，AB 垂直x 轴于B 点，若S △AOB ＝3，则k 的值为（） A 、6B 、3C 、+3或-3D 、+6或-65.（2009年娄底）市一小数学课外兴趣小组的同学每人制作一个面积为200cm 2的矩形学具进行展示. 设矩形的宽为x cm ，长为y cm ，那么这些同学所制作的矩形长y （cm ）与宽x （cm ）之间的函数关系的图象大致是 ( )6.在同一直角坐标平面内，如果直线1y x k =与双曲线2k y x=没有交点，那么1k 和2k 的关系一定是（）A.1k <0,2k >0B.1k >0，2k <0C.1k 、2k 同号D.1k 、2k 异号7.（09河池）如图5，A 、B 是函数2y x=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴，△ABC 的面积记为S ，则（） A ． 2S = B ． 4S = C ．24S << D ．4S >8.（2009丽水市）如图，点P 在反比例函数1y x =(x > 0)的图象上，且横坐标为2. 若将点P 先向右平移两个单位，再向上平移一个单位后所得的像为点P '.则在第一象限内，经过点P '的反比例函数图象的解析式是( )A ．)0(5>-=x xy B .)0(5>=x x yC . )0(6>-=x x yD . )0(6>=x xy9.（09恩施市）一张正方形的纸片，剪去两个一样的小矩形得到一个“E ”图案，如图所示，设小矩形的长和宽分别为x 、y ，剪去部分的面积为20，若2≤x ≤10，则y 与x 的函数图象是（）10.在同一坐标系中，函数ky x=和3y kx =+的图象大致是二、填空题： 11．如果函数122--=m xm y 是反比例函数，那么=m ____________.12．已知y 与x 成反比例，且当2-=x 时，3=y ，则y 与x 的函数关系是_________，当3-=x 时，=y _____________。

新人教版初二数学下册第17章反比例函数单元测试题及答案

八年级（下）第17章《反比例函数》班级姓名得分一、选择题（每小题3分，共24分）1．如果x 、y 之间的关系是10(0)ax y a -+=≠，那么y 是x 的（） A ．正比例函数 B ．反比例函数 C ．一次函数D ．二次函数2．函数y ＝－4x的图象与x 轴的交点的个数是（）A ．零个B ．一个C ．两个D ．不能确定3．反比例函数y ＝－4x的图象在（）A ．第一、三象限B ．第二、四象限C ．第一、二象限D ．第三、四象限 4．已知关于x 的函数y ＝kx 和y ＝－kx（k ≠0）它们在同一坐标系中的大致图象是（• ）5．已知反比例函数y ＝xk的图象经过点（m ，3m ），m ≠0，则此反比例函数的图象在（） A ．第一、二象限 B ．第一、三象限 C ．第二、四象限 D ．第三、四象限6．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （ kPa ）是气体体积V （ m 3）的反比例函数，其图象如图所示．当气球内的气压大于120 kPa 时，气球发将爆炸．为了安全起见，气球的体积应（） A ．不小于54m 3B ．小于54m 3C ．不小于45m 3D ．小于45m 37．如果点P 为反比例函数xy 4=的图象上一点，PQ ⊥x 轴，垂足为Q ，那么△POQ 的面积为（）A ．2B ． 4C ．6D ．8)第6题8．已知：反比例函数xmy 21-=的图象上两点A （x 1，y 1），B （x 2， y 2）当x 1＜0＜x 2时， y 1＜y 2，则m 的取值范围（）A ．m ＜0B ．m ＞0C ．m ＜21 D ．m ＞21二、填空题（每小题3分，共30分）9．有m 台完全相同的机器一起工作，需m 小时完成一项工作，当由x 台机器（x 为不大于m 的正整数）完成同一项工作时，所需的时间y 与机器台数x 的函数关系式是____. 10．已知y 与x 成反比例，且当x 32=-时，y =5，则y 与x 的函数关系式为__________. 11．反比例函数xy 3=的图象在第一象限与第象限. 12．某食堂现有煤炭500吨，这些煤炭能烧的天数y 与平均每天烧煤的吨数x 之间的函数关系式是 . 13．若nxm y ++=2)5(是反比例函数，则m 、n 的取值是 .14．两位同学在描述同一反比例函数的图象时，甲同学说：这个反比例函数图象上任意一点到两坐标轴的距离的积都是3；乙同学说：这个反比例函数的图象与直线y =x 有两个交点，你认为这两位同学所描述的反比例函数的解析式是 . 15．在ABC △的三个顶点A （2，－3）、B （－4，－5）、C （－3，2）中，可能在反比例函数(0)ky k x=>的图象上的点是． 16．如果反比例函数4ny x-=的图象位于第二、四象限，则n 的取值范围是_______；如果图象在每个象限内，y 随x 的增大而减小，则n 的取值范围是 .17．如图，△P 1OA 1、△P 2A 1 A 2是等腰直角三角形，点P 1、P 2在函数4(0)y x x=>的图象上，斜边OA 1、A 1 A 2都在x 轴上，则点A 2的坐标是 .18．两个反比例函数k y x =和1y x=在第一象限内的图象如图所示，点P 在k y x =的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x=的图象于点B ，当点P 在k y x =的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等；④当点A 是PC 的中点时，点B 一定是PD 的中点．其中一定正确的是（把你认为正确结论的序号都填上，少填或错填不给分）．12 第17题三、解答题（共66分） 19．（8分）反比例函数xky =的图象经过点A （2 ，3）.（1）求这个函数的解析式；（2）请判断点B （1 ，6）是否在这个反比例函数的图象上，并说明理由.20．（9分）已知三角形的一边为x ，这条边上的高为y ，三角形的面积为3，写出y 与x 的函数表达式，并画出函数的图象.21．（10分）如图，一次函数y =kx ＋b 的图像与反比例函数xmy =的图像相交于A 、B 两点，（1）利用图中条件，求反比例函数和一次函数的解析式（2）根据图像写出使一次函数的值大于反比例函数的值的x 的取值范围.22．（12分）近视眼镜的度数y （度）与镜片焦距x （米）成反比例，已知800度近视眼镜镜片的焦距为0.125米，（1）求y 与x 的函数关系；（2）若张华同学近视眼镜镜片的焦距为0.25米，你知道他的眼睛近视多少度吗？23．（12分）对于取消市场上使用的杆秤的呼声越来越高，原因在于一些不法商贩在卖货时将秤砣挖空，或更换较小称砣，使砣较轻，从而欺骗顾客. （1）如图，对于同一物体，哪个图用的是标准秤砣，哪个用的是较轻的秤砣？（2）在称同一物体时，所称得的物体质量y （千克）与所用秤砣质量x （千克）之间满足关系. （3）当砣较轻时，称得的物体变重，这正好符合哪个函数的哪些性质？24．（12分）联想电脑公司新春期间搞活动，规定每台电脑0.7万元，交首付后剩余的钱数y 与时间t 的关系如图所示：（1）根据图象写出y 与t 的函数关系式.（2）求出首付的钱数. （3）如果要求每月支付的钱数不少于400元，那么还至少几个才能将所有的钱全部还清？图1图2月)y (）八年级（下）第17章《反比例函数》答案一、选择题1．B ；2． A ；3． B ；4． A ；5． B ；6． C ；7．A ；8． C ．二、填空题9．y ＝x m 2 10．152y x=- 11．三 12．y ＝x 50013．m ≠－5 n ＝－3 14．y ＝x 3 15．B16.n ＞4，n ＜4 17．（0） 18．①②④ 三、解答题 19．（1）y ＝x6；（2）在 20． y ＝6x，图像略 21．（1）2y x=-，1y x =--;（2） 2x <-或0x <<122．（1）100y x=，（2）400度 23．（1）图②是用与秤配套的秤砣，图①则使用较轻的秤砣.（2）反比例. （3）函数y =xk（k ＞0），当x 变小时，y 增大 24．（1）y ＝t 6000 ；（2）7000－6000＝1000（元）；（3）400＝t6000，t ＝15 28．（1）8xy =-；（2）126。

数学：第17章《反比例函数》章水平测试(一)(人教版八年级下)

第17章反比例函数单元水平测试(一)一、选择题（每小题2分，共20分）1．三角形的面积为152cm ，这时底边上的高y cm 与底边x cm 间的函数关系的图象大致是（）．2．双曲线43y x=-经过点（8，a ），则a 的值为（）． A ．43- B ．16- C ．16 D ．323-3．如果反比例函数12my x-=的图象在所在的每个象限内y 都是随着x 的增大而减小，那么m 的取值范围是（）．A ．m ＞12 B ．m ＜12 C ．m ≤12 D ．m ≥124．已知反比例函数xky =的图象经过点（2，6），下列说法正确的是（）．A ．当x ＜0时，y ＞0B ．函数的图象只在第一象限C ．y 随着x 的增大而增大D ．点（4，－3）不在此函数的图象上 5．若m ＜－1，则下列函数：（1）(0)my x x=>；（2）1y mx =-+ （3）y mx =（4）(1)y m x =+，其中，y 随着x 的增大而增大的函数是（）．A ．（1）、（2）B ．（2）、（3）C ．（1）、（3）D ．（3）、（4）6．如果y ＝y 1＋y 2，其中1y 与x 成正比例，2y 与x －2成反比例，且x ＝1时，y ＝－1；x ＝3时，y ＝5,那么y 的解析式为（）．A ．22--=x x yB ．22-+=x x yC ．22++=x x yD ．22---=x x y 7．点A （－2，1y ）与点B （－1，2y ）都在反比例函数ky x=的图象上，则1y 和2y 的大小关系是（）．A ．1y ＞2yB ．1y ＝2yC ．1y ＜2yD ．无法确定x A y Ox By O x CyO xDyOxyP 1P 2A 1A 28．函数229(2)mm y m x --=+是反比例函数，则m 的值是（）．A. m =4或m =-2B. m =4C. m =-2D. m =-19．函数y kx b =+与y k xkb =≠()0的图象可能是（）．A B C D10．如图，△P 1OA 1、△P 2A 1A 2是等腰直角三角形，点P 1、P 2在函数4(0)y x x=>的图象上，斜边OA 1、A 1A 2都在x 轴上，则22OA 等于（）． A ．8 B ．16 C ．32 D ．64 二、填空题（每小题3分，共24分）11．已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是h ＝__________,这时h 是a 的__________． 12．已知反比例函数xm y 23-=，当______m 时，其图象的两个分支在第一、三象限内；当______m 时，其图象在每个象限内y 随x 的增大而增大．13．如图，面积为3的矩形OABC 的一个顶点B 在反比例函数xky =的图象上，另三点在坐标轴上，则k ＝ . 14．在反比例函数3y x=的图象上，和x 轴距离为1的点的坐标是 . 15．若反比例函数ky x=，当x ＝3＋2时，y ＝3－2，则这个反比例函数的图象一定在第象限．16．如果一次函数b kx y +=的图象经过第二、三、四象限，则反比例函数xkby =的图象位于第象限内．17．已知函数xay ax y -==4和的图象有两个交点，其中一个交点的横坐标为1，则两个函数图象的交点坐标是．18．已知一次函数2y x =+与反比例函数ky x=的图象的一个交点为P （a ，b ），且P 到原点的距离是10，则k ＝．三、解答题（共56分）19．正比例函数x y 2=与双曲线xky =的一个交点坐标为A （2，m ）．（1）求出点A 的坐标；（2）求反比例函数关系式．20．如图所示，在平面直角坐标系中，第一象限的角平分线 OM 与反比例函数的图像相交于点M ，已知OM 的长是22．（1）求点M 的坐标；（2）求此反比例函数的关系式．21．如图，A 、B 、C 为反比例函数图像上的三个点，分别从A 、B 、C 向x 轴、y 轴作垂线，构成三个矩形ADOE ，BGOF ，CHOI ，它们的面积分别是1S 、2S 、3S ，试比较1S 、2S 、3S 的大小并说明理由．22．点A 为反比例函数图象上一点，它到原点的距离为13，到y 轴的距离为5，求这个反比例函数的解析式．23．已知1223y y y =-，1y 与x 成正比例，2y 与x 成反比例，当x ＝1时，y ＝1；当x ＝2时，y ＝5．（1）请写出y 和x 之间的函数关系式；（2）当x ＝1时，求y 的值．24．已知关于x 的一次函数y ＝kx ＋3b 和反比例函数xbk y 52+=的图象都经过点A （1，－2），求一次函数和反比例函数的解析式．25．如图，已知点A （2，a ）在反比例函数xy 8=的图象上，（1）求a 的值；（2）如果直线b x y +=34也经过点A ，且与x 轴交于点C ，连接AO ，求△AOC 的面积．26．如图，RtΔABO 的顶点A 是双曲线y ＝kx 与直线y ＝x ＋(k ＋1)在第四象限的交点,AB⊥x 轴于B,且AOBS △＝ 32 ，求这两个函数的解析式．Oxy.AC27．已知反比例函数ky x=与一次函数21y x =-的图象交于点A （a ，b ），且一次函数21y x =-经过点B （1a +，b k +），AE⊥x 轴于E ，AF⊥y 轴于F ，求矩形OFAE 的面积．28．已知反比例函数)0(≠=k xky 和一次函数8+-=x y （1）若一次函数和反比例函数的图象的交于点（4，m ），求m 和k ；（2）k 满足什么条件时，这两个函数图象有两个不同的交点；（3）设（2）中的两个交点A 、B ，试判断∠AOB 是锐角还是钝角？参考答案1．D 2．B 3．B 4．D 5．A 6．B 7．D 8．B 9．A 10．C 11．2s a 、反比例函数 12．＞32 、＜3213．－3 14．（3，1）和（－3，－1） 15．二、四 16．一、三 17．（1，2）和（－1，－2） 18．4819．（1）A 点坐标是（2，4）（2）反比例函数解析式8y x =． 20．（1）M 点坐标是（2，2）（2）反比例函数解析式4y x=．21．1S ＝2S ＝3S 22．反比例函数解析式60y x =或60y x=-． 23．（1）23y x x=-（2）y ＝1 24．一次函数解析式42y x =-，反比例函数解析式2y x=-． 25．（1）a ＝4 （2）△AOC 的面积是2．26．设A 点坐标是（x ，y ），∵AOB S △＝ 32 ，∴12OB AB ＝32，∴1322x y =，∵A 点在第四象限，∴xy ＝－3，∴k ＝－3， ∴反比例函数解析式3y x=-，一次函数解析式2y x =-． 27．将A （a ，b ）代入ky x=中，得k ab =，∵一次函数21y x =-经过A （a ，b ），B （1a +，b k +），∴2121a ba b ab-=⎧⎨+=+⎩，∴ab ＝2，∵AE⊥x 轴，AF⊥y 轴，∴AF＝a ，AE ＝b ，∴矩形OFAE 的面积＝ab＝2．28．（1）m ＝4，k ＝16 （2）当k ＜0或0＜k ＜16时，两个函数图象有两个不同的交点（3）当k ＜0时，∠AOB 是是钝角，当0＜k ＜16时，∠AOB 是锐角．。

人教版初中数学第17章反比例函数章水平测试(二)及答案

第17章反比例函数单元水平测试一、选择题（每小题2分，共20分）1．点P （－3，4）一定在下列哪个函数的图象上（）．A ．12x y -= B ．x y 12-= C ．xy 34-= D ．623+-=x y2．在第三象限中，下列函数中：①y ＝－3x ；②y ＝x8；③y ＝－2x ＋5；④y ＝－5x －6，y 随x 的增大而减小的有（）．A ．1个B ．2个C ．3个D ．4个 3．若ｙ与－3ｘ成反比例，ｘ与z4成正比例，则ｙ是ｚ的（）． A ．正比例函数 B ．反比例函数 C ．一次函数 D ．不能确定 4．双曲线ky x=经过点(),m m - ()0m ≠，则它的两个分支分别在（）． A ．第一、二象限内；B ．第二、四象限内；C ．第一、三象限内；D ．第三、四象限内 5．已知反比例函数(0)ky k x=<的图象上有同一象限内两点A （1x ，1y ），B （2x ，2y ），且12x x <，则12y y -的值是（）．A ．正数B ．负数C ．非正数D ．不能确定 6．正比例函数y ＝k 1x 和反比例函数xk y 2=交于A （1、m ），B （n ，－2）两点，则m n +等于（）．A ．3B ．－1C ．1D ．－3 7．如图所示，A （1x ，1y ）、B （2x ，2y ）、C （3x ，3y ）是函数xy 1=的图象在第一象限分支上的三个点，且1x ＜2x ＜3x ，过 A 、B 、C 三点分别作坐标轴的垂线，得矩形ADOH 、BEON 、CFOP ，它们的面积分别为S 1、S 2、S 3，则下列结论中正确的是（）．A ．S 1＜S 2＜S 3B ．S 3 ＜S 2＜ S 1C ．S 2＜ S 3＜ S 1D ．S 1＝S 2＝S 3 8．如图，在同一直角坐标系中，函数y ＝kx －k 与ky x=(k ≠0)的图象大致是（）．ABCD9．已知反比例函数xy 1=的图像经过P （m ，n ），则化简)1)(1(n n m m +-的结果正确的是（）．A ．2m 2B ．2n 2C ．n 2－m 2D ．m 2－n 2 10．若点（1π-，1y ），（－π，2y ），（21a +，3y ）都是反比例函数4y x=上的点，则下列各式中，正确的是（）．A ．1y ＞2y ＞3yB ．2y ＞1y ＞3yC ． 3y ＞1y ＞2yD ．3y ＞2y ＞1y 二、填空题（每小题3分，共24分）11．把一张一百元人民币换成其他面额的，其换成的元数x 和换成的张数y 的关系如下表：由上表得换成的张数y （张）与换成的元数x （元）之间的函数关系式是． 12．函数2y x=-的图像，在每一个象限内，y 随x 的增大而． 13．若函数图象上任意一点的的横、纵坐标之积等于－5，那么这个函数是_________函数，其解析式是．14．已知正比例函数x m y )12(-=与反比例函数xmy -=3的图象交点在第一、三象限，则m 的取值范围为．15．函数y ＝x4，当y≥－2时，x 的取值范围是（可结合图像解） 16．已知反比例函数xky =图象与直线x y 2=和1+=x y 的图象过同一点，则k ＝．17．P 是反比例函数图像上一点，且点P 到x 轴的距离为3，到y 轴的距离为2，则该函数的表达式为． 18．若反比例函数y ＝xk 3-的图像位于一、三象限内，正比例函数y ＝(2k －9)x 过二、四象限，则k 的整数值是．三、解答题（共56分）19．现有一水塔，水塔内装有水20m 3，如果每小时从排水管中放水x （m 3），则要经过y （h ）就可以把水放完．（1）求y 与x 之间的函数关系式；（2（3）当x＝4时，求时间y的值．20．已知y－1与x成反比例关系，且点（－2，3）在其图象上，求y与x的函数解析式．21．某空调厂的装配车间原计划用2个月时间（每月以30天计算），每天组装150台空调.（1）从组装空调开始，每天组装的台数m（单位：台／天）与生产的时间t（单位：天）之间有怎样的函数关系？（2）由于气温提前升高、厂家决定这批空调提前十天上市，那么装配车间每天至少要组装多少空调？22．请分别写出反比例函数3yx=和2yx=-的图象的性质的两个共同点和不同点．23．已知：反比例函数xky =和一次函数12-=x y ，其中一次函数的图像经过点（k ，5）. （1）试求反比例函数的解析式；（2）在同一平面直角坐标系中画出上述两函数的图像上，根据图象判断这两个函数图象有没有交点？如果有，清说明交点在哪些象限内．24．如图，一次函数y ax b =+的图象与反比例函数ky x=的图象交于M 、N 两点．（1）求反比例函数和一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．25．已知反比例函数xmy 3-=和一次函数1-=kx y 的图象都经过点m P (，)3m - ⑴ 求点P 的坐标和这个一次函数的解析式；⑵ 若点M(a ，1y )和点N (1+a ，2y )都在这个一次函数的图象上．试通过计算或利用一次函数的性质，说明1y 大于2ym ）N26．已知双曲线4y x=-与直线y kx b =+有一个公共点A （m ，2），直线y kx b =+与y 轴交于B 点，且AOB S △＝4。

新人教版九年级数学下册第十七章《反比例函数》单元检测题(含答案)-

第十七章反比例函数单元检测题（时间90分钟，满分100分）一、耐心填一填：（每题4分，共24分）1．若函数y=kx中，当x=2时，y=-3，则函数解析式是_______．2．函数y=kx-1的图象分布在第一、三象限内，则k的取值范围是_______．3．若关于x、y的函数y=5x25k 是反比例函数，则k=________．4．反比例函数y=-34x的比例系数k=_____，•若点（-3，a）•在它的图象上，则a=___．5．若y是x的反比例函数，x是z的正比例函数，则y是z的______函数．6．设函数y=-2x与y=-x+1的图象交于A、B•两点，•O•为坐标原点，•则△AOB•面积为_____．二、精心选一选（每题4分，共28分）7．若反比例函数y=kx的图象过点（-2，1），则k等于（）A．-2 B．2 C．- D．8．若反比例函数y=-2x的图象经过点（a，-a），则a为（）A．2 B．-2 C．±2 D．±29．若函数y=-kx的图象在第二、四象限，则（）A．k>0 B．k<0 C．k=0 D．k为任何实数10．若函数y=kx（k≠0）图象在第二、四象限内，则点（k，-1-k）在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限11．若函数y=kx的图象过点（1，-2），则直线y=kx+1不经过（）A．第一象限 B．第二象限 C．第三象限 D．第四象限12．函数y=k（x-1）与y=-kx在同一直角坐标系内的图象大致是（）13．A、B两城间的距离为15千米，一人行路的平均速度每小时不少于3千米，也不多于5千米，则表示此人由A到B的行路速度x（千米/小时）与所用时间y（小时）•的关系y=15x的函数图象是（）三、问答题（14题10分，15、16题12分，17题4分，共48分）14．（本题10分）某工程队原定每天修路50米，10天可将这一路段全部修好．（1）该路段多长？（2）如果使每天修路的长度达到y （米），那么所需时间x （天）将如何变化？（3）写出y 与x 的函数关系式，并画出图象；（4）如果准备在5天内将路修好，那么每天至少修路多少米？（5）工程队为了保证施工质量，每天修路不得超过80米，•那么最少多长时间能把路修好？15．（本题12分）已知函数y=2x 与y=8x 在第一象限的交点为A ，直线y=43x+b 经过点A•并交x 轴于点B ，求点B 的坐标．16．（本题12分）某校科技小组进行野外考察，途中遇到一片十几米宽的烂泥湿地．为了安全、迅速通过这片湿地，他们沿着前进路线铺了若干块木块，构筑成一条临时近道．木板对地面的压强()Pa p 是木板面积()2m S 的反比例函数，其图象如下图所示．（1）请直接写出这一函数表达式和自变量取值范围；（2）当木板面积为20.2m 时，压强是多少？（3）如果要求压强不超过6000Pa ，木板的面积至少要多大？17．（本题14分）已知关于x 的一次函数y=mx+3n 和反比例函数y=25m n x+的图象都过点（1，-2），求：（1）一次函数和反比例函数的解析式；（2）两个函数图象的另一个交点的坐标．0 200 40600 ()1.5400A ， /Pa p 2/m S 4 3 2.5 2 1.5 1参考答案1．y=-6x 2．k>0 3．k ±2 4．-34 14 5．反比例 6．327．A 8．C 9．•A •10．B 11．C 12．A 13．D14．（1）500 （2）x 随y 的增大而减小（3）y=500x，图略（•4）100米（5）x=50025804=，最小7天 15．直线y=43x+43，B （-1，0） 16．（1）()6000p S S=>（解析式与自变量取值范围各1分）．（2）当0.2S =时，60030000.2p ==．即压强是3000Pa ．（3）由题意知，6006000S ≤，0.1S ∴≥．即木板面积至少要有20.1m ． 17．（1）y=4x-6，y=-2x（2）交点坐标为（12，-4）。

第17章反比例函数单元复习测试(含答案)(人教新课标初二下)doc初中数学

337第17章反比例函数单元复习测试（含答案）（人教新课标初二下）doc 初中数学第17章反比例函数（时刻：120分钟分数：120分）得分 _______、选择题〔每题3分，共30分〕11 .以下函数，①y=2x ，②y=x ，③y=x 1，④y= 是反比例函数的个数有〔丨.x 1A . 0个B . 1个C . 2个D . 3个22 .反比例函数y= 的图象位于〔〕xA .第一、二象限B .第一、三象限C .第二、三象限D .第二、四象限3.矩形的面积为10,那么它的长y 与宽x 之间的关系用图象表示大致为〔〕k4.关于x 的函数y=k 〔 x+1丨和y=-〔 k 工0〕它们在同一坐标系中的大致图象是〔？〕.k5 .点〔3, 1〕是双曲线y=-〔 2 0〕上一点，那么以下各点中在该图象上的点是〔丨.x11A .〔 —，-9〕B .〔 3, 1〕C .〔 -1 , 3〕D .〔 6,-—〕326 .某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P 〔kPa 〕是气体体积 V 〔m 3〕体积应〔丨.24A.不大于一卅B35 不小于24 m33524.不大于一* .不小于2437的反比例函数，其图象如下图，当气球内的气压大于140kPa时，？气球将爆炸，为了安全起见，气体k 11. 一个反比例函数 y=k 〔 k z 0〕的图象通过点 P 〔-2 , -1〕，那么该反比例函数的解析式是 ________________ x12 .关于x 的一次函数y=kx+1和反比例函数 y=—的图象都通过点〔2, m 〕，那么一次函数的解析式是x13 . 一批零件300个，一个工人每小时做 15个，用关系式表示人数 x?与完成任务所需的时刻 y 之间的函数关系式为 _________ .114 .正比例函数y=x 与反比例函数y=—的图象相交于 A C 两点，AB 丄x 轴于B, CD?丄x 轴于D,如下图,x200 150 J (XI50 0.5 t.O L5 2 v (m l )（第6题）（7.某闭合电路中，电源电压为定值，电流中电流I 与电阻R 之间的函数关系的图象，663A . I=B .1=-C . 1=-R RiI 〔 A 〕与电阻那么用电阻2R 〔Q 丨成反比例，如右图所表示的是该电路 R 表示电流I?的函数解析式为〔〕.8 .函数y=—与函数y=x 的图象在同一平面直角坐标系内的交点个数是〔 xB . 2个〕.A . 1个 9 •假设函数 y=〔 m+2C . 3个D . 0个|m|-3是反比例函数，那么 m 的值是〔〕.-2.土 210 .点 A 〔-3 , y i 〕 ,B 〔-2 , y 2〕4,C 〔3, y 3〕都在反比例函数 y=—的图象上，那么〔丨.xA . y i <y 2<y 3B . y 3<y 2<y iC . y 3<y i <y 2D . y 2<y i <y 3二、填空题〔每题分，共27分〕4(0.8,120) It那么四边形ABCD 勺为 ________（第14题）第15题）(第19题）〔用” > 填空〕19 .两个反比例函数 y= — , y=—在第一象限内的图象如下图，点P 1, P 2, P 3 .......... P 2005,在反比例函数y=—X纵坐标分不是1, 3, ?5?……,?共2005年连续奇3y= 的图象交点依次是 Q 1〔X 1, y 1〕，Q 2〔x 2,x\\ . !! \\ . “ \\ !!> 、< 、 — 的图象上, 数，过点 y 2〕，Q 3 x x它们的横坐标分不是 X 1, X 2, X 3,…X 2005, P l , P 2, P 3,…，P 2005分不作y 轴的平行线与〔X 3, y 3〕，…， Q 2005〔 X 2005, y 2005〕，那么 y 2005 = 三、不定项选择题〔每题 4分，共8分，错选一项得 0分，？对而不全酌情给分〕 20 .当>0时，两个函数值1A . y=3x 与 y=x1 C . y=-2x+6 与 y=xy , 一个随x 增大而增大，另一个随x 的增大而减小的是〔？丨.c 匕1 .y=-3x 与 y=x 1 .y=3x-15 ^与 y=-—x1 在y=」的图象中，阴影部分面积为1的有〔〕.x四、运算题.〔8分〕如图，一次函数 y=kx+b y= m 〔 m 甘0〕的图象在第一象限交于x〔1〕求点A 、B 、D 的坐标；22. 〔k z 0〕的图象与x 轴、y 轴分不交于 A 、B?两点，且与反比例函数 C 点，CD 垂直于x 轴，垂足为 D, ?假设OA=OB=OD=1 求一次函数和反比例函数的解析式.15•如图，P 是反比例函数图象在第二象限上的一点，且矩形是 ___________ .3n 916.反比例函数丫=注_9的图象每一象限内，y 随x 的增大而增大，那么n=10 n 2X17. _______________________________________________________________ 一次函数y=3x+m 与反比例函数y= _3的图象有两个交点，当m= ________________________________________ 时有一个交点的纵坐标为 6.x k18. 假设一次函数y=x+b 与反比例函数y= 图象，在第二象限内有两个交点，？那么kxPEOF 勺面积为8，那么反比例函数的表达式x25 .〔 12分〕如图，一次函数 y=kx+b 的图象与反比例函数y=m 的图象交于A B 两点.823.〔 10分〕如图，点 A 〔4, m 〕，B 〔-1 , n 〕在反比例函数 y 的图象上，直线 AB?分不与x 轴，y 轴x相交于C 、D 两点，〔1〕求直线AB 的解析式.〔2〕C D 两点坐标.〔3〕S A AOC : S ^BOD 是多少？24.〔 11分〕y=y i -y 2, y i 与.x 成正比例，y 与x 成反比例，且当 x=1时，y=-14 , x=4时，y=3.求〔1〕y 与x 之间的函数关系式. 〔2〕自变量x 的取值范畴.1〔3〕当x=—时，y 的值.4〔1〕利用图中的条件，求反比例函数和一次函数的解析式. 〔2〕依照图象写出使一次函数的值大于反比例函数的值的x 的取值范畴.526 .〔14分〕如图，双曲线y在第一象限的一支上有一点C〔1, 5〕，?过点C?的直线y=kx+b〔k>0〕x与x轴交于点A〔a, 0〕.〔1〕求点A的横坐标a与k的函数关系式〔不写自变量取值范畴〕.〔2〕当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△ COA?勺面积.1答案：1. B 2 . D 3 . A 4 . A 5 . B 6 . B 7 . A 8 . B 9 . A 10 . Dk b 0解得k 1b 1• 一次函数的解析式为 y=x+1 ,••点C 在一次函数y=x+1的图象上，？且CDL x 轴, • C 点的坐标为〔1, 2〕，又••点C 在反比例函数y=m 〔 m^ 0〕的图象上，x〔2〕依照图象可知，一次函数的图象在反比例函数的图象的上方时, 的值，即x>2或-1<x<0 .26.解：〔1 点 C 〔 1, 5〕在直线 y=-kx+b 上，• 5=-k+b ,又•••点 A 〔a , 0〕也在直线 y=-kx+b 上，-ak+b=0，二 b=ak11. y=2 12 . y=x+1 13 x .y=-20 14 . 2x15 . y=--x16. n=-3 17 . m=5 18 .<,> 22.解：〔1〕T OA=OB=OD=1•••点A B 、D 的坐标分不为 19 . 2004. 5 20 . A 、B 21 . A C 、DA 〔-1 , 0〕〔2〕•••点 AB 在一次函数 y=kx+b 〔 k 工 0〕 ,B 〔0, 1〕，的图象上，D 〔 1, 0〕. 23 . 24 . 25 . ••• m=2 ? •••反比例函数的解析式为〔1〕〔1〕 2 y=. x D 〔 0, y=2x-6 ;〔 2〕C 〔3, 0〕， y=2、. x - ^!提示：设 y=k 1 .. x -x自变量x 取值范畴是 -6〕；〔 3〕S A AOC S A BO =1 : k，再代入求k 1, k 2的值.xx>0 . 当 x=-时，y=2 J 1 -16「=255.4 V4解：〔1〕由图中条件可知，双曲线通过点•••仁口，• m=2, •••反比例函数的解析式为2A 〔 2,1〕2 y=_. x又点B 也在双曲线上，• n = — =-2，•点1B 的坐标为〔-1 , -2丨.•••直线y=kx+b 通过点A 、B.1 2k b解得k 12 k b b• 一次函数的解析式为 y=x-1 .?一次函数的值大于反比例函数5 将b=ak 代入5=-k+a 中得5=-k+ak , • a= +1.k 〔2〕由于D点是反比例函数的图象与直线的交点5 y 二9•' ak=5+k，•‘• y=-8k+5③y 9k ak将①代入③得:5 =-8k+5 ,• k=5-,a=1099-X 10X 5=25• A〔10,0〕，又知〔1, 5〕，•'• S^COA =2。

(最新整理)第十七章《反比例函数》单元测试题(含答案)-

________函数，比例系数为_______．
18．如果一次函数 y=mx+n 与反比例函数 y= 3n m 的图象相交于点( 1 ,2)，那么该直线与双曲
x
2
线的另一个交点的坐标为_________．
三、解答题（6 分,6 分，6 分，7 分,8 分，8 分，9 分,计 50 分) 19．在同一坐标系内,画出函数 y= 8 与 y=2x 的图象，并求出交点坐标．
O
x
C
y
4
O 4x
D
二、填空题(3 分×8=24 分） 11．如果一个反比例函数 y= k 的图象经过点(2，—1）,那么这个反比例函数的解析式为
x _________． 12．要使函数 y= k （k 是常数，k≠0）的图象的两个分支分别在第、三象限内，则 k的值为
x ________．（请写出两个符号上述要求的数值)．
x
-3-
第十七章《反比例函数》单元测试题(含答案)-
16．当 x〉0 时,反比例函数 y=m x2m23m6 随 x 的减小而增大，则 m 的值为________，图象在第
_______象限．
17．已知 y 与 3m 成反比例,比例系数为 k1，m 又与 6x 成正比例，比例系数为 k2,那么 y 与 x 成
第十七章《反比例函数》单元测试题(含答案)-
第十七章《反比例函数》单元测试题(含答案)-
编辑整理：
尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（第十七章《反比例函数》单元测试题(含答案)-）的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为第十七章《反比例函数》单元测试题(含答案)-的全部内容。

人教版初中数学第17章反比例函数章水平测试(四)及答案

第17章反比例函数单元水平测试一、选择题（每小题3分，共30分） 1、观察下列函数：5y x =， 3y x -=， 91y x =-， 5x y =.其中反比例函数有（） A 、1个 B 、2个 C 、3个 D 、4个 2、双曲线1k y x-=在第一、三象限内，则k 的取值范围是（） A 、0k ＞ B 、1k ＞ C 、k ＜0 D 、k ＜1 3、反比例函数2y x =，3y x =-，14y x=的共同特点是（）A 、图像位于相同的象限内B 、自变量取值范围是全体实数C 、在第一象限内y 随x 的增大而减小D 、图像都不与坐标轴相交 4、若y 与x 成反比例，且当3x =时，1y =，则y 是x 的函数关系式是（） A 、3y x = B 、3y x = C 、13y x = D 、13y x =5、已知函数25(1)my m x -=+是反比例函数，且图像在第二、四象限内，则m 的值是（）A 、2B 、2-C 、2±D 、12- 6、已知点M (－2，3 )在双曲线xky =上，则下列各点一定在该双曲线上的是( ) A 、 (3，-2 )B 、(-2，-3 )C 、 (2，3 )D 、 (3，2)7、在同一坐标系中，正比例函数x y =与反比例函数xy 2=的图象大致是（）8、在反比例函数1ky x-=的图象的每一条曲线上，y x 都随的增大而增大，则k 的值可以是（） A 、1-B 、0C 、1D 、29、一个直角三角形的两直角边长分别为y x ，，其面积为2，则y 与x 之间的关系用图像表示大致为（）10、对于函数3y x=，下列判断正确的是（） A 、图像经过点（-1，3） B 、图像在第二、四象限C 、图像所在的每一个象限内，y 随x 的增大而减小D 、不论x 取何值时，总有0y ＞二、填空题（每小题3分，共30分）11、已知函数2(1)a y a x -=-，当a =_____时，它的图像是双曲线 12、反比例函数 xm y 1+=的图像经过点（2，1），则m 的值是 13、若正比例函数y kx =在每一个象限内y 随x 的增大而减小，那么反比例函数k y x=-在每一个象限内y 随x 的增大而_________ 14、已知点A 是反比例函数3y x=-图像上的一点．若AB 垂直于y 轴，垂足为B ，则AOB △ 的面积= ．15、若11(,)A x y ，22(,)B x y 是双曲线xy 3=上的两点，且120x x ＞＞，则1y 2y （填“＞”“＝”“＜”）．16、在同一坐标系内，正比例函数32y x =-与反比例函数3y x=-图像的交点在第_____象限 17、点A(2，1)在反比例函数y kx=的图像上，当1﹤x ﹤4时，y 的取值范围是 .18、在对物体做工一定的情况下，力F （牛）与物体在力的方向上移动的距离s （米）成反比例函数关系，点 P （15，2）在函数图像上，当力达到20牛时，物体在力的方向上移动的距离是____ 米。

反比例函数》测试题(含答案)

反比例函数》测试题(含答案)1、选择题（每小题5分，共50分）1、若点（x1.-1）、(x2.-2)、(x3.1)都在反比例函数y= k/x 上，则它们之间的大小关系是（）A．x1<x3<x2B．x2<x1<x3C．x1<x2<x3D．x2<x3<x12、若反比例函数y=k/x的图象经过点(m，3m)，其中m≠0，则此反比例函数的图象在（）A．第一、二象限；B．第一、三象限；C．第二、四象限；D．第三、四象限3、在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线y=3/x上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小4、函数y=-kx与函数y=k/x的图象的交点个数是（）A。

0B。

1C。

2D.不确定5、函数y=6-x与函数y=k/x的图象交于A、B两点，设点A的坐标为（x1,y1），则边长分别为x1、y1的矩形面积和周长分别为（）A。

4，12B。

4，6C。

8，12D。

8，66、已知y1+y2=y，其中y1与x成反比例,且比例系数为k1，而y2与x2成正比例,且比例系数为k2，若x=-1时,y=0，则k1,k2的关系是( )A.k1+k2=0B.k1k2=1C.k1-k2=0D.k1k2=-17、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标系中的图象不可能是（）18、如图，直线y=mx与双曲线y=k/(x-1)交与A、B两点，过点A作AM⊥x轴，垂足为M，连接BM，若S△ABM=2，则k的值是（）A、2B、m-2C、mD、49、如图，点A在双曲线y=6/x上，且OA＝4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为( )A.47B.5C.27D.2210、如图，反比例函数y= k/x的图象经过点(1,2)，则k=（）。

二、填空题（每小题5分，共20分）11、若y=k/x是反比例函数，且x1y1=x2y2，则k=______。

八年级下册数学第十七章反比例函数单元测试一(附答案)

八年级下册数学第十七章反比例函数单元测试一（附答案）学校:___________姓名：___________班级：___________考号：___________一、选择题 1．若反比例函数ky x=的图象经过点(3)m m ，，其中0m ≠，则此反比例函数的图象（） A ．第一、二象限 B ．第一、三象限 C ．第二、四象限 D ．第三、四象限 2．若反比例函数xy 4-=的图象经过点（a ，-a ）则a 的值为（） A ．2B ．-2C ．2±D ．±23．（2011贵州六盘水，8，3分）若点（－3，y 1）、（－2，y 2）、（1，y 3）在反比例函数xy 2=的图像上，则下列结论正确的是（） A ．y 1> y 2> y 3 B ．y 2> y 1> y 3 C ．y 3> y 1> y 2 D ．y 3> y 2> y 1 4．若A(x 1，y 1)，B(x 2，y 2），C(x 3，y 3)是反比例函数y=x3图象上的点，且x 1＜x 2 ＜0＜x 3，则y 1、y 2、y 3的大小关系正确的是 ( ) A y 3＞y 1＞y 2 B y 1＞y 2＞y 3C y 2＞y 1＞y 3D y 3＞y 2＞y 15．已知关于x 的函数y=k (x-1) 和ky x =-(0)k ≠,它们在同一坐标系中的图象大致是( )6．函数x y 2=的图象经过的点是（）A.（2，1）B.（2，－1）C.（2，4）D.（21-，2）7．如图，已知菱形ABCD 的边长为2㎝，︒=∠60A ，点M 从点A 出发，以1㎝／s 的速度向点B 运动，点N 从点A 同时出发，以2㎝／s 的速度经过点D 向点C 运动，当其中一个动点到达端点时，另一个动点也随之停止运动. 则△AMN 的面积y (㎝2) 与点M 运动的时间t (s)的函数的图像大致是（）8．下列各点中，在反比例函数8y x=图象上的是 A ．（－1，8）B ．（－2，4）C ．（1，7）D ．（2，4）9．若函数x m y 2+=的图象在其象限内y 的值随x 值的增大而增大，则m 的取值范围是（A ）2->m （B ）2-<m （C ）2>m （D ）2<m 10．下列四个点中，有三个点在同一反比例函数xky =的图象上，则不在这个函数图象上的点是 ( )A ．(5，1)B ．(－1，5)C ．(35，3)D ．(－3，35-)二、填空题11．如图，一次函数y=mx 与反比例函数y=x k的图象交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM,若ABM S ∆=3，则k 的值是 .12．如图，点A 在双曲线y=的第一象限的那一支上，AB 垂直于x 轴与点B ，点C 在x 轴正半轴上，且OC=2AB ，点E 在线段AC 上，且AE=3EC ，点D 为OB 的中点，若△ADE 的面积为3，则k 的值为．yxO12 3yx3yxO12 3（A ）（B ）（C ）（D ） yxO12 313．两个反比例函数48,y y x x==-的图象在第一象限，第二象限如图，点P 1、P 2、P 3……P 2012在4y x=的图象上，它们的横坐标分别是有这样规律的一行数列1，3，5，7，9，11，……，过点P 1、P 2、P 3、……、P 2012分别做x 轴的平行线，与8y x=-的图象交点依次是Q 1 、Q 2、Q 3、……、Q 2012，则点Q 2012的横坐标是．14．如图，直线2-==kx y (k ＞0)与双曲线xky =在第一象限内的交点面积为R ，与x 轴的交点为P ，与y 轴的交点为Q ；作RM ⊥x 轴于点M ，若△OPQ 与△PRM 的面积是4：1，则=k15．如图，在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====，过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、，得直角三角形1112233344455OPA A P A A P A A P A A P A 2、、、、，并设其面积分别为12345S S S S S 、、、、，则5S 的值为。

八年级数学下册第十七章反比例函数单元综合测试(含解析) 新人教版

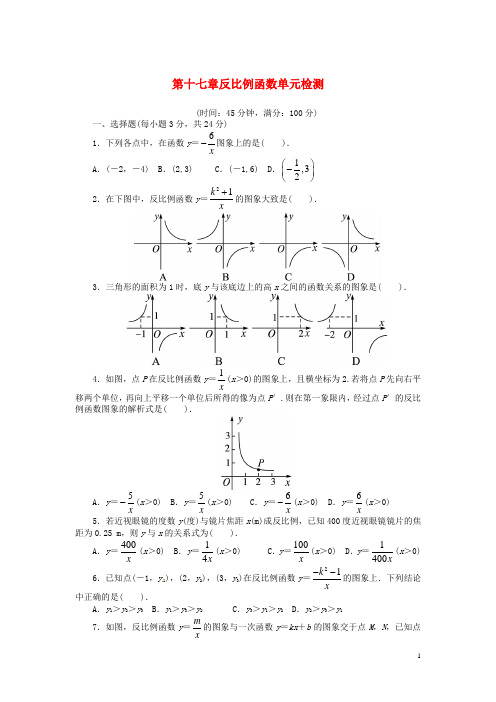
第十七章反比例函数单元检测(时间：45分钟，满分：100分)一、选择题(每小题3分，共24分)1．下列各点中，在函数y ＝6x-图象上的是( )． A ．(－2，－4) B ．(2,3) C ．(－1,6) D ．1,32⎛⎫- ⎪⎝⎭2．在下图中，反比例函数y ＝21k x+的图象大致是( )．3．三角形的面积为1时，底y 与该底边上的高x 之间的函数关系的图象是( )．4．如图，点P 在反比例函数y ＝1x(x ＞0)的图象上，且横坐标为2.若将点P 先向右平移两个单位，再向上平移一个单位后所得的像为点P ′.则在第一象限内，经过点P ′的反比例函数图象的解析式是( )．A ．y ＝5x -(x ＞0) B ．y ＝5x(x ＞0) C ．y ＝6x -(x ＞0) D ．y ＝6x(x ＞0) 5．若近视眼镜的度数y (度)与镜片焦距x (m)成反比例，已知400度近视眼镜镜片的焦距为0.25 m ，则y 与x 的关系式为( )．A ．y ＝400x(x ＞0) B ．y ＝14x (x ＞0)C ．y ＝100x (x ＞0) D ．y ＝1400x (x ＞0) 6．已知点(－1，y 1)，(2，y 2)，(3，y 3)在反比例函数y ＝21k x--的图象上．下列结论中正确的是( )．A ．y 1＞y 2＞y 3B ．y 1＞y 3＞y 2C ．y 3＞y 1＞y 2D ．y 2＞y 3＞y 17．如图，反比例函数y ＝mx的图象与一次函数y ＝kx ＋b 的图象交于点M ，N ，已知点M 的坐标为(1,3)，点N 的纵坐标为－1，根据图象信息可得关于x 的方程mx＝kx ＋b 的解为( )．A ．－3,1B ．－3,3C ．－1,1D ．3，－18．在平面直角坐标系中，直线y ＝6－x 与函数y ＝4x(x ＞0)的图象相交于A ，B 两点，设点A 的坐标为(x 1，y 1)，那么长为x 1，宽为y 1的矩形面积和周长分别为( )．A ．4,12B ．8,12C ．4,6D ．8,6 二、填空题(每小题4分，共20分)9．已知反比例函数y ＝kx 的图象经过点(1，－2)，则k ＝__________. 10．如图是反比例函数y ＝kx(k ≠0)在第二象限内的图象，若图中的矩形OABC 的面积为2，则k ＝__________.11．如图，反比例函数y ＝kx的图象位于第一、三象限，其中第一象限内的图象经过点A (1,2)，请在第三象限内的图象上找一个你喜欢的点P ，你选择的P 点坐标为__________．12．过反比例函数y ＝kx(k ≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B ，C ，如果△ABC 的面积为3，则k 的值为__________．13．双曲线y 1、y 2在第一象限的图象如图所示，y 1＝4x，过y 1上的任意一点A ，作x 轴的平行线交y 2于B ，交y 轴于C ，若S △AOB ＝1，则y 2的解析式是__________．三、解答题(共56分)14．(本小题满分10分)如图所示，在平面直角坐标系中，一次函数y ＝kx ＋1的图象与反比例函数y ＝9x的图象在第一象限相交于点A ，过点A 分别作x 轴、y 轴的垂线，垂足分别为点B ，C ．如果四边形OBAC 是正方形，求一次函数的关系式．15．(本小题满分10分)由物理知识知道，在力F (N)的作用下，物体会在力F 的方向上发生位移s (m)，力F 所做的功W (J)满足：W ＝Fs .当W 为定值时，F 与s 之间的函数图象如图所示．(1)力F 所做的功是多少？(2)试确定F 与s 之间的函数表达式； (3)当F ＝4 N 时，s 是多少？16．(本小题满分12分)已知如图中的曲线是反比例函数y ＝5mx(m 为常数)图象的一支．(1)求常数m 的取值范围；(2)若该函数的图象与正比例函数y ＝2x 的图象在第一象限的交点为A (2，n )，求点A 的坐标及反比例函数的解析式．17．(本小题满分12分)如图所示，一次函数y ＝ax ＋b (a ≠0)的图象与反比例函数y ＝kx(k ≠0)的图象交于M ，N 两点．(1)求反比例函数与一次函数的解析式；(2)根据图象写出使反比例函数的值大于一次函数的值的x的范围．18．(本小题满分12分)给出下列命题：命题1：点(1,1)是直线y＝x与双曲线y＝1x的一个交点；命题2：点(2,4)是直线y＝2x与双曲线y＝8x的一个交点；命题3：点(3,9)是直线y＝3x与双曲线y＝27x的一个交点；…….(1)请观察上面命题，猜想出命题n(n是正整数)；(2)证明你猜想的命题n是正确的．参考答案1. 答案：C2. 答案：D3. 答案：C4. 答案：D5. 答案：C 设y ＝k x ，将(0.25,400)代入y ＝kx，得k ＝100， ∴y ＝100x(x ＞0)． 6. 答案：B 因为－k 2－1＜0，所以反比例函数y ＝21k x--的图象在第二、四象限，(2，y 2)，(3，y 3)在同一象限，y 随x 的增大而增大，即y 2＜y 3＜0，又y 1＞0，所以y 1＞y 3＞y 2.7. 答案：A 由M (1,3)代入y ＝mx得，m ＝3，所以y ＝3x ，将N 点纵坐标－1代入y ＝3x，得x ＝－3. 所以N (－3，－1)，根据图象的意义知，方程mx＝kx ＋b 的解就是它们的交点坐标的横坐标，所以方程的解为－3或1.8. 答案：A 因为y ＝6－x 与函数y ＝4x的图象相交于A ，B ，则有点A (x 1，y 1)的坐标满足两个关系式y 1＝6－x 1，y 1＝14x ，且x 1＞0，y 1＞0. 所以长为x 1，宽为y 1的矩形面积为x 1y 1＝4，矩形周长为2(y 1＋x 1)＝2×6＝12，故选A. 9. 答案：－2 10. 答案：－211. 答案：答案不唯一，如(－1，－2) x ，y 满足xy ＝2且x ＜0，y ＜0即可． 12. 答案：6或－6 根据反比例函数的几何意义可得出S △ABC ＝12|k |，所以|k |＝6，则k ＝±6.13. 答案：y 2＝6x y 1＝4x，过y 1上的任意一点A ，作x 轴的平行线交y 2于B ，交y 轴于C ，S △AOB ＝1.∴△CBO 面积为3，∴y 2的解析式是y 2＝6x. 14. 解：∵S 正方形OBAC ＝OB 2＝9，∴OB ＝AB ＝3， ∴点A 的坐标为(3,3)．∵点A 在一次函数y ＝kx ＋1的图象上， ∴3k ＋1＝3，解得k ＝23. ∴一次函数的关系式是y ＝23x ＋1. 15. 解：(1)W ＝Fs ＝2×7.5＝15(J)．(2)F ＝15s. (3)当F ＝4 N 时，s ＝15154F =＝3.75(m)． 16. 解：(1)∵这个反比例函数的图象分布在第一、三象限，∴5－m ＞0，解得m ＜5.(2)∵点A (2，n )在正比例函数y ＝2x 的图象上， ∴n ＝2×2＝4，则A 点的坐标为(2,4)．又∵点A 在反比例函数y ＝5mx-的图象上， ∴4＝52m-，即5－m ＝8. ∴反比例函数的解析式为y ＝8x. 17. 分析：(1)利用点N 的坐标可求出反比例函数的表达式，据此求点M 的坐标．由两点M ，N 的坐标可求出一次函数的表达式；(2)反比例函数的值大于一次函数的值表现在图象上，就是双曲线在直线的上方，由此可求出x 的范围．解：(1)把N (－1，－4)代入y ＝k x 中，得－4＝1k -，所以k ＝4.反比例函数的表达式为y ＝4x. 又点M (2，m )在双曲线上，所以m ＝2，即点M (2,2)．把M (2,2)，N (－1，－4)代入y ＝ax ＋b 中，得22,4.a b m a b +=⎧⎨-+=-⎩解得2,2.a b =⎧⎨=-⎩故一次函数的表达式为y ＝2x －2.(2)由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值．18. 解：(1)命题n ：点(n ，n 2)是直线y ＝nx 与双曲线y ＝3n x的一个交点(n 是正整数)．(2)把2,x n y n=⎧⎨=⎩代入y ＝nx ，左边＝n 2，右边＝n ·n ＝n 2， ∵左边＝右边，∴点(n ，n 2)在直线上．同理可证：点(n ，n 2)在双曲线上，∴点(n ，n 2)是直线y ＝nx 与双曲线y ＝3n x的一个交点，命题正确．。

第17章反比例函数复习单元测试题(人教新课标初二下)doc初中数学

第17章反比例函数复习单元测试题（人教新课标初"）doc 初中数学第十七章反比例函数班不 ___________ 姓名 ___________________座号___________ 成绩 _______________、选择〔每题 3分，共30分〕 i .以下函数是反比例函数的是（）那么a 与b 的关系是V 62 -x A . yB3x.y x x C.y3Dy 4x 822.反比例函数y —xA .第一、二象限的图象位于〔〕正比例函数y ax ，反比例函数，在同一坐标系中，这两个函数的图象没有交点,同号 B .异号.互为倒数 D .乘积为0占八〔3, 1〕是双曲线y k(k x0）上一点，那么以下各点中在该图象上的点是〔5.某闭合电路中，电源的电压为定值，电流反比例。

如图表示的是该电路中电流用电阻 R 表示电流 A. I2 B.R6.函数yk(x 1)和 yC D .第二、四象限II 的函数解析式为〔-1 , 3〕 Ck〔 k 工0〕在同一坐标系中的大致图象是 ?〕假如函数y (a 3)x 囘4为反比例函数，那么a三角形的三个顶点 A 〔 3, -2丨、B 〔 1, 6〕、C 〔 1,-6丨中，可能在同一反比例函数y图象上的是一个梯形的面积是 40，它的上底是下底的一半，假设上底为 x ，高为y ，那么y 与x 的函数关系式为 ________________ 。

1 115.假设函数y 4x 与y —的图象有一个交点是〔一，2〕,那么另一个交点坐标是_x2三、解答题：〔共 50分〕k16.反比例函数y的图象通过点 A (2 , -8)。

〔 1〕求那个函数的解析式；x〔2〕请判定点B (-4 , 4)是否在那个反比例函数的图象上，并讲明理由。

〔6分〕9.A.假设y 与x 成正比，y 与z 的倒数成正比，z 那么是x 的〔 A .正比例函数 B •反比例函数C •二次函数D如图，P 是反比例函数图象在第二象限上的一点，且矩形为8,那么反比例函数的表达式是〔八4 4 A . y B . yC . yxx〕8 Dx一次函数y kx b 的图象通过第一、 kb y的图象通过〔 xA .第一、三象限B .第二、四象限 C.第一、四象限D .第二、三象限10. 点A [ -3，yJ, B 〔-2 , y 〕 ,c 〔 3, y 3〕都在反比例函数 4y的图象上，x那么〔〕A .Y 1 y y 3B .y 3 y 2 y 1C .y 3y 1 y 2D . y 2y 1 土二、填空题: 〔每题 4分，共 20分〕12. 13.14.〕那么反比例函数〕一个函数的图象是双曲线, 且通过点〔3,-5〕，那么该函数的解析式为11.O17．一司机驾驶汽车从甲地去乙地，以 80千米 /小时的平均速度用 6小时到达目的地。

完整版)反比例函数练习题含答案

完整版)反比例函数练习题含答案测试1 反比例函数的概念一、填空题1.一般的，形如 y=k/x 的函数称为反比例函数，其中x是自变量，y是因变量。

自变量x的取值范围是x≠0.2.写出下列各题中所要求的两个相关量之间的函数关系式，并指出函数的类别。

1) 商场推出分期付款购电脑活动，每台电脑元，首付4000元，以后每月付y元，x个月全部付清，则y=(8000+)/x，是反比例函数。

2) 某种灯的使用寿命为1000小时，它的使用天数y与平均每天使用的小时数x之间的关系式为 y=1000/x，是反比例函数。

3) 设三角形的底边、对应高、面积分别为a、h、S。

当a=10时，S与h的关系式为 S=10h/2，是正比例函数；当S=18时，a与h的关系式为 h=36/a，是反比例函数。

4) 某工人承包运输粮食的总数是w吨，每天运x吨，共运了y天，则 y=w/x，是反比例函数。

3.下列各函数 y=1/(k2+1)、y=x/(x5+x12)、y=14-3x、y=2x和y=3x-1 中，是y关于x的反比例函数的有：①y=1/(k2+1)、② y=x/(x5+x12)、③ y=2x。

4.若函数 y=m/(x-1) (m是常数) 是反比例函数，则 m=1，解析式为 y=1/(x-1)。

5.近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜片的焦距为0.25m，则 y=1000/x。

二、选择题6.已知函数 y=3x/(kx+1)，当x=1时，y=-3，那么这个函数的解析式是 y=3x/(3k+1)。

(解析：由 y=-3=3/(3k+1) 可得 k=-1/3，代入原式得 y=3x/(3x-1)。

)7.已知 y 与 x 成反比例，当 x=3 时，y=4，那么 y=3 时，x 的值等于 4/3.三、解答题8.已知 y 与 x 成反比例，当 x=2 时，y=3.1) 求y 与x 的函数关系式：y=k/x，代入已知条件得k=6，因此函数关系式为 y=6/x。

人教版初中数学17章反比例函数章水平测试(三)及答案

第17章反比例函数单元水平测试一、选择题（每小题2分，共20分）1．下列各变量之间是反比例函数关系的是（）．A ．存入银行的利息和本金;B ．在耕地面积一定的情况下，人均占有耕地面积与人口数C ．汽车行驶的时间与速度;D ．电线的长度与其质量 2．函数x k y =的图象经过点（2，8），则下列各点不在xky =图像上的是（）． A ．（4，4） B ．（－4，－4） C ．（8，2） D ．（－2，8） 3．如果反比例函数xky =的图象经过点（－1，5），那么直线1y kx =+一定不经过（）． A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 4．函数y kx =-与k y x=（k ≠0）的图象的交点的个数是（）． A. 2 B.1 C. 0 D.不确定5．若点（3，4）是反比例函数xm m y 122++=图象上一点，则此函数图象必经过点（）．A.（3，－4）B.（2，－6）C.（4，－3）D. （2，6） 6．已知不等式ax b +＞0的解集为x ＞b a-，那么双曲线ay x =的图象上的点一定位于（）．A ．第一象限B ．第二象限C ．第一、三象限D ．第二、四象限 7．函数1y x=-的图象上有两点),(11y x A 、),(22y x B 且21x x <，那么下列结论正确的是（）．A.21y y <B.21y y >C.21y y =D.1y 与2y 之间的大小关系不能确定8．一条直线与双曲线xy 1=的交点是A （a ，4），B （－1，b ），则这条直线的解析式为（） A ．34-=x y B ．341+=x y C ．34+=x y D ．34--=x y9．函数y ＝－kx ＋k 与y ＝xk-（k≠0）在同一坐标系中的图象可能是（）．10．如图，点P 是x 轴上的一个动点，过点P 作 x 轴的垂线PQ 交双曲线xy 1=于点Q ，连结OQ ，当点P 沿x 轴正半方向运动时，Rt △QOP 面积（）．A ．逐渐减小B ．逐渐增大C ．保持不变D ．无法确定二、填空题（每小题3分，共24分）11．一般地，函数是反比例函数，其图象是，当k <0时，图象两支在象限内． 12．反比例函数y ＝x2，当y ＝6时，x =_________． 13．近视眼镜的度数y （度）与焦距x （米）的函数关系式为100y x=，已知某同学近视眼镜镜片的焦距为0. 25米，则该同学配的镜片的度数是__________度．14．若函数的图象经过点（2，1），则函数的表达式可能是____________（写出一个即可）． 15．已知函数y ＝x k 的图像过点（31，43），则函数的关系式是，当y ＝65时，x＝．16．若函数y ＝4x 与y ＝x 1的图象有一个交点是（21，2），则另一个交点坐标是 _．17．点P 在反比例函数y ＝x6-的图像上，若点P 的纵坐标小于－1，则点P 的横坐标的取值范围是． 18．直线y ＝－2x─2与双曲线y ＝xk相交于点A ，与x 、y 轴交于点B 、C ，AD ⊥x 轴于点D ，如果ADB S △＝COB S △，那么k ＝．三、解答题（共56分）19．有一个水池，池内原有水500升，现在以每分钟20升注入水，35分钟可注满水池．（1）水池的容积是多少？（2）若每分钟注入的水量达到Q 升，注满水池需要t 分钟，写出t 与Q 之间的关系式．（3）若要20分钟注满水池，每分钟的注水量应达到多少升？20．甲、乙两地相距12千米，一辆汽车从甲地开往乙地，若设汽车的平均速度为每小时x 千米，到达乙地所用的时间为y 小时，（1）y 与x 之间的函数关系式为；（2）画出该函数的图象．21．在反比例函数y ＝42008k x-图像的每一条曲线上，y 随x 的增大而减小，求k 的取值范围．22．我们学过反比例函数，例如小明准备用20元钱去买单价为x 元/千克的水果，那么他能够购买的水果的重量y （千克）与x 之间就是反比例函数关系．函数解析式是xy 20=，其中x ＞0．请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数的量的实例，并写出它的函数关系式．你自己能完成吗？实例：_______________________________________________________________________ ___________________．函数关系式：____________________________．23．已知反比例函数xky =与一次函数b kx y +=的图象都经过点（－2，－1），求这两个函数解析式．24．面积一定的梯形，其上底长是下底长的21，设下底长x ＝10 cm 时，高y ＝6 cm （1）求y 与x 的函数关系式；（2）求当y ＝5 cm 时，下底长多少？25．若反比例函数xy 6=与一次函数4-=mx y 的图象都经过点A （a ，2）（1）求点A 的坐标；（2）求一次函数4-=mx y 的解析式．26、如图所示，直线l 1的方程为y =－x +l ，直线l 2的方程为y =x +5，且两直线相交于点P ，过点P 的双曲线ky x=与直线l 1的另一交点为Q （3，M ）. （1）求双曲线的解析式．（2）根据图象直接写出不等式kx＞－x +l 的解集．27．已知点A （－2，0）和点B （2，0），点P 在函数y ＝x1-的图像上，如果△PAB 的面积是6，求点P 的坐标．28．如图，反比例函数1k y x=图象在第一象限的分支上有一点C （1，3），过点C 的直线2y k x b =+〔k ＜ 0〕与x 轴交于点A （a ，0）.（1）求反比例函数的解析式；（2）求A 点横坐标a 和2k 之间的函数关系式；（3）当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时，求△COA 的面积.参考答案1．B 2．D 3．C 4．C 5．D 6．C 7．D 8．C 9．A 10．C11．(0)k y k x =≠、双曲线、第二和第四 12．13 13．400 14．2y x = 15．14y x =、310 16．（12-，－2） 17．0＜x ＜6 18．－419．（1）1200升（2）1200t Q=（3）60升 20．（1）12y x=（x ＞0）（2）略 21．k ＞50222．京沪高速公路全长约为1262km ，汽车沿京沪高速公路从上海驶往北京，汽车完成全程所需的时间t （h ）与行驶的平均速度v (km/h)是反比例函数关系，1262t v= 23．一次函数解析式23y x =+，反比例函数解析式2y x= 24．（1）60y x=（2）下底长12cm ． 25．（1）A 点坐标（3，2）（2）24y x =- 26．解：（1）依题意：15y x y x =-+⎧⎨=+⎩ 解得：23x y =-⎧⎨=⎩∴双曲线的解析式为：y =6x-（2）－2＜x ＜0或x>3 27．P 点坐标是（13，－3）或（－13，3） 28．（1）3y x = （2）a ＝225k k - （3）△COA 面积是6.。

反比例函数单元测试卷含答案

反比例函数单元测试卷含答案一、选择题1. 反比例函数的一般形式是：A. y = kxB. y = ax + bC. y = k/xD. y = mx + c答案: C2. 当x为0时，反比例函数的值为：A. 0B. 1C. 无定义D. 任意值答案: C3. 若反比例函数的k值为正数，x趋近于无穷大，y会趋近于：A. 正无穷大B. 负无穷大C. 0D. 不存在极限答案: B4. 反比例函数的图像是一条：A. 直线B. 抛物线C. 余弦曲线D. 双曲线答案: D5. 若反比例函数的x值为正数，y值为负数，那么k值是：A. 正数B. 负数C. 零D. 无法确定答案: B二、计算题1. 已知反比例函数y = 5/x，当x = 2时，求y的值。

答案: 2.52. 已知反比例函数y = 3/x，当y = 6时，求x的值。

答案: 0.5三、简答题1. 什么是反比例函数？答案: 反比例函数是一种函数关系，当自变量x的值增大时，因变量y的值会减小，并且二者之间呈现出一种倒数关系。

它的一般形式为y = k/x，其中k为常数。

2. 反比例函数的图像有什么特点？答案: 反比例函数的图像是一条双曲线。

当x趋近于无穷大或无穷小时，函数的值趋近于零。

两支曲线的对称轴为y轴，并在y 轴上有一个渐近线。

3. 如何确定反比例函数的常数k的值？答案: 可以通过已知点的坐标进行求解。

将已知的x和y的值代入反比例函数的一般形式中，解方程得到k的值。

以上就是反比例函数单元测试卷的答案。

希望能对你的学习有所帮助！。

第17章反比例函数单元测试题(含答案)

第17章《反比例函数》单元测试题（满分１００分，时间４０分钟）班级： __________ 姓名：__________学号: __________一、选择题（每题4分，共２4分）1.下列函数中, y 是x 的反比例函数的是（）A 、21x y =B 、52+=x yC 、xy=8D 、53+=x y2. 已知反比例函数)0(≠=k xky 上有一个点（－４，－２），则点（）在此函数图象上。

A 、Ａ（３,４）B 、Ｂ(2，４)C 、Ｃ（－４，２）D 、Ｄ（４，－２）３. 若反比例函数y =xk 3-的图像在每一个象限内，y 随x 的增大而增大，则有（） A 、 k 0≠ B 、k 3≠ C 、k<3 D 、k>3４.设A( 1x ，1y ) B (2x ，2y )是反比例函数xy 5= 图像上的两点，若1x <2x <0 则1y 与 2y之间的关系是（）。

A 、1y <2y <0B 、2y <1y <0C 、1y >2y >0D 、2y >1y >0 ５.一次函数y=kx —1 与反比例函数)0(≠=k xky 的图像的形状大致是（）A B C D6.如图2，双曲线上两点Ａ、Ｂ,ＡＰ垂直ｘ轴，垂足为Ｐ，ＢＤ垂直于x 轴，垂足为Ｄ。

连接ＯＡ、ＯＢ,设△AOP 的面积为S 1，△BOD 面积为S 2，则S 1与S 2的大小关系是（）。

A 、S 1=S 2B 、S 1<S 2C 、S 1>S 2D 、无法确定二、填空题（每题4分，共24分） 7.已知反比例函数y=xk的图像经过点（3 ，—2）则此函数的解析式为____________，当x>0时 y 随x 的增大而____________。

8.写出一个具有性质“在每个象限内y 随x 的增大而减小”的反比例函数的表达式为___________。

9. 某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 .（写出自变量的取值范围）x10．直线b x y +-=5与双曲线xy 2-= 相交于点p (—2 ，m ) ，则 b=____________。

八年级数学第十七章反比例函数单元测试题(含答案)

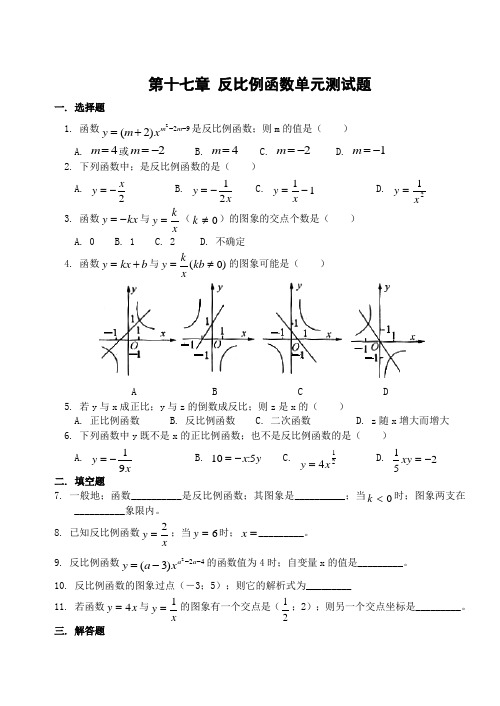
第十七章反比例函数单元测试题一. 选择题1. 函数y m x m m =+--()2229是反比例函数；则m 的值是（） A. m =4或m =-2 B. m =4 C. m =-2 D. m =-12. 下列函数中；是反比例函数的是（） A. y x =-2B. y x =-12 C. y x=-11D. y x =123. 函数y kx =-与y k x=（k ≠0）的图象的交点个数是（） A. 0 B. 1 C. 2 D. 不确定 4. 函数y kx b =+与y kxkb =≠()0的图象可能是（）A B C D5. 若y 与x 成正比；y 与z 的倒数成反比；则z 是x 的（）A. 正比例函数B. 反比例函数C. 二次函数D. z 随x 增大而增大 6. 下列函数中y 既不是x 的正比例函数；也不是反比例函数的是（） A. y x=-19B. 105=-x y :C.y x=412D.152xy =- 二. 填空题7. 一般地；函数__________是反比例函数；其图象是__________；当k <0时；图象两支在__________象限内。

8. 已知反比例函数y x=2；当y =6时；x =_________。

9. 反比例函数y a x a a =---()3224的函数值为4时；自变量x 的值是_________。

10. 反比例函数的图象过点（－3；5）；则它的解析式为_________ 11. 若函数y x =4与y x =1的图象有一个交点是（12；2）；则另一个交点坐标是_________。

三. 解答题12. 直线y kx b =+过x 轴上的点A （32；0）；且与双曲线y kx=相交于B 、C 两点；已知B点坐标为（-12；4）；求直线和双曲线的解析式。

13. 已知一次函数y x =+2与反比例函数y k x=的图象的一个交点为P （a ；b ）；且P 到原点的距离是10；求a 、b 的值及反比例函数的解析式。

八年级下册数学第十七章反比例函数单元测试一(附答案)s

八年级下册数学第十七章反比例函数单元测试一（附答案）学校:___________姓名：___________班级：___________考号：___________一、选择题1．矩形ABCD 中，8cm 6cm AD AB ==，．动点E 从点C 开始沿边CB 向点B 以2cm/s 的速度运动，动点F 从点C 同时出发沿边CD 向点D 以1cm/s 的速度运动至点D 停止．如图可得到矩形CFHE ，设运动时间为x （单位：s ），此时矩形ABCD 去掉矩形CFHE 后剩余部分的面积为y(单位：2cm )，则y 与x 之间的函数关系用图象表示大致是下图中的( )2．对反比例函数4y x=，下列说法不正确．．．的是（） A.它的图像在第一、三象限 B.点（-1，-4）在它的图像上C.当x ＜0时，y 随x 的增大而减小D.当x ＞0时，y 随x 的增大而增大3．（2011•福州）如图是我们学过的反比例函数图象，它的函数解析式可能是（）A 、2y x =B 、4y x =C 、3y x=-D 、12y x =4．（）A ．图象经过点（1，-1）B ．图象位于第二、四象限C ．图象是中心对称图形D ．当x ＜0时，y 随x 的增大而增大 5．一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝满足（） A 、当x ＞0时，y ＞0 B 、在每个象限内，y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限Oy (cm 2)x (s)48 16 4 6 A ．Oy (cm 2)x (s)48 16 4 6B ．Oy (cm 2)x (s)48 16 4 6C ．Oy (cm 2)x (s)48 16 46 D ．AD F CE H B6．给出下列命题：①反比例函数x y 2=的图象经过一、三象限，且y 随x 的增大而减小；②对角线相等且有一个内角是直角的四边形是矩形；③我国古代三国时期的数学家赵爽，创制了一幅“勾股圆方图”，用形数结合得到方法，给出了勾股定理的详细证明（右图）；④相等的弧所对的圆周角相等.其中正确的是（）（A ）③④ （B ）①②③ （C ）②④ （D ）①②③④7．已知点（-1，1y ），（2，2y ），（3，3y ）在反比例函数xk y 12--=的图像上. 下列结论中正确的是（）A ．321y y y >>B ．231y y y >>C ．213y y y >>D ． 132y y y >> 8．在反比例函数y=2x的图象上的一个点的坐标是（） A ．（2，1） B ．（-2，1） C ．（2，12） D ．（12，2） 9．已知反比例函数xm y 5-=的图象在第二、四象限，则m 的取值范围是 A. 5≥m B. 5>m C. 5≤m D. 5<m10．下列各点中，在函数y=－x3的图象上的是A ．（3，1）B ．（－3，1）C ．（31，3） D ．（3，－31）二、填空题11．已知2y -与x 成反比例，当2x =时，4y =，则当3y =时，x = .12．在直角坐标系中，□OCBA 的边OC 在x 轴的正半轴上，点O 为坐标原点，点B 的坐标为（10，4），点M 为对角线AC 、OB 的交点，反比例函数的图象经过点M ，则该反比例函数的解析式为__ _．13．14．如图，直线y ＝kx(k ＞0)与双曲线xy 4=交于A （x 1，y 1），B （x 2，y 2）两点，则2x 1y 2－7x 2y 1＝___________．15．已知反比例函数xky =（0≠k ）的图像经过点A （－3，2），那么k = ． 16．在同一平面直角坐标系中，若一个反比例函数的图象与一次函数=-2+6y x 的图象无．公共点，则这个反比例函数的表达式是（只写出符合条件的一个即可）．三、计算题17．（本题满分8分）如图所示，反比例函数y ＝x4的图象与一次函数y ＝kx －3的图象在第一象限内相交于点A (4，m)．（1）求m 的值及一次函数的解析式；（2）若直线x ＝2与反比例和一次函数的图象分别交于点B 、C ，求线段BC 的长．18．如图，过y 轴上点A 的一次函数与反比例函数相交于B 、D 两点，B （﹣2，3），BC ⊥x 轴于C ，四边形OABC 面积为4．（1）求反比例函数和一次函数的解析式；（2）求点D 的坐标；（3）当x 在什么取值范围内，一次函数的值大于反比例函数的值．（直接写出结果）四、解答题19．（2011内蒙古赤峰，20，10分）如图，点D 在双曲线上，AD 垂直x 轴，垂足为A ，点C 在AD 上，CB 平行于x 轴交双曲线于点B ，直线AB 与y 轴交于点F ，已知AC ： AD=1：3，点C 的坐标为（2，2）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第17章《反比例函数》单元测试题
一、填空题（每题3分共30分） 1.已知反比例函数y=
x
k
的图像经过点（3 ，—2）则此函数的解析式为____________ 当x>0时 y 随x 的增大而____________
2.写出一个具有性质“在每个象限内y 随x 的增大而减小”的反比例函数的表达式为_______
3.反比例函数4
22
)1(---=m m
x m y 当x <0时 y 随x 的增大而增大则 m 的值是________
4.已知正比例函数y=ax 和反比例函数x
b
y = 在同一坐标系中两图像无交点，则 a 和 b 的关系式是___________
5.在函数x a y 12--= （a 为常数）的图像上三点（—1 ，1y ），（4
1- 2y ），（21
3y ）
则函数值1y 、2y 、3y 的大小关系是__________________.
6.若一个三角形的面积是82cm 则其底边长y(cm) 与这边上的高x(cm)之间的关系是__________
7.直线b x y +-=5与双曲线x
y 2
-= 相交于点p (—2 ，m ) 则 b=____________ 8.已知反比例函数)0(≠=
k x
k
y ，当x>0 时，y 随x 增大而增大，那么一次函数 y=kx —k 的图像经过_______________象限。

9.有一面积为120的梯形，其上底是下底长的
3
2
，若上底长为x ，高为y ，则y 与x 的函数关系式为____________ ；当高为10时x=___________. 10.反比例函数x
y 6
=
的图像上，横坐标和纵坐标都是整数的点的个数是_____________ 二、选择题（每题3分共30分）
11.下列函数中 y 是x 的反比例函数的是（）
A 、2
1x y =
B 、xy=8
C 、52+=x y
D 、53+=x y
12.当x>0时，四个函数 y= —x ，y=2x+1，x y 1-=，x
y 2
= ，其中y 随x 的增大而增大的函数
有（）
A 、1 个
B 、2 个
C 、3 个
D 、4个 13.设A( 1x 1y ) B (2x 2y )是反比例函数x
y 2
-
= 图像上的两点若1x <2x <0 则1y 与 2y 之间的关系是（）
A 、1y <2y <0
B 、2y <1y <0
C 、2y >1y >0
D 、1y >2y >0
14.一次函数y=kx —1 与反比例函数)0(≠=
k x
k
y 的图像的形状大致是（）
A B C D 15.已知一次函数y=kx+b 的图像经过第一二四象限则反比例函数x
kb
y =
的图像在（） A 、第一二象限 B 、第三四象限 C 、第一三象限 D 、第二四象限 16.如果点P 为反比例函数x
y 6
=
的图像上的一点， PQ 垂直于x 轴，垂足为Q ，那么po ∆Q 的面积为（）
A 、12
B 、6
C 、3
D 、1.5 17.已知函数2
2-=m mx
y 是反比例函数且图像的两个分支在第二，四象限则m 的值是（）
A 、1
B 、—1
C 、1±
D 、不能确定 18.反比例函数x
k
y =与直线y= -2x 相交与点A ， A 点的横坐标为 -1，则此反比例函数的解析式为（）
A 、x y 2=
B 、x y 21=
C 、x y 2-=
D 、x
y 21-=
19.若反比例函数y =x
k 3
-的图像在每一个象限内，y 随x 的增大而增大，则有（）
A 、 K 0≠
B 、K 3≠
C 、K<3
D 、K>3
20.已知XF 所做的功是15焦，则XF 与物体在力的方向上通过的距离S 的图像大致是下图中的（）
A B C D 三、解答题（共40分）
21.（本小题5分）已知y 是x 的反比例函数，当x ＝2时，y ＝6. ⑴写出y 与x 的函数关系式； ⑵求当x ＝4时，y 的值.
S
F
S
F
F
F
S
S
x
y
o C
A B
2 4 -4 -2 x
y
A B
O 22.（本小题6分）已知21y y y +=，若1y 与2x 成正比例关系，2y 与
2
31
+x 成反比例关系，且
当X=-1时，ｙ＝３．由ｘ＝１时，ｙ＝－３时，求ｙ与ｘ的函数关系式？
23.（本小题6分）如图所示：已知直线ｙ＝
x 21 与双曲线ｙ＝)0(>k x
k
交于Ａ、Ｂ两点，且点Ａ的横坐标为４。

⑴求ｋ的值；⑵ 若双曲线ｙ＝)0(>k x
k
上的一点C 的纵坐标为8，求△AOC 的面积？
24.（本小题7分）已知反比例函数y=
x
m
的图像经过点A （1 ，—3），一次函数y=kx+b 的图像经过点A 与点C (0 ，—4)，且与反比例函数的图像相交于另一点B 。

⑴ 试确定这两个函数的表达式？⑵ 求点B 的坐标？
分钟）
25.（本小题8分）如图，反比例函数y ＝
x
k
的图象与一次函数y ＝mx ＋b 的图象交于A （1，3），B （n ，－1）两点.
⑴ 求反比例函数与一次函数的解析式；
⑵ 根据图象回答：当x 取何值时，反比例函数的值大于一次函数的值.
26.（本小题8分）为了预防流感，某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放
过程中，室内每立方米空气中含药量y （毫克）与时间x （分钟）成正比例；药物释放完毕后，y 与x 成反比例，如图所示.根据图中提供的信息，解答下列问题：
⑴ 写出从药物释放开始，y 与x 之间的两个函数关系式及相应的自变量取值范围；
⑵ 据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么
从药物释放开始，至少需要经过多少小时后，学生才能进入教室？
参考答案
一、填空题
1. y= —
x 6 增大 2. y=x
3
(答案不唯一) 3. —1 4. 异号 5. 3y <1y <2y 6 y=x
16
7. —9 8.一二四
9 ｙ＝x
96
９.６１０．８个
二、选择题
1１Ｂ 1２B 1３Ｃ 1４Ｃ 1５Ｄ 1６Ｃ 1７Ｂ 1８Ｃ 1９Ｃ 2０Ｂ三、解答题 21.⑴ y ＝
，⑵.3；
22． 2322
--=x x y 23.⑴ k=8 ⑵15=∆COA s 24. ⑴x
y 3
-= ，4-=x y ⑵（3 —1） 25.⑴x
y 3
=
，y ＝x ＋2 ， ⑵从图像可知：当x ＜－3或0＜x ＜1时，反比例函数的值大于一次函数的值； 26.（1）当0≤x ≤12时，x y 43=
；当x ≥12时，x y 108
=。

（2）当y ＝0.45时，代入x
y 108
=中，得x ＝240（分钟）＝4（小时）
则从药物释放开始，至少需要经过4小时后，学生才能进入教室.。