五年级数学图形复习
五年级数学上册,图形与几何,整理和复习

例1、下面是某城市部分路线示意图。
(1)火车站的位置用(1,1)表示,请用数对表示出下面的位置:商业城(),游戏城()。
(2)儿童公园的位置用(3,5)表示,请在图上标出儿童公园的位置。
分析与解答:用数对表示物体位置时,要先表示列数,再表示行数,由于商业城在第4列和第1行的交点上,所以商业城的位置用对可以表示为(4,1),而游戏城在第6列和第2行的交点上,故游戏城用数对可以表示为(6,2);根据数对确定物体的位置时,看数对的两个数字表示的是哪一列,哪一行,列和行的交点处就是物体的位置,由于儿童公园的位置用数对表示为(3,5),说明它的位置在第3列和第5行的交点处,在该点标出儿童公园的位置(如图)。
方法二:可以把这个图形按图二的方法分成一个梯形和一个长方形,这个梯形的上底是4㎝,下底是8㎝,高是10-5=5(㎝),它的面积是(4+8)×5÷2=30(㎝²);这个长方形的长是5㎝,宽是4㎝,它的面积是5×4=20(㎝²),所以这个图形的面积是30+20=50(㎝²)。
方法三:也可以像图三那样把这个图形分成一个三角形和一个直角梯形,这个三角形的底是8㎝,高是10-5=5(㎝),它的面积是8×5÷2=20(㎝²),这个直角梯形的上底是5㎝,下底是10㎝,高是4㎝,它的面积是(5+10)×4÷2=30(㎝²),所以这个图形的面积是20+30=50(㎝²)。
方法四:还可以把这个图形按图四的方法分成两个三角形,一个三角形的底是5㎝,高是4㎝,它的面积是5×4÷2=10(㎝²),另一个三角形的底是10㎝,高是8㎝,它的面积是10×8÷2=40(㎝²),所以这个图形的面积是10+40=50(㎝²)。
方法五:还可以按图五的方法把这个图形补成长方形,从图上可以看到,这个图形的面积等于长方形面积减去梯形面积,长方形的长是10㎝,宽是8㎝,它的面积是10×8=80(㎝²),梯形的上底是5㎝,下底是10㎝,高是8-4=4(㎝),它的面积是(5+10)×4÷2=30(㎝²),所以这个图形的面积是80-30=50(㎝²)。
五年级上册数学教案- 总复习 图形与几何-北师大版

五年级上册数学教案-总复习图形与几何-北师大版教学目标:1. 让学生掌握图形与几何的基本知识和技能。
2. 培养学生运用图形与几何知识解决问题的能力。
3. 培养学生的空间想象力和创新意识。
教学内容:1. 点、线、面、体的基本概念和性质。
2. 平面图形的分类和性质。
3. 立体图形的分类和性质。
4. 图形的变换。
教学重点:1. 点、线、面、体的基本概念和性质。
2. 平面图形的分类和性质。
3. 立体图形的分类和性质。
教学难点:1. 点、线、面、体的基本概念和性质。
2. 平面图形的分类和性质。
3. 立体图形的分类和性质。
教学准备:1. 教学课件或黑板。
2. 教学素材或教具。
教学过程:一、导入1. 引导学生回顾图形与几何的基本概念和性质。
2. 提问学生:什么是点、线、面、体?它们有什么性质?二、新课导入1. 讲解平面图形的分类和性质。
2. 讲解立体图形的分类和性质。
3. 讲解图形的变换。
三、课堂练习1. 让学生完成课堂练习题。
2. 对学生的答案进行讲解和评价。
四、课堂小结1. 让学生回顾本节课所学内容。
2. 提问学生:什么是平面图形?什么是立体图形?它们有什么性质?五、作业布置1. 布置课后作业:完成课后练习题。
2. 提醒学生:下节课我们将学习图形与几何的应用。
教学反思:本节课是五年级上册数学教案-总复习图形与几何的教学内容。
通过本节课的教学,学生应该掌握图形与几何的基本知识和技能,能够运用图形与几何知识解决问题。
在教学过程中,要注意引导学生积极参与课堂讨论和练习,培养学生的空间想象力和创新意识。
同时,要注意关注学生的学习情况,及时解答学生的疑问,提高教学效果。
人教版五年级数学上册期末总复习《图形与几何》(附答案)

人教版五年级数学上册
期末总复习《图形与几何》(附答案)
一、填空。
1.平行四边形的面积是20 m2,如果底和高都扩大2倍,它的面积是()m2。
2.右图的平行四边形面积是15cm2,阴影部分面积是()cm2。
3.小明坐在第3行第5列的位置,用数对表示是()。
二、判断。
1.(5,7)点右移3格后的位置用数对表示是(2,7)。
()
2.梯形的上、下底各扩大2倍,面积扩大4倍。
()
3.底和高分别相等的两个三角形面积相等。
()
三、计算下面图形的面积。
(单位:cm)
四、生活中的数学。
1.一个平行四边形的荔枝园,量得底是240米,高40米。
如果每4平方米种一棵荔枝树,这个荔枝园共可种荔枝多少棵?
2.一间房子的侧面如下图,如果每平方米用砖190块,砌这堵墙大约需要多少块砖?
五、求下图阴影部分的面积。
(单位:dm)
参考答案
一、1.80 2.7.5 3.5,3
二、1.× 2.× 3.√
三、1500(cm2)300(cm2)
四、1.240×40÷4=2400(棵)答:荔枝园共可种荔枝2400棵。
2.(8×1.5÷2+
3.2×8)×190=(6+25.6)×190=31.6×190=6004(块)答:砌这堵墙大约需要6004块砖。
五、4×7-4×(7-5)÷2=24(dm2)
答:阴影部分的面积是24 dm2。
【精选】苏教版五年级下册数学期末复习《图形与几何、统计与概率》专项练习(含答案)

【精选】苏教版五年级下册数学期末复习《图形与几何、统计与概率》专项练习(含答案)一、做一做。
(第5题3分,第7题5分,其余每空1分,共24分)1.当圆规两脚之间的距离是6厘米时,画出的圆的直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
2.有大、小两个圆,大圆的直径是小圆半径的4倍,则大圆半径是小圆半径的( ),大圆周长是小圆周长的( ),大圆面积是小圆面积的( )。
3.将一张半径是2cm的圆形纸片,连续对折三次,得到的图形的圆心角是( )度,周长是( )cm。
4.某5A级景区2022年接待游客情况如图。
根据下面的统计图回答问题。
(1)4月份接待游客( )万人,6月份接待游客( )万人。
(2)( )月份接待的游客人数最多,( )月份接待的游客人数最少。
(3)8月份接待的游客人数是10月份接待游客人数的( )。
5.如图是由5个半径是2厘米的圆组成的图形,连接这些圆的圆心形成了一个正五边形。
(1)这个图形有( )条对称轴,在图上画一画。
(2)这个五边形的周长是( )厘米。
6.人民公园有一个圆形水池,池边每隔4米栽一棵树,一共栽了314棵树,这个水池的直径是( )米,占地面积是( )公顷。
7.测量右图中的有关数据,并求出图中圆的面积。
(1)需要测量出( )的长度,从而得出圆的直径是( )厘米。
(2)圆的半径是( )厘米。
(3)要求圆的面积,可列式计算为:_________________8.如图,一个半径为2厘米的圆在一个长16厘米、宽12厘米的长方形内滚动一周后(无滑动),又回到了原来的位置,这个圆的圆心共移动了( )厘米。
二、选择。
(将正确答案的字母填在括号里)(每小题2分,共12分)1.下面不适合制作成折线统计图的是( )。
A.某地每天的气温变化情况B.轩轩家每月的用电量的变化情况C.某校各年级的男、女生人数D.某校历年一年级新生入学人数变化情况2.圆的直径是正方形的对角线,则正方形的面积( )圆的面积。
沪教五年级下册数学课件6.5 总复习:图形与几何(平面图形的认识) (共9张)

从“角”的角度整理
从“角”的角度整理
三角形分类
锐角三角形
直角三角形
钝角三角形
从“边”的角度整理
3cm
4cm
3cm
4cm
3cm
6cm
任选三根小棒可以围成什么样的三角形,想好后和同桌交流一下。
3
3
3 等边三角形
3
4 3
4
4
4
3
等腰三角形
4 6
3
46 Βιβλιοθήκη 般三角形整合“三角形”的关系
3
3
3 等边三角形
(锐角三角形)
3
4 3
4
4
4
4
3
6
等腰三角形
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
自主整理“四边形”
小组合作:
1.它们各有什么特征?(先填表) 2.请思考、讨论如下问题?
⑴ 梯形和平行四边形最大的区别是什么? ⑵ 为什么说正方形和长方形是特殊的平行四边形? ⑶ 为什么说正方形是特殊的长方形? 3.画一画它们的关系图?
简单整理“圆”
自由交流:
1.圆和以上图形最大的区别是什么? 2.圆能分类吗? 3.圆有什么特征?
半径定大小 圆心定位置
趣味拼图
敬请指导!
都二
能分
运浇
用灌
好,
“八
二分
八等
定待
律;
”二
,分
我管
们教
一,
起八
,分
静放
待手
花;
开二
。分
成
➢ Pure of heart, life is full of sweet and joy!
人教版五年级下册数学图形与几何领域解决问题部分总复习(一)(课件)

22÷4 ≈ 5(个)
10÷4 ≈ 2(个)
10÷5= 2(个)
5÷2.5=2(个)
5÷2.5=2(个)
4×2×2=16 (个) 5×2×2=20(个)
16<20 答:最多可以放20个这样的盒子。
丝带打结处 长32厘米。
5cm
22cm
10cm
至少需要多长的丝带?
22×2+10×2+5×4+32 =44+20+20 +32
一般都是长方形(也可
面 能有一组相对的面是正 都是面积相等的
方形),相对的完全相 正方形。
同。
棱
有12条棱 相对的一组棱长度相等。 长度都相等。
顶点
有8个顶点
正方体可以看成是长、宽、高都相等的长方体。我们 可以用下图来表示长方体和正方体的关系。
长方体 正方体
名称 图形及条件
表面积
体积
长方体 正方体
2.每日计算题:
=116(cm)
答:至少需要116厘米长的丝带。
20cm
32cm
20cm
32cm
8cm
32cm 5cm
20cm
32cm
20cm
11cm
5cm 11cm
5cm
7cm 1cm
6cm 2cm
5cm
3cm
4cm
4cm
7×1=7(cm2 ) 6×2=12(cm2 ) 5×3=15(cm2 )
4×4=16(cm2 )
图形与几何领域解决问题部分 总复习(一)
五年级下册
长方体和正方体的认识
长方体的认识 正方体的认识
长 方
长方体和正方体的表面积
表面积的含义
体
表面积计算
小学数学五年级下册总复习全部

小红家的客厅长四八分米,宽三 二分米.现在给客厅的地面铺正方 形地砖,有三种砖,你帮小红家想一 想,选择哪种地砖能铺得即整齐又 不会有余料?
边长三分米
边长六分米
边长八分米
分析:求出四八和三二的公因数,这个公因数是
地砖的边长.
复习长方体和正方体
一、建构知识网络
第一课时
长方形 正方形
等边三角形 按边分 等腰三角形
[二]简单图形旋转九0°的画法
一.找出图形的关键点或线段. 二.借助三角板[或量角器]作原图形线段或关键点与旋转中心所在线段的垂线. 三.在所做垂线上量出与原线段相等的长度[即找出原图关键点的对应点]. 四.顺次连接所画出的对应点.
[一]画出图一的全部对称轴. [二]画出图二向上平移三格后的图形.
七、一九
偶数
二
四、六、八、一0、
一二、一四、一六、
二.出示判断题:
[一]自然数中,除了奇数就是偶数.[ ]
[二]所有的奇数都是质数.
[]
[三]所有的合数都是偶数.
[]
[四]自然数中,除了质数就是合数.[ ]
[五]质数与质数的积还是质数. [ ]
[六]一个数越大,它的因数的个数就越多.
[]
注意:奇数里既有质数也有合数还有一. 质数里除了二以外都是奇数. 偶数里除了二以外全是合数.
10
单位:厘米
8 15
后
上
一左
前
右
0●
八
下
一
五 长方体六个面的面积,就是长方体的表面积.
二.正方体表面积的含义 [一]正方体棱长与每个面边长的关系
后 上 左前右 下
正方体展开图的每个面都是正方形, 边长就是正方体的棱长,每个面的面 积都等于棱长乘棱长。
图形复习五年级数学

直线型面积计算(1)对于三角形的面积计算,我们除了熟练运用基本的计算公式,在技巧性很强的奥数题中还要根据相应的性质和结论来解题,下面就是我们小学奥数常用的三条性质:【例 1】 如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.E BA E BA【分析】 本题是等底等高的两个三角形面积相等的应用.连接BH 、CH . ∵AE EB =, ∴S S AEH BEH = .同理,S S BFH CFH = ,S =S CGH DGH ,∴11S S 562822==⨯=阴影长方形ABCD (平方厘米).[铺垫]你有多少种方法将任意一个三角形分成:⑴2个面积相等的三角形; ⑵3个面积相等的三角形; ⑶4个面积相等的三角形.[分析] ⑴如右图,D 、E 、F 分别是对应边上的中点,这样就将三角形分成了2个面积相等的三角形;CBAEA B CFCB A⑵如右图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点;答案不唯一;①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如BCD ACD S S ∆∆=; 反之,如果BCD ACD S S ∆∆=,则可知直线AB 平行于CD .DC BAED A BC FC BADGDA BC⑶如下图,答案不唯一,以下仅供参考.(5)(4)(3)(2)(1)【例 2】 如图,三角形ABC 的面积为1,其中3AE AB =,2BD BC =,三角形BDE 的面积是多少?EDCB AEDC B A【分析】 连接CE .∵3AE AB =,∴2BE AB =,2BCE ACB S S ∆∆=.又∵2BD BC =,∴244BDE BCE ABC S S S ∆∆∆===.【例 3】 如图,三角形ABC 中,2DC BD =,3CE AE =,三角形ADE 的面积是20平方厘米,三角形ABC 的面积是多少?ECBA 【分析】 ∵3CE AE =,∴4AC AE =,4ADC ADE S S ∆∆=;又∵2DC BD =,∴32BC DC =,361202ABC ADC ADE S S S ∆∆∆===(平方厘米).[铺垫]如图,三角形ABC 被分成了甲、乙两部分,4BD DC ==,3BE =,6AE =,甲部分面积是乙部分面积的几分之几?乙甲E CBAABCDE[分析] 连接AD .∵3BE =,6AE =,∴13BE AB =,13BDE ABD S S ∆∆=.又∵4BD DC ==,∴12ABD ABC S S ∆∆=,∴1136BDE ABD ABC S S S ∆∆∆==,∴15S S =乙甲.[拓展]如图,在三角形ABC 中,8BC =厘米,6AD =厘米,E 、F 分别为AB 和AC 的中点,那么三角形EBF 的面积是多少平方厘米?FE CAFE CA[分析] ∵F 是AC 的中点,∴12ABF ABC S S ∆∆=,同理12BEF ABF S S ∆∆=,∴111866442BEF ABC S S ∆∆==⨯⨯⨯=(平方厘米).【例 4】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.F EDCB A AB CDEF【分析】 本题是性质的反复使用(还可以用燕尾定理,但本讲不用这种方法,燕尾定理我们会放到五年级春季再讲).连接AE 、CD . ∵S 1S 1S 1ABC ABC DBC == ,, ∴S 1DBC = .同理可得其它,最后三角形DEF 的面积18=.[拓展]如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH[分析] 连接BD .设1DCB S S = ,2DAB S S =∵CB BF =,∴2CDF CDB CDB CB BFS S S CB∆∆∆+==,又∵DC CG =,∴12CFG CDF S S S ∆∆==, 同理22AEH S S ∆=, ∴2CFG AEH ABCD S S S ∆∆+=连接AC ,同理2HDG BEF ABCD S S S ∆∆+=∴5EFGH CFG AEH HDG BEF ABCD ABCD S S S S S S S ∆∆∆∆=++++=,111355ABCD EFGH S S ==(平方米).[拓展]如图,已知长方形ADEF 的面积16,三角形ADB 的面积是3,三角形ACF 的面积是4,那么三角形ABC 的面积是多少?F CA F CA[分析] 连接对角线AE . ∵ADEF 是长方形∴12ADE AEF ADEF S S S ∆∆==∴38ADB ADE S DB DE S ∆∆==, 12ACF AEF S FC EF S ∆∆== ∴58BE DE DB DE DE -==,12CE FE CF EF EF -== ∴1515162822BEC S ∆=⨯⨯⨯=∴132ABC ADEF ADB ACF CBE S S S S S ∆∆∆∆=---= .[拓展]如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF GABCD EF G[分析] 连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEF ABCD ABCD S S S =⨯⨯= 长方形长方形.因为12AED ABCD S S = 长方形,11::5:1210AG GF ==,所以510AGD GDF S S == ,所以12AFD S = .因为16AFD ABCD S S = 长方形,所以长方形ABCD 的面积是72平方厘米.【例 5】 (第八届小数报数学竞赛决赛试题)如下图,E 、F 分别是梯形ABCD 的下底BC 和腰CD 上的点,DF FC =,并且甲、乙、丙3个三角形面积相等.已知梯形ABCD 的面积是32平方厘米.求图中阴影部分的面积.BC【分析】 因为乙、丙两个三角形面积相等,底DF FC =.所以A 到CD 的距离与E 到CD 的距离相等,即AE 与CD 平行,四边形ADCE 是平行四边形,阴影部分的面积=平行四边形ADCE 的面积的12,所以阴影部分的面积=乙的面积2⨯.从而阴影部分的面积23212.85=⨯=(平方厘米).[拓展]如图,在平行四边形ABCD 中,BE EC =,2CF FD =.求阴影面积与空白面积的比.B[分析] 因为BE EC =,2CF FD =,所以14ABE ABCD S S =四边形,16ADF ABCD S S = 四边形. 因为2AD BE =,所以2AG GE =,所以11312BGE ABE ABCD S S S == 四边形,2136ABG ABE ABCD S S S == 四边形.同理可得,18ADH ABCD S S = 四边形,124DHF ABCD S S = 四边形.因为12B C D A B C D S S = 四边形,所以空白部分的面积111112()21224683ABCD ABCD S S =--++=四边形四边形,所以阴影部分的面积是13A B C D S 四边形.12:1:233=,所以阴影面积与空白面积的比是1:2.【例 6】 如图所示,四边形ABCD 与AEGF 都是平行四边形,请你证明它们的面积相等.GFEB AGFEB A【分析】 本题主要是让学生了解并会运用等底等高的两个平行四边形面积相等和三角形面积等于与它等底等高的平行四边形面积的一半.证明:连接BE .(我们通过ABE 把这两个看似无关的平行四边形联系在一起.)∵在平行四边形ABCD 中,12ABE S AB AB =⨯⨯ 边上的高,∴1S S 2ABG ABCD = (也就是等积变换的重要依据③的特殊情况).同理,1S S 2ABE AEGF = ,∴平行四边形ABCD 与AEGF 面积相等.[拓展]如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?A BGC E F DABGCEF D[分析] 本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半.证明:连接AG .(我们通过ABG 把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G 12AB S AB AB =⨯⨯ 边上的高,∴1S S 2ABG ABCD = (三角形面积等于与它等底等高的平行四边形面积的一半)同理,1S S 2ABG EFGB = .∴正方形ABCD 与长方形EFGB 面积相等. 长方形的宽8810 6.4=⨯÷=(厘米).【例 7】 如图,正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,求图中三角形BFD 的面积为多少平方厘米?HGFED C BAHG FED C BA【分析】 连接CF .∵BD ,CF 都是正方形的对角线∴45DBC FCE ∠=∠=︒,BD ∥CF .∴BFD ∆与BCD ∆同底等高,11010502BFD BCD S S ∆∆==⨯⨯=(平方厘米) .【例 8】 (03年西城某重点中学小升初分班考题)右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC的面积.AA【分析】 这道题似乎缺少大正方形的边长这个条件,实际上本题的结果与大正方形的边长没关系.连接AD (见右上图),可以看出,三角形ABD 与三角形ACD 的底都等于小正方形的边长,高都等于大正方形的边长,所以面积相等.因为三角形AGD 是三角形ABD 与三角形ACD 的公共部分,所以去掉这个公共部分,根据差不变性质,剩下的两个部分,即三角形ABG 与三角形GCD 面积仍然相等.根据等量代换,求三角形ABC 的面积等于求三角形BCD 的面积,等于4428⨯÷=.[拓展](小学数学夏令营五年级组试题)如图,四边形ABCD 和四边形DEFG 都是正方形,已知三角形AFH 的面积为6平方厘米,求三角形CDH 的面积.[分析] 通常求三角形的面积,都是先求它的底和高.题目中没有一条线段的长度是已知的,所以我们只能通过创造等积的方法来求.直接找三角形HDC 与三角形AFH 的关系还很难,而且也没有利用“四边形ABCD 和四边形DEFG 是正方形”这一条件.我们不妨将它们都补上梯形DEFH 这一块.寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系.经过验算,可以知道它们的面积是相等的.从而得到三角形HDC 与三角形AFH 面积相等,也是6平方厘米.【例 9】 如右图,在平行四边形ABCD 中,直线CF 交AB 于E ,交DA 延长线于F ,若1ADE S = ,求BEF 的面积.AB CDEFABCDEF[分析] 本题主要是让学生并会运用等底等高的两个三角形面积相等(或夹在一组平行线之间的三角形面积相等)和等量代换的思想.连接AC .∵AB ∥CD ,∴ADE ACE S S = .同理AD ∥BC ,∴ACF ABF S S = .又ACF ACE AEF S S S =+ ,ABF BEF AEF S S S =+ ,∴ ACE BEF S S = ,即 1BEF ADE S S == .【例10】 (小学数学奥林匹克决赛试题)右图中,ABCD 是74⨯的长方形,DEFG 是102⨯的长方形,求三角形BCO 与三角形EFO 的面积之差.【分析】 直接求出三角形BCO 与三角形EFO 的面积之差,不太容易做到.如果利用差不变性质,将所求面积之差转化为另外两个图形的面积之差,而这两个图形的面积之差容易求出,那么问题就解决了. 法1:连结BE (见右图).三角形BCO 与三角形EFO 都加上三角形BEO ,则原来的问题转化为求三角形BEC 与三角形BEF 的面积之差. 所求为4(107)22(107)23⨯-÷-⨯-÷=. 法2:连结CF (见右图).三角形BCO 与三角形EFO 都加上三角形CFO ,则原来的问题转化为求三角形BCF 与三角形ECF 的面积之差. 所求为4(107)22(107)23⨯-÷-⨯-÷=. 法3:延长BC 交GF 于H (见右图).三角形BCO 与三角形EFO 都加上梯形COFH ,则原来的问题转化为求三角形BHF 与矩形CEFH 的面积之差. 所求为(42)(107)22(107)3+⨯-÷-⨯-=. 法4:延长AB ,FE 交于H (见右图).三角形BCO 与三角形EFO都加上梯形BHEO ,则原来的问题转化为求矩形BHEC 与直角三角形BHF 的面积之差.所求为4(107)(4⨯--+⨯-÷=.【例11】 如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?OA BCDE F GOA B CDE F G O A B C DE FGH O AB CD E FGH OAB CDE FGBE【分析】 三角形ABC 的面积+三角形CDE 的面积(133549)+++=长方形面积+阴影部分面积;又因为三角形ABC 的面积=三角形CDE 的面积12=长方形面积,所以可得:阴影部分面积13354997=++=.1. 如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果24AB =厘米,8BC =厘米,求三角形ZCY 的面积.ABC DZ Y【分析】 ∵Y 是BD 的中点,Z 是DY 的中点,∴1122ZY DB =⨯⨯,14ZCY DCB S S = ,又∵ABCD 是长方形,∴11124442ZCY DCB ABCD S S S ==⨯= (平方厘米).2. 如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?A BCD EA BCDE【分析】 连接BE .∵13AE EC = ∴13ABE ABC S S ∆∆=.又∵15AD AB =∴11515ADE ABE ABC S S S ∆∆∆==,∴1515ABC ADE S S ∆∆==.3. 两个正方形组成右图所示的组合图形.已知组合图形的周长是52厘米,4DG =厘米,求阴影部分的面积.A【分析】 组合图形的周长并不等于两个正方形的周长之和,因为CG 部分重合了.用组合图形的周长减去DG ,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(524)316-÷=(厘米).又由两个正方形的边长之差是4厘米,可求出大正方形边长(164)210=+÷=(厘米),小正方形边长(164)26=-÷=(厘米).阴影部分面积410266238BDG BFG S S =+=⨯÷+⨯÷= (平方厘米).4. 在右图中,平行四边形ABCD 的边BC 长10厘米,直角三角形ECB 的直角边EC 长8厘米.已知阴影部分的总面积比三角形EFG 的面积大10平方厘米,求平行四边形ABCD 的面积.[分析] 因为阴影部分比三角形EFG 的面积大10平方厘米,都加上梯形FGCB 后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边行ABCD 比直角三角形ECB 的面积大10平方厘米,所以平行四边形ABCD 的面积等于10821050⨯÷+=平方厘米.5. 右图中,4CA AB ==厘米,三角形ABE 比三角形CDE 的面积大2平方厘米,求CD 的长.ABCD E【分析】 连结CB .三角形DCB 的面积为44226⨯÷-=平方厘米,6243CD =⨯÷=厘米.直线型面积计算(2)在小学的学习中几何是一个很重要的部分,每一个几何图形都非常美妙,几何图形的美妙不仅来源于它的外形,更重要的是在几何模型上出现的那些美妙的规律,下面我们就一起来看看几个美妙的几何模型:模型一:任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.模型二:梯形中比例关系(“梯形蝴蝶定理”):A BCDOba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.模型三:相似三角形性质:GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形【例 9】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?B【分析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯ ,那么6BGC S = ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=.【例 10】 (2006年南京智力数学冬令营)如下图,梯形ABCD 的AB ∥CD ,对角线AC ,BD 交于O ,已知AOB 与BOC 的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD 【分析】 根据梯形蝴蝶定理,2::25:35AOB BOC S S a ab == ,可得:5:7a b =,再根据梯形蝴蝶定理,2222::5:725:49AOB DOC S S a b === ,所以49DOC S = (平方厘米).那么梯形ABCD 的面积为25353549144+++=(平方厘米).[铺垫]梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA BC D [分析] 根据梯形蝴蝶定理,2::2:3AOB BOC S S ab b == ,可以求出:2:3a b =,再根据梯形蝴蝶定理,2222::2:34:9AOD BOC S S a b === .通过利用已有几何模型,我们轻松解决了这个问题,而没有像以前一样,为了某个条件的缺乏而千辛万苦进行构造假设,所以,请同学们一定要牢记几何模型的结论.【例 11】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABC DOH GA B C D O靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCD S S = ,这可以向模型一蝴蝶定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个“不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题. 解法一:∵::1:3ABD BDC AO OC S S ∆∆==, ∴236OC =⨯=,∴:6:32:1OC OD ==.解法二:作AH BD ⊥于H ,CG BD ⊥于G . ∵13ABD BCD S S ∆∆=,∴13AH CG =,∴13AOD DOC S S ∆∆=,∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.【例 12】 在边长为1的正方形ABCD 中,2BE EC =,2DF FC =.求四边形ABGD 的面积.ABCDE FGABCDE FG【分析】 题目要求四边形ABGD 的面积,可以发现这个四边形是个“不良四边形”,需要对它进行改造.通常在一个四边形中画辅助线,会想到画对角线,又注意到E 、F 都是三等分点,如果连接EF ,因为EF ∥BD ,则可以构造一个梯形,从而应用梯形蝴蝶定理快速求解.因为2BE EC =,2DF FC =,所以:3:1BD EF =.根据梯形蝴蝶定理可以知道,等腰梯形BDFE 四部分面积比为1:3:3:9;而等腰梯形BDFE 的面积为:111141122339⨯⨯-⨯⨯=,所以9113394BDG BDFE S S =⨯=+++ ,得11311244ABGD ADB BDG S S S =+=⨯⨯+= .【例 13】如图,正方形ABCD 面积为1,M 是AD 边上的中点.求图中阴影部分的面积.【分析】 因为M 是AD 边上的中点,所以12AM =,可得34AMCB S =梯形,由于:1:2AM BC =,根据梯形蝴蝶定理可以知道 22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯= ()(),所以阴影部分面积占梯形面积的22412249+=+++,所以341493S =⨯=阴影.【例 14】 如图,在长方形ABCD 中,6AB =,2AD =,AE EF FB ==,求阴影部分的面积.DD【分析】 如图,连接DE ,DE 将阴影部分的面积分为两个部分,其中三角形AED 的面积为26322⨯÷÷=.由于:1:3E F D C =,根据梯形蝴蝶定理,:3:1DEO EFO S S = ,所以34DEO DEF S S = ,而2D E F A D ES S == ,所以32 1.54D E O S =⨯= ,阴影部分的面积为2 1.5 3.5+=.相似三角形性质【例 7】 在图中的正方形中,A ,B ,C 分别是所在边的中点,CDO 的面积是ABO 面积的几倍?A BCD OE FA BCD O【分析】 连接BC ,易知OA ∥EF ,根据相似三角形性质,可知::OB OD AE AD =,且::1:2OA BE DA DE ==,所以CDO 的面积等于CBO 的面积;由1124OA BE AC ==可得3CO OA =,所以3CDO CBO ABO S S S == ,即CDO 的面积是ABO 面积的3倍.【例 8】 如图,线段AB 与BC 垂直,已知4AD EC ==,6BD BE ==,那么图中阴影部分面积是多少?A BCDA BDA BD【分析】 解法一:这个图是个对称图形,且各边长度已经给出,不妨连接这个图形的对称轴看看.作辅助线BO ,则图形关于BO 对称,有ADO CEO S S = ,DBO EBO S S = ,且:4:62:3ADO DBO S S == . 设ADO 的面积为2份,则DBO 的面积为3份,直角三角形ABE 的面积为8份.因为610230ABE S =⨯÷= ,而阴影部分的面积为4份,所以阴影部分的面积为308415÷⨯=.解法二:连接DE 、AC .由于4AD EC ==,6BD BE ==,所以DE ∥AC ,根据相似三角形性质,可知::6:103:5DE AC BD BA ===,根据梯形蝴蝶定理,()()22:::3:35:35:59:15:15:25DOE DOA COE COA S S S S =⨯⨯= ,所以()():1515:915152515:32AD E C S S =++++=阴影梯形,即1532ADECS S =阴影梯形; 又11101066=3222ADEC S =⨯⨯-⨯⨯梯形,所以151532ADEC S S ==阴影梯形.【例 9】 右图中正方形的面积为1, E 、F 分别为AB 、BD 的中点,13GC FC =.求阴影部分的面积.AB EABE【分析】 题中条件给出的都是比例关系,由此可以初步推断阴影部分的面积要通过比例求解,而图中出现最多的就是三角形,那么首先想到的就是利用相似三角形的性质.阴影部分为三角形,已知底边为正方形边长的一半,只要求出高,便可求出面积. 可以作FH 垂直BC 于H ,GI 垂直BC 于I .根据相似三角形性质,::1:3CI CH CG CF ==,又因为CH HB =,所以:1:6CI CB =,即():61:65:6BI BC =-=,所以115522624BGE S =⨯⨯=.【例10】 如图,长方形ABCD 中,E 为AD 的中点,AF 与BE 、BD 分别交于G 、H ,OE 垂直AD 于E ,交AF 于O ,已知5AH cm =,3HF cm =,求AG .ABC DEFGHO【分析】 由于AB ∥DF ,利用相似三角形性质可以得到::5:3AB DF AH HF ==,又因为E 为AD 中点,那么有:1:2OE FD =,所以3:5:10:32AB OE ==,利用相似三角形性质可以得到::10:3AG GO AB OE ==, 而()()1153422AO AF cm ==⨯+=,所以()104041313AG cm =⨯=.【例11】 ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为AB 、BC 的中点,则图中阴影部分的面积为____平方厘米.BB【分析】 注意引导学生利用三角形的中位线定理以及平行线的相关性质.设G 、H 分别为AD 、DC 的中点,连接GH 、EF 、BD .可得1=4AED ABCD S S 平行四边形,对角线BD 被EF 、AC 、GH 平均分成四段,又OM ∥EF ,所以23::2:344DO ED BD BD ==,()()::32:31:3OE ED ED OD ED =-=-=,所以 11117263434AEO ABCD S S =⨯=⨯⨯= 平行四边形(平方厘米),212ADO AEO S S =⨯= (平方厘米).同理可得6CFM S = 平方厘米,12CDM S = 平方厘米. 所以 366624ABC AEO CFM S S S --=--= (平方厘米), 于是,阴影部分的面积为24121248++=(平方厘米).练习5. (第十届华杯赛)如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【分析】 根据蝴蝶定理,ABD AO CBD CO =三角形的面积三角形的面积,所以35AO CO =,又1AO =,所以53CO =.6. 如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.ODC BA 【分析】 根据梯形蝴蝶定理,22::4:9AOB ACOD S S a b == ,所以:2:3a b =,2:::3:2AOD AOB S S ab a b a === ,31.2 1.82AOD COB S S ==⨯= ,1.2 1.8 1.82.77.5ABCD S =+++=梯形.7. 已知三角形ABC 的面积为a ,:2:1AF FC =,E 是BD 的中点,且EF ∥BC ,交CD 于G ,求阴影部分的面积.【分析】 已知:2:1A F F C =,且EF ∥BC ,利用相似三角形性质可知::2:3EF BC AF AC ==,所以23EF BC =,且:4:9A E F ABC S S = . 又因为E 是BD 的中点,所以EG 是三角形DBC 的中位线,那么12EG BC =,12::3:423EG EF ==,所以:1:4GF EF =,可得:1:8CFG AFE S S = ,所以:1:18CFG ABC S S = ,那么18CFG aS = .8. 在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.A BCDEF【分析】 根据相似三角形性质可知::1:2EF AF BE AD ==,所以33ABE BEF S S == (平方厘米),那么412ABCD ABE S S == (平方厘米).。
人教版小学数学五年级数学下册期末阶段专项复习 《图形操作题》(含答案)

人教版小学数学五年级下册期末阶段专项复习——《图形操作题》班级:_________ 姓名:__________1.分别画出下面几何体从正面、上面和左面看到的图形。
2.(1)画出图形A绕点O逆时针旋转90°后的图形B。
(2)画出图形A向右平移6格后的图形C。
3.按照变化规律画出第四个图形。
4.在直线上描点表示下面各数。
3 432581685.观察图形,给风车的叶片写上相应的颜色。
6.画出三角形ABO绕点O顺时针旋转90°后得到的图形。
7.涂色表示下面各分数。
8.画出下面左图中小旗子的轴对称图形,画出右图中的三角形绕点O逆时针旋转90°后的图形。
9.画出三角形绕A点逆时针分别旋转90°和180°后的图形。
10.观察图形,画一画。
11.观察图形,画一画。
12.请你先在下面的方格图中设计一个具有对称美的图形。
13.画图。
把下面的图形绕点O先顺时针旋转90度,再向右平移5格得到的图形。
(每小格均为正方形)14.先画出图形A绕点O按顺时针方向旋转135°得到的图形B,再画出图形B向右平移7格后的图形C。
15.如图是由几个同样的小正方体所组成的几何体从上面看到的图形,小正方形中的数字表示在该位置上的小正方体的个数,在下列方格图中画出从正面和左面看到的图形。
16.以O点为顶点画一个面积是6cm2的三角形(1小格为1cm2),再画出绕O点逆时针旋转90°后的图形。
17.操作。
(1)以虚线m为对称轴作图形A的轴对称图形,得到图形B。
(2)将图形A绕点O逆时针旋转90°,得到图形C。
18.在下面的方格纸上画出面积是16平方米的长方形和正方形,并把正方形的34涂上阴影。
19.根据下列分数涂上你喜欢的颜色。
3 4121320.画一画。
(1)画出三角形AOB向左平移4格后的图形。
(2)画出三角形AOB绕点O逆时针旋转90°后的图形。
21.用直线上的点表示出12和54。
新人教版五年级数学上册期末总复习——图形与几何

(3)10×4+8×(10-5)×(8-4)÷2
=40+10 =50(平方厘米)
8厘米
5厘米
10厘米
4厘米
组合图形的面积: 把求组合图形的面积转化成求几个简单图形面积的和或差。 例题2.计算下面图形的面积,你能想出几种方法?
(4)8×10÷2+5×4÷2 =40+10 =50(平方厘米)
8厘米
5厘米
考点真题训练: 1.下面方格图中不规则图形的面积大约是( B )cm2。(每个小正方形的面积看
作1cm2) A.26 B.39
C.80 D.100
2.右图中每个小方格的边长表示1cm,不规则图形的面积最接近
( C )平方厘米。 A.28 B.38 C.48 D.58
一定相等;三角形DEC与三角形( AEB )的面积一定相等。
A
D
E
B
C
7.下图是某公园一块近似平行四边形的空地,面积是4800平方米,计划沿着 与80米长的底边垂直的方向修一条宽2米的小路,其余的地方铺上草坪。
(1)计划修的小路长多少米? 4800÷80=60(米) 答:计划修的小路长60米。
小路 80m
新人教版五年级数学上册
期末总复习 二 图形与几何
考点一 数对 用数对表示物体的位置时,要先写该物体所在位置对应的列数,再写出该物 体所在位置对应的行数,中间用逗号隔开。 (列,行)
根据数对确定物体的位置时,看数对的两个数表示的是哪一列,哪一行,列 和行的交叉处就是物体的位置。
例题.下面是某城市部分路段示意图。
6cm 6cm
(6+10.5)×6÷2 =16.5×3 =49.5(平方厘米)
3.一张平行四边形的纸,量得相邻两条边的长度分别是2分米和1.5分米,其中 一条边上的高是1.6分米,这张平行四边形纸的面积是( 2.4)平方分米。
小学五年级数学图形的变换整理和复习

图形的变换整理和复习五年级数学教案第一单元图形的变换单元分析:本单元教材注意利用学生已有知识引导学生探索新知识,加强了直观教学图形的特征,并设计了大量的活动,帮助学生理解图形的性质和变换,发展空间观念。
单元教学目标:1、进一步认识图形的轴对称,探索图形成轴对称的特征和性质,能在方格纸上画出一个图形的轴对称图形;2、进一步认识图形的旋转,探索旋转的特征和性质,能在方格纸上把简单图形旋转 90 度。
3、初步学会运用对称、平移和旋转的方法在方格纸上设计图案,进一步增强空间观念。
4、在上述活动中,欣赏图形变换所创造出的美,进一步感受对称、平移和旋转在生活中的应用,体会数学的价值。
单元教学重难点:重点:(1)探索图形成轴对称的性质和特征。
(2)探索图形旋转的特性和性质。
难点:(1)能在方格纸上画出一个图形的轴对称图形。
(2)能在方格纸上把简单图形旋转 90 度。
课时分配:轴对称-------1 课时欣赏设计------1 课时旋转---------1 课时整理复习-------1 课时日期: 日期轴对称教学目标: 1、进一步认识图形的轴对称,感受对称在生活中的应用,体会数学的价值。
2、探索图形成轴对称的基本性质。
3、通过观察、思考和动手操作,培养探索与实践的能力,发展空间观念。
教学重难点:1、进一步认识图形的轴对称。
2、探索图形成轴对称的基本性质。
教学准备:主题图课件、其他有关轴对称的图片或实物。
教学过程:一、创设情境,引入新知。
1、呈现现实生活中利用对称、平移和旋转设计出的许多美丽的事物或图案。
(仔细观察美丽的对称图案)2、引导:大家仔细观察这些漂亮的图案,想一想它们有什么特征?(独立思考,集体交流:这些图案有的是通过对称得到的;还有的是通过平移和旋转得到的)3、过渡:对于这些类型的图形,大家以前也有些接触,现在我们再来深入学习这些图形有什么特征。
这一单元分别介绍(板书):图形的轴对称、旋转、平移。
今天我们主要学习图形的轴对称。
人教版五年级数学上册总复习图形与几何(附答案)

人教版五年级数学上册总复习图形与几何(附答案)第3课时图形与几何(1) (教材P112~114)一、填一填。
21.一个平行四边形的底是8cm,高是10cm,这个平行四边形的面积是(80)cm²;与它等底等高的三角形的面积是(40)cm²。
22.一个三角形的面积是10m²,高是4m,这个三角形的底是(5)m。
23.如下图,大平行四边形被分成三块,在分成的这三块中,三角形①的面积是30cm²,平行四边形②的面积是(44)cm²,梯形③的面积是(66)cm²。
二、计算下列图形的面积。
(单位:m²)三、求阴影部分的面积。
大正方形的边长是8cm,小正方形的边长是6cm。
四、生活中的数学。
21.学校准备给面积是720m²的平行四边形水池安装围栏,围栏长多少米?22.图中每个小方格表示10cm,请你估算这个海豚图案的面积。
(不满1格的都按半格计算)五、___有一块长方形铁皮,长100cm,宽60cm,他准备把这块铁皮剪成一些如下图所示的直角三角形,最多能剪多少个这样的直角三角形?第3课时图形与几何(1)一、1.(4,5)2.(6,4)二、略三、阴影部分的面积为(28)cm²。
四、21.围栏长为(117.6)m。
22.海豚图案的面积约为(140)cm²。
五、最多能剪成(40)个这样的直角三角形。
第4课时图形与几何(2) (教材P112~114)一、填一填。
1.学校组织五年级学生去看电影,___坐在第4列,第5行,用(4,5)表示,___坐在第8列、第6行,应该用(8,6)表示。
2.若将电影票上的“6排5号”用(5,6)表示,那么电影票上的“2排3号”用(3,2)表示;(4,6)表示的位置是(第6列,第4行)。
二、选一选。
(将正确答案的序号填在括号里)1.有三个点a、b、c,用数对表示是a(4,5),b(6,5),c(4,6),在同一行的是(AC)。
人教版五年级数学期末复习要点(附十大重点题目)

人教版五年级数学期末复习要点(附十大重点题目),给孩子收藏!据统计,如果在期末考试之前能有半个月或以上时间复习的,那么考生的总体成绩都会比平时明显提高。
图形变换的基本方式是平移、对称和旋转。
1、轴对称:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
(1)学过的轴对称平面图形:长(正)方形、圆形、等腰三角形、等边三角形、等腰梯形……等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴,正方形有4条对称轴,等腰梯形有1条对称轴,任意梯形和平行四边形不是轴对称图形。
(2)圆有无数条对称轴。
(3)对称点到对称轴的距离相等。
(4)轴对称图形的特征和性质:①对应点到对称轴的距离相等;②对应点的连线与对称轴垂直;③对称轴两边的图形大小、形状完全相同。
(5)对称图形包括轴对称图形和中心对称图形。
平行四边形(除棱形)属于中心对称图形。
2、旋转:在平面内,一个图形绕着一个顶点旋转一定的角度得到另一个图形的变化较做旋转,定点O叫做旋转中心,旋转的角度叫做旋转角,原图形上的一点旋转后成为的另一点成为对应点。
(1)生活中的旋转:电风扇、车轮、纸风车(2)旋转要明确绕点,角度和方向。
(3)长方形绕中点旋转180度与原来重合,正方形绕中点旋转90度与原来重合。
等边三角形绕中点旋转120度与原来重合。
旋转的性质:(1)图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;(2)其中对应点到旋转中心的距离相等;(3)旋转前后图形的大小和形状没有改变;(4)两组对应点非别与旋转中心的连线所成的角相等,都等于旋转角;(5)旋转中心是唯一不动的点。
3、对称和旋转的画法:旋转要注意:顺时针、逆时针、度数1、整除:被除数、除数和商都是自然数,并且没有余数。
整数与自然数的关系:整数包括自然数。
2、因数、倍数:大数能被小数整除时,大数是小数的倍数,小数是大数的因数。
例:12是6的倍数,6是12的因数。
五年级数学上册教学课件《多边形的面积 整理和复习》

b a S = ab
h a S = ah
h a S = ah÷2 a
h S =b(a+b)h÷2
平行四边形、三角形和梯形面积计算公 式的推导都用到了转化的方法。
3.梯形的变化
a
a
h
h
b
b
当梯形的上底和下底相等时就成了平行四边形;当
梯形的上底为 0 时就成了三角形。长方形、正方形、
平行四边形、三角形和梯形之间都可以互相转化。
变式训练
2. 如图,一个梯形的上、下底分别是 6 cm、10 cm, 已知涂色部分的面积是 24 cm2 ,这个梯形的面 积是多少平方厘米。
6 cm
三角形的高是:
24×2÷10 = 4.8 ( cm ) S梯形 = ( 6 + 10 )×4.8÷2 = 38.4 ( cm2) 10 cm 答:这个梯形的面积是 38.4 cm2 。
课后作业
1.从教材整理和复习中选取; 2.从课时练中选取。
板书设计
整理和复习
平行四边形的面积 S = ah 三角形的面积 S = ah÷2 多边形的面积 梯形的面积 S =(a+b)h÷2 组合图形的面积①添补求差法 ②分割求和法
不规则图形的面积 ①数方格 ②转化
10 cm 5cm
6cm 12 cm
方法六:割补拼成一个梯形
S梯形= [12+12+(12 - 6)]×5÷2 = 30×5÷2 = 75(cm2)
10 cm 5cm
6cm 12 cm
右面是由一副七巧板拼 出的正方形,边长为12 cm, 你能计算出其中每个图形的 面积吗?
①②各占正方形的四分之一; ④⑤⑦各占八分之一; ③⑥各占十六分之一。 先求正方形的面积,再求各部分的 面积。
人教版小学数学五年级数学下册期末阶段专项复习 《图形计算》(含答案)

人教版小学数学五年级下册期末阶段专项复习——《图形计算》班级:_________ 姓名:__________1.计算下面图形的表面积和体积。
(单位:厘米)2.求下图的体积。
3.计算下列图形的表面积和体积(单位:厘米)。
4.计算下面立体图形的体积。
5.下图是有两个面为正方形的长方体表面积展开图,请算出它的表面积。
6.分别求出下面图形的表面积和体积。
(单位:cm)7.求出下面图形的体积、表面积、棱长总和各是多少?8.计算如图图形的表面积和体积。
(单位:厘米)9.下图是一个长方体的展开图,根据所给的数据计算这个长方体的表面积。
(单位:cm)10.下图是一个底面为正方形的长方体,计算这个长方体的表面积。
11.计算下面图形的体积。
(单位:cm)12.求长方体的表面积。
(单位:厘米)13.计算正方体的表面积和体积。
14.下图是一个长方体的展开图,计算下面各立体图形的表面积和体积。
(单位:cm)15.如图是一个长方体的表面展开图,根据图上有关数据,计算这个长方体的体积。
16.算一算。
求下图的表面积和体积。
(单位:厘米)17.计算下面图形的体积。
(单位:cm)18.如图,请计算礼品盒的表面积和体积。
19.求体积。
(单位:厘米)20.如图,求围成的长方体的体积。
(单位∶厘米)参考答案:1.52平方厘米;24立方厘米2.0.125立方分米3.表面积:1712平方厘米;体积:4320立方厘米4.489cm35.550cm26.表面积:1620cm2;体积:3528cm37.285dm3;278.5dm2;84dm8.358平方厘米;408立方厘米9.184cm210.450平方厘米11.208cm312.158平方厘米13.1350cm2;3375cm314.正方体:150cm2;125cm3;长方体:64cm2;28cm3 15.3480cm16.844平方厘米;1416立方厘米17.365立方厘米18.1300平方厘米;3000立方厘米19.327立方厘米20.90立方厘米。
人教版五年级数学下册图形与几何、统计专项复习卷(含答案)

人教版五年级数学下册图形与几何专项复习卷(含答案)满分:100分试卷整洁分:2分(72分)一、用心思考,正确填写。
(第1、2小题各4分,其余每空2分,共30分)1.[旋转](1)放( )kg的物品,指针顺时针旋转45°。
(2)放( )kg的物体,指针顺时针旋转90°。
(3)放4 kg物品,指针( )时针旋转( )°。
2.[单位换算]在括号里填上合适的数。
2.8 m3=( )dm3 1.05 dm3=( )cm31800 mL=( )L 540 L=( )dm33.[长方体的体积]一根长2 m的长方体钢材,沿横截面截成两段后,表面积增加了0.6 dm2,这根长方体钢材的体积是( )dm3。
4.[长方体的体积]一个长方体包装箱,相交于一个顶点的三条棱的长度分别是5 dm、3 dm、4 dm,这个包装箱的占地面积最大是( )dm2,体积是( )dm3。
5.[长方体体积公式的应用]一个长方体容器,从里面量长4 dm,宽3 dm,能容纳30 L水。
这个长方体容器的高是( )dm。
6.[旋转]从8时55分到9时15分,分针旋转了( )°。
7.[长方体的表面积和体积]一个长方体的长、宽、高都扩大到原来的2倍,这个长方体的表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
8.[探索图形]右图是用小正方体拼成的大正方体,在它的表面涂色。
三面涂色的小正方体有( )个,没有涂色的小正方体有( )个。
9.[观察物体]一个立体图形从正面看到的形状是,从左面看到的形状是,搭这个立体图形至少要( )个小正方体,最多要( )个小正方体。
二、认真辨析,合理选择。
(将正确答案的序号填在括号里)(10分)1.[旋转]图形绕点O旋转以后,得到的图形可能是( )。
A. B. C. D.2.[表面积]右图是由同样大小的正方体组成的两个图形,它们的表面积相比较,( )。
A.一样大B.①大C.②大D.无法比较3.[观察物体]小明搭的积木从上面看到的形状是,上面的数字表示在这个位置上所用正方体的个数。
五年级数学下册 期中复习专项训练《图形计算》 (北师大版)
北师大版小学数学
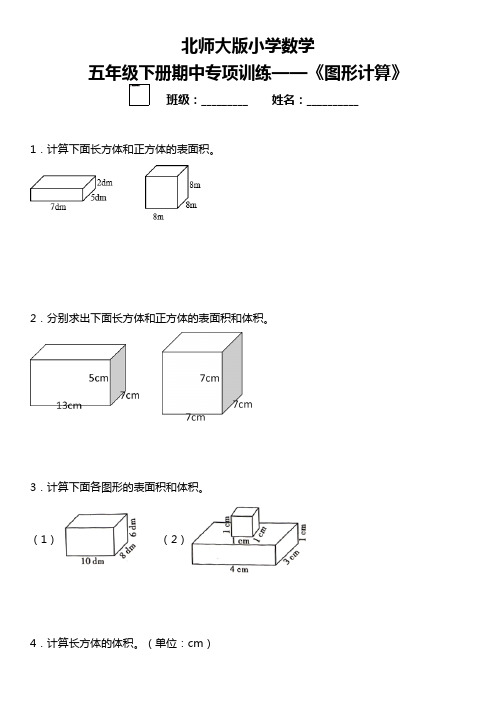
班级:_________ 姓名:__________ 1.计算下面长方体和正方体的表面积。
2.分别求出下面长方体和正方体的表面积和体积。
3.计算下面各图形的表面积和体积。
(1)(2)
4.计算长方体的体积。
(单位:cm)
5.计算出下面图形的表面积。
6.计算正方体的表面积。
(单位:cm)
7.求下面图形的表面积和体积(单位:dm)。
8.计算下面长方体的表面积和体积。
(长=6cm,宽=5cm,高=3cm)
9.计算下面图形的表面积和体积。
10.计算组合图形的表面积和体积。
11.求下面正方体的表面积与长方体的体积。
(1)(2)
12.求下面长方体的表面积和体积。
13.计算出下面图形体积。
14.计算下面图形的体积和表面积。
参考答案:1.118dm2;384m2
2.长方体:表面积382cm2;体积455cm3;
正方体:294cm2;体积343cm3
3.(1)表面积:376平方分米;体积:480立方分米(2)表面积:42平方厘米;体积:13立方厘米
4.96cm3
5.220厘米2
6.150 cm2
7.表面积:340平方分米;体积:400立方分米8.126平方厘米;90立方厘米
9.表面积:330平方厘米;
体积350立方厘米
10.表面积:186;体积:152
11.96平方厘米;56立方厘米
12.表面积:128平方厘米;体积:96立方厘米13.200立方厘米;216立方厘米
14.体积:576立方厘米;
表面积:432平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第一课时) 教学设计
《多边形的面积》整理和复习
复习内容:义务教育教科书五年级上册第103 页及相关内容
复习目标:
l.复习平行四边形、三角形和梯形的面积计算公式的由来,体会转化思想。
能应用公式计算图形的面积和解决一些简单的实际问题。
2.沟通多边形面积计算公式之间的联系,实现知识的网络结构化,进一步培养学生自主整理知识的能力。
3.激发学生的学习兴趣,培养学生的反思意识。
复习重点: 整理本单元所学的面积计算公式,理解计算公式之间的联系,形成知
识网络。
复习难点: 能正确应用多边形面积公式解决简单的实际问题。
复习准备: 课前发放如下复习资料,学生独立自主完成。
《多边形的面积》整理和复习
l.想一想: 本单元我们学过哪些平面图形的面积? 它们的公式分别是什
么? 是怎样推导出来
的? 这些平面图形的面积计算公式之间有什么联系?
2.请用表格或画图的方式将本单元的知识进行整理。
在你认为紫握的较好的板块旁画上;
在容易出错的地方做上标记,或者举例说明。
3.在学习多边形面积时,哪类题目容易出错? 收集一道易错的题日。
4.如果你还学有余力,请设计一道综合性、思考性较强的题目与大家分享。
复习过程:
课前热身:一分钟口算。
知识再现,揭示课题。
师: 今天这节课咱们对本单元《多边形的而积》进行整理和复习。
现在就让我们
跟随的电子课本,一起来回顾一下。
(课件)
问: 本单元都学过哪些知识呢?
二、自主梳理,建构网络。
1.小组交流课前自主整理的材料
節;先在小组内交流你的整理,听了别人的发言后还可以完善你的整理。
最后每组推选一位同学在全班作交流。
2.全班交流。
生汇报: (1) 平行四边形的面积;
62) 三角形的面积;
(3) 梯形的面积。
3.构建知识网络
(1) 转化
而:这些公式的推导过程中,
都有什么相同的地方吗?
师小绍它们都是把没学过的图形转化成已学过的图形,都是利用已有的面积公式推出新的面积公式。
(2) 动态变化构建联系
播放梯形动画
问: 你看到了什么? 这由仆么图形变成了什么图形?
预设:
(1) 两湍延长; 当上底两端延长到和下底相等时,它就变成了长方形。
(2)一端延长: 当梯形的上底与下底相等时,它就变成了平行四边形。
(3) 缩短为0时: 当梯形的上底为0时,它就变成了三角形。
功画演1
师小结: 由此可见,当在一定条件下,这些图形都是可以互相转化的。
但无论怎
样变化,这些平面图形的面积始终和什么有关一一和底和高有关。
问; 通过本节课的整理,对于多边形面秒的知识,你还有什么疑惑吗?
三、
练习应用,内化方法。
l.基本练习; 求出下列图形的面积。
2.辨析概念
四、思维提升,巩固提高
l.在方格纸上可出一个面积是16cm?的三角形、平行四边形或者梯形。
@ 学生白主完成
@ 交流经验
2.交流“易错题”
五、反思回顾,质疑提升。
师:酒过今天的整理和复习,你有什么新的收获吗? 下节课我们将利用这些多边形的面积知识和转化的思想来复习组合图形和不规则图形的面积。
