平方差公式和完全平方公式
平方差公式与完全平方公式

平方差公式: ( a+b) ( a-b)= a 2- b 2即:两数和与这两数差的积,等于它们的平方差。
平方差公式的特点:(1)左边是两个二项式相乘,这两项中有一项相同,另一项互为相反数;(2)右边是乘式中两项的平方差(相同项的平方减去相反项的平方);(3)公式中的a 和b 可以是有理数,也可以是单项式或多项式.一、请你填一填:1. __________))((=+-y x y x ,=-+)2131)(3121(x y y x 。
2.=--+-)51)(51(a a ,(5--a )( )=225a -,22)(______)(n m n m +-=+。
3.=-=+=-22,7,4y x y x y x 则若 。
4. 18201999⨯=________, 403×397=________, 110199100+⨯= ,1241221232⨯-= 。
5.)1)(1(2+-x x ( )14-=x .6.+=--++a c b a c b a [))((( )][-a ( )]7.=+-+---))((d c b a d c b a [( )+( )][( )-( )]8. 化简22)()(c b a c b a +--++的结果为 。
二、请你选一选:9.乘法等式中的字母b a ,表示( )A.只能是数B.只能是单项式C.只能是多项式D.单项式、•多项式都可以10.下列计算,能用平方差公式的是( )A.)532)(325(3223a c b bc a +- B.))((n m n m --+ C.)23)(32(-+x x D.)4332)(4332(3232n m n m --- 11.下列各式中,计算正确的是( )A.2)2)(2(2-=+-x x x B.43)23)(2(2-=-+x x xC.))((c ab c ab +-=222c b a - D.22))((y x y x y x -=+--初二数学个性化讲义 平方差公式与完全平方公式佛山学习前线教育培训中心12.20022-2001×2003的计算结果是( )A. 1B.-1C.2D.-213.计算22)23()32(b a b a ---的正确结果是( )A.0 B.22131213b ab a +- C.2255b a +- D.224125b ab a ---14.等式)(b a --( ))(22a b +=44b a -中,括号内应填( )A.b a - B.b a +- C.b a -- D.b a +15.下面计算)7)(7(b a b a ---++-正确的是( )A.原式=22)(7)]7()][7([b a b a b a +-=++----B.原式=22)7(])7(][)7([b a b a b a -+=-+-++-C.原式=22)(7)](7)[7(b a b a b a +--=+--++-D.原式=22)(7)](7)[7(b a b a b a ++=+--++-16.下列式中能用平方差公式计算的有( )①)21)(21(y x y x +-, ②)3)(3(a bc bc a ---, ③)3)(3(y x y x +++-, ④(100+1)(100-1) A.1个 B.2个 C.3个 D.4个17.可以运用平方差公式运算的有( )个①)21)(21(x x --+- ②)21)(21(x x +-- ③)2)(2(b ab b ab ---A .1B .2C .3D .018.代数式)1()1)(1)(1(42+-++-y y y y 的值是( )A .0B .2C .-2D .不能确定三、解答题:19.利用平方差公式计算:⑴ 502×498 ⑵ 1.01× 0.99 ⑶ 30.8×29.220.先化简,再求值:⑴)2)(2()2)(2(y x y x y x y x -----+,其中8,8-==y x ;⑵)4)(2)(2(22y x y x y x --+,其中1,2-==y x .完全平方公式: (a +b)2 =a 2+2ab+b 2 ; (a- b)2 =a 2-2ab+b 2即两数和(或差)的平方等于它们的平方之和加上(或减去)这两个数之积的2倍。
平方差公式和完全平方公式

平方差公式:两个数的和乘两个数的差的乘积,等于这两个数的平方差 例1:(X+2)(X-2) (2x+21y) (2x-21y) (a+b-c)(a-b+c)(-3x-2y )(3x-2y) (2x+y-z+10)(2x-y+z+10)练习:1、计算(x-2y )(-2y-x)-(3x+4y)(-3x+4y) (x-2)(16+x 4)(2+x)(4+x 2)(2a+b-c-3d)(2a-b-c+3d) (m+n+p+q )(m-n-p-q )例2: 98×102 982(用平方差公式)练习:103×97 118×122 1032例3:(1+xy2)(1-xy2)(-1-x2y4) (x+2y)(x-2y)-(2x-y)(-2x-y),其中x=8. y=8练习:11、(1-2a)(1+2a)(1+4a2)(1+16a4),其中a=-22、(x-y)(x2+y2)(x4+y4)¨¨¨¨(x16+y16)3、(22+1)(24+1)(28+1)(216+1)完全平方公式:1、两个数和的平方,等于这两个数的平方和,加上这两个数积的2倍。
2、两个数差的平方,等于这两个数的平方和,减去这两个数积的2倍。
例4:(2a+3b)2 598 2 (-m-4n)2 (a-2b)2练习:102289.82 (-2a-b)2例5:()?, 2)()3(.,1,2)2(.)1(,51)1(222222222应为多少则如果的值求若的值求已知znmnmznmxyyxyxaaaa++=+-=+=-+=+练习:1、已知x+y=7,xy=2,求:①2x2+2y2的值;②(x-y)2的值.2、如果x+y=6, xy=7, 那么x2+y2=,(x-y)2=。
3、(09深圳)用配方法将代数式a2+4a-5变形,结果正确的是()A.(a+2)2-1B.(a+2)2-5C.(a+2)2+4D.(a+2)2-94、已知x-1÷x=3,求x2-1÷x25、已知x 2 – 4=0,求代数式x(x+1)2 –x(x 2+x)-x-7的值一、科学记数法:1、绝对值大于10的数:na 10⨯ (1≤a 〈10 ,n 是原数的整数位数减1〉 2、绝对值小于1的数:n a -⨯10 (1≤a 〈10,n 是有效数字前0的个数)1米=1000000微米=100万微米 1米=100000000010亿纳米例6:(1)用科学记数法表示下列各数: 696000000 300000000 0.146 -0.000000017例7:人体内的某种细胞中,每个细胞的面积约为1.9×10-12平方米,在一平方厘米的面积内,一层这样的细胞大约有多少万个? 练习:1、100张100元的新版人民币约0.9 cm 厚,则每张新版100元人民币的厚度为________cm(用科学记数法表示).2、人体内一种细胞的直径为 4.3微米,用科学记数法表示这种细胞的直径为 米。
平方差公式和完全平方公式

第三讲 平方差公式和完全平方公式【名言警句】细节决定成败!【知识点归纳讲解】(一)平方差公式:(a+b)(a-b)=a 2-b 2 两数和与这两数差的积,等于它们的平方差. 特征:①左边:二项式乘以二项式,两数(a 与b )的和与它们差的乘积. ②右边:这两数的平方差. 平方差公式的常见变形:①位置变化:如()()()()22a b b a b a b a b a +-=+-=-②符号变化:如()()()()()2222a b a b b a b a b a b a ---=---+=--=-⎡⎤⎡⎤⎣⎦⎣⎦或()()()()()2222a b a b a b a b a b a b ---=-+-=--=-+ ③系数变化:如()()()()()22ma mb a b m a b a b m a b +-=+-=-(二)完全平方公式()()22222222a b a ab b a b a ab b+=++-=-+ 完全平方公式常见变形:① 符号变化:如()()22222a b a b a ab b --=+=++ ()()22222a b a b a ab b -+=-=-+②移项变化:()()22222222a b a ab b a b a ab b +=++-=-+⇒()()22222222a b a b ab a b a b ab+=+-+=-+⇒()()224a b a b ab +--=【经典例题讲解】(一)平方差公式例1:计算:()()()()2244a b b a b a b a ---+-例2:计算:①(2x+y )(2x-y) ②(y x 3121+)(y x 3121-)③(-x+3y)(-x-3y) ④(2a+b)(2a-b)(4)22b a +.【同步演练】应用平方差公式计算(1)()()a a 2121+- (2)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+3121312122x x (3)()()y x y x 3232+---例3:某初级中学得到政府投资,进行了校园改造建设,他们的操场原来是长方形,改建后变为正方形,正方形的边长比原来的长方形少6米,比原来的长方形的宽多了6米,问操场的面积比原来大了还是小了?相差多少平方米?(二)完全平方公式例1:已知2291822a b ab a b +==+,,求的值例2:利用完全平方公式计算:(1)1022 (2)1972【同步演练】利用完全平方公式计算:(1)982 (2)2032例3:计算:(1))3)(3(-+++b a b a (2))2)(2(-++-y x y x【同步演练】)3)(3(+---b a b a例4:若22)2(4+=++x k x x ,则k =若k x x ++22是完全平方式,则k =例:5:完全平方公式的推广()2222222a b c a b c ab ac bc ++=+++++()222222222a b c d a b c d ab bc cd ad +++=+++++++附加题:若实数222,,9,a b c a b c ++=满足()()()222a b b c c a -+-+-则代数式的最大值是多少?【课堂检测】 (一)平方差公式 一、填空题1、=--+-)2)(2(y y _______.2、=-+)2)(2(y x y x ______.3、=-+)3121)(3121(b a b a ______. 4、=---))((22x a x a _______. 5、=++-))()((22b a b a b a _______. 6、=-+-))((y x y x _______. 7、=+-----+))(())((y x y x y x y x _______. 8、+xy (_______)-xy (_______)81122-=y x . 二、选择题9、下列各式中,能直接用平方差公式计算的是( ) (A ))22)(2(b a b a +--; (B ))2)(2(a b b a +-; (C ))2)(2(b a b a +--; (D ))2)(2(b a a b ++-.10、下列各式中,运算结果是223625y x -的是( ) (A ))56)(56(x y x y --+- ; (B ))56)(65(x y y x +-; (C ))56)(56(x y x y ++- ; (D ))65)(65(y x y x +--. 三、解答题11.计算)2)(2())((n m n m n m n m -+-+-.12.先化简后求值2),2)(2()2)(2(22-=-+--+x x x x x .13.解方程4)2()1)(1(2=---+x x x x .(二)完全平方公式 一、填空题1、=-+)2)(2(b a b a _______.2、)5(x +-_______225x -=. 用平方差公式计算并填空3、)218(5.75.8+=⨯__ ___4363=. 4、=⨯95105_______.5、=-+22)2()2(y x y x (_______)2. 二、选择题6、=+----))((y x y x _______.( )(A )22y x +-;(B )22y x -;(C )22y x --;(D )22y x +.7、如果16)(2-=+a m a p ,则( )(A )4),4(=+=m a p ; (B )4),4(-=-=m a p (C )4),4(-=+=m a p ; (D )4,4=+-=m a p . 三、解答题8、解不等式x x x x x 3)6()3)(3(>+-+-.9、解方程)1)(1(2)3)(12(+-=+-x x x x .10、先化简后求值)5)(5(2)4)(3(-+-+-x x x x ,其中10-=x11、一个梯形上底是)(b a +㎝,下底是)(b a -㎝,高为)2(b a +㎝,求梯形的面积,若2,215==b a ,求这个梯形的面积.【课后作业】一、填空题(每题2分,共28分)1.(34=⋅a a ____()⨯____34)+=a ; 2.=-⋅-54)()(x y y x _________; 3.()(23=m _____)(_____23)⨯=m ; 4.=-⋅--535)(])([a a _________; 5.=⨯3)87(_________3387⨯=; 6.(8164=y x ______2); 7.已知长方形的长是m 4,它的面积是nm 20,则它的宽是_________;8.=⋅+-222483)41(6y x x y x xy _________;9.=⋅+n m 2)7(_________;10.=+--)()(b a a a b b _________; 11.=++))((t z y x _________; 12.=+++-))()()((4422b a b a b a b a _________; 13.=++-+-))((c b a c b a _________; 14.=--+22)()(b a b a _________. 二、选择题(每题3分,共12分)15.下列各式中正确的是( )(A )222)(b a b a -=-; (B )2222)2(b ab a b a ++=+; (C )222)(b a b a +=+; (D )2222)(b ab a b a +-=+-.16.计算)102.2()105.3(53⨯⨯⨯的结果并用科学记数法表示,正确的结果是( ) (A )770000000;(B )71077⨯;(C )8107.7⨯;(D )7107.7⨯.17.20072006)32()23(⋅-的计算结果是( )(A )23-;(B )32-;(C )32;(D )23.18.下列计算正确的是( )(A )1262432a a a a a =⋅+⋅; (B )252212)2(3bc a c a ab =⋅;(C )322322+=⋅⋅+⋅n n a a a a a a ; (D )432222)21()2(y x y x xy -=-⋅-.三、简答题:(每题6分,共30分)19.计算:4453)()(a a a a -+-20.结果用)(y x -的幂的形式表示62323)(2])[(])[(y x x y y x -+-+-.21.用简便方法计算63720052006)2()81()125.0()8(⨯+-⨯-22.计算453210)2()(b a ab b a +⋅- .23.计算)1()1(22++-++x x x x x . 24.计算))()((22b a b a b a -+-.四、解答题(每题5分,共20分)25.解方程)2(2)2()1(-=++-x x x x x x26.化简并求值31,3),3)(3(==--b a a b b a 其中.27.化简并求值2,)1()12(22-=-++x x x 其中.28.计算2)(c b a --29.综合题(10分,每小题5分)(1)已知一个圆的半径若增加2厘米,则它的面积就增加39平方厘米,求这个圆的直径.(用π的代数式表示这个圆的直径)(2)阅读:若一家商店的销售额10月比9月份增长(减少)10%,则设这家商店9月10月份销售额的增长率为0.1(-0.1);理解:甲、乙两店9月份的销售额均为a万元,在10月到11月这两个月中,甲,问到商店的销售额的平均每月增长率为x,乙商店的销售额平均每月的增长率为x11月底时,甲商店的销售额比乙商店的销售额多多少万元(用a和x的代数式表示结果).【课后作业】家长意见及建议:家长签字:日期:年月日。
平方差和完全平方公式应用举例

平方差和完全平方公式应用举例一、平方差公式平方差公式描述了两个数(或代数式)的乘积与它们的差之间的关系:(a+b)(a-b)=a²-b²这个公式的应用在代数运算中非常常见,下面我们通过几个具体的例子来说明它的应用。
例子1:计算(7+2)(7-2)根据平方差公式,我们有:(7+2)(7-2)=7²-2²=49-4=45所以,(7+2)(7-2)=45例子2:计算(x+1)(x-1)根据平方差公式,我们有:(x+1)(x-1)=x²-1²=x²-1所以,(x+1)(x-1)=x²-1二、完全平方公式完全平方公式描述了一个一次多项式的平方的表达式:(a + b)² = a² + 2ab + b²这个公式的应用也非常广泛,下面我们通过几个具体的例子来说明它的应用。
例子3:展开(x+2)²根据完全平方公式,我们有:(x+2)²=x²+2(x)(2)+2²=x²+4x+4所以,(x+2)²=x²+4x+4例子4:展开(3+2x)²根据完全平方公式,我们有:(3+2x)²=3²+2(3)(2x)+(2x)²=9+12x+4x²所以,(3+2x)²=4x²+12x+9这些例子展示了平方差和完全平方公式在解题中的应用。
它们可以用来简化计算过程,化简表达式和方程。
例如,当我们需要计算两个数的乘积或平方时,我们可以利用平方差公式,将计算过程转化为相加或相减的操作,从而简化计算。
另外,完全平方公式可用于展开一个一次多项式的平方,从而获取更多的信息。
这在求解方程和证明等问题中经常会遇到。
总结起来,平方差和完全平方公式是代数中常用的公式,它们的应用在代数运算、化简表达式、求解方程和证明等问题中都具有重要的作用。
平方差公式与完全平方公式

Word 文档平差公式与完全平公式(a+b )2 = a 2+2ab+b 2(a -b )2=a 2-2ab+b2(a+b )(a -b )=a 2-b 2应用1、平差公式的应用:例1、利用平差公式进行计算: (1)(5+6x )(5-6x ) (2)(x +2y )(x -2y ) (3)(-m +n )(-m -n ) 解:例2、计算:(1)(y x 41--)(y x 41+-) (2)(-m -n )(m -n )(3)(m +n )(n -m )+3m 2(4)(x+y )(x -y )(x 2-y 2)解:例3、计算:(1)103×97 (2)118×122 (3)32203119⨯ 解:应用2、完全平公式的应用: 例4、计算:(1)(2x -3)2(2)(4x+5y )2(3)(y x 21-)2 (4)(-x -2y )2(5)(-x+y 21)2解:例5、利用完全平公式计算:(1)1022 (2)1972 (3)199992-19998×20002解:试一试:计算:123456789×123456787-1234567882=_______________Word 文档应用3、乘法公式的综合应用: 例6、计算:(1)(x+5)2-(x+2)(x -2)(2)(a+b+3)(a+b -3) (3)(a -b+1)(b -a+1)(4)(a+b -c )2解: 例7、(1)若4ax x 412++是完全平式,则:a=________________(2)若4x 2+1加上一个单项式M 使它成为一个完全平式,则M=_______________ 例8、(1)已知:3a1a =+,则:__________a1a 22=+(2)已知:5a 1a =-,则:__________a 1a 22=+(3)已知:a+b=5,ab=6,则:a 2+b 2=_______(4)已知:(a+b )2=7,(a -b )2=3,则:a 2+b 2= ,ab=例9、计算:(1))1011()411)(311)(211(2222----ΛΛ (2))12()12)(12)(12)(12(32842+++++ΛΛ解:例10、证明:x 2+y 2+2x -2y+3的值总是正的。
注意完全平方公式和平方差公式不同

注意完全平方公式和平方差公式不同:结果不同:完全平方公式的结果是三项,即(a +b)2=a2 2ab+b2;平方差公式的结果是两项,即(a+b)(a−b)=a2−b2.在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab 时不少乘2;第一(二)个数被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键有时需要进行变形,使变形后的式子符合应用完全平方公式的条件,即为“两数和(或差)的平方”,然后应用公式计算。
例1 运用完全平方公式计算:(1)(x+2y)2; (2)(2a-5)2;(3) (-2s+t)2; (4) (-3x-4y)2.例1 利用完全平方公式计算:第一数的平方减去第一数与第二数乘积的2倍,加上第二数的平方(1) (2x−3)2 ;(2) (4x+5y)2 ; (3) (mn−a)2例2:计算(1)(-2 x-1)2 (2)(2x+1) 2(3)(2x-1) 2 (4)(1-2x) 2(1)(-2 x-1)2 = [-(2x+1) ]2=(2x) 2 +2 ×2x ×1+1 2=4x 2 +4x+1(2) (2x+1) 2=(2x) 2 +2 ×2x ×1+1 2=4x 2 +4x+1(2)(3) (2x-1) 2= (2x) 2-2 ×2x ×1 +1 2=4x 2- 4x+1(4) (1-2x) 2 = 12- 2 ×1 ×2x + (2x) 2=1-4x+4x 2运用完全平方公式计算:1 (a+6) 22 (4+x) 23 (x-7) 24 (8-y) 25 (3a+b) 26 (4x+3y) 27 (–2x+5y) 28 (-a-b) 29 (x/2-3y) 210 (3x/4-2y/3) 2=a 2+12a+36=16+8x+x 2=x 2-14x+49=64-16y+y 2=9a 2+6ab+b 2=16x 2+24xy+9y 2=4x 2-20xy+25y 2 =a 2+2ab+b 2= x 2 /4-3xy+9y 2=9 x 2 /16-xy+4 y 2 /9。
平方差公式与完全平方差公式

平方差公式与完全平方公式平方差公式:22))((b a b a b a -=-+说明:相乘的两个二项式中,a 表示的是完全相同的项,+b 和-b 表示的是互为相反数的两项。
所以说,两个二项式相乘能不能用平方差公式,关键看是否存在两项完全相同的项,两项互为相反数的项。
熟悉公式:(5+6x)(5-6x)中 是公式中的a , 是公式中的b(5+6x)(-5+6x)中 是公式中的a , 是公式中的b(x-2y)(x+2y)中 是公式中的a , 是公式中的b(-m+n)(-m-n)中 是公式中的a , 是公式中的b(a+b+c )(a+b-c)中 是公式中的a , 是公式中的b(a-b+c )(a-b-c)中 是公式中的a , 是公式中的b将下列各式转化成平方差形式(1) 36-x 2 (2)a 2-91b 2 (3) x 2-16y 2 (4) x 2y 2-z 2 (5) (x+2)2-9 (6)(x+a)2-(y+b)2 (7) 25(a+b)2-4(a -b)2例1:计算下列各题1.(a+3)(a-3)2..( 2a+3b)(2a-3b)3. (1+2c)(1-2c)4. (-x+2)(-x-2)5. (a+2b)(a-2b)6. (2x+12)(2x-12)例2:计算下列各题:1、 1998×20022、1.01×0.99 3.(20-19)×(19-89)例3::计算下列各题1、(a+b )(a-b)(a 2+b 2)2、(a+2)(a-2)(a 2+4)3、(x-12)(x 2+ 14)(x+ 12)例4:计算下列各题1、(-2x-y )(2x-y)2、(y-x)(-x-y) 3.(-2x+y)(2x+y) 4.(4a-1)(-4a-1)5.(b+2a)(2a-b)6.(a+b)(-b+a)例5;计算下列各题1.(a+2b+c )(a+2b-c)2.(a+b-3)(a-b+3)3.(m-n+p)(m-n-p)完全平方公式完全平方公式:2222)(b ab a b a +±=± 注意不要漏掉2ab 项熟悉公式1、a 2+b 2=(a+b)2 =(a-b)22、(a-b )2=(a+b)2 ; (a+b)2=(a-b)23、(a+b)2 +(a-b )2=4、(a+b)2 --(a-b )2=5.将下列各式转化成完全平方式形式(1)a 2-4a +4 (2)a 2-12ab +36b 2 (3)25x 2+10xy +y 2(4)16a 4+8a 2+1 (5) (m +n)2-4(m +n)+4 (6) 16a 4-8a 2+1(7)249114x x --例1:计算下列各题1、2)(y x +2、2)23(y x -3、2)21(b a +4、2)12(--t5、2)313(c ab +- 6、2)2332(y x + 7、2)121(-x 8、(0.02x+0.1y)2 例2:利用完全平方公式计算:(1)1022 (2)1972 (3)982 (4)2032例3:(1)若22)2(4+=++x k x x ,求k 值。
平方差完全平方公式

【知识点】一、平方差公式:(a+b )(a-b)=a 2-b 2两数和与这两数差的积,等于它们的平方之差。
1、即:(a+b )(a-b) = 相同符号项的平方 - 相反符号项的平方2、平方差公式可以逆用,即:a 2-b 2=(a+b )(a-b)。
3、能否运用平方差公式的判定①有两数和与两数差的积 即:(a+b )(a-b)或(a+b )(b-a) ②有两数和的相反数与两数差的积 即:(-a-b )(a-b)或(a+b )(b-a) ③有两数的平方差 即:a 2-b 2 或-b 2+a 2二、完全平方公式:(a+b)2=a 2+2ab+b 2(a-b)2=a 2-2ab+b 2两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
1、完全平方公式也可以逆用,即a 2+2ab+b 2=(a+b)2a 2-2ab+b 2=(a-b)22、能否运用完全平方式的判定 ①有两数和(或差)的平方即:(a+b)2或 (a-b)2或 (-a-b)2或 (-a+b)2②有两数平方,加上(或减去)它们的积的2倍,且两数平方的符号相同。
即:a 2+2ab+b 2或a 2-2ab+b 2或-a 2-2ab-b 2或 -a 2+2ab-b 2探索练习:1、计算下列各式: (1)()()22-+x x (2)()()a a 3131-+ (3)()()y x y x 55-+2、观察以上算式及其运算结果,你发现了什么规律?3、猜一猜:()()=-+b a b a -平方差公式1、平方差公式:两数和与这两数差的积,等于它们的平方差,即22))((b a b a b a -=-+。
2、其结构特征是:①公式左边是两个二项式相乘,两个二项式中第一项相同,第二项互为相反数; ②公式右边是两项的平方差,即相同项的平方与相反项的平方之差。
随堂练习:1、下列各式中哪些可以运用平方差公式计算 (1)()()c a b a -+ (2)()()x y y x +-+ (3)()()ab x x ab ---33 (4)()()n m n m +--2、判断:(1)()()22422b a a b b a -=-+ ( ) (2)1211211212-=⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+x x x ( ) (3)()()22933y x y x y x -=+-- ( )(4)()()22422y x y x y x -=+--- ( ) (5)()()6322-=-+a a a ( ) (6)()()933-=-+xy y x ( )3、计算下列各式:(1)()()b a b a 7474+- (2)()()n m n m ---22 (3)()()33221221--+-+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-x x x x4、填空:(1)()()=-+y x y x 3232 (2)()()116142-=-aa(3)()949137122-=⎪⎭⎫ ⎝⎛-b a ab (4)()()229432y x y x -=-+5、求()()()22y x y x y x +-+的值,其中2,5==y x6、计算:(1)()()c b a c b a --+- (2)()()()()()42212122224++---+-x x x x x x【例】运用平方差公式计算:102×98; 59.8×60.2;运用平方差公式计算:完全平方公式探索:一块边长为a 米的正方形实验田,因需要将其边长增加b 米,形成四块实验田,以种植不同的新品种。
平方差公式与完全平方公式知识点总结

平方差公式与完全平方公式知识点总结一、平方差公式(a+b)(a-b)=a2-b2 归纳小结公式的变式,准确灵活运用公式:① 位置变化,(x+y)(-y+x)=x2-y2② 符号变化,(-x+y)(-x-y)=(-x)2-y2= x2-y2③ 指数变化,(x2+y2)(x2-y2)=x4-y4④ 系数变化,(2a+b)(2a-b)=4a2-b2⑤ 换式变化,[xy+(z+m)][xy-(z+m)]=(xy)2-(z+m)2=x2y2-(z+m)(z+m)=x2y2-(z2+zm+zm+m2)=x2y2-z2-2zm-m2⑥ 增项变化,(x-y+z)(x-y-z)=(x-y)2-z2=(x-y)(x-y)-z2=x2-xy-xy+y2-z2=x2-2xy+y2-z2⑦ 连用公式变化,(x+y)(x-y)(x2+y2)=(x2-y2)(x2+y2)=x4-y4⑧ 逆用公式变化,(x-y+z)2-(x+y-z)2 =[(x-y+z)+(x+y-z)][(x-y+z)-(x+y-z)] =2x(-2y+2z)=-4xy+4xz完全平方公式活用: 把公式本身适当变形后再用于解题。
这里以完全平方公式为例,经过变形或重新组合,可得如下几个比较有用的派生公式:灵活运用这些公式,往往可以处理一些特殊的计算问题,培养综合运用知识的能力。
例1、已知,,求的值。
例2、已知,,求的值。
解:∵ ∴ ∴=∵,∴ 例3 已知,求的值。
解:三、学习乘法公式应注意的问题(一)、注意掌握公式的特征,认清公式中的“两数”、例1 计算(-2x2-5)(2x2-5)分析:本题两个因式中“-5”相同,“2x2”符号相反,因而“-5”是公式(a+b)(a-b)=a2-b2中的a,而“2x2”则是公式中的b、例2 计算(-a2+4b)2分析:运用公式(a+b)2=a2+2ab+b2时,“-a2”就是公式中的a,“4b”就是公式中的b;若将题目变形为(4b-a2)2时,则“4b”是公式中的a,而“a2”就是公式中的b、(解略)(二)、注意为使用公式创造条件例3 计算(2x+y-z+5)(2x-y+z+5)、分析:粗看不能运用公式计算,但注意观察,两个因式中的“2x”、“5”两项同号,“y”、“z”两项异号,因而,可运用添括号的技巧使原式变形为符合平方差公式的形式、例5 计算(2+1)(22+1)(24+1)(28+1)、分析:此题乍看无公式可用,“硬乘”太繁,但若添上一项(2-1),则可运用公式,使问题化繁为简、(三)、注意公式的推广计算多项式的平方,由(a+b)2=a2+2ab+b2,可推广得到:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc、可叙述为:多项式的平方,等于各项的平方和,加上每两项乘积的2倍、例6 计算(2x+y-3)2解:原式=(2x)2+y2+(-3)2+22xy+22x(-3)+2y(-3)=4x2+y2+9+4xy-12x-6y、(四)、注意公式的变换,灵活运用变形公式例7 已知:x+2y=7,xy=6,求(x-2y)2的值、例10 计算(2a+3b)2-2(2a+3b)(5b-4a)+(4a-5b)2分析:此题可以利用乘法公式和多项式的乘法展开后计算,但逆用完全平方公式,则运算更为简便、四、怎样熟练运用公式:熟悉常见的几种变化有些题目往往与公式的标准形式不相一致或不能直接用公式计算,此时要根据公式特征,合理调整变化,使其满足公式特点、常见的几种变化是:1、位置变化如(3x+5y)(5y-3x)交换3x和5y的位置后即可用平方差公式计算了、2、符号变化如(-2m-7n)(2m-7n)变为-(2m+7n)(2m-7n)后就可用平方差公式求解了(思考:不变或不这样变,可以吗?)3、数字变化如98102,992,912等分别变为(100-2)(100+2),(100-1)2,(90+1)2后就能够用乘法公式加以解答了、4、系数变化如(4m+)(2m-)变为2(2m+)(2m-)后即可用平方差公式进行计算了、(四)、注意公式的灵活运用有些题目往往可用不同的公式来解,此时要选择最恰当的公式以使计算更简便、如计算(a2+1)2(a2-1)2,若分别展开后再相乘,则比较繁琐,若逆用积的乘方法则后再进一步计算,则非常简便、即原式=[(a2+1)(a2-1)]2=(a4-1)2=a8-2a4+1、对数学公式只会顺向(从左到右)运用是远远不够的,还要注意逆向(从右到左)运用、如计算(1-)(1-)(1-)…(1-)(1-),若分别算出各因式的值后再行相乘,不仅计算繁难,而且容易出错、若注意到各因式均为平方差的形式而逆用平方差公式,则可巧解本题、即原式=(1-)(1+)(1-)(1+)…(1-)(1+)=… ==、有时有些问题不能直接用乘法公式解决,而要用到乘法公式的变式,乘法公式的变式主要有:a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab等、用这些变式解有关问题常能收到事半功倍之效、如已知m+n=7,mn=-18,求m2+n2,m2-mn+ n2的值、面对这样的问题就可用上述变式来解,即m2+n2=(m+n)2-2mn=72-2(-18)=49+36=85,m2-mn+ n2= (m+n)2-3mn=72-3(-18)=103、下列各题,难不倒你吧?!1、若a+=5,求(1)a2+,(2)(a-)2的值、2、求(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1)+1的末位数字、(答案:1、(1)23;(2)21、2、6 )五、乘法公式应用的五个层次乘法公式:(a+b)(a-b)=a2-b2,(ab)=a22ab+b2,(ab)(a2ab+b2)=a3b3、第一层次──正用即根据所求式的特征,模仿公式进行直接、简单的套用、例1计算 (-2x-y)(2x-y)、、第二层次──逆用,即将这些公式反过来进行逆向使用、例2计算第三层次──活用:根据待求式的结构特征,探寻规律,连续反复使用乘法公式;有时根据需要创造条件,灵活应用公式、例3化简:(2+1)(22+1)(24+1)(28+1)+1、分析直接计算繁琐易错,注意到这四个因式很有规律,如果再增添一个因式“2-1”便可连续应用平方差公式,从而问题迎刃而解、解原式=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216、第四层次──变用:解某些问题时,若能熟练地掌握乘法公式的一些恒等变形式,如a2+b2=(a+b)2-2ab,a3+b3=(a +b)3-3ab(a+b)等,则求解分简单、明快、例5已知a+b=9,ab=14,求2a2+2b2的值、解:∵a+b=9,ab=14,∴2a2+2b2=2[(a+b)2-2ab]=2(92-214)=106,第五层次──综合后用:将(a+b)2=a2+2ab+b2和(a-b)2=a2-2ab+b2综合,可得 (a+b)2+(a-b)2=2(a2+b2);(a+b)2-(a-b)2=4ab;等,合理地利用这些公式处理某些问题显得新颖、简捷、例6计算:(2x+y-z+5)(2x-y+z+5)、解:原式=[(2x+y-z+5)+(2x-y+z+5)]2-[(2x+y-z+5)-(2x-y+z+5)]2=(2x+5)2-(y-z)2=4x2+20x+25-y2+2yz-z2乘法公式的使用技巧:①提出负号:对于含负号较多的因式,通常先提出负号,以避免负号多带来的麻烦。
第三讲-平方差完全平方公式

平方差公式、完全平方公式一、知识目标:熟练掌握平方差公式和完全平方公式。
二、知识梳理:1. 平方差公式1).平方差公式:两数和与这两数差的积,等于它们的平方差,即。
2). 结构特征:①公式左边是两个二项式相乘,两个二项式中第一项相同,第二项互为相反数;②公式右边是两项的平方差,即相同项的平方与相反项的平方之差。
2.完全平方公式1).完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍,即;2).结构特征:①公式左边是二项式的完全平方;②公式右边共有三项,是二项式中二项的平方和,再加上或减去这两项乘积的2倍三、经典例题:例一、计算:(1)2001×1999 (2)998×1002(3)(a-b)(a+b)(4)(-a+b)(-a-b)(5)(a-b)(-a-b)(6)(a+b)(-a+b)练习1、计算:(1)(4b2-a)((-2b)2+a)(2)(3a+2b)(3a-2b)(3)(a5-b2)(a5+b2)(4)(a-b)(a+b)(a2+b2)2 (5))2)(1(2)1(22+--+a a a a(6))2)(2()2)(2(22x x x x x x -+++-例二、计算:(1)(-a-b )2(2)(b-a )2(3)(-a-b )2 +(-a+b )2(4)(b-a )2+4ab练习2、计算:(1)(4m+n )2(2)(y-12)2(3)22(1)(1)ab ab +--(4)(2x-y )2-4(x-y )(x+2y )例三、(1)若2212,6,x y x y x y -=+=-则=练习3、(2)已知63)122)(122(=-+++b a b a ,则=+b a ____________例四、(1)已知2,4==+xy y x ,则2)(y x -=练习4、(2)已知3)(,7)(22=-=+b a b a ,求=+22b a ________,=ab ________例五、22)()(c b a c b a +--++练习5、()()()()()42212122224++---+-x x x x x x例六、已知0132=+-x x ,求221x x +和441x x +的值。
平方差公式和完全平方公式
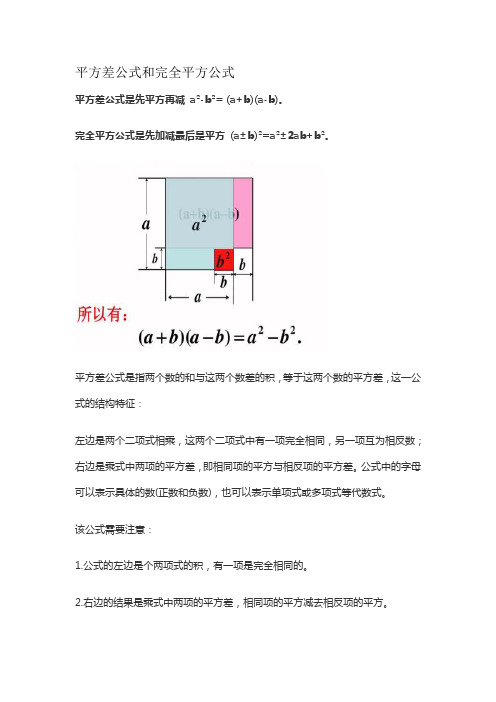
平方差公式和完全平方公式平方差公式是先平方再减a²-b²= (a+b)(a-b)。
完全平方公式是先加减最后是平方(a±b)²=a²±2ab+b²。
平方差公式是指两个数的和与这两个数差的积,等于这两个数的平方差,这一公式的结构特征:左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;右边是乘式中两项的平方差,即相同项的平方与相反项的平方差。
公式中的字母可以表示具体的数(正数和负数),也可以表示单项式或多项式等代数式。
该公式需要注意:1.公式的左边是个两项式的积,有一项是完全相同的。
2.右边的结果是乘式中两项的平方差,相同项的平方减去相反项的平方。
3.公式中的a,b 可以是具体的数,也可以是单项式或多项式。
完全平方公式指两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
为了区别,会叫做两数和的完全平方公式,或叫做两数差的完全平方公式。
这个公式的结构特征:1.左边是两个相同的二项式相乘,右边是三项式,是左边二项式中两项的平方和,加上或减去这两项乘积的2倍;2.左边两项符号相同时,右边各项全用“+”号连接;左边两项符号相反时,右边平方项用“+”号连接后再“-”两项乘积的2倍(注:这里说项时未包括其符号在内)。
公式中的字母可以表示具体的数(正数或负数),也可以表示单项式或多项式等数学式。
该公式需要注意:1.左边是一个二项式的完全平方。
2.右边是二项平方的和,加上(或减去)这两项乘积的二倍,a和b可是数,单项式,多项式。
3.不论是(a+b)2还是(a-b)2,最后一项都是加号,不要因为前面的符号而理所当然的以为下一个符号。
4.不要漏下一次项。
5.切勿混淆公式。
6.运算结果中符号不要错误。
7.变式应用难,不易于掌握。
平方差公式、完全平方公式

1平方差公式与完全平方公式1. 平方差公式:两个数的和与这两个数的差的积等于这两个数的平方差。
这个公式叫做乘法的平方差公式()()22b a b a b a -=-+2. 公式的结构特征①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数 ②右边是乘式中两项的平方差(相同项的平方减去相反项的平方) 一.基础部分【题型一】利用平方差公式计算 1. 位置变化:(1)()()x x 2525+-+(2)()()ab x x ab -+符号变化:(3)()()11--+-x x(4)⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛-m n n m 321.01.032系数变化:(5)()()n m n m 3232-+(6)⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--b a b a 213213 指数变化:(7)()()222233x yy x ++-(8)()()22225252b aba --+-2.增项变化(1)()()z y x z y x ++-+- (2)()()939322+++-x x x x3.增因式变化(1)()()()1112+-+x x x(2)⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-2141212x x x【题型二】利用平方差公式判断正误 4.下列计算正确的是( )A .()()()()2222425252525y x y x y x y x -=-=-+B .22291)3()1()31)(31(a a a a +=+-=--+-C .()()()()222249232332x y x y x y y x -=-=--- D .()()8242-=-+x x x【题型三】运用平方差公式进行一些数的简便运算例 5.用平方差公式计算.2 (1)397403⨯ (2)41304329⨯(3)1000110199⨯⨯ (4)2008200620072⨯-【题型四】平方差公式的综合运用 6.计算:(1)))(()2)(2(222x y y x y x y x x +-++-- (2)()()()()111142+-++-x x x x【题型五】利用平方差公式进行化简求值与解方程7.化简求值:())32)(32()23(32a b a b b a a b +---+,其中2,1=-=b a .【题型六】逆用平方差公式8.已知02,622=-+=-y x y x ,求5--y x 的值.课堂练习 一、选择1、下列运算正确的是( )A 、223)3)(3(y x y x y x -=-+B 、229)3)(3(y x y x y x -=-- C 、229)3)(3(y x y x y x --=-+- D 、229)3)(3(y x y x y x -=--+- 2、下列算式可用平方差公式的是( )A 、(m+2m )(m-2m)B 、(-m-n )(m+n)C 、(-m-n )(m-n)D 、(m-n )(-m+n) 3、计算2)55)(5151(y y x y x -+-+的结果是( ) A 、x 2B 、-x 2C 、2y 2-x 2D 、x 2-2y 24.计算(a m+b n)(a 2m-b 2n)(a m-b n)正确的是 ( ) A.a 4m-2a 2m b 2n+b 4mB.a 4m-b 4C.a 4m+b 4nD.a 2m+b 2n+2a m b n二、填空题三、解答题7.计算:①)2)(2(b a b a --+- ②2009200720082⨯-③))()((22b a b a b a +-+ ④.,12,222的值求若b a b a b a +=-=-四、用完全平方公式计算:(1)4992 (2)9982 (3)532 (4)88245。
八年级上数学人教版《 平方差公式、完全平方公式》笔记

《平方差公式、完全平方公式》笔记
一、平方差公式
1.公式描述:两数和乘两数差,等于两数平方差。
2.公式结构:(a+b)(a−b)=a2−b2
3.公式说明:此公式是整式乘法中的重要公式之一,它适用于任何具有此结
构的式子,可以简化计算。
4.公式应用:在解决数学问题时,此公式可以用于计算两数之和与两数之差
的积,也可以用于分解因式和求值。
二、完全平方公式
1.公式描述:首平方又末平方,二倍首末在中央;和的平方加再加,先减后
加差平方。
2.公式结构:(a+b)2=a2+2ab+b2,(a−b)2=a2−2ab+b2
3.公式说明:此公式是整式乘法中的另一个重要公式,它适用于任何具有此
结构的式子,可以简化计算。
4.公式应用:在解决数学问题时,此公式可以用于计算一个数的平方加上或
减去两倍的此数与另一数的积再加上或减去两倍的此数的平方,也可以用于分解因式和求值。
三、注意事项
1.在使用公式时要注意公式的结构以及字母的含义,避免出现错误。
2.在进行计算时要注意运算顺序和符号,确保计算结果的准确性。
3.在解决实际问题时要注意公式的应用范围和限制条件,避免出现错误的应
用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平方差公式与完全平方公式(a+b )2 = a 2+2ab+b 2(a -b )2=a 2-2ab+b2(a+b )(a -b )=a 2-b 2应用1、平方差公式的应用:例1、利用平方差公式进行计算: (1)(5+6x )(5-6x ) (2)(x +2y )(x -2y ) (3)(-m +n )(-m -n ) 解:例2、计算:(1)(y x 41--)(y x 41+-) (2)(-m -n )(m -n )(3)(m +n )(n -m )+3m 2(4)(x+y )(x -y )(x 2-y 2)解:例3、计算:(1)103×97 (2)118×122 (3)32203119⨯ 解:应用2、完全平方公式的应用: 例4、计算:(1)(2x -3)2(2)(4x+5y )2(3)(y x 21-)2 (4)(-x -2y )2(5)(-x+y 21)2解:例5、利用完全平方公式计算:(1)1022 (2)1972 (3)199992-19998×20002解:试一试:计算:123456789×123456787-1234567882=_______________应用3、乘法公式的综合应用: 例6、计算:(1)(x+5)2-(x+2)(x -2)(2)(a+b+3)(a+b -3) (3)(a -b+1)(b -a+1)(4)(a+b -c )2解: 例7、(1)若4ax x 412++是完全平方式,则:a=________________(2)若4x 2+1加上一个单项式M 使它成为一个完全平方式,则M=_______________ 例8、(1)已知:3a1a =+,则:__________a1a 22=+(2)已知:5a 1a =-,则:__________a 1a 22=+(3)已知:a+b=5,ab=6,则:a 2+b 2=_______(4)已知:(a+b )2=7,(a -b )2=3,则:a 2+b 2= ,ab=例9、计算:(1))1011()411)(311)(211(2222---- (2))12()12)(12)(12)(12(32842+++++解:例10、证明:x 2+y 2+2x -2y+3的值总是正的。
【模拟试题】一、耐心填一填1、计算:(2+3x )(-2+3x )=_____________;(-a -b )2=______________.*2、一个多项式除以a 2-6b 2得5a 2+b 2,那么这个多项式是_________________.3、若ax 2+bx+c=(2x -1)(x -2),则a=________,b=_______,c=_________.4、已知 (x -ay ) (x + ay ) = x 2-16y 2, 那么 a = ______________.5、多项式9x 2+1加上一个单项式后,使它能成为一个整式的完全平方,那么加上的单项式可以是____________.(填上一个你认为正确的即可)6、计算:(a -1)(a+1)(a 2-1)=__________.7、已知x -y=3,x 2-y 2=6,则x+y=________.8、若x+y=5,xy=6,则x 2+y 2=__________.9、利用乘法公式计算:1012=___________;1232-124×122=____________.10、若A=(2-1)(2+1)(22+1)(24+1)……(232+1)+1,则A 的个位数字是___________.二、精心选一选(每小题3分,共30分)1、计算结果是2x 2-x -3的是( ) A.(2x -3)(x+1) B.(2x -1)(x -3) C.(2x+3)(x -1) D.(2x -1)(x+3) 2、下列各式的计算中,正确的是( )A.(a+5)(a -5)=a 2-5B.(3x+2)(3x -2)=3x2-4 C.(a+2)(a -3)=a 2-6 D.(3xy+1)(3xy -1)=9x 2y 2-13、计算(-a+2b )2,结果是( )A. -a 2+4ab+b 2B. a 2-4ab+4b 2C. -a 2-4ab+b 2D. a 2-2ab+2b 24、设x+y=6,x -y=5,则x 2-y 2等于( )A. 11B. 15C. 30D. 605、如果(y+a )2=y 2-8y+b ,那么a 、b 的值分别为( )A. a=4,b=16B. a=-4,b=-16C. a=4,b=-16D. a=-4,b=166、若(x -2y )2=(x+2y )2+m ,则m 等于( ) A. 4xy B. -4xy C . 8xy D. -8xy 7、下列式子中,可用平方差公式计算的式子是( ) A.(a -b )(b -a ) B.(-x+1)(x -1) C.(-a -b )(-a+b ) D.(-x -1)(x+1)8、当a=-1时,代数式(a+1)2+a (a -3)的值等于( )A. -4 B . 4 C. -2 D. 2 9、两个连续奇数的平方差是( ) A. 6的倍数 B . 8的倍数 C. 12的倍数 D. 16的倍数10、将正方形的边长由acm 增加6cm ,则正方形的面积增加了( )A. 36cm 2B. 12acm 2C.(36+12a )cm 2D. 以上都不对三、用心做一做 1、化简求值(1)(x+4)(x -2)(x -4),其中x=-1(2)x (x+2y )-(x+1)2+2x ,其中x=251,y=-25.2、对于任意有理数a 、b 、c 、d ,我们规定cadb =ad-bc ,求y y x 3)(- )(2y x x+的值。
3、一个正方形的一边增加3cm ,相邻一边减少3cm ,所得矩形面积与这个正方形的每边减去1cm ,所得正方形面积相等,求这矩形的长和宽.整式单元复习【知识结构】【应用举例】一、选一选,看完四个选项后再做决定呀! 1. 下列说法正确的是( )A. 225a b 的次数是5 B. 23x yx +--不是整式 C. x 是单项式 D. 3243xy x y +的次数是72. 已知:166x y =-=,,n 为自然数,则442n n x y+的值是( )A.112B. 136-C. 136D. 112-3. 光的速度为每秒约3×108米,地球和太阳的距离约是1.5×1011米,则太阳光从太阳射到地球需要( )A. 5×102秒B. 5×103秒C. 5×104秒D. 5×105秒4. 如果118m m x x x -+=,则m 的值为( ) A. 8 B. 3 C. 4 D. 无法确定5. 若()(1)x t x ++的积中不含有x 的一次项,则t 的值为( )A. 0B. 1C. 1-D. ±16. 如图,在边长为a 的正方形内部,以一个顶点为圆心,a 为半径画弧经过与圆心相邻的两个顶点,那么阴影部分的面积为( )A.241a π B. 22πa a -C. 221π2a a -D. 221π4a a - 7. 如果2222210x xy y x y ++--+=,则x y +=( )A. 0B. 1C. 1-D. ±1二、填一填,要相信自己的能力!1. 325x y -的系数是 次数是 .2. =⋅+3332a a )a ( .3. 已知2a a m -+是关于a 的一个完全平方式,那么m = .4. 1003997⨯= .5. 23228)a a (]a )a a [(÷÷⋅÷ .6. 一个正方体的棱长是2×103毫米,则它的表面积是平方毫米,它的体积是 立方毫米.7. 若除式为21x +,商式为21x -,余式为2x ,则被除式为 .8. 三个连续奇数,中间一个是21n +,则这三个数的和是 .三、做一做,要注意认真审题呀! 1. 化简:(25)(25)(21)(23)m m m m -+---;解:2. 化简求值:2(2)(2)()2(2)(2)a b a b a b a b a b +--+--+·(a+2b ),其中2b ,21a -==解:3. 已知21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,……(1)你能按此推测264的个位数字是多少吗?(2)根据上面的结论,结合计算,请估计一下:(2-1)(2+1)(22+1)(24+1)…(232+1)的个位数字是多少吗?解:6. 已知2326212ab c ===,,,试找出a 、b 、c之间的等量关系.解:7. 已知除式是5m 2,商式是2341m m --,余式是23m -,求被除式.【模拟试题】(答题时间:45分钟)一、选一选,看完四个选项后再做决定呀! 1. 下列运算正确的是( )A. 2628a a a += B. 220a a ÷=C.D. a a 1a 2=⋅-*2. 若单项式4123a xy --与313a b x y +是同类项,则两个单项式的积是( )A. 64x y B. 32x y -C. 3283x y -D. 64x y -*3. 如果关于x 的多项式2ax abx b -+与22bx abx a ++的和是一个单项式,那么a 与b 的关系是( )A. a b =B. a b =-或2b a =-C. a b =或0b =D. 1ab =4. 已知33282n⨯=,则n 的值为( ) A. 18 B. 7 C. 8 D. 125. 计算2002200120032(1.5)(1)3⎛⎫⨯⨯- ⎪⎝⎭的结果是( ) A. 23 B. 23- C. 32 D. 32-6. 设(3)(7)(2)(8)A x x B x x =--=--,,则A ,B 的关系为( )A. A >BB. A <BC. A =BD. 无法确定7. 若32144mnx y x y x ÷=,则( ) A. 51m n ==, B. 50m n ==, C. 60m n ==, D. 61m n ==,8. 三个连续奇数,最小的一个为n ,则它们的积为( )A. 3268n n n ++B. 3232n n n ++C. 3386n n n ++ D. 34n n - 二、填一填,要相信自己的能力!(每小题3分,共30分)1. 观察下列单项式:23452481632x x x x x ---,,,,,…根据你发现的规律,第n 个单项式是 .第2008个单项式是 .2. 多项式32223x x y y -+是 次项式,最高次项的系数是 .3. )a ()a (a 43-⋅-- .4. 已知2()P ab =-,则2P -= .5.437()()x x -÷-=,02(2005)3--+= .6. 2213213x x x ⎛⎫--+-= ⎪⎝⎭. 7. 如果22()4x a x kx +=++,则a = ,k = .8. 22(6)(6)x x ---= .三、做一做,要注意认真审题呀!1.计算:344321044)x (5x 2)x 2(x 2)x 2(⋅+-⋅+-.2.化简求值:2[(2)(2)4(2)]3y x x y x y y -----÷,其中13x y ==-,.3.一个多项式与多项式22242a b b ab --+的差比24ab b -小223a b b --,求这个多项式.4. 在28x px ++与23x x q -+的积中不含3x 与x 的项,求p ,q 的值.5已知312a b ab +==-,,求下列各式的值. (1)22a b +;(2)22a ab b -+;(3)2()a b -. .一元一次方程的解法【典型例题】例1、已知方程122x =与38x kx +=的解相同,则k = .例2、已知:2x =-是方程215(2)3mx x =+-的解. 求:(1)m 的值;(2)式子20062)1711(+-m m 的值.例3、若134x x -=,变形为4312x x -=,其依据是______________.例4、已知19303x y --=,经过观察与思考,可求得3x y -的值是( )A. 1-B. 3C. 1D.19例5、下列是一元一次方程的是( ) A. 872240+=⨯ B. 938x x =- C. 53y -D. 210x x +-=【能力提升】:已知2x =时,式子234ax x +-的值为10,求当2x =-时,这个式子的值是多少?例6、解方程:(1)2131x x +=+;(2)72xx =+.解:例7、解方程:2559x x -+=-+. 解:例8、解方程:2(3)5(1)2x x +--=.解: 例9、解方程:124332x x x -+--=. 解:例10、解方程 2211632x x x -+--=+解:【【模拟试题】一、填一填,要相信自己的能力!1. 若253x x =-+,则2x + 3=,依据是 . 2. 若134x x -=,变形为4312x x -=,其依据是 .3. 下列各数:0, 1,2,1-,2-,其中是一元一次方程71032xx -=+的解的是 . 4. 写出一个一元一次方程,使它的解为2-,这个方程可以是 .5. 某数的一半减去3所得的差比该数的2倍大3,若设该数为x ,可列方程为 .6. 甲、乙两运输队,甲队32人,乙队28人,若从乙队调x 人到甲队,那么甲队人数恰好是乙队人数的2倍,列出方程322(28)x x +=-所依据的相等关系是 . (填题目中的原话)7. 已知4x =是关于x 的一元一次方程(即x 为未知数)332xa x -=+的解,则a = .8. 甲、乙两个工程队共有100人,甲队人数比乙队人数的4倍少10人,求甲、乙两个工程队各有多少人?如果设乙队有x 人,那么甲队有 人,由题意可得方程为 .二、选一选,看完四个选项后再做决定呀!1. 在①231x y +-;②17158+=-+;③1112x x -=+;④23x y +=中,方程有( )A. 1个B. 2个C. 3个D. 4个 2. 下列是一元一次方程的是( ) A. 872240+=⨯ B. 938x x =- C. 53y -D. 210x x +-=3. 2x =是下列哪个方程的解( )A. 26x =B. (3)(2)0x x --=C. 230x -=D. 063=⋅x4. x y ,是两个有理数,“x 与y 的和的2倍等于4”用式子表示为( )A. 24x y ++=B. 24x y +=C. 2()4x y +=D. 以上都不对5. 根据下列条件可列出一元一次方程的是( ) A. a 与1的和的3倍 B. 甲数的2倍与乙数的3倍的和C. a 与b 的差的20%D. 一个数的3倍是5 6. 下列方程求解正确的是( )A. 32x =-的解是23x =- B. 232x x +=-的解是1x =C. 351x x =-的解是12x =-D. 334x =的解是3x =7. 对于等式1213x x +=,下列变形正确的是( )A. 1213x x -=-B. 1213x x -=-C. 1213x x -= D. 32x x -=8. 下列等式必能成立的是( ) A. 2470y +=B. 12p p +=-C. 2332a b b a +=+D. 7|11|8x -=-三、做一做,要注意认真审题呀!1.已知2x =时,式子234ax x +-的值为10,求当2x =-时,这个式子的值是多少?2.某风景区集体门票的收费标准是:20人以内(含20人)每人25元;超过20人的,超过的人数每人10元.(1)对有x人(x大于或等于20人)的旅行团,应收多少门票费?(用含x的式子表示).(2)班主任老师带领初一(2)班的全体同学去该风景区游玩,买门票共用去840元,问他们共有多少人?平行线与相交线单元复习1、余角与补角的定义,判定方法。
