AMC 美国数学竞赛试题 详解 英文版
AMC 美国数学竞赛 2002 AMC 10A 试题及答案解析

2002 AMC 10A1、The ratio is closest to which of the following numbers?SolutionWe factor as . As , ouranswer is .2、For the nonzero numbers , , , define.Find .Solution. Ouranswer is then .Alternate solution for the lazy: Without computing the answer exactly,we see that , , and . The sumis , and as all the options are integers, the correct one is obviously .3、According to the standard convention for exponentiation,.If the order in which the exponentiations are performed is changed, how many other values are possible?SolutionThe best way to solve this problem is by simple brute force.It is convenient to drop the usual way how exponentiation is denoted,and to write the formula as , where denotes exponentiation. We are now examining all ways to add parentheses to this expression. There are 5 ways to do so:1.2.3.4.5.We can note that . Therefore options 1 and 2 are equal, and options 3 and 4 are equal. Option 1 is the one given in the problem statement. Thus we only need to evaluate options 3 and 5.Thus the only other result is , and our answer is .4、For how many positive integers does there exist at least one positive integer such that ?infinitely manySolutionSolution 1For any we can pick , we get , therefore theanswer is .Solution 2Another solution, slightly similar to this first one would be using Simon's Favorite Factoring Trick.Let , thenThis means that there are infinitely many numbers that can satisfythe inequality. So the answer is .5、Each of the small circles in the figure has radius one. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region.SolutionThe outer circle has radius , and thus area . The littlecircles have area each; since there are 7, their total area is . Thus,our answer is .6、Cindy was asked by her teacher to subtract from a certain numberand then divide the result by . Instead, she subtracted and thendivided the result by , giving an answer of . What would heranswer have been had she worked the problem correctly?SolutionWe work backwards; the number that Cindy started with is. Now, the correct result is . Ouranswer is .7、If an arc of on circle has the same length as an arc of oncircle , then the ratio of the area of circle to the area of circle isSolutionLet and be the radii of circles A and B, respectively.It is well known that in a circle with radius r, a subtended arc oppositean angle of degrees has length .Using that here, the arc of circle A has length . The arcof circle B has length . We know that they are equal,so , so we multiply through and simplify to get . As all circles are similar to one another, the ratio of the areas is just thesquare of the ratios of the radii, so our answer is .8、Betsy designed a flag using blue triangles, small white squares, anda red center square, as shown. Let be the total area of the bluetriangles, the total area of the white squares, and the area of thered square. Which of the following is correct?SolutionThe blue that's touching the center red square makes up 8 triangles, or 4 squares. Each of the corners is 2 squares and each of the edges is 1, totaling 12 squares. There are 12 white squares, thus we have.9、There are 3 numbers A, B, and C, such that ,and . What is the average of A, B, and C?More than 1SolutionNotice that we don't need to find what A, B, and C actually are, just their average. In other words, if we can find A+B+C, we will be done.Adding up the equations gives soand the average is . Our answer is .10、Compute the sum of all the roots of.SolutionSolution 1We expand to get which isafter combining like terms. Using the quadratic partof Vieta's Formulas, we find the sum of the roots is . Solution 2Combine terms to get, hence the rootsare and , thus our answer is .11、Jamal wants to store computer files on floppy disks, each ofwhich has a capacity of megabytes (MB). Three of his files requireMB of memory each, more require MB each, and theremaining require MB each. No file can be split between floppydisks. What is the minimal number of floppy disks that will hold all the files?SolutionA 0.8 MB file can either be on its own disk, or share it with a 0.4 MB. Clearly it is not worse to pick the second possibility. Thus we will have 3 disks, each with one 0.8 MB file and one 0.4 MB file.We are left with 12 files of 0.7 MB each, and 12 files of 0.4 MB each.Their total size is MB. The total capacity of 9 disks is MB, hence we need at least 10 more disks. And wecan easily verify that 10 disks are indeed enough: six of them will carry two 0.7 MB files each, and four will carry three 0.4 MB files each.Thus our answer is .12、Mr. Earl E. Bird leaves his house for work at exactly 8:00 A.M. every morning. When he averages miles per hour, he arrives at hisworkplace three minutes late. When he averages miles per hour, hearrives three minutes early. At what average speed, in miles per hour, should Mr. Bird drive to arrive at his workplace precisely on time?SolutionSolution 1Let the time he needs to get there in be t and the distance he travelsbe d. From the given equations, we know that and. Setting the two equal, we have andwe find of an hour. Substituting t back in, we find . From, we find that r, and our answer, is .Solution 2Since either time he arrives at is 3 minutes from the desired time, the answer is merely the harmonic mean of 40 and 60. The harmonicmean of a and b is . In this case, a and b are 40 and 60,so our answer is , so .Solution 3A more general form of the argument in Solution 2, with proof:Let be the distance to work, and let be the correct average speed.Then the time needed to get to work is .We know that and . Summing these twoequations, we get: .Substituting and dividing both sides by , we get ,hence .(Note that this approach would work even if the time by which he is late was different from the time by which he is early in the other case - we would simply take a weighed sum in step two, and hence obtaina weighed harmonic mean in step three.)13、Give a triangle with side lengths 15, 20, and 25, find the triangle's smallest height.SolutionSolution 1This is a Pythagorean triple (a 3-4-5 actually) with legs 15 and 20. Thearea is then . Now, consider an altitude drawn to anyside. Since the area remains constant, the altitude and side to which it is drawn are inversely proportional. To get the smallest altitude, it must be drawn to the hypotenuse. Let the length be x; we have, so and x is 12. Our answer is then.Solution 2By Heron's formula, the area is , hence the shortest altitude'slength is .14、Both roots of the quadratic equation are prime numbers. The number of possible values of isSolutionConsider a general quadratic with the coefficient of being and theroots being and . It can be factored as which is just. Thus, the sum of the roots is the negative of the coefficient of and the product is the constant term. (In general, this leads to Vieta's Formulas).We now have that the sum of the two roots is while the product is. Since both roots are primes, one must be , otherwise the sumwould be even. That means the other root is and the product mustbe . Hence, our answer is .15、Using the digits 1, 2, 3, 4, 5, 6, 7, and 9, form 4 two-digit prime numbers, using each digit only once. What is the sum of the 4 prime numbers?SolutionOnly odd numbers can finish a two-digit prime number, and a two-digit number ending in 5 is divisible by 5 and thus composite,hence our answer is .(Note that we did not need to actually construct the primes. If we had to, one way to match the tens and ones digits to form four primes is , , , and .)16、Let . What is?SolutionLet . Since one ofthe sums involves a, b, c, and d, it makes sense to consider 4x. We have. Rearranging, we have , so .Thus, our answer is .17、Sarah pours four ounces of coffee into an eight-ounce cup and fourounces of cream into a second cup of the same size. She then transfers half the coffee from the first cup to the second and, after stirring thoroughly, transfers half the liquid in the second cup back to the first. What fraction of the liquid in the first cup is now cream?SolutionWe will simulate the process in steps.In the beginning, we have:▪ounces of coffee in cup▪ounces of cream in cupIn the first step we pour ounces of coffee from cup to cup ,getting:▪ounces of coffee in cup▪ounces of coffee and ounces of cream in cupIn the second step we pour ounce of coffee and ounces of cream from cup to cup , getting:▪ounces of coffee and ounces of cream in cup▪the rest in cupHence at the end we have ounces of liquid in cup , and outof these ounces is cream. Thus the answer is .18、A cube is formed by gluing together 27 standard cubicaldice. (On a standard die, the sum of the numbers on any pair of opposite faces is 7.) The smallest possible sum of all the numbers showing on the surface of the cube isSolutionIn a 3x3x3 cube, there are 8 cubes with three faces showing, 12 with two faces showing and 6 with one face showing. The smallest sum with three faces showing is 1+2+3=6, with two faces showing is 1+2=3, and with one face showing is 1. Hence, the smallest possiblesum is . Our answer is thus.19、Spot's doghouse has a regular hexagonal base that measures oneyard on each side. He is tethered to a vertex with a two-yard rope.What is the area, in square yards, of the region outside of the doghouse that Spot can reach?SolutionPart of what Spot can reach is of a circle with radius 2, whichgives him . He can also reach two parts of a unit circle, whichcombines to give . The total area is then , which gives .20、Points and lie, in that order, on , dividing it intofive segments, each of length 1. Point is not on line . Point lieson , and point lies on . The line segments andare parallel. Find .SolutionAs is parallel to , angles FHD and FGA are congruent. Also,angle F is clearly congruent to itself. From SSS similarity,; hence . Similarly, . Thus,.21、The mean, median, unique mode, and range of a collection of eight integers are all equal to 8. The largest integer that can be an element of this collection isSolutionAs the unique mode is , there are at least two s.As the range is and one of the numbers is , the largest one can beat most .If the largest one is , then the smallest one is , and thus the meanis strictly larger than , which is a contradiction.If the largest one is , then the smallest one is . This means that wealready know four of the values: , , , . Since the mean of all thenumbers is , their sum must be . Thus the sum of the missing fournumbers is . But if is the smallest number,then the sum of the missing numbers must be at least ,which is again a contradiction.If the largest number is , we can easily find the solution. Hence, our answer is .NoteThe solution for is, in fact, unique. As the median must be , thismeans that both the and the number, when ordered by size,must be s. This gives the partial solution . For themean to be each missing variable must be replaced by the smallestallowed value.22、A sit of tiles numbered 1 through 100 is modified repeatedly by the following operation: remove all tiles numbered with a perfect square, and renumber the remaining tiles consecutively starting with 1. How many times must the operation be performed to reduce the number of tiles in the set to one?SolutionSolution 1The pattern is quite simple to see after listing a couple of terms.Solution 2Given tiles, a step removes tiles, leaving tiles behind. Now,, so in the next step tilesare removed. This gives , another perfect square.Thus each two steps we cycle down a perfect square, and insteps, we are left with tile, hence our answer is.23、Points and lie on a line, in that order, with and. Point is not on the line, and . The perimeterof is twice the perimeter of . Find .SolutionFirst, we draw an altitude to BC from E.Let it intersect at M. As triangle BEC is isosceles, we immediately get MB=MC=6, so the altitude is 8. Now, let . Using the Pythagorean Theorem on triangleEMA, we find . From symmetry,as well. Now, we use the fact that the perimeter of is twice the perimeter of .We have so. Squaring both sides, we havewhich nicely rearranges into. Hence, AB is 9 so our answer is .24、Tina randomly selects two distinct numbers from the setand Sergio randomly selects a number from the set. The probability that Sergio's number is larger than the sum of the two numbers chosen by Tina isSolutionThis is not too bad using casework.Tina gets a sum of 3: This happens in only one way (1,2) and Sergio can choose a number from 4 to 10, inclusive. There are 7 ways that Sergio gets a desirable number here.Tina gets a sum of 4: This once again happens in only one way (1,3). Sergio can choose a number from 5 to 10, so 6 ways here.Tina gets a sum of 5: This can happen in two ways (1,4) and (2,3). Sergio can choose a number from 6 to 10, so 2*5=10 ways here.Tina gets a sum of 6: Two ways here (1,5) and (2,4). Sergio can choose a number from 7 to 10, so 2*4=8 here.Tina gets a sum of 7: Two ways here (2,5) and (3,4). Sergio can choose from 8 to 10, so 2*3=6 ways here.Tina gets a sum of 8: Only one way possible (3,5). Sergio chooses 9 or 10, so 2 ways here.Tina gets a sum of 9: Only one way (4,5). Sergio must choose 10, so 1 way.In all, there are ways. Tina chooses twodistinct numbers in ways while Sergio chooses a number inways, so there are ways in all. Since , ouranswer is .25、In trapezoid with bases and , we have ,, , and . The area of isSolutionSolution 1It shouldn't be hard to use trigonometry to bash this and find the height, but there is a much easier way. Extend and to meet atpoint :Since we have , with the ratio ofproportionality being . Thus So the sides of are , which we recognize to be aright triangle. Therefore (we could simplify some of the calculation using that the ratio of areas is equal to the ratio of the sides squared),Solution 2Draw altitudes from points and :Translate the triangle so that coincides with . We getthe following triangle:The length of in this triangle is equal to the length of the original, minus the length of . Thus .Therefore is a well-known right triangle. Its area is, and therefore its altitude is.Now the area of the original trapezoid is.。
美国数学竞赛AMC8 -- 2005年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2005年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:If x is the number, then 2x=60 and x=30. Dividing the number by 2 yields 15.中文解析:按照Connie的计算,这个数乘以2是60,可知这个数是30. 应该做的计算是30除以2,因而正确答案应该是15. 答案是B。
Problem 2Answer: CSolution:Karl paid 5*2.5=$12.5. 20% of this cost that he saved is 12.5*0.2=$2.5.中文解析:Karl按原价买了5个文件夹,支付的费用是:2.5*5=12.5. 折扣价是:1.25*0.8=10。
如果Karl 等一天,可以省2.5元。
答案是C.Problem 3Answer: DSolution:Rotating square ABCD counterclockwise 45° so that the line of symmetry BD is a vertical line makes it easier to see that 4 squares need to be colored to match its corresponding square.中文解析:如上图所示,以BD为对称轴,标蓝色的方块需要涂黑。
共4块,答案是D。
Problem 4Answer: CSolution:The perimeter of the triangle is 6.1+8.2+9.7=24cm. A square's perimeter is four times its side length, since all its side lengths are equal. If the square's perimeter is 24, the side length is24/4=6, and the area is 6*6=36.中文解析:三角形的周长是:6.1+8.2+9.7=24. 正方形的周长和三角形相等,也是24,则其边长是24/4=6. 其面积是:6*6=36. 答案是C。
AMC 美国数学竞赛 2000 AMC 10 试题及答案解析

USA AMC 10 20001In the year , the United States will host the International Mathematical Olympiad. Let , , and be distinct positive integers such that the product . What's the largest possible value of the sum ?SolutionThe sum is the highest if two factors are the lowest.So, and .2Solution.3Each day, Jenny ate of the jellybeans that were in her jar at the beginning of the day. At the end of the second day, remained. How many jellybeans were in the jar originally?Solution4Chandra pays an online service provider a fixed monthly fee plus an hourly charge for connect time. Her December bill was , but in January her bill was because she used twice as much connect time as in December. What is the fixxed monthly fee?SolutionLet be the fixed fee, and be the amount she pays for the minutes she used in the first month.We want the fixed fee, which is5Points and are the midpoints of sides and of . As moves along a line that is parallel to side , how many of the four quantities listed below change?(a) the length of the segment(b) the perimeter of(c) the area of(d) the area of trapezoidSolution(a) Clearly does not change, and , so doesn't change either.(b) Obviously, the perimeter changes.(c) The area clearly doesn't change, as both the base and its corresponding height remain the same.(d) The bases and do not change, and neither does the height, so the trapezoid remains the same.Only quantity changes, so the correct answer is .6The Fibonacci Sequence starts with two 1s and each term afterwards is the sum of its predecessors. Which one of the ten digits is the last to appear in thet units position of a number in the Fibonacci Sequence?SolutionThe pattern of the units digits areIn order of appearance:.is the last.7In rectangle , , is on , and and trisect . What is the perimeter of ?Solution.Since is trisected, .Thus,.Adding, .8At Olympic High School, of the freshmen and of the sophomores took the AMC-10. Given that the number of freshmen and sophomore contestants was the same, which of the following must be true?There are five times as many sophomores as freshmen.There are twice as many sophomores as freshmen.There are as many freshmen as sophomores.There are twice as many freshmen as sophomores.There are five times as many freshmen as sophomores.SolutionLet be the number of freshman and be the number of sophomores.There are twice as many freshmen as sophomores.9If , where , thenSolution, so ...10The sides of a triangle with positive area have lengths , , and . The sides of a second triangle with positive area have lengths , , and . What is the smallest positive number that is not a possible value of ?SolutionFrom the triangle inequality, and . The smallest positive number not possible is , which is .11Two different prime numbers between and are chosen. When their sum is subtracted from their product, which of the following numbers could be obtained?SolutionTwo prime numbers between and are both odd.Thus, we can discard the even choices.Both and are even, so one more than is a multiple of four.is the only possible choice.satisfy this, .12Figures , , , and consist of , , , and nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure 100?SolutionSolution 1We have a recursion:.I.E. we add increasing multiples of each time we go up a figure. So, to go from Figure 0 to 100, we add.Solution 2We can divide up figure to get the sum of the sum of the firstodd numbers and the sum of the first odd numbers. If you do not see this, here is the example for :The sum of the first odd numbers is , so for figure , there are unit squares. We plug in to get , which is choice13There are 5 yellow pegs, 4 red pegs, 3 green pegs, 2 blue pegs, and 1 orange peg to be placed on a triangular peg board. In how many ways can the pegs be placed so that no (horizontal) row or (vertical) column contains two pegs of the same color?SolutionIn each column there must be one yellow peg. In particular, in the rightmost column, there is only one peg spot, therefore a yellow peg must go there.In the second column from the right, there are two spaces for pegs. One of them is in the same row as the corner peg, so there is only one remaining choice left for the yellow peg in this column.By similar logic, we can fill in the yellow pegs as shown:After this we can proceed to fill in the whole pegboard, so there is only arrangement of the pegs. The answer is14Mrs. Walter gave an exam in a mathematics class of five students. She entered the scores in random order into a spreadsheet, which recalculated the class average after each score was entered. Mrs. Walter noticed that after each score was entered, the average was always an integer. The scores (listed in ascending order) were , , , , and . What was the last score Mrs. Walter entered? SolutionThe sum of the first scores must be even, so we must choose evens or the odds to be the first two scores.Let us look at the numbers in mod .If we choose the two odds, the next number must be a multiple of , of which there is none.Similarly, if we choose or , the next number must be a multiple of , of which there is none.So we choose first.The next number must be 1 in mod 3, of which only remains.The sum of the first three scores is . This is equivalent to in mod .Thus, we need to choose one number that is in mod . is the only one that works.Thus, is the last score entered.15Two non-zero real numbers, and , satisfy . Which of the following is a possible value of ?SolutionSubstituting , we get16The diagram shows lattice points, each one unit from its nearest neighbors. Segment meets segment at . Find the length of segment .SolutionSolution 1Let be the line containing and and let be the line containing and . If we set the bottom left point at , then , , , and .The line is given by the equation . The -intercept is , so . We are given two points on , hence we cancompute the slope, to be , so is the lineSimilarly, is given by . The slope in this case is , so . Plugging in the point gives us , so is the line .At , the intersection point, both of the equations must be true, soWe have the coordinates of and , so we can use the distance formula here:which is answer choiceSolution 2Draw the perpendiculars from and to , respectively. As it turns out, . Let be the point on for which ., and , so by AA similarity,By the Pythagorean Theorem, we have ,, and . Let , so , thenThis is answer choiceAlso, you could extend CD to the end of the box and create two similar triangles. Then use ratios and find that the distance is 5/9 of the diagonal AB. Thus, the answer is B.17Boris has an incredible coin changing machine. When he puts in a quarter, it returns five nickels; when he puts in a nickel, it returns five pennies; and when he puts in a penny, it returns five quarters. Boris starts with just one penny. Which of the following amounts could Boris have after using the machine repeatedly?SolutionConsider what happens each time he puts a coin in. If he puts in a quarter, he gets five nickels back, so the amount of money he has doesn't change. Similarly, if he puts a nickel in the machine, he gets five pennies back and the money value doesn't change. However, if he puts a penny in, he gets five quarters back, increasing the amount of money he has by cents.This implies that the only possible values, in cents, he can have are the ones one more than a multiple of . Of the choices given, the only one is18Charlyn walks completely around the boundary of a square whose sides are each km long. From any point on her path she can see exactly km horizontally in all directions. What is the area of the region consisting of all points Charlyn can see during her walk, expressed in square kilometers and rounded to the nearest whole number?SolutionThe area she sees looks at follows:The part inside the walk has area . The part outside the walk consists of four rectangles, and four arcs. Each of the rectangles has area . The four arcs together form a circle with radius . Therefore the total area she can see is, which rounded to the nearest integer is .19Through a point on the hypotenuse of a right triangle, lines are drawn parallel to the legs of the triangle so that the trangle is divided into a square and two smaller right triangles. The area of one of the two small right triangles is times the area of the square. The ratio of the area of the other small right triangle to the area of the square is SolutionLet the square have area , then it follows that the altitude of one of the triangles is . The area of the other triangle is .By similar triangles, we haveThis is choice(Note that this approach is enough to get the correct answer in the contest. However, if we wanted a completely correct solution, we should also note that scaling the given triangle times changes each of the areas times, and therefore it does not influence the ratio of any two areas. This is why we can pick the side of the square.)20Let , , and be nonnegative integers such that . What is the maximum value of ? SolutionThe trick is to realize that the sum is similar to the product .If we multiply , we get.We know that , therefore.Therefore the maximum value of is equal to the maximum value of . Now we will find this maximum.Suppose that some two of , , and differ by at least . Then this triple is surely not optimal.Proof: WLOG let . We can then increase the value ofby changing and .Therefore the maximum is achieved in the cases where is a rotation of . The value of in this case is . And thus the maximum of is.21If all alligators are ferocious creatures and some creepy crawlers are alligators, which statement(s) must be true?I. All alligators are creepy crawlers.II. Some ferocious creatures are creepy crawlers.III. Some alligators are not creepy crawlers.SolutionWe interpret the problem statement as a query about three abstract concepts denoted as "alligators", "creepy crawlers" and "ferocious creatures". In answering the question, we may NOT refer to reality -- for example to the fact that alligators do exist.To make more clear that we are not using anything outside the problem statement, let's rename the three concepts as , , and .We got the following information:▪If is an , then is an .▪There is some that is a and at the same time an .We CAN NOT conclude that the first statement is true. For example, the situation "Johnny and Freddy are s, but only Johnny is a "meets both conditions, but the first statement is false.We CAN conclude that the second statement is true. We know that there is some that is a and at the same time an . Pick one such and call it Bobby. Additionally, we know that if is an , then is an. Bobby is an , therefore Bobby is an . And this is enough to prove the second statement -- Bobby is an that is also a .We CAN NOT conclude that the third statement is true. For example, consider the situation when , and are equivalent (represent the same set of objects). In such case both conditions are satisfied, but the third statement is false.Therefore the answer is .22One morning each member of Angela's family drank an -ounce mixture of coffee with milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. How many people are in the family?SolutionThe exact value "8 ounces" is not important. We will only use the fact that each member of the family drank the same amount.Let be the total number of ounces of milk drank by the family and the total number of ounces of coffee. Thus the whole family drank a total of ounces of fluids.Let be the number of family members. Then each family member drank ounces of fluids.We know that Angela drank ounces of fluids.As Angela is a family member, we have .Multiply both sides by to get .If , we have .If , we have .Therefore the only remaining option is .23When the mean, median, and mode of the list are arranged in increasing order, they form a non-constant arithmetic progression. What is the sum of all possible real values of ? SolutionAs occurs three times and each of the three other values just once, regardless of what we choose the mode will always be .The sum of all numbers is , therefore the mean is .The six known values, in sorted order, are . From this sequence we conclude: If , the median will be . If , the median will be . Finally, if , the median will be .We will now examine each of these three cases separately.In the case , both the median and the mode are 2, therefore we can not get any non-constant arithmetic progression.In the case we have , because. Therefore our three values inorder are . We want this to be an arithmetic progression. From the first two terms the difference must be . Therefore thethird term must be .Solving we get the only solution for this case: . The case remains. Once again, we have ,therefore the order is . The only solution is when , i. e., .The sum of all solutions is therefore .24Let be a function for which . Find the sum of all values of for which .SolutionIn the definition of , let . We get: . As we have , we must have , in other words .One can now either explicitly compute the roots, or use Vieta's formulas. According to them, the sum of the roots ofis . In our case this is .(Note that for the above approach to be completely correct, we should additionally verify that there actually are two distinct real roots. This is, for example, obvious from the facts that and .)25In year , the day of the year is a Tuesday. In year , the day is also a Tuesday. On what day of the week did the of year occur?SolutionClearly, identifying what of these years may/must/may not be a leap year will be key in solving the problem.Let be the day of year , the day of year and the day of year .If year is not a leap year, the day will bedays after . As , that would be a Monday.Therefore year must be a leap year. (Then is days after .) As there can not be two leap years after each other, is not a leap year. Therefore day is days after . We have . Therefore is weekdays before , i.e., is a.(Note that the situation described by the problem statement indeed occurs in our calendar. For example, for we have=Tuesday, October 26th 2004, =Tuesday, July 19th, 2005 and =Thursday, April 10th 2003.)。
美国数学竞赛AMC8 -- 2008年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2008年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:50-12-24=14中文解析:总共花的钱是:12+12*2=36元。
剩余50-36=14元。
答案是BProblem 2Answer: ASolution:We can derive that c=8,L=6, U=7,and E=1. Therefore, the answer is 8671.中文解析:这10个字母的对应关系是: B -0;E-1; S-2; ......K -9. 按照这个对应关系:C-8,L-6,U-7,E-1. 即8671. 答案是A。
Problem 3Answer: ASolution:We can go backwards by days, but we can also backwards by weeks. If we go backwards by weeks, we see that February 6 is a Friday. If we now go backwards by days, February 1 is a Sunday.中文解析:13日是周五,则13-7=6,即6日也是周五,则倒推2月1日是周日。
答案是A。
Problem 4Answer: CSolution:The area outside the small triangle but inside the large triangle is 16-1=15. This is equally distributed between the three trapezoids. Each trapezoid has an area of 15/3=5.中文解析:大三角形的面积等于小的等边三角形的面积加上3个梯形的面积。
据此,三个梯形的面积是16-1=15. 每个梯形的面积是15/3=5. 答案是C。
AMC 美国数学竞赛试题+详解 英文版

2013 AMC8 Problems1.Danica wants to arrange her model cars in rows with exactly 6 cars in each row. She now has 23 model cars. What is the smallest number of additional cars she must buy in order to be able to arrange all her cars this way?2.A sign at the fish market says, "50% off, today only: half-pound packages for just $3 perpackage." What is the regular price for a full pound of fish, in dollars?What is the value of?3.4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill? 5.Hammie is in thegrade and weighs 106 pounds. His quadruplet sisters are tiny babiesand weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11.Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12.At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13.When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14.Abe holds 1 green and 1 red jelly bean in his hand. Bea holds 1 green, 1 yellow, and 2 red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?15.If , , and , what is the product of , , and ?16.A number of students from Fibonacci Middle School are taking part in a community serviceproject. The ratio of -graders to -graders is , and the the ratio of -graders to-graders is . What is the smallest number of students that could be participating in the project?17.The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18.Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?19.Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20.A rectangle is inscribed in a semicircle with longer side on the diameter. What is thearea of the semicircle?21.Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23.Angle of is a right angle. The sides of are the diameters of semicirclesas shown. The area of the semicircle on equals , and the arc of the semicircle onhas length . What is the radius of the semicircle on ?24.Squares , , and are equal in area. Points and are the midpointsof sides and , respectively. What is the ratio of the area of the shaded pentagonto the sum of the areas of the three squares?25.A ball with diameter 4 inches starts at point A to roll along the track shown. The track iscomprised of 3 semicircular arcs whose radii are inches, inches, andinches, respectively. The ball always remains in contact with the track and does notslip. What is the distance the center of the ball travels over the course from A to B?2013 AMC8 Problems/Solutions1. ProblemDanica wants to arrange her model cars in rows with exactly 6 cars in each row. She now has 23 model cars. What is the smallest number of additional cars she must buy in order to be able to arrange all her cars this way?Solution:In order to have her model cars in perfect, complete rows of 6, Danica must have a number ofcars that is a multiple of 6. The smallest multiple of 6 which is larger than 23 is 24, so she'll need to buy more model car.2.A sign at the fish market says, "50% off, today only: half-pound packages for just $3 per package." What is the regular price for a full pound of fish, in dollars?ProblemSolution: The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.What is the value of?3. ProblemNotice that we can pair up every two numbers to make a sum of 1:SolutionTherefore, the answer is .4. ProblemEight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill.What was the total bill?Each of her seven friends paidto cover Judi's portion. Therefore, Judi's portion mustbe. Since Judi was supposed to payof the total bill, the total bill must be.Solution5.Hammie is in thegrade and weighs 106 pounds. His quadruplet sisters are tiny babiesand weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these fivechildren or the median weight, and by how many pounds?ProblemLining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds. SolutionThe average weight of the five kids is .Therefore, the average weight is bigger, bypounds, making the answer.6. The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example,. What is the missing number in the top row?ProblemSolutionLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.Solution 1: Working BackwardsWe see that, making.It follows that, so.Another way to do this problem is to realize what makes up the bottommost number. Thismethod doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Solution 2: Jumping Back to the StartAgain, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7. Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass,Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clearthe crossing at a constant speed. Which of the following was the most likely number of cars inthe train?ProblemIf Trey saw, then he saw.Solution 12 minutes and 45 seconds can also be expressed asseconds.Trey's rate of seeing cars,, can be multiplied byon the top andbottom (and preserve the same rate):. It follows that the most likely number of cars is.2 minutes and 45 seconds is equal to.Solution 2Since Trey probably counts around 6 cars every 10 seconds, there are groups of 6cars that Trey most likely counts. Since, the closest answer choice is.8. A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?ProblemFirst, there areways to flip the coins, in order.Solution The ways to get two consecutive heads are HHT and THH. The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9. The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then onwhich jump will he first be able to jump more than 1 kilometer?ProblemThis is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that. SolutionHowever, because the first term isand not, the solution to the problem is10. What is the ratio of the least common multiple of 180 and 594 to the greatest common factorof 180 and 594?ProblemTo find either the LCM or the GCF of two numbers, always prime factorize first. Solution 1The prime factorization of . The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in bothfactorizations and multiply. = 18. Thus the answer = =.We start off with a similar approach as the original solution. From the prime factorizations, the GCF is 18.Similar SolutionIt is a well known fact that. So we have,.Dividing by 18 yields .Therefore, .11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?ProblemWe use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, letrepresent the time.SolutionOn Monday, he was at a rate of . So,.For Wednesday, he walked at a rate of . Therefore,.On Friday, he walked at a rate of. So,. Adding up the hours yields++=.We now find the amount of time Grandfather would have taken if he walked atperday. Set up the equation,.To find the amount of time saved, subtract the two amounts: -=.To convert this to minutes, we multiply by 60.Thus, the solution to this problem is12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?ProblemFirst, find the amount of money one will pay for three sandals without the discount. We have.SolutionThen, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. ProblemWhen Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?Let the two digits be and. SolutionThe correct score was . Clara misinterpreted it as. The difference between thetwo iswhich factors into. Therefore, since the difference is a multiple of 9,the only answer choice that is a multiple of 9 is.14.Abe holds 1 green and 1 red jelly bean in his hand. Bea holds 1 green, 1 yellow, and 2 red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?ProblemThe probability that both show a green bean is. The probability that both show ared bean is . Therefore the probability isSolution15. If ,, and , what is the product of, , and ?ProblemSolutionTherefore,.Therefore,.To most people, it would not be immediately evident that , so we can multiply 6'suntil we get the desired number:, so.Therefore the answer is16. A number of students from Fibonacci Middle School are taking part in a community serviceproject. The ratio of-graders to-graders is, and the the ratio of-graders to-graders is . What is the smallest number of students that could be participating inthe project?ProblemSolutionWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Solution 1: AlgebraTherefore, the ratio of 8th graders to 7th graders to 6th graders is. Since the ratiois in lowest terms, the smallest number of students participating in the project is.The number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and7th graders. The numbers ofstudents isSolution 2: Fakesolving17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?ProblemThe mean of these numbers is. Therefore the numbers are, so the answer isSolution 1Let thenumber be . Then our desired number is.Solution 2Our integers are , so we have that.Let the first term be. Our integers are. We have,Solution 318.Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?ProblemThere arecubes on the base of the box. Then, for each of the 4 layers abovethe bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are4 feet left), there arecubes. Hence, the answer is.Solution 1 We can just calculate the volume of the prism that was cut out of the originalbox. Each interior side of the fort will be 2 feet shorter than each side of the outside. Since thefloor is 1 foot, the height will be 4 feet. So the volume of the interior box is.Solution 2The volume of the original box is . Therefore, the number of blockscontained in the fort is19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?ProblemIf Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, ifHannah did worse than Bridget, there is no way Bridget could have known that she didn't getthe highest in the class. Therefore, Hannah did better than Bridget, so our order isSolution20. Arectangle is inscribed in a semicircle with longer side on the diameter. What is thearea of the semicircle?ProblemSolutionA semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem,. The area is21. ProblemSamantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?SolutionThe number of ways to get from Samantha's house to City Park is, and the number ofways to get from City Park to school is. Since there's one way to go through CityPark (just walking straight through), the number of different ways to go from Samantha's house to City Park to school22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?ProblemThere are 61 vertical columns with a length of 32 toothpicks, and there are 33 horizontal rowswith a length of 60 toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks. Thus, our answer isSolution23.Angleof is a right angle. The sides ofare the diameters of semicircles as shown. The area of the semicircle on equals, and the arc of the semicircle onhas length . What is the radius of the semicircle on?ProblemIf the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagorean theorem says that the other side has length 15, so the radius is.Solution 1We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of the largest is , and the middle one is , so the radius is .Solution 224. Squares, , andare equal in area. Pointsandare the midpointsof sidesand, respectively. What is the ratio of the area of the shaded pentagonto the sum of the areas of the three squares?ProblemSolution 1First let(whereis the side length of the squares) for simplicity. We can extenduntil it hits the extension of. Call this point. The area of trianglethen isThe area of rectangleis. Thus, our desired area is. Now, the ratio of the shaded area to the combined area of the three squares is.Solution 2Let the side length of each square be 1.Let the intersection ofandbe .Since, . Sinceand are vertical angles, theyare congruent. We also haveby definition.So we haveby congruence. Therefore,.Since andare midpoints of sides,. This combined withyields.The area of trapezoidis.The area of triangleis.So the area of the pentagon is .The area of the 3 squares is . Therefore, .Solution 3Let the intersection of andbe .Now we haveand .Because both triangles has a side on congruent squares therefore.Becauseand are vertical angles. Also bothand are right angles so .Therefore by AAS (Angle, Angle, Side) . Then translating/rotating the shadedinto the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25.A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, andinches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of the ball travels over the course from A to B?ProblemThe radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departurefrom the length of the track means that the answer is .Solution 1The total length of all of the arcs is . Since we want the path fromthe center, the actual distance will be shorter. Therefore, the only answer choice less thanis . This solution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump. Solution 2。
2023年AMC10美国数学竞赛A卷附中文翻译和答案

2023AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) (B)(C)(D) (E)4. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) (C) (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A∪B, the union of A and B?(A) 5 (B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) (B) (C)(D) (E)8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7 (B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A) (B)(C)(D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13 (B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) (B)(C)(D) (E)15. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A) (B) (C) (D) (E)17. In the eight-term sequence A, B, C, D, E, F, G, H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17 (B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B?(B) (C) (D) (E)(A)19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2023, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) (B) (C) (D) (E)21. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) (B) (C) (D) (E)22. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A) (B) (C) (D) (E)an integer. A point X in the interior of R is25. Let R be a square region andcalled n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500 (B) 1560 (C) 2320 (D) 2480 (E) 25002023AMC10美国数学竞赛A卷1. 某通讯公司手机每月基本费为20美元, 每传送一则简讯收 5美分(一美元=100 美分)。
AMC8(美国数学竞赛)历年真题、答案及中英文解析

AMC8(美国数学竞赛)历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析:AMC8-2020年:真题 --- 答案---解析(英文解析+中文解析)AMC8 - 2019年:真题----答案----解析(英文解析+中文解析)AMC8 - 2018年:真题----答案----解析(英文解析+中文解析)AMC8 - 2017年:真题----答案----解析(英文解析+中文解析)AMC8 - 2016年:真题----答案----解析(英文解析+中文解析)AMC8 - 2015年:真题----答案----解析(英文解析+中文解析)AMC8 - 2014年:真题----答案----解析(英文解析+中文解析)AMC8 - 2013年:真题----答案----解析(英文解析+中文解析)AMC8 - 2012年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 2010年:真题----答案----解析(英文解析+中文解析)AMC8 - 2009年:真题----答案----解析(英文解析+中文解析)AMC8 - 2008年:真题----答案----解析(英文解析+中文解析)AMC8 - 2007年:真题----答案----解析(英文解析+中文解析)AMC8 - 2006年:真题----答案----解析(英文解析+中文解析)AMC8 - 2005年:真题----答案----解析(英文解析+中文解析)AMC8 - 2004年:真题----答案----解析(英文解析+中文解析)AMC8 - 2003年:真题----答案----解析(英文解析+中文解析)AMC8 - 2002年:真题----答案----解析(英文解析+中文解析)AMC8 - 2001年:真题----答案----解析(英文解析+中文解析)AMC8 - 2000年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1998年:真题----答案----解析(英文解析+中文解析)AMC8 - 1997年:真题----答案----解析(英文解析+中文解析)AMC8 - 1996年:真题----答案----解析(英文解析+中文解析)AMC8 - 1995年:真题----答案----解析(英文解析+中文解析)AMC8 - 1994年:真题----答案----解析(英文解析+中文解析)AMC8 - 1993年:真题----答案----解析(英文解析+中文解析)AMC8 - 1992年:真题----答案----解析(英文解析+中文解析)AMC8 - 1991年:真题----答案----解析(英文解析+中文解析)AMC8 - 1990年:真题----答案----解析(英文解析+中文解析)AMC8 - 1989年:真题----答案----解析(英文解析+中文解析)AMC8 - 1988年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1986年:真题----答案----解析(英文解析+中文解析)AMC8 - 1985年:真题----答案----解析(英文解析+中文解析)◆AMC介绍◆AMC(American Mathematics Competitions) 由美国数学协会(MAA)组织的数学竞赛,分为 AMC8 、 AMC10、 AMC12 。
amc 美国数学竞赛 amc 10b 试题及答案解析

2004 AMC 10BProblem 1Each row of the Misty Moon Amphitheater has 33 seats. Rows 12 through 22 are reserved for a youth club. How many seats are reserved for this club?There are rows of seats, giving seats.Problem 2How many two-digit positive integers have at least one 7 as a digit?Ten numbers () have as the tens digit. Nine numbers () have it as the ones digit. Number is in both sets.Thus the result is .Problem 3At each basketball practice last week, Jenny made twice as many free throws as she made at the previous practice. At her fifth practice she made48 free throws. How many free throws did she make at the first practice?At the fourth practice she made throws, at the third one it was , then we get throws for the second practice, and finally throws at the first one.Problem 4A standard six-sided die is rolled, and P is the product of the five numbers that are visible. What is the largest number that is certain to divide P?Solution 1The product of all six numbers is . The products of numbers that can be visible are , , ..., . The answer to this problem is their greatest common divisor -- which is , where is the least common multiple of . Clearly and the answer is .Solution 2Clearly, can not have a prime factor other than , and .We can not guarantee that the product will be divisible by , as the number can end on the bottom.We can guarantee that the product will be divisible by (one of and will always be visible), but not by .Finally, there are three even numbers, hence two of them are always visible and thus the product is divisible by . This is the most we can guarantee, as when the is on the bottom side, the two visible even numbers are and , and their product is not divisible by .Hence .Problem 5In the expression , the values of , , , and are , , , and , although not necessarily in that order. What is the maximum possible value of the result?If or , the expression evaluates to .If , the expression evaluates to .Case remains.In that case, we want to maximize where .Trying out the six possibilities we get that the best one is, where .Problem 6Which of the following numbers is a perfect square?Using the fact that , we can write:▪▪▪▪▪Clearly is a square, and as , , and are primes, none of the other four are squares.Problem 7On a trip from the United States to Canada, Isabella took U.S. dollars. At the border she exchanged them all, receiving Canadian dollars for every U.S. dollars. After spending Canadian dollars, she had Canadian dollars left. What is the sum of the digits of ?Solution 1Isabella had Canadian dollars. Setting up an equation we get, which solves to , and the sum of digits of isSolution 2Each time Isabelle exchanges U.S. dollars, she gets Canadian dollars and Canadian dollars extra. Isabelle received a total of Canadian dollars extra, therefore she exchanged U.S. dollars times. Thus .Problem 8Minneapolis-St. Paul International Airport is 8 miles southwest of downtown St. Paul and 10 miles southeast of downtown Minneapolis. Which of the following is closest to the number of miles between downtown St. Paul and downtown Minneapolis?The directions "southwest" and "southeast" are orthogonal. Thus the described situation is a right triangle with legs 8 miles and 10 mileslong. The hypotenuse length is , and thus the answer is .Without a calculator one can note that . Problem 9A square has sides of length 10, and a circle centered at one of its vertices has radius 10. What is the area of the union of the regions enclosed by the square and the circle?The area of the circle is , the area of the square is . Exactly of the circle lies inside the square. Thus the total area is.Problem 10A grocer makes a display of cans in which the top row has one can and each lower row has two more cans than the row above it. If the display contains cans, how many rows does it contain?The sum of the first odd numbers is . As in our case , we have .Problem 11Two eight-sided dice each have faces numbered 1 through 8. When the dice are rolled, each face has an equal probability of appearing on the top. What is the probability that the product of the two top numbers is greater than their sum?Solution 1We have , hence if at least one of the numbers is , the sum is larger. There such possibilities.We have .For we already have , hence all other cases are good.Out of the possible cases, we found that in the sum is greater than or equal to the product, hence in it is smaller. Therefore the answer is .Solution 2Let the two rolls be , and .From the restriction:Since and are non-negative integers between and , either , , orif and only if or .There are ordered pairs with , ordered pairs with , and ordered pair with and . So, there areordered pairs such that .if and only if and or equivalently and . This gives ordered pair .So, there are a total of ordered pairs with .Since there are a total of ordered pairs , there are ordered pairs with .Thus, the desired probability is .Problem 12An annulus is the region between two concentric circles. The concentric circles in the figure have radii and , with . Let be a radius of the larger circle, let be tangent to the smaller circle at , and let be the radius of the larger circle that contains . Let , , and . What is the area of the annulus?The area of the large circle is , the area of the small one is , hence the shaded area is .From the for the right triangle we have , hence and thus the shaded area is .Problem 13In the United States, coins have the following thicknesses: penny, mm; nickel, mm; dime, mm; quarter, mm. If a stack of these coins is exactly mm high, how many coins are in the stack?All numbers in this solution will be in hundreds of a millimeter.The thinnest coin is the dime, with thickness . A stack of dimes has height .The other three coin types have thicknesses , , and . By replacing some of the dimes in our stack by other, thicker coins, we can clearly create exactly all heights in the set.If we take an odd , then all the possible heights will be odd, and thus none of them will be . Hence is even.If the stack will be too low and if it will be too high. Thus we are left with cases and .If the possible stack heights are , with the remaining ones exceeding .Therefore there are coins in the stack.Using the above observation we can easily construct such a stack. A stack of dimes would have height , thus we need to add . This can be done for example by replacing five dimes by nickels (for ), and one dime by a penny (for ).Problem 14A bag initially contains red marbles and blue marbles only, with moreblue than red. Red marbles are added to the bag until only of the marbles in the bag are blue. Then yellow marbles are added to the baguntil only of the marbles in the bag are blue. Finally, the number of blue marbles in the bag is doubled. What fraction of the marbles now in the bag are blue?We can ignore most of the problem statement. The only important information is that immediately before the last step blue marbles formed of the marbles in the bag. This means that there were blue and other marbles, for some . When we double the number of blue marbles, there will be blue and other marbles, hence bluemarbles now form of all marbles in the bag.Problem 15Patty has coins consisting of nickels and dimes. If her nickels were dimes and her dimes were nickels, she would have cents more. How much are her coins worth?Solution 1She has nickels and dimes. Their total cost iscents. If the dimes were nickels and vice versa, she would havecents. This value should be cents more than the previous one. We get , which solves to . Her coins are worth .Solution 2Changing a nickel into a dime increases the sum by cents, and changing a dime into a nickel decreases it by the same amount. As the sum increased by cents, there are more nickels than dimes. As the total count is , this means that there are nickels and dimes.Problem 16Three circles of radius are externally tangent to each other and internally tangent to a larger circle. What is the radius of the large circle?The situation in shown in the picture below. The radius we seek is . Clearly . The point is clearly the center of the equilateral triangle , thus is of the altitude of this triangle. We get that . Therefore the radius we seek is.WARNING. Note that the answer does not correspond to any of the five options. Most probably there is a typo in option D.Problem 17The two digits in Jack's age are the same as the digits in Bill's age, but in reverse order. In five years Jack will be twice as old as Bill will be then. What is the difference in their current ages?Solution 1If Jack's current age is , then Bill's current age is .In five years, Jack's age will be and Bill's age will be .We are given that . Thus .For we get . For and the value is not an integer, and for it is more than . Thus the only solution is , and the difference in ages is .Solution 2Age difference does not change in time. Thus in five years Bill's age will be equal to their age difference.The age difference is , hence it is a multiple of . Thus Bill's current age modulo must be .Thus Bill's age is in the set .As Jack is older, we only need to consider the cases where the tens digit of Bill's age is smaller than the ones digit. This leaves us with the options .Checking each of them, we see that only works, and gives the solution .Problem 18In the right triangle , we have , , and . Points , , and are located on , , and , respectively, so that , , and . What is the ratio of the area of to that of ?First of all, note that , and therefore.Draw the height from onto as in the picture below:Now consider the area of . Clearly the triangles and are similar, as they have all angles equal. Their ratio is ,hence . Now the area of can be computed as= . Similarly we can find that as well.Hence , and the answer is .Problem 19In the sequence , , , , each term after the third is found by subtracting the previous term from the sum of the two terms that precede that term. For example, the fourth term is. What is the term in this sequence?Solution 1We already know that , , , and . Let's compute the next few terms to get the idea how the sequence behaves. We get ,, , and so on.We can now discover the following pattern: and . This is easily proved by induction. It follows that.Solution 2Note that the recurrence can be rewritten as.Hence we get that and alsoFrom the values given in the problem statement we see that .From we get that .From we get that .Following this pattern, we get.Problem 20In points and lie on and , respectively. If and intersect at so that and , what is ?Solution (Triangle Areas)We use the square bracket notation to denote area.Without loss of generality, we can assume . Then , and . We have , so we need to find the area of quadrilateral .Draw the line segment to form the two triangles and . Let , and . By considering trianglesand , we obtain , and by considering triangles and , we obtain . Solving, we get , , so the area of quadrilateral is .ThereforeSolution (Mass points)The presence of only ratios in the problem essentially cries out for mass points.As per the problem, we assign a mass of to point , and a mass of to . Then, to balance and on , has a mass of .Now, were we to assign a mass of to and a mass of to , we'd have . Scaling this down by (to get , which puts and in terms of the masses of and ), we assign a mass of to and a mass of to .Now, to balance and on , we must give a mass of . Finally, the ratio of to is given by the ratio of the mass of tothe mass of , which is .Solution (Coordinates)Affine transformations preserve ratios of distances, and for any pair of triangles there is an affine transformation that maps the first one onto the second one. This is why the answer is the same for any , and we just need to compute it for any single triangle.We can choose the points , , and . This way we will have , and . The situation is shown in the picture below:The point is the intersection of the lines and . The points on the first line have the form , the points on the second line have the form . Solving for we get , hence.The ratio can now be computed simply by observing the coordinates of , , and :Problem 21Let ; ; and ; ; be two arithmetic progressions. The set is the union of the first terms of each sequence. How many distinct numbers are in ?The two sets of terms are and.Now . We can compute. We will now find .Consider the numbers in . We want to find out how many of them lie in . In other words, we need to find out the number of valid values of for which .The fact "" can be rewritten as ", and ".The first condition gives , the second one gives .Thus the good values of are , and their count is .Therefore , and thus .Problem 22A triangle with sides of 5, 12, and 13 has both an inscribed and a circumscribed circle. What is the distance between the centers of those circles?This is obviously a right triangle. Pick a coordinate system so that the right angle is at and the other two vertices are at and .As this is a right triangle, the center of the circumcircle is in the middle of the hypotenuse, at .The radius of the inscribed circle can be computed using the well-known identity , where is the area of the triangle and its perimeter. In our case, and , thus . As the inscribed circle touches both legs, its center must be at .The distance of these two points is then.Problem 23Each face of a cube is painted either red or blue, each with probability 1/2. The color of each face is determined independently. What is the probability that the painted cube can be placed on a horizontal surface so that the four vertical faces are all the same color?Label the six sides of the cube by numbers to as on a classic dice. Then the "four vertical faces" can be: , , or .Let be the set of colorings where are all of the same color, similarly let and be the sets of good colorings for the other two sets of faces.There are possible colorings, and there are goodcolorings. Thus the result is . We need to compute .Using the we can writeClearly , as we have two possibilities for the common color of the four vertical faces, and two possibilities for each of the horizontal faces.What is ? The faces must have the same color, and at the same time faces must have the same color. It turns out thatthe set containing just the two cubes where all six faces have the same color.Therefore , and the result is .Problem 24In we have , , and . Point is on the circumscribed circle of the triangle so that bisects . What is the value of ?Problem 25A circle of radius is internally tangent to two circles of radius at points and , where is a diameter of the smaller circle. What is the area of the region, shaded in the picture, that is outside the smaller circle and inside each of the two larger circles?The area of the small circle is . We can add it to the shaded region, compute the area of the new region, and then subtract the area of the small circle from the result.Let and be the intersections of the two large circles. Connect them to and to get the picture below:Now obviously the triangles and are equilateral with side .Take a look at the bottom circle. The angle is , hence the sector is of the circle. The same is true for the sector of the bottom circle, and sectors and of the top circle.If we now sum the areas of these four sectors, we will almost get the area of the new shaded region - except that each of the two equilateral triangles will be counted twice.Hence the area of the new shaded region is, and the area of the original shared region is .。
amc 美国数学竞赛 00 amc 0b 试题及答案解析

2003 AMC 10B1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pinkpill, and Al’s pills cost a total of for the two weeks. How much doesone green pill cost?Solution3、The sum of 5 consecutive even integers is less than the sum of thefirst consecutive odd counting numbers. What is the smallest of theeven integers?Solution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the figure. She plants one flower per square foot in each region. Asters cost 1 each,begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easterlilies 3 each. What is the least possible cost, in dollars, for hergarden?Solution5、Moe uses a mower to cut his rectangular -foot by -foot lawn.The swath he cuts is inches wide, but he overlaps each cut byinches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?Solution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length ofa “-inch” television screen is closest, in inches, to which of thefollowing?Solution7、The symbolism denotes the largest integer not exceeding . Forexample. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and .Which of the following is a possible first term?Solution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?Solution11、A line with slope intersects a line with slope at the point .What is the distance between the -intercepts of these two lines?Solution12、Al, Betty, and Clare split among them to be invested indifferent ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubledtheir money, whereas Al has managed to lose . What was Al’soriginal portion?Solution.13、Let denote the sum of the digits of the positive integer . Forexample, and . For how many two-digitvalues of is ?Solution14、Given that , where both and are positive integers,find the smallest possible value for .Solution15、There are players in a singles tennis tournament. Thetournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players aregiven a bye, and the remaining players are paired off to play. Aftereach round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?Solution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is theratio of the cone’s height to its radius?Solution18、What is the largest integer that is a divisor offor all positive even integers ?Solution19、Three semicircles of radius are constructed on diameter of asemicircle of radius . The centers of the small semicircles divideinto four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside thesmaller semicircles?Solution20、In rectangle , and . Points and are onso that and . Lines and intersect at . Findthe area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes onthe hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at11:15 AM on February , , on what date will the chimeoccur?Solution23、A regular octagon has an area of one square unit.What is the area of the rectangle ?Solution24、The first four terms in an arithmetic sequence are , , ,and , in that order. What is the fifth term?Solution25、How many distinct four-digit numbers are divisible by and haveas their last two digits?Solution。
美国数学竞赛AMC8 -- 2008年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2008年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:50-12-24=14中文解析:总共花的钱是:12+12*2=36元。
剩余50-36=14元。
答案是BProblem 2Answer: ASolution:We can derive that c=8,L=6, U=7,and E=1. Therefore, the answer is 8671.中文解析:这10个字母的对应关系是: B -0;E-1; S-2; ......K -9. 按照这个对应关系:C-8,L-6,U-7,E-1. 即8671. 答案是A。
Problem 3Answer: ASolution:We can go backwards by days, but we can also backwards by weeks. If we go backwards by weeks, we see that February 6 is a Friday. If we now go backwards by days, February 1 is a Sunday.中文解析:13日是周五,则13-7=6,即6日也是周五,则倒推2月1日是周日。
答案是A。
Problem 4Answer: CSolution:The area outside the small triangle but inside the large triangle is 16-1=15. This is equally distributed between the three trapezoids. Each trapezoid has an area of 15/3=5.中文解析:大三角形的面积等于小的等边三角形的面积加上3个梯形的面积。
据此,三个梯形的面积是16-1=15. 每个梯形的面积是15/3=5. 答案是C。
美国中学数学竞赛(AMC12-12级)(附答案)

2004 AMC12 试题1. 爱丽每小时的工资为美金20元,其中的1.45%要缴地方税,试问爱丽每小时的工资中要付地方税美金多少分?(美金1元二美金100分)(A) 0.0029 (B) 0.029 (C) 0.29 (D) 2.9 (E) 292. 于AMC2的测验中,每答对一题可得6分,答错可得0分,未作答可得2.5分.假设凯琳在25题中有8题未作答,她至少要答对几题,总分才会不低于100 分?(A) 11(B) 13(C) 14(D) 16(E) 173.滿足x 2y100的正整数序对(x, y)有多少組?(A) 33(B) 49(C) 50(D) 99(E) 1004.白婆婆有6个女儿、没有儿子,有些女儿也恰有6个女儿,其他的女儿没有孩子. 白婆婆有女儿及外孙女共30位,没有外曾孙女. 试问白婆婆的女儿及外孙女中有多少位没有女儿?(A) 22 (B) 23 (C) 24 (D) 25 (E) 265.直线y mx(A) mb 1 (B) 1 mb 0 (C) mb 0 (D) 0 mb 1 (E) mb 16.设u 2 20042005, V 20042005, W 2003 20042004, X 2 20042004Y 20042004, Z 20042003.試问以下何者值最大?(A) U V (B) V W (C) W X (D) X Y (E) Y Z7. 一种代币的游戏,其规那么如下:每回持有最多代币者须分给其他每一位参与游戏者一枚代币,并放一枚代币於回收桶中;当有一位游戏参与者没有代币时,那么游戏结束.假设A、B C三人玩此游戏,在游戏开始时分别持有15、14及13枚代币.试问游戏从开始到结束,共进行了多少回?(A) 36 (B) 37 (C) 38 (D) 39 (E) 409. 有一个将花生酱装在圆桶状瓶子内出售的公司 .市场研究建议瓶子较粗时可增加销售量.假设瓶子的直径增加25%,而体积仍维持不变,那么 瓶子的高度应减少百分之多少?(A) 10(B) 25(C) 36(D) 50(E) 6010. 有49个连续整数,它的和为75,則它们排在最中间的数为何?(A) 7(B) 72(C) 73(D) 74(E) 7511. 某国的硬币中有1分、5分、10分及25分四种,在保拉的皮包 內硬币的平均值为20分.假设再增加一枚25分的硬币,平均值則增为 21分.試问她的皮包內有多少枚10分的硬币?(A) 0(B) 1(C) 2(D) 3(E) 412. 设A (0, 9) , B (0,12).点A 、B 在直线y x 上, 且AA 与BB 交于点 C (2,8).試问AB的长度是多少?(A) 2(B) 2 2(C) 3(D) 22(E) 3“13. 以S 表示坐标平面上所有的点(a,b)所形成的集合,其中a,b 等于1, 0,或1.試问有多少条相异的直线至少通过集合 S 中的两个点?(A) 8(B) 20(C) 24(D) 27(E) 3614. 三个实数的数列形成一个等差数列,首项是9.假设将第二项加2、第 三项加20可使得这三个数变为等比数列,那么这个等比数列中第三项 最小可能是多少?(A) 1(B) 4(C) 36(D) 49(E) 8115.小美与小雯在一个圆形的跑道上向相反的方向跑 ,开始两人分别从8.如下图EAB 及 ABC 为直角,厢 4 , BC 6 , AE 8, AC 与BE 交于D 点.試问 差为多少?(A) 2(B) 4(C) 5 (D) 8 (E) 9ADE 与BDC 面积之圆形跑道直径的两端起跑.小美跑了 100公尺时她们第一次相遇;在 第一次相遇后小雯跑了 150公尺时她们第二次相遇.假设她们跑的速 度都分别维持固定不变,试问此圆形跑道的长度是多少公尺?(A) 250(B) 300(C) 350(D) 400(E) 50016.使函数 log 2004{log 2003{log 2002{log 2001 X}}}有定义的集合为 之值是多少?(A) 0(B) 20012002(C) 20022003(D) 20032004{xx c}.試问 c(E) 20012°°丹317.函数f 满足以下性质: (i) f(1) 1,且(ii)对任意的正整数n ,f(2n) n f(n).试问f(2100)之值为何?(A) 1(B) 299(C) 2100(D) 24950 18.如下图,ABCD 是边长2的正方形.在正方形 的内部作一个以AB 为直径的半圆,且自C 点引 此半圆的切线交AD 边于E 点•试问CE 的长度是 多少?(E) 5 ■.5(E) 29999(B) 5 (C) 6 (D)?19.如下图,A B C 三圆彼此外切且均内切于圆等,圆A 的半径1且通过圆D 的圆心.试问圆B 的半径是多少?D.B 、C 两圆相(A)3(B)于(C) 土 (D) |20.从0与1之间的数,随机独立取出两实数a 与b,并将a, b 之和记 作c.分别以A, B, C 表示最接近a, b, c 的整数.试问 的机率为何?(A) 1(B) !(C) 1(D) 2(E) 443 23421.假设n 02nCOS5,那么Cos2之值是多少?(A) 15 (B) I (C) ±55(D) ?(E)上5522.三个半径为1的球彼此外切且放置在一水平面上,一个半径为2 的大球放在它们的上面 .试问大球的最高点至平面的距离是多 少?C 2004 0,且 P (x)=0 有 2004个复数根 z a k b k i , 20042004b k 为实数,a ib i 0,且a kb k .k 1k 1试问以下哪一项可能不是 0 ?2004(A) C 0(B)C2003(C) b z b s L b s 004 (D)a kk 124. 设A 、B 为平面上的两点,其中AB 1.令S 为平面上所有半径是1且 能盖住线段AB 之圆的并集,則S 的面积是多少?(A) 2.3(B) -(C) 33(D)卫 3(E) 4 2 33 2325. 对每一个整数n 4,令a n 表示n 进位的循环小数0.133n .把乘积a 4a 5L a 99写成—的形式,其中m P 为正整数,且p 尽可能小.试问mp!之值是多少?(A) 98(B) 101(C) 132(D) 798(E) 962Q屈o J123 52(A) 3(B) 3 -(C) 3 -(D)2349(E) 3 2、223.多项式P(x) GX C 0 ,的系数都是实数, 1 k 2004,其中 a k ,2004(E)C kk 12004C 2004X 2003C 2003XL答案:1 ( E )2 ( C )3 ( B )4 ( E )5 ( B )6 ( A )7 ( B )8 ( B )9 ( C )10 ( C ) 11 ( A )12 ( B )13 ( B )14 ( A )15 ( C ) 16 ( B )17 ( D )18 ( D )19 ( D )20( E ) 21 ( D )22 ( B )23 ( E )24 ( C )25 ( E )。
美国数学竞赛AMC8 -- 2006年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2006年真题解析(英文解析+中文解析) \Problem 1Answer: DSolution:The three prices round to $2, $5, and $10, which has a sum of 17.中文解析:三件商品价格先近似取整,然后求和:2+5+10=17. 答案是D。
Problem 2Answer: CSolution:As the AMC 8 only rewards 1 point for each correct answer, everything is irrelevant except the number Billy answered correctly,13.中文解析:正确的题目每题1分,错误或没做的题目都是0分,做对13题的得分应该是13. 答案是C。
Problem 3Answer: ASolution:When Elisa started, she finished a lap in 25/10=2.5 minutes. Now, she finishes a lap is 24/12=2 minutes. The difference is 2.5-2=0.5中文解析:开始25分钟游10圈,平均2.5分钟游1圈。
后来24分钟游12圈,平均2分钟游1圈。
速度从2.5分钟提高到2分钟,提高了0.5分钟,即1/2 分钟。
答案是A。
Problem 4Answer: BSolution:If the spinner goes clockwise 2+1/4 revolutions and then counterclockwise 3+3/4 revolutions, it ultimately goes counterclockwise 1+1/2 which brings the spinner pointing east.中文解析:最初方向指向西,转整数圈不改变指针方向。
2020 AMC 10B (美国数学竞赛)真题加详解

2020 AMC 10B Solution Problem1What is the value ofSolutionWe know that when we subtract negative numbers, .The equation becomesProblem2Carl has cubes each having side length , and Kate has cubes each having side length . What is the total volume of these cubes?SolutionA cube with side length has volume , so of these will have a total volume of .A cube with side length has volume , so of these will have a total volume of .~quacker88Problem 3The ratio of to is , the ratio of to is , and the ratioof to is . What is the ratio of toSolution 1WLOG, let and .Since the ratio of to is , we can substitute in the value of toget .The ratio of to is , so .The ratio of to is then so our answeris ~quacker88Solution 2We need to somehow link all three of the ratios together. We can start by connecting the last two ratios together by multiplying the last ratio by two., and since , we can link themtogether to get .Finally, since , we can link this again to get: ,so ~quacker88Problem4The acute angles of a right triangle are and , where andboth and are prime numbers. What is the least possible value of ?SolutionSince the three angles of a triangle add up to and one of the anglesis because it's a right triangle, .The greatest prime number less than is . If ,then , which is not prime.The next greatest prime number less than is . If ,then , which IS prime, so we have our answer ~quacker88 Solution 2Looking at the answer choices, only and are coprime to . Testing , the smaller angle, makes the other angle which is prime, therefore our answerisProblem5How many distinguishable arrangements are there of 1 brown tile, 1 purple tile, 2 green tiles, and 3 yellow tiles in a row from left to right? (Tiles of the same color are indistinguishable.)SolutionLet's first find how many possibilities there would be if they were all distinguishable, then divide out the ones we overcounted.There are ways to order objects. However, since there's ways to switch the yellow tiles around without changing anything (since they're indistinguishable) and ways to order the green tiles, we have to divide out these possibilities.~quacker88SolutionWe can repeat chooses extensively to find the answer. Thereare choose ways to arrange the brown tiles which is . Then from the remaining tiles there are choose ways to arrange the red tiles. And now from the remaining two tiles and two slots we can see there are two ways to arrange the purple and brown tiles, giving us an answerofProblem6Driving along a highway, Megan noticed that her odometershowed (miles). This number is a palindrome-it reads the same forward and backward. Then hours later, the odometer displayed the next higher palindrome. What was her average speed, in miles per hour, during this -hour period?SolutionIn order to get the smallest palindrome greater than , we need to raise the middle digit. If we were to raise any of the digits after the middle, we would be forced to also raise a digit before the middle to keep it a palindrome, making it unnecessarily larger.So we raise to the next largest value, , but obviously, that's not how place value works, so we're in the s now. To keep this a palindrome, our number is now .So Megan drove miles. Since this happened over hours, she drove at mph. ~quacker88 Problem7How many positive even multiples of less than are perfect squares?SolutionAny even multiple of is a multiple of , so we need to find multiples of that are perfect squares and less than . Any solution that we want will be in theform , where is a positive integer. The smallest possible value isat , and the largest is at (where the expression equals ). Therefore, there are a total of possible numbers.-PCChess Problem8Points and lie in a plane with . How many locations forpoint in this plane are there such that the triangle with vertices , ,and is a right triangle with area square units?Solution 1There are options here:1. is the right angle.It's clear that there are points that fit this, one that's directly to the rightof and one that's directly to the left. We don't need to find the length, we just need to know that it is possible, which it is.2. is the right angle.Using the exact same reasoning, there are also solutions for this one.3. The new point is the right angle.(Diagram temporarily removed due to asymptote error)The diagram looks something like this. We know that the altitude tobase must be since the area is . From here, we must see if there are valid triangles that satisfy the necessary requirements.First of all, because of the area.Next, from the Pythagorean Theorem.From here, we must look to see if there are valid solutions. There are multiple ways to do this:We know that the minimum value of iswhen . In this case, the equationbecomes , which is LESSthan . . The equationbecomes , which is obviously greater than . We canconclude that there are values for and in between that satisfy the Pythagorean Theorem.And since , the triangle is not isoceles, meaning we could reflectit over and/or the line perpendicular to for a total of triangles this case.Solution 2Note that line segment can either be the shorter leg, longer leg or thehypotenuse. If it is the shorter leg, there are two possible points for that cansatisfy the requirements - that being above or below . As such, thereare ways for this case. Similarly, one can find that there are also ways for point to lie if is the longer leg. If it is a hypotenuse, then thereare possible points because the arrangement of the shorter and longer legs can be switched, and can be either above or below the line segment. Therefore, the answer is .Problem9How many ordered pairs of integers satisfy theequationSolutionRearranging the terms and and completing the square for yields theresult . Then, notice that can onlybe , and because any value of that is greater than 1 will causethe term to be less than , which is impossible as must be real. Therefore, plugging in the above values for gives the orderedpairs , , , and gives a totalof ordered pairs.Solution 2Bringing all of the terms to the LHS, we see a quadraticequation in terms of . Applying the quadratic formula, weget In order for to be real, which it must be given the stipulation that we are seekingintegral answers, we know that the discriminant, must benonnegative. Therefore, Here, we see that we must split the inequality into a compound, resultingin .The only integers that satisfy this are . Plugging thesevalues back into the quadratic equation, we see that both produce a discriminant of , meaning that there is only 1 solution for .If , then the discriminant is nonzero, therefore resulting in two solutions for .Thus, the answer is .~TiblisSolution 3, x firstSet it up as a quadratic in terms of y:Then the discriminant is This will clearly only yield real solutionswhen , because it is always positive. Then . Checking each one: and are the same when raised to the 2020th power:This has only has solutions , so are solutions. Next, if :Which has 2 solutions, so andThese are the only 4 solutions, soSolution 4, y firstMove the term to the other side toget . Because for all , then . If or , the right side is and therefore . When , the right side become , therefore . Our solutions are , , , . There are solutions, so the answer is - wwt7535Problem 10A three-quarter sector of a circle of radius inches together with its interior can be rolled up to form the lateral surface area of a right circular cone by taping together along the two radii shown. What is the volume of the cone in cubicinches?SolutionNotice that when the cone is created, the radius of the circle will become the slant height of the cone and the intact circumference of the circle will become the circumference of the base of the cone.We can calculate that the intact circumference of the circle is . Since that is also equal to the circumference of the cone, the radius of the cone is . We also have that the slant height of the cone is . Therefore, we use the Pythagorean Theorem to calculate that the height of the coneis . The volume of the coneis -PCChessSolution 2 (Last Resort/Cheap)Using a ruler, measure a circle of radius 4 and cut out the circle and then the quarter missing. Then, fold it into a cone and measure the diameter to be 6cm . You can form a right triangle with sides 3, 4, and then through the Pythagorean theorem the height is found tobe . The volume of a cone is . Plugging in we findProblem11Ms. Carr asks her students to read any 5 of the 10 books on a reading list. Harold randomly selects 5 books from this list, and Betty does the same. What is the probability that there are exactly 2 books that they both select?SolutionWe don't care about which books Harold selects. We just care that Bettypicks books from Harold's list and that aren't on Harold's list.The total amount of combinations of books that Betty can selectis .There are ways for Betty to choose of the books that are on Harold's list.From the remaining books that aren't on Harold's list, thereare ways to choose of them.~quacker88Problem12The decimal representation of consists of a string of zeros after the decimal point, followed by a and then several more digits. How many zeros are in that initial string of zeros after the decimal point?Solution 1Now we do some estimation. Notice that , which meansthat is a little more than . Multiplying itwith , we get that the denominator is about . Notice that whenwe divide by an digit number, there are zeros before the first nonzero digit. This means that when we divide by the digitinteger , there are zeros in the initial string after the decimal point. -PCChessSolution 2First rewrite as . Then, we know that when we write this in decimal form, there will be 40 digits after the decimal point. Therefore, we just have to findthe number of digits in .and memming (alternatively use the factthat ),digits.Our answer is .Solution 3 (Brute Force)Just as in Solution we rewrite as We thencalculate entirely by hand, first doing then multiplying that product by itself, resulting in Because this is digits,after dividing this number by fourteen times, the decimal point is beforethe Dividing the number again by twenty-six more times allows a stringof zeroes to be formed. -OreoChocolateSolution 4 (Smarter Brute Force)Just as in Solutions and we rewrite as We can then look at the number of digits in powersof . , , , , ,, and so on. We notice after a few iterations that every power of five with an exponent of , the number of digits doesn't increase. This means should have digits since thereare numbers which are from to , or digits total. This means our expression can be written as , where is in therange . Canceling gives , or zeroes before the since the number should start on where the one would be in . ~aop2014 Solution 5 (Logarithms)Problem13Andy the Ant lives on a coordinate plane and is currently at facingeast (that is, in the positive -direction). Andy moves unit and thenturns degrees left. From there, Andy moves units (north) and thenturns degrees left. He then moves units (west) and againturns degrees left. Andy continues his progress, increasing his distance each time by unit and always turning left. What is the location of the point at which Andy makes the th leftturn?Solution 1You can find that every four moves both coordinates decrease by 2. Therefore, both coordinates need to decrease by two 505 times. You subtract, giving you theanswer of ~happykeeperProblem14As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length 2 so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded region — inside the hexagon but outside all of the semicircles?Solution 1Let point A be a vertex of the regular hexagon, let point B be the midpoint of the line connecting point A and a neighboring vertex, and let point C be the second intersection of the two semicircles that pass through point A. Then, , since B is the center of the semicircle with radius 1 that C lies on, , since B is the center of the semicircle with radius 1 that A lies on,and , as a regular hexagon has angles of 120,and is half of any angle in this hexagon. Now, using the sinelaw, , so . Since the angles in a triangle sum to 180, is also 60. Therefore, is an equilateral triangle with side lengths of 1.Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagonis . Since the area of an equilateral triangle can be foundwith the formula , where is the side length of the equilateral triangle,the area of an equilateral triangle with side lengths of 1 is . Since the area of a circle can be found with the formula , the area of a sixthof a circle with radius 1 is . In each sixth of the hexagon, thereare two equilateral triangles colored white, each with an area of , and onesixth of a circle with radius 1 colored white, with an area of . The rest of the sixth is colored gray. Therefore, the total area that is colored white in each sixthof the hexagon is , which equals , and the total areacolored white is , which equals . Since the area colored gray equals the total area of the hexagon minus the area colored white,the area colored gray is , whichequals .Solution 2First, subdivide the hexagon into 24 equilateral triangles with side length1:Now note that the entire shadedregion is just 6 times this part:The entire rhombus is just 2 equilatrial triangles with side lengths of 1, so it has an area of:The arc that is not included has an area of:Hence, the area ofthe shaded region in that section is For a final areaof:Problem15Steve wrote the digits , , , , and in order repeatedly from left to right, forming a list of digits, beginning He thenerased every third digit from his list (that is, the rd, th, th, digits from the left), then erased every fourth digit from the resulting list (that is, the th, th, th, digits from the left in what remained), and then erased every fifth digit from what remained at that point. What is the sum of the three digits that were then in the positions ?Solution 1After erasing every third digit, the list becomes repeated. After erasing every fourth digit from this list, the listbecomes repeated. Finally, after erasing every fifth digit from this list, the list becomes repeated. Since this list repeats every digits andsince are respectively in we have that the th, th, and st digits are the rd, th, and thdigits respectively. It follows that the answer is~dolphin7Problem16Bela and Jenn play the following game on the closed interval of the real number line, where is a fixed integer greater than . They take turns playing, with Bela going first. At his first turn, Bela chooses any real number in theinterval . Thereafter, the player whose turn it is chooses a real numberthat is more than one unit away from all numbers previously chosen by either player. A player unable to choose such a number loses. Using optimal strategy, which player will win the game?SolutionNotice that to use the optimal strategy to win the game, Bela must select themiddle number in the range and then mirror whatever number Jennselects. Therefore, if Jenn can select a number within the range, so can Bela. Jenn will always be the first person to run out of a number to choose, so theanswer is .Solution 2 (Guessing)First of all, realize that the value of should have no effect on the strategy at all. This is because they can choose real numbers, not integers, so even if is odd, for example, they can still go halfway. Similarly, there is no reason the strategy would change when .So we are left with (A) and (B). From here it is best to try out random numbers and try to find the strategy that will let Bela win, but if you can't find it, realize thatit is more likely the answer is since Bela has the first move and thus has more control.Problem17There are people standing equally spaced around a circle. Each person knows exactly of the other people: the people standing next to her or him, as well as the person directly across the circle. How many ways are there forthe people to split up into pairs so that the members of each pair know each other?SolutionLet us use casework on the number of diagonals.Case 1: diagonals There are ways: either pairs with , pairs with , and so on or pairs with , pairs with , etc.Case 2: diagonal There are possible diagonals to draw (everyone else pairs with the person next to them.Note that there cannot be 2 diagonals.Case 3: diagonalsNote that there cannot be a case with 4 diagonals because then there would have to be 5 diagonals for the two remaining people, thus a contradiction.Case 4: diagonals There is way to do this.Thus, in total there are possible ways. Problem18An urn contains one red ball and one blue ball. A box of extra red and blue balls lie nearby. George performs the following operation four times: he draws a ball from the urn at random and then takes a ball of the same color from the box and returns those two matching balls to the urn. After the four iterations the urn contains six balls. What is the probability that the urn contains three balls of each color?SolutionLet denote that George selects a red ball and that he selects a blue one. Now, in order to get balls of each color, he needs more of both and .There are 6cases:(wecan confirm that there are only since ). However we canclump , ,and together since they are equivalent by symmetry.andLet's find the probability that he picks the balls in the order of .The probability that the first ball he picks is red is .Now there are reds and blue in the urn. The probability that he picks red again is now .There are reds and blue now. The probability that he picks a blue is .Finally, there are reds and blues. The probability that he picks a blue is . So the probability that the case happensis . However, since the case is the exactsame by symmetry, case 1 has a probability of chance of happening.andLet's find the probability that he picks the balls in the order of .The probability that the first ball he picks is red is .Now there are reds and blue in the urn. The probability that he picks blue is .There are reds and blues now. The probability that he picks a red is . Finally, there are reds and blues. The probability that he picks a blue is .So the probability that the case happensis . However, since the case is the exactsame by symmetry, case 2 has a probability of chance of happening.andLet's find the probability that he picks the balls in the order of .The probability that the first ball he picks is red is .Now there are reds and blue in the urn. The probability that he picks blueis .There are reds and blues now. The probability that he picks a blue is .Finally, there are reds and blues. The probability that he picks a red is .So the probability that the case happensis . However, since the case is the exactsame by symmetry, case 3 has a probability of chance of happening.Adding up the cases, we have ~quacker88 Solution 2We know that we need to find the probability of adding 2 red and 2 blue balls insome order. There are 6 ways to do this, since there are ways to arrange in some order. We will show that the probability for each of these 6 ways is the same.We first note that the denominators should be counted by the same number. This number is . This is because 2, 3, 4, and 5 represent how many choices there are for the four steps. No matter what the stepinvolves numbers to choose from.The numerators are the number of successful operations. No matter the order, the first time a red is added will come from 1 choice and the second time will come from 2 choices, since that is how many reds are in the urn originally. Thesame goes for the blue ones. The numerator must equal . Therefore, the probability for each of the orderingsof is . There are 6 of these, so the total probabilityis .Solution 3First, notice that when George chooses a ball he just adds another ball of the same color. On George's first move, he either chooses the red or the blue witha chance each. We can assume he chooses Red(chance ), and then multiply the final answer by two for symmetry. Now, there are two red balls andone blue ball in the urn. Then, he can either choose another Red(chance ), in which case he must choose two blues to get three of each, withprobability or a blue for two blue and two red in the urn, withchance . If he chooses blue next, he can either choose a red then a blue, or ablue then a red. Each of these has a for total of . The total probability that he ends up with three red and three blueis . ~aop2014 Solution 4Let the probability that the urn ends up with more red balls be denoted . Since this is equal to the probability there are more blue balls, the probabilitythere are equal amounts is . the probability no more blues are chosen plus the probability only 1 more blue is chosen. The firstcase, .The second case, . Thus,the answer is .~JHawk0224Solution 5By conditional probability after 4 rounds we have 5 cases: RRRBBB, RRRRBB,RRBBBB, RRRRRB and RBBBBB. Thus the probability is . Put .~FANYUCHEN20020715Edited by KinglogicSolution 6Here X stands for R or B, and Y for the remaining color. After 3 rounds one can either have a 4+1 configuration (XXXXY), or 3+2 configuration (XXXYY). Theprobability of getting to XXXYYY from XXXYY is . Observe that the probability of arriving to 4+1 configuration is ( to get from XXY toXXXY, to get from XXXY to XXXXY). Thus the probability of arriving to 3+2configuration is also , and the answer isSolution 7We can try to use dynamic programming to solve this problem. (Informatics Olympiad hahaha)We let be the probability that we end up with red balls and blue balls. Notice that there are only two ways that we can end up with red balls and blue balls: one is by fetching a red ball from the urn when wehave red balls and blue balls and the other is by fetching a blue ball from the urn when we have red balls and blue balls.Then wehaveThen we start can with and try to compute .The answer is .Problem19In a certain card game, a player is dealt a hand of cards from a deckof distinct cards. The number of distinct (unordered) hands that can be dealt to the player can be written as . What is the digit ?Solution 1We're looking for the amount of ways we can get cards from a deck of ,which is represented by .We need to get rid of the multiples of , which will subsequently get rid of the multiples of (if we didn't, the zeroes would mess with the equation since you can't divide by 0), , leaves us with 17.Converting these into, we have~quacker88 Solution 2Since this number is divisible by but not , the last digits must be divisible by but the last digits cannot be divisible by . This narrows the options down to and .Also, the number cannot be divisible by . Adding up the digits, weget . If , then the expression equals , a multiple of . This would mean that the entire number would be divisible by , which is not what we want. Therefore, the only option is -PCChessSolution 3It is not hard to check that divides thenumber,As , using wehave .Thus , implying so the answer is .Solution 4As mentioned above,We can divide both sidesof by 10 to obtain which means is simply the units digit of the left-hand side. This valueisProblem20Let be a right rectangular prism (box) with edges lengths and ,together with its interior. For real , let be the set of points in -dimensional space that lie within a distance of some point . The volumeof can be expressed as ,where and are positive real numbers. What isSolutionSplit into 4 regions:1. The rectangular prism itself2. The extensions of the faces of3. The quarter cylinders at each edge of4. The one-eighth spheres at each corner ofRegion 1: The volume of is 12, soRegion 2: The volume is equal to the surface area of times . The surfacearea can be computed to be ,so .Region 3: The volume of each quarter cylinder is equal to . The sum of all such cylinders must equal times the sum of the edge lengths. This can be computed as , so the sum of the volumes of the quarter cylinders is , soRegion 4: There is an eighth of a sphere of radius at each corner. Since there are 8 corners, these add up to one full sphere of radius . The volume of thissphere is , so .Using these values,Problem21In square , points and lie on and , respectively, so that Points and lie on and , respectively, and points and lie on so that and . See the figure below. Triangle , quadrilateral ,quadrilateral , and pentagon each has area Whatis ?SolutionSince the total area is , the side length of square is . We see that since triangle is a right isosceles triangle with area 1, we can determinesides and both to be . Now, considerextending and until they intersect. Let the point of intersection be .We note that is also a right isosceles triangle with side and find it's area to be . Now, we notice that is also a rightisosceles triangle and find it's area to be . This is also equalto or . Since we are looking for , we want two times this. That gives .~TLiuSolution 2Since this is a geometry problem involving sides, and we know that is , we can use our ruler and find the ratio between and . Measuring(on the booklet), we get that is about inches and isabout inches. Thus, we can then multiply the length of by the ratioof of which we then get We take the square of that andget and the closest answer to that is . ~Celloboy (Note that this is just a strategy I happened to use that worked. Do not press your luck with this strategy, for it was a lucky guess)Solution 3Draw the auxiliary line . Denote by the point it intersects with , and by the point it intersects with . Last, denote by the segment , and by the segment . We will find two equations for and , and then solve for .Since the overall area of is ,and . In addition, the areaof .The two equations for and are then:Lengthof :Area of CMIF: .Substituting the first into the second,yieldsSolving for gives ~DrBSolution 4Plot a point such that and are collinear and extend line topoint such that forms a square. Extend line to meetline and point is the intersection of the two. The area of this square is equivalent to . We see that the area of square is , meaning each side is of length 2. The area of the pentagon is .Length , thus . Triangle is isosceles, and the area of this triangleis . Adding these two areas, we get . --OGBooger Solution 5 (HARD Calculation)We can easily observe that the area of square is 4 and its side length is 2 since all four regions that build up the square has area 1. Extend and let the intersection with be . Connect , and let the intersectionof and be . Notice that since the area of triangle is 1and , ,therefore . Let ,。
美国数学竞赛AMC题目及答案

2.3.What is the value of ?4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill?5.Hammie is in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13. When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .15. If , , and , what is the product of , , and ?16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle?21. Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22. Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23. Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length .What is the radius of the semicircle on ?24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B?1.2.The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.3.Notice that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .4.Each of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .5.The median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer.6.Solution 1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7.If Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is .8.First, there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9.This is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11. We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation, .To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are, so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there arecubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained inthe fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class.Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways toget from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22. There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks.Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagoreantheorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of thelargest is , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits theextension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to thecombined area of the three squares is .Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . Thissolution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.古希腊哲学大师亚里士多德说:人有两种,一种即“吃饭是为了活着”,一种是“活着是为了吃饭”.一个人之所以伟大,首先是因为他有超于常人的心。
美国数学竞赛AMC8 -- 2005年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2005年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:If x is the number, then 2x=60 and x=30. Dividing the number by 2 yields 15.中文解析:按照Connie的计算,这个数乘以2是60,可知这个数是30. 应该做的计算是30除以2,因而正确答案应该是15. 答案是B。
Problem 2Answer: CSolution:Karl paid 5*2.5=$12.5. 20% of this cost that he saved is 12.5*0.2=$2.5.中文解析:Karl按原价买了5个文件夹,支付的费用是:2.5*5=12.5. 折扣价是:1.25*0.8=10。
如果Karl 等一天,可以省2.5元。
答案是C.Problem 3Answer: DSolution:Rotating square ABCD counterclockwise 45° so that the line of symmetry BD is a vertical line makes it easier to see that 4 squares need to be colored to match its corresponding square.中文解析:如上图所示,以BD为对称轴,标蓝色的方块需要涂黑。
共4块,答案是D。
Problem 4Answer: CSolution:The perimeter of the triangle is 6.1+8.2+9.7=24cm. A square's perimeter is four times its side length, since all its side lengths are equal. If the square's perimeter is 24, the side length is24/4=6, and the area is 6*6=36.中文解析:三角形的周长是:6.1+8.2+9.7=24. 正方形的周长和三角形相等,也是24,则其边长是24/4=6. 其面积是:6*6=36. 答案是C。
AMC美国数学竞赛AMC.B 试题及答案解析
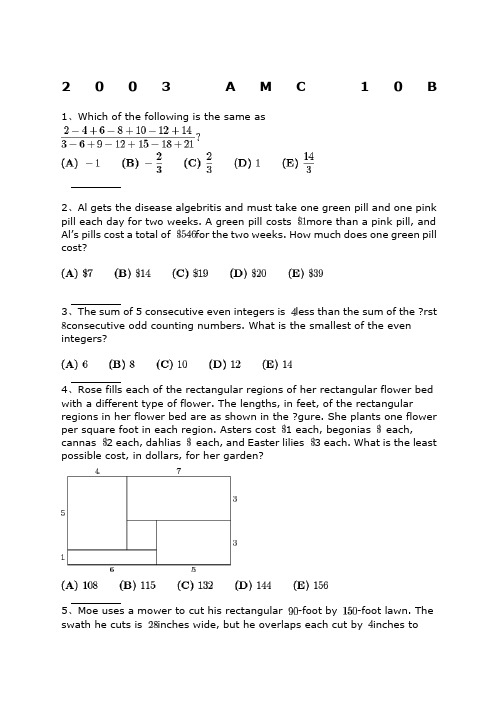
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013 AMC8 Problems1.Danica wants to arrange her model cars in rows with exactly 6 cars in each row. She now has 23 model cars. What is the smallest number of additional cars she must buy in order to be able to arrange all her cars this way?2.A sign at the fish market says, "50% off, today only: half-pound packages for just $3 perpackage." What is the regular price for a full pound of fish, in dollars?What is the value of?3.4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill? 5.Hammie is in thegrade and weighs 106 pounds. His quadruplet sisters are tiny babiesand weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11.Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12.At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13.When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14.Abe holds 1 green and 1 red jelly bean in his hand. Bea holds 1 green, 1 yellow, and 2 red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?15.If , , and , what is the product of , , and ?16.A number of students from Fibonacci Middle School are taking part in a community serviceproject. The ratio of -graders to -graders is , and the the ratio of -graders to-graders is . What is the smallest number of students that could be participating in the project?17.The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18.Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?19.Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20.A rectangle is inscribed in a semicircle with longer side on the diameter. What is thearea of the semicircle?21.Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23.Angle of is a right angle. The sides of are the diameters of semicirclesas shown. The area of the semicircle on equals , and the arc of the semicircle onhas length . What is the radius of the semicircle on ?24.Squares , , and are equal in area. Points and are the midpointsof sides and , respectively. What is the ratio of the area of the shaded pentagonto the sum of the areas of the three squares?25.A ball with diameter 4 inches starts at point A to roll along the track shown. The track iscomprised of 3 semicircular arcs whose radii are inches, inches, andinches, respectively. The ball always remains in contact with the track and does notslip. What is the distance the center of the ball travels over the course from A to B?2013 AMC8 Problems/Solutions1. ProblemDanica wants to arrange her model cars in rows with exactly 6 cars in each row. She now has 23 model cars. What is the smallest number of additional cars she must buy in order to be able to arrange all her cars this way?Solution:In order to have her model cars in perfect, complete rows of 6, Danica must have a number ofcars that is a multiple of 6. The smallest multiple of 6 which is larger than 23 is 24, so she'll need to buy more model car.2.A sign at the fish market says, "50% off, today only: half-pound packages for just $3 per package." What is the regular price for a full pound of fish, in dollars?ProblemSolution: The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.What is the value of?3. ProblemNotice that we can pair up every two numbers to make a sum of 1:SolutionTherefore, the answer is .4. ProblemEight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill.What was the total bill?Each of her seven friends paidto cover Judi's portion. Therefore, Judi's portion mustbe. Since Judi was supposed to payof the total bill, the total bill must be.Solution5.Hammie is in thegrade and weighs 106 pounds. His quadruplet sisters are tiny babiesand weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these fivechildren or the median weight, and by how many pounds?ProblemLining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds. SolutionThe average weight of the five kids is .Therefore, the average weight is bigger, bypounds, making the answer.6. The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example,. What is the missing number in the top row?ProblemSolutionLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.Solution 1: Working BackwardsWe see that, making.It follows that, so.Another way to do this problem is to realize what makes up the bottommost number. Thismethod doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Solution 2: Jumping Back to the StartAgain, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7. Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass,Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clearthe crossing at a constant speed. Which of the following was the most likely number of cars inthe train?ProblemIf Trey saw, then he saw.Solution 12 minutes and 45 seconds can also be expressed asseconds.Trey's rate of seeing cars,, can be multiplied byon the top andbottom (and preserve the same rate):. It follows that the most likely number of cars is.2 minutes and 45 seconds is equal to.Solution 2Since Trey probably counts around 6 cars every 10 seconds, there are groups of 6cars that Trey most likely counts. Since, the closest answer choice is.8. A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?ProblemFirst, there areways to flip the coins, in order.Solution The ways to get two consecutive heads are HHT and THH. The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9. The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then onwhich jump will he first be able to jump more than 1 kilometer?ProblemThis is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that. SolutionHowever, because the first term isand not, the solution to the problem is10. What is the ratio of the least common multiple of 180 and 594 to the greatest common factorof 180 and 594?ProblemTo find either the LCM or the GCF of two numbers, always prime factorize first. Solution 1The prime factorization of . The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in bothfactorizations and multiply. = 18. Thus the answer = =.We start off with a similar approach as the original solution. From the prime factorizations, the GCF is 18.Similar SolutionIt is a well known fact that. So we have,.Dividing by 18 yields .Therefore, .11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?ProblemWe use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, letrepresent the time.SolutionOn Monday, he was at a rate of . So,.For Wednesday, he walked at a rate of . Therefore,.On Friday, he walked at a rate of. So,. Adding up the hours yields++=.We now find the amount of time Grandfather would have taken if he walked atperday. Set up the equation,.To find the amount of time saved, subtract the two amounts: -=.To convert this to minutes, we multiply by 60.Thus, the solution to this problem is12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?ProblemFirst, find the amount of money one will pay for three sandals without the discount. We have.SolutionThen, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. ProblemWhen Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?Let the two digits be and. SolutionThe correct score was . Clara misinterpreted it as. The difference between thetwo iswhich factors into. Therefore, since the difference is a multiple of 9,the only answer choice that is a multiple of 9 is.14.Abe holds 1 green and 1 red jelly bean in his hand. Bea holds 1 green, 1 yellow, and 2 red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?ProblemThe probability that both show a green bean is. The probability that both show ared bean is . Therefore the probability isSolution15. If ,, and , what is the product of, , and ?ProblemSolutionTherefore,.Therefore,.To most people, it would not be immediately evident that , so we can multiply 6'suntil we get the desired number:, so.Therefore the answer is16. A number of students from Fibonacci Middle School are taking part in a community serviceproject. The ratio of-graders to-graders is, and the the ratio of-graders to-graders is . What is the smallest number of students that could be participating inthe project?ProblemSolutionWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Solution 1: AlgebraTherefore, the ratio of 8th graders to 7th graders to 6th graders is. Since the ratiois in lowest terms, the smallest number of students participating in the project is.The number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and7th graders. The numbers ofstudents isSolution 2: Fakesolving17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?ProblemThe mean of these numbers is. Therefore the numbers are, so the answer isSolution 1Let thenumber be . Then our desired number is.Solution 2Our integers are , so we have that.Let the first term be. Our integers are. We have,Solution 318.Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?ProblemThere arecubes on the base of the box. Then, for each of the 4 layers abovethe bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are4 feet left), there arecubes. Hence, the answer is.Solution 1 We can just calculate the volume of the prism that was cut out of the originalbox. Each interior side of the fort will be 2 feet shorter than each side of the outside. Since thefloor is 1 foot, the height will be 4 feet. So the volume of the interior box is.Solution 2The volume of the original box is . Therefore, the number of blockscontained in the fort is19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?ProblemIf Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, ifHannah did worse than Bridget, there is no way Bridget could have known that she didn't getthe highest in the class. Therefore, Hannah did better than Bridget, so our order isSolution20. Arectangle is inscribed in a semicircle with longer side on the diameter. What is thearea of the semicircle?ProblemSolutionA semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem,. The area is21. ProblemSamantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?SolutionThe number of ways to get from Samantha's house to City Park is, and the number ofways to get from City Park to school is. Since there's one way to go through CityPark (just walking straight through), the number of different ways to go from Samantha's house to City Park to school22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?ProblemThere are 61 vertical columns with a length of 32 toothpicks, and there are 33 horizontal rowswith a length of 60 toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks. Thus, our answer isSolution23.Angleof is a right angle. The sides ofare the diameters of semicircles as shown. The area of the semicircle on equals, and the arc of the semicircle onhas length . What is the radius of the semicircle on?ProblemIf the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagorean theorem says that the other side has length 15, so the radius is.Solution 1We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of the largest is , and the middle one is , so the radius is .Solution 224. Squares, , andare equal in area. Pointsandare the midpointsof sidesand, respectively. What is the ratio of the area of the shaded pentagonto the sum of the areas of the three squares?ProblemSolution 1First let(whereis the side length of the squares) for simplicity. We can extenduntil it hits the extension of. Call this point. The area of trianglethen isThe area of rectangleis. Thus, our desired area is. Now, the ratio of the shaded area to the combined area of the three squares is.Solution 2Let the side length of each square be 1.Let the intersection ofandbe .Since, . Sinceand are vertical angles, theyare congruent. We also haveby definition.So we haveby congruence. Therefore,.Since andare midpoints of sides,. This combined withyields.The area of trapezoidis.The area of triangleis.So the area of the pentagon is .The area of the 3 squares is . Therefore, .Solution 3Let the intersection of andbe .Now we haveand .Because both triangles has a side on congruent squares therefore.Becauseand are vertical angles. Also bothand are right angles so .Therefore by AAS (Angle, Angle, Side) . Then translating/rotating the shadedinto the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25.A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, andinches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of the ball travels over the course from A to B?ProblemThe radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departurefrom the length of the track means that the answer is .Solution 1The total length of all of the arcs is . Since we want the path fromthe center, the actual distance will be shorter. Therefore, the only answer choice less thanis . This solution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump. Solution 2。
