第三次课厂商行为理论
第四章 厂商行为理论

第二节 成本理论与收益
一、成本的概念
(一)会计成本和机会成本
会计成本是指厂商在生产过程中按市场价格直接支付 的一切费用,这些费用一般均可以通过会计账目反映出来。 机会成本是指人们将资源用于某种用途而放弃的在其 他用途中所能得到的最高收益。
(二)显性成本与隐性成本
显性成本是指厂商在生产要素市场上购买或租用所需 要的生产要素的实际支出;隐性成本是指厂商自己所拥有 的用于该企业生产过程的那些生生产 一单位产品所消耗的不变成本。其公式为: 平均可变成是企业在短期内平均每生产一 单位产品所消耗的可变成本。其公式为: 平均总成本(Average Cost,简称AC)是 企业在短期内平均每生产一单位产品所消耗的 全部成本,它等于平均不变成本和平均可变成 本之和。 边际成本是企业在短期内每增加一单位产 量时所增加的成本。其公式为:
(五)长期生产函数分析的应用
1.生产要素的最适组合
既定成本条件下,唯一的等成本线AB和等产量曲线Q2 的相切点E,才是实现既定成本条件下的最大产量的要素组 合。 为了实现既定成本条件下 的最大产量,企业必须选择最 优的生产要素组合,使得两要 素的边际替代率等于两要素的 价格比例。即:
2.生产的规模报酬 (1)规模报酬递增 规模报酬递增是指产量增加的比例大于各种生产要素 增加的比例。例如,当全部的生产要素劳动和资本都增加 100%时,产量的增加大于100%。 (2)规模报酬固定 规模报酬固定是指产量增加的比例等于各种生产要素 增加的比例。 (3)规模报酬递减 规模报酬递减是指产量增加的比例小于各种生产要素 增加的比例。
三、长期成本分析
(一)长期总成本
长期总成本(Long Total Cost,简称LTC)是指企业长 期内在每一个产量水平上通过选择最优的生产规模所能达到 的最低总成本。
经济学原理-第05章 厂商行为理论PPT

第二节 厂商生产行为分析
二、厂商短期生产行为分析
(一)总产量、平均产量和边际产量
第二节 厂商生产行为分析
二、厂商短期生产行为分析
(一)总产量、平均产量和边际产量
图5-2 产量曲线
第二节 厂商生产行为分析
二、厂商短期生产行为分析
(一)总产量、平均产量和边际产量
总产量、平 均产量和边 际产量之间
的关系
MRTSL,K
K L
dK dL
(5-10)
△K前面加一个负号,表示增加劳动的投入就必须减少资本 的投入,二者变动方向相反。
第二节 厂商生产行为分析
三、厂商长期生产行为分析
(一)等产量线 等产量曲线具有以下特征:
在某一特定投入组合的边际技术替代率是这一 组和所能生产的等产量曲线在这一点的斜率。
MRTSL,K
生产要素的最佳组合发生在等成本线与等产量线的相
切之点上,那么要求等成本线的斜率-PL/PK必须等于等 产量线的斜率MPL/MPK(等产量线的斜率的绝对值就是边 际技术替代率且为负数),即:
MPL MPK
PL
PK
(5-14)
第二节 厂商生产行为分析
三、厂商长期生产行为分析
(四)生产扩展线
在生产要素价格、生产技术水平和其他条件不 变的情况下,如果企业改变成本,等成本线会发生 平移;如果厂商改变产量,等产量线会发生平移。 这些不同的等成本线与不同的等产量线相切,形成 不同的生产均衡点。这些生产均衡点的轨迹就是生 产扩展线。
公司制 企业
第二节 厂商生产行为分析
一、生产和生产函数
(一)生产和生产要素
生产是指与人类创造物质财富和精神财富有 关的一切活动。它不仅仅局限于创造有形的物质 产品的活动,而且也包括金融、贸易、运输、家 庭服务等各种服务性的活动。在生产过程中要投 入各种生产要素并生产产品,因此,生产也就是 把投入变为产出的过程。
经济学基础第4章厂商行为理论4.1 课件PPT

第二阶段才是可变投入的合理区域
2019/10/28
5
三、边际收益递减规律
在其他投入不变的情况下,一种要素的投入量增加到 一定水平后,增加的单位投入所带来的总产出的增量递减 (边际产量递减)。这是一条经验规律。
边际收益递减的前提条件是:技术不变;其他要素的 投入量不变;生产要素的数量超过一定量。
“一个和尚担水吃,两个和尚抬水吃,三个和尚没有水 吃。”
当经济利润为零时,厂商仍可得到正常利润。
2019/10/28
23
三、利润最大化的原则:MR=MC
• MR>MC ,每增加一单位产品所增加的收益大于这 一单位的成本,厂商有利可图,必然扩大产量;
• MR<MC ,每增加一单位产品所增加的收益小于这 一单位的成本,厂商会亏损,必然减少产量;
• 只有在MR=MC时,厂商既不扩大,也不缩小产量, 而是维持产量,表明该赚的利润都赚到,即实现生 产者利润最大化。
第4章 厂商行为理论
很多人都想成为大老板,赚大钱,可是 又不愿意赚小钱,问题是小钱都不会赚的人, 是发现不了赚大钱的机会的。作为一个企业的 管理者,在赚钱的过程中,首先要熟悉一般的 生产企业的目标,以及其基本动作规律。
2019/10/28
经济学,培育聪明的大脑:汤健雄主讲
1
生产企业结构图
2019/10/28
成本曲线在超过Q1以后,在SAC2的下方。
同样,当产量超
过Q2时,由于扩大规
成
模后的成本低于前一
本
SAC1
SAC6
规模下相同产出的成
SAC2
SAC4 SAC5
本,厂商将把生产规
SAC3
模扩大到SAC3。
结果,厂商的长
第三章 厂商理论
第三章 厂商理论在这一章中我们研究经济的供给,分析厂商的行为。
这一章中的厂商是处于完全竞争的经济环境中,它们的市场力量很小,不能影响与左右市场的价格,只是市场价格的接受者。
厂商理论是微观经济学中第二重要的要素。
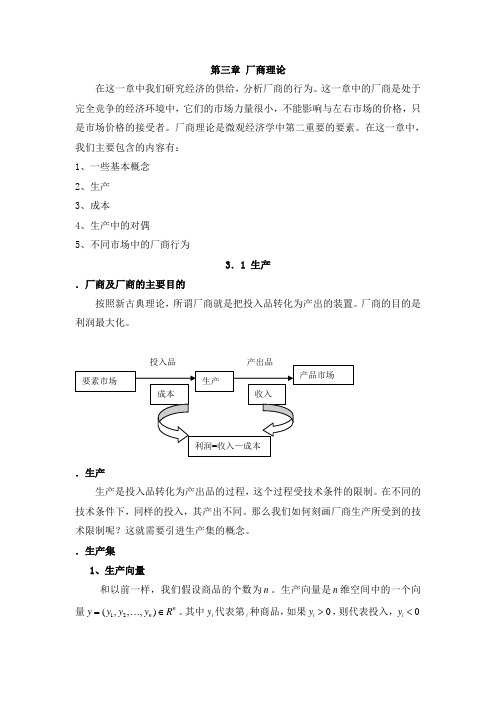
在这一章中,我们主要包含的内容有: 1、一些基本概念 2、生产 3、成本 4、生产中的对偶5、不同市场中的厂商行为3.1 生产.厂商及厂商的主要目的按照新古典理论,所谓厂商就是把投入品转化为产出的装置。
厂商的目的是利润最大化。
.生产生产是投入品转化为产出品的过程,这个过程受技术条件的限制。
在不同的技术条件下,同样的投入,其产出不同。
那么我们如何刻画厂商生产所受到的技术限制呢?这就需要引进生产集的概念。
.生产集 1、生产向量和以前一样,我们假设商品的个数为n 。
生产向量是n 维空间中的一个向量12(,,,)n n y y y y R =∈。
其中i y 代表第i 种商品,如果0i y >,则代表投入,0i y <则代表产出,如果0i y =则意味着第i 种商品既没有被生产也没有被用来做投入。
例如,如果4n =,(2,1,5,0)y =--意味着用2个单位的商品1和1个单位的商品2可以生产出5个单位的商品3。
2、生产集n 维空间中的生产向量有无穷多,但不是每一个生产向量都是技术上可行的,我们把所有技术上可行的生产向量构成的集合称为生产集,记为Y 。
Y 代表了厂商所受到的技术限制。
3、生产函数生产集是目前刻画厂商生产所受到的技术限制的最一般的方法,因为它允许有多种投入与多种产出。
但在一般的情况下,我们更关心的是多种投入1,2(,,) 0=≥n i x x x x x 与一种产出y 之间的关系,这就是在新古典理论中,用一个生产函数:++→nf R R 来描述生产过程的方法。
假设 3.1 生产函数的性质生产函数:++→n f R R 是nR +上的:(1)、连续(投入的微小变化只会带来产量的微小变化); (2)、严格递增(多投入,多产出); (3)、严格拟凹;(4)、(0)0=f (没有投入,就没有产出)。
厂商行为 ppt课件

10
2、单一生产要素连续投入的三个生产阶段 即:边际报酬递减规律的3阶段
Q
Ⅰ
F TP
ⅡⅢ
E AP
L
0
A B MP
•第一个阶段,平均产出递 增,因为生产的规模效益 正在表现出来; (一个和尚挑水吃) •第二个阶段,平均产出递 减, 总产出增长的速度放 慢; (二个和尚抬水吃) •第三个阶段,边际产出为 负, 总产出绝对下降。 (三个和尚没水吃,需减 员增效)
13
A.等产量曲线: 图示
等产量线凸向原点的原因:边际技术替代率递减 K
18
11
7
5
Q
O
123 4
L
14
特殊形状的等产量线
固定技术系数的等产量曲线
K
要素完全替代的等产量曲线
K
6
6
5
5
4
Q 2=200 4
3
3
2
Q 1=100 2
Q 1=100
1
1
O1 2 3 4
L
O1 2 3 4
L
15
2.边际技术替代率
长期总成本(LTC) 长期平均成本(LAC) 长期边际成本(LMC)
34
1. 长期总成本
长期总成本:是指厂商在长期中在各种产量水平上通
过改变生产规模所能达到的最低总成本。
LTC是STC的包络曲线 LTC曲线从原点出发向右上方倾斜 LTC曲线是扩展线的转换形态
35
LTC是STC的包络曲线
不同的短期总成本曲线STC表示不同的生产规模(FC不 同) 。
• 显成本(Explicit Cost) :厂商在生产要素 市场上购买或租用的生产要素的实际支出。
厂商行为理论

1、在土地上施肥量越多越好吗? 2、为什么存在边际产量递减规律?
4
分析
生产者行为分析中我们假定生产者都是具有完全理性 的经济人,目标是实现利润最大化。利润最大化的实 现涉及三个问题:
①投入的生产要素与产量的关系,也就是如何使用各种 生产要素,使成本最小,产量最大; ②成本与收益的关系,要使利润最大化,就要使扣除成 本后的收益达到最大化,并确定一个利润最大化的原则; ③市场问题,即厂商处于不同的市场结构时,应如何确 定产品的产量与价格,以便实现利润最大化。
二、生产要素最适组合的等产量线分析
(一)等产量曲线:表 示两种生产要素L、K的不 同数量的组合可以带来相 等产量的一条曲线。
线上任何一点,L、K组合不 同,但产量却相同。
K
Q f L, K Q0
与无差异曲线的比较?
Q L
23
(二)等产量线的特征
表明:实现同样产量,增加 一种要素,必须减少另种。 K
综上所述,厂商在第一阶段进行生产是极其有利的。但如果 厂商在第一阶段就停止增加劳动量,那就不能得到继续增加 劳动投入量的全部好处,任何厂商都会将生产进行到第二阶 段。所以,生产要素的合理投入区域是第二阶段(L1-L2)。
第二节 最优的生产要素组合
一、生产要素最适组合的边际分析
生产要素最适组合的原则是:在成本与生产要素价格既 定的条件下,厂商应该选择最佳的要素投入量,使所购 买的各种生产要素的边际产量与价格的比例相等。用K 表示资本,MPk代表资本的边际产量,Pk代表资本的价格, Qk代表购买的资本量;用L表示劳动,MPl代表劳动的边 际产量,Pl代表劳动的价格,Ql代表购买的劳动量;M表 示货币成本,MPm表示货币的边际产量,则生产要素最 适组合条件可表示为:
第三章 厂商理论精选版

(5)代理理论
(阿尔钦、德姆塞茨、詹森和麦克林) 代理理论主要研究企业内部的组织结构与企业中的代理关系。
(阿尔钦、德姆塞茨)企业是一种“团队生产”方式,无法准确计量团队个 体成员的努力程度和对团队整体成果的贡献程度。因此,团队中必须的监督, 并且最适合、最有效的监督者是最终剩余的索取者。 (詹森和麦克林)管理者不是企业的所有者,产生代理成本。管理者(代理人) 代表所有者(委托人)行使资产的经营与管理职能,但管理者和所有者存在着 对立的利益。所有者监督管理者的成本非常高。
The limit to the size of the firm is set where its costs of organizing a transaction become equal to the cost of carry it out through the market. 不完全契约理论
(6)产权理论 (诺思、马克思、德姆塞茨、科斯) 产权理论主要是研究权力分配对于效率的影响。 企业产权及其分解。(归属权、占有权、支配权和使用权) 当契约不完全时,没有在契约中详细规定的那部分权利应该归 谁所有?
gjgj
9
现代企业理论认为企业是将一组生产要素连结起来的特殊合约。 合约的不完备性决定了合约中存在未经指定的权利,剩余控制 权(residual rights of control)是行使合约中未经指定权利的权 利;剩余索取权(claim to residue)是占有由企业总收益与总成 本的之差构成的剩余(residue)的权利。 在以个人企业 (Individual Proprietorship)为代表的古典型企业中,企业的 剩余完全由企业所有者占有,这种制度安排由于企业经营者与 所有者身份的统一内生地解决了经营者的激励问题。在现代企 业制度中,企业的所有权与经营权是分离的:所有者将企业的 经营管理责任交由经营者承担,并通过对经营者的有效监督来 保障其权益。这是一种典型的委托—代理关系:经营者受股东 的委托负责企业的经营活动,委托人(股东)追求剩余的最大, 代理人(经营者)追求自身报酬的最大,给定企业的收益,二 者的利益相互侵蚀;由所有者完全占有剩余的制度安排对企业 的经营者存在着激励不足。
(完整版)第三次课厂商行为理论

第三次课 厂商行为理论 (2015-9-25,星期五)第一部分 厂商理论(厂商行为分析) 一、厂商的最优选择对应于消费者的最优选择,厂商对生产要素的最优抉择为()crK wL t s K L f Max KL ≤+..,,()()rK wL c K L f V --+=μ,000=--=∂∂=-∂∂=∂∂=-∂∂=∂∂rK wL c Vr K fK V w L fL V μμμ 从而有r w K f L f =∂∂∂∂,或者rwMP MP K L =。
即厂商在最优决策时,劳动的边际产量与资本的边际产量之比,等于(两种生产要素相应的价格)工资与利率之比。
拉格朗日乘子μ的含义为r K f w L f ∂∂=∂∂=μ,或者rMP w MP KL ==μ。
也就是说,μ是最优化状态时单位要素价格所获得之边际产量。
二、几个弹性概念1、产出弹性在技术水平及其它投入要素价格水平保持不变的情况下,仅某一种投入要素变动时,产量的相对变动与投入量的相对变动之比。
设有生产函数()βαK AL K L f Q ==,α==∆∆=∂∂=LLL AP MP Q L L Q L L Q Q E β==∆∆=∂∂=KKK AP MP Q K K Q K K Q Q E2、生产力弹性e E在技术水平及投入要素价格水平保持不变条件下,所有要素都按同一比例变动时,产出的相对变动对投入要素的相对变动之比。
Q X dX dQ X dX Q dQ E e ==,dK KfdL L f dQ ∂∂+∂∂=βα+=+=K L e E E E3、替代弹性σE 在最优状态时r w MP MP K L =,如果rw (相对价格)变化,则会导致L K(要素投入比例)变化,以及K L MP MP (边际技术替代率)变化。
定义LK相对变化对K L MP MP 相对变化之比为劳动对资本的替代弹性。
⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=L K MP MP MP MP d L K d MP MP MP MP d L K L K d E K L K L K L K L σ 1=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=βαβαβαβασL K d L K d L K L K L K d L K d E三、生产要素需求利润π是总收入与总成本的函数()00,222111221121=-∂∂=∂∂=-∂∂=∂∂---=-=r x fp x r x fpx b x r x r x x pf cpq ππππ1x f p∂∂为要素1x 边际产量的价值,2x fp ∂∂为要素2x 边际产量的价值。
专题3 微观经济学:厂商理论

2013-8-20
40
这说明在这一阶段,不变要素资本的投 入量相对过多,生产者增加可变要素劳 动的投入量是有利有。 或者说,生产者只要增加可变要素劳动 的投入量,就可以较大幅度地增加总产 量。
2013-8-20
41
因此,任何理性的生产者都不会在这一 阶段停止生产,而是连续增加可变要素 劳动的投入量,以增加总产量并将生产 扩大到第II阶段。
二、生产:投入与产出 1、生产:厂商投入生产要素到产品产出的过 程。 2、 生产要素 劳动(L) ——工资 资本(K)——利息 土地(N)——地租
企业家才能(E, entrepreneurship) ——利润
2013-8-20 3
三、生产函数
1、定义: 表示产量与生产要素投入量 之间的关系 。P85,严格的定义。 Q = f(L,K,N,E)--- 生产函数 其中N是固定的,E难以估算,所以, Q = f(L,K)
38
2013-8-20
四、生产要素的合理投入区间 根据短期生产的总产量曲线、平均产量 曲线和边际产量曲线之间的关系,可将 短期生产划分为三个阶段。如图所示。
2征为:劳动的 平均产量始终是上升的,且达到最大值 ;劳动的边际产量上升达到最大值,然 后开始下降,且劳动的边际产量始终大 于劳动的平均产量;劳动的总产量始终 是增加的。
29
2013-8-20
我们简单地归纳一下: 只要边际产量是正的,总产量是增加的 ;只要边际产量是负的,总产量是减少 的;当边际产量为零时,总产量达到最 大值点。
2013-8-20
30
进一步地,由于在边际报酬递减规律作 用下的边际MPL曲线先上升,在B’点达到 最大值,然后再下降,所以,相应的总 产量TPL曲线的斜率先是递增的,在B点 为拐点,然后再是递减的。也就是说, MPL曲线的最大值点B’和TPL曲线的拐点B 是相互对应的。
《经济学之厂商理论》课件

VS
反垄断政策
厂商理论有助于理解市场垄断的形成机制 ,为反垄断政策的制定提供依据。政策制 定者可以利用厂商理论分析垄断企业的行 为,制定有效的反垄断措施。
厂商理论在企业决策中的应用
投资决策
厂商理论指导企业进行投资决策,通过分析 市场供求、成本和收益等因素,确定最佳的 投资方案。
定价策略
厂商理论为企业制定定价策略提供指导,帮 助企业理解市场需求和竞争状况,制定合理 的价格策略。
创新与差异化
为了在竞争中获得优势, 寡头厂商会不断进行技术 创新和产品差异化,提高 产品质量和降低成本。
05
厂商理论的实践应用
厂商理论在政策制定中的应用
产业政策
厂商理论为政策制定者提供了产业政策 制定的理论基础,例如,通过分析市场 结构、竞争状况等因素,制定有利于特 定产业的政策,提高产业竞争力。
的最大产量之间的关系。
02 03
特性
生产函数具有规模收益递增、规模收益递减和规模收益不变三种特性, 分别表示随着生产规模的扩大,产量增加的比例大于、小于和等于投入 要素增加的比例。
形式
生产函数有多种形式,如柯布-道格拉斯生产函数、CES生产函数等, 这些函数描述了不同生产要素之间的替代关系和边际产量。
厂商的目标与决策
目标
厂商的目标是追求利润最大化,即厂 商在生产过程中追求产出的边际收益 等于边际成本。
决策
厂商的决策包括生产什么、生产多少 、如何生产和为谁生产等,这些决策 基于厂商的成本和收益分析,以及市 场供求状况。
厂商的生产函数
01
定义
生产函数表示在一定技术条件下,各种生产要素的投入量与其所能生产
经济学之厂商理论
目录
• 厂商理论概述 • 完全竞争市场中的厂商 • 垄断市场中的厂商 • 寡头市场中的厂商 • 厂商理论的实践应用
第6章 厂商行为理论

第6章厂商行为理论第6章厂商行为理论6.1 知识要点本章要求掌握厂商行为的收入最大化法则以及不同的市场结构下的市场绩效。
1、基本概念(1)收益函数:厂商收益与销售量有关,收益对产量的关系被称为收益函数。
(2)利润函数:利润是总收益与总成本的差额,收益和成本都是产量的函数,因此,利润也是产量的函数。
(3)利润最大化条件:MR = MC2、市场结构的划分(1)市场集中度常用指标:CR4;HHI。
(2)常见的市场结构的划分市场结构厂商数目产品差别化规模经济完全竞争多无不明显垄断竞争多有不明显寡头垄断少有或无明显完全垄断一无明显3、不同市场结构下的市场均衡(1)完全竞争市场。
在这种市场结构下,厂商面临的是一条水平的需求曲线,因此厂商决策是P=MR=MC。
(2)垄断竞争市场。
在这种市场结构下,厂商面临的需求曲线是向右下倾斜的,但是竞争的存在又使得超额利润不会长期存在,因此在这种市场上P=AC>MR。
(3)寡头垄断市场。
在这种市场结构下,单个厂商的行为决策不仅要考虑需求而且要考虑其他厂商的决策对自己,以及自己的决策对其他厂商的影响,因此需要借助博弈论的方法分析这种市场上的均衡。
(4)完全垄断。
完全垄断厂商面临的需求曲线是市场的需求曲线,因此在这种市场上P>MR=MC。
6.2 习题解答【关键概念复习】在B栏中寻找与A栏中术语相应的解释,并将序号填在术语前边。
A B2 市场结构1.又称纯粹竞争,是指一种不受任何阻碍和干扰的竞争。
该市场是指没有任何垄断因素的市场。
1 完全竞争2.是某一个行业中垄断与竞争的程度。
4 完全垄断3.市场是有许多出售相似而不相同产品的企业的市场结构,是既有竞争因素、又有垄断因素的一种市场类型。
3 垄断竞争4.通常称为垄断市场。
在这种市场中,一种产品被某一家企业独家控制。
6 自然垄断5.少数几家厂商控制整个(或绝大部分)市场产品的生产和销售的市场组织。
5 寡占市场6.由生产的技术特性造成规模经济引起的垄断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三次课 厂商行为理论
(2015-9-25,星期五)
第一部分 厂商理论(厂商行为分析)
一、厂商的最优选择
对应于消费者的最优选择,厂商对生产要素的最优抉择为
从而有,或者。
即厂商在最优决策时,劳动的边际产量与资本的边际产量之比,等于(两种生产要素相应的价格)工资与利率之比。
拉格朗日乘子的含义为,或者。
也就是说,是最优化状态时单位要素价格所获得之边际产量。
二、几个弹性概念
1、产出弹性
在技术水平及其它投入要素价格水平保持不变的情况下,仅某一种投入要素变动时,产量的相对变动与投入量的相对变动之比。
设有生产函数
2、生产力弹性
在技术水平及投入要素价格水平保持不变条件下,所有要素都按同一比例变动时,产出的相对变动对投入要素的相对变动之比。
,
3、替代弹性
在最优状态时,如果(相对价格)变化,则会导致(要素投入比例)变化,以及(边际技术替代率)变化。
定义相对变化对相对变化之比为劳动对资本的替代弹性。
三、生产要素需求
利润是总收入与总成本的函数
为要素边际产量的价值,为要素边际产量的价值。
利润最大化时各种投入要素边际产量的价值要等于要素本身的价格。
根据以上等式,求得厂商对两种生产要素的需求函数和。
与利润最大化时相对应,成本最小化之最优要素需求函数为
四、要素价格变化对要素需求的影响
设有生产函数,如果,,且有,则为严格凹函数,利润最大化问题有解。
如果生产函数呈规模报酬递减,则利润最大化问题有解。
如果生产函数呈规模报酬不变或规模报酬递增,则利润可能没有极大值。
由于,求各因素之全微分,则有,求得如下(其中),即生产函数为严格凹函数)
设有,由于,则有对的影响。
也就是说,价格提高,的投入量下降,贵的少用;价格下降,的投入量提高,贱的多用。
设有,由于,则有对的影响。
也就是说,价格提高,的投入量下降;价格下降,的投入量提高。
设有,由于,则有产出品价格对的影响,亦即产出品价格上升,将会驱使厂商增加生产要素投入。
假设为劳动力投入量,则商品价格上涨,相应增加;而不是相反。
假设存在人浮于事,人力资源投入过度,则;在这种情况下,人多瞎捣乱;当然,。
也是由于人浮于事,所以的产出弹性。
五、短期成本函数
设有生产函数,分别为要素价格,则成本函数为
为条件需求函数,即在产出量给定“条件”下的要素需求函数,则有成本函数。
短期成本函数与长期成本函数的区别在于:一是在短期存在固定成本,而在长期,由于所有的要素都是可变的,因此无所谓固定成本。
二是在短期生产规模是给定的,而在长期,生产规模是可以抉择的。
假定生产要素的价格给定不变,则成本就仅仅是产量的函数
平均总成本
平均可变成本;平均固定成本
边际成本
平均总成本与边际成本,,。
在平均成本最小处,边际成本等于平均成本。
六、长期成本函数
假设生产规模为,则短期成本函数可以表达为,建立隐函数。
由对求偏导,并令该偏导为零,即有。
表示当变化时,厂商充分利用了的潜力,得到最佳的与之间的关系,由得到即为长期成本函数。
譬如,假设有短期成本函数
建立隐函数
由,则有,
这就是长期成本函数。
七、学习曲线
企业的长期平均成本曲线()有时可能逐渐下降,这可能来自于企业随产出量的积累而不断进行的“学习”,“学习”是指“边干边学”(Learning by doing)。
数学描述
考虑两个时期,。
每个时期有产出量,于是两时期产量分别为。
第一期的成本为,第二期的成本为。
“学习效应”是指。
也就是说,第一期的产出量越多,则第二期的生产成本下降越大。
通常,学习效应是以累计产量对降低平均成本的作用来表示,譬如,其中表示单位产出的劳动投入量,表示累计产量,表示常系数。
系数表示学习效应的大小。
如果,则,为常数,不存在学习效应;如果,则。
当时,,学习效应是充分的。
譬如,假设学习曲线为。
累计产量为20时,总用工量为200;累计产量为40时,总用工量为360。
则有:,;从而有,,从而求得,所以学习曲线为。
可以预测,累计产量为80时,单位产量用工为,总用工量为。
八、规模报酬与范围经济
关于规模报酬
边际成本严格递减、平均成本严格递减、成本函数的次可加性,这三个概念都是存在规模报酬的数学表达式,表述如下
首先,如果对于所有可能出现的产量,如果,则边际成本严格递减。
其次,如果对于所有的和都满足,有,则平均成本严格递减。
第三,如果对于产量,有,则成本函数就是严格次可加的(sub-additivity)。
次可加是指,在一个有限的产量变化范围内,共同生产一组产出量的总和会比分别生产它们节约成本。
当仅仅是和两种产量时,规模报酬的表达式可以简化为。
集约化城市建设,节约配套费用。
对于范围经济,数学表达式也是,不过此时表示商品的产出量。
范围经济说明,由一家企业集团联合生产若干种产出,要比家企业分别生产各自商品节省成本。
譬如,当时,范围经济的表达式可以简化为。
对于范围经济存在的原因,可能是:第一,生产过程相互关联,既种粮又养猪;第二,需求方面的相互关联,shopping mall既饮食娱乐,又购物;第三,规避风险,不易于被市场或融资风险一网打尽;等等。
对于一种要素,边际报酬递减;
对于一种商品,规模报酬递减;
对于多种商品,范围经济优势。
九、利润函数
1、数学表达式
也就是说,在产出品价格和投入要素价格给定的前提下,厂商抉择要素投入量和产出量,从而达到利润最大化目标。
利润函数只有当规模报酬递减时才存在,利润函数仅仅依赖于。
2、霍特林引理(Hotelling lemma)
,即为供给函数;
,即为要素需求函数。
十、供给函数的确定
第一,从利润函数计算供给函数
假设生产函数为,为的单价,为的单价(为固定投入量),为产出
单价,求利润函数,以及供给函数(即利润最大化时的生产函数)。
计算:
根据利润最大化条件,有,
把带入方程,有
由霍特林引理求供给函数
第二,从生产函数计算供给函数
如果一个生产函数是一个严格凹函数(满足),则利润极大化问题有解。
可以先直接求出要素的条件需求函数,将该要素的条件需求函数带入生产函数,即求得厂商的供给函数。
譬如,假设某厂商的短期生产函数为,如果(表示固定投入)为16,计算厂商的短期供给函数。
计算:厂商的生产函数为,因而利润函数为(假设为固定投入的租金),根据利润极大化一解条件,有
得到,所以,,带入原生产函数得到短期厂商供给函数为。
如果假定给定且保持不变,则供给只表达与之间的函数关系。
第三,从成本函数计算供给函数
厂商的利润表达式为
若厂商利润最大化问题有解,则必满足价格等于边际成本这一条件(必要条件),从而由求解供给函数。
譬如,某厂商短期成本函数为,,按照,短期供给函数即为,或者。
十一、几个说明
1、技术进步作用的测定
2、非利润最大化厂商行为分析
1)保证获利基础上的产出最大化
在这种情况下,厂商尽可能扩大产出,直至利润为零,即;或者。
与利润最大化企业不同,在给定商品价格的前提下,不是按价格等于边际成本来决定产出水平,而是按价格等于平均成本来决定产出水平,对于具有型的平均成本曲线,厂商的供应函数即为平均成本函数的上升段,供应函数随价格而递增。
2)厂商追求成本利润率最大化
这种指标在计划经济(PLANNED ECONOMY)中常常采用,如果
极值存在,其一阶条件为:,或者。
厂商按边际成本与平均成本相等的点安排生产,由于厂商的决策与商品的价格无关,即。
也就是说,企业供应函数为一常数,对价格无反应。
3)单位职工的利润最大化
这种模式有可能适合企业自治或企业利润由职工承包的情况。
企业追求的是平均职工收入的最大化,即
式中为职工人数。
由理论分析可知,这类企业对价格信号的反应是不清晰的,甚至有可能是反常规的,商品价格越高,企业的投入与产出越小。
3、欧拉等式(Euler´s Equation)
考察生产函数,如果对于所有正实数,下列关系式都能成立:,则该函数称为次齐次函数。
齐次函数满足欧拉恒等式
如果=1,总产品刚好能够支付生产要素所有者的报酬,即所谓“耗尽原则”;>1,生产要素的报酬高于总产品;<1,生产要素的报酬小于总产品。
4、生产函数举例
不妨将营销努力(包括商品质量改进以及增加推销费用等)视为一种投入,则产出函数可用或者来表达,如图所示。
