2018最新四年级奥数.几何.风筝模型和梯形蝴蝶定理(C级).学生版
四年级下册数学竞赛试题-几何.风筝模型和梯形蝴蝶定理C级.学生版-全国通用

6风筝模型和梯形蝴蝶定理例题精讲【例11【巩固1【例21C、、/如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;(2) AG:GC在^ABC中-B D=2:1,DC如图,平行四边形是2、4、4 和6.=?AE=I:3,求OB=?EC OEABCD的对角线交于0点,△ CEF、△ OEF、△ ODF、△ BOE的面积依次求:⑴求△ OCF的面积;⑵求△ GCE的面积.D【巩固】如右上图,已知 BO=2DO C0=5AO 阴影部分的面积和是 11平方厘米,求四边形 ABCD 的面积。
那么三角形DBE 的面积是O如图,边长为1的正方形ABCD 中,BE =2EC , CF =FD ,求三角形AEG 的面积.如图,长方形ABCD 中,BE: EC =2:3,DF :FC =1:2,三角形DFG 的面积为2平方厘米,求 长方形ABCD 的面积.如图,在 MBC 中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于0 ,若AAOM 、虫ABO和人BON 的面积分别是3、2、1,则人MNC 的面积是如图4,在三角形 ABC 中,已知三角形 ADE 三角形DCE 三角形BCD 的面积分别是 89、28、26,-J f -I ”【例3】【巩固】【例4】 【巩固】CB【例5】已知ABCD是平行四边形,B C:CE=3:2,三角形ODE的面积为6平方厘米。
贝9阴影部分的面积是平方厘米。
AB E【巩固】在梯形ABCD中,上底长5厘米,下底长10厘米,S郎OC=20平方厘米,则梯形ABCD的面积是平方厘米。
【例6】如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH 的面积是23,求四边形EGFH的面积.【巩固】如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为在下图的正方形 ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1如图所示,BD 、CF 将长方形ABCD 分成4块,心DEF 的面积是4平方厘米,ACED 的面积是6 平方厘米.问:四边形 ABEF 的面积是多少平方厘米?如图, MBC 是等腰直角三角形,DEFG 是正方形,线段 AB 与CD 相交于K 点.已知正方形DEFG 的面积48, AK : KB =1:3,则虫BKD 的面积是多少?如图所示,ABCD 是梯形,AADE 面积是1.8,心ABF 的面积是9,也BCF 的面积是27 .那么阴影 MEC 面积是多少?【例7】 平方厘米,那么正方形 ABCD 面积是平方厘米.【巩固】【例8】【巩固】方厘米,则四边形 PMON 勺面积是平方厘米。
2018四年级奥数.几何.风筝模型和梯形蝴蝶定理(B级).学生版

MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
Page 2 of 9
【巩固】在△ABC 中 BD =2:1, AE =1:3,求 OB =?
DC
EC
OE
【例 3】 如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、 △ODF 、△BOE 的面积依次 是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.
【巩固】如右上图,已知 BO=2DO,CO=5AO,阴影部分的面积和是 11 平方厘米,求四边形 ABCD 的面积。
【例 4】 如图,边长为 1 的正方形 ABCD 中, BE 2EC , CF FD ,求三角形 AEG 的面积.
A
D
G F
B
EC
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
方厘米,则四边形 PMON 的面积是
平方厘米。
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
Page 6 of 9
课堂检测
【随练 1】 如图, S2 2 , S3 4 ,求梯形的面积.
【随练 2】 如左下图,E 是长方形 ABCD 边 AB 的中点,已知三角形 EBF 的面积是 1 平方厘米,求长方形 ABCD 的面积。
A
D
O
B
C
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(B).学生版
Page 4 of 9
【巩固】在梯形 ABCD 中,上底长 5 厘米,下底长 10 厘米, S BOC 20 平方厘米,则梯形 ABCD 的面积是 平方厘米。
风筝模型和梯形蝴蝶定理

风筝模型和梯形蝴蝶定理知识框架板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)例题精讲【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDC BA76【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?CB【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=?【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BA【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.A B【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
奥数专题:蝴蝶定理和风筝定理
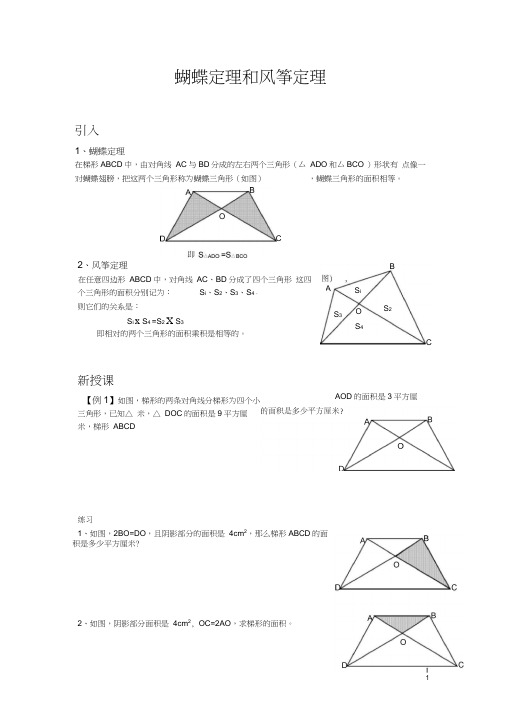
蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形ABCD 中,由对角线 AC 与BD 分成的左右两个三角形(厶 ADO 和厶BCO )形状有 点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图),蝴蝶三角形的面积相等。
2、风筝定理在任意四边形 ABCD 中,对角线 AC 、BD 分成了四个三角形 这四个三角形的面积分别记为: S i 、S 2、S 3、S 4。
则它们的关系是:S i x S 4 =S 2 X S 3即相对的两个三角形的面积乘积是相等的。
新授课【例1】如图,梯形的两条对角线分梯形为四个小三角形,已知△ 米,△ DOC 的面积是9平方厘米,梯形 ABCD练习1、如图,2BO=DO ,且阴影部分的面积是 4cm 2,那么梯形ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是 4cm 2, OC=2AO ,求梯形的面积。
CBAS i S 2O S 3S 4CAOD 的面积是3平方厘【例2】如图,BD , CF 将长方形ABCD 分成四块,红色三角形的面积是4平方厘米,黄色三角形的面积是 8平方厘米,那么绿色四边形的面积是多少平方厘米?练习1如图,BD ,CF 将长方形ABCD 分成4块,红色三角形面积是 面积是6平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形 ABCD 的面积是36平方厘米,对角线 AC 、BD 交于0点,E 为CD 上一点,已知四边形 EFOG 的面积是3平方厘米,则阴影部分的面积为多少平方厘米?【例3】如图,四边形ABCD 是边长为18厘米的正方形,已知CE 的长是ED 的2倍。
求:(1)三角形CEF 的面积,(2)DF 的长度练习 正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍。
三角形DEF 的面积是多少平 方厘米? CF 长多少厘米?4平方厘米,黄色三角形DDFC【例4】正方形ABCD 和正方形CEFG ,且正方形 ABCD 边长为10厘米,则图中三角形BDF 面积为多少平方厘米?2、三个正方形 ABCD 、BEFG 、FHKP 如图排列,正方形 BEFG 的边长是3厘米,求三角形 DEK 的面积。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理一、蝴蝶定理的定义与公式蝴蝶定理是小学奥数几何篇中的一个重要模型,它描述了在等腰三角形中,一条平行于底边的线段将底边平分,并且这条线段与等腰三角形的两腰相交于同一点时,该线段的中点与等腰三角形的顶点、底边的中点以及两腰上的交点形成一个等腰三角形。
蝴蝶定理的公式如下:设等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,则AG=BG=CG。
二、蝴蝶定理的应用1. 在等腰三角形中求边长:通过蝴蝶定理,可以快速求出等腰三角形中未知边的长度。
例如,已知等腰三角形ABC中,AB=AC,底边BC 的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求AG的长度。
解答:根据蝴蝶定理,AG=BG=CG,又因为AB=AC,所以AG=AB/2=a。
2. 在等腰三角形中求角度:通过蝴蝶定理,可以求出等腰三角形中未知角的度数。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求∠AGB的度数。
解答:由于AG=BG=CG,所以△AGB是等边三角形,∠AGB=60°。
3. 在等腰三角形中求面积:通过蝴蝶定理,可以求出等腰三角形中未知部分的面积。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求△AGB的面积。
解答:由于△AGB是等边三角形,所以△AGB的面积=(a^2 √3)/ 4。
小学奥数-几何五大模型(蝴蝶模型)

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?A【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?B【解析】 ⑴根据蝴蝶定理,123BGCS ⨯=⨯,那么6BGCS=;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)任意四边形、梯形与相似模型【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
看到题目中给出条件:1:3ABDBCDSS=,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。
小学奥数_几何五大模型[蝴蝶模型]
![小学奥数_几何五大模型[蝴蝶模型]](https://img.taocdn.com/s3/m/a427fc5431b765ce05081466.png)
模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?A【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?B【解析】 ⑴根据蝴蝶定理,123BGCS ⨯=⨯,那么6BGCS=;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的任意四边形、梯形与相似模型面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
看到题目中给出条件:1:3ABD BCD S S =,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。
小学几何之蝴蝶定理

几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4)S 的对应份数为(a+b )2定理4:相似三角形性质CBEFDA1)Hh C c B b A a ===2) S 1 ∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、例1 如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD分割成四个三角形。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理(附答案)在小学奥数的几何部分,蝴蝶定理是一个非常有用的工具,它可以帮助我们解决一些复杂的几何问题。
蝴蝶定理主要描述了在四边形中,当两条对角线互相垂直时,四边形被分成四个小三角形,而这四个小三角形的面积之间存在一定的关系。
蝴蝶定理的内容如下:设四边形ABCD中,AC和BD是互相垂直的对角线,交于点O。
设四个小三角形的面积分别为S1、S2、S3、S4。
那么,蝴蝶定理可以表述为:S1 + S2 = S3 + S4。
这个定理听起来可能有些抽象,但实际上它的应用非常广泛。
我们可以通过蝴蝶定理来解决一些看似复杂的问题。
下面,我将通过一些例子来展示蝴蝶定理的应用。
例1:在四边形ABCD中,AC和BD是互相垂直的对角线,且AC =8cm,BD = 6cm。
如果三角形ABC的面积是24cm²,那么三角形ADC的面积是多少?解答:根据蝴蝶定理,我们有S1 + S2 = S3 + S4。
由于三角形ABC的面积是24cm²,所以S1 = 24cm²。
又因为AC = 8cm,BD = 6cm,我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 8cm6cm = 24cm²。
因此,三角形ADC的面积也是24cm²。
例2:在四边形ABCD中,AC和BD是互相垂直的对角线,且AC = 10cm,BD = 5cm。
如果三角形ABC的面积是20cm²,那么三角形ADC的面积是多少?解答:同样地,根据蝴蝶定理,我们有S1 + S2 = S3 + S4。
由于三角形ABC的面积是20cm²,所以S1 = 20cm²。
又因为AC = 10cm,BD = 5cm,我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 10cm 5cm = 25cm²。
因此,三角形ADC的面积是25cm²。
小学奥数几何模型 之 蝴蝶模型 例题+作业 带答案

小学奥数几何模型之蝴蝶模型例题+作业带答案小学几何模型之蝴蝶模型在这一节中,我们将介绍蝴蝶模型的几何形状,并通过例题和练来帮助大家更好地理解和掌握这一模型。
梯形中的蝴蝶模型蝴蝶模型通常出现在梯形中,其中梯形的两个翅膀相等,即左边等于右边。
例题1下面是一道关于梯形的例题:在梯形ABCD中,AD平行于BC,对角线AC和BD相交于点O。
已知三角形AOD与三角形DOC的面积分别是16平方厘米与24平方厘米,求梯形ABCD的面积。
解题思路:首先,我们可以计算出△AOB的面积为24平方厘米。
接着,根据相似三角形的性质,我们可以得到△BOC的面积为36平方厘米。
最后,将所有三角形的面积相加,即可得到梯形ABCD的面积为100平方厘米。
练1现在是你们自己来练的时间了。
在梯形ABCD中,AD平行于BC,对角线AC和BD相交于点O。
已知三角形DOC与三角形BOC的面积分别是35平方厘米与49平方厘米,求三角形AOD的面积。
解题思路:首先,我们可以计算出△AOB的面积为35平方厘米。
接着,根据相似三角形的性质,我们可以得到△AOD的面积为25平方厘米。
例题2下面是一道关于长方形的例题:长方形ABCD被一些直线分成了若干部分。
已知三角形ADG的面积是7平方厘米,三角形BCH的面积是9平方厘米,求四边形EGFH的面积。
解题思路:我们可以通过连接EF来得到四边形EGFH。
接着,将已知的三角形面积相加,即可得到四边形EGFH的面积为16平方厘米。
练2现在是你们自己来练的时间了。
长方形ABCD被一些直线分成了若干部分。
已知三角形ADG的面积是24平方厘米,三角形BHC的面积是17平方厘米,求四边形GEHF的面积。
解题思路:我们可以通过连接EF来得到四边形GEHF。
接着,将已知的三角形面积相加,即可得到四边形GEHF的面积为41平方厘米。
风筝模型除了蝴蝶模型,风筝模型也是几何学中常见的模型之一。
例题3下面是一道关于不规则四边形的例题:一个不规则四边形被两条对角线分成四个小三角形。
奥数专题:蝴蝶定理和风筝定理

蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形ABCD 中,由对角线 AC 与BD 分成的左右两个三角形(厶 ADO 和厶BCO )形状有 点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图),蝴蝶三角形的面积相等。
2、风筝定理在任意四边形 ABCD 中,对角线 AC 、BD 分成了四个三角形 这四个三角形的面积分别记为: S i 、S 2、S 3、S 4。
则它们的关系是:S i x S 4 =S 2 X S 3即相对的两个三角形的面积乘积是相等的。
新授课【例1】如图,梯形的两条对角线分梯形为四个小三角形,已知△ 米,△ DOC 的面积是9平方厘米,梯形 ABCD练习1、如图,2BO=DO ,且阴影部分的面积是 4cm 2,那么梯形ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是 4cm 2, OC=2AO ,求梯形的面积。
CBAS i S 2O S 3S 4CAOD 的面积是3平方厘【例2】如图,BD , CF 将长方形ABCD 分成四块,红色三角形的面积是4平方厘米,黄色三角形的面积是 8平方厘米,那么绿色四边形的面积是多少平方厘米?练习1如图,BD ,CF 将长方形ABCD 分成4块,红色三角形面积是 面积是6平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形 ABCD 的面积是36平方厘米,对角线 AC 、BD 交于0点,E 为CD 上一点,已知四边形 EFOG 的面积是3平方厘米,则阴影部分的面积为多少平方厘米?【例3】如图,四边形ABCD 是边长为18厘米的正方形,已知CE 的长是ED 的2倍。
求:(1)三角形CEF 的面积,(2)DF 的长度练习 正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍。
三角形DEF 的面积是多少平 方厘米? CF 长多少厘米?4平方厘米,黄色三角形DDFC【例4】正方形ABCD 和正方形CEFG ,且正方形 ABCD 边长为10厘米,则图中三角形BDF 面积为多少平方厘米?2、三个正方形 ABCD 、BEFG 、FHKP 如图排列,正方形 BEFG 的边长是3厘米,求三角形 DEK 的面积。
小学奥数之几何蝴蝶定理问题

几何之蝴蝶(húdié)定理一、基本(jīběn)知识点定理(dìnglǐ)1:同一三角形中,两个三角形的高相等,则面积之比等于(děngyú)对应底边之比。
S1 : S2 = a : b定理(dìnglǐ)2:等分点结论( 鸟头定理)如图,三角形△AED的面积占三角形△ABC的面积的定理3:任意四边形中的比例关系( 蝴蝶定理)1) S1∶S2 =S4∶S3或 S1×S3 = S2×S4上、下部分的面积之积等于左、右部分的面积之积2)AO∶OC = (S1+S2)∶(S4+S3)梯形中的比例关系( 梯形蝴蝶定理)1)S1∶S3 =a2∶b2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S1∶S3∶S2∶S4 =a2∶b2∶ab∶ab4)S的对应份数为(a+b)2定理4:相似三角形性质1)2) S1∶S2 = a2 ∶A2定理(dìnglǐ)5:燕尾定理S△ABE ∶ S△AEC = S△BGE ∶ S△GEC = BE∶ECS△BGA ∶ S△BGC = S△AGF ∶ S△GFC = AF∶FCS△ADC ∶ S△DCB = S△ADG ∶ S△DGB = AD∶DB二、例题(lìtí)例1、如图,,,已知阴影(yīnyǐng)部分面积为平方厘米,的面积(miàn jī)是多少平方厘米?例2、有一个(yī ɡè)三角形ABC的面积为1,如图,且,,,求三角形的面积.例3、如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且BE=AB,已知四边形EDCA的面积是35,求三角形ABC 的面积.例4如图,ABCD是直角梯形,求阴影(yīnyǐng)部分的面积和。
(单位(dānwèi):厘米)例5、两条对角线把梯形(tīxíng)ABCD分割成四个三角形。
四年级奥数.几何.风筝模型和梯形蝴蝶定理

板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)知识框架风筝模型和梯形蝴蝶定理【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDCBA76【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?321GDCBA【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=? 例题精讲【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BA【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.A B【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
四年级风筝模型和梯形蝴蝶定理

风筝模型和梯形蝴蝶定理知识框架风筝模型:板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)例题精讲【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDCBA76【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?321GDCBA【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=?【例 3】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGFEDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
小学几何之蝴蝶定理

CFEF几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b 定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的 定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4 上、下部分的面积之积等于左、右部分的面积之积 2)AO ∶OC = (S 1+S 2)∶(S 4+S 3) 梯形中的比例关系( 梯形蝴蝶定理) 1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab 4)S 的对应份数为(a+b )2 定理4:相似三角形性质 1)HhC c B b A a === 2) S 1 ∶S 2 = a 2 ∶A 2 定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶EC S △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FC S △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且AD 13BE BC =,14CF CA =,求三角形DEF 的面积.AB 上的一点,且BE=13AB,例3、如图,在三角形ABC 中,,D 为BC 的中点,E 已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、例1 如图,ABCD 是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD 分割成四个三角形。
小学奥数 蝴蝶定理 知识点+例题+练习 (分类全面)

重点 蝴蝶定理公式 难点 蝴蝶定理公式
教学过程
蝴蝶定理
1、
在梯形 ABCD 中,由对角线 AC 与 BD 分成的左右两个三角形(△ADO 和△BCO)形状有点像一
对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图),蝴蝶三角形的面积相等。
A
B
O
D
D
E
C
B
F
1、如图,2BO=DO,且阴影部分的面积是 4cm2,那么梯形 ABCD 的面积是多少平方厘米?
A
B
O
D
C
2、如图,某公园的外轮廓是四边形 ABCD,被对角线 AC、BD 分成四个部分,△AOB 面积为 1 平方千米,△BOC 面积为 2 平方千米,△COD 的面积为 3 平方千米,公园由陆地面积是 6.92 平方千米和人工湖组成,求人工湖的面积是多少平方千米?
A
D
O
B
C
E
例 4、如图,四边形 ABCD 是边长为 18 厘米的正方形,已知 CE 的长是 ED 的 2 倍。求: (1)三角形 CEF 的面积,(2)DF 的长度
A
DF
E
B C
巩固、正方形 ABCD 的边长是 12 厘米,已知 DE 是 EC 长度的 2 倍。三角形 DEF 的面积是多少 平方厘米?CF 长多少厘米?
ADຫໍສະໝຸດ BEFC
3
例 5、正方形 ABCD 和正方形 CEFG,且正方形 ABCD 边长为 10 厘米,则图中三角形 BDF 面积为 多少平方厘米?
A
D
G
F
H
B
C
E
巩固、正方形 ADEB 和正方形 ECFG 底边对齐,两个正方形边长分别为 6 厘米和 4 厘米,三角 形 BDF 的面积是多少平方厘米?
奥数专题:蝴蝶定理和风筝定理

蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形ABCD 中,由对角线AC 与BD 分成的左右两个三角形(△ADO 和△BCO )形状有点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图),蝴蝶三角形的面积相等。
即S △ADO =S △BCO2、风筝定理在任意四边形ABCD 中,对角线AC 、BD 分成了四个三角形(如图),这四个三角形的面积分别记为:S 1 、S 2 、S 3 、S 4。
则它们的关系是:S 1×S 4 =S 2×S 3即相对的两个三角形的面积乘积是相等的。
新授课【例1】如图,梯形的两条对角线分梯形为四个小三角形,已知△AOD 的面积是3平方厘米,△DOC 的面积是9平方厘米,梯形ABCD 的面积是多少平方厘米?练习1、如图,2BO=DO ,且阴影部分的面积是4cm 2,那么梯形ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是4cm 2,OC=2AO ,求梯形的面积。
A BCD O S 1 S 2S 3 S 4【例2】如图,BD ,CF 将长方形ABCD 分成四块,红色三角形的面积是4平方厘米,黄色三角形的面积是8平方厘米,那么绿色四边形的面积是多少平方厘米?练习1、如图,BD ,CF 将长方形ABCD 分成4块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形ABCD 的面积是36平方厘米,对角线AC 、BD 交于O 点,E 为CD 上一点,已知四边形EFOG 的面积是3平方厘米,则阴影部分的面积为多少平方厘米?【例3】如图,四边形ABCD 是边长为18厘米的正方形,已知CE 的长是ED 的2倍。
求: (1)三角形CEF 的面积,(2)DF 的长度练习正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍。
三角形DEF 的面积是多少平方厘米?CF 长多少厘米?CC【例4】正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中三角形BDF 面积为多少平方厘米?练习1、如图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积。
2018四年级奥数.几何.风筝模型和梯形蝴蝶定理(C级).学生版

课后作业
【作业 1】 (2003 北京市第十九届小学生“迎春杯”数学竞赛)四边形 ABCD 的对角线 AC 与 BD 交
于点
O
(如图)所示。如果三角形
ABD
的面积等于三角形
BCD
的面积的
1 3
,且
AO
2
,
DO 3 ,那么 CO 的长度是 DO 的长度的_________倍。
MSDC 模块化分级讲义体系
【例 2】 如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、 △ODF 、△BOE 的面积依次 是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.
【巩固】如右上图,已知 BO=2DO,CO=5AO,阴影部分的面积和是 11 平方厘米,求四边形 ABCD 的面积。
Page 1 of 10例题讲【例 1】 如图,四边形被两条对角线分成 4 个三角形,其中三个三角形的面积已知,求:⑴三角形 BGC 的面积;⑵ AG : GC ?
【巩固】在△ABC 中 BD =2:1, AE =1:3,求 OB =?
DC
EC
OE
欢迎关注:奥数轻松学
余老师薇芯:69039270
A
F
D
4
E6
B
C
【作业 4】 如图所示,长方形 ABCD 内的阴影部分的面积之和为 70,四边形 EFGO 的面积为 10,长方
形的面积是
.
MSDC 模块化分级讲义体系
四年级奥数.几何.风筝模型和梯形蝴蝶定理(C 级).学生版
Page 8 of 10
【作业 5】 如图,已知 D 是 BC 中点, E 是 CD 的中点, F 是 AC 的中点.三角形 ABC 由①~⑥这 6 部 分组成,其中②比⑤多 6 平方厘米.那么三角形 ABC 的面积是多少平方厘米?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识框架
板块一
风筝模型:(又叫任意四边形模型)
S 4
S 3
S 2
S 1O D
C
B
A ①1243::S S S S =或者1324S S S S ⨯=⨯②()()
1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.
板块二梯形模型的应用
梯形中比例关系(“梯形蝴蝶定理”):
A B
C
D
O b
a S 3
S 2
S 1S 4
①22
13::S S a b =②221324::::::S S S S a b ab ab =;③S 的对应份数为()2
a b +.
梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)
风筝模型和梯形蝴蝶定理
例题精讲
【例1】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC
的面积;⑵:AG GC =?
【巩固】在△ABC 中
DC BD =2:1,EC AE =1:3,求OE
OB
=?欢迎关注:“奥数轻松学”
【例2】如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次
是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.
【巩固】如右上图,已知BO=2DO,CO=5AO,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
【例3】如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG 的面积.
A
B
C
D
E
F
G
【巩固】如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求
长方形ABCD 的面积.
A
B
C
D F G
【例4】如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO
∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是
.
【巩固】如图4,在三角形ABC 中,已知三角形ADE、三角形DCE、三角形BCD 的面积分别是89、28、26,
那么三角形DBE 的面积是。
欢迎关注:
“奥数轻松学”
【例5】已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米。
则阴影部分的面
积是
平方厘米。
【巩固】在梯形ABCD 中,上底长5厘米,下底长10厘米,20=∆BOC S 平方厘米,则梯形ABCD 的面积是
平方厘米。
【例6】如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH
的面积是23,求四边形EGFH 的面积.欢迎关注:“奥数轻松学”
H
G F
E
D
C
B A
【巩固】如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三
角形1的面积为________.
3
21【例7】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1
平方厘米,那么正方形ABCD 面积是
平方厘米.
A B
C
D
E
F 【巩固】如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是4平方厘米,CED ∆的面积是6
平方厘米.问:四边形ABEF 的面积是多少平方厘米?
6
4A
B C
D
E
F
【例8】如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形
DEFG 的面积48,:1:3AK KB =,则BKD ∆
的面积是多少?
【巩固】如图所示,ABCD 是梯形,ADE ∆面积是1.8,ABF ∆的面积是9,BCF ∆的面积是27.那么阴影
AEC ∆面积是多少?
欢迎关注:“奥数轻松学”
【例9】如图,正六边形面积为6,那么阴影部分面积为多少?
【巩固】如图,在一个边长为6的正方形中,放入一个边长为2的正方形,保持与原正方形的边平行,现在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的面积为.
【例10】如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15四边形EFGO的面积为______.
【巩固】如图5所示,矩形ABCD的面积是24平方厘米,、三角形ADM与三角形BCN的面积之和是7.8平方厘米,则四边形PMON的面积是平方厘米。
课堂检测
【随练1】如左下图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1平方厘米,求长方形
ABCD 的面积。
【随练2】
正方形ABCD 的边长为6,E 是BC 的中点(如图)。
四边形OECD 的面积为。
【随练3】
如图,在长方形ABCD 中,6AB =厘米,2AD =厘米,AE EF FB ==,求阴影部分的面积.
课后作业
【作业1】
(2003北京市第十九届小学生“迎春杯”数学竞赛)四边形ABCD 的对角线AC 与BD 交于点O (如图)所示。
如果三角形ABD 的面积等于三角形BCD 的面积的
1
3
,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
【作业2】
如图面积为12平方厘米的正方形ABCD 中,,E F 是DC 边上的三等分点,求阴影部分的面积.
欢迎关注:“奥数轻松学”
【作业3】如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是4平方厘米,CED ∆的面
积是6平方厘米.问:四边形ABEF 的面积是多少平方厘米?
6
4A
B C
D
E
F
【作业4】如图所示,长方形ABCD 内的阴影部分的面积之和为70,四边形EFGO 的面积为10,长方
形的面积是
.
【作业5】
如图,已知D 是BC 中点,E 是CD 的中点,F 是AC 的中点.三角形ABC 由①~⑥这6部
分组成,其中②比⑤多6平方厘米.那么三角形ABC 的面积是多少平方厘米?
⑥
⑤
④
③
②①
B
F
E
D C
A
【作业6】如图,正方形ABCD 中,2BE EC =,CF FD =,三角形AEG 的面积是1,求正方形ABCD
的面积.
A
B
C
D
E
F
G
教学反馈
学生对本次课的评价
○特别满意○满意○一般
家长意见及建议
家长签字:。
