小学奥数几何之蝴蝶定理
小学奥数几何篇 五大模型——蝴蝶定理(附答案)

五大模型——蝴蝶模型例1. 四边形ABCD的对角线AC与BD交于点O,如果三角形ABD1,且AO=2,DO=3,那么CO的长的面积等于三角形BCD的面积3度是DO的长度的倍例2. 如图,平行四边形ABCD的对角线交与点O点,△CEF、△OEF、△ODF、△BOE的面积依次是2、4、4和6 求:(1)△OCF 的面积;(2)求△GCE的面积例3.如图,边长为1的正方形ABCD中,BE=3EC,CF=FD,求三角形AEG的面积。
例4. 如图,边长为1的正方形ABCD的边长为10厘米,E为AD 中点,F为CE中点,G为BF中点,求三角形BDG的面积例5. 如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知AOB于BOC的面积分别为25平方厘米于35平方厘米,那么梯形ABCD的面积是平方厘米例6.梯形ABCD的对角线AC与BD交与点O,已知梯形上底为2,2,求三角形AOD与且三角形ABO的面积等于三角形BOC面积的3三角形BOC的面积之比。
例7. 如下图,一个长方形一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH的面积是23,求四边形EGFH 的面积。
例8. 右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米例9. 如图,长方形ABCD被CE、DF分成四块,已知期中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为平方厘米例10. 如图,正六边形面积为6,那么阴影部分面积为多少?蝴蝶模型习题1、如图,长方形ABCD中,BE:EC=2:3,DF:FC=1:2,三角形DFC面积为2平方厘米,求长方形ABCD的面积.2、梯形的下底是上底的1.5倍,三角形OBC的面积是9cm2,问三角形AOD的面积是多少?3、如图,长方形中,若三角形1的面积与三角形3的面积比为4:5,四边形2的面积为36,则三角形1的面积为4、如图,长方形ABCD中,阴影部分是直角三角形且面积为54,OD的长是16,OB的长是9,那么四边形OECD的面积是多少?5、如图,△ABC是等腰三角形,DEFG是正方形,线段AB与CD相较于K点,已知正方形DEFG的面积48,AK:KB=1:3,则△BKD的面积是多少?答案【例1】因为AO : OC =S∆ABD : S∆BDC= 1: 3 ,所以OC = 2⨯3 = 6 ,所以OC : OD = 6: 3 = 2:1.解法二:作AH ⊥BD于H ,CG ⊥BD 于G .因为S所以S ∆ABD=1S3=1S∆BCD,所以AH =1 CG ,3,∆AOD 3 ∆DOCAO =1CO ,3OC = 2⨯3 = 6 ,OC : OD = 6: 3 = 2:1.C【例2】⑴⑴BCD 的面积为2 + 4 + 4 + 6 =16 ,⑴BCO 和∆CDO 的面积都是16 ÷ 2 = 8 ,所以⑴OCF 的面积为8 - 4 = 4 ;⑴由于⑴BCO 的面积为8,⑴BOE 的面积为6,所以⑴OCE 的面积为8 - 6 = 2 ,根据蝴蝶定理,EG : FG =S∆COE : S∆COF= 2 : 4 = 1: 2所以S∆GCE : S∆GCF=EG : FG = 1: 2 ,S∆GCE =11+ 2S∆CEF=1⨯ 2 =2 .33【例3】A DFB EC 连接EF .因为BE = 2EC ,CF =FD ,所以S∆DEF = (1⨯1⨯1)S2 3 2ABCD=1S12ABCD.因为S∆AED =1S2ABCD,由蝴蝶定理,AG : GF =1 : 12 12= 6 :1 ,所以S∆AGD = 6S∆GDF=6S7∆ADF=6⨯1S74ABCD=3S14ABCD.所以S∆AGE =S∆AED-S∆AGD=1S2ABCD-3 S14ABCD=2S7ABCD=2,7【例4】A E DB C设BD 与CE 的交点为O ,连接BE 、DF .由蝴蝶定理EO : OC =S BED : S BCD ,而SBED =1S4ABCD,SBCD=1S2ABCD,所以EO : OC =SBED : SBCD= 1: 2 ,故EO =1EC .3F 为CE 中点,所以EF =1 EC ,2故EO: EF = 2: 3,FO : EO =1: 2 .由蝴蝶定理SBFD : SBED=FO : EO = 1: 2 ,所以SBFD =1S2BED=1S8ABCD,SBGD =1S2BFD=1S16ABCD=1⨯10⨯10 = 6.2516AOB BOC AOB DOC 梯形蝴蝶定理B① S 1 : S 3 C= a 2 : b 2② S : S : S : S = a 2 : b 2 : ab : ab ; 1 3 2 4 ③ S 的对应份数为(a + b )2【例 5】由梯形蝴蝶定理, S : S = a 2 : ab = 25 : 35 , 可得 a : b = 5: 7 ,再根据梯形蝴蝶定理, S : S = a 2 :b 2 = 52 : 72 = 25 : 49 , 所以S DOC = 49梯形 ABCD 的面积为25 + 35 + 35 + 49 =144【例 6】由蝴蝶定理, S AOB : S BOC = ab : b 2 = 2 : 3得a : b = 2: 3,S AOD : S BOC = a 2 : b 2 = 22 : 32 = 4 : 9O∆OCD ∆OCD【例 7】AF BDE C如图,连结 EF ,显然 ADEF 和 BCEF 都是梯形, 于是 EFG 的面积等于三角形 ADG 的面积三角形 BCH 的面积等于三角形 EFH 的面积所以四边形 EGFH 的面积是11+ 23 = 34.【例 8】A DB C连接 AE .由于 AD 与 BC 平行,所以 AECD 也是梯形,那么S ∆OCD = S ∆OAE .据蝴蝶定理, S ∆OCD ⨯ S ∆OAE = S ∆OCE ⨯ S ∆OAD = 2 ⨯ 8 = 16 故 S 2 = 16 ,所以S = 4另解:在平行四边形 ABED 中, S ∆ADE =1 S2 ABED = 1 ⨯(16 + 8) = 12 2 所以S ∆AOE = S ∆ADE - S ∆AOD = 12 - 8 = 4根据蝴蝶定理,阴影部分的面积为8⨯ 2 ÷ 4 = 4【例 9】A EBD连接 DE 、CF . EDCF 为梯形,所以S ∆EOD = S FOC , 又根据蝴蝶定理, S ∆EOD ⋅ S ∆FOC = S ∆EOF ⋅ S ∆COD 所以S ∆EOD = 4 , S ∆ECD = 4 + 8 = 12ABCD 面积为12⨯2 = 24S ∆EOD ⋅ S ∆FOC = S ∆EOF ⋅ S ∆COD = 2 ⨯ 8 = 16 ,四边形OFBC 的面积为24 - 5 - 2 -8 = 9 (平方厘米).【例 10】连接阴影图形的长对角线,此时六边形被平分为两半根据六边形的特殊性质,和梯形蝴蝶定理把六边形分为 18 份 阴影部分占了其中 8 份,所以阴影部分的面积 8 ⨯ 6 = 8 .183∆ AOD ∆ AOD ∆BOC123作业题答案1.AD FBEC连接 AE , FE .因为 BE : EC = 2: 3 , DF : FC =1: 2 ,所以S = (3 ⨯ 1 ⨯ 1)S = 1S. DEF 5 3 2长方形ABCD10 长方形ABCD 因为S= 1 S , A G : GF = 1 : 1= 5 :1,所以S = 5S = 10 平方厘米,所AED2 长方形ABCD 2 10AGD GDF 以 S = 12 平方厘米.因为S = 1S ,所以长方形 ABCD 的面积是72 平方 AFD厘米.2.AFDA D6 长方形ABCDBC根据梯形蝴蝶定理, a : b =1:1.5 = 2: 3 , S : S = a 2:b 2 = 22 : 32 = 4 : 9 , 所以S = 4(cm 2 ) .3.O 做辅助线如下:利用梯形模型,这样发现四边形 2 分成左右两边,其面积正好等于三角形 1 和三角形 3,所以 1 的面积就是36 ⨯44 + 5= 16 ,3 的面积就是 36 ⨯54 + 5= 20 .4.ADBEC因为连接 ED 知道⑴ABO 和⑴EDO 的面积相等即为54 ,又因为OD ⑴OB =16⑴9 ,所以 ⑴AOD 的面积为54 ÷ 9⨯16 = 96 ,根据四边形的对角线性质知道:⑴BEO 的面积为:54⨯54 ÷ 96 = 30.375 ,所以四边形OECD 的面积为: 54 + 96 - 30.375 =119.625 (平方厘米).5.BM C由于 DEFG 是正方形,所以 DA 与 BC 平行,那么四边形 ADBC 是梯形.在梯形ADBC 中,∆BDK 和∆ACK 的面积是相等的.而 AK : KB =1: 3 ,所以∆ACK 的面积是∆ABC 面积的 1 = 1 ,那么∆BDK 的面积也是∆ABC 面积的 1.1+ 3 4 4由于∆ABC 是等腰直角三角形,如果过 A 作 BC 的垂线,M 为垂足,那么 M 是BC 的中点,而且 AM = DE ,可见∆ABM 和∆ACM 的面积都等于正方形 DEFG 面积的一半,所以∆ABC 的面积与正方形 DEFG 的面积相等,为 48. 那么∆BDK 的面积为48⨯ 1= 12 .4。
小学奥数 蝴蝶定理(1) 知识点+例题+练习 (分类全面)

B O
A
D
6
3、如图,BD,CF 将长方形 ABCD 分成 4 块,红色三角形面积是 4 平方厘米,黄色三角形 面积是 6 平方厘米,则绿色四边形的面积是多少平方厘米?
A
F 红
D
绿E
黄
B
C
4、如图,甲、乙两图形都是正方形,它们的边长分别是 10 厘米和 12 厘米,求阴影部分的面 积。
F
E
G A
Aห้องสมุดไป่ตู้
B
G
F
D
E
C
例 6、正方形 ADEB 和正方形 ECFG 底边对齐,两个正方形边长分别为 6 厘米和 4 厘米,三角 形 ACG 的面积是多少平方厘米?
A
B
G F
D
E
C
4
如图,小正方形的边长 6 厘米,阴影部分面积多少平方厘米?
例 7、已知三角形 ABC 的面积是 64 平方厘米,是平方四边形 DEFC 面积的 2 倍,求阴影部分 的面积。
C
2、
即 S =S △ADO △BCO
在任意四边形 ABCD 中,对角线 AC、BD 分成了四个三角形(如图),
这四个三角形的面积分别记为:S1 、S2 、S3 、S4。
B
A
S1
S3 O
S2
S4
D
C
则它们的关系是:
S1×S4 =S2×S3 即相对的两个三角形的面积乘积是相等的。
1
例 1、如图,梯形的两条对角线分梯形为四个小三角形,已知△AOD 的面积是 3 平方厘米,△ DOC 的面积是 9 平方厘米,梯形 ABCD 的面积是多少平方厘米?
B甲C
乙
D
5、正方形 ABCD 和正方形 CEFG,且正方形 ABCD 边长为 8 厘米,则图中阴影(三角形 BDF)部 分的面积为多少平方厘米?
小学几何之蝴蝶定理

小学几何之蝴蝶定理在小学几何的奇妙世界里,有一个充满趣味和智慧的定理——蝴蝶定理。
它就像一把神奇的钥匙,能帮助我们轻松解开许多几何难题。
那什么是蝴蝶定理呢?咱们先来看一个简单的图形。
想象有一个四边形,它的两条对角线相交于一点。
然后,分别从这个交点向四边形的四条边作垂线。
这时,你会发现一个有趣的现象:在两条对角线上相对的两个三角形的面积乘积相等。
比如说,有一个四边形 ABCD,对角线 AC 和 BD 相交于点 O,过点 O 分别作 AB、BC、CD、DA 的垂线,垂足分别为 E、F、G、H。
那么,三角形 AOB 和三角形 COD 的面积乘积就等于三角形 AOD 和三角形 BOC 的面积乘积。
这就是蝴蝶定理的基本内容。
可能有的小朋友会问了,为什么会有这样神奇的定理呢?咱们来试着证明一下。
假设三角形 AOB 的面积为 S₁,三角形 BOC 的面积为 S₂,三角形COD 的面积为 S₃,三角形 AOD 的面积为 S₄。
因为三角形的面积等于底乘以高除以 2,而三角形 AOB 和三角形BOC 都以 BO 为底边,它们的高分别是 AE 和 CF。
所以,S₁/S₂=(AE×BO/2) /(CF×BO/2) = AE/CF。
同理,三角形 AOD 和三角形 COD 都以 DO 为底边,它们的高分别是 AH 和 CG。
所以,S₄/S₃=(AH×DO/2) /(CG×DO/2) =AH/CG。
又因为三角形 AEO 和三角形 CGO 相似(因为对顶角相等,直角相等),所以 AE/CF = AH/CG。
从而得出 S₁×S₃= S₂×S₄,这就证明了蝴蝶定理。
蝴蝶定理在解决实际问题中可有大用处啦!比如,有一道这样的题目:在一个四边形中,两条对角线相交,其中一条对角线被交点分成 3 厘米和 5 厘米两段,另一条对角线被交点分成 2 厘米和 4 厘米两段。
求这个四边形中相对的两个三角形的面积比。
小学奥数之蝴蝶定理

小学奥数---蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4)S 的对应份数为(a+b )2定理4:相似三角形性质CBEFDA1)Hh C c B b A a ===2) S 1 ∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、例1 如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD分割成四个三角形。
奥数专题:蝴蝶定理和风筝定理

蝴蝶定理和风筝定理引入1、蝴蝶定理在梯形 ABCD 中,由对角线 AC 与 BD 分成的左右两个三角形(△ ADO 和△ BCO )形状有 点像一对蝴蝶翅膀,把这两个三角形称为蝴蝶三角形(如图) , 蝴蝶三角形的面积相等。
2、风筝定理在任意四边形 ABCD 中,对角线 AC 、 BD 分成了四个三角形 这四个三角形的面积分别记为: S 1 、S 2 、S 3 、 S 4。
则它们的关系是:S 1× S 4 =S 2× S 3 即相对的两个三角形的面积乘积是相等的。
新授课【例 1】如图,梯形的两条对角线分梯形为四个小三角形,已知△ 米,△ DOC 的面积是 9 平方厘米,梯形 ABCD练习1、如图, 2BO=DO ,且阴影部分的面积是 4cm 2,那么梯形 ABCD 的面积是多少平方厘米?2、如图,阴影部分面积是 4cm 2,OC=2AO ,求梯形的面积。
CBAS 1 S 2O S 3 S 4CAOD 的面积是 3 平方厘例 2】如图, BD ,CF 将长方形 ABCD 分成四块,红色三角形的面积是 4平方厘米,黄色三角形的面积是 8 平方厘米,那么绿色四边形的面积是多少平方厘米?练习1、如图, BD ,CF 将长方形 ABCD 分成 4块,红色三角形面积是 面积是 6 平方厘米,则绿色四边形的面积是多少平方厘米?2、如图,平行四边形 ABCD 的面积是 36平方厘米,对角线 AC 、BD 交于 O 点,E 为 CD 上一点,已知四边形 EFOG 的面积是 3 平方厘米,则阴影部分的面积为多少平方厘米?例 3】如图, 四边形 ABCD 是边长为 18 厘米的正方形, 已知 CE 的长是 ED 的 2 倍。
求: 1)三角形 CEF 的面积,( 2)DF 的长度练习 正方形 ABCD 的边长是 12 厘米,已知 DE 是 EC 长度的 2 倍。
三角形 DEF 的面积是多少平 方厘米? CF 长多少厘米?4 平方厘米,黄色三角形DDFC【例 4】正方形 ABCD 和正方形 CEFG ,且正方形 ABCD 边长为 10 厘米,则图中三角形BDF 面积为多少平方厘米?2、三个正方形 ABCD 、BEFG 、FHKP 如图排列,正方形 BEFG 的边长是 3 厘米,求三角形 DEK 的面积。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理一、蝴蝶定理的定义与公式蝴蝶定理是小学奥数几何篇中的一个重要模型,它描述了在等腰三角形中,一条平行于底边的线段将底边平分,并且这条线段与等腰三角形的两腰相交于同一点时,该线段的中点与等腰三角形的顶点、底边的中点以及两腰上的交点形成一个等腰三角形。
蝴蝶定理的公式如下:设等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,则AG=BG=CG。
二、蝴蝶定理的应用1. 在等腰三角形中求边长:通过蝴蝶定理,可以快速求出等腰三角形中未知边的长度。
例如,已知等腰三角形ABC中,AB=AC,底边BC 的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求AG的长度。
解答:根据蝴蝶定理,AG=BG=CG,又因为AB=AC,所以AG=AB/2=a。
2. 在等腰三角形中求角度:通过蝴蝶定理,可以求出等腰三角形中未知角的度数。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求∠AGB的度数。
解答:由于AG=BG=CG,所以△AGB是等边三角形,∠AGB=60°。
3. 在等腰三角形中求面积:通过蝴蝶定理,可以求出等腰三角形中未知部分的面积。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求△AGB的面积。
解答:由于△AGB是等边三角形,所以△AGB的面积=(a^2 √3)/ 4。
小学几何之蝴蝶定理大全

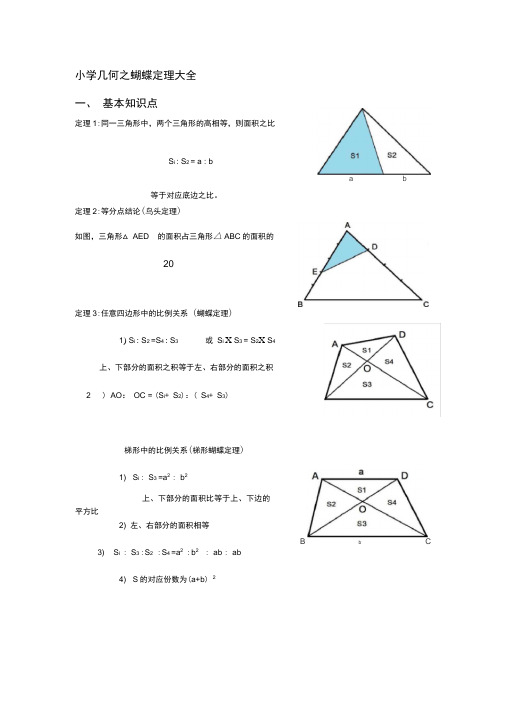
小学几何之蝴蝶定理大全一、基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比等于对应底边之比。
定理2:等分点结论(鸟头定理)如图,三角形△ AED的面积占三角形△ ABC的面积的3 15 4 20定理3:任意四边形中的比例关系(蝴蝶定理)1 )S i:S2 =S : S3 或S i X S3 = S 2 x S上、下部分的面积之积等于左、右部分的面积之积2 ) AO: OC = (S i+ S2):( S+ S3)梯形中的比例关系(梯形蝴蝶定理)A ________ Z_______ 01 )S i : S3 =a2:b2上、下部分的面积比等于上、下边的平方比B b C2)左、右部分的面积相等2 23 ) S : S B : S2: S4 =a : b : ab : ab)S的对应份数为(a+b)定理4:相似三角形性质a b _c _hA B C H2 22 ) S i : S = a : A定理5:燕尾定理S △ ABG : S △ AGC = S △ BGE : S △ GEC = BE : ECS△BGA :S △ BGC=:S △AGF :S △GFC :=AF:FCS△AGC :S △ BCG=:S △ADG :S △DGB :=AD:DB二、例题分析例1、如图,AD DB , AE EF FC,已知阴影部分面积为5平方厘米, 多少平方厘米ABC的面积是例2、有一个三角形ABC的面积为1,如图,且AD - AB,BE21CF CA,求4三角形DEF的面积.例3、如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且1丄AB,已知四边形EDCA勺面积是35,求三角形ABC的面积.(单位:厘米)例4、例1如图,ABCD是直角梯形,求阴影部分的面积和。
例5、两条对角线把梯形 ABCD 分割成四个三角形。
已知两个三角形的面积(如图所示) ,求另两个三角形的面积各是多少(单位:平方厘米)例6、如下图,图中 B0=2DO 阴影部分的面积是 4平方厘米,求梯形 ABCD 勺面积是多少平 方厘米例7、(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD 被对角线 AC BD 分成四个部分,△ AOB 面积为1平方千米,△ BOC 面积为2平方千米,△ COD 勺面积为3平方千米,公园陆地的面积例8、如图:在梯形 ABCD 中,三角形 AOD 的面积为9平方厘米,平方厘米,求梯形 ABCD 勺面积。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理(附答案)在小学奥数的几何部分,蝴蝶定理是一个非常有用的工具,它可以帮助我们解决一些复杂的几何问题。
蝴蝶定理主要描述了在四边形中,当两条对角线互相垂直时,四边形被分成四个小三角形,而这四个小三角形的面积之间存在一定的关系。
蝴蝶定理的内容如下:设四边形ABCD中,AC和BD是互相垂直的对角线,交于点O。
设四个小三角形的面积分别为S1、S2、S3、S4。
那么,蝴蝶定理可以表述为:S1 + S2 = S3 + S4。
这个定理听起来可能有些抽象,但实际上它的应用非常广泛。
我们可以通过蝴蝶定理来解决一些看似复杂的问题。
下面,我将通过一些例子来展示蝴蝶定理的应用。
例1:在四边形ABCD中,AC和BD是互相垂直的对角线,且AC =8cm,BD = 6cm。
如果三角形ABC的面积是24cm²,那么三角形ADC的面积是多少?解答:根据蝴蝶定理,我们有S1 + S2 = S3 + S4。
由于三角形ABC的面积是24cm²,所以S1 = 24cm²。
又因为AC = 8cm,BD = 6cm,我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 8cm6cm = 24cm²。
因此,三角形ADC的面积也是24cm²。
例2:在四边形ABCD中,AC和BD是互相垂直的对角线,且AC = 10cm,BD = 5cm。
如果三角形ABC的面积是20cm²,那么三角形ADC的面积是多少?解答:同样地,根据蝴蝶定理,我们有S1 + S2 = S3 + S4。
由于三角形ABC的面积是20cm²,所以S1 = 20cm²。
又因为AC = 10cm,BD = 5cm,我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 10cm 5cm = 25cm²。
因此,三角形ADC的面积是25cm²。
小学几何之蝴蝶定理

小学几何之蝴蝶定理在小学几何的奇妙世界里,有一个充满趣味和智慧的定理——蝴蝶定理。
它就像一把神奇的钥匙,能帮助我们轻松解开许多几何难题。
蝴蝶定理的名字听起来很有趣,是不是让你联想到了一只美丽的蝴蝶在几何图形中翩翩起舞?其实,这个定理之所以叫这个名字,是因为它的图形看起来有点像一只蝴蝶。
那蝴蝶定理到底说的是什么呢?咱们先来看看它的基本形式。
假设有一个梯形,两条对角线相交于一点。
在这个梯形中,通过对角线相交点作两条平行于梯形底边的直线,分别与梯形的两条腰相交。
那么,位于梯形上下两个部分的三角形面积相等。
比如说,有一个梯形 ABCD,上底是 AD,下底是 BC,对角线 AC和 BD 相交于点 O。
过点 O 作 EF 平行于 AD 和 BC,分别交 AB 于点E,交 CD 于点 F。
那么三角形 AOD 和三角形 BOC 的面积是相等的。
可能有的同学会问,为什么会这样呢?我们来试着解释一下。
为了更好地理解,我们可以把梯形的面积看作是由多个部分组成的。
首先,三角形 ABD 和三角形 ACD 的面积是相等的,因为它们都以AD 为底边,并且顶点 B 和 C 到 AD 的距离是相等的,也就是这两个三角形的高相等。
那么,三角形 ABD 的面积减去三角形 AOD 的面积,就等于三角形AOB 的面积;三角形 ACD 的面积减去三角形 AOD 的面积,就等于三角形 DOC 的面积。
因为三角形 ABD 和三角形 ACD 的面积相等,所以三角形 AOB 的面积就等于三角形 DOC 的面积。
蝴蝶定理在解决实际问题中非常有用。
比如,当我们已知梯形中某些部分的面积,要求其他部分的面积时,就可以运用这个定理来快速找到答案。
再举个例子,假如梯形 ABCD 中,三角形 AOD 的面积是 6 平方厘米,三角形 BOC 的面积是 9 平方厘米,那么三角形 AOB 的面积是多少呢?根据蝴蝶定理,我们知道三角形 AOB 的面积乘以三角形 DOC的面积等于三角形 AOD 的面积乘以三角形 BOC 的面积。
小学几何之蝴蝶定理

CFEF几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b 定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的 定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4 上、下部分的面积之积等于左、右部分的面积之积 2)AO ∶OC = (S 1+S 2)∶(S 4+S 3) 梯形中的比例关系( 梯形蝴蝶定理) 1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab 4)S 的对应份数为(a+b )2 定理4:相似三角形性质 1)HhC c B b A a === 2) S 1 ∶S 2 = a 2 ∶A 2 定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶EC S △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FC S △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且AD 13BE BC =,14CF CA =,求三角形DEF 的面积.AB 上的一点,且BE=13AB,例3、如图,在三角形ABC 中,,D 为BC 的中点,E 已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、例1 如图,ABCD 是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD 分割成四个三角形。
小升初奥数 几何(蝴蝶模型)

S4
S3 B
① S2 S4 ② S1 : S3 a 2 : b2 ③ S1 : S3 : S2 : S4 a 2 : b2 : ab : ab ④ S 的对应份数为 a b .
2
b
C
基础篇: 【一】 如图,某公园的外轮廓是四边形 ABCD,被对角线 AC、BD 分成四个部分,△AOB 面积为 1 平方千米, △BOC 面积为 2 平方千米, △COD 的面积为 3 平方千米, 公园由陆地面积是 6.92 平方千米和人工湖组成,求人工湖的面积是多少平方千米?
A 2 B C 1 G 3 D
【分析】 ⑴根据蝴蝶定理, S
BGC
1 2 3 ,那么 S
BGC
6;
⑵根据蝴蝶定理, AG : GC 1 2 : 3 6 1: 3 . 【三】 图中的四边形土地的总面积是 52 公顷,两条对角线把它分成了四个小三角形,其中两个小 三角形的面积分别是 6 公顷和 7 公顷,求四个三角形中最大的一个的面积。
C
B O A D
【分析】 根据蝴蝶定理求得 S△ AOD 3 1 2 1.5 平方千米,公园四边形 ABCD 的面积是
1 2 3 1.5 7.5 平方千米,所以人工湖的面积是 7.5 6.92 0.58 平方千米
【二】 如图, 四边形被两条对角线分成 4 个三角形, 其中三个三角形的面积已知, 求: ⑴三角形 BGC 的面积;⑵ AG : GC ?
米), SECD 4 8 12 (平方厘米).那么长方形 ABCD 的面积为 12 2 24 平方厘 米,四边形 OFBC 的面积为 24 5 2 8 9 (平方厘米).
【八】 如图,正方形 ABCD 面积为 3 平方厘米, M 是 AD 边上的中点.求图中阴影部分的面积. C B
蝴蝶定理定理

蝴蝶定理定理
蝴蝶定理是古代欧氏平面几何中最精彩的结果之一。
这个命题最早出现在1815年,由W。
G。
霍纳提出证明。
而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,题目的图形像一只蝴蝶。
这个定理的证法不胜枚举,至
今仍然被数学爱好者研究,在考试中时有各种变形。
蝴蝶定理:设M为圆内弦PQ的中点,过M作弦AB和CD。
设AD 和BC各相交PQ于点X和Y,则M是XY的中点。
蝴蝶定理的证明
该定理实际上是射影几何中一个定理的特殊情况,有多种推广(详见定理推广):
1.M作为圆内弦的交点是不必要的,可以移到圆外。
2.圆可以改为任意圆锥曲线。
3.将圆变为一个筝形,M为对角线交点。
4.去掉中点的条件,结论变为一个一般关于有向线段的比例式,称为“坎迪定理”,不为中点时满足。
小学几何之蝴蝶定理

小学几何之蝴蝶定理在小学几何的奇妙世界里,有一个充满趣味和智慧的定理,那就是蝴蝶定理。
它就像一把神奇的钥匙,能帮助我们轻松解决许多看似复杂的几何问题。
让我们先来看看蝴蝶定理到底说的是什么。
蝴蝶定理通常是指在一个梯形中,连接两条对角线,会形成四个三角形。
位于梯形对角线两侧的两个三角形的面积相等。
简单来说,就像是一只蝴蝶的两个翅膀,面积是一样的。
那为什么这个定理如此重要呢?想象一下,当我们面对一个梯形的图形,需要计算其中某些部分的面积时,如果能够运用蝴蝶定理,就可以省去很多繁琐的计算步骤,迅速得出答案。
这对于提高我们解决问题的效率和准确性可是非常有帮助的。
为了更好地理解蝴蝶定理,让我们通过一些具体的例子来感受一下它的神奇之处。
比如说,有一个梯形 ABCD,其中 AB 平行于 CD,两条对角线 AC 和 BD 相交于点 O。
假设三角形 AOD 的面积是 6 平方厘米,三角形BOC 的面积是 8 平方厘米。
那么根据蝴蝶定理,三角形 AOB 的面积就等于三角形 DOC 的面积。
那我们怎么来求出这两个未知三角形的面积呢?我们可以这样思考:因为三角形 AOD 和三角形 BOC 的面积已知,我们设三角形 AOB 的面积为 x 平方厘米,那么三角形 DOC 的面积也为 x 平方厘米。
根据梯形中三角形面积的关系,我们可以得到:三角形 AOD 的面积乘以三角形 BOC 的面积等于三角形 AOB 的面积乘以三角形 DOC 的面积。
也就是 6×8 = x×x,解得 x =4√3 平方厘米。
再来看一个例子。
有一个梯形,上底是 4 厘米,下底是 6 厘米,高是 5 厘米。
连接两条对角线后,其中一个三角形的面积是 10 平方厘米。
那么另一个与它相对的三角形的面积是多少呢?我们先根据梯形的面积公式:(上底+下底)×高÷2,算出这个梯形的总面积是(4 + 6)×5÷2 = 25 平方厘米。
小学几何之蝴蝶定理大全
小学几何之蝴蝶定理大全一、基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比S i : S2 = a : ba b等于对应底边之比。
定理2:等分点结论(鸟头定理)如图,三角形△AED的面积占三角形△ ABC的面积的20定理3:任意四边形中的比例关系(蝴蝶定理)1) S i : S2 =S4 : S3 或S i X S3 = S2X S4上、下部分的面积之积等于左、右部分的面积之积2 ) AO: OC = (S i+ S2):( S4+ S3)梯形中的比例关系(梯形蝴蝶定理)1) S i : S3 =a2: b2上、下部分的面积比等于上、下边的平方比2) 左、右部分的面积相等B b C3) S i : S3 : S2 : S4 =a2: b2: ab : ab4) S的对应份数为(a+b) 2定理4:相似三角形性质2) S i : S 2 = a 2 : A 2定理5:燕尾定理S AABG:S A AGC : =S A BGE : :S A GEC =BE : ECS A BGA : :S A BGC : =S A AGF :S A GFC =AF : FC S A AGC : :S A BCG : =S A ADG:S A DGB=AD :DB二、例题分析例1、如图,AD DB , AE EF FC ,已知阴影部分面积为 5平方厘米, 多少平方厘米?ABC 的面积是例2、有一个三角形 ABC 的面积为1,如图,且AD - AB , BE21例3、如图,在三角形 ABC 中,,D 为BC 的中点,E 为AB 上的一点,且 BE=—AB,已知四边3例4、例1如图,ABCD 是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形 ABCD 分割成四个三角形。
已知两个三角形的面积(如图所示) 另两个三角形的面积各是多少?(单位:平方厘米)例6、如下图,图中 BO=2DO 阴影部分的面积是 4平方厘米,求梯形 ABCD 勺面积是多少平三角形DEF 的面积.-BC , CF3-CA ,求 4形EDCA 勺面积是35,求三角形 ABC 的面积.,求B方厘米?例7、(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC、BD分成四个部分,△ AOB 面积为1平方千米,△ BOC面积为2平方千米,△ COD的面积为3平方千米,公园陆地的面积是6.92平方千米,求人工湖的面积是多少平方千米?例8、如图:在梯形ABCD中,三角形AOD的面积为9平方厘米25平方厘米,求梯形ABCD的面积。
最新小学奥数之几何蝴蝶定理问题

几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4)S 的对应份数为(a+b )2定理4:相似三角形性质CFEADBCBEFDA1)HhC c B b A a ===2) S 1 ∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABE ∶ S △AEC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △ADC ∶ S △DCB = S △ADG ∶ S △DGB = AD ∶DB二、 例题例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD分割成四个三角形。
小学几何之蝴蝶定理

几何之蝴蝶定理一、 根本常识点定理1:统一三角形中,两个三角形的高相等,则面积之比等于对应底边之比.S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的定理3:随意率性四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上.下部分的面积之积等于左.右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上.下部分的面积比等于上.下边的平方比2)左.右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2∶ab ∶ab4)S 的对应份数为(a+b )2定理4:类似三角形性质1) H hC c B b A a ===2) S 1∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABG ∶S △AGC = S △BGE ∶S △GEC = BE ∶ECS △BGA ∶S △BGC = S △AGF ∶S △GFC = AF ∶FCS △AGC ∶S △BCG = S △ADG ∶S △DGB = AD ∶DB二、 例题剖析例 1.如图,AD DB =,AE EF FC ==,已知暗影部分面积为5平方厘米,ABC 的面积是若干平方厘米? 例2.有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3.如图,在三角形ABC 中,,D 为BC的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4.例1 如图,ABCD 是直角梯形,求暗影部分的面积和.(单位:厘米)例5.两条对角线把梯形ABCD 朋分成四个三角形.已知两个三角形的面积(如图所示),求另两个三角形的面积各是若干?(单位:平方厘米)例6.如下图,图中BO=2DO,暗影部分的面积是4平方厘米,求梯形ABCD 的面积是若干平方厘米?例7.(小数报比赛运动试题)如图,某公园的外轮廓是四边形ABCD,被对角线AC.BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园陆地的面积是6.92平方千米,求人C B E F D A CFE A DB工湖的面积是若干平方千米?例8.如图:在梯形ABCD中,三角形AOD的面积为9平方厘米,三角形BOC的面积为25平方厘米,求梯形ABCD的面积.例9.(2003北京市第十九届小学生“迎春杯”数学比赛)四边形ABCD的对角线AC与BD交于点O(如图)所示.假如三角形ABD的面积等于三角形BCD的面积的13,且2AO=,3DO=,那么CO的长度是DO的长度的_________倍.例10.左下图所示的ABCD的边BC长10cm,直角三角形BCE的直角边EC长8cm,已知两块暗影部分的面积和比△EFG的面积大10cm2,求CF的长.例11.长方形ABCD的面积为36平方厘米,E.F.G分离为边AB.BC.CD的中点,H为AD边上的任一点.求图中暗影部分的面积是若干?例12.如图,甲.乙两图形都是正方形,它们的边长分离是10厘米和12厘米,求暗影部分的面积.例13.如图,大正方形ABCD的边长为6,依以下前提求三角形BDF的面积.例14.(右图是一块长方形耕地,它由四个小长方形拼合而成,个中三个小长方形的面积分离为15.18.30公顷,问图中暗影部分的面积是若干?例15.如下图,已知D是BC的中点,E是CD的中点,F是AC的中点,且ADG ∆的面积比EFG ∆的面积大6平方厘米.?的面积是多少平方厘米ABC ∆ 三、 演习题1.如图,四边形ABCD 中,AC 和BD 订交于O 点,三角形ADO 的面积=5,三角形DOC 的面积=4,三角形AOB 的面积=15,求三角形BOC 的面积是若干?2.如图所示,BD,CF 将长方形ABCD 分成4块,△DEF 的面积是4cm 2,△CED 的面积是6cm 2.问:四边形ABEF 的面积是若干平方厘米?3.如右图BE=31BC,CD=41AC,那么三角形AED 的面积是三角形ABC 面积的______.5.如图所示,已知ABCD 是长方形,AE:ED=CF:FD=1:2,三角形DEF 的面积是16平方厘米,求三角形ABE 的面积是若干平方厘米?6、 如右图,ABCD 是梯形,ABED 是平行四边形,己知三角面积如下图所示(单位:平方厘米),暗影部分的面积是若干平方厘米.7.正方形ABFD 的面积为100平方厘米,直角三角形ABC 的面积,比直角三角形(CDE 的面积大30平方厘米,求DE 的长是若干?8、 已知ABC∆中,12AB AC cm ==,ABC ∆的面积是2cm ,P 是BC 上随意率性一点,P 到AB ,AC 的距离是,x y ,那么x y +=;9.如右图所示,已知三角形ABC 面积为1,延伸AB 至D,使BD=AB;延伸BC至E,使CE=2BC;延伸CA至F,使AF=3AC,求三角形DEF的面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例11、长方形ABCD的面积为36平方厘米,E、F、G分别为边AB、BC、CD的中点,H为AD边上的任一点。求图中阴影部分的面积是多少?
例12、如图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积。
例8、如图:在梯形ABCD中,三角形AOD的面积为9平方厘米,三角形BOC的面积为25平方厘米,求梯形ABCD的面积。
例9、(2003北京市第十九届小学生“迎春杯”数学竞赛)
四边形 的对角线 与 交于点 (如图)所示。
如果三角形 的面积等于三角形 的面积的 ,且
, ,那么 的长度是 的长度的_________倍。
定理5:燕尾定理
S△ABG∶S△AGC= S△BGE∶S△GEC= BE∶EC
S△BGA∶S△BGC= S△AGF∶S△GFC= AF∶FC
S△AGC∶S△BCG= S△ADG∶S△DGB= AD∶DB
二、例题
例1、如图, , ,已知阴影部分面积为 平方厘米, 的面积是多少平方厘米?
例2、有一个三角形 的面积为1,如图,且 , , ,求三角形 的面积.
2)AO∶OC = (S1+S2)∶(S4+S3)
梯形中的ቤተ መጻሕፍቲ ባይዱ例关系(梯形蝴蝶定理)
1)S1∶S3=a2∶b2
上、下部分的面积比等于上、下边的平方比
2)左、右部分的面积相等
3)S1∶S3∶S2∶S4=a2∶b2∶ab∶ab
4)S的对应份数为(a+b)2
定理4:相似三角形性质
1)
2)S1∶S2= a2∶A2
例6、如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?
例7、(小数报竞赛活动试题)
如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米,公园陆地的面积是6.92平方千米,求人工湖的面积是多少平方千米?
例13、如图,大正方形ABCD的边长为6,依以下条件求三角形BDF的面积。
例14、(右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为15、18、30公顷,问图中阴影部分的面积是多少?
例15、如下图,已知D是BC的中点,E是CD的中点,F是AC的中点,且 的面积比 的面积大6平方厘米。
三、练习题
1、如图,四边形ABCD中,AC和BD相交于O点,三角形ADO的面积=5,三角形DOC的面积=4,三角形AOB的面积=15,求三角形BOC的面积是多少?
2、如图所示,BD,CF将长方形ABCD分成4块,△DEF的面积是4cm ,△CED的面积是6cm 。问:四边形ABEF的面积是多少平方厘米?
几何之蝴蝶定理
一、基本知识点
定理1:同一三角形中,两个三角形的高相等,则面积之比
等于对应底边之比。
S1: S2= a : b
定理2:等分点结论(鸟头定理)
如图,三角形△AED的面积占三角形△ABC的面积的
定理3:任意四边形中的比例关系(蝴蝶定理)
1)S1∶S2=S4∶S3或S1×S3= S2×S4
上、下部分的面积之积等于左、右部分的面积之积
7、正方形ABFD的面积为100平方厘米,直角三角形ABC的面积,比直角三角形(CDE的面积大30平方厘米,求DE的长是多少?
8、已知 中, , 的面积是 , 是 上任意一点, 到 , 的距离是 ,那么 ;
9、如右图所示,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
例3、如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且BE= AB,已知四边形EDCA的面积是35,求三角形ABC的面积.
例4、例1如图,ABCD是直角梯形,求阴影部分的面积和。(单位:厘米)
例5、两条对角线把梯形ABCD分割成四个三角形。已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)
3、如右图BE= BC,CD= AC,那么三角形AED的面积是三角形ABC面积的______.
5、如图所示,已知ABCD是长方形,AE:ED=CF:FD=1:2,三角形DEF的面积是16平方厘米,求三角形ABE的面积是多少平方厘米?
6、如右图, 是梯形, 是平行四边形,己知三角面积如下图所示(单位:平方厘米),阴影部分的面积是多少平方厘米。
