南京邮电大学数值代数实验

合集下载

南邮数据库基础教程实验报告

实验报告〔２０1 5 / ２０1 6 学年第二学期〕课程名称数据库系统与设计实验名称数据库系统程序设计与分析实验时间２０1 6年6月3/17/22/24 日指导单位指导教师学生班级学号学院(系) 电脑学院专业实验报告实验报告insert into PC values(1010,,2048,300,770);insert into PC values(1011,,2048,160,959);insert into PC values(1012,,1024,160,649);insert into PC values(1013,,512,80,529);insert into Laptop values(2001,,2048,240,,3673);insert into Laptop values(2002,,1024,80,,949);insert into Laptop values(2003,,512,60,,549);insert into Laptop values(2004,,512,60,,1150);insert into Laptop values(2005,,1024,120,,2500);insert into Laptop values(2006,,2048,80,,1700);insert into Laptop values(2007,,1024,120,,1429);insert into Laptop values(2008,,1024,100,,900);insert into Laptop values(2009,,512,80,,680);insert into Laptop values(2010,,2048,160,,2300);insert into Printer values(3001,'true','ink_jet',99); insert into Printer values(3002,'false','laster',239); insert into Printer values(3003,'true','laster',899); insert into Printer values(3004,'true','ink_jet',120); insert into Printer values(3005,'false','laster',120);insert into Printer values(3006,'true','ink_jet',100); insert into Printer values(3007,'true','laster',200);insert into Product values('A',1001,'pc');insert into Product values('A',1002,'pc');insert into Product values('A',1003,'pc');insert into Product values('A',2004,'laptop');insert into Product values('A',2005,'laptop');insert into Product values('A',2006,'laptop');insert into Product values('B',1004,'pc');insert into Product values('B',1005,'pc');insert into Product values('B',1006,'pc');insert into Product values('B',2007,'laptop');insert into Product values('C',1007,'pc');insert into Product values('D',1008,'pc');insert into Product values('D',1009,'pc');insert into Product values('D',1010,'pc')insert into Product values('D',3004,'printer');insert into Product values('D',3005,'printer');insert into Product values('E',1011,'pc');insert into Product values('E',1012,'pc');insert into Product values('E',1013,'pc');insert into Product values('E',2001,'laptop');insert into Product values('E',2002,'laptop');insert into Product values('E',2003,'laptop');insert into Product values('E',3001,'printer');insert into Product values('E',3002,'printer');insert into Product values('E',3003,'printer');insert into Product values('F',2008,'laptop');insert into Product values('F',2009,'laptop');insert into Product values('G',2010,'laptop')insert into Product values('H',3006,'printer');insert into Product values('H',3007,'printer');实验二A〕SELECT maker,speedFrom Product,Laptopwhere Laptop.hd>=30 AND Laptop.model=Product.modelB〕SELECT Product.model,priceFrom Product,PCWhere Product.maker='B'AND Product.model=PC.model UNIONSELECT Product.model,priceFrom Product,LaptopWhere Product.maker='B'AND Product.model=Laptop.model UNIONSELECT Product.model,priceFROM Product,PrinterWHERE Product.maker='B'AND Product.model=Printer.modelC〕SELECT makerFrom Product PWhere P.type='laptop'EXCEPTSELECT makerFrom Product PWhere P.type='pc'D〕SELECT DISTINCT p.hdFROM PC p,PC qWHERE q.hd=p.hd AND p.model>q.modelE〕SELECT p.model AS MODEL1,q.model AS MODEL2FROM PC p,PC qWHERE p.speed=q.speed AND p.ram=q.ram AND p.model>q.modelF〕SELECT p.makerFROM (SELECT E.maker,F.modelFROM Product E,PC FWHERE F.speed> 3.0 AND E.model=F.modelUNIONSELECT G.maker,H.modelFROM Product G,Laptop HWHERE H.speed> 3.0 AND G.model=H.model)pGROUP BY p.makerHAVING COUNT(p.model)>= 2实验三A〕SELECT makerFROM Product,(SELECT modelFROM PCWHERE PC.speed>)pWHERE Product.model=p.modelSELECT makerFROM Product JOIN PCON Product.model=PC.modelWHERE speed>B〕SELECT p.priceFROM Printer pWHERE p.price>=ALL(SELECT priceFROM Printer)SELECT MAX(price)AS price FROM PrinterC〕SELECT p.modelFROM Laptop pWHERE p.speed<=(SELECT MIN(speed)FROM PC)SELECT p.modelFROM Laptop pWHERE p.speed<=ALL(SELECT speedFROM PC)D〕SELECT p.modelFROM (SELECT model,priceFROM PCUNIONSELECT model,priceFROM LaptopUNIONSELECT model,priceFROM Printer)pWHERE p.price>=ALL(SELECT priceFROM PCUNIONSELECT priceFROM LaptopUNIONSELECT priceFROM Printer)E〕SELECT makerFROM ProductWHERE model=(SELECT modelFROM PrinterWHERE price=(SELECT MIN(price)AS priceFROM Printer))SELECT p.makerFROM Product p,Printer qWHERE p.model=q.model AND q.price<=ALL(SELECT priceFROM Printer)F〕SELECT makerFROM Product p,PC qWHERE p.model=q.modelAND q.ram<=ALL(SELECT ramFROM PC)AND q.speed>=ALL(SELECT speedFROM PC)实验四A〕SELECT AVG(speed)AS AVGSPEEDFROM PCB〕SELECT AVG(speed)AS AVGSPEEDFROM PCWHERE price> 1000C〕SELECT AVG(price)AS AVGPRICEFROM PCWHERE model IN(SELECT modelFROM ProductWHERE maker='A')D〕SELECT AVG(p.price)AS AVGPRICEFROM (SELECT model,priceFROM PCUNIONSELECT model,priceFROM Laptop)pWHERE p.model IN(SELECT modelFROM ProductWHERE maker='D')E〕SELECT speed,AVG(price)AS AVGPRICEFROM PCGROUP BY speedF〕SELECT maker,AVG(screen)AS AVGSCREENFROM Product p JOIN Laptop q ON p.model=q.model GROUP BY makerG〕SELECT makerFROM ProductWHERE type='PC'GROUP BY makerHAVING COUNT(model)>= 3H〕SELECT maker,MAX(price)AS MAXPRICEFROM Product p JOIN PC q ON p.model=q.model GROUP BY makerI〕SELECT speed,AVG(price)AS AVGPRICEFROM PCWhere speed>GROUP BY speedJ〕SELECT AVG(hd)AS AVGHDFROM Product p JOIN PC q ON p.model=q.model WHERE maker IN(SELECT makerFROM ProductWhere type='Printer')实验报告。

南邮数据结构实验一

实验报告（2014 / 2015 学年第一学期）课程名称数据结构实验名称二叉树基本操作以及哈夫曼编码译码系统实验时间年月日指导单位指导教师学生姓名班级学号学院(系) 专业二叉树的基本运算：一、问题描述1.设计递归算法，实现二叉树的运算：删除一棵二叉树，求一棵二叉树的高度，求一棵二叉树中叶子节点数，复制一棵二叉树，交换一棵二叉树的左右子树2.设计算法，自上而下，自左向右即按层次遍历一棵二叉树3.设计main函数，测试上述每个运算二、系统分析和概要设计首先用maketree构造一棵二叉树，然后遍历二叉树，然后交换每个结点的左右子树，接着算出输得高度和叶子节点，最后删除。

三、详细设计2. 核心算法建立二叉树的void MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right)和计算叶子节点的int Size();3. 算法分析删除一棵二叉树，求一棵二叉树的高度，求一棵二叉树中叶子节点数，复制一棵二叉树等都是用递归的方法实现。

四、程序代码流程图#include<iostream.h>template<class T>struct BTNode{BTNode(){lChild=rChild=NULL;}BTNode(const T &x){element=x;lChild=rChild=NULL;}BTNode(const T &x,BTNode<T>* l,BTNode<T>* r){element=x;lChild=l;rChild=r;}T element;BTNode<T>* lChild,* rChild;};template<class T>class BinaryTree{public:BinaryTree(){root=NULL;}~BinaryTree(){Clear();}void Copy(BinaryTree<T> &r) const;bool IsEmpty()const{return root == NULL;}void Clear();void Exchange();bool Root(T& x)const;int GetHeight();void MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right);void BreakTree(T& x,BinaryTree<T>& left,BinaryTree<T>& right);void PreOrder(void (*Visit)(T &x));void LevelOrder(void (*Visit)(T& x));int Size();BinaryTree<T>(BinaryTree<T> &t)root=Copy(t.root);}// void InOrder(void (*Visit)(T &x));// void PostOrder(void (*Visit)(T &x));BTNode<T>* Copy(BTNode<T>* t);protected:BTNode<T> * root;private:static int number;void Clear(BTNode<T>* &t);void Exchange(BTNode<T>* t);int GetHeight(BTNode<T>* t);int Size(BTNode<T>* t);void PreOrder(void (*Visit)(T &x),BTNode<T>* t);void LevelOrder(void (*Visit)(T& x),BTNode<T>* t); // void InOrder(void (*Visit)(T &x),BTNode<T>* t);// void PostOrder(void (*Visit)(T &x),BTNode<T>* t); };template <class T>bool BinaryTree<T>::Root(T &x)const{if(root){x=root->element;return true;}elsereturn false;}template <class T>void BinaryTree<T>::Clear(){Clear(root);}template <class T>void BinaryTree<T>::Clear(BTNode<T>* &t){if(t)Clear(t->lChild);Clear(t->rChild);delete t;t=NULL;}}template <class T>void BinaryTree<T>::MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right) {if(root||&left==&right)return;root=new BTNode <T>(x,left.root,right.root);left.root=right.root=NULL;}template <class T>void BinaryTree<T>::BreakTree(T& x,BinaryTree<T>& left,BinaryTree<T>& right) {if(!root||&left==&right||left.root||right.root)return;x=root->element;left.root=root->lChild;right.root=root->rChild;delete root;root=NULL;}template <class T>BTNode<T>* BinaryTree<T>::Copy(BTNode<T>* t){if(!t)return NULL;BTNode<T>*q=new BTNode<T>(t->element);q->lChild=Copy(t->lChild);q->rChild=Copy(t->rChild);return q;}template <class T>void Visit(T &x){cout<<x<<" ";}template <class T>void BinaryTree<T>::PreOrder(void (*Visit)(T& x)){PreOrder(Visit,root);}template <class T>void BinaryTree<T>::PreOrder(void (*Visit)(T& x),BTNode<T>* t) {if(t){Visit(t->element);PreOrder(Visit,t->lChild);PreOrder(Visit,t->rChild);}}template <class T>void BinaryTree<T>::Exchange(){Exchange(root);}template <class T>void BinaryTree<T>::Exchange(BTNode<T>* t){if(!t)return;BTNode<T>* temp;temp=t->lChild;t->lChild=t->rChild;t->rChild=temp;Exchange(t->lChild);Exchange(t->rChild);}template <class T>int BinaryTree<T>::GetHeight(){return GetHeight(root);}int BinaryTree<T>::GetHeight(BTNode<T>* t){int templ;int tempr;if(!t)return 0;templ=GetHeight(t->lChild);tempr=GetHeight(t->rChild);if(templ++>tempr++)return templ;elsereturn tempr;}template <class T>int BinaryTree<T>::number=0;template <class T>int BinaryTree<T>::Size(){Size(root);return number;}template <class T>int BinaryTree<T>::Size(BTNode<T>* t){if(t!=NULL){Size(t->lChild);if(t->lChild ==NULL&&t->rChild ==NULL)number++;Size(t->rChild);}return number;}template <class T>void BinaryTree<T>::LevelOrder(void (*Visit)(T& x)) {PreOrder(Visit,root);}void BinaryTree<T>::LevelOrder(void (*Visit)(T& x),BTNode<T>* t) {BTNode *quene[50],*p;int pre=1,rear=1;quene[++pre]=t;while(pre!=0){p=quene[++rear];cout<<p->element<<" ";if(p->lChild !=NULL)quene[++pre]=p->rChild ;if(p->rChild !=NULL)quene[++pre]=p->lChild ;}}void main(){BinaryTree <char> a,b,x,y,z;y.MakeTree('E',a,b);z.MakeTree('F',a,b);x.MakeTree('C',y,z);y.MakeTree('D',a,b);z.MakeTree('B',y,x);cout<<"二叉树z的先序遍历:"<<endl;z.PreOrder(Visit);cout<<endl;cout<<"层次遍历二叉树:";z.LevelOrder(Visit);cout<<endl;BinaryTree<char> q(z);cout<<"复制的二叉树q的先序遍历:"<<endl;q.PreOrder(Visit);cout<<endl;cout<<"树的高度:";cout<<z.GetHeight()<<endl;cout<<"叶子节点数量:";cout<<z.Size()<<endl;z.Exchange();cout<<"二叉树左右子树交换后的先序遍历:"<<endl;z.PreOrder(Visit);cout<<endl;}五、测试用例和运行结果测试用例如main函数中所示，结果如下图所示。

资料：数学实验(南邮)答案2

第二次题库1、设⎪⎩⎪⎨⎧=+=+32/)7(11x x x x n n n ，数列}{n x 是否收敛？若收敛，其值为多少？精确到6位有效数字。

>> f=inline('(x+7/x)/2'); syms x; x0=3; for i=1:1:20 x0=f(x0);fprintf('%g,%g\n',i,x0); end 1,2.66667 2,2.64583 3,2.64575 4,2.64575 5,2.64575 6,2.64575 7,2.64575 8,2.64575 9,2.64575 10,2.64575 11,2.64575 12,2.64575 13,2.64575 14,2.64575 15,2.64575 16,2.64575 17,2.64575 18,2.64575 19,2.64575 20,2.64575本次计算运行到第三次结果稳定，可得：数列}{n x 收敛，收敛到2.645752、设 ,131211pp p n n x ++++= }{n x 是否收敛？若收敛，其值为多少？精确到17位有效数字。

学号为单号，取7=p >> s=0; for i=1:1:200 s=s+1/i^7;fprintf('%g,%20.17f\n',i,s); end1, 1.00000000000000000 2, 1.00781250000000000 3, 1.00826974737082750 4, 1.00833078252707750 5, 1.00834358252707750 6, 1.00834715477216210 7, 1.00834836903784100 8, 1.00834884587499920 9, 1.00834905495015730 10, 1.00834915495015730 …………………………… 181, 1.00834927738191870 182, 1.00834927738191890 183, 1.00834927738191920 184, 1.00834927738191940 185, 1.00834927738191960 186, 1.00834927738191980 187, 1.00834927738192000 188, 1.00834927738192030 189, 1.00834927738192050190, 1.00834927738192070 191, 1.00834927738192070 192, 1.00834927738192070 193, 1.00834927738192070 194, 1.00834927738192070 195, 1.00834927738192070 196, 1.00834927738192070 197, 1.00834927738192070 198, 1.00834927738192070 199, 1.00834927738192070 200, 1.00834927738192070运行至第190次后稳定，值为1.00834927738192070书上题库：(实验四) 1，2，4，7（1），8，12（改为：对例2，取 120,55,25,5.4=a 观察图形有什么变化．），13，14 。

南京邮电大学实验报告模版 2

实验报告（2014 / 2015 学年第一学期）课程名称计算机操作系统实验名称虚拟存储中页面置换算法的模拟实现实验时间2014 年12 月19 日指导单位南京邮电大学指导教师崔衍学生姓名班级学号学院(系) 物联网院专业网络工程实验报告- 2 -- 1 -二、实验原理及内容实验三#include <iostream.h>#include<stdlib.h>#include<conio.h>#include<stdio.h>#define Bsize 4typedef struct BLOCK//声明一种新类型——物理块类型{int pagenum;//页号int accessed;//访问字段，其值表示多久未被访问}BLOCK;int pc;//程序计数器，用来记录指令的序号int n;//缺页计数器，用来记录缺页的次数static int temp[320];//用来存储320条随机数BLOCK block[Bsize]; //定义一大小为4的物理块数组//************************************************************* void init( ); //程序初始化函数int findExist(int curpage);//查找物理块中是否有该页面int findSpace( );//查找是否有空闲物理块int findReplace( );//查找应予置换的页面void display ( );//显示void suijishu( );//产生320条随机数,显示并存储到temp[320]void pagestring( );//显示调用的页面队列void OPT( );//OPT算法void LRU( );// LRU算法void FIFO( );//FIFO算法//************************************************************* void init( ){for(int i=0;i<Bsize;i++){block[i].pagenum=-1;block[i].accessed=0;- 1 -{for(int i=0; i<Bsize; i++){if(block[i].pagenum != -1){ printf(" %02d",block[i].pagenum);}}cout<<endl;}//-------------------------------------------------------------void suijishu( ){ int flag=0;cin>>pc;cout<<"******按照要求产生的320个随机数：*******"<<endl;for(int i=0;i<320;i++){temp[i]=pc;if(flag%2==0) pc=++pc%320;if(flag==1) pc=rand( )% (pc-1);if(flag==3) pc=pc+1+(rand( )%(320-(pc+1)));flag=++flag%4;printf(" %03d",temp[i]);if((i+1)%10==0) cout<<endl;}}//-------------------------------------------------------------void pagestring( ){for(int i=0;i<320;i++){printf(" %02d",temp[i]/10);if((i+1)%10==0) cout<<endl;}}//-------------------------------------------------------------void OPT( ){int exist,space,position ;- 2 -int curpage;for(int i=0;i<320;i++){if(i%100==0) getch( );pc=temp[i];curpage=pc/10;exist = findExist(curpage);if(exist==-1){space = findSpace ( );if(space != -1){block[space].pagenum = curpage;display( );n=n+1;}else{for(int k=0;k<Bsize;k++){for(int j=i;j<320;j++){if(block[k].pagenum!= temp[j]/10){block[k].accessed = 1000;}//将来不会用，设置为一个很大数else{block[k].accessed = j;break;}}}position = findReplace( );block[position].pagenum = curpage;display( );n++;- 3 -}}}cout<<"缺页次数:"<<n<<endl;cout<<"缺页率:"<<(n/320.0)*100<<"%"<<endl;}//-------------------------------------------------------------void LRU( ){int exist,space,position ;int curpage;for(int i=0;i<320;i++){if(i%100==0) getch( );pc=temp[i];curpage=pc/10;exist = findExist(curpage);if(exist==-1){space = findSpace( );if(space != -1){block[space].pagenum = curpage;display( );n=n+1;}else{position = findReplace( );block[position].pagenum = curpage;display( );n++;}}else block[exist].accessed = -1;//恢复存在的并刚访问过的BLOCK中页面accessed为-1 for(int j=0; j<4; j++)- 4 -}cout<<"缺页次数:"<<n<<endl;cout<<"缺页率:"<<(n/320.0)*100<<"%"<<endl;}//------------------------------------------------------------- void FIFO( ){int exist,space,position ;int curpage;for(int i=0;i<320;i++){if(i%100==0) getch( );pc=temp[i];curpage=pc/10;exist = findExist(curpage);if(exist==-1){space = findSpace( );if(space != -1){block[space].pagenum = curpage;display( );n=n+1;}else{position = findReplace( );block[position].pagenum = curpage;display( );n++;block[position].accessed--;}}for(int j=0; j<Bsize; j++)- 5 -}cout<<"缺页次数:"<<n<<endl;cout<<"缺页率:"<<(n/320.0)*100<<"%"<<endl;}//************************************************************* void main( ){int select;cout<<"请输入第一条指令号(0~320)：";suijishu( );cout<<"*****对应的调用页面队列*******"<<endl;pagestring( );do{cout<<"****************************************"<<endl;cout<<"------1:OPT 2:LRU 3:FIFO 4:退出-----"<<endl;cout<<"****************************************"<<endl;cout<<" 请选择一种页面置换算法:";cin>>select;cout<<"****************************************"<<endl;init( );switch(select){case 1:cout<<"最佳置换算法OPT:"<<endl;cout<<"*****************"<<endl;OPT( );break;case 2:cout<<"最近最久未使用置换算法LRU:"<<endl;cout<<"**************************"<<endl;LRU( );break;case 3:cout<<"先进先出置换算法FIFO:"<<endl;cout<<"*********************"<<endl;FIFO( );break;- 6 -default: ;}}while(select!=4); }实验结果：实验四Login用户登录bool chklogin(char *users, char *pwd){int i;for(i=0; i<8; i++){if( (strcmp(users,usrarray[i].name)==0) && (strcmp(pwd,usrarray[i].pwd)==0)) return true;}return false;}Create创建文件int create(){temp=initfile(" ",0);cin>>temp->filename;cin>>temp->content;if(recent->child==NULL){temp->parent=recent;temp->child=NULL;recent->child=temp;temp->prev=temp->next=NULL;cout<<"文件建立成功!"<<endl;}else{ttemp=recent->child;while(ttemp->next){。

南京邮电大学-数值计算实践报告

数值计算实践I 、方程求根一、实验目的熟悉和掌握Newton 法,割线法,抛物线法的方法思路，并能够在matlab 上编程实现二、问题描述(1).给定一个三次方程,分别用Newton 法,割线法,抛物线法求解. 方程的构造方法:(a)根:方程的根为学号的后三位乘以倒数第二位加1再除以1000. 假设你的学号为B06060141,则根为141*(4+1)/1000=0.564(b)方程:以你的学号的后三位数分别作为方程的三次项,二次项,一次项的系数,根据所给的根以及三个系数确定常数项. 例如:你的学号是B06060141,则你的方程是x 3+4x 2+x+a 0=0的形式. 方程的根为0.564,因此有0.5643+4*0.5642+0.564+a0=0,于是a0=-2.015790144 你的方程为x 3+4x 2+x-2.015790144=0.(2)假设方程是sinx+4x 2+x+a0=0的形式（三个系数分别是学号中的数字），重新解决类似的问题(3)构造一个五次方程完成上面的工作.四次方程的构造:将三次多项式再乘以(x-p*)2得到对应的五次多项式(p*为已经确定的方程的根,显然,得到的五次方程有重根).(4)将（2）中的方程同样乘以(x-p*)得到一个新的方程来求解注:(1)Newton 法取0.5为初值,割线法以 0,1为初值,抛物线法以0,0.5,1为初值, (2)计算精度尽量地取高.终止准则：根据ε<--||1n n p p 来终止(3)可供研究的问题：（一）ε的取值不同对收敛速度有多大的影响（二）将注（1）中的初值该为其它的初值，对收敛性以及收敛速度有无影响（三）能否求出方程的所有的根（4）实验报告的撰写实验报告包含的内容：（一）实验目的（二）问题描述（三）算法介绍（包括基本原理）（四）程序（五）计算结果（六）结果分析（七）心得体会三、算法介绍在本问题中，我们用到了newton 法，割线法，抛物线法。

南邮数据结构上机实验三图的基本运算及飞机换乘次数最少问题

实验报告（2015 / 2016学年第二学期）课程名称数据结构A实验名称图的基本运算及飞机换乘次数最少问题实验时间2016 年 5 月19 日指导单位计算机科学与技术系指导教师骆健学生姓名班级学号学院(系) 管理学院专业信息管理与信息系统实习题名:图的基本运算班级姓名学号日期2016.05.19一、问题描述验证教材中关于在邻接矩阵和邻接表两种不同的储存结构上实现图的基本运算的算法(见程序9.1~程序9.8)，在邻接矩阵存储结构上实现图的深度和广度优先遍历算法，设计主函数，测试上述运算。

二、概要设计文件graph.cpp中在该文件中定义图数据结构的抽象模板类Graph。

邻接矩阵类MGraph是从抽象类Graph派生得来，邻接表类LGraph也是从抽象类Graph派生得来。

主函数的代码如图所示。

三、详细设计1.类和类的层次设计程序定义了Graph类，以及邻接矩阵类MGraph和邻接表类LGraph以及循环列表类SeqQueue。

邻接矩阵类MGraph继承了Graph的数据成员n和e，重载了Graph的纯虚函数。

保护数据成员T** a指向动态生成的二维数组，用以存储邻接矩阵。

邻接表类LGraph也继承了Graph的数据成员n和e及重载了Graph的纯虚函数，边结点由类ENode定义，每个结点有三个域adjVex、w和nextArc。

邻接表的表头组成为一维数组，a是指向该数组的指针。

（a）循环队列类（b）模版类Graph， MGraph和LGraph2.核心算法深度优先搜索用栈来实现：1)把根节点压入栈中2)每次从栈中弹出一个元素，搜索所有在它下一级的元素，把这些元素压入栈中。

并把这个元素记为它下一级元素的前驱3)找到所要找的元素时结束程序4)如果遍历整个树还没有找到，结束程序广度优先搜索使用队列来实现：1)把根节点放到队列的末尾2)每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。

南京邮电大学数值代数实验

数值代数实验数值线性代数实验一一、实验名称：矩阵的LU分解.二、实验目的：用不选主元的LU分解和列主元LU分解求解线性方程组Ax=b, 并比较这两种方法.三、实验内容与要求（1）用所熟悉的计算机语言将不选主元和列主元LU分解编成通用的子程序，然后用编写的程序求解下面的84阶方程组将计算结果与方程组的精确解进行比较，并就此谈谈你对Gauss消去法的看法.（2）写出追赶法求解三对角方程组的过程，并编写程序求该实验中的方程组Gauss消去法：用消去法解方程组的基本思想是用逐次消去未知数的方法把原来方程组Ax=b化为与其等价的三角方程组，而求解三角方程组就容易了。

换句话说，上述过程就是用行的初等变换将原方程组系数矩阵化为简单形式，从而将求解原方程组的问题转化为求解简单方程组的问题。

利用Gauss消去法对线性方程组Ax=b进行求解。

用MATLAB建立m文件DelGauss.m,程序如下：function x=DelGauss(a,b)[n,m]=size(a);nb=length(b);det=1;x=zeros(n,1);for k=1:n-1for i=k+1:nif a(k,k)==0returnendm=a(i,k)/a(k,k);for j=k+1:na(i,j)=a(i,j)-m*a(k,j);endb(i)=b(i)-m*b(k);enddet=det*a(k,k);enddet=det*a(n,n);for k=n:-1:1for j=k+1:nb(k)=b(k)-a(k,j)*x(j);endx(k)=b(k)/a(k,k);End在matlab中输入如下：结果如下：方程组的精确解为x1=x2=…=x84=1.0000，与Gauss消去法求得的解差距很大，所得结果不够准确，计算简单但其消元过程有时不能进行到底而使求解出现解失真的情况。

数值线性代数实验二一、实验名称：实对称正定矩阵的A的Cholesky分解.二、实验目的：用平方根法和改进的平方根方法求解线性方程组Ax=b.三、实验内容与要求用所熟悉的计算机语言将Cholesky分解和改进的Cholesky分解编成通用的子程序，然后用编写的程序求解对称正定方程组Ax=b，其中（1）b随机的选取，系数矩阵为100阶矩阵（2）系数矩阵为40阶Hilbert矩阵，即系数矩阵A的第i行第j列元素为，向量b的第i个分量为（3）用实验一的程序求解这两个方程组，并比较所有的计算结果，然后评价各个方法的优劣。

南京邮电大学实验报告模版

南京邮电大学实验报告模版南京邮电大学实验报告模版实验报告课程名称实验名称计算机操作系统虚拟存储中页面置换算法的模拟实现2014 实验时间指导单位指导教师年12 月19 日南京邮电大学崔衍学生姓名学院(系) 物联网院班级学号专业网络工程实验报告实验名称虚拟存储中页面置换算法的模拟实现实验类型上机实验实验学时一、实验目的和要求目的：通过请求页式存储管理中页面置换算法模拟设计，了解虚拟存储技术的技术特点，掌握请求页式存储管理的页面置换算法要求：(1)设计实现下面算法，并输出下述各种算法的命中率。

①先进先出的算法；②最近最少使用算法先淘汰最不常用的页地址。

(2)多次反复运行改进后的程序，观察并记录运行结果，并分析原因。

指导教师崔衍4 实验时间二、实验环境(实验设备) Vc++ - 2 - 二、实验原理及内容实验三#include #include #include #include #define Bsize 4 typedef struct BLOCK//声明一种新类型——物理块类型{ int pagenum;//页号int accessed;//访问字段，其值表示多久未被访问}BLOCK; int pc;//程序计数器，用来记录指令的序号int n;//缺页计数器，用来记录缺页的次数static int temp[320];//用来存储320条随机数BLOCK block[Bsize]; //定义一大小为4的物理块数组//********************************* **************************** void init( );//程序初始化函数int findExist(int curpage);//查找物理块中是否有该页面int findSpace( );//查找是否有空闲物理块int findReplace( );//查找应予置换的页面void display ( );//显示void suijishu( );//产生320条随机数,显示并存储到temp[320] void pagestring( );//显示调用的页面队列void OPT( );//OPT 算法void LRU( );// LRU算法void FIFO( );//FIFO 算法//********************************* **************************** void init( ) { for(int i=0;iblock[i].pagenum=-1;block[i].accessed=0; - 3 - pc=n=0;} } //------------------------------------------------------------- int findExist(int curpage) { for(int i=0; i if(block[i].pagenum == curpage ) return i;//检测到内存中有该页面，返回block中的位置} return -1; } //------------------------------------------------------------- int findSpace( ) {for(int i=0; i if(block[i].pagenum == -1) return i;//找到空闲的block，返回block中的位置}return -1; }//------------------------------------------------------------- int findReplace( ) { int pos = 0; for(int i=0; i if(block[i].accessed >block[pos].accessed) pos = i;//找到应予置换页面，返回BLOCK中位置} return pos; } //------------------------------------------------------------- void display( ) - 4 - { for(int i=0;i if(block[i].pagenum != -1) { printf(\ } cout //------------------------------------------------------------- void suijishu( ) { int flag=0; cin>>pc; cout if(flag%2==0) pc=++pc20;if(flag==1) pc=rand( )% (pc-1); if(flag==3) pc=pc+1+(rand( )%(320-(pc+1))); flag=++flag%4; printf(\ if((i+1) ==0) cout //------------------------------------------------------------- void pagestring( ) {for(int i=0;i printf(\if((i+1) ==0) cout //------------------------------------------------------------- void OPT( ) { int exist,space,position ; - 5 - int curpage; for(int i=0;i if(i 0==0) getch( ); pc=temp[i];curpage=pc/10; exist = findExist(curpage); if(exist==-1) { space = findSpace ( );if(space != -1) { block[space].pagenum = curpage; display( );n=n+1;} else { for(int k=0;k for(int j=i;j if(block[k].pagenum!= temp[j]/10) { block[k].accessed = 1000;}//将来不会用，设置为一个很大数else{ block[k].accessed = j; break; }}} position = findReplace( ); block[position].pagenum = curpage; display( );n++; - 6- } } } cout cout //------------------------------------------------------------- void LRU( ) { int exist,space,position ; int curpage; for(int i=0;i if(i 0==0) getch( ); pc=temp[i];curpage=pc/10; exist = findExist(curpage); if(exist==-1) { space = findSpace( );if(space != -1) { block[space].pagenum = curpage; display( );n=n+1;} else { position = findReplace( ); block[position].pagenum = curpage; display( );n++;} } else block[exist].accessed = -1;//恢复存在的并刚访问过的BLOCK中页面accessed 为-1for(int j=0; j- 7 - {block[j].accessed++;} } cout cout//------------------------------------------------------------- void FIFO( ) { int exist,space,position ; int curpage;for(int i=0;i if(i 0==0) getch( ); pc=temp[i];curpage=pc/10; exist = findExist(curpage); if(exist==-1){ space = findSpace( );if(space != -1) { block[space].pagenum = curpage; display( );n=n+1;} else { position = findReplace( ); block[position].pagenum = curpage; display( );n++; block[position].accessed--;} } for(int j=0; j- 8 - block[j].accessed++; } cout cout//************************************************************* void main( ) { int select; cout cout cout>select; cout switch(select){ case 1:cout case 2:cout case 3:cout- 9 - default: ;}}while(select!=4); } 实验结果：- 10 - 实验四Login用户登录bool chklogin(char *users, char *pwd) { int i; for(i=0; i>temp->filename; cin>>temp->content;if(recent->child==NULL){ temp->parent=recent; temp->child=NULL; recent->child=temp; temp->prev=temp->next=NULL; coutchild; while(ttemp->next) { - 11 - ttemp=ttemp->next;if(strcmp(ttemp->filename,temp->filename)==0&&ttemp->isdir==0) { printf(\对不起,文件已存在!\return 1; } } ttemp->next=temp; temp->parent=NULL; temp->child=NULL; temp->prev=ttemp; temp->next=NULL; coutchild==NULL) { coutchild; while(temp) { if(temp->isdir) {coutnext; } cout cin>>filename; if(recent->child==NULL) { coutchild->filename,filename)==0) { coutchild->contentchild;while(temp->next){ if(strcmp(temp->next->filename,filenam e)==0) {coutnext->content>filename; if(recent->child==NULL) { coutchild->filename,filename)==0) { recent->child->isopen=1;//设置文件标记为打开cin>>recent->child->content; recent->child->isopen=0;//设置文件标记为关闭cout { temp=recent->child; while(temp->next) { if(strcmp(temp->next->filename,filenam e)==0) { recent->child->isopen=1;//设置文件标记为打开cin>>temp->next->content;recent->child->isopen=0;//设置文件标记为关闭cout>filename; temp=new fnode; if(recent->child) { temp=recent->child; while(temp->next && (strcmp(temp->filename,filename)!=0 || temp->isdir!=0)) temp=temp->next; if(strcmp(temp->filename,filename)!=0) { coutparent==NULL){ temp->prev->next=temp->next; if(temp->next)temp->next->prev=temp->prev;temp->prev=temp->next=NULL; - 14 - } else { if(temp->next) temp->next->parent=temp->parent;temp->parent->child=temp->next; } delete temp; cout>temp->filename; if(recent->child==NULL){ temp->parent=recent; temp->child=NULL;recent->child=temp; temp->prev=temp->next=NULL; } else { ttemp=recent->child; while(ttemp->next) { ttemp=ttemp->next; if(strcmp(ttemp->filename,temp->filename)==0&&ttemp->isdir==1) { printf(\对不起,目录已存在!\return 1; } } ttemp->next=temp; temp->parent=NULL; temp->child=NULL; temp->prev=ttemp; temp->next=NULL; } return 1; - 15 -} 切换目录int dir(){ int i=0,j=0; temp=new fnode; temp=recent; if(temp!=root) {coutchild==NULL) { coutchild; while(temp) { if(temp->isdir) {coutnext; } cout- 17 - 四、实验小结通过课程设计,加深了对操作系统的认识,了解了操作系统中各种资源分配算法的实现,特别是对虚拟存储,页面置换有了深入的了解,并能够用高级语言进行模拟演示。

南邮数学实验答案

第一次练习题1、求032=-x e x 的所有根。

>>x=-5:0.01:5;y=exp(x)-3*x.^2;plot(x,y);grid on>> fsolve('exp(x)-3*x.^2',-1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =-0.4590>> fsolve('exp(x)-3*x.^2',1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =0.9100>> fsolve('exp(x)-3*x.^2',4)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =3.73312、求下列方程的根。

南邮数学实验参考答案(选题版)

syms x y;>> a=int(int(exp(x^2+y^2),x,0,1),y,0,1) a =(pi*erfi(1)^2)/41.7、n=20;for i=1:(n-2)a(1)=1;a(2)=1;a(i+2)=a(i+1)+a(i);enda'ans =112358132134558914423337761098715972584418167651.8、>> A=[-2,1,1;0,2,0;-4,1,303/1000]; >> inv(A)0.0893 0.1027 -0.29460 0.5000 01.1786 -0.2946 -0.5893>> eig(A)ans =-0.8485 + 1.6353i-0.8485 - 1.6353i2.0000>> [p,D]=eig(A)p =0.2575 - 0.3657i 0.2575 + 0.3657i 0.24250 0 0.97010.8944 0.8944 0.0000D =-0.8485 + 1.6353i 0 00 -0.8485 - 1.6353i 00 0 2.0000 >> det(A)ans =6.7880>> A^6ans =45.0194 4.7452 -6.37180 64.0000 025.4870 -6.3718 30.3452>> A.^6ans =1.0e+003 *0.0640 0.0010 0.00100 0.0640 04.0960 0.0010 0.0000 1.9、M文件定义如下：function y=f(x)if x>=0&&x<=1/2y=2*x;else if x>1/2&&x<=1y=2-2*x;endend命令窗口执行：fplot(@f,[0,1])1.10、t=-8:0.1:8;x=cos(t);y=sin(t);z=t;plot3(x,y,z,'r');hold onx1=2*cos(t);y1=2*sin(t);z1=t;plot3(x1,y1,z1)grid on1.11、>> A=[4 -2 2;-3 0 5;1 5*303 3];>> B=[1 3 4;-2 0 -3;2 -1 -1];>> det(A)ans =-39418>> 2*A-Bans =7 -7 0-4 0 130 3031 7>> A*Bans =12 10 207 -14 -17-3023 0 -4544>> A.*Bans =4 -6 86 0 -152 -1515 -3>> A*B^-1ans =-0.4211 -1.4737 0.7368-1.0000 -2.0000 -3.0000637.7368 716.5789 398.2105>> A^-1*Bans =0.3467 0.5763 0.99950.0015 -0.0017 -0.0013-0.1920 0.3458 -0.0003>> A^2ans =24 3022 4-7 7581 9 -4538 4543 7586>> A'ans =4 -3 1-2 0 15152 5 31.12、syms x;fplot('(1/(sqrt(2*pi)*514/600))*exp(-((x)^2)/2)',[-3,3],'r') hold onfplot('(1/(sqrt(2*pi)*514/600))*exp(-((x-1)^2)/2)',[-3,3],'b') hold onfplot('(1/(sqrt(2*pi)*514/600))*exp(-((x+1)^2)/2)',[-3,3],'g') hold offlegend('u为0','u为-1','u为1')syms x;fplot('(1/(sqrt(2*pi)*1))*exp(-((x)^2)/2)',[-3,3],'r')hold onfplot('(1/(sqrt(2*pi)*2))*exp(-((x)^2)/2)',[-3,3],'b')hold onfplot('(1/(sqrt(2*pi)*4))*exp(-((x)^2)/2)',[-3,3],'--')hold onfplot('(1/(sqrt(2*pi)*5.14))*exp(-((x)^2)/2)',[-3,3],'g')hold off1.15、ezplot('exp(x)-3*303*x.^2',[-10,10]);grid onfsolve('exp(x)-3*303*x.^2',0)ans =-0.0326第二次练习：2.1、f=inline('(x+7/x)/2');syms x;x0=3;for i=1:1:15x0=f(x0);fprintf('%g,%g\n',i,x0);end结果如下：1,2.666672,2.645833,2.645754,2.645755,2.645756,2.645757,2.645758,2.645759,2.6457510,2.6457511,2.6457512,2.6457513,2.6457514,2.6457515,2.645752.2、同2.1的方法，把f=inline('(x+7/x)/2');把未知表达式改一下就可以了；2.3、f=inline('1-2*abs(x-1/2)');x=[];y=[];x(1)=rand;y(1)=0;x(2)=x(1);y(2)=f(x(1));for i=1:10000x(1+2*i)=y(2*i);x(2+2*i)=x(1+2*i);y(1+2*i)=x(1+2*i);y(2+2*i)=f(x(2+2*i));endplot(x,y,'r');hold on;syms x;ezplot(x,[0,1]);ezplot(f(x),[0,10]);axis([0,1,0,1]);hold off答案如下：2.4、以α=3.5为例；其他的把α改变就可以了；f=inline('3.5（是α的取值）*x*(1-x)');x=[];y=[];x(1)=0.5;y(1)=0;x(2)=x(1);y(2)=f(x(1));for i=1:10000x(1+2*i)=y(2*i);x(2+2*i)=x(1+2*i);y(1+2*i)=x(1+2*i);y(2+2*i)=f(x(2+2*i));endplot(x,y,'r');hold on;syms x;ezplot(x,[0,1]);ezplot(f(x),[0,1]);axis([0,1,0,1]);hold off结果如下：整体结果如下：3.3 3.5 3.56 3.568 3.6 3.84序列收敛情况不收敛循环周期为2不收敛循环周期为4不收敛循环周期为8混沌混沌不收敛循环周期为32.5、对着书上的代码先输入到M文件里，然后再在命令窗口输入执行命令如：Martin(303,303,303,5000);即可。

南邮数字信号处理实验报告(带问题答案小结)

南京邮电大学实验报告实验名称熟悉MATLAB环境快速傅里叶变换(FFT)及其应用 IIR数字滤波器的设计FIR数字滤波器的设计课程名称数字信号处理A班级学号_ 12006311____ 姓名_______张文欣_____________开课时间 2014/2015学年，第二学期实验一熟悉MATLAB环境一、实验目的（1）熟悉MA TLAB的主要操作命令。

（2）学会简单的矩阵输入和数据读写。

（3）掌握简单的绘图命令。

（4）用MATLAB编程并学会创建函数。

（5）观察离散系统的频率响应。

二、实验内容(1) 数组的加、减、乘、除和乘方运算。

输入A=[1 2 3 4]，B=[3,4,5,6]，求C=A+B，D=A-B，E=A.*B,F=A./B,G=A.^B 。

并用stem语句画出A、B、C、D、E、F、G。

n = 0:1:3;A=[1 2 3 4];subplot(4,2,1)stem(n,A)xlabel('n')ylabel('A')B=[3,4,5,6];subplot(4,2,2)stem(n,B)xlabel('n')ylabel('B')C=A+B;subplot(4,2,3)stem(n,C)xlabel('n')ylabel('C')D=A-BSubplot(4,2,4)stem(n,D)xlabel('n')ylabel('D')E=A.*Bsubplot(4,2,5)stem(n,E)xlabel('n')ylabel('E')F=A./Bsubplot(4,2,6)stem(n,F) xlabel('n') ylabel('F')G=A.^B subplot(4,2, 7) stem(n,G) xlabel('n') ylabel('G')nAnBnCnDnEnFnG(2) 用MATLAB 实现下列序列： a) 08(). 0n 15nx n =≤≤ n=0:1:15; x1=0.8.^n; stem(n,x1) xlabel('n') ylabel('x(n)')title('2(a)')nx (n )b) 023(.)() 0n 15j nx n e+=≤≤ n=0:1:15;i=sqrt(-1); a = 0.2+3*i; x2=exp(a*n); figuresubplot(1,2,1) stem(n,real(x2)) xlabel('n')ylabel('x(n)实部') subplot(1,2,2) stem(n,imag(x2)) xlabel('n')ylabel('x(n)虚部')nx (n )实部nx (n )虚部2(b)c) 3012502202501()cos(..)sin(..)x n n n ππππ=+++ 0n 15≤≤ n=0:1:15;x3=3*cos(0.125*pi*n+0.2*pi) + 2*sin(0.25*pi*n+0.1*pi); stem(n,x3) xlabel('n') ylabel('x(n)') title('2(c)')nx (n )2(c)(4) 绘出下列时间函数的图形，对x 轴、y 轴以及图形上方均须加上适当的标注： a)2()sin() 0t 10s x t t π=≤≤t=0:0.001:10; x=sin(2*pi*t); plot(t,x,'r-')xlabel('t'),ylabel('x(t)'),title('sin(2\pit)')-1-0.8-0.6-0.4-0.200.20.40.60.81tx (t )sin(2πt)b) 100()cos()sin() 0t 4s x t t t ππ=≤≤ t=0:0.001:4;x=cos(100*pi*t).*sin(pi*t); plot(t,x,'b-')xlabel('t'),ylabel('x(t)'),title('cos(100\pit)*sin(\pit)')-1-0.8-0.6-0.4-0.200.20.40.60.81tx (t )cos(100πt)*sin(πt)(6)给定一因果系统12121106709()()/(..)H z z z z ----=++-+，求出并绘制H (z )的幅频响应和相频响应。

南京邮电大学实验课程安排表(2011-12-1)-最终稿

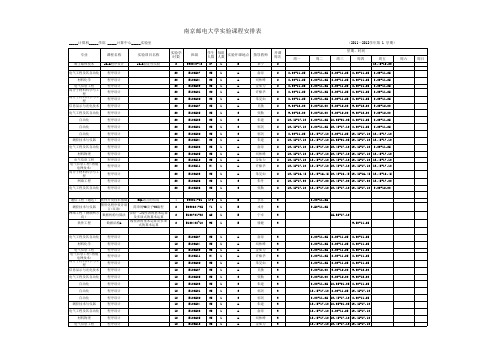
学生每组实验开课地点人数人数
87 35 35 35 32 35 35 35 35 35 35 35 35 35 35 34 35 35 35 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 B A A A A A A C C C C A A A A A A C C
13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-16:45 13:45-16:45 13:45-16:45 13:45-16:45 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 13:45-17:10 9:00-12:00 9:00-12:00 9:00-12:00 9:00-12:00
150 104 71 109 120 183
1 1 1 1 1 1
B B B B B B
B100408 B100405 B100402 B100403 B100401 B100407 B100409 33 30 40 37
1 1 1 1 1 1 1 1 1
A A A A A A C C C
李频蒋凌云张琳肖甫张迎周王海艳闵丽娟李超徐小龙
（2011～2012学年第 1 学期）实验学时数
2 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20
课程名称

南邮Matlab实验报告三参考模板

Matlab上机实验报告实验名称：MATLAB的数值运算班级：自动化二班学号： B11050216姓名：李鹏飞南京邮电大学2013年4月9日一、实验目的1．学习MATLAB 的基本矩阵运算； 2．学习MATLAB 的点运算；3．学习复杂运算。

二、实验基本知识1.基本矩阵运算；2.多项式运算；3.代数方程组；4.数值微积分。

三、上机练习1. 给a,b,c 赋如下数据:]6,46,23,4,2,6,3,8,0,1[,3568382412487,278744125431-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=c b a1)求a+b,a*b,a.*b,a/b,a./b,a^2,a.^2,length(c)的结果.2)求c 中所有元素的平均值、最大值.3)求d=b(2:3,[1,3]).程序代码：（1）>> a=[1,3,4;5,12,44;7,8,27]; >> b=[-7,8,4;12,24,38;68,-5,3]; >> c=[1,0,8,3,6,2,-4,23,46,6]; >> d=a+b d =-6 11 8 17 36 82 75 3 30>> e=a*be =301 60 1303101 108 6081883 113 413 >> f=a.*bf =-7 24 1660 288 1672476 -40 81 >> g=a/bg =0.0966 0.0945 0.0080-3.6125 1.5838 -0.5778-1.9917 0.9414 -0.2682>> h=a./bh =-0.1429 0.3750 1.00000.4167 0.5000 1.15790.1029 -1.6000 9.0000>> i=a^2i =44 71 244373 511 1736236 333 1109 >> j=a.^2j =1 9 1625 144 1936 49 64 729 >> k=length(c) k =10（2）>> l=max(c) l =46>> m=mean(c) m =9.1000（3）>> d=b(2:3,[1,3]) d =12 3868 32.求解方程⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001987654321X ，并对所得结果作出解释。

南京邮电大学实验课程安排表

多项式加法和乘法运算的设计与实现
3
B080401-05 130 1
操作系统结构分析
4 B070301-3 105 1
信息安全综合实验
网络攻防
3 B060302
31 1
数据结构B
二叉树类及其实现
4 B080222-25 143 1
软件开发技术基础(SQL Server,Delphi)
4 080045-49 156 1
1-2 8:30-11:30 8:30-11:30 8:30-11:30 8:30-11:30 8:30-11:30
1-2 8:30-11:30 8:30-11:30 8:30-11:30 8:30-11:30 8:30-11:30
1-2 8:30-11:30 8:30-11:30 8:30-11:30 8:30-11:30 8:30-11:30
单链表类及其实现
Linux常用命令及Vi编辑器的使用单链表类及其实现入侵检测入侵检测
2 B080214-16 106 1
2 B070308-10 110 1
16 B080309
30 1
16 B080303
32 1
4 070032-34 100 1
4 B080222-25 143 1
4 B070308-10 110 1
4
13:45-17:10
4
9:50-12:15
4
9:50-12:15
4
13:45-17:10
100 1
教2-316
孙知信 4
18:30-21:05
31 1 30 1 32 1 156 1 31 1 34 1
教2-316 教2-316 教2-316 教2-316 教2-316 教2-316

南邮数学实验报告

@1.1>> syms x>> limit(((1+1514*x^2)^(1/2)-cos(1514*x))/x^2)ans =1146855>> syms x>> limit(((1+1514*x^2)^(1/2)-cos(1514*x))/x,inf)ans =1514^(1/2)@1.2>> syms x>> diff(exp(x)*cos(1514*x/1000),x,2)ans =-323049/250000*exp(x)*cos(757/500*x)-757/250*exp(x)*sin(757/500*x)>> syms x>> p=diff(exp(x)*cos(1514*x/1000),6);>> subs(p,x,0)ans =33.3859@1.3>> syms x>> int(exp(-1514*x^2),x,0,inf)ans =1/3028*1514^(1/2)*pi^(1/2)@1.4>> syms x>> taylor((1514/1000+x)^(1/3),5,0)ans =1/500*757^(1/3)*500^(2/3)+1/2271*757^(1/3)*500^(2/3)*x-500/5157441*757^(1/3)*500^(2/3 )*x^2+1250000/35137645533*757^(1/3)*500^(2/3)*x^3-1250000000/79797593005443*757^(1 /3)*500^(2/3)*x^4@1.5x=randint(1,2,[1,1515]);>> for n=3:1:10x(n)=x(n-1)+x(n-2);end>> disp(x)1033 575 1608 2183 3791 5974 9765 15739 25504 41243@1.6>> A=[4,-2,2;-3,0,5;1,5,3*1514];det(A)ans =-27392>> A=[4,-2,2;-3,0,5;1,5,3*1514];inv(A)ans =0.0009 -0.3320 0.0004-0.4976 -0.6632 0.00090.0005 0.0008 0.0002’>> A=[4,-2,2;-3,0,5;1,5,3*1514];eig(A)ans =1.0e+003 *0.0052-0.00124.5420>> A=[4,-2,2;-3,0,5;1,5,3*1514];B=[1,3,4;-2,0,-3;2,-1,1]; A/B ans =1.0e+003 *0 0 0.0020-0.0027 -0.0080 -0.0081-1.2944 -4.5360 -3.8883>> A=[4,-2,2;-3,0,5;1,5,3*1514];B=[1,3,4;-2,0,-3;2,-1,1]; A\B ans =0.6656 0.0024 1.00000.8306 -1.4938 0-0.0006 0.0014 0@1.7@1.8t=-1514/2:25:1514/2; >> x=(1514/20)*cos(t); >> y=(1514/20)*sin(t); >> z=t;>> plot3(x,y,z);grid ont=-1514/2:0.1:1514/2; x=cos(t)+(t.*sin(t));y=sin(t)-t.*cos(t);z=-t;plot3(x,y,z);grid on@1.9M:function y=f(x)if x>0y=(1000/1514)*exp((-1000/1514)*x);elseif x<=0y=0;endend>> hold on>> fplot('f(x)',[-8,8],'r -')>> fplot('g(x)',[-8,8],'b -')>> fplot('h(x)',[-8,8],'m -')>> fplot('z(x)',[-8,8],'y -')>> hold off@1.10ezplot('sin(x^2+(1514/1000)*y^2)-cos(x*y)',[-5,5,-5,5])x y22@1.11x=-5:0.2:5;y=x;[X Y]=meshgrid(x,y);Z=1514*X.^2+Y.^4;mesh(X,Y,Z);@1.12Syms xfplot('exp(x)-3*1514/1614*x^2',[-5,5]);grid on fsolve('exp(x)-3*1514/1614*x^2',-1)fsolve('exp(x)-3*1514/1614*x^2',1)fsolve('exp(x)-3*1514/1614*x^2',4)ans =-0.4710ans =0.9665ans =3.5922syms x>> diff(exp(x)-3*1514/1614)*x^2)ans =exp(x)-1514/269*xsyms xfplot('exp(x)-1514/269*x',[-5,5]);grid onfsolve('exp(x)-1514/269*x',0)ans =0.2218fsolve('exp(x)-1514/269*x',3)ans =2.7333体会：对应一个不甚了解的函数，先画出其图形，可增加我们对它的了解，再在了解的基础上进行其他运算，得到该函数的其他性质。

数学实验报告南邮

实验名称：线性方程组的求解方法实验目的：1. 理解线性方程组的概念及其解法。

2. 掌握高斯消元法和克拉默法则求解线性方程组的方法。

3. 通过实验验证不同方法的计算效率和适用范围。

实验时间：2023年X月X日实验地点：南京邮电大学计算机实验室实验器材：1. 计算机2. 数学软件（如MATLAB、Mathematica等）3. 纸张和笔实验步骤：一、实验准备1. 确定实验所需线性方程组，例如：\[\begin{cases}2x + 3y - z = 4 \\-x + 2y + 3z = -1 \\3x - 2y + 4z = 5\end{cases}\]2. 熟悉高斯消元法和克拉默法则的原理。

二、实验实施1. 高斯消元法求解（1）将线性方程组转化为增广矩阵：\[\begin{bmatrix}2 &3 & -1 & | &4 \\-1 & 2 & 3 & | & -1 \\3 & -2 &4 & | & 5\end{bmatrix}\]（2）进行行变换，将增广矩阵转化为行最简形式：\[\begin{bmatrix}1 & 0 & 0 & | & 1 \\0 & 1 & 0 & | & 1 \\0 & 0 & 1 & | & 1\end{bmatrix}\]（3）根据行最简形式得到方程组的解：\(x = 1, y = 1, z = 1\)。

2. 克拉默法则求解（1）计算系数矩阵的行列式：\[D = \begin{vmatrix}2 &3 & -1 \\-1 & 2 & 3 \\3 & -2 & 4\end{vmatrix}\]（2）计算增广矩阵的行列式：\[D_x = \begin{vmatrix}4 & 3 & -1 \\-1 & 2 & 3 \\5 & -2 & 4\end{vmatrix}\]（3）计算\(D_y\)和\(D_z\)，分别对应\(x\)、\(y\)、\(z\)的系数矩阵和增广矩阵的行列式。

南邮数据结构上机实验四内排序算法的实现以及性能比较

实验报告（2015 / 2016学年第二学期）课程名称数据结构A实验名称内排序算法的实现以及性能比较实验时间2016 年 5 月26 日指导单位计算机科学与技术系指导教师骆健学生姓名耿宙班级学号B14111615学院(系) 管理学院专业信息管理与信息系统实习题名:内排序算法的实现及性能比较班级 B141116 姓名耿宙学号 B14111615 日期2016.05.26 一、问题描述验证教材的各种内排序算法，分析各种排序算法的时间复杂度；改进教材中的快速排序算法，使得当子集合小于10个元素师改用直接插入排序；使用随即数发生器产生大数据集合，运行上述各排序算法，使用系统时钟测量各算法所需的实际时间，并进行比较。

系统时钟包含在头文件“time.h”中。

二、概要设计文件Sort.cpp中包括了简单选择排序SelectSort()，直接插入排序InsertSort()，冒泡排序BubbleSort()，两路合并排序Merge()，快速排序QuickSort()以及改进的快速排序GQuickSort()六个内排序算法函数。

主主函数main的代码如下图所示：三、详细设计1.类和类的层次设计在此次程序的设计中没有进行类的定义。

程序的主要设计是使用各种内排序算法对随机生成的数列进行排列，并进行性能的比较，除此之外还对快速排序进行了改进。

下图为主函数main的流程图：main()2.核心算法1)简单选择排序：简单选择排序的基本思想是：第1趟，在待排序记录r[1]~r[n]中选出最小的记录，将它与r[1]交换；第2趟，在待排序记录r[2]~r[n]中选出最小的记录，将它与r[2]交换；以此类推，第i趟在待排序记录r[i]~r[n]中选出最小的记录，将它与r[i]交换，使有序序列不断增长直到全部排序完毕。

2)直接插入排序：插入排序的思想是将一组无序的元素分别插入一个已经有序的的数组里，并保证插入后的数组也是有序的。

当所有无序组的元素都插入完毕时，一个有序数组构造完成。

南京邮电大学数值代数实验

南邮数据库基础教程实验报告

南邮数据结构实验一

资料：数学实验(南邮)答案2

南京邮电大学实验报告模版 2

南京邮电大学-数值计算实践报告

南邮数据结构上机实验三图的基本运算及飞机换乘次数最少问题

南京邮电大学 数值代数实验

南京邮电大学实验报告模版

南邮数学实验答案

南邮 数学实验参考答案(选题版)

南邮 数字信号处理实验报告(带问题答案小结)

南京邮电大学实验课程安排表(2011-12-1)-最终稿

南邮Matlab实验报告三参考模板

南京邮电大学实验课程安排表

南邮 数学实验 报告

数学实验报告南邮

南邮数据结构上机实验四内排序算法的实现以及性能比较

南京邮电大学数值代数实验

南邮数学实验参考答案(选题版)

南邮数字信号处理实验报告(带问题答案小结)

南邮数学实验报告