第1章实验数据及模型参数
multisim教程实验指导书第一章
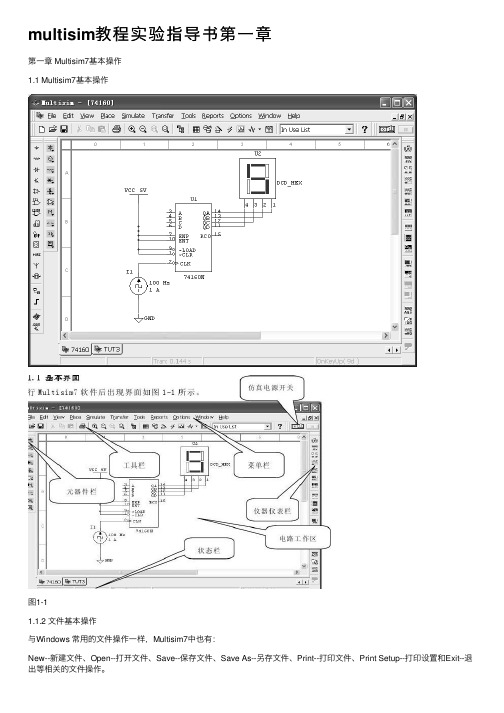
multisim教程实验指导书第⼀章第⼀章 Multisim7基本操作1.1 Multisim7基本操作图1-11.1.2 ⽂件基本操作与Windows 常⽤的⽂件操作⼀样,Multisim7中也有:New--新建⽂件、Open--打开⽂件、Save--保存⽂件、Save As--另存⽂件、Print--打印⽂件、Print Setup--打印设置和Exit--退出等相关的⽂件操作。
以上这些操作可以在菜单栏File ⼦菜单下选择命令,也可以应⽤快捷键或⼯具栏的图标进⾏快捷操作。
1.1.3 元器件基本操作常⽤的元器件编辑功能有:90 Clockwise--顺时针旋转90?、90 CounterCW--逆时针旋转90?、Flip Horizontal--⽔平翻转、Flip Vertical--垂直翻转、Component Properties--元件属性等。
这些操作可以在菜单栏Edit ⼦菜单下选择命令,或⽤Edit ⼦菜单右边显⽰的快捷键进⾏快捷操作,也可以选中元器件后右击⿏标选择相应命令。
例对三极管操作如图1-2所⽰:图1-21.1.4 ⽂本基本编辑对⽂字注释⽅式有两种:直接在电路⼯作区输⼊⽂字或者在⽂本描述框输⼊⽂字,两种操作⽅式有所不同。
1. 电路⼯作区输⼊⽂字单击Place / Text 命令或使⽤Ctrl+T 快捷操作,然后⽤⿏标单击需要输⼊⽂字的位置,输⼊需要的⽂字。
⽤⿏标指向⽂字块,单击⿏标右键,在弹出的菜单中选择Color 命令,选择需要的颜⾊。
双击⽂字块,可以随时修改输⼊的⽂字。
2. ⽂本描述框输⼊⽂字利⽤⽂本描述框输⼊⽂字不占⽤电路窗⼝,可以对电路的功能、实⽤说明等进⾏详细的说明,可以根据需要修改⽂字的⼤⼩和字体。
单击View/ Circuit Description Box 命令或使⽤快捷操作Ctrl+D ,打开电路⽂本描述框,如图1-3所⽰,在其中输⼊需要说明的⽂字,可以保存和打印输⼊的⽂本。
第1章 动态数学模型概述-v1.

主要形式: ② 脉冲响应g(t) ③ 频率响应G(jω )
2019/7/16
化工过程动态数学模型(化工与环境学院)
30
第1章 过程动态数学模型概述
(2)现代辨识方法 特点:① 从概率统计的观点对系统进行辨识, 尽可能抑制噪声影响; ② 需要处理大量数据,计算量大,只能 采用计算机进行; ③ 数学模型表达式,限于离散型,例如 差分方程(脉冲传递函数)。
化工过程动态数学模型(化工与环境学院)
5
第1章 过程动态数学模型概述
(3)化工过程
按照物质、能量内部联系的性质,所有的化工过程一般可分 为:流体力学过程、传热过程、扩散过程、化学过程和机械过 程。
按其性质,过程还可分为确定过程和随机过程。 在确定过程中,输入值是按确定的规律连续变化的。确定过 程可用经典的解析方法和数值方法描述。如带搅拌器的混合均 匀的流通式反应器就是确定过程的一个例子。 在随机过程中,输入值的变化是不规则的,且往往是不连续 的。此时,输出值与输入值并无一定的对应关系。描述随机过 程要用概率统计的方法。在接触催化过程中,产品的产率随催 化剂的活性而变,而催化剂的活性与它的老化程度有关。
2019/7/16
化工过程动态数学模型(化工与环境学院)
14
第1章 过程动态数学模型概述
(8)生产过程自动监控系统
2019/7/16
化工过程动态数学模型(化工与环境学院)
15
第1章 过程动态数学模型概述
基本概念(二)
(1)建立动态数学模型的目标及意义 建立数学模型对新工艺的研究、工艺过程的放大
开发、过程设计、生产过程的技术改造、产品的质 量管理与生产控制、操作人员的训练,以及控制系 统的设计与分析等具有重要的意义。
DOE实验设计之最佳参数分析

2010-5-17中级方差分析1第二章回归模型设计第一节数学模型分析实验设计的模型当各自变量处于什么值时,响应(y 值)最好?12(,,......)n y f X X X =2010-5-17中级方差分析24 因子实验设计的回归函数1、确定该方程的各项的系数2、当各自变量处于什么值时,响应最好?12011223344112213314423524634(,,......)n y f X X X y a a X a X a X a X b X X b X X b X X b X X b X X b X X ε==+++++++++++在回归函数中,如果某个a(正值)系数大,则该因子随着水平值的增高,响应值y增大,如果某个a(负值)系数大,则该因子随着水平值的增高,响应值y减小,(a系数绝对值的大小决定主效应的强弱,显著);如果某个b系数(绝对值)大,则该两个因子的交互作用强,b系数绝对值的大小决定主效应的强弱,显著)。
1、确定回归函数(确定a系数和b系数)2、在回归函数中找出因子的最佳参数。
2010-5-17中级方差分析3例:制作某种食品必须加A、B、C三种添加剂,并将食品烘焙。
A、B、C三种添加剂的量和食品烘焙时间D都与加工后的食品中的防腐剂含量有关。
A、B、C三种添加剂量和食品烘焙时间的取值范围为:A 2~3B 0.2~0.3C 0.6~0.8D 25~30通过12次实验,找出A、B、C四个因子各取什么值,食品中的防腐剂含量最低。
2010-5-17中级方差分析4一、创建因子设计及实验统计→DOE→因子→创建因子设计2010-5-17中级方差分析5因子参数2010-5-17中级方差分析6得到正交表2010-5-17中级方差分析7输入数据得:2010-5-17中级方差分析8二、分析数据统计→DOE→因子→分析因子设计2010-5-17中级方差分析9选择图形2010-5-17中级方差分析10存储2010-5-17中级方差分析112010-5-17中级方差分析12数据分析A 因子不显著、B 因子显著、C 因子显著、D 因子显著;交互作用AD显著。
最新大学物理实验1-实验报告模板

最新大学物理实验1-实验报告模板实验名称:测量物体的密度实验目的:1. 掌握测量固体和液体密度的基本方法。
2. 熟悉使用比重瓶和电子天平的操作。
3. 分析实验误差,提高实验数据的准确性。
实验原理:密度定义为物体质量与体积的比值,即 \( \rho = \frac{m}{V} \)。
本实验通过测量物体的质量和体积来计算其密度。
对于固体,体积可通过排水法测量;对于液体,体积可通过比重瓶直接测量。
实验仪器:1. 电子天平2. 比重瓶3. 烧杯4. 移液管5. 蒸馏水6. 待测固体样品7. 待测液体样品实验步骤:1. 使用电子天平测量待测固体样品的质量 \( m \)。
2. 将适量的蒸馏水倒入烧杯中,使用移液管将部分水转移到比重瓶中。
3. 将待测固体样品完全浸入比重瓶中的水中,并记录比重瓶中水的体积变化 \( V_{water} \)。
4. 计算固体样品的体积 \( V = V_{water} \)。
5. 根据密度公式计算固体样品的密度 \( \rho = \frac{m}{V} \)。
6. 重复上述步骤,测量不同液体样品的密度。
7. 记录所有数据,并进行必要的误差分析。
实验数据与结果:(此处填写实验数据表格,包括样品编号、质量m、体积V、计算出的密度ρ以及可能的误差分析)结论:通过本次实验,我们成功地测量了不同固体和液体样品的密度,并掌握了使用比重瓶和电子天平进行密度测量的方法。
实验结果与理论值相近,但在实际操作中存在一定的系统误差和随机误差,这些误差来源包括仪器的精度限制、操作者的技术水平等。
未来可以通过改进实验方法和提高操作精确度来减少误差,提高实验结果的准确性。
第1章 第2节 种群数量的变化

第2节种群数量的变化一、种群数量的增长、变化曲线及其应用1.建构种群增长模型的方法(1)数学模型:是用来描述一个系统或它的性质的数学形式。
(2)构建数学模型的方法步骤:观察研究对象,提出问题→提出合理的假设→根据实验数据,用适当的数学形式对事物的性质进行表达,即建立数学模型→通过进一步实验或观察等,对模型进行检验或修正。
(3)根据教材中“细菌数量增长规律”分析:若N表示细菌数量,n表示第n代,则细菌增长的方程式模型为N n=2n;曲线模型为:2.种群的“J”形增长(1)模型假设:食物和空间条件充裕、气候适宜、没有天敌和其他竞争物种等(即理想条件)。
(2)建立模型①参数的含义:N t:t年后种群的数量;N0:种群的起始数量;t:时间(年数);λ:该种群数量是前一年种群数量的倍数。
②数学方程式:N t=N0λt。
③曲线图(如下)3.种群的“S”形增长(1)模型假设:自然界的资源和空间总是有限的。
(2)对曲线的分析①a 点以前是生物对环境的适应期,种群数量增长较慢的原因是个体数量少,因此增长速率很小。
②ab 段是快速增长期,种群数量快速增长,K 2时增长速率达到最大,此时食物、空间相对充裕,天敌数量少。
③bc 段,随着种群密度的增加,个体间因食物、空间和其他生活条件的争夺而导致种内竞争加剧,使种群出生率降低,死亡率升高。
④达到K 值时,种群出生率等于死亡率,种群数量保持相对稳定。
(3)K 值的含义:又称为环境容纳量,指一定的环境条件所能维持的种群最大数量。
(4)应用①野生大熊猫数量锐减的原因:栖息地遭到破坏,食物减少和活动范围缩小,K 值变小。
②应对措施:建立自然保护区,改善栖息环境,提高环境容纳量。
4.种群数量的波动(1)影响因素⎩⎪⎨⎪⎧自然因素人为因素:人类活动的影响 (2)数量变化:大多数种群的数量总是在波动中;处于波动状态的种群,在某些特定条件下可能出现种群爆发。
长久处于不利的条件下,种群数量会出现持续性的或急剧的下降。
OPNET实验报告

篇一:opnet仿真实验报告南京航空航天大学opnet仿真实验报告计算机网络实验目录1.1 实验一 ............................................................................. . (3)1.2 实验二 ............................................................................. . (3)第二章opnet网络建模及仿真方法 (3)2.1 opnet简介 ............................................................................. . (3)2.2 opnet仿真关键技术 ............................................................................. .. (4)2.2.1 层次化建模技术 ............................................................................. .. (4)2.2.2 离散事件仿真机制 ............................................................................. .. (4)2.2.3 仿真调度机制 ............................................................................. (4)2.2.4 通信机制 ............................................................................. . (4)2.3 opnet仿真流程 ............................................................................. (5)第三章实验仿真过程 ............................................................................. .. (5)3.1 实验一单台服务器场景仿真过程 (6)3.1.1 建立网络拓扑结构 ............................................................................. .. (6)3.1.2 收集统计量 ............................................................................. (8)3.1.3 运行仿真 ............................................................................. . (9)3.1.4 60台pc场景1_expand_60 .................................................................... .. 103.1.5 90台pc场景1_expand_90 .................................................................... . (11)3.2 实验一多台服务器场景仿真过程 (12)3.3 实验二用opnet对rip仿真分析 (13)第四章实验仿真结果及分析.............................................................................. . (13)4.1 单台服务器场景仿真结果及分析 (13)4.1.1 整个网络平均延迟对比曲线图 (14)4.1.2 服务器与交换机链路的平均吞吐量对比曲线图 (14)4.1.3 服务器cpu负载变化对比曲线图,见图16. (15)4.2 多台服务器场景仿真结果及分析 (16)4.2.1 整个网络平均延迟对比曲线图 (16)4.2.2 服务器与交换机链路的平均吞吐量对比曲线图 (16)4.2.3 服务器cpu负载变化对比曲线图 (17)4.3 用opnet对rip仿真结果及分析 (18)4.3.1 rip协议概述 ............................................................................. .. (18)4.3.2 rip的工作原理 ............................................................................. .. (18)4.3.3 rip路由更新机制 ............................................................................. . (20)4.3.4 建立网络拓扑结构 ............................................................................. (21)4.3.5 仿真结果 ............................................................................. .. (23)4.3.6 对rip协议的总结.............................................................................. .. (28)第五章实验心得体会以及不足 ............................................................................. . (29)5.1 心得和体会 ............................................................................. . (29)5.2 实验中的不足 ............................................................................. (29)opnet仿真实验报告第一章实验任务1.1 实验一–设置一个仿真场景,假设pc有n台,服务器有m台,交换机和路由器根据n值进行配置1)整个网络平均延迟对比曲线图2)服务器与交换机链路的平均吞吐量对比曲线图3)服务器cpu负载变化对比曲线图–当n=90,m分别取值1和2时,设置仿真场景,配置连接设备,服务器配置同上,给出m 不同取值时:1)整个网络平均延迟对比曲线图2)服务器与交换机链路的平均吞吐量对比曲线图3)服务器cpu负载变化对比曲线图。
31第1章31_804pn结交流小信号模型

半导体器件物理(1)半导体器件物理(I )第1章pn结外加电压为:只需将电流源I D 换为小信号电导g dg d 的数值则根据直流工作点电流I D 值计算不新增模型参数。
外加电压只取交流信号。
1-8 pn 结模型和模型参数三. pn 结交流小信号模型半导体器件物理(I )第1章pn结1-8 pn 结模型和模型参数四.描述二极管模型的其他模型参数在PSpice 软件采用的二极管模型中,还同时考虑许多其他特性。
例如:噪声模型;模型参数随温度变化的模型(包括:IS 、ISR 、RS 、IKF 、BV 、CJ0等模型参数随温度的变化)使二极管模型参数总数达到29个。
半导体器件物理(I )第1章pn结1-8 pn 结模型和模型参数五. 器件模型参数值的优化确定1. 基本原理记器件模型为I=I(θ,V),其中θ代表一组模型参数。
若测量一组端特性数据为(V1,I1)、(V2,I2)、……、(Vn,In)若外加电压为Vi ,电流测量值为Ii ,按模型计算的电流应该为I(θ,Vi)。
如果模型和模型参数绝对精确,则这两个值应该相等,即Ii= I(θ,Vi)。
由于存在各种误差,上述等式不可能完全成立。
但是从工程应用要求,测量值与模型计算值之差应该比较小。
数学上可表示为误差平方和最小:第1章pn结1-8 pn结模型和模型参数五. 器件模型参数值的优化确定2. 适用工具(例)(1) PSpice/Model Editor(2) PSpice/Optimizor与PSpice/Model Editor的综合应用只要测量器件的端特性数据,采用相关软件工具就可以优化提取得到相关的模型参数数值。
半导体器件物理(I)第1章pn结1-8 pn结模型和模型参数上面基于pn结各种特性的分析介绍了模拟仿真软件Spice中采用的pn结模型。
下一个知识点将开始介绍双极晶体管的放大原理。
半导体器件物理(I)。
快速运动实验设计:高速摄影与运动轨迹分析

会议论文
作者3 et al. (年份) 标题3 作者4 et al. (年份) 标题4
专著
作者5 (年份) 书名1 作者6 (年份) 书名2
附录
在第23页,附录将收 录实验中的原始数据、 实验记录和补充材料。 通过提供更多关于研 究的详细信息和数据 支持,读者可以更深 入地了解本研究的内 容和方法,为进一步 研究提供参考依据。
轨迹数据处理工具
01 轨迹数据处理软件选择
选择合适的软件用于导入、处理和分析运动 轨迹数据。
02 轨迹数据分析插件介绍
介绍常用的轨迹数据分析插件,以及它们的 功能和特点。
03 数据可视化工具应用
利用数据可视化工具展示运动轨迹数据的分 析结果,直观地呈现数据变化和趋势。
轨迹分析实例
通过具体实例展示轨迹分析的步骤和计算方法, 以及如何结合图表和数据结果说明轨迹分析在快 速运动实验中的应用和重要性。这些实例有助于 解释轨迹分析的实际操作过程,加深对运动轨迹 分析方法的理解。
激光传感器应用
激光传感器 原理
激光测距原理
激光传感器 在快速运动 实验中的作
用
精准时间测量
激光传感器 与高速摄影 的结合应用
高速运动轨迹测 量
快速摄影数据处理
数据采集
高速摄影数据采集方法包 括高速相机参数设置和实 时观测 数据存储和管理需要考虑 数据量大、实验重复性等 因素
图像处理
图像去噪和增强可以提高 数据处理的准确性 图像配准和轨迹提取是分 析中关键的步骤
03 数据统计分布
对数据进行统计学处理
实验结果比较
不同实验数 据的差异分
析
数据差异性对比
验证实验结 果的准确性
结果准确性验证
计量经济学ppt第一章

1.2 What is Econometrics About
◆计量经济学家时常被指责为:使用大铁锤去砸开花 生,却对数据不足以及成功运用这些技术所需的但却 不可靠的许多假设熟视无睹。
“计量经济理论就像仔细斟酌过的法国食谱,清楚、精确地 说明了混合调味料需要调几次,需要多少克拉的香料,以及在恰 好474度下需要多少毫秒烘烤混合物。可是,当统计学的”厨师“ 转向原材料时,却发现没有仙人掌水果的核,因此用几块哈密瓜 代替;当食谱要求采用粉条时他却用麦片;他还用绿色胡椒代替 咖喱,用鹌鹑蛋代替海龟蛋,还用一罐松脂油代替1883的 Chalifougnac。”(Valavanis,1959)
Page 5
1.1 什么是计量经济学
Principles of Econometrics, 4th Edition
Chapter 1: An Introduction to Econometrics
Page 6
1.1.1 计量经济学的概念
计量经济学( Econometrics):是经济理论、统计学和数学 的结合。
原因之三:
新的检验要求新的计量经济学方法,从
而催生新的理论的诞生。 这也提示我们,在学习计量经济学时,应回到经济学 之中,应与经济现实相结合,对感兴趣的经济理论或假
设进行检验。
Principles of Econometrics, 4th Edition
Chapter 1: An Introduction to Econometrics Page 15
Principles of Econometrics, 4th Edition
Chapter 1: An Introduction to Econometrics Page 10
离散模型的参数估计及阶次辨识

北京工商大学《系统建模与辨识》课程上机实验报告()专业名称:上机题目:离散模型的参数估计及阶次辨识专业班级:学生姓名:学号:指导教师:年月目录目录 (2)第一章实验目的 (3)第二章实验内容 (4)第三章基本最小二乘法 (6)3.1基本最小二乘法原理 (6)3.2基本最小二乘法实验结果 (7)3.3源程序代码 (12)第四章递推广义最小二乘法 (15)4.1递推广义最小二乘法原理 (15)4.2递推广义最小二乘法实验结果 (16)4.3源程序代码 (19)第五章遗忘因子递推最小二乘算法 (21)5.1遗忘因子递推最小二乘算法原理 (21)5.2遗忘因子递推最小二乘算法实验结果 (21)5.3源程序代码 (25)第六章递推随机逼近算法 (29)6.1递推随机逼近算法原理 (29)6.2递推随机逼近算法实验结果 (30)6.3源程序代码 (34)第七章AIC模型定阶 (37)7.1 AIC模型定阶原理 (37)7.2 AIC模型定阶实验结果 (37)7.3源程序代码 (37)第八章实验总结 (41)参考文献 (41)通过实验掌握几种常用的模型参数估计算法和阶次辨识理论,具体的模型参数估计方法包括基本最小二乘法、递推广义最小二乘法(RELS)、衰减因子的递推最小二乘法和递推随机逼近算法,并在实验的基础上总结体会不同辨识方法的适用范围和优缺点。
《过程辨识》书P538实验2 离散模型的参数估计及阶次辨识,选择模拟的是第一个过程,采用基本最小二乘法、递推广义最小二乘法(RELS )、遗忘因子递推最小二乘法和递推随机逼近算法对被辨识系统进行参数估计,采用AIC 进行模型定阶。
1. 系统模拟图如图1所示图 1 系统模拟图 其中()()()()⎪⎪⎩⎪⎪⎨⎧=+-=+=+-=----------1.705.115.0.705.111211211211z D z z z C zz z B z z z A (1-1)输入信号()u k 采用幅值为1的M 序列,其特征多项式由实验者根据具体需要确定;()v k 是均值为零,方差为2v σ服从正态分布的不相关噪声,方差2v σ的大小由信噪比η确定。
数据分析与预测方法实践指导书

数据分析与预测方法实践指导书第1章数据分析概述 (3)1.1 数据分析的意义与价值 (3)1.2 数据分析的基本步骤 (4)1.3 数据分析的方法与工具 (4)第2章数据预处理 (5)2.1 数据清洗 (5)2.1.1 缺失值处理 (5)2.1.2 异常值处理 (5)2.1.3 重复值处理 (5)2.2 数据整合 (6)2.2.1 数据合并 (6)2.2.2 数据标准化 (6)2.2.3 数据一致性检查 (6)2.3 数据变换 (6)2.3.1 数据规范化 (6)2.3.2 数据离散化 (6)2.3.3 特征提取与选择 (6)2.4 数据规约 (6)2.4.1 数据降维 (7)2.4.2 数据压缩 (7)2.4.3 数据聚合 (7)第3章描述性统计分析 (7)3.1 频数分析与图表展示 (7)3.1.1 频数统计 (7)3.1.2 图表展示 (7)3.2 分布特性分析 (7)3.2.1 分布形态 (7)3.2.2 集中趋势 (7)3.2.3 离散程度 (8)3.3 关联性分析 (8)3.3.1 交叉表 (8)3.3.2 相关系数 (8)3.3.3 协方差矩阵 (8)3.4 异常值分析 (8)3.4.1 箱线图法 (8)3.4.2 基于规则的方法 (8)3.4.3 距离法 (8)3.4.4 统计模型法 (8)第4章假设检验与参数估计 (8)4.1 假设检验基本概念 (8)4.2 单样本检验 (9)4.4 参数估计 (9)第5章回归分析 (10)5.1 线性回归 (10)5.1.1 一元线性回归 (10)5.1.2 多元线性回归 (10)5.2 多元线性回归 (10)5.2.1 多元线性回归模型 (10)5.2.2 多元线性回归的假设检验 (10)5.2.3 应用实例 (10)5.3 逻辑回归 (10)5.3.1 逻辑回归模型 (10)5.3.2 模型评估与优化 (10)5.3.3 应用实例 (10)5.4 非线性回归 (11)5.4.1 非线性回归模型 (11)5.4.2 模型建立与参数估计 (11)5.4.3 应用实例 (11)第6章时间序列分析 (11)6.1 时间序列基本概念 (11)6.2 平稳性检验 (11)6.3 自相关与偏自相关分析 (11)6.4 时间序列预测方法 (12)第7章聚类分析 (12)7.1 聚类分析基本概念 (12)7.2 层次聚类法 (12)7.3 划分聚类法 (13)7.4 密度聚类法 (13)第8章分类与预测方法 (14)8.1 决策树 (14)8.1.1 基本原理 (14)8.1.2 特征选择 (14)8.1.3 决策树算法 (14)8.1.4 决策树剪枝 (14)8.2 随机森林 (14)8.2.1 基本原理 (14)8.2.2 随机森林算法 (14)8.2.3 超参数调优 (14)8.3 支持向量机 (14)8.3.1 基本原理 (15)8.3.2 核函数 (15)8.3.3 SVM算法 (15)8.4 神经网络 (15)8.4.1 基本原理 (15)8.4.3 神经网络算法 (15)8.4.4 神经网络优化方法 (15)第9章优化方法及其应用 (15)9.1 线性规划 (15)9.1.1 基本概念与理论 (15)9.1.2 线性规划的数学模型 (15)9.1.3 线性规划的求解方法 (16)9.2 非线性规划 (16)9.2.1 基本概念与理论 (16)9.2.2 非线性规划的数学模型 (16)9.2.3 非线性规划的求解方法 (16)9.3 整数规划 (16)9.3.1 基本概念与理论 (16)9.3.2 整数规划的数学模型 (16)9.3.3 整数规划的求解方法 (16)9.4 动态规划 (16)9.4.1 基本概念与理论 (16)9.4.2 动态规划的数学模型 (16)9.4.3 动态规划的求解方法 (17)第10章数据分析与预测在实际应用中的案例分析 (17)10.1 金融领域应用案例 (17)10.1.1 风险控制 (17)10.1.2 信用评估 (17)10.1.3 投资决策 (17)10.2 电商领域应用案例 (17)10.2.1 用户行为分析 (17)10.2.2 推荐系统 (17)10.2.3 库存管理 (18)10.3 医疗领域应用案例 (18)10.3.1 疾病预测 (18)10.3.2 药物研发 (18)10.3.3 医疗资源分配 (18)10.4 能源领域应用案例 (18)10.4.1 能源消耗预测 (18)10.4.2 电力负荷预测 (18)10.4.3 新能源利用 (18)第1章数据分析概述1.1 数据分析的意义与价值数据分析作为一种科学的方法论,在现代社会的各个领域具有极高的应用价值。
第1章 用Multisim设计电路实验

第1章 用Multisim 设计电路实验Multisim 电路仿真器是一个完整的系统设计工具,不仅可以作为专业软件真实地仿真、分析电路的工作,也可以在电子实验课中作为虚拟实验平台对电路进行测试。
Multisim 提供了众多仿真分析方法、测试仪表和大量的元器件模型,为电路分析、模拟电路和数字电路的分析设计带来了极大的方便。
与EWB 以前版本比,Multisim 在编辑电路原理图,设置仿真参数等,都有新的方法和要求。
下面用Multisim 设计一些电路实验。
1.1 基本电路的分析与测试1.1.1 欧姆定律的验证一、实验目的验证欧姆定律的正确性。
二、实验准备欧姆定律的表达式为:IR U s =也可表示为:RU I s =当R 不变、变化时,s U I 与成正比;当不变、s U s U R 变化时,I与R 成反比。
以下面电路进行分析:图1-1-1 欧姆定律电路三、实验步骤1.编辑图2.1-1电路:分别从电源库、元件库和指示部件库中调用所需电源、电阻和电压表、电流表。
其中电位器、电阻选用虚拟元件。
注:放置元件和电压、电流表时,可调整摆放位置,选择此元器件或仪表,点击右键,选择使用左右、上下、顺旋转90度或逆旋转90度功能。
标注性文字1、2用Place 菜单中的(或点击鼠标右键)Place Text 命令完成。
然后按电路图的形式连接起来。
元器件参数设置如下:开关J1键值为Space键,电位器R1设为10Ω的变阻器,对电压源V1进行分压处理,变阻键选择字母A,在仿真时,按A键,变阻器的阻值随着一旁的百分比改变而减少,按Shift+A键,则阻值随着百分比改变而增大。
电位器R2设为100Ω的变阻器,用来改变电路的电阻值,变阻键选择字母B。
确定电流表、电压表属性中Mode为DC。
2.如图1-1-1连接线路。
3.进行仿真,设定R2=0,R3=10Ω,设R=R2+R3,将开关拨向1,按A键,将电源电压设置为表2.1-1第一列所示的各个值,并激活电路,将测试到的电压和电流的结果填入表2.1-1第二列中。
第一章 数学建模概论 数学模型与实验 国家级精品课程课件 20页

2、国际数学建模竞赛(MCM)
创办于1985年,由美国运筹与管理学会,美国工业与应 用数学学会和美国数学会联合举办,开始主要是美国的大学 参赛,90年代以来有来自中国、加拿大、欧洲、亚洲等许多 国家的大学参加,逐渐成为一项全球性的学科竞赛。上一年 11月份报名,每个大学限报4队,每个系限报2队,2月上旬 比赛,4月份评奖。9篇优秀论文刊登在 “The Journal of Undergraduate Mathematics and Its Applications(UMAP)” 专刊上。详见 /
用实际问题的实测数据等 来检验该数学模型
不符合实际 符合实际
交付使用,从而可产生 经济、社会效益
建模过程示意图
七、怎样撰写数学建模的论文? 1、摘要:问题、模型、方法、结果 2、问题重述 3、模型假设 4、分析与建立模型 5、模型求解 6、模型检验 7、模型改进、评价、推广等 8、参考文献 9、附录
数学模型与实验
十一、 资料查询
校内:校图书馆提供电子资源,搜索软件查询 校外:, ,
数学模型与实验
十二 数学建模示例
椅子能在不平的地面上放稳吗 问题分析 通常 ~ 三只脚着地 模 型 假 设
放稳 ~ 四只脚着地
• 四条腿一样长,椅脚与地面点接触,四脚 连线呈正方形; • 地面高度连续变化,可视为数学上的连续 曲面; • 地面相对平坦,使椅子在任意位置至少三 只脚同时着地。
1、中国大学生数学建模竞赛(CUMCM)
创办于1990年,由教育部高教司和中国工业与应用数学 学会共同举办,全国几乎所有大专院校都有参加,每年6月份 报名,9月下旬比赛,11月份评奖。优秀论文刊登在《数学 的实践与认识》或?工程数学?每年第一期上。详见
第一节单容自衡水箱液位特性测试实验

第一节 单容自衡水箱液位特性测试实验一、实验目的1.掌握单容水箱的阶跃响应测试方法,并记录相应液位的响应曲线;2.根据实验得到的液位阶跃响应曲线,用相应的方法确定被测对象的特征参数K 、T 和传递函数;3.掌握同一控制系统采用不同控制方案的实现过程。
二、实验设备1.实验对象及控制屏、SA-11挂件一个、SA-13挂件一个、SA-14挂件一个、计算机一台(DCS 需两台计算机)、万用表一个;2.SA-12挂件一个、RS485/232转换器一个、通讯线一根;3.SA-21挂件一个、SA-22挂件一个、SA-23挂件一个;4.SA-31挂件一个、SA-32挂件一个、SA-33挂件一个、主控单元一个、数据交换器两个,网线四根;5.SA-41挂件一个、CP5611专用网卡及网线;6.SA-42挂件一个、PC/PPI 通讯电缆一根。
三、实验原理所谓单容指只有一个贮蓄容器。
自衡是指对象在扰动作用下,其平衡位置被破坏后,不需要操作人员或仪表等干预,依靠其自身重新恢复平衡的过程。
图2-1所示为单容自衡水箱特性测试结构图及方框图。
阀门F1-1、F1-2和F1-8全开,设下水箱流入量为Q 1,改变电动调节阀V 1的开度可以改变Q 1的大小,下水箱的流出量为Q 2,改变出水阀F1-11的开度可以改变Q 2。
液位h 的变化反映了Q 1与Q 2不等而引起水箱中蓄水或泄水的过程。
若将Q 1作为被控过程的输入变量,h 为其输出变量,则该被控过程的数学模型就是h 与Q 1之间的数学表达式。
根据动态物料平衡关系有Q 1-Q 2=A dtdh (2-1) 将式(2-1)表示为增量形式ΔQ 1-ΔQ 2=A dth d ∆ (2-2) 式中:ΔQ 1,ΔQ 2,Δh ——分别为偏离某一平衡状态的增量;A ——水箱截面积。
在平衡时,Q 1=Q 2,dtdh =0;当Q 1 发生变化时,液位h 随之变化,水箱出 图2-1 单容自衡水箱特性测试系统 口处的静压也随之变化,Q 2也发生变化 (a )结构图 (b )方框图。
第一章 统计建模

聚类分析
聚类分析是一种数值分类方法。所研究的样 本或者变量之间存在程度不同的相似性,要 求设法找出一些能够度量它们之间相似程度 的统计量作为分类的依据,将相似程度大的 样本聚合为一类,把另外一些彼此之间相似 程度大的样本聚合为另外一类⋯⋯关系密切 的聚合到一个小的分类单位,关系疏远的聚 合到一个大的分类单位,直到把所有样品都 聚合完毕,把不同的类型一个个划分出来, 形成一个由小到大的分类系统。
判别分析
判别分析是在已知研究对象分成若干类型(或 组别)并已取得各种类型的一批已知样品的观 测数据,在此基础上根据某些准则建立判别式, 然后对未知类型的样品进行判别分类。对于聚 类分析来说,一批给定样品要划分的类型事先 并不知道,正需要通过聚类分析来给以确定类 型的。正因为如此,判别分析和聚类分析往往 联合起来使用,例如判别分析是要求先知道各 类总体情况才能判断新样品的归类,当总体分 类不清楚时,可先用聚类分析对原来的一批样 品进行分类,然后再用判别分析建立判别式以 对新样品进行判别。
第三部分
往年试题分析
历年来的CUMCM题
1992年A题:施肥效果分析 B题:实验数据分解 1993年A题:非线性交调的频率设计 B题:足球队排名次 1994年A题:逢山开路 B题:锁具装箱 1995年A题:一个飞行管理问题 B题:天车与冶炼炉的作业调度
第二部分
统计学基础知识简介
统计学基础知识简介
统计是“认识社会的最有力的武器之 一”——列宁 什么是统计学?
一封统计学博士的情书
亲爱的莲: 我们的感情,在组织的亲切关怀下、 在领导的亲自过问下,一年来正沿着健康 的道路蓬勃发展。这主要表现在: (一)我们共通信121封,平均3.01天一 封。其中你给我的信51封,占42.1%; 我给你的信70封,占57.9%。每封信平 均1502字,最长的达5215字,最短的也 有624字。
第一章PSASP概述及基础数据库

第四章暂态稳定计算一、实验目的理解电力系统分析中暂态稳定计算的相关概念,掌握PSASP暂态计算的过程。
学会根据相对功角判断系统的稳定性。
二、预习要求复习《电力系统分析》中有关暂态稳定计算的内容,了解有关暂态稳定计算的功能,理解常用暂态稳定计算方法,掌握系统暂态稳定性的判断方法。
三、实验内容(一)PSASP暂态稳定计算概述电力系统暂态稳定是指电力系统受到大干扰后,各同步发电机保持同步运行并过渡到新的或恢复到原来稳态运行方式的能力。
电力系统遭受大干扰之后是否能继续保持稳定运行的主要标志:一是各机组之间的相对角摇摆是否逐步衰减;二是局部地区的电压是否崩溃。
通常大干扰后的暂态过程会出现两种可能的结局:一种是各发电机转子间相对角度随时间的变化呈摇摆状态,且振荡幅值逐渐衰减,各机组之间的相对转速最终衰减为零,各节点电压逐渐回升到接近正常值,使系统回到扰动前的稳态运行状态,或者过渡到一个新的稳态运行状态。
在此运行状态下,所有发电机仍然保持同步运行。
这种结局,电力系统是暂态稳定的。
另一种结局是暂态过程中某些发电机转子之间的相对角度随时间不断增大,使这些发电机之间失去同步或者局部地区电压长时间很低。
这种结局,电力系统是暂态不稳定的,或称电力系统失去暂态稳定。
暂态稳定计算的数学模型包括一次电网的数学描述(网络方程)和发电机,负荷,无功补偿,直流输电,发电机的调压器、调速器、电力系统稳定器、继电保护等一次设备和二次装置动态特性的数学描述(微分方程)以及各种可能发生的扰动方式和稳定措施的模拟等。
因此PSASP暂态稳定计算(ST)的数学模型可归为以下三个部分:①电网的数学模型,即网络方程;②发电机、负荷等一次设备和二次自动装置的数学模型,即微分方程;③扰动方式和稳定措施的模拟,如电网的简单故障或复杂故障及冲击负荷、快关汽门、切机、切负荷、切线路等。
这些因素的作用结果是改变系统参数或状态变量。
(二)数据准备以WEPRI-36节点系统为例,其系统图如下:PSASP程序中给出了WEPRI-36节点系统的基础数据,为方便起见,就从WEPRI-36系统导入数据。
01 第一章 流变参数

切速率 γ& ,η0 是零剪切粘度,γ&c 为一临界剪切速率。当 γ& ≤ γ&c 时,粘度保持不变( η = η0 ),
表现为牛顿行为。因此,零剪切粘度与流场剪切速率无关,其大小仅仅取决于聚合物分子
结构、温度与压力。很多聚合物的零剪切粘度可从文献中查得。当 γ& > γ&c 时, η 与 Ψ1 都随 着 γ& 的增大而减小,表现出非牛顿行为。从微观机理上看,非牛顿行为是聚合物大分子链拉
(1-13)
式中 T0 为参考温度,η0 为参考温度 T0 下的粘度,aT 为转换因子, C10 与 C02 是常数,可由
下式求得
C02 = Cg2 + T0 − Tg , C10 = C1gCg2 C02
(1-14)
式中 C1g 与 Cg2 分别为 Tg 下的两个常数。某些聚合物的 C1g 与 Cg2 可由文献查得。
模型。当 a < 1 时,转变速度减慢,转变区域扩大。对于很多聚合物流体,特别是聚合物熔
体,当 γ& 增大到一定程度时,大分子链容易发生断裂。因此,聚合物流变曲线的第二个粘度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m
m
Q (a ,b ) (p (x i)yi)2 (a bi xyi)2
i 1
i 1
(1-11)
Q (a , b)的极小值需满足:
Q (a a,b)2im 1(abixyi)0 Q (a b,b)2im 1(abixyi)xi 0
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
Rma(x x i)yi
(1-5)
1im
• (3)用各点误差的平方和表示
m
RR 2 ( (xi)yi)2
i 1
R称为均方误差
或RQ(x 2)(1-6-) Y 2
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.2 拟合的标准
• 由于计算均方误差的最小值的原则容易实 现而被广泛采用。按均方误差达到极小构 造拟合曲线的方法称为最小二乘法。同时 还有许多种其他的方法构造拟合曲线,感 兴趣的读者可参阅有关教材。本章主要讲 述用最小二乘法构造拟合曲线。
i 1
i 1
拟合得二次方程为:
1.0
p0.248 04 .05 0t90 5.070t02 1(15-10) 0.8 0.6
压 力, P ( M P a )
相关系数为R为0.99972, 平均绝对偏差SD为0.0056。 具体拟合曲线见图1-4
0.4 y=0.24845+0.00957 x+0.00015 x 2
20
30
40
50
DME饱和蒸汽t 压和温度之间的
线性拟合
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.2 拟合的标准
实例
如果采用二次拟合,通过计算下述均方误差:
m
m
Q ( a 0 ,a 1 ,a 2 )(p ( ti) p i)2( a 0 a 1 ti a 2 ti2 p i)2 (1-9)
0.2
0.0
-30
-20
-10
0
10
20
30
40
50
温 度 , t(℃ )
图1-4 DME饱和蒸汽压和温度之间的
二次拟合
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.2 拟合的标准
实例
比较图1-3和图1-4以及各自的相关系数和平均绝对 偏差可知:
• 对于DME饱和蒸汽压和温度之间的关系,在实验 温度范围内用二次拟合曲线优于线性拟合。
表1-2 DME饱和蒸气压和温度的关系
由表1-2的数据观测可得,DME的饱和蒸汽压和温 度有正相关关系。
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.2 拟合的标准
实例
• 如果以直线拟合p=a+bt,即拟合函数是一条直线。 通过计算均方误差Q ( a , b )最小值而确定直线方 程(见图1-3)
1.5
1.3.1 单变量拟合
1.6
线性拟合
• 整理得到拟合曲线满足的方程:
ya1b1Tc1T2
பைடு நூலகம்
(1-2)
y a2
c2 b2(T45)2
(1-3)
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.2 拟合的标准
向量Q与Y之间的误差或距离有以下几种定义方法:
• (1)用各点误差绝对值的和表示
m
R1 (xi)yi
(1-4)
• (2)用各i点1 误差按绝对值的最大值表示
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.3 单变量拟合和多变量拟合
• 1.3.1单变量拟合
• 1.3.2 多变量的曲线拟合
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.3.1 单变量拟合
1.6
线性拟合
• 给定一组数据(xi,yi),i=1, 2 , …, m ,做拟合直线 p (x)=a + bx , 均方误差为 :
第1章 实验数据及模型参数 拟合方法
• 1.1 问题的提出 • 1.2拟合的标准 • 1.3单变量拟合和多变量拟合 • 1.4解矛盾方程组 • 1.5梯度法拟合参数 • 1.6吸附等温曲线回归
总202目0/3/录31
1.1
1.2
1.3
1.4
1.5
1.6
1.1 问题的提出 200 150
100
Y Y
2
4
6
8
10
X
无法同时满足某特定函数的数据序列
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.1 问题的提出
• 在化学化工中,许多模型也要利用数据拟合技术, 求出最佳的模型和模型参数。
• 如在某一反应工程实验中,我们测得了如表1-1所示 的实验数据:
序号
1
2
温度 T 10
20
1.0
m
m
Q (a ,b ) (p (ti)p i)2 (a bi tp i)2(1-7) 0.8
i 1
i 1
0.6
拟合得到得直线方程为:
p
0.4
p0.303204.01t21(1-8) 0.2
相关系数R为0.97296, 平均绝对偏差SD为0.05065。
0.0 -30
图1-3
-20
-10
0
10
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.2 拟合的标准
实例
• 实验测得二甲醇(DME)的饱和蒸汽压和 温度的关系如下表 :
序号
温度 ℃
蒸气压 MPa
1
-23.7
0.101
2
-10
0.174
3
0
0.254
4
10
0.359
5
20
0.495
6
30
0.662
7
40
0.880
转化率 y 0.1 0.3
3
4
5
6
7
8
30
40
50
60
70
80
0.7 0.94 0.95 0.68 0.34 0.13
表1-1
总202目0/3/录31
本章目录
1.1
1.2
1.3
1.4
1.5
1.6
1.1 问题的提出
• 确定在其他条件不变的情况下,转化率y和 温度T的具体关系,现拟用两种模型去拟合 实验数据,两种模型分别是:
• 二次拟合曲线具有局限性,由图1-4观察可知,当 温度低于-30℃时,饱和压力有升高的趋势,但在 拟合的温度范围内,二次拟合的平均绝对偏差又小 于一次拟合,故对物性数据进行拟合时,不仅要看 在拟合条件下的拟合效果,还必须根据物性的具体 性质,判断在拟合条件之外的物性变化趋势,以便 使拟合公式在已做实验点数据之外应用。
• 化工设计及化工模拟 计算中,有大量的物 性参数及各种设备参 数。实验测量得到的 常常是一组离散数据 序列(xi ,yi)
• 图1-1所示为“噪声”
• 图1-2所示为无法同时 满足某特定的函数
50
0
-2
0
2
4
6
8
10 12 14 16 18 20
X
图1-1 含有噪声的数据
20
15
10
5
0 0
图1-2
