11-第十一章-图形的运动-七年级(上)-知识点汇总-沪教版

合集下载

(2023年最新)沪教版七年级上册数学第十一章图形的运动含答案

沪教版七年级上册数学第十一章图形的运动含答案一、单选题(共15题，共计45分)1、经过轴对称变换后所得的图形，与原图形相比（）A.形状没有改变，大小没有改变B.形状没有改变，大小有改变C.形状有改变，大小没有改变D.形状有改变，大小有改变2、如图，在△ABC中，∠C＝90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC＝6，NC＝，则四边形MABN的面积是（）A. B. C. D.3、点A（﹣2，3）关于x轴的对称点A′的坐标为（）A.（2，﹣3）B.（﹣2，3）C.（﹣2，-3）D.（ 2，3）4、如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为（）cm2．A.4B.8C.12D.165、如图，MN是⊙O的直径，点A是半圆上的三等分点，点B是劣弧AN的中点，点P是直径MN上一动点.若MN=2 ，AB=1，则△PAB周长的最小值是（）A.2 +1B. +1C.2D.36、如图，把△ABC经过一定的变换得到△A′B′C′，如果△ABC边上点P的坐标为（a，b），那么这个点在△A′B′C′中的对应点P′的坐标为（）A.（﹣a，b﹣2）B.（﹣a，b+2）C.（﹣a+2，﹣b）D.（﹣a+2，b+2）7、如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF= ，则BC的长是（）A. B. C.3 D.8、如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB 上A′处，折痕为CD，则∠A′DB=（）A.40°B.30°C.20°D.10°9、点关于轴对称的点的坐标是（）A. B. C. D.10、将点P（2，1）沿x轴方向向左平移3个单位，再沿y轴方向向上平移2个单位，所得的点的坐标是（）A.（5，﹣1）B.（﹣1，﹣1）C.（﹣1，3）D.（5，3）11、已知M（a，3）和N（4，b）关于x轴对称，则（a+b）2020的值为（）A.1B.-1C.7 2020D.-7 202012、如图，将△ABC沿BC方向平移1个单位得到△DEF，若△ABC的周长等于8，则四边形ABFD的周长等于（）A.9B.10C.11D.1213、如图，在中，，，，将折叠，使点落在边上的点处，是折痕，则的周长为（）A.6B.8C.12D.1414、在平面直角坐标系中，对进行循环往复的轴对称变换，若原来点的坐标是，则经过第2019次变换后所得的点的坐标是（）A. B. C. D.15、如图，半径为4的与含有角的直角三角板ABC的边AC切于点A，将直角三角板沿CA边所在的直线向左平移，当平移到AB与相切时，该直角三角板平移的距离为A.2B.C.4D.二、填空题(共10题，共计30分)16、如图，已知∠MON＝40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，∠APB的度数是________°.17、如图，平行四边形ABCD中，∠B＝30°，AB≠BC ，将△ABC沿AC翻折至△AB′C ，连结B ′D. 若，∠AB ′D＝75°，则BC=________．18、把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上，若∠EFG=55°，则∠1=_________°，∠2=________°．19、如图，四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为________．20、如图，已知正方形ABCD的边长为8，点E是正方形内部一点，连接BE，CE，且∠ABE＝∠BCE，点P是AB边上一动点，连接PD，PE，则PD+PE的长度最小值为________.21、从平面镜子中看到镜子对面电子钟示数的像如图所示，这时的时刻应是________.22、如图，Rt△ABC中，∠B＝90°，BC＝4，AC＝5，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于________.23、如图，大矩形长是10厘米，宽是8厘米，阴影部分宽为2厘米，则空白部分面积________.24、如图，长方形ABOC中点A坐标为（4，5），点E是x轴上一动点，连接AE，把∠B沿AE折叠，当点B落在y轴上时点E的坐标为________．25、如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=6，DH=2，平移距离CF为3，则BE=________，阴影部分面积为________．三、解答题(共5题，共计25分)26、如图所示，△ABC平移后得到了△DEF，D在AB上，若∠A=26°，∠E=74°，求∠1，∠2，∠F，∠C的度数．27、如图，在平面直角坐标系中，每个小正方形的边长为1cm，△ABC各顶点都在格点上，点A，C的坐标分别为（﹣1，2）、（0，-1），结合所给的平面直角坐标系解答下列问题：（1）AC的长等于多少？（2）画出△ABC向右平移2个单位得到的△，求A点的对应点A1的坐标。

图形的沪教版七年级《图形的运动》单元复习-带答案

注意：画图要保留痕迹，最后要有结论。

热身练习一、填空题：1、在平面内，将一个图形沿着某个方向移动一定距离，这样的图形运动称为平移。

平移前后的两个图形中，对应边相等，对应点的连线相等。

2、在平面内，将一个图形绕一个定点，沿某个方向转动一个角度α（00<α<3600），这样的图形运动称为旋转。

这个定点称为旋转中心，转动的角度称为旋转角。

3、旋转前后的两个图形中，对应边相等，对应点到旋转中心的距离相等。

4、如果一个图形沿一条直线对折，对折后的两部分能完全重合，那么这个图形就是轴对称图形，这条直线就是它的对称轴。

5、如果一个图形沿一条直线折叠，如果它能与另一个图形完全重合，那么这两个图形成轴对称，这条直线就是对称轴，折叠后重合的对应点就是对称点。

二、选择题：1、如图：△OAB绕点O逆时针旋转600到△OCD的位置。

已知∠AOB =350，则∠AOD=( D )A. 450B. 200 C . 400 D.2502、下列图形中，是中心对称图形的是（D ）A. B. C. D.3、下列四个多边形：①等边三角形；②正方形；③正五边形；④正六边形。

其中，既是轴对称图形又是中心对称图形的是（ C ）A．①②B．②③C．②④D．①④4、如图，下列图案是我国几家银行的标志，其中轴对称图形有（ C ）A．1个B．2个C．3个D．4个5、在下列三角形中是轴对称图形的是（C ）A．锐角三角形B．直角三角形C．等腰三角形D．不等边三角形6、将一张纸片沿图1中①、②的虚线对折得图1中的③，然后剪去一个角，展开平铺后的图形如图1中的④，则图1中的③沿虚线的剪法是（A ）7、下列图形中，对称轴最多的是（A ）A.圆B.等腰梯形C.正五边形D.正方形三、解答题：1、作出线段AB关于直线MN的对称图形答案：略2、已知：图A、图B，分别是6×6正方形网格上的两个轴对称图形（阴影部分），其面积分别为S A、S B，（网格中最小的正方形面积为一个平方单位）。

沪教版数学七年级上-第十一章图形的运动11.1平移练习一和参考答案.(精选)

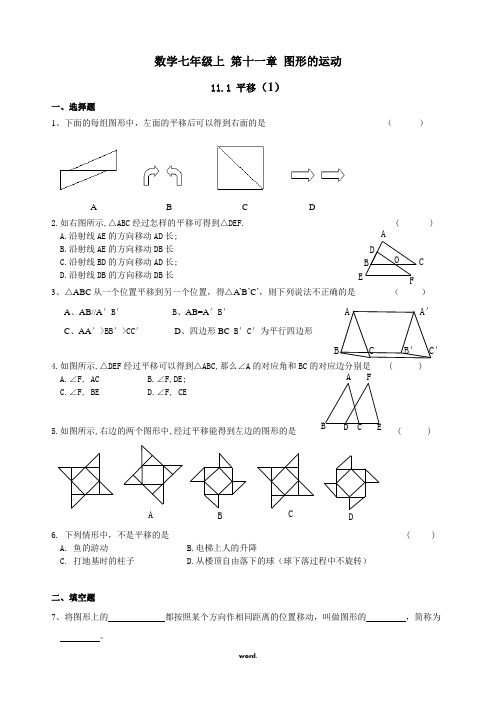
数学七年级上第十一章图形的运动11.1 平移（1）一、选择题1、下面的每组图形中，左面的平移后可以得到右面的是（）A B C D2.如右图所示,△ABC经过怎样的平移可得到△DEF. ( )A.沿射线AE的方向移动AD长;B.沿射线AE的方向移动DB长C.沿射线BD的方向移动AD长;D.沿射线DB的方向移动DB长3、△ABC从一个位置平移到另一个位置，得△A’B’C’，则下列说法不正确的是（）A、AB//A′B′B、AB=A′B′ A A′C、AA′>BB′>CC′D、四边形BC B′C′为平行四边形B C B′ C′4.如图所示,△DEF经过平移可以得到△ABC,那么∠A的对应角和BC的对应边分别是 ( )A.∠F, ACB.∠F,DE;C.∠F, BED.∠F, CE5.如图所示,右边的两个图形中,经过平移能得到左边的图形的是 ( )DCBA6. 下列情形中，不是平移的是 ( )A. 鱼的游动B.电梯上人的升降C. 打地基时的柱子D.从楼顶自由落下的球（球下落过程中不旋转）二、填空题7、将图形上的都按照某个方向作相同距离的位置移动，叫做图形的，简称为。

OFECBADFBA8. 图形平移后，图形的和都不变.9、图形移动后，对应点之间的距离、对应线段的长度、对应角的大小 . 10. 图形移动后，对应点之间的距离叫做。

11、如图，线段AD 经过平移到达BC 位置， A D那么图形ABCD 为形.B C12.如图所示,平移△ABC 可得到△DEF,如果∠A=52°, ∠C=63°,那么∠E= •度,∠EDF 度， ∠F= 度,∠DOB= 度.如果AB=6,BE=4,则DE= ,DB= .13.如图所示,长方体中,平移后能得到棱DD 1的棱有 . 14.小明的一本书一共有102页,在这102页的页码中有两个数码的,并且这两个数码经过平移其中一个能得到另一个,则这样的页共有________页.15. 某商场地下室层高4米，由一楼到地下室的电梯长10米。

第11章图形的运动(知识清单)-(沪教版)[001]

第11章图形的运动知识清单【考点剖析】1.平移：..⎧⎪⎪⎨⎪⎪⎩：将图形上所有点按某个方向作相同距离的位置移动：平移后各对应点之间的距离；平移的：平移后，对应点之间距离、对应线段长度、对应角大小相等平移后图形的大小、形定义平移的距离性质状都不变. 2.旋转：...︒⎫⎬⎭：把一个图形绕一定点旋转一个图中心对称一个定义：将一个图形上所有点绕一定点按某个方向转动一个角度. 定点叫旋转中心；转动的角度叫旋转角.性质：图形旋转后，对应点到旋转中心的距离相等；对应线段的长度、对应角的大小相等；旋转对称图形一个角度中心对称图形18旋转前后图形的大小与形状不变：把一图形绕一定点旋转后与初始图形重合：把一图形绕一定点旋转后与初始图形重合0}⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩两个图角度后与另一个图！形重合. 3.翻折.⎧⎪⎧⎪⎨⎪⎨⎪⎪⎪⎩⎩轴对称图形轴对称性质：把一个图沿某一条直线折叠，直线两旁的部分能完全重合定义：把一个图沿某直线翻折，能与另一个图形重合.：：两个图关于一条直线对称，这两图对应线段的长度、对应角的大小相等，它们的形状相同、大小相等. 要点一、图形的平移平移的概念将图形上的所有点都按照某个方向作相同距离的位置移动，叫做图形的平移运动，简称为平移．如图：平移三角形ABC 就可以得到三角形A ′B ′C ′，点Ａ和点A ′，点B 和B ′，点C 和点C ′是对应点，线段ＡＢ和ＡB ′，BC 和B ′C ′，AC 和A ′C ′是对应线段，∠Ａ与∠A ′，∠Ｂ与∠Ｂ′∠Ｃ与∠Ｃ′是对应角．平移的性质图形平移后，对应点之间的距离、对应线段的长度、对应角的大小相等．图形平移后，图形的大小、形状都不变。

要点诠释：１、平移后各对应点之间的距离叫做图形平移的距离．２、平移的两个要素：平移的方向和平移的距离．要点二、图形的旋转旋转的概念在平面内，将一个图形上的所有点绕一个定点按照某个方向转动一个角度，这样的运动叫做图形的旋转．这个定点叫做旋转中心（如点O ），转动的角度叫做旋转角(如∠AO A ′)．如图：三角形A ′B ′C ′是三角形ABC 绕点O 旋转所得，则点Ａ和点A ′，点B 和B ′，点C 和点C ′是对应点，线段ＡＢ和ＡB ′，BC 和B ′C ′，AC 和A ′C ′是对应线段，,∠ＢＯＢ′,∠ＣＯＣ′是旋转角．要点诠释：旋转的三个要素：旋转中心、旋转方向和旋转角度．旋转的性质(1)对应点到旋转中心的距离相等（OA= OA ′）； C'B'A'AB C(2)对应线段的长度相等（ＡＢ＝ＡB′）；(3)对应点与旋转中心所连线段的夹角等于旋转角（∠ＡＯA′）；要点诠释：１、图形绕某一点旋转，既可以按顺时针旋转也可以按逆时针旋转．２、旋转前后图形的大小和形状没有改变．旋转对称图形与中心对称图形的比较：中心对称把一个图形绕着某一个点旋转180°后，和另一个图形重合，那么叫做这两个图形关于这个点对称也叫做这两个图形中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点．要点诠释：１、中心对称是旋转角为180°的旋转对称；２、寻找对称中心，只需分别联结两对对应点，所得两条直线的交点就是对称中心；３、对称点所连线段经过对称中心，而且被对称中心平分．。

A4版打印沪教版七年级上册数学第十一章图形的运动含答案

沪教版七年级上册数学第十一章图形的运动含答案一、单选题(共15题，共计45分)1、如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（）A.a= bB.a=2 bC.a=2bD.a=4b2、如图，∠AOB＝30º，∠AOB内有一定点P，且OP＝10．在OA上有一动点Q，OB上有一动点R．若ΔPQR周长最小，则最小周长是（）A.10B.C.20D.3、如图：一张宽度相等的纸条折叠后，若∠ABC=120°，则∠1的度数是( )A.80°B.70°C.60°D.50°4、如图所示，如果把△ABC的顶点A先向下平移3格，再向左平移1格到达A'点，连接A'B，则线段A'B与线段AC的关系是 ( )A.垂直B.相等C.平分D.平分且垂直5、如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（）A.4.5B.4C.3D.26、如图，在中，，，点、在上，将、分别沿、翻折，点、分别落在点、的位置，再将、分别沿、翻折，点与点恰好重合于点，则的度数是（）A.90°B.120°C.135°D.150°7、如图，一张△ABC纸片，小明将△ABC沿着DE折叠并压平，点A与A′重合，若∠A=78°，则∠1+∠2=（）A.156°B.204°C.102°D.78°8、将抛物线y=x2+2先向左平移1个单位，再向下平移3个单位，所得的抛物线解析式是（）A.y=（x+1）2+1B.y=（x+1）2﹣1C.y=（x﹣1）2﹣1D.y=（x-1）2+19、下列生活中的现象，属于平移的是（）A.升降电梯从底楼升到顶楼B.闹钟的钟摆的运动C.DVD片在光驱中运行D.秋天的树叶从树上随风飘落10、给出下列说法：①射线是轴对称图形；②角的平分线是角的对称轴；③轴对称图形的对称点一定在对称轴的两侧；④平行四边形是轴对称图形；⑤平面上两个全等的图形一定关于某条直线对称，其中正确的说法有（）A.4个B.3个C.2个D.1个11、如图，在矩形中，，动点满足，则点到两点距离之和的最小值为（）A. B. C. D.12、如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为（）A. B. C. D.13、生活中有人喜欢把请人传送的便条折成图丁形状，折叠过程如图所示（阴影部分表示纸条反面），如果折成图丁形状的纸条宽x cm, 并且一端超出P点1 cm，另一端超出P点2 cm，那么折成的图丁所示的平面图形的面积为cm2. ( )A. B. C. D.14、点A（3，2）关于x轴对称的点的坐标为（）A.（3，－2 ）B.（－3，2）C.（－3，－2 ）D.（ 3，2）15、如图，边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD 沿直线DF折叠，点C落在对角线BD上的点E处，折痕DF交AC于点M，则OM=( )A. B. C. D.二、填空题(共10题，共计30分)16、点A（2，-1）关于x轴对称的点的坐标是________.17、点A（—3，4）关于轴对称的点的坐标是________.18、若点A（m+2，3）与点B（﹣4，n+5）关于y轴对称，则m+n=________．19、如图，在Rt△ABC中，∠C＝90°，BC＝2 ，AC＝2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D 交AB于点F.若△AB′F为直角三角形，则AE的长为________或________20、在平面直角坐标系内，把点P（6，3）先向左平移2个单位长度，再向上平移4个单位长度后得到的点的坐标是________．21、如图，将▱ABCD沿EF对折，使点A落在点C处，若∠A=60°，AD=4，AB=8，则AE的长为________．22、如图，矩形ABCD中，AB=3cm，BC=4cm，则图中四个小矩形的周长之和为________.23、如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则DP的长为________．24、已知P1点关于x轴的对称点P2(3－2a，2a－5)是第三象限内的整点(横、纵坐标都为整数的点，称为整点)，则P1点的坐标是________25、如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB方向平移得到△DEF，若四边形ABED的面积等于8，则平移的距离为________．三、解答题(共5题，共计25分)26、已知点A 和点B 关于轴对称，求的值．27、如图的方格纸中，每个小正方形的边长均为1，有线段AB和线段CD，线段的端点均在小正方形的顶点上．（1）在方格纸中画出分别以线段AB，CD为一边的两个三角形，使这两个三角形关于某条直线成轴对称，且两个三角形的顶点均在小正方形的顶点上．（2）请直接写出一个三角形的面积．28、如图，点A、B、C、D在一条直线上，CE与BF交于点G，∠A＝∠1，CE∥DF，求证：∠E＝∠F29、如图①，将一张直角三角形纸片ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形，再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样的两个矩形为“叠加矩形”．请完成下列问题：（1）如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如能，请在图②中画出折痕；（2）如图③，在正方形网格中，以给定的BC为一边，画出一个斜△ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；（3）如果一个三角形所折成的“叠加矩形” 为正方形，那么它必须满足的条件是．30、如图，在矩形ABCD中，AB=5，BC=4，将矩形ABCD翻折，使得点B落在CD 边上的点E处，折痕AF交BC于点F，求FC的长．参考答案一、单选题(共15题，共计45分)1、C2、A3、C4、D5、B6、B7、A9、A10、D11、A12、C13、C14、A15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、28、29、。

沪教版七年级数学--图形的运动

沪教版七年级数学--图形的运动教师姓名：未提供学科：数学教学目标：1.掌握旋转对称图形和中心对称图形的概念。

2.能够判别给出图形是否是旋转对称图形或中心对称图形。

3.能够画出给定条件的旋转对称图形或中心对称图形。

4.理解轴对称图形的概念并能够找出轴对称图形的对称轴。

教学重难点：理解和应用旋转对称图形和中心对称图形的概念。

教学设计：一、平移1.平移的意义：平移是指在平面内将一个图形上的所有点按照某个方向作相同距离的移动，这样的图形运动叫做平移。

平移不改变图形的形状和大小。

2.平移的特征：①平移前后图形的形状和大小不变，位置改变。

②新图形与原图形的对应点的连线平行且相等。

③新图形与原图形的对应线段平行且相等，对应角相等。

3.基础练：1.填空：1) 将线段AB向右平移3cm得到线段CD，如果AB=5 cm，则CD=8 cm。

2) 将∠XXX向上平移10cm得到∠EFG，如果∠ABC=52°，则∠EFG=52°，BF=10 cm。

3) 将面积为30cm²的等腰直角三角形ABC向下平移20cm，得到△MNP，则△MNP是等腰直角三角形，它的面积是30cm²。

2.图中小船经过平移到了新的位置，你发现少了什么？请补上。

3.如图1，在四边形ABCD中，AD∥BC，AB=CD，AD＜BC，要探究∠B与∠C的关系，可以采用平移的方法（如图2、3）。

请你分别说明图形的形状判断∠B与∠C的关系并叙述理由，同时你还有其他方法吗？请在图1中画出你的方案。

二、旋转1.旋转的概念在平面内，将一个图形绕一个定点旋转一定的角度，这样的图形运动称为图形的旋转。

这个定点称为旋转中心，旋转的角度称为旋转角。

2.旋转的特征旋转前后图形的形状和大小不变，位置改变。

新图形与原图形的对应点到旋转中心的距离相等，对应角度相等。

3.基础练：如图，单摆上小球的转动，由位置P转到位置P′，像这样的运动就叫做旋转，这悬挂点就叫做小球旋转的旋转中心。

图形的运动(沪教版七年级第十一章复习)

线所成的角度都是旋转角．（４）对应点到旋转中心的距离相等．
1、下列图形中，只有一条对称轴的是（ C ）．
A
B
C
D
2、下列图形中，是轴对称图形的为（ D ）．
A
B
C
D
3、下面的希腊字母中, 是轴对称图形的是（ D）．
ΧδλΨ
A
B
C
D
4、下列图形中，是中心对称图形的是（ A ）． A.菱形； B.等腰梯形；
C
A
D B
E
.O
F
旋转中心在对应点连线的垂直平分线上。
2.在等腰直角△ABC中，∠C=900，画出以AC的中点O为旋转中心的对称图形。
B’
CC’
O
AA’
B
3.已知：如图，在△ABC中，∠BAC=1200，以BC为边向形外作等边三角形△BCD，把△ABD绕着点D按顺时针方向旋转600 后得到△ECD，若AB=3，AC=2，求∠BAD 的度数与AD的长.
到了什么位置？点M转到了线段AC的中点上
例3 如图△ABC为等边三角形,△ABP旋转后能与△CBP1重合,那么（1）旋转中心是哪一点？点B
(2）最小旋转角是几度？ 60°
（3）联结PP1后，三角形BPP1是
A
什么三角形？
等边三角形
P
B
C
P1
例4、如图，四边形ABCD是正方形，△ DCE 旋转后能与 △ DAF重合，那么
第十一章
复习与小结
第十一章
复习与小结
知识梳理
图形的运动包括图形的平移、旋转、翻折，图形在运动的过程中，对应线段、对应角的大小不变，改变的是图形的位置。
平移：对应点的连线平行且相等．旋转：对应线段的夹角相等，这个夹角就是

11-第十一章-图形的运动-七年级(上)-知识点汇总-沪教版

第十一章图形的运动11.1 图形的平移1、平移的定义：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

平移后各对应点之间的距离叫做图形平移的距离。

2、关键：（1）平移不改变图形的形状和大小（也不会改变图形的方向，但改变图形的位置）。

（2）图形平移三要素：原位置、平移方向、平移距离。

3、平移的规律(性质)：经过平移，对应点所连的线段平行且相等，对应线段平行且相等、对应角相等。

4、简单的平移作图：平移作图要注意：①方向；②距离。

整个平移作图，就是把整个图案的每一个特征点按一定方向和一定的距离平行移动。

11.2 图形的旋转1、旋转的定义：在平面内，将一个图形饶一个定点沿某个方向转动一个角度，这样的运动叫做图形的旋转。

这个定点称为旋转中心；转动的角称为旋转角。

2、关键：（1）旋转不改变图形的形状和大小（但会改变图形的方向，也改变图形的位置）。

（2）图形旋转四要素：原位置、旋转中心、旋转方向、旋转角。

3、旋转的规律(性质)：经过旋转，图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等。

(旋转前后两个图形的对应线段相等、对应角相等)4、简单的旋转作图：旋转作图要注意：①旋转方向；②旋转角度。

整个旋转作图，就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。

11.3 旋转对称图形与中心对称图形1、旋转对称图形：把一个图形绕着一个定点旋转一个角度α后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角（旋转角α满足0<α<360）2、中心对称图形：如果把一个图形绕着一个定点旋转180后，与初始图形重合，那么这个图形叫做中心对称图形，这个点叫做对称中心。

11.4 中心对称把一个图形绕着一个定点旋转180后，与另一个图形重合，那么叫做这两个图形关于这点对称，也叫做这两个图形成中兴对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点。

七年级数学上册第十一章课件(11.1-11.3 共3个专题)沪教版

和
称为A对B应C三角形。
点A与点 A叫做对应点，∠A和∠ 称为A对应角。
C A
C′ A′
点C 的对应点是点，C 线段BC 的对应线段
是线段BC，
B
B′ ∠C 的对应角是 C，
线段、射线、直线、角、三角形、长方形、圆，经过平移后分别是怎样的图形？平移后形状没有变化！
我们身边有哪些平移的例子？
1.(1)说说下面的这些运动哪些是平移，哪些不是平移，为什么？
（2）下列各组图形中图（2）可以由图（1）平
移得到的是（）B
A
B
C
(3)在下面的六幅图案中，(2)(3)(4)(5)(6)中的
哪个图案可以通过平移图案(1)得到？
（3）
如图，将△ABC平移到 AB的C位置，把△ABC
平移后各对应点之间的距离叫做图形平移的距离。
2.(1)如图,四边形EFGH是由四边形ABCD平移得
到的,已知AD=5,∠B=70°,则 ( ) B
A. FG=5, ∠G=70° B. EH=5, ∠F=70°
C. EF=5, ∠F=70° D. EF=5，∠E=70°
A
E
5
B 70°
D
F
H
C
G
(2)将线段AB向右平移3cm得到线段CD, 如果 AB=5 cm,则CD= c5m.
B
D
A
C
3cm
例1：怎么画出将△ABC向右平移5格后的图形？
A
A1
B
B1
C
C1
3.（1）请将图中的“蘑菇”向左平移6个格,再向下平移2个格.（附:图2）
（2）怎样画⊙O向左平移6个方格后的图形⊙O’。（附：图3）

11-第十一章-图形的运动-七年级(上)-知识点汇总-沪教版

(2023年最新)沪教版七年级上册数学第十一章 图形的运动含答案

图形的沪教版七年级 《图形的运动》单元复习-带答案

沪教版数学七年级上-第十一章图形的运动11.1平移练习一和参考答案.(精选)

第11章 图形的运动(知识清单)-(沪教版)[001]

A4版打印沪教版七年级上册数学第十一章 图形的运动含答案

沪教版七年级数学--图形的运动

图形的运动(沪教版 七年级第十一章复习)

11-第十一章-图形的运动-七年级(上)-知识点汇总-沪教版

七年级数学上册第十一章课件(11.1-11.3 共3个专题)沪教版

(2023年最新)沪教版七年级上册数学第十一章图形的运动含答案

图形的沪教版七年级《图形的运动》单元复习-带答案

第11章图形的运动(知识清单)-(沪教版)[001]

A4版打印沪教版七年级上册数学第十一章图形的运动含答案

图形的运动(沪教版七年级第十一章复习)