视觉SLAM十四讲 第七讲 视觉里程计(1)
视觉slam十四讲 引用

视觉SLAM十四讲引言视觉SLAM(Simultaneous Localization and Mapping)是一种通过摄像头获取图像数据,并在其中实时地定位和构建地图的技术。
它在无人驾驶、增强现实、机器人导航等领域有着广泛的应用。
《视觉SLAM十四讲》是一本经典的教材,本文将对该教材进行探讨和总结。
什么是视觉SLAM视觉SLAM是一种通过计算机视觉技术来实现实时定位和地图构建的技术。
通过摄像头获取图像,利用SLAM算法来实时地对机器人的位置和运动进行估计,并同时构建地图。
与传统的SLAM技术相比,视觉SLAM能够减少对其他传感器的依赖,提高系统的自主性和灵活性。
视觉SLAM的基本流程视觉SLAM的基本流程包括图像预处理、特征提取与匹配、运动估计、地图更新等步骤。
具体步骤如下:1.图像预处理–图像去畸变:对图像进行去除镜头畸变的处理,提高后续特征提取和匹配的效果。
–图像降噪:通过滤波等方法降低图像中的噪声,提高图像质量。
2.特征提取与匹配–特征提取:通过提取图像中的角点、边缘等特征点,用于后续的特征匹配和运动估计。
–特征匹配:通过比较两幅图像中的特征点,找到它们之间的对应关系,用于后续的运动估计和地图更新。
3.运动估计–单目SLAM:通过分析图像序列中的特征点的运动,估计机器人的运动轨迹。
–双目SLAM:利用双目摄像头获取的图像,通过立体视觉的方法来估计机器人的运动轨迹。
–深度估计SLAM:通过利用深度传感器获取的深度信息,估计机器人的运动轨迹。
4.地图更新–同步优化:通过对图像序列中的特征点和机器人的位姿进行联合优化,得到更精确的运动轨迹和地图。
–闭环检测:通过对图像序列中的特征点和地图进行匹配,检测是否存在闭环,进而修正运动估计和地图。
视觉SLAM算法简介视觉SLAM算法有很多种,常用的包括特征点法、直接法、半直接法等。
•特征点法:通过提取图像中的特征点,利用这些特征点之间的关系来进行定位和地图构建。
单目视觉里程计完整版介绍

研究对象
机器人模型
地面移动平台
相机位置固定
俯仰角为0°
研究对象
输入图像
图像来源:/datasets/kitti/eval_odometry.php
流程步骤
步骤
方法
特征提取
SURF算法
图像处理
特征追踪
金字塔LK光流法
RANSAC
八点法
位姿解算
对极几何
SVD
= , =
+
+
, − + , +
= − = −
−
2
2
特征追踪
流程步骤
步骤
方法
特征提取
SURF算法
图像处理
特征追踪
金字塔LK光流法
RANSAC
八点法
位姿解算
对极几何
SVD
运动估计
尺度估计
运动估计
尺度估计
地面特征
特征提取
一般角点特征不具有尺度不变性,SURF特征点则有尺度不变性
流程步骤
步骤
方法
特征提取
SURF算法
图像处理
特征追踪
金字塔LK光流法
RANSAC
八点法
位姿解算
对极几何
SVD
运动估计
尺度估计
地面特征
特征追踪
LK算法基于三个前提假设:亮度恒定、运动幅度小、局部一致性
特征追踪
基于尺度估计的
单目视觉里程计研究
智能机器人全自主移动
研究定位
SLAM
传感器
声纳
激光
功能
SLAM14讲第七章特征点法

SLAM14讲第七章特征点法视觉前端和优化后端视觉⾥程计VO-根据相邻图像的信息估计处粗略的相机运动,给后端较好的估计值【⼀】特征提取与匹配:特征点法——运⾏稳定,对光照、动态物体不敏感主要问题:根据图像来估计相机运动特征点-路标-有代表性的点-图像信息的⼀种表达形式-在相机运动之后保持稳定-⾓点|边缘|区块仅灰度值:受光照、形变、物体材质的影响严重【×】SIFT\SURF\ORB——可重复性、可区别性、⾼效、局部特征点=关键点(图像中的位置、朝向、⼤⼩)+描述⼦(向量,周围像素)依据【外观相似的特征有相似的描述⼦原则】SIFT尺度不变特征变换 5228.7msFAST关键点——计算速度很快,没有描述⼦,不具有⽅向性ORB(旋转、尺度不变性)——速度极快的⼆进制描述⼦BRIEF 1000点/15.3msSURF 217.3ms7.1 ORB特征Oriented FAST关键点(FAST+特征点主⽅向)+BRIEF特征⼦1 FAST关键点FAST⾓点:检测局部像素像素灰度变化明显的地⽅(只⽐较像素亮度⼤⼩)FAST-9/11/12(半径为3的圆上16个像素点中有N个⼤于或⼩于中⼼点的阈值120%/80%)FAST-12预测试:第1/5/9/13个点的情况#⾮极⼤值抑制:⼀定区域内仅保留响应极⼤值的⾓点,避免集中【缺点1】FAST特征点量⼤且不确定,往往希望对图像提取固定数量的特征【改进】固定数量N,原始FAST⾓点计算Harries响应值【缺点2】FAST不具有⽅向信息【改进】由构建图像⾦字塔并在每⼀层检测⾓点实现尺度不变性,灰度质⼼(以图像块灰度值作为权重的中⼼)法实现特征旋转2 BRIEF描述⼦关键点附近两个像素p和q的⼤⼩关系,1/0,128维,随机选取旋转后的Steer BRIEF特征7.2 特征匹配(数据关联)#场景⼤量重复纹理导致的误匹配问题计算特征点之间的描述⼦距离,通常汉明距离,⼆进制不同位数的个数特征点多时,⽤快速近似最近邻FLANN算法#include <iostream>#include <opencv2/core/core.hpp>#include <opencv2/features2d/features2d.hpp>#include <opencv2/highgui/highgui.hpp>using namespace std;using namespace cv;int main ( int argc, char** argv ){if ( argc != 3 ) //确认输⼊为两张图⽚{cout<<"usage: feature_extraction img1 img2"<<endl;return1;}//-- 读取图像// imread C++ 模型// include <opencv2/imgcodecs.hpp>// Mat cv::imread( const String & filename, int flags = IMREAD_COLOR)// 返回MAT类型,读取失败时返回空矩阵 Mat::data = NULL// 参数1:filename 读取的图⽚⽂件名绝对/相对路径要加后缀// 参数2:flags 读取标记,读取图⽚的⽅式,默认为IMREAD_COLOR(好像没影响)Mat img_1 = imread ( argv[1], IMREAD_COLOR );Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );//-- 初始化std::vector<KeyPoint> keypoints_1, keypoints_2;//关键点-放置keypoint对象的⼀个vectorMat descriptors_1, descriptors_2;//描述⼦,cv::Mat类型//OpenCV提供FeatureDetector实现特征检测及匹配;//FeatureDetetor是虚类,通过定义FeatureDetector的对象可以使⽤多种特征检测⽅法。
视觉SLAM十四讲学习笔记1——ch1预备知识ch2初始SLAM

视觉SLAM⼗四讲学习笔记1——ch1预备知识ch2初始SLAM第⼀章SLAM(Simultaneous Localization and Mapping(同时定位与地图构建)):搭载特定传感器的主体,在没有环境先验信息的情况下,于运动过程中建⽴环境的模型,同时估计⾃⼰的运动。
第⼆章考虑携带于机器⼈本体上的传感器——IMU、激光、相机。
SLAM⼀般分为激光SLAM和视觉SLAM(相机),⽬前激光SLAM技术⽐较成熟,相机SLAM仍在发展过程中。
视觉SLAM⼀般分为3种:单⽬相机(Monocular)、双⽬相机(Stereo)、深度相机(Stereo)单⽬相机:没有深度,必须通过移动相机产⽣深度。
双⽬相机:通过视差计算深度。
深度相机:通过物理⽅法测量深度。
(量程较⼩、易受⼲扰、功耗较⼤)视觉SLAM整体流程图: 视觉⾥程计(Visual Odometry,VO):视觉⾥程计的任务是估算相邻图像间相机的运动,以及局部地图的样⼦(VO ⼜称为前端) 后端优化(Optimization):后端接受不同时刻视觉⾥程计测量的相机位姿,以及回环检测的信息,对它们进⾏优化,得到全局⼀致的轨迹和地图(由于接在 VO 之后,⼜称为后端) 回环检测(Loop Closing):回环检测判断机器⼈是否到达过先前的位置。
如果检测到回环,它会把信息提供给后端进⾏处理。
建图(Mapping):它根据估计的轨迹,建⽴与任务要求对应的地图。
视觉⾥程计:根据相邻的图像估计相机的运动,不可避免地存在漂移。
⽬前基本存在两种主要⽅法:特征点法(第七讲)、直接法(第⼋讲)后端优化:从带有噪声的数据中优化轨迹和地图,解决状态估计的问题。
后端优化要考虑状态估计的不确定性有多⼤——即最⼤后验概率估计(MAP)。
后端优化的⽅法前期以EKF为代表,现在以图优化为代表。
(第⼗讲、第⼗⼀讲)回环检测:词袋模型(第⼗⼆讲)建图:(第⼗三讲)SLAM问题的数学描述: 前⼀个⽅程为运动⽅程,描述了从k-1时刻到k时刻,机器⼈的位置是如何变化的。
《视觉SLAM十四讲》笔记(ch7)

《视觉SLAM⼗四讲》笔记(ch7)ch7 视觉⾥程计1本章⽬标:1.理解图像特征点的意义,并掌握在单副图像中提取出特征点及多副图像中匹配特征点的⽅法2.理解对极⼏何的原理,利⽤对极⼏何的约束,恢复出图像之间的摄像机的三维运动3.理解PNP问题,以及利⽤已知三维结构与图像的对应关系求解摄像机的三维运动4.理解ICP问题,以及利⽤点云的匹配关系求解摄像机的三维运动5.理解如何通过三⾓化获得⼆维图像上对应点的三维结构本章⽬的:基于特征点法的vo,将介绍什么是特征点,如何提取和匹配特征点,以及如何根据配对的特征点估计相机运动和场景结构,从⽽实现⼀个基本的两帧间视觉⾥程计。
特征点:⾓点、SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)、SURF、、ORB(后三个是⼈⼯设计的特征点,具有更多的优点)特征点的组成:1.关键点:指特征点在图像⾥的位置2.描述⼦:通常是⼀个向量,按照某种⼈为设计的⽅式,描述了该关键点周围像素的信息。
相似的特征应该有相似的描述⼦(即当两个特征点的描述⼦在向量空间上的距离相近,认为这两个特征点是⼀样的)以ORB特征为代表介绍提取特征的整个过程:ORB特征:OrientedFAST关键点+BRIEF关键⼦提取ORB特征的步骤:1.提取FAST⾓点:找出图像中的“⾓点”,计算特征点的主⽅向,为后续BRIEF描述⼦增加了旋转不变特性FAST⾓点:主要检测局部像素灰度变化明显的地⽅特点:速度快缺点:1).FAST特征点数量很⼤且不确定,但是我们希望对图像提取固定数量的特征2).FAST⾓点不具有⽅向信息,并且存在尺度问题解决⽅式:1).指定要提取的⾓点数量N,对原始FAST⾓点分别计算Harris响应值,然后选取前N个具有最⼤响应值的⾓点作为最终的⾓点集合2).添加尺度和旋转的描述 尺度不变性的实现:构建图像⾦字塔,并在⾦字塔的每⼀层上检测⾓点(⾦字塔:指对图像进⾏不同层次的降采样,以获得不同分辨率的图像)特征旋转的实现:灰度质⼼法(质⼼:指以图像块灰度值作为权重的中⼼)2.计算BRIEF描述⼦:对前⼀步提取出的特征点周围图像区域进⾏扫描特点:使⽤随机选点的⽐较,速度⾮常快,由于使⽤了⼆进制表达,存储起来也⼗分⽅便,适⽤于实时的图像匹配在不同图像之间进⾏特征匹配的⽅法:1.暴⼒匹配:浮点类型的描述⼦,使⽤欧式距离度量⼆进制类型的描述⼦(⽐如本例中的BRIEF描述⼦),使⽤汉明距离度量缺点:当特征点数量很⼤时,暴⼒匹配法的运算量会变得很⼤2.快速近似最近邻(FLANN):适合匹配特征点数量极多的情况实践部分:1.OpenCV的图像特征提取、计算和匹配的过程:演⽰如何提取ORB特征并进⾏匹配代码: 1 #include <iostream>2 #include <opencv2/core/core.hpp>3 #include <opencv2/features2d/features2d.hpp>4 #include <opencv2/highgui/highgui.hpp>56using namespace std;7using namespace cv;89int main(int argc,char** argv)10 {11if(argc!=3)12 {13 cout<<"usage:feature_extraction img1 img2"<<endl;14return1;15 }1617//读取图像18 Mat img_1=imread(argv[1],CV_LOAD_IMAGE_COLOR);19 Mat img_2=imread(argv[2],CV_LOAD_IMAGE_COLOR);2021//初始化22 vector<KeyPoint> keypoints_1,keypoints_2;//关键点,指特征点在图像⾥的位置23 Mat descriptors_1,descriptors_2;//描述⼦,通常是向量24 Ptr<ORB> orb=ORB::create(500,1.2f,8,31,0,2,ORB::HARRIS_SCORE,31,20);2526//第⼀步:检测OrientFAST⾓点位置27 orb->detect(img_1,keypoints_1);28 orb->detect(img_2,keypoints_2);2930//第2步:根据⾓点位置计算BRIEF描述⼦31 orb->compute(img_1,keypoints_1,descriptors_1);32 orb->compute(img_2,keypoints_2,descriptors_2);3334 Mat outimg1;35 drawKeypoints(img_1,keypoints_1,outimg1,Scalar::all(-1),DrawMatchesFlags::DEFAULT);36 imshow("1.png的ORB特征点",outimg1);37 Mat outimg2;38 drawKeypoints(img_2,keypoints_2,outimg2,Scalar::all(-1),DrawMatchesFlags::DEFAULT);39 imshow("2.png的ORB特征点",outimg2);4041//第3步:对两幅图像中的BRIEF描述⼦进⾏匹配,使⽤Hamming距离42 vector<DMatch> matches;43//特征匹配的⽅法:暴⼒匹配44 BFMatcher matcher(NORM_HAMMING);45 matcher.match(descriptors_1,descriptors_2,matches);46// for(auto it=matches.begin();it!=matches.end();++it)47// {48// cout<<*it<<" ";49// }50// cout<<endl;5152//第4步:匹配点对筛选53 distance是min_dist5455double min_dist=10000,max_dist=0;5657//找出所有匹配之间的最⼩距离和最⼤距离,即最相似的和最不相似的和最不相似的两组点之间的距离58for(int i=0;i<descriptors_1.rows;++i)59 {60double dist=matches[i].distance;61// cout<<dist<<endl;62if(dist<min_dist) min_dist=dist;63if(dist>max_dist) max_dist=dist;64 }6566 printf("--Max dist:%f\n",max_dist);67 printf("--Min dist:%f\n",min_dist);6869//当描述⼦之间的距离⼤于两倍的最⼩距离时,即认为匹配有误70//但有时候最⼩距离会⾮常⼩,设置⼀个经验值作为下限71 vector<DMatch> good_matches;72for(int i=0;i<descriptors_1.rows;++i)73 {74if(matches[i].distance<=max(2*min_dist,30.0))75 {76 good_matches.push_back(matches[i]);77 }78 }7980//第5步:绘制匹配结果81 Mat img_match;82 Mat img_goodmatch;83 drawMatches(img_1,keypoints_1,img_2,keypoints_2,matches,img_match);84 drawMatches(img_1,keypoints_1,img_2,keypoints_2,good_matches,img_goodmatch);85 imshow("所有匹配点对",img_match);86 imshow("优化后匹配点对",img_goodmatch);87 waitKey(0);8889return0;90 }实验结果:1.png中提取到的特征点2.png中提取到的特征点匹配结果: 所有点对匹配结果 优化后的匹配点对结果(筛选依据是Hamming距离⼩于最⼩距离的两倍)结果分析:尽管在这个例⼦中利⽤⼯程经验优化筛选出正确的匹配,但并不能保证在所有其他图像中得到的匹配都是正确的,所以,在后⾯的运动估计中,还要使⽤去除误匹配的算法。
视觉里程计原理(一)特征提取(SURF算法)

MPIG Seminar0045Feature Extraction陈伟杰Machine Perception and Interaction Group (MPIG)cwj@Feature ExtractionRefined based on the book:Mastering OpenCV with Practical Computer VisionProjects_full.pdfandBay H, Tuytelaars T, Van Gool L. Surf: Speeded up robust features [M]. Computer vision–ECCV 2006. Springer. 2006: 404-417.or F for [R|t]Drawing pathThe main steps of Visual Odometryimages parametersFeature ExtractionFeaturematchingCompute EFirstFeature Extraction What feature is?Characteristics can be easily identified in imagesEdges Corners Blobslines pointsHarris SIFT SURF Commonly used algorithm:•Corner extractor•Fast operation •Poor resolution •Not applicable when scalechanges •Blobs extractor•Slow operation•Good resolution•Scale invariance•Upgrade fromSIFT•Speed up•More robustSURF(Speed Up Robust Feature) opencv2/nonfree/features2d.hppSurfFeatureDetectordetector()SurfDescriptorExtractorSURF(Speed Up Robust Feature)Integral imageii x,y = i=0i≤x j=0j≤yI(i,j)(x,y)ACB D1234ii 1= A ii 2= A + BD =ii 1+ii 4−ii 2−ii 3SURF(Speed Up Robust Feature)Hessian matrixH x,σ=L xx(x,σ)L xy(x,σ) L xy(x,σ)L yy(x,σ)L x,σ=Gσ∗I(x,y)Gσ=ð2g(σ)ðx2g(σ) is Gaussian function andσis varianceIt’s the image conversion like frequency domain transformApproximation of Hessian matrixDetHapprox=D xx D yy−0.9D xy2L yy L xyD yy DxyWe can use integral image to compute easily nowH x,σ=L xx(x,σ)L xy(x,σ)L xy(x,σ)L yy(x,σ) Filter templateSURF(Speed Up Robust Feature)scale space (image pyramid)SIFT SURF Change size of filter only Easier and fasterPositioning feature points3×3 window“x”is extreme point when it’s themax or the min of 26 points aroundSetting a threshold value tif x>t, x is feature pointThe larger t is, the less points will beSURF feature descriptorMain directionStatistics harr wavelet feature around the feature point with the range of 60°in a circle of radius6s(s is the scale of the feature point)The max value is main directionSURF feature descriptormain directionfeature point 20s Every descriptor has4*4*4=64 dimensional vectorMat img1 = imread( "chapel00.png");Mat img2 = imread("chapel01.png");int minHessian = 400;SurfFeatureDetector detector( minHessian );std::vector<KeyPoint> keypoints1, keypoints2;detector.detect(img1, keypoints1);detector.detect(img2, keypoints2);// computing descriptorsSurfDescriptorExtractor extractor;Mat descriptors1, descriptors2;pute(img1, keypoints1, descriptors1);pute(img2, keypoints2, descriptors2);CODE//--Draw keypoints Mat img_keypoints_1; Mat img_keypoints_2;drawKeypoints( img1, keypoints1, img_keypoints_1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );drawKeypoints( img2, keypoints2, img_keypoints_2, Scalar::all(-1), DrawMatchesFlags::DEFAULT );//--Show detected (drawn) keypoints imshow("Keypoints 1", img_keypoints_1 );imshow("Keypoints 2", img_keypoints_2 );waitKey(0);return 0;800 400200 minHessian。
12_视觉里程计1_ICP算法

12_视觉⾥程计1_ICP算法前⾔ICP的英⽂全称为Iterative Closest Point,即为迭代最近点。
它在激光雷达应⽤频率很⾼,主要是在点云配准领域。
ICP算法在是是视觉SLAM中应⽤也⾮常多,这个算法还是很重要。
我们下⾯的讨论还是基于视觉SLAM,好了我们开始吧!ICP算法流程ICP算法顾名思义,就是找最近点。
算法流程如下:step1:预处理点云step2:寻找对应点(最近点)step3:根据对应点,计算R和tstep4:对点云进⾏转换,计算误差step5:不断迭代,直⾄误差⼩于某⼀个值3D-3D: ICP假设我们有⼀组配对好的3D点如下:\boldsymbol{P}=\left\{\boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{n}\right\}, \quad \boldsymbol{P}^{\prime}=\left\{\boldsymbol{p}_{1}^{\prime}, \cdots, \boldsymbol{p}_{n}^{\prime}\right\}现在我们想要找到⼀个欧式变换,使得\forall i, \boldsymbol{p}_{i}=\boldsymbol{R} \boldsymbol{p}_{i}^{\prime}+\boldsymbol{t}.上述的这个问题就可以使⽤ICP算法求解。
这⾥主要需要注意下,如果仅考虑3D点之间的变换,此时和相机并没有关系。
在RGB-D SLAM中⽤ICP问题指代匹配好的两组点间的运动估计问题(跟激光SLAM有区别,激光SLAM通常是未知的情况)。
ICP求解主要是两种⽅式,⼀种是SVD,另⼀种是⾮线性优化⽅式求解。
SVD⽅法根据前⾯描述的ICP问题,令第i对点的误差为:\boldsymbol{e}_{i}=\boldsymbol{p}_{i}-\left(\boldsymbol{R} \boldsymbol{p}_{i}^{\prime}+\boldsymbol{t}\right).这⾥解释⼀下,我们⽤⼀个点\boldsymbol{p}_{i}^{\prime}(第⼆幅图中数据)来估算另⼀个点\boldsymbol{p}_{i}时(在第⼀幅中数据,即为观测坐标),必然会产⽣误差。
【视觉SLAM十四讲课后作业答案】第五讲:特征点法视觉里程计
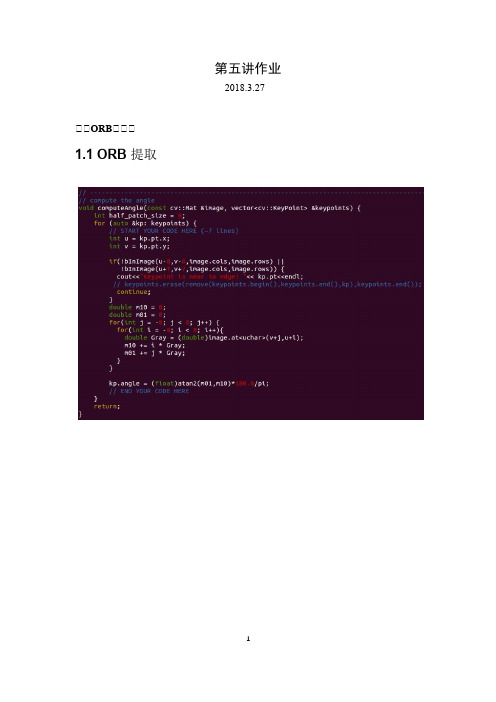
第五讲作业2018.3.27一一ORB一一一1.1 ORB 提取1.2 ORB 描述1.3 暴力匹配问题回答如下:1.ORB 的描述子是用许多对像素点坐标(此处坐标需要经过旋转校正)所在位置的灰度值的大小对比来组成,对比结果为0 和1,假设有256 对像素点,那么ORB 的特征点描述子便有256 个0 或1 组成,因此称ORB 是一种二进制特征;2.ORB 匹配时是计算两个描述子之前的汉明距离,即计算两个二进制值在每一位上不相等的个数,当然我们希望这个不相等的个数越少越好,当个数为0,则说明两个描述子的特征完全一致,随着个数越多,说明两个特征不一致的程度也就越高,因此若将阈值取小,则匹配点对的数量越少,但是误匹配几率越小,反之,若将阈值调高,则匹配出的点对数量增加,但误匹配几率也增加。
3.匹配出107 组点,耗时为3329.67ms 。
若在CMakeLists 中增加-O2 编译优化,则耗时可减小至160.675ms,若改为-O3 编译优化,耗时可继续减小至154.373ms。
一一一E一一R,t三一一G-N 一一Bundle Adjustment问题回答如下:1.重投影误差:(ξ) = P uv − 1 Kexp(ξ∧)P wz c2.雅可比矩阵为:f xJ(ξ)=−zc0 [0z c −−f x zx2c2−−ff xy zx cc−2y c z c f2x2+ff yx zzxx c c c2c2y2c−f y zfx c x z c y c ] z cf y f y y c f y y cc3.更新之前估计:T k+1 exp T k四一一ICP一一一一一一11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从理论到实践
高翔 清华大学 2016年冬
2
第七讲 视觉里程计(1)
Chapter 7: Visual Odometry (1)
3 第七讲 视觉里程计(1)
• 本讲目标
• 理解图像特征点的意义, 并掌握在单幅图像中提取出特征点,及多幅图像中匹配特征点 的方法。 • 理解对极几何的原理,利用对极几何的约束,恢复出图像之间的摄像机的三维运动。 • 理解PNP问题,及利用已知三维结构与图像的对应关系,求解摄像机的三维运动。 • 理解ICP问题,及利用点云的匹配关系,求解摄像机的三维运动。 • 理解如何通过三角化,获得二维图像上对应点的三维结构。
• 两步计算位姿:
• 由匹配点计算E
• 由E恢复R,t
• 对极约束的性质: • 乘任意非零常数依然满足 • E共五个自由度 • 当成普通矩阵的话,有八个自由度 • 可用八点法求解
17 7.3 2D-2D:对极几何
• 八点法求E
• 将E看成通常3x3的矩阵,去掉因子后剩八个自由度
• 一对匹配点带来的约束:
八对点构成方程组
• 向量形式:
18 7.3 2D-2D:对极几何
• 从E计算R, t:奇异值分解
四个可能的解,但只有一个深度为正
19 7.3 2D-2D:对极几何
• SVD过程中:
• 取 因为E的内在性质要求它的奇异值为
• 最少可使用五个点计算R,t,称为五点法
• 但需要利用E的非线性性质,原理较复杂
• 如果匹配的是RGB-D图,得到3D-3D间的关系
——PnP
——ICP
14 7.3 2D-2D:对极几何
• 几何关系:
• P在两个图像的投影为
• 两个相机之间的变换为
• • 在第二个图像上投影为
• 记 ,称为极线,反之亦然
称为极点
• 实践当中:
• • 通过特征匹配得到,P未知, 何
• 世界坐标: • 以第一个图为参考系,投影方程:
• 使用归一化坐标(去掉内参):
对极约束:
• 齐次关系: • 两侧左乘:
带内参的形式:
• 再一步左乘:
16 7.3 2D-2D:对极几何
• 对极约束刻画了 • 定义:
• Essential矩阵 • Fundamental矩阵
共面的关系
• 在内参已知的情况下,可以使用E
• 当特征点在平面上时(例如俯视或仰视),使用H恢复R,t
• 否则,使用E或F恢复R,t
• 求得R,t后:
• 利用三角化计算特征点的3D位置(即深度)
24
7.4 实践:对极约束求解相机运动
25 7.5 三角化
• 已知运动时,求解特征点的3D位置
• 几何关系:
• 求 时,两侧乘
• 反之亦然
• 或者同时解
20 7.3 2D-2D:对极几何
• 八点法的讨论
• 用于单目SLAM的初始化
• 尺度不确定性:归一化 t 或特征点的平均深度
• 纯旋转问题:t=0 时无法求解 • 多于八对点时:最小二乘或RANSAC
21 7.3 2D-2D:对极几何
• 从单应矩阵恢复R,t:
• 八点法在特征点共面时会退化
• 设特征点位于某平面上:
• 求 的最小二乘解
26 7.5 三角化
• 三角化中的问题:
• 解得深度的质量与平 移相关 • 但是平移大时特征匹 配可能不成功
• 方程
• 系数矩阵伪逆不可靠 • 行列式近零
特例:相机前进时,虽然有位移,但位于图像中心的点无法三角化(没有视差)
27
7.6 实践:三角测量
• 在FAST基础上计算旋转
9 7.1 特征点法
• BRIEF
• BRIEF-128:在特征点附近的128次像素比较
BRIEF的比较pattern • ORB:旋转之后的BRIEF描述
• BRIEF是一种二进制描述,需要用汉明距离度量
10 7.1 特征点法
• 特征匹配
• 通过描述子的差异判断哪些特征为同一个点
• 两个图像特征点的坐标关系:
或
中间记为H
22 7.3 2D-2D:对极几何
• 该式是在非零因子下成立的
• 去掉第三行:
• 一对点提供两个约束 • 写成关于H的线性方程:
• 类似八点法
• 先计算H • 再用H恢复R,t,n,d,K
23 7.3 2D-2D:对极几何
• 小结 • 2D-2D情况下,只知道图像坐标之间的对应关系
• 特征点周围的图像信息——描述子(Descriptor)
• 例子:SIFT/SURF/ORB
见OpenCV features2d模块
8 7.1 特征点法
• 例子:ORB特征
• 关键点:Oriented FAST
• 描述:BRIEF
• FAST
• 连续N个点的灰度有明显差异
• Oriented FAST
4 第七讲 视觉里程计(1)
• 从本讲开始,开始介绍SLAM系统的重要算法
• 视觉里程计:特征点法和直接法
• 后端优化
• 回环检测 • 地图构建
5
7.1 特征点法
6 7.1 特征点法
• 经典SLAM模型中以位姿——路标(Landmark)来描述SLAM过程 • 路标是三维空间中固定不变的点,能够在特定位姿下观测到
• 数量充足,以实现良好的定位
• 较好的区分性,以实现数据关联
• 在视觉SLAM中,可利用图像特征点作为SLAM中的路标
7 7.1 特征点法
• 特征点:图像当中具有代表性的部分
• 可重复性
• 可区别性
• 高效 • 本地
• 特征点的信息
• 位置、大小、方向、评分等——关键点
特征描述应该在光照、视角发生少量变化时 仍能保持一致
• 暴力匹配:比较图1中每个特征和图2特征的距离
• 加速:快速最近邻(FLANN)
11
7.2 实践:特征提取和匹配
12
7.3 2D-2D:对极几何
13 7.3 2D-2D:对极几何
• 特征匹配之后,得到了特征点之间的对应关系
• 如果只有两个单目图像,得到2D-2D间的关系 ——对极几何
• 如果匹配的是帧和地图,得到3D-2D间的关系
