(完整word)数列题型及解题方法归纳总结,推荐文档
数列解题技巧归纳总结-打印

数列解题技巧归纳总结-打印等差数列前n 项和的最值问题:1、若等差数列{}na 的首项1a>,公差0d <,则前n 项和nS 有最大值。
(ⅰ)若已知通项na ,则nS 最大⇔1nn aa+≥⎧⎨≤⎩; (ⅱ)若已知2nS pn qn=+,则当n 取最靠近2q p -的非零自然数时nS 最大;2、若等差数列{}na 的首项10a <,公差0d >,则前n 项和nS 有最小值(ⅰ)若已知通项na ,则nS 最小⇔1nn aa+≤⎧⎨≥⎩; (ⅱ)若已知2nS pn qn=+,则当n 取最靠近2q p -的非零自然数时nS 最小;数列通项的求法:⑴公式法:①等差数列通项公式;②等比数列通项公式。
⑵已知nS (即12()na a a f n +++=)求na ,用作差法:{11,(1),(2)nn n S n a S S n -==-≥。
已知12()n aa a f n =求n a ,用作商法:(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩。
⑶已知条件中既有nS 还有na ,有时先求nS ,再求na ;有时也可直接求na 。
⑷若1()n na a f n +-=求na 用累加法:11221()()()nnn n n a a a a a a a ---=-+-++- 1a +(2)n ≥。
⑸已知1()n na f n a +=求n a ,用累乘法:121121n n n n n a a aa a a aa---=⋅⋅⋅⋅(2)n ≥。
⑹已知递推关系求na ,用构造法(构造等差、等比数列)。
特别地,(1)形如1nn aka b-=+、1nnn aka b -=+(,k b 为常数)的递推数列都可以用待定系数法转化为公比为k 的等比数列后,再求na ;形如1nnn aka k -=+的递推数列都可以除以nk 得到一个等差数列后,再求na 。
(2)形如11n nn a a ka b --=+的递推数列都可以用倒数法求通项。
(完整word版)数列知识点归纳及习题总结
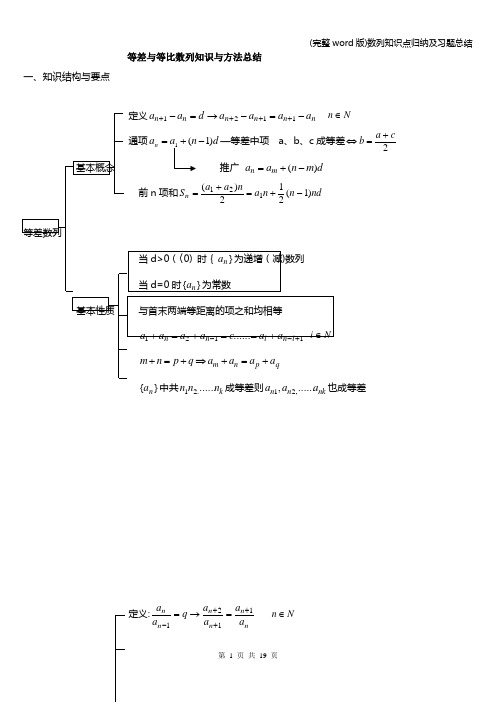
等差与等比数列知识与方法总结一、知识结构与要点N2cab+=⇔}{na中共k nnn.......21成等差则nknnaaa......,,21也成等差定义:nnnnnnaaaaqaa1121+++-=→=Nn∈通项 →⋅=-11n n q a a 等比中项:a b c 成等比数列ac b =⇒2基本概念推广m n m n q a a -⋅=前n 项和=n S )1(11)1()1(111≠--=--=q qqa a qq a q n a n n 等比数列与首末两端等距离的两项之积相等 1121......+--⋅===i n i n n a a a a a a q p n m a a a a q p n m ⋅=⋅⇒+=+}{n a 成等比,若k n n n ,...,21 成等差则nk n a a a ,...,21成等比基本性质 当101>>q a 或1001<<<q a 时 {}n a 为递增数列当101><q a 或1001<<>q a 时 {}n a 为递减数列当 q<0时 {}n a 为摆动数列 当 q=1时 {}n a 为常数数列二、等差数列、等比数列基础知识与方法概括 (一).一般数列数列的定义及表示方法;数列的项与项数;有穷数列与无穷数列;递增(减)、摆动、循环数列;数列{a n }的通项公式a n ;数列的前n 项和公式S n ;一般数列的通项a n 与前n 项和S n 的关系:⎩⎨⎧≥-===-)2()1(111n S S n S a a n nn(二)等差数列1.等差数列的概念[定义]如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
即:成等比数列}{)0,0,2(1n n n n a q a n d a a ⇔≠≠≥=-- 2.等差数列的判定方法(1)定义法:对于数列{}n a ,若d a a n n =-+1(常数),则数列{}n a 是等差数列。
(完整word)(经典)高中数学最全数列总结及题型精选,推荐文档

高中数学:数列及最全总结和题型精选一、数列的概念(1) 数列定义:按一定次序排列的一列数叫做数列; 数列中的每个数都叫这个数列的项。
记作a n ,在数列第一个位置的项叫第 1项(或首项),在第二个位置的叫第2项,……,序号为n 的项叫第n 项(也叫通项)记作 a n ; 数列的一般形式: 印,a 2, a 3,……,a n ,……,简记作a n 。
(2) 通项公式的定义:如果数列 {a n }的第n 项与n 之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式。
例如:①:r , 2 , 3 , 4, 51 n 2k 1② 同一个数列的通项公式的形式不一定唯一。
例如‘ a n = ( 1)n ='(k Z);1,n 2k③ 不是每个数列都有通项公式。
例如‘ 1, 1.4 , 1.41 , 1.414 ,…… (3) 数列的函数特征与图象表示:从函数观点看‘数列实质上是定义域为正整数集N (或它的有限子集)的函数 f(n)当自变量n 从1开始依次取值时对应的一系列函数值 f (1), f (2), f (3),……,f(n),……•通常用a n 来代替f n ‘其图象是一群孤立点。
(4) 数列分类:①按数列项数是有限还是无限分:有穷数列和无穷数列;②按数列项与项之间的大小关系 分:递增数列、递减数列、常数列和摆动数列。
例:下列的数列‘哪些是递增数列、递减数列、常数列、摆动数列? (1) 1 , 2 , 3 , 4 , 5 , 6,… (2)10, 9, 8, 7, 6, 5, …(3) 1,0, 1,0, 1,0,… (4)a, a, a, a, a,…二、等差数列(一)、等差数列定义:一般地‘如果一个数列从第2项起‘每一项与它的前一项的差等于同一个常数‘那么这个数列就叫等差数列‘这个常数叫做等差数列的公差‘公差通常用字母 _d 表示。
用递推公式表示为 a n a n1 d(n 2)或 a n 1 a n d(n 1)例:等差数列a n 2n 1 , a n a n 1 ___________________ (二)、等差数列的通项公式: a n a 1 (n 1)d ;说明:等差数列(通常可称为A P 数列)的单调性:d 0为递增数列‘ d 0为常数列‘ d 0为递减数列。
(完整word版)数列常见题型总结经典(超级经典)

高中数学《数列》常有、常考题型总结题型一数列通项公式的求法1.前 n 项和法(知 S n 求 a n ) a nS 1(n 1)S n S n 1(n 2)例 1、已知数列 { n } 的前 n 项和 S n 12nn 2 ,求数列{| a n|} 的前 n 项和T na1、若数列 {a n } 的前 n项和 S2n,求该数列的通项公式。
n2、若数列 { a n } 的前 n 项和 S n3 a n 3 ,求该数列的通项公式。
23、设数列 {} 的前,知足 T2Sn 2,a n n 项和为S n ,数列{ S n } 的前n 项和为T nnn求数列 { a n } 的通项公式。
2. 形如 a n 1 a nf (n) 型(累加法)( 1)若 f(n) 为常数 , 即: a n 1 a n d , 此时数列为等差数列,则 a n =a 1(n 1)d .( 2)若 f(n) 为 n 的函数时,用累加法 .例 1. 已知数列{ a n }知足 a 1 1, a n3n 11. 已知数列a n 的首项为 1,且 a n 1a n 2. 已知数列 { a n } 知足 a 1 3 , a na n 13. 形如an 1( )f n 型(累乘法)a na n 1 ( n 2) , 证明 a n 3n122n(n N * ) 写出数列a n 的通项公式 .1 ( n 2) ,求此数列的通项公式 .n(n 1)( 1)当 f(n) 为常数,即:a n 1q (此中 q 是不为 0 的常数),此数列为等比且 a n = a 1 q n 1 .a n( 2)当 f(n) 为 n 的函数时 , 用累乘法 .例 1、在数列 { a n } 中 a 11, a nn a n 1 (n 2) ,求数列的通项公式。
n 1 1、在数列 { a n } 中 a 11, a n n 1a n 1 (n 2) ,求 a n 与 S n 。
(完整word版)数列知识点复习总结,推荐文档

数列高考知识点大扫描数列基本概念数列是一种特殊函数,对于数列这种特殊函数,着重讨论它的定义域、值域、增减性和最值等方面的性质,依据这些性质将数列分类:依定义域分为:有穷数列、无穷数列; 依值域分为:有界数列和无界数列;依增减性分为递增数列、递减数列和摆动数列。
数列的表示方法:列表法、图象法、解析法(通项公式法及递推关系法); 数列通项:()n a f n =2、等差数列1、定义 当n N ∈,且2n ≥ 时,总有 1,()n n a a d d +-=常,d 叫公差。
2、通项公式 1(1)n a a n d =+-1)、从函数角度看 1()n a dn a d =+-是n 的一次函数,其图象是以点 1(1,)a 为端点, 斜率为d 斜线上一些孤立点。
2)、从变形角度看 (1)()n n a a n d =+--, 即可从两个不同方向认识同一数列,公差为相反数。
又11(1),(1)n m a a n d a a m d =+-=+-,相减得 ()n m a a n m d -=-,即()n m a a n m d =+-. 若 n>m ,则以 m a 为第一项,n a 是第n-m+1项,公差为d ; 若n<m ,则 m a 以为第一项时,n a 是第m-n+1项,公差为-d.3)、从发展的角度看 若{}n a 是等差数列,则12(2)p q a a a p q d +=++- ,12(2)m n a a a m n d +=++-, 因此有如下命题:在等差数列中,若2m n p q r +=+= , 则2m n p q r a a a a a +=+=.3、前n 项和公式由 1211,n n n n n S a a a S a a a -=+++=+++L L , 相加得 12n n a a S n +=, 还可表示为1(1),(0)2n n n S na d d -=+≠,是n 的二次函数。
数列题型及解题方法归纳总结2推荐文档

知识框架数列的概念数列的分类数列的通项公式数列的递推关系函数角度理解求和公式及性质,掌握了典型题型的解法和数学思想法的应用,就有可能在高考中顺利地解决数列问题。
一、典型题的技巧解法数列两个基本数列等差数列的定义a n等差数列的通项公式等差数列等差数列的求和公式等差数列的性质a n等比数列的定义3na na n 1a nS na mq(nd(na1 (nn /2(a12)1)da n) na ia p a q (mn(n 1)d2q)2)等比数列的通项公式等比数列等比数列的求和公式a nS n等比数列的性质公式法分组求和错位相减求和裂项求和倒序相加求和累加累积归纳猜想证明分期付款数列的应用一八其他数列求和岂a n q1a i(1q n a1(q a n a m a p a q(m nn、q )/(q1 q1)p q)1)1、求通项公式(1)观察法。
(2)由递推公式求通项。
对于由递推公式所确定的数列的求解,通常可通过对递推公式的变换转化成等差数列或等比数列问题。
(1)递推式为a n+1=a+d及a n+1=qa n(d,q为常数)例1、已知{a n}满足a n+1=a n+2,而且a1=1。
求a n。
例1、解■/a n+1-a n=2为常数••• {a n}是首项为1,公差为2的等差数列--a n=1+2 (n-1 )即a n=2n-11例2、已知{a n}满足a n 1— a n,而a1 2,求a. =?2解V 是常数••七J是以2为首项.公比为扌的等匕嗷列5 -2 • L z --^―(2)递推式为a n+1=a n+f (n)1例3、已知{a n}中a1,a n 1解:由已知可知a n 1 a nan14n2 1求a n.1 丄(_匚(2n 1)(2n 1) 2(2n 112n1)令n=1,2,…,(n-1 ),代入得(n-1 )个等式累加,即(a2-a 1)+ (a3-a2)+… +(a n-a n-1 )掌握了数列的基本知识,特别是等差、等比数列的定义、通项公式、1(1 亠 32 2n 1 4n 2★ 说明只要和f (1) +f (2) +…+f ( n-1 )是可求的,就可以由a”i=a n+f (n)以n=1, 2,…,(n-1)代入,可得n-1个等式累加而求a n⑶递推式为a n+1=p@+q (p, q为常数)例4、{a n}中,a1 1,对于n> 1 (n € N)有a n 3a n 1 2,求a..解法一:由已知递推式得a n+1=3a n+2, a n=3a n-1+2。
(word完整版)数列全部题型归纳(非常全面,经典),推荐文档

数列百通通项公式求法 (一)转化为等差与等比1、已知数列{}n a 满足11a =,211n n a a -=+(,n N *∈2≤n ≤8),则它的通项公式n a 什么2.已知{}n a 是首项为2的数列,并且112n n n n a a a a ---=,则它的通项公式n a 是什么3.首项为2的数列,并且231n n a a -=,则它的通项公式n a 是什么4、已知数列{}n a 中,10a =,112n na a +=-,*N n ∈.求证:11n a ⎧⎫⎨⎬-⎩⎭是等差数列;并求数列{}n a 的通项公式;5.已知数列{}n a 中,13a =,1222n n a a n +=-+,如果2n n b a n =-,求数列{}n a 的通项公式(二)含有n S 的递推处理方法1)知数列{a n }的前n 项和S n 满足log 2(S n +1)=n +1,求数列{a n }的通项公式.2.)若数列{}n a 的前n 项和n S 满足,2(2)8n n a S +=则,数列n a3)若数列{}n a 的前n 项和n S 满足,111,0,4n n n n a S S a a -=-≠=则,数列na4)12323...(1)(2)n a a a na n n n +++=++求数列n a(三) 累加与累乘(1)如果数列{}n a 中111,2nn n a a a -=-=(2)n ≥求数列n a(2)已知数列}{n a 满足31=a ,)2()1(11≥-+=-n n n a a n n ,求此数列的通项公式(3) 12+211,2,=32n n n a a a a a +==-,求此数列的通项公式.(4)若数列{}n a 的前n 项和n S 满足,211,2n n S n a a ==则,数列n a(四)一次函数的递推形式1. 若数列{}n a 满足1111,12n n a a a -==+(2)n ≥,数列n a2 .若数列{}n a 满足1111,22n n n a a a -==+ (2)n ≥,数列n a(五)分类讨论(1)2123(3),1,7n n a a n a a -=+≥==,求数列n a(2)1222,(3)1,3nn a n a a a -=≥==,求数列n a(六)求周期16 (1) 121,41nn na a a a ++==-,求数列2004a(2)如果已知数列11n n n a a a +-=-,122,6a a ==,求2010a拓展1:有关等和与等积(1)数列{n a }满足01=a ,12n n a a ++=,求数列{a n }的通项公式(2)数列{n a }满足01=a ,12n n a a n ++=,求数列{a n }的通项公式(3).已知数列满足}{n a )(,)21(,3*11N n a a a n n n ∈=⋅=+,求此数列{a n }的通项公式.拓展2 综合实例分析1已知数列{a n }的前n 项和为n S ,且对任意自然数n ,总有()1,0,1n n S p a p p =-≠≠(1)求此数列{a n }的通项公式(2)如果数列{}n b 中,11222,,n b n q a b a b =+=<,求实数p 的取值范围2已知整数列{a n }满足31223341 (3)n n n n a a a a a a a a --+++=,求所有可能的n a3已知{}n a 是首项为1的正项数列,并且2211(1)0(1,2,3,)n n n n n a na a a n +++-+==L ,则它的通项公式n a 是什么4已知{}n a 是首项为1的数列,并且134n n n a a a +=+,则它的通项公式n a 是什么5、数列{}n a 和{}n b 中,1,,+n n n a b a 成等差数列,n b ,1+n a ,1+n b 成等比数列,且11=a ,21=b ,设nn n b a c =,求数列{}n c 的通项公式。
word完整版等差等比数列知识点梳理及经典例题推荐文档

word完整版等差等⽐数列知识点梳理及经典例题推荐⽂档(3)8A 、等差数列知识点及经典例题⼀、数列由a n 与S n 的关系求a n由S n 求a n 时,要分n=1和n > 2两种情况讨论,然后验证两种情况可否⽤统⼀的解析式表⽰,若不能,则⽤分段1例〗根据下列条件,确定数列a n 的通项公式。
⑴⑷=1 .⼬I =3%+2孑 (2 ) a\ = 1,4+i = C n+ 1) Ofl ?分析:(1)可⽤构造等⽐数列法求解; (2)可转化后利⽤累乘法求解; (3)将⽆理问题有理化,⽽后利⽤a n 与S n 的关系求解。
丁⽿初=3兔+ 2,⼆%知+ 1=3(弘+1⼋⼆詈异=3⼯丽临为等⽐数列拾⽐+⼆為+ 1 = 2 * 3" 1 , A ^ = 2 * 3^-1.E^H =(n+> ?-=服得 S T =(A ±^!当 42 时=5⼀5-='為f "(為⼫O(2) ■!.⽚?1⼀⼇「?| ^⼀ J ........................ 「「⼇记.故"—<-累乘可得,函数的形式表⽰为a nS (n 1) Si S n 1 (n 2)解答:(1)—(cud- a, i+4)(弼―a?- I〉,⼆(召+為⼁)(的—编| —4) = QrTcin>0,「*爲+ 4 i>CbA O H —I —4=0,即%—久1=4, 化数列为等差数列,"差d=4.丁⼫ +2)⼜a? = S* =-------- g ----- ?A a. -2??:%=2⼗4(川⼀1〉=如⼀2?⼀⼆、等差数列及其前n项和(⼀)等差数列的判定1、等差数列的判定通常有两种⽅法:第⼀种是利⽤定义,a n a n 1 d(常数)(n 2),第⼆种是利⽤等差中项,即2a.务1 %i(n 2)。
2、解选择题、填空题时,亦可⽤通项或前n项和直接判断。
(1)通项法:若数列{a n}的通项公式为n的⼀次函数,即a n=An+B,则{a n}是等差数列;(2)前n项和法:若数列{a.}的前n项和S n是S n An2Bn的形式(A, B是常数),则{a“}是等差数列。
数列全部题型归纳(非常全面,经典!)(精编文档).doc

【最新整理,下载后即可编辑】数列百通 通项公式求法 (一)转化为等差与等比1、已知数列{}n a 满足11a =,n a =,n N *∈2≤n ≤8),则它的通项公式n a 什么2.已知{}n a 是首项为2的数列,并且112n n n n a a a a ---=,则它的通项公式n a 是什么3.首项为2的数列,并且231n n a a -=,则它的通项公式n a 是什么4、已知数列{}n a 中,10a =,112n na a +=-,*N n ∈.求证:11n a ⎧⎫⎨⎬-⎩⎭是等差数列;并求数列{}n a 的通项公式;5.已知数列{}n a 中,13a =,1222n n a a n +=-+,如果2n n b a n =-,求数列{}n a 的通项公式(二)含有n S 的递推处理方法1)知数列{a n }的前n 项和S n 满足log 2(S n +1)=n +1,求数列{a n }的通项公式.2.)若数列{}n a 的前n 项和n S 满足,2(2)8n n a S +=则,数列n a3)若数列{}n a 的前n 项和n S 满足,111,0,4n n n n a S S a a -=-≠=则,数列n a4)12323...(1)(2)n a a a na n n n +++=++ 求数列n a(三) 累加与累乘(1)如果数列{}n a 中111,2n n n a a a -=-=(2)n ≥求数列n a(2)已知数列}{n a 满足31=a ,)2()1(11≥-+=-n n n a a n n ,求此数列的通项公式 (3) 12+211,2,=32n n n a a a a a +==-,求此数列的通项公式.(4)若数列{}n a 的前n 项和n S 满足,211,2n n S n a a ==则,数列n a(四)一次函数的递推形式1. 若数列{}n a 满足1111,12n n a a a -==+(2)n ≥,数列n a2 .若数列{}n a 满足1111,22n n n a a a -==+(2)n ≥,数列n a(五)分类讨论(1)2123(3),1,7n n a a n a a -=+≥==,求数列n a(2)1222,(3)1,3nn a n a a a -=≥==,求数列n a(六)求周期 16 (1)121,41nn na a a a ++==-,求数列2004a(2)如果已知数列11n n n a a a +-=-,122,6a a ==,求2010a拓展1:有关等和与等积(1)数列{n a }满足01=a ,12n n a a ++=,求数列{a n }的通项公式(2)数列{n a }满足01=a ,12n n a a n ++=,求数列{a n }的通项公式(3).已知数列满足}{n a )(,)21(,3*11N n a a a n n n ∈=⋅=+,求此数列{a n }的通项公式.拓展2 综合实例分析1已知数列{a n }的前n 项和为n S ,且对任意自然数n ,总有()1,0,1n n S p a p p =-≠≠ (1)求此数列{a n }的通项公式(2)如果数列{}n b 中,11222,,n b n q a b a b =+=<,求实数p 的取值范围 2已知整数列{a n }满足31223341 (3)n n n na a a a a a a a --+++=,求所有可能的n a3已知{}n a 是首项为1的正项数列,并且2211(1)0(1,2,3,)n n n n n a na a a n +++-+==,则它的通项公式n a 是什么4已知{}n a 是首项为1的数列,并且134nn n a a a +=+,则它的通项公式n a 是什么5、数列{}n a 和{}n b 中,1,,+n n n a b a 成等差数列,n b ,1+n a ,1+n b 成等比数列,且11=a ,21=b ,设nnn b a c =,求数列{}n c 的通项公式。
数列题型及解题方法归纳总结材料(最新整理)

(8)当遇到 an1
an1
d或 an1 an1
q 时,分奇数项偶数项讨论,结果可
能是分段形式。
数列求和的常用方法:
(1)公式法:①等差数列求和公式;②等比数列求和公式。
(2)分组求和法:在直接运用公式法求和有困难时,常将“和式”中“同类项”
先合并在一起,再运用公式法求和。
(3)倒序相加法:若和式中到首尾距离相等的两项和有其共性或数列的通项与
2
因此所求数列的前 n 项的和为
例 10、解 Sn 0 Cn0 3Cn1 6Cn2 3nCnn
∴ Sn=3n·2n-1 (4)、错位相减法
如果一个数列是由一个等差数列与一个等比数列对应项相乘构成的,可把和 式的两端同乘以上面的等比数列的公比,然后错位相减求和.
例 11、 求数列 1,3x,5x2,…,(2n-1)xn-1 前 n 项的和.
(n 2)
[练习]
a n a1 f (2) f (3) …… f (n) ∴a n a 0 f (2) f (3) …… f (n)
文档大全
[练习]
数列 a n ,a1 1,a n 3n1 a n1 n 2 ,求a n
(a n
1 2
3n
1 )
6、等比型递推公式
着写的两个和式相加,然后求和。
例 10、求和: Sn 3Cn1 6Cn2 3nCnn
【例 8】 求数列 1,(3+5),(7+9+10),(13+15+17+19),…前 n 项的和。
解
本题实际是求各奇数的和,在数列的前 n 项中,共有 1+2+…+n=
1 n(n 1) 个奇数, 2
数列解题技巧归纳总结-打印

等差数列前n 项和的最值问题:1、若等差数列{}n a 的首项10a >,公差0d <,则前n 项和n S 有最大值。
(ⅰ)若已知通项n a ,则n S 最大⇔10n n a a +≥⎧⎨≤⎩;(ⅱ)若已知2n S pn qn =+,则当n 取最靠近2qp-的非零自然数时n S 最大; 2、若等差数列{}n a 的首项10a <,公差0d >,则前n 项和n S 有最小值 (ⅰ)若已知通项n a ,则n S 最小⇔10n n a a +≤⎧⎨≥⎩;(ⅱ)若已知2n S pn qn =+,则当n 取最靠近2qp-的非零自然数时n S 最小; 数列通项的求法:⑴公式法:①等差数列通项公式;②等比数列通项公式。
⑵已知n S (即12()n a a a f n +++=)求n a ,用作差法:{11,(1),(2)n n n S n a S S n -==-≥。
已知12()n a a a f n =求n a ,用作商法:(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩。
⑶已知条件中既有n S 还有n a ,有时先求n S ,再求n a ;有时也可直接求n a 。
⑷若1()n n a a f n +-=求n a 用累加法:11221()()()n n n n n a a a a a a a ---=-+-++- 1a +(2)n ≥。
⑸已知1()n n a f n a +=求n a ,用累乘法:121121n n n n n a a aa a a a a ---=⋅⋅⋅⋅(2)n ≥。
⑹已知递推关系求n a ,用构造法(构造等差、等比数列)。
特别地,(1)形如1n n a ka b -=+、1nn n a ka b -=+(,k b 为常数)的递推数列都可以用待定系数法转化为公比为k 的等比数列后,再求n a ;形如1n n n a ka k -=+的递推数列都可以除以n k 得到一个等差数列后,再求n a 。
(完整版)数列题型及解题方法归纳总结,推荐文档

建议收藏下载本文,以便随时学习! 4、叠乘法
可转化为等比数列,设a n x c a n1 x
例如:数列a n 中,a1
3,
a n1 an
n
n
1
,求a
n
a n ca n1 c 1x
解: a 2 · a 3 …… a n 1 · 2 …… n 1 ,∴ a n 1
a1 a2
a n1 2 3
1、公式法
可能是分段形式。 数列求和的常用方法:
2、 由S n 求a n
(1)公式法:①等差数列求和公式;②等比数列求和公式。
(2)分组求和法:在直接运用公式法求和有困难时,常将“和式”中“同类
项”先合并在一起,再运用公式法求和。
(3)倒序相加法:若和式中到首尾距离相等的两项和有其共性或数列的通项
与组合数相关联,则常可考虑选用倒序相加法,发挥其共性的作用求和(这
an=3(an-an-1)
因此数列{an+1-an}是公比为 3 的等比数列,其首项为 a2-a1=(3×1+2)-
1=4
∴an+1-an=4·3n-1
∵an+1=3an+2 ∴3an+2-an=4·3n-1
即
an=2·3n-1-1 解法二: 上法得{an+1-an}是公比为 3 的等比数列,于是有:a2-a1=4,a3-
⑵已知 Sn (即 a1 a2 an f (n) )求 an ,用作差法:
我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙龙课反倒是龙卷风前一天
4
文德教育
建议收藏下载本文,以便随时学习! (8)当遇到 an1
an1
d或 an1 an1
(word完整版)归纳综合数列知识点归纳,推荐文档

必修5 第二章 数列 (复习1)一 、等差数列知识点1、等差数列定义:一般地,如果一个数列从第2项起, 那么这个数列就叫等差数列,这个常数叫做等差数列的 ,公差通常用字母d 表示。
用递推公式表示为1(2)n n a a d n --=≥或1(1)n n a a d n +-=≥。
2、等差数列的通项公式:1(1)n a a n d =+-;说明:等差数列 的单调性: 为数列当 为常数列, 为递减数列。
3、等差中项的概念:定义:如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差其中A = a ,A ,b 成等差数列⇔ 。
4、等差数列的前n 和的求和公式: 。
5、等差数列的性质:(1)在等差数列{}n a 中,从第2项起,每一项是它相邻二项的等差中项;(2)在等差数列{}n a 中,相隔等距离的项组成的数列是AP ,如:1a ,3a ,5a ,7a ,……;3a ,8a ,13a ,18a ,……;(3)在等差数列{}n a 中,对任意m ,n N +∈,n a = ,d = ()m n ≠;(4)在等差数列{}n a 中,若m ,n ,p ,q N +∈且m n p q +=+,则 ; 说明:设数列{}n a 是等差数列,且公差为d ,(Ⅰ)若项数为偶数,设共有2n 项,则①S 奇-S 偶nd =; ② 1n n S aS a +=奇偶; (Ⅱ)若项数为奇数,设共有21n -项,则①S 偶-S 奇n a a ==中;②1S nS n =-奇偶。
6、数列最值(1)10a >,0d <时,n S 有最大值;10a <,0d >时,n S 有最小值;(2)n S 最值的求法:①若已知n S ,可用二次函数最值的求法(n N +∈);②若已知n a ,则n S 最值时n 的值(n N +∈)可如下确定100n n a a +≥⎧⎨≤⎩或10n n a a +≤⎧⎨≥⎩。
变式训练1, 根据各题的条件,求等差数列{}n a 的前n 项和n S ,(1)12,5,10a d n === (2)12,6,12n a a n =-==(3)102,5,8a d n =-=-=2. 在1和15之间插入25个数,使得所得到的的27个数成等差数列。
(完整)数列题型及解题方法归纳总结,推荐文档

1 2
5
文德教育
n 2时,a n Sn Sn1 …… 3·4 n1
a n ca n1 d c、d为常数,c 0,c 1,d 0
建议收藏下载本文,以便随时学习! 4、叠乘法
可转化为等比数列,设a n x c a n1 x
例如:数列a n 中,a1
3,
a n1 an
n n 1 ,求an
a n ca n1 c 1x
解: a 2 · a 3 …… a n 1 · 2 …… n 1 ,∴ a n 1
a1 a2
a n1 2 3
n
a1 n
又a 1
3,∴a n
3 n
5、等差型递推公式
由a n a n1 f (n),a1 a 0,求a n ,用迭加法
令(c 1)x d,∴x d c1
(3)形如 an1 ank 的递推数列都可以用对数法求通项。
(7)(理科)数学归纳法。
4
文德教育
建议收藏下载本文,以便随时学习! (8)当遇到 an1
an1
d或 an1 an1
q 时,分奇数项偶数项讨论,结果
求数列通项公式的常用方法:
1、公式法
可能是分段形式。 数列求和的常用方法:
2、 由S n 求a n
∴a n
c
d
1是首项为a
1
c
d ,c为公比的等比数列 1
∴a n
c
d 1
a1
c
d
1
·c
n
1
n
2时,a 2 a3
a1 a2
f (2)
f
(3)
两边相加,得:
…… ……
a n a n1 f (n)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1知识框架111111(2)(2)(1)(1)()22()n n n n n n m p q n n n n a q n a a a qa a d n a a n d n n n S a a na d a a a a m n p q --=≥=⎧⎪←⎨⎪⎩-=≥⎧⎪=+-⎪⎪-⎨=+=+⎪⎪+=++=+⎪⎩两个基等比数列的定义本数列等比数列的通项公式等比数列数列数列的分类数列数列的通项公式函数角度理解的概念数列的递推关系等差数列的定义等差数列的通项公式等差数列等差数列的求和公式等差数列的性质1111(1)(1)11(1)()n n n n m p q a a q a q q q q S na q a a a a m n p q ---=≠--===+=+⎧⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎪⎨⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎩⎩⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎧⎨⎩⎩等比数列的求和公式等比数列的性质公式法分组求和错位相减求和数列裂项求和求和倒序相加求和累加累积归纳猜想证明分期付款数列的应用其他⎪⎪⎪⎪⎪⎪⎪⎪⎪掌握了数列的基本知识,特别是等差、等比数列的定义、通项公式、求和公式及性质,掌握了典型题型的解法和数学思想法的应用,就有可能在高考中顺利地解决数列问题。
一、典型题的技巧解法 1、求通项公式 (1)观察法。
(2)由递推公式求通项。
对于由递推公式所确定的数列的求解,通常可通过对递推公式的变换转化成等差数列或等比数列问题。
(1)递推式为a n+1=a n +d 及a n+1=qa n (d ,q 为常数) 例1、 已知{a n }满足a n+1=a n +2,而且a 1=1。
求a n 。
例1、解 ∵a n+1-a n =2为常数 ∴{a n }是首项为1,公差为2的等差数列∴a n =1+2(n-1) 即a n =2n-1 例2、已知{}n a 满足112n n a a +=,而12a =,求n a =?(2)递推式为a n+1=a n +f (n )例3、已知{}n a 中112a =,12141n n a a n +=+-,求n a . 解: 由已知可知)12)(12(11-+=-+n n a a n n )121121(21+--=n n令n=1,2,…,(n-1),代入得(n-1)个等式累加,即(a 2-a 1)+(a 3-a 2)+…+(a n -a n-1)22434)1211(211--=--+=n n n a a n ★ 说明 只要和f (1)+f (2)+…+f (n-1)是可求的,就可以由a n+1=a n +f (n )以n=1,2,…,(n-1)代入,可得n-1个等式累加而求a n 。
(3)递推式为a n+1=pa n +q (p ,q 为常数)例4、{}n a 中,11a =,对于n >1(n ∈N )有132n n a a -=+,求n a .解法一: 由已知递推式得a n+1=3a n +2,a n =3a n-1+2。
两式相减:a n+1-a n =3(a n -a n-1)因此数列{a n+1-a n }是公比为3的等比数列,其首项为a 2-a 1=(3×1+2)-1=4∴a n+1-a n =4·3n-1 ∵a n+1=3a n +2 ∴3a n +2-a n =4·3n-1 即 a n =2·3n-1-1解法二: 上法得{a n+1-a n }是公比为3的等比数列,于是有:a 2-a 1=4,a 3-a 2=4·3,a 4-a 3=4·32,…,a n -a n-1=4·3n-2, 把n-1个等式累加得: ∴an=2·3n-1-1(4)递推式为a n+1=p a n +q n (p ,q 为常数))(3211-+-=-n n n n b b b b 由上题的解法,得:n n b )32(23-= ∴nn nn n b a )31(2)21(32-==(5)递推式为21n n n a pa qa ++=+思路:设21n n n a pa qa ++=+,可以变形为:211()n n n n a a a a αβα+++-=-,想于是{a n+1-αa n }是公比为β的等比数列,就转化为前面的类型。
求n a 。
3(6)递推式为S n 与a n 的关系式关系;(2)试用n 表示a n 。
∴)2121()(1211--++-+-=-n n n n n n a a S S∴11121-+++-=n n n n a a a ∴n n n a a 21211+=+ 上式两边同乘以2n+1得2n+1a n+1=2na n +2则{2na n }是公差为2的等差数列。
∴2na n = 2+(n-1)·2=2n数列求和的常用方法:1、拆项分组法:即把每一项拆成几项,重新组合分成几组,转化为特殊数列求和。
2、错项相减法:适用于差比数列(如果{}n a 等差,{}n b 等比,那么{}n n a b 叫做差比数列)即把每一项都乘以{}n b 的公比q ,向后错一项,再对应同次项相减,转化为等比数列求和。
3、裂项相消法:即把每一项都拆成正负两项,使其正负抵消,只余有限几项,可求和。
适用于数列11n n a a +⎧⎫⎨⎬⋅⎩⎭和1n n a a +⎧⎫⎨⎬+⎪⎪⎩⎭(其中{}n a 等差)可裂项为:111111()n n n n a a d a a ++=-⋅,111()n n n n a a da a ++=-+等差数列前n 项和的最值问题:41、若等差数列{}n a 的首项10a >,公差0d <,则前n 项和n S 有最大值。
(ⅰ)若已知通项n a ,则n S 最大⇔10n n a a +≥⎧⎨≤⎩;(ⅱ)若已知2n S pn qn =+,则当n 取最靠近2q p-的非零自然数时n S 最大;2、若等差数列{}n a 的首项10a <,公差0d >,则前n 项和n S 有最小值(ⅰ)若已知通项n a ,则n S 最小⇔10n n a a +≤⎧⎨≥⎩;(ⅱ)若已知2n S pn qn =+,则当n 取最靠近2qp-的非零自然数时n S 最小;数列通项的求法:⑴公式法:①等差数列通项公式;②等比数列通项公式。
⑵已知n S (即12()n a a a f n +++=L )求n a ,用作差法:{11,(1),(2)n n n S n a S S n -==-≥。
已知12()n a a a f n =g g L g 求n a ,用作商法:(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩。
⑶已知条件中既有n S 还有n a ,有时先求n S ,再求n a ;有时也可直接求n a 。
⑷若1()n n a a f n +-=求na 用累加法:11221()()()n n n n n a a a a a a a ---=-+-++-L1a +(2)n ≥。
⑸已知1()n n a f n a +=求n a ,用累乘法:121121n n n n n a a aa a a a a ---=⋅⋅⋅⋅L (2)n ≥。
⑹已知递推关系求n a ,用构造法(构造等差、等比数列)。
特别地,(1)形如1n n a ka b -=+、1nn n a ka b -=+(,k b 为常数)的递推数列都可以用待定系数法转化为公比为k 的等比数列后,再求n a ;形如1n n n a ka k -=+的递推数列都可以除以nk 得到一个等差数列后,再求n a 。
(2)形如11n n n a a ka b--=+的递推数列都可以用倒数法求通项。
(3)形如1kn n a a +=的递推数列都可以用对数法求通项。
(7)(理科)数学归纳法。
(8)当遇到q a a d a a n n n n ==--+-+1111或时,分奇数项偶数项讨论,结果可能是分段形式。
数列求和的常用方法:(1)公式法:①等差数列求和公式;②等比数列求和公式。
(2)分组求和法:在直接运用公式法求和有困难时,常将“和式”中“同类项”先合并在一起,再运用公式法求和。
(3)倒序相加法:若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联,则常可考虑选用倒序相加法,发挥其共性的作用求和(这也是5等差数列前n 和公式的推导方法). (4)错位相减法:如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成,那么常选用错位相减法(这也是等比数列前n 和公式的推导方法).(5)裂项相消法:如果数列的通项可“分裂成两项差”的形式,且相邻项分裂后相关联,那么常选用裂项相消法求和.常用裂项形式有:①111(1)1n n n n =-++; ②1111()()n n k k n n k=-++; ③2211111()1211k k k k <=---+,211111111(1)(1)1k k k k k k k k k-=<<=-++--; ④1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++ ;⑤11(1)!!(1)!n n n n =-++;⑥=<<= 二、解题方法:求数列通项公式的常用方法:1、公式法2、n n a S 求由(时,,时,)n a S n a S S n n n ==≥=--12111 3、求差(商)法{}如:满足……a a a a n n n n 121212251122+++=+<>解:n a a ==⨯+=1122151411时,,∴n a a a n n n ≥+++=-+<>--2121212215212211时,……<>-<>=12122得:n n a∴a n n =+21∴a n n n n ==≥⎧⎨⎩+141221()()[练习]{}数列满足,,求a S S a a a n n n n n +==++111534 (注意到代入得:a S S S S n n n n n+++=-=1114 {}又,∴是等比数列,S S S n n n144==n a S S n n n n ≥=-==--23411时,……·4、叠乘法{}例如:数列中,,,求a a a a nn a n n n n 1131==++ 解:a a a a a a n n a a nn n n 213211122311·……·……,∴-=-= 又,∴a a nn 133==5、等差型递推公式6由,,求,用迭加法a a f n a a a n n n -==-110()n a a f a a f a a f n n n ≥-=-=-=⎫⎬⎪⎪⎭⎪⎪-22321321时,…………两边相加,得:()()()a a f f f n n -=+++123()()()…… ∴……a a f f f n n =++++023()()() [练习]{}()数列,,,求a a a a n a n n n n n 111132==+≥--()()a n n=-1231 6、等比型递推公式()a ca d c d c c d n n =+≠≠≠-1010、为常数,,, ()可转化为等比数列,设a x c a x n n +=+-1 ()⇒=+--a ca c x n n 11令,∴()c x d x dc -==-11∴是首项为,为公比的等比数列a d c a dc c n +-⎧⎨⎩⎫⎬⎭+-111 ∴·a d c a d c c n n +-=+-⎛⎝ ⎫⎭⎪-1111∴a a d c c dc n n =+-⎛⎝⎫⎭⎪---1111[练习]{}数列满足,,求a a a a a n n n n 11934=+=+()a n n =-⎛⎝ ⎫⎭⎪+-843117、倒数法例如:,,求a a a a a n nn n 11122==++由已知得:1221211a a a a n n n n+=+=+ ∴11121a a n n +-= ∴⎧⎨⎩⎫⎬⎭=111121a a n 为等差数列,,公差为 ()()∴=+-=+11112121a n n n ·7∴a n n =+212.数列求和问题的方法 (1)、应用公式法等差、等比数列可直接利用等差、等比数列的前n 项和公式求和,另外记住以下公式对求和来说是有益的。
