北京化工大学数理统计两类错误势函数共28页文档

合集下载

2019-概率论与数理统计(柴中林)第20讲-PPT课件-文档资料

当 H0: 1=2 为真时，有
(XY) S m1n1 ~tmn2.
从而
P S|X m 1 Yn |1tm n2(/2 ).
拒绝域为
| S
XY| m1n1
tmn2(/2)
P|0X .1/1100| z/2，
即 P |X 1 | ( 0 . 0 1 /1 ) z / 2 0 .
故可， c 取 (0 .1 /1)z 0 /2.
于是，我们就得到如下检验准则:
当| X10|c时接，受原H假 0；设当|X10|c时拒，绝原H假 0. 设
此检验法称作 t 检验法。
例1(续例8.1.1) : 假设2未知，检验
H0: μ =10；H1: μ≠10.
解：n=10, =0.05, 0=10， t10-1( /2)=t9(0.025)=2.2622，
计X 算 0 .0,S 得 5 2 0 .0,S 5 0 .2.24
而 0. 0X 5 0S ntn 1( /2 )0 .1.6
通常用 α 和 β 记犯第一、第二类错误的概率，即
P{拒绝 H0|H0为真 }， P{接受 H0|H0为假 }.
在检验问题中，犯“弃真”和“取伪” 两类错误都总是不可避免的，并且减少犯第一类错误的概率，就会增大犯第二类错误的概率;反之亦所然以。，犯两类错误的概率不能同时得到控制。
H0:μ =10，其c 中 (0 .1 / 1)0 z/2.
现在我们来分析一下：取上述 c 后，如果 H0 是正确的，却被我们拒绝了。这时，犯第一类错误的概率是多少呢？
分析: 因为当原假设 H0: μ =10 成立时，有
X10~N(0, 1). 0.1/ 10

北交大2010-2011学年第二学期数理统计学期末考试试卷(B卷)答案

北京交通大学2010~2011学年第二学期数理统计学期末考试试卷（B 卷）答案一．（本题满分10分）设总体X 存在二阶矩，记()μ=X E ，()2var σ=X ，()n X X X ,,,21 是从该总体中抽取的一个样本，X 是其样本均值，2S 是其样本方差．⑴ 证明：()μ=X E ，()nX 2var σ=．⑵ 证明：()22σ=S E ．解：⑴ ()()μμμ=⋅===⎪⎭⎫ ⎝⎛=∑∑∑===n n n X E n X n E X E n i ni i n i i 1111111，()()n n n n X n X n X n i n i i n i i 22212212111var 11var var σσσ=⋅===⎪⎭⎫ ⎝⎛=∑∑∑===．⑵ ()()()()⎭⎬⎫⎩⎨⎧----=⎭⎬⎫⎩⎨⎧--=∑∑==2121221111μμX n X E n X X n E S E n i i n i i()()⎭⎬⎫⎩⎨⎧----=∑=21211μμX nE X E n n i i()()()()⎭⎬⎫⎩⎨⎧----=∑=21211X E X nE X E X E n n i i i()()⎭⎬⎫⎩⎨⎧--=∑=X n X n n i ivar var 111 ()2222121111σσσσσ=--=⎭⎬⎫⎩⎨⎧⋅--=∑=n n n n n n i ．二．（本题满分10分）设总体X 服从参数为p 的几何分布，其分布列为{}1-==k pq k X P () ,3,2,1=k ．其中10<<p 是未知参数，p q -=1．n X X X ,,,21 是取自该总体中的一个样本．试求参数p 的极大似然估计量．解：似然函数为 (){}{}{}{}n n n n x X P x X P x X P x X x X x X P p L ======== 22112211,,,()()()()nx nx x x nk k n p p p p p p p p ----∑-=--⋅-==1211111111所以，()()p n x p n p L n k k -⎪⎭⎫⎝⎛-+=∑=1ln ln ln 1．对p 求导，得 ()01ln 1=---=∑=pn x p n p L dp d nk k ，解方程，得xp 1=．因此p 的极大似然估计量为Xp1ˆ=．三．（本题满分10分）设总体X 服从区间()θ,0上的均匀分布，其中0>θ是未知参数，()n X X X ,,,21 是从该总体中抽取的一个样本．⑴ 试判断()n X n n 1ˆ+=θ是否为未知参数θ的无偏估计量？⑵ 试判断()n X nn 1ˆ+=θ是否为未知参数θ的相合估计量？解：X 的密度函数与分布函数分别为()⎪⎩⎪⎨⎧<<=其它01θθx x f ， ()⎪⎩⎪⎨⎧≥<<≤=θθθx x x x x F 1000．所以()n X 的密度函数为()()()()()⎪⎩⎪⎨⎧<<==--其它011θθx nx x f x F n x f nn n n ．所以，()()()()()()⎰⎰-+∞∞-⋅+=+=+=⎪⎭⎫ ⎝⎛+=θθθ011111ˆdx nx x n n dx x xf n n X E n n X n n E E n n n n nθθθθ=+⋅+=⋅+=⎰1110n n n n dx x n n n n n所以，()n X nn 1ˆ+=θ是未知参数θ的无偏估计量．又 ()()()()()()⎰⎰-+∞∞-⋅⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+=θθθ012222222221111ˆdx nx x n n dx x f x n n X E n n X n n E E n n n n n ()()2222221211θθθθ++=+⋅⎪⎭⎫⎝⎛+=⋅⎪⎭⎫ ⎝⎛+=⎰n n n n n n n dx x n n n n n 所以，()()()()()()()221ˆˆˆvar 222222+=-++=-=n n n n n E E θθθθθθ由Chebyshev 不等式，对任意给定的0>ε，有{}()()021ˆvar ˆ0222→+⋅=≤≥-≤n n P θεεθεθθ， ()∞→n ．所以，对任意给定的0>ε，有{}0ˆlim =≥-∞→εθθP n ．这表明，()n X nn 1ˆ+=θ是未知参数θ的相合估计量．四．（本题满分10分）设总体()2,~σμN X ，其中μ与2σ都未知，+∞<<∞-μ，02>σ，()n X X ,,1 是取自该总体中的一个样本．对于给定的显著性水平10<<α，试求检验假设2020:σσ≥H ()2021:σσ<H ．的拒绝域．解：取检验统计量()()202122011σσS n X X T ni i -=-=∑=．当0H 成立，且22σσ=时，()()()1~112221220--=-=∑=n S n X X T ni i χσσ．当原假设0H 成立时，由观测值()n x x ,,1 可知比值22σs 应当大于1，因此比值()2021σs n -应当比较大；反之，如果我们通过样本观测值()nx x ,,1 ，发现()2021σs n -偏小，自然就有理由认为0H不成立．于是，拒绝域可以取作形如()()⎭⎬⎫⎩⎨⎧<-=c s n x x W n 202111:,,σ ．对给定的显著性水平()10<<αα，当0H 成立，并且22σσ=时，由()ασ=⎭⎬⎫⎩⎨⎧<-c S n P 2021，故取临界值()12-=n c αχ．即有 ()()αχσασ=⎭⎬⎫⎩⎨⎧-<-11220220n S n P ，对任意+∞<<∞-μ成立．因此，我们得到当202σσ=时，显著性水平α下的一个检验的拒绝域()()()⎭⎬⎫⎩⎨⎧-<-=11:,,22021n s n x x W n αχσ ．当原假设0H 成立，且202σσ>时，有()()222211σσS n S n -<-．而且当原假设0H 成立，且总体为()2,σμN 时，有()()1~1222--n S n χσ，所以此时有，(){}()()⎭⎬⎫⎩⎨⎧-<-=∈11,,220211n S n P W X X P n αχσ ()()αχσα=⎭⎬⎫⎩⎨⎧-<-≤11222n S n P ，对任意+∞<<∞-μ成立．因此原假设2020:σσ≤H 的拒绝域为()()()⎭⎬⎫⎩⎨⎧-<-=11:,,22211n s n x x W n αχσ ．五．（本题满分10分）检验某批矿砂中的含镍量，随机抽取7份样品，测得含镍量百分比分别为：67.2 33.3 69.3 01.3 98.3 15.3 69.3假设这批矿砂中的含镍量的百分比服从正态分布，试在显著性水平05.0=α下检验这批矿砂中的含镍量的百分比是否为25.3．解：设X 表示这批矿砂中的含镍量的百分比，则()2,~σμN X ．25.3:0=μH ()25.3:1≠μH由于总体方差未知，故用检验统计量n SX T 25.3-=当0H 成立时，()1~25.3--=n t n SX T ．由于显著性水平05.0=α，7=n ，所以()4469.26025.0=t ．因此检验的拒绝域为()⎭⎬⎫⎩⎨⎧≥-=4469.225.3:,,,7211n sx x x x W由样本观测值，得36.3=x ，455668007.0=s 所以，4469.2638694486.0745*******.025.336.325.3<=-=-n sx所以，不拒绝0H ，可以认为这批矿砂中的含镍量的百分比为25.3．六．（本题满分10分）设总体X 的密度函数为()()⎩⎨⎧≤>=+-ax ax x a x f 01θθθθ；其中0>a 是已知常数，而0>θ是未知参数．()n X X X ,,,21 是取自该总体中的一个样本．试给出未知参数的一个充分统计量．证明：样本()n X X X ,,,21 的联合密度函数为()()()⎪⎩⎪⎨⎧=>=∏∏=+-=其它；0,,2,1,111n i a x x a x f i ni i ni i θθθθ()()()⎩⎨⎧=>=+-其它0,,2,1,121n i a x x x x a i n n n θθθ(){}a x a x a x ni i n n n I x a >>>+-=⋅⎪⎪⎭⎫ ⎝⎛=∏,,,1121 θθθ令()()1,+-=θθθθt a t g n n ，(){}a x a x a x n n I x x x h >>>=,,,2121,,, ，则 ()()n n i i ni i x x x h x g x f ,,,,2111 ⋅⎪⎪⎭⎫⎝⎛=∏∏==θθ；并且(){}a x a x a x n n I x x x h >>>=,,,2121,,, 与未知参数θ无关，因此由因子分解定理知，∏==ni iX T 1是未知参数θ的充分统计量．七．（本题满分10分）一试验用来比较4种不同药品解除外科手术后疼痛的延续时间（单位：小时），结果如下表：假定各种疼痛的延续时间服从正态分布，而且方差相等，试在显著性水平05.0=α下检验这4种不同药品解除外科手术后的疼痛时间是否有显著性影响．解：0H ：4种不同药品解除外科手术后的疼痛时间无显著性差异．所以有14310016176812211112=⨯-=⎪⎪⎭⎫ ⎝⎛-=∑∑∑∑====r i n j ij ri n j ij T i iX n X S ， 3333.1081001613333.7331122112121=⨯-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=∑∑∑∑====r i n j ij ri n j ij i A i i X n X n S ， 6667.343333.108143=-=-=A T E S S S ．八．（本题满分10分）随机地检查一本书的100页，记录各页中印刷错误的个数，其结果为试在显著性水平05.0=α下，能否认为一页的印刷错误的个数服从Poisson 分布？解：0H ：一页的印刷错误的个数服从Poisson 分布． λ的极大似然估计值为()1162504231924013601001ˆ=⨯+⨯+⨯+⨯+⨯+⨯+⨯=λ选取统计量 ()∑=-=ri i i i pn pn n 122ˆˆχ，则当∞→n 时，()()1ˆˆ2122--→-=∑=m r pn pn n ri i i i χχ． {}!!ˆˆ1ˆk e ek k X Pk --===λλ， () ,2,1,0=k ．因此，我们有 {}367879441.00ˆˆ0===X P p， {}367879441.01ˆˆ1===X P p ， {}18393972.02ˆˆ2===X P p， {}06131324.03ˆˆ3===X P p ， {}01532831.04ˆˆ4===X P p， {}00306566.05ˆˆ5===X P p ， {}00051094.06ˆˆ6===X P p， {}000083248.04ˆ1ˆ67==-=∑=k X P p ．计算结果列下表：本题中4=r ，1=m ，05.0=α，所以，()()9915.521295.021==---χχαm r ．所以检验的拒绝域为 {}9915.521>=χW ．由观测值，得9915.546070748.1<，所以不拒绝0H ，可以认为一页的印刷错误的个数服从Poisson 分布．九．（本题满分10分）为考察促进剂与氧化锌对橡胶定伸强力的影响，选用3种不同的促进剂和4种不同分量的氧化锌组合配方，同样的配方重复试验2次，测得300%的定伸强力如下表：试在显著性水平01.0=α检验不同的促进剂，不同分量的氧化锌以及他们的交互作用对橡胶定伸强力是否有显著性影响？解：A H 0：不同的促进剂对橡胶定伸强力无显著性影响；B H 0：不同分量的氧化锌对橡胶定伸强力无显著性影响； B A H ⨯0：促进剂与氧化锌对橡胶定伸强力无显著性影响．令35-=X Y ，得新数据表为表2表33=r ，4=s ，2=t ，所以24243=⨯⨯=⨯⨯=t s r n ．242401492411221112=⨯=⎪⎪⎭⎫ ⎝⎛=∑∑∑===r i s j t k ijk X rst n T ， 9583333.21024240131121112=-=-=∑∑∑===n T X S ri sj tk ijkT ，583333.56242401812531212=-=-=∑=⋅⋅n T T st S r i i A ， 125.132242401613931212=-=-=∑=⋅⋅n T T rt S s j j B ，∑∑∑∑∑==⋅===-=r i s j ij ri sj tk ijkE T t XS 11211121 ()5.1725873112568125481369949103621311=-=+++++++++++⨯-=，75.45.17125.132583333.569583333.210=---=---=⨯E B A T B A S S S S S ．方差分析表拒绝A H 0，认为不同的促进剂对橡胶定伸强力有显著性影响；拒绝B H 0，认为不同分量的氧化锌对橡胶定伸强力有显著性影响；b 11不拒绝B A H ⨯0，可以认为促进剂与氧化锌对橡胶定伸强力无显著性影响．十．（本题满分10分）下表列出了自1952-2004年各届奥运会男子10000米赛跑冠军的成绩（冠军成绩以min 计）⑴ 求Y 关于x 的线性回归方程x b a yˆˆˆ+=； ⑵ 试在显著性水平05.0=α下检验假设：()0:0:10≠=b H b H ．解：⑴ 对数据作变换，① 时间x 原取值改为 ,2,1（即自1952年算作奥运万米第一次记录，其后第二次，第三次等）．② 把万米记录均减去20（分）来算（这样在使用经验回归方程时，得到的时间加上20就是实际所要求的时间）．得经整理的数据及计算如下表：b 12()5.227105*********=⨯-=-=∑∑i i xx x n x l ， ()()65.359.1111051416.8031=⨯⨯-=-=∑∑∑i i i i xy y x n y x l ，()5892857.79.11114199.9011222=⨯-=-=∑∑i i yy y n y l ，设所求的回归函数为bx a +，则有1567.0ˆ-==xxxy l l b ， 168.9ˆ1ˆ=-=∑∑i i x n b y n a．因此经验回归方程为 x y15677.0168.9ˆ-=． ⑵ 需在显著性水平05.0=α下检验假设()0::10≠=b H b H ．5892857.7==yy T l S ，()586237475.55.2271567.0ˆ22=⨯-==xxR l b S ， 003048225.2586237475.55892857.7=-=-=R T E S S S ．方差分析表来源平方和自由度均方和 F 比临界值显著性回归R 5.586237475 1 5.586237475 33.4664()75.412,195.0=F显著残差E 2.003048225 12 0.166920685总和7.589285713所以，拒绝0H ，认为0≠b ，即回归效果显著．信你自己罢！只有你自己是真实的，也只有你能够创造你自己。

概率论与数理统计课后习题答案(非常全很详细)

P(B) P(A)P(B A) P(A)P(B A)
第 5 页共 101 页
5
0.2 0.1
1 0.02702
0.8 0.9 0.2 0.1 37
即考试及格的学生中不努力学习的学生仅占 2.702%
(2) P(A B) P(AB)
P(A)P(B A)
P(B) P(A)P(B A) P(A)P(B A)
可以看出，用第二种方法简便得多. （3）由于是有放回的抽取，每次都有 N 种取法，故所有可能的取法总数为 Nn 种，n
次抽取中有
m
次为正品的组合数为
C
m n
种，对于固定的一种正、次品的抽取次序，
m 次取得正品，都有 M 种取法，共有 Mm 种取法，nm 次取得次品，每次都有 NM 种取法，共有（NM）nm 种取法，故
【解】 P（A∪B∪C）=P(A)+P(B)+P(C)P(AB)P(BC)P(AC)+P(ABC)
111 1 3
=+ + =
4 4 3 12 4
7. 从 52 张扑克牌中任意取出 13 张，问有 5 张黑桃，3 张红心，3 张方块，2 张梅花的概率是多少？
【解】
p=
C153C133C133C123
P( A1
B)
P( A1B) P(B)
P(B
A 1
)
P(
A1
)
2
P(B Ai )P( Ai )
i0
2 / 31/ 3
1
1/ 31/ 3 2 / 31/ 3 11/ 3 3
28. 某工厂生产的产品中 96%是合格品，检查产品时，一个合格品被误认为是次品的概率
为 0.02，一个次品被误认为是合格品的概率为 0.05，求在被检查后认为是合格品产品确

2017《概率论与数理统计（经管类）》（课程代码04183）附答案

《概率论与数理统计(经管类)》(课程代码04183) 第一大题：单项选择题1、事件A与事件B的和事件可以表示为 [B ]∙ A.∙ B.A+B∙ C.∙ D.2、“事件A发生而B不发生”，可以表示为[C]∙ A.∙ B.B-A∙ C.A-B∙ D.3、设事件A={1，2，3，4}，事件B={4，5，6，7}则事件AB为[D]∙ A.{2}∙ B.{3}∙ C.{6}∙ D.{4}4、若事件A与B互不相容，则概率P（A+B）为[D]∙ A.P（A）-P（B）∙ B.P（B）-P（A）∙ C.（AB）-P（BA）∙ D.P（A）+P（B）5、事件A与B相互独立，则概率P（AB）为[C]∙ A.P（A）∙ B.P（B）∙ C.P（A）P（B）∙ D.06、随机变量X服从0-1分布，概率P（X=1）=p，则P（X=0）为[A]∙ A.1-p∙ B.1∙ C.0∙ D.p（1-p）7、设X为离散型随机变量，其分布律为P（）= ，k=1，2，3则有[B] ∙ A.∙ B.∙ C.∙ D.8、设随机变量X在[-1，2]上服从均匀分布，则随机变量X的概率密度f(x)为（A）∙ A.∙ B.∙ C.∙ D.9、F（x）为随机变量X的分布函数，则有[A] ∙ A.∙ B.∙ C.∙ D.10、设C为常数，其期望E（C）为 [B]∙ A.0∙ B.C∙ C.∙ D.不存在11、X为随机变量，则方差D（-2X）为[A]∙ A.4D（X）∙ B.-2D（X）∙ C.2D（X）∙ D.D（X）12、事件A与事件B的积事件可以表示为 [B]∙ A.∙ B.AB∙ C.∙ D.13、“事件A包含在事件B中”，可以表示为[C]∙ A.∙ B.∙ C.∙ D.14、设事件A={2，5，8}，B={3，6，9}则事件AB为 [D]∙ A.{2，5，8，3，6，9}∙ B.{5}∙ C.{6}∙ D.φ15、对任意事件A与B，概率P（A+B）[ A ]∙ A.P（A）+P（B）-P（AB）∙ B.P（A）+P（B）∙ C.P（A）-P（AB）∙ D.P（B）-P（AB）16、抛掷一枚质地均匀的硬币，出现正面的概率为p，则反面的概率为[ A ]∙ A.1-p∙ B.1∙ C.0∙ D.（1-p）p17、设C为常数，则方差D（C）为 [ A ]∙ A.0∙ B.C∙ C.∙ D.E(C)18、事件A与事件B互不相容可以表示为[ B ]∙ A.∙ B.∙ C.∙ D.19、设事件A={0，1，2}，B={3，4，0}则事件AB为[ D ]∙ A.{0，1，2，3，4}∙ B.{1，2，3，4}∙ C.{}∙ D.{0}20、三事件A，B，C互不相容，则概率P（A+B+C）为 [ B ]∙ A.P（A）-P（B）+P（C）∙ B.P（A）+P（B）+P（C）∙ C.P（B）+P（C）-P（A）∙ D.P（C）-P（A）-P（B）21、事件A与B独立，则概率P（）为[B ]∙ A.∙ B.∙ C.P（B）∙ D.022、随机变量X只取两个可能取值0，1，若; 则P（X=0）为; [ A;] ∙ A.∙ B.1∙ C.0∙ D.23、离散型随机变量X的概率分布是P（X=X k）=a，k=1,2,3,,则a的取值为[ C ] ∙ A.a＞0∙ B.a≥ 0∙ C.0≤a≤ 1∙ D.a＜124、X，Y为随机变量，则期望E（X+Y）为 [ C ]∙ A.E（X）∙ B.E（Y）∙ C.E（X）+E（Y）∙ D.X+Y25、设C为常数，X为随机变量，则方差D（C+X）为 [ D ] ∙ A.C+D（X）∙ B.C∙ C. +D（X）∙ D.D（X）26、F（x）为随机变量X的分布函数，下面不成立的是[ A ]∙ A.∙ B.∙ C.∙ D.0≤F（x）≤127、设A，B为两个互不相容事件，则下列各式中错误的是（ C ）∙ A.P（AB）=0∙ B.∙ C.P（AB）=P（A）P（B）∙ D.P（B-A）=P（B）28、设随机变量X~B ，则P{X 1}=（ C ）∙ A.∙ B.∙ C.∙ D.29、C∙ A.∙ B.∙ C.∙ D.30、B∙ A.∙ B.2x∙ C.∙ D.2y31、B∙ A.∙ B.∙ C.N(0,7)∙ D.N(0,25)32、设A与B互为对立事件，且P（A）>0，P（B）>0，则下列各式中错误的是（ A ）∙ A.∙ B.P（B|A）=0∙ C.P（AB）=0∙ D.P（A∪B）=133、一批产品共10件，其中有2件次品，从这批产品中任取3件，则取出的3件中恰有一件次品的概率为( D )∙ A.∙ B.∙ C.∙ D.34、设A，B为两个随机事件，且P（AB）>0，则P（A|AB）=（ D ）∙ A.P（A）∙ B.P（AB）∙ C.P（A|B）∙ D.135、下列各函数中，可作为某随机变量概率密度的是（ A ）∙ A.∙ B.∙ C.∙ D.36、某种电子元件的使用寿命X（单位：小时）的概率密度为任取一只电子元件，则它的使用寿命在150小时以内的概率为（ B ）∙ A.∙ B.∙ C.∙ D.37、D∙ A.-1∙ B.∙ C.∙ D.138、设随机变量X的概率密度为则常数c等于（ B ）∙ A.∙ B.∙ C.1∙ D.539、设二维随机变量（X，Y）的分布律为则P{X=Y}=（ A ）∙ A.0.3∙ B.0.5∙ C.0.7∙ D.0.840、设随机变量X服从参数为2的指数分布，则下列各项中正确的是（ A ）∙ A.E（X）=0.5，D（X）=0.25∙ B.E（X）=2，D（X）=2∙ C.E（X）=0.5，D（X）=0.5∙ D.E（X）=2，D（X）=441、设随机变量X服从参数为3的泊松分布，Y~B（8，），且X，Y相互独立，则D（X-3Y-4）=（C ）∙ A.-13∙ B.15∙ C.19∙ D.2342、设E(X),E(Y),D(X),D(Y)及Cov(X,Y)均存在，则D(X-Y)=（ C ）∙ A.D(X)+D(Y)∙ B.D(X)-D(Y)∙ C.D(X)+D(Y)-2Cov(X,Y)∙ D.D(X)-D(Y)+2Cov(X,Y)43、已知D（X）=1，D（Y）=25，ρXY=0.4，则D（X-Y）=（ B ）∙ A.6∙ B.22∙ C.30∙ D.4644、D∙ A.—0.8∙ B.—0.16∙ C.0.16∙ D.0.845、B∙ A.∙ B.∙ C.∙ D.46、C∙ A.∙ B.∙ C.∙ D.47、A∙ A.∙ B.∙ C.∙ D.48、D∙ A.0.2∙ B.0.4∙ C.0.6∙ D.0.849、D∙ A.∙ B.∙ C.∙ D.50、已知随机变量X服从参数为2的泊松分布，则随机变量X的方差为（ D ）∙ A.-2∙ B.0∙ C.∙ D.251、( C ) ∙ A.0.5∙ B.0.6∙ C.0.66∙ D.0.752、同时抛掷3枚均匀的硬币，则恰好有两枚正面朝上的概率为（ C ）∙ A.0.125∙ B.0.25∙ C.0.375∙ D.0.5053、设A、B相互独立，且P(A)>0，P(B)>0，则下列等式成立的是（ B ）∙ A.P(AB)=0∙ B.∙ C.P(A)+P(B)=1∙ D.P(A|B)=054、设随机变量X的概率密度为则常数=（ D ）∙ A.∙ B.∙ C.3∙ D.455、C∙ A.∙ B.∙ C.∙ D.56、100件产品中有3件次品，从中任取3件，则3件全是次品的概率为（B）∙ A.∙ B.∙ C.∙ D.57、 C∙ A.A发生且B发生∙ B.B不同时发生∙ C.A、B至少有一个发生∙ D.A、B至多有一个发生58、设X、Y独立，且X~N(2,1)，Y~N(3,2)，则3X-2Y~ （C）∙ A.N(1,36)∙ B.N(0,36)∙ C.N(0,17)∙ D.N(1,17)59、已知D(X)=4，E(X2)=20，则E2(X)= （ C）∙ A.4∙ B.5∙ C.16∙ D.1860、 C∙ A.∙ B.∙ C.∙ D.161、若事件A、B互不相等，P(A)=0.5，P(B)=0.2，则P(A+B)= （A）∙ A.0.7∙ B.0.5∙ C.0.3∙ D.0.262、若事件A、B独立，则P(B|A)= （B）∙ A.P(A)∙ B.P(B)∙ C.P(A|B)∙ D.P(AB)63、 B ∙ A.∙ B.∙ C.2∙ D.464、设a、b为常数，则有D(aX+b)= （B）∙ A.a2D(X)+b∙ B.a2D(X)∙ C.aD(X)+b∙ D.aD(X)65、袋中有4个白球2个黑球，从中任取2球，则取得两个黑球的概率是（A）∙ A.∙ B.∙ C.∙ D.66、设X、Y是随机变量，c为常数，则有（ D ）∙ A.D(X+Y)=D(X)+D(Y)∙ B.D(X-Y)=D(X)-D(Y)∙ C.D(X+c)=D(X)+c∙ D.D(X+c)=D(X)67、掷3枚均匀的硬币，出现3个正面的概率是（D）∙ A.∙ B.∙ C.∙ D.68、 B ∙ A.∙ B.∙ C.∙ D.69、掷两粒均匀的骰子，点数之和为12的概率是（A）∙ A.∙ B.∙ C.∙ D.70、设f(x)是连续型随机变量X的密度函数，则它的分布函数F(x)= （C）∙ A.∙ B.∙ C.∙ D.71、掷两粒均匀的骰子，恰好出现一个一点的概率是（D）∙ A.∙ B.∙ C.∙ D.72、设X服从[-1,a]上的均匀分布，且E(X)=7，则a= （A）∙ A.15∙ B.14∙ C.8∙ D.773、设X~N(-1,9)，Y=4X-3，则D(Y)= （B）∙ A.141∙ B.144∙ C.33∙ D.3674、掷两枚均匀的硬币，设X表示出现的正面数，则E(X)= （）∙ A.0.5∙ B.1∙ C.1.5∙ D.275、设X~N(1,4)，Y=2X+1，则Y服从的分布为（）∙ A.N(3,4)∙ B.N(3,8)∙ C.N(3,6)∙ D.N(3,20)76、设事件A、B互不相等，P(A)=0.2，P(B)=0.3，则P(B|A)= （）∙ A.0∙ B.0.2∙ C.0.3∙ D.177、事件A、B独立，则有（）∙ A.P(A+B)=P(A)+P(B)∙ B.P(AB)=P(A)•P(B)∙ C.P(A-B)=P(A)-P(B)∙ D.P(B-A)=P(B)-P(A)78、∙ A.∙ B.∙ C.∙ D.79、若P(AB)=0，则称事件A、B （）∙ A.相互独立∙ B.互不相等∙ C.相互对立∙ D.为样本空间的一个划分80、将4封信随机投入3个邮筒，则基本事件总数有（）∙ A.12个∙ B.24个∙ C.81个∙ D.64个81、∙ A.∙ B.∙ C.∙ D.82、设X~B(n,0.6)，且D(X)=2.4，则n= （）∙ A.6∙ B.8∙ C.10∙ D.1283、两个人生日相同的概率是（）∙ A.∙ B.∙ C.∙ D.84、∙ A.∙ B.∙ C.∙ D.85、则a= （）∙ A.0.1∙ B.0.3∙ C.0.4∙ D.0.786、则E(X2)= （）∙ A.1.1∙ B.1.7∙ C.3.1∙ D.2.587、设X服从p=0.6的0-1分布，则E(X)= （）∙ A.0.24∙ B.0.3∙ C.0.4∙ D.0.688、设C服从[0,4]上的均匀分布，则P(X>3)= （）∙ A.∙ B.∙ C.∙ D.89、且E(X)=3，则a= （）∙ A.4∙ B.6∙ C.7∙ D.890、已知D(X)=4，D(Y)=25，COV(X,Y)=4，则 = （）∙ A.0.4∙ B.0.04∙ C.0.8∙ D.0.08第二大题：填空题1、设事件A与B互不相容，P（A）=0.2，P（B）=0.3，则P（）=____0.5_____.2、一个盒子中有6颗黑棋子、9颗白棋子，从中任取两颗，则这两颗棋子是不同色的概率为__18/35__.3、甲、乙两门高射炮彼此独立地向一架飞机各发一炮，甲、乙击中飞机的概率分别为0.4，0.5，则飞机至少被击中一炮的概率为_ 0.7_.4、设随机变量X~N（1，4），已知标准正态分布函数值Φ（1）=0.8413，为使P{X<a}<0.8413，则常数a< ___3___.5、抛一枚均匀硬币5次，记正面向上的次数为X，则P{X≥1}=____31/32___6、随机变量X的所有可能取值为0和x，且P{X=0}=0.3，E（X）=1，则x=10/7_.7、设随机变量X的分布律为则D（X）=18、设随机变量X服从参数为3的指数分布，则D（2X+1）=_4/9_9、设二维随机变量（X，Y）的概率密度为f (x, y)= 则P{X≤ }=_1/2_10、11、312、设事件A，B相互独立，且P（A）=0.2，P（B）=0.4，则P（A∪B）=__0.5。

(完整word版)清华大学杨虎应用数理统计课后习题参考答案3

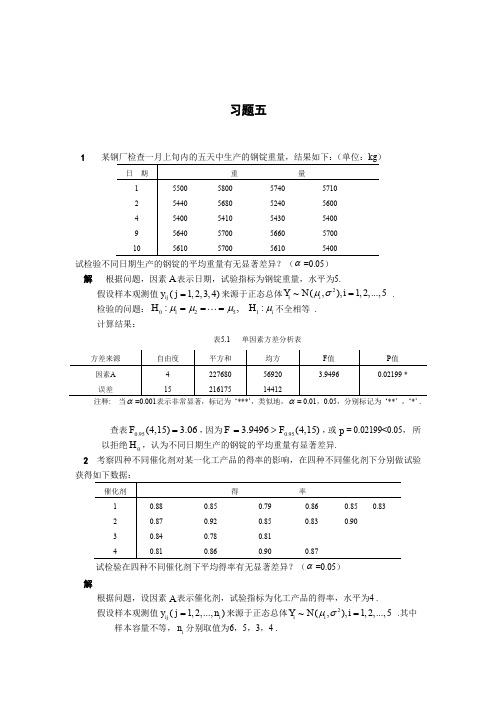
习题五1试检验不同日期生产的钢锭的平均重量有无显著差异？（α=0.05）解根据问题，因素A 表示日期，试验指标为钢锭重量，水平为5.假设样本观测值(1,2,3,4)ij y j =来源于正态总体2~(,),1,2,...,5i i Y N i μσ= .检验的问题：01251:,:i H H μμμμ===不全相等 .计算结果：表5.1 单因素方差分析表注释: 当=0.001表示非常显著，标记为 ‘***’，类似地，= 0.01，0.05，分别标记为 ‘**’ ，‘*’ .查表0.95(4,15) 3.06F =，因为0.953.9496(4,15)F F =>，或p = 0.02199<0.05，所以拒绝0H ，认为不同日期生产的钢锭的平均重量有显著差异.2 考察四种不同催化剂对某一化工产品的得率的影响，在四种不同催化剂下分别做试验试检验在四种不同催化剂下平均得率有无显著差异？（α=0.05）解根据问题，设因素A 表示催化剂，试验指标为化工产品的得率，水平为4 .假设样本观测值(1,2,...,)ij i y j n =来源于正态总体2~(,),1,2,...,5i i Y N i μσ= .其中样本容量不等，i n 分别取值为6，5，3，4 .检验的问题：012341:,:i H H μμμμμ===不全相等 .计算结果：表5.2 单因素方差分析表查表0.95(3,14) 3.34F =，因为0.952.4264(3,14)F F =<，或p = 0.1089 > 0.05，所以接受0H ，认为在四种不同催化剂下平均得率无显著差异 .3 试验某种钢的冲击值（kg ×m/cm2），影响该指标的因素有两个，一是含铜量A ，另试检验含铜量和试验温度是否会对钢的冲击值产生显著差异？（α=0.05）解根据问题，这是一个双因素无重复试验的问题，不考虑交互作用.设因素,A B 分别表示为含铜量和温度，试验指标为钢的冲击力，水平为12.假设样本观测值(1,2,3,1,2,3,4)ij y ij ==来源于正态总体2~(,),1,2,3,ij ij Y N i μσ=1,2,3,4j = .记i α⋅为对应于i A 的主效应；记j β⋅为对应于j B 的主效应；检验的问题：（1）10:i H α⋅全部等于零，11:i H α⋅不全等于零；（2）20:j H β⋅全部等于零，21:j H β⋅不全等于零；计算结果：表5.3 双因素无重复试验的方差分析表查表0.95(2,6) 5.143F =，0.95(3,6) 4.757F =，显然计算值,A B F F 分别大于查表值，或p = 0.0005，0.0009 均显著小于0.05，所以拒绝1020,H H ，认为含铜量和试验温度都会对钢的冲击值产生显著影响作用.设每个工人在每台机器上的日产量都服从正态分布且方差相同 .试检验：（α=0.05）1）操作工之间的差异是否显著？ 2）机器之间的差异是否显著？3）它们的交互作用是否显著？解根据问题，这是一个双因素等重复(3次)试验的问题，要考虑交互作用.设因素,A B 分别表示为机器和操作，试验指标为日产量，水平为12. 假设样本观测值(1,2,3,1,2,3,4)ijk y i j ==来源于正态总体2~(,),1,2,3,ij ij Y N i μσ= 1,2,3,4j =，1,2,3k = .记i α⋅为对应于i A 的主效应；记j β⋅为对应于j B 的主效应；记ij γ为对应于交互作用A B ⨯的主效应；检验的问题：（1）10:i H α⋅全部等于零，11:i H α⋅不全等于零；（2）20:j H β⋅全部等于零，21:j H β⋅不全等于零；（3）30:ij H γ全部等于零，31:ij H γ不全等于零；计算结果：表5.4 双因素无重复试验的方差分析表查表0.95(3,24) 3.01F =，0.95(2,24) 3.4F =，0.95(6,24) 2.51F =，计算值 3.01,A F <3.4, 2.51B A B F F ⨯>>，或0.05A p >>，而,B A B p p ⨯均显著小于0.05，所以拒绝2030,H H ，接受10H ，认为操作工之间的差异显著，机器之间的差异不显著，它们之间的交互作用显著 . 5 某轴承厂为了提高轴承圈退火的质量，制定因素水平分级如下表所示因素上升温度℃ 保温时间(h)出炉温度℃水平1 800 6 400 水平28208500试填好正交试验结果分析表并对试验结果进行直观分析和方差分析 .解根据题意，这是一个3因素2水平的试验问题 .试验指标为硬度的合格率 .应选择正交表44(2)L 来安排试验，随机生成正交试验表如下：方差来源自由度平方和均方 F 值 P 值因素A 因素B 相互效应A ×B误差总和3 2 6 24 352.750 27.167 73.5 41.333 144.750.917 13.583 12.250 1.7220.5323 7.8871 7.11290.6645 0.00233** 0.00192**由此可见第三号试验条件为：上升温度800℃、保温时间6h 、出炉温度500℃ . 直观分析需要计算K 值，计算结果如下：表5.6 计算表直观分析由计算的K 值知，因素A 、B 、C 的极差分别为70，40，40，因此主次关系为A B C >=，B ，C 相当 .由于试验指标为硬度的合格率，应该是越大越好，所以各确定因素的水平分别是121,,A B C ，即最佳的水平组合是121A B C ，即最佳搭配为：上升温度800℃、保温时间8h 、出炉温度400℃.采用方差分析法，计算得下表：表5.7 方差分析表方差来源平方和自由度均方差 F 值 A 1225 1 1225 1 B 400 1 400 0.33 C 400 1 400 0.33 误差 1225 1 1225 总和32504如果显著性检验水平取0.1α=，则查表得0.9(1,1)39.9F =，显然计算的F 值1,0.33A B C F F F ===均小于查表值，所以认为三个因素对结果影响都显著 .6问应选用哪张正交表安排试验，并写出第8号试验的条件；如果9组试验结果为（单位：kg/100m 2）：62.925，57.075，51.6，55.05，58.05，56.55，63.225，50.7，54.45，试对该正交试验结果进行直观分析和方差分析.解该问题属于3因素3水平的试验问题，试验指标为水稻产量 .根据题意应选择正交表49(3)L 来安排试验，随机生成正交表如下：由表可知，第8号试验的条件：品种（A 3）珍珠矮11号，插值密度（B 2）3.75棵/100m 2 ，施肥量（C 1）0.75kg/100m 2纯氨；直观分析需要计算K 值，计算结果如下：表5.9 计算表同上题进行直观分析，得出K 值的大小关系为：111312212223333132,,K K K K K K K K K >>>>>>由直观分析看出：本例较好的水平搭配是：113A B C 采用方差分析法，计算得下表：表5.10 方差分析表方差来源平方和自由度均方差F 值A 1.759 2 0.879 0.0223B 65.861 2 32.931 0.8361C 6.660 2 3.330 0.0845 误差78.776 239.388 39.3880.9(2,2)9F =，所以认为三个因素对结果影响都不显著.7 在阿魏酸的合成工艺考察中，为了提高产量，选取了原料配比A ，吡啶量B 和反应时间C 三个因素，它们各取了7个水平如下：原料配比A ：1.0，1.4，1.8，2.2，2.6，3.0，3.4 吡啶量B ：10，13，16，19，22，25，28 反应时间C ：0.5，1.0，1.5，2.0，2.5，3.0，3.5试选用合适的均匀设计表安排试验，并写出第7号试验的条件；如果7组试验的结果（收率）为：0.33，0.336，0.294，0.476，0.209，0.451，0.482，试对该均匀试验结果进行直观分析并通过回归分析发现可能更好的工艺条件.解根据题意选择均匀设计表47(7)U 来安排试验，有3个因素，根据使用表，实验安排如：表5.11 试验安排表所以第7号实验的条件为：原配料比3.4，吡啶量28ml，反应时间3.5h.通过直观分析，最好的实验条件是：原配料比3.4，吡啶量28ml，反应时间3.5h.通过回归分析，最合适的实验条件是：原配料比2.6，吡啶量16ml，反应时间0.5h.习题六1 从某中学高二女生中随机选取8名，测得其升高、体重如下：在绝对距离下，试用最短距离法和离差平方和法对其进行聚类分析.解由R软件，用最短距离（左）和差离平方和法（右）对题目进行聚类分析如下图6.1，表6.1和表6.2：最短距离法离差平方和法图6.1 聚类树形图表6.1 聚类附表(最短距离法)表6.2 聚类附表(离差平方和法)2 已知五个变量的距离矩阵为03674012340444401592343331).;2);3)036034022020401000⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭试用最短距离法和最长距离法对这些变量进行聚类，并画出聚类图和二分树.解针对距离矩阵1），采用两种方法计算如下. ①最短距离法的聚类步骤如下：12345036740159036020w w w w w ⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭a ）将()236,1w w f h =合并为一类，，{}11456,,,,H w w w h =距离矩阵如下0743023060⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭{}()457457),,,2b w w h w w f h ==合并为一类，{}2167,,,H w h h =距离矩阵如下：034030⎛⎫ ⎪⎪ ⎪⎝⎭{}()()1681689),,3,3c w h h w h f h f h ===合并为一类，最后，，聚类图和树状图如图6.2：图6.2 聚类图（左）与树状图（右）②最长距离法与最短距离法类似，步骤如下： a ）()236,1w w f h =合并为一类，{}11456,,,,H w w w h =距离矩阵如下0746025090⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭ {}(){}4574572167),,,2,,,b w w h w w f h H w h h ===合并为一类，距离矩阵如下：067090⎛⎫⎪⎪ ⎪⎝⎭{}()()1681689),,69c w h h w h f h f h ===合并为一类，最后，，，聚类图和树状图如图6.3：图6.3 聚类图（左）与树状图（右）（2）针对距离矩阵2）012340234034040⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭①最短距离法的聚类步骤如下 a ）()216,1w w f h =合并为一类，{}13456,,,,0342043040H w w w h =⎛⎫⎪⎪ ⎪ ⎪⎝⎭距离矩阵如下{}()367367),,,2b w h h w h f h ==合并为一类，{}24567,,,,H w w h h =聚类矩阵如下：043040⎛⎫⎪⎪ ⎪⎝⎭{}(){}()4784789879),,3,,4c w h h w h f h h w h f h ====合并为一类，最后，，聚类图和树状图如图6.4：图6.4 聚类图（左）与树状图（右）②由于本题数据的特殊性，最长距离法与最短距离法结果相同（略）. (3)044440333022010⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪⎝⎭最短距离法的聚类步骤如下a ) ()456,1w w f h =合并为一类，{}11236,,,,H w w w h =距离矩阵如下0444033020⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭{}(){}36736724567),,,2,,,,b w h h w h f h H w w h h ===合并为一类，距离矩阵如下：044030⎛⎫⎪⎪ ⎪⎝⎭{}(){}()4784789879),,3,,4c w h h w h f h h w h f h ====合并为一类，最后，，，聚类图和树状图如图6.5：图6.5 聚类图（左）与树状图（右）由于本题数据的特殊性，最长距离法与最短距离法结果相同(略).3 在一项关于作物对土壤营养的反应的研究中，要测定土壤的总磷量和总氮量（占干物质重的百分比），今对10份土样测得数据如下：在绝对距离下，试用重心法对其进行聚类分析.解由R软件得到重心法聚类分析的结果如图6.6与表6.3：图6.6 聚类树形图表6.3 聚类过程记录表4 1975年Dagnelie收集了11年的气象数据资料如下表其中：x 1—前一年11月12日的降水量；x 2—7月均温；x 3—7月降雨量；x 4—月日辐射，试对这四个气象因子进行主成分分析. 解由R 软件分析得到如下表6.4，6.5：表6.4 各主成分的重要性:主成分1 主成分2 主成分3 主成分4 标准差 1.6103349 0.9890848 0.53407741 0.37854199 方差贡献率 0.6482947 0.2445722 0.07130967 0.03582351 累积贡献率0.64829470.89286680.964176491.00000000表6.5 因子荷载:主成分1 主成分2 主成分3 主成分4 X1 0.291 0.871 0.332 -0.214 X2 -0.506 0.425 -0.742 -0.111 X3 0.577 0.136 -0.418 0.688 X4-0.5710.2050.4040.685由于前两个主成分对应的累积贡献率已经达到89.287，因此选取主成分的数目为2.5 对某初中12岁的女生进行体检，测量其身高x 1、体重x 2、胸围x 3和坐高x 4，共测得58个样本，并算得1234(,,,)x x x x x ='的样本协方差为19.9410.5023.566.5919.7120.958.637.97 3.937.55S ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭ 试进行样本主成分分析.解首先计算样本的相关系数矩阵：10.484410.32240.887210.70330.59760.31251⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭设相关系数矩阵的特征值和特征向量分别为d 和v 阵，计算得到0.0546000 0 0.312600= 000.96470 000 2.6681d ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭即四个特征值依次为：2.6681，0.9647，0.3126，0.0546，前两个主成分的累计贡献率为：90.8471%，因此提取主成分为2.四个特征根相应的特征向量为0.06000.70600.5333 0.4620 0.7317 0.17430.34040.5642=0.60570.19320.60400.48060.30690.65870.48460.4870v -⎛⎫ ⎪-⎪ ⎪--- ⎪-⎝⎭ 因此，两个主成分的表达式为：112340.060.73170.60570.3069z x x x x =+-- 212340.7060.17430.19320.6587z x x x x =-+-+6 比较因子分析和主成分分析模型的异同，阐明两者的关系. 解（1）提取公因子的方法主要有主成分法和公因子法.若采取主成分法，则主成分分析和因子分析基本等价，该法从解释变量的变异的角度出发，尽量使变量的方差能被主成分解释；而公因子法主要从解释变量的相关性角度，尽量使变量的相关程度能被公因子解释，当因子分析目的重在确定结构时则用到该法.（2）主成分分析和因子分析都是在多个原始变量中通过他们之间的内部相关性来获得新的变量，达到既减少分析指标个数，又能概括原始指标主要信息的目的.但他们各有其特点：主成分分析是将n 个原始变量提取m 个支配原始变量的公因子，和1个特殊因子，各因子之间可以相关或不相关.（3）统用降维的方法，但差异也很明显：主成分分析把方差划分为不同的正交成分，而因子分析则把方差化分为不同的起因因子；因子分析中的特征值的计算只能从相关系数矩阵出发，且必须把主成分划分为因子.（4）因子分析提取的公因子比主成分分析提取的主成分更具有可解释性.（5）两者分析的实质及重点不同.主成分的数学模型为Y AX =，因子分析的数学模型为X AF ε=+.因而可知主成分分析是实际上是线性变换，无假设检验，而因子分析是统计模型，某些因子模型是可以得到假设检验的；主成分分析主要综合原始数据的信息，而因子分析重在解释原始变量之间的关系.（6）SPSS 数据的实现：两者都通过“analyze data reduction Factor···”过程实现，但主成分分析主要使用“descriptires ”,“extraction ”,“stores ”对话框，而因子分析处使用这些外，还可使用“rotaction ”对话框进行因子旋转.7 试对第4题的变量作因子分析，并将结果和上面的结果进行比较. 解用SPSS 分析，计算结果如下表6.6-6.8：表6.6 反应压缩比情况表提取方法: 主成分法计算的相关系数矩阵的特征值和方差贡献率：表6.7 方差解释度提取方法: 主成分法表6.8 主成分矩阵8 为研究某一树种的叶片形态，选取50片叶测量其长度x 1（mm ）和宽度x 2（mm ），按样本数据求得其平均值和协方差矩阵为：129048134,92,4845x x S ⎛⎫=== ⎪⎝⎭求出相关系数阵R ，并由R 出发作因子分析；解1）求相关系数矩阵：904810.7303,48900.73031S R ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭ 2）用R 软件求R 的特征根及其相应的特征向量，软件输出结果如下：$values[1] 2.99393809 0.07273809 $vectors[,1] [,2] [1,] 0.7071068 -0.7071068 [2,] 0.7071068 0.7071068122.9939,0.0727,λλ∴==12(),()0.7071,0.7071-0.7071,0.7071T Tηη==3) 求载荷矩阵A ：1.22350.19071.22350.1907A -⎛⎫= ⎪⎝⎭4）22121.5333, 1.5333,h h == 0.98810.154*0.98810.154A -⎛⎫= ⎪⎝⎭12121,1,0.3043,0.3043u u v v ===-=，222222000011112,0,()0.9074,20i i iii i i i i i A u B v C u v D u v =========-===∑∑∑∑9 1981年，生物学家Grogan 和Wirth 对两种蠓虫Af 和Apf 根据其触角长度x 1和翼长x 2进行了分类，分类的数据资料如下：Af 1 2 3 4 5 6 7 8 x 1 1.24 1.36 1.38 1.38 1.38 1.40 1.48 1.54 x 2 1.27 1.74 1.64 1.82 1.90 1.70 1.82 1.82 Apf 1 2 3 4 5 6 x 1 1.14 1.18 1.20 1.26 1.28 1.30 x 2 1.78 1.96 1.86 2.00 2.00 1.96 （1）试建立Af 和Apf 的Fisher 判别模型；（2）对样本（1.24，1.80），（1.28，1.84），（1.40，2.04）进行判别分类. 解（1）建立Fisher 判别模型991122121111(,)(1.42,1.75),(,)(1.23,1.93)99T TT T i i i i i i x x y y μμ======∑∑120.08480.1490.01980.0218,0.1490.39120.02180.039A A ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭12120.0080.0130.0130.0332A A n n ⎛⎫+== ⎪+-⎝⎭∑()120.19,0.18Tμμ-=-，()()121 1.325,1.842T μμ+= 1345.05135.42135.4283.33--⎛⎫= ⎪-⎝⎭∑，带入Fisher 判别函数 ()12345.05135.42[(,)(1.325,1.84)]0.19,0.18135.4283.33Tx x -⎛⎫-- ⎪-⎝⎭1291.301741.336944.534x x =--（2）把三个样本（1.24，1.80），（1.28，1.84）,(1.4,2.04)带入模型，得到结果：三个样本均属于Apf 类.10 在两个玉米品种之间进行判别：137玉米G 1和甜玉米G 2，选取的两个变量是：x 1—玉米果穗长；x 2—玉米果穗直径，两个类的样本容量为n 1＝n 2＝40，实际算得两个类的样本均值和样本协方差为：121218.5625.348.120 4.4589.661 3.720,,,5.98 4.12 4.458 4.350 3.720 3.410x x S S ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭试建立G 1，G 2的Bayes 类线性判别函数.解因为已知两类的样本均值和样本协方差为：12(18.56,5.98),(25.34,4.12)T T x x ==，128.120 4.4589.661 3.720,4.458 4.350 3.720 3.410S S ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭可计算得到修正的公共协方差矩阵和逆矩阵12120.2280.1450.1450.0992A A n n ⎛⎫+== ⎪+-⎝⎭∑，15.6393.738.25147.38--⎛⎫= ⎪-⎝⎭∑()()()121216.78,1.86,21.95,5.052TTμμμμ-=-+= 带入Fisher 判别函数()112121(())()2T W x x μμμμ-=-+-∑ ()()12 5.6393.73[(,)21.95,5.05] 6.78,1.868.25147.38Tx x -⎛⎫=-- ⎪-⎝⎭1274.396.951141.29x x =-+-。

02197--概率论与数理统计（二）

02197--概率论与数理统计（二）[单项选择题]1.设分别为随机变量的分布函数，为使是某一随机变量的分布函数，在下列给定的各组值中应取（A、）。

2.设是随机变量，其分布函数分别为，为使是某一随机变量的分布函数，在下列给定的各组数值中应取（C、）3.设随机变量的概率分布为且满足，则的相关系数为（A、0）4.设A、B、C为三个事件，P（AB）＞0且P（C|AB）=1，则有（C、P（C）≥P （A）+P（B）-1）5.设x?,x?,··· ···,x?为正态总体N（μ，4）的一个样本，表示样本均值，则μ的置信度为1-α的置信区间为（D、）6.设总体X服从正态分布N（μ，σ2），X?，X?，··· ···，X n是来自X 的样本，则σ2的最大似然估计为( A、 )7.设是未知参数的一个估计量，若，则是的( D.有偏估计 )8.在对单个正态总体均值的假设检验中，当总体方差已知时，选用( B、u检验法)9.若X～t(n)那么χ2～（A、F(1,n)）10.对于事件A，B，下列命题正确的是（D、）11.设X~N(μ,σ2),那么当σ增大时，P{|X-μ|＜σ}=（C、不变）12.已知随机变量X的密度函数f(x)=(λ>0,A为常数)，则概率P{λ＜X＜λ+a}（a>0）的值（C、与λ无关，随a的增大而增大）13.设随机事件A与B互不相容，且P(A)＞0,P(B)＞0，则 (D、)。

14.设 X1, X2为来自总体N(μ, 1) 的一个简单随机样本, 则下列估计量中μ的无偏估计量中最有效的是 ( A、设随机变量X的概率密度为f(x),则f(x)一定满足【C、】16.设随机变量X与Y的方差分别是25和16，协方差为8，则相关系数ρXY=【C、】17.已知随机变量与相互独立，且它们在区间[-1,3]和[2,4]上服从均匀分布，则【A、3】18.若X,Y相互独立,则下列正确的是【C、】设X~N(0,1), Y~N(μ,σ2), 则Y与X之间的关系是【A、】设A, B为随机事件, A错误!未找到引用源.B,（B、）A，B，C是任意事件，在下列各式中，不成立的是（B、（A∪B）－A=B）设随机变量且相互独立，根据切比雪夫不等式有（D、≥5/12）设A,B,C为三个事件，且A,B相互独立，则以下结论中不正确的是（D、）设离散型随机变量X和Y的联合概率分布为,若X,Y独立，则α,β的值为（A、）设总体X的数学期望为μ,X?，X?，··· ···，X n为来自X的样本，则下列结论中正确的是（A、X?是μ的无偏估计量）已知是来自总体的样本，则下列是统计量的是（B、）设X，Y是相互独立的两个随机变量，它们的分布函数分别为F x(x),F y(y),则Z = max {X,Y} 的分布函数是（C、）对于任意两个随机变量X和Y，若E(XY)=E(X)-E(Y)，则(B、D(X+Y)=D(X)+D(Y) ) 设A，B为任二事件，则（D、）设Φ（x）是标准正态分布函数，则Φ（0）= 【B、】设随机变量X与Y相互独立，且P{X≤1}=1/4,P{Y≤1}=1/3,则P{X≤1,Y≤1}=【C、】设随机事件A与B互不相容，且, ,则【D、】设A和B相互独立，，，则【B、】袋中有5个白球和3个黑球，从中任取两个，则取到的两个球是白球的概率是【A、】下列关于“统计量”的描述中，不正确的是【C、统计量表达式中不含有参数】设A,B为随机事件,则下列说法正确的是【B、】设随机变量X的取值范围是[-1,1]，以下函数可以作为X的概率密度的是【C、】已知随机变量X的分布函数为C、7/12设随机变量X服从参数为的指数分布，则下列各项中正确的是(D、)设二维随机变量(X, Y)的概率密度为,则常数c=(A、)将一枚硬币重复郑n次，以X和Y分别表示正面向上和反面向上的次数，则X 与Y的相关系数等于（A、-1）是来自总体X~N（0,1）的一部分样本，设：，则Z/Y~（D、F（8,8））X?,X?独立,且分布率为(i=1,2),那么下列结论正确的是（C、P{X?=X?}=1/2）下列二无函数中，( B、) 可以作为连续型随机变量的联合概率密度。

清华大学杨虎应用数理统计课后习题参考答案2

习题三1 正常情况下，某炼铁炉的铁水含碳量2(4.55,0.108)X N .现在测试了5炉铁水，其含碳量分别为4.28，4.40，4.42，4.35，4.37. 如果方差没有改变，问总体的均值有无显著变化？如果总体均值没有改变，问总体方差是否有显著变化（0.05α=）？解由题意知 2~(4.55,0.108),5,0.05X N n α==，1/20.975 1.96u u α-==，设立统计原假设 0010:,:H H μμμμ=≠ 拒绝域为{}00K x c μ=->，临界值1/21.960.108/0.0947c u α-==⋅=，由于 0 4.364 4.550.186x c μ-=-=>，所以拒绝0H ，总体的均值有显著性变化.设立统计原假设 22220010:,:H H σσσσ=≠ 由于0μμ=，所以当0.05α=时22220.0250.97511()0.03694,(5)0.83,(5)12.83,n i i S X n μχχ==-===∑2210.02520.975(5)/50.166,(5)/5 2.567c c χχ====拒绝域为 {}222200201//K s c s c σσ=><或由于220/ 3.167 2.567S σ=>，所以拒绝0H ，总体的方差有显著性变化. 2 一种电子元件，要求其寿命不得低于1000h .现抽测25件，得其均值为x =950h .已知该种元件寿命2(100,)X N σ，问这批元件是否合格（0.05α=）？解由题意知 2(100,)X N σ，设立统计原假设0010:,:,100.0.05.H H μμμμσα≥<==拒绝域为{}00K x c μ=-> 临界值为 0.050.0532.9c u u =⋅=⋅=-由于 050x c μ-=-<，所以拒绝0H ，元件不合格.3 某食品厂用自动装罐机装罐头食品，每罐标准重量为500g ，现从某天生产的罐头中随机抽测9罐，其重量分别为510，505，498，503，492，502，497，506，495（g ），假定罐头重量服从正态分布. 问 (1)机器工作是否正常（0.05α=）？ 2）能否认为这批罐头重量的方差为5.52（0.05α=）？解（1）设X 表示罐头的重量(单位：g). 由题意知2(,)XN μσ,μ已知设立统计原假设 0010:500,:H H μμμμ==≠,拒绝域 {}00K x c μ=-> 当0.05α=时，2500.89,34.5, 5.8737x s s ===临界值 12(1) 4.5149c t n α-=-⋅=，由于00.8889x c μ-=<，所以接受0H ，机器工作正常.（2）设X 表示罐头的重量(单位：g). 由题意知2(,)XN μσ，σ已知设立统计原假设 222220010: 5.5,:H H σσσσ==≠拒绝域为 {}{}222200102K s c sc σσ=<> 当α=0.05时，可得2220.0250.97512500.89,34.5,(5) 2.7,(5)19.02,0.3, 2.11x s c c χχ======由于22001.0138s K σ=∈,所以接受0H ，可以认为方差为25.5.4 某部门对当前市场的鸡蛋价格情况进行调查，抽查某市20个集市上鸡蛋的平均售价为3.399（元/500克），标准差为0.269（元/500克）.已知往年的平均售价一直稳定在 3.25（元/500克）左右，问该市当前的鸡蛋售价是否明显高于往年？（0.05α=）解设X 表示市场鸡蛋的价格（单位：元/克），由题意知2(,)XN μσ设立统计原假设 0010: 3.25,:H H μμμμ==>, 拒绝域为 {}00K x c μ=->当α=0.05时，13.399,0.269,20,0.0992x n c ασμ-====⋅=临界值由于0 3.399 3.250.149.x c μ-=-=>所以拒绝0H ，当前的鸡蛋售价明显高于往年.5 已知某厂生产的维尼纶纤度2(,0.048)X N μ，某日抽测8根纤维，其纤度分别为1.32，1.41，1.55，1.36，1.40，1.50，1.44，1.39，问这天生产的维尼纶纤度的方差2σ是否明显变大了（0.05α=）？解由题意知 2(,0.048)XN μ，0.05α=设立统计原假设 2222220010:0.048,:0.048H H σσσσ==>=拒绝域为{}2200K s c σ=>，当0.05α=时，2220.950.951.4213,0.0055,(7)14.07,(7)7 2.0096x s c χχ=====由于220 2.3988s c σ=>，所以拒绝0H ，认为强度的方差明显变大.6 某种电子元件,要求平均寿命不得低于2000h ，标准差不得超过130h .现从一批该种元件中抽取25只,测得寿命均值1950h ,标准差148h s =.设元件寿命服从正态分布，试在显著水平 α=0.05下, 确定这批元件是否合格. 解设X 表示电子元件的平均寿命（单位：h ），由题意知2(,)X N μσ设立统计原假设 0010:=2000H <H μμμμ≥，：拒绝域为 {}00K x c μ=-<当0.05α=时，1950,148,(1)50.64x s c t n α===-=-临界值由于 050x c μ-=->，所以接受0H ，即这批电子元件的寿命是合格的. 7 设n X X X ,...,,21为来自总体(,4)XN μ的样本，已知对统计假01:1;: 2.5H H μμ== 的拒绝域为0K {}2>=X .1）当9=n 时，求犯两类错的概率α与β；2）证明：当n →∞时，α→0，β→0.解（1）由题意知 {}010~(,4),:1;: 2.5,2,9.X N H H K X n μμμ===>= 犯第一类错误的概率为()21 1.51(1.5)0.0668.X P X P αμ⎫=>==>==-Φ=⎪⎭犯第二类错误的概率为()2 2.50.75(0.75)1(0.75)0.2266.X P X P βμ⎫=≤==≤=-⎪⎭=Φ-=-Φ=（2）若0:1H μ=成立，则(1,4)X N}{}{00000()=11)n P H H P X c P X c nc αμμσ=≥+=-<+=-Φ否定成立当n →∞时，0)1ncσΦ→，所以0()n n α→→∞同理 }{0010=<+=+c )/)()=0()n P X c n βμμμσΦ-→Φ-∞→∞ 8 设需要对某一正态总体,4()N μ的均值进行假设检验H 0：μ= 15，H 1：μ< 15 取检验水平α=0.05，试写出检验H 0的统计量和拒绝域.若要求当H 1中的μ=13时犯第二类错误的概率不超过β=0.05，估计所需的样本容量n . 解由题意知 (,4)XN μ,σ已知, 设立统计原假设 01:15,:15H H μμ=<则拒绝域为}{015K X c =-<，其中临界值0.05c μ=⋅=-犯第二类错误的概率1513130.05P X P Xβ⎛⎫⎛⎫=->==->≤⎪⎭⎝⎝即1.65)0.95Φ≥, 化简得23.311n≥≈.9 设nXXX,...,,21为来自总体X～2(,)Nμσ的样本，2σ为已知, 对假设：0011:;:H Hμμμμ==其中01μμ≠，试证明：22011212()()nαβσμμμμ--=+⋅-解（1）10>μμ当时,由题意知00110:;:;H Hμμμμμ==>犯第一，二类错误分别为,αβ，则有001(|)P X c c uααμμμ-=>+=⇒=011100(|))XP X c P uαβμμμμμ-=≤+==≤=⇒()()220 11111120010 u u u u n u u ββααβαβσμμμ------=-=⇒+==+-（2）10μμ≤当时由题意知00110:,:H Hμμμμμ==≤，犯第一，二类错误分别为,αβ，则有00(|)P X c c uααμμμ=<+=⇒=()()01100220 1111120010 (|))XP X c P uu u u u n u uαβααβαββμμμμμσμμ-----=≥+==≥+=⇒=⇒+==+-10设171,...,XX为总体2(0,)X N σ样本，对假设：2201:9,: 2.905H Hσσ==的拒绝域为}{24.93K s=<. 求犯第Ⅰ类错误的概率α和犯第Ⅱ类错的概率β.解由题意知2(0,)X N σ,222~().nsnχσ统计假设为2201:9,: 2.905H Hσσ==. 拒绝域为}{24.93K s=<则犯第一，二类错误的概率,αβ分别是()()22222221717417174497.3040.0259999171744 3.319120.48810.750.253.319 3.319s s P s P P s P s P ασβσ⎛⎫⎛⎫⨯⨯=<==<=<== ⎪ ⎪⎝⎭⎝⎭⎛⎫⨯=<==-<==-= ⎪⎝⎭11 设总体是密度函数是1,01(;)0,x x f x θθθ-<<=⎧⎨⎩其他统计假设 01:1,:2H H θθ==.现从总体中抽取样本21,X X ,拒绝域2134ΚX X =≤⎧⎫⎨⎬⎩⎭，求：两类错误的概率,αβ 解由题意知010213:1;:2,, 2.4H H K X n X θθ⎧⎫===≤=⎨⎬⎩⎭当12121,0,11(;1) 1.~(0,1),(,)0,x x f x X U f x x θ<<⎧===⎨⎩时，其他此时 212121231431(,)0.250.75ln 0.75.4x x P X f x x dx dx X αθ≤⎛⎫=≤===+⎪⎝⎭⎰⎰当1212122,014,0,12(;2).(,)0,0,x x x x x x f x f x x θ<<<<⎧⎧===⎨⎨⎩⎩时，其他其他此时 21212123143992(,)ln 0.75.4168x x P X f x x dx dx X βθ>⎛⎫=>===+⎪⎝⎭⎰⎰12 设总体2(,)X N μσ，根据假设检验的基本原理，对统计假设：00110:,:()()H H μμμμμσ==>已知；0010:,:H H μμμμσ≥<（未知），试分析其拒绝域. 解由题意知 2(,)XN μσ,当00110:,:()H H μμμμμ==>成立时()01X P X c P αμμμ=->==>=-Φ{}1100,u c u K X c ααμ--===->所以拒绝域为 }{00K X c μ=->当0010:,:H H μμμμ≥<成立时00()()X P X c P X c P αμμμμ⎛⎛⎫⎫=-<≥≥-<=<=Φ}{00,c K X c ααμμμ===-<所以拒绝域为}{00K X c μ=-< 13 设总体2(,)X N μσ根据假设检验的基本原理，对统计假设：（1）22220010:,:()H H σσσσμ=>已知；（2）22220010:,:()H H σσσσμ≤>未知试分析其拒绝域.解由题意知 2~(,)X N μσ（1）假设统计假设为 22220010:=,:>H H σσσσ 其中μ已知当0H 成立时，拒绝域形式为 2020=>sK c σ⎧⎫⎪⎨⎬⎪⎭⎩由222220=(n)ns ns χσσ，可得220=>nsP nc ασ⎧⎫⎪⎨⎬⎪⎭⎩ 所以 21-=()nc n αχ，由此可得拒绝域形式为2201-201=>()sK n n αχσ⎧⎫⎪⎨⎬⎪⎭⎩ （2）假设统计假设为 22220010:<,:>H H σσσσ 其中μ未知当0H 成立时，选择拒绝域为 2020=>sK c σ⎧⎫⎪⎨⎬⎪⎭⎩，由222(-1)(1)n s n χσ-得 ()()()()222201111n s n s P n c P n c ασσ⎧⎫⎧⎫--⎪⎪⎪⎪=>-≤>-⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭所以21(1)(1)n c n αχ--=-，由此可得拒绝域形式为2201-201=>(1)1s K n n αχσ⎧⎫⎪-⎨⎬-⎪⎭⎩14 从甲、乙两煤矿各取若干样品，得其含灰率（%）为,甲:24.3, 20.8, 23.7, 21.3,17.4, 乙:18.2, 16.9, 20.2, 16.7 .假定含灰率均服从正态分布且2212=σσ，问甲、乙两煤矿的含灰率有无显著差异（=0.05α）？解由题意知 2212(,),Y (,)XN N μσμσ设统计假设为 012112:=;:H H μμμμ≠ 其中12=5,=4n n 当=0.05α时1/2122.3238,(2) 2.3646w s t n n α-==+-=临界值1-12=(+2) 3.6861w c t n n s α-⋅= 拒绝域为}{0 3.6861K x y c =->= 而 03.5,,.x y c H -=<接受认为没有差别15 设甲、乙两种零件彼此可以代替，但乙零件比甲零件制造简单，造价也低.经过试验获得它们的抗拉强度分别为（单位：kg/cm 2）：甲：88，87，92，90，91 乙：89，89，90，84，88假定两种零件的抗拉强度都服从正态分布，且21σ =22σ.问甲种零件的抗拉强度是否比乙种的高（=0.05α）？解由题意知 2212(,),Y (,)XN N μσμσ设统计假设为 012112:=;:H H μμμμ≠，其中12=5,=5n n 当=0.05α时122.2136,(2) 1.86,w s t n n α==+-=-临界值1-212=(+2) 2.2136w c t n n s α-⋅= 拒绝域为}{0 2.2136K x y c =->=而 1.6x y c -=<，所以接受0H ，认为甲的抗拉强度比乙的要高.16 甲、乙两车床生产同一种零件.现从这两车床产生的产品中分别抽取8个和9个，测得其外径（单位：mm ）为：甲：15.0，14.5，15.2，15.5，14.8，15.1，15.2，14.8乙：15.2，15.0，14.8，15.2，15.0，15.0，14.8，15.1，14.8假定其外径都服从正态分布，问乙车床的加工精度是否比甲车床的高（=0.05α）？解由题意知 2212(,),Y (,)XN N μσμσ设统计假设为 2222012112:;:H H σσσσ≥<，其中12=8,=9n n当=0.05α时 220.0955,0.0261x y s s ==，临界值 12(1,1)0.2684c F n n α=--=拒绝域为202x ys K c s ⎧⎫⎪⎪=<⎨⎬⎪⎪⎭⎩，而22 3.6588x y s F c s ==>，接受0H ，认为乙的精度高.17 要比较甲、乙两种轮胎的耐磨性，现从甲、乙两种轮胎中各取8个，各取一个组成一对，再随机选取8架飞机，将8对轮胎磨损量（单位：mg ）数据列表如下：试问这两种轮胎的耐磨性有无显著差异？(=0.05α). 假定甲、乙两种轮胎的磨损量分别满足2212(,),Y (,)XN N μσμσ且两个样本相互独立.解由题意知 2212(,),Y (,)X N N μσμσ设统计假设为 012112:=;:H H μμμμ≠，其中12===8n n n 当=0.05α时，令()221/211,320,102200,319.69,(1) 2.36461n ZZ i Z X Y z s z z s t n n α-==-==-==-=-∑ 拒绝域为}{0K z c =>，临界值1-2=(1)2138Z c t n s α-⋅= 而320z c =<，所以接受0H ，认为两种轮胎耐磨性无显著差异.18 设总体2212(,),Y (,)X N N μσμσ, 由两总体分别抽取样本 X ：4.4，4.0，2.0，4.8 Y ：6.0，1.0，3.2，0.41）能否认为12μμ= (=0.05α)? 2）能否认为2212σσ= (=0.05α)？解 (1) 由题意知 2212(,),Y (,)XN N μσμσ设统计假设为 012112:=;:H H μμμμ≠，其中12==4=n n n令Z X Y =-，则有22111.15,()9.02331n z i z s z z n ===-=-∑，当=0.05α时，1-2=(1) 3.1824c t n α-=，1-2=(1)/ 4.78Z c t n s α-⋅= 拒绝域为}{0K z c =>，而 1.15z c =<，所以012,.H μμ=接受认为 (2) 由题意知 2212(,),Y(,)XN N μσμσ设统计假设为 2222220111:=;:H H σσσσ≠，其中12==4=n n n 其中221.5467, 6.4367x y s s ==，拒绝域为2201222>x x y y s s K c c s s ⎧⎫⎪⎪=<⎨⎬⎪⎪⎭⎩或临界值 1/21221212(1,1)0.0648,(1,1)15.4392c F n n c F n n αα-=--==--=而22201220.2403,,.X Ys F H s σσ===接受认为19 从过去几年收集的大量记录发现，某种癌症用外科方法治疗只有2%的治愈率.一个主张化学疗法的医生认为他的非外科方法比外科方法更有效.为了用实验数据证实他的看法，他用他的方法治疗200个癌症病人，其中有6个治好了.这个医生断言这种样本中的3%治愈率足够证实他的看法.（1）试用假设检验方法检验这个医生的看法；（2）如果该医生实际得到了4.5%治愈率，问检验将证实化学疗法比外科方法更有效的概率是多少？解 (1) 记每个病人的治愈情况为X ，则有(1,) XB p设统计假设为 0010:=0.02;:0.02H p p H p p >≤=，其中200,0.05n α==拒绝域为}{00K x p c =-<，临界值10.0163c αμ-== 而 000.01,,0.02.x p c H p -=<>拒绝不能认为(2) 不犯第二类错误的概率101 4.5%P X u p p αβ-⎧⎫⎪⎪-=>=⎨⎬⎪⎪⎭⎩由(1,) XB p ，可得 (1),p p EX p DX n-==由中心极限定理得1 4.5%10.72X P p β⎧⎫⎪-=>=⎬⎪⎭=-Φ=20 在某公路上，50min 之间，观察每15s 内通过的汽车数，得下表通过的汽车数量0 1 2 3 4 ≥5 次数f92 68 28 11 1 0问能否认为通过的汽车辆数服从泊松分布（=0.10α）？解设统计假设为 0010:()(),()(),200.0.10H F x F x H F x F x n α====4001ˆ,0.805.j j H X j n λν====∑若成立记 ˆ1,2,3,4ˆ(),!j j j p P x j e j λλ-==-=则有ˆ0.8050102143243500.8050.4471,0.805*0.3599,*0.144920.8050.805*0.0389,*0.0078,10.0014,34j j p e e p p p p p p p p p p λ--=============-=∑检验统计量的值为()2522210.9500 2.1596(1)(4)9.848,~(),0.805.jj n j jnp m r np H X P ανχχχλλ-=-==<--===∑不拒绝认为且21 对某厂生产的汽缸螺栓口径进行100次抽样检验，测得100数据分组列表如下：组限10.93～10.9510.95～10.9710.97～10.9910.99～11.01频数 582034 组限 11.01～11.0311.03～11.0511.05～11.0711.07～11.09 频数1766 4试对螺栓的口径X 的分布做假设检验（=0.05α）.解设X 表示螺栓的口径，2(,)XN μσ，分布函数为()F x ，统计假设为0010:()(),:()()H F x F x H F x F x =≠，其中100,0.05,2n r α===在0H 成立的情况下，计算得88221111ˆˆ11.0024,()0.00101888j j j j i i X x v x v μσμ====⋅==-⋅=∑∑ 由ˆ11.0024(0,1)ˆ0.00319X X N μσ--=得0810.9311.002411.0911.00242.2689,, 2.74520.003190.00319x x --==-==所以110887()()0.0386,,()()0.0140p x x p x x =Φ-Φ==Φ-Φ=检验统计量的值为2822210.951()13.825(1)(5)11.07j j nj jv np m r np αχχχ-=-==>--==∑由此应该20,~(,).H X N μσ拒绝不能认为22 检查产品质量时，每次抽取10个产品检验，共抽取100次，得下表：次品数0 1 2 3 4 5 6 7 8 9 10 频数 35 40 18 5 1 1 0 0 0 0 0 问次品数是否服从二项分布（=0.05α）？解设X 表示抽取的次品数，2(,)XN μσ，分布函数为()F x ，统计假设为0010:()(),:()()H F x F x H F x F x =≠，其中10,0.05n α==在0H 成立的情况下，01ˆNjj X pjvN N===∑计算得00101192280101102103371010010*******(1),0,1,,10;ˆˆˆ(1)0.3487,(1)0.3874,(1)0.1937ˆˆ(1)0.0574,(1)10,jj N j j N p C p p j p C p p p C p p p C p p p C p pp C p p--=-==-==-==-==-==-= 检验统计量的值为0020()21022210.9505.1295(1)(9)16.92jj n j jnp m r np ανχχχ-=-==<--==∑因此0,~(10,0.1).H X B 不拒绝认为23 请71人比较A 、B 两种型号电视机的画面好坏，认为A 好的有23人，认为B 好的有45人，拿不定主意的有3人，是否可以认为B 的画面比A 的好（=0.10α）？解设X 表示A 种型号电视机的画面要好些，Y 表示B 中型号电视机画面要好些分布函数分别为()X F x ，()Y F x ，统计假设为01:()(),:()(),10,100.0.05X Y X Y H F x F x H F x F x N n α=≠===由题意知++=23=45,=+n n n n n --，检验统计量 ,min()s n n +-=而23(68)25s s α=<=，所以0,.H B 拒绝认为的画面好24 为比较两车间（生产同一种产品）的产品某项指标的波动情况，各依次抽取12个产品进行测量，得下表甲 1.13 1.26 1.16 1.41 0.86 1.39 1.21 1.22 1.20 0.62 1.18 1.34 乙 1.21 1.31 0.99 1.59 1.41 1.48 1.31 1.12 1.60 1.38 1.60 1.84 问这两车间所生产的产品的该项指标分布是否相同（=0.05α）？解设,X Y 分别表示甲乙两车间所生产产品的指标分布，分布函数分别()X F x ()Y F x ，统计假设为01:()(),:()(),.0.05,12,X Y X Y H F x F x H F x F x n m α=≠===检验统计量为秩和T ，易知T 的样本值为112T =且(150,300)T N拒绝域为012K u u α-⎧⎫⎪=>⎨⎬⎪⎭⎩而0.9752.194 1.96u u =>=，所以0,.H 拒绝认为指标分布不相同25 观察两班组的劳动生产率(件/h)，得下表：问两班组的劳动生产率是否相同（α=0.05）？解设,X Y 分别表示两个组的劳动生产率，分布函数分别为(),X F x ()Y F x ，统计假设为01:()(),:()(),.0.05,9,9X Y X Y H F x F x H F x F x n m α=≠===检验统计量为秩和T ，易知T 的样本值为73T = 拒绝域形式为}{01212,<K T t T t t t =<>其中而12(9,9)=66,(9,9)105t t =，因此T K ∈, 所以0,.H 接受认为劳动生产率相同26 观观察得两样本值如下：Ⅰ 2.36 3.14 7.52 3.48 2.76 5.43 6.54 7.41 Ⅱ 4.38 4.25 6.54 3.28 7.21 6.54 问这两样本是否来自同一总体（α=0.05）？解设,X Y 分别表示Ⅰ，Ⅱ两个样本，分布函数分别是(),X F x ()Y F x ，统计假设为01:()(),:()(),.0.05,6,8,X Y X Y H F x F x H F x F x n m α=≠===检验统计量为秩和T ，易知T 的样本值为49T = 拒绝域形式为}{01212,<K T t T t t t =<>其中而12(6,8)=32,(6,8)58t t =，因此0T K ∈, 所以0,.H 接受认为来自同一总体 27 某种动物配偶的后代按体格的属性分为三类，各类的数目是：10，53，46,按照某种遗传模型其比率之比应为：22)1(:)1(2:p p p p --，问数据与模型是否相符（05.0=α）？解设体格的属性为样本X ，由题意知(2,1)X B p -其密度函数为()f x ，其中22(,)(1)0,1,2xxx f x p C p p x -=-=统计假设为0010:()(),:()()H F x F x H F x F x =≠似然函数为222211(1)(1)i iii nnx x x x n nxnxi i L C pp pp C--===-=-∏∏解得最大似然统计量为 ˆ12xp=- 则 220ˆˆ 1.330.1121pp === 1ˆˆˆ2(1)0.4454p p p =-= 22ˆˆ(1)0.4424p p =-= 拒绝域为}{2201(1)K m r αχχ-=>--而 ()21022210.950ˆ0.9134(1)(9) 3.8414ˆjj n j j np m r npανχχχ-=-==<--==∑所以0,.H 不拒绝认为与模型相符28 在某地区的人口调查中发现：15729245个男人中有3497个是聋哑人.16799031个女人中有3072个是聋哑人.试检验“聋哑人与性别无关”的假设（05.0=α）.解设X 表示男人中聋哑人的个数，Y 表示女人中聋哑人的个数，其分布函数分别表示为()X F x ，()Y F x . 统计假设为01:(,)()(),:(,)()()X Y X Y H F x y F x F x H F x y F x F x =≠拒绝域为}{2201(1)K m r αχχ-=>--而21022210.950ˆ()62.64(1)(1) 3.84ˆj j n j jv np m r np αχχχ-=-==>--==∑ 所以0,.H 拒绝认为聋哑与性别相关 29 下表为某药治疗感冒效果的联列表：试问该药疗效是否与年龄有关（α=0.05）？解设X 表示该药的疗效与年龄有关，Y 表示该药的疗效与年龄无关，其分布函数分别表示为(),X F x ()Y F x . 统计假设为01:(,)()(),:(,)()(),3,3,0.05,X Y X Y H F x y F x F x H F x y F x F x r s α=≠===拒绝域为}{2201(1)K m r αχχ-=>--而 ()21022210.950ˆ13.59(1)(4)9.488ˆj j n j j np m r npανχχχ-=-==>--==∑所以0,.H 拒绝认为疗效与年龄相关30 某电子仪器厂与协作的电容器厂商定，当电容器厂提供的产品批的不合格率不超过3%时以高于95%的概率接受，当不合格率超过12%时，将以低于10%的概率接受.试为验收者制订验收抽样方案.解由题意知，010.03,0.12,0.05,0.1p p αβ====代入式子 01()1()L p L p αβ=-⎧⎨=⎩()L p 选用式子()()()(1)(1)L P X d P U np p np p φ=≤=≤≈--计算求得 66,4n d ==，于是抽查方案是：抽查66件产品，如果抽得的不合格产品4X ≤，则接受这批产品，否则拒绝这批产品.31 假设一批产品的质量指标2(,)XN μσ（2σ已知），要求质量指标值越小越好.试给出检验抽样方案（,n c ）的计算公式.若2σ未知，又如何确定检验抽样方案（,n c ）？若质量高时指质量指标在一个区间时，又如何确定检验抽样方案（,n c ）?解 (1) 解方程组01()1()L L μαμβ=-⎧⎨=⎩ 得 ()201u u n αβσμμ⎛⎫+⎪= ⎪-⎝⎭10u u c u u αβαβμμ+=+ (2) 若2σ未知，用*2M 估计2σ，从而得出公式()2*201u u M n αβμμ⎛⎫+⎪= ⎪-⎝⎭10u u c u u αβαβμμ+=+习题四1 下表数据是退火温度x (C 0)对黄铜延性η效应的试验结果，η是以延伸率计算的，且设为正态变量，求η对x 的样本线性回归方程.x (C 0)300 400 500 600 700 800 y (%)40 50 55 60 67 70解利用回归系数的最小二估计：101ˆˆˆxyxx l l y xβββ⎧=⎪⎨⎪=-⎩其中2211,n nxy i i xx i i i l x y nxy l x nx ===-=-∑∑ 代入样本数据得到：10ˆˆ0.0589,24.6286ββ==样本线性回归方程为：ˆ24.62860.0589yx =+2 证明线性回归函数中(1)回归系数1β的置信水平为α-1的置信区间为211ˆˆ(2)n αβ--；(2)回归系数0β的置信水平为α-1的置信区间为2ˆ(2)n αβ-±-.证 (1) 由于211ˆ,xx N l σββ⎛⎫ ⎪⎝⎭()0,1N222(2)ES n χσ-又因为：，()222ˆ2(2)n n σχσ--故所以()2t n -易知 {}11ˆ1p cββα-<=-，1P α<=-⎪⎭⎩其中()122n α--所以1β的置信水平为α-1的置信区间为211ˆˆ(2)n αβ-- (2) 由0ˆβ～2201(,())xxnx N l βσ+，得 ()0,1N ，()222ˆ2(2)n n σχσ--，0ˆβ与2ˆσ相互独立，所以：()2T t n ==-根据11221(2)(2)P T t n P t n ααα--⎫⎪⎛⎫⎪-=<-=<- ⎪⎪⎝⎭⎪⎪⎭()()0001122ˆˆ22P n n ααβββ--⎛⎫ ⎪ ⎪=--<<+- ⎪ ⎪ ⎪⎝⎭得到0β的置信度为1α-的置信区间()012ˆ2n αβ--.3 某河流溶解氧浓度（以百万分之一计）随着水向下游流动时间加长而下降.现测得8组数据如下表所示.求溶解氧浓度对流动时间的样本线性回归方程，并以α=0.05对回归显著性作检验.流动时间t （天） 0.5 1.0 1.6 1.8 2.6 3.2 3.8 4.7 溶解氧浓度（百万分之一）0.28 0.29 0.29 0.18 0.17 0.18 0.10 0.12解利用101ˆˆˆtyttl l y t βββ⎧=⎪⎨⎪=-⎩其中2211,n n ty i i tt i i i l t y nty l t nt ===-=-∑∑ 代入样本数据得到： 10ˆˆ0.0472,0.3145ββ=-= 所以，样本线性回归方程为：ˆ0.31450.0472yt =- 拒绝域形式为：{}21ˆc β>()20.95ˆ1,6,0.0058ttF c c l σ==>而21ˆ0.0022β=，所以回归模型不显著. 4 假设X 是一可控制变量，Y 是一随机变量,服从正态分布.现在不同的X 值下分别对Y 进行观测，得如下数据i x0.25 0.37 0.44 0.55 0.60 0.62 0.68 0.70 0.73 i y2.57 2.31 2.12 1.92 1.75 1.71 1.60 1.51 1.50 i x 0.75 0.82 0.84 0.87 0.88 0.90 0.95 1.00 i y1.41 1.33 1.31 1.25 1.20 1.19 1.15 1.00(1)假设X 与Y 有线性相关关系，求Y 对X 样本回归直线方程，并求2σ=DY 的无偏估计；(2)求回归系数210σββ、、的置信度为95%的置信区间； (3)检验Y 和X 之间的线性关系是否显著（=0.05α）； (4)求Y 置信度为95%的预测区间；(5)为了把Y 的观测值限制在)68.1,08.1(，需把x 的值限制在什么范围？（=0.05α）解 (1) 利用101ˆˆˆxyxx l l y x βββ⎧=⎪⎨⎪=-⎩其中2211,n nxy i i xx i i i l x y nxy l x nx ===-=-∑∑计算得10ˆˆ2.0698, 3.0332ββ=-= 所以，样本线性回归方程为：ˆ 3.0332 2.0698yx =-，22ˆ0.002015ES σ== (2) 根据第二题，1β的置信区间为()112ˆˆ2n αβ-±-，代入值计算得到：()1 2.1825, 1.9571β∈--，0β的置信区间为()02ˆ2n αβσ-±-，代入数值计算得到：()0 2.95069,3.1160β∈.(3) 根据F 检验法，其拒绝域形式为 }{201ˆK c β=> 而 12ˆ(2),xxc tn l ασ-=- 显然10K β∈，所以Y 和X 之间具有显著的线性关系.(4)()221(0,(1))xxxx yN l nσ-++,()2ˆ1()1(0,1)xxx x s x N l n -=++令222ˆ(2)(2),(2)ˆ()n nt n s x σχσσ---则有 1122ˆˆˆ((2),(2))y ytn yt n αα--∈--(5) 根据(4)的结论，令 22ˆˆ1.68 1.08yyαα--+=-=，解得 (0.7802,0.8172)x ∈5 证明对一元线性回归系数0ˆβ,1ˆβ相互独立的充分必要条件是0=x . 证 ""⇒()()()()()010011111ˆˆˆˆˆˆcov ,E y x ββββββββββ=--=---2110111101ˆˆˆˆ()E y x y x βββββββββ=---++2211011101ˆy xE y x ββββββββ=---++ ()2211ˆx E ββ=-- 222221111ˆˆˆ()xx E D E l σββββ=+=+ 若要()01ˆˆcov ,0ββ=，那么0x =.反之显然也成立，命题的证.6 设n 组观测值),...,2,1)(,(n i y x i i =之间有关系式：i i i i x x y εεββ，+-+=)(10～),...,2,1)(,0(2n i N =σ（其中∑==ni i x n x 11），且n εεε,...,,21相互独立.(1) 求系数10,ββ的最小二乘估计量10ˆ,ˆββ； (2) 证明∑∑∑===-+-=-ni i n i i i n i i y y y y y y 121212)ˆ()ˆ()(，其中∑==n i i y n y 11 (3) 求10ˆ,ˆββ的分布. 解 (1) 最小化残差平方和：2201[()]Ei i S y x x ββ=---∑01ββ求，的偏导数[][]220101012()02()()0E Ei i i i i S S y x x y x x x x ββββββ∂∂=----==-----=∂∂∑∑， 01ˆˆ,xyxxl y l ββ==得到：(2) 易知()()()22221111ˆˆˆˆˆˆ()()2()nnnniiiiiii i i i i i i i y y y yy y y y yy y y y y ====-=-+-=-+-+--∑∑∑∑ 其中01ˆˆˆ()()xyi i i xxl yx x y x x l ββ=+-=+-，将其代入上式可得 1ˆˆ()()0niiii y yy y =--=∑ 所以,∑∑∑===-+-=-ni i n i i i ni iy y yy y y121212)ˆ()ˆ()( (3)20ˆ~(0,),i N y εσβ=，200ˆ~(,)N nσββ∴同理，易得211ˆ~(,)xxN l σββ∴7 某矿脉中13个相邻样本点处某种金属的含量Y 与样本点对原点的距离X 有如下观测值 ix 2 3 4 5 7 8 10 i y 106.42 108.20 109.58 109.50 110.00 109.93 110.49 ix 11 14 15 16 18 19 i y 110.59 110.60 110.90 110.76 111.00 111.20分别按(1)x b a y +=；(2)x b a y ln +=；(3)xba y +=. 建立Y 对X 的回归方程，并用相关系数221TES S R -=指出其中哪一种相关最大.解 (1)令v y a bv ==+，根据最小二乘法得到，正规方程：101ˆˆˆvy vv l l y vβββ⎧=⎪⎨⎪=-⎩，最后得到10ˆˆ1.1947,106.3013ββ==所以：样本线性回归方程为：ˆ106.3013y=+10.8861R = (2) 令ln ,v x y a bv ==+101ˆˆˆvyvv l l y vβββ⎧=⎪⎨⎪=-⎩，得到10ˆˆ1.714,106.3147ββ== 所以：样本线性回归方程为：ˆ106.3147 1.714ln yx =+，20.9367R = (3) 令1,v y a bv x==+ 101ˆˆˆvy vv l l y vβββ⎧=⎪⎨⎪=-⎩，得到10ˆˆ111.4875,9.833ββ==- 所以：样本线性回归方程为：ˆ111.48759.833yx =-，30.987R = 综上，123R R R <<,所以第三种模型所表示的X Y 与的相关性最大. 8 设线性模型⎪⎩⎪⎨⎧++=+-=+=3213221211122εββεββεβy y y其中i ε～),0(2σN （1,2,3.i =）且相互独立，试求1β、2β的LS 估计.解令()()1231212310,,,21,(,),,,12T TT Y y y y X βββεεεε⎡⎤⎢⎥==-==⎢⎥⎢⎥⎣⎦则线性模型可转化为 Y X βε=+ 根据 222TTTTES Y X Y Y Y X X X ββββ=-=-+，令 20ES β∂=∂ 可得 ()1ˆTT X X X Y β-=即 112322311ˆˆ(23),(2)66Y Y Y Y Y ββ=++=--+ 9 养猪场为估算猪的毛重，随机抽测了14头猪的身长1x (cm)，肚围2x (cm)与体重y (kg)，得数据如下表所示，试求一个22110x b x b b y ++=型的经验公式.解由多元线性模型得：()2140,Y X I βεεσ=+⎧⎪⎨=⎪⎩()()()0121212,,,,,,TTTn n Y y y y ββββεεεε===()114149145581516215271159621627416971ˆ172741787918084190851929419891110395T T X X X X Y β-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦代入数值得到：12ˆ15.93840.52230.4738yx x =-++ 同样得到：12ˆ15.93840.52230.4738yx x =-++ 10 某种商品的需求量y ，消费者的平均收入1x 和商品价格2x 的统计数据如下表所示.试求y 对1x 、2x 的线性回归方程. 1i x1000 600 1200 500 300 400 1300 1100 1300 300 2i x 5 7 6 6 8 7 5 4 3 9 y100 75 80 70 50 65 90 100 110 60解建立回归模型201122=+++(0,)Y x x N βββεεσ其中根据2()=0E S ββ∂∂，可求得β的LS 估计为 -1ˆ=(X X)T T X Y β代入x ，得0=111.6918,β 1=0.0143,β 2=7.1882,β-则回归方程为：12ˆ111.69180.01437.1882yx x =+-11 设n 组观测值),...,2,1)(,(n i y x i i =之间有如下关系：i i i i i x x y εεβββ，+++=2210～),...,2,1)(,0(2n i N =σ，且n εεε,...,,21相互独立.(1)求系数210,,βββ的最小二乘估计量21ˆ,ˆ,ˆβββ； (2)设n i x x y i i i ,...,2,1,ˆˆˆˆ2210=++=βββ，∑==n i i y n y 11，证明：∑∑∑===-+-=-ni i ni i i ni i y y y y y y 121212)ˆ()ˆ()(解 (1) ()()()0121212,,,,,,TTTn n Y y y y ββββεεεε===1222211111Tn n X x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭()1ˆT T X X X Y β-=(2)()()()22221111ˆˆˆˆˆˆ()()2()nnnniiiiiii i i i i i i i y y y yy y y y yy y y y y ====-=-+-=-+-+--∑∑∑∑()()11ˆˆˆˆ()0nT T i i i i x x x x y yy y β-==--=∑其中:y=x ，将其代入，得到 ()22211ˆˆ()()nni i i i i i y y y yy y ==∴-=-+-∑∑ 12(1)求形如210的回归方程；(2)对上述回归方程的显著性作检验； (3)求当x =5.5时Y 的估计值.解 (1) 令212,xx x x ==，求得回归方程为：2ˆ 3.4167 2.72620.3905yx x =+- (2) 拒绝域形式为：{}21ˆc β> ()20.9521ˆ1,6ˆxxF c l σβ=>而，所以回归方程具有显著性 (3) 将 5.5x =代入回归方程，得到ˆ 6.5982y=13 设y 和变量12,x x 有形为ε++=2211x b x b y ,2(0,)N εσ的回归方程模型，试用最小二乘法求出12b b 和的估计.解令 ()()()121212,,,,,TT Tn Y y y y βββεεε===1112121222Tn n x x x X x x x ⎛⎫=⎪⎝⎭残差平方和为 222T T T T E S Y X Y Y Y X X X ββββ=-=-+令 20E S β∂=∂，得到 112ˆ(,)()T T T X X X Y βββ-==.。

北航数理统计第二次数理统计大作业判别分析

数理统计大作业（二）全国各省发展程度的聚类分析及判别分析指导教师院系名称材料科学与工程院学号学生姓名2015 年 12 月21 日目录全国各省发展程度的聚类分析及判别分析 (1)摘要： (1)引言 (1)1实验方案 (2)1.1数据统计 (2)1.2聚类分析 (3)1.3判别分析 (4)2结果分析与讨论 (5)2.1聚类分析结果 (5)2.2聚类分析结果分析： (8)2.3判别分析结果 (9)2.4 Fisher判别结果分析： (11)参考文献： (16)全国各省发展程度的聚类分析及判别分析摘要：利用SPSS软件对全国31个省、直辖市、自治区(浙江、安徽、甘肃除外)的主要经济指标进行多种聚类分析，分析选择最佳聚类类数，并对浙江、湖南、甘肃进行类型判别分析。

通过这两个方法对全国各省进行发展分类。

本文选取了7项社会发展指标作为决定发展程度的影响因素，其中经济因素为主要因素，同时评估城镇化率和人口素质因素。

各项数据均来自2014年国家统计年鉴。

分析结果表明：北京市和上海市和天津市为同一类；江苏省和山东省和广东省为同一类型；河北、湖北、河南、湖南、四川、辽宁为同一类；其余的为另一类。

关键词：聚类分析、判别分析、发展引言聚类分析是根据研究对象的特征对研究对象进行分类的多元统计分析技术的总称。

它直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。

系统聚类分析又称集群分析，是聚类分析中应用最广的一种方法，它根据样本的多指标（变量）、多个观察数据，定量地确定样品、指标之间存在的相似性或亲疏关系，并据此连结这些样品或指标，归成大小类群，构成分类树状图或冰柱图。

判别分析是根据多种因素(指标)对事物的影响来实现对事物的分类，从而对事物进行判别分类的统计方法。

判别分析适用于已经掌握了历史上分类的每一个类别的若干样品，希望根据这些历史的经验（样品），总结出分类的规律性（判别函数）来指导未来的分类。

南开大学22春“金融学”《概率论与数理统计》期末考试高频考点版(带答案)试卷号：2

南开大学22春“金融学”《概率论与数理统计》期末考试高频考点版（带答案）一.综合考核(共50题)1.设X~N(0,1)，有常数c满足P(x=c)=P(xc)，则c=()。

A.1B.0C.1/2D.-1参考答案：B2.协方差cov(X，Y)的绝对值越大，说明XY的线性关系越强。

()A.正确B.错误参考答案：A3.设X,Y是两个相互独立的随机变量，它们的分布函数分别为FX(x), FY(y)，令Z=Min(X,Y),则FZ(z)=1-[1-FX(z)]*[1-FY(z)]。

()A.正确B.错误参考答案：A4.随机变量X的期望是E(X)，随机变量Y的期望E(Y)，X与Y满足E[X+Y]=E[X]+E[Y]，则X与Y不一定相互独立。

()A.正确B.错误参考答案：AA，B为两个互不相容事件，则下列各式中错误的是()。

参考答案：C6.袋中有4个白球和5个黑球，采用放回抽样，连续从中取出3个球，取到的球顺序为黑白黑的概率为()。

A.7/50B.100/729C.17/48D.43/125参考答案：B7.正态分布是一种连续分布。

()A.正确B.错误参考答案：A8.如果三个事件相互独立，则任意一事件与另外两个事件的积、和、差均相互独立。

()A.正确B.错误参考答案：A9.实际推断原理：一次试验小概率事件不会发生。

()A.正确B.错误参考答案：B10.F(X，Y)一定大于等于FX(x)*FY(y)。

()A.正确B.错误参考答案：B11.设X~N(0，1)，有常数c满足P(x>=c)=P(xA.1B.0C.1/2D.-1参考答案：B12.在事件A发生的条件下事件B发生的概率，简称为B的()。

A.估计量B.条件概率C.统计概率D.概率参考答案：B13.设X~N(2，σ2)，P(2A.0.3B.0.2C.0.4D.0.5参考答案：B14.如果随机试验E具有以下特点：(1)样本空间S中所含样本点为有限个，(2)一次试验，每个基本事件发生的可能性相同。

课程代码为04183的概率论与数理统计-试题及答案(2008年1月、4月、7月、10月)

课程代码为04183的概率论与数理统计-试题及答案（2007年4月、7月、10月） 2008年1月高等教育自学考试全国统一命题考试概率论与数理统计（经管类）试卷课程代码 4183一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.设事件A 与B 相互独立,且P(A)>0,P(B)>0,则下列等式成立的是（）A.AB=φB.P(A B )=P(A)P(B )C.P(B)=1-P(A)D.P(B |A )=0 2.设A 、B 、C 为三事件，则事件C B A =（）A.A C BB.A B CC.( A B )CD.( A B )C3. 设随机变量X 的取值范围是(-1,1),以下函数可作为X 的概率密度的是（）4.设随机变量X~N(1，4)，Φ（1）=8413.0，Φ（0）=0.5，则事件{1≤X ≤3}的概率为（）A.0.1385B.0.2413C.0.2934D.0.34135.设随机变量（X ，Y ）的联合概率密度为f(x,y)=则A=（） A.21 B.1 C.23 D.2 6.Y X0 5 041 61 2 31 41则P{XY=0}=（） A. 41 B.125 C.43 D.17.设X~B （10，31），则E （X ）=（） A.31 B.1C.310 D. 10 8.设X~N （1，23），则下列选项中，不成立．．．的是（） A.E （X ）=1B.D （X ）=3C.P （X=1）=0D.P （X<1）=0.59.设且P(A)=0.8,1000021X ,,X ,X 相互独立,令Y=则由中心极限定理知Y 近似服从的分布是（）A.N(0,1)B.N(8000,40)C.N(1600,8000)D.N(8000,1600)二、填空题（本大题共15小题，每小题2分，共30分）请在每小题的空格中填上正确答案。

中国地质大学(北京)概率论与数理统计期末备考题集（全新整理汇总）3723

3723--中国地质大学(北京)概率论与数理统计期末备考题集3723奥鹏期末考试题集合集单选题：（1）对于事件A,B,下列命题正确的是().A.若A,B互不相容,则与也互不相容B.若A,B相容,那么与也相容C.若A,B互不相容,且概率都大于零,则A,B也相互独立D.若A,B相互独立,那么与也相互独立.正确选项：D（2）在一次假设检验中,下列说法正确的是().A.既可能犯第一类错误也可能犯第二类错误B.如果备择假设是正确的,但作出的决策是拒绝备择假设,则犯了第一类错误C.增大样本容量,则犯两类错误的概率都不变D.如果原假设是错误的,但作出的决策是接受备择假设,则犯了第二类错误正确选项：A（3）对总体X~N(μ,σ2)的均值?和作区间估计,得到置信度为95%的置信区间,意义是指这个区间().A.平均含总体95%的值B.平均含样本95%的值C.有95%的机会含样本的值D.有95%的机会的机会含μ的值正确选项：D（4）在假设检验问题中,犯第一类错误的概率α的意义是().A.在H0不成立的条件下,经检验H0被拒绝的概率B.在H0不成立的条件下,经检验H0被接受的概率C.在H0成立的条件下,经检验H0被拒绝的概率D.在H0成立的条件下,经检验H0被接受的概率正确选项：C（5）在一次假设检验中,下列说法正确的是().A.第一类错误和第二类错误同时都要犯B.如果备择假设是正确的,但作出的决策是拒绝备择假设,则犯了第一类错误C.增大样本容量,则犯两类错误的概率都要变小D.如果原假设是错误的,但作出的决策是接受备择假设,则犯了第二类错误正确选项：C（6）在一个确定的假设检验中,与判断结果相关的因素有().A.样本值与样本容量B.显著性水平C.检验统计量D.A,B,C同时成立正确选项：D（7）对正态总体的数学期望?进行假设检验,如果在显著水平0.05下接受H0:μ=μ0,那么在显著水平0.01下,下列结论中正确的是().A.必须接受H0B.可能接受,也可能拒绝H0C.必拒绝H0D.不接受,也不拒绝H0正确选项：A（8）已知P(A)=0.4,P(B)=0.6,P(B|A)=0.5,则P(A|B)=().A.1/2B.1/3C.10/3D.1/5正确选项：B（9）甲.乙两人独立的对同一目标各射击一次,其中命中率分别为0.6和0.5,现已知目标被命中,则它是乙命中的概率是().A.3/5B.5/11C.5/8D.6/11正确选项：C（10）某人射击时,中靶的概率为2/3,如果射击直到中靶子为止,则射击次数为3的概率().A.2/27B.2/9C.8/27D.1/27正确选项：A（11）变量X的密度函数为,则常数C=().A.3B.4C.1/4D.1/3正确选项：B（12）设随机变量X～N(μ,σ2),则随着σ的增大,概率为().A.单调增加B.单调减少C.保持不变D.增减不定正确选项：C（13）设随机变量X和Y均服从正态分布X～N(μ,42),Y～N(μ,52),记,则().A.对任何实数μ都有p1=p2B.对任何实数μ都有p1<p2C.仅对个别值有p1=p2D.对任何实数μ都有p1>p2正确选项：A（14）袋中有50个乒乓球,其中20个黄的,30个白的,现在两个人不放回地依次从袋中随机各取一球.则第二人取到黄球的概率是().A.1/5B.2/5C.3/5D.4/5正确选项：B（15）事件”甲种产品畅销,乙种产品滞销”,则其对立事件A为().A.”甲种产品滞销,乙种产品畅销”B.”甲.乙两种产品均畅销”C.”甲种产品滞销”D.”甲种产品滞销或乙种产品畅销”正确选项：D（16）常见随机变量的分布中,数学期望和方差一定相等的分布是()A.二项分布B.标准正态分布C.指数分布D.泊松分布.正确选项：D（17）设是未知参数?的一个估计量,若则是?的().A.极大似然估计B.矩法估计C.相合估计D.有偏估计正确选项：B（18）在对单个正态总体均值的假设检验中,当总体方差已知时,选用().A.t检验法B.u检验法C.F检验法D.σ2检验法正确选项：B（19）设A和B为两个任意事件,且,P(B)0,则必有().A.AB.BC.CD.D正确选项：B（20）设A和B为两个任意事件,则下列关系成立的是().A.AB.BC.CD.D正确选项：C（21）设A和B为两个任意事件,且,则必有().A.AB.BC.CD.D正确选项：D（22）设每次实验成功的概率为p(0p1)则在三次独立重复试验中至少一次成功的概率为().A.p3B.1-p3C.(1-p)3D.1-(1-p)3正确选项：B（23）设一随机变量X的密度函数,F(x)是X的分布函数,则对任意实数a有().A.AB.BC.CD.D正确选项：B（24）设X和Y相互独立,且分别服从N(0,1)和N(1,1)则().A.AB.BC.CD.D正确选项：B（25）总体方差D等于().A.AB.BC.CD.D正确选项：C（26）设X1,X2,…,Xn为来自总体的一个样本,为样本均值,EX未知,则总体方差DX的无偏估计量为().A.AB.BC.CD.D正确选项：B（27）设总体X~f(x,θ),θ为未知参数,X1,X2,…,Xn为X的一个样本,θ1(X1,X2,…,Xn).θ2(X1,X2,…,Xn)为两个通缉量(θ1,θ2)为θ的置信度为1-α的置信区间,则应有().A.P{θ1θθ2}=αB.P{θθ2}=1-αC.P{θ1θθ2}=1-αD.P{θθ1}=α正确选项：C（28）在假设建设检验中,记H0为检验假设,则所谓犯第一类错误的是().A.H0为真时,接受H0B.H0不真时,接受H0C.H0不真时,拒绝H0D.H0为真时,拒绝H0正确选项：D（29）设A,B,C表示三个随机事件,则ABC表示A.A,B,C中至少有一个发生B.A,B,C都同时发生C.A,B,C中至少有两个发生D.A,B,C都不发生.正确选项：A（30）已知事件A,B相互独立,且P(A)=0.5,P(B)=0.8,则P(AB)=()A.0.65B. 1.3C.0.9D.0.3正确选项：C（31）设X~B(n,p),则有()A.E(2X-1)=2npB.E(2X+1)=4np+1C.D(2X+1)=4np(1-p)+1AD.D(2X-1)=4np(1-p)正确选项：D（32）X的概率函数表(分布律)是x-01p1/4a5/12则a=()A.1/3;B.0;C.5/12;D.1/4.正确选项：A（33）在n次独立重复的贝努利试验中,设P(A)=p,那么A事件恰好发生k次的概率为().A.pk;B.()pk(1-p)n-k;C.pn-k(1-p)k;D.pk(1-p)n-k正确选项：B（34）设X的概率函数表是().x-01p1/41/41/2则它的数学期望E(X)和方差D(X)分别是A.1/4,1/16;B.1/2,3/4;C.1/4,11/16;D.1/2,11/16.正确选项：C（35）设随机变量X的密度函数,则常数A=().A.1;B.1/;C.1/2;D..正确选项：A（36）若T~t(n),下列等式中错误的是().A.P{T0}=P{T0};B.P{T1}=P{T1};C.P{T=0}=0.5;D.P{Tt}=P{T-t}.正确选项：C（37）设X~N(1,12),它有容量为n1的样本Xi,i=1,2,…n1;Y~N(2,22),它有容量为n2的样本Yj,j=1,2,…n2.它们均相互独立,和分别是它们样本平均值,s12和s22分别是它们样本方差,12,22未知但是相等.则统计量应该服从的分布是().A.t(n1+n2);B.t(n1+n2-1);C.t(n1+n2-2);D.F(n1-1,n2-1).正确选项：C（38）设X~N(1,2),它有容量为n1的样本Xii=1,2,…n1;Y~N(2,2),它有容量为n2的样本Yjj=1,2,…n2.均相互独立,s12和s22分别是它们样本方差.则统计量应该服从的分布是().A.2(n1+n2-2);B.F(n2-1,n1-1);C.t(n1+n2-2);D.F(n1-1,n2-1).正确选项：D（39）若1和2同是总体平均数的无偏估计,则下面叙述中,不正确的是().A.21-2仍是总体平均数的无偏估计;B.1-2仍是总体平均数的无偏估计;C.1+2仍是总体平均数的无偏估计D.1+2仍是总体平均数的无偏估计.正确选项：B（40）假设检验时,当样本容量n固定时,缩小犯第Ⅰ类错误的概率,则犯第Ⅱ类错误的概率().A.一般要变小;B.一般要变大;C.可能变大也可能变小;D.肯定不变.正确选项：B（41）设X~N(,2),和2均未知,是样本平均值,s2是样本方差,则(-t0.05,+t0.05)作为的置信区间时,其置信水平为().A.0.1;B.0.2;C.0.9;D.0.8.正确选项：C（42）已知一元线性回归直线方程为=+4x,且=3,=6.则=().A.0;B.6;C.2;D.-6.正确选项：D（43）设(x1,y1),(x2,y2),...(xn,yn)是对总体(X,Y)的n次观测值,YY=,XX=分别是关于Y,关于X的校正平方和及XY=是关于X和Y的校正交叉乘积和,则它们的一元回归直线的回归系数=().A.;B.;C.;D..正确选项：A（44）设A,B为两个事件,则=().A.;B.B;C.A;D..正确选项：D（45）若X~N(0,1),(x)是它的密度函数,(x)是它的分布函数,则下面叙述中不正确的是().A.(-x)=-(x);B.(x)关于纵轴对称;C.(0)=0.5;D.(-x)=1-(x).正确选项：A（46）对单个总体X~N(,2)假设检验,2未知,H0:0.在显著水平下,应该选().A.t检验;B.F检验;C.2检验;D.u检验.正确选项：A（47）甲乙两人各自同时向敌机射击,已知甲击中敌机的概率为0.8,乙击中敌机的概率为0.5,则恰有一人击中敌机的概率().A.0.8B.0.5C.0.4D.0.6正确选项：B（48）设X~N(μ,0.32),容量n=9,均值,则未知参数μ的置信度为0.95的置信区间是.(查表Z0.025=1.96)A.(4.808,6.96)B.(3.04,5.19)C.(4.808,5.19)D.(3.04,6.96)正确选项：C填空题：（1）设X1,X2,…,X16是来自总体的简单随机样本,已知,令则统计量服从分布##(必须写出分布的参数).1、正确选项：N(0,1)（2）设,而1.70,1.75,1.70,1.65,1.75是从总体X中抽取的样本,则μ的矩估计值为##.1、正确选项：（3）设X~U[a,1],X1,…,Xn是从总体X中抽取的样本,求a的矩估计为##.1、正确选项：（4）已知F0.1(8,20)=2,则F0.9(20,8)=##.1、正确选项：0.5（5）设某个假设检验问题的拒绝域为W,且当原假设H0成立时,样本值(x1,x2,…,xn)落入W的概率为0.15,则犯第一类错误的概率为##1、正确选项：0.15（6）设样本的频数分布为X01234频数13212则样本方差s2=##1、正确选项：2（7）设X1,X2,?,Xn为来自正态总体N(μ,σ2)的一个简单随机样本,其中参数μ和σ2均未知,记,,则假设H0:μ=0?的t检验使用的统计量是##.(用和Q表示)1、正确选项：（8）设总体X~N(μ,σ2),X1,X2,…,Xn为来自总体X的样本,则样本均值=## 1、正确选项：（9）设总体X~b,(np),0p1,X1,X2,?…,Xn为其样本,则n的矩估计是##.1、正确选项：（10）设总体X~[U,θ]?,(X1,X2,…,Xn)是来自X的样本,则θ的最大似然估计量是##1、正确选项：（11）测得自动车床加工的10个零件的尺寸与规定尺寸的偏差(微米)如下:+2,+1,-2,+3,+2,+4,-2,+5,+3,+4.则零件尺寸偏差的数学期望的无偏估计量##1、正确选项：2（12）设X1,X2,X3,X4是来自正态总体N(0,2)2的样本,令Y=(X1+X2)2+(X3-X4)2,则当C=##时CY~x2(2).1、正确选项：1/8（13）设容量n=10的样本的观察值为(8,7,6,9,8,7,5,9,6),则样本均值样本方差##.1、正确选项：s2=2（14）设A.B为随机事件,P(A)=0.5,P(B)=0.6,P(B|A)=0.8则P(B|A)=##1、正确选项：0.7（15）若事件A和事件B相互独立,P(A)=α?,P(B)=0.3,,则α=##1、正确选项：3/7（16）设X~N(2,σ2),且P{2x4}=0.3,则P{x0}=##1、正确选项：2（17）一射手对同一目标独立地进行四次射击,若至少命中一次的概率为80/81,则该射手的命中率为##1、正确选项：2/3（18）三个人独立地解答一道难题,他们能单独正确解答的概率分别为1/5.1/3.1/4,则此难题被正确解答的概率为##1、正确选项：3/5（19）设有一箱产品由三家工厂生产的其中1/2是第一加工厂生产的,其余两家工厂各生产1/4,又知第一.第二工厂生产的产品有2%的次品,第三工厂生产的产品有4%的次品,现从箱中任取一只,则取到的次品的概率为##1、正确选项：2.5%（20）一个盒子中有10个球,其中有3个红球,2个黑球,5个白球,从中取球两次,每次取一个(有放回)则:第二次取到黑球的概率为##1、正确选项：0.2（21）由长期统计资料得知,某一地区在4月下雨(记事件A)的概率为4/15,刮风(记作事件B)概率为7/15,刮风又下雨(记作事件C)概率为1/10则:p(B|A)=## 1、正确选项：3/8（22）一盒子中黑球.红球.白球各占50%,30%,20%,从中任取一球,结果不是红球,则取到的是白球的概率为##1、正确选项：2/7（23）某公共汽车站甲.乙丙动人分别独立地等1.2.3路汽车,设每个人等车时间(单位分钟)均服从[0,5]上的均匀分布,则三人中至少有两个人等车时间不超过2分钟的概率为##1、正确选项：0.352（24）若随机变量X~(2,σ2)且p{2X4}=0.3,则p{X2}=##1、正确选项：0.5（25）若随机变量X~N(-1,1),Y~N(3,1)且X和Y相互独立,设随机变量Z=X-2Y+7,则Z~##.1、正确选项：N(0,5)（26）设随机变量X~N(1,22),则EX2=##1、正确选项：5计算题：（1）已知100个产品中有5个次品,现从中有放回地取3次,每次任取1个,求在所取的3个中恰有2个次品的概率.正确选项：（2）某人进行射击,设每次射击的命中率为0.02,独立射击400次,试求至少击中两次的概率.正确选项：的分布律为于是所求概率为（3）已知100个产品中有5个次品,现从中无放回地取3次,每次任取1个,求在所取的3个中恰有2个次品的概率.正确选项：（4）某一城市每天发生火灾的次数X服从参数的泊松分布,求该城市一天内发生3次或3次以上火灾的概率.正确选项：由概率的性质,得（5）某公共汽车站从上午7时起,每15分钟来一班车,即7:00,7:15,7:30,7:45等时刻有汽车到达此站,如果乘客到达此站时间X是7:00到7:30之间的均匀随机变量,试求他候车时间少于5分钟的概率.正确选项：以7:00为起点0,以分为单位,依题意为使候车时间少于5分钟,乘客必须在7:10到7:15之间,或在7:25到7:30之间到达车站,故所求概率为（6）某元件的寿命X服从指数分布,已知其平均寿命为1000小时,求3个这样的元件使用1000小时,至少已有一个损坏的概率.正确选项：由题设知,X的分布函数为由此得到各元件的寿命是否超过1000小时是独立的,用表示三个元件中使用1000小时损坏的元件数,则所求概率为（7）设某项竞赛成绩(65,100),若按参赛人数的10%发奖,问获奖分数线应定为多少?正确选项：设获奖分数线为则求使成立的即查表得解得故分数线可定为78.（8）设随机变量具有以下的分布律,试求的分布律.正确选项：Y所有可能的取值0,1,4,由即得Y的分布律为0140.10.70.2（9）已知随机变量X的分布函数,求正确选项：随机变量的分布密度为故（10）设,求标准正态分布的水平0.05的上侧分位数和双侧分位数.正确选项：由于查标准正态分布函数值表可得而水平0.05的双侧分位数为它满足:查标准正态分布函数值表可得分布.（11）设为X的一个样本,求:(1)样本均值的数学期望与方差;(2)正确选项：由于样本容量所以于是由得故（12）,则求常数A.期望EX及方差DX.正确选项：,得A=1。

(2021年整理)概率论与数理统计(经管类)综合试题1-5_(课程代码_4183)

（完整）概率论与数理统计(经管类)综合试题1-5_(课程代码_4183) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）概率论与数理统计(经管类)综合试题1-5_(课程代码_4183)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）概率论与数理统计(经管类)综合试题1-5_(课程代码_4183)的全部内容。

Ⅱ、综合测试题概率论与数理统计(经管类）综合试题一（课程代码 4183）一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.下列选项正确的是（ B ）.A 。

AB A B +=+ B.()A B B A B +-=-C 。

（A-B ）+B =A D. AB AB =2。

设()0,()0P A P B >>，则下列各式中正确的是（ D )。

A 。

P (A -B )=P （A )-P (B ） B.P （AB ）=P （A )P (B ）C. P (A +B )=P （A ）+P （B ）D. P (A +B )=P （A ）+P （B )-P (AB )3。

同时抛掷3枚硬币,则至多有1枚硬币正面向上的概率是（ D )。

A. 18B. 16C. 14D. 124.一套五卷选集随机地放到书架上，则从左到右或从右到左卷号恰为1，2，3，4，5顺序的概率为（ B ）。

A.1120 B. 160 C. 15 D. 125。

设随机事件A ，B 满足B A ⊂，则下列选项正确的是 ( A ）。

数理统计CH方差分析0000

2020/1/20
王玉顺：数理统计06_方差分析
8
6 方差分析
(3)多个独立正态总体均值相等检验犯第一类错误的概率
同理，a个独立正态总体均值相等假设等价于m个均值差假设同时成立：
H0 : 1 2
H01 : 1 2 0

a

H
02
:
1

3

0

a
m

2
nj
或N

j
,
2
nj

x

1 n
a j 1
nj i 1
xij
~
N

,
2
n

其中

1 n
a
njj
j 1
推论样本均值的概率分布
2020/1/20
王玉顺：数理统计06_方差分析
24
6.1 单向分组数据方差分析
两种统计假设等价
(4)单向分组数据统计假设
j j
xij j ij j +ij

ij
~
N (0,
2)

j 1,2,
,a；i 1,2,
,nj
推论xij ~ N ( j , 2 )或xij ~ N ( j , 2)
2020/1/20
王玉顺：数理统计06_方差分析
22
j 1
j 1
j 1
2020/1/20
王玉顺：数理统计06_方差分析
23
6.1 单向分组数据方差分析
(3)单向分组数据统计模型
xij j ij j ij xij ~ N j , 2

北京化工大学自动控制原理2015--2016,2020年考研初试真题

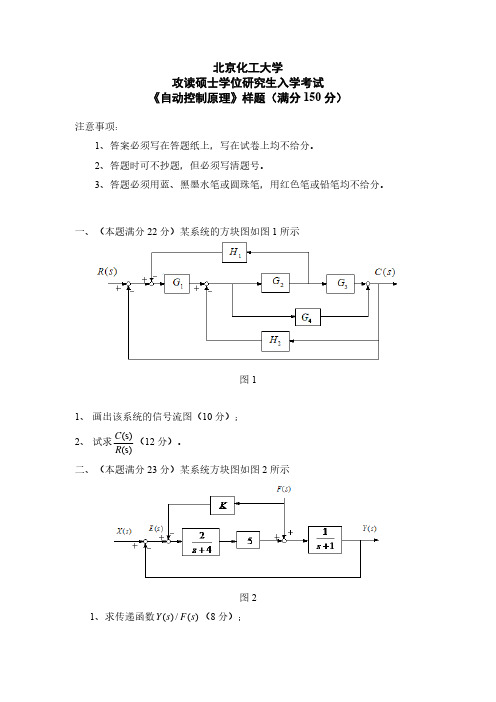
（3）（6 分）说明比例微分环节对系统稳定性的影响。
六、（15 分）考虑如下线性时不变系统：
x(t) = Ax(t)+ Bu(t)
y(t)
=
Cx(t ) +
Du(t
)
第2页共 4 页
北京化工大学 2015 年攻读硕士学位研究生入学考试《自动控制原理》试题
其中 A R22, B R2 1, C R1 2, D R1 。1
达式。（2）（4 分）判断系统的能控性和能观性。
八、（21 分）考虑如下系统：
2 1 1 1
x(t) = 0 1
0
x(t
)
+
0
u(t
)
1 0 0
0
（1）（7 分）根据可控性，对上述系统进行分解；
（2）（5 分）将可控部分的极点都配置在-1，请给出状态反馈增益矩阵
K1 ；
（3）（6 分）请解释能否将整个系统的三个极点都配置在-1；如果能，
G(s)
K (0.5s 1)2 (0.5s 1)(2s 1)
，
1、绘制系统的根轨迹（要求有计算过程）（8 分）；
2、确定系统稳定时 K 的取值范围（4 分）；
3、写出根轨迹分离点处对应的 K 值（3 分）。
五、(本题满分 15 分)
针对开环系统
G(s)
s
1
1
1、试设计一个连续控制器，使得闭环系统的自然频率为 1，且阻尼系数为 0.7。
（1）（5 分）试求数字控制器 D(z)的脉冲传递函数；（2）（5 分）试求采样系统的闭环脉冲传递函数；（3）（5 分）当 k=1，R(t)=t 时，试求系统的稳态偏差 E1() 。
九、（15 分）给定非线性系统 x x x 0 ，试分析该系统奇点的性质，

自考04183概率论与数理统计经管类总结2数理统计部份

高等教育自学考试辅导《概率论与数理统计（经管类）》第二部份数理统计部份专题一统计量及抽样的散布近几年试题的考点散布和分数散布最高分数分布最低分数分布平均分数分布样本的分布 2 1样本矩 2 1合计4/100 0/100 2/100一、整体与样本：所考察对象的全部称为整体；组成整体的每一个大体元素称为个体。

：从整体中随机抽取n个个体x1,x2…,x n称为整体的一个样本，个数n称为样本容量。

若是整体X的样本x1,x2…,x n知足：（1）x1与X有相同散布，i＝1，2，…，n；（2）x1,x2…,x n彼此独立，那么称该样本为简单随机样本，简称样本。

取得简单随机样本的方式称为简单随机抽样方式。

（1）联合散布函数：设整体X的散布函数为F（x），x1,x2…,x n为该整体的一个样本，那么联合散布函数为二、统计量及其散布1.统计量、抽样散布：设x1,x2…,x n为取自某整体的样本，假设样本函数T=T（x1,x2…,x n）不含任何未知参数，那么称T为统计量；统计量的散布称为抽样散布。

：设x1,x2…,x n为取自某整体X的样本，（2）样本均值的性质：①若称样本的数据与样本均值的差为偏差，则样本偏差之和为零，即②偏差平方和最小，即对任意常数C，函数时取得最小值.（5）样本矩（7）正态分布的抽样分布A.应用于小样本的三种统计量的分布的为自由度为n的X2散布的α分位点.求法：反查X 2散布表.[答疑编号1]答案：D[答疑编号2]答案：[答疑编号3]答案：B [答疑编号4]答案：1 [答疑编号5]答案：B [答疑编号6]解析：故填20. [答疑编号7]答案：n解析：[答疑编号8]答案：解析：此题考核正态散布的叠加原理和x2－散布的概念。

根据课本P82，例题3－28的结果，若X～N（0，1），Y～N（0,1）,且X与Y彼此独立，那么X＋Y～N（0＋0，1＋1）＝N（0，2）。

此题，已知X1、X2、X3、X4为来自整体X～N（0，1）的样本，因此X1、X2、X3、X4彼此独立且服从同散布N（0，1），那么X1+X2～N（0，2），X3+X4～N（0，2）；从而，,那么以下选项中正确的选项是（）[答疑编号9]答案：A解析：本题考察课本p140，4.一些重要结论。

北京交通大学22春“物流管理”《概率论与数理统计》期末考试高频考点版(带答案)试卷号：1

北京交通大学22春“物流管理”《概率论与数理统计》期末考试高频考点版（带答案）一.综合考核(共50题)1.对于任意两个随机变量X和Y，若E(XY)=EX*EY，则()。

A.D(XY)=DX*DYB.D(X+Y)=DX+DYC.X和Y相互独立D.X和Y互不相容参考答案：B2.相继掷硬币两次，则事件A={两次出现同一面}应该是()A.Ω={(正面，反面)，(正面，正面)}B.Ω={(正面，反面)，(反面，正面)}C.{(反面，反面)，(正面，正面)}D.{(反面，正面)，(正面，正面)}参考答案：C3.从0到9这十个数字中任取三个，问大小在中间的号码恰为5的概率是多少?()A.1/5B.1/6C.2/5D.1/8参考答案：B4.炮弹爆炸时产生大、中、小三块弹片。

大、中、小三块弹片打中某距离的装甲车的概率分别等于0.1，0.2，0.4。

当大、中、小三块弹片打中装甲车时其打穿装甲车的概率分别为0.9，0.5，0.01。

今有一装甲车被一块炮弹弹片打穿(在上述距离)，则装甲车是被大弹片打穿的概率是()A.0.761B.0.647参考答案：D5.若随机变量X服从正态分布N(a，b)，随机变量Y服从正态分布N(c，d)，则X+Y所服从的分布为正态分布。

()A.错误B.正确参考答案：B6.在参数估计的方法中，矩法估计属于()方法A.点估计B.非参数性C.极大似然估计D.以上都不对参考答案：A7.如果两个事件A、B独立，则()A.P(AB)=P(B)P(A∣B)B.P(AB)=P(B)P(A)C.P(AB)=P(B)P(A)+P(A)D.P(AB)=P(B)P(A)+P(B)参考答案：B8.二元正态分布的边缘概率密度是一元正态分布。

()A.错误B.正确参考答案：B设随机变量的数学期望E(ξ)=μ，均方差为σ，则由切比雪夫不等式，有{P(|ξ-μ|≥3σ)}≤()A.1/9B.1/8C.8/9D.7/8参考答案：A10.设g(x)与h(x)分别为随机变量X与Y的分布函数，为了使F(x)=ag(x)+bh(x)是某一随机变量的分布函数，在下列各组值中应取()A.a=3/5，b=-2/5B.a=-1/2，b=3/2C.a=2/3，b=2/3D.a=1/2，b=-2/3参考答案：A11.某单位有200台电话机，每台电话机大约有5%的时间要使用外线电话，若每台电话机是否使用外线是相互独立的，该单位需要安装()条外线，才能以90%以上的概率保证每台电话机需要使用外线时而不被占用。