流体力学综合实验台实验指导书
流体力学实验指导书

《流体力学》实验指导书目录实验装置简介及实验安排…………………………………………………… 1-2 实验一:伯努利方程验证实验………………………………………………… 3-8 实验二:雷诺实验…………………………………………………………… 9-12实验装置简介及实验安排实验装置:流体力学综合实验台是一个多功能实验装置,用此实验台可进行伯努利方程(能量方程)验证实验、雷诺实验、沿程阻力测定实验、局部阻力测定实验、毕托管测速实验和文丘里流量计实验等多个流体力学实验。
实验装置如图1-1所示。
1—供水箱,水泵;2—实验桌;3—层流测针;4—恒压水箱;5—彩色墨水罐;6—差压板;7—沿程阻力实验管;8—局部阻力实验管;9—伯努利实验管;10—雷诺实验管;11—伯努利差压板;12—毕托管;13—计量水箱;14—回水管。
图1-1 多功能流体力学综合实验台针对轮机工程专业36学时或32学时的流体力学课程,我们开设两个实验,即伯努利方程验证实验和雷诺实验。
在雷诺实验中,学生可以借助该实验装置观察层流和湍流(紊流)特征以及它们之间的转换特征,掌握测定临界雷诺数Re 的方法。
在伯努利方程实验中,学生可以借助该实验装置验证总流的伯努利方程,观察流体流动过程中的能量守恒关系,同时可以掌握流速、流量和压强等要素的实验量测技能。
实验学时分配:实验一:伯努利方程验证实验 2学时实验二:雷诺实验 2学时实验分组:每个实验7-8人一组,每个自然班分成四组。
实验一:伯努利方程验证实验一、实验目的1.掌握伯努利方程式中各项的物理意义及它们之间的转换关系; 2.验证流体总流的能量方程;3.掌握流速、流量、压强等动水力学水力要素的实验量测技术; 4.学习使用测压管、总压管测水头的实验技能及绘制水头线的方法。
二、实验原理1.伯努利方程(能量方程)在伯努利实验管路中沿水流方向取n 个过流断面。
在动能修正系数α近似取为1的情况下,可以列出进口断面(1)至任一断面(i )的能量方程式(i = 2,3,……,n )i ,i i i h gv p z g v p z -+++=++1f 2211122γγ (1)式中,z 、γp 和gv 22分别为位置水头(位头)、压力水头(压头)和速度水头(动头),单位为m (水柱);i ,h -1f 为从过流断面1到断面n 的水头损失,单位也是m (水柱)。
《流体力学》实验指导书

实验(一)流体静力学综合性实验一、实验目的和要求掌握用测压管测量流体静压强的技能;通过测量静止液体点的静水压强,加深理解位臵水头、压强水头、及测管水头的基本概念;观察真空现象,加深对真空度的理解;验证不可压缩流体静力学基本方程;测量油的重度。
二、实验装臵本实验装臵如图1.1所示图1.1流体静力学综合性实验装臵图1.测压管2.带标尺测压管3.连通管4.真空测压管5.U 型测压管6.通气阀7.加压打气球8.截止阀9.油柱 10.水柱 11.减压放水阀说明:1.所有测压管液面标高均以标尺(测压管2)零度数为基准;2.仪器铭牌所注▽B 、▽C 、▽D 系测点B 、C 、D 标高;若同时取标尺零点作为静力学基本方程的基准,则▽B 、▽C 、▽D 亦为ZB 、ZC 、ZD3.本仪器中所有阀门旋柄顺管轴线为开。
4.测压管读数据时,视线与液面保持水平,读凹液面最低点对应的数据。
三、实验原理1在重力作用下不可压缩流体静力学基本方程const γpz =+或h p p γ+=0式中:z —被测点在基准面以上的位臵高度;p —被测点的静水压强,用相对压强表示,以下同;0p —水箱中液面的表面压强γ—液体容重; h —被测点的液体深度。
上式表明,在连通的同种静止液体中各点对于同一基准面的测压管水头相等。
利用液体的平衡规律,可测量和计算出连通的静止液体中任意一点的压强,这就是测压管测量静水压强的原理。
压强水头γp和位臵水头z 之间的互相转换,决定了夜柱高和压差的对应关系:h γp ∆=∆ 对装有水油(图1.2及图1.3)U 型侧管,在压差相同的情况下,利用互相连通的同种液体的等压面原理可得油的比重So 有下列关系:21100h h h γγS w+==图1.2 图1.3据此可用仪器(不用另外尺)直接测得So 。
四、实验方法与步骤1.搞清仪器组成及其用法。
包括: 1)各阀门的开关;2)加压方法 关闭所有阀门(包括截止阀),然后用打气球充气; 3)减压方法 开启筒底阀11放水4)检查仪器是否密封 加压后检查测管1、2、5液面高程是否恒定。
流体力学实验指导书

《流体力学》实验指导书适用专业:环境工程专业前言一、实验的意义和目的实验是流体力学课程的组成部分之一。
流体力学问题是错综复杂的,其复杂性在于其影响因素很多。
由于人们对流体运动规律认识的局限性,因此还有许多问题并非由理论分析就能解决,往往有赖于实验;在某些场合,实验已成为解决问题的主要途径。
通过流体力学实验教学其目的在于加强学生对流动现象的感性认识,验证所学理论,提高理论分析能力;培养基本实验进呢过,了解现代量测技术;培养严谨踏实的科学作风。
二、实验须知1、实验前必须预习。
预习时,应仔细阅读实验指导书及有关的教材资料,明确实验的目的、要求和有关的实验原理,了解操作步骤和有关的仪器设备,做到心中有数。
2. 严肃认真的进行实验。
到实验室后,必须保持安静,不得谈笑喧哗,不准碰动与本实验无关的设备。
实验时,应按实验书的要求,全神贯注地按步骤进行操作,并注意多观察流体运动现象,多思考分析问题,及时记录实验原始数据。
3. 保持良好的科学作风,实验时,应尊重原始数据,不得任意更改;实验后,应进行必要的检查和补充,经指导教师同意后,方可离开实验室;应及时整理实验数据,认真编写实验报告。
由于时间仓促,水平有限,书中的缺点和错误在所难免,恳切希望读者批评指正。
目录实验一、流体静压强实验实验二、平面静水总压力实验实验三、能量方程实验实验四、动量方程实验实验五、沿程水头损失实验实验六、局部水头损失实验实验一:静水压强实验实验学时:1课时 实验类型:验证实验要求:必修 一、实验目的1、验证静止液体中,C gpZ =+ρ。
2、建立液体表面压强a p p >0,a p p <0的概念,并观察真空现象。
二、实验仪器三、实验原理、方法和手段静水压强测定及静水压强基本方程gh p p ρ+=0………(1) C gpZ =+ρ………(2) Z -被测点在基准面以上的位置高度; p -被测点的静水压强;0p -水箱中液面的表面压强; h -被测点的淹没深度利用等压面与连通器原理。
流体力学实验指导书

篇一:流体力学实验指导书1流体力学(水力学)实验指导书黎强张永东编西南大学工程技术学院建筑系二零零八年九月流体力学综合实验台简介流体力学综合实验台为多用途实验装置,其结构示意图如图1所示。
图1 流体力学综合试验台结构示意图1.储水箱2.上、回水管3.电源插座4.恒压水箱5.墨盒6.实验管段组7.支架8.计量水箱9.回水管 10.实验桌利用这种实验台可进行下列实验:一、雷诺实验;二、能量方程实验;三、管路阻力实验;1.沿层阻力实验2.局部阻力实验;四、孔板流量计流量系数和文丘里流量系数的测定方法;五、皮托管测流速和流量的方法。
一、雷诺实验1.实验目的(1)观察流体在管道中的流动状态;(2)测定几种状态下的雷诺数;(3)了解流态与雷诺数的关系。
2.实验装置本实验的实验装置为:(1)流体力学综合实验台;(2)雷诺实验台。
在流体力学综合实验台中,雷诺实验涉及的部分有高位水箱、雷诺数实验管、阀门、伯努力方程实验管道、颜料水(蓝墨水)盒及其控制阀门、上水阀、出水阀,水泵和计量水箱等,秒表及温度计自备。
雷诺实验台部件种类同综合实验台雷诺实验部分。
3.实验前准备(1)、将实验台的各个阀门置于关闭状态。
开启水泵,全开上水阀门,把水箱注满水,再调节上水阀门,使水箱的水有少量溢流,并保持水位不变。
(2)、用温度计测量水温。
4.实验方法(1)、观察状态打开颜料水控制阀,使颜料水从注入针流出,颜料水和雷诺实验管中的水迅速混合成均匀的淡颜色水,此时雷诺实验管中的流动状态为紊流;随着出水阀门的不断的关小,颜料水与雷诺实验管中的水渗混程度逐渐减弱,直至颜料水与雷诺实验管中形成一条清晰的线流,此时雷诺实验管中的流动为层流。
(2)测定几种状态下的雷诺系数全开出水阀门,然后在逐渐关闭出水阀门,直至能开始保持雷诺实验管内的颜料水流动状态为层流状态。
按照从小流量到大流量的顺序进行实验,在每一个状态下测量体积流量和水温,并求出相应的雷诺数。
流体力学实验指导书.

《流体力学》实验指导书郭广思王连琪沈阳理工大学2006年10月一伯努利方程综合性实验(一)实验目的伯努利方程是水力学三大基本方程之一,反映了水流在流动时,位能、压能、动能之间的关系。
1.了解总水头线和测压管水头线在局部阻力和沿程阻力处的变化规律;2.了解总水头线在不同管径段的下降坡度,即水力坡度J的变化规律;3.了解总水头线沿程下降和测压管水头线升降都有可能的原理;4.用实例流量计算流速水头去核对测压板上两线的正确性;不同管径流速水头的变化规律(二)设备简图本实验台由高位水箱、供水箱、水泵、测压板、有机玻璃管道、铁架、量筒等部件组成,可直观地演示水流在不同管径、不同高程的管路中流动时,上述三种能量之间的复杂变化关系。
(三)实验原理过水断面的能量由位能、压能、动能三部分组成。
水流在不同管径、不同高程的管路中流动时,三种能量不断地相互转化,在实验管道各断面设置测压管及测速管,即可演示出三种能量沿程变化的实际情况。
测压管中水位显示的是位能和压能之和,即伯努利方程中之前两项:gp Z ρ+,测速管中水位显示的是位能、压能和动能之和。
即伯努利方程中三项之和:gv g p Z 22++ρ。
将测压管中的水位连成一线,称为测压管水头线,反映势能沿程的变化;将测速管中的水位连成一线,称为总水头线,反映总能量沿程的变化,两线的距离即为流速水头g v 2/2。
本实验台在有机玻璃实验管道的关键部位处,设置测压管及测速管,适当的调节流量就可把总水头线和测压管水头线绘制于测压板上。
注:计算所的流速水头值是采用断面平均流速求得,而实测流速水头值是根据断面最大速度得出,显然实测值大于计算值,两者相差约为1.3倍。
(四)实验步骤1.开动水泵,将供水箱内之水箱至高位水箱;2.高位水箱开始溢流后,调节实验管道阀门,使测压管,测速管中水位和测压板上红、黄两线一致;3.实验过程中,始终保持微小溢流;4.如水位和红黄两线不符,有两种可能:一是连接橡皮管中有气泡,可不断用手挤捏橡皮管,使气泡排出;二是测速管测头上挂有杂物,可转动测头使水流将杂物冲掉。
《流体力学》实验指导书
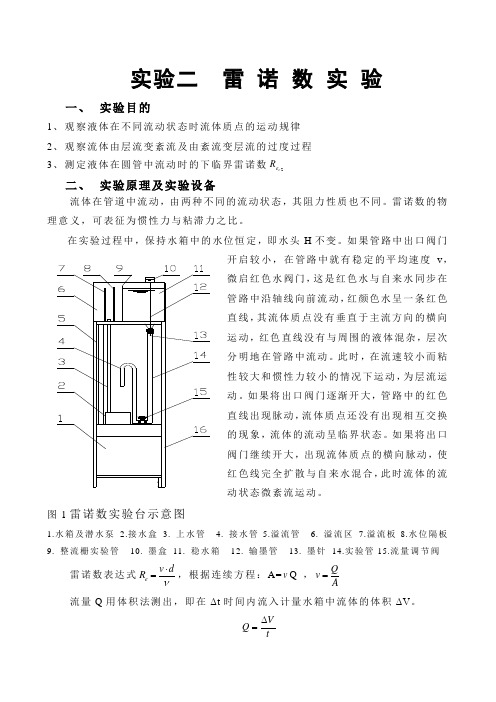
实验二 雷 诺 数 实 验一、 实验目的1、 观察液体在不同流动状态时流体质点的运动规律2、 观察流体由层流变紊流及由紊流变层流的过度过程3、 测定液体在圆管中流动时的下临界雷诺数2c e R二、 实验原理及实验设备流体在管道中流动,由两种不同的流动状态,其阻力性质也不同。
雷诺数的物理意义,可表征为惯性力与粘滞力之比。
在实验过程中,保持水箱中的水位恒定,即水头H 不变。
如果管路中出口阀门开启较小,在管路中就有稳定的平均速度v ,微启红色水阀门,这是红色水与自来水同步在管路中沿轴线向前流动,红颜色水呈一条红色直线,其流体质点没有垂直于主流方向的横向运动,红色直线没有与周围的液体混杂,层次分明地在管路中流动。
此时,在流速较小而粘性较大和惯性力较小的情况下运动,为层流运动。
如果将出口阀门逐渐开大,管路中的红色直线出现脉动,流体质点还没有出现相互交换的现象,流体的流动呈临界状态。
如果将出口阀门继续开大,出现流体质点的横向脉动,使红色线完全扩散与自来水混合,此时流体的流动状态微紊流运动。
图1雷诺数实验台示意图1.水箱及潜水泵2.接水盒3. 上水管4. 接水管5.溢流管6. 溢流区7.溢流板8.水位隔板9. 整流栅实验管 10. 墨盒 11. 稳水箱 12. 输墨管 13. 墨针 14.实验管15.流量调节阀雷诺数表达式e v dR ν⋅=,根据连续方程:A=v Q ,Qv A=流量Q 用体积法测出,即在Δt 时间内流入计量水箱中流体的体积ΔV 。
tVQ ∆=42d A π=式中:A —管路的横截面积;d —实验管内径;V —流速;ν—水的粘度。
三、实验步骤1、准备工作:将水箱充满,将墨盒装上墨水。
启动水泵,水至经隔板溢流流出,将进水阀门关小,继续向水箱供水,并保持溢流,以保持水位高度H 不变。
2、缓慢开启阀门7,使玻璃管中水稳定流动,并开启红色阀门9,使红色水以微小流速在玻璃管内流动,呈层流状态。
3、开大出口阀门15,使红色水在玻璃管内的流动呈紊流状态,在逐渐关小出口阀门15,观察玻璃管中出口处的红色水刚刚出现脉动状态但还没有变为层流时,测定此时的流量。
流体力学实验指导书

《流体力学实验指导书》一、电液比例综合测试实验台简介该实验台是根据《液压气动传动》通用教材设计而成,集可编程控制器和数据转换卡、液压元件模块为一体,除可进行常规的液压基本控制回路实验外,还可进行液压,组合应用实验及液压技术课程设计,元件的性能测试。
实验台配置了完备的各种类型传感器,包括压力传感器、流量传感器、转速传感器、功率传感器、位移传感器等,以满足各项实验参数测试的需要。
实验台是采用快速拼装结构,实验人员可根据实验项目原理图,选用相应的液压元件快速组成液压实验回路,通过电磁换向阀动作的控制和相关液压阀的调节进行实验。
实验台计算机测试控制系统实现实验参数(压力、流量、转速、功率、位移等)的自动数据检测、自动处理计算和存储等,还能实现回路电磁阀的自动控制,提高了实验台操作的自动化和智能化水平。
实验台可以同时进行16路实验数据的采集和8个二位电磁阀的控制。
1、性能与特点1、实验台采用台式结构,便利于多名学生的安装、测试。
2、操作平台面积大,可集成多个子系统。
3、阀体固定安装在操作平台上,管路连接采用快速接头,在背面连接,保证正面整洁。
4、实验用管件采用金属线,耐压胶管,压力可达到31.5Mpa。
5、测试方法实用、可靠。
实验装置由实验台架、液压泵站、电气测控单元等几部分组成。
3、液压站原理操作面板分布图A1.仪表数显区, A2.比例放大器与检测区,A3.PLC控制区, A4.传感器接口与手动控制区,A5.基础实验行程控制区, A6.液压站控制区。
5、数显区:功率表--—--定量叶片泵的实时功率。
转速表--—--定量叶片泵的实时转速。
流量表——--流过流量传感器的实时流量。
图A1 数显区分布图1、功率数显表;2、转速数显表;3、流量数显表;6.液压站控制区主系统控制区——定、变量泵的启动与停止,液压系统的供压与卸荷,冷却与加热以及总停的控制。
实验时先确定总停按钮为开启状态,即顺时钟旋转一定角度,自动升起为开。
流体力学综合实验装置实验指导书

《三》实验管道中液流循环如下 (见实验装置)
1 / 31
流体力学综合实验装置
1、实验台潜水泵供水到恒压水箱,水箱内液体分别由实验管 A(雷诺实验及沿 程阻力系数测定实验) 、实验管 B(伯努利方程实验) 、实验管 C(局部阻力系数测定实 验)、实验管 D 毕托管测流速、文丘里、孔板和毕托管实验) 经流量计流入辅助水箱, 再返回到供水水箱中循环使用。 2、雷诺实验:颜色水容器的颜色水径调节阀调节,进入实验管 A,随 A 管内的流 动水一起运动,显示有色的流线;经辅助水箱,辅助水箱排尽阀直接排入地沟; 3、实验中基准水平面的选取 用本实验装置做以上各项实验时,其基准水平面一律选择为工作台面板的上平面。 4、本实验指导书中各项实验所涉及的运算,均采用国际单位制。
《二》实验台参数
1、水泵:型号 HQB-4500;最大扬程:8m;最大流量:75L/min;额定功率 100W; 电源:单相~220V。 2、恒压水箱:长×宽×高=300×350×600; 3、实验管 A:管径内径 Φ14,长约 1.0 (m),雷诺数实验管; 4、实验管 B:小管内径 Φ14,大管内径 Φ30,轴线高度差 70,总长约 1.0 (m); 伯努利方程实验管; 5、实验管 C:管内径 Φ14,大管内径Φ30,总长约 1.0 (m);突然扩大和突然缩 小阻力测定;毕托管的测定速实验和文丘里实验; 6、实验管 D:管内径 Φ14,沿程损失实验管,沿程损失计算长度 L=0.75 (m); 7、实验管 E:管内径Φ14, 闸阀和弯头阻力实验管 8、实验台总尺寸:长×宽×高=1800×500×1700。
λ=64/Re
(2)对于水力滑管紊流流动可取
8 / 29
流体力学综合实验装置
=
0.3164 5 < Re ( ) 10 Re1/4
流体力学实验指导书( 建环专业)

目录实验一静水压强实验•••••••••••••••••••••••••••••••••••••••••••1实验二伯努利方程式的验证•••••••••••••••••••••••••••••••••••••3实验三雷诺实验••••••••••••••••••••••••••••••••••••••••••••••6实验四管道沿程阻力实验••••••••••••••••••••••••••••••••••••••9实验五管道局部阻力系数的测定••••••••••••••••••••••••••••••••12实验一静水压强实验(一)实验目的1、测定静止液体中某点的静水压强,加深对静压公式p=p0+γh的理解;2、测定有色液体的重度,并通过实验加深理解位置水头,压强水头及测压管水头的基本概念,观察静水中任意两点测压管水头Z+p/γ=常数。
p=p0+γh式中:P——被测点的静水压强;P0——水箱中水面的表面压强;γ——液体重度;h——被测点在表面以下的竖直深度。
可知在静止的液体内部某一点的静水压强等于表面压强加上液体重度乘以该点在液面下的竖直深度。
(四)实验步骤1、打开密封水箱E顶上空气阀门a,此时水箱内水面上的压强p0=p a。
观察各测压连通管内液面是否平齐,如果不齐则检查各管内是否阻塞并加以勾通。
2、读取A点、B点的位置高度Z A、Z B。
3、关闭空气阀门a,转动手柄,抬高长方形小水箱F至一定高度,此时表面压力P0>P a,待水面稳定后读各测压管中水位标高▽=▽I(I=1、2、3、4、5),并记入表中。
4、在保持P0>P a的条件下,改变长方形小水箱F高度,重复进行2-3次。
5、打开空气阀门a,使水箱内的水面上升,然后关闭空气阀门a,下降长方形小水箱。
6、在P0<P a的条件下,改变水箱水位重复进行2-3次。
(五)对表中数据进行分析单位:mm实验二 伯努利方程式的验证(一)实验目的:1、观察流体(水)在管内作恒定流动时,位置水头(Z )、压强水头(rp )和速度水头(V 2/2g )三者沿程变化的规律,加深对能量方程的理解。
流体力学综合实验指导书

流体力学综合实验实验指导书第 1 页共13页流体力学综合实验一、实验目的1)能进行光滑管、粗糙管、闸阀局部阻力测定实验,测出湍流区阻力系数与雷诺数关系曲线图;2)能进行离心泵特性曲线测定实验,测出扬程、功率和效率与流量的关系曲线图;3)学习工业上流量、功率、转速、压力和温度等参数的测量方法,使学生了解涡轮流量计、C1000、电动调节阀以及相关仪表的原理和操作;二、装置整体流程图:1-离心泵;2-进口压力变送器;3-铂热电阻(测量水温);4-出口压力变送器;5-电气仪表控制箱;6-均压环;7-粗糙管;8-光滑管(离心泵实验中充当离心泵管路);9-局部阻力管;10-管路选择球阀;11-涡轮流量计;12-局部阻力管上的闸阀;13-电动调节阀;14-差压变送器;15-水箱图1 实验装置流程示意图第 2 页共13页第 3 页 共 13页离心泵特性测定实验一、基本原理离心泵的特性曲线是选择和使用离心泵的重要依据之一,其特性曲线是在恒定转速下泵的扬程H 、轴功率N 及效率η与泵的流量Q 之间的关系曲线,它是流体在泵内流动规律的宏观表现形式。
由于泵内部流动情况复杂,不能用理论方法推导出泵的特性关系曲线,只能依靠实验测定。
1.扬程H 的测定与计算取离心泵进口真空表和出口压力表处为1、2两截面,列机械能衡算方程:f h gug p z H g u g p z ∑+++=+++2222222111ρρ (1-1)由于两截面间的管长较短,通常可忽略阻力项f h ∑,速度平方差也很小故可忽略,则有 (=H gp p z z ρ1212)-+- 210(H H H ++=表值)(1-2) 式中: 120z z H -=,表示泵出口和进口间的位差,m ;和ρ——流体密度,kg/m 3 ; g ——重力加速度 m/s 2;p 1、p 2——分别为泵进、出口的真空度和表压,Pa ;H 1、H 2——分别为泵进、出口的真空度和表压对应的压头,m ; u 1、u 2——分别为泵进、出口的流速,m/s ; z 1、z 2——分别为真空表、压力表的安装高度,m 。
流体力学实验指导书_2

实验一 雷诺实验一、实验目的与要求1、了解流体的流动形态:观察实际的流线形状,判断其流动形态的类型;2、熟悉雷诺准数的测定和计算方法;3、确立“层流与湍流与Re 之间有一定关系”的概念。
二、基本原理流体在流动过程中有3种不同的流动形态,即层流、湍流和介于两者之间的过渡流。
雷诺用实验的方法研究流体流动时,发现影响流体流动类型的因素除了流速u 以外,还有管径d 、流体的密度ρ以及粘度μ,由这四个物理量组成的无因次数群μρdu =Re称之为雷诺数。
实验证明,流体在直管内流动时:当Re ≤2000时,流体的流动类型为层流。
当Re ≥4000时,流体的流动类型为湍流。
当2000<Re <4000,流体的流动类型可能是层流,也可能为湍流,将这一范围称之为不稳定的过渡区。
从雷诺数的定义式来看,对于同一管路d 为定值时,u 仅为流量的函数。
对于流体水来讲,ρ及μ仅为温度的函数。
因此确定了温度及流量即可计算出雷诺数Re 。
三、实验装置及流程实验装置如图所示,实验时水从玻璃水槽3流进玻璃管4(内径20mm ),槽内水由自来水供应,供水量由阀6控制,槽壁外有进水稳定槽7及溢流槽10,过量的水进溢流槽10排入图1-3 雷诺示范实验装置1-红墨水瓶 2.6.8.12-阀门 3-玻璃水槽 4-带喇叭口玻璃管(Φ20) 5-进水管 7-进水稳定槽 9-转子流量计 10-溢流槽 11-排水管下水道。
实验时打开阀门8,水即由玻璃槽进入玻璃管,经转子流量计9后,流进排水管排出,用阀8调节水量,流量由转子流量计9测得。
高位墨水瓶贮藏墨水之用,墨水由经墨水调节阀2流入玻璃管4。
四、实验数据记录表表1-2 雷诺实验数据记录表水温__________[℃] 水粘度_______________[10-3×Pa·S]水密度_____________[kg/m3] 管内径_______________[mm]五、讨论1、流量从小做到大,当刚开始湍流,测出雷诺数是多少?与理论值2000有否差距?请分析原因。
流体力学实验指导书

实验一 能量转换实验一、实验目的1、熟悉流体在流动中各种能量和压头的概念及其转换关系,加深对伯努利方程的理解;2、观察流速随管径变化的规律。
二、实验原理1、全压头的分析:全压头为静压头与动压头之和,任意两截面间的能量方程为12222121w ,12v p v p Z Z h g 2g g 2g ρρ-++=++- 。
图一所示实验装置中,从实验可以观测到B 截面的全压头低于A 截面的全压头,这符合伯努利方程。
2、A 、B 截面间静压头的分析:由于两截面同处于一水平位置,B 截面面积比A 截面面积大。
这样B 处的流速比A 处小。
设流体从A 流到B 的压头损失为w ,A B h -以A-B 截面列伯努利方程。
22A AB Bw ,A B p v p v ()()h g 2g g 2gρρ-+=++ B A Z Z =22B A A B w ,A B p p v v ()()h g g 2g 2gρρ--=-- 即两截面处的静压头之差是由动压头减小和两截面间的压头损失来决定。
3、C 、D 截面间静压头的分析:出口阀全开时,在C 、D 间列伯努利方程,由于C 、D 截面积相等即动能相等,则: CD C D w ,C D p p ()(Z Z )h g gρρ--=-- C 、D 截面静压头的增大值,决定于)(D C Z Z -和w ,C D h -当)(D C Z Z -大于w ,C D h -时,静压头的增值为正,反之,静压头的增值为负。
4、压头损失的计算:以出口阀全开时,从C 到D 的压头损失w ,C D h -为例,在C 、D 两截面间列伯努利方程得:22C CD DC D w ,C D p v p v Z Z h g 2g g 2gρρ-++=+++ 所以,压头损失的算法之一是用全压头来计算: 22C CD D w ,C DC D p v p v h ()()(Z Z )g 2gg 2g ρρ-⎡⎤=+-++-⎢⎥⎣⎦压头损失的算法之二是用静压头来计算:(D C V V =) C Dw ,C D C D p p h ()(Z Z )g gρρ-=-+- 三、实验装置与设备参数 1、设备参数截面直径()mm以D 截面中心AB CD为基准面()mm第一套142814140=D ZA Z .、B Z 、110=C Z第二套142814140=D ZA Z .、B Z 、120=C Z2、实验装置图一 能量转换实验装置图四、实验方法与注意事项 1、实验方法:(1)向低位水槽灌注一定数量的蒸馏水,关闭水箱进水调节阀门及实验测试导管出口调节阀门,然后启动离心泵。
流体力学综合实验指导书

流体力学综合实验一、实验目的1.能进行光滑管、粗糙管、闸阀局部阻力测定,测出湍流区阻力系数与雷诺数关系曲线图;2.能进行离心泵特性曲线测定,测出扬程、功率和效率与流量的关系曲线图;3.学习工业上流量、功率、转速、压力和温度等参数的测量方法,了解涡轮流量计、C1000、电动调节阀以及相关仪表的原理和操作。
二、装置整体流程图:1-水箱;2-进口压力变送器;3-离心泵;4-出口压力变送器;5-涡沦流量计;6-管路选择球阀;7-均压环;8-连接均压环和压力变送器球阀;9-局部阻力管上的闸阀;10-差压变送器;11-出水管路闸阀;12-水箱放水阀;13-宝塔接头;14-温度传感器;15-离心泵的管路阀;16-旁路阀;17-电动调节阀;图1 实验装置流程示意图实验三、离心泵特性测定实验一、基本原理离心泵的特性曲线是选择和使用离心泵的重要依据之一,其特性曲线是在恒定转速下泵的扬程H 、轴功率N 及效率η与泵的流量Q 之间的关系曲线,它是流体在泵内流动规律的宏观表现形式。
由于泵内部流动情况复杂,不能用理论方法推导出泵的特性关系曲线,只能依靠实验测定。
1. 流量的测定流量是在实验过程中设定值,可直接设定流量3m 3/h ——12m 3/h 共取10组数据。
也可设定出口阀的开度从10%——100%共取10组数据。
2.扬程H 的测定与计算 取离心泵进口真空表和出口压力表处为1、2两截面,列机械能衡算方 程: fHgu gp z H gu g p z ∑+++=+++2222222111ρρ (1-1) 由于两截面间的管长较短,通常可忽略阻力项f H ∑,速度平方差也很小故可忽略,则有 (=H gp p z z ρ1212)-+- (1-2)式中: 12z z -,表示泵出口和进口间的位差,m ;ρ——流体密度,kg/m 3 ; g ——重力加速度 m/s 2;p 1、p 2——分别为泵进、出口的真空度和表压,Pa ; u 1、u 2——分别为泵进、出口的流速,m/s ; z 1、z 2——分别为真空表、压力表的安装高度,m 。
流体力学实验指导书

流体力学实验指导书《流体力学》课程实验指导书流体传动与控制研究所流体传动与控制实验室编学院:姓名:班级:学号:指导老师:武汉科技大学机械自动化学院二0一四年七月目录实验一、伯努力方程实验..............................................2 实验二、雷诺实验..........................................................5 实验三、沿程水头损失实验.................................. . (7)1实验一伯努力方程实验一、实验目的要求1.验证伯努力方程;2.通过对动水力学诸多水力现象的实验分析研讨,进一步掌握有压管流中动水力学的能量转换特性;3.掌握流速、流量、压强等动水力学水力要素的实验量测技能。
二、实验装置本实验的装置如下图所示。
本仪器测压管有两种:1.毕托管测压管(表1中标*的测压管),用以测读毕托管探头对准点的总水头,pv2?pu2?(因一般H??Z,须注意一般情况下H'与断面总水头H??Z2g?不同,?2g'u ≠ v),它的水头线只能定性表示总水头变化趋势;2.普通测压管(表1中未标*者),用以定量量测测压管水头。
实验流量用阀13调节,流量由体积时间法(量筒、秒表另备)、重量时间法(电子称另备)或电测法测量(以下实验类同)。
三、实验原理在实验管路中沿管内水流方向取n个过水断面。
可以列出进口断面(1)至另一断面(i)的能量方程(i=2,3,??,n)Z1?p11v122g?Zi?piivi22g?hw1?i2取α1=α2=?αn=1,选好基准面,从已设置的各断面的测压管中读出Z?p值,测出通过管路的流量,即可计算出断面平均流速v及?v22g,从而即可得到各断面测管水头和总水头。
四、实验方法与步骤1.熟悉实验设备,分清哪些测管是普通测压管,那些是毕托管测压管,以及两者功能的区别。
流体力学实验指导书20151007.(DOC)

工 程 流 体 力 学实验指导与实验报告姓 名:学 号:班 级:西南科技大学制造科学与工程学院中心实验室二零一五年十月目录实验说明 (I)TXZH-3型流体力学综合实验装置说明.............................................................................................. I I一、装置组成 (II)二、实验内容 (II)三、实验台参数 (II)四、实验装置组成 (III)实验一雷诺实验 (1)一、实验目的 (1)二、实验装置 (1)三、实验原理 (1)四、实验方法与步骤 (1)实验报告一雷诺实验 (4)1. 实验数据表 (4)2. 计算过程 (4)3. 实验结果分析 (5)4. 思考题 (5)实验二伯努利方程实验 (6)一、实验目的 (6)二、实验装置 (6)三、实验原理 (6)四、实验方法和步骤 (7)五、实验数据记录 (8)实验报告二伯努利方程实验 (9)1. 实验数据表 (9)2. 计算过程 (9)3. 实验结果分析 (10)4. 思考题 (11)实验三文丘里实验 (12)一、实验目的 (12)二、实验装置 (12)三、实验原理 (12)四、实验操作与步骤 (13)五、实验数据记录 (13)实验报告三文丘里实验 (14)1. 实验数据表 (14)2. 计算过程 (14)3. 实验结果分析 (15)4. 思考题 (15)实验说明工程流体力学实验作为《液压与气压传动》课程的随课实验,开设该实验的目的是通过本实验的教学,使学生初步了解流体力学的研究方法,学习流体力学实验中有关参数(如温度、流量、水位、测压管水头、总水头等)的测量;培养学生观测实验现象、正确记录与处理数据和运用所学知识分析实验结果的可靠性的能力。
通过实验验证工程流体力学主要理论的正确性,巩固加深对这些理论的理解。
培养学员严肃、认真的科学态度和严格、细致的工作作风。
流体力学综合实验台实验指导书.

流体力学综合实验流体力学综合实验台为多用途实验装置,其结构示意图如图1所示。
图1 流体力学综合试验台结构示意图1.储水箱2.上、回水管3.电源插座4.恒压水箱5.墨盒6.实验管段组7.支架8.计量水箱9.回水管10.实验桌利用这种实验台可进行下列实验:一、雷诺实验;二、能量方程实验;三、管路阻力实验;1.沿层阻力实验2.局部阻力实验;四、孔板流量计流量系数和文丘里流量系数的测定方法;五、皮托管测流速和流量的方法。
一、雷诺实验1.实验目的(1)观察流体在管道中的流动状态;(2)测定几种状态下的雷诺数;(3)了解流态与雷诺数的关系。
2.实验装置在流体力学综合实验台中,雷诺实验涉及的部分有高位水箱、雷诺数实验管、阀门、伯努力方程实验管道、颜料水(蓝墨水)盒及其控制阀门、上水阀、出水阀,水泵和计量水箱等,秒表及温度计自备。
3.实验前准备(1)、将实验台的各个阀门置于关闭状态。
开启水泵,全开上水阀门,把水箱注满水,再调节上水阀门,使水箱的水有少量溢流,并保持水位不变。
(2)、用温度计测量水温。
4.实验方法 (1)、观察状态打开颜料水控制阀,使颜料水从注入针流出,颜料水和雷诺实验管中的水迅速混合成均匀的淡颜色水,此时雷诺实验管中的流动状态为紊流;随着出水阀门的不断的关小,颜料水与雷诺实验管中的水渗混程度逐渐减弱,直至颜料水与雷诺实验管中形成一条清晰的线流,此时雷诺实验管中的流动为层流。
(2)测定几种状态下的雷诺系数全开出水阀门,然后在逐渐关闭出水阀门,直至能开始保持雷诺实验管内的颜料水流动状态为层流状态。
按照从小流量到大流量的顺序进行实验,在每一个状态下测量体积流量和水温,并求出相应的雷诺数。
实验数据处理举例:设某一工况下具体积流量Q=3.467×10-5m 3/s ,雷诺实验管内径d=0.014m ,实验水温T=5℃,查水的运动粘度与水温曲线,可知微v=1.519×10-6m 2/s 。
流体力学实验指导书(新版)

《水力学》实验教学指导书及报告姓名:班级:学号:唐山学院土木工程系序言水力学是应用性较强的专业技术基础课。
从学科的发展来看,水力学属于技术基础学科,实验方法和实验技术是促进其发展的重要研究手段。
由于流体运动的复杂性,水力学的研究及应用就更加离不开科学实验,其发展很大程度上取决于实验技术的进步。
因此,水力学实验是巩固和加深理论知识的学习、探求流体运动规律、解决工程实际问题的重要环节,通过实验教学,掌握各种实验方法,规范操作,提高实验技能。
一、实验教学目的:(1)观察流动现象,增强感性认识,提高实验分析能力。
(2)根据实测资料验证水力学基本理论,以加强和巩筑理论知识的学习。
(3)学会使用基本的测量仪器,掌握测量技术。
(4)培养分析实验数据,整理实验成果和编写实验报告的能力。
(5)培养严谨踏实的科学态度和合作精神,为未来进行研究和实际工作打下基础。
二、实验教学要求:(1)每次实验前,预习教材中有关内容及实验指导书,了解本次实验的目的、原理、步骤和所要验证的理论。
(2)认真听取指导教师讲解,弄清实验方法和步骤后,方能动手实验。
(3)实验中,应注意观察实验现象,细心读取实验数据,并做相应的记录,原始数据不得任意修改。
(4)实验小组内每位学生亲自动手、相互配合、共同完成实验。
(5)实验态度严肃、方法严密,一丝不苟进行操作。
(6)实验完毕应清理设备及实验室,实验设备摆放整齐。
三、实验报告要求:(1)实验报告是实验资料的总结、是实验的成果。
通过完成实验报告,可以提高分析问题的能力,要求必须独立完成并按规定时间交给指导教师。
(2)实验报告一般包括以下几项内容:①班级、姓名、同组人及实验日期。
②实验名称及实验目的。
③实验原理。
④实验装置简图及仪器。
⑤流动现象的描述及实验原始记录。
⑥计算实验结果。
(3)报告要求字体工整,语言通顺,计算结果无误,所绘表格、曲线清楚、连续,书面整洁,无胡乱涂画现象。
目录实验一水的流线、流动形态及能量转化实验(综合性实验) 实验二静水压强实验实验三雷诺实验实验四沿程阻力系数测定实验实验五局部阻力系数测定实验实验六文丘里流量计实验实验七恒定流动量定理实验实验一 水的流线、流动形态及能量转化实验(综合性实验)一、实验目的1.应用流动显示仪演示各种不同边界条件下的水流形态,以增强对流体运动特性的认识。
流体力学实验指导书-2011年

流体力学实验指导书(二)流体力学综合实验台为多用途实验装置,利用这种实验台可进行下列实验:一、雷诺数实验(必做);二、沿程水头损失与流速的关系(必做)三、能量方程验证实验(必做);四文丘里流量计校正实验其结构示意图如图0-1所示。
图0-1 流体力学综合试验台结构示意图1.储水箱2.上水流量调节阀3. 回水管4.恒压水箱5.颜料供给系统6.标尺组及滑板7.测压管固定板 8. 雷诺实验流量调节9.综合流量调节、切断阀10. 接水箱该实验装置流量计量采用体积法。
每次测定一定定容积和接水时间,从而计算实验过程中的流量或标准流量。
实验一、雷诺实验(必做)1、实验目的(1)观察流体在管道中的流动状态;(2)测定几种状态下的雷诺数;(3)了解流态与雷诺数的关系。
2、实验装置在流体力学综合实验台中,雷诺实验涉及的部分有高位水箱、雷诺数实验管、调节尾部阀门、颜料水(可由甲基兰配制或蓝墨水)盒及其控制阀门、上水阀、出水阀,水泵和计量水箱等,温度计自备。
能量方程实验管道上的阀门始终处于关闭状态。
3、实验前准备(1)、将实验台的各个阀门置于关闭状态。
开启水泵,全开水箱下的上水阀门,把水箱注满水,再调节上水阀门,使水箱的水有少量溢流,并保持水位不变。
(2)、用温度计测量水温。
图1-1 流体力学综合试验台雷诺实验示意图1.储水箱2.上水流量调节阀3.恒压水箱4.颜料流量调节阀5.墨盒6.实验管段7.流量调节阀8.计量水箱9.回水管 10.实验桌4、实验方法(1)、观察状态检查系统正常后,接通电源,打开水泵开关上水。
关闭能量方程实验管道上的阀门。
调节上水流量调节阀2使恒压水箱中的溢流板有少量溢流。
调节流量调节阀7,排除实验管内的气泡,然后把流量调小,约管内水为层流状态。
打开颜料水控制阀,使颜料水从注入针流出,颜料水和雷诺实验管中的水迅速混合成均匀的淡颜色水,此时雷诺实验管中的流动状态为紊流;随着出水阀门的不断的关小,颜料水与雷诺实验管中的水掺混程度逐渐减弱,直至颜料水与雷诺实验管中形成一条清晰的线流,此时雷诺实验管中的流动为层流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体力学综合实验流体力学综合实验台为多用途实验装置,其结构示意图如图1所示。
图1 流体力学综合试验台结构示意图1.储水箱2.上、回水管3.电源插座4.恒压水箱5.墨盒6.实验管段组7.支架8.计量水箱9.回水管10.实验桌利用这种实验台可进行下列实验:一、雷诺实验;二、能量方程实验;三、管路阻力实验;1.沿层阻力实验2.局部阻力实验;四、孔板流量计流量系数和文丘里流量系数的测定方法;五、皮托管测流速和流量的方法。
一、雷诺实验1.实验目的(1)观察流体在管道中的流动状态;(2)测定几种状态下的雷诺数;(3)了解流态与雷诺数的关系。
2.实验装置在流体力学综合实验台中,雷诺实验涉及的部分有高位水箱、雷诺数实验管、阀门、伯努力方程实验管道、颜料水(蓝墨水)盒及其控制阀门、上水阀、出水阀,水泵和计量水箱等,秒表及温度计自备。
3.实验前准备(1)、将实验台的各个阀门置于关闭状态。
开启水泵,全开上水阀门,把水箱注满水,再调节上水阀门,使水箱的水有少量溢流,并保持水位不变。
(2)、用温度计测量水温。
4.实验方法 (1)、观察状态打开颜料水控制阀,使颜料水从注入针流出,颜料水和雷诺实验管中的水迅速混合成均匀的淡颜色水,此时雷诺实验管中的流动状态为紊流;随着出水阀门的不断的关小,颜料水与雷诺实验管中的水渗混程度逐渐减弱,直至颜料水与雷诺实验管中形成一条清晰的线流,此时雷诺实验管中的流动为层流。
(2)测定几种状态下的雷诺系数全开出水阀门,然后在逐渐关闭出水阀门,直至能开始保持雷诺实验管内的颜料水流动状态为层流状态。
按照从小流量到大流量的顺序进行实验,在每一个状态下测量体积流量和水温,并求出相应的雷诺数。
实验数据处理举例:设某一工况下具体积流量Q=3.467×10-5m 3/s ,雷诺实验管内径d=0.014m ,实验水温T=5℃,查水的运动粘度与水温曲线,可知微v=1.519×10-6m 2/s 。
流 速 s m FQ V /255.0014.0410467.325=⨯⨯==-π 20756=-根据实验数据和计算结果,可绘制出雷诺数与流量的关系曲线(图2)。
不同温度下,对应的曲线斜率不同。
3)测定下临界雷诺数调整出水阀门,使雷诺实验管中的流动处于紊流状态,然后缓慢地逐渐关小出水阀门,观察管内颜色水流的变动情况。
当关小某一程度时,管内的颜料水开始成为一条线流,即为紊流转变为层流的下临界状态。
记录下此时的相应的数据,求出下临界雷诺数。
4)观察层流状态下的速度分布关闭出水阀门,用手挤压颜料水开关的胶管二到三下,使颜料水在一小段管内扩散到整的断面。
然后,在微微打开出水阀门,使管内呈层流流动状态,这是即可观察到水在层流流动时呈抛物状,演示出管内水流流速分布。
注:每调节阀门一次,均需等待稳定几分钟。
关小阀门过程中,只许渐小,不许开打。
随着出水流量减小,应当调小上水阀门,以减少溢流流量引发的振动。
二、能量方程实验1、实验目的(1)、观察流体流经能量方程实验管时的能量转化情况,并对实验中出现的现象进行分析,从而加深对能量方程的理解。
(2)、掌握一种测量流体流速的原理。
2、实验装置流体力学综合实验台中,能量方程实验部分涉及的有上水箱、能量方程实验管、上水阀门、出水阀门、水泵、测压管板(图中未给出)和计量水箱等。
3、实验前准备工作开启水泵,全开水阀门使水箱注满水,再调节上水阀门,使水箱水位始终保持不变,并有少量溢出。
4、实验方法(1)、能量方程实验调节出水阀门至一定开度,测定能量方程实验管的四个断面四组测压管的液柱高度,并利用计量水箱和秒表测定流量。
改变阀门的开度,重复上面方法进行测试。
根据测试数据的计算结果,绘出某一流量下各种水头线(如图3),并运用能量方程进行分析,解释各测点各种能头的变化规律。
可以看出,能量损失沿着流体流动方向增大的;Ⅰ与Ⅲ比较,两点管径相同,所以动能头基本相同,但Ⅲ点的压力能头比Ⅰ增大了,这是由于位置能转化而得来的;Ⅰ与Ⅱ比较,其位置能头相同,但Ⅱ点比Ⅰ点的压力能头大,这是图3 各种水头线由于管径变粗;速度减慢,动能头转化为压力能头;Ⅲ与Ⅳ比较,位置能头相同,但压力能头小了,可明显看出,是压力能头转化为速度能头了。
实验结果还清楚的说明了连续方程,对于不可压缩的流体稳定流动,当流量一定时,管径粗的地方流速小,细的地方流速大。
2)测速能量方程实验管上的四组测压管的任一组都相当与一个皮托管,可测得管内的流体速度。
由于本实验台将总测压管置与能量方程实验管的轴线,所以测得的动压水头代表了轴心处的最大速度。
皮托管求点速度的公式为:h==2gk2=c∆ku∆hcg式中u---毕托管测点处的点速度;c---毕托管的教正系数;∆h---毕托管全压水头与静水压水头差。
ϕg=2Hu∆联立上两式可得H∆''ϕ=/hc∆式中u--- 测点处流速,有毕托管测定;''ϕ---测点流速系数;∆---管嘴的作用水头;H在进行能量方程实验的同时,就可以测定出各点的轴心速度和平均速度。
测试结果记入表二中,如果用皮托管求出所在截面的理论平均速度,可根据该截面中心处的最大流速。
雷诺数与平均流速的关系,参考有关流体力学求出。
表2-1表2-2三沿程水头损失与流速的关系1.实验目的1)验证沿程水头损失与平均流速的关系。
2)对照雷诺实验,观察层流和紊流两种流态及其转换过程。
2.实验前准备工作将实验台个阀门置于关闭状态,开启实验管道阀门,将泵开启,检验系统是否有泄露;排放导压胶管中的空气。
3.实验原理对沿程阻力两测点的断面列能量方程w h g u a pg P Z g u a pg P Z +++=++2//2//2211112222 因实验管段水平,切为均匀流动: r w h h u u d d Z Z ====∴;;;212121得:h pg P pg P hr ∆=-=//21上式中: w h :测压管水头差即为沿程水头损失。
由此式求得沿程水头损失,同时根据实测流量计算平均流速V ,将所得w h ,V 数据点绘在对数坐标纸上,就可确定沿程水头损失与流速的关系。
4.实验步骤1)开启调节阀门,测读测压计水面差; 2)用体积法测量流量,并计算出平均流速;3)将实验的w h 与计算得出的u 值标入对数坐标纸内,绘出lgh r -lgu 关系曲线; 4)调节阀门逐次由大到小,共测定10次; 5.实验数据及曲线绘制仪器常数:d= cm, A= cm 2L= m, t= ℃表 3-178910四沿程阻力系数的测定单1 实验原理对沿程阻力两点的端面列能量方程得=hr∆=//-hPpgPpg12由达西公式:⋅⋅=λ/2gudLhr2/用体积法测得流量, 并计算出断面平均流速,即可求得沿程阻力系数λ2/2u L gdh r ⋅=λ2 实验步骤及要求1)本实验共进行粗细不同管径的两组实验,每组各作出6个实验; 2)开启进水阀门,使压差达到最大高度,作为第一个实验点; 3)测读水柱高度,并计算高度差; 4)用体积法测量流量,并测量水温;5)用不同符号将粗细管首的实验点绘制成lg$e-lg100λ对数曲线。
绘图:实验数据记录:d粗= cm,L= m vρKg/cm2 d细= cm,t= c水表4-1表4-2五 局部阻力损失实验1 实验目的1)掌握三点法,四点法测量局部阻力系数的技能;2)通过对圆管突扩局部阻力系数的包达公式和突缩局部阻力系数的经验公式的实验验证与分析,熟悉用理论分析法和经验法建立函数式的途径。
3)加深对局部阻力损失机理的解释; 2 实验原理写出局部阻力前后两断面的能量方程根据曲线推导条件,扣除沿程水头损失可得:1)突然扩大采用三点法计算,下式中21-f h 由32-f h 按流长比例换算得出: ]]2/)/[(]2/)/[(2122222111-+++-++=f ie h g au y p Z g au y p Z h]2//[21g au h ie e=ξ理论221)/1(A A e-=ξg au h e is 2/25==ξ2)突然缩小采用四点法计算,下式中B 点为突缩点,h f4-B 由h f3-4换算得出,h fB-5由h f5-6换算得出。
实测 ])2/)/[())2/)/[(5255542444--+++--++=fB B f fs h g au Y P Z h g au Y P Z h]2//[25g au h is s =ξ 经235)/1(5.0A A e-=ξg au h e is 2/25==ξ3 实验方法与步骤1)测记实验有关的常数。
2)打开水泵,排除实验管道中的滞留气体及测压管气体。
3)打开出水阀至最大开度,等流量稳定后,测记测压管读数,同时用体积法计量流量。
4)打开出水阀开度3-4次,分别测记压管读数及流量。
4 实验分析与讨论1)分析比较突扩与突缩在相应条件下的局部损失大小关系2)结合流动演示的水力现象,分析局部阻力损失机理何在?产生突扩与突缩局部阻力损失的主要部位在那里?怎样减小局部阻力损失。
表5-1表4-2六 阀门局部阻力系数的测定1 实验目的1)测定阀门不同开度时:全开,<30o , <45o 三种的阻力系数。
2)掌握局部阻力系数的测定方法。
2 实验原理对Ⅰ,Ⅳ两断面列能量方程式,可求得阀门的局部水头损失与2(I 1+I 2)长度上沿程水头损失之和,用h w1表示,则有下式:1411/)(h pg P P h w ∆=-=同理对Ⅱ,Ⅲ两断面列能量方程式,可求得阀门局部水头损失与L+L 2长度上的沿程水头损失之和,用h w2表示:2322/)(h pg P P h w ∆=-=所以阀们的局部水头损失ξh 应为122h h h ∆-∆=ξ亦12222/h h g ∆-∆=⋅μξ 所以阀门的局部阻力系数应为:212/2)2(μξg h h ⋅∆-∆=式中: μ为管道断面的平均流速。
3 实验步骤及要求1)本实验共进行三组实验,阀门全开,<30o , <45o 每组做三个实验点。
2)开启进水阀门,是压差达到测压计可测量的最大高度。
3)测读压差,同时用体积法测量流量。
4)每组各个实验点的压差值不要太接近。
5)变换阀门开启角度重复上述步骤。
6)绘制)(ξf a =曲线。
阀门局部阻力系数实验记录表6-1:七 文丘里流量计实验一 实验目的1)通过测定流量系数,掌握文丘里流量计测量管道流量的技术。
2)验证能量方程的正确性。
二 实验原理根据能量方程式和连续性方程式,可得不计阻力作用的文氏管过水能力关系式h K P Z P Z g d dd Q ∆=+-+-=)]()[(21)(4'221142121γγπ其中:1)(442121-=d dd K π)()(2211γγP Z P Z h +-+=∆ 式中:h ∆ 为两断面测压管水头差由于阻力的存在,实际通过流量Q 恒小于Q ’。
