运筹学最短路问题
合集下载
运筹学05_图与网络分析2-最短路
v4
v7
－1
42
终 点
lij
P(t)1j
起 v1 v2 v3 v4 v5 v6 v7 v8 t=1 t=2 t=3 t=4 点
v1 0 -1 -2 3 0 0 0 0
v2 6 0 2 -1 -5 -5 -5
v3 -3 0 -5 1 -2 -2 -2 -2
v4 8 0 2 3 -7 -7 -7
60
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 0 5 5 1 4 0 6 v5 2 3 0 v6 2 2 0
61
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 05 5 1 4 0 6 3 23 0 v6 2 2 0
54
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 v3 2 0 5 1 1 4 0 4 v5 2 3 0 v6 2 2 0
55
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 v3 2 0 5 1 1 4 0 4+2 v5 2 3 0 v6 2 2 0
0
2
7
1
5 3 5 55 7
1
3
3
1
4
6
7
5
12
③从已标号的点出发，找与这
(1,2)
2
些相邻点最小权数（距离）者， 找到之后：标号；边变红。
2
0
2
7
1
5 3 5 55 7
1
3
3
1
34 5 6
7
13
④重复上述步骤，直至全部的
(1,2)
点都标完。
2
2
0
2
运筹学——.图与网络分析-最短路
可选择的最短路为
(v5 , v6 ), (v5 , v7 ).
min{ k24, k34, k56, k57} min{9,10,13,14} 9
① 给(v2 , v4 )
划成粗
线②。给v4 标号（9）。
③ 划第5个弧。
v2 (4) 5 v4(9) 9 v6 (13)
4 4
v1 (0)
1
75
v2 (4)
5
v4
9
v6
4
1
v1 (0)
4
75
5
v8
①
64
1
②
v3(6)
7 v5 6
v7
③
3）接着往下考察，有三条路可走：(v1, v3 ), (v2, v4 ), (v2 , v5 ).
可选择的最短路为
min{ k13, k24, k25} min{l13, l12 d24,l12 d25} min{ 6,4 5,4 4} 6
第6章 图与网络分析
本章内容重点
图的基本概念与基本定理 树和最小支撑树 最短路问题 网络最大流
引
言
图论是应用非常广泛的运筹学分 支，它已经广泛地应用于物理学控制论，信 息论，工程技术，交通运输，经济管理，电 子计算机等各项领域。对于科学研究，市场 和社会生活中的许多问题，可以同图论的理 论和方法来加以解决。例如，各种通信线路 的架设，输油管道的铺设，铁路或者公路交 通网络的合理布局等问题，都可以应用图论 的方法，简便、快捷地加以解决。
若已知设备在各年的购买费，及不同机器役龄时的残值与 维修费，如表2所示.
项目 购买费 机器役龄 维修费 残值
第1年 11 0-1 5 4
运筹学课件 最短路、最大流、邮路
第i年 价格 ai 使用寿命 费用 bi 1 11 0－1 b1 5 2 11 1－2 b2 6 3 12 2－3 b3 8 4 12 3－4 b4 11 5 13 4－5 b5 18
最短路径问题的应用
例 设备更新问题
把求总费用最小问题化为最短路径问题。用点 i (i=1,2,3,4,5)表示第 i 年买进一台新 设备。增设一点 6 表示第五年末。从i点到i+1,……, 6 各画一条弧，弧（i , j）表示在 第 i 年买进的设备一直使用到第 j 年年初（第 j －1年年末）。求1点到6点的最短路径。 路径的权数为购买和维修费用。 弧（i , j）的权数为第i年的购置费ai＋从第i年使用至第j-1年末的维修费之和。 从第i年使用至第j-1年末的维修费：b1+…+bj-i
1 1 2 3 4 5 2 16 3 22 16
（使用寿命为j-i年） 具体权数计算结果如下：
5 41 30 23 17 6 59 41 31 23 18
如：（2－4）权数为：a2+b1+b2=11＋5＋6=22
4 30 22 17
通过一个网络的最短路径
例 设备更新问题 ：
2 16 30 22 41 4 23
最大流问题
两个重要结论： 1、任何一个可行流的流量都不会超过任一截集的容量。 2、若对于一个可行流f *，网络中有一个截集（ V1*，V1*）， 使v（ f *）=C(V1*，V1 *)，则f *必是最大流，而（ V1*， V1 *）必是所有截集中容量最小的一个，即最小截集。
定理：可行流f *是最大流，当且仅当不存在关于f *的增广链。 于是有如下结论：最大流量最小截量定理：任一个网络中，从vs 到vt的最大流量等于分离vs，vt的最小截集的容量。
最短路径问题的应用
例 设备更新问题
把求总费用最小问题化为最短路径问题。用点 i (i=1,2,3,4,5)表示第 i 年买进一台新 设备。增设一点 6 表示第五年末。从i点到i+1,……, 6 各画一条弧，弧（i , j）表示在 第 i 年买进的设备一直使用到第 j 年年初（第 j －1年年末）。求1点到6点的最短路径。 路径的权数为购买和维修费用。 弧（i , j）的权数为第i年的购置费ai＋从第i年使用至第j-1年末的维修费之和。 从第i年使用至第j-1年末的维修费：b1+…+bj-i
1 1 2 3 4 5 2 16 3 22 16
（使用寿命为j-i年） 具体权数计算结果如下：
5 41 30 23 17 6 59 41 31 23 18
如：（2－4）权数为：a2+b1+b2=11＋5＋6=22
4 30 22 17
通过一个网络的最短路径
例 设备更新问题 ：
2 16 30 22 41 4 23
最大流问题
两个重要结论： 1、任何一个可行流的流量都不会超过任一截集的容量。 2、若对于一个可行流f *，网络中有一个截集（ V1*，V1*）， 使v（ f *）=C(V1*，V1 *)，则f *必是最大流，而（ V1*， V1 *）必是所有截集中容量最小的一个，即最小截集。
定理：可行流f *是最大流，当且仅当不存在关于f *的增广链。 于是有如下结论：最大流量最小截量定理：任一个网络中，从vs 到vt的最大流量等于分离vs，vt的最小截集的容量。
管理运筹学 第7章 最短路实例
管 理 运 筹 学
8
§4 最大流问题
• 最大流问题：给一个带收发点的网络，其每条弧的赋权称之为容量， 在不超过每条弧的容量的前提下，求出从发点到收点的最大流量。 一、最大流的数学模型 例6 某石油公司拥有一个管道网络，使用这个网络可以把石油从采地 运送到一些销售点，这个网络的一部分如下图所示。由于管道的直径 的变化，它的各段管道（vi,vj）的流量cij（容量）也是不一样的。cij的 单位为万加仑/小时。如果使用这个网络系统从采地 v1向销地 v7运送石 油，问每小时能运送多少加仑石油？
2 0 0
2 0 2 1
3 v6 4
3 01
2
v7
3 5
3 1 v4
第五次迭代：选择路为v1 v2 v3 v5 v7 。弧（ v2 , v3 ）的顺流容 量为2，决定了pf=2，改进的网络流量图如下图：
1 v2 0 5 2 3 0 0 2 3 v5 2 0 0 0
管 理 运 筹 学
15
20
v1 1
3
(a)
图11-12
管 理 运
(b)
筹 学
(c)
5
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤：
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边（如果有两条或两条 以上的边都是权数最大的边，则任意去掉其中一条）。
3、如果所余下的图已不包含圈，则计算结束，所余下的图即 为最小生成树，否则返回第1步。
§2 最短路问题
例 设备更新问题。某公司使用一台设备，在每年年初，公司就要 决定是购买新的设备还是继续使用旧设备。如果购置新设备，就要支 付一定的购置费，当然新设备的维修费用就低。如果继续使用旧设备， 可以省去购置费，但维修费用就高了。请设计一个五年之内的更新设 备的计划，使得五年内购置费用和维修费用总的支付费用最小。 已知：设备每年年初的价格表
8
§4 最大流问题
• 最大流问题：给一个带收发点的网络，其每条弧的赋权称之为容量， 在不超过每条弧的容量的前提下，求出从发点到收点的最大流量。 一、最大流的数学模型 例6 某石油公司拥有一个管道网络，使用这个网络可以把石油从采地 运送到一些销售点，这个网络的一部分如下图所示。由于管道的直径 的变化，它的各段管道（vi,vj）的流量cij（容量）也是不一样的。cij的 单位为万加仑/小时。如果使用这个网络系统从采地 v1向销地 v7运送石 油，问每小时能运送多少加仑石油？
2 0 0
2 0 2 1
3 v6 4
3 01
2
v7
3 5
3 1 v4
第五次迭代：选择路为v1 v2 v3 v5 v7 。弧（ v2 , v3 ）的顺流容 量为2，决定了pf=2，改进的网络流量图如下图：
1 v2 0 5 2 3 0 0 2 3 v5 2 0 0 0
管 理 运 筹 学
15
20
v1 1
3
(a)
图11-12
管 理 运
(b)
筹 学
(c)
5
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤：
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边（如果有两条或两条 以上的边都是权数最大的边，则任意去掉其中一条）。
3、如果所余下的图已不包含圈，则计算结束，所余下的图即 为最小生成树，否则返回第1步。
§2 最短路问题
例 设备更新问题。某公司使用一台设备，在每年年初，公司就要 决定是购买新的设备还是继续使用旧设备。如果购置新设备，就要支 付一定的购置费，当然新设备的维修费用就低。如果继续使用旧设备， 可以省去购置费，但维修费用就高了。请设计一个五年之内的更新设 备的计划，使得五年内购置费用和维修费用总的支付费用最小。 已知：设备每年年初的价格表
10.3_最短路问题
B）Dijkstra算法和Ford算法都适用于任意边的情况 C）Dijkstra算法仅适用于所有边的权非负的情况，Ford算
法适用于所有边的权为任意实数的情况 D）Dijkstra算法适用于所有边的权为任意实数的情况，
Ford算法适用于所有边的权非负情况
29
OR:SM
试试看——选择题
• 2、以下说法中错误的是（ ）。
4
8
1
v4
vt
1
7
3
6
1
2
v6
7
OR:SM
vs
方式之一：单标号算法
第一步：
T(vs)=∞
v1
2
3
P(vs)=0 vs
9
10
4 7
T(vs)=∞
v2 1
4
3
v3
2
T(vs)=∞
T(vs)=∞
v5
8 1
v4 T(vs)=∞
7
vt T(vs)=∞
6
1
v6
T(vs)=∞
8
OR:SM
方式之一：单标号算法
第二步：
第4年 19 3-4 18
第5年 24 4-5 27
[解]设以vi(i=1,2,3,4,5)表示“第i年初购进一台新设备”这 种状态，以v6表示“第5年末”这种状态；以弧(vi, vj)表示 “第i年初购置的一台设备一直使用到第j年初”这一方案，以
wij表示这一方案所需购置费和维护费之和。于是，该问题就 可归结为从图中找出一条从v1到v6的最短路问题。其网络模型 如下：
本章小结
图论是应用十分广泛的运筹学分支，它已广泛应用在物 理、化学、控制论、信息论、科学管理、电子计算机等 各个领域。
法适用于所有边的权为任意实数的情况 D）Dijkstra算法适用于所有边的权为任意实数的情况，
Ford算法适用于所有边的权非负情况
29
OR:SM
试试看——选择题
• 2、以下说法中错误的是（ ）。
4
8
1
v4
vt
1
7
3
6
1
2
v6
7
OR:SM
vs
方式之一：单标号算法
第一步：
T(vs)=∞
v1
2
3
P(vs)=0 vs
9
10
4 7
T(vs)=∞
v2 1
4
3
v3
2
T(vs)=∞
T(vs)=∞
v5
8 1
v4 T(vs)=∞
7
vt T(vs)=∞
6
1
v6
T(vs)=∞
8
OR:SM
方式之一：单标号算法
第二步：
第4年 19 3-4 18
第5年 24 4-5 27
[解]设以vi(i=1,2,3,4,5)表示“第i年初购进一台新设备”这 种状态，以v6表示“第5年末”这种状态；以弧(vi, vj)表示 “第i年初购置的一台设备一直使用到第j年初”这一方案，以
wij表示这一方案所需购置费和维护费之和。于是，该问题就 可归结为从图中找出一条从v1到v6的最短路问题。其网络模型 如下：
本章小结
图论是应用十分广泛的运筹学分支，它已广泛应用在物 理、化学、控制论、信息论、科学管理、电子计算机等 各个领域。
运筹学论文最短路问题
运筹学论文——旅游路线最短问题摘要：随着社会的发展，人民的生活水平的提高，旅游逐渐成为一种时尚，越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节，是选择旅游时间最短，旅游花费最少还是旅游路线最短等问题随之出现，如何决策成为一道难题。
然而，如果运用运筹学方法来解决这一系列的问题，那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列，给出问题的解法，确定最短路线，实现优化问题。
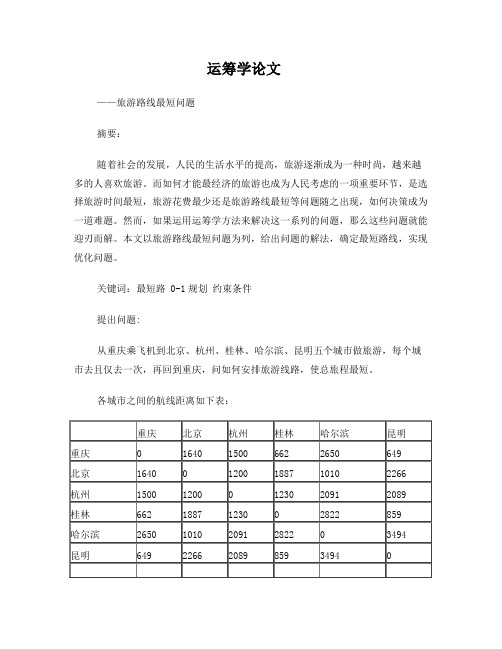
关键词：最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游，每个城市去且仅去一次，再回到重庆，问如何安排旅游线路，使总旅程最短。
各城市之间的航线距离如下表：问题分析：1．这是一个求路线最短的问题，题目给出了两两城市之间的距离，而在最短路线中,这些城市有的两个城市是直接相连接的（即紧接着先后到达的关系），有些城市之间就可能没有这种关系，所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了，有些则没有用。
这是一个0-1规划的问题，也是一个线性规划的问题。
2．由于每个城市去且仅去一次，最终肯定是形成一个圈的结构，这就导致了这六个城市其中有的两个城市是直接相连的，另外也有两个城市是不连接的。
这就可以考虑设0-1变量，如果两个城市紧接着去旅游的则为1，否则为0。
就如同下图3．因为每个城市只去一次，所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
LINGO解法：为了方便解题，给上面六个城市进行编号，如下表（因为重庆是起点，将其标为1）重庆北京杭州桂林哈尔滨昆明1 2 3 4 5 6假设：设变量x11。
如果x11=1,则表示城市i与城市j直接相连（即先后紧接到达关系），否则若x11=0，则表示城市i与城市j不相连。
特别说明：xij和xji是同一变量，都表示表示城市i与城市j是否有相连的关系。
这里取其中xij (i<j)的变量。
模型建立：由于这是一个最短路线的问题，且变量已经设好。
运筹学课件(第十讲)—最短路问题
如果P是D中从vs到vj的最短路，vi是P中的一点，那么从vs沿P到vi路也是 从vs到vi的最短路。
Dijkstra法的适用条件
求出一点到图中任意点最短路
求解思路
从vs出发，逐步地向外探索最短路。执行过程中，与每个点记下一个数， 它或者表示从vs到该点的最短路的权（称为P(perpetual)标号），或者是 从vs到该点的最短路的权的上界（称为T(temporary)标号），方法的每一 步是去修改T标号，并且把某一个T标号点改为P标号点，从而使D中P标 号顶点多一个，这样最多经过p-1步就可以求出从vs到各点的最短路。
（2）起点发出的流的总和(称为流量)，必须等于终点接收的流的总 和；
（3）各中间点流入的流量之和必须等于从该点流出的流量之和，即 流入的流量之和与流出的流量 之和的差为0，也就是说各中间点只 起转运作用，它既不产出新的物资，也不得截留过境的物资．
Operation Research
网络最大流的基本概念（3）
第八讲
Operation Research
网络最大流的基本概念（6）
增广链的基本概念
第八讲
Operation Research
第八讲
Operation Research
第八讲
Operation Research
实例：寻找图中增广链
第八讲
Operation Research
第八讲
网络最大流的基本概念（7）
运筹学课程
Operation Research
最短路问题
定义
第八讲
求最短路有两种算法，一是求从某一点至其他各点之间最短距离的Dijkstra(狄 克斯屈拉)算法；另一种是求网络图上任意两点之间最短距离的矩阵算法.
Dijkstra法的适用条件
求出一点到图中任意点最短路
求解思路
从vs出发，逐步地向外探索最短路。执行过程中，与每个点记下一个数， 它或者表示从vs到该点的最短路的权（称为P(perpetual)标号），或者是 从vs到该点的最短路的权的上界（称为T(temporary)标号），方法的每一 步是去修改T标号，并且把某一个T标号点改为P标号点，从而使D中P标 号顶点多一个，这样最多经过p-1步就可以求出从vs到各点的最短路。
（2）起点发出的流的总和(称为流量)，必须等于终点接收的流的总 和；
（3）各中间点流入的流量之和必须等于从该点流出的流量之和，即 流入的流量之和与流出的流量 之和的差为0，也就是说各中间点只 起转运作用，它既不产出新的物资，也不得截留过境的物资．
Operation Research
网络最大流的基本概念（3）
第八讲
Operation Research
网络最大流的基本概念（6）
增广链的基本概念
第八讲
Operation Research
第八讲
Operation Research
第八讲
Operation Research
实例：寻找图中增广链
第八讲
Operation Research
第八讲
网络最大流的基本概念（7）
运筹学课程
Operation Research
最短路问题
定义
第八讲
求最短路有两种算法，一是求从某一点至其他各点之间最短距离的Dijkstra(狄 克斯屈拉)算法；另一种是求网络图上任意两点之间最短距离的矩阵算法.
运筹学-14最短路
9
[1,v1]
[9,v5] [12,v5] [10,v5]
v1 v3 v2 v5 v8 12
v1 v9Leabharlann • 有向图的最短路问 题我会了，可是无
向图的最短路问题 怎样求？
最短路问题
• 一个旅行者从城市V1出发到V10，各城市之间的 距离如图所示，问如何确定旅行路线，才能使
总旅程最短？
2. X,X ’= 3. v9标号[]
求从v 1到各点的最短路(3)
v1 v3 v2
5
v1 v3
3
[5,v3]
[6,v2]
[]
v1 v4
1
v1 v3 v2 v5
6
v1 v3 v2 v5 v6
v1 v3 v2 v5 v7
[0,0]
[3,v1]
10
一旦找到v的最短路就把顶点v割是一个弧集每一条弧计算kijij最小到不了该点标号法dijkstrs算法到各点的最短路11v标号00002minxxminvmin06321105到各点的最短路200min6463661101091211min6466110941012111310vmin66941213到各点的最短路300有向图的最短路问题我会了可是无向图的最短路问题怎样求
(1, V1)
标号法
(10, V4)
[0，0]
(9,V7) (5, V8)
(8, V6)
(3,V1)
(11, V8)
V3：(10,V4) X=V1,V2,V8,V6,V7,V4,V3, X’=V5,V9,V10
(X,X’)={(V8,V9)(V7,V9)(V7,V10)(V3,V10)(V4,V5)(V7,V5)(V3,V5)}