运筹学论文最短路问题
最优算法中的最短路问题讨论

最优算法中的最短路问题讨论
最优算法是在给定的图中找到两个节点之间的最短路径的一种方法。
最短路问题是图论中的经典问题,有很多不同的算法可以解决它。
最著名且常用的最短路径算法是Dijkstra算法和A*算法。
Dijkstra算法是一种用于在带权有向图中找到从一个节点到其
他节点的最短路径的算法。
它基于贪婪算法的思想,通过不断选择当前路径中权重最小的节点来逐步构建最短路径。
Dijkstra算法适用于边权重非负的情况。
A*算法是一种更高效的最短路径算法,它结合了Dijkstra算法的贪婪策略和启发式(heuristic)函数的估计来减少搜索空间。
A*算法通过估计每个节点到目标节点的剩余距离来确定下一
步选择的节点,从而更快地找到最短路径。
A*算法适用于边
权重非负且有启发式函数可以使用的情况。
除了Dijkstra算法和A*算法之外,还有其他一些用于解决最
短路径问题的算法,如Bellman-Ford算法和Floyd-Warshall算
法等。
在选择最优算法时,需要考虑图的规模、边权重的分布、需求的时间和空间复杂度等因素。
不同算法在不同场景下的表现也会有所不同。
因此,选择最合适的最短路径算法需要综合考虑这些因素。
最短路问题的求解方法

最短路问题的求解方法最短路问题是图论中的一个经典问题,它在很多实际应用中都有着重要的作用。
在现实生活中,我们经常需要求解最短路径,比如在地图导航、网络通信、交通运输等领域。
因此,研究最短路问题的求解方法具有重要的理论意义和实际应用价值。
在图论中,最短路问题的求解方法有很多种,其中比较经典的有Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
这些算法各有特点,适用于不同的场景和要求。
下面我们就逐一介绍这些算法的原理和求解方法。
Dijkstra算法是一种用于求解单源最短路径的算法,它采用贪心策略,每次找到当前距离最短的节点进行松弛操作,直到所有节点都被遍历。
Dijkstra算法的时间复杂度为O(V^2),其中V为节点的个数。
这种算法适用于边权值为正的图,可以求解从单个源点到其他所有点的最短路径。
Bellman-Ford算法是一种用于求解单源最短路径的算法,它可以处理边权值为负的图,并且可以检测负权回路。
Bellman-Ford算法的时间复杂度为O(VE),其中V为节点的个数,E为边的个数。
这种算法适用于一般情况下的最短路径求解,但是由于其时间复杂度较高,不适用于大规模图的求解。
Floyd-Warshall算法是一种用于求解所有点对最短路径的算法,它可以处理边权值为正或负的图,但是不能检测负权回路。
Floyd-Warshall算法的时间复杂度为O(V^3),其中V为节点的个数。
这种算法适用于求解图中所有点对之间的最短路径,可以同时求解多个源点到多个目标点的最短路径。
除了上述几种经典的最短路求解算法外,还有一些其他的方法,比如A算法、SPFA算法等。
这些算法在不同的场景和要求下有着各自的优势和局限性,需要根据具体情况进行选择和应用。
在实际应用中,最短路问题的求解方法需要根据具体的场景和要求进行选择,需要综合考虑图的规模、边权值的情况、时间效率等因素。
同时,对于大规模图的求解,还需要考虑算法的优化和并行化问题,以提高求解效率。
网络最短路的解集结构及有关问题

郑州大学硕士学位论文网络最短路的解集结构及有关问题姓名:张振坤申请学位级别:硕士专业:运筹学与控制论指导教师:罗来兴;林诒勋2002.5.1中文摘要网络最短路问题是一个基本的离散最优化问题,一般的有限状态多阶段决策过程都可以转化为它。
因此,最短路问题有着很广泛的应用意义。
f其定义如下㈨:给定一个有向或无向图(网络)N=(V,A)和每一个弧ej∈A上的非负权。
;>/o,其中y为点集,A为弧集。
最短路问题就是求从一个始点s到另一个终点t的一条路,使得路上弧的总权和最/j,J本文所研究的问题是对网络最短路问题的进一步讨论,由以下3个部分组成:1.网络最短路的最优镌.0瞄;2.网络最短路的曩垡童掺结构;3.多端最短路的缝蕉攥型。
(1.网络最短路的最优解邻域\文[6,9]介绍了第k条最短路的概念和算法。
在此基础上,第二章讨论了最短路的最优解邻域的求解问题,得到了求解一个网络N的等势网络N。
的算法思想、求解网络N的所有最短路的算法2.1以及求解所有处于最优解邻域中的非最短路的算法2.2。
定理1网络N的等势网络N。
包含N中所有的(s。
t)最短路,并且N。
可以在多项式时间内找到,算法复杂性为O(m),其中m=IAI。
定理2在网络N的任意一条长度小于或等于£‘+e的(5,t)路中,任意中间顶点{的位势嘶必小于或等于z。
+e。
定理3在网络Ⅳ中,对任意一条通过顶点i∈V\“的路P,若路P的路长z≤£。
+e,则必有”f+?ti7≤Z’+£2网络最短路的最优解集结构本文在第三章中研究了网络最短路的最优解集结构:首先讨论了一个网络N具有唯一一条最短路的充要条件;其次,借助于2一变换的定义,着重探讨了网络最短路的2一变换图的结构性质。
定理4对等势予网络N。
中一个(s,t)有向路P,它是N中唯一一条最短路的充分必要条件是:在N。
中不存在起点和终点都在P上的等长2一重路。
定理5网络N的最短路2一变换图为平凡图,当且仅当网络N只有一条最短路。
最短路问题实际案例

最短路问题实际案例介绍最短路问题是图论中的一个经典问题,其目标是找到两个顶点之间的最短路径。
这个问题在日常生活中有着广泛的应用,例如导航系统、网络路由以及物流配送等场景中都需要解决最短路问题。
本文将通过实际案例来深入探讨最短路问题及其应用。
什么是最短路问题?最短路问题是指在一个给定的图中,找到两个顶点之间的最短路径。
通常情况下,路径的长度可以通过边的权重来衡量。
最短路问题可以分为单源最短路问题和全源最短路问题,前者是指从一个固定的起点出发,求到图中其他所有顶点的最短路径;后者是指求图中任意两个顶点之间的最短路径。
实际案例:导航系统导航系统是最短路问题的一个典型应用。
当我们使用导航系统来规划路线时,系统需要找到最短路径以优化我们的行车时间。
下面以一个具体案例来说明导航系统如何解决最短路问题。
案例场景假设我们身处一座陌生的城市,想要前往城市中心的一个著名景点。
我们打开导航系统,输入起点和终点信息。
导航系统会根据地图数据自动生成最短路径,并提供导航指引。
导航系统的实现导航系统实现最短路径规划的过程可以分为以下几个步骤:1.构建路网图:将城市中的道路以及交叉口等信息转化为图的形式。
图中的节点表示交叉口,边表示道路,边的权重可以表示行驶距离、时间等。
2.选择算法:根据实际需求选择合适的最短路径算法。
常见的算法有Dijkstra算法、Bellman-Ford算法和A*算法等。
3.计算最短路径:根据选定的算法,在路网图上计算起点到终点的最短路径。
算法会考虑边的权重以及路径的方向等因素。
4.导航指引:根据计算得到的最短路径,导航系统会生成具体的导航指引,包括行驶指示、路口转向、距离和预计时间等信息。
优化策略导航系统通过不断的优化,提高了最短路径的计算效率和准确性。
以下是几种常见的优化策略:1.路网数据更新:导航系统会及时更新路网数据,包括道路信息、交通状况等。
这样可以保证计算得到的最短路径更准确。
2.平行算法:为了加快计算速度,导航系统采用并行算法来计算最短路径。
最短路问题(整理版)

最短路问题(short-path problem)若网络中的每条边都有一个权值值(长度、成本、时间等),则找出两节点(通常是源节点与结束点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题,我们通常归属为三类:单源最短路径问题(确定起点或确定终点的最短路径问题)、确定起点终点的最短路径问题(两节点之间的最短路径)1、Dijkstra算法:用邻接矩阵a表示带权有向图,d为从v0出发到图上其余各顶点可能达到的最短路径长度值,以v0为起点做一次dijkstra,便可以求出从结点v0到其他结点的最短路径长度代码:procedure dijkstra(v0:longint);//v0为起点做一次dijkstrabegin//a数组是邻接矩阵,a[i,j]表示i到j的距离,无边就为maxlongintfor i:=1 to n do d[i]:=a[v0,i];//初始化d数组(用于记录从v0到结点i的最短路径), fillchar(visit,sizeof(visit),false);//每个结点都未被连接到路径里visit[v0]:=true;//已经连接v0结点for i:=1 to n-1 do//剩下n-1个节点未加入路径里;beginmin:=maxlongint;//初始化minfor j:=1 to n do//找从v0开始到目前为止,哪个结点作为下一个连接起点(*可优化) if (not visit[j]) and (min>d[j]) then//结点k要未被连接进去且最小begin min:=d[j];k:=j;end;visit[k]:=true;//连接进去for j:=1 to n do//刷新数组d,通过k来更新到达未连接进去的节点最小值,if (not visit[j]) and (d[j]>d[k]+a[k,j]) then d[j]:=a[k,j]+d[k];end;writeln(d[n]);//结点v0到结点n的最短路。
运筹学论文最短路问题
运筹学论文——旅游路线最短问题摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
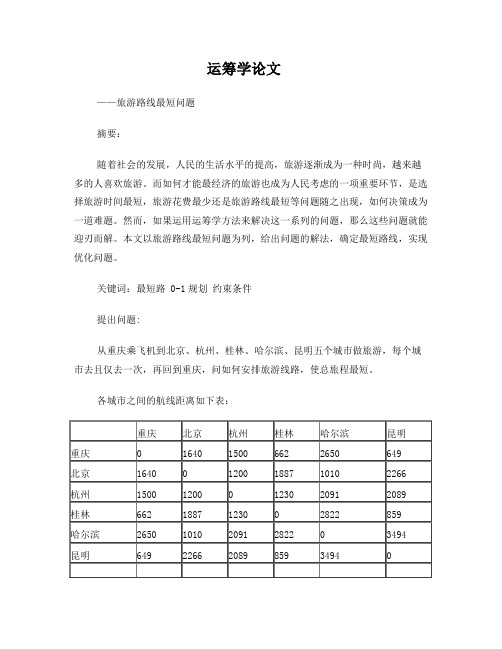
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图3.因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
LINGO解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)重庆北京杭州桂林哈尔滨昆明1 2 3 4 5 6假设:设变量x11。
如果x11=1,则表示城市i与城市j直接相连(即先后紧接到达关系),否则若x11=0,则表示城市i与城市j不相连。
特别说明:xij和xji是同一变量,都表示表示城市i与城市j是否有相连的关系。
这里取其中xij (i<j)的变量。
模型建立:由于这是一个最短路线的问题,且变量已经设好。
运筹学05_图与网络分析2-最短路

根 据 Dijkstra 算 法 , 可 以 得 出 从 v1 到 v2 最 短路权是2,但是这显然不对,因为从v1到 v2的最短路是(v1, v3, v2),权是-1。
2
v1
v2
2
-3
vh 3
38
有向图某些权值为负
逐次逼近算法
1、先对图中各个点按照Dijkstra算法标号,称之为第 一次标号,令m=1,转入第二步;
2.5
3
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
27
v5
3
5
3
3 0 v1
v2
3
2
v6
2.5
3
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
28
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
29
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
h
60
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 0 5 5 1 4 0 6 v5 2 3 0 v6 2 2 0
h
61
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 05 5 1 4 0 6 3 23 0 v6 2 2 0
最短路问题的实际应用论文

金华双龙洞旅游路线中最短路问题摘要:金华双龙洞景点分布较多,通过对其旅游路线的设置,转化为图论内容中的最短路情景进行讨论,建立模型,并通过搜索资料,利用几种方法解决路线最小的问题。
关键字:数学建模最短路问题 lingo Dijkstra法 flod算法一、研究背景:在旅游过程中,我们常常感觉到自己一天下来走了很多路,回到宾馆脚痛的不行。
但其实我们可以利用运筹学的知识,通过建立数学模型,转化为图论的内容。
从而较为合理的制定出选择的路线(即最短路问题)。
因而这次的小论文,我主要探究一下几个问题:1.从景点进口到出口的最短路程。
(最短路问题)2.从景点到出口的最长路线。
3.建立的模型是否满足能回到起点(古典图论问题)二、研究内容:根据从互联网中搜索的资料,金华双龙洞的主要景点:景区进口双龙洞,冰壶洞,朝真洞,桃源洞,黄大仙祖宫五个,其余为小景点(若要加入,同样可以按照以下问题的研究方法进行讨论)现在忽略。
问题总假设:分别设置双龙洞,冰壶洞,朝真洞,桃源洞,黄大仙祖宫五个景点为A,B,C,D,E五点,根据现实及假设,可以得到如图所示的路线图:再利用用Dijkstra算法求解无负权网络的最短路。
同时也可以利用此法算出最长路程。
问题一的解决:以A为景点出口,E为出口。
故A点标号为P(a)=0 给其余所有的T标号T(i)=+∞考虑与A相邻的两个顶点BC,两个顶点为T标号,故修改这两个点的标号为:T(b)=min[T(b),P(a)+l12]=min[+∞,0+3]=3T(c)=min[T(c),P(a)+l13]=min[+∞,0+2]=2比较所有T标号,T(c)最小,所以令P(c)=2再考察(C,B)(C,D)(C,E)的端点:同理可得T(b)=6 T(d)=6.8 T(e)=10.2(显然已经到终点但还需要看看其余路线长短)故又令P(b)=6.综合分析只有一条线路即A→C→B→D→E 此时总路程为2+4+3+8.4=16.4>10.2所以,最短路程为A→C→E。
最短路问题

[网络图中最短路问题—专题研究报告!报告人:张鹏学号:班级:035109012011年5月12日%…网络图中最短路问题…【问题导引】网络分析在电子导航、交通旅游、城市规划以及电力、通讯等各种管网、管线的布局设计中发挥了重要作用。
而最短路问题是网络分析中最基本、最关键的问题。
最短路径不仅指一般地理意义上的距离最短,还可以引申到其他的度量,如时间,费用等等。
这些都可以抽像为在图中找出任意两点间的一条通路,使这条通路上的权值和最小。
最短路问题作为图与网络技术研究的一个经典问题,在工程规划、地理信息系统、通信和军事运筹学等领域有十分广泛的应用。
举例如下:}【案例一】:如图的交通网络,图中的点表示交通节点,每条边表示两个节点间的一条通路,边上的数字表示路段的长度,有向边表示单行道,无向边表示可双向行驶。
若有一批货物要从1号顶点运往11号顶点,问运货车应沿哪条线路行驶,才能最快地到达目的地【案例分析与建模】:这是实际生活中经常遇到的一类问题,首先对该问题做如下假设以便抽象为数学模型。
假设一:各路段路况相同,车辆在各路段以相同的速度行驶。
~假设二:各路段均一路畅通,即不存在堵车问题。
在以上两种假设的前提下,此问题即转化为在图中选一条从节点1到节点11的通路,使得路径总长度最短,即典型的最短路问题模型。
将图抽象为距离矩阵表示,即可建立数学模型,设计算法求解。
【算法设计】:对于最短路模型,传统的Dijkstra算法和floyd算法为两种有效的求解方法。
利用Dijkstra算法求解案例一中的问题。
!算法思路:采用标号作业法,每次迭代产生一个永久标号, 从而生长一颗以v0为根的最短路树,在这棵树上每个顶点与根节点之间的路径皆为最短路径。
S: 具有永久标号的顶点集;l(v): v的标记;f(v):v的父顶点,用以确定最短路径;"输入:输入加权图的带权邻接矩阵w=[w(vi,vj)]nxm.1)初始化:令l(v0)=0,S=Ø; v≠v0 ,l(v)= ;2)更新l(v), f(v):寻找不在S中的顶点u,使l(u)为最小.把u加入到S中,然后对所有不在S中的顶点v,如l(v)>l(u)+w(u,v),则更新l(v),f(v), 即l(v)l(u)+w(u,v),f(v)u;3)重复步骤2), 直到所有顶点都在S中为止。
运筹学-最短路问题

V1 0 V2 2 V3 5 D = V4 − V5 − V6 − V7 −
பைடு நூலகம்
v2
2 0 2 4 6 − −
v3
5 2 0 1 − 3 −
v4
− 4 1 0 4 1 4
v5
− 6 − 4 0 − 1
v6
− − 3 1 − 0 2
v7
− − − 4 1 2 0
二、最短路算法: 最短路算法:
1. D氏标号法(Dijkstra) 氏标号法(Dijkstra) (1)求解思路 求解思路——从始点出发,逐步顺序 从始点出发, 从始点出发 逐步顺序 地向外探寻,每向外延伸一步都要求是最 地向外探寻,每向外延伸一步都要求是最 短的。 短的。 (2)使用条件 使用条件——网络中所有的弧权均 网络中所有的弧权 网络中所有的弧权均 非负, 非负,即 wij ≥ 0 。
(4) 计算步骤及例:
第三步:若网络图中已无T标号点 标号点, 第三步:若网络图中已无 标号点,停止 计算。否则 令 计算。否则,令 二步。 二步。 此时,要注意将第二步中的 此时,
T ( v j0 ) =
min {T ( v )}
v j ∈s j
,
然后将 标号改成P 然后将 v j0 的T 标号改成 标号 ,转入第
步骤 考察点 T标号点集 标号点集 v1 0
标 v2
标号) 号( 表P标号) 标号 v3 v4 v5 v6 v7
1 2 3 4 5 6
v1 v2 v3 v4 v6 v5
{v2,…,v7} , {v3,…,v7} , {v4,…,v7} , {v5,v6,v7} {v5,v7} {v7}
2
5 2+2 4
运筹学及其应用10.2 最短路问题

3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 6,2 2
∞,1
v9
6
3
3 4
10 4
v6 2 v7 ∞,1
11,4
∞,1
v8
18
v2 5,3 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 6,2 2
∞,1
v9
6
3
3 4
10 4
v6 2 v7 9,5
10,5
12,5
v8
19
v2 5,3 1
9
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 ∞,1 2
6
3
4 10
4
v6
2
v7
∞,1
∞,1
∞,1
v9
3
∞,1
v8
10
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 ∞,1 2
6
3
4 10
4
v6
2
v7
∞,1
∞,1
∞,1
v9
3
∞,1
v8
11
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
军事运筹理论中最短路问题的解法探讨

【 4+ 4 j
} - 8
1 最 短 路 问题 的 求 法
例 1 :给定 一个 图 1 所 示 的线
路 网络 . 图 1上 两点 间连 线 上 的数
其 相应 决策 U 3 ( C ) = D 。
类 似地 . 可算 得 当k = 2时 . 有
f 2 ( B 1 ) = 1 0 ,u 2 ( B 1 ) = C 3 , f 2 ( B 2 ) = 9 ,U 2 ( B 2 ) = C 3 ,
分 别 用动 态规 划 法 、 D i j k s t r a算 法 的求 解 , 探 讨 各 自的特 点及 适 用 范 围 . 并提 出一 般 通 用 的求 解
方 法— — 迭 代 法 。
关键 词 : 最短路 问题 ; 动 态规 划 ; D i j k s t r a算法 ; 迭代 法
中 图分 类 号 : E 9 1 1 文 献标 识码 : A d o i : 1 0 . 3 9 6 9 / j . i s s n . 1 6 6 5 — 2 2 7 2 . 2 0 1 4 . 0 3 . 0 7 6
,
d c,,。,) +f 。 ) ( 4 (
)
到 的方法 之 间有何 区别 ?它们 之 间
有 联 系 吗? 为 了解 决 这 个 问题 . 下
= ai r n{ 【
f 2 + 3 1
5+ 4 J
} = 5
其相 应决 策 U 3 ( C ) = D 。
C 4 Dz) +f a D2 f 3 ( c ) = mi n【 d 3 ( (
且 经 常 被 作 为 解 决 其 它 优 化 问 题 的一 个基 本工 具 最短 路在 图 与 网
运筹学最短路问题实验报告

运筹学最短路问题实验报告
姓名:雷超敏
学号:
班级:安全101
指导教师:冯树虎
一、实验目的:
1、学会独立建模能力,并用模型解决相关现实问题。
2、通过实验,把所学的运筹学理论知识与实践相结合,从而强化相关理论知识。
3、进一步加强对现实问题的认识,提高独立运用理论知识解决现实问题。
4、通过上机实验检验运筹学理论,发现相关理论知识的适用范围及不足。
二、实验任务:
1、提出一个有关运筹学的实际问题;
2、建立模型;
3、运用软件进行求解;
4、撰写分析报告。
三、实验软件
Excel2003。
运筹学最短路问题及程序

运筹学最短路问题----------关于旅游路线最短及程序摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:重庆北京杭州桂林哈尔滨昆明重庆0 1640 1500 662 2650 649北京1640 0 1200 1887 1010 2266杭州1500 1200 0 1230 2091 2089桂林662 1887 1230 0 2822 859哈尔滨2650 1010 2091 2822 0 3494昆明649 2266 2089 859 3494 0问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图3. 因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)重庆北京杭州桂林哈尔滨昆明123456假设:设变量x11。
浅谈最短路的数学模型解问题

浅谈最短路的数学模型解问题在生产与科学实验中,有一类活动的过程,由于它的特殊性,可将过程分为若干个互相联系的阶段,在它的每一个阶段都需要做出决策,从而使整个过程达到最好的活动效果。
因此,各个阶段的决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展。
当各个阶段决策确定后,就组成了一个决策序列,因而也就决定了整个过程的一条活动路线。
这种把一个问题可看作一个前后关联且具有链状结构的多阶段过程就称为多阶段决策过程,这种问题就称为多阶段决策问题,而最短路问题是这类问题中的比较典型的一种。
现在我们一起来探讨这类问题的特点和解决方法。
问题1(最小价格的管道铺设方案)如下图用点表示城市,现有共7个城市。
点与点之间的连线表示城市间有道路相连。
连线旁的数字表示道路的长度。
现计划从城市A到城市D铺设一条天然气管道,请设计出最小价格管道铺设方案。
首选我们要明确以下2点:(1)管道长短与成本价格之间有什么关系?显然,管道越短,成本越低。
(2)你能在众多管道路线中找到一条最短的管道路线吗?答案是肯定的。
这是一般人都有的最直接最原始的思路。
我们在这里就是要寻找一个比较简便的方法。
本题的实质就是求从城市A到城市D的一条最短路。
1、建立数学模型:Min{d(xk,xk+1)+f(xk+1)}的含义是:前一个阶段距离加上后一状态变量到终点的最短距离,然后在这些距离和中取最小者,即为所求的最短距离。
其中xk+1=u(xk),即从状态xk出发,采取决策uk到达下一状态xk+1;Sk表示从状态xk 出发的所有可能选取的决策的集合;而f4(x4)=0称为边界条件,因为状态x4=D已经是终点;各个决策路径xk+1=u(xk)都是所有决策的集合Sk中的一种,即xk+1=u(xk)∈Sk。
2、模型求解:①从最后一个阶段即第三阶段开始,按f3的定义有②第二个阶段有2个状态,而每个状态又有3个决策可选取,因此有B1到D的最短路长得B1到D的最短路径B2到D的最短路长得B2到D的最短路径③当k=1时,有A到D的最短路长得A到D的最短路径,故从A到D的最短弧长为6,路径为最短路问题是最重要的优化问题之一,它不仅可以直接应用于解决生产实际的许多问题,如管道铺设、线路安排、厂区布局、设备更新等等,而且经常被作为一个基本工具,用于解决其它优化问题。
最短路问题

最短路问题摘要若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,也是应用最广泛的问题之一。
在实际生活应用中许多优化问题都可以使用这个模型。
如管路铺设、线路安装、厂区布局和设备更新等。
在运筹学的介绍中求最短路问题的方法有很多,在本次论文研究中,我们主要介绍几种已成熟的最短路问题求解的方法并运用Matlab软件进行数学建模对问题运用Floyd算法进行求解。
关键词:最短路问题;求解方法;Floyd法;MATLAB软件THE PROBLEM OF SHORT-PATH PROBLEMABSTRACTIf the network each edge has a value (the length, cost, time, etc.), then find the two-node (usually the source node and well nodes) between the right and the smallest total path is the shortest path problem. The shortest path problem is a typical network theory to solve the problem is one of the most widely used one of the issues. Many applications in real life optimization problems can use this model. Such as pipeline laying, line installation, plant layout and equipment updates. In the introduction to operations research problems for the most short-circuit a lot, in this thesis, we introduce some of the most mature way to short-circuit problem solving and mathematical modeling using Matlab software using Floyd algorithm for the problem SolutionKey words: The shortest path problem;Solution;Floyd method;MATLAB software目录1 问题的提出 (1)2 最短路问题 (1)3 最短路问题解法介绍 (2)3.1迪克施特拉(dijkstra)算法. (2)3.2逐次逼近算法.............................. . (2)3.3 Floyd算法.............................. (3)4 问题假设 (3)5 符号说明 (4)6 模型的建立 (4)6.1 模型的准备工作 (4)6.2 建立模型 (5)7 模型求解 (5)8 模型验证及结果分析 (7)8.1 模型验证 (7)8.2 问题分析 (8)参考文献 (9)附录 (10)1 问题提出有9点S、2A、3A、1B、2B、1C、2C、T,各点之间的路程如下图所示,各点到T的最短路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学论文——旅游路线最短问题摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:重庆北京杭州桂林哈尔滨昆明重庆0 1640 1500 662 2650 649北京1640 0 1200 1887 1010 2266杭州1500 1200 0 1230 2091 2089桂林662 1887 1230 0 2822 859哈尔滨2650 1010 2091 2822 0 3494昆明649 2266 2089 859 3494 0问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图实线代表两个城市相连为1,虚线代表没有相连为03.因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
LINGO解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)假设:设变量x11。
如果x11=1,则表示城市i与城市j直接相连(即先后紧接到达关系),否则若x11=0,则表示城市i与城市j不相连。
特别说明:xij和xji是同一变量,都表示表示城市i与城市j是否有相连的关系。
这里取其中xij (i<j)的变量。
模型建立:由于这是一个最短路线的问题,且变量已经设好。
目标函数min=1640*x12+1500*x13+662*x14+2650*x15+649*x16+1200*x23+1 887*x24+1010*x25+2266*x26+1230*x34+2091*x35+2089*x36+2822 *x45+859*x46+3494*x56;约束条件:1.上面目标函数中的变量是表示两个城市是否直接相连接的关系,且最短路线是可以形成圈的,如下图实线代表两个城市相连为1,虚线代表没有相连为0如上图城市a和城市b有直接相连接的关系,所以之间变量为1,而城市a 与城市e则没有直接相连接的关系,之间变量为0。
其余的也有同样约束,所以有下面的约束。
条件1:变量xij为0-1变量@bin(xij)2.最短旅程路线中,每一个城市都要和其他两个城市相连接,即有一个进入路线和一个出去路线,所以含第i个城市的所有变量xij和xji之和为2。
所以又有如下的约束条件2:城市1(重庆)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2x12+x13+x14+x15+x16=2城市2(北京)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2x12+x23+x24+x25+x26=2城市3(杭州)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2x13+x23+x34+x35+x36=2城市4(桂林)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2x14+x24+x34+x45+x46=2城市5(哈尔滨)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2x15+x25+x35+x45+x56=2城市6(昆明)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2x16+x26+x36+x46+x56=2则可以编制程序如下!目标函数最小;min=1640*x12+1500*x13+662*x14+2650*x15+649*x16+1200*x23+1887*x24+1010 *x25+2266*x26+1230*x34+2091*x35+2089*x36+2822*x45+859*x46+3494*x56; !变量0-1约束;!城市1(重庆)与城市2(北京)之间关系变量x12的0-1约束;@bin(x12);!城市1(重庆)与城市3(杭州)之间关系变量x13的0-1约束;@bin(x13);!城市1(重庆)与城市4(桂林)之间关系变量x14的0-1约束;@bin(x14);!城市1(重庆)与城市5(哈尔滨)之间关系变量x15的0-1约束;@bin(x15);!城市1(重庆)与城市6(昆明)之间关系变量x16的0-1约束;@bin(x16);!城市2(北京)与城市3(杭州)之间关系变量x23的0-1约束;@bin(x23);!城市2(北京)与城市4(桂林)之间关系变量x24的0-1约束;@bin(x24);!城市2(北京)与城市5(哈尔滨)之间关系变量x25的0-1约束;@bin(x25);!城市2(北京)与城市6(昆明)之间关系变量x26的0-1约束;@bin(x26);!城市3(杭州)与城市4(桂林)之间关系变量x34的0-1约束;@bin(x34);!城市3(杭州)与城市5(哈尔滨)之间关系变量x35的0-1约束;@bin(x35);!城市3(杭州)与城市6(昆明)之间关系变量x36的0-1约束;@bin(x36);!城市4(桂林)与城市5(哈尔滨)之间关系变量x45的0-1约束;@bin(x45);!城市4(桂林)与城市6(昆明)之间关系变量x46的0-1约束;@bin(x46);!城市5(哈尔滨)与城市6(昆明)之间关系变量x56的0-1约束;@bin(x56);!条件约束,即每个城市的连接路线约束;!城市1(重庆)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2;x12+x13+x14+x15+x16=2;!城市2(北京)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2;x12+x23+x24+x25+x26=2;!城市3(杭州)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2;x13+x23+x34+x35+x36=2;!城市4(桂林)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2;x14+x24+x34+x35+x46=2;!城市5(哈尔滨)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2;x15+x25+x35+x45+x56=2;!城市6(昆明)有且仅有一个进入路线和一个出去路线,所以和它连接的路线条数为2;x16+x26+x36+x46+x56=2;运行结果如下Global optimal solution found.Objective value: 7598.000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX12 0.000000 1640.000X13 0.000000 1500.000X14 0.000000 662.0000X15 1.000000 2650.000X16 1.000000 649.0000X23 1.000000 1200.000X24 0.000000 1887.000X25 1.000000 1010.000X26 0.000000 2266.000X34 1.000000 1230.000X35 0.000000 2091.000X36 0.000000 2089.000X45 0.000000 2822.000X46 1.000000 859.0000X56 0.000000 3494.000Row Slack or Surplus Dual Price1 7598.000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.000000上面显示旅程最短的距离是7598可以看出求出的所有变量的值都是0或1,其中x15=1,x16=1,x23=1,x25=1,x34=1,x46=1,这说明了城市1(重庆)和城市5(哈尔滨)相连接城市1(重庆)和城市6(昆明)相连接城市2(北京)和城市3(杭州)相连接城市2(北京)和城市5(哈尔滨)相连接城市3(杭州)和城市4(桂林)相连接城市4(桂林)和城市6(昆明)相连接形成的圈是“重庆(1)-哈尔滨(5)-北京(2)-杭州(3)-桂林(4)-昆明(6)-重庆(1)”,如下图最短旅程的旅游线路:重庆→哈尔滨→北京→杭州→桂林→昆明→重庆(上图外环线)或者也可以按这条路线的逆方向旅行,即重庆→昆明→桂林→杭州→北京→哈尔滨→重庆(上图内环线)总旅程:2650+1010+1200+12301+859+649=7598感想:运筹学就是教我们如何优化作业,得到最优解或者满意解。
现实中有许多的事情都需要优化的,当我们去旅游是,我们会考虑走哪些条路线时费用最少;生产物品时,我们要考虑定货批量和库存持有成本与定货成本之间的关系,从而找到最佳的定货批量;当我们考虑管道的铺设问题时,我们要考虑如何选择铺设的路线才能使铺设管道用料最少,从而找到最少用料的路线等等问题。
这些都需要我们去优化找到比较满意的答案。
