第35届全国中学生物理竞赛决赛试题(word版).docx

合集下载

第35届全国中学生物理竞赛决赛训练试题第01套-解答v1

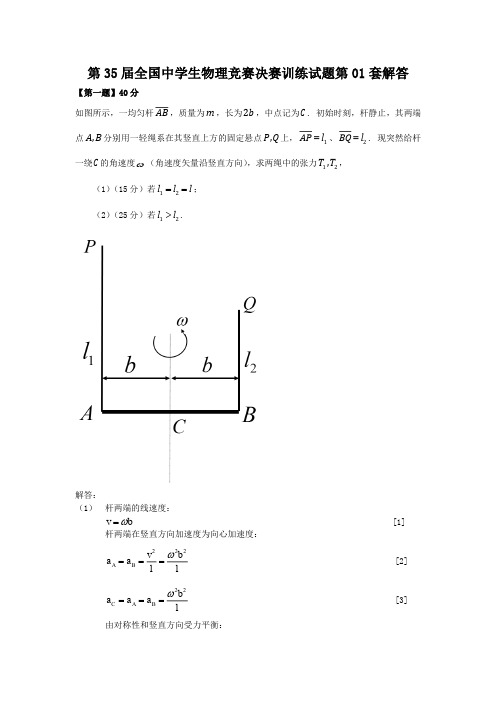
第35届全国中学生物理竞赛决赛训练试题第01套解答【第一题】40分如图所示，一均匀杆AB ，质量为m ，长为2b ，中点记为C . 初始时刻，杆静止，其两端点,A B 分别用一轻绳系在其竖直上方的固定悬点,P Q 上，=1AP l 、=2BQ l . 现突然给杆一绕C 的角速度ω（角速度矢量沿竖直方向），求两绳中的张力12,T T ，（1）（15分）若==12l l l ；（2）（25分）若>12l l .解答：（1）杆两端的线速度：v b ω= [1] 杆两端在竖直方向加速度为向心加速度：222A B v b a a l l ω=== [2]22C A B b a a a lω===[3]由对称性和竖直方向受力平衡：12T T = [4] 12C T T mg ma +-= [5]解得：22121()2b T T m g lω==+ [6][1][2][4][5]各2分 [3]3分 [6]4分（2）同（1）的第一步：22211A v b a l l ω== [7]22222B v b a l l ω== [8]设：A C a a b β=- [9]BC a a b β=+[10]可解得：2212122C l l a b l l ω+=[11]212122l l b l l βω-=[12]平衡和牛顿第二定律：21T b T b I β-=[13] 2211(2)123I m b mb ==[14] 12C T T mg ma +-=[15]解得：221211221(b )23l l T m g l l ω+=+[16]221221221(b )23l l T m g l l ω+=+[17][7][8][11][12][13][15]各2分[9][10][14]各1分 [16][17]各5分【第二题】40分如图，这时是一种三角打孔机的结构。

其中持钻架A被限制平行运动，A中间有一个正三角形的内孔，边长为l。

2019年第35届全国中学生物理竞赛预赛试卷(纯WORD版)

2019年第35届全国中学生物理竞赛预赛试卷(纯WORD版)个电压值的差C.保持电流方向不变,改变磁场方向(B→-B),求出改变前后的两个电压值的差D.同时改变电流方向和磁场方向,求出改变前后的两个电压值的差5.如图,一根长为L的均匀细杆质量为m,可绕过其中一端点O作为转动轴在竖直平面内转动。

现将杆从竖直向下的位置缓慢放开,使其绕O匀速旋转,旋转速度为。

设在杆上距离O的位置为x处有一质量为M的小球,小球与杆的碰撞是完全弹性碰撞。

当小球与杆相碰后,杆的角速度为'。

若碰撞后小球向上弹起的高度为h,则h与L、M、m、、'的关系式为[]A.h=ML 22mg MLB.h=ML 2mg ML2C.h=2ML 2mg MLD.h=2ML 22mg ML6.一物体沿x轴正方向做直线运动,第1秒的位移为1m,第2秒的位移为3m。

则第3秒的位移为[]A.5mB.7mC.9mD.11m7.如图,一平板电由两块平行的金属板组成,板间距为d,面积为S。

一电荷为Q的点电荷从板间距离为L处沿垂直于板面方向飞向电。

最终停在下金属板上。

若点电荷在飞行过程中做功W,则电荷Q与电的电容C、板间电势差V和电场强度E的关系式为[] A.W=Q2d20C=20SdB.V=QC,C.E=Q0SB.W=Q2dC=0S2dD.V=Q2C,D.E=Q20S8.如图,一电阻为R的电阻器,两端分别接有电压为U的电源和一电容为C的电。

一开始电未充电,然后接通电源,此时电的电荷Q(t)随时间t的变化关系式为[]A.Q(t)=CU(1-e-t/RC)B.Q(t)=CU(1-e-t/2RC)C.Q(t)=CU(1-e-t/3RC)D.Q(t)=CU(1-e-t/4RC)9.如图,一根长为L的均匀细杆质量为m,可绕过其中一端点O作为转动轴在竖直平面内转动。

现将杆从竖直向下的位置缓慢放开,使其绕O匀速旋转,旋转速度为。

设在杆上距离O的位置为x处有一质量为M的小球,小球与杆的碰撞是完全弹性碰撞。

2023年全国中学生物理竞赛决赛试卷

全国中学生物理竞赛决赛理论考试试题也许用到的物理常量和公式：真空中的光速82.99810/c m s =⨯；地球表面重力加速度大小为g ；普朗克常量为h ，2h π=； 2111ln ,1121x dx C x x x+=+<--⎰。

1、（15分）山西大同某煤矿相对于秦皇岛的高度为c h 。

质量为t m 的火车载有质量为c m 的煤，从大同沿大秦铁路行驶路程l 后到达秦皇岛，卸载后空车返回。

从大同到秦皇岛的过程中，火车和煤总势能的一部分克服铁轨和空气做功，其余部分由发电机转换成电能，平均转换效率为1η，电能被所有存储于蓄电池中以用于返程。

空车在返程中由储存的电能驱动电动机克服重力和阻力做功，储存的电能转化为对外做功的平均转换效率为2η。

假设大秦线轨道上火车平均每运营单位距离克服阻力需要做的功与运营时（火车或火车和煤）总重量成正比，比例系数为常数μ，火车由大同出发时携带的电能为零。

（1）若空车返回大同时尚有剩余的电能，求该电能E 。

（2）问火车至少装载质量为多少的煤，才干在不此外提供能量的条件下刚好返回大同？（3）已知火车在从大同到达秦皇岛的铁轨上运营的平均速率为v ，请给出发电机的平均输出功率P 与题给的其它物理量的关系。

2、（15分）如图a ，AB 为一根均质细杆，质量为m ，长度为2l ；杆上端B 通过一不可伸长的软轻绳悬挂到固定点O ，绳长为1l 。

开始时绳和杆均静止下垂，此后所有运动均在同一竖直面内。

（1）现对杆上的D 点沿水平方向施加一瞬时冲量I ，若在施加冲量后的瞬间，B 点绕悬点O 转动的角速度和杆绕其质心转动的角速度相同，求D 点到B 点的距离和B点绕悬点O 转动的初始角速度0ω。

（2）设在某时候，绳和杆与竖直方向的夹角分别为1θ和2θ（如图b 所示），绳绕固定点O 和杆绕其质心转动的角速度分别为1ω和2ω，求绳绕固定点O 和杆绕其质心转动的角加速度1α和2α3、（15分）火星大气可视为仅由很稀薄的2CO 组成，此大气的摩尔质量记为μ，且同一高度的大气可视为处在平衡态的抱负气体。

第35届全国中学生物理竞赛决赛训练试题第07套-解答v2

第35届全国中学生物理竞赛决赛训练试题第07套解答【第一题】40分如图所示，有一长为2l的轻质细杆，两端各固连一个质量为m的小球（A和B），中点处有一原长为0，劲度系数为k的轻质弹簧，弹簧一端与杆的中点相连，另一端与一个套在杆上质量也是m的小球C相连，这个小球可以沿杆无摩擦滑动. 初始时系统静止在光滑水平桌面上，一个质量也是m的小球D以速度v0与小球B发生弹性正碰，v0垂直于杆.(1)求碰后瞬间四个小球的速度.(2)在碰后的运动中，如果小球C稍稍偏离杆的中点，为了在中点附近相对于杆做简谐振动，弹簧的劲度系数k至少多大？(3)在(2)的条件下，求出振动的周期.答案(1)选择杆中点为转轴，ABC系统的转动惯量I0=2ml2[1]设碰后ABC系统质心速度（即C的速度）为v C，角速度为ω0，小球D的速度为v D，则有动量守恒mv0=3mv C+mv D[2]角动量守恒mv0l=mv D l+I0ω0[3]机械能守恒1 2mv02=123mv C2+12mv D2+12I0ω02[4]联立解得v C=4v011v D=−v011ω0=6v011l[5] 则有v A=v C−ω0l=−2v011v B=v C+ω0l=10v011[6] (18分，每式2分)(2)在ABC系统质心系研究此问题. 假设杆中点到质心的距离为x，则小球C到质心的距离为2x，C偏离杆中点共3x. 此时系统绕质心的转动惯量I=m(l+x)2+m(l−x)2+m(2x)2=2ml2+6mx2[7] 角动量守恒，有Iω=I0ω0[8] 所以转动动能为T1=12Iω2=L22I=L24m(l2+3x2)[9]其中L=I0ω0=12mv0l/11表示系统的角动量. 研究径向运动时，转动动能化为有效势能的一部分. 有效势能V eff=12k(3x)2+T1=12k(3x)2+L24m(l2+3x2)[10]利用小量展开1/(1+α)≈1−α，有V eff≈92kx2−3L24ml4x2+L24ml2[11]要形成简谐振动，x=0处V eff应极小，即要求9 2k−3L24ml4>0[12]所以k min=L26ml4=24mv02121l2[13](14分，每式2分)(3)由(14)式，等效劲度系数K=9k−3L22ml4=9k−216mv02121l2[14]径向运动的动能T2=12(2m)ẋ2+12(2ẋ)2=3mẋ2[15]等效质量M=6m[16] 所以周期T=2π√MK =2π√2m3k−72mv02121l2[17](8分，每式2分)【第二题】40分如图所示，在水平地面上放着一个物体，其由两个全同的刚体在O点光滑铰接组成。

2018第35届全国中学生物理竞赛（决赛）试题答案出炉！

2018第35届全国中学⽣物理竞赛（决赛）试题答案出炉！
10⽉25⽇⾄11⽉1⽇，2018年第35届全国中学⽣物理竞赛决赛在上海举⾏，全国32个省份（含澳门）365名考⽣参加了本次决赛。

第35届全国中学⽣物理竞赛决赛将于10⽉31⽇颁奖。

10⽉28⽇，来⾃全国各地共365名省队学员在上海交通⼤学闵⾏校区顺利完成了第35届物理竞赛决赛的实验考试。

据竞委会的赛程安排，参加决赛的全体考⽣被随机分为三批次，每批两组共A-F六组。

三批次学⽣分布在上午、下午和晚上完成了3⼩时40分钟的考试。

截⽌到10⽉28⽇晚E、F组同学实验考试结束，第35届全国中学⽣物理竞赛全国决赛就正式结束了！
决赛⽇程回顾
25⽇全天报到，26⽇看考场，27⽇上午考理论，28⽇⼀天考实验，30⽇进⾏闭幕式，11⽉1⽇离开。

理论考试：
【时间】10⽉27⽇ 09:00-12:00
【地点】上海中学
实验考试：
【时间】10⽉28⽇
A、B组学⽣ 08:00-11:40
C、D组学⽣ 12:40-16:20
E、F组学⽣ 17:20-21:00
【地点】上海交通⼤学闵⾏校区
颁奖⼤会：
【时间】10⽉31⽇ 19:30-21:30
【地点】上海中学⼤礼堂
提醒：第35届物理竞赛决赛试题及答案请在⾃主招⽣指南后台回复“35届物理决赛”领取！
-END-
⊙来源 | ⽹络，清⼤紫育⾃主招⽣指南（ID：mxzzzsw）整理，转载请先联系协商授权并标明明确来源!。

第35届全国中学生物理竞赛复赛理论考试试题(word版)(汇编)

2018年第35届全国中学生物理竞赛复赛理论考试试题2018年9月22日一，（40分）假设地球是一个质量分布各向同性的球体。

从地球上空离地面高度为h 的空间站发射一个小物体，该物体相对于地球以某一初速度运动，初速度方向与其到地心的连线垂直。

已知地球半径为R ，质量为M ，引力常量为G 。

地球自转及地球大气的影响可忽略。

（1）若该物体能绕地球做周期运动，其初速度的大小应满足什么条件？（2）若该物体的初速度大小为v 0，且能落到地面，求其落地时速度的大小和方向（即速度与其水平分量之间的夹角），以及它从开始发射直至落地所需的时间。

已知对于2040c b ac <∆=->，有322()b C c =-+- ，式中C 为积分常数。

二，（40分）如图，一劲度系数为k的轻弹簧左端固定，右端连一质量为m的小球，弹簧水平水平，它处于自然状态时小球位于坐标原点O；小球课在水平地面上滑动，它与地面之间的摩擦因数为。

初始时小球速度为0，将此时弹簧相对于其原长的伸长记为-A0（A0>0但是它并不是已知量）。

重力加速度大小为g，假设最大静摩擦力等于滑动摩擦力（1）如果小球至多只能向右运动，求小球最终静止的位置，和此种情形下A0应满足的条件；（2）如果小球完成第一次向右运动至原点右边后，至多只能向左运动，求小球最终静止的位置，和此种情形下A0应满足的条件；（3）如果小球只能完成n次往返运动（向右经过原点，然后向左经过原点，算1 次往返）（4）如果小球只能完成n次往返运动，求小球从开始运动直至最终静止的过程中运动的总路程。

三、（40 分）如图，一质量为M 、长为l 的匀质细杆AB 自由悬挂于通过坐标原点O 点的水平光滑转轴上（此时，杆的上端A 未在图中标出，可视为与O 点重合），杆可绕通过O 点的轴在竖直平面（即 x -y 平面， x 轴正方向水平向右）内转动；O 点相对于地面足够高，初始时杆自然下垂；一质量为m 的弹丸以大小为v 0 的水平速度撞击杆的打击中心（打击过程中轴对杆的水平作用力为零）并很快嵌入杆中。

2019年第35届全国中学生物理竞赛预赛真题试卷(纯WORD版)

第35届全国中学生物理竞赛预赛试卷本卷共16题,满分200分一、选择题.本题共5小题,每小题6分,在每小题给出的4个选项中,有的小题只有一项符合题意,有的小题有多项符合题意.把符合题意的选项前面的英文字母写在每小题后面的方括号内.全部选对的得6分,选对但不全的得3分,有选错或不答的得0分。

1.居里夫人发现了元素钋(Po),其衰变的核反应方程式为206082a c eb d b f P P αγ→++,其中,a 、b 、c 、d 、e 、f 的值依次为[ ]A.211、84、4、2、1、0B.210、84、4、2、0、0C.207、84、1、1、0、1D.207、83、1、1、0、02.如图,一劲度系数为k 的轻弹簧上端固定在天花板上,下端连接一质量为m 的小球,以小球的平衡位置O 作为坐标原点,x 轴正方向朝下。

若取坐标原点为系统势能的零点,则当小球位于坐标为x 0的位置时,系统的总势能为[ ]A.20012kx mgx -B.001()2k x mgx k+- C.201()2mg k x k + D.2012kx3.库伦扭摆装置如图所示,在细银丝下悬挂一根绝缘棒,棒水平静止;棒的两端各固定一相同的金属小球a 和b,另一相同的金属小球c 固定在插入的竖直杆上,三个小球位于同一水平圆周上,圆心银丝为棒的悬点O 。

细银丝自然悬挂时,a 、c 球对0点的张角α=4°。

现在使a 和c 带相同电荷,库伦力使细银丝扭转,张角a 增大,反向转动细银丝上端的旋钮可使张角a 变小;若将旋钮缓慢反向转过角度β=30°,可使小球a 最终回到原来位置,这时细银丝的扭力矩与球a 所受球c 的静电力的力矩平衡。

设细银丝的扭转回复力矩与银丝的转角B 成正比。

为使最后a 、c 对0点的张角α=2°,旋钮相对于原自然状态反向转过的角度应为[ ]A.β=45°B.β=60°C.β=90°D.β=120°4.霍尔传感器的结构如图所示,图中H为一块长方体半导体薄片外加磁场的磁感应强度B 和外加电流/的方向如相应箭头所示(B与长方体的后两个表面及电流均垂直),电压表(可判断直流电压的正负)按图中方式与H的上下表面相连。

第35届全国中学生物理竞赛模拟试题(精品范文).doc

【最新整理，下载后即可编辑】第35届全国中学生物理竞赛模拟试题★ 理论部分一、足球比赛，一攻方队员在图中所示的 A 处沿 Ax 方向传球，球在草地上以速度 v 匀速滚动，守方有一队员在图中 B 处，以 d 表示 A ，B 间的距离，以 θ 表示 AB 与Ax之间的夹角，已知 θ ＜90° ．设在球离开 A 处的同时，位于 B 处的守方队员开始沿一直线在匀速运动中去抢球，以 v p 表示他的速率．在不考虑场地边界限制的条件下，求解以下问题（要求用题中给出的有关参量间的关系式表示所求得的结果）：1．求出守方队员可以抢到球的必要条件．2．如果攻方有一接球队员处在 Ax 线上等球，以 l r 表示他到 A 点的距离，求出球不被原在 B 处的守方队员抢断的条件．3．如果攻方有一接球队员处在 Ax 线上，以L 表示他离开 A 点的距离．在球离开 A 处的同时，他开始匀速跑动去接球，以 v r 表示其速率，求在这种情况下球不被原在 B 处的守方队员抢断的条件．二、卫星的运动可由地面观测来确定；而知道了卫星的运动，又A可以用它来确定空间飞行体或地面上物体的运动．这都涉及时间和空间坐标的测定．为简化分析和计算，不考虑地球的自转和公转，把它当做惯性系．1．先来考虑卫星运动的测定．设不考虑相对论效应．在卫星上装有发射电波的装置和高精度的原子钟．假设从卫星上每次发出的电波信号，都包含该信号发出的时刻这一信息．（I）地面观测系统（包含若干个观测站）可利用从电波中接收到的这一信息，并根据自己所处的已知位置和自己的时钟来确定卫星每一时刻的位置，从而测定卫星的运动．这种测量系统至少需要包含几个地面观测站？列出可以确定卫星位置的方程．（II）设有两个观测站D1，D2，分别位于同一经线上北纬θ和南纬θ（单位：（°））处．若它们同时收到时间τ之前卫星发出的电波信号．（i）试求出发出电波时刻卫星距地面的最大高度H；（ii）当D1，D2处观测站位置的纬度有很小的误差△θ时，试求H的误差；（iii）如果上述的时间τ有很小的误差τ△，试求H 的误差．2．在第1（II）小题中，若θ= 45°，τ= 0.10 s ．（i）试问卫星发出电波时刻卫星距地面最大高度H 是多少千米？（ii）若△θ= ±1.0′′ ，定出的H 有多大误差？（iii）若τ△= ±0.010 μs ，定出的H 有多大误差？假设地球为半径R = 6.38 ×103 km 的球体，光速c = 2.998 ×108 m / s ，地面处的重力加速度g = 9.81 m / s2．3．再来考虑根据参照卫星的运动来测定一个物体的运动．设不考虑相对论效应．假设从卫星持续发出的电波信号包含卫星运动状态的信息，即每个信号发出的时刻及该时刻卫星所处的位置．再假设被观测物体上有一台卫星信号接收器（设其上没有时钟），从而可获知这些信息．为了利用这种信息来确定物体的运动状态，即物体接收到卫星信号时物体当时所处的位置以及当时的时刻，一般来说物体至少需要同时接收到几个不同卫星发来的信号电波？列出确定当时物体的位置和该时刻的方程．4．根据狭义相对论，运动的钟比静止的钟慢．根据广义相对论，钟在引力场中变慢．现在来考虑在上述测量中相对论的这两种效应．已知天上卫星的钟与地面观测站的钟零点已经对准．假设卫星在离地面h = 2.00 ×104 km 的圆形轨道上运行，地球半径R、光速c 和地面重力加速度g 取第2小题中给的值．（I）根据狭义相对论，试估算地上的钟经过24h 后它的示数与卫星上的钟的示数差多少？设在处理这一问题时，可以把匀速直线运动中时钟走慢的公式用于匀速圆周运动．（II）根据广义相对论，钟在引力场中变慢的因子是(1－2φ/ c2 )1 / 2 ，φ是钟所在位置的引力势（即引力势能与受引力作用的物体质量之比；取无限远处引力势为零）的大小．试问地上的钟24 h 后，卫星上的钟的示数与地上的钟的示数差多少？三、致冷机是通过外界对机器做功，把从低温处吸取的热量连同外界对机器做功所得到的能量一起送到高温处的机器；它能使低温处的温度降低，高温处的温度升高．已知当致冷机工作在绝对温度为T1 的高温处和绝对温度为T2 的低温处之间时，若致冷机从低温处吸取的热量为Q，外界对致冷机做的功为W，则有QW≤T2T1－T2，式中“=”对应于理论上的理想情况．某致冷机在冬天作为热泵使用（即取暖空调机），在室外温度为－5.00℃的情况下，使某房间内的温度保持在20.00℃．由于室内温度高于室外，故将有热量从室内传递到室外．本题只考虑传导方式的传热，它服从以下的规律：设一块导热层，其厚度为l ，面积为S，两侧温度差的大小为T，则单位时间内通过导热层由高温处传导到低温处的热量为H = k △Tl S ，其中k 称为热导率，取决于导热层材料的性质．1．假设该房间向外散热是由面向室外的面积S = 5.00 m2、厚度 l = 2.00 mm 的玻璃板引起的．已知该玻璃的热导率 k = 0.75 W / ( m • K )，电费为每度0.50元．试求在理想情况下该热泵工作12 h 需要多少电费？2．若将上述玻璃板换为“双层玻璃板”，两层玻璃的厚度均为2.00mm ，玻璃板之间夹有厚度 l 0 = 0.50 mm 的空气层，假设空气的热导率 k 0 = 0.025 W / ( m • K )，电费仍为每度0.50元．若该热泵仍然工作12 h ，问这时的电费比上一问单层玻璃情形节省多少？四、如图1所示，器件由相互紧密接触的金属层( M )、薄绝缘层( I )和金属层( M )构成．按照经典物理的观点，在I 层绝缘性能理想的情况下，电子不可能从一个金属层穿过绝缘层到达另一个金属层．但是，按照量子物理的原理，在一定的条件下，这种渡越是可能的，习惯上将这一过程称为隧穿，它是电子具有波动性的结果．隧穿是单个电子的过程，是分立的事件，通过绝缘层转移的电荷量只能是电子电荷量－e ( e = 1.60 ×10－19 C )的整数倍，因此也称为单电子隧穿，MIM 器件亦称为隧穿结或单电子隧穿结．本题涉及对单电子隧穿过程控制的库仑阻塞原理，由于据此可望制成尺寸很小的单电子器件，这是目前研究得很多、有图1应用前景的领域．1．显示库仑阻塞原理的最简单的做法是将图1的器件看成一个电容为C的电容器，如图2所示．电容器极板上的电荷来源于金属极板上导电电子云相对于正电荷背景的很小位移，可以连续变化．如前所述，以隧穿方式通过绝缘层的只能是分立的单电子电荷．如果隧穿过程会导致体系静电能量上升，则此过程不能发生，这种现象称为库仑阻塞．试求出发生库仑阻塞的条件即电容器极板间的电势差V AB= V A－V B 在什么范围内单电子隧穿过程被禁止．2．假定V AB = 0.10 mV是刚能发生隧穿的电压．试估算电容C 的大小．3．将图1的器件与电压为V 的恒压源相接时，通常采用图2所示的双结构器件来观察单电子隧穿，避免杂散电容的影响．中间的金属块层称为单电子岛．作为电极的左、右金属块层分别记为S ，D ．若已知岛中有净电荷量－ne ，其中净电子数n 可为正、负整数或零，e 为电子电荷量的大小，两个MIM 结的电容分别为C S 和C D．试证明双结结构器件的静电能中与岛上净电荷量相关的静电能（简称单电子岛的静电能）为U n=(－ne )22( C S +C D )．4．在图3给出的具有源( S )、漏( D )电极双结结构的基础上，通过和岛连接的电容C G 添加门电极( G )构成如图4给出的单电子三极管结构，门电极和岛间没有单电子隧穿事件发生．在V 较小且固定的情况下，通过门电压V G 可控制岛中的净电子数n ．对于V G 如何控制n ，简单的模型是将V G 的作用视为岛中附加了等效电荷q0 =CGVG．这时，单电子岛的静电能可近似为U n=(－ne+q)2 /2C∑，式中C∑= C S+C D+C G ．利用方格图（图5），考虑库仑阻塞效应，用粗线画出岛中净电子数从n = 0开始，C G V G / e 由0增大到3的过程中，单电子岛的静电能U n 随C G V G 变化的图线（纵坐标表示U n，图3 图4图5U n( e2 / 2C∑)C G V Ge取U n的单位为e2 / 2C；横坐标表示C G V G ，取C G V G的单位为e）．要求标出关键点的坐标，并把n = 0 ，1 ，2 ，3时C G V G / e 的变化范围填在表格中．（此小题只按作图及所填表格（表1）评分）．表1n 0 1 2 3C G VG/ e变化范围五、折射率n = 1.50 、半径为R的透明半圆柱体放在空气中，其垂直于柱体轴线的横截面如图所示，图中O 点为横截面与轴线的交点．光仅允许从半圆柱体的平面AB 进入，一束足够宽的平行单色光沿垂直于圆柱轴的方向以入射角i射至AB 整个平面上，其中有一部分入射光束能通过半圆柱体从圆柱面射出．这部分光束在入射到AB 面上时沿y 轴方向的长度用d 表示．本题不考虑光线在透明圆柱体内经一次或多次反射后再射出柱体的复杂情形．1．当平行入射光的入射角i 在0°～90°变化时，试求d 的最小值dmin和最大值d max．2．在如图所示的平面内，求出射光束与柱面相交的圆弧对zO 点的张角与入射角i 的关系．并求在掠入射时上述圆弧的位置．六、根据广义相对论，光线在星体的引力场中会发生弯曲，在包含引力中心的平面内是一条在引力中心附近微弯的曲线．它距离引力中心最近的点称为光线的近星点．通过近星点与引力中心的直线是光线的对称轴．若在光线所在平面内选择引力中心为平面极坐标（r ，φ）的原点，选取光线的对称轴为坐标极轴，则光线方程（光子的轨迹方程）为r =GM / c2a cosφ+a2 ( 1 + sin2φ)，G 是万有引力恒量，M 是星体质量，c 是光速，a 是绝对值远小于1的参数．现在假设离地球80.0光年处有一星体，在它与地球连线的中点处有一白矮星．如果经过该白矮星两侧的星光对地球上的观测者所张的视角是1.80×10－7rad ，试问此白矮星的质量是多少千克？已知G = 6.673 ×10－11 m3 / ( kg •s2 )七、1．假设对氦原子基态采用玻尔模型，认为每个电子都在以氦核为中心的圆周上运动，半径相同，角动量均为：= h / 2π，其中h 是普朗克常量．（I）如果忽略电子间的相互作用，氦原子的一级电离能是多少电子伏？一级电离能是指把其中一个电子移到无限远所需要的能量．（II）实验测得的氦原子一级电离能是24.6 eV ．若在上述玻尔模型的基础上来考虑电子之间的相互作用，进一步假设两个电子总处于通过氦核的一条直径的两端．试用此模型和假设，求出电子运动轨道的半径r0、基态能量E0以及一级电离能E+，并与实验测得的氦原子一级电离能相比较．已知电子质量m = 0.511 MeV / c2，c是光速，组合常量c =197.3 MeV • fm = 197.3 eV • nm ，ke2 = 1.44 MeV • fm = 1.44 eV • nm ，k是静电力常量，e 是基本电荷量．2．右图是某种粒子穿过云室留下的径迹的照片．径迹在纸面内，图的中间是一块与纸面垂直的铅板，外加恒定匀强磁场的方向垂直纸面向里．假设粒子电荷的大小是一个基本电荷量e：e = 1.60 ×10－19 C ，铅板下部径迹的曲率半径r d= 210 mm ，铅板上部径迹的曲率半径r u= 76.0 mm ，铅板内的径迹与铅板法线成θ= 15.0°，铅板厚度d = 6.00 mm ，磁感应强度B = 1.00 T ，粒子质量m = 9.11 ×10－31 kg = 0.511 MeV / c2．不考虑云室中气体对粒子的阻力．（I）写出粒子运动的方向和电荷的正负．（II）试问铅板在粒子穿过期间所受的力平均为多少牛？（III）假设射向铅板的不是一个粒子，而是从加速器引出的流量为j= 5.00 ×1018 / s 的脉冲粒子束，一个脉冲持续时间为 =2.50 ns ．试问铅板在此脉冲粒子束穿过期间所受的力平均为多少牛？铅板在此期间吸收的热量又是多少焦？第35届全国中学生物理竞赛模拟试题参考解答一、1 ．解法一：设守方队员经过时间t 在Ax 上的C 点抢到球，用l 表示A 与C 之间的距离，lp表示B 与C之间的距离（如图1所示），则有l = vt ，lp = v p t （1）图1和l 2p= d2 + l2 －2dl cosθ．（2）解式（1），（2）可得l =d1－( v p / v)2{cosθ±[ (vpv)2 －sin2θ]1/ 2 }．（3）由式（3）可知，球被抢到的必要条件是该式有实数解，即vp≥v sinθ．（4）解法二：设BA 与BC 的夹角为φ（如图1）．按正弦定理有lp sinθ=lsinφ．利用式（1）有vpv= sinθsinφ．从sinφ≤1可得必要条件（4）．2．用l min 表示守方队员能抢断球的地方与A 点间的最小距离．由式（3）知l min =d1－( v p / v)2{cosθ±[ (vpv)2 －sin2θ]1/ 2 }．（5）若攻方接球队员到A 点的距离小于l min ，则他将先控制球而不被守方队员抢断．故球不被抢断的条件是lr＜lmin．（6）由（5），（6）两式得l r ＜d1－( v p / v)2{cosθ±[ (vpv)2 －sin2θ]1 /2 }（7）由式（7）可知，若位于Ax 轴上等球的攻方球员到A 点的距离l r 满足该式，则球不被原位于B 处的守方球员抢断．3．解法一：如果在位于B 处的守方球员到达Ax 上距离A 点lmin的C1 点之前，攻方接球队员能够到达距A 点小于lmin处，球就不会被原位于B 处的守方队员抢断（如图2所示）．若L≤l min 就相当于第2小题．若L＞l min ，设攻方接球员位于Ax 方向上某点E 处，则他跑到C1点所需时间trm= ( L－l min ) /vr；（8）守方队员到达C1 处所需时间t pm = ( d2+ l 2min－2dl mincosθ)1 / 2/v p．球不被守方抢断的条件是图2trm＜tpm．（9）即L＜vrvp( d2 + l2min－2dl min cosθ)1 / 2 + l min ，（10）式中l min 由式（5）给出．解法二：守方队员到达C1 点的时间和球到达该点的时间相同，因此有tpm= l min / v ．从球不被守方队员抢断的条件（9）以及式（8）可得到L＜( 1 + vr/ v)l min （11）式中l min也由式（5）给出．易证明式（11）与（10）相同．二、1．（I）选择一个坐标系来测定卫星的运动，就是测定每一时刻卫星的位置坐标x，y，z．设卫星在t时刻发出的信号电波到达第i 个地面站的时刻为t i．因为卫星信号电波以光速c 传播，于是可以写出(x－x i )2+ (y－y i )2+ (z －z i )2= c2(t－t i )2( i = 1 ，2 ，3 )，（1）式中x i，y i，z i是第i个地面站的位置坐标，可以预先测定，是已知的；t i 也可以由地面站的时钟来测定；t 由卫星信号电波给出，也是已知的．所以，方程（1）中有三个未知数x，y，z，要有三个互相独立的方程，也就是说，至少需要包含三个地面站，三个方程对应于式（1）中i = 1 ，2 ，3 的情况．（II）（i）如图所示，以地心O 和两个观测站D1，D2的位置为顶点所构成的三角形是等腰三角形，腰长为R ．根据题意，可知卫星发出信号电波时距离两个观测站的距离相等，都是L= cτ．（2）当卫星P 处于上述三角形所在的平面内时，距离地面的高度最大，即H．以θ表示D1，D2 所处的纬度，由余弦定理可知L2= R2 + ( H+R )2 －2R( H+R ) cosθ．（3）由（2），（3）两式得H = (cτ)2 －(R sinθ)2 －R ( 1－cosθ) ．（4）式（4）也可据图直接写出．（ii）按题意，如果纬度有很小的误差△θ，则由式（3）可知，将引起H发生误差△H ．这时有L2 = R2 + ( H +△H + R )2 －2R ( H +△H + R ) cos ( θ+△θ)．（5）将式（5）展开，因△θ很小，从而△H也很小，可略去高次项，再与式（3）相减，得△H = －R ( R +H ) sinθ△θH +( 1－cosθ) R，（6）其中H 由（4）式给出．（iii）如果时间τ有τ△的误差，则L 有误差△L = cτ△．（7）由式（3）可知，这将引起H 产生误差△H ．这时有( L +△L )2 = R2 + ( H +△H + R )2 －2R ( H +△H + R ) cosθ．（8）由式（7），（8）和（3），略去高次项，可得△H =c2ττ△H + R ( 1－cosθ)，（9）其中H 由式（4）给出．2．（i）在式（4）中代入数据，算得H = 2.8 ×104 km ．（ii）在式（6）中代入数据，算得△H =25m ．（iii）在式（9）中代入数据，算得△H = ±3.0 m ．3．选择一个坐标系，设被测物体待定位置的坐标为x，y，z，待定时刻为t ，第i 个卫星在t i 时刻的坐标为x i，y i，z i．卫星信号电波以光速传播，可以写出(x－x i )2 + (y－y i )2 + (z －z i )2 = c2 (t－t i )2( i = 1 ，2 ，3 ，4 )，（10）由于方程（1）有四个未知数t ，x，y，z，需要四个独立方程才有确定的解，故需同时接收至少四个不同卫星的信号．确定当时物体的位置和该时刻所需要的是式（10）中i = 1 ，2 ，3 ，4 所对应的四个独立方程．4．（I）由于卫星上钟的变慢因子为[ 1－( v/ c)2] 1 / 2 ，地上的钟的示数T 与卫星上的钟的示数t 之差为T－t = T－1－(vc )2T= [ 1－1－(vc )2] T ，（11）这里v 是卫星相对地面的速度，可由下列方程定出：v2r= GMr2，（12）其中G 是万有引力常量，M 是地球质量，r 是轨道半径．式（11）给出v = GMr =gr R =gR + h R ，其中R 是地球半径，h 是卫星离地面的高度，g = GM / R2是地面重力加速度；代入数值有v = 3.89 km / s ．于是( v / c )2 ≈1.68 ×10－10，这是很小的数．所以[ 1－(vc )2 ]1 / 2 ≈1－12(vc )2．最后，可以算出24 h 的时差T－t ≈12(vc )2T=12gR2c2 ( R + h )T = 7.3μs ．（13）（II）卫星上的钟的示数t与无限远惯性系中的钟的示数T0之差t－T= 1－2φc2T0－T0= ( 1－2φc2－1 )T0 ．（14）卫星上的钟所处的重力势能的大小为φ=GMR + h=R2R + hg．（15）所以φc2=gR2c2 ( R + h )；代入数值有φ/ c2 = 1.68 ×10－10，这是很小的数．式（14）近似为t －T 0 ≈－ φc 2T 0 ．（16）类似地，地面上的钟的示数 T 与无限远惯性系的钟的示数之差T －T 0 = 1－2E φ c 2 T 0－T 0 = ( 1－2Eφ c 2 －1 )T 0 ．（17）地面上的钟所处的重力势能的大小为E φ= GM R=gR ．（18）所以 Eφ c 2 = gR c 2 ；代入数值有E φ/ c 2 = 6.96 ×10－10 ，这是很小的数．与上面的情形类似，式（17）近似为T －T 0 ≈－ Eφ c 2T 0 ．（19）（16），（19）两式相减，即得卫星上的钟的示数与地面上的钟的示数之差t －T ≈－ Eφφ- c 2T 0 ．（20）从式（19）中解出 T 0 ，并代入式（20）得t －T ≈－ E φφ- c 2 / (1－ E φ c 2 )T ≈－ Eφφ- c 2 T = gR c 2 hR + h T ．（21）注意，题目中的 24 h 是指地面的钟走过的时间 T ．最后，算出 24 h 卫星上的钟的示数与地面上的钟的示数之差t －T = 46μs ．（22）三、1．依题意，为使室内温度保持不变，热泵向室内放热的功率应与房间向室外散热的功率相等．设热泵在室内放热的功率为 q ，需要消耗的电功率为 P ，则它从室外（低温处）吸收热量的功率为 q －P ．根据题意有q －P P≤ T 2T 1－T 2 ，（1）式中 T 1 为室内（高温处）的绝对温度，T 2 为室外的绝对温度．由（1）式得P ≥ T 1－T 2T 1q ．（2）显然，为使电费最少，P 应取最小值；即式（2）中的“≥”号应取等号，对应于理想情况下P 最小．故最小电功率Pmin =T1－T2T1q ．（3）又依题意，房间由玻璃板通过热传导方式向外散热，散热的功率H =k T1－T2lS ．（4）要保持室内温度恒定，应有q = H ．（5）由（3）～（5）三式得Pmin=kS ( T1－T2 )2lT1．（6）设热泵工作时间为t，每度电的电费为c，则热泵工作需花费的最少电费Cmin= P min tc ．（7）注意到T1 = 20.00 K + 273.15 K = 293.15 K ，T2 = －5.00 K + 273.15 K = 268.15 K ，1度电= 1 kW • h ．由（6），（7）两式，并代入有关数据得Cmin =( T1－T2 )2T1l Sktc = 23.99元．（8）所以，在理想情况下，该热泵工作12 h 需约24元电费．2．设中间空气层内表面的温度为T i，外表面的温度为T0 ，则单位时间内通过内层玻璃、中间空气层和外层玻璃传导的热量分别为H1=kT1－T il S ，（9）H2=k0Ti－T0lS ，（10）H3=kT－T2lS ．（11）在稳定传热的情况下，有H1=H2=H3．（12）由（9）～（12）四式得k T1－T il= k0Ti－T0l和T1－T i = T0－T2．（13）解式（13）得T i =lk + lklk + 2lkT1+lklk + 2lkT2．（14）将（14）式代入（9）式得H1 =kklk + 2lk( T1－T2)S ．（15）要保持室内温度恒定，应有q = H1．由式（3）知，在双层玻璃情况下热泵消耗的最小电功率P′min =kklk + 2lk( T1－T2 )2T1S ．（16）在理想情况下，热泵工作时间t需要的电费C ′min= P′min tc ；（17）代入有关数据得C′min= 2.52元．（18）所以，改用所选的双层玻璃板后，该热泵工作12 h 可以节约的电费△C min = C min －C′min= 21.47 元．（19）四、1．先假设由于隧穿效应，单电子能从电容器的极板A 隧穿到极板B．以Q 表示单电子隧穿前极板A 所带的电荷量，VAB表示两极板间的电压（如题目中图3所示），则有VAB= Q/ C ．（1）这时电容器储能U= 1 2CV2AB．（2）当单电子隧穿到极板B后，极板A所带的电荷量为Q′= Q + e ，（3）式中e 为电子电荷量的大小．这时，电容器两极板间的电压和电容器分别储能为V′AB =Q + eC，U′=12CV ′2AB．（4）若发生库仑阻塞，即隧穿过程被禁止，则要求U′－U ＞0 ．（5）由（1）～（5）五式得V AB ＞－12eC ．（6）再假设单电子能从电容器的极板B隧穿到极板A．仍以Q表示单电子隧穿前极板A所带的电荷量，VAB表示两极板间的电压．当单电子从极板B隧穿到极板A时，极板A所带的电荷量为Q′ = Q－e ．经过类似的计算，可得单电子从极板B 到极板A的隧穿不能发生的条件是V AB ＜12eC ．（7）由（6），（7）两式知，当电压V AB 在－e / 2C～e / 2C 之间时，单电子隧穿受到库仑阻塞，即库仑阻塞的条件为－12eC ＜V AB ＜12eC ．（8）2．依题意和式（8）可知，恰好能发生隧穿时有V AB =12eC = 0.10mV ．（9）由式（9），并代入有关数据得C =8.0 ×10－16 F ．（10）3．设题目中图3中左边的MIM 结的电容为C S，右边的MIM 结的电容为C D ．双结结构体系如图a所示，以Q1 ，Q2 分别表示电容C S ，C D所带的电荷量．根据题意，中间单电子岛上的电荷量为－ne = Q2－Q1．（11）体系的静电能为C S 和C D 中静电能的总和，即U = Q212C S+Q222C D；（12）图a电压V = Q1CS+Q2CD．（13）由（11）～（13）三式解得U = 12CV2+(Q2－Q1)22 ( C S + C D )．（14）由于V为恒量，从式（13）可知体系的静电能中与岛上净电荷相关的静电能U n= (－ne )2 / 2 (C S + C D )．4．U n 随C G V G 变化的图线如图b；C G V G / e 的变化范围如表2．表2n 0 1 2 3C G VG/ e 的变化范围0～0.5 0.5～1.5 1.5～2.5 2.5～3.0U n( e2 / 2C )五、1．在图1中，z轴垂直于AB面．考察平行光束中两条光线分别在AB面上C与C′点以入射角i 射入透明圆柱时的情况，r 为折射角，在圆柱体中两折射光线分别射达圆柱面的D和D′，对圆柱面其入射角分别为i2与i′2 ．在△OCD中，O点与入射点C的距离y c由正弦定理得y c sin i2=Rsin ( 90° + r)，即y c =sin i2cos rR ．（1）同理在△OC ′D′中，O 点与入射点C ′的距离有y c′sin i′2=Rsin ( 90°－r)，即y c′=sin i′2cos rR ．（2）当改变入射角i时，折射角r 与柱面上的入射角i2与i′2 亦图1随之变化．在柱面上的入射角满足临界角i20= arcsin ( 1 / n) ≈41.8°（3）时，发生全反射．将i2 = i′2 = i20 分别代入式（1），（2）得y o c =y o c ′=sin i20cos rR ，（4）即d= 2y o c= 2sin i20 cos rR ．（5）当y c ＞y o c和y c ′＞y o c ′时，入射光线进入柱体，经过折射后射达柱面时的入射角大于临界角i20 ，由于发生全反射不能射出柱体．因折射角r随入射角i 增大而增大．由式（4）知，当r = 0 ，即i = 0（垂直入射）时，d 取最小值dmin= 2R sin i20 = 1.33 R ．（6）当i →90°（掠入射）时，r→41.8°．将r =41.8°代入式（4）得dmax= 1.79 R．（7）2．由图2可见，φ是Oz 轴与线段OD 的夹角，φ′是Oz 轴与线段图2OD ′ 的夹角．发生全反射时，有φ = i 20 + r ，（8）φ′ = i 20 － r ，（9）和 θ = φ + φ′ = 2i 20≈83.6° ．（10）由此可见，θ 与 i 无关，即 θ 独立于 i ．在掠入射时，i ≈90° ，r = 41.8° ，由式（8）,（9）两式得φ = 83.6° ，φ′ = 0°．（11）六、由于方程r= GM / c 2a cos φ + a 2 ( 1 + sin 2φ)（1）是 φ 的偶函数，光线关于极轴对称．光线在坐标原点左侧的情形对应于 a ＜ 0 ；光线在坐标原点右侧的情形对应 a ＞ 0 ．右图是 a ＜ 0 的情形，图中极轴为 Ox ，白矮星在原点O 处．在式（1）中代入近星点坐标 r = r m ，φ = π ，并注意到 a 2| a | ，有a ≈－GM / c 2r m ．（2）经过白矮星两侧的星光对观测者所张的视角 θS 可以有不同的表y S r x O Er m φ达方式，相应的问题有不同的解法．解法一：若从白矮星到地球的距离为d，则可近似地写出θS≈2r m/ d．（3）在式（1）中代入观测者的坐标r = d，φ= －π/ 2，有a2≈GM/ 2c2d．（4）由（2）与（4）两式消去a，可以解出rm= 2GMd / c2 ．（5）把式（5）代入式（3）得θS≈8GM / c2d；（6）即M≈θ2Sc2d/ 8G ，（7）其中d = 3.787 ×1017 m ；代入数值就可算出M≈2.07 ×1030 kg ．（8）解法二：光线射向无限远处的坐标可以写成r→∞，φ= －π2+θ2．（9）近似地取 θS ≈θ ，把式（9）代入式（1），要求式（1）分母为零，并注意到 θ1，有a θ / 2 + 2a 2 = 0 ．所以 θS ≈θ = －4a = 8GM / c 2d ，（10）其中用到式（4），并注意到 a ＜ 0 ．式（10）与式（6）相同，从而也有式（8）．解法三：星光对观测者所张的视角 θS 应等于两条光线在观测者处切线的夹角，有sinθS2=△( r cos φ )△r= cos φ－r sin φ△φ△r ．（11）由光线方程（1）算出△φ / △r ，有sin θS2 = cos φ－r sin φGM / c 2r 2a sin φ = cos φ－ GM c 2ra；代入观测者的坐标r = d ， = －π / 2 以及 a 的表达式（4），并注意到 θS 很小，就有θS≈2GM c 2d2c 2dGM=8GM c 2d，与式（6）相同．所以，也得到了式（8）．解法四：用式（2）把方程（1）改写成－r m = r cosφ－GMc2rmr[ (r cosφ )2 + 2 (r sinφ)2 ] ，即x= －r m + GMc2rmr( x2+2y2 ) ．（12）当y→－∞时，式（12）的渐近式为x = －rm －2GMc2rmy．这是直线方程，它在x轴上的截距为－r m ，斜率为1－2GM/ c2r m≈1－tan ( θS / 2 ) ≈－1θS/ 2．于是有θS ≈4GM/c2r m ．r m用式（5）代入后，得到式（6），从而也有式（8）．七、1．（I）氦原子中有两个电子，一级电离能E+ 是把其中一个电子移到无限远处所需要的能量满足He + E+ →He+ + e－．为了得到氦原子的一级电离能E+ ，需要求出一个电子电离以后氦离子体系的能量E*．这是一个电子围绕氦核运动的体系，下面给出两种解法．解法一：在力学方程2ke2r2= mv2 r中，r 是轨道半径，v 是电子速度．对基态，用玻尔量子化条件（角动量为）可以解出r=2/ 2ke2m ．（1）于是氦离子能量E* = p22m－2ke2r= －2k2e4m2，（2）其中p0 为基态电子动量的大小；代入数值得E* = －2( ke2 )2mc2(c)2≈－54.4eV ．（3）由于不计电子间的相互作用，氦原子基态的能量E0 是该值的2倍，即E=2E* ≈－108.8 eV ．（4）氦离子能量E*与氦原子基态能量E0之差就是氦原子的一级电离能E+ =E*－E= －E*≈54.4 eV ．（5）解法二：氦离子能量E*= p22m－2ke2r．把基态的角动量关系rp =代入，式（3）可以改写成E* = 22mr2－2ke2r=22m(1r－2ke2m2)2－2k2e4m2．因基态的能量最小，式（4）等号右边的第一项为零，所以半径和能量r 0 = 22ke2m，E*= －2k2e4m2分别与（1），（2）两式相同．（II）下面，同样给出求氦原子基态能量E0和半径r0的两种解法．解法一：利用力学方程mv2r= 2ke2r2－ke2( 2r )2=7ke24r2和基态量子化条件rmv =，可以解出半径r= 42/ 7ke2m，（6）于是氦原子基态能量E 0= 2 (p22m－2ke2r) +ke22r0= －49k2e4m162；（7）代入数值算得E 0= －49( ke2 )2mc216(c)2≈－83.4 eV ，（8）r 0 =4 (c)27ke2mc2≈ 0.0302 nm ．所以，氦原子的一级电离能E+ =E*－E≈29.0 eV ．（9）这仍比实验测得的氦原子一级电离能24.6 eV 高出4.4 eV ．解法二：氦原子能量E = 2 (p22m－2ke2r) +ke22r=2mr2－7ke22r可以化成E = 2m( 1r－7ke2m42)2－49k2e4m162．当上式等号右边第一项为零时，能量最小．由此可知，基态能量与半径E 0 =－49k2e4m162，r0=427ke2m分别与（7），（6）两式相同．2．（I）粒子从下部射向并穿过铅板向上运动，其电荷为正．（II）如题图所示，粒子的运动速度v 与磁场方向垂直，洛伦兹力在纸面内；磁力不改变荷电粒子动量的大小，只改变其方向．若不考虑云室中气体对粒子的阻力，荷电粒子在恒定磁场作用下的运动轨迹就是曲率半径为一定值的圆弧；可以写出其运动方程qBv=|△p△t| =p△φ△t=pvr，（1）其中q 是粒子电荷，v 是粒子速度的大小，p 是粒子动量的大小，△φ是粒子在△t时间内转过的角度，r是轨迹曲率半径．于是有p= qBr ．（2）按题意，q=e ．用p d 和p u 分别表示粒子射入铅板和自铅板射出时动量的大小，并在式（1）中代入有关数据，可以算得pd=63.0 MeV / c ，p u= 22.8 MeV / c ．（3）注意到当pc mc2 时应使用狭义相对论，从p=mv1－( v / c)2．（4）中可以得到v=c1+( mc / p)2．（5）用v d 和v u 分别表示粒子进入和离开铅板时的速度大小．把式（2）以及m = 0.511 MeV / c2代入式（3），可得vd≈c，v u≈c．（6）于是，粒子穿过铅板的平均速度v= ( 1 / 2 ) ( v d + v u ) ≈c．用△t表示粒子穿过铅板的时间，则有v cosθ△t =d．（7）再用△p du表示粒子穿过铅板动量改变量的大小，铅板所受到的平均力的大小f = △p du△t=pd－p ud / (v cosθ)≈( p d－p u ) c cosθd；（8）代入有关数值得f ≈ 1.04 ×10－9。

第35届全国中学生物理竞赛决赛训练试题第03套-解答

第35届全国中学生物理竞赛决赛训练试题第03套解答【第一题】40分如图所示，一个质量为m ，半径为R 的匀质圆环静止竖立在地面上，二者间的摩擦系数为μ.图中A 点所在直径与竖直方向夹角为()0/2θθπ<<，现在在A 点瞬间给予圆环一个冲量I ，与竖直方向夹角为()0/2φφπ<<.假设收到冲击后圆环竖直方向上速度为零。

(1) 参数μ,θ,ϕ满足何种条件时，圆环最低点（M 处）将与地面发生滑动？ (2) 分别在发生滑动与不发生滑动的条件下求出末态圆环的质心速度和转动角速度. (3) 在一定条件下，圆环可能在一段时间之后滚回初始位置. 这要求参数μ,θ,ϕ满足何种条件？解答：(1) 由于冲量是瞬间作用的，可以不考虑重力的作用. 考虑到圆环竖直方向没有运动，地面支持力的冲量为cos I ϕ.设摩擦力冲量为i .先确定冲量i 的方向，如果地面光滑，则容易看出sin C v I ϕ=,()sin //C I mR v R ωϕθ=-<，故最低点速度向右，由此判断摩擦力向左. 水平方向动量定理：sin C mv I i ϕ=- [1]对质心C 的角动量定理：()2sin mR IR iRωϕθ=-+ [2]假设底部没有滑动，则C v R ω= [3]联立以上三式可解得()sin sin 2I i ϕϕθ--⎡⎤⎣⎦= [4]而摩擦力可提供的冲量最大为max cos i I μϕ=,故发生滑动摩擦的条件是()sin sin cos 2ϕϕθμϕ--⎡⎤⎣⎦<[5](16分，判断摩擦力方向2分，[3]式2分，其他四式各3分)（2）不发生滑动摩擦的情况下，联立[1]-[3]式可解得()sin sin 2C I v mϕϕθ+-⎡⎤⎣⎦=,()sin sin 2I mRϕϕθω+-⎡⎤⎣⎦=[6] 发生滑动得情况下，联立[1]、[2]式以及cos i I μϕ=可解得sin cos c I I v mϕμϕ-=, ()cos sin I I mR μϕϕθω+-=[7](12分，两种情况各6分)（3）要滚离初始位置再滚回，首先要求I 作用完成后圆环底部与地面有相对滑动（否则将一直匀速纯滚动，不可能滚回来），即要满足[5]式.在这个前提下，就有可能质心速度向右，但逆时针转动，在地面摩擦力作用下达到纯滚动时向左运动，最终回到初始位置. 以地面上的固定点M 为参考点，I 作用完成后的运动中，重力与支持力的力矩相互抵消，摩擦力过M 点不产生力矩，故圆环角动量守恒. 圆环能滚回来要求初始时角动量向纸面外（逆时针转动）.由于冲量I 作用过程中支持力和摩擦力对M 点也没有力矩，故这就要求M 在I 的延长线上方，即/2ϕθ<.所以参数应满足的条件为()cos sin sin /2/2μϕϕϕθϕθ⎧<--⎡⎤⎪⎣⎦⎨<⎪⎩ [8](12分，利用上一问解得的速度和角速度计算纯滚动速度时得到结果也可，其他方法也可)【第二题】40分在数轴的原点有一只球形猪，每过0t 时间，猪就会随机向左或者向右走单位长度1。

第35届全国中学生物理竞赛决赛训练试题第05套解答v4

第35届全国中学生物理竞赛决赛训练试题第05套解答【第一题】40分疯狂的科学家想制造一条太空锁链.在地球赤道上两处，立起等长的足够坚固、长度可调的两根柱子，忽略地球自转，地球半径为R ，地表重力加速度为g .在两根柱子的顶端之间连接一根质量线密度为λ的链条，链条处于平衡状态. 锁链所能承受的最大张力为max T .若要求锁链最低点距离地心为0r 、有张力2002gR T r λ=，已知2max 00gR T T r λ<+，求在锁链恰好不断裂时：（1）端点处链条切线与柱子的夹角C α；（2）锁链的形状()r θ；（3）两根柱子之间的夹角C φ；解答：易知引力势能为：2P R E mg r=-[1]由虚功原理，可以得到r 处张力T 的大小：()20011T T ds dsgR r r λ⎛⎫-=- ⎪⎝⎭()20011T T ds dsgR r r λ⎛⎫-=-⎪⎝⎭20011T T gR r r λ⎛⎫=+- ⎪⎝⎭[2]由于对称性，取一半锁链对地心有力矩平衡：00sin Tr T r α=[3]极坐标下有几何关系：sin α==[4]联立以上方程可得：22000011T gR T r r r λ⎡⎤⎛⎫+-=⎢ ⎪⎝⎭⎣ [5]作换元1u r=：()200011gR u u T u λ⎡⎤+-=⎢⎣进一步整理：()20000gR u u u u T λ⎡⎤+-=⎢⎥⎣⎦[6]由于θ↑r ↑u ↓，于是：d θ= [7]代入2002T gR u λ=及00r r θ==可以得到:()1arcsin1022rrπθθ⎡⎤⎛⎫=-+>⎪⎢⎥⎝⎭⎣⎦[8]()0rθ=>[9]()()()0r rθθθ=-<[10] 由[2]可知：11max0max220013CT T Trr gR r gRλλ--⎛⎫⎛⎫-=-=-⎪ ⎪⎝⎭⎝⎭[11]代入[3]有Cα：()2max00max02max max02arcsin1arcsin3CT TT T rgRT g T r gRλαλλ-⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦[12]代入[8]有：max0212arcsin422C CT rgRπφθλ⎡⎤⎛⎫==--⎢⎥⎪⎝⎭⎦[13][1-5]共10分[8][9]共10分[12]10分[13]10分【第二题】40分记太阳质量为sM、地球质量为eM、火星质量为MM、地球半径为er、火星半径为mr.认为地球和火星在同一平面内绕太阳圆周运动，轨道半径分别为eR和mR. 现通过某种机制使火星突然获得一指向太阳的速度v.（1）（15分）若火星此后的轨道可以与地球轨道相交，求v的最小值.（2）（25分）在（1）的条件下，设火星在到达地球轨道附近时地球恰在轨道上该位置，在地球与火星的间距d满足,,e m e mr r d R R<<<<时，火星相对地球的速度的矢量线与地球球心的距离为b（如图）. 若火星和地球可以发生碰撞，求b的最大值.解答：（1） 202m s mm m mv GM M M R R = [1]0m m m m t e M v R M v R =[2]()()22221122s m s m m m m m t m eGM M GM M M v v M v v R R +-=+-[3]由t v =22212m ms e m e R v GM v R R R ⎛⎫=--++ ⎪⎝⎭[4]则可知v ≥[5][1]-[4]共10分[5]5分（2） ()2220rel t e m v v v v =-+[6]由0e v =2231rels em v GM v R R ⎛=--+ ⎝[7]质心系角动量守恒()rel rel m e v b v r r μμ'=+[8]能量守恒221122e m rel relm eGM M v v r r μμ'=-+ [9]其中约化质量e me mM M M M μ=+可解得)max m e b r r =+[10][6]-[9]共15分[10]10分【第三题】（40分）如图所示, 一个粗糙的, 半径为b 的半球固定在水平面上, 其顶部有一个半径a 的匀质薄球壳. 重力加速度为g .1两球球心的连线与地面夹角为0θ。

第35届全国中学生物理竞赛决赛训练试题第06套-解答v2

第35届全国中学生物理竞赛决赛训练试题第06套【第一题】40分根据伯努利定律，流体沿着一条稳定、不可压缩的流线移动时，根据能量守恒，其动能、势能总保持为常数，也就是212v gh P const ρρ++= （1）由于圆柱比较简单，我们先计算一个质心cx v 水平运动，角速度ω（方向为图示中y 方向），半径为R ，高度为h （对称轴为y 轴，>>h R ）的圆柱受到的合力。

假设其表面的空气和圆柱保持同样的速度，并且假设圆柱转动比较快以至于其表面流体的流动可以看做沿着表面的流管进行流动，并且不同位置的高度差可以忽略，如图请先用对称性分析受到的合力方向再计算出其大小。

（13分）（2）假如圆柱质心以cz v 竖直运动，其他条件和（1）中一样，求受到的气体压力的大小和方向。

（5分）（3）作为一个简单的假设，只考虑流体对圆柱平动的影响而不考虑对其转动的影响，圆柱以初速度00ˆˆ(0)c y z v v y v z =+，角速度ˆy ωω=，求速度与时间的关系。

（12分）解答：（1）关于x-z 平面对称，合力无y 分量，速度大小关于y-z 平面对称，合力无x 分量，故合力应该延z 方向。

以柱为系，认为系统为定常理想流体。

则流体的定常流动如图所示，可以认为如图情形在y 方向是无限延伸的。

流体流场为u v +，其中u 为向x 轴负方向常量，v 为环流场，在R 处速度为R ω，随着距离圆柱的距离增大衰减。

对于环路12,C C ，分别是无限靠近圆柱和远离圆柱的两个环路，它们之间用两个从上和从下无限靠近x 轴的路径连接起来。

考察体积内流体动量变化为零()()()()120C C pds u v u v ds ρ-+++⋅=⎰【1】则有()()()()()()()()12--C C Fpds u v u v ds h pds u v u v ds ρρ=+++⋅=+++⋅⎰⎰【2】对于稳定流体()()2011=22P u v u v P u ρρ++++()()()()2201---2C F P v u v ds u u v ds v u ds v v ds h ρρρρρ⎛⎫⎛⎫=⋅++⋅+⋅+⋅ ⎪ ⎪⎝⎭⎝⎭⎰考虑到在环路2C 上<<v u ，()u v ds +⋅为环路内流体流量，则净流量为零，上式化简为()()()()()22=--=-C C Fu v ds v u ds h u v ds ρρ⋅+⋅⨯⨯⎰⎰可知合力为y 方向，其大小为()()2----x y y x C x y Fuv ds v uds h u v dx v dy ρρ=+=⎰⎰ 【3】由茹可夫斯基定理，以及将u 代换成cx v22cx F hR v πρω=【1】【2】各3分，结果方向2分，大小2分（2）在计算F 时，x 轴与z 轴是等地位的，所以圆柱延z 轴方向运动时所受到的力为22cz F hR v πρω=- 【4】负号代表方向沿x 轴负方向。