fluent动态网格自适应
fluent中scale-adaptive simulation介绍

fluent中scale-adaptive simulation介绍Fluent中的Scale-Adaptive Simulation (SAS) 是一种用于计算流体力学 (CFD) 模拟的自适应网格方法,它可以在不同空间尺度上直接模拟流体流动。
SAS 可以在不同尺度下揭示流体流动中的复杂特性,并为各种应用提供更准确和可靠的结果。
SAS 是一种结合了雷诺平均N-S方程 (RANS) 模型和大涡模拟(LES) 方法的模拟技术。
在传统的RANS模拟中,流体流动被假设是平稳和各向同性的,而忽略了湍流的尺度和时间相关性。
然而,在某些流动情况下,湍流的尺度变化和空间相关性对结果的准确性具有重要影响。
相比之下,LES方法可以解决流动中的尺度和相关性问题,但计算成本较高。
SAS方法在不同的空间尺度上组合了RANS和LES方法的优点,以平衡计算效率和准确性。
SAS的核心思想是在CFD模拟中引入一个尺度自适应方法,根据流动场的特性来选择合适的网格尺度进行模拟。
该方法基于雷诺应力的局部尺度来调整模型的二阶湍流粘度。
通过自适应地调整模型的粘度值,SAS方法可以在不同的网格尺度上更准确地模拟湍流流动,并解决RANS方法在处理局部尺度流动时的不足。
为了实现尺度自适应,SAS引入了一个形如子网格的尺度函数。
该尺度函数基于湍流的空间和时间尺度,它可以自适应地调整网格的大小和分辨率。
在SAS中,子网格的尺度将根据当地的湍流动力学来确定。
当流动中存在大尺度的涡旋时,子网格的尺度将调整为较大值以更好地保持这些结构。
而当流动中存在小尺度的涡旋时,子网格的尺度将减小以捕获更多的细节。
SAS方法在多个领域得到了广泛的应用,包括空气动力学、船舶流体力学、涡轮机械、燃烧和环境工程等。
通过适当选择尺度函数和调整模型的湍流粘度,SAS可以在不同尺度下模拟出更准确和可靠的结果。
相比传统的RANS方法,SAS方法能够更好地预测湍流结构、细节和湍流交互。
05-第五章 FLUENT适应性网格技术

第五章 适应性网格技术FLUENT的解适应性网格细化的特性允许用户在几何的和数值的解数据的基础上细化和/或粗糙化网格。
另外,为建立和查看用户化的适应场,FLUENT提供了特殊应用的工具。
本章从以下10节详细介绍适应性处理。
5.1 使用适应性网格5.2 网格适应过程5.3 边界适应5.4 梯度适应5.5 各向同性适应5.6 区域适应5.7 体积适应5.8 y+和y*适应5.9 管理适应标识5.10 适应性控制5.11 用光滑和交换的方式改善网格5.1 使用适应性网格在FLUENT中,非结构网格的功能有两个重要的优势:与结构网格相比,缩短设置时间合并网格的解适应性细化的能力使用解适应性细化可以添加网格中需要的单元,从而能够使流场得到更好的解决。
当适应性被合适的利用时,由于解被用来决定添加更多单元的地方,因此所得到的网格对于流动的解是最理想的。
换言之,网格中包含多余的单元不会浪费计算资源,这发生在结构网格中是比较有代表性的情形。
进一步而言,网格细化对解的影响可以在不用完全重新生成网格的情况下来研究。
!在一个并行计算中,任何时候执行网格适应性,一个负荷平衡步将被FLUENT在缺省下执行。
可以通过如下的命令关闭自动负荷平衡:(disable-load-balance-after-adaption)若返回到默认行为,则使用下面的命令:(enable-load-balance-after-adaption)注意,自动负荷平衡将不发生在与动态适应相关联的情况下。
5.1.1 适应性的例子这一小节介绍怎样在可压缩、湍流流动经过一个2D涡轮叶栅的解中有效地使用适应性。
最初的网格,如图5.1.1所示,在叶片周围是非常细的。
表面节点分布为叶片几何提供了足够的定义,并且使湍流边界层不用进一步适应而能够得到完全解决。
另一方面,进口、出口和周期边界处的网格是比较粗糙的。
为保证在叶片通道里的流动得到适当地解决,解适应性细化被用来建立网格,如图5.1.2所示。
fluent介绍

fluent目录简介基本特点优点其他相关编辑本段简介CFD商业软件介绍之一——Fluent通用CFD软件包,用来模拟从不可压缩到高度可压缩范围内的复杂流动。
由于采用了多种求解方法和多重网格加速收敛技术,因而FLUENT能达到最佳的收敛速度和求解精度。
灵活的非结构化网格和基于解的自适应网格技术及成熟的物理模型,使FLUENT在转捩与湍流、传热与相变、化学反应与燃烧、多相流、旋转机械、动/变形网格、噪声、材料加工、燃料电池等方面有广泛应用。
编辑本段基本特点FLUENT软件具有以下特点:☆FLUENT软件采用基于完全非结构化网格的有限体积法,而且具有基于网格节点和网格单元的梯度算法;☆定常/非定常流动模拟,而且新增快速非定常模拟功能;☆FLUENT软件中的动/变形网格技术主要解决边界运动的问题,用户只需指定初始网格和运动壁面的边界条件,余下的网格变化完全由解算器自动生成。
网格变形方式有三种:弹簧压缩式、动态铺层式以及局部网格重生式。
其局部网格重生式是FLUENT所独有的,而且用途广泛,可用于非结构网格、变形较大问题以及物体运动规律事先不知道而完全由流动所产生的力所决定的问题;☆FLUENT软件具有强大的网格支持能力,支持界面不连续的网格、混合网格、动/变形网格以及滑动网格等。
值得强调的是,FLUENT软件还拥有多种基于解的网格的自适应、动态自适应技术以及动网格与网格动态自适应相结合的技术;☆FLUENT软件包含三种算法:非耦合隐式算法、耦合显式算法、耦合隐式算法,是商用软件中最多的;☆FLUENT软件包含丰富而先进的物理模型,使得用户能够精确地模拟无粘流、层流、湍流。
湍流模型包含Spalart-Allmaras模型、k-ω模型组、k-ε模型组、雷诺应力模型(RSM)组、大涡模拟模型(LES)组以及最新的分离涡模拟(DES)和V2F模型等。
另外用户还可以定制或添加自己的湍流模型;☆适用于牛顿流体、非牛顿流体;☆含有强制/自然/混合对流的热传导,固体/流体的热传导、辐射;☆化学组份的混合/反应;☆自由表面流模型,欧拉多相流模型,混合多相流模型,颗粒相模型,空穴两相流模型,湿蒸汽模型;☆融化溶化/凝固;蒸发/冷凝相变模型;☆离散相的拉格朗日跟踪计算;☆非均质渗透性、惯性阻抗、固体热传导,多孔介质模型(考虑多孔介质压力突变);☆风扇,散热器,以热交换器为对象的集中参数模型;☆惯性或非惯性坐标系,复数基准坐标系及滑移网格;☆动静翼相互作用模型化后的接续界面;☆基于精细流场解算的预测流体噪声的声学模型;☆质量、动量、热、化学组份的体积源项;☆丰富的物性参数的数据库;☆磁流体模块主要模拟电磁场和导电流体之间的相互作用问题;☆连续纤维模块主要模拟纤维和气体流动之间的动量、质量以及热的交换问题;☆高效率的并行计算功能,提供多种自动/手动分区算法;内置MPI并行机制大幅度提高并行效率。
第8讲 自适应网格和fluent计算数据的后处理(学生用)

FLUENT模拟中的关键问题与数据后处理以混合问题为例:一、自定义函数(p57)使用命令:Define>Custom Field Function打开自定义函数设计对话框:以定义速度水头为例:显示自定义函数的数值分布:使用命令:Display>Contours…取消Filled选项,保留其它默认设置,点击Display点击Close,结果见下图:二、使用二阶离散化方法重新计算为了提高计算精度,对于计算当中的变量可以在离散格式中,提高其精度:1)使用命令:Solve>Controls>Solution在条目下,选择能量项,并选择,此时要修改相应的能量方程的松弛因子为 0.8。
点击OK。
2)再进行200次计算:得到的结果明显改善:提高精度后的结果和前的结果比较三、 自适应网格FLUENT 设置自适应网格的目的是为了提高计算精度。
1. Display>contours…,选择温度作为显示对象;2. 取消node values 选项,再点击display ,看到单元边界不光滑,即梯度很大,其范围也会显示出来;从图中可以明显的看到,单元间边界很不光滑了。
为了改进梯度变化较大的区域的精度,我们必须建立梯度比较大的网格组合,以便于细分网格,提高计算精度。
3.在contours of 下拉菜单中,选择adption…和adaption function;显示用于改进计算精度的网格图:取消node values选项;点击display;4.把梯度范围大于0.01的显示出来,取消Options项下的Auto Range,设定min为0.01,把梯度大于0.01的边界节点显示出来:如果把min设置为0.005,网格数量明显增加:5.对高温度梯度的范围进行改进:使用Adapt>Gradient对计算区域重新修正;取消上表中的Coarsen选项,点击Compute,Fluent将修正Min和Max,把threshold值改为0.01,点击Mark,这时实际上对比较高梯度的网格节点进行了标记。
自适应网格生成算法与应用

自适应网格生成算法与应用自适应网格生成算法是一种重要的数值计算方法,广泛应用于科学计算、工程模拟和物理仿真等领域。
本文将详细介绍自适应网格生成算法的原理和应用,并探讨其在不同领域中的实际应用案例。
一、自适应网格生成算法的原理自适应网格生成算法是一种基于网格重构的数值计算方法。
其核心思想是根据问题的特性和求解需求,在计算过程中动态调整网格的大小和形状,以提高数值计算的效率和精度。
自适应网格生成算法通常包括以下几个步骤:1. 初始网格生成:根据问题的几何形状和边界条件,生成初始的网格。
2. 误差估计:通过计算网格单元内部的数值误差或局部残差,评估当前网格的精度。
3. 网格划分:根据误差估计结果,确定需要细分的网格单元,并对其进行细分操作。
4. 网格合并:根据误差估计结果,确定需要合并的网格单元,并对其进行合并操作。
5. 网格重构:根据细分和合并操作的结果,对整个网格进行重构,以适应新的问题求解需求。
6. 计算求解:在重构后的网格上进行数值计算,并更新问题的解。
7. 收敛判断:通过对比前后两次计算结果,判断数值计算是否收敛,若未收敛,则返回第二步。
二、自适应网格生成算法的应用自适应网格生成算法在科学计算、工程模拟和物理仿真等领域得到了广泛应用,能够提高计算效率和精度,降低计算成本。
下面将分别从这几个领域进行具体介绍。
1. 科学计算:自适应网格生成算法在科学计算中的应用非常广泛。
例如,对于流体力学中的空气动力学问题,通过自适应网格生成算法,可以在物体表面和流动区域自动调整网格的密度,以捕捉流动细节,提高计算精度和效率。
2. 工程模拟:工程模拟是一个复杂的过程,需要对多个物理场耦合求解。
自适应网格生成算法可以根据不同物理场的特性,分别调整网格在不同区域的分布和密度,以适应多个物理场的求解需求,从而提高工程模拟的准确性和可信度。
3. 物理仿真:自适应网格生成算法在物理仿真中也有重要应用。
例如,在计算结构强度和变形时,通过自适应网格生成算法,可以根据不同部位的应力和应变分布,自动调整网格的大小,以更好地捕捉局部细节,提高仿真结果的准确性。
adapt在fluent意思

adapt在fluent意思在计算机科学中,adapt一词通常用于描述软件或系统的自适应性。
它指的是软件或系统能够自动适应不同的环境和需求,以便更好地满足用户的要求。
在这篇文章中,我们将探讨adapt在流体力学仿真软件Fluent中的应用。
Fluent是一款用于流体力学仿真的软件,它广泛应用于航空航天、汽车工业、能源、环境保护、医学等领域。
在Fluent中,adapt是一个非常重要的功能,它可以使仿真更加准确和高效。
简单来说,adapt是Fluent中的一个网格自适应工具,它可以自动调整网格,以便更好地适应计算区域内的流动情况。
这一过程通常包括以下几个步骤:1. 评估网格质量:在进行自适应之前,Fluent会评估网格的质量,以确定哪些区域需要进行调整。
它会检查网格的几何形状、网格单元的形状和大小等因素,以确定是否需要进行改进。
2. 生成新网格:一旦确定了需要进行调整的区域,Fluent会生成一个新的网格。
这个网格通常比原来的网格更加密集,以便更好地适应流动情况。
3. 重新计算:在生成新的网格之后,Fluent会重新计算流动情况,并将结果与之前的计算进行比较。
如果新的计算结果更加准确,那么就会继续使用新的网格进行计算。
如果新的计算结果没有改进,那么就会回退到之前的网格。
通过这样的自适应过程,Fluent可以更加准确地模拟流动情况,提高仿真的精度和效率。
这对于需要进行流体力学仿真的领域来说非常重要,比如航空航天领域中的飞行器气动力学分析、汽车工业中的空气动力学分析等。
除了在流体力学仿真中的应用之外,adapt在其他领域中也有着广泛的应用。
比如,在机器学习中,adapt可以指机器学习算法的自适应性,即算法可以根据数据的变化自动调整参数和模型,从而提高预测的准确率。
在智能控制领域中,adapt可以指控制系统的自适应性,即控制系统可以根据外部环境的变化自动调整控制策略,从而更好地适应环境。
adapt是一个非常重要的概念,它可以帮助软件和系统更好地适应不同的环境和需求,提高其性能和效率。
Fluent的自适应网格问题

加密网格的话有两种参考标准一种是y+值,一种是y*值,一般来说,要加密网格主要是为了是y+值满足需求,具体的情况看楼主你的需要...根据y+值来加密网格的步骤如下:运行fluent,导入cas and dat 文件后,点击adapt——Yplus/Ystar..。
,之后出现选择界面,一般情况可以保持默认界面,当然也可以根据自己的需求选择选项,一般type项选择Yplus,然后点击compute,在min及max项会出现你的选择壁面的Y+值,在其下方,有minallowed 和maxallowed,输入你所需要的Y+值范围,点击Mark按钮,会标记出不符合要求的部分,然后点击adapt,就可以了,这部分区域的网格会加密,以适应你的要求Y*的步骤也是这样的但是前提是要知道你的计算的y+值范围,而这个值一般是估计值,且跟计算有关的,是个不确定量,所以一般只作参考用希望能帮到你......另外,希望给加分啊,呵呵追问我点完adpat,Yplus/Ystar这个是灰的,不能点。
回答额,你计算了吗?或者说你导入的是cas & dat 文件吗?如果不是,你都没有一个y+值的范围,怎么可能让软件给你加密网格???...(这是基本条件)追问当然计算了,我保存完再导入cas& dat也不行回答那你试试计算完,直接点adapt试试.....还真没遇到过你说的情况追问adapt都能点只是里面的Yplus/Ystar不能点,是灰色的fluent里的常见问题(一)(2011-02-26 09:44:43)1什么叫松弛因子?松弛因子对计算结果有什么样的影响?它对计算的收敛情况又有什么样的影响?1、亚松驰(Under Relaxation):所谓亚松驰就是将本层次计算结果与上一层次结果的差值作适当缩减,以避免由于差值过大而引起非线性迭代过程的发散。
用通用变量来写出时,为松驰因子(Relaxation Factors)。
Fluent中的动网格

Fluent中的动网格动网格是目前求解计算域变化问题的常用方法。
参考Fluent帮助,可以知道动网格技术与一般流动计算设置的主要区别在于网格更新方法和更新域设置。
这里就这两方面问题的一点体会作一简单记录。
一、网格更新方法弹簧近似光滑法将任意两网格节点之间的连线理想地看成一条弹簧,并通过近似弹簧的压缩或拉伸实现网格和计算域的改变。
该方法网格拓扑不变,无需网格的插值处理,对结构化(四边形、六面体)和非结构化(三角形、四面体)网格同样适用。
但不适合于大变形情况,当计算区域变形较大时,变形后的网格质量变差,严重影响计算精度。
动态分层法在运动边界相邻处根据运动规律动态增加或减少网格层数,以此来更新变形区域的网格。
该方法适用于结构化网格,通过设置适当的分层和缩减系数,更新后的网格依然为较为均匀的结构化网格,对计算精度影响较小。
对于运动域具有多自由度和任意变形情况,该方法处理起来非常困难。
网格重生方法在整个网格更新区域内依据设定的最大和最小网格尺寸判断需要进行网格重生的网格,并依据设置的更新频率进行网格重生处理。
该方法适用于非结构化网格,能够较好的应用于任意变形的计算区域处理。
二、更新域设置更新域设置是动网格设置中的一项重要工作,最常用的设置是刚体运动域和变形域,这里针对这两种域的设置注意事项和技巧作一简单介绍。
1、域动网格一般来讲,设置为刚体运动域的区域一般为壁面类边界,通过设置固壁的运动,模拟计算域内物体的运动。
由于固壁边界有时形状较为复杂,壁面附近网格尺度与周围网格尺度存在较大差别,网格更新时变形较大。
在这种情况下,可以设置一个包含固壁运动边界的计算域,通过该计算域的整体运动模拟域内物体的运动,在有的地方将这种方法称为域动网格法。
在域动网格法中,需要设置包含运动物体的内部计算域、内部计算域界面均为刚体运动域。
如下图所示。
2、动态分层法中的分界面在应用动态分层网格更新方法时,当分层界面在计算域内部时,需要采用Split interface(这里称分界面)将运动域运动范围与固定计算域区分开来,以保证动态分层网格处理(如果运动域网格与固定域网格没有分界面,动态分层无法执行)。
fluent网格自适应

1.读入文件.file--read--case找到.msh文件打开2.网格检查grid-check网格检查会报告有关网格的任何错误,特别make sure最小体积不能使负值;3.平滑和交换网格. grid-smooth/swap---点击smooth再点击swap,重复多次;4.确定长度单位grid-scale----.在units conversion中的grid was created in中选择相应的单位,.点击change length units给出相应的范围,点击scal,然后关闭;5.显示网格.display--grid建立求解模型1.define-models-solver(求解器)2.设置湍流模型.define-models-viscous3.选择能量方程define-models-energy4 设置流体物理属性define-materials,进行设置,然后点击change/create,弹出的对话框点NO。
可以从材料库database选择材料和拷贝属性,也可以在properties栏编辑属性,然后点击change/create。
5设置边界条件define-boundary conditions,根据给定条件设置6.求解solver-initialize-initializecomputer from列表中选择要计算的点,点击init,close7监控display-monitors--surface设置surface monitors的个数,勾选plot,点击define,在这里面修改和选择一些选项;然后保存:file-writer-case7 迭代.solver --iterate,会出现检测结果8,显示计算结果.8.1 利用不同颜色显示速度分布display--contours,勾选filled(就是填充),在contours of 选择,点击computer,点击display。
FLUENT动网格技术简介

FLUENT动网格技术简介FLUENT动网格简介在固体有限元计算中,网格运动实非什么稀奇事儿。
而且在绝多数固体计算的基本物理量是网格的节点位移,所以,固体计算中,网格节点运动是对的,没有运动反而不正常了。
也可以这么说:正因为计算域内部节点间的相对运动,才导致了内应力的产生。
流体计算与固体完全不同。
其根源在于它们使用的网格类型不同。
当前固体有限元计算采用的是拉格朗日网格,而流体计算则大多数采用的欧拉网格。
如果说把拉格朗日网格中的节点点看作是真实世界的物质原子的话,那么欧拉网格的节点则好比是真实世界中的一个个传感器,它们总是呆在相同的位置,真实的记录着各自位置上的物理量。
正常情况下,欧拉网格系统是这样的:计算域和节点保持位置不变,发生变化的是物理量,网格节点就像一个个布置在计算域中的传感器,记录该位置上的物理量。
这其实是由流体力学研究方法所决定的。
宏观与微观的差异决定了固体力学计算采用拉格朗日网格,流体计算采用欧拉网格。
关于这部分的详细解说,可以参阅任何一本计算流体动力学书籍。
世界是公平的。
有利必有弊。
朗格朗日网格适合计算节点位移,然而对于过大的网格变形却难以处理。
欧拉网格生来可以处理大变形(因为节点不动),然而对于对于节点运动的处理,则是其直接软肋。
然而很不幸的是,现实生活中有太多网格边界运动的实例。
如汽车发动机中的气缸运动、阀门开启与关闭、机翼的运动、飞机投弹等等等等举不胜举。
计算流体动力学计算的基本物理量通常为:速度、温度、压力、组分。
并不计算网格节点位移。
因此要让网格产生运动,通常给节点施加的物理约束是速度。
CFD中的动网格大体分为两类:(1)显式规定的网格节点速度。
配合瞬态时间,即可很方便的得出位移。
当然一些求解器(如FLUENT)也支持稳态动网格,这时候可以直接指定节点位移。
(2)网格节点速度是通过求解得到的。
如6DOF模型基本上都属于此类。
用户将力换算成加速度,然后将其积分成速度。
对于第一类动网格问题,在fluent中通常可以使用profile与UDF 进行网格设置,通过规定节点或区域的速度、角速度或位移等方式来显式确定网格的运动,通常大部分的动网格问题都归于此类。
fluent命令介绍、网格划分、参数使用
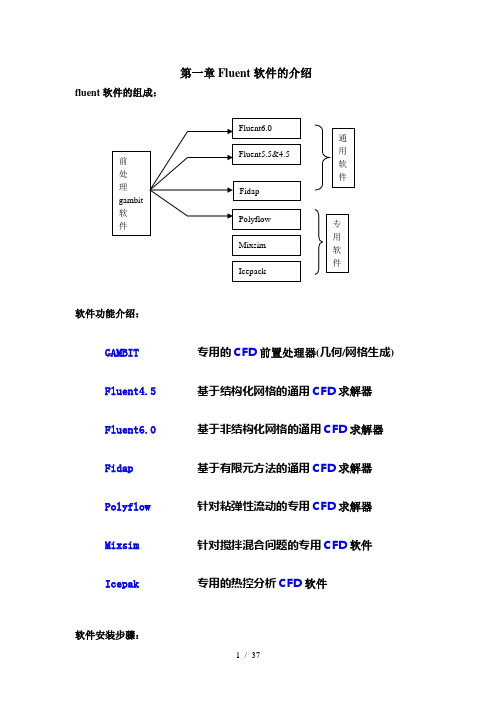
第一章Fluent 软件的介绍fluent 软件的组成:软件功能介绍:GAMBIT 专用的CFD 前置处理器(几何/网格生成) Fluent4.5 基于结构化网格的通用CFD 求解器 Fluent6.0 基于非结构化网格的通用CFD 求解器 Fidap 基于有限元方法的通用CFD 求解器 Polyflow 针对粘弹性流动的专用CFD 求解器 Mixsim 针对搅拌混合问题的专用CFD 软件 Icepak专用的热控分析CFD 软件软件安装步骤:step 1: 首先安装exceed软件,推荐是exceed6.2版本,再装exceed3d,按提示步骤完成即可,提问设定密码等,可忽略或随便填写。
step 2: 点击gambit文件夹的setup.exe,按步骤安装;step 3: FLUENT和GAMBIT需要把相应license.dat文件拷贝到FLUENT.INC/license目录下;step 4:安装完之后,把x:\FLUENT.INC\ntbin\ntx86\gambit.exe命令符拖到桌面(x为安装的盘符);step 5: 点击fluent源文件夹的setup.exe,按步骤安装;step 6: 从程序里找到fluent应用程序,发到桌面上。
注:安装可能出现的几个问题:1.出错信息“unable find/open license.dat",第三步没执行;2.gambit在使用过程中出现非正常退出时可能会产生*.lok文件,下次使用不能打开该工作文件时,进入x:\FLUENT.INC\ntbin\ntx86\,把*.lok文件删除即可;3.安装好FLUENT和GAMBIT最好设置一下用户默认路径,推荐设置办法,在非系统分区建一个目录,如d:\usersa) win2k用户在控制面板-用户和密码-高级-高级,在使用fluent用户的配置文件修改本地路径为d:\users,重起到该用户运行命令提示符,检查用户路径是否修改;b) xp用户,把命令提示符发送到桌面快捷方式,右键单击命令提示符快捷方式在快捷方式-起始位置加入D:\users,重起检查。
Fluent理论手册3—滑移网格及动网格理论
31
图 3.2.2 转子 子-定子相互 互作用
图 3.2.3 3 风机
3.2.1 滑移网 网格技术
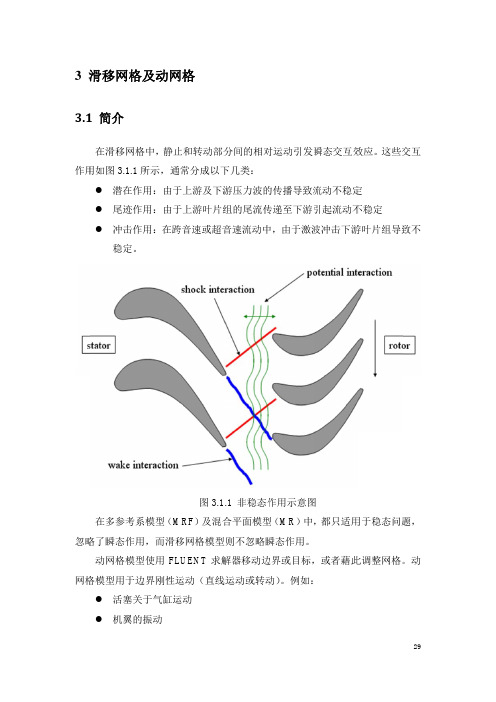
滑移网格 格技术使用两 两个或多个 个计算区域 (如果使用独 独立区域生 生成网格,则 则需 要在 在计算开始 始前将网格文 文件进行合 合并, 如用户 户手册 6.3.15 节: 读入多 多网格文件 件) 。 每一 一个计算区域与其相邻 邻的区域间 间至少存在一 一个分界面 面。 相邻计算 算区域的分界 界面 形成 成“网格分 分界”的形式 式,相隔计 计算区域将会 会关于网格 格分界面进行 行运动。 在计算中,一个计算 算区域相对于 于另一个计 计算域沿着网格分界滑 滑动(旋转或 或平 ,图 3.2.4 及 3.2.5 为两个计算区 移) 为 区域在初始 始位置以及在 在便后一段 段时间后的先 先对 位置 置。 分界面上 上网格并不需 需要进行对 对齐,由于流 流动的非稳态 态特性,因 因此在计算中 中需 要使 使用瞬态分 分析。
34
模型中将各区域连接起来。
3.3.1 动网格更新方法
ANSYS FLUENT 中有三组网格运动方法对变形区域网格进行运动边界指定: 光顺方法(smoothing methods) 动态层(dynamic layering) 局部重构方法(local remeshing methods)
图 3.1 .1 非稳态作 作用示意图 图 在多参考 考系模型 (MRF M ) 及混合 合平面模型 型 (MR) 中, 都只适用 用于稳态问题 题, 忽略 略了瞬态作用,而滑移 移网格模型 型则不忽略瞬 瞬态作用。 模型使用 FL LUENT 求解 解器移动边 边界或目标, ,或者藉此 此调整网格。 。动 动网格模 网格 格模型用于 于边界刚性运 运动(直线 线运动或转动 动) 。例如: 活塞关 关于气缸运 运动 机翼的 的振动
FLUENT不收敛的解决方法

FLUENT不收敛的解决方法解决FLUENT不收敛的问题是一个复杂的过程,因为它涉及到多个因素的相互影响。
下面是一些解决FLUENT不收敛问题的常用方法:1.初始条件的选择:在开始数值求解之前,需要确定一个合适的初始条件。
初始条件对于解的收敛性至关重要。
初始条件应该尽可能接近真实的解,以便尽快地达到收敛状态。
2.网格的质量:网格的质量对于解的收敛性有重要影响。
不合适的网格质量可能导致剧烈的数值振荡和不收敛。
因此,在进行数值求解之前,要确保网格是充分细化和适当分布的。
3.边界条件的设置:边界条件是数值求解的重要组成部分。
正确选择和设置边界条件可以帮助解决不收敛的问题。
边界条件应该与实际情况相适应,并且在数值上稳定。
4.松弛因子的调整:松弛因子是迭代求解过程中的一个重要参数。
它可以控制数值振荡的幅度和求解的速度。
调整松弛因子可以帮助改善解的收敛性。
通常,可以通过逐步调整松弛因子的值来找到合适的取值。
5.改变求解方法:FLUENT提供了多种求解方法,包括迭代解法、隐式解法等。
在遇到不收敛的情况下,可以尝试改变求解方法。
例如,从显式求解器切换到隐式求解器,或者改变迭代收敛准则等。
6.缩小时间步长:时间步长是时间离散化的重要参数。
当模拟流体现象有快速变化时,时间步长可能需要相应缩小。
缩小时间步长可以提高求解的稳定性和收敛性。
7.考虑物理特性:在建立数学模型和设定边界条件时,要充分考虑物理特性。
不合理的模型和边界条件可能导致不收敛的问题。
合理的物理模型和边界条件可以提高解的收敛性。
8.自适应网格:自适应网格技术可以根据流场的变化情况动态调整网格,从而提高求解的精度和收敛性。
在遇到不收敛的问题时,可以尝试使用自适应网格技术。
9.并行计算:FLUENT支持并行计算,可以利用多个处理器进行求解。
并行计算可以加速求解过程,并有助于解决不收敛的问题。
通过提高计算效率,可以增加求解的稳定性和收敛性。
10.稳定化技术:当遇到不稳定的流场时,可以尝试使用稳定化技术来提高求解的稳定性。
网格自适应

3. 对于 3D网格,减小Minimum Skewness为0.6,重复 smoothing/swapping过程
Yplus/Ystar自适应
使壁面网格满足湍流壁面函数和湍流模型 的要求
Adapt -> Yplus/Ystar...
湍流壁面网格要求
壁面函数
标准和非网格处于过渡区
边界层中的网格单元不能太少
增强壁面处理
网格最好足够细,分辨粘性底,双层模型占主导
造成网格线相交,产生负体积 执行光顺前需保存case文件
Skewness-Based Smoothing
算法:移动节点,减小偏斜度 问题:
可能最大偏斜度降低,平均偏斜度升高 建议只对偏斜度非常高的单元进行光顺
Minimum Skewness:0.4 for 2D;0.8 for 3D.
面交换(swapping )
提高三角形和四面体网格的质量 三角形网格面交换:约束优化的Delaunay网格
交换
四面体网格面交换
skewness-based光顺与交换联用
1. skewness-based smoothing, Minimum Skewness of 0.8 for 3D, or 0.4 for 2D
动态梯度自适应设置
采用Hanging node 方法 设置Min # of Cells, Max # of Cells,超过限
制时自动调整加密和合并阈值 设置Max Level of Refine(一般设为2) 和
Min Cell Volume
等值面自适应 Adapt -> Iso-Value...
fluent 动网格

Remeshing方法中的一些参数设定:Remeshing中的参数Minimum length scale和Maximum Length Scale,这两个参数你可以参考mesh scale info中的值,仅是参考,因为mesh scale info中的值是整个网格的评价值,设置的时候看一下动网格附近的网格和整个网格区域的大小比较,然后确定这两个参数,一般来讲,动网格附近的网格较密,这些值都比整体的小,所以在设置时通常设置为比mesh scale info中的Minimum length scale大一点,比Maximum Length Scale小一点。
以上是一般来讲的设置思路。
下面是我在NACA0012翼型动网格例子中的设置:Remeshing中的参数设定:为了得到较好的网格更新,本例在使用局部网格重新划分方法时,使用尺寸函数,也就是Remeshing+Must Improve Skewness+Size Function的策略。
将Minimum Length Scale及Maximum Length Scale均设置为0,为了使所有的区域都被标记重新划分;Maximum Cell Skewness(最大单元畸变),参考Mesh Scale Info…中的参考值0.51,将其设定为0。
4,以保证更新后的单元质量;Size Remesh Interval(依照尺寸标准重新划分的间隔),将这个值设定为1,在FLUENT,不满足最大网格畸变的网格在每个时间步都会被标记,而后重新划分,而不满足最小,最大及尺寸函数的网格,只有在Current Time=(Size Remesh Interval)*delta t的时候,才根据这些尺寸的标准标记不合格的单元进行重新划分,为了保证每步的更新质量,将其修改为1,就是每个时间都根据尺寸的标准标记及更新网格.Size Function Resolution(尺寸函数分辨率),保持默认的3;Size Function Variation(尺寸函数变量):建议使用一个小值,在0.1到0。
fluent 非定常计算的 自适应时间步控制

fluent 非定常计算的自适应时间步控制摘要:1.Fluent 的自适应时间步控制概述2.非定常计算的概念3.自适应时间步控制的实现方法4.自适应时间步控制的优势与应用正文:【1.Fluent 的自适应时间步控制概述】Fluent 是一款广泛应用于流体力学领域的计算流体力学(CFD)软件,能够模拟各种流体流动问题。
在Fluent 中,时间步控制是模拟过程中一个重要的参数,它直接影响到计算结果的准确性和效率。
自适应时间步控制是Fluent 中的一种高级技术,能够在计算过程中动态调整时间步长,以适应不同的计算需求。
【2.非定常计算的概念】非定常计算是指在计算流体流动问题时,流场的物理参数随时间变化而变化。
这与定常计算不同,定常计算假设流场的物理参数不随时间变化。
非定常计算能够更准确地模拟现实世界中的流体流动问题,但同时也增加了计算的复杂性和难度。
【3.自适应时间步控制的实现方法】自适应时间步控制通过在计算过程中动态调整时间步长,以适应不同的计算需求。
具体实现方法包括以下几种:(1)根据流场的变化速率调整时间步长。
当流场的变化速率较大时,需要使用较小的时间步长,以保证计算结果的准确性;当流场的变化速率较小时,可以使用较大的时间步长,以提高计算效率。
(2)根据计算的收敛性调整时间步长。
当计算收敛速度较快时,可以使用较小的时间步长,以提高计算精度;当计算收敛速度较慢时,可以使用较大的时间步长,以减少计算时间。
(3)结合以上两种方法,实时调整时间步长,以达到最优的计算效果。
【4.自适应时间步控制的优势与应用】自适应时间步控制具有以下优势:(1)提高计算效率:通过动态调整时间步长,能够在保证计算结果准确性的同时,减少计算时间。
(2)提高计算精度:根据流场的变化情况调整时间步长,能够使得计算结果更加接近真实值。
(3)简化操作:自适应时间步控制可以自动进行参数调整,减少了用户的操作难度。
自适应时间步控制在Fluent 中的应用非常广泛,适用于各种非定常计算流体流动问题,如湍流、多相流、热传导等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fluent动态网格自适应详解
动态网格自适应用于,瞬态求解计算时,按照一定方法动态的加密某一区域,以实现对该区域物理变量的高精度捕捉。
比如,利用VOF计算液流雾化时,连续的流体会雾化成细小的液滴,且液滴的大小和位置是时时变化的,此时就要用动态网格自适应,去动态的捕捉液滴的位置,并相应的加密此处网格,用以更精确的捕捉液滴的形状。
如下:
1,网格自适应设置
Method-gradient:一般选择gradient(梯度)自适应方法,本方法可以有效的捕捉两相交界面处的网格,便于更好的细化此处网格。
Coarsen threshold:粗化阀值。
这个数值的意思是,低于这个阀值的网格将被标记并粗化,还原成原来的网格。
也就是说当液滴运动到其他位置后,之前位置被细化的网格将被粗化,还原成原来的粗网格。
如果这个值设为0,那么所有被细化的网格将不会被粗化,也就是不会被还原成原来的粗网格。
只有这个值大于0,粗化才有意义。
如本案例中,粗化阀值为0.001,也就是从体积分数梯度的:MIN(1.42E-14)到0.001,这之间的网格将被粗化,还原成原来的网格。
Refine Threshold:细化阀值。
这个数值的意思是,高于这个数值的网格将被标记并细化。
拿本案例来说,体积分数梯度大于这个数值的位置,网格才被加密。
Dynamic:选择这个按钮,说明是在瞬态仿真中,要时时的去细化网格。
瞬态网格自适应,必须选择这个按钮才有效果。
Interval:这个数值的意思是,细化网格的频率。
如果数值为1,就是每个时间步长都要进行网格自适应计算。
数值为10,就是每10个步长进行一次网格自适应计算。
Normalization:包括三种正规化方法。
Standard、scale和normalize,当进行瞬态网格自适应计算时,推荐scale和normalize。
2,设置细化水平
这里的细化水平的也就是网格细化的程度,数值越大表示网格细化的越厉害。
默认为2.。
