中考数学专题训练-旋转模型几何变换三种模型手拉手-半角-对角互补

合集下载

中考数学专题训练旋转模型几何变换的三种模型手拉手半角对角互补

中考数学专题训练旋转模型几何变换的三种模型手拉手半角对角互补Company Document number：WTUT-WT88Y-W8BBGB-BWYTT-19998几何变换的三种模型手拉手、半角、对角互补⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎧⎪⎨⎪⎩⎪⎪⎩等腰三角形手拉手模型等腰直角三角形（包含正方形）等边三角形（包含费马点）特殊角旋转变换对角互补模型一般角特殊角角含半角模型一般角等线段变换（与圆相关）【练1】（2013北京中考）在ABC △中，AB AC =，BAC α∠=（060α︒<<︒），将线段BC 绕点B 逆时针旋转60°得到线段BD ．（1）如图1，直接写出ABD ∠的大小（用含α的式子表示）；（2）如图2，15060BCE ABE ∠=︒∠=︒，，判断ABE △的形状并加以证明；（3）在（2）的条件下，连结DE ，若45DEC ∠=︒，求α的值．真题演练知识关联图【练2】（2012年北京中考）在ABC △中，BA BC BAC α=∠=，，M 是AC 的中点，P 是线段上的动点，将线段PA 绕点P 顺时针旋转2α得到线段PQ ．（1）若α=60︒且点P 与点M 重合（如图1），线段CQ 的延长线交射线BM 于点D ，请补全图形，并写出CDB ∠的度数；（2）在图2中，点P 不与点B M ，重合，线段CQ 的延长线与射线BM 交于点D ，猜想CDB ∠的大小（用含α的代数式表示），并加以证明；（3）对于适当大小的α，当点P 在线段BM 上运动到某一位置（不与点B ，M 重合）时，能使得线段CQ 的延长线与射线BM 交于点D ，且PQ QD =，请直接写出α的范围．例题精讲考点1：手拉手模型：全等和相似包含：等腰三角形、等腰直角三角形（正方形）、等边三角形伴随旋转出全等，处于各种位置的旋转模型，及残缺的旋转模型都要能很快看出来（1）等腰三角形旋转模型图（共顶点旋转等腰出伴随全等）（2）等边三角形旋转模型图（共顶点旋转等边出伴随全等）（3）等腰直角旋转模型图（共顶点旋转等腰直角出伴随全等）（4）不等边旋转模型图（共顶点旋转不等腰出伴随相似）【例1】（14年海淀期末）已知四边形ABCD和四边形CEFG都是正方形，且AB CE>．（1）如图1，连接BG、DG．求证：BG DE=；（2）如图2，如果正方形ABCD的边长为2，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG BD∥，BG BD=．①求BDE∠的度数；②请直接写出正方形CEFG的边长的值．【题型总结】手拉手模型是中考中最常见的模型，突破口常见的有哪些信息常见的考试方法有哪些【例2】（2014年西城一模）四边形ABCD 是正方形，BEF ∆是等腰直角三角形，90BEF ∠=︒，BE EF =，连接DF ，G 为DF 的中点，连接EG ，CG ，EC 。

旋转模型(手拉手模型、脚拉脚模型、半角模型)典型例题含答案

旋转模型（综合）考察点1：“手拉手”模型（绕点旋转）手拉手模型，亦称为共顶点等腰型，一定会出现旋转型全等。

其衍生模型有等腰对补角模型和等腰旁等角模型。

辅助线作法：通常情况下，绕等腰三角形的顶点旋转，旋转角度为等腰三角形顶角的度数；难一点的情况，还需过旋转点作被旋转三角形的高，以及旋转后三角形的高。

解题时：证明全等通常用的是边角边，难点在于如何先说明夹角相等。

模型回顾：A AA C一、旋转全等图2图1（2）如图2，连接EO ，求证：EO 平分∠AED（1）如图1，连接AC ，BD ，求证：①△OAC ≌△OBD ；②∠AEB=α1. 在△OAB 和△OCD 中，OA=OB ，OC=OD ，∠AOB=∠COD=α，直线AC 与直线BD 相交于点E 。

DDA1. 解：在△OAC 和△OBD 中OE 平分∠AED在Rt △OME 和Rt △ONE 中OM=ONOE=OE∠OEM=∠OEN 过点O 作OM ⊥AC ，ON ⊥BDOM=ONOA=OB∠OAM=∠OBN∠OMA=∠ONB=90°（2）OAM ≌△OBN 图1图2∠AEB=∠AOB=α∠OAC=∠OBD∠OFA=∠EFB在△OAF 和△BEF 中∠OAC=∠OBD△OAC ≌△OBD②①△OAC ≌△OBD（1）OA=OB∠AOC=∠BODOC=ODC C二、等腰旁等角模型图4图3图2图1（4）如图4，若∠ADC=90°+12α，求证：∠ADB=α。

（3）如图3，若α=90°，∠ABD=∠ACD ，求证：∠DAC=∠DBC ；（2）如图2，若α=90°，∠DAC=∠DBC ，求证：∠BDC=45°；1. 如图，在四边形ABCD 中，CA=CB ，∠ACB=α，连接BD 。

（1）如图1，若α=90°，∠ADC=135°，求证：BD ⊥AD ；C∠CDE=45°∠BDC=45°BD ⊥ADBDC ≌△ACE BC=AC∠BCD=∠ACECD=CE ∠BDC=∠CED=45°在△BCD 和△ACD 中A 、D、E 三点共线∠CDE=45°∠ADC=135°∠CDE=∠CED=45°△CDE 1. 证明:（1）将CD 绕点C 顺时针旋转90°得到CE∠BDC=45°DCF CF=CD∠DCF=90°∠ACB=90°∠BCF=∠ACDCF=CD∠BCF=∠ACD在△BCF 和△ACD 中BC=AC∠DBC=∠DACBF=AD BCF ≌△ACD （2）在BD 上取一点F ，使得BF=AD 图2∠ADB=∠ADC-∠BDC=（90°+12α）-（90°-12α）=α∠BDC=∠P=90°-12αD 、G 、H 三点共线∠∠ADC=90°+12α（4）将CD 绕点C 顺时针旋转α，得到CP ，连接DP 、AP∠P=∠CDP=90°-12αCD=CP∠PCD=在△BDC 和△ACP 中BC=AC∠BCD=∠ACPCD=CPBCD ≌△ACPBCH ≌△ACD BC=AC∠BCH=∠ACDCH=CD在△BCH 和△ACD 中∠DAC=∠DBCD 、G 、H 三点共线∠CDG=45°∠CDH=45°∠ACD=∠ABD∠CGD=∠BGA ∠CDG=∠BAG=45°在△DCG 和△ABG 中△CDH ∠CDH=45°（3）将CD 绕点C 逆时针旋转90°得到CH ，连接BH 、DH图3三、等腰对补角模型1.如图，已知△ABC为等边三角形，D是BC下方一点，连接AD。

专题3.1 旋转重难点模型(5大类型)(解析版)

专题3.1 旋转重难点模型（5大类型）【题型1 手拉手模型】【题型2 “半角”模型】【题型3 构造旋转模型解题】【题型4 奔驰模型】【题型5 费马点模型】模型一：“手拉手”模型模型特征：两个等边三角形或等腰直角三角形或正方形共顶点。

模型说明：如图1，▲ABE，▲ACF都是等边三角形，可证▲AEC≌▲ABF。

如图2，▲ABD，▲ACE都是等腰直角三角形，可证▲ADC≌▲ABE如图2，四边形ABEF，四边形ACHD都是正方形，可证▲ABD≌▲AFC模型二：“半角”模型模型特征：大角含半角+有相等的边，通过旋转“使相等的边重合，拼出特殊角”模型说明：（1）如图，在正方形ABCD中，∠EAF=45°，将▲ADF绕点A顺时针旋转90°，得到▲ABG 可证▲AEF≌AEG，所以可到DF+BE=EF（2）如图，在等腰直角▲ABC中，∠MAN=45°，将▲ACN绕点A顺时针旋转90°，得到▲ABQ，可证▲AMN≌▲AMQ，所以可得CN²+BM²=MN²（3）如图，等腰▲ABC中，AB=BC，∠DBE=将▲CBD绕点B逆时针旋转∠CBA 的度数得到▲ABD’可证▲DBE≌▲D’BE。

模型三：构造旋转模型解题方法指导：若一个图形中含有相等的线段和特殊的角度，通常是以等线段的公共端点为旋转中心进行旋转，使得相等的边重合，得出特殊的图形.常见图形旋转：（1）“等边三角形”的旋转方法归纳：将等边三角形内的一个小三角形，旋转60度，从而使小三角形的一边与原等边三角形的边重合，连接小三角形的钝角顶点，得三角形．通过旋转将不相关的线段转化到同一个三角形中，将分散的已知条件集中起来，使问题得以解决．模型四：奔驰模型模型五：费马点模型【费马点问题】问题：如图1，如何找点P使它到△ABC三个顶点的距离之和PA+PB+PC最小？图文解析：如图1，把△APC绕C点顺时针旋转60°得到△A′P′C，连接PP′．则△CPP′为等边三角形，CP=PP′，PA=P′A′，∴PA+PB+PC= P′A′+PB+PP′BC′．∵点A′可看成是线段CA绕C点顺时针旋转60°而得的定点，BA′为定长∴当B、P、P′、A′四点在同一直线上时，PA+PB+PC最小．最小值为BA.′【题型1“手拉手”模型】【典例1】（2022春•西安期末）如图，在△ABC中，BC＝5，以AC为边向外作等边△ACD，以AB为边向外作等边△ABE，连接CE、BD．（1）若AC＝4，∠ACB＝30°，求CE的长；（2）若∠ABC＝60°，AB＝3，求BD的长．【解答】解：（1）∵△ABE与△ACD是等边三角形，∴AC＝AD，AB＝AE，∴∠DCA＝∠CAD＝∠EAB＝60°，∴∠EAB+∠BAC＝∠CAD+∠BAC，即∠EAC＝∠BAD．在△EAC和△BAD中，，∴△EAC≌△BAD（SAS），∴EC＝BD，又∵∠ACB＝30°，∴∠DCB＝∠ACB+∠DCA＝90°，∵CD＝AC＝4，BC＝5，∴BD＝＝＝，∴CE＝；（2）如图，作EK垂直于CB延长线于点K．∵△ABE与△ACD是等边三角形，∴AC＝AD，AB＝AE，∴∠DCA＝∠CAD＝∠EAB＝60°，∴∠EAB+∠BAC＝∠CAD+∠BAC，即∠EAC＝∠BAD．在△EAC和△BAD中，，∴△EAC≌△BAD（SAS），∴EC＝BD，∵∠ABC＝60°，∠ABE＝60°，∴∠EBK＝60°，∴∠BEK＝30°，∴BK＝BE＝，∴EK＝＝＝，∴EC＝＝＝7，∴BD＝EC＝7．【变式1-1】（2022秋•荔湾区校级期中）以△ABC的AB，AC为边分别作正方形ADEB，正方形ACGF，连接DC，BF．（1）CD与BF有什么数量与位置关系？说明理由．（2）利用旋转的观点，在此题中，△ADC可看成由哪个三角形绕哪点旋转多少角度得到的．【解答】解：（1）CD＝BF且CD⊥BF，理由如下：∵四边形ABED和四边形ACGF都是正方形，∴AD＝AB，AC＝AF，∠DAB＝∠CAF＝90°，又∵∠DAC＝∠DAB+∠BAC，∠BAF＝∠CAF+∠BAC，∴∠DAC＝∠BAF，在△DAC与△BAF中，，∴△DAC≌△BAF（SAS），∴DC＝BF，∴∠AFB＝∠ACD，又∵∠AFN+∠ANF＝90°，∠ANF＝∠CNM，∴∠ACD+∠CNM＝90°，∴∠NMC＝90°，∴BF⊥CD；（2）∵AD＝AB，AC＝AF，CD＝BF，∠DAB＝∠CAF＝90°，∴△ADC可看成是△ABF绕点A顺时针旋转90°得到的．【变式1-2】（2022九上·吉林期末）如图①，在△ABC中，∠C=90°，AC=BC=AD=BE，AD⊥BE成立．点D，E分别在边AC，BC上，且CD=CE=（1）将△CDE绕点C逆时针旋转90°时，在图②中补充图形，并直接写出BE的长度；（2）当△CDE绕点C逆时针旋转一周的过程中，AD与BE的数量关系和位置关系是否仍然成立？若成立，请你利用图③证明，若不成立请说明理由；（3）将△CDE绕点C逆时针旋转一周的过程中，当A，D，E三点在同一条直线上时，请直接写出AD的长度．【答案】（1）解：如图所示，BE=（2）解：AD=BE，AD⊥BE仍然成立.证明：延长AD交BE于点H，∵∠ACB=∠DCE=90°，∠ACD=∠ACB−∠BCD，∠BCE=∠DCE−∠BCD，∴∠ACD=∠BCE，又∵CD=CE，AC=BC，∴△ACD≅△BCE，∴AD=BE，∠1=∠2，在Rt△ABC中，∠1+∠3+∠4=90°，∴∠2+∠3+∠4=90°，∴∠AHB=90°，∴AD⊥BE.（3）AD或AD=+1【题型2“半角”模型】【典例2】（秋•锦江区期末）在△ABC中，AB＝AC，点E，F是边BC所在直线上与点B，C不重合的两点．（1）如图1，当∠BAC＝90°，∠EAF＝45°时，直接写出线段BE，CF，EF的数量关系；（不必证明）（2）如图2，当∠BAC＝60°，∠EAF＝30°时，已知BE＝3，CF＝5，求线段EF的长度；（3）如图3，当∠BAC＝90°，∠EAF＝135°时，请探究线段CE，BF，EF的数量关系，并证明．【解答】解：（1）结论：EF2＝BE2+CF2．理由：∵∠BAC＝90°，AB＝AC，∴将△ABE绕点A逆时针旋转90°得△ACG，连接FG，如图1中，∴AG＝AE，CG＝BE，∠ACG＝∠B，∠EAG＝90°，∴∠FCG＝∠ACB+∠ACG＝∠ACB+∠B＝90°，∴FG2＝FC2+CG2＝BE2+FC2；又∵∠EAF＝45°，而∠EAG＝90°，∴∠GAF＝90°﹣45°＝45°，∴∠EAF＝∠GAF，∵AF＝AF，AE＝AG，∴△AEF≌△AGF（SAS），∴EF＝FG，∴EF2＝BE2+CF2．（2）如图2中，∵∠BAC＝60°，AB＝AC，∴将△ABE绕点A逆时针旋转60°得△ACG，连接FG，作GH⊥BC交BC的延长线于H．∵∠BAC＝60°，∠EAF＝30°，∴∠BAE+∠CAF＝∠CAG+∠CAF＝∠FAG＝30°，∴∠EAF＝∠FAG，∵AF＝AF，AE＝AG，∴△AEF≌△AGF（SAS），∴EF＝FG，在Rt△CGH中，∵CG＝BE＝3，∠GCH＝60°，∴∠CGH＝30°，∴CH＝CG＝，GH＝CH＝，在Rt△FGH中，FG＝＝＝7，∴EF＝FG＝7．（3）结论：EF2＝EC2+BF2理由：如图3中，将△AEC绕点A顺时针旋转90°，得到△ABG，连接FG．∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵△ACE≌△ABG，∴∠CAE＝∠BAG，EC＝BG，∠ACE＝∠ABG＝45°，∴∠CAB＝∠EAG＝90°，∠GBF＝90°，∴∠FAG＝360°﹣∠EAF﹣∠EAG＝360°﹣135°﹣90°＝135°，∴∠FAE＝∠FAG，∵FA＝FA，AG＝AE，∴△FAE≌△FAG（SAS），∴EF＝FG，在Rt△FBG中，∵∠FBG＝90°，∴FG2＝BG2+BF2，∵FG＝EF，BG＝EC，∴EF2＝EC2+BF2．【变式2-1】（春•金牛区校级期中）类比探究：（1）如图1，等边△ABC内有一点P，若AP＝8，BP＝15，CP＝17，求∠APB的大小；（提示：将△ABP绕顶点A旋转到△ACP′处）（2）如图2，在△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点，且∠EAF＝45°．求证：EF2＝BE2+FC2；（3）如图3，在△ABC中，∠C＝90°，∠ABC＝30°，点O为△ABC内一点，连接AO、BO、CO，且∠AOC＝∠COB＝∠BOA＝120°，若AC＝1，求OA+OB+OC的值．【解答】解：（1）如图1，将△APB绕着点A逆时针旋转60°得到△ACP′，∴△ACP′≌△ABP，∴AP′＝AP＝8、CP′＝BP＝15、∠AP′C＝∠APB，由题意知旋转角∠PA P′＝60°，∴△AP P′为等边三角形，∴P P′＝AP＝8，∠A P′P＝60°，∵PP′2+P′C2＝82+152＝172＝PC2，∴∠PP′C＝90°，∴∠APB＝∠AP′C＝∠A P′P+∠P P′C＝60°+90°＝150°（2）如图2，把△ABE绕着点A逆时针旋转90°得到△ACE′，则AE′＝AE，CE′＝CE，∠CAE′＝∠BAE，∵∠BAC＝90°，∠EAF＝45°，∴∠BAE+∠CAF＝∠CAF+∠CAE′＝∠FAE′＝45°，∴∠EAF＝∠E′AF，且AE＝AE'，AF＝AF，∴△AEF≌△AE′F（SAS），∴EF＝E′F，∵∠B+∠ACB＝90°，∴∠ACB+∠ACE′＝90°，∴∠FCE′＝90°，∴E′F2＝CF2+CE′2，∴EF2＝BE2+CF2；（3）如图3，将△AOB绕点B顺时针旋转60°至△A′O′B处，连接OO′，∵在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，∴AB＝2，∴BC＝＝，∵△AOB绕点B顺时针方向旋转60°，∴△A′O′B如图所示；∠A′BC＝∠ABC+60°＝30°+60°＝90°，∵∠ACB＝90°，AC＝1，∠ABC＝30°，∴AB＝2AC＝2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，∴△BOO′是等边三角形，∴BO＝OO′，∠BOO′＝∠BO′O＝60°，∵∠AOC＝∠COB＝∠BOA＝120°，∴∠COB+∠BOO′＝∠BO′A′+∠BO′O＝120°+60°＝180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C＝＝，∴OA+OB+OC＝A′O′+OO′+OC＝A′C＝．【变式2-2】（2022春•西山区校级月考）如图，已知正方形ABCD，点E、F分别是AB、BC边上，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM．（1）求证：△EDF≌△MDF；（2）若正方形ABCD的边长为5，AE＝2时，求EF的长？【解答】（1）证明：∵四边形ABCD是正方形，∴∠A＝∠B＝∠DCF＝90°，AD＝AB＝BC＝5，由旋转得：∠A＝∠DCM＝90°，DE＝DM，∠EDM＝90°，∴∠DCF+∠DCM＝180°，∴F、C、M三点在同一条直线上，∵∠EDF＝45°，∴∠FDM＝∠EDM﹣∠EDC＝45°，∴∠EDF＝FDM，∵DF＝DF，∴△EDF≌△MDF（SAS）；（2）设CF＝x，∴BF＝BC﹣CF＝5﹣x，由旋转得：AE＝CM＝2，∴BE＝AB﹣AE＝3，FM＝CF+CM＝2+x，∵△EDF≌△MDF，∴EF＝FM＝2+x，在Rt△EBF中，BE2+BF2＝EF2，∴9+（5﹣x）2＝（2+x）2，∴x＝，∴EF＝2+x＝，∴EF的长为．【变式2-3】（2022秋•山西期末）阅读以下材料，并按要求完成相应的任务：从正方形的一个顶点引出夹角为45°的两条射线，并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型．半角模型可证出多个几何结论，例如：如图1，在正方形ABCD中，以A为顶点的∠EAF＝45°，AE、AF与BC、CD边分别交于E、F两点．易证得EF＝BE+FD．大致证明思路：如图2，将△ADF绕点A顺时针旋转90°，得到△ABH，由∠HBE＝180°可得H、B、E三点共线，∠HAE＝∠EAF＝45°，进而可证明△AEH≌△AEF，故EF＝BE+DF．任务：如图3，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，∠BAD＝120°，以A为顶点的∠EAF＝60°，AE、AF与BC、CD边分别交于E、F两点．请参照阅读材料中的解题方法，你认为结论EF＝BE+DF是否依然成立，若成立，请写出证明过程；若不成立，请说明理由．【解答】解：成立．证明：将△ADF绕点A顺时针旋转120°得到△ABM，∴△ABM≌△ADF，∠ABM＝∠D＝90°，∠MAB＝∠FAD，AM＝AF，MB＝DF，∴∠MBE＝∠ABM+∠ABE＝180°，∴M、B、E三点共线，∴∠MAE＝∠MAB+∠BAE＝∠FAD+∠BAE＝∠BAD﹣∠EAF＝60°，∴∠MAE＝∠FAE，∵AE＝AE，AM＝AF，∴△MAE≌△FAE（SAS），∴ME＝EF，∴EF＝ME＝MB+BE＝DF+BE．【题型3构造旋转模型解题】【典例3】（九上·江津期中）请阅读下列材料：，PC=1、求∠BPC问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长，问题得到解决．为，BP= ，PC=1．求∠BPC度数的大小和正方形ABCD的边长．点P，且PA=【解答】解：如图，将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A．；∴AP′=PC=1，BP=BP′=连接PP′，在Rt△BP′P中，，∠PBP′=90°，∵BP=BP′=∴PP′=2，∠BP′P=45°；，在△AP′P中，AP′=1，PP′=2，AP=∵12+22=2，即AP′2+PP′2=AP2；∴△AP′P是直角三角形，即∠AP′P=90°，∴∠AP′B=135°，∴∠BPC=∠AP′B=135°．过点B作BE⊥AP′，交AP′的延长线于点E，∴∠BEP′=90°，∵∠AP′B=135°，∴∠EP′B=45°，∴△BEP′是等腰直角三角形，，∵BP′=∴EP′=BE=1，∴AE=AP′+EP′=2；；∴在Rt△ABE中，由勾股定理，得AB=∴∠BPC=135°，正方形边长为【变式3-1】（九上·南昌月考）如图，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1，求∠BPC的度数和等边三角形ABC的边长．【解答】解：∵ΔABC是等边三角形∴∠ABC=60°将ΔBPC绕点B顺时针选转60°，连接B P′∴AP'=CP=1，BP′=PB=，∠BPC= ∠P′BA，∠A P′B=∠BPC ∵∠PBC+∠ABP=∠ABC=60°∴∠AB P′+∠ABP=∠ABC=60°∴ΔP′PB是等边三角形∴PP′=，∠P P′B=60°∵A P′=1，AP=2∴A P′2+P P′2=A P2∴ΔP P′A为直角三角形∴∠BPC=∠A P′B=150°过点B做BM⊥A P′，交AP′的延长线于点M∴∠M P′B=30°，BM=32∴P′M=32∴AM=1+32=52由勾股定理得：AB=∴等边三角形ABC的边长为．【变式3-2】（九上·德州期中）当图形具有邻边相等的特征时，我们可以把图形的一部分绕着公共端点旋转，这样将分散的条件集中起来，从而达到解决问题的目的．（1）如图1，等腰直角三角形ABC内有一点P，连接AP，BP，CP，∠APB＝135°，为探究AP，BP，CP三条线段间的数量关系，我们可以将△ABP，绕点A逆时针旋转90°得到△ACP'，连接PP'，则PP'＝ AP，△CPP'是三角形，AP，BP，CP三条线段的数量关系是．（2）如图2，等边三角形ABC内有一点P，连接AP、BP、CP，∠APB＝150°，请借助第一问的方法探究AP、BP、CP三条线段间的数量关系．（3）如图3，在四边形ABCD中，AD∥BC，点P在四边形的内部，且PD＝PC，∠CPD ＝90°，∠APB＝135°，AD＝4，BC＝5，请直接写出AB的长．【解答】（1P C2=B P2+2A P2（2）解：如图所示，将△ABP绕点B顺时针旋转60°得到△CB P′，连接P P′，由旋转的性质可得：B P′=BP，∠C P′B=∠APB=150∘，∠PB P′=60∘，A P′=AP，C P′=AP，∴△BP P′是等边三角形，∴BP=P P′，∠B P′P=60∘，∴∠P P′C=∠C P′B−∠B P′P=90∘，∴P C2=P P′2+P′C2，∴P C2=B P2+A P2；（3）解：AB=【题型4奔驰模型解题】【典例4】（2023•崂山区模拟）阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA＝3，PB＝4，PC＝5，求∠APB的度数．小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．请你回答：图1中∠APB的度数等于　150°　．参考小伟同学思考问题的方法，解决下列问题：（1）如图3，在正方形ABCD内有一点P，且PA＝，PB＝1，PD＝，则∠APB的度数等于　135°　，正方形的边长为；（2）如图4，在正六边形ABCDEF内有一点P，且PA＝2，PB＝1，PF＝，则∠APB的度数等于　120°　，正六边形的边长为．【答案】见试题解答内容【分析】阅读材料：把△APB绕点A逆时针旋转60°得到△ACP′，根据旋转的性质可得P′A＝PA，P′C＝PB，∠PAP′＝60°，然后求出△APP′是等边三角形，根据等边三角形的性质求出PP′＝PA＝3，∠AP′P＝60°，再利用勾股定理逆定理求出∠PP′C＝90°，然后求出∠AP′C，即为∠APB的度数；（1）把△APB绕点A逆时针旋转90°得到△ADP′，根据旋转的性质可得P′A＝PA，P′D＝PB，∠PAP′＝90°，然后判断出△APP′是等腰直角三角形，根据等腰直角三角形的性质求出PP′，∠AP′P＝45°，再利用勾股定理逆定理求出∠PP′D＝90°，然后求出∠AP′D，即为∠APB的度数；再求出点P′、P、B三点共线，过点A作AE⊥PP′于E，根据等腰直角三角形的性质求出AE＝PE＝PP′，然后求出BE，在Rt△ABE中，利用勾股定理列式求出AB即可；（2）把△APB绕点A逆时针旋转120°得到△AFP′，根据旋转的性质可得P′A＝PA，P′F＝PB，∠PAP′＝120°，然后求出△APP′是底角为30°的等腰三角形，过点A作AM⊥PP′于M，设PP′与AF相交于N，求出AM＝1，再求出PP′，∠AP′P＝30°，再利用勾股定理逆定理求出∠PP′F＝90°，然后求出∠AP′F，即为∠APB的度数；根据P′F、AM的长度得到P′F＝AM，利用“角角边”证明△AMN和△FP′N全等，根据全等三角形对应边相等可得AN＝FN，P′N＝MN，然后求出MN，在Rt△AMN中，利用勾股定理列式求出AN，然后求出AF即可．【解答】解：阅读材料：把△APB绕点A逆时针旋转60°得到△ACP′，由旋转的性质，P′A＝PA＝3，P′D＝PB＝4，∠PAP′＝60°，∴△APP′是等边三角形，∴PP′＝PA＝3，∠AP′P＝60°，∵PP′2+P′C2＝32+42＝25，PC2＝52＝25，∴PP′2+P′C2＝PC2，∴∠PP′C＝90°，∴∠AP′C＝∠AP′P+∠PP′C＝60°+90°＝150°；故∠APB＝∠AP′C＝150°；（1）如图3，把△APB绕点A逆时针旋转90°得到△ADP′，由旋转的性质，P′A＝PA＝2，P′D＝PB＝1，∠PAP′＝90°，∴△APP′是等腰直角三角形，∴PP′＝PA＝×2＝4，∠AP′P＝45°，∵PP′2+P′D2＝42+12＝17，PD2＝2＝17，∴PP′2+P′D2＝PD2，∴∠PP′D＝90°，∴∠AP′D＝∠AP′P+∠PP′D＝45°+90°＝135°，故，∠APB＝∠AP′D＝135°，∵∠APB+∠APP′＝135°+45°＝180°，∴点P′、P、B三点共线，过点A作AE⊥PP′于E，则AE＝PE＝PP′＝×4＝2，∴BE＝PE+PB＝2+1＝3，在Rt△ABE中，AB＝＝＝；（2）如图4，∵正六边形的内角为×（6﹣2）•180°＝120°，∴把△APB绕点A逆时针旋转120°得到△AFP′，由旋转的性质，P′A＝PA＝2，P′F＝PB＝1，∠PAP′＝120°，∴∠APP′＝∠AP′P＝（180°﹣120°）＝30°，过点A作AM⊥PP′于M，设PP′与AF相交于N，则AM＝PA＝×2＝1，P′M＝PM＝＝＝，∴PP′＝2PM＝2，∵PP′2+P′F2＝（2）2+12＝13，PF2＝2＝13，∴PP′2+P′F2＝PF2，∴∠PP′F＝90°，∴∠AP′F＝∠AP′P+∠PP′F＝30°+90°＝120°，故，∠APB＝∠AP′F＝120°，∵P′F＝AM＝1，∵△AMN和△FP′N中，，∴△AMN≌△FP′N（AAS），∴AN＝FN，P′N＝MN＝P′M＝，在Rt△AMN中，AN＝＝＝，∴AF＝2AN＝2×＝．故答案为：150°；（1）135°，；（2）120°，．【变式4-1】（2023春•广东期中）18．如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10．若将△PAC绕点A逆时针旋转后，得到△MAB．（1）∠MAP＝　60　°，连接PM，则PM＝　6　；（2）求∠APB的度数．【答案】（1）60，6；（2）150°．【分析】（1）连接MP，根据等边三角形的性质得AB＝AC，∠BAC＝60°，再根据旋转的性质得AM＝AP，∠MAP＝∠BAC＝60°，BM＝CP＝10，则可判断△AMP为等边三角形；（2）根据旋转可以得到MP＝AP＝6，∠APM＝60°，在△PBM中通过计算得到PM2+PB2＝BM2，根据勾股定理的逆定理得∠BPM＝90°，然后利用∠APB＝∠APM+BPM进行计算即可．【解答】解：（1）如图，连接MP，∵△ABC为等边三角形，∴AB＝AC，∠BAC＝60°，∵△PAC绕点A逆时针旋转后，得到△MAB，∴AM＝AP，∠MAP＝∠BAC＝60°，BM＝CP＝10，∴△AMP为等边三角形，∴MP＝AP＝6，∠APM＝60°；故答案为：60，6；（2）在△PBM中，PM＝6，BM＝10，PB＝8，∵62+82＝102，∴PM2+PB2＝BM2，∴∠BPM＝90°，∴∠APB＝∠APM+BPM＝60°+90°＝150°．【变式4-2】（2023春•古田县期中）阅读材料，解决问题：（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为5，12，13，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB＝　150°　；（2）请你利用第（1）题的解答思想方法，解答下面问题，已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF2＝BE2+FC2．【答案】（1）150°；（2）证明见解析．【分析】（1）根据旋转变换前后的两个三角形全等，全等三角形对应边相等，全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答；（2）把△ABE绕点A逆时针旋转90°得到△ACE′，根据旋转的性质可得AE′＝AE，CE′＝CE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，再求出∠E′AF＝45°，从而得到∠EAF＝∠E′AF，然后利用“边角边”证明△EAF和△E′AF全等，根据全等三角形对应边相等可得E′F＝EF，再利用勾股定理列式即可得证．【解答】解：（1）∵△ACP′≌△ABP，∴AP′＝AP＝5、CP′＝BP＝12、∠AP′C＝∠APB，′′由题意知旋转角∠PAP′＝60°，∴△APP′为等边三角形，PP′＝AP＝5，∠A P′P＝60°，在△PP′C中，PP′＝5，CP′＝12，PC＝13，而52+122＝132，∴△PP′C为直角三角形，且∠PP′C＝90°，∴∠APB＝∠AP′C＝∠AP′P+∠PP′C＝60°+90°＝150°；故答案为：150°；（2）证明：如图，把△ABE绕点A逆时针旋转90°得到△ACE′，由旋转的性质得，AE′＝AE，CE′＝BE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，∵∠EAF＝45°，∴∠E′AF＝∠CAE′+∠CAF＝∠BAE+∠CAF＝∠BAC﹣∠EAF＝90°﹣45°＝45°，∴∠EAF＝∠E′AF，在△EAF和△E′AF中，，∴△EAF≌△E′AF（SAS），∴E′F＝EF，∵∠CAB＝90°，AB＝AC，∴∠B＝∠ACB＝45°，∴∠E′CF＝45°+45°＝90°，由勾股定理得，E′F2＝CE′2+FC2，即EF2＝BE2+FC2．【变式4-4】（2022春•侯马市期末）如图①，△ABC和△ADE中，∠BAC＝∠DAE＝90°，点D、E分别在边AB、AC上，∠ABC＝∠ADE＝45°．（1）如图②，将△ADE绕点A逆时针旋转到如图位置，若∠BAD＝30°，求∠BAE的度数；（2）如图②，将△ADE绕点A逆时针旋转过程中，当旋转角度α＝　45°或225°　时，直线AC与DE垂直（0°＜α≤360°）；（3）如图③，△ADE绕点A在平面内自由旋转，连接BD，且AD＝4，AB＝10，求BD的最大值和最小值．【答案】（1）120°；（2）45°或225°；（3）BD的最大值是14，最小值是6．【分析】（1）根据∠DAE＝90°，即可得∠BAE的度数；（2）分两种情况画出图形，根据角的和差即可求解；（3）当AD旋转到射线BA的延长线上时，BD最大；当AD旋转到线段AB 上时，BD最小，分别画出图形即可求解．【解答】解：（1）∵∠BAD＝30°，∠DAE＝90°，∴∠BAE＝∠BAD+∠DAE＝30°+90°＝120°．（2）①垂足在线段AC上时，∵AC⊥DE，∠ADE＝45°，∴∠DAC＝45°，∵∠BAC＝90°，∴∠BAD＝45°，即旋转角度α＝45°；②垂足在线段AC延长线上时，∵AC⊥DE，∠ADE＝45°，∴∠DAH＝45°，∵∠BAC＝90°，∴旋转角度α＝90°+180°﹣45°＝225°；故答案为：45°或225°．（3）当AD旋转到线段BA的延长线上时，BD最大，此时BD＝AB+AD＝10+4＝14．当AD旋转到线段AB上时，BD最小，此时BD＝AB﹣AD＝10﹣4＝6．∴BD的最大值是14，最小值是6．【题型5费马点模型解题】【典例5】（秋•邗江区期末）背景资料：在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小．这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．如图①，当△ABC三个内角均小于120°时，费马点P在△ABC内部，此时∠APB＝∠BPC＝∠CPA＝120°，此时，PA+PB+PC的值最小．解决问题：（1）如图②，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB＝　150°　；基本运用：（2）请你利用第（1）题的解答思想方法，解答下面问题：如图③，△ABC中，∠CAB＝90°，AB＝AC，E，F为BC上的点，且∠EAF ＝45°，判断BE，EF，FC之间的数量关系并证明；能力提升：（3）如图④，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点P为Rt△ABC的费马点，连接AP，BP，CP，求PA+PB+PC的值．【答案】见试题解答内容【分析】（1）根据旋转变换前后的两个三角形全等，全等三角形对应边相等，全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答；（2）把△ABE绕点A逆时针旋转90°得到△ACE′，根据旋转的性质可得AE′＝AE，CE′＝CE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，再求出∠E′AF＝45°，从而得到∠EAF＝∠E′AF，然后利用“边角边”证明△EAF和△E′AF全等，根据全等三角形对应边相等可得E′F＝EF，再利用勾股定理列式即可得证．（3）将△APB绕点B顺时针旋转60°至△A′P′B处，连接PP′，根据直角三角形30°角所对的直角边等于斜边的一半求出AB＝2AC，即A′B的长，再根据旋转的性质求出△BPP′是等边三角形，根据等边三角形的三条边都相等可得BP＝PP′，等边三角形三个角都是60°求出∠BPP′＝∠BP′P＝60°，然后求出C、P、A′、P′四点共线，再利用勾股定理列式求出A′C，从而得到PA+PB+PC＝A′C．【解答】解：（1）∵△ACP′≌△ABP，∴AP′＝AP＝3、CP′＝BP＝4、∠AP′C＝∠APB，由题意知旋转角∠PA P′＝60°，∴△AP P′为等边三角形，P P′＝AP＝3，∠A P′P＝60°，易证△P P′C为直角三角形，且∠P P′C＝90°，∴∠APB＝∠AP′C＝∠A P′P+∠P P′C＝60°+90°＝150°；故答案为：150°；（2）EF2＝BE2+FC2，理由如下：如图2，把△ABE绕点A逆时针旋转90°得到△ACE′，由旋转的性质得，AE′＝AE，CE′＝BE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，∵∠EAF＝45°，∴∠E′AF＝∠CAE′+∠CAF＝∠BAE+∠CAF＝∠BAC﹣∠EAF＝90°﹣45°＝45°，∴∠EAF＝∠E′AF，在△EAF和△E′AF中，，∴△EAF≌△E′AF（SAS），∴E′F＝EF，∵∠CAB＝90°，AB＝AC，∴∠B＝∠ACB＝45°，∴∠E′CF＝45°+45°＝90°，由勾股定理得，E′F2＝CE′2+FC2，即EF2＝BE2+FC2．（3）如图④，将△APB绕点B顺时针旋转60°至△A′P′B处，连接PP′，∵在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，∴AB＝2，∴BC＝＝，∵△APB绕点B顺时针方向旋转60°，∴△A′P′B如图所示；∠A′BC＝∠ABC+60°＝30°+60°＝90°，∴AB＝2AC＝2，∵△APB绕点B顺时针方向旋转60°，得到△A′P′B，∴A′B＝AB＝2，BP＝BP′，A′P′＝AP，∴△BPP′是等边三角形，∴BP＝PP′，∠BPP′＝∠BP′P＝60°，∵∠APC＝∠CPB＝∠BPA＝120°，∴∠CPB+∠BPP′＝∠BP′A′+∠BP′P＝120°+60°＝180°，∴C、P、A′、P′四点共线，在Rt△A′BC中，A′C＝＝＝，∴PA+PB+PC＝A′P′+PP′+PC＝A′C＝．【变式5-1】（2022秋•大冶市期末）如图，D是等边三角形ABC外一点，连接AD，BD，CD，已知BD＝8，CD＝3，则当线段AD的长度最小时，①∠BDC＝　60°　；②AD的最小值是　5　．【答案】①60°；②5．【分析】以BD为边向外作等边三角形BDE，连接CE，判定△ABD≌△CBE，即可得出CE＝AD，再根据C，D，E三点共线时，CE有最小值，即可得到AD的最小值为5，此时∠BDC＝60°．【解答】解：如图所示，以BD为边向外作等边三角形BDE，连接CE，∵△BDE，△ABC均为等边三角形，∴BE＝BD，AB＝BC，∠ABC＝∠DBE＝60°，∴∠ABD＝∠CBE，在△ABD和△CBE中，，∴△ABD≌△CBE（SAS），∴CE＝AD，∵BE＝BD＝DE＝8，CD＝3，∴当C，D，E三点共线时，CE有最小值，∴CE＝DE﹣CD＝8﹣3＝5，∴AD的最小值为5，此时∠BDC＝60°．故答案为：①60°；②5．【变式5-2】（2022•荷塘区模拟）在△ABC中，若其内部的点P满足∠APB＝∠BPC＝∠CPA＝120°，则称P为△ABC的费马点．如图所示，在△ABC中，已知∠BAC＝45°，设P为△ABC的费马点，且满足∠PBA＝45°，PA＝4，则△PAC的面积为　4　．【答案】4．【分析】如图，延长BP交AC于D，先说明△ABD是等腰直角三角形，△ADP 是30°的直角三角形，可得PD和AD的长，根据费马点的定义可得∠APC＝120°，从而可知△PDC也是30°的直角三角形，可得CD的长，根据三角形的面积公式可得结论．【解答】解：如图，延长BP交AC于D，∵∠BAC＝∠PBA＝45°，∴∠ADB＝90°，AD＝BD，∵P为△ABC的费马点，∴∠APB＝∠CPA＝120°，∴∠BAP＝180°﹣120°﹣45°＝15°，∴∠PAC＝45°﹣15°＝30°，∴∠APD＝60°，Rt△PAD中，∵PA＝4，∴PD＝2，AD＝2，∵∠APC＝120°，∴∠CPD＝120°﹣60°＝60°，Rt△PDC中，∠PCD＝30°，∴CD＝2，∴AC＝AD+CD＝2+2＝4，∴△PAC的面积为＝＝4．故答案为：4．。

中考数学专题讲练旋转(解析版)

旋转一．半角模型“半角”旋转模型，经常会出现在等腰直角三角形、正方形中，在一般的等腰三角形中也会有涉及．二．等腰三角形旋转模型等腰三角形的旋转模型比较多，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化，证明的基本思想“SAS”．1．一般等腰三角形的旋转2．等边三角形的旋转3．等腰直角三角形的旋转三．对角互补模型四边形对角互补模型多数题目给出的条件会以四边形或三角形等旋转为载体．四．旋转相似模型共顶点相似的一般三角形模型：如图，图中ABD ACE∆∆∽，得到AB AD BDAC AE CE==，ABD ACE∠=∠，ADB AEC∠=∠，BAD CAE∠=∠，则有ABC ADE∆∆∽．一．考点：1．旋转全等模型；2．旋转相似模型；3．旋转中的轨迹与最值问题；二．重难点：1．这类题的关键是找到题目中所给的特殊条件，结合问题所要证明或者求解的边长角度问题，再去选择是要构造旋转全等还是通过已经得到的旋转全等的性质进一步证明．2．观察图形发现旋转得到的相似；3．通过添加辅助线构造旋转相似或者去挖掘隐含的相似图形．三．易错点：1．在利用旋转构造全等的时候注意辅助线的做法问题；2．构造旋转全等时候一定要有相等边长的条件．3．全等是相似的一个特例，旋转有时候也会出现全等，注意和旋转全等的区别和联系．题模一：旋转与全等例1.1.1已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．【答案】图2成立，证明见解析，图3不成立，图3中AE、CF、EF的关系是AE﹣CF=EF【解析】∵AB⊥AD，BC⊥CD，AB=BC，AE=CF，在△ABE和△CBF中，∴△ABE≌△CBF（SAS）；∴∠ABE=∠CBF，BE=BF；∵∠ABC=120°，∠MBN=60°，∴∠ABE=∠CBF=30°，∴AE=12BE，CF=12BF；∵∠MBN=60°，BE=BF，∴△BEF为等边三角形；∴AE+CF=12BE+12BF=BE=EF；图2成立，图3不成立．证明图2．延长DC至点K，使CK=AE，连接BK，在△BAE和△BCK中，则△BAE≌△BCK，∴BE=BK，∠ABE=∠KBC，∵∠FBE=60°，∠ABC=120°，∴∠FBC+∠ABE=60°，∴∠FBC+∠KBC=60°，∴∠KBF=∠FBE=60°，在△KBF和△EBF中，∴△KBF≌△EBF，∴KF=EF，∴KC+CF=EF，即AE+CF=EF．图3不成立，AE、CF、EF的关系是AE﹣CF=EF．例1.1.2（1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD．求证：EF=BE+FD；（2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？（3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【答案】（1）证明见解析（2）成立（3）EF=BE﹣FD 【解析】（1）延长EB到G，使BG=DF，连接AG．∵∠ABG=∠ABC=∠D=90°，AB=AD，∴△ABG≌△ADF．∴AG=AF，∠1=∠2．∴∠1+∠3=∠2+∠3=∠EAF=12∠BAD．∴∠GAE=∠EAF．又AE=AE，∴△AEG≌△AEF．∴EG=EF．∵EG=BE+BG．∴EF=BE+FD（2）（1）中的结论EF=BE+FD仍然成立．（3）结论EF=BE+FD不成立，应当是EF=BE﹣FD．证明：在BE上截取BG，使BG=DF，连接AG．∵∠B+∠ADC=180°，∠ADF+∠ADC=180°，∴∠B=∠ADF．∵AB=AD，∴△ABG≌△ADF．∴∠BAG=∠DAF，AG=AF．∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD．∴∠GAE=∠EAF．∵AE=AE，∴△AEG≌△AEF．∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD．例 1.1.3如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．【答案】（1）见解析（2）见解析（3）△ACN仍为等腰直角三角形【解析】（1）证明：如图1，∵EN∥AD，∴∠MAD=∠MNE，∠ADM=∠NEM．∵点M为DE的中点，∴DM=EM．在△ADM和△NEM中，∴△ADM≌△NEM．∴AM=MN．∴M为AN的中点．（2）证明：如图2，∵△BAD和△BCE均为等腰直角三角形，∴AB=AD，CB=CE，∠CBE=∠CEB=45°．∵AD∥NE，∴∠DAE+∠NEA=180°．∵∠DAE=90°，∴∠NEA=90°．∴∠NEC=135°．∵A，B，E三点在同一直线上，∴∠ABC=180°﹣∠CBE=135°．∴∠ABC=∠NEC．∵△ADM≌△NEM（已证），∴AD=NE．∵AD=AB，∴AB=NE．在△ABC和△NEC中，∴△ABC≌△NEC．∴AC=NC，∠ACB=∠NCE．∴∠ACN=∠BCE=90°．∴△ACN为等腰直角三角形．（3）△ACN仍为等腰直角三角形．证明：如图3，延长AB交NE于点F，∵AD∥NE，M为中点，∴易得△ADM≌△NEM，∴AD=NE．∵AD=AB，∴AB=NE．∵AD∥NE，∴AF⊥NE，在四边形BCEF中，∵∠BCE=∠BFE=90°∴∠FBC+∠FEC=360°﹣180°=180°∵∠FBC+∠ABC=180°∴∠ABC=∠FEC在△ABC和△NEC中，∴△ABC≌△NEC．∴AC=NC，∠ACB=∠NCE．∴∠ACN=∠BCE=90°．∴△ACN为等腰直角三角形．例1.1.4如图，△AEF中，∠EAF=45°，AG⊥EF于点G，现将△AEG沿AE折叠得到△AEB，将△AFG沿AF折叠得到△AFD，延长BE和DF相交于点C．（1）求证：四边形ABCD是正方形；（2）连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．（3）若EG=4，GF=6，2，求AG、MN的长．【答案】（1）见解析（2）MN2=ND2+DH2；理由见解析（3）AG=12；2【解析】（1）证明：∵△AEB由△AED翻折而成，∴∠ABE=∠AGE=90°，∠BAE=∠EAG，AB=AG，∵△AFD由△AFG翻折而成，∴∠ADF=∠AGF=90°，∠DAF=∠FAG，AD=AG，∵∠EAG+∠FAG=∠EAF=45°，∴∠ABE=∠AGE=∠BAD=∠ADC=90°，∴四边形ABCD 是矩形，∵AB=AD ，∴四边形ABCD 是正方形；（2）MN 2=ND 2+DH 2，理由：连接NH ，∵△ADH 由△ABM 旋转而成，∴△ABM ≌△ADH ，∴AM=AH ，BM=DH ，∵由（1）∠BAD=90°，AB=AD ，∴∠ADH=∠ABD=45°，∴∠NDH=90°，∴△AMN ≌△AHN ，∴MN=NH ，∴MN 2=ND 2+DH 2；（3）设AG=BC=x ，则EC=x ﹣4，CF=x ﹣6，在Rt △ECF 中，∵CE 2+CF 2=EF 2，即（x ﹣4）2+（x ﹣6）2=100，x 1=12，x 2=﹣2（舍去）∴AG=12，∵AG=AB=AD=12，∠BAD=90°，∴22AB AD +221212+2，∵2，∴MD=BD ﹣2﹣22，设NH=y，在Rt△NHD中，∵NH2=ND2+DH2，即y2=（2y）2+（22，解得2，即2．题模二：旋转与相似例1.2.1如图1，点P在正方形ABCD的对角线AC上，正方形的边长是a，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N．（1）操作发现：如图2，固定点P，使△PEF绕点P旋转，当PM⊥BC时，四边形PMCN是正方形．填空：①当AP=2PC时，四边形PMCN的边长是________；②当AP=nPC时（n是正实数），四边形PMCN的面积是___________．（2）猜想论证如图3，改变四边形ABCD的形状为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF 的两条直角边PE、PF分别交BC、DC于点M、N，固定点P，使△PEF绕点P旋转，则PMPN=__________．（3）拓展探究如图4，当四边形ABCD满足条件：∠B+∠D=180°，∠EPF=∠BAD时，点P在AC上，PE、PF分别交BC，CD于M、N点，固定P点，使△PEF绕点P旋转，请探究PMPN的值，并说明理由．【答案】（1）①13a②()221an+（2）ab（3）见解析【解析】（1）①如图2，∵PM⊥BC，AB⊥BC ∴△PMC∽△ABC又∵AP=2PC∴PMAB=13，即PMa=13∴PM=13a，即正方形PMCN的边长是13a②当AP=nPC时（n是正实数），PMAB=11n+∴PM=11n+a∴四边形PMCN的面积=（11n+a）2=()221an+（2）如图3，过P作PG⊥BC于G，作PH⊥CD于H，则∠PGM=∠PHN=90°，∠GPH=90°∵Rt△PEF中，∠FPE=90°∴∠GPM=∠HPN∴△PGM∽△PHN由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==∵AB=a，BC=b∴PG PHa b=，即PGPH=ab（3）如图4，过P作PG∥AB，交BC于G，作PH∥AD，交CD于H，则∠HPG=∠DAB ∵∠EPF=∠BAD∴∠EPF=∠GPH，即∠EPH+∠HPN=∠EPH+∠GPM∴∠HPN=∠GPM∵∠B+∠D=180°∴∠PGC+∠PHC=180°又∵∠PHN+∠PHC=180°∴∠PGC=∠PHN∴△PGM∽△PHN由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==即PG AB PH AD=②∴由①②可得，PMPN=ABAD例1.2.2数学活动课上，小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动．操作：使点D落在线段AB的中点处并使DF过点C（如图1），然后将其绕点D顺时针旋转，直至点E落在AC的延长线上时结束操作，在此过程中，线段DE与AC或其延长线交于点K，线段BC与DF相交于点G（如图2，3）．探究1：在图2中，求证：△ADK∽△BGD．探究2：在图2中，求证：KD平分∠AKG．探究3：①在图3中，KD仍平分∠AKG吗？若平分，请加以证明；若不平分，请说明理由．②在以上操作过程中，若设AC=BC=8，KG=x，△DKG的面积为y，请求出y与x的函数关系式，并直接写出x的取值范围．【答案】探究1：见解析；探究2：见解析；探究3：①KD仍平分∠AKG②y=2x，其中≤≤4838x【解析】探究1，∵∠KAD=∠KDG=∠DBG=45°，∴∠KDA+∠BDG=135°．∵∠BDG+∠BGD=135°，∴∠KDA=∠BGD，∴△ADK∽△BGD；探究2，∵△ADK∽△BGD，∵点D是线段AB的中点，∴BD=AD，∵∠KAD=∠KDG=45°，∴△ADK∽△DCK，∴∠AKD=∠DKC，∴KD平分∠AKG．探究3，①KD仍平分∠AKG．理由如下：∵同探究1可得△ADK∽△BGD，同探究2可得，△ADK∽△DGK，∴∠AKD=∠DKG，∴KD仍平分∠AKG；②如图，过点D作DM⊥AC于点M，DN⊥KG于点N，由①知线段KD平分∠AKG，∴DM=DN．∵AC=BC=8，点D是线段AB的中点，∠KAD=45°，∴DM=DN=4．∵KG=x，∴S△DKG=y=12×4x=2x，对于图3的情况同理可得y=2x，综上所示，y=2x，其中38．题模三：旋转中的轨迹与最值问题例1.3.1如图，点P是平行四边形ABCD对角线BD上的动点，点M为AD的中点，已知AD=8，AB=10，∠ABD=45°，把平行四边形ABCD绕着点A按逆时针方向旋转，点P的对应点是点Q，则线段MQ的长度的最大值与最小值的差为．【答案】18﹣2【解析】如图，作AP1⊥BD垂足为P1，∵∠DBA=45°，AB=10，∴∠P1AB=∠DBA=45°，AP1=P12，∵AM=MD=12AD=4，当AP1旋转到与射线AD的重合时（点P1与点E重合），ME就是MQ最小值24，当点P2与B重合时，旋转到与DA的延长线重合时（点P2与点F重合），此时MF就是MQ最大值=AM+AF=14，∴MQ的最大值与最小值的差=14﹣（2﹣4）=18﹣2故答案为18﹣2例 1.3.2如图，菱形ABCD中，AB=2，∠C=60°，我们把菱形ABCD的对称中心O称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为______；经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为______．（结果都保留π）【答案】3231+nπ【解析】∵菱形ABCD中，AB=2，∠C=60°，∴△ABD是等边三角形，BO=DO=1，223AD DO-第一次旋转的弧长6033ππ⨯=∵第一、二次旋转的弧长和60360323ππ⨯⨯=，第三次旋转的弧长为：601 1803ππ⨯=∵3n÷3=n，故经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为：n 23π+3π）231+nπ．例1.3.3如图1，点O为正方形ABCD的中心．（1）将线段OE绕点O逆时针方向旋转90︒，点E的对应点为点F，连结EF，AE，BF，请依题意补全图1；（2）根据图1中补全的图形，猜想并证明AE与BF的关系；（3）如图2，点G是OA中点，△EGF是等腰直角三角形，H是EF的中点，90EGF∠=︒，22AB=2GE=，△EGF绕G点逆时针方向旋转α角度，请直接写出旋转过程中BH的最大值．【答案】（1）见解析（2）AE⊥BF（3）25+【解析】（1）正确画出图形；………………1分（2）延长EA 交OF 于点H ，交BF 于点G …2分∵O 为正方形ABCD 的中心，∴OB OA =，∠AOB ＝90……3分∵OE 绕点O 逆时针旋转90角得到OF∴∠AOB ＝∠EOF ＝90∴∠EOA ＝∠FOB ……4分在△EOA 和△FOB 中，∴BF AE =.……5分∴∠OFB +∠FHG =90∴AE ⊥BF ……6分（3）BH 的最大值为25+……8分随练1.1 在ABC ∆中，2AB BC ==，90ABC ∠=︒，BD 为斜边AC 上的中线，将ABD ∆绕点D 顺时针旋转α(0180α︒<<︒)得到EFD ∆，其中点A 的对应点为点E ，点B 的对应点为点F ，BE 与FC 相交于点H .（1）如图1，直接写出BE 与FC 的数量关系：____________;（2）如图2，M 、N 分别为EF 、BC 的中点.求证：MN =__________;（3）连接BF ，CE ，如图3，直接写出在此旋转过程中，线段BF 、CE 与AC 之间的数量关系：____________________________.【答案】（1）BE FC =；（2）22FC ；（3）222BF CE AC +=. 【解析】（1）BE FC =；（2）证明：如图，∵AB BC =，90ABC ∠=︒，BD 为斜边中线，∴12BD AD CD AC ===，BD AC ⊥ ∵EFD ∆是由ABD ∆旋转得到的，∴DE DF DB DC ===，90EDF ADB BDC ∠=∠=∠=︒∴EDF BDF BDC BDF ∠+∠=∠+∠，即BDE FDC ∠=∠，∴BDE FDC ∆∆≌，∴BE FC =且12∠=∠又∵34∠=∠，∴90FHE FDE ∠=∠=︒ ,即BE CF ⊥连接BF ，取BF 中点G ，连接MG 、NG .∵M 为EF 中点，G 为BF 中点，N 为BC 中点又∵EB FC =，BE FC ⊥∴MG NG =，90MGN ∠=︒，∴MGN ∆为等腰直角三角形，∴2MN =. （3）222BF CE AC +=.随练1.2 在菱形ABCD 中，120BAD ∠=︒，4AB =，把一个含60°角的三角板与这个菱形叠合，使三角板的60°角的顶点与点A 重合，两边分别落在AB 、AC 上．将三角板绕点A 按逆时针旋转，设旋转角为α．（1）如图①，当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你通过观察或测量写出图中现有的两组相等线段(菱形的边和对角线除外)．（2）如图②，当60120α︒<<︒时，三角板的两边分别与BC 、CD 的延长线相交于点E 、F ，你在(1)中得到的结论还成立吗?若成立，请你选择一组加以证明；若不成立，请你说明理由．（3）当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你求出这个三角板与这个菱形重合部分的面积．【答案】见解析【解析】（1）BE CF =，AE AF =，CE DF =．写出两组即可．（2）（1）中的结论仍然成立．如图，BE CF =的结论仍然成立．证明如下：∵在菱形ABCD 中，120BAD ∠=︒，又由题意可知，60EAF ∠=︒，∴BAE CAF ∠=∠．在△BAE 和△CAF 中，∴△BAE ≌△CAF ．∴BE CF =．（3）当060α︒<<︒时，三角板与这个菱形重合部分的面积就是四边形AECF 的面积．由题意可证△BAE ≌△CAF ．∴四边形AECF 的面积就是△ABC 的面积．∵4AB =，∴所求图形的面积为43随练1.3如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）（1）如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；（2）如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．【答案】（1）DM=FM，DM⊥FM（2）DM⊥FM，DM=FM【解析】（1）如图2，DM=FM，DM⊥FM，证明：连接DF，NF，∵四边形ABCD和CGEF是正方形，∴AD∥BC，BC∥GE，∴AD∥GE，∴∠DAM=∠NEM，∵M是AE的中点，∴AM=EM，在△MAD与△MEN中，∴△MAD≌△MEN，∴DM=MN，AD=EN，∵AD=CD，∴CD=NE，∵CF=EF，∠DCF=∠DCB=90°，在△DCF与△NEF中，∴△DCF≌△NEF，∴DF=NF，∠CFD=∠EFN，∵∠EFN+∠NFC=90°，∴∠DFC+∠CFN=90°，∴∠DFN=90°，∴DM⊥FM，DM=FM（2）猜想：DM⊥FM，DM=FM，证明如下：如图3，连接DF，NF，连接DF，NF，∵四边形ABCD是正方形，∴AD∥BC，∵点E、B、C在同一条直线上，∴AD∥CN，∴∠ADN=∠MNE，在△MAD与△MEN中，∴△MAD≌△MEN，∴DM=MN，AD=EN，∵AD=CD，∴CD=NE，∵CF=EF，∵∠DCF=90°+45°=135°，∠NEF=180°﹣45°=135°，∴∠DCF=∠NEF，在△DCF与△NEF中，∴△MAD≌△MEN，∴DF=NF，∠CFD=∠EFN，∵∠CFD+∠EFD=90°，∴∠NFE+∠EFD=90°，∴∠DFN=90°，∴DM ⊥FM ，DM=FM ．随练 1.4 已知：在ABC △中，AB AC =，点D 为BC 边的中点，点F 在AB 上，连结DF 并延长到点E ,使BAE BDF ∠=∠，点M 在线段DF 上，且ABE DBM ∠=∠．（1）如图，当45ABC ∠=°时，求证：2AE MD =；（2）如图，当60ABC ∠=°时，则线段AE MD 、之间的数量关系为____________；（3）在（2）的条件下，延长BM 到P ，使MP BM =，连接CP ，若727AB AE ==，，求tan EAB ∠的值．【答案】（1）见解析（2）2AE MD =（33 【解析】该题考查的是四边形综合．（1）如图，连结AD又∵45ABC ∠=°∴cos BD AB ABC =∠即2AB BD =∴△ABE ∽△DBM（2）与（1）类似可知△DBM ∽△ABE ，又60ABC ∠=︒，（3）如图2连结AD 、EP ，∵△ABE ∽△DBM又∵BM MP =∴△BEP 等边三角形∴EM BP ⊥即90BMD ∠=︒在Rt △AEB 中，27AE =7AB =， tan EAB ∠的值为3随练 1.5 在等边ABC ∆的两边AB ，AC 所在直线上分别有两点M N D ，，为ABC ∆外一点，且60MDN ∠=︒，120BDC ∠=︒，BD CD =，探究：当点M N ，分别在直线AB AC ，上移动时，BM NC MN ，，之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系．（1）如图①，当点M N ，在边AB AC ，上，且DM DN =时，BM NC MN ，，之间的数量关系式_________；此时Q L=__________ （2）如图②，当点M N ，在边AB AC ，上，且DM DN ≠时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明；（3）如图③，当点M N ，分别在边AB CA ，的延长线上时，若AN x =，则Q =_________（用x L ，表示）【答案】见解析【解析】 (Ⅰ)BM 、NC 、MN 之间的数量关系BM NC MN +=．此时23Q L =． (Ⅱ)猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE BM =，连结DE ．∵BD CD =，且120BDC ∠=︒．又△ABC 是等边三角形，∴90MBD NCD ∠=∠=︒．在△MBD 与△ECD 中，BM CE MBD ECD BD DC =⎧⎪∠=∠⎨⎪=⎩∴△MBD ≌△ECD (SAS)．∴DM DE =，BDM CDE ∠=∠．在△MDN 与△EDN 中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩∴△MDN ≌△EDN (SAS)．△AMN 的周长Q AM AN MN =++而等边△ABC 的周长3L AB =(Ⅲ)如图③，当M 、N 分别在AB 、CA 的延长线上时，若AN x =，则223Q x L=+（用x、L表示）．随练1.6（1）正方形ABCD中，对角线AC与BD相交于点O，如图1，请直接猜想并写出AO与CD 之间的数量关系：；（2）如图2，将（1）中的△BOC绕点B逆时针旋转得到△BO1C1，连接AO1，DC1，请猜想线段AO1与DC1的数量关系，并证明你的猜想；（3）如图3，矩形ABCD和Rt△BEF有公共顶点，且∠BEF=90°，∠EBF=∠ABD=30°，则AEDF=______．【答案】（1）AO=2CD．理由如下：∵四边形ABCD为正方形，∴AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=2 CD，故答案为AO=2 CD；（2）∵四边形ABCD为正方形，∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC和△OBC都是等腰直角三角形，∵△BOC绕点B逆时针方向旋转得到△BO1C1，∴∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，∴BC121，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC1∽△BAO1，（3）在R t△EBF中，cos∠EBF=EB FB在R t△ABD中，cos∠ABD=AD BD，∵∠EBF=∠ABD=30°，∵∠EBF+∠FBA=∠ABD+∠FBA，即∠EBA=∠FBD，∴△AEB∽△FBD，故答案为3【解析】（1）根据正方形的性质得AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，由勾股定理得到AO与CD之间的数量关系；（2）如图2根据正方形的性质得AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，得到△ABC和△OBC都是等腰直角三角形，求出AC=2AB BC=2BO，得到BD=2AB，因为△BOC绕点B逆时针方向旋转得到△BO1C1，所以∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，BC1=2BO1，由∠1+∠3=45°，∠2+∠3=45°，得到∠1=∠2，于是得到△BDC1∽△BAO1，求出结论；（3）如图3在R t△ABD中，cos∠ABD=ABBD，在Rt△EBF中，cos∠EBF=EBFB因为∠EBF=∠ABD=30°得到BE ADBF BD=3，再由∠EBF+∠FBA=∠ABD+∠FBA，得到∠EBA=∠FBD，△AEB∽△FBD，由相似的性质得到解．解：（1）AO=2CD．理由如下：如图1，∵四边形ABCD为正方形，∴AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=2 CD，故答案为AO=2 CD；（2）如图2，∵四边形ABCD为正方形，∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC和△OBC都是等腰直角三角形，∵△BOC绕点B逆时针方向旋转得到△BO1C1，∴∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，∴BC121，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC1∽△BAO1，（3）如图3 在R t△EBF中，cos∠EBF=EB FB在R t△ABD中，cos∠ABD=AD BD，∵∠EBF=∠ABD=30°，∵∠EBF+∠FBA=∠ABD+∠FBA，即∠EBA=∠FBD，∴△AEB∽△FBD，故答案为3．随练1.7如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF 相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是______．【答案】2【解析】如图点P运动的路径是以G为圆心的弧EF，在⊙G上取一点H，连接EH、FH．∵四边形AOCB是正方形，∴∠AOC=90°，∴∠AFP=12∠AOC=45°，∵EF是⊙O直径，∴∠EAF=90°，∴∠APF=∠AFP=45°，∴∠H=∠APF=45°，∴∠EGF=2∠H=90°，∵EF=4，GE=GF，∴2，∴EF的长9022π•2．随练1.8已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．【答案】（1）见解析；（2）①∠CMD=135°②2π【解析】（1）如图1中，∵CA=CB，∠ACB=90°，∴∠A=∠ABC=45°，∵△CEF是由△CAD旋转逆时针α得到，α=90°，∴CB与CE重合，∴∠CBE=∠A=45°，∴∠ABF=∠ABC+∠CBF=90°，∵BG=AD=BF，∴∠BGF=∠BFG=45°，∴∠A=∠BGF=45°，∴GF∥AC．（2）①如图2中，∵CA=CE，CD=CF，∴∠CAE=∠CEA，∠CDF=∠CFD，∵∠ACD=∠ECF，∴∠ACE=∠CDF，∵2∠CAE+∠ACE=180°，2∠CDF+∠DCF=180°，∴∠CAE=∠CDF，∴A、D、M、C四点共圆，∴∠CMF=∠CAD=45°，∴∠CMD=180°﹣∠CMF=135°．②如图3中，O是AC中点，连接OD、CM．∵AD=DB，CA=CB，∴CD⊥AB，∴∠ADC=90°，由①可知A、D、M、C四点共圆，∴当α从90°变化到180°时，点M 在以AC 为直径的⊙O 上，运动路径是弧CD ，∵OA=OC ，CD=DA ，∴DO ⊥AC ，∴∠DOC=90°，∴CD ∧的长=901180π=2π． ∴当α从90°变化到180°时，点M 运动的路径长为2π．随练1.9 如图1，点O 是正方形ABCD 两对角线的交点，分别延长OD 到点G ，OC 到点E ，使OG=2OD ，OE=2OC ，然后以OG 、OE 为邻边作正方形OEFG ，连接AG ，DE ．（1）求证：DE ⊥AG ；（2）正方形ABCD 固定，将正方形OEFG 绕点O 逆时针旋转α角（0°＜α＜360°）得到正方形OE ′F ′G ′，如图2．①在旋转过程中，当∠OAG ′是直角时，求α的度数；②若正方形ABCD 的边长为1，在旋转过程中，求AF ′长的最大值和此时α的度数，直接写出结果不必说明理由．【答案】（1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①α=30°；②α=315°．【解析】（1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①在旋转过程中，∠OAG′成为直角有两种情况：（Ⅰ）α由0°增大到90°过程中，当∠OAG′=90°时，∵OA=OD=12OG=12OG′， ∴在Rt △OAG′中，sin ∠AG′O='OA OG =12， ∴∠AG′O=30°，∵OA ⊥OD ，OA ⊥AG′，∴OD ∥AG′，∴∠DOG′=∠AG′O=30°，即α=30°；（Ⅱ）α由90°增大到180°过程中，当∠OAG′=90°时，同理可求∠BOG′=30°，∴α=180°﹣30°=150°．综上所述，当∠OAG′=90°时，α=30°或150°．②如图3，当旋转到A、O、F′在一条直线上时，AF′的长最大，∵正方形ABCD的边长为1，∴2，∵OG=2OD，∴2∴OF′=2，∴2+2，∵∠COE′=45°，∴此时α=315°．作业1如图1，在△ABC中，∠BAC=90°，AB=AC．（1）若点M为AC上的任意一点，过M作MN⊥BC于点N，取BM的中点D，连接AD、DM，求证：AD=DN．（2）如图2，若M为BC上的任意一点，以线段CM为底边作等腰Rt△MCN，此时，取BM的中点D，连接AD、DN，则AD与DN有怎样的数量关系？说明理由．（3）如图3，在（2）的条件下将Rt△MNC绕C点旋转任意角度，连接BM，取BM的中点D，再连接AD、DN，则（2）中的结论仍然成立吗，它们之间又有怎样的位置关系？请说明理由．【答案】（1）见解析；（2）AD=DN；（3）AD=DN，AD⊥DN【解析】（1）证明：解法一：如图1中，延长AD到K，使得DK=AD，连接AN、KN、KM．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KMC=∠BAC=90°，∵AB=AC，∠BAC=90°，∴∠C=45°，∵MN⊥BC，∴∠MNC=90°，∠NMC=45°=∠KMC=∠C，∴MN=NC，在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，即AD=DN．解法二：根据直角三角形斜边中线性质，可知AD=12BM，DN=12BM，由此即可证明．（2）如图2中，结论：AD=DN．理由：延长AD到K，使得DK=AD，连接AN、KN、KM．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KMN=∠B=45°，∵∠NMC=∠NCM=∠ACB=45°∴MN=NC，∠KMN=∠ACN=90°在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，即AD=DN．（3）如图3中，结论：AD=DN，AD⊥DN．理由：延长AD到K，使得DK=AD，连接AN、KN、KM，延长KN交AC于G．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KGC=∠BAC=90°，∴∠ACN+∠NMG=180°，∵∠KMN+∠NMG=180°，∴∠ACN=∠NMK，在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，DN⊥AK，即AD=DN．AD⊥DN．作业2已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．【答案】（1）见解析（2）成立（3）见解析【解析】本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质．（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG．（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG=CG；再证出△DMG≌△FNG，得到MG=NG；再证明△AMG≌△ENG，得出AG=EG；最后证出CG=EG．（3）结论依然成立．还知道EG⊥CG．（1）证明：∵四边形ABCD是正方形，∴∠DCF=90°，在Rt△FCD中，∵G为DF的中点，∴CG=12 FD，同理，在Rt△DEF中，EG=12 FD，∴CG=EG．（1）（1）中结论仍然成立，即EG=CG．证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．在△DAG与△DCG中，∵AD=CD，∠ADG=∠CDG，DG=DG，∴△DAG≌△DCG（SAS），∴AG=CG；在△DMG与△FNG中，∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG（ASA），∴MG=NG；∵∠EAM=∠AEN=∠AMN=90°，∴四边形AENM是矩形，在矩形AENM中，AM=EN，在△AMG与△ENG中，∵AM=EN，∠AMG=∠ENG，MG=NG，∴△AMG≌△ENG（SAS），∴AG=EG，∴EG=CG．证法二：延长CG至M，使MG=CG，连接MF，ME，EC，在△DCG与△FMG中，∵FG=DG，∠MGF=∠CGD，MG=CG，∴△DCG≌△FMG．∴MF=CD，∠FMG=∠DCG，∴MF∥CD∥AB，∴EF⊥MF．在Rt△MFE与Rt△CBE中，∵MF=CB，∠MFE=∠EBC，EF=BE，∴△MFE≌△CBE∴∠MEF=∠CEB．∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°，∴△MEC为直角三角形．∵MG=CG，∴EG=12 MC，∴EG=CG．（3）（1）中的结论仍然成立．理由如下：过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB于N．由于G为FD中点，易证△CDG≌△MFG，得到CD=FM，又因为BE=EF，易证∠EFM=∠EBC，则△EFM≌△EBC，∠FEM=∠BEC，EM=EC∵∠FEC+∠BEC=90°，∴∠FEC+∠FEM=90°，即∠MEC=90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG=CG，EG⊥CG．作业3在△ABC中，∠ACB=90°，∠A＜45°，点O为AB中点，一个足够大的三角板的直角顶点与点O重合，一边OE经过点C，另一边OD与AC交于点M．（1）如图1，当∠A=30°时，求证：MC2=AM2+BC2；（2）如图2，当∠A≠30°时，（1）中的结论是否成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由；（3）将三角形ODE绕点O旋转，若直线OD与直线AC相交于点M，直线OE与直线BC相交于点N，连接MN，则MN2=AM2+BN2成立吗？答：____（填“成立”或“不成立”）【答案】（1）见解析；（2）不成立；（3）成立【解析】（1）证明：如图1，过A作AF⊥AC交CO延长线于F，连接MF，∵∠ACB=90°，∴BC∥AF，∴△BOC∽△AOF，∵O为AB中点，∴OA=OB，∴AF=BC，CO=OF，∵∠MOC=90°，∴OM是CF的垂直平分线，∴CM=MF，在Rt△AMF中，由勾股定理得：MF2=AM2+AF2=AM2+BC2，即MC2=AM2+BC2；（2）还成立，理由是：如图2，过A作AF⊥AC交CO延长线于F，连接MF，∵∠ACB=90°，∴BC∥AF，∴△BOC∽△AOF，∵OA=OB，∴AF=BC，CO=OF，∵∠MOC=90°，∴OM是CF的垂直平分线，∴CM=MF，在Rt△AMF中，由勾股定理得：MF2=AM2+AF2=AM2+BC2，即MC2=AM2+BC2；（3）成立．作业4在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．请直接写出AC1与BD1的数量关系和位置关系．（2）如图2，若四边形ABCD是菱形，AC=6，BD=8，判断AC1与BD1的数量关系和位置关系，并给出证明；（3）如图3，若四边形ABCD是平行四边形，AC=6，BD=12，连接DD1，设AC1=kBD1，请直接写出k 的值和AC12+（kDD1）2的值．【答案】（1）AC1⊥BD1（2）AC1=34BD1，AC1⊥BD1，理由见解析（3）AC12+（kDD1）2=36【解析】（1）AC1=BD1，AC1⊥BD1；理由：如图1，∵四边形ABCD是正方形，∴OC=OA=OD=OB，AC⊥BD，∴∠AOB=∠COD=90°，∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OC1=OC，OD1=OD，∠COC1=∠DOD1，∴OC1=OD1，∠AOC1=∠BOD1=90°+∠AOD1，在△AOC 1和△BOD 1中1111AO OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩ ，∴△AOC 1≌△BOD 1（SAS ）；∴AC 1=BD 1，∵∠AOB=90°，∴∠OAB+∠ABP+∠OBD 1=90°，∴∠OAB+∠ABP+∠OAC 1=90°，∴∠APB=90°，则AC 1⊥BD 1；故AC 1 与BD 1的数量关系是：AC 1=BD 1；AC 1 与BD 1的位置关系是：AC 1⊥BD 1；（2）AC 1=34BD 1，AC 1⊥BD 1．理由：∵四边形ABCD 是菱形，∴OC=OA=12AC ，OD=OB=12BD ，AC ⊥BD ． ∵△C 1OD 1由△COD 绕点O 旋转得到，∴O C 1=OC ，O D 1=OD ，∠CO C 1=∠DO D 1．∴O C 1=OA ，O D 1=OB ，∠AO C 1=∠BO D 1，∴△AO C 1∽△BOD 1．∴∠O AC 1=∠OB D 1．又∵∠AOB=90°，∴∠O AB+∠ABP+∠OB D 1=90°．∴∠O AB+∠ABP+∠O AC 1=90°．∴∠APB=90°．∴AC 1⊥BD 1．∵△AO C 1∽△BOD 1，即AC 1=34BD 1，AC 1⊥BD 1．（3）如图3，与（2）一样可证明△AOC1∽△BOD1，∴k=12；∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OD1=OD，而OD=OB，∴OD1=OB=OD，∴△BDD1为直角三角形，在Rt△BDD1中，BD12+DD12=BD2=144，∴（2AC1）2+DD12=144，∴AC12+（kDD1）2=36．作业5在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．（一）尝试探究如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD 上，∠EAF=30°，连接EF．（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=________度，线段BE、EF、FD之间的数量关系为________．（2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．（二）拓展延伸如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF=30°，BE=1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．【答案】解：（一）（1）：30 ，BE+DF=EF（2）BE﹣DF=EF（二）3【解析】解：（一）（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′，则∠1=∠2，BE=DE′，AE=AE′，∵∠BAD=60°，∠EAF=30°，∴∠1+∠3=30°，∴∠2+∠3=30°，即∠FAE′=30°∴∠EAF=∠FAE′，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，即EF=DF+DE′，∴EF=DF+BE，即线段BE、EF、FD之间的数量关系为BE+DF=EF，故答案为：30，BE+DF=EF；（2）如图3，在BE上截取BG=DF，连接AG，在△ABG和△ADF中，∴△ABG≌△ADF（SAS），∴∠BAG=∠DAF，且AG=AF，∵∠DAF+∠DAE=30°，∴∠BAG+∠DAE=30°，∵∠BAD=60°，∴∠GAE=60°﹣30°=30°，∴∠GAE=∠FAE，在△GAE和△FAE中，∴△GAE≌△FAE（SAS），∴GE=FE，又∵BE﹣BG=GE，BG=DF，∴BE﹣DF=EF，即线段BE、EF、FD之间的数量关系为BE﹣DF=EF；（二）如图4，将△ABE 绕点A 逆时针旋转60°得到△A ′B ′E ′，则AE=AE ′，∠EAE ′=60°，∴△AEE ′是等边三角形，又∵∠EAF=30°，∴AN 平分∠EAF ，∴AN ⊥EE ′，∴直角三角形ANE 中，AN 3AE = ∵在等边△ABC 中，AM ⊥BC ，∴∠BAM=30°， ∴AM 3AB =，且∠BAE+∠EAM=30°，又∵∠MAN+∠EAM=30°，∴∠BAE=∠MAN ，∴△BAE ∽△MAN ， ∴MN AM =BE AB ，即MN 31= ∴3．作业6 探索绕公用顶点的相似多边形的旋转：（1）如图1，已知：等边ABC ∆和ADE ∆，根据__________（指出三角形的全等或相似），可得到CE 与BD 的大小关系为：__________．（2）如图2，正方形ABCD 和正方形AEFG ，求：FCEB 的值；（3）如图3，矩形ABCD 和矩形AEFG ，AB kBC =，AE kEF =，求：FCEB 的值．【答案】（1）全等，相等；（223）21k +．【解析】解：（1）如图1，ABC ∆和ADE ∆都是等边三角形，在AEC ∆和ADB ∆中，AE ADCAE BADAC AB =⎧⎪∠=∠⎨=⎪⎩，AEC ADB ∴∆≅∆，CE BD ∴=；（2）如图2，四边形ABCD 和四边形AEFG 都是正方形，（3）连接FA 、CA ，如图3，四边形ABCD 和四边形AEFG 都是矩形，AB kBC =，AE kEF =，作业7 如图，边长为6的等边三角形ABC 中，E 是对称轴AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针转60°得到FC ，连接DF ．则在点E 运动过程中，DF 的最小值是（）A ． 6B ． 3C ． 2D ． 1.5【答案】D【解析】取线段AC 的中点G ，连接EG ，如图所示．∵△ABC 为等边三角形，且AD 为△ABC 的对称轴，∴CD=CG=12AB=3，∠ACD=60°， ∵∠ECF=60°，∴∠FCD=∠ECG ．在△FCD 和△ECG 中，FC EC FCD ECG DC GC =⎧⎪∠=∠⎨⎪=⎩，∴△FCD ≌△ECG （SAS ），∴DF=GE ．当EG ∥BC 时，EG 最小，∵点G 为AC 的中点，∴此时EG=DF=12CD=32．作业8 已知等边△ABC 边长为2，放置在如图的水平桌面上，将△ABC 水平向右作无滑动翻滚，使△ABC 首次落回开始的位置，则等边△ABC 的中心O 经过的路径长为_________．【答案】433π．【解析】如图，过点C作CD⊥AB于D，则CD一定经过点O，∵CD=32BC=3，∴OC=23CD=233，根据等边三角形的性质，∠BCD=12∠ACB=12×60°=30°，∴每一次翻滚中心O旋转的角度为：180°﹣2×30°=120°，等边三角形翻滚3次翻滚一周，∴点O旋转的角度为：120°×3=360°，∴中心O经过的路径长是：2π•OC=2π×233=433π，故答案为：433π．作业9已知，点O是等边△ABC内的任一点，连接OA，OB，OC．（1）如图1，已知∠AOB=150°，∠BOC=120°，将△BOC绕点C按顺时针方向旋转60°得△ADC．①∠DAO的度数是；②用等式表示线段OA，OB，OC之间的数量关系，并证明；（2）设∠AOB=α，∠BOC=β．①当α，β满足什么关系时，OA+OB+OC有最小值？请在图2中画出符合条件的图形，并说明理由；②若等边△ABC的边长为1，直接写出OA+OB+OC的最小值．【答案】（1）①90°；②OA2+OB2=OC2；证明见解析（2）①α=β=120°，OA+OB+OC有最小值；图形见解析【解析】（1）①∠AOB=150°，∠BOC=120°，∴∠AOC=360°﹣120°﹣150°=90°，。

中考数学专题训练-旋转模型几何变换三种模型手拉手-半角-对角互补

几何变换的三种模型手拉手、半角、对角互补知识关联图「等腰三角形手拉手模型I等腰直角三角形（包含正方形）.等边三角形（包含费马点）特殊角旋转变换对角互补模型一般角角含半角模型!特殊角一般角等线段变换（与圆相关）真题演练【练1】（2013北京中考）在厶ABC中，AB=AC，/BAC •（ 0：；" .：60），将线段BC 绕点B逆时针旋转60°得到线段BD .（1）如图1，直接写出/ABD的大小（用含:-的式子表示）；（2）如图2，乙BCE =150 , ABE =60，判断△ABE的形状并加以证明；（3）在（2）的条件下，连结DE ,若.DEC =45，求〉的值.【练2】（2012年北京中考）在厶ABC中，BA二BC , BAC = , M是AC的中点，P是线段上的动点，将线段PA绕点P顺时针旋转2〉得到线段PQ .（1 ）若》且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D，请补全图形，并写出• CDB的度数；（2）在图2中，点P不与点B，M重合，线段CQ的延长线与射线BM交于点D，猜想.CDB 的大小（用含:的代数式表示），并加以证明；（3）对于适当大小的:-，当点p在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ =QD，请直接写出:-的范围.例题精讲考点1:手拉手模型：全等和相似包含：等腰三角形、等腰直角三角形（正方形）、等边三角形伴随旋转出全等，处于各种位置的旋转模型，及残缺的旋转模型都要能很快看出来（1 ）等腰三角形旋转模型图（共顶点旋转等腰出伴随全等）（2 ）等边三角形旋转模型图（共顶点旋转等边出伴随全等）（3）等腰直角旋转模型图（共顶点旋转等腰直角出伴随全等）（4）不等边旋转模型图（共顶点旋转不等腰出伴随相似）【例1】(14年海淀期末)已知四边形ABCD和四边形CEFG都是正方形，且AB . CE •(1) 如图1，连接BG、DG •求证：BG =DE ;(2) 如图2，如果正方形ABCD的边长为.2，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG // BD , BG二BD •①求.BDE的度数；②请直接写出正方形CEFG的边长的值.【例2】（2014年西城一模）四边形ABCD是正方形，A BEF是等腰直角三角形,.BEF =90，BE二EF，连接DF，G 为DF 的中点，连接EG，CG，EC 。

初三上学期旋转专题之旋转(全等)模型教案(有答案)

旋转（全等）模型互动精讲题型一、手拉手模型1、已知：如图1，点C为线段AB上一点，△ACM，△CBN都是等边三角形，AN交MC于点E，BM交CN于点F.(1)求证：AN=BM；(2)求证：△CEF为等边三角形；(3)将△ACM绕点C按逆时针方向旋转90∘,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).2、已知△ABC ，以AC 为边在△ABC 外作等腰△ACD ，其中AC=AD 。

⑴如图①，若∠DAC=2∠ABC ，AC=BC ，四边形ABCD 是平行四边形，则∠ABC=________；⑵如图②，若∠ABC=30°，△ACD 是等边三角形，AB=3，BC=4，求BD 的长； ⑶如图③，若∠ACD 为锐角，作AH ⊥BC 于H ，当2224BC AH BD +=时，∠DAC=2∠ABC 是否成立？若不成立，请说明你的理由；若成立，证明你的结论。

③②①AH CBDDCBADCBA题型二、角含半角模型3、已知：如图1在Rt △ABC 中，∠BAC=90°，AB=AC ，点D 、E 分别为线段BC 上两动点，若∠DAE=45°．探究线段BD 、DE 、EC 三条线段之间的数量关系．小明的思路是：把△AEC 绕点A 顺时针旋转90°，得到△ABE '，连结E 'D ，使问题得到解决．请你参考小明的思路探究并解决下列问题：⑴ 猜想BD 、DE 、EC 三条线段之间存在的数量关系式，并对你的猜想给予证明； ⑵ 当动点E 在线段BC 上，动点D 运动在线段CB 延长线上时，如图2，其它条件不变，⑴中探究的结论是否发生改变？说明你的猜想并给予证明．图1ABCDE图2AB CDE4、在等边△ABC 的两边AB ，AC 所在直线上分别有两点M ，N ，D 为△ABC 外一点，且∠MDN=60°,∠BDC=120°，BD=CD ，探究：当点M ，N 分别爱直线AB ，AC 上移动时，BM ，NC ，MN 之间的数量关系及AMN ∆的周长与等边AB C ∆的周长L 的关系．⑴如图①，当点M ，N 在边AB ，AC 上，且DM=DN 时，BM ，NC ，MN 之间的数量关系式________；此时LQ=__________. ⑵如图②，当点M ，N 在边AB ，AC 上，且DN DM ≠时，猜想(1)问的两个结论还成立吗？写出你的猜想并加以证明；⑶如图③，当点M ，N 分别在边AB ，CA 的延长线上时，若AN=x ，则Q =________(用x ，L 表示)图（1）图（2）图（3）N M DCBANM DCBANMDCBA题型三、对角互补模型5、已知：∠MAN ，AC 平分∠MAN ．⑴在图1中，若∠MAN=∠DCB=90°，证明：AC AD AB 2=+．⑵在图2中，若∠MAN=120°，∠DCB=60°，探究AB 、AD 、AC 三者之间的数量关系，并给出证明；⑶在图3中：若∠MAN=()︒︒1800 α，∠DCB=α-180︒，则AB+AD= AC （用含α的三角函数表示,直接写出结果，不必证明）图3图2图1ABM CDNAB MCDNNMDCB A题型四、直角三角形斜边中点6、在等腰直角△ABC 中，∠ACB=90°，AC=BC ，M 是AB 的中点，点P 从B 出发向C 运动， MQ ⊥MP 交AC 于点Q ，试说明△MPQ 的形状和面积将如何变化．7、等腰直角三角形ABC ，∠ABC=90°AB=2,O 为AC 中点，∠EOF=45°，求△BEF 的周长．APMCQ BOFE CBA题型五、等线段共点8、如图，P 为正方形ABCD 内一点，PA ＝1，PD ＝2，PC ＝3，将△PAD 绕着D 点按逆时针旋转90°到△DCM 的位置（1）求∠APD 的度数。

初中数学九大几何模型

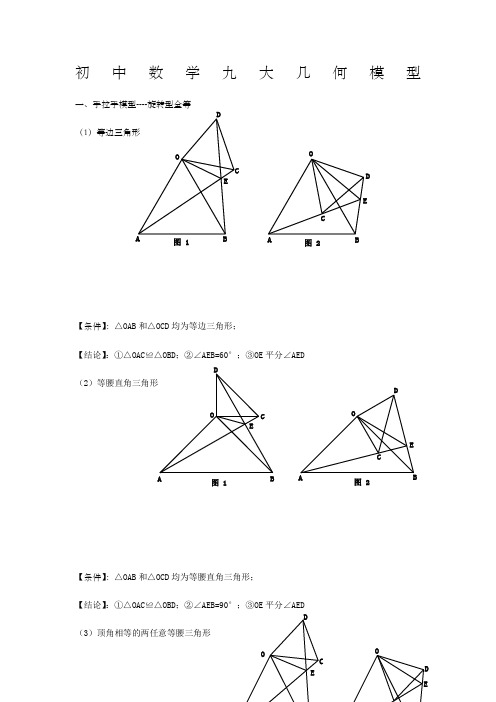
初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED（2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED（3）顶角相等的两任意等腰三角形OB C DE图 1OABCD E图 2OABCDE图 1OACDE图 2OCDEOD E【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AED二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90° 将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ；OAB COBCDEOB CDEOA CD③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB B C AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ；③2△OCD △OCE OC 21S S =-（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=AOBCDE 图 1A OBCDEM N图 2A OBCDEF图 3A O BCDEMN 图 4证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

旋转中的三种常见模型(学生版)-初中数学

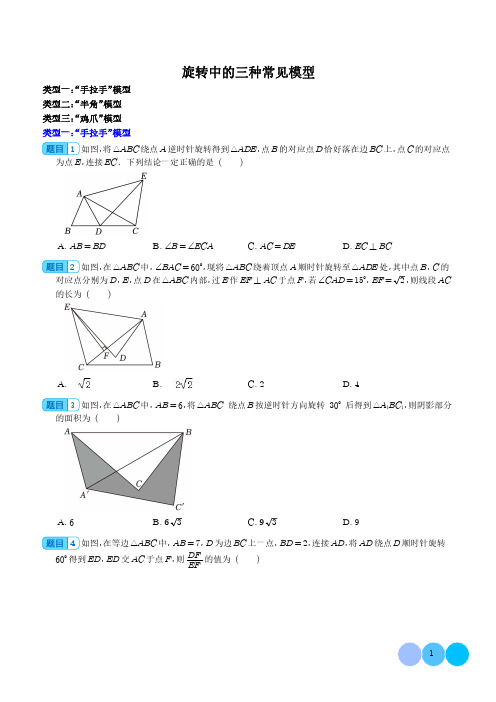
旋转中的三种常见模型类型一：“手拉手”模型类型二：“半角”模型类型三：“鸡爪”模型类型一：“手拉手”模型1如图，将△ABC绕点A逆时针旋转得到△ADE，点B的对应点D恰好落在边BC上，点C的对应点为点E，连接EC．下列结论一定正确的是()A.AB=BDB.∠B=∠ECAC.AC=DED.EC⊥BC2如图，在△ABC中，∠BAC=60°，现将△ABC绕着顶点A顺时针旋转至△ADE处，其中点B，C的对应点分别为D，E，点D在△ABC内部，过E作EF⊥AC于点F，若∠CAD=15°，EF=2，则线段AC 的长为()A. B. C.2 D.43如图，在△ABC中，AB=6，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分的面积为()A.6B.63C.93D.94如图，在等边△ABC中，AB=7，D为边BC上一点，BD=2，连接AD，将AD绕点D顺时针旋转60°得到ED，ED交AC于点F，则DFEF的值为()A.3B.52C.332D.945如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=2，将△ABC绕顶点C逆时针旋转得到△A′B′C′，若点M、P分别是BC、A′B′的中点，连接PM．则线段PM的最大值是()A.4B.3C.2D.16如图，△ABC是边长为8的等边三角形，D是BC的中点，E是直线AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．则在点E的运动过程中，DF的最小值是()A.2B.2.5C.3D.3.57在△ABC中，∠ABC=60°，将△ABC在平面内绕点B顺时针旋转α(0°<α<90°)得到△DBE，其中点A的对应点为点D，连接CE．(1)若α=30°，如图①，求∠BEC的度数；(2)当点D在边BC上时，如图②，若DC=2，AC=19，求AB的长．8如图，△ABC中，AB=BC，点O是△ABC内一点，将△ABO旋转后能与△BCD重合(1)旋转中心是点；(2)若∠ACB=70°，旋转角是度；(3)若∠ACB=60°，请判断△BOD的形状并说明理由．9如图，在△ABC中，∠BAC=90°，AB=AC=103cm，点D为△ABC内一点，∠BAD=15°，AD =62，连接BD，将△ABD绕点A按逆时针方向旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，(1)求∠AFD的度数．(2)求△ADE中DE边上的高．(3)求CF的长．10△ABC和△ADE都是等边三角形．(1)将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有P A+PB=PC(或P A+PC=PB)成立(不需证明)；(2)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC之间有怎样的数量关系？并加以证明；(3)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC之间有怎样的数量关系？并加以证明．类型二：“半角”模型11如图，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，已知AD=6(正方形的四条边都相等，四个内角都是直角)，DF=2，则S△AEF=()A.6B.12C.15D.3012如图，在菱形ABCD中，AB=43，∠BAD=60°，对角线AC，BD相交于点O，点E是对角线AC 上的一个动点，连结BE，将BE绕点B按逆时针方向旋转60°，得到BF，连接OF，则OF的最小值是()A.23B.32C.3 D.3213如图，正方形ABCD边长为1，∠ECF=45°，CF=CE，则下列结论：①∠1=∠2=22.5°；②AC垂直平分EF；③△AEF的周长是2；④DE+BF>EF；⑤点A到EF的距离是2-1．其中正确的结论有()A.2个B.3个C.4个D.5个14如图△ABC中，AB=AC，∠BAC=120°，∠DAE=60°，BD=5，CE=8，求DE的长．15如图，在△ABC中，CA=CB，∠ACB=120°，E为AB上一点，∠DCE=60°，∠DAE=120°，求证：DE-AD=BE．16如图，点E与F分别在正方形ABCD的边BC与CD上，∠EAF=45°，以点A为旋转中心，将△ADF按顺时针方向旋转90°得到△ABF'．已知DF=5cm，BE=3cm，求EF的长．17如图，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连接EF，试猜想EF，BE，DF 之间的数量关系，并证明你的猜想．18如图，四边形ABCD是正方形，E，F分别在直线AB，AD上，且∠ECF=45°，连接EF．(1)当E，F分别在边AB，AD上时，如图1．请探究线段EF，BE，DF之间的数量关系，并写出证明过程；(2)当E，F分别在BA，AD的延长线上时，如图2．试探究线段EF，BE，DF之间的数量关系，并证明．19如图，在四边形ABCD中，点M、N分别在边CD、BC上．连接AM、AN．(1)如图1，四边形ABCD为正方形时，连结MN，且∠MAN=45°，①已知CM=6，CN=8，求MN的长；②已知DM：CM=3：2，求AB：BN的值；(2)如图2，四边形ABCD为矩形，∠AMD=2∠BAN，点N为BC的中点，AN=6，AM=8，求AD的长．类型三：“鸡爪”模型20如图，等边△ABC内部有一点P，且P A=8，PB=15，PC=17，则∠APB的度数为()A.150°B.135°C.120°D.165°21如图，P为等边△ABC内的一点，且P到三个顶点A，B，C的距离分别为6，8，10，则△ABC的面积为()A.36+253B.253C.18+253D.18+50322如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④；⑤．其中正确的结论是()A.①②③⑤B.①②③④C.①②③④⑤D.①②③23如图，△ABC是等边三角形，点P为三角形内一点，连接P A、PB、PC，且P A=2，PB=1，PC= 5，则阴影部分的面积为．24如图，P是等边△ABC内一点，且P A=6，PC=8，PB=10，D是△ABC外一点，且△ADC≌△APB，求∠APC的度数．25如图，点O是等边三角形ABC内的一点，∠BOC=150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．(1)求∠ODC的度数；(2)若OB=4，OC=5，求AO的长．26(1)探究发现：下面是一道例题及解答过程，请补充完整：如图①在等边△ABC内部，有一点P，若∠APB=150°，求证：AP2+BP2=CP2．证明：将△APC绕A点逆时针旋转60°，得到△AP′B，连接PP′，则△APP′为等边三角形，∴∠APP′=60°，P A=PP′，PC=．∵∠APB=150°，∴∠BPP'=90°∴P′P2+BP2=2，即P A2+PB2=PC2．(2)类比延伸：如图②在等腰ABC中，∠BAC=90°，内部有一点P，若∠APB=135°，试判断线段P A、PB、PC之间的数量关系，并证明．27(1)如图1，P是等边三角形ABC内一点，P A=6，PB=8，PC=10．若P′是△ABC外的一点，且△P′AB≌△P AC．求PP′的长度及∠APB的度数．(2)如图2，Q是等边三角形ABC内一点，QA=5，QB=12，∠AQB=150°，求CQ的长．28在等边三角形ABC的内部有一点D，连接BD，CD，以点B为中心，把BD逆时针旋转60°得到HD′，连接AD′，DD′．以点C为中心，把CD顺时针旋转60°得到CD″，连接AD″，DD″．(1)判断∠D′BA和∠DBC的大小关系，并说明理由；(2)求证：D′A=DC；(3)求证：四边形AD'DD″是平行四边形．。

旋转中的三种全等模型(手拉手、半角、对角互补模型)—2023-2024学年九年级数学上册(解析版)

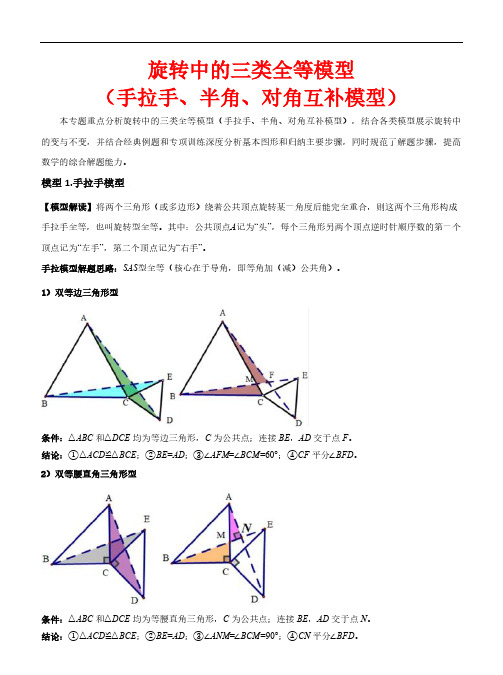
旋转中的三类全等模型（手拉手、半角、对角互补模型）本专题重点分析旋转中的三类全等模型（手拉手、半角、对角互补模型），结合各类模型展示旋转中的变与不变，并结合经典例题和专项训练深度分析基本图形和归纳主要步骤，同时规范了解题步骤，提高数学的综合解题能力。

模型1.手拉手模型【模型解读】将两个三角形（或多边形）绕着公共顶点旋转某一角度后能完全重合，则这两个三角形构成手拉手全等，也叫旋转型全等。

其中：公共顶点A记为“头”，每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”，第二个顶点记为“右手”。

手拉模型解题思路：SAS型全等（核心在于导角，即等角加（减）公共角）。

1）双等边三角形型条件：△ABC和△DCE均为等边三角形，C为公共点；连接BE，AD交于点F。

结论：①△ACD≌△BCE；②BE=AD；③∠AFM=∠BCM=60°；④CF平分∠BFD。

2）双等腰直角三角形型条件：△ABC和△DCE均为等腰直角三角形，C为公共点；连接BE，AD交于点N。

结论：①△ACD≌△BCE；②BE=AD；③∠ANM=∠BCM=90°；④CN平分∠BFD。

3）双等腰三角形型条件：△ABC和△DCE均为等腰三角形，C为公共点；连接BE，AD交于点F。

结论：①△ACD≌△BCE；②BE=AD；③∠ACM=∠BFM；④CF平分∠BFD。

4）双正方形形型条件：△ABCFD和△CEFG都是正方形，C为公共点；连接BG，ED交于点N。

结论：①△△BCG≌△DCE；②BG=DE；③∠BCM=∠DNM=90°；④CN平分∠BNE。

【答案】(1)40；(2)60；(3)【分析】（1）证明△COD是等边三角形，得到∠ODC=60°，即可得到答案；∠=∠ADC-∠ODC求出答案；（3）由△BOC≌△ADC，推出∠ADC=∠BOC=150°，AD=OB=8，根据（2）利用ODA△COD 是等边三角形，得到∠ODC=60°，OD=4OC =，证得△AOD 是直角三角形，利用勾股定理求出．【详解】（1）解：∵CO=CD ，∠OCD=60°，∴△COD 是等边三角形；∴∠ODC=60°，∵∠ADC=∠BOC=100α=︒，∴ODA ∠=∠ADC -∠ODC=40°，故答案为：40；（2）∵∠ADC=∠BOC=120α=︒，∴ODA ∠=∠ADC -∠ODC=60°，故答案为：60；（3）解：当150α=︒，即∠BOC=150°，∴△AOD 是直角三角形．∵△BOC ≌△ADC ，∴∠ADC=∠BOC=150°，AD=OB=8，又∵△COD 是等边三角形，∴∠ODC=60°，OD=4OC =，∴∠ADO=90°，即△AOD 是直角三角形，∴OA =故答案为：【点睛】本题以“空间与图形”中的核心知识（如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等）为载体，内容由浅入深，层层递进．试题中几何演绎推理的难度适宜，蕴含着丰富的思想方法（如运动变化、数形结合、分类讨论、方程思想等），能较好地考查学生的推理、探究及解决问题的能力．备用图【答案】(1)△BEF 是等边三角形(2)证明见解析(3)131−【分析】（1）根据旋转即可证明△BEF 是等边三角形；（2）由△EBF 是等边三角形，可得FB=EB ，再证明∠FBA=∠EBC ，又因为AB=BC ，所以可证明△FBA ≌△EBC ，进而可得AF=CE ；（3）当点D ，E ，F 在同一直线上时，过B 作BM ⊥EF 于M ，再在Rt △BMD 中利用勾股定理列方程求解即可．（1）∵将线段EB 绕点E 顺时针旋转60°得到线段EF ，∴EB=EF ，60FEB =︒∠∴△BEF 是等边三角形（2）∵等边△ABC 和△BEF ∴BF=BE ，AB=BC ，60EBF ABC ∠=∠=︒∴EBF ABE ABC ABE ∠+∠=∠+∠即∠FBA=∠EBC∴△FBA ≌△EBC （SAS ）∴AF=CE（3）图形如图所示：过B 作BM ⊥EF 于M ，∵△BEF 是等边三角形∴2BE EM =，BM =∵点D 是AB 的中点，∴142BD AB == 在Rt △BMD 中，222BM DM BD +=∵DE=2∴222)(2)4EM ++=解得EM 或EM =（舍去）∴21BE EM == 【点睛】本题考查了旋转的性质，全等三角形的判定和性质，勾股定理的运用，旋转的性质，等边三角形的判定和性质，解一元二次方程，利用手拉手模型构造全等三角形是解题的关键．例3．（2022·吉林·九年级期末）如图①，在ABC 中，90C ∠=︒，AC BC ==点D ，E 分别在边AC ，BC 上，且CD CE =AD BE =，AD BE ⊥成立．（1）将CDE △绕点C 逆时针旋转90︒时，在图②中补充图形，并直接写出BE 的长度；（2）当CDE △绕点C 逆时针旋转一周的过程中，AD 与BE 的数量关系和位置关系是否仍然成立？若成立，请你利用图③证明，若不成立请说明理由；（3）将CDE △绕点C 逆时针旋转一周的过程中，当A ，D ，E 三点在同一条直线上时，请直接写出AD 的长度．【答案】（1）补充图形见解析；BE =（2）AD BE =，AD BE ⊥仍然成立，证明见解析；（3）1AD或1=AD ．【分析】（1）根据旋转作图的方法作图，再根据勾股定理求出BE 的长即可；（2）根据SAS 证明E ACD BC ≅∆∆得AD=BE ，∠1=∠2，再根据∠1+∠3+∠4=90°得∠2∠3+∠4=90°，从而可得出结论；（3）分两种情况，运用勾股定理求解即可．【详解】解：（1）如图所示，根据题意得，点D 在BC 上，∴BCE ∆是直角三角形，且由勾股定理得，BE ==（2）AD BE =，AD BE ⊥仍然成立. 证明：延长AD 交BE 于点H ，∵90ACB DCE ∠=∠=︒，ACD ACB BCD ∠=∠−∠，BCE DCE BCD ∠=∠−∠，∴ACD BCE ∠=∠，又∵CD CE =，AC BC =，∴ACD BCE ≅△△，∴AD BE =，12∠=∠，在Rt ABC 中，13490∠+∠+∠=︒，∴23490∠+∠+∠=︒，∴90AHB ∠=︒，∴AD BE ⊥.（3）①当点D 在AC 上方时，如图1所示，同（2）可得ACD BCE ≅△△∴AD=BE 同理可证BE AE ⊥在Rt △CDE 中，CD CE =2=在Rt △ACB 中，AC BC =AB ==设AD=BE=x ，在Rt △ABE 中，222BE AE AB +=∴222(2)x x ++=解得,1x ∴ 1AD =②当点D 在AC 下方时，如图2所示，同（2）可得ACD BCE ≅△△∴AD=BE 同理可证BE AE ⊥在Rt △CDE 中，CD CE =2=在Rt △ACB 中，AC BC =AB ==设AD=BE=x ，在Rt △ABE 中，222BE AE AB +=∴222(2)x x +−=解得,x = ∴ 1AD .所以,AD 1【点睛】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识，熟练解答本题的关键．例4．（2022·黑龙江·虎林市九年级期末）已知Rt △ABC 中，AC =BC ，∠ACB ＝90°，F 为AB 边的中点，且DF =EF ，∠DFE ＝90°，D 是BC 上一个动点．如图1，当D 与C 重合时，易证：CD 2＋DB 2＝2DF 2；（1）当D 不与C 、B ，CD 、DB 、DF 有怎样的数量关系，请直接写出你的猜想，不需证明．（2）当D 在BC 的延长线上时，如图3，CD 、DB 、DF 有怎样的数量关系，请写出你的猜想，并加以证明．【答案】（1）CD2+DB2=2DF2 ；（2）CD2+DB2=2DF2，证明见解析【分析】（1）由已知得222DE DF =，连接CF ，BE ，证明CDF BEF ∆≅∆得CD=BE ，再证明BDE ∆为直角三角形，由勾股定理可得结论；（2）连接CF ，BE ，证明CDF BEF ∆≅∆得CD=BE ，再证明BDE ∆为直角三角形，由勾股定理可得结论．【详解】解：（1）CD2+DB2=2DF2证明：∵DF=EF ，∠DFE ＝90°，∴222DF EF DE += ∴222DE DF =连接CF ，BE ，如图∵△ABC 是等腰直角三角形，F 为斜边AB 的中点∴CF BF =， CF AB ⊥，即90CFB ∠=︒ ∴45FCB FBC ∠=∠=︒，90CFD DFB ∠+∠=︒又90DFB EFB ∠+∠=︒ ∴CFD EFB ∠=∠在CFD ∆和BFE ∆中CF BF CFD BFE DF EF =⎧⎪∠=∠⎨⎪=⎩ ∴CFD ∆≅BFE ∆∴CD BE =，45EBF FCB ∠=∠=︒ ∴454590DBF EBF ∠+∠=︒+︒=︒ ∴222DB BE DE +=∵CD BE =，222DE DF =∴CD2+DB2=2DF2 ；（2）CD2+DB2=2DF2 证明：连接BE∵CF=BF ，DF=EF 又∵∠DFC+∠CFE=∠EFB+∠CFB=90°∴∠DFC=∠EFB ∴△DFC ≌△EFB ∴CD=BE ，∠DCF=∠EBF=135°∵∠EBD=∠EBF －∠FBD=135°－45°=90° 在Rt △DBE 中，BE2+DB2=DE2∵ DE2=2DF2 ∴ CD2+DB2=2DF2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键，学会添加常用辅助线，构造全等三角形解决问题．例5．（2022·山西大同·九年级期中）综合与实践：已知ABC 是等腰三角形，AB AC =．（1）特殊情形：如图1，当DE ∥BC 时，DB ______EC ．（填“＞”“＜”或“＝”）；（2）发现结论：若将图1中的ADE 绕点A 顺时针旋转α（0180α︒<<︒）到图2所示的位置，则（1）中的结论还成立吗？请说明理由．（3）拓展运用：某学习小组在解答问题：“如图3，点P 是等腰直角三角形ABC 内一点，90BAC ∠=︒，且1BP =，2AP =，3CP =，求BPA ∠的度数”时，小明发现可以利用旋转的知识，将BAP △绕点A 顺时针旋转90°得到CAE V ，连接PE ，构造新图形解决问题．请你根据小明的发现直接写出BPA ∠的度数．【答案】（1）=；（2）成立，理由见解析；（3）∠BPA=135°．【分析】（1）由DE ∥BC ，得到∠ADE=∠B ，∠AED=∠C ，结合AB=AC ，得到DB=EC ；（2）由旋转得到的结论判断出△DAB ≌△EAC ，得到DB=CE ；（3）由旋转构造出△APB ≌△AEC ，再用勾股定理计算出PE ，然后用勾股定理逆定理判断出△PEC 是直角三角形，在简单计算即可．【详解】解：（1）∵DE ∥BC ，∴∠ADE=∠B ，∠AED=∠C ，∵AB=AC ，∴∠B=∠C ，∴∠ADE=∠AED AD=AE ，∴DB=EC ，故答案为：=；（2）成立．证明：由①易知AD=AE ，∴由旋转性质可知∠DAB=∠EAC ，在△DAB 和△EAC 中AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩，∴△DAB ≌△EAC （SAS ），∴DB=CE ；（3）如图，将△APB 绕点A 旋转90°得△AEC ，连接PE ，∴△APB ≌△AEC ，∴AE=AP=2，EC=BP=1，∠PAE=90°，∴∠AEP=∠APE=45°，在Rt △PAE 中，由勾股定理可得，在△PEC 中，PE2=（2=8，CE2=12=1，PC2=32=9，∵PE2+CE2=PA2，∴△PEC 是直角三角形，∴∠PEC=90°，∴∠AEC=135°，又∵△APB ≌△AEC ，∴∠BPA=∠CEA=135°．【点睛】本题主要考查了旋转的性质，平行线的性质，全等三角形的性质和判定，勾股定理及其逆定理，解本题的关键是构造全等三角形，也是本题的难点．【答案】（1）见解析；（2）48；（3）15︒【分析】（1）通过边角边判定三角形全等；（2）连接,BD GE ，设,BG DE 交于点O ，,DE CG 交于点M ，先证明DE BG ⊥，由勾股定理可得2222DG BE DB GE +=+；（3）作CK GE ⊥于点K ，则122CK GE ==，且1452GCK GCE ∠=∠=︒，由含30度角的直角三角形的性质求解．【详解】（1）四边形ABCE 与CEFG 为正方形，CG CE =，90BCG DCE ∠=∠=︒，90BCG α=∠︒+，90DCE α∠=︒+，BCG DCE ∴∠=∠，在BCG 和DCE △中，BC DC BCG DCECG CE =⎧⎪∠=∠⎨⎪=⎩BCG DCE ∴≌ (SAS)，（2）连接,BD GE ，设,BG DE 交于点O ，,DE CG 交于点M ，90BCG α=∠︒+，90DCE α∠=︒+，BCG DCE ∴∠=∠，在△BCG 和DCE △中，BC DC BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩()SAS BCG DCE ∴△≌，BGC DEC ∠=∠，GMO EMC ∠=∠，18090GOM GMO BGC EMC DEC GCE ∴∠=︒−∠−∠=︒−∠−∠=∠=︒DE BG ∴⊥，由勾股定理得222DG DO GO =+，222BE OB OE =+，22222222DG BE DO GO OB OE DB GE ∴+=+++=+，4,AB CG ==，BD ∴==4GE ==，2222(448DG BE ++∴==，(3)作CK GE ⊥于点K ，如图，△CEG 为等腰直角三角形，122CK GE ==，且1452GCK GCE ∠=∠=︒，在Rt CDK 中，12CK CD =，30CDK ∴∠=︒，903060DCK ∴∠=︒−︒=︒， 604515DCG DCK GCK =∠−∠=︒−︒=︒∠．∴15α=︒．【点睛】本题考查四边形与三角形的综合问题，解题关键是熟练掌握正方形与直角三角形的性质，通过添加辅助线求解．模型2.半角模型【模型解读】半角模型概念：过多边形一个顶点作两条射线，使这两条射线夹角等于该顶角一半思想方法：通过旋转构造全等三角形，实现线段的转化1）正方形半角模型条件：四边形ABCD是正方形，∠ECF=45°；结论：①△BCE≌△DCG；②△CEF≌△CGF；③EF＝BE＋DF；④∆AEF的周长=2AB；⑤CE、CF分别平分∠BEF和∠EFD。

2020年中考高频考点——旋转在几何中的常见模型分析(2)

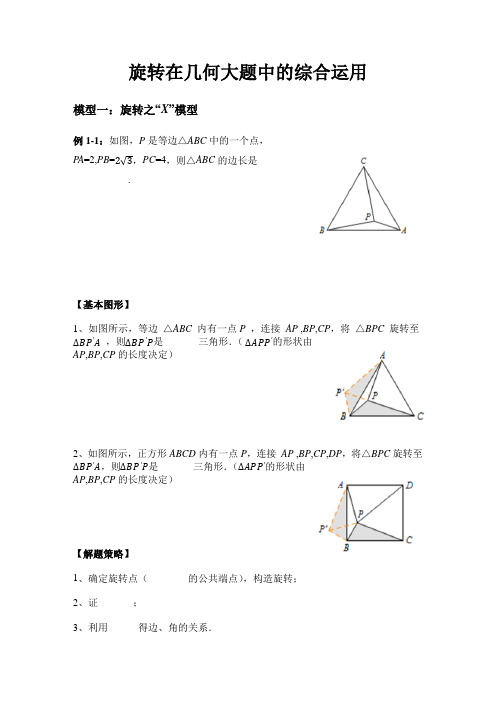
旋转在几何大题中的综合运用模型一：旋转之“X”模型例1-1：如图，P是等边△ABC中的一个点，P A=2,PB=2√3，PC=4，则△ABC的边长是___________.【基本图形】1、如图所示，等边△ABC内有一点P，连接AP ,BP,CP，将△BPC旋转至∆BP′A，则∆BP′P是_______三角形．（ ∆APP′的形状由AP,BP,CP的长度决定）2、如图所示，正方形ABCD内有一点P，连接AP ,BP,CP,DP，将△BPC旋转至∆BP′A，则∆BP′P是_______三角形．（∆APP′的形状由AP,BP,CP的长度决定）【解题策略】1、确定旋转点（________的公共端点），构造旋转；2、证_______；3、利用______得边、角的关系．【经典例题】例1-2：问题背景：如图①设P是等边△ABC内一点，P A＝6，PB＝8，PC＝10，求∠APB的度数．小君研究这个问题的思路是：将△ACP绕点A逆时针旋转60°得到△ABP'，易证：△APP'是等边三角形，△PBP'是直角三角形，所以∠APB＝∠APP'+∠BPP'＝150°．简单应用：（1）如图2，在等腰直角△ABC中，∠ACB＝90°．P为△ABC内一点，且P A＝5，PB＝3，PC＝2，则∠BPC＝_________°（2）如图3，在等边△ABC中，P为△ABC内一点，且P A＝5，PB＝12，∠APB ＝150°，则PC＝__________．拓展廷伸：①如图4，∠ABC＝∠ADC＝90°，AB＝BC．求证：BD＝AD+DC．②若图4中的等腰直角△ABC与Rt△ADC在同侧如图5，若AD＝2，DC＝4，请直接写出BD的长．模型二：旋转之手拉手模型例2-1：如果两个等边△ABD和等边△BCE，连接AE与CD，证明：（1）AE与DC的夹角为60°；（2）AE与DC的交点设为H，BH平分∠AHC.【基本图形】1、如图所示，在等腰△ABC与等腰△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，连接BD，CE，则△ABD≌_______.2、如图所示，在等腰直角△ABC和等腰直角△ADE中，∠ACB=∠AED=90°，连接BD，CE，则△AEC∽_______.【解题策略】1、找旋转点（___________的公共端点）,构造旋转；2、证________或________；3、利用_______或_______得到边、角的关系.【经典例题】例2-2：如图1，在△ABC中，BC=4，以线段AB为边作△ABD，使得AD=BD，连接DC，再以DC为边作△CDE，使得DC=DE，∠CDE=∠ADB=α.(1)如图2,当∠ABC=45∘且α=90∘时，用等式表示线段AD，DE之间的数量关系(2)将线段CB沿着射线CE的方向平移，得到线段EF，连接BF，AF.①若α=90∘，依题意补全图3，求线段AF的长；②请直接写出线段AF的长(用含α的式子表示).模型三：旋转之对角互补模型例3-1：菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180∘，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF.(1)如图1,当∠ABC=90∘时，△OEF的形状是___；(2)如图2,当∠ABC=60∘时，请判断△OEF的形状，并说明理由；【基本图形】1、如图所示，在等腰Rt△ABC中，点O为斜边AB的中点，点E ,F分别是AC ,BC 上两点，且∠EOF+∠ACB=180°，则∠EOF=90°①若过点O分别作AC，BC的垂线段，垂足为M，N，则△MOE≌_________.②若连接OC，则△EOC≌_________.2、如图所示，点D为∠ABC的平分线BD上一点，点E，F分别为∠ABC两边上的点，且∠ABC+∠EDF=180°.过点D分别作AB，BC的垂线段，垂足为H，G，则△DHE≌_________.3、如图，在∠AOB中，C是其中任意一点，满足∠AOB+∠ACB=180°，过C向两边作垂线，垂足分别为E、D，则有△CBE∽________.【解题策略】1、找旋转点（两互补角中_______角所对的动角的顶点），构造旋转；2、证_______或_______；3、利用_______或_______得到边、角的关系．【经典例题】例3-2：如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD 上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E.(1)求证：P A=PE；(2)若将(1)中的正方形变为矩形,其余条件不变(如图2)，且AD=10，DC=8，求AP:PE；(3)在(2)的条件下,当P滑动到BD的延长线上时(如图3)，请你直接写出AP:PE的比值。

模型构建专题：旋转中的常见模型(解析版)

模型构建专题：旋转中的常见模型【考点导航】目录【典型例题】【类型一“手拉手”模型】【变式1等边三角形--等腰直角三角形】【变式2特殊三角形--矩形】【变式3特殊三角形--正方形】【类型二“半角”模型】【典型例题】【类型一“手拉手”模型】1(2023秋·河南信阳·九年级统考期末)△ABC和△ADE都是等边三角形．将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+PC=PB)成立．(1)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(2)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．【答案】(1)PB=PA+PC，证明见解析(2)PC=PA+PB【分析】(1)在BP上截取BF=PC，连接AF，证明△ABD≌△ACE SAS，得和△BAF≌△CAP SAS AF=AP，∠BAF=∠CAP，再证明△AFP是等边三角形，得PF=PA，最后由线段的和可得结论；(2)在PC上截取CM=PB，连接AM，证明△ABD≌△ACE SAS，得AM=和△AMC≌△APB SAS AP，∠BAP=∠CAM，再证明△AMP是等边三角形，得PM=PA，最后由线段的和可得结论．【详解】(1)解：PB=PA+PC，理由如下：如图②，在BP上截取BF=PC，连接AF，∵△ABC、△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAC+∠CAD=∠CAD+∠DAE，即∠DAB=∠EAC，∴△ABD≌△ACE SAS，∴∠ABD=∠ACE，∵AB=AC，BF=CP，∴△BAF≌△CAP SAS，∴AF=AP，∠BAF=∠CAP，∴∠BAC=∠PAF=60°，∴△AFP是等边三角形，∴PF=PA，∴PB=BF+PF=PC+PA；(2)解：PC=PA+PB，理由如下：如图③，在PC上截取CM=PB，连接AM，∵△ABC、△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAC+∠CAD=∠CAD+∠DAE，即∠DAB=∠EAC，∴△ABD≌△ACE SAS，∴∠ABD=∠ACE，∵AB=AC，PB=CM，∴△AMC≌△APB SAS，∴AM=AP，∠BAP=∠CAM，∴∠BAC=∠PAM=60°，∴△AMP是等边三角形，∴PM=PA，∴PC=PM+CM=PA+PB．【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质，熟练掌握等边三角形的性质、全等三角形的判定与性质，添加适当的辅助线，是解题的关键．【变式1等边三角形--等腰直角三角形】1(2023春·吉林长春·七年级校考期末)【阅读材料】两个顶角相等的等腰三角形，若它们的顶角具有公共的顶点，且当把它们底角的顶点连接起来时会形成一组全等三角形，则把具有这种规律的图形称为“手拉手”图形，如图1，在“手拉手”图形中，若∠BAC=∠DAE，AB=AC，AD=AE，则△ABD≌△ACE．(1)【材料理解】在图1中证明．(2)【问题解决】如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE，AB=AC，AD=AE，线段DE与线段AC交于点F，延长ED交BC于点G，求证：∠BAD=∠CGE．下面是小明的部分证明过程：证明：∵AB=AC，AD=AE，∴∠ABC=∠ACB=12180°-∠BAC，∠AED=∠ADE=12180°-∠DAE∵∠BAC=∠DAE，∴∠ACB=∠AED．请你补全余下的证明过程．(3)【结论应用】如图3，△ABC是等腰三角形，∠BAC=100°，D、E分别为边AB、AC上的点，且满足AD =AE，连接DE，将△ADE以点A为旋转中心按逆时针方向旋转，旋转角为α0°<α<360°，当线段DE 与△ABC的腰有交点，且直线DE垂直于△ABC的腰时，直接写出α的值．【答案】(1)证明见解析(2)证明见解析(3)50°或310°【分析】(1)根据∠BAC=∠DAE得∠BAD=∠CAE，再结合全等三角形的判定条件SAS证明即可；(2)根据三角形内角和定理，证明∠FAE=∠FGC，结合∠BAD=∠CAE，即可证明∠BAD=∠CGE；(3)根据直线DE垂直于△ABC的腰AB和AC时的图，结合三角内角和定理分别求出∠DAD1和∠DAD2的度数，再结合逆时针旋转方向求出旋转角即可．【详解】(1)证明：∵∠BAC=∠DAE，∴∠BAD=∠CAE，在△ABD和△ACE中，AB=AC∠BAD=∠CAE AD=AE∴△ABD≌△ACE SAS，(2)：∵AB=AC，AD=AE，∴∠ABC=∠ACB=12180°-∠BAC，∠AED=∠ADE=12180°-∠DAE∵∠BAC=∠DAE，∴∠ACB=∠AED，又∵∠AFE=∠CFG，∴∠FAE=∠EGC，∵∠BAC=∠DAE，∴∠BAD=∠CAE，∴∠BAD=∠CGE．(3)DE旋转至垂直AC时，如图4所示，∵∠BAC=100°，AD=AE，∴∠ADE=∠AED=40°，∵△ADE以点A为旋转中心按逆时针方向旋转至△AD1E1，∴∠AD2P=∠ADE=40°，∵D1E1⊥AC于点P，∴∠APD1=90°，∴∠D1AP=50°，∴∠DAD1=∠DAE-∠D1AP=50°，∴DE旋转至垂直AC时，△ADE以点A为旋转中心按逆时针方向旋转角度为50°；DE旋转至垂直AB时，如图5所示，∵△ADE以点A为旋转中心按逆时针方向旋转至△AD2E2，∴∠AD2P=∠ADE=40°，∵D2E2⊥AB于点P，∴∠APD2=90°，∴∠D2AP=50°，∴∠DAD2=50°，∴DE旋转至垂直AB时，△ADE以点A为旋转中心按逆时针方向旋转角度为：360°-50°=310°．【点睛】本题考查了全等三角形的判定、等腰三角形的性质、三角形的内角和和图形的旋转，熟练掌握各个性质定理是解题的关键．【变式训练】1(2023春·河北张家口·八年级统考期中)已知△AOB和△MON都是等腰直角三角形2 2OA<OM<OA，∠AOB=∠MON=90°．(1)如图①，连AM，BN，求证：△AOM≌△BON；(2)若将△MON绕点O顺时针旋转．①如图②，当点N恰好在AB边上时，求证：BN2+AN2=2ON2；②当点A，M，N在同一条直线上时，若OB=5，ON=4，请直接写出线段BN的长．【答案】(1)见解析(2)①见解析；②17+22或17-22【分析】(1)利用SAS证明△AOM≌△BON即可；(2)①连接AM，证明△AOM≌△BON，得AM=BN，结合等腰直角三角形的性质，即可证BN2+AN2=2ON2；②分当点N在线段AM上时，和当点M在线段AN上时，两种情况分类讨论．情况一：当点N在线段AM上时，连接BN，过点O作OH⊥MN于H，根据△AOM≌△BON，得AM=BN，根据等腰直角三角形的性质和勾股定理，先算出MH，AH，再根据BN=AM=AH+MH计算即可；情况二：当点M在线段AN上时，连接BN，过点O作OH⊥MN于H，先利用SAS证△AOM≌△BON，得AM=BN，再根据等腰直角三角形的性质和勾股定理，算出MH，AH，最后根据BN=AM=AH-MH计算即可．【详解】(1)证明：∵∠AOB=∠MON=90°，∴∠MON+∠AON=∠AOB+∠AON，即∠AOM=∠BON，∵△MON和△AOB是等腰直角三角形，∴OM =ON ，OA =OB ，在△AOM 和△BON 中，OM =ON∠AOM =∠BON OA =OB，∴△AOM ≌△BON SAS ；(2)解：①证明：如下图，连接AM ，∵∠AOB =∠MON =90°，∴∠MON -∠AON =∠AOB -∠AON ，即∠AOM =∠BON ，∵△MON 和△AOB 是等腰直角三角形，∴OM =ON ，OA =OB ，∠OAB =∠OBA =45°，在△AOM 和△BON 中，OM =ON∠AOM =∠BON OA =OB，∴△AOM ≌△BON SAS ，∴∠MAO =∠OBA =45°，AM =BN ，∴∠MAN =∠MAO +∠OAB =90°，∴AM 2+AN 2=MN 2，∵△MON 是等腰直角三角形，∴MN =2ON ，MN 2=2ON 2，∴BN 2+AN 2=2ON 2．②情况一：如下图，当点N 在线段AM 上时，连接BN ，过点O 作OH ⊥MN 于H ，∵由(1)得△AOM ≌△BON ，∴AM =BN ，∵△MON 和△MON 都是等腰直角三角形，OB =5，ON =4，∠AOB =∠MON =90°，OH ⊥MN ，∴MN =2ON =42，OA =OB =5，MH =HN =OH =12MN =22，∴AH =OA 2-OH 2=52-22 2=17，∴BN =AM =AH +MH =17+22；情况二：如下图，当点M 在线段AN 上时，连接BN ，过点O 作OH ⊥MN 于H ，∵∠AOB =∠MON =90°，∴∠AON -∠MON =∠AON -∠AOB ，即∠AOM =∠BON ，∵△MON 和△AOB 都是等腰直角三角形，OB =5，ON =4，∠AOB =∠MON =90°，OH ⊥MN ，∴OM=ON =4，OA =OB =5，MN =2ON =42，MH =HN =OH =12MN =22，在△AOM 和△BON 中，OM =ON∠AOM =∠BON OA =OB，∴AM =BN ，∴AH =OA 2-OH 2=52-22 2=17，BN =AM =AH -MH =17-22，综上，线段BN 的长为17+22或17-22．【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质，等腰直角三角形的性质，勾股定理等知识，结合图形正确判断全等三角形是解题的关键．2(2023春·江西吉安·八年级校联考期中)如图1，在△ABC 中，∠A =90°，AB =AC =2+1，点D ，E 分别在边AB ，AC 上，且AD =AE =1，连接DE ．现将△ADE 绕点A 顺时针方向旋转，旋转角为α(0°<α<360°)，如图2，连接CE ，BD ，CD ．(1)当0°<α<180°时，如图2，求证：CE =BD ；(2)当α=90°时，如图3，延长CE 交BD 于点F ，求证：CF 垂直平分BD ；(3)在旋转过程中，当△BCD 的面积最大时，直接写出此时旋转角α的度数和△BCD 的面积．【答案】(1)见解析(2)见解析(3)α=135°，32+52【分析】(1)利用 “SAS ”证得△ACE ≌△ABD 即可得到结论；(2)利用 “SAS ”证得△ACE ≌△ABD ，推出∠ACE =∠ABD ，计算得出AD =BC =2+2，利用等腰三角形“三线合一”的性质即可得到结论；(3)观察图形，当点D 在线段BC 的垂直平分线上时，△BCD 的面积取得最大值，利用等腰直角三角形的性质结合三角形面积公式即可求解．【详解】(1)解：根据题意：AB =AC ，AD =AE ，∠CAB =∠EAD =90°，∵∠CAE +∠BAE =∠BAD +∠BAE =90°，∴∠CAE =∠BAD ，在△ACE 和△ABD 中，AC =AB∠CAE =∠BAD AE =AD，∴△ACE ≌△ABD SAS ，∴CE =BD ；(2)解：根据题意：AB =AC ，AD =AE ，∠CAB =∠EAD =90°，在△ACE 和△ABD 中，AC =AB∠CAE =∠BAD AE =AD，∴∠ACE =∠ABD ，∵∠ACE +∠AEC =90°，且∠AEC =∠FEB ，∴∠ABD +∠FEB =90°，∴∠EFB =90°，∴CF ⊥BD ，∵AB =AC =2+1，AD =AE =1，∠CAB =∠EAD =90°，∴BC =2AB =2+2，CD =AC +AD =2+2，∴BC =CD ，∵CF ⊥BD ，∴CF 是线段BD 的垂直平分线；(3)解：△BCD 中，边BC 的长是定值，则BC 边上的高取最大值时△BCD 的面积有最大值，∴当点D 在线段BC 的垂直平分线上时，△BCD 的面积取得最大值，如图：∵AB =AC =2+1，AD =AE =1，∠CAB =∠EAD =90°，DG ⊥BC 于G ，∴AG =12BC =2+22，∠GAB =45°，∴DG =AG +AD =2+22+1=2+42，∠DAB =180°-45°=135°，∴△BCD 的面积的最大值为：12BC ⋅DG =12(2+2)2+42 =32+52，旋转角α=135°．【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，线段垂直平分线的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题．【变式2特殊三角形--矩形】1(2023春·福建福州·八年级统考期末)矩形ABCO 的边长OA =3，AB =5，将矩形ABCO 绕点O 顺时针旋转角α得到矩形DEFO ，点A 、B 、C 的对应点分别为D 、E 、F ．(1)如图1，当DE 过点C 时，求DC 的长；(2)如图2，当点D 落在AC 上时，连结CE 、OE ．①四边形OACE 是何特殊的四边形？请说明理由；②证明点B 、C 、E 三点共线．【答案】(1)4(2)①四边形是OACE 为平行四边形，理由见解析；②证明见解析【分析】(1)根据旋转的性质可得OD的长度，在Rt△CDO中，根据勾股定理即可求解；(2)①矩形DEFO是由矩形ABCO旋转所得，则有OA=OD，可证△AOC≌△ODE(SAS)，AC∥OE，再结合平行四边形的判定方法即可求证；②根据平行的性质即可求解．【详解】(1)解：∵OC=5，OA=3，由旋转的性质得：OD=OA=3，在Rt△CDO中，∠ODC=∠OAB=90°，由勾股定理得：DC=OC2-OD2=52-32=4．(2)解：①四边形OACE是平行四边形，理由如下：如图所示，∵矩形DEFO是由矩形ABCO旋转所得，∴∠AOC=∠ODE=90°，OA=OD，OC=DE，∴△AOC≌△ODE(SAS)，∴∠CAO=∠EOD，AC=OE，∵OA=OD，∴∠DAO=∠ADO，∴∠ADO=∠DOE，∴AC∥OE，又∵AC=OE，∴四边形是OACE为平行四边形；②证明：∵矩形ABCO中，BC∥AO，由上述①可知，四边形是OACE为平行四边形，即CE∥AO，∴点B、C、E三点共线．【点睛】本题主要考查平行四边形的判定和性质，矩形的旋转的性质，勾股定理求线段长度的综合，掌握以上知识是解题的关键．【变式训练】1(2023春·湖北武汉·八年级统考期末)【探索发现】(1)如图1，正方形ABCD的对角线相交于点O，点O又是正方形A1B1C1O的一个顶点，而且这两个正方形的边长相等，我们知道，无论正方形A1B1C1O绕点O怎么转动，总有ΔAEO≅ΔBFO，连接EF，求证：AE2+CF2=EF2．【类比迁移】(2)如图2，矩形ABCD的中心O是矩形A1B1C1O的一个顶点，A1O与边AB相交于点E，C1 O与边CB相交于点F，连接EF，矩形A1B1C1O可绕着点O旋转，判断(1)中的结论是否成立，若成立，请证明，若不成立，请说明理由；【迁移拓展】(3)如图3，在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，直角∠EDF的顶点D在边AB 的中点处，它的两条边DE和DF分别与直线AC，BC相交于点E，F，∠EDF可绕着点D旋转，当BF= 1cm时，直接写出线段EF的长度．【答案】(1)见解析；(2)仍然成立，证明见解析；(3)EF=5或525cm【分析】(1)根据正方形的性质证明△AOE ≌△BOF ，推出AE =BF ，得到BE =CF ，然后根据勾股定理和线段的代换即可证得结论；(2)连接AC ，证明△AOE ≌△COG ，可得AE =CG ,OE =OG ，然后根据勾股定理和线段的代换证明即可；(3)设CE =x ，分两种情况：当点F 在边BC 上，点F 在边CB 延长线上时，结合(2)的结论利用勾股定理构建方程求解即可．【详解】(1)证明：∵四边形ABCD 、A 1B 1C 1O 都是正方形，∴OA =OB ,∠OAE =∠OBF =45°,∠AOB =∠EOF =∠ABC =90°，AB =BC ，∴∠AOE =∠BOF ，∴△AOE ≌△BOF ，∴AE =BF ，∴BE =CF ，在直角三角形BEF 中，BE 2+BF 2=EF 2，∴AE 2+CF 2=EF 2；(2)AE 2+CF 2=EF 2仍然成立；证明：连接AC ，∵O 是矩形ABCD 的中心，∴O 在AC 上，且AO =CO ，延长EO 交CD 于G ，连接FG ，∵四边形ABCD 是矩形，∴∠BCD =90°,AB ∥CD ，∴∠BAO =∠DCO ,∠AEO =∠CGO ，∴△AOE ≌△COG ，∴AE =CG ,OE =OG ，又∵矩形A 1B 1C 1O 中，∠EOF =90°，∴OF 垂直平分EG ，∴EF =GF ，在直角三角形FCG 中，CG 2+CF 2=FG 2，∴AE 2+CF 2=EF 2；(3)当点F 在边BC 上时，如图，因为BF =1，所以CF =3，根据(2)的结论可得：AE 2+BF 2=EF 2，设CE =x ，则AE =3-x ，则3-x 2+12=x 2+22，解得x =1，即CE =1，∴EF =CE 2+CF 2=12+22=5(cm )；当点F 在边CB 延长线上时，如图，同理可证：AE 2+BF 2=EF 2，设CE =x ，则AE =3+x ，∵EF 2=CE 2+CF 2=AE 2+BF 2，∴x 2+52=x +3 2+12，解得：x =52，即CE =52，∴EF =52+52 2=525(cm )；综上，EF =5或525cm ．【点睛】本题考查了正方形的性质、矩形的性质、勾股定理、全等三角形的判定和性质等知识，熟练掌握相关图形的性质定理、灵活利用方程思想是解题的关键．【变式3特殊三角形--正方形】1(2023·山西大同·校联考三模)综合与实践：问题情景：如图1、正方形ABCD 与正方形AEFG 的边AB ，AE AB <AE 在一条直线上，正方形AEFG 以点A 为旋转中心逆时针旋转，设旋转角为α，在旋转过程中，两个正方形只有点A 重合，其它顶点均不重合，连接BE ，DG ．(1)操作发现：当正方形AEFG 旋转至如图2所示的位置时，求证：BE =DG ；(2)操作发现：如图3，当点E 在BC 延长线上时，连接FC ，求∠FCE 的度数；(3)问题解决：如图4，如果α=45°，AB =2，AE =42，请直接写出点G 到BE 的距离．【答案】(1)见解析(2)∠FCE =45°(3)1655【分析】(1)根据正方形的性质可得AB =AD ，∠BAE +∠EAD =90°，AE =AG ，∠EAD +∠DAG =90°，从而证明△ABE ≅△ADG SAS ，即可得出结论；(2)过F 作FH ⊥BE ，垂足为H ，证明△ABE ≌△EHF AAS ，可得AB =EH ，BE =FH ，从而可得BE =CH =FH ，再由∠EHF =90°，即可求解；(3)连接GB ，GE ，过点B 作BH ⊥AE 于点H ，根据正方形的性质可得AB ∥GE ，从而可得S △BEG =S △AEG =12S 正方形AEFG =16，再利用勾股定理求得BE =25，再由S △BEG =12×BE ×h =16，即可求解．【详解】(1)证明：∵四边形ABCD 是正方形，∴AB =AD ，∠BAE +∠EAD =90°，又∵四边形AEFG 是正方形，∴AE =AG ，∠EAD +∠DAG =90°，∴∠BAE =∠DAG ．在△ABE 与△ADG 中，AB =AD ,∠BAE =∠DAG AE =AG ,，∴△ABE ≅△ADG SAS ，∴BE =DG ；(2)解；过F作FH⊥BE，垂足为H，∵∠AEF=∠ABE=∠EHF=90°，∴∠AEB+∠FEH=90°，∠FEH+∠EFH=90°，∴∠AEB=∠EFH，∵四边形AEFG是正方形，∴AE=EF，在△ABE与△EHF中，∠ABE=∠EHF ∠AEB=EFH AE=EF，∴△ABE≌△EHF AAS，∴AB=EH，BE=FH，∴AB=BC=EH，∴BC+EC=EH+EC，∴BE=CH=FH，又∵∠EHF=90°，∴∠FCE=45°，(3)解：如图，连接GB，GE，过点B作BH⊥AE于点H，∵GE是正方形AEFG的对角线，∴∠AEG=45°，∵∠EAB=45°，∴AB∥GE，∴S△BEG=S△AEG=12S正方形AEFG=12×42×42=16，∵AB=2，∴BH=AH=2，∴HE=42-2=32，在Rt△BHE中，BE=22+322=25，设点G到BE的距离为h，∵S△BEG=12×BE×h ，∴1 2×25×h=16，解得：h=1655，∴点G到BE的距离为1655．【点睛】本题考查正方形的性质、平行线性质、勾股定理、全等三角形的判定与性质，熟练掌握正方形的性质是解题的关键．【变式训练】1(2023·全国·九年级专题练习)问题情境：小红同学在学习了正方形的知识后，进一步进行以下探究活动：在正方形ABCD的边BC上任意取一点G，以BG为边长向外作正方形BEFG，将正方形BEFG绕点B顺时针旋转．特例感知：(1)当BG在BC上时，连接DF，AC相交于点P，小红发现点P恰为DF的中点，如图①．针对小红发现的结论，请给出证明；(2)小红继续连接EG，并延长与DF相交，发现交点恰好也是DF中点P，如图②，根据小红发现的结论，请判断△APE的形状，并说明理由；规律探究：(3)如图③，将正方形BEFG绕点B顺时针旋转α，连接DF，点P是DF中点，连接AP，EP，AE，△APE 的形状是否发生改变？请说明理由．【答案】(1)见解析；(2)△APE是等腰直角三角形，理由见解析；(3)△APE的形状不改变，见解析【分析】(1)连接BD，BF，BP，根据正方形的性质求出∠DBF=90°，证明△APD≌△APB，推出BP= DP，再利用余角的性质求出∠PBF=∠PFB，推出PB=PF即可；(2)根据正方形的性质直接得到∠CAE=∠PEA=45°，推出AP=EP,∠APE=90°，得到△APE是等腰直角三角形；(3)延长EP至点M，使PM=EP，连接MA,MD，证明△MPD≌△EPF SAS，得到DM=EF,∠DMP=∠PEF，推出BG∥DM，设DF交BC于点H，交BG于点N，得到∠MDN=∠DNB，由AD∥BC得到∠ADN=∠BHN，推出∠ADM=∠BHN+∠BNH=180°-∠HBN，进而得到∠ADM=∠ABE，再证明△ADM≌△ABE SAS，得到AM=AE，∠DAM=∠BAE，证得∠APE=90°，再由∠MAE=90°，根据等腰三角形的三线合一的性质求出∠MAP=∠PAE=45°，即可证得△APE是等腰直角三角形．【详解】(1)证明：连接BD，BF，BP，如图，∵四边形ABCD，BEFG都是正方形，∴∠CBD=45°=∠FBG，∴∠DBF=90°，∵四边形ABCD是正方形，∴∠DAC=∠BAC=45°，又∵AP=AP，∴△APD≌△APB SAS，∴BP=DP，∴∠PDB=∠PBD，∵∠PDB+∠PFB=90°=∠PBD+∠PBF，∴∠PBF=∠PFB，∴PB=PF，∴PD=PF，即点P恰为DF的中点；(2)△APE是等腰直角三角形，理由如下：∵四边形ABCD，BEFG都是正方形，∴∠CAE=∠PEA=45°∴AP=EP,∠APE=90°，∴△APE是等腰直角三角形；(3)△APE的形状不改变，延长EP至点M，使PM=EP，连接MA,MD，∵四边形ABCD、四边形BEFG都是正方形，∴AB=AD，∠BAD=∠ABC=∠EBG=90°，BE=EF，BG∥EF，∵点P为DF的中点，∴PD=PF，∵∠DPM=∠EPF，∴△MPD≌△EPF SAS，∴DM=EF,∠DMP=∠PEF，∴BE=DM，DM∥EF，∴BG∥DM，设DF交BC于点H，交BG于点N，∴∠MDN=∠DNB，∵AD∥BC，∴∠ADN=∠BHN，∵∠BHN+∠BNH+∠HBN=180°，∴∠ADM=∠ADN+∠MDN=∠BHN+∠BNH=180°-∠HBN，∵∠ABE=360°-∠ABC-∠EBG-∠HBN=180°-∠HBN，∴∠ADM=∠ABE，又∵AD=AB，∴△ADM≌△ABE SAS，∴AM=AE，∠DAM=∠BAE，∵PM=EP，∴AP⊥ME，即∠APE=90°，∵∠DAM+∠MAB=90°，∴∠BAE+∠MAB=90°，即∠MAE=90°，∴∠MAP=∠PAE=45°，∴∠PEA=45°=∠PAE，∴AP=EP，∴△APE是等腰直角三角形．【点睛】此题考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，平行线的性质等，(3)中作辅助线利用中点构造全等三角形是解题的难点，熟练掌握各性质和判定定理是解题的关键．【类型二“半角”模型】1(2023春·福建漳州·八年级校考期中)(1)【发现证明】老师在数学课上提出一个问题：如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，∠EAF =45°，请试判断BE 、EF 、FD 之间的数量关系，小聪把△ABE 绕点A 逆时针旋转90°至△ADG ，发现EF =BE +FD ，请你利用图1证明上述结论．(2)【类比引申】如图2，四边形ABCD 中，∠BAD ≠90°，AB =AD ，∠B +∠D =180°，点E 、F 分别在边BC 、CD 上，要使得EF =BE +FD 仍然成立，则∠EAF 与∠BAD 应满足什么数量关系？请说明理由．(3)【探究应用】如图3，在某公园的同一水平面上，四条通道围成四边形ABCD ．已知AB =AD =80米，∠B =60°，∠ADC =120°，∠BAD =150°，道路BC 、CD 上分别有景点E 、F ，且AE ⊥AD ，DF =403-1 )米，现要在E 、F 之间修一条笔直道路，求这条道路EF的长，【答案】(1)见解析；(2)∠BAD =2∠EAF ；(3)403+40 米【分析】(1)根据旋转的性质，得到AE =AG ，∠BAE =∠GAD ，从而证明∠GAF =∠EAF ，可证△AEF ≌△AGF SAS 得出EF =GF =GD +DF 即可；(2)仿照(1)的方法将△ADF 绕点A 顺时针旋转∠BAD 至△ABM ，则可通过的相同的方法证明△EAF ≌△EAM ，即可证出；(3)将△ABE 绕点A 逆时针旋转150°至△ADG ，连接AF ，过A 作AH ⊥GD ，垂足为H ，得到点G 在CD 的延长线上，求出AH ，HF ，得到∠HAF =45°，求出∠DAF =15°，进而得到∠EAF =∠EAD -∠DAF =90°-15°=75°，推出∠BAD =150°=2×75°=2∠EAF ，由此得到EF =BE +DF 求出结果．【详解】(1)解：∵△ABE 绕点A 逆时针旋转90°至△ADG ，∴△ABE ≌△ADG SAS ，∴∠BAE =∠GAD ，AE =AG ，∴∠GAD +∠DAF =∠BAE +∠DAF =90°-45°=45°，∴∠GAF =∠EAF =45°，在△AEF 和△AGF 中，GA =EA∠GAF =∠EAF AF =AF，∴△AEF ≌△AGF SAS ，∴EF =GF =GD +DF =BE +DF ；(2)解：∠BAD =2∠EAF ，理由如下：将△ADF 绕点A 顺时针旋转∠BAD 至△ABM ，∵△ADF 绕点A 顺时针旋转∠BAD 至△ABM ，∴△ABM ≌△ADF ，∴AF =AM ，∠DAF =∠BAM ，∠D =∠ABM ，∵∠BAD =2∠EAF ，∴∠DAF +∠BAE =∠BAM +∠BAE =∠EAF ，∴∠EAF =∠EAM ，∵∠ABE +∠D =180°，∴∠ABE +∠ABM =180°，则点M 、B 、E 共线，∴EM =BE +BM ，在△EAF 和△EAM 中，AF =AM∠EAF =∠EAM AE =AE，∴△EAF ≌△EAM ，∴EF =EM =BE +BM =BE +DF ，即EF =BE +DF ；(3)解：将△ABE 绕点A 逆时针旋转150°至△ADG ，连接AF ，过A 作AH ⊥GD ，垂足为H ，∵∠BAD =150°，∠DAE =90°，∴∠BAE =60°，∵∠B =60°，∴△ABE 是等边三角形，∴BE =AB =80米，根据旋转的性质得到∠ADG =∠B =60°，AG =AE ，∠DAG =∠BAE ，DG =BE ，∵∠ADF =120°，∴∠GDF =180°，即点G 在CD 的延长线上，又∵AH =80×32=403，HF =HD +DF =40+403-1 =403，∵AH ⊥GD ，∴∠HAF =45°，∴∠DAF =∠HAF -∠HAD =45°-30°=15°，∴∠EAF =∠EAD -∠DAF =90°-15°=75°，∴∠BAD =150°=275°=2∠EAF ，根据(2)中结论有：EF =BE +DF =80+403-1 =403+40 (米)，即这条道路EF 的长为403+40 米．【点睛】本题考查了全等三角形，旋转的性质，对于大角中等于其中包含的小角的2倍的问题，可利用题中旋转的方法补全三角形，再通过证明三角形全等的方法求解相关线段．【变式训练】1(2023春·河南信阳·八年级校考期中)通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．原题：如图1，点E 、F分别在正方形ABCD 的边BC 、CD 上，∠EAF =45°，连接EF ，则EF =BE +DF ，试说明理由．(1)梳理∵AB=CD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．∵∠ADC=∠B=90°，∴∠FDG=180°，点F、D、G共线．根据，易证△AFG≌，得EF=BE+DF．(2)引申如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°，若∠B、∠D都不是直角，则当∠B与∠D满足等量关系时，仍有EF=BE+DF．(3)联想拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，猜想BD、DE、EC 应满足的等量关系，并写出推理过程．【答案】(1)SAS，△AFE(2)∠B+∠D=180°(3)DE2=BD2+EC2，见解析【分析】1 把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，再证明△AFG≌△AFE进而得到EF=FG，即可得EF=BE+DF；2 ∠B+∠D=180°时，EF=BE+DF，与1 的证法类同；3 根据△AEC绕点A顺时针旋转90°得到△ABE'，根据旋转的性质，可知△AEC≌△ABE'得到BE = EC，AE =AE，∠C=∠ABE ，∠EAC=∠E AB，根据Rt△ABC中的，AB=AC得到∠E BD=90°，所以E B2+BD2=E D2，证△AE'D≌△AED，利用DE=DE 得到DE2=BD2+EC2；【详解】(1)证明：∵AB=AD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．∴∠BAE=∠DAG，∵∠BAD=90°，∠EAF=45°，∴∠BAE+∠DAF=45°，∴∠EAF=∠FAG，∵∠ADC=∠B=90°，∴∠FDG=180°，在△AFE和△AFG中AE=AG∠EAF=∠FAG AF=AF，∴△AFE≌△AFG SAS，∴EF=FG，即：EF=BE+DF．(2)解：延长CD 至点G ，连接AG ，如图所示，∠B +∠D =180°时，EF =BE +DF ；∵AB =AD ，∴把△ABE 绕点A 逆时针旋转90°至△ADG ，可使AB 与AD 重合，∴∠BAE =∠DAG ，BE =DG ，∵∠BAD =90°，∠EAF =45°，∴∠BAE +∠DAF =45°，∴∠EAF =∠FAG ，当∠FDG =180°，点F 、D 、G 共线时，在△AFE 和△AFG 中AE =AG∠FAE =∠FAG AF =AF，∴△AFE ≌△AFG SAS ，∴EF =FG ，∵FG =DF +DG =DF +BE ，即：EF =BE +DF ．故答案为：∠B +∠D =180°；(3)解：猜想：DE 2=BD 2+EC 2．把△AEC 绕点A 顺时针旋转90°得到△ABE ，连接DE ，∴△AEC ≌△ABE ，∴BE =EC ，AE =AE ，∠C =∠ABE ，∠EAC =∠E AB ，在Rt △ABC 中，AB =AC ，∴∠ABC =∠ACB =45°，∴∠ABC +∠ABE =90°，即∠E BD =90°，∴E B 2+BD 2=E D 2，又∵∠DAE =45°，∴∠BAD +∠EAC =45°，∴∠E AB +∠BAD =45°，即∠E AD =45°，在△AE D 和△AED 中，AE =AE∠E AD =∠DAEAD =AD∴△AE D ≌△AED SAS ，∴DE =DE ，∴DE 2=BD 2+EC 2．【点睛】此题主要考查了几何变换，关键是正确画出图形，证明△AFG ≌△AEF .此题是一道综合题，难度较大，题目所给例题的思路，为解决此题做了较好的铺垫．。

专项17旋转中的几何模型归类(3大类型)(原卷版)

专项17 旋转中的几何模型归类（3大类型）类型一：“手拉手”模型模型特征：两个等边三角形或等腰直角三角形或正方形共顶点。

模型说明：如图1，▲ABE，▲ACF都是等边三角形，可证▲AEC≌▲ABF。

如图2，▲ABD，▲ACE都是等腰直角三角形，可证▲ADC≌▲ABE如图2，四边形ABEF，四边形ACHD都是正方形，可证▲ABD≌▲AFC类型二：“半角”模型模型特征：大角含半角+有相等的边，通过旋转“使相等的边重合，拼出特殊角”模型说明：（1）如图，在正方形ABCD中，∠EAF=45°，将▲ADF绕点A顺时针旋转90°，得到▲ABG可证▲AEF≌AEG，所以可到DF+BE=EF（2）如图，在等腰直角▲ABC中，∠MAN=45°，将▲ACN绕点A顺时针旋转90°，得到▲ABQ，可证▲AMN≌▲AMQ，所以可得CN²+BM²=MN²（3）如图，等腰▲ABC中，AB=BC，∠DBE=将▲CBD绕点B逆时针旋转∠CBA的度数得到▲ABD’可证▲DBE≌▲D’BE。

类型三：构造旋转模型解题方法指导：若一个图形中含有相等的线段和特殊的角度，通常是以等线段的公共端点为旋转中心进行旋转，使得相等的边重合，得出特殊的图形.常见图形旋转：方法归纳：将等边三角形内的一个小三角形，旋转60度，从而使小三角形的一边与原等边三角形的边重合，连接小三角形的钝角顶点，得三角形．通过旋转将不相关的线段转化到同一个三角形中，将分散的已知条件集中起来，使问题得以解决．【考点1 “手拉手”模型】【典例1】（2021春•西安期末）如图，在△ABC中，BC＝5，以AC为边向外作等边△ACD，以AB为边向外作等边△ABE，连接CE、BD．（1）若AC＝4，∠ACB＝30°，求CE的长；（2）若∠ABC＝60°，AB＝3，求BD的长．【变式11】（2021秋•荔湾区校级期中）以△ABC的AB，AC为边分别作正方形ADEB，正方形ACGF，连接DC，BF．（1）CD与BF有什么数量与位置关系？说明理由．（2）利用旋转的观点，在此题中，△ADC可看成由哪个三角形绕哪点旋转多少角度得到的．【变式12】（2021九上·吉林期末）如图①，在△ABC中，∠C=90°，AC=BC=√6，点D，E分别在边AC，BC上，且CD=CE=√2，此时AD=BE，AD⊥BE成立．（1）将△CDE绕点C逆时针旋转90°时，在图②中补充图形，并直接写出BE的长度；（2）当△CDE绕点C逆时针旋转一周的过程中，AD与BE的数量关系和位置关系是否仍然成立？若成立，请你利用图③证明，若不成立请说明理由；（3）将△CDE绕点C逆时针旋转一周的过程中，当A，D，E三点在同一条直线上时，请直接写出AD的长度．【考点2 “半角”模型】【典例2】（2017秋•锦江区期末）在△ABC中，AB＝AC，点E，F是边BC所在直线上与点B，C不重合的两点．（1）如图1，当∠BAC＝90°，∠EAF＝45°时，直接写出线段BE，CF，EF的数量关系；（不必证明）（2）如图2，当∠BAC＝60°，∠EAF＝30°时，已知BE＝3，CF＝5，求线段EF的长度；（3）如图3，当∠BAC＝90°，∠EAF＝135°时，请探究线段CE，BF，EF的数量关系，并证明．【变式21】（2021春•金牛区校级期中）类比探究：（1）如图1，等边△ABC内有一点P，若AP＝8，BP＝15，CP＝17，求∠APB的大小；（提示：将△ABP绕顶点A旋转到△ACP′处）（2）如图2，在△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点，且∠EAF＝45°．求证：EF2＝BE2+FC2；（3）如图3，在△ABC中，∠C＝90°，∠ABC＝30°，点O为△ABC内一点，连接AO、BO、CO，且∠AOC＝∠COB＝∠BOA＝120°，若AC＝1，求OA+OB+OC的值．【变式22】（2022春•西山区校级月考）如图，已知正方形ABCD，点E、F分别是AB、BC 边上，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM．（1）求证：△EDF≌△MDF；（2）若正方形ABCD的边长为5，AE＝2时，求EF的长？【变式23】（2022春•路北区期末）如图，在边长为6的正方形ABCD内作∠EAF＝45°，AE交BC于点E，AF交CD于点F，连接EF，将△ADF绕点A顺时针旋转90°得到△ABG．（1）求证：GE＝FE；（2）若DF＝3，求BE的长为．【变式24】（2021秋•山西期末）阅读以下材料，并按要求完成相应的任务：从正方形的一个顶点引出夹角为45°的两条射线，并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型．半角模型可证出多个几何结论，例如：如图1，在正方形ABCD中，以A为顶点的∠EAF＝45°，AE、AF与BC、CD边分别交于E、F两点．易证得EF＝BE+FD．大致证明思路：如图2，将△ADF绕点A顺时针旋转90°，得到△ABH，由∠HBE＝180°可得H、B、E三点共线，∠HAE＝∠EAF＝45°，进而可证明△AEH≌△AEF，故EF＝BE+DF．任务：如图3，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，∠BAD＝120°，以A为顶点的∠EAF＝60°，AE、AF与BC、CD边分别交于E、F两点．请参照阅读材料中的解题方法，你认为结论EF＝BE+DF是否依然成立，若成立，请写出证明过程；若不成立，请说明理由．【考点3 构造旋转模型解题】【典例3】（2017九上·江津期中）请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB= √3，PC=1、求∠BPC 度数的大小和等边三角形ABC的边长．李明同学的思路是：将∠BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得∠P′PB是等边三角形，而∠PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边∠ABC的边长为√7，问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA= √5，BP= √2，PC=1．求∠BPC度数的大小和正方形ABCD的边长．【变式31】（2020九上·南昌月考）如图，在等边三角形ABC内有一点P，且PA=2，PB=√3，PC=1，求∠BPC的度数和等边三角形ABC的边长．【变式32】（2021九上·德州期中）当图形具有邻边相等的特征时，我们可以把图形的一部分绕着公共端点旋转，这样将分散的条件集中起来，从而达到解决问题的目的．（1）如图1，等腰直角三角形ABC内有一点P，连接AP，BP，CP，∠APB＝135°，为探究AP，BP，CP三条线段间的数量关系，我们可以将∠ABP，绕点A逆时针旋转90°得到∠ACP'，连接PP'，则PP'＝AP，∠CPP'是三角形，AP，BP，CP三条线段的数量关系是．（2）如图2，等边三角形ABC内有一点P，连接AP、BP、CP，∠APB＝150°，请借助第一问的方法探究AP、BP、CP三条线段间的数量关系．（3）如图3，在四边形ABCD中，AD∠BC，点P在四边形的内部，且PD＝PC，∠CPD ＝90°，∠APB＝135°，AD＝4，BC＝5，请直接写出AB的长．1.（2021九上·鲅鱼圈期中）△ABC与△CDE都是等边三角形，连接AD、BE．（1）如图①，当点B、C、D在同一条直线上时，则∠BCE=度；（2）将图①中的△CDE绕着点C逆时针旋转到如图②的位置，求证：AD=BE．2．（2021九上·宜春期末）如图（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．则：①∠ACB的度数为；②线段BE，CE与AE之间的数量关系是．（2）拓展研究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上．若CE=√2，BE=2，求AB的长度．（3）探究发现：图1中的△ACB和△DCE，在△DCE旋转过程中，当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．3.（2021秋•夏河县期中）已知△ABC为等边三角形．（1）如图，P为△ABC外一点，∠BPC＝120°，连接P A，PB，PC，求证：PB+PC＝P A；（2）如图，P为△ABC内一点，若P A＝12，PB＝5，PC＝13，求∠APB的度数．4.（2021九上·伊通期末）如图，已知正方形ABCD的边长为6，E，F分别是AB、BC 边上的点，且∠EDF＝45°，将∠DAE绕点D逆时针旋转90°，得到∠DCM．（1）求证：EF＝MF；（2）若AE＝2，求FC的长．5．（2019九上·西城期中）在∠ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，将线段AD绕点A逆时针旋转90°得到AE，连结EC．如果AB=AC，∠BAC=90°．①当点D在线段BC上时（与点B不重合），如图1，请你判断线段CE、BD之间的位置和数量关系（直接写出结论）；②当点D在线段BC的延长线上时，请你在图2画出图形，判断①中的结论是否仍然成立，并证明你的判断．6．（2022春•临渭区期末）数学探究课上老师出了这样一道题：“如图，等边△ABC中有一点P，且P A＝3，PB＝4，PC＝5，试求∠APB的度数．”小明和小军探讨时发现了一种求∠APB度数的方法，下面是这种方法的一部分思路，请按照下列思路要求画图或判断．（1）在图中画出△APC绕点A顺时旋转60°后的△AP1B，并判断△AP1P的形状是；（2）试判断△BP1P的形状，并说明理由；（3）由（1）、（2）两问可知：∠APB．7．（2022春•丹江口市期末）（1）如图1，已知，正方形ABCD和正方形CEFG，点G在BC延长线上，点E在CD边上，则BE与DG的数量关系为，BE与DG的位置关系为；（2）将（1）中的正方形CEFG绕点C旋转至图2时，（1）中的结论是否成立？若成立，请给以证明；若不成立，请说明理由；（3）若AB＝5，CE＝，在正方形CEFG绕点C旋转一周过程中，当A，F，G三点在一条直线上时，请画出图形，并直接写出AG长．8．（2021秋•十堰期末）正方形ABCD中，点F为正方形ABCD内的点，△BFC绕着点B 按逆时针方向旋转90°后与△BEA重合．（1）如图①，若正方形ABCD的边长为2，BE＝1，FC＝，求证：AE∥BF．（2）如图②，若点F为正方形ABCD对角线AC上的点（点F不与点A、C重合），试探究AE、AF、BF之间的数量关系并加以证明．9．（2021秋•宁津县期末）如图，正方形ABCD中，点E，F分别为AB，AD的中点，以AE，AF为边作正方形AEGF．（1）在图1中，线段DF与CG之间有怎样的数量关系？说明理由；（2）在图2中，将正方形AEGF绕点A顺时针旋转一定角度（旋转角小于90°）后，得到正方形AE'G'F'，连接DF'，CG'，则线段DF′与CG′之间的数量关系是否仍然成立，请说明理由．10.（2020秋•饶平县校级期末）如图，O是等边△ABC内一点，OA＝3，OB＝4，OC＝5，将线段BO绕点B逆时针旋转60°得到线段BO′．（1）求点O与O′的距离；（2）求∠AOB的度数．11．（大兴安岭）已知：正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．当∠MAN绕点A旋转到BM＝DN时（如图1），易证BM+DN＝MN．（1）当∠MAN绕点A旋转到BM≠DN时（如图2），线段BM、DN和MN之间有怎样的数量关系？写出猜想，并加以证明；（2）当∠MAN绕点A旋转到如图3的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想．。

中考数学九大几何模型标准版

初中数学九大几何模型、手拉手模型 - 旋转型全等条件】：△ OAB 和△ OCD 均为等边三角形；条件】：△ OAB 和△ OCD 均为等腰直角三角形；结论】：①△ OAC ≌△ OBD ；②∠ AEB=90°；③ OE 平分∠ AEDD EAED 1）等边三角形D结论】：①△ OAC ≌△ OBD ；②∠ AEB=60°；③ OE 平分∠、模型二：手拉手模型 -- 旋转型相似（1）一般情况【条件】：CD ∥AB ，将△ OCD 旋转至右图的位置 O OD EA A结论】：①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ；②延长 AC 交 BD 于点 E ，必有∠ BEC=∠ BOA2）特殊情况条件】：CD ∥ AB ，∠ AOB=90°将△ OCD 旋转至右图的位置 A 结论】：①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ； ②延长 AC 交 BD 于点 E ，必有∠ BEC=∠ BOA ； ③ A BD C O O C D O O A B tan ∠OCD ；④BD ⊥AC ； ⑤连接 AD 、BC ，必有 AD 2 BC 2 AB 2三、模型三、对角互补模型1）全等型 -90 ° 条件】：①∠ AOB=∠ DCE=90°；② OC 平分∠ AOB结论】：① CD=CE ；② OD+OE= 2 OC ；③ S △DCE CD ；⑥S△BCD证明提示： ①作垂直，如图 2，证明△ CDM ≌△ CEN ②过点 C 作 CF ⊥ OC ，如图 3，证明△ ODC ≌△ FEC ※当∠ DCE 的一边交 AO 的延长线于 D 时（如图 4）： S△OCDS以上三个结论：① CD=CE ；② OE-OD= 2 OC ； ③ S △ OCE S △ OCD2）全等型 -120 °条件】：①∠ AOB=2∠ DCE=120°；② OC 平分∠ AOB32 结论】：① CD=CE ；② OD+OE=O ；C ③ S △DCES △OCDS △OCEOC 2 4证明提示：①可参考“全等型 -90 °”证法一；②如右下图：在 OB 上取一点 F ，使 OF=OC ，证明△ OCF 为等边三角形。

旋转模型、手拉手模型、半角模型

Math 唐老师1旋转模型综合应用第2页，共14页1．如图①，在ABC中，90C AC BC ∠=︒==，D E ，分别在边AC BC ，上，且CD CE ==时AD BE AD BE =⊥，成立．(1)将CDE 绕点C 逆时针旋转90︒时，在图②中补充图形，并求出BE 的长度；(2)当CDE 绕点C 逆时针旋转一周的过程中，AD 与BE 的数量关系和位置关系是否仍然成立？若成立，请你利用图③证明，若不成立请说明理由；(3)将CDE 绕点C 逆时针旋转一周的过程中，当A D E ，，三点在同一条直线上时，请画出图形并直接写出AD 的长度．2．如图，在等边三角形ABC 中，点E 是边AC 上一定点，点D 是直线BC 上一动点，以DE 为一边作等边三角形DEF ，连接CF ．（1）如图1，若点D 在边BC 上，直接写出CE ，CF 与CD 之间的数量关系；（2）如图2，若点D 在边BC 的延长线上，请探究线段CE ，CF 与CD 之间存在怎样的数量关系？并说明理由；（3）如图3，若点D 在边CB 的延长线上，请直接写出CE ，CF 与CD 之间的数量关系．Math唐老师3（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．则：①∠AEB的度数为°；②线段AD、BE之间的数量关系是．（2）拓展研究：如图2，△ACB和△DCE均为等腰三角形，且∠ACB＝∠DCE＝90°，点A、D、E在同一直线上，若AD＝a，AE＝b，AB＝c，求a、b、c之间的数量关系．（3）探究发现：图1中的△ACB和△DCE，在△DCE旋转过程中，当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．3第4页，共14页手拉手模型综合应用手拉手模型的定义：有两个顶角相等而且有公共顶点的等腰三角形开成的图形。

初中数学模型题库半角模型+旋转原理+手拉手模型

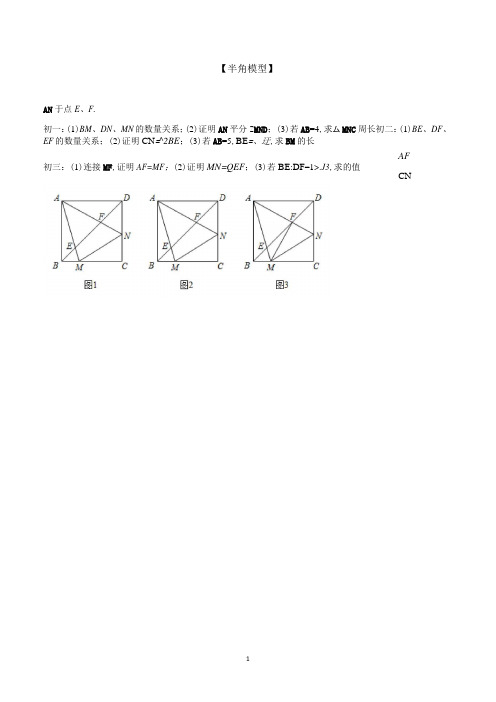
【半角模型】AN于点E、F.初一：(1)BM、DN、MN的数量关系；(2)证明AN平分Z MND；(3)若AB=4,求厶MNC周长初二：(1)BE、DF、EF的数量关系；(2)证明CN=^2BE；(3)若AB=5,BE=、迂,求BM的长AF初三：(1)连接MF,证明AF=MF；(2)证明MN=QEF；(3)若BE:DF=1>.J3,求的值CN且Z MAN=60°,BD分别交AM、AN于点E、F.初一：1) BM、DN、MN的数量关系；(2)证明AN平分Z MND；(3)若BD=4,求厶MNC周长(2)证明CN€2BE；(3)若AB=5,BE二訂，求BM的长初二：若BE=2,DF=4,求EF的长;1)的值且Z MAN=30°,BD分别交AM、AN于点E、F.初一：(1)BM、DN、MN的数量关系；(2)证明AN平分Z MND；(3)若BC=4,求厶MNC周长2^/3初二：(1)若BE=4,DF=2,求EF的长；(2)证明CN二—計BE；(3)若AB=9,BE=3,求BM的长2点3^AF 初三：(1)连接MF,证明AF丄MF；(2)证明MN=三_EF；(3)若BE:DF=2:(3-1),求而的旋转原理】1、如图，等腰△ABC中，AB=AC.(1)如图1,Z BDC=Z BAC=60°,猜想DA、DB、DC数量关系并证明;(2)如图2,Z BDC=Z BAC=90。

,猜想DA、DB、DC数量关系并证明;(3)如图2,Z BDC=Z BAC,猜想DE、DB、DC数量关系并证明；2、如图，等腰△ABC中，AB=AC.(1)如图1,Z BAC=60°,Z BDC=120。

，猜想DA、DB、DC数量关系并证明;(2)如图2,Z BDC=Z BAC=90。

,猜想DA、DB、DC数量关系并证明；(3)如图2,Z BAC=120°,Z BDC=60°,猜想DA、DB、DC数量关系并证明;(4)如图4,Z BDC+Z BAC=180°，证明AD平分/BDC.【对称中心】1、如图，△ABC是等边三角形，点E、F为直线BC、AC上的动点，且BE=CF,连接AE、BF.(1)如图1,当点E、F分别在边BC、CA上时，求直线AE、BF的夹角；(2)如图2,当点E、F分别在边BC、CA的延长线上时，直线AE、BF的夹角大小是否改变？(3)如图3,当点E、F分别在边BC、CA上时，以AB为边作等边△ABD.①连接DG,直接写出Z DGA的度数以及GA、GB、GD的数量关系；②作DH丄AG于点H,猜想GA、GB、GH数量关系并证明；A E A AE BGG C D B BC C F F@2團3 Si2、(1)如图1,在正方形ABCD 中，E 、F 、G 分别为边AD 、BC 、CD 上的动点，连接BG 、EF ,若BG 丄EF, 求证BG =EF ；(2) 如图2,在菱形ABCD 中，Z B V 90。

专题31 对角互补模型-2023年中考数学总复习真题探究与变式训练(全国通用,含解析)(原卷版)

模块二常见模型专练专题31 对角互补模型例1（2021·安徽安庆·中考真题）如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN 与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）A．4B．3C．2D．1例2（2022·贵州遵义·统考中考真题）探究与实践“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．该小组继续利用上述结论进行探究．提出问题：如图1，在线段同侧有两点，，连接，，，，如果，那么，，，四点在同一个圆上．探究展示：如图2，作经过点，，的，在劣弧上取一点（不与，重合），连接，则（依据1）点，，，四点在同一个圆上（对角互补的四边形四个顶点共圆）点，在点，，所确定的上（依据2）点，，，四点在同一个圆上(1)反思归纳：上述探究过程中的“依据1”、“依据2”分别是指什么？依据1：__________；依据2：__________．(2)图3，在四边形中，，，则的度数为__________．(3)拓展探究：如图4，已知是等腰三角形，，点在上（不与的中点重合），连接．作点关于的对称点，连接并延长交的延长线于，连接，．①求证：，，，四点共圆；②若，的值是否会发生变化，若不变化，求出其值；若变化，请说明理由．例3（2020·湖南益阳·统考中考真题）定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形，根据以上定义，解决下列问题：（1）如图1，正方形中，是上的点，将绕点旋转，使与重合，此时点的对应点在的延长线上，则四边形为“直等补”四边形，为什么？（2）如图2，已知四边形是“直等补”四边形，，，，点到直线的距离为．①求的长．②若、分别是、边上的动点，求周长的最小值．对角互补模型特指在四边形中，存在一对对角互补，而且有一组邻边相等的几何模型。

初中数学专题一旋转中的几何模型(手拉手模型、对角互补模型)(解析版)

专题一旋转中的几何模型模型一　“手拉手”模型模型特征：两个等边三角形或等腰直角三角形或正方形共顶点．模型说明：如图1，△ABE，△ACF都是等边三角形，可证△AEC≌△ABF.如图2，△ABD，△ACE都是等腰直角三角形，可证△ADC≌△ABE.如图3，四边形ABEF，四边形ACHD都是正方形，可证△ABD≌△AFC.图1 图2 图3等腰图形有旋转，辩清共点旋转边，关注三边旋转角，全等思考边角边。

1【问题提出】(1)如图①，△ABC,△ADE均为等边三角形，点D,E分别在边AB，AC上．将△ADE绕点A沿顺时针方向旋转，连结BD,CE．在图②中证明△ADB≅△AEC．[学以致用](2)在(1)的条件下，当点D,E,C在同一条直线上时，∠EDB的大小为度．[拓展延伸](3)在(1)的条件下，连结CD．若BC=6,AD=4直接写出△DBC的面积S的取值范围．【思路点拨】(1)根据“手拉手”模型，证明△ADB≅△AEC即可；(2)分“当点E在线段CD上”和“当点E在线段CD的延长线上”两种情况，再根据“手拉手”模型中的结论即可求得∠EDB的大小；(3)分别求出△DBC的面积最大值和最小值即可得到结论【详解】(1)∵ABC,ADE均为等边三角形，∴AD=AE，AB=AC，∴∠DAE-∠BAE=∠BAC-∠BAE，即∠BAD=∠CAE在△ADB和△AEC中，AD=AE∠BAD=∠CAE AB=AC∴ABD ≅ACE (SAS )；(2)当D ,E ,C 在同一条直线上时，分两种情况：①当点E 在线段CD 上时，如图，∵△ADE 是等边三角形，∴∠ADE =∠AED =60°，∴∠AEC =180°-∠AED =120°，由(1)可知，△ADB ≅△AEC ，∴∠ADB =∠AEC =120°，∴∠EDB =∠ADB -∠ADE =120°-60°=60°②当点E 在线段CD 的延长线上时，如图，∵△ADE 是等边三角形，∴∠ADE =∠AED =60°∴∠ADC =180°-∠ADE =120°，由(1)可知，△ADB ≅△AEC∴∠ADB =∠AEC =60°，∴∠EDB =∠ADB +∠ADE =60°+60°=120°综上所述，∠EDB 的大小为60°或120°(3)过点A 作AF ⊥BC 于点F ，当点D 在线段AF 上时，点D 到BC 的距离最短，此时，点D 到BC 的距离为线段DF 的长，如图：∵ΔABC 是等边三角形，AF ⊥BC ，BC =6∴AB =BC =6，BF =12BC =3∴AF =AB 2-BF 2=62-32=33∴DF =33-4此时S .DBC =12BC ⋅DF =12×6×(33-4)=93-12；当D 在线段FA 的延长线上时，点D 到BC 的距离最大，此时点D 到BC 的距离为线段DF 的长，如图，∵ΔABC 是等边三角形，AF ⊥BC ，BC =6∴AB =BC =6，BF =12BC =3，∴AF =AB 2-BF 2=62-32=33∵AD =4∴DF =AF +AD =33+4此时，S .DBC =12BC ⋅DF =12×6×(33+4)=93+12；综上所述，△DBC 的面积S 取值是93-12≤5≤93+12【点评】利用“手拉手”模型，构造对应边“拉手线”组成的两个三角形全等是解题关键2已知正方形ABCD 和等腰直角三角形BEF ，BE =EF ，∠BEF =90°，按图1放置，使点F 在BC 上，取DF 的中点G ，连接EG ，CG ．(1)探索EG，CG的数量关系和位置关系并证明；(2)将图(1)中△BEF绕点B顺时针旋转45°，再连接DF，取DF中点G(见图2)，(1)中的结论是否仍然成立？证明你的结论；(3)将图(1)中△BEF绕点B顺时针转动任意角度(旋转角在0°到90°之间)，再连接DF，取DF中点G(见图3)，(1)中的结论是否仍然成立？证明你的结论．【思路点拨】(1)首先证明B、E、D三点共线，根据直角三角形斜边上的中线等于斜边的一半，即可证明EG=DG= GF=CG，得到∠EGF=2∠EDG，∠CGF=2∠CDG，从而证得∠EGC=90°；(2)首先证明△FEG≌△DHG，然后证明△ECH为等腰直角三角形．可以证得：EG=CG且EG⊥CG；(3)首先证明：△BEC≌△FEH，即可证得：△ECH为等腰直角三角形，从而得到：EG=CG且EG⊥CG．【解题过程】解：(1)EG=CG且EG⊥CG．证明如下：如图①，连接BD．∵正方形ABCD和等腰Rt△BEF，∴∠EBF=∠DBC=45°．∴B、E、D三点共线．∵∠DEF=90°，G为DF的中点，∠DCB=90°，∴EG=DG=GF=CG．∴∠EGF=2∠EDG，∠CGF=2∠CDG．∴∠EGF+∠CGF=2∠EDC=90°，即∠EGC=90°，∴EG⊥CG．(2)仍然成立，证明如下：如图②，延长EG交CD于点H．∵BE⊥EF，∴EF∥CD，∴∠1=∠2．又∵∠3=∠4，FG=DG，∴△FEG≌△DHG，∴EF=DH，EG=GH．∵△BEF为等腰直角三角形，∴BE=EF，∴BE=DH．∵CD=BC，∴CE=CH．∴△ECH为等腰直角三角形．又∵EG=GH，∴EG=CG且EG⊥CG(3)仍然成立．证明如下：如图③，延长CG至H，使GH=CG，连接HF交BC于M，连接EH、EC．∵GF=GD，∠HGF=∠CGD，HG=CG，∴△HFG≌△CDG，∴HF=CD，∠GHF=∠GCD，∴HF∥CD．∵正方形ABCD，∴HF=BC，HF⊥BC．∵△BEF是等腰直角三角形，∴BE=EF，∠EBC=∠HFE，∴△BEC≌△FEH，∴HE=EC，∠BEC=∠FEH，∴∠BEF=∠HEC=90°，∴△ECH为等腰直角三角形．又∵CG=GH，∴EG=CG且EG⊥CG．针对训练11已知ΔABC是等边三角形，AD⊥BC于点D，点E是直线AD上的动点，将BE绕点B顺时针方向旋转60°得到BF，连接EF，CF，AF．(1)问题发现：如图1，当点E在线段AD上时，且∠AFC=35°，则∠FAC的度数是；(2)结论证明：如图2，当点E 在线段AD 的延长线上时，请判断∠AFC 和∠FAC 的数量关系，并证明你的结论；(3)拓展延伸：若点E 在直线AD 上运动，若存在一个位置，使得ΔACF 是等腰直角三角形，请直接写出此时∠EBC 的度数．【答案】(1)55°；(2)∠AFC +∠FAC =90°，见解析；(3)15°或75°【解析】(1)55°，理由：∵ΔABC 是等边三角形，∴AB =AC =BC ，∠ABC =∠BAC =∠ACB =60°，∵AB =AC ，AD ⊥BC ，∴∠BAD =30°，∵将BE 绕点B 顺时针方向旋转60°得到BF ，∴BE =BF ，∠EBF =60°，∴∠EBF =∠ABC ，在△ADC 和△BDA 中，AB =BC∠ABE =∠FBC BE =BF，∴ΔABE ≌ΔCBF SAS ，∴∠BAE =∠BCF =30°，∴∠ACF =90°，∴∠AFC +∠FAC =90°；∵∠AFC =35°，∴∠FAC =55°；(2)结论：∠AFC +∠FAC =90°，理由如下：∵ΔABC 是等边三角形，∴AB =AC =BC ，∠ABC =∠BAC =∠ACB =60°，∵AB =AC ，AD ⊥BC ，∴∠BAD =30°，∵将BE 绕点B 顺时针方向旋转60°得到BF ，∴BE =BF ，∠EBF =60°，∴∠EBF =∠ABC ，在△ADC 和△BDA 中，AB =BC∠ABE =∠FBC BE =BF，∴ΔABE ≌ΔCBF SAS ，∴∠BAE =∠BCF =30°，∴∠ACF =90°，∴∠AFC +∠FAC =90°；(3)∠EBC =15°或75°分两种情况：①点E 在点A 的下方时，如图：∵ΔACF 是等腰直角三角形，∴AC =CF ，由(2)得ΔABE ≌ΔCBF ，∴CF =AE ，∴AC =AE =AB ，∴∠ABE =180°-30°2=75°，∴∠EBC =∠ABE -∠ABC =75°-60°=15°；②点E 在和点A 的上方时，如图：同理可得∠EBC =∠ABE +∠ABC =75°．2已知四边形ABCD 是正方形，将线段CD 绕点C 逆时针旋转α(0°<α<90°)，得到线段CE ，联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F ．(1)如图，当BE =CE 时，求旋转角α的度数；(2)当旋转角α的大小发生变化时，∠BEF 的度数是否发生变化?如果变化，请用含α的代数式表示；如果不变，请求出∠BEF 的度数；(3)联结AF ，求证：DE =2AF ．【答案】(1)30°；(2)不变；45°；(3)见解析【解析】(1)证明：在正方形ABCD 中, BC =CD .由旋转知，CE=CD,又∵BE =CE ,∴BE =CE =BC ,∴△BEC 是等边三角形，∴∠BCE=60°.又∵∠BCD=90°,∴α=∠DCE=30°.(2)∠BEF的度数不发生变化.在△CED中，CE=CD,∴∠CED=∠CDE=180°-α2=90°-α2，在△CEB中,CE=CB,∠BCE=90°-α,∴∠CEB=∠CBE=180°-∠BCE2=45°+α2,∴∠BEF=180°-∠CED-∠CEB=45°.(3)过点A作AG∥DF与BF的延长线交于点G，过点A作AH∥GF与DF交于点H，过点C作CI⊥DF于点I易知四边形AGFH是平行四边形，又∵BF⊥DF，∴平行四边形AGFH是矩形.∵∠BAD=∠BGF=90°，∠BPF=∠APD，∴∠ABG=∠ADH.又∵∠AGB=∠AHD=90°，AB=AD，∴△ABG≌△ADH.∴AG=AH，∴矩形AGFH是正方形.∴∠AFH=∠FAH=45°，∴AH=AF∵∠DAH+∠ADH=∠CDI+∠ADH=90°∴∠DAH=∠CDI又∵∠AHD=∠DIC=90°，AD=DC，∴△AHD≌△DIC∴AH=DI，∵DE=2DI，∴DE=2AH=2AF模型二　对角互补模型对角互补模型的特征：外观呈现四边形，且对角和为180°。

中考数学能力提升(几何之几何模型)

中考数学能力提升（几何之几何模型）（一）初中几何常见模型解析模型一：手拉手模型 - 全等（ 1 ）等边三角形条件：均为等边三角形结论：① ；② ；③ 平分。

（ 2 ）等腰条件：均为等腰直角三角形结论：① ；② ；③ 平分。

（ 3 ）任意等腰三角形条件：均为等腰三角形结论：① ；② ；③ 平分。

模型二：手拉手模型 - 相似（ 1 ）一般情况条件：，将旋转至右图位置结论：右图中① ；②延长 AC 交 BD 于点 E ，必有（ 2 ）特殊情况条件：，，将旋转至右图位置结论：右图中① ；②延长 AC 交 BD 于点 E ，必有；③ ；④ ；⑤连接 AD 、 BC ，必有；⑥ （对角线互相垂直的四边形）模型三：对角互补模型若将条件“ OC 平分”与结论“ CD=CE ”互换，则有：条件：① ；② CD=CE ；结论：① OC 平分；② ；③（ 1 ）全等型 -90°条件：① ；② OC 平分结论：① CD=CE; ② ；③证明提示：①作垂直，如图，证明；②过点 C 作, 如上图（右），证明；当的一边交 AO 的延长线于点 D 时：以上三个结论：① CD=CE （不变）；② ；③ 此结论证明方法与前一种情况一致，可自行尝试。

（ 2 ）全等型 -120°条件：① ；② 平分；结论：① ；② ；③证明提示：①可参考“ 全等型 -90° ”证法一；②如图：在 OB 上取一点 F ，使 OF=OC ，证明为等边三角形。

当的一边交 AO 的延长线于点 D 时（如上图右）：原结论变成：① ；② ；③ ；可参考上述第②种方法进行证明。

（ 3 ）全等型 - 任意角条件：① ；② ；结论：① 平分；② ；③ .当的一边交 AO 的延长线于点 D 时（如右上图）：原结论变成：① ；② ；③ ；可参考上述第②种方法进行证明。

✧请思考初始条件的变化对模型的影响。

如图所示，若将条件“ 平分”去掉，条件①不变，平分，结论变化如下：结论：① ；② ；③ .对角互补模型总结：①常见初始条件：四边形对角互补；注意两点：四点共圆及直角三角形斜边中线；②初始条件“角平分线”与“两边相等”的区别；③两种常见的辅助线作法；④注意下图中平分时，相等是如何推导的？模型四：角含半角模型 90 °角含半角要旋转（ 1 ）角含半角模型 90 ° -1条件：①正方形；② ；结论：① ；② 的周长为正方形周长的一半；也可以这样：条件：①正方形；②结论：（ 2 ）角含半角模型 90 ° -2条件：①正方形；② ；结论：辅助线如下图所示：（ 3 ）角含半角模型 90 ° -3条件：① ；② ；结论：若旋转到外部时，结论仍然成立。

旋转中的三种常见模型(原卷版)—2024-2025学年九年级数学上册(人教版)

旋转中的三种常见模型类型一：“手拉手”模型类型二：“半角”模型类型三：“鸡爪”模型类型一：“手拉手”模型1．如图，将△ABC绕点A逆时针旋转得到△ADE，点B的对应点D恰好落在边BC上，点C的对应点为点E，连接EC．下列结论一定正确的是（）A．AB＝BD B．∠B＝∠ECA C．AC＝DE D．EC⊥BC2．如图，在△ABC中，∠BAC＝60°，现将△ABC绕着顶点A顺时针旋转至△ADE处，其中点B，C的对应点分别为D，E，点D在△ABC内部，过E作EF⊥AC于点F，若∠CAD＝15°，，则线段AC的长为（）A．B．C．2D．43．如图，在△ABC中，AB＝6，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分的面积为（）A．6B．C．D．94．如图，在等边△ABC中，AB＝7，D为边BC上一点，BD＝2，连接AD，将AD绕点D顺时针旋转60°得到ED，ED交AC于点F，则的值为（）A．3B．C．D．5．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，BC＝2，将△ABC绕顶点C逆时针旋转得到△A′B′C′，若点M、P分别是BC、A′B′的中点，连接PM．则线段PM的最大值是（）A．4B．3C．2D．16．如图，△ABC是边长为8的等边三角形，D是BC的中点，E是直线AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．则在点E的运动过程中，DF的最小值是（）A．2B．2.5C．3D．3.57．在△ABC中，∠ABC＝60°，将△ABC在平面内绕点B顺时针旋转α（0°＜α＜90°）得到△DBE，其中点A的对应点为点D，连接CE．（1）若α＝30°，如图①，求∠BEC的度数；（2）当点D在边BC上时，如图②，若DC＝2，，求AB的长．8．如图，△ABC中，AB＝BC，点O是△ABC内一点，将△ABO旋转后能与△BCD重合（1）旋转中心是点；（2）若∠ACB＝70°，旋转角是度；（3）若∠ACB＝60°，请判断△BOD的形状并说明理由．9．如图，在△ABC中，∠BAC＝90°，，点D为△ABC内一点，∠BAD＝15°，，连接BD，将△ABD绕点A按逆时针方向旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，（1）求∠AFD的度数．（2）求△ADE中DE边上的高．（3）求CF的长．10．△ABC和△ADE都是等边三角形．（1）将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有PA+PB＝PC（或PA+PC＝PB）成立（不需证明）；（2）将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；（3）将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明．类型二：“半角”模型11．如图，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，已知AD＝6（正方形的四条边都＝（）相等，四个内角都是直角），DF＝2，则S△AEFA．6B．12C．15D．3012．如图，在菱形ABCD中，，∠BAD＝60°，对角线AC，BD相交于点O，点E是对角线AC 上的一个动点，连结BE，将BE绕点B按逆时针方向旋转60°，得到BF，连接OF，则OF的最小值是（）A．B．C．D．13．如图，正方形ABCD边长为1，∠ECF＝45°，CF＝CE，则下列结论：①∠1＝∠2＝22.5°；②AC 垂直平分EF；③△AEF的周长是2；④DE+BF＞EF；⑤点A到EF的距离是．其中正确的结论有（）A．2个B．3个C．4个D．5个14．如图△ABC中，AB＝AC，∠BAC＝120°，∠DAE＝60°，BD＝5，CE＝8，求DE的长．15．如图，在△ABC中，CA＝CB，∠ACB＝120°，E为AB上一点，∠DCE＝60°，∠DAE＝120°，求证：DE﹣AD＝BE．16．如图，点E与F分别在正方形ABCD的边BC与CD上，∠EAF＝45°，以点A为旋转中心，将△ADF 按顺时针方向旋转90°得到△ABF'．已知DF＝5cm，BE＝3cm，求EF的长．17．如图，点E，F分别在正方形ABCD的边BC，CD上，∠EAF＝45°，连接EF，试猜想EF，BE，DF 之间的数量关系，并证明你的猜想．18．如图，四边形ABCD是正方形，E，F分别在直线AB，AD上，且∠ECF＝45°，连接EF．（1）当E，F分别在边AB，AD上时，如图1．请探究线段EF，BE，DF之间的数量关系，并写出证明过程；（2）当E，F分别在BA，AD的延长线上时，如图2．试探究线段EF，BE，DF之间的数量关系，并证明．19．如图，在四边形ABCD中，点M、N分别在边CD、BC上．连接AM、AN．（1）如图1，四边形ABCD为正方形时，连结MN，且∠MAN＝45°，①已知CM＝6，CN＝8，求MN的长；②已知DM：CM＝3：2，求AB：BN的值；（2）如图2，四边形ABCD为矩形，∠AMD＝2∠BAN，点N为BC的中点，AN＝6，AM＝8，求AD的长．类型三：“鸡爪”模型20．如图，等边△ABC内部有一点P，且PA＝8，PB＝15，PC＝17，则∠APB的度数为（）A．150°B．135°C．120°D．165°21．如图，P为等边△ABC内的一点，且P到三个顶点A，B，C的距离分别为6，8，10，则△ABC的面积为（）A．B．C．D．22．如图，O是等边△ABC内一点，OA＝3，OB＝4，OC＝5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB＝150°；④；⑤．其中正确的结论是（）A．①②③⑤B．①②③④C．①②③④⑤D．①②③23．如图，△ABC是等边三角形，点P为三角形内一点，连接PA、PB、PC，且PA＝2，PB＝1，，则阴影部分的面积为．24．如图，P是等边△ABC内一点，且PA＝6，PC＝8，PB＝10，D是△ABC外一点，且△ADC≌△APB，求∠APC的度数．25．如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．（1）求∠ODC的度数；（2）若OB＝4，OC＝5，求AO的长．26．（1）探究发现：下面是一道例题及解答过程，请补充完整：如图①在等边△ABC内部，有一点P，若∠APB＝150°，求证：AP2+BP2＝CP2．证明：将△APC绕A点逆时针旋转60°，得到△AP′B，连接PP′，则△APP′为等边三角形，∴∠APP′＝60°，PA＝PP′，PC＝．∵∠APB＝150°，∴∠BPP'＝90°∴P′P2+BP2＝，即PA2+PB2＝PC2．（2）类比延伸：如图②在等腰ABC中，∠BAC＝90°，内部有一点P，若∠APB＝135°，试判断线段PA、PB、PC之间的数量关系，并证明．27．（1）如图1，P是等边三角形ABC内一点，PA＝6，PB＝8，PC＝10．若P′是△ABC外的一点，且△P′AB≌△PAC．求PP′的长度及∠APB的度数．（2）如图2，Q是等边三角形ABC内一点，QA＝5，QB＝12，∠AQB＝150°，求CQ的长．28．在等边三角形ABC的内部有一点D，连接BD，CD，以点B为中心，把BD逆时针旋转60°得到HD′，连接AD′，DD′．以点C为中心，把CD顺时针旋转60°得到CD″，连接AD″，DD″．（1）判断∠D′BA和∠DBC的大小关系，并说明理由；（2）求证：D′A＝DC；（3）求证：四边形AD'DD″是平行四边形．。

中考数学专题训练旋转模型几何变换的三种模型手拉手、半角、对角互补

几何变换的三种模型手拉手、半角、对角互补【练1】（2013北京中考）在ABC △中，AB AC =，BAC α∠=（060α︒<<︒），将线段BC 绕点B 逆【练2】，请补全（2CDB ∠的（3知识关联图真题演练考点1：手拉手模型：全等和相似包含：等腰三角形、等腰直角三角形（正方形）、等边三角形伴随旋转出全等，处于各种位置的旋转模型，及残缺的旋转模型都要能很快看出来（1）等腰三角形旋转模型图（共顶点旋转等腰出伴随全等）（2）等边三角形旋转模型图（共顶点旋转等边出伴随全等）例题精讲>．【例1】（14年海淀期末）已知四边形ABCD和四边形CEFG都是正方形，且AB CE（1）如图1，连接BG、DG．求证：BG DE=；（2）如图2，如果正方形ABCD，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG BD=．∥，BG BD①求BDE∠的度数；②请直接写出正方形CEFG的边长的值．【例2】（2014年西城一模）四边形ABCD 是正方形，BEF ∆是等腰直角三角形，90BEF ∠=︒，BE EF =，连接DF ，G 为DF 的中点，连接EG ，CG ，EC 。

（1）如图24-1，若点E 在CB 边的延长线上，直接写出EG 与GC 的位置关系及EC GC 的值；（2）将图24-1中的BEF ∆绕点B 顺时针旋转至图24-2所示位置，请问（1）中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；【例3】（2015年海淀九上期末）如图1，在ABC △ 中，4BC =，以线段AB 为边作ABD △，使得AD BD =，连接DC ，再以DC 为边作CDE △，使得DC DE =，CDE ADB α∠=∠=．（1）如图2 ，当45ABC ∠=︒且90α=︒时，用等式表示线段AD DE ，之间的数量关系；【例4】（13年房山一模）（1）如图1，ABC△都是等边三角形，且B、C、D三点共线，联结AD、BE相△和CDE交于点P，求证：BE AD=．（2）如图2，在BCD△中，120△外部作等边BCD∠<，分别以BC、CD和BD为边在BCD△和等边BDFABC△、等边CDE△，联结AD、BE和CF交于点P，下列结论中正确的是_______（只填序号即可）①AD BE CF∠=∠；③60==；②B E C A D C∠=∠=∠=；DPE EPC CPA （3）如图2，在（2）的条件下，求证：PB PC PD BE++=．考点2：角含半角模型：全等秘籍：角含半角要旋转：构造两次全等【例1】（2012年西城期末）已知：如图，正方形ABCD的边长为a，BM，DN分别平分正方形的两个外角，且满足45MAN∠=︒，连结MC，NC，MN．猜想线段BM，DN和MN之间的等量关系并证明你的结论．【例2】（2014年平谷一模）（1）如图1，点E F 、分别是正方形ABCD 的边BC CD 、上的点，45EAF ∠=︒，连接EF ，则EF BE FD 、、之间的数量关系是：EF BE FD =+．连结BD ，交AE AF 、于点M N 、，且 MN BM DN 、、满足222DN BM MN +=，请证明这个等量关系；（2）在ABC △中， AB AC =，点D E 、分别为BC 边上的两点．①如图2，当60BAC ∠=︒，30DAE ∠=︒时，BD DE EC 、、应满足的等量关系是__________________；都是【例2】已知：点P 是MON ∠的平分线上的一动点，射线PA 交射线OM 于点A ，将射线PA 绕点P 逆时针旋转交射线ON 于点B ，且使180APB MON ∠+∠=．（1）利用图1，求证：PA PB =；（2）如图1，若点C 是AB 与OP 的交点，当3POB PCB S S ∆∆=时，求PB 与PC 的比值；图1 图2ABC（【练1】（2015年昌平九上期末）如图，已知ABC 和ADE 都是等腰直角三角形， 90BAC DAE ∠=∠=︒，AB AC =，AD AE =．连接BD 交AE 于M ,连接CE 交AB 于N ，BD 与CE 交点为F ，连接AF ．（1）如图1，求证：BD CE ⊥；（2）如图1，求证：AF 是CFD ∠的平分线；全能突破【练2】（2014西城九上期末）已知：ABC △，DEF △都是等边三角形，M 是BC 与EF 的中点，连接AD ，BE .（1）如图1，当EF 与BC 在同一条直线上时，直接写出AD 与BE 的数量关系和位置关系；（2）ABC △固定不动，将图1中的DEF 绕点M 顺时针旋转α（o 0≤α≤o 90）角，如图2所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由；（3）△ABC 固定不动，将图1中的DEF 绕点M 旋转α（o 0≤α≤o 90）角，作DH BC⊥【练3】（2014年朝阳一模24题）在ABC △中，AC BC =，在AED △中，AD ED =，点D 、E 分别在CA 、AB 上，（1）图①，若90ACB ADE ∠=∠=︒，则CD 与BE 的数量关系是______________；（2）若120ACB ADE ∠=∠=︒，将AED △绕点A 旋转至如图②所示的位置，则CD 与BE 的数量关系是______________；（3）若2(090)ACB ADE αα∠=∠=<<︒，将AED △绕点A 旋转至如图③所示的位置，探究线段CD 与BE 的数量关系，并加以证明（用含α的式子表示）【练4】， ACF ，连接45DAE ︒＝，可证FAE DAE ≌，得．解FCE ，可求得EF (即DE 的长．的度数是_________________Rt ABC ____参考小辉思考问题的方法，解决问题：【练5】 A、点（1）在BAC ∠的旋转过程中，AEQ ∠的大小是否改变，若不变写出它的度数，若改变，写出它的变化范围（直接在答题卡上写出结果，不必证明）；（2）探究APQ ∆与AEF ∆的面积的数量关系，写出结论并加以证明．E C【练6】（2015年延庆九上期末）已知：ABC △是O 的内接三角形，AB AC =，在BAC ∠所对弧AC上，任取一点D ，连接AD BD CD ，，，（1）如图1，BAC α∠=，直接写出ADB ∠的大小（用含α的式子表示）；（2）如图2，如果∠60BAC =︒，求证：BD CD AD +=；（3）如图3，如果∠120BAC =︒，那么BD CD +与AD 之间的数量关系是什么？写出猜测并加以证明；（4）如果BAC α∠=，直接写出BD CD +与AD 之间的数量关系.【练7】（1)如图，在四边形ABCD 中，90AB AD B D =∠=∠=︒，，E F 、分别是边BC CD 、上的点，且12EAF =BAD ∠∠．求证：EF BE FD =+;(2) 如图在四边形ABCD 中，180AB AD B+D =∠∠=︒，，E F 、分别是边BC CD 、上的点，且12EAF BAD ∠=∠， (1)中的结论是否仍然成立？不用证明． (3) 如图，在四边形ABCD 中，AB AD =，180B ADC ∠+∠=︒，E F ，分别是边BC CD ，延长线上的点，且1EAF BAD ∠=∠， (1)中的结论是否仍然成立？若成立，请证明；若不成【练ABC 中，PA PB PC 、、APC 绕点，得到EDC ，连接的长即为所求．）请你写出图2中，________；【练9】（2014年西城二模）在ABC ，BAC ∠为锐角，AB AC >， AD 平分BAC ∠交BC 于点D ．（1）如图1，若ABC 是等腰直角三角形，直接写出线段AC ，CD ，AB 之间的数量关系；（2）BC 的垂直平分线交AD 延长线于点E ，交BC 于点F ．①如图2，若60ABE ∠=︒，判断AC ，CE ，AB 之间有怎样的数量关系并加以证明；【练10】 (2014年1月西城八年级期末试题—附加题) 已知：如图，MAN ∠为锐角，AD 平分MAN ∠，点B ，点C 分别在射线AM 和AN 上， AB AC =.（1）若点E 在线段CA 上，线段EC 的垂直平分线交直线AD 于点F ，直线BE 交直线AD 于点G ，求证：EBF CAG ∠=∠；（2）若（1）中的点E 运动到线段CA 的延长线上，（1）中的其它条件不变，猜想EBF ∠与CAG∠的数量关系并证明你的结论.【练11】（2014海淀一模）在ABC △中，AB AC =，将线段AC 绕着点C 逆时针旋转得到线段CD ，旋转角为α，且0180α︒<<︒，连接AD ，BD ．（1）如图1，当100BAC ∠=︒，60α=︒时，CBD ∠的大小为__________；（2）如图2，当100BAC ∠=︒，20α=︒时，求M 的大小；（3）已知BAC ∠的大小为m （60120m ︒<<︒），若M 的大小与（2）中的结果相同，请直接写出α的大小．1234。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

几何变换的三种模型手拉手、半角、对角互补⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎧⎪⎨⎪⎩⎪⎪⎩等腰三角形手拉手模型等腰直角三角形（包含正方形）等边三角形（包含费马点）特殊角旋转变换对角互补模型一般角特殊角角含半角模型一般角等线段变换（与圆相关）【练1】（2013北京中考）在ABC△中，AB AC=，BACα∠=（060α︒<<︒），将线段BC绕点B逆时针旋转60°得到线段BD．（1）如图1，直接写出ABD∠的大小（用含α的式子表示）；（2）如图2，15060BCE ABE∠=︒∠=︒，，判断ABE△的形状并加以证明；（3）在（2）的条件下，连结DE，若45DEC∠=︒，求α的值．知识关联图真题演练【练2】（2012年北京中考）在ABC △中，BA BC BAC α=∠=，，M 是AC 的中点，P 是线段上的动点，将线段PA 绕点P 顺时针旋转2α得到线段PQ ．（1）若α=60︒且点P 与点M 重合（如图1），线段CQ 的延长线交射线BM 于点D ，请补全图形，并写出CDB ∠的度数；（2）在图2中，点P 不与点B M ，重合，线段CQ 的延长线与射线BM 交于点D ，猜想CDB ∠的大小（用含α的代数式表示），并加以证明；（3）对于适当大小的α，当点P 在线段BM 上运动到某一位置（不与点B ，M 重合）时，能使得线段CQ 的延长线与射线BM 交于点D ，且PQ QD =，请直接写出α的范围．例题精讲考点1：手拉手模型：全等和相似包含：等腰三角形、等腰直角三角形（正方形）、等边三角形伴随旋转出全等，处于各种位置的旋转模型，及残缺的旋转模型都要能很快看出来（1）等腰三角形旋转模型图（共顶点旋转等腰出伴随全等）（2）等边三角形旋转模型图（共顶点旋转等边出伴随全等）（3）等腰直角旋转模型图（共顶点旋转等腰直角出伴随全等）（4）不等边旋转模型图（共顶点旋转不等腰出伴随相似）【例1】（14年海淀期末）已知四边形ABCD 和四边形CEFG 都是正方形，且AB CE >．（1）如图1，连接、．求证：BG DE =；（2）如图2，如果正方形ABCD 的边长为，将正方形CEFG 绕着点旋转到某一位置时恰好使得CG BD ∥，BG BD =． ①求BDE ∠的度数；②请直接写出正方形CEFG 的边长的值．【题型总结】手拉手模型是中考中最常见的模型，突破口常见的有哪些信息常见的考试方法有哪些【例2】（2014年西城一模）四边形ABCD是正方形，BEF∆是等腰直角三角形，90BEF∠=︒，BE EF=，连接DF，G为DF的中点，连接EG，CG，EC。

（1）如图24-1，若点E在CB边的延长线上，直接写出EG与GC的位置关系及EC GC的值；（2）将图24-1中的BEF∆绕点B顺时针旋转至图24-2所示位置，请问（1）中所得的结论是否仍然成立若成立，请写出证明过程；若不成立，请说明理由；图图【例3】（2015年海淀九上期末）如图1，在ABC △ 中，4BC =，以线段AB 为边作ABD △，使得AD BD =，连接DC ，再以DC 为边作CDE △，使得DC DE =，CDE ADB α∠=∠=．（1）如图2 ，当45ABC ∠=︒且90α=︒时，用等式表示线段AD DE ，之间的数量关系；B（2）将线段CB 沿着射线CE 的方向平移，得到线段EF ，连接BF AF ，．若 90α=︒，依题意补全图3，求线段AF 的长；请直接写出线段AF 的长（用含α的式子表示）．BBB图2 图3 备用图图1【例4】（13年房山一模）（1）如图1，ABC △和CDE △都是等边三角形，且B 、C 、D 三点共线，联结AD 、BE 相交于点P ，求证：BE AD =．（2）如图2，在BCD △中，120BCD ∠<o ，分别以BC 、CD 和BD 为边在BCD △外部作等边ABC △、等边CDE △和等边BDF △，联结AD 、BE 和CF 交于点P ，下列结论中正确的是_______（只填序号即可）①AD BE CF ==；②BEC ADC ∠=∠；③60DPE EPC CPA ∠=∠=∠=o ；（3）如图2，在（2）的条件下，求证：PB PC PD BE ++=．FAB 图1图2A考点2：角含半角模型：全等秘籍：角含半角要旋转：构造两次全等FED CBA G FED CBA AB CDEFFED CBA GABCDEFGABCD E ABCD E F【例1】（2012年西城期末）已知：如图，正方形ABCD 的边长为a ，BM ，DN 分别平分正方形的两个外角，且满足45MAN ∠=︒，连结MC ，NC ，MN ．猜想线段BM ，DN 和MN 之间的等量关系并证明你的结论．【例2】（2014年平谷一模）（1）如图1，点E F 、分别是正方形ABCD 的边BC CD 、上的点，45EAF ∠=︒，连接，则EF BE FD 、、之间的数量关系是：EF BE FD =+．连结，交AE AF 、于点M N 、，且 MN BM DN 、、满足222DN BM MN +=，请证明这个等量关系；（2）在ABC △中， AB AC =，点D E 、分别为边上的两点．①如图2，当60BAC ∠=︒，30DAE ∠=︒时，BD DE EC 、、应满足的等量关系是__________________；②如图3，当BAC ∠=，90)<︒，DAE ∠=α21时，BD DE EC 、、应满足的等量关系是____________________．【参考：1cos sin 22=+αα】A B CD EF 图1B C DE 图2ADE 图3AMN考点3：对角互补模型常和角平分线性质一起考，一般有两种解题方法（全等型—90°）OABCE DNOM A BCE D（全等型—120°）（全等型—任意角）OEDCBA OFEDCBA OEDCBA【例1】四边形ABCD 被对角线分为等腰直角三角形和直角三角形，其中和都是直角，另一条对角线的长度为2，求四边形ABCD 的面积．DCB A【例2】已知：点是MON ∠的平分线上的一动点，射线交射线于点，将射线绕点逆时针旋转交射线于点，且使180APB MON ∠+∠=o ．（1）利用图1，求证：PA PB =；（2）如图1，若点是与的交点，当3POB PCB S S ∆∆=时，求PB 与PC 的比值；CAOPBMNTTNM BP OAC图1 图2【例3】 (初二期末)已知：如图，在ABC △中，AB AC =，BAC ∠=α，且60120α︒<<︒．P为ABC △内部一点，且PC AC =，120PCA α∠=︒-．（1）用含α的代数式表示APC ∠，得APC ∠ =_______________________；（2）求证：BAP PCB ∠=∠；（3）求PBC ∠的度数．BCPA（【练1】（2015年昌平九上期末）如图，已知ABC V 和ADE V 都是等腰直角三角形，90BAC DAE ∠=∠=︒，AB AC =，AD AE =．连接BD 交AE 于M ,连接CE 交AB于N ，BD 与CE 交点为F ，连接AF ．（1）如图1，求证：BD CE ⊥；（2）如图1，求证：AF 是CFD ∠的平分线；（3）如图2，当2AC =，15BCE ∠=︒时，求CF 的长.FEDCBA图1NM图2ABCDEF MN全能突破【练2】（2014西城九上期末）已知：ABC △，DEF △都是等边三角形，M 是BC 与EF的中点，连接AD ，BE .（1）如图1，当EF 与BC 在同一条直线上时，直接写出AD 与BE 的数量关系和位置关系；（2）ABC △固定不动，将图1中的DEF V 绕点M 顺时针旋转α（o 0≤α≤o 90）角，如图2所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由；（3）△ABC 固定不动，将图1中的DEF V 绕点M 旋转α（≤α≤）角，作DH BC⊥于点H ．设 BH x ＝，线段AB ，BE ，ED ，DA 所围成的图形面积为S ．当6AB ＝，2DE ＝时，求S 关于x 的函数关系式，并写出相应的x 的取值范围．图2备用图图1【练3】（2014年朝阳一模24题）在ABC △中，AC BC =，在AED △中，AD ED =，点D 、E 分别在CA 、AB 上，（1）图①，若90ACB ADE ∠=∠=︒，则CD 与BE 的数量关系是______________；（2）若120ACB ADE ∠=∠=︒，将AED △绕点A 旋转至如图②所示的位置，则CD 与BE 的数量关系是______________；（3）若2(090)ACB ADE αα∠=∠=<<︒，将AED △绕点A 旋转至如图③所示的位置，探究线段CD 与BE 的数量关系，并加以证明（用含α的式子表示）【练4】（2015年燕山九上期末）小辉遇到这样一个问题：如图1，在Rt ABC △中，90BAC ∠︒＝，AB AC ＝，点，E 在边BC 上，45DAE ∠︒＝．若3BD ＝，1CE ＝，求DE 的长．D小辉发现，将绕点A 按逆时针方向旋转90o ，得到ACF V ，连接EF （如图2），由图形旋转的性质和等腰直角三角形的性质以及45DAE ∠︒＝，可证FAE DAE V V ≌，得FE DE ＝．解FCE V ，可求得EF (即DE )的长．请回答：在图2中，FCE ∠的度数是__________，DE 的长为_______Rt ABC V ____．参考小辉思考问题的方法，解决问题：如图3，在四边形ABCD 中，AB AD ＝，180B D ∠∠︒＋＝．E F ，分别是边BC CD ，上的点，且12EAF BAD ∠∠＝．猜想线段BE EF FD ，，之间的数量关系并说明理由．图1ABC DE图2FABCDE图3EFDABC【练5】（11年石景山一模）已知：如图，正方形ABCD 中，,为对角线，将BAC ∠绕顶点逆时针旋转α(045α<<o o )，旋转后角的两边分别交于点、点，交,于点、点，联结、．（1）在BAC ∠的旋转过程中，AEQ ∠的大小是否改变，若不变写出它的度数，若改变，写出它的变化范围（直接在答题卡上写出结果，不必证明）；（2）探究APQ ∆与AEF ∆的面积的数量关系，写出结论并加以证明．QFC DBAP E【练6】（2015年延庆九上期末）已知：ABC △是O e 的内接三角形，AB AC =，在BAC∠所对弧AC 上，任取一点D ，连接AD BD CD ，，，（1）如图1，BAC α∠=，直接写出ADB ∠的大小（用含的式子表示）；（2）如图2，如果60BAC =︒，求证：BD CD AD +=；（3）如图3，如果120BAC =︒，那么BD CD +与AD 之间的数量关系是什么写出猜测并加以证明；（4）如果BAC α∠=，直接写出BD CD +与AD 之间的数量关系.AA图1图2图3【练7】（1)如图，在四边形ABCD 中，90AB AD B D =∠=∠=︒，，分别是边BC CD 、上的点，且12EAF =BAD ∠∠．求证：EF BE FD =+;(2) 如图在四边形ABCD 中，180AB AD B+D =∠∠=︒，，分别是边BC CD 、上的点，且12EAF BAD ∠=∠， (1)中的结论是否仍然成立不用证明．(3) 如图，在四边形ABCD 中，AB AD =，180B ADC ∠+∠=︒，分别是边BC CD ，延长线上的点，且12EAF BAD ∠=∠， (1)中的结论是否仍然成立若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．EFDCBAEFD CBAEFDCBA【练8】小华遇到这样一个问题，如图1, ABC V 中，ACB ∠=30o ，65BC AC ==，，在ABC V内部有一点P ，连接PA PB PC 、、，求PA PB PC ++的最小值．小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，并让折线的两个端点为定点，这样依据“两点之间，线段最短”，就可以求出这三条线段和的最小值了．他先后尝试了翻折、旋转、平移的方法，发现通过旋转可以解决这个问题．他的做法是，如图2，将APC V 绕点C 顺时针旋转60o ，得到EDC V ，连接PD BE 、，则BE 的长即为所求．（1）请你写出图2中，PA PB PC ++的最小值为________；（2）参考小华的思考问题的方法，解决下列问题：①如图3，菱形ABCD 中，ABC ∠=60o ，在菱形ABCD 内部有一点P ，请在图3中画出并指明长度等于PA PB PC ++最小值的线段（保留画图痕迹，画出一条即可）；②若①中菱形ABCD 的边长为4，请直接写出当PA PB PC ++值最小时PB 的长．B图3B图2B图1【练9】（2014年西城二模）在ABC V ，BAC ∠为锐角，AB AC >，AD 平分BAC ∠交BC 于点D ．（1）如图1，若ABC V 是等腰直角三角形，直接写出线段AC ，CD ，AB 之间的数量关系；（2）BC 的垂直平分线交AD 延长线于点E ，交BC 于点F ．①如图2，若60ABE ∠=︒，判断AC ，CE ，AB 之间有怎样的数量关系并加以证明；②如图3，若3AC AB AE +=，求BAC ∠的度数．【练10】(2014年1月西城八年级期末试题—附加题) 已知：如图，MAN ∠为锐角，AD 平分MAN ∠，点B ，点C 分别在射线AM 和AN 上， AB AC =.（1）若点E 在线段CA 上，线段EC 的垂直平分线交直线AD 于点F ，直线BE 交直线AD 于点G ，求证：EBF CAG ∠=∠；（2）若（1）中的点E 运动到线段CA 的延长线上，（1）中的其它条件不变，猜想EBF∠与CAG ∠的数量关系并证明你的结论.【练11】（2014海淀一模）在ABC △中，AB AC =，将线段AC 绕着点C 逆时针旋转得到线段CD ，旋转角为α，且0180α︒<<︒，连接AD ，BD ．（1）如图1，当100BAC ∠=︒，60α=︒时，CBD ∠的大小为__________；（2）如图2，当100BAC ∠=︒，20α=︒时，求M 的大小；（3）已知BAC ∠的大小为m （60120m ︒<<︒），若M 的大小与（2）中的结果相同，请直接写出α的大小．1、旋转的基本模型特征2、费马点问题3、角平分线和垂直平分线辅助线，中点辅助线4、线段旋转的特点小结与复习图2DCBA图1AB。

中考数学专题训练-旋转模型几何变换三种模型手拉手-半角-对角互补

中考数学专题训练旋转模型几何变换的三种模型手拉手半角对角互补

旋转模型(手拉手模型、脚拉脚模型、半角模型)典型例题含答案

专题3.1 旋转重难点模型(5大类型)(解析版)

中考数学专题讲练 旋转(解析版)

中考数学专题训练-旋转模型几何变换三种模型手拉手-半角-对角互补

初三上学期旋转专题之旋转(全等)模型教案(有答案)

初中数学九大几何模型

旋转中的三种常见模型(学生版)-初中数学

旋转中的三种全等模型(手拉手、半角、对角互补模型)—2023-2024学年九年级数学上册(解析版)

2020年中考高频考点——旋转在几何中的常见模型分析(2)

模型构建专题：旋转中的常见模型(解析版)

专项17旋转中的几何模型归类(3大类型)(原卷版)

中考数学九大几何模型标准版

旋转模型、手拉手模型、半角模型

初中数学模型题库 半角模型+旋转原理+手拉手模型

专题31 对角互补模型-2023年中考数学总复习真题探究与变式训练(全国通用,含解析)(原卷版)

初中数学专题一 旋转中的几何模型(手拉手模型、对角互补模型)(解析版)

中考数学能力提升(几何之几何模型)

旋转中的三种常见模型(原卷版)—2024-2025学年九年级数学上册(人教版)

中考数学专题训练 旋转模型几何变换的三种模型手拉手、半角、对角互补

中考数学专题讲练旋转(解析版)

初中数学模型题库半角模型+旋转原理+手拉手模型

初中数学专题一旋转中的几何模型(手拉手模型、对角互补模型)(解析版)

中考数学专题训练旋转模型几何变换的三种模型手拉手、半角、对角互补