多相流的数值模拟
空气动力学中的多相流数值模拟研究

空气动力学中的多相流数值模拟研究空气动力学是一个重要的学科,在包括汽车、飞机、火箭、风力发电等领域中都有广泛的应用。
多相流是空气动力学研究的一个重要领域,它描述了多种相互作用的流体混合物的运动及其特性。
多相流中的物理现象非常复杂,数值模拟成为了研究多相流的重要手段之一。
在本文中,我们将重点介绍空气动力学中的多相流数值模拟研究,包括模拟方法、模拟能力和应用实例。
1. 模拟方法针对多相流的研究,我们需要选择合适的数值模拟方法来对流体流动进行数值计算。
在多相流数值模拟中,传统的方法是欧拉—拉格朗日方法,即在欧拉参考系下求解连续性、动量和能量方程,同时在拉格朗日参考系下求解离散粒子的运动方程。
这种方法适用于颗粒密度很小,而运动方向与流体变化方向差异很大的情况。
但是,当颗粒密度很大,占据了流体相邻空间的时候,欧拉—拉格朗日方法不再适用。
随着计算机技术的发展,欧拉—欧拉方法逐渐成为多相流数值模拟的主流方法。
在欧拉—欧拉方法中,我们假设颗粒是与流体连续的,同时运用控制方程来描述颗粒的运动。
这种方法特别适合处理颗粒密度很大,对流体流动有严重影响的情况。
而在实际应用中,往往要结合欧拉和拉格朗日两种方法,来完整地描述复杂的多相流体。
2. 模拟能力多相流数值模拟的模拟能力是衡量模拟方法好坏的重要指标。
在多相流数值模拟中,颗粒的碰撞、聚集、分散等过程都是非常复杂的。
区分性、可读性、精度和稳定性是衡量模拟方法的关键因素。
区分性:在多相流中,需要区分不同物质的属性,如密度、粘度、颗粒大小等。
高质量的模拟能够很好地完成这些工作。
可读性:模拟能够提供可读性较高的结果,可以方便地分析和理解实验过程并得出结论。
精度:模拟方法可以准确快速地计算出所需的结果,高精度的模拟能够提供更准确的结果数据,能够满足工程应用的需求。
稳定性:稳定性是在数值模拟中最重要的指标之一。
对于多相流体而言,它的稳定性直接影响了模拟计算中的误差和稳定性。
3. 应用实例多相流数值模拟在工程应用中有着广泛的应用。
多相流动过程的数值模拟与优化

多相流动过程的数值模拟与优化随着科技的不断发展,多相流动过程的数值模拟与优化在工业领域中扮演着越来越重要的角色。
多相流动是指在同一空间中同时存在两种或多种不同相态的流体,如气体与液体、液体与固体等。
通过数值模拟与优化,可以更好地理解多相流动的特性,并为工业过程的改进和优化提供依据。
在多相流动的数值模拟中,最常用的方法是计算流体力学(CFD)。
CFD基于流体动力学原理,通过对流体流动进行离散化和数值求解,得到流场的分布情况。
对于多相流动,CFD可以用来模拟不同相态的流体在空间中的分布、速度和压力等参数的变化。
通过数值模拟,可以直观地观察到多相流动的行为,如气泡的形成和破裂、液滴的运动轨迹等。
然而,多相流动的数值模拟也面临着一些挑战。
首先,多相流动中的相态转变和界面行为往往非常复杂,需要考虑到液体与气体之间的相互作用、表面张力的影响等因素。
这就要求数值模拟的模型和算法能够准确地描述这些现象。
其次,多相流动的规模往往非常庞大,需要消耗大量的计算资源和时间。
因此,如何提高计算效率也是一个重要的问题。
为了克服这些挑战,研究人员提出了许多优化方法。
首先,可以通过改进数值模型来提高模拟的准确性。
例如,引入更精确的界面模型、考虑表面张力的影响、修正流体力学方程等。
其次,可以采用并行计算和高性能计算技术来提高计算效率。
并行计算可以将计算任务分配给多个处理器同时进行,从而加快计算速度。
高性能计算技术则可以利用更强大的计算资源,处理更大规模的问题。
此外,还可以利用人工智能和机器学习等技术,对模拟结果进行分析和优化。
通过建立模型和算法,可以根据模拟结果自动调整参数,优化多相流动过程。
除了数值模拟与优化,多相流动的实验研究也是不可或缺的。
实验可以提供直接的观测数据,验证数值模拟的准确性,并为模型的改进提供依据。
实验研究还可以用来探索多相流动的微观机理和宏观行为,为数值模拟提供更准确的边界条件和参数。
因此,实验与数值模拟应该相互结合,共同推动多相流动的研究。
多相流模型数值模拟(中文)
va
po r
– 欧拉显式
po r
liq
Байду номын сангаасui
d
Actual interface shape
Geo-reconstruct (piecewise linear) Scheme
– 欧拉隐式
• 定常和非定常都使用相同的求解器,在差的网格 单元上有固定的数值差分方法 –使用高阶VOF离 散(HRIC, CICSAM)
Stokes数
• 系统载入媒介粒子时, 根据Stokes数选择合适的模型。
– Stokes数(St)是粒子(分散内相)时间松弛系数(τd)和流动特征 时间比例(τc)的比值。
St =
2 ρd d d 其中 . τ d = 18 μ c
τd τc
,τ c =
D U
– D 和 U 是问题中的特征长度和速度标量。 – 如果 St << 1, 粒子流动将会跟随流场流动。 – 如果 St > 1, 粒子流动独立于流场流动。
• 几种有效的子模型方法:
– 散布相的加热/冷却 – – – – 流体液滴的汽化和蒸发 燃烧粒子的挥发演变和燃烧 喷雾模型中液滴的分裂和融合 腐蚀/衍生
DPM模型的适用条件
• 流域: • 填充体积: • 填充粒子: • 建立湍流模型: • Stokes数: • 案例
– – – – – – 气旋 喷雾干燥器 粒子的分离和分类 浮质散布 液体燃料 媒的燃烧
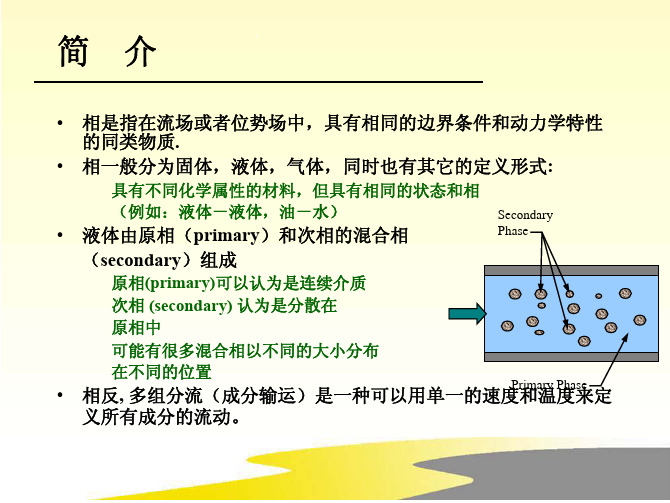
Primary Phase
选择多相流模型
• 为能选择合理的模型,用户需要推理得到下列 形式的一些流动参数:
– 流动域
• 微粒 (连续介质中的气泡,液滴和固体颗粒) • 分层 (流体分界面的长度和域的长度成正比)
多相流体力学的数值模拟及其应用

多相流体力学的数值模拟及其应用引言多相流体力学是研究多种不同物质在相互作用下流动行为的学科领域。
它在工程、环境、生物等多个领域都有重要的应用价值。
随着计算机技术的不断发展,数值模拟成为研究多相流体力学的重要手段之一。
本文将介绍多相流体力学数值模拟的基本原理和方法,并探讨其在工程和科学研究中的应用。
一、多相流体力学的基本概念1.1 多相流体的定义多相流体是指由两种或更多种不同物质组成的流体系统。
它们可以是气体和液体的组合,也可以是液体和固体的组合。
在多相流体中,不同相之间存在各种各样的相互作用,如表面张力、颗粒间作用力等。
1.2 多相流体的分类根据不同的分类标准,多相流体可以分为不同的类型。
按照相间分布的均匀性,可以将多相流体分为均质和非均质两类。
均质多相流体是指各相之间存在均匀分布的情况,如气泡在液体中的分布。
非均质多相流体是指各相之间存在不均匀分布的情况,如液滴在气体中的分布。
1.3 多相流体的力学性质多相流体的力学性质是研究多相流体力学的重要内容。
它包括各个相的速度分布、压力分布、浓度分布等。
多相流体的力学性质直接影响多相流体的流动行为,并对多相流体的应用产生重要影响。
二、多相流体力学的数值模拟方法2.1 多相流体力学方程多相流体力学方程是研究多相流体力学的基本方程。
它从守恒性原理出发,通过质量守恒、动量守恒和能量守恒等方程来描述多相流体的运动行为。
2.2 多相流体的计算模型多相流体的计算模型是进行多相流体力学数值模拟的基础。
常见的多相流体计算模型包括欧拉法、拉格朗日法和亚欧拉法等。
2.3 多相流体力学的数值方法多相流体力学的数值方法是进行多相流体力学数值模拟的关键环节。
常见的多相流体力学数值方法包括有限体积法、有限元法、边界元法等。
2.4 多相流体力学的边界条件多相流体力学的边界条件在数值模拟中起着重要作用。
它们可以分为速度边界条件、压力边界条件和浓度边界条件等。
三、多相流体力学数值模拟的应用3.1 多相流体流动的数值模拟多相流体流动的数值模拟在工程和科学研究中有着广泛的应用。
多相流动的基础知识和数值模拟方法

多相流动的基础知识和数值模拟方法多相流动是指在同一空间中存在两种及以上物质的流动现象。
在工程领域中,多相流动具有广泛应用,如化工反应器中的气液流动、石油勘探中的油水混合流动等。
本文将介绍多相流动的基础知识,并探讨一些常用的数值模拟方法。
一、多相流动的分类多相流动可以根据不同的分类标准进行分类,常见的分类方法包括:1.根据组分:固液流动、气液流动、固气流动等;2.根据速度:稳定流动、不稳定流动、湍流等;3.根据形态:离散相、连续相、两相界面等。
二、多相流动的基础知识1.多相流动的基本方程多相流动的基本方程包括连续性方程、动量方程和能量方程。
在连续性方程中,考虑到多相流动中各相的质量守恒关系;在动量方程中,引入各相之间的相互作用力和速度差等因素;在能量方程中,考虑到各相之间的相变、传热等现象。
2.多相流动的相互作用多相流动中的不同相之间存在相互作用力,如液固两相之间的颗粒间碰撞力、气液两相之间的表面张力等。
这些相互作用力对多相流动的行为和特性具有重要影响。
3.多相流动的模型为了更好地描述多相流动的行为,研究者们提出了多种多相流动模型,如两流体模型、Eulerian-Eulerian模型和Eulerian-Lagrangian模型等。
不同的模型适用于不同的多相流动情况,选择合适的模型对于准确描述多相流动至关重要。
三、多相流动的数值模拟方法数值模拟是研究多相流动的重要手段之一,常用的数值模拟方法包括:1.有限体积法有限体积法是常用的求解多相流动的数值方法之一,它将流动域划分为网格单元,通过离散化各个方程,利用差分格式求解模拟区域内的物理量。
2.多尺度方法多尺度方法考虑到多相流动中存在不同尺度的现象和作用力,通过将流动域划分为不同的区域进行求解,以更好地描述多相流动的行为。
常见的多尺度方法有多尺度网格方法和多尺度时间方法。
3.相场方法相场方法是一种常用的描述多相流动界面的方法,它通过引入相场函数来表示相界面,并利用Cahn-Hilliard方程等对相场函数进行求解,从而获得界面位置和形状等信息。
多相流动动力学的数值模拟与分析

多相流动动力学的数值模拟与分析多相流动是指在流体中同时存在两种或两种以上的物质,这些物质可以是气体、液体或固体。
由于多相流动的复杂性,数值模拟成为研究多相流动的有效手段之一。
数值模拟可以通过计算机模拟多相流动的各种特性,如相互作用、相变、物理效应等,以更深入地理解多相流动动力学行为。
本文将介绍多相流动动力学的数值模拟与分析方法和应用,包括模型、算法以及重要应用领域。
多相流动动力学模型在数值模拟中,多相流动动力学模型是处理多相流动问题的基础。
多相流动模型可以大致分为两类:欧拉-欧拉模型和欧拉-拉格朗日模型。
欧拉-欧拉模型使用两个或多个连续性方程对每个相的物质守恒和动量守恒进行建模。
这些方程用于描述不同相之间的相互作用,包括不同相之间的质量和能量传递。
欧拉-欧拉模型被广泛应用于处理多孔介质中的多相流,如油藏、地下水系统等。
欧拉-拉格朗日模型则使用一个欧拉方程对流体整体进行建模,用于描述流体的运动和相互作用。
该模型建立在欧拉方程的基础上,使用另一种拉格朗日方程来描述固体颗粒运动。
欧拉-拉格朗日模型通常用于研究一个或多个固体颗粒在流体中的运动,例如颗粒悬浮在液体中的情况。
多相流动动力学算法在多相流动动力学数值模拟中,有多种算法可供选择。
以下是几种常用的多相流动动力学算法:Lattice-Boltzmann方法:Lattice-Boltzmann方法是Lattice-Gas方法的一种改进。
该算法将连续性方程转化为离散空间和时间的微分方程,从而简化了计算过程。
Lattice-Boltzmann方法已经被广泛应用于湍流数值模拟、多孔流动和多相流动等领域。
有限元法:有限元法通过将流场划分为多个小区域来离散化流 field。
这种方法对任意复杂的几何形状和流动条件都有一个准确的数值解,已被广泛用于数值模拟和工程设计中。
元胞自动机方法:元胞自动机方法是一种离散事件方法,通过定义哪些工作单元(mesh cell)可以容纳颗粒,颗粒在各个时间步长内向相邻工作单元的移动,来模拟多相流动的行为。
多相流的数值模拟和实验研究

多相流的数值模拟和实验研究多相流是指由两种或两种以上不同物质组成的两相或多相混合物所表现出来的流动现象。
对多相流的研究具有重要的理论和实际意义,它对于理解自然界的物理现象和化学过程,以及各种工业生产过程的优化和控制有着重要的意义。
由于多相流的复杂性,传统的实验和经验研究方法很难对其进行全面而准确的理论分析和实验研究,因此,数值模拟技术成为多相流研究的重要手段。
一、多相流的数学及物理模型多相流的模型是描述多相流动行为、相间传质、相间传热及相间反应过程的数学模型。
对于粒子数量较少的多相流应用连续介质模型,人们将不同相之间人为的断裂为一个个离散的颗粒,在一段时间内它们遵循阻力、碰撞、转移等物理规律分别运动。
在三维颗粒动力学(Discrete Element Method,DEM)模拟中,将某物质视作一堆颗粒的集合,部分颗粒之间具有碰撞和摩擦等相互作用。
相较于欧拉模型,DEM直接模拟颗粒的运动,颗粒运动的规律和特性可直接反映在输出的数据中。
对于粒子数量较多的多相流,例如颗粒流和气固两相流,需要采用欧拉模型。
欧拉模型将多相流看作为运动的连续介质,通过对流动状态中各相界面的移动和膨胀收缩来描绘多相流的运动及相间耦合反馈关系。
其中最重要的问题是对各相之间的相互作用关系、相互传递关系、相互转移关系进行描述和计算。
其中最经典的方法是用Navier-Stokes方程和质量守恒方程来描述多相流的欧拉模型,但是由于微观尺度的混沌运动和相互作用关系的复杂性,欧拉模型仅能模拟在能量和数量分布方面相对均一的现象。
二、多相流的数值模拟多相流的数值模拟将多相流视为连续介质,通过数值解法在离散化的时间和空间网格上对多相流动的各项参数进行计算,从而通过计算机模拟的方法来模拟多相流的运动行为。
数值模拟的过程通常包括以下几个方面的内容:建立数学模型、数值解法、模型验证和优化等。
1.建立数学模型多相流动的数学模型是研究多相流动过程的基础,在多相流动的数值模拟中,合适的模型对于准确得到各相的体积分数、速度以及温度等参数具有重要意义。
多相流体数值模拟及应用研究

多相流体数值模拟及应用研究随着科技的不断进步,工程领域中涉及到的流体力学问题越来越复杂,例如,一些液体和气体混合的现象,会出现多相流体,导致传统的单相流动的理论无法满足实际需要。
因此,多相流体数值模拟成为解决这一问题的有效途径。
本篇文章将介绍多相流体数值模拟及其应用研究,其中包括模拟方法、模型及其在工程中的实际应用等方面。
一、多相流体数值模拟的基本原理多相流体是指相互作用的不同物质间形成的复杂流态体系,多相流体数值模拟是一种研究这种复杂流体动力学特性的研究方法。
基本原则是将复杂的多相系统看作一系列在空间和时间上组合而成的相互作用粒子,通过计算机模拟这些悬浮在主流内的物质运动及相互作用,以预测和研究多相流动系统中的一系列相应物理现象。
多相流体数值模拟的基本步骤包括模型选择、碎片单元建模、流体力学方程及物理模型的设定、网格划分及离散化、求解和后处理等步骤。
模拟精度的提升则需要从多个方面进行优化。
这包括:程序的高效性、模型的有效性、精度及稳定性等。
其中,数值方法是数值模拟的核心,旨在解决方程组的离散求解过程。
二、多相流体数值模拟中的模型及其应用1. Euler-Lagrange方法Euler-Lagrange方法是最常用的粒子装置模型之一,本质上是一种粒子追踪方法,其中,流体相的宏观行为由Navier-Stokes方程组来描述,而悬浮粒子的轨迹则独立计算。
其优点是模型精度高,但是计算速度较慢,因此只适用于小规模的模拟。
2. Euler-Euler方法Euler-Euler方法是一种多相流动模型,通过使用一套Navier-Stokes方程来描述流体相和颗粒相的彼此交互。
这对于颗粒真实的排列及运动具有高度的准确性。
但是,这种方法只适用于均质系统,而对于粗糙介质的流动研究效果并不理想。
3. Lattice-Boltzmann方法Lattice-Boltzmann方法是一种用于模拟速度分布函数的方法,与传统的方法不一样,它快速计算大量计算单元的流动,但计算结果的精度相对较低。
多相流热动力学基础(数值模拟)

两相流动力学的数理模型一、均相流动模型均相流动模型就是把气液两相混合物看作一种均匀介质,这种介质具有均一的流动参数,其物理特性参数取两相介质相应参数的平均值。
因此可按单相介质处理均相流模型的流体力学问题。
由于这种模型回避了相之间的相互作用,对非均匀混合的情况误差较大。
使用均相流模型对于泡状流(尤其是沫状流和雾状流)具有较高的精确性;对于弹状流和块状流需要进行时间平均修正;对于分层流、波状流和环状流,则误差较大。
均流模型的基本假设是:①气液两相流的实际流动速度相等;②两相介质间处于热力学平衡状态,压力、密度等互为单值函数;③在计算摩擦阻力和压力损失时使用单相介质阻力系数。
由上述假设可知:u u u l g ==,滑动比1g l s u u ==,真实含气率与体积含气率相等αβ=,真实密度与流动密度相等()ρρ'=。
对于稳定的一维均相流动,其基本方程有 1、连续性方程根据质量守恒原理,可得M==常数uA ρ (1) 2、动量方程在一维流场中任取一长为dz 的微小流段,其直径为D,过流断面面积为A,如图一所示,现沿流动方向建立动量方程。
图一 均相流动模型作用在微小流段上的质量力只有重力,其沿z方向的分力为θρ-sin gAdz ; 作用在微小流段上的表面力有压力A )dp p (pA +-和切向力dF -。
由动量定律,可得如下动量方程:Mdu sin gAdz dF Adp =θρ--- (2) 或写成AdzMdu sin g AdzdF dz dp +θρ+-=(3)3、能量方程利用工程流体力学中的热焓形式能量方程di )2u(d )sin gz (d dwdw dq 2f ++θ++= (4)根据热力学第一定律dp pd de )p (d de di υ+υ+υ+==υ+=pd de dq 故 di =dp dq υ+ 由此可得dw )2u(d dz sin g dwdp 2f ++θ+υ-= (5)式中:dq ──单位质量流体吸收的热量,包括由外界直接吸收的热量和由机械能散失转变 成的热量;dw ──单位质量流体对外所作的功;f dw ──单位质量流体由于摩擦而散失的机械能; di ──单位质量流体焓的增量; de ──单位质量流体内能的增量; υ──两相混合物的比容,υ=ρ1。
纳米级多相流动数值模拟研究

纳米级多相流动数值模拟研究一、前言多相流动是指在一个体积内同时存在两种或两种以上的流体,其中至少有一种流体存在于不连续的分散相状态。
多相流动涉及到许多的物理和化学过程,例如泡沫、气泡、液滴、固体颗粒等,这些现象都存在于许多工业和工程领域,例如化工、能源、环保、食品等。
因此,多相流动的研究一直是一个热门的话题,而纳米级的多相流动研究更是近年来的研究热点。
二、多相流动的数值模拟方法多相流动的数值模拟旨在描述和预测多相体系中的流动行为及其相关流体力学量,例如速度、压力、流量等。
数值模拟方法主要分为两大类:欧拉方法和拉格朗日方法。
欧拉方法假定分散相为无限小粒子,而连续相为连续介质,因此分散相的位置和速度随时间而变化。
而拉格朗日方法则是描述分散相的运动情况,不考虑连续相特征。
纳米级多相流动的数值模拟相较于传统多相流动的数值模拟更为复杂和困难,因为纳米级的分散相可能与连续相相互作用,并受到湍流的影响。
因此,涉及到多尺度、多物理过程和多相互作用的数值模拟方法,例如分子动力学、格子气体动力学和混合有限元等方法,逐渐成为研究纳米级多相流动的主流方法。
三、纳米级的多相流动研究应用纳米级多相流动的研究在许多领域中都有重要应用。
例如,在制药业中,纳米级的胶体化合物混合均匀性对于生产高质量新药是必要的,因此对于分散相的数量和分布进行了详细研究。
在能源领域中,纳米级的燃料油和润滑油流动性能对于机械设备的性能具有重要作用。
在纳米流体力学中,纳米级材料的流动性能研究旨在开发新的纳米流体等领域。
四、纳米级多相流动的挑战及未来发展方向纳米级多相流动的研究具有极大的挑战性。
目前,我们对于纳米尺度上分散相与连续相交互的理解仍然不够深入,因此需要开发新的理论模型和数值方法。
同时,新技术的发展,例如高性能计算和多尺度模拟,为纳米级多相流动的研究提供了新的途径。
未来,纳米级多相流动的研究将面临更多的挑战和机遇。
例如,新的纳米材料的开发和应用,以及新的多相流动现象的探测和研究等。
多相流动的数值模拟

多相流动的数值模拟引言在石油、化工、冶金等领域,多相流动是一类十分重要的现象。
它对于流体力学、化学反应等方面的研究都有着重要的意义。
在实验室内研究多相流动往往受到条件的限制,因此人们常常借助数值模拟的方法来探究多相流动的规律。
随着高性能计算技术的进步,多相流动的数值模拟得到了显著的发展。
概述多相流动是指两种以上物质同时存在于同一空间内、流动行为相互影响的现象。
其中流体中两相之间相对运动存在的现象称为相互作用。
两相之间的相互作用表现为牛顿第三定律:相互作用力相等,方向相反。
多相流动的计算方法目前主要有多介质方法、连续介质方法等。
多介质方法:将流体划分为两个或以上相分离的单相流,依据一个对象在单相流中的位置,判定该对象处于哪个相中,并且根据两相之间物质交换规律,计算两个相之间的相互作用和传质传热情况。
多介质方法的优点是可以明确地区分出多种物质,但是在相界面上,流体速度及物理量的梯度会达到无穷大,时间步长受到的限制较大。
连续介质方法:将两个相或多个相混合在一起作为一个流体进行数值模拟。
连续介质方法将相互作用作为成分间的扩散流。
连续介质方法的优点是计算机容易处理,且时间步长相对较大。
缺点是得到的结果是平均化的量,难以表达相之间的详细信息。
多相流动的数值模拟方法主要有欧拉法、拉格朗日法和欧拉-拉格朗日方法。
欧拉法:与连续介质方法相似,欧拉法以物质点的质量为基础来进行计算。
以两相为例,沿任何一条雷诺迹线,可以得到该点处气相和液相的不同体积分数。
欧拉法的优点是可以精确的描述流体的宏观特征,计算快速简单,缺点是欧拉法忽略了颗粒之间的相互作用。
拉格朗日法:是以颗粒为基础,采用颗粒运动方程和颗粒轨迹计算颗粒的定位和速度。
拉格朗日法的优点是可以精确的描述颗粒间的相互作用,计算精度高。
缺点是需要像物理颗粒模型这样的复杂的计算,计算量很大。
欧拉-Lagrange方法:欧拉-Lagrange方法采用欧拉法描述流体的运动,采用Lagrange法描述颗粒间的相互作用。
多相流数值模拟方法研究

多相流数值模拟方法研究随着计算机科技和数值计算方法的不断发展,多相流数值模拟方法成为了研究流体力学、化工工程等领域的重要手段。
多相流涉及多种物质的相互作用和流动,具有非常复杂的物理过程和数学模型,因此需要深入研究数值模拟方法及其应用。
一、多相流数值模拟方法概述多相流体系中存在气液、液液、气固、液固等不同相态组合,这些相态组合具有各自的物理特性和运动规律。
因此,研究多相流的数值模拟方法需要充分考虑这些相之间的相互作用和运动规律。
多相流数值模拟方法主要有欧拉-欧拉方法、欧拉-拉格朗日方法和连续介质方法。
欧拉-欧拉方法是一种流场和相态特性都用欧拉坐标系描述的方法,数学模型比较简单,计算效率较高,但不适合描述某些特殊情况,例如相态变化。
欧拉-拉格朗日方法是一种在欧拉坐标系下描述流场,而在拉格朗日坐标系下描述相态特性的方法,适用于描述相态变化的过程。
连续介质方法是一种将不同相态视为连续介质的方法,通过给定介质性质及其守恒方程来求解流场和相态特性,适用于处理比较稠密的多相流体系。
二、多相流数值模拟方法的发展趋势随着数值计算方法的不断发展和数值计算机的性能提升,多相流数值模拟方法已经取得了很多进展。
未来,多相流数值模拟方法的发展趋势主要包括以下几个方面:1. 多物理场耦合模拟多相流在实际应用中往往涉及到多物理场的相互作用,如流动、传热、化学反应等。
因此,在多相流数值模拟中,需要考虑不同物理场之间的相互作用和耦合关系,以获得准确的模拟结果。
2. 多尺度、多分辨率模拟多相流动物理过程涉及到不同时间和空间尺度,因此需要在多尺度和多分辨率上进行模拟。
通过采用不同的数值计算方法和模型,可以在更精细的尺度上描述多相流行为,提高模拟精度和计算效率。
3. 高性能计算多相流数值模拟需要处理大量的计算数据和复杂的数学模型,因此需要充分发挥高性能计算的优势,提高数值计算效率和模拟精度。
4. 计算模型优化多相流数值模拟中需要考虑多种物理过程和数值计算模型,对计算模型进行优化可以提高模拟效率和准确度。
多相流的数值模拟

颗粒轨道模型
连续流体相的质量守恒方程:
t xj
vj nkmk
n
k
、m k
分别为第k中颗粒的数密度和单个颗粒重量,m k
dmk dt
;
第k组颗粒的连续方程: k t xj
kvkj
nk mk
k nkmk 为k相颗粒的表现密度;
优点: 为数值模拟气-液两相流这种复杂的流体动力学问题提供了一
种有效途径(启发FLIC方法和VOF方法)。 缺点: 需要对计算区域内每一个空间位置上的流体质点进行跟踪,计
m pd dv tp pi F diF vm iFpiF BiF M iF si
颗粒运动的阻力
Basset力
Saffman力
附加质量力
压力剃度力
Magnus力
简化后的单颗粒运动方程:
dvi dtk
vi
vki /rk
gi
适用:流场中一相须是弥散于连续介质中的独立的颗粒、气泡或液滴。 适用模型:处理稀疏的气-固两相流或弥散的气-液,液-液两相流问题。
Q k 为各组颗粒与连续相流体之间的对流换热;q r 为连续流体相的 辐射热; S 连续流体相中第s组分的反应率。
第k组颗粒的能量方程:
、 表示单位体积中连续流体相与颗粒相由于变质量造 成的热量源。
13
颗粒轨道模型 优点: 计算简单,节省存储空间和运算时间 当由弥散颗粒由比较复杂的变化经历时,可较好的追踪 颗粒的运动 缺点:
7
连续介质力学模型 欧拉—拉格朗日类模型 特点:连续相的介质的运动由经典的Navier-Stokes方程控制, 而分散相的运动则由独立的动量方程控制。 适用范围:用于解决由连续相(气体或者液体)和分散相(如 液滴或气泡)组成的弥散多相流动体系。
多相流体的数值模拟及计算方法

多相流体的数值模拟及计算方法随着科技的不断发展,数值模拟成为了多领域科学研究的重要手段。
在工程领域中,多相流体的数值模拟显得尤为重要,因为多相流体系统中的相互作用十分复杂,实验条件受到限制,因此数值模拟成为了研究这些系统的主要手段之一。
一、多相流体的数值模拟多相流体包括两个或两个以上物理相或化学相的混合物,比如液体、气体、固体等。
在多相流流场中,不同相之间互相作用,流体间相互作用形成了复杂的流动现象,如空气中的雾、汽车燃烧室中的燃气和固体颗粒等。
如何对这些现象进行准确模拟,是工程领域中多相流体研究的一大挑战。
数值模拟在多相流体研究中的作用不言而喻。
数值模拟能够模拟多相流体流动的各种现象,如液滴、气泡、颗粒等运动轨迹、质量传递过程、界面着生和破裂过程等。
数值模拟方法主要有拉格朗日方法和欧拉方法两种。
拉格朗日方法主要适用于离散相数目较少、相互之间相对独立的情况。
该方法通过在每个离散相质点上解运动方程来描述相的运动,然后通过在每个极小团上解质量、动量和能量守恒方程来描述其与流体场的相互作用。
而欧拉方法适用于离散相数目较多或相互依赖较多的情况。
该方法将全多相流看做是一种非连续的流体,将其称为“均相流”。
根据物理实验数据的观察和分析,多相流体的数值模拟可以分为不同的模型,如气-液两相模型、沸腾模型、涡流破碎模型、松弛模型等,而不同的模型又需要不同的求解算法。
二、多相流体数值模拟的计算方法在多相流体模拟中,需要解决连续相和离散相之间的相互作用,因此需要涉及到两套计算方法。
前者是连续相计算,主要基于欧拉方法;后者则是离散相计算,主要基于拉格朗日方法。
两种方法的计算过程都十分复杂,需要对流场的参数进行求解。
多相流的数值模拟使用的计算方法有:有限体积法(FVM)和有限元法(FEM)。
FVM是应用广泛的计算数值方法,它将集成区域划分为有限数量的小单元,然后使用控制方程组来求解每个单元的值。
FEM则是将连续体分成小单元,通过建立节点来对其进行离散化。
多相流的数值模拟综述

颗粒轨道模型 假设: 颗粒相是离散体系,与连续流体相之间有速度差; 弥散颗粒相无自身的湍流扩散,湍流粘性和湍流导热; 颗粒群按初始尺寸分布分组,每组颗粒在任何时刻都有相同
的的尺寸、速度;
每组颗粒从某一初始位置开始沿着各自独立的轨道运动,互 不干扰,互不碰撞; 颗粒相作用于流体的质量,动量及能量源都以一个等价的量 均匀分布于流体相所在的单元内。
5
多相流数值模拟中的常用特殊参数 容积气流率 气相体积流量和两相体积流量之比为体积含气率,又称容 QG / Q QG / QG QL 积气流率,用 表示: 相函数 相函数表示两相流气体(液体)相的体积(在二维空间中,对 应的参数是面积)在局部单个网格区域中所占据的份额。 Level Set函数 Level Set函数是一个高阶空间分布函数,它的零等值面可 被用来指示相界面的位置和形状。 加权参数 为了计算方便和便于进行试验数据拟合,常对多相流的真 实参数进行权重因子的加权。 运动参数 静止参数
多相流的数值模拟
机械设计及理论(3)班 叶圣军 136091321
1
• 本章主要内容
多相流数值模拟的特点
多相流数值模拟中常用的特殊参数 多相流数值模拟方法的分类 连续介质力学模型 其他多相流数值模拟方法 多相流数值模拟中的困难及发展方向
2
• 多相流数值模拟的特点
数值模拟也叫计算机模拟,它以计算机为手段,通过数
mp
dv pi dt p
Fdi Fvmi Fpi FBi FMi Fsi
附加质量力 压力剃度力
颗粒运动的阻力
Basset力
Saffman力 Magnus力
简化后的单颗粒运动方程:
多相流的数值模拟及其在化工领域中的应用

多相流的数值模拟及其在化工领域中的应用随着科学技术的不断发展,多相流的研究和应用越来越广泛。
在化工领域中,多相流模拟已经成为一种不可或缺的工具。
本文将从多相流模拟的基本原理、常用数值方法以及它在化工领域中的具体应用方面进行探讨。
多相流模拟的基本原理多相流指的是两种或两种以上的物质在同一空间中同时存在、相互作用和运动的流动场景。
一般情况下,其中一种物质是流体,另一种物质可以是气体、固体或者液体。
需要指出的是,多相流模拟是一项复杂的任务,因为不同物质间存在多种多样的相互作用。
为了描述不同物质间相互作用的影响,研究者通常使用各种流动参数来描述对流、对流湍流和粘流的影响,例如密度、粘度、流速和能量等。
常用的数值方法对于多相流动的数值模拟,现在已经有了非常成熟的方法,如欧拉-拉格朗日(Euler-Lagrange)、欧拉-欧拉(Euler-Euler)和欧拉-格作懦耜觯?例如,欧拉-拉格朗日方法将运动颗粒视为离散的物质,而将连续的流体视为连续的介质。
这种方法通过使用描述颗粒与流体间相互作用的不同模型,可以比较准确地预测颗粒行为。
但是这种方法也存在一些局限性,例如需要较大的计算资源以及模型的不确定性。
而欧拉-欧拉方法则是将连续相视为由不同物质组成的混合物。
欧拉-欧拉方法具有很强的应用性,且通常是基于保守律的守恒原理进行建模。
相对而言,欧拉-格作懦耜觯则是将界面位移视为流体介质的一个附加变量,主要用于描述表面张力产生的影响。
多相流模拟在化工领域中的应用多相流模拟技术在化学工业中的应用非常广泛,其中涉及到了许多重要的技术过程,例如喷雾干燥、气固流化床、结晶等。
喷雾干燥是一种将液态物质喷雾进入热空气中使其蒸发,得到干燥的固态颗粒的过程。
在这个过程中,究竟有多少颗粒剩余或是蒸发还需进行计算。
气固流化床技术是指固态颗粒在液态或气态流体的作用下呈现出流体化现象。
这个技术非常重要,因为它可以使固态物质在密集状态下表现出流体性质。
24_多相流的数值模拟课件

18
小滑移模型 较均相模型有以下改进:
➢按尺寸分组的各弥散颗粒相的速度不再等于当地的流体相速度, 各弥散相之间的速度也不再相等; ➢弥散颗粒相的运动由流体的运动引起,颗粒相的滑移则由颗粒相 相对于多相流整体的湍流扩散所致;湍流脉动的相互作用是造成颗 粒相与连续流体相之间相对运动的基本因素;弥散颗粒相与连续流 体相之间的滑移是颗粒相在连续流体中湍流扩散的表现。 ➢各相之间存在阻力作用,在动量方程中增加阻力项。
➢ 缺点
• 描述两相流的变量几乎增加一倍 • 描述两相流的基本方程组比单相流要复杂的多 • 需要确定相之间的相互作用 • 相分布的描述困难 • 两相流守恒方程的求解困难 • 气-液相界面的数学描述困难 • 气-液相界面上表面张力的计算困难
4
4
• 多相流数值模拟中的常用特殊参数
相分布参数
➢ 浓度 浓度表示固体相的质量在局部计算区域中所占据的质量(或
19
19
颗粒拟流体模型(多流体模型)
特点:将弥散颗粒相与连续流体相均看作是连续介质,对颗粒相的 处理方法与对连续介质相的处理方法类似,认为颗粒相是欧拉坐标 系中与连续相流体相互渗透的一种“假想”流体。
较之小滑移模型:考虑速度和温度滑移的同时,认为滑移与颗粒相 的扩散是两种不同的作用,而且颗粒相的扩散是独立于流体相扩散 之外的另一种运动特性。引入了颗粒相粘相、扩散和导热系数这些 与连续流体类似的物理性质。
颗粒运动的阻力
Basset力
Saffman力
附加质量力
压力剃度力
Magnus力
简化后的单颗粒运动方程:
适用:流场中一相须是弥散于连续介质中的独立的颗粒、气泡或液滴。 适用模型:处理稀疏的气-固两相流或弥散的气-液,液-液两相流问题。
微观尺度下的多相流数值模拟

微观尺度下的多相流数值模拟第一章:绪论多相流是指在同一空间中含有两种或两种以上物质的流动现象,广泛存在于自然界和工程技术中,其研究对于理解自然现象和工程优化具有重要意义。
微观尺度下的多相流数值模拟是多相流研究中的重要分支之一,能够通过模拟微观尺度物理规律,预测宏观流动现象,具有重要的理论和实践价值。
第二章:基本理论2.1 多相流的分类多相流可以分为不同的分类,通常根据液相和气相的比例、相对速度和物质性质等进行划分。
比如按液相和气相比例可以将多相流分为气液两相流、气固两相流、液固两相流、液液两相流等。
2.2 多相流物理规律在微观尺度下,多相流通常表现为两相或多相之间的相互作用和微观尺度物理规律的相互作用。
液相和气相之间存在着表面张力和离心力等作用,气固两相流存在着气固之间的摩擦和碰撞,液固两相流存在着接触角和黏附力等相互作用。
2.3 微观尺度下的数值模拟微观尺度下的数值模拟是多相流研究中的重要手段,其基本原理是通过数值方法模拟物理规律,并预测复杂的宏观流动现象。
微观尺度下的数值模拟主要包括直接数值模拟方法、分子动力学模拟方法、格子Boltzmann方法和离散元素法等。
第三章:多相流数值模拟方法3.1 直接数值模拟方法直接数值模拟方法是通过求解流体局部的Navier-Stokes方程和控制方程,来预测多相流的宏观行为。
该方法在处理液液两相和气液两相流时较为适用,但处理气固两相流时由于流场的复杂性和离散问题,其应用较为有限。
3.2 分子动力学模拟方法分子动力学模拟方法是通过建立分子-分子之间的相互作用力模型,模拟粒子之间的运动,并通过统计物理学原理来得到宏观量的物理规律。
该方法在处理气固两相流和液固两相流时具有较高的精度和适用性,但其计算时间较长,需要注意计算负荷问题。
3.3 格子Boltzmann方法格子Boltzmann方法是数值计算流体物理学研究中的一种计算方法,该方法主要采用格子模型对多相流进行数值模拟。
复杂多相流动的数值模拟和优化设计

复杂多相流动的数值模拟和优化设计随着科学技术的进步,复杂多相流的数值模拟方法已成为研究和优化工业过程的重要工具之一。
复杂多相流动涉及多种相态的流体,例如气体、液体、固体颗粒和气泡等。
复杂多相流动具有许多的挑战性质,例如物理现象高度复杂、非线性、不确定性等。
解决这些问题对于提升产品质量、降低生产成本、改善环境保护等方面都有着重要的意义。
下面本文将从数值模拟和优化设计两个方面分别进行介绍。
一、复杂多相流动的数值模拟数值模拟方法是最常用的研究流体力学问题的方法之一。
在复杂多相流动的数值模拟中,通常采用Eulerian-Eulerian(E-E)方法、Eulerian-Lagrangian(E-L)方法和Lagrangian-Lagrangian(L-L)方法等模拟方法进行研究。
其中E-E方法是将每种相态各自建立一个连续的运动方程,解出各自的速度和压力,并采用传质项和多相相互传递项等处理复杂多相流体中多种相的相互作用,从而实现趋近于真实流动特性的模拟。
该方法较为有效,但由于需要处理复杂的多相相互作用和传质过程,因此较为耗费计算资源和时间。
相比之下,E-L方法因可以对连续相和分散相分别进行处理,因此不需要考虑多相相互作用的问题,计算量相对较小。
但具有不稳定性及误差较大等缺点。
L-L方法通常用于流体中颗粒或气泡的移动轨迹跟踪和粒子聚合等复杂多相流动的研究,因为它是在Lagrangian视角下对多相进行处理的。
但本方法的计算结果和实际情况相比较而言存在一定误差。
总之,各种方法都有各自的优缺点,需要根据实际研究需求选择合适的数值模拟方法。
无论采用何种方法进行数值模拟,都需要在模型建立、边界条件设置、计算程序设计等等方面花费大量的人力、物力和财力,才能取得更加准确的模拟结果。
二、复杂多相流动的优化设计复杂多相流动的优化设计是指在实际生产过程中,通过改变流体的性质和流场结构,从而使产品质量提高、生产成本降低、环境污染减少等目的的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Basset力
Saffman力 Magnus力
简化后的单颗粒运动方程:
dvi dt k
vi v ki / rk g i
适用:流场中一相须是弥散于连续介质中的独立的颗粒、气泡或液滴。 适用模型:处理稀疏的气-固两相流或弥散的气-液,液-液两相流问题。
College of Energy and Power Engineering
LJ
20
颗粒拟流体模型(多流体模型)
基本假设: 流场中弥散颗粒相与连续流体相共存并渗透,但分别具有各 自的速度、浓度、温度和体积分数等,而且每个计算单元内 只有一个值; 在做体积平均后,每一尺寸组的颗粒相在空间中具有连续的 速度分布、温度分布和容积分数的分布; 每个尺寸的颗粒相除了与连续流体相具有质量、动量和能量 间的相互作用之外,还具有自身的湍流脉动,并由此造成颗 粒相自身的质量、动量和能量的湍流输运,因而具有其自身 的湍流粘性、扩散和导热等湍流输运性质; 弥散颗粒相可按初始尺寸分布为不同组群; 连续流体相和颗粒相都在欧拉方程系内描述。
均 相 模 型 小 滑 移 模 型 欧拉 欧拉类模型 颗 粒 拟 流 体 模 型 气 -液 两 相 流 的 双 流 体 模 型
College of Energy and Power Engineering
LJ
16
均相模型 假设:
连续流体相和弥散颗粒相间保持动量平衡,无滑移速度; 连续相和弥散颗粒相之间保持动量平衡,无温度差; 弥散颗粒相被看作是连续流体相的一种组分,是有湍流扩散 的连续介质,且各相的湍流扩散系数均相等,与其他流体组 分一样以相同的速率扩散; 弥散颗粒相可按初始尺寸分组,也可按当地尺寸分布分组,
计算简单,节省存储空间和运算时间 当由弥散颗粒由比较复杂的变化经历时,可较好的追踪 颗粒的运动
缺点: 不能全面考虑颗粒的质量,动量及能量的扩散过程 在复杂的流场内给出连续,关于颗粒速度和浓度的空间 场分布 以上缺点会导致计算结果和实验结果有较大误差!
College of Energy and Power Engineering
v
k
ki
vi / rk vi S FM i
College of Energy and Power Engineering
LJ
12
颗粒轨道模型 第k组颗粒的动量方程:
t
k v ki
x j
k v kj v ki
t
x j
k
v kj n k m k
k n k m k 为k相颗粒的表现密度;
连续流体相的动量方程:
t
vi
x j
v v
j i
e xi x j p gi
v j vi x x j i
其他多相流数值模拟方法
多相流数值模拟中的困难及发展方向
College of Energy and Power Engineering LJ 2
多相流数值模拟的特点
数值模拟也叫计算机模拟,它以计算机为手段,通过数
值计算和图像显示的方法,达到对工程问题和物理问题乃 至自然界各类问题研究的目的。多相流数值模拟即对两相 或多相流动系统进行数值模拟。
College of Energy and Power Engineering LJ 11
颗粒轨道模型
连续流体相的质量守恒方程:
t
x j
v n
j
k
mk
n k 、 k 分别为第k中颗粒的数密度和单个颗粒重量, k m m
dm k dt
;
第k组颗粒的连续方程: k
College of Energy and Power Engineering LJ 19
颗粒拟流体模型(多流体模型)
特点:将弥散颗粒相与连续流体相均看作是连续介质,对颗粒相的 处理方法与对连续介质相的处理方法类似,认为颗粒相是欧拉坐标 系中与连续相流体相互渗透的一种“假想”流体。
较之小滑移模型:考虑速度和温度滑移的同时,认为滑移与颗粒相 的扩散是两种不同的作用,而且颗粒相的扩散是独立于流体相扩散 之外的另一种运动特性。引入了颗粒相粘相、扩散和导热系数这些 与连续流体类似的物理性质。
College of Energy and Power Engineering LJ 6
多相流数值模拟方法分类 根据数学和物理原理不同,将多相流数值模拟主要分为以下三类: 经典的连续介质力学方法(欧拉-拉格朗日方法和欧拉-欧拉
方法) 建立在统计分子动力学基础上的分子动力学模拟方法 介观层次上的模拟方法(格子-Boltzmann方法) 从应用角度,将多相流数值模拟主要分为以下三类: 宏观整体特性的数值模拟 局部场分布特性的数值模拟
k rk
vi v ki k g i vi S k
Fk , M i
连续流体相的能量方程:
e T c pT x v j c pT x x t j j T j
S Q S q r n k Q k c P TS
单颗粒在流体中的受力及运动情况
College of Energy and Power Engineering LJ 9
单颗粒动力学模型(单向耦合模型)
在拉格朗日坐标中,一般形式的颗粒运动方程为: dv pi mp Fdi Fvmi F pi FBi FM i Fsi dt p
College of Energy and Power Engineering LJ 4
多相流数值模拟中的常用特殊参数
相分布参数 浓度 浓度表示固体相的质量在局部计算区域中所占据的质量(或 体积)份额,对应的浓度参数则称为质量(或体积)的浓度。 容积含气率和截面含气率 含气率表示气体相的体积在局部计算区域中所占据的份额, V 也叫空泡率,表示为: V g / V ,其中, g 表示控制单元内 气体相的体积,而 V 表示控制单元的体积。 质量气流率 气-液两相流中气相质量流量 W 所占两相质量流量的份额称 为质量气流率,用 x 表示:x WG / WG W L
微观层次的深入分析
College of Energy and Power Engineering LJ 7
连续介质力学模型
欧拉—拉格朗日类模型 特点:连续相的介质的运动由经典的Navier-Stokes方程控制, 而分散相的运动则由独立的动量方程控制。 适用范围:用于解决由连续相(气体或者液体)和分散相(如 液滴或气泡)组成的弥散多相流动体系。
不同尺寸组就是不同相;
相与相之间的相互作用类似与流体混合物中各组分之间的相 互作用,弥散颗粒相和连续流体相之间的阻力忽略不计。
College of Energy and Power Engineering LJ 17
均相模型
优点: 处理方法简单,可用成熟的、单相流体的数值模拟方法来 处理两相流问题。 缺点: 没有考虑颗粒相与连续相之间的速度和温度滑移和阻力作 用,与实际情况的差别较大,在实际中应用不多。
G
College of Energy and Power Engineering
LJ
5
多相流数值模拟中的常用特殊参数 容积气流率 气相体积流量和两相体积流量之比为体积含气率,又称容 积气流率,用 表示: QG / Q QG / QG Q L 相函数 相函数表示两相流气体(液体)相的体积(在二维空间中,对 应的参数是面积)在局部单个网格区域中所占据的份额。 Level Set函数 Level Set函数是一个高阶空间分布函数,它的零等值面可 被用来指示相界面的位置和形状。 加权参数 为了计算方便和便于进行试验数据拟合,常对多相流的真 实参数进行权重因子的加权。 运动参数 静止参数
College of Energy and Power Engineering
LJ
18
小滑移模型
较均相模型有以下改进: 按尺寸分组的各弥散颗粒相的速度不再等于当地的流体相速度,
各弥散相之间的速度也不再相等;
弥散颗粒相的运动由流体的运动引起,颗粒相的滑移则由颗粒相 相对于多相流整体的湍流扩散所致;湍流脉动的相互作用是造成 颗粒相与连续流体相之间相对运动的基本因素;弥散颗粒相与连 续流体相之间的滑移是颗粒相在连续流体中湍流扩散的表现。 各相之间存在阻力作用,在动量方程中增加阻力项。
为各组颗粒与连续相流体之间的对流换热;q r 为连续流体相的 辐射热; S 连续流体相中第s组分的反应率。 第k组颗粒的能量方程:
Qk
、 表示单位体积中连续流体相与颗粒相由于变质量造 成的热量源。
College of Energy and Power Engineering LJ 13
颗粒轨道模型 优点:
v k , j v kc , j v kd , j
College of Energy and Power Engineering LJ 15
连续介质力学模型
欧拉—欧拉类模型 特点:把弥散颗粒相和连续流体相一样看作连续介质,同时在 欧拉坐标系中考虑弥散颗粒相和连续流体相的运动。 适用范围:模拟弥散相浓度较高的场合。
单 颗 粒 动 力 学 模 型 欧拉 拉格朗日类模型 颗 粒 轨 道 模 型
College of Energy and Power Engineering
LJ
