触摸屏的校准方法
电阻式触摸屏校准算法分析
电阻式触摸屏校准算法分析<一> 算法分析电阻式触摸屏在X,Y坐标方向上是线性的,比如S32采用的触摸屏,理论上Xmin=0,Xmax=1023,Ymin=0,Ymax=1023。
但是实际的触摸屏,往往是xmin>0,xmax<1023,ymin>0,ymax<1023。
所以就需要校准。
此文讨论的校准算法,其原理就是利用触摸屏的线性特性,针对被校准的触摸屏,获取其真正的x,y的范围,即xmin,ymin,xmax,ymax将其记录下来。
以后当触摸事件发生,将触摸屏报告的原始坐标(x,y)按比例投射到0~1023的坐标上即可。
注意,TP与LCD在相同的坐标方向上,具有相似性,即比例一致性。
看看对原始坐标的处理:If (x<xmin) x=0;Else if (x>xmax) x=xmax-xmin;Else x=1023*(x-xmin)/(xmax-xmin);If (y<ymin) y=0;Else if (y>ymax) y=ymax-ymin;Else y=1023*(y-ymin)/(ymax-ymin);可见,对原始坐标,先减去一个0位置的偏移量(x-xmin),然后求得它X范围上的比率((x-xmin)/(xmax-xmin)),再乘以1023,就得到了投射到(0~1023)上的坐标。
再看看校准算法。
在以下的讨论中,所谓物理坐标,指触摸屏上的坐标PT;所谓逻辑坐标,指LCD上的坐标PL。
LCD的宽度(W)对应TP的X方向,LCD的高度(H)对应TP的Y方向。
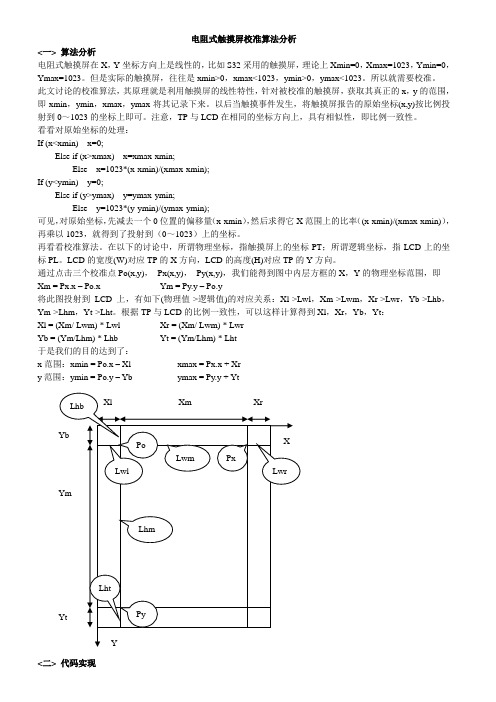
通过点击三个校准点Po(x,y),Px(x,y),Py(x,y),我们能得到图中内层方框的X,Y的物理坐标范围,即Xm = Px.x – Po.x Ym = Py.y – Po.y将此图投射到LCD上,有如下(物理值->逻辑值)的对应关系:Xl->Lwl,Xm->Lwm,Xr->Lwr,Yb->Lhb,Ym->Lhm,Yt->Lht。
屏幕4点校准算法

屏幕4点校准算法介绍屏幕4点校准算法是一种用于校准触摸屏幕的方法。
通过测量用户点击屏幕时的坐标,并与屏幕上实际显示的坐标进行比较,可以计算出触摸屏幕的误差,并进行校准,从而提高触摸屏幕的准确性和灵敏度。
本文将详细介绍屏幕4点校准算法的原理、步骤和应用。
原理屏幕4点校准算法的原理基于触摸屏幕在不同位置的响应误差是不一样的。
通常情况下,由于制造过程中的一些偏差和材料差异,触摸屏幕在边缘和角落的响应误差较大,而在中心位置的响应误差较小。
因此,通过在触摸屏幕的四个角落进行校准,可以得到一个精确的校准参数,从而减小触摸屏幕的误差。
步骤屏幕4点校准算法的步骤如下:步骤1:选择参考点首先,需要选择四个参考点,一般选取屏幕的四个角落。
这四个参考点的坐标需要事先确定,并且要尽可能分布在屏幕的不同位置。
步骤2:用户操作用户需要按照指示在屏幕上分别点击四个参考点位置。
系统会记录下用户点击时的坐标。
步骤3:计算校准参数根据用户点击时的坐标和事先确定的参考点坐标,可以计算出校准参数。
校准参数可以通过线性插值或者其他数学模型得到,具体的计算方法要根据具体情况而定。
步骤4:应用校准参数最后,将计算出的校准参数应用到触摸屏幕上,以校正触摸屏幕的误差。
校准参数可以通过软件或者硬件的方式进行应用。
应用屏幕4点校准算法广泛应用于各类触摸屏设备,例如智能手机、平板电脑、工控机等。
通过校准触摸屏幕,可以提高用户的触控体验,减少误操作,并且可以精确地控制光标的位置。
总结屏幕4点校准算法是一种用于校准触摸屏幕的方法,通过选择参考点、用户操作、计算校准参数和应用校准参数等步骤,可以提高触摸屏幕的准确性和灵敏度。
该算法广泛应用于各类触摸屏设备,可以改善用户的触摸体验。
触摸屏校正方法

用久了出现在触摸不准不灵敏的时候的校正方法:
1、将触摸屏背面的四个拨码开关,第一个设置为ON,其余三个拨码开关位置保持不变。
正常情况下四个拨码开关均在OFF的位置,如下图:
将第一个拨码开关设置为ON (上图)
2、按一下拨码开关旁边的黑色的Reset(复位)按钮或者将人机界面重新上电。
3、人机界面启动后,会要求对触控面板进行触控校正。
校正的方法为人机界面屏幕上出现的十字光标在什么位置就触控一下这个位置,直到十字光标消失,人机界面会继续往下执行启动过程
4、校正完之后,会弹出如下对话框,询问是否要恢复为出厂设置密码如下图,请选择NO 校正完成。
记得把第一个将第一个拨码开关设置回OFF
TK6070需要把J3端子的1-2短接就行,校准完成后在恢复到7-8短接。
电容屏触摸校准方法

电容屏触摸校准方法
电容屏触摸校准是确保触摸屏准确响应用户输入的重要步骤。
以下是电容屏触摸校准的一般方法:
1. 手动校准,在某些设备上,可以通过进入设置菜单中的触摸屏校准选项来手动进行校准。
在这种情况下,系统会显示一些目标点,用户需要按照指示用手指精确地点击这些点,以便系统能够准确地识别屏幕的触摸位置。
2. 自动校准,许多设备在启动时会自动进行触摸屏校准,系统会通过内置的算法自动识别触摸屏的特征并进行校准。
这种方法通常更简单,用户无需进行手动操作。
3. 使用校准工具,一些设备可能配备了专门的校准工具,用户可以通过这些工具进行更精细的触摸屏校准,以确保触摸屏在不同位置都能准确响应。
4. 软件校准,在一些情况下,触摸屏校准可以通过安装特定的校准软件来实现,这些软件通常提供了更多的参数和选项,用户可以根据自己的需求进行定制化的校准。
无论采用哪种方法,触摸屏校准都是非常重要的,它可以确保设备在日常使用中能够准确响应用户的操作,提高了用户体验。
在进行触摸屏校准时,用户需要确保环境安静,避免干扰,以获得最佳的校准效果。
同时,定期进行触摸屏校准也是一个好习惯,可以确保设备长期保持良好的触摸性能。
触摸屏校准方法

嵌入式Linux和MiniGUI结合的解决方案已经成为很多嵌入式系统的图形化方案之一,而触摸屏也是很多嵌入式系统首选的输入设备,因此触摸屏的校准也成为很多嵌入式系统开发过程中常常碰到的问题之一。
嵌入式Linux是一种可以进行裁减、修改使之能在嵌入式计算机系统上运行的操作系统,既继承了Internet上的无限的开放源代码资源,又具有嵌入式操作系统的特性。
该系统具有较高的稳定性和安全性、良好的硬件支持、标准兼容性和资源丰富等功能。
而触摸屏是一种方便、快捷的输入设备,附着在显示器的表面,与显示器配合使用,在工业控制场合得到了广泛的应用。
然而在实际的嵌入式程序移植的过程中,由于触摸屏尺寸的不同,以及GUI(Graphic User Interface)方案选择和IAL(Input Abstract Layer)的差异,一般开发板制造商并不提供触摸屏的校正程序。
本文介绍的正是笔者在制作实际的嵌入式Linux数控机床人机接口过程中,提出的一套基于嵌入式Linux和MiniGUI的通用触摸屏校准程序设计方案。
MiniGUI简介MiniGUI()是国内最有影响的自由软件项目之一, MiniGUI 项目的目标是为基于 Linux 的实时嵌入式系统提供一个轻量级的图形用户界面支持系统。
该项目自1998年底开始到现在,已历经7年多的开发过程,到目前为止,已经比较成熟和稳定,并且在许多实际产品或项目中得到了广泛应用。
MiniGUI 为应用程序定义了一组轻量级的窗口和图形设备接口。
利用这些接口,每个应用程序可以建立多个窗口,而且可以在这些窗口中绘制图形且互不影响。
用户也可以利用MiniGUI 建立菜单、按钮、列表框等常见的 GUI 元素。
MiniGUI 可以具有两种截然不同的运行时模式:MiniGUI-Threads或者MiniGUILite。
运行在 MiniGUI-Threads 上的程序可以在不同的线程中建立多个窗口,但所有的窗口在一个进程中运行。
触摸屏校准方法!!!

触摸屏及ADS7846/HT20462009-05-15 10:17四线电阻式触摸屏,上图我们看到,触摸屏一般是上线和下线为一组。
左右线为一组,用万用表可以量到阻值。
上下的线阻为(Y+ Y-)阻值为 500欧----680欧。
左右线阻(X+ X-)阻值为 350欧----450欧。
jz4740,的中断计算程序#define SPCS_HIGH v_pSSIGPIORegs->group[SPI_EN_PIN/32].DATS = 1 <<(SPI_EN_PIN%32)#define SPCS_LOW v_pSSIGPIORegs->group[SPI_EN_PIN/32].DATC = 1 << (SPI_EN_PIN%32)#define SPCK_HIGH v_pSSIGPIORegs->group[SPI_CLK_PIN/32].DATS = 1 <<(SPI_CLK_PIN%32)#define SPCK_LOW v_pSSIGPIORegs->group[SPI_CLK_PIN/32].DATC = 1 <<(SPI_CLK_PIN%32)#define SPDA_HIGH v_pSSIGPIORegs->group[SPI_DATA_PIN/32].DATS = 1 <<(SPI_DATA_PIN%32)#define SPDA_LOW v_pSSIGPIORegs->group[SPI_DATA_PIN/32].DATC = 1 <<(SPI_DATA_PIN%32)#define SPDAIN v_pSSIGPIORegs->group[SPI_DATARX_PIN/32].PIN & (1 <<(SPI_DATARX_PIN % 32))//insert 0 ,not insert 1;#define SPDABUSY v_pSSIGPIORegs->group[SPI_BUSY_PIN/32].PIN & (1 <<(SPI_BUSY_PIN % 32))//insert 0 ,not insert 1;//------------------------------------------------------------------------------ void delay(int k){int i;for(i=0;i<k;i++);}void start()//SPI开始{SPCK_LOW;SPCS_HIGH;SPDA_HIGH;SPCK_HIGH;SPCS_LOW;}void WriteCharTo7843(unsigned char num) //SPI写数据{unsigned char count=0;SPCK_LOW;for(count=0;count<8;count++){if ( (num & 0x80) == 0x80)SPDA_HIGH;elseSPDA_LOW;SPCK_LOW;delay(3);SPCK_HIGH;delay(3);num <<= 1;}}int ReadFromCharFrom7843() //SPI 读数据{unsigned char count=0;WORD Num=0;for(count=0;count<12;count++){Num<<=1;SPCK_HIGH;delay(3); //下降沿有效SPCK_LOW;delay(3);if(SPDAIN)Num++;}return(Num);}INT WINAPI SpiISR( VOID ){while ( !g_SpiISR.bISTExist ){int X=0,Y=0,X_,y_;WaitForSingleObject( g_SpiISR.hIntrEvent, INFINITE );Sleep(30);//中断后延时以消除抖动,使得采样数据更准确start(); //启动SPIWriteCharTo7843(0x90); //送控制字 10010000 即用差分方式读X坐标详细请见有关资料delay(2);while(SPDABUSY);SPCK_HIGH; delay(4);SPCK_LOW; delay(4);X=ReadFromCharFrom7843();WriteCharTo7843(0xD0); //送控制字 11010000 即用差分方式读Y坐标详细请见有关资料delay(2);while(SPDABUSY);SPCK_HIGH; delay(4);SPCK_LOW; delay(4);Y=ReadFromCharFrom7843();SPCS_HIGH;RETAILMSG(1, (TEXT("SpiISR X=%d,Y=%d\r\n"),X,Y));InterruptDone( g_SpiISR.dwSwIntr );}return ( 0 );}控制字ADS7846的控制字由表1所列,其中S为数据传输起始标志位,该位必为“1”,A2~A0进行通道选择。
光洋触摸屏校准方法

光洋触摸屏校准方法
嘿,朋友们!今天咱就来唠唠光洋触摸屏校准这档子事儿。
你想想看啊,这触摸屏就好比是我们和机器沟通的一个小窗口,要
是这个窗口歪了斜了,那咱和机器的交流不就乱套啦!所以校准它可
太重要啦!
那怎么校准呢?别急,听我慢慢道来。
首先呢,咱得找到校准的入口,就像你找家门钥匙孔一样,得找对地方才行。
一般在系统设置里
能找到相关的选项,你就可着劲儿地找吧!
然后呢,进入校准模式,这时候屏幕上可能会出现一些小点点或者
线条啥的,嘿,这就是让你瞄准的目标呢!就好像打靶一样,你得把
你的手指准确地按在那些点上。
这时候你可别马虎呀,得集中注意力,一个点一个点地认真去校准。
要是你马马虎虎的,那校准出来的效果能好吗?那肯定不行呀!
哎呀,你说这触摸屏校准不就跟咱平时走路一样嘛,得一步一步走
稳了,才能走得顺溜。
要是东倒西歪的,那不就摔跟头啦!
校准的过程中,你可能会觉得有点繁琐,但是没办法呀,谁让咱要
让这触摸屏乖乖听话呢!你就耐心点,就当是和它培养感情啦!
等你把所有的点都校准好了,嘿,那感觉,就好像你给这触摸屏整
了个容一样,焕然一新呀!
这时候你再去试试操作,哇塞,那叫一个顺手,就跟你使唤自己的胳膊腿儿一样自然。
所以说呀,朋友们,可别小瞧了这光洋触摸屏校准,它可是能让你的使用体验大大提升呢!别嫌麻烦,认真去做,你肯定会有收获的。
好好对待你的触摸屏,它也会好好为你服务的哟!这不就是咱和机器和谐共处的小秘密嘛!你说是不是呀?。
有效处理手机触摸屏失灵的情况

有效处理手机触摸屏失灵的情况手机触摸屏失灵是我们在日常使用手机时经常遇到的问题之一。
当我们的手机触摸屏出现失灵时,可能会给我们的生活和工作带来不便。
因此,有效处理手机触摸屏失灵的情况是非常重要的。
本文将介绍一些常见的手机触摸屏失灵原因以及相应的解决方法,帮助读者更好地应对这一问题。
一、常见手机触摸屏失灵原因1.触摸屏脏污触摸屏使用时间长了,表面容易积聚灰尘、污垢等杂质,导致触摸屏失灵。
此时,我们可以使用干净柔软的布轻轻擦拭触摸屏表面,清除污垢,恢复触摸屏的灵敏度。
2.触摸屏受潮手机触摸屏进水或者受潮后,容易导致触摸屏失灵。
在这种情况下,我们应该立即将手机关机,并将手机放入干燥通风的地方晾干。
切记不要用电吹风或者暴晒阳光直接照射手机,以免损坏手机内部元件。
3.触摸屏硬件故障有时候,手机触摸屏失灵是由于硬件故障引起的。
这时候,我们可以尝试重启手机,看是否能够解决问题。
如果重启后触摸屏仍然无法正常使用,建议及时联系手机售后维修服务中心进行检修。
二、有效处理手机触摸屏失灵的方法1.软件问题处理有时候,手机触摸屏失灵是由于软件问题引起的。
我们可以尝试通过以下方法解决:(1)清理手机缓存:打开手机设置,找到应用管理,选择清理缓存,清理手机缓存可以帮助提高手机的运行速度,并有助于解决触摸屏失灵问题。
(2)更新系统:有时候,手机触摸屏失灵是由于系统版本过旧引起的。
我们可以打开手机设置,选择系统更新,更新手机系统到最新版本,以修复触摸屏失灵问题。
2.触摸屏校准有时候,手机触摸屏失灵是由于校准问题引起的。
我们可以尝试通过以下方法进行校准:(1)打开手机设置,选择显示设置,找到触摸屏校准选项,按照屏幕上的指示进行校准操作。
(2)如果手机没有触摸屏校准选项,我们可以尝试在应用商店中搜索并下载触摸屏校准软件,按照软件的指引进行校准操作。
3.专业维修服务如果以上方法都无法解决手机触摸屏失灵问题,建议及时联系手机售后维修服务中心进行专业维修。
触摸屏为什么点不准之触摸屏校准教程

触摸屏为什么点不准之触摸屏校准教程嵌入式环境下,触摸屏是鼠标的替代也是升级输入设备,下面我们来研究一下触摸屏。
1.基础知识触摸屏的原理这里不讲,只说下大体思路,触摸屏硬件能够接收到来自用于的触摸,通过若干方式,把数据转换成坐标,此时,坐标是物理坐标,即触摸屏的坐标,而不是显示设备的坐标,显示设备的坐标由软件来定义,而触摸屏的物理坐标是固定的。
所以,当我们点击触摸屏,数据被送给驱动,驱动送给应用程序时,我们得到的数据还不是真正的显示设备数据哦,比如点击一点,硬件传来的是(189,123),(我们约定x在前),这时如果我们说,屏幕上的(189,123)点有点击,这时不正确的,这个很容易明白的,物理的点只是采样到的点,并不是真正意义上的显示设备的坐标,毕竟显示坐标由我们来定。
那么怎么办呢?~这时,需要校准触摸屏,所有的触摸屏使用前,必须要经过校准。
2.触摸屏校准原理以上说了触摸屏需要校准的原因,问题出在,物理坐标和屏幕坐标并不匹配,不匹配有两个方面:第一,物理坐标的1个单位和屏幕坐标的1个单位并不相等,我们知道屏幕坐标1个单位一般是一个像素,而物理坐标的1个单位并不是1个像素.第二,假设我们把屏幕的左上角定义为(0,0),那么触摸屏的左上角的物理坐标并不是(0,0)(我们点击之后的物理采样数据)。
综上,校准有两个方面:第一,物理采样坐标与屏幕像素坐标的对应关系,也就是伸缩系数,即单位物理采样数据代表几个单位屏幕像素数据,x坐标和y坐标各有一个伸缩系数,分别记作:xScale和yScale。
计算方法很简单,为了精确,可以采样屏幕上的四个点,让用户点击,比如(20,20),(20,200),(300, 200),(300,20),通过横着的线段除以物理采样的数据线段,得到了x的伸缩系数。
同理可以得到y的伸缩系数。
第二,物理坐标的相对于屏幕像素坐标的偏移,假如我们不计算偏移,只计算伸缩系数的话,假设用户在屏幕点(20,20)点击,我们经过转换物理采样数据,即乘上伸缩系数,发现,校准后的数据并不是(20,20)点,原因就是因为有偏移,原因是触摸屏的物理采样数据,在左上角并不是(0,0),而是某个正数对,采样到的数据不会是0的,这就是偏移产生的原因,所以,在计算过伸缩系数之后,比如点击屏幕(20,20),采样到的数据是(45,78),而第一步计算出的伸缩系数分别是0.78和0.67,那么物理坐标转换成屏幕坐标后是(45*0.78,78*0.67),此时虽然我们得到了物理坐标对应的屏幕坐标,但是现在屏幕坐标和我们(20,20)所在的屏幕坐标并不在一个坐标系,即(0,0)点不同,所以我们要减去一个坐标系偏移,假设分别是xOffset和yOffset,那么两个坐标做差便得到了xOffset和yOffset。
android实现触摸屏校准

android实现触摸屏校准并根据读取到事件类型的不同分成三类(KEYBOARD、TOUCHSCREEN、TRACKBALL),分别进行处理,例如键盘事件会调用dispatchKey((KeyEvent)ev.event, 0, 0)以将事件通过Binder发送给具有焦点的窗口应用程序,然后调用mQueue.recycleEvent(ev)继续等侍键盘事件的发生;如果是触摸屏事件则调用dispatchPointer(ev,(MotionEvent)ev.event, 0, 0),这里会根据事件的种类(UP、DOWN、MOVE、OUT_SIDE等)进行判断并处理,比如Cancel或将事件发送到具有权限的指定的窗口中去;3.移植方案a.Android本身并不带触摸屏校准。
Android获取到的数据就是驱动上报的原始数据。
b.方案一: 移植TSLIB,通过TSLIB产生pointercal 校准参数文件。
c.方案二: 从Android框架层获取OnTouch事件产生pointercal 校准参数文件d.方案一: 数据的校准在驱动中完成。
即把pointercal 的参数数据通过某种方式(sysfs)传递给驱动程序进行校准。
e.方案二: 驱动上报原始点,原始点在框架层拦截后进行校验处理。
4.TSLIB移植过程a.修改源码以适应android的文件结构。
b.设定Android.mk 编译选项,生成库即应用。
i.etc/ts.conf module_raw inputii.src/ts_config.c #define TS_CONF "/system/etc/ts.conf"iii.src/ts_load_module.cchar *plugin_directory="/system/lib/ts/plugins/";iv.tests/fbutils.cchar *defaultfbdevice = "/dev/graphics/fb0";v.COPY ts.conf 到/system/etc/ts.confvi.init.rc. mkdir /data/etc/pointercalvii.通过ts_calibrate 产生pointercal 数据文件。
手机触屏校准的操作方法

手机触屏校准的操作方法手机触屏校准是一种调整手机触摸面板灵敏度和精确度的操作,它能够帮助手机更好地识别用户的点击和滑动动作。
当我们使用手机时发现触摸屏幕的精准度出现问题,例如点击位置偏移、按住滑动无法进行等情况,就需要进行触屏校准。
下面将详细介绍手机触屏校准的操作方法。
首先,打开手机的“设置”界面,一般可以在主屏幕上找到设置图标,一般为一个齿轮或者是齿轮加线的图标。
在设置界面中,找到并点击“显示”选项,可能需要向下滑动才能找到它。
在一些手机上,可能需要点击“设备”、“系统”或者“其他”选项才能找到“显示”。
在“显示”选项中,寻找“触控校准”或者“屏幕校准”等类似选项。
不同品牌的手机设置界面可能略有不同,但大多数手机都有类似的校准选项。
点击“触控校准”选项进入触屏校准界面。
在这个界面中,你将看到屏幕上出现一系列小方块或者“+”符号。
接下来,你需要按照屏幕上的指示进行校准。
一般情况下,你需要按照顺序点击小方块或者“+”符号,以确保手机能够准确识别触摸位置。
当你点击每个小方块或者“+”符号时,屏幕上会出现震动或者声音提示,表示触摸已经被识别。
请确保你用手指轻按触摸屏幕,而不是用其他工具。
在完成所有的触摸校准点后,你可能需要点击“完成”或者“保存”按钮来保存校准结果。
有些手机会在校准完成后自动退出校准界面。
完成触屏校准后,你可以测试校准结果是否理想。
打开一个应用程序或者网页,试着在屏幕上点击和滑动,观察是否有明显的延迟或者偏移。
如果校准结果不理想,你可以重新进行校准。
有些手机提供了多种校准模式,例如“普通”和“高级”等,你可以尝试不同的模式来找到最适合你的校准结果。
除了通过手机设置界面进行触屏校准外,还有一些手机可以通过特定的触摸手势或快捷键来进行校准。
你可以查看手机的使用手册或者在互联网上搜索关于你手机型号的触屏校准方法,以获取更加准确的操作步骤。
需要注意的是,触屏校准过程可能会因手机品牌和型号而异,以上是比较通用的操作方法。
如何解决手机触摸屏失灵的问题

如何解决手机触摸屏失灵的问题手机已经成为现代人生活中不可或缺的工具,而触摸屏作为手机的主要输入方式,更是被广泛使用。
然而,有时我们可能会遇到手机触摸屏失灵的问题,这给我们的使用带来了很大的困扰。
本文将为大家介绍一些解决手机触摸屏失灵问题的方法。
一、清洁触摸屏表面触摸屏失灵的一个常见原因是表面的污垢或油脂。
为了解决这个问题,我们可以使用干净柔软的布或专用的手机屏幕清洁剂轻轻擦拭触摸屏表面。
请注意不要使用过于湿润的布或清洁剂,以免进一步损坏触摸屏。
二、重启手机有时,触摸屏失灵可能是由于手机系统出现故障引起的。
在这种情况下,我们可以尝试重启手机来解决问题。
长按手机的电源键,选择重启选项,等待手机重新启动后,再次尝试触摸屏是否恢复正常。
三、更新系统和应用程序另一个导致触摸屏失灵的原因可能是手机系统或应用程序的bug。
为了解决这个问题,我们可以尝试更新手机系统和应用程序。
打开手机的设置菜单,找到系统更新或应用程序更新选项,检查是否有可用的更新。
如果有更新,按照提示进行操作,等待更新完成后,再次测试触摸屏是否正常工作。
四、校准触摸屏有时触摸屏失灵可能是由于触摸屏校准出现问题导致的。
为了解决这个问题,我们可以尝试重新校准触摸屏。
打开手机的设置菜单,找到触摸屏校准选项,按照提示进行操作。
校准完成后,重启手机,再次测试触摸屏是否恢复正常。
五、检查硬件问题如果以上方法都无法解决触摸屏失灵的问题,那么可能是手机触摸屏硬件出现了故障。
这时候,我们可以尝试将手机关机,取下手机电池和SIM卡,等待几分钟后重新安装,再次开机测试。
如果问题仍然存在,建议将手机送修或咨询专业的手机维修人员。
总结:手机触摸屏失灵是一个常见的问题,但通过一些简单的方法,我们可以尝试解决。
首先,清洁触摸屏表面,确保没有污垢或油脂。
其次,尝试重启手机,更新系统和应用程序,校准触摸屏,以解决可能由软件问题引起的失灵。
最后,如果问题仍然存在,可能是硬件问题,建议寻求专业的维修服务。
触摸屏技术的原理及触控精度改进方法

触摸屏技术的原理及触控精度改进方法触摸屏技术被广泛应用于各种电子设备中,如智能手机、平板电脑、个人电脑等。
它作为一种直观且便捷的交互方式,在现代科技领域发挥着重要的作用。
本文将介绍触摸屏技术的基本原理,并探讨改进触控精度的方法。
一、触摸屏技术的原理触摸屏技术的基本原理是通过触控板传感器检测用户手指的位置和动作,进而实现相应的操作。
触摸屏主要分为电阻式触摸屏、电容式触摸屏和声表面波触摸屏三种类型。
1. 电阻式触摸屏电阻式触摸屏使用两层导电薄膜间的电阻变化来检测手指触摸位置。
当手指触摸触摸屏表面时,上下两层电阻薄膜产生反应,触发电流流过手指,从而测量手指的位置。
这种触摸屏的特点是价格相对较低,但由于屏幕需要产生压力,其触摸体验不够灵敏。
2. 电容式触摸屏电容式触摸屏利用触摸产生的静电场来检测手指位置。
触摸屏表面覆盖有一层导电物质,当手指接近时,导电物质所形成的感应电场发生变化,触摸屏传感器便可通过探测电流的变化来确定手指的位置。
这种触摸屏具有高灵敏度和响应速度快的特点,但价格较高。
3. 声表面波触摸屏声表面波触摸屏采用超声波传感器来检测手指的位置。
超声波传感器通过产生机械波并在触摸屏表面传播,当手指触摸屏时,机械波会发生反射,传感器便可通过分析反射信号来确定手指位置。
这种触摸屏具有高灵敏度和良好的可见光透过性,但价格较高。
二、触控精度的改进方法为提高触摸屏的触控精度,可采取以下方法:1. 优化触摸屏传感器触摸屏传感器是影响触控精度的核心元件,不同类型的触摸屏传感器具有各自的特点和适用范围。
在选择触摸屏时,可以根据应用需求和用户群体选择最适合的触摸屏类型,以提高触控精度。
2. 提高采样率采样率是指触摸屏在单位时间内获取触摸数据的次数。
提高采样率可以使触摸屏更加灵敏,减少延迟,并提高触控精度。
通过提高芯片的处理速度和优化触控算法,可以实现较高的采样率。
3. 降低触摸的误判率触摸屏在使用过程中可能会出现误触现象,影响触控精度。
如何校准触摸屏基准参数

如何校准触摸屏基准参数在触摸屏修理工作中,我们发觉电阻式触摸屏在嵌入式系统中用的较多,电阻式触摸屏可分为四线、五线、七线等几种,接下来,我们主要以WinCE触摸屏为例,分析如何校准触摸屏基准参数问题:在我们顺当完成驱动程序安装以及各种功能就都已经预备就绪了,现在就可以实际操作触摸屏幕了。
但一般来说,电阻式触摸屏需要校准,也就是说在驱动启动过程中MDD层要调用相应的DDSI函数来读取注册表中的校正数据校正触摸屏。
抱负状况下,校准程序只要在嵌入式设备初次加电测试过程中运行一次就可以了,参考值会被存储在非易失性存储器中,以免让用户在以后的加电启动期间再做校准。
不过,高质量的触摸屏驱动程序是应当要向用户供应一种进入校准例程的途径,从而在由于温度漂移或其它因素造成校准不精确时进行重新校准。
在抱负状况下,校正触摸屏基准只需两组原始数据,即在屏幕对角读取的最小和最大值。
但在实际应用中,由于很多电阻式触摸屏存在明显的非线性,假如只在最小和最大值之间简洁的插入位置数值会导致驱动程序特别的不精确。
因此,在WinCE中需要猎取多个校准点,常用的校准点数量为5个。
方法如下:1、首先驱动程序在函数DdsiTouchPanelGetDeviceCaps 中设置校准点的个数;2、是系统在TouchDriverCalibrationPointGet中猎取每个校准点的屏幕坐标;3、是在屏幕界面的校准点坐标处显示一个位置符号,用户需要精确地在位置符号按下触摸屏;4、驱动程序通过TouchPanelReadCalibrationPoint函数读取相应的触摸屏坐标值;5、然后再开头下一个校准点,直到循环设定的次数后将采集到的触摸屏坐标值和校准点屏幕坐标送到TouchPanelSetCalibration函数中进行处理,该函数将产生校准基准参数。
校准完成之后,触摸屏便可以开头正常的操作了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本文介绍的校准方法需要三个目标点/或测试点,然后依次进行触摸测试,以确定该显示屏特有的校准因数。
最后通过这些校准因数将触摸屏的对应点与实际显示的对应点完全对应起来。
误差的来源
有几个误差源会影响触摸屏控制器,使之无法产生正确的对应点X和Y坐标。
最主要的误差源是电气噪声、机械误差及放大因子。
此外,操作者的误操作也会有所影响,如手指或铁笔按压时间不够长或压力不够大。
以上所有误差均会产生无用数据,必须对它进行纠正补偿才能使触摸屏正常工作。
在各种电气系统中,由热效应或电磁效应以及系统设计缺陷引起的电气噪声无处不在。
在触摸屏中,由于AD转换器的前端电路具有高输入阻抗,因此特别容易受到电气噪声的影响。
除了对带有触摸屏控制器的电路小心布局外,我们通常在AD转换器输入端增加低通滤波器来解决这一问题。
此外也可选择软件方法,舍弃AD转换中的最小的一、两位,并用算法将一些落在允许误差范围之外的数据点从采样流中去除。
这种软件算法也可消除由使用者产生的误差。
本文所阐述的校准方法可用来解决由于机械误差和放大因素引起的误差。
图3中的圆圈表示触摸屏下的LCD显示的图形,椭圆则表示当用户顺着LCD显示的图像画圈时,触摸屏对应点的集合,不过有所夸大。
这个重建的图形显然经过一系列旋转、移位和放大,而且在每个方向变换的参数不一样。
校准的重点则是将触摸屏上显示的这个重建图形经过变换,换算出与LCD显示的图形相一致的对应点集合。
校准的数学基础
为了得到一个通用解决方案,我们将每个点描述为一个数学参量。
如图4所示,可将LCD显示器上的每个点当作一个矢量PD,而该点在触摸屏上对应的点则当作矢量P。
此外,我们假设一个参量M,通过这个参量可将PD与P进行换算,即
PD=MP(1)这里的M是一个转换矩阵,也是我们要研究的对象。
如果能得到转换矩阵M中相关的数值,那么给定触摸屏上任一点P,我们就可换算出它在LCD显示器上的对应点PD。
现在假设LCD显示器上的任一点都与触摸屏上的某点相对应,但要经过旋转、移位和放大处理。
如果按矢量的长度和角度将每个点用(X,Y)两个坐标来表示,则LCD显示器和触摸屏上的点都可通过以下方程式来表达:
如果触摸屏在校准时与显示屏之间存在一个角度差异,为了进行补偿,要进行旋转处理,即θr=θD-θ,θr 是角度差。
这样我们便可得到一个中间点:
将每个点的X坐标和Y坐标以不同的因子放大,得到KX和KY。
考虑放大因子可以得到以下方程式,它更准确地描述了LCD显示器与触摸屏上点与点之间的对应关系:
最后,我们加上位移因子XT和YT,得到LCD显示器与触摸屏上点与点之间的对应方程式:
为了将方程式5再次变换以求取方程式中的未知量,假设触摸屏和LCD显示器上点与点之间有一个角度差θr,但这一角度极小,因此sinθr≈θr,而cosθr≈1.0。
根据这一假设我们得出另两个十分有用的近似方程式:
通过以下组合,方程式5可重新表示为:
方程式7的优点在于,它采用触摸屏坐标描述了LCD显示器上的点坐标。
上述方程式也可转换为:
利用我们原先的假设(即实际情况中的放大、旋转和位移因数均为常量),除X和Y之外,上述方程式右边的各项均为常量。
通过采用更方便的方式表达XD和YD坐标,我们可以得到触摸屏与LCD显示器各点之间的对应关系方程式:
可见,只有当触摸屏和LCD显示器间的角度差非常小时,才可运用上述公式。
校准矩阵
一般的校准算法常选取2-5个采样点来收集校准信息。
假设LCD显示器上的对应点可以通过触摸屏上的点转换得到,只需正好3个采样点我们就可得到校准数据。
需要3个采样点的原因在于方程式9a和9b有三个未知量。
从这3个采样点我们可获得足够的信息来建立并求解这一联立方程组。
采样点的选取也应当考虑到实际情况。
它们必须能得出非冗余的联立方程组,它们不能太靠近触摸屏的边缘(此处呈现非线性),此外它们的间隔必须足够宽,以便尽可能减少放大误差。
图5所示的P0、P1和P2这三个点符合这些条件。
这些点距触摸屏边缘约10%,分布足够散,得出以下非冗余方程式:
从而求出A、B、C、D、E和F的值。
一旦这些参数值定下来,便可利用方程式9,通过触摸屏上的原始数据计算出它在LCD显示器上的对应点。
上述联立方程组的未知量已求解出,此处不再推导。
直接跳过中间步骤得出最后结论,将K作为各方程式的公分母,便可得出未知量:
软件实现
实际的软件实现过程相对简单。
可从/code.htm上得到程序样本,它包括三个文件:alibrate.c、calibrate.h和sample.c。
第一个文件包含两个函数setCalibrationMatrix()和getDisplayPoint()。
前者实现了方程式13-18,后者则实现了方程式9。
D,而该点在触摸屏上对应的点则当作矢量P。
"hspace=12
src="/Article/UploadFiles/200504/20050420001204188.GIF"align=right vspace=12>启动文件包含了各种声明,另一个源文件则实现了一个控制台应用程序,这一程序执行校准功能,并示范如何在器件中使用这些函数。
sample.c中的代码假设在调用这些函数前,器件中实现了一个执行程序来采集校准数据。
表1是建议的校准步骤,将这些步骤执行完毕就实现了校准过程,此时设备便可开始从触摸屏系统接收精确的位置信息。
触摸屏控制器中设有中断程序,当程序将数字转换器的输出数据过滤后,它需要调用函数getDisplay-Point()。
通常,getDisplay-Point()函数调用是将触摸屏某点数据存入用户输入队列以前的最后一个步骤。
表1:建议的校准步骤。
=======================================
1.用全组数值调用setCalibrationMatrix()以设置显示屏驱动器,并提供原始存取数据(见sample.c)。
这样就不需要为存取数据构造特殊的函数。
你只需要按照与程序一样的机制获取纵坐标。
2.在坐标(XD0,YD0)画出第一个目标。
3.收集从触摸屏返回的数据,并存储在坐标(X0,Y0)。
4.在坐标(XD1,YD1)画出第二个目标。
5.收集从触摸屏返回的数据,并存储在坐标(X1,Y1)。
6.在坐标(XD2,YD2)画出第三个目标。
7.收集从触摸屏返回的数据,并存储在坐标(X2,Y2)。
8.采用参考显示数据和其产生的触摸屏数据作为变量,调用setCalibrationMatrix()函数。
=================================
其它考虑因素
执行采样函数是为了保证每次都获得准确结果,因而它的中间值未经过放大。
由于多数数字转换器提供的原始数据为10位,因此需要进行整数型32位数学运算,方程式15和18会产生31位的符号数。
执行这些方程式时要使用分辨率高达1,024点的触摸屏数字转换器,它适用于分辨率高达512点(宽度或高度)的显示器。
如果要在大面积的触摸屏中使用这些公式,就必须使用64位整数或将缩小输出值和中间结果,以免在计算校准因子时寄存器出现溢出。
函数getDisplayPoint()与校准矩阵有关,后者包括一套有效参量,这种采样结构使用自动变量来表明LCD 显示器和触摸屏的对应点间以及校准矩阵间的关系,不过在实际执行中,校准矩阵最好是一个全局结构,并在启动时正确初始化。
这些代码可从/code.htm免费下载,并用于多种场合。
不过该代码未经过任何优化处理。
本文小节
本文描述的触摸屏校准方法简单、灵活并可纠正一些常见的机械性误差。
这些误差(位移、放大、旋转)都是由于LCD显示器与触摸屏之间的不对应引起的。
尽管可通过机械方法来弥补,但是软件方法无需使用机械设备,且更能保证产品质量。
本文来自:USB中国开发论坛()详细出处参考:
/thread-18681-1-19.html。
