第五讲 统计检验(2)与预测
统计预测方法及预测模型

• 运算过程:
中南大学
统 计 预 测
ˆt ) 2 离差平方和 et ( yt y
(二)统计预测的步骤
确定预测目的 搜索和审核资料
选择预测模型和方法
分析预测误差,改进预测模型
提出预测报告
10.2
10.2.1 10.2.2
趋势外推法
趋势外推法概述 多项式曲线趋势外推法
10.2.3
10.2.4 10.2.5
指数曲线趋势外推法
生长曲线趋势外推法 曲线拟合优度分析
统 计 预 测
趋势外推法的基本思想
1993 200
1994 300
1995 350
1996 400
1997 500
1998 630
1999 700
利润额 yt
y a
2002 2003
中南大学
y ae
10000
统 bt 计 预 测
总需求量(件)
9000
y a bx cx
45 45 40 40 35 35 30 30 25 25 20 20 15 15 10 10 55 00
10.2.1
趋势外推法概述
一、趋势外推法概念和假定条件
趋势外推法概念:
当预测对象依时间变化呈现某种上升或下降趋势,没有明显的 季节波动,且能找到一个合适的函数曲线反映这种变化趋势时,就 可以用趋势外推法进行预测。 运用趋势外推法进行预测是基于两个基本假设: 一是决定过去预测对象发展的因素,在很大程度上仍将决定其未 来的发展; 二是预测对象发展过程一般是渐进变化,而不是跳跃式变化。 趋势外推法的突出特点是选用一定的数学模型来拟合预测变量的变 动趋势,并进而用模型进行预测。
● 某些客观事物的发展变化相对于时间推移,常表现出一定的规律性:
第五讲-指标体系及权重确定

,说明在固定m,p的情况下,单纯由q的变动引起的X的变动, 即由于平均开放床位数的增加,使得1988年1季度较1987年 同期的住院收入增加了0.35%。
.
3.平均床位周 q q1 1m m 转 1 0p p0 0次 5 41 8数 7 5 ..4 82 3 4 6指 9 4 1.8 3 3 0% 数 2
,说明在固定q,p的情形下,单纯由m的变动而引起的X的 变动,即由于病床周转次数的下降,使得住院收入减少了 6.18%。
4.出院者人 q q 1 均 1 m m 1 1p p 1 0 费 4 68 1用 ..5 0 8 0 3 4 6 8 1 指 1 8.2 9 0 5 % 数 5 6
,说明在固定q,m的情形下,单纯由p的变动而引起的X的 变动,即由于人均费用的增加,使住院收入增加了25.79%。
.
综合指数是编制总指数的基本计算形式。它一方面,我 们可利用综合指数的方法来进行因素分析;当我们可以把某个 总量指标分解为两个或多个因素指标时,如果固定其中的一个 或几个指标,便可观察出其中某个指标的变动程度;另一方面, 也可以综合观察多个指标同时变动时,对某一现象或结果影响 的程度和方向,进而评价其优劣。
得:W1=0.6370,W2=0.2583,W3=0.1047。
.
用同样方法可获得其他分层中各项目的权重系数,见表5-9 表5-9 第二层、第三层子目标权重系数
.
(4)求组合权重 病床使用率的组合权重系数
C1=0.6370*0.2970=0.1892; 治疗有效率的组合权重系数
C2=0.6370*0.5396*0.6670=0.2292 重患收治率的组合权重系数
1.30,那么加权后的权数分配为A:B:C:D=114:83:51: 27,经归一化处理后,A:B:C:D=0.41:0.30:0.19:0.10。
统计预测ppt课件

递推公式:Mt+2= Mt+1+( Xt+1-Xt-n+1 ) / n
2018/10/24
17
2018/10/24
18
2018/10/24
19
三、指数平滑法
2018/10/24
20
2018/10/24
21
第四节
回归分析预测法
一、回归分析预测法前提与基础 ——相关关系
相关关系的概念与种类 相关关系的分类
相关分析的内容与步骤
相关关系判断 相关表 相关图(散点图、散布图) 相关系数计算与判断
2018/10/24 23
•相关系数 r
1 ( x x )( y y ) n r 1 1 2 2 (x x) ( y y) n n 其他公式: r n xy x y n x ( x )
类推全局。
2018/10/24 10
二、集体经验判断法
(专家小组意见法)
含义——利用集体经验、 智慧,思考、分析、判断 综合后预测未来。
做法——组成专家小组集 中讨论 成员面对面预测 (包括理由) 综合处理,得最 终预测结果
2018/10/24 11
例1 某企业为制定下半年的生产计划,组织了一次由总经 理主持,有市场部、销售部、财务部、生产部四位部门经理 参加的销售预测会,在了解了市场上对产品的需求、本企业 和同行企业的销售情况等背景资料之后,进行了个人意见的 交流和讨论,并填写了下列预测值估计表。
•函数关系——确定性关系,现象之间存在着确定
数量依存关系。 •相关关系——不确定关系,现象之间存在着不确定 数量依存关系。
2018/10/24
22
相关关系的种类
中国医科大学研究生医学统计学 第五讲 计数资料及卡方检验2

(四)注意资料的可比性 用以比较的资料应是同质的,除 了要比较的处理因素外,其它条件应 基本相同。对于不同时期、地区、条 件下的资料应注意是否齐同。
• (五)对比不同时期资料应注意客观 条件是否相同 例如,疾病报告制度完善和资料完整 的地区或年份,发病率可以“升高”; 居民因医疗普及,就诊机会增加,或诊 断技术提高,也会引起发病率“升高” 。因此在分析讨论时,应根据各方面情 形全面考虑,慎重对待。
2 ( A T ) 2 RC RC TRC
=
[b- (b+c)/2]2
+
[c- (b+c)/2]2
(b+c)/2 [(c- b)/2]2 (b+c)/2
(b+c)/2
= [ (b-c)/2]2 +
(b+c)/2
= (b-c)2/2
(b+c)/2
(b c) 2 bc
H0:总体B = C H1:总体B≠C α= 0.05 b + c = 12 + 2 = 14 < 40。
本资料若不校正时,X2=4.35,P<0.05,结 论与之相反。
最小理论频数TRC的判断: R行与C列中,行合计数中的最小 值与列合计数中的最小值所对应
格子的理论频数最小。
如本例,第2行与第2列所对应的格子 理论频数最小(4.67)。
第二节 配对设计的四格表资料的χ2检验
(一)配对四格表形式 B 甲种属性 + 合计 A乙种属性 + 合计 a b a+b c d c+d a+c b+d n=a+b+c+d
无效 b d b+d
统计与预测的基本方法

统计与预测的基本方法统计与预测的基本方法是中小学数学课程中的一部分,它涉及到数据的收集、整理、分析和解释。
以下是统计与预测的基本知识点:1.数据收集:数据收集是统计与预测的第一步,可以通过调查、观察、实验等方式获取。
收集数据时要注意数据的真实性、完整性和可靠性。
2.数据整理:数据整理包括数据的清洗、排序和分类。
常用的整理方法有制作表格、绘制图表等,以便更好地理解和分析数据。
3.数据分析:数据分析是对数据进行解释和推理的过程。
常用的分析方法有描述性统计、推断性统计和概率论等。
描述性统计包括计算均值、中位数、众数等,推断性统计包括假设检验和置信区间等。
4.数据预测:数据预测是根据已有的数据来估计未来的趋势或结果。
常用的预测方法有趋势分析、时间序列分析和回归分析等。
5.概率论:概率论是统计与预测的基础,它研究随机事件的可能性。
常用的概率计算方法有排列组合、条件概率和贝叶斯定理等。
6.假设检验:假设检验是用来判断样本数据是否支持某个假设的方法。
常用的假设检验方法有t检验、卡方检验和F检验等。
7.置信区间:置信区间是用来估计总体参数的一个范围。
常用的置信区间计算方法有t分布、正态分布和卡方分布等。
8.相关性分析:相关性分析是用来衡量两个变量之间关系的强度和方向。
常用的相关性分析方法有皮尔逊相关系数和斯皮尔曼等级相关系数等。
9.线性回归:线性回归是用来建立自变量和因变量之间线性关系的模型。
常用的线性回归方法有最小二乘法和最大似然估计等。
10.时间序列分析:时间序列分析是用来研究时间上的数据变化的规律。
常用的时间序列分析方法有平稳性检验、自相关函数和滑动平均模型等。
11.指数平滑:指数平滑是一种用于时间序列预测的方法,它根据历史数据的权重来预测未来的趋势。
12.决策树:决策树是一种用于分类和回归的方法,它通过树状结构来表示不同特征的组合,并预测相应的结果。
13.聚类分析:聚类分析是一种无监督学习方法,它将数据分为若干个类别,以发现数据中的潜在模式和结构。
统计预测概述(精)

统计预测的概念和作用
• 统计预测的概念
• 统计预测:如何用科学的统计方法对事物的 未来发展进行定量推测,并计算概率置信区 间。
• 统计预测三要素:实际资料是预测的依据, 经济理论是预测的基础,预测模型是预测的 手段。
统计预测与经济预测的联系与区别
联系:
• A.都是以经济现象的数值作为研究对象 • B.直接或间接地为宏观和微观的市场预测、管理
3、预测结果的表达常常是预测区间或预测 范围
• 由于预测对象的不确定性,所以,预测结果 只能是一个区间估计。有人认为,在表达预 测结果时缺少这种衡量预测精度的范围,就 仅仅完成了预测任务的一半。
预测的分类
• 按预测对象所处的具体领域类
• 可以分为社会预测、经济预测、科学预测、技术 预测和军事预测五大类。各大类还可再分,例如: 经济预测可分为需求预测、资源预测、价格预测 等。
• 均方误差就是预测误差的平方的平均值。既
MSE
E(e2 )
1 n
1 t 1
(xt
xˆt )2
• 平均绝对百分误差
• 平均绝对百分误差的计算公式如下:
MAPE 1 n xt xˆt 100%
n t1 xt
• 可消除单位的不同产生的影响,判断方法。
• 这些规律是通过对客观事物和现象的过去经 验和资料进行定性和定量分析,经过一番 “去伪存真、去粗取精、由此及彼、由表及 里”的加工制作而发现的。并往往用数学模 型加以描述。这种认识既可以用来评价过去, 也可以用来预测未来。
• 预测为决策降低决策风险提供依据。
预测的特点
1、预测一般是不太准确的
• 由于预测所研究的是不确定的事物和现象,影 响它们的因素多而复杂,很难完全把握,这就 决定了预测结果的不准确性。
统计预测

(4)
进行指数曲线模型拟合。对模型 :
ˆt aebt y
两边取对数:
ˆ ln yt ln a bt
产生序列 ln y ,之后进行普通最小二乘估计 t 该模型。最终得到估计模型为: ˆ ln yt ln 303.69 0.0627t
ˆ yt 303.69 e0.0627t
指数曲线预测模型:
yt aebt 一般形式: ˆ
ˆ yt a bct 修正的指数曲线预测模型 :
ˆ 对数曲线预测模型:yt a b ln t
L 1 ae bt
bt
皮尔曲线趋势外推法:yt
龚珀兹曲线预测模型 :ˆ t ka y
三、趋势模型的选择
图形识别法:
这种方法是通过绘制散点图来进行的,即将时间序列 的数据绘制成以时间t为横轴,时序观察值为纵轴的图形, 观察并将其变化曲线与各类函数曲线模型的图形进行比较, 以便选择较为合适的模型。 差分法: 利用差分法把数据修匀,使非平稳序列达到平稳序列。 一阶向后差分可以表示为: yt yt yt 1
只需要因变量的历史资 料,是一切反复预测中 最简易的方法,但建立 模型所费的时间与自适 应过滤法不相上下
计算器
移动平均法
短期
不带季节变动的 反复预测 具有或不具有季 节变动的反复预 测
适用于趋势型态的 性质随时间而变化, 而且没有季节变动 的反复预测
计算器
在用计算机 建立模型后 进行预测时, 只需计算器 就行了
多项式曲线外推模型:
一次(线性)预测模型: yt b0 b t ˆ 1
ˆ 二次(二次抛物线)预测模型: yt b0 b t b2t 2 1
2 3 ˆ 三次(三次抛物线)预测模型:yt b0 b1t b2t b3t
统计预测参考答案

统计预测参考答案统计预测参考答案统计预测是一种利用数学和统计学方法来预测未来事件或趋势的技术。
它可以应用于各个领域,如经济学、社会学、医学等,对于决策和规划具有重要意义。
本文将探讨统计预测的原理、方法和应用,并分享一些统计预测的参考答案。
一、统计预测的原理和方法统计预测的原理基于大量的历史数据和概率理论。
通过对过去事件的统计分析,我们可以找到事件之间的规律和趋势,从而预测未来可能发生的情况。
统计预测的方法主要包括时间序列分析、回归分析和假设检验等。
时间序列分析是一种常用的统计预测方法,它通过对时间序列数据的分析,找出其中的趋势和周期性变化。
例如,我们可以通过分析过去几年的销售数据,来预测未来一段时间内的销售情况。
时间序列分析常用的方法有移动平均法、指数平滑法和ARIMA模型等。
回归分析是一种用于研究变量之间关系的统计方法。
它通过建立数学模型,来描述自变量和因变量之间的关系,并利用这个模型来进行预测。
回归分析常用的方法有线性回归、多项式回归和逻辑回归等。
例如,我们可以通过回归分析来预测一个人的身高与体重之间的关系。
假设检验是一种用于验证统计推断的方法。
它通过对样本数据的分析,来判断某个假设是否成立。
例如,我们可以通过假设检验来判断某个广告活动是否对销售额产生了显著影响。
二、统计预测的应用统计预测在各个领域都有广泛的应用。
在经济学中,统计预测可以用于预测GDP增长率、股市走势等。
在社会学中,统计预测可以用于预测人口增长、犯罪率等。
在医学中,统计预测可以用于预测疾病的传播趋势、患者的康复情况等。
统计预测在决策和规划中起着重要的作用。
通过对过去数据的分析和预测,决策者可以做出更加明智的决策,避免风险和损失。
例如,企业可以通过统计预测来确定产品的需求量,以便制定生产计划和库存策略。
政府可以通过统计预测来预测人口增长和城市发展趋势,以便规划城市建设和基础设施建设。
三、统计预测的参考答案统计预测的参考答案是通过对历史数据的分析和模型建立,得出的预测结果。
《统计预测》PPT课件
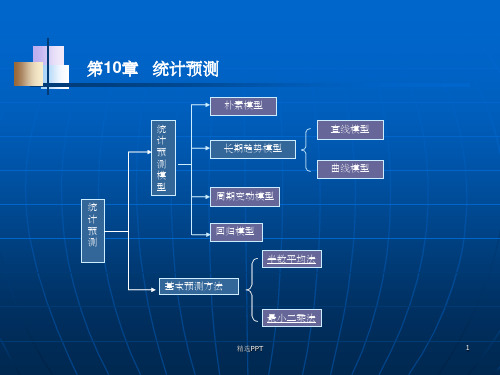
算具体数值。例如投资方向预
预测。
测,消费者需求倾向预测等等。
宏观预测 微观预测 定性预测 定量预测 短期预测 中期预测 长期预测
精选PPT
4
返回
统计预测的步骤
搜集、审核、整理资料 选择预测模型和预测方法 进行预测 分析预测误差和改进预测
精选PPT
5
返回
9—2统计预测模型与基本预测方法
统计预测模型 基本预测方法
精选PPT
17
返回
平均增(减)量预测模型
这种模型是用本期观测值与以前逐期平均增减量之和,作为下一期 的预测值。其公式为:
y t 1y t
(y n i 1 y i 1 )y ty n n 1 y 1
该模型适用于预测对象时间数列预测期增减量同于全时期平均增减 量的情形。
精选PPT
18
返回
增减速度预测模型
这种模型是把本期观测值与本期增减速度之积与本期观测值之和, 作为下一期的预测值。其公式为:
y t1yt(1yty t y 1t1)yt(yy t t1)
该模型适用于预测对象各期增减的绝对量虽不等,但却存在相对 稳定的增减速度的情形。
精选PPT
19
返回
平均发展速度预测模型
这种模型是把本期观测值与时间数列全时期的平均发展速度之积, 作为下一期的预测值。其公式为:
精选PPT
6
返回
统计预测模型
(一)简单预测模型 (二)长期趋势模型 (三)周期性变动模型 (四)回归模型
精选PPT
7
返回
简单预测模型
观测值预测模型 固定平均数预测模型 移动平均数预测模型 增减量预测模型 平均增(减)量预测模型 增减速度预测模型 平均发展速度预测模型
统计学中的数据分析与预测技巧

统计学中的数据分析与预测技巧统计学是一门应用数学,其中数据分析与预测技巧是非常重要的组成部分。
统计学旨在收集、分类、分析和解释数据,以便从中推断结论和进行预测。
数据分析是统计学的一个重要步骤。
数据分析旨在将数据转化为有意义的信息。
数据分析可以通过统计方法、计算机科学和机器学习技术来完成。
数据分析可以揭示数据之间的关系和趋势,从而提供有关业务和市场的深入见解。
预测技术是数据分析的一部分。
它旨在使用历史数据来预测未来事件的发生。
预测建立在趋势和循环性规律性的基础上。
预测技术可以在不同行业中得到广泛应用,如金融、医疗保健、零售和制造业等。
统计学的数据分析与预测技巧包括以下方面:1. 描述统计学描述统计学是用来总结和描述数据的一种方法。
描述统计学包括测量中心趋势、离散程度和分布类型等方面。
常见的描述统计学方法包括均值、中位数、众数、方差、标准差和百分位数。
2. 探索性数据分析探索性数据分析(EDA)旨在通过可视化和统计方法来发现数据之间的关系和趋势。
EDA的目标是从数据中发现新的见解和洞察力。
EDA包括散点图、箱形图、直方图和核密度估计图等。
3. 数据挖掘数据挖掘是一种通过计算机处理大量数据来揭示隐藏模式和知识的技术。
数据挖掘可以用来预测未来事件、识别趋势和定位机会。
数据挖掘技术包括聚类分析、决策树、随机森林和神经网络等。
4. 统计推断统计推断是基于样本数据来推断总体数据的一种方法。
它可以估计平均值、方差、比例和相关系数等。
统计推断还可以用来测试假设和确定置信区间和偏差。
5. 时间序列分析时间序列分析是一种通过时间顺序排列的一系列数据来预测未来趋势和周期性的方法。
此方法可以被用在摄氏温度、设备故障情况和股票价格等方面。
时间序列分析技术包括趋势分析、季节性分析和周期性分析等。
总之,统计学中的数据分析与预测技巧是非常重要的。
数据分析可以提供有关趋势和模式的深入见解,而预测技术可以在业务和市场推理中提供参考意见。
统计分析与预测公开课教案

统计分析与预测公开课教案第一节:统计分析的基本概念与应用(1000字)统计分析是一种通过收集、整理、分析和解释数据来揭示数据背后规律的方法。
它在各个领域都有广泛的应用,包括市场调研、经济预测、医学研究等。
本节将介绍统计分析的基本概念和应用。
首先,统计分析的基本概念包括数据收集、数据整理、数据分析和数据解释。
数据收集是指通过各种方式获取数据,可以是实地调查、问卷调查、实验观察等。
数据整理是指对收集到的数据进行整理、清洗和转换,使其适合进行进一步的分析。
数据分析是指通过统计方法对数据进行计算、描述和推断,以揭示数据背后的规律。
数据解释是指对分析结果进行解释和说明,得出结论并提出相应的建议。
其次,统计分析的应用非常广泛。
在市场调研中,统计分析可以帮助企业了解消费者的需求和偏好,为产品开发和营销策略提供依据。
在经济预测中,统计分析可以通过对历史数据的分析,预测未来的经济走势,为政府和企业的决策提供参考。
在医学研究中,统计分析可以帮助医生和研究人员分析大量的临床数据,发现疾病的风险因素和治疗效果,指导临床实践。
第二节:统计分析的基本方法与技巧(1000字)统计分析涉及到许多基本方法和技巧,本节将介绍其中的一些重要内容。
首先,描述统计是统计分析的基础。
描述统计包括数据的集中趋势和离散程度的度量。
集中趋势可以通过平均值、中位数和众数等指标来描述,离散程度可以通过方差、标准差和四分位数等指标来描述。
描述统计可以帮助我们了解数据的分布情况和变异程度。
其次,推断统计是统计分析的核心。
推断统计是通过从样本中获取信息,推断总体的特征。
推断统计包括参数估计和假设检验。
参数估计是通过样本数据估计总体参数的值,例如通过样本均值估计总体均值。
假设检验是通过对样本数据进行统计推断,判断总体参数是否符合某种假设。
第三节:预测分析的基本方法与应用(1000字)预测分析是一种通过历史数据和趋势来预测未来情况的方法。
它在经济、金融、市场等领域都有重要的应用。
统计学中的统计分析与模型预测

统计学中的统计分析与模型预测统计学被广泛地应用于各类数据的分析和处理。
统计分析和模型预测是统计学的两个重要领域,是所有统计学应用的基础。
一、统计分析统计分析是一种用来解释数据的方法。
它可以用来确定数据中出现的模式、变化和异常。
在统计分析中,人们经常使用各种矩阵、频率表、图表和其他工具来揭示数据中的有关因素。
当人们在分析数据时,往往会先计算各种统计量,比如均值、中位数和标准差等。
以此为基础,可以进行更高级的分析,比如回归分析、协方差分析和方差分析等。
这些分析方法可以帮助人们提取出数据之间的关系,并加强对数据背后因果关系的理解。
二、模型预测在统计学中,模型预测是指利用已知数据来预测未来发展趋势的方法。
为了做到这一点,需要建立一个合适的模型,以确保有足够的预测值。
常用的模型包括线性回归模型、时间序列模型和多项式回归模型等。
准确的预测模型对于许多领域的决策都是至关重要的,比如经济、营销、金融和医疗等。
一个好的模型应该能够处理大数据、适应各种情况,并同样准确地预测未来数据。
三、统计分析与模型预测的联系统计分析与模型预测两者之间有着密不可分的联系。
统计分析通过对数据的探索来揭示数据间的关系和可能的变化趋势,为模型预测提供了必要的前提和条件。
而模型预测则可以通过对数据的模拟来验证与进一步完善统计分析的结果。
一个好的预测模型需要依据统计学原理,对数据进行有针对性的分析。
通过建立合理的模型,可以进一步准确地预测未来的发展趋势和变化。
预测结果的准确性,也反过来验证了统计分析的可靠性和正确性。
四、统计分析与模型预测的应用统计分析与模型预测在现代社会中有着广泛的应用。
从商业领域到医疗卫生,甚至到政府各级部门,都需要使用统计学方法进行数据分析和预测。
比如,在金融领域中,统计分析可以帮助投资者分析市场行情并制定相应投资策略。
而模型预测则可以预测股票和市场的趋势,指导投资者在股市中实现利润最大化。
在医疗卫生领域中,统计分析和模型预测也扮演着重要的角色。
统计预测与决策PPT课件( 16页)

•
2、孤单一人的时间使自己变得优秀,给来的人一个惊喜,也给自己一个好的交代。
•
3、命运给你一个比别人低的起点是想告诉你,让你用你的一生去奋斗出一个绝地反击的故事,所以有什么理由不努力!
•
4、心中没有过分的贪求,自然苦就少。口里不说多余的话,自然祸就少。腹内的食物能减少,自然病就少。思绪中没有过分欲,自然忧就少。大悲是无泪的,同样大悟
设时间序列为 x 1 , x 2 , . . . , 移动平均法可以表示为: 1t
F t 1xtxt 1...xtN 1/NN tN 1xi
式中: x t 为最新观察值;
F t 1 为下一期预测值。
由移动平均法计算公式可以看出,每 一新预测值是对前一移动平均预测值的修
悲心,饶益众生为他人。
•
14、梦想总是跑在我的前面。努力追寻它们,为了那一瞬间的同步,这就是动人的生命奇迹。
•
15、懒惰不会让你一下子跌倒,但会在不知不觉中减少你的收获;勤奋也不会让你一夜成功,但会在不知不觉中积累你的成果。人生需要挑战,更需要坚持和勤奋!
•
16、人生在世:可以缺钱,但不能缺德;可以失言,但不能失信;可以倒下,但不能跪下;可以求名,但不能盗名;可以低落,但不能堕落;可以放松,但不能放纵;可以虚荣,
•
7、生命的美丽,永远展现在她的进取之中;就像大树的美丽,是展现在它负势向上高耸入云的蓬勃生机中;像雄鹰的美丽,是展现在它搏风击雨如苍天之魂的翱翔中;像江
河的美丽,是展现在它波涛汹涌一泻千里的奔流中。
•
8、有些事,不可避免地发生,阴晴圆缺皆有规律,我们只能坦然地接受;有些事,只要你愿意努力,矢志不渝地付出,就能慢慢改变它的轨迹。
(1)移动平均法有两种极端情况
第5讲 预处理技术之五:推断统计

依据什么做出决策?
1. 若假设为H0:=500,H1:≠ 500。样本均 值为495,拒绝H0吗?样本均值为502,拒 绝H0吗?
2. 做出拒绝或不拒绝原假设的依据是什么? 3. 传统上,做出决策所依据的是样本统计量,
现代检验中人们直接使用由统计量算出的犯
第Ⅰ类错误的概率,即所谓的值
(=0.01)
左侧检验
50个零件尺寸的误差数据 (mm) 1.26 1.19 1.31 0.97 1.81 1.13 0.96 1.06 1.00 0.94 0.98 1.10 1.12 1.03 1.16 1.12 1.12 0.95 1.02 1.13 1.23 0.74 1.50 0.50 0.59 0.99 1.45 1.24 1.01 2.03 1.98 1.97 0.91 1.22 1.06 1.11 1.54 1.08 1.10 1.64 1.70 2.37 1.38 1.60 1.26 1.17 1.12 1.23 0.82 0.86
4. 总是有符号 , 或
H0 : = 某一数值 H0 : 某一数值 H0 : 某一数值
例如, H0 : 10cm
备择假设
1. 也称“研究假设”,H1或Ha表示 2. 所表达的含义是总体参数发生了变化或变量之间
有某种关系
3. 备择假设通常用于表达研究者自己倾向于支持的 看法,然后就是想办法收集证据拒绝原假设,以 支持备择假设
临界值
H0
2008年8月
用统计量决策
(右侧检验 )
抽样分布
置信水平
Region of Rejection
拒绝H0
1 -
2
Region of Nonrejection
【第五章统计估计和假设检验】

【第五章统计估计和假设检验】第五章统计估计和假设检验统计学的基本问题就是根据样本所提供的信息对总体的分布以及分布的数字特征作出统计推断。
统计推断包括两大部分:一是统计估计,二是假设检验。
统计估计问题就是根据样本的数字特征来估计总体参数的数字特征,因此通常也称作参数估计。
参数估计根据所得出结论的方式不同有两种形式:点估计和区间估计。
假设检验就是对关于总体分布的一些数字特征或分布函数所做的假设进行检验,以判断其正确性。
假设检验也分为两类:一类是对总体分布的一些数字特征进行检验,称为参数假设检验;另一类是要求根据样本所提供的信息对关于分布函数的假设进行检验,此时只检验分布,而不对参数作检验,这称作非参数的假设检验。
非参数检验将在第六章进行讨论,本章着重讨论参数检验。
第一节点估计一、点估计的极大似然法点估计就是以单个数据对总体参数值作出估计。
若未知的总体参数为,这时是一个未知的常数。
我们根据抽样样本的观察值构造一个统计量()来估计总体参数。
由于抽样的随机性,统计量是一个随机变量。
点估计就是将的具体值作为的估计值。
显然,这样做必然会有误差产生。
这种误差就称为抽样误差。
极大似然法是一种对参数点估计的重要方法之一。
我们先用一个例子说明其原理。
例5-1。
设有一批产品,质量上分为正品与次品。
产品的次品率有两种估计:0.1和0.4,今随机抽样15件产品,发现只有一件是次品。
现根据这一抽样情况,来决定用哪一种次品率来估计更为可靠呢?记A =“抽取15件产品,只有一件是次品”,设抽得正品用X=0,抽得次品用X=1来表示。
抽样结果只有X=0 与X=1 两种情形,于是,可得事件A发生的概率为:P(A)= 其中:是这批产品的次品率。
若次品率=0.1,则P(A)=×0.1=0.0229 若次品率=0.4,则P(A)=×0.4=0.0003。
现在事件A 既然在一次观察中就发生了,直观地我们可以认为事件A发生的概率P(A)不会小,故应选择使P(A)较大的次品率作为产品的次品率的估计更为可靠些。
统计预测和决策讲义课件.pptx

回总目录 回本章目录
第四节 定性预测的其他方法
[解答] • 加权平均法:根据各部门负责人对市场情况的熟悉程
度以及他们在以往预测判断中的准确程度,分别给予 不同部门负责人不同的评定等级,在综合处理时,采 用不同的加权系数。如定销售部门负责人的加权系数 为2,其他两个部门负责人的加权系数为1,从而下一 年度笔记本电脑的销售预测值为:
回总目录 回本章目录
第四节 定性预测的其他方法
二、厂长(经理)评判意见法
• 优点:迅速、及时和经济;集中了各个方面有经验人 员的意见,使预测结果比较准确可靠;不需要大量的 统计资料,适合于对那些不可控因素较多的产品进行 销售预测;如果市场发生了变化,可以立即进行修正。
• 缺点:预测结果容易受主观因素的影响;对市场变化、 顾客的愿望等问题了解不细,因此预测结果一般化。
房产需求量(套)
1
2111 2144 2156 2200 2222 2244 2267 2278 2311
2
1978 2100 2133 2156 2200 2222 2267 2278 2500
3
2044 2100 2133 2144 2244 2267 2289 2311 2444
回总目录 回本章目录
415 570 770 585(千件) 3
回总目录 回本章目录
第二节 德尔菲法
[解答] • 加权平均预测:将最可能销售量、最低销售量和最高
销售量分别按0.50、0.20和0.30的概率加权平均,则预 测平均销售量为:
570 0.50 415 0.20 770 0.30 599(千件)
回总目录 回本章目录
《STATA第五讲》课件

总结词:在Stata编程中,宏和循环结构的使用可能会 带来一些问题。
错误与调试
详细描述:熟悉常见的语法错误提示,根据错误提示检 查代码;采用逐步调试方法,设置断点、单步执行和查 看变量值,定位和修正逻辑错误。
2023
REPORTING
THANKS
感谢观看
2023
PART 06
Stata常见问题解答
REPORTING
数据处理问题解答
总结词
当遇到数据导入困难时,可能是由于文件格 式、编码或分隔符不正确所致。
详细描述
确保数据文件格式(如.csv、.dta等)与 Stata软件兼容;检查文件编码(如UTF-8 、ANSI等),确保与软件设置一致;确认 数据字段分隔符(如逗号、制表符等)是否 正确。
Stata是一种统计分析软件,专门用于数据管理和统 计分析。
02
它提供了广泛的数据分析工具,包括描述性统计、 回归分析、方差分析、生存分析等。
03
Stata具有易于使用的界面和强大的编程语言,使数 据分析变得简单而高效。
Stata的用途
数据分析
Stata提供了各种数据分析工具, 可以帮助用户进行数据探索、描 述性统计和复杂统计分析。
Cox比例风险模型
研究多个因素对生存时间的影响,并假设风险函 数与时间无关。
ABCD
Kaplan-Meier曲线
非参数方法描述生存函数随时间的变化。
时间依赖性Cox模型
在某些情况下,风险函数可能随时间变化,可以 使用此模型进行描述。
2023
PART 04
Stata编程基础
REPORTING
Stata命令基础
数据管理
Stata具有强大的数据管理功能, 可以方便地导入、导出数据,进 行数据清洗和整理。
计量经济学重点笔记第五讲

第五讲 自相关高斯-马尔科夫假定五是:(,)0,i j Cov i j εε=≠如果该假定不成立,那么称模型的误差项是序列相关的。
由于序列相关主要针对于时间序列数据,因此我们把脚标i 改写为t ,把样本容量N 改写为T 。
笔记:1、如果基于横截面数据的回归模型其误差项是相关的,则称为空间自相关。
但是要记住,除非观察顺序具有某种逻辑或者经济上的意义,否则,在横截面数据回归中,观察顺序是可以随意的,因此,也许在某种观测顺序下误差项呈现出一种模式的自相关但在另一种观测顺序下又呈现出另外一种模式的自相关。
然而,当我们处理时间序列时,观测服从时间上的一种自然顺序。
2、在时间序列模型中,误差项经常被称之为冲击(Shock)。
对经济系统的冲击经常具有持续性,从而这为误差项序列相关提供了现实依据。
一、 自相关的后果与仅仅违背同方差假定一样,仅仅违背序列无关假定并不影响OLS 估计量所具有的线性、无偏性、一致性等性质。
在误差项序列相关的情况下,OLS 估计法并没有利用这个信息,故OLS 估计量不是最有效的。
我们下面来推导在误差项序列相关情况下OLS 估计量的方差表达。
假定真实模型是:t 01t t y x ββε=++则12ˆ12222()()()()(())()()[()]t t t t t t t t tx x Var x x x x Var x x Var x x x x βεδβεε-=+---==--∑∑∑∑∑∑ 在假定五:0,0t t jj εεδ+=≠下,有:122ˆ222()[()]tt t x x x x βεδδ-=-∑∑但如果假定五不成立,那么正确的方差表达式应该是:12ˆ1221122()2()()[()]t t t j T T tt t t j t j t x x x x x x x x βεεεδδδ+--+==-+--=-∑∑∑∑所以, OLS 法下通常的系数估计量方差的表示是错误的,一般来说它小于真实的方差。
统计预测与分析

第一章经济预测的基本问题● 1.1 预测的基本概念● 1.2 经济预测的产生和发展● 1.3 预测的分类● 1.4 预测方法的选择● 1.5 预测的步骤● 1.6 预测精度的确定●1.1 预测的基本概念⏹预测(forecast):借助对过去的探讨去寻求对未来的了解。
⏹应用领域:经济、政治、军事、教育、科技、气象等。
⏹※经济预测:根据经济发展的历史资料,现在掌握的经济信息以及主观的经验教训,客观环境条件,对经济活动未来可能产生的后果和可能发展过程作出科学的预见。
⏹例如:根据接受调查的63位经济学家的平均预测,美国第四季度经济增长速度将减缓至0.5%。
1.2 经济预测的产生和发展经济预测是随着社会经济发展和人们参与商品交换、市场竞争逐步形成和发展的。
中国:2000年以前就出现了经济预测的萌芽。
春秋末期,政治、外交、军事、大商人范蠡:“论其有余不足,则知贵贱;贵上极则贱,贱下极则反贵”。
据此规律预测市场行情,成为巨商。
不足:经验预测或定性预测,即依靠预测者的个人学识和经验所判断的,不能满足现代化大生产所带来的社会经济发展要求。
发展:将经济学、数学、统计学以及稍后发展的计量经济学、运筹学、信息论、系统论、控制论等应用于经济预测,逐步丰富和发展了预测的理论和方法,使经济预测走上了数学化、模型化及定量化。
理论基础:20世纪40年代凯恩斯主义的兴起。
技术条件:电子计算体系的创立。
社会应用:各国预测机构大量产生,如:美国“麦格劳—希尔公司”,美国政府智囊团“兰德公司”。
中国:经济预测起步较晚,研究和应用不理想。
为适应我国新的经济体制和经济发展的要求,许多科研机关和高等院校都成立了专门的预测研究机构。
1.3 预测的分类按时期长短分(1)长期经济预测:对5年以上的经济发展情况所做的预测,为经济长期规划和战略目标的制定提供依据。
例如:在商业领域中,可以商品的生产和销售发展方向、产品有关技术发展趋势,生产要素的供应变化趋势等作出总体预测和战略预测。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、变量的显著性检验
从拟合优度中看出,拟合优度越高,就说明样本 回归线对观测值的拟合就越好,但这只是推测,被 解释变量与解释变量之间的线性关系是否显著,或 者解释变量对被解释变量是否有显著的线性影响, 需要我们去研究,这就是变量的显著性检验。
回归分析中,主要是针对变量X前的参 数真值是否为零来检验。
2
,则在显著性水平
下拒绝原假设 H0 : k 0 ,即认为 X 对 Y 有显著影响 ►若
p
2
,则在显著性水平
下不拒绝原假设 H0 : k 0 ,即认为 X 对 Y 没有显著
影响
规则:当 p 时,P值越小,越能拒绝原假设 H 0
12
对于一元线性回归方程中的0,可构造如下t 统计量进行显著性检验:
(较复杂不具体证明)
ˆ 2 ei2 (n 2)代替 2时,对 e F标准化的变量 t 当用 为
t
eF E (eF ) SE (eF)
^
ˆF YF Y
1 ( X F X )2 ˆ 1 2 n x i
~ t (n 2)
23
构建个别值的预测区间
给定显著性水平 ,查 t 分布表得自由度为n—2 的临界值 t 2 (n 2) ,则有
2
26
若对于前面的例子,我们得到了总体均值 E Y X 1000 的95%的置信区间为
533.05,814.62
如何解释?
给定 X 0 1000 在重复抽样中,每100个类似于(533.05,814.62) 的区间将有95个包含着真实的均值。 如果我们对每一个X值求类似于(533.05,814.62) 的95%的 置信区间,把这些区间的端点连接起来,我们就得到如图 所展示的一个关于总体回归函数的置信带。 同样我们也可得到Y的个别值在 X 1000的95%的置信区间为 (372.03,975.65) 如果我们对每一个X值求类似于(372.03,975.65)的95%的置 信区间,把这些区间的端点连接起来,我们就得到如图所 展示的一个关于Y的个别值的置信带。
预测值、平均值、个别值的关系
SRF
点预测值
PRF
真实平均值 E YF X F
个别值
F
XF
YF
eF
ˆ 是真实平均值预测值的点估计,也是个别值预测本思想:
ˆ 值不一定等于真实总 由于存在抽样波动,预测的 Y F 体条件均值 E YF X F 。 ˆ 和 E YF X F 都有关的统计量 必须找出与 Y F
2
^
~ t (n 2)
给定 , 查 t 分布表得 ▼如果 t * t (n 2)
2
t (n 2)
则拒绝原假设 H 0 : 2 0 ▼如果 t * t (n 2)
2
则不拒绝原假设 H0 : 2 0
检验步骤:
(1)对总体参数提出假设 H0: 1=0, H1:10
P(t 2 t t 2 ) 1
P(t 2 t
^
ˆ E (Y X ) Y F F F ˆ ) SE(Y F
^
t 2 ) 1
^
ˆ F t SE(Y ˆ F )] E(Y X ) [Y ˆ F t SE(Y ˆ F )]} 1 p{[Y 2 F F 2
ˆ 的分布分析 具体做法:从 Y
F
ˆ ˆX ˆ Y F 0 1 F
ˆ ˆ X ) E( ˆ ) X E( ˆ ) X ˆ ) E( E(Y F 0 1 F 0 F 1 0 1 F
ˆ Var Y F
1 X X 2 F 2 2 xi n
相对于显著性水平 的临界值为: 计算的统计量为:
t (单侧)或 t 2(双侧)
t
*
(小概率事件) (大概率事件)
1
t 2
0
t
*
t 2
统计量 t
6
2、变量的显著性检验
确立假设:原假设为
备择假设为
H 0 : 1 0
H1 : 1 0
(本质:检验 1 是否为0,即检验 X i 是否对Y有显著影响)
回归分析结果的报告
经过模型的估计、检验,得到一系列重要的数 据,为了简明、清晰、规范的表述这些数据,计量 经济学通常采用以下规范化的方式:
ˆ 103.172 0.777 X Y i i t
2
估计的样本回归函数 标准误差SE 估计的t统计量
98.41 0.0425 1.048 18.29
平均值的预测区间
于是,在1-的置信度下,总体均值 EYF X F 的置信区间为
2 2 ( X X ) ( X X ) 1 1 F F ˆF t ˆF t ˆ ˆ [Y , Y ] 2 2 2 2 n n xi xi
个别预测值的置信区间
基本思想:
1、假设检验 I. II. 先根据实际问题的要求提出一个论断, 称为原假设, 然后根据样本信息,看能得到什么结 果,如果导致一个不合理的结果,拒 绝原假设。
III.
判断结果合理与否,是基于“小概 率事件不易发生”这一原理的。
注意这里的“接受和拒绝”
基本概念回顾: 临界值与概率、大概率事件与小概率事件
0
Yˆ ~ N (
F
X ,
1 F
2
(
1 n
(X
0
X )2
)) x
2 i
E YF
t
ˆ X Y F 0 1 F ˆ 1 XF X 2 n x i
2
t n 2
给定显著性水平α,查 t 分布表,得自由度n-2的临界值,则有
25
(2)平均值和个别值预测区间都不是常数, 是随 X F 的变化而变化的,当 X F X 时,预测区间最小。 (3)预测区间上下限与样本容量有关,当样本容量 n→∞时,个别值的预测区间只决定于随机扰 动的方差。
预测区间
1 (XF X ) ˆ ˆ 1 YF Y F t 2 2 n xi
当 2 未知,且样本容量较小时
只能用 ˆ
2
2 去代替 ,可利用 t分布作 t 检验:
t
*
ˆ 2 2 ˆ) SE ( 2
^
ˆ 2 ˆ) SE ( 2
^
~ t (n 2)
t
*
ˆ 2 2 ˆ) SE ( 2
^
ˆ 2 ˆ) SE ( 2
ˆ F t SE(e )] Y [Y ˆ F t SE(e )]} 1 P{[Y 2 F F 2 F
因此,一元回归时Y的个别值的置信度为 1 的预测区间 上下限为
2 ( X X ) 1 ˆ ˆ 1 F 2 YF Y F t 2 n xi
(2)以原假设H0构造t统计量,并由样本计算其值
t*
ˆ 0 1 S ˆ
1
(3)给定显著性水平,查t分布表,得临界值t /2(n-2)
(4) 比较,判断
注意1:
一个“大”的 t
注意2:
是与原假设相抵触的迹象。
观察t分布表,当自由度为20或更大时,计算的t值 如果是2.5或3或更大,则我们就不需要再查阅t分 布表以评定所估的参数的显著性,它必定是要拒 绝原假设,即该变量通过了显著性检验。 当自由度小于20时,我们要查阅t分布表。
2.4 一元线性回归模型的统计检验 2.5 一元线性回归分析的应用:预测问题
一、参数的区间估计 一、拟合优度检验 二、拟合优度检验 三、变量的显著性检验 三、参数的置信区间估计
二、变量的显著性检验
三、参数的置信区间估计
ˆ ˆ 1 P 1 1 1
ˆ t 1 1 : t n 2 ˆ se 1
^
^
被解释变量Y区间预测的特点
(1)Y平均值的预测值与真实平均值有误差,主要
是受抽样波动影响
预测区间
2 ( X X ) 1 F ˆF t ˆ YF Y 2 2 n x i
Y个别值的预测值与真实个别值的差异,不仅受抽 样波动影响,而且还受随机扰动项的影响 预测区间
2 ( X X ) 1 F ˆF t ˆ YF Y 1 2 2 n x i
R 0.9766 df 8 可决系数和自由度 F 2859 DW 1.85 F统计量 DW统计量
2.5 一元线性回归分析的应用:预测问题
计量经济预测是一种条件预测:
模型设定的关系式不变 所估计的参数不变 解释变量在预测期的取值已作出预测
预测的类型
对被解释变量的预测分为:平均值和个别值预测 对被解释变量的预测又分为点预测和区间预测
显著性水平 —
犯第一类错误的概率——拒绝了真值的假设的概率 经典假设检验方法的痛处 —选择 的武断
用 P 值判断参数的显著性
假设检验的 p 值:
p 值是基于既定的样本数据所计算的统计量,拒绝 原假设的最低显著性水平。 统计分析软件中通常都给出了检验的 p 值
相对于显著性水平 计算的统计量:
t ˆ
2
X
2 i
ˆ 0 0
2 i
n x
2 i
ˆ 0 S ˆ
0
~ t (n 2)
在上述收入-消费支出例中,首先计算2的估计值
ˆ
2
e
2 i
n2
y
n2
ˆ 2 x2 1 i
3354955 0.6702 7425000 2734 10 2
