物理化学知识点总结(热力学第一定律)

合集下载

物理化学上热力学第一定律知识框架图总结

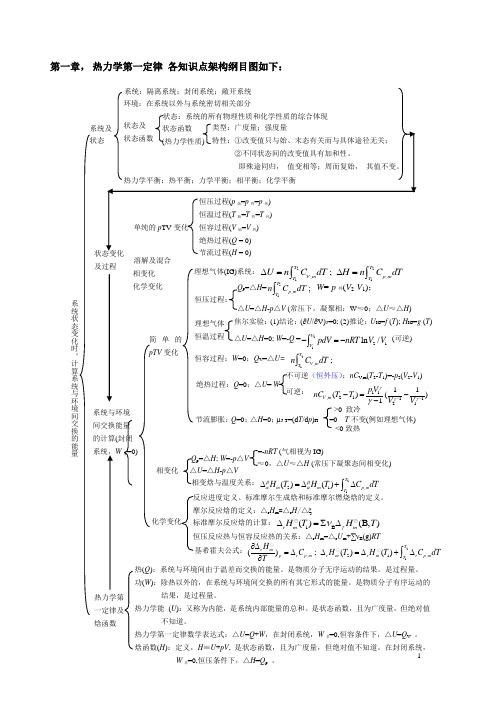
1第一章，热力学第一定律各知识点架构纲目图如下：及过程溶解及混合化学变化相变化热(Q )：系统与环境间由于温差而交换的能量。

是物质分子无序运动的结果。

是过程量。

功(W )：除热以外的，在系统与环境间交换的所有其它形式的能量。

是物质分子有序运动的结果，是过程量。

热力学能 (U )：又称为内能，是系统内部能量的总和。

是状态函数，且为广度量，但绝对值不知道。

热力学第一定律数学表达式：△U =Q +W ，在封闭系统，W 非=0,恒容条件下，△U =Q V 。

焓函数(H )：定义，H ≡U +pV , 是状态函数，且为广度量，但绝对值不知道。

在封闭系统，W 非=0,恒压条件下，△H =Q p 。

热力学第一定律及焓函数系统与环境间交换能量的计算(封闭系统，W 非=0)简单的pTV 变化理想气体(IG)系统：2211,,;T TV m p mT T U n C dT H n C dT ∆=∆=⎰⎰ 理想气体恒温过程焦尔实验：(1)结论：(∂U /∂V)T =0; (2)推论：U IG =f (T ); H IG =g (T ) △U =△H =0; W =-Q =2121ln /VVpdV nRT V V -=-⎰ (可逆)恒容过程：W =0；Q V =△U= 21,;TV mT n C dT ⎰绝热过程：Q =0；△U = W 不可逆（恒外压）：nC V ,m (T 2-T 1)=-p 2(V 2-V 1) 可逆： 11,21112111()()1V m p V nC T T V V γγγγ---=-- Q p =△H =21,;T p m T n C dT ⎰W =-p 外(V 2-V 1)； △U =△H -p △V (常压下，凝聚相：W ≈0；△U ≈△H )恒压过程：节流膨胀：Q =0；△H =0；μJ-T =(d T /d p )H =0 T 不变(例如理想气体) <0致热 >0 致冷相变化 △U =△H -p △VQ p =△H ; W =-p △V≈0，△U ≈△H (常压下凝聚态间相变化)=-nRT (气相视为IG) 相变焓与温度关系：2121,()()Tm m p mT H T H T C dT ββαα∆=∆+∆⎰化学变化摩尔反应焓的定义：△r H m =△r H /△ξ 恒压反应热与恒容反应热的关系：△r H m =△r U m +∑νB (g)RT标准摩尔反应焓的计算：1B ()(B,)r m f mH T H T ν∆=∑∆反应进度定义、标准摩尔生成焓和标准摩尔燃烧焓的定义。

物理化学知识点(全)

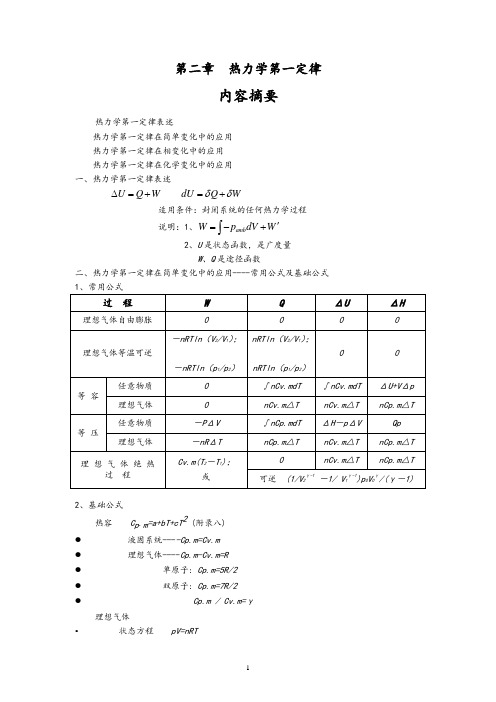
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用热力学第一定律在相变化中的应用热力学第一定律在化学变化中的应用一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件：封闭系统的任何热力学过程说明：1、amb W p dV W '=-+⎰2、U 是状态函数，是广度量W 、Q 是途径函数二、热力学第一定律在简单变化中的应用----常用公式及基础公式过程WQΔUΔH理想气体自由膨胀理想气体等温可逆－nRTln （V 2/V 1）；－nRTln （p 1/p 2） nRTln （V 2/V 1）；nRTln （p 1/p 2）0 0等容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等压任意物质－P ΔV ∫nCp.mdT ΔH －p ΔV Qp 理想气体－nR ΔT nCp.m △TnCv.m △T nCp.m △T 理想气体绝热过程 Cv.m(T 2－T 1)；或nCv.m △TnCp.m △T可逆 (1/V 2γ-1－1/ V 1γ-1)p 0V 0γ/(γ－1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m － p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = －Δ蒸发H m (T)Δ凝固H m (T) = －Δ熔化H m (T) Δ凝华H m (T) = －Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点： 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。

《物理化学》知识点汇总

《物理化学》知识点汇总热力学系统：热力学系统是指热力学研究的对象，是物质或物质的集合体。

状态：状态是指热力学系统中物质的宏观性质及其变化的状态。

热力学第一定律：能量守恒定律在热力学中的表现形式，它说明能量不能被创造或消失，只能从一种形式转化为另一种形式。

能量守恒：能量既不能被创造也不能被消失，它只能从一种形式转化为另一种形式。

热力学第二定律：热力学中描述自然过程方向性的定律，它表明，在一个封闭系统中，自发过程总是向熵增加的方向进行。

熵增：在封闭系统中，自发过程总是向熵增加的方向进行，也就是说，系统总是朝着更大的混乱状态发展。

相平衡：在热力学中，相平衡是指不同物相之间达到的平衡状态。

化学平衡：在化学反应中，反应物和生成物之间达到的平衡状态。

化学动力学：研究化学反应速率以及反应机制的科学。

表面化学：研究表面吸附、表面反应等表面现象的化学分支。

胶体分散系：由一种或多种物质在另一种物质中分散而成的系统。

以上是《物理化学》中的一些重要知识点，这些知识点是理解物理化学概念和应用的基础。

在学习过程中，需要不断巩固和深化对这些知识点的理解，以更好地掌握物理化学这门学科。

《经济法基础》是会计专业技术资格考试中的一门科目，主要考察考生对经济法相关知识的掌握程度和应用能力。

考试内容涉及广泛，包括经济法的基本概念、市场主体、市场秩序、宏观调控、劳动法等。

考试形式为闭卷、笔试，考试时间为90分钟。

经济法的基本概念：经济法的定义、特征、原则等。

市场主体：各类企业、个体工商户、农村承包经营户等市场主体的设立、变更和终止的相关法律规定。

市场秩序：市场竞争、市场准入、市场退出等方面的法律规定。

宏观调控：产业政策、财税政策、货币政策等宏观调控手段的法律规定。

劳动法：劳动者的权利和义务，劳动合同的签订和履行，劳动安全卫生、社会保险等方面的法律规定。

经济法涉及的法律法规众多，需要考生具备较为扎实的法律基础。

考试内容涉及面广，考生需要全面掌握各个方面的知识。

物理化学知识点总结(热力学第一定律)

热力学第一定律一、基本概念1.系统与环境敞开系统：与环境既有能量交换又有物质交换的系统。

封闭系统：与环境只有能量交换而无物质交换的系统。

（经典热力学主要研究的系统）孤立系统：不能以任何方式与环境发生相互作用的系统。

2.状态函数：用于宏观描述热力学系统的宏观参量，例如物质的量n、温度T、压强p、体积V等。

根据状态函数的特点，我们把状态函数分成：广度性质和强度性质两大类。

广度性质：广度性质的值与系统中所含物质的量成正比，如体积、质量、熵、热容等，这种性质的函数具有加和性，是数学函数中的一次函数，即物质的量扩大a倍，则相应的广度函数便扩大a倍。

强度性质：强度性质的值只与系统自身的特点有关，与物质的量无关，如温度，压力，密度，摩尔体积等。

注：状态函数仅取决于系统所处的平衡状态，而与此状态的历史过程无关，一旦系统的状态确定，其所有的状态函数便都有唯一确定的值。

二、热力学第一定律热力学第一定律的数学表达式：对于一个微小的变化状态为：dU=公式说明：dU表示微小过程的内能变化，而δQ和δW则分别为微小过程的热和功。

它们之所以采用不同的符号，是为了区别dU是全微分，而δQ和δW不是微分。

或者说dU与过程无关而δQ和δW却与过程有关。

这里的W既包括体积功也包括非体积功。

以上两个式子便是热力学第一定律的数学表达式。

它们只能适用在非敞开系统，因为敞开系统与环境可以交换物质，物质的进出和外出必然会伴随着能量的增减，我们说热和功是能量的两种传递形式，显然这种说法对于敞开系统没有意义。

三、体积功的计算1.如果系统与环境之间有界面，系统的体积变化时，便克服外力做功。

将一定量的气体装入一个带有理想活塞的容器中，活塞上部施加外压。

当气体膨胀微小体积为dV时，活塞便向上移动微小距离dl，此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积因为我们假设活塞没有质量和摩擦，所以此活塞实际上只代表系统与环境之间可以自由移动的界面。

物理化学知识点归纳

物理化学知识点归纳物理化学是化学学科的一个重要分支，它综合运用物理学的原理和方法来研究化学现象和过程。

以下是对物理化学一些重要知识点的归纳：一、热力学第一定律热力学第一定律，也就是能量守恒定律，表明能量可以在不同形式之间转换，但总量保持不变。

在热力学中，通常用公式△U ＝ Q ＋ W来表示，其中△U 是系统内能的变化，Q 是系统吸收或放出的热量，W 是系统对外做功或外界对系统做功。

例如，在一个绝热容器中进行的化学反应，如果体系对外做功，那么内能就会减少；反之，如果外界对体系做功，内能就会增加。

二、热力学第二定律热力学第二定律有多种表述方式，其中克劳修斯表述为：热量不能自发地从低温物体传到高温物体。

开尔文表述为：不可能从单一热源取热使之完全变为有用功而不产生其他影响。

熵（S）的概念在热力学第二定律中至关重要。

对于一个孤立系统，熵总是增加的，这意味着系统总是朝着更加混乱和无序的方向发展。

比如，混合气体自发扩散后，不会自动分离回到初始状态，因为这个过程熵增加了。

三、热力学第三定律热力学第三定律指出，绝对零度（0K）时，纯物质完美晶体的熵值为零。

这一定律为计算物质在不同温度下的熵值提供了基准。

四、化学平衡化学平衡是指在一定条件下，可逆反应中正逆反应速率相等，反应物和生成物的浓度不再随时间改变的状态。

平衡常数（K）是衡量化学平衡的重要参数。

对于一个一般的化学反应 aA ＋ bB ⇌ cC ＋ dD，平衡常数 K 的表达式为：K ＝ C^cD^d ／ A^aB^b （其中方括号表示物质的浓度）。

影响化学平衡的因素包括温度、浓度、压强等。

例如，对于吸热反应，升高温度会使平衡向正反应方向移动；增加反应物浓度，平衡也会向正反应方向移动。

五、相平衡相平衡研究的是多相体系中各相的组成、性质以及它们之间的相互转化规律。

相律是描述相平衡体系中自由度、组分数和相数之间关系的定律，其表达式为 F ＝ C P ＋ 2，其中 F 是自由度，C 是组分数，P 是相数。

物理化学热力学第一定律总结

物理化学热力学第一定律总结热力学第一定律是热力学中最基本的定律之一，并且与能量守恒原理密切相关。

它陈述了一个闭合系统内部的能量转换过程。

根据热力学第一定律，能量是不能从真空中产生的，也不能消失，它只能在系统内部进行转化。

该定律可以用以下公式表达：ΔU=Q-W其中，ΔU表示系统内部能量的变化，Q表示系统吸收的热量，W表示系统对外界做的功。

这个公式说明了能量的守恒，即系统吸收的热量和对外界做的功之和等于系统内部能量的变化。

当系统从外界吸收热量时，其内部能量会增加，而当系统对外界做功时，其内部能量会减少。

这种能量的转化是一个相互依存的过程，可以通过热力学第一定律进行描述。

热力学第一定律的应用十分广泛，并且在实际问题中具有重要的意义。

以下是热力学第一定律在不同领域的应用：1.在化学反应中，热力学第一定律可以用来计算反应的焓变。

通过测量反应前后系统吸收或释放的热量，可以计算出反应的焓变，从而了解反应的能量转化和方向。

2.在工程领域，热力学第一定律常用于能量转换设备的设计和优化中。

例如，蒸汽轮机、内燃机和制冷机等能量转换系统的效率可以通过热力学第一定律进行评估和计算。

3.在生物学领域，热力学第一定律可以用于研究生物体内的能量转化过程。

例如，通过测量生物体吸收的热量和对外界做的功，可以计算出生物代谢的能量转换效率。

热力学第一定律的重要性在于揭示了能量守恒的基本原理，为能量转化和能量利用提供了基础理论支持。

它对于研究和解决实际问题具有重要指导意义。

热力学第一定律的应用可以帮助我们评估能量转换过程的效率，优化能量利用方式，并促进可持续发展。

总之，物理化学热力学第一定律表述了能量守恒的原则，描述了能量转化和能量守恒的过程。

它在化学、工程、生物等领域具有广泛的应用，并对能量转换和利用提供了理论支持。

热力学第一定律的理解和应用可以帮助我们更好地理解能量转换过程，优化能量利用方式，并实现可持续发展的目标。

物理化学热力学一定律、二定律复习

H nC p,m dT
T1
T2
H Qp
此式适用于W′＝0、dp＝0的封闭系统所进行的一切过程
理想气体恒温pVT 变化:
U 0

H 0
4. 化学反应热效应
由生成焓求反应焓 r H m B f H m B 由燃烧焓求反应焓 r H m B c H m B
2. 单纯pVT变化过程的熵变
V2 T2 S nR ln nCV ,m ln V1 T1 p1 T2 S nR ln nC p ,m ln p2 T1
将C p ,m、CV ,m看成定值
p2 V2 S nCV ,m ln nC p ,m R ln p1 V1
3. 相变化过程的熵变
U QV 适用于W ' 0, dV 0的封闭系统所进行的一切过程。
H U ( pV )，式中：( pV ) p2V2 pV1 1
此式适用于封闭系统的一切过程。
此式适用于n、Cp,m恒定的理想气体单纯pVT变化的一切过程；或n、Cp,m恒定的任意单相纯物质的恒压变温过程。
熵判据
不可逆自发隔离系统：S 0 或 dS 0 可逆平衡自发 S隔离 S系统 S环境 0 平衡
V2 p1 nR ln 理想气体的恒温可逆和不可逆过程：T S nR ln V1 p2
纯物质的恒压变温可逆和不可逆过程： p S nC p ,m ln T2 T1 纯物质的恒容变温可逆和不可逆过程：V S nCV ,m ln T2 T1 理想气体pVT都变的可逆过程：
5. 理想气体的绝热可逆方程：
T2
T1
Cv ,m

物理化学知识点总结

第一章热力学第一定律一、基本概念系统与环境，状态与状态函数，广度性质与强度性质，过程与途径，热与功，内能与焓。

二、基本定律热力学第一定律：ΔU =Q +W 。

焦耳实验：ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = －p e d V恒外压过程：W = －p e ΔV可逆过程：1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热：Q V =ΔU （封闭系统不作其他功）等压热：Q p =ΔH （封闭系统不作其他功）焓的定义：H =U +pV ; d H =d U +d(pV )焓与温度的关系：ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义：V V )(T U C ∂∂=；p p )(T H C ∂∂=定压热容与定容热容的关系：nR C C =-V p 热容与温度的关系：C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程：ΔU =0 ; ΔH =0 ; W =－Q =⎰-p e d V 等容过程：W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程：W =－p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程：Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程：Q =0 ; 利用C V (T 2-T 1)=－p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化：ΔH =Q =n Δ＿H ；Ｗ＝－p (V 2-V 1)=－pV g =－nRT ; ΔU =Q +W3、热化学物质的标准态；热化学方程式；盖斯定律；标准摩尔生成焓。

摩尔反应热的求算：)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律：)(])([,p B C T H m p BB m r ∑=∂∆∂ν。

物理化学基本知识点与公式总结

3、气体组分的化学势
RT lnp/p
B

B

RT
ln p B /p

RT lnp/p
B

B

RT lnpBB/p
化学平衡总结
化学平衡总结
1、标准平衡常数
K 0 ( pBeq p0 )B
Qp
H

T2 T1
nC
p,m
dT
n,
C
为常数
p,m
nCp,m (T2 T1)
Cp,m-CV,m=R（理想气体）单原子理想气体： CV,m=3/2 R
双原子理想气体：CV,m=5/2 R
多原子理想气体：CV,m=3R
可逆相变
Q2 相变过程的热力学计算
不可逆相变
状态函数法
Q3
热力学第一定律
可不逆可相逆
热力学
第三定律
PVT
程程程过程程程
程
变相变
热力学基本方程
Maxwell关系式
过程判据
S判据
0 dS隔离 0
0
不可逆,自发可逆, 平衡不可能
不可逆 dSiso dSsys dSamb 0 可逆
A判据 A 0
A=U-TS
自发进行
nC p ,m
ln

T2 T1

nR
ln

p1 p2

S

nCV ,m
ln

p2 p1

nC p ,m
ln

V2 V1

物理化学热力学第一定律精要

dH = C p dT
DU = QV =
ò
T1
CV dT
W ：系统对环境做功系统吸热 Q＞0 ，系统放热 Q＜0 ；系统对环境做功W ＜0 ，环境对系统做功W ＞0 。 3. 体积功 dW = -pe dV pe ：外压。（1）自由膨胀： pe = 0 （2）恒压膨胀：（V2＞V1 ） ①一次：W = -pe ( V2 -V1 ) ②二次： W = -pe¢( V ¢ -V1 ) - pe ( V2 -V ¢) （V1＜V ¢＜V2 ， pe¢＜pe ）（3）准静态膨胀（可逆过程）（V2＞V1 ）
æ ¶D H ö ÷ r ÷ ç DC p = ç ÷ ç ÷ ç è ¶T ÷ ø p
T2
T1
n BC p,m (B)
Dr H m = å (n B DbH m )
dW = dU = CV dT
10. 绝热可逆过程的过程方程
pV = K1
热容比 g =
g
TV
C p,m CV ,m
g -1
= K2
T p
g
1-g
= K3
不准确，用作估算。 19. 离子摩尔生成焓
11. 理想气体的绝热功
1 定义： H2 (g) ¾¾ H+ (aq, ¥) + e2
双原子分子多原子分子单原子分子
CV ,m 3 R 2 5 R 2 3R
C p,m 5 R 2 7 R 2 4R
Ventta Lab.
9. 理想气体的绝热过程 Q=0
Dr H m = -å (n B DcH m )
dU = dW
18. 键焓定义：某个键在 1 mol 各种化合物中键能的平均值称为该键的键焓 DbH m 。

物理化学知识点归纳

第二章热力学第一定律一、热力学基本概念1.状态函数状态函数,是指状态所持有的、描述系统状态的宏观物理量，也称为状态性质或状态变量.系统有确定的状态，状态函数就有定值；系统始、终态确定后，状态函数的改变为定值；系统恢复原来状态，状态函数亦恢复到原值。

2.热力学平衡态在指定外界条件下，无论系统与环境是否完全隔离,系统各个相的宏观性质均不随时间发生变化,则称系统处于热力学平衡态。

热力学平衡须同时满足平衡（△T=0)、力平衡（△p=0）、相平衡（△μ=0）和化学平衡（△G=0）4个条件.二、热力学第一定律的数学表达式1.△U=Q+W或dU=ΔQ+δW=δQ—p amb dV+δW`规定系统吸热为正，放热为负.系统得功为正，对环境做功为负。

式中p amb为环境的压力,W`为非体积功。

上式适用于封闭系统的一切过程.2．体积功的定义和计算系统体积的变化而引起的系统和环境交换的功称为体积功.其定义式为:δW=-p amb dV（1）气体向真空膨胀时体积功所的计算 W=0（2）恒外压过程体积功 W=p amb （V 1—V 2）=-p amb △V 对于理想气体恒压变温过程 W=—p △V=—nR △T （3）可逆过程体积功 W r =⎰21p V V dV(4）理想气体恒温可逆过程体积功W r =⎰21p V V dV =—nRTln(V 1/V 2）=—nRTln （p 1/p 2）（5）可逆相变体积功 W=-pdV三、恒热容、恒压热，焓 1.焓的定义式H def U + p V 2．焓变(1）△H=△U+△（pV)式中△（pV)为p V 乘积的增量，只有在恒压下△（pV)=p(V 2—V 1)在数值上等于体积功。

（2）△H=⎰21,T T m p dT nC此式适用于理想气体单纯p VT 变化的一切过程，或真实气体的恒压变温过程,或纯的液、固态物质压力变化不大的变温过程。

3. 内能变（1）△U=Qv式中Qv 为恒热容.此式适用于封闭系统，W`=0、dV=0的过程。

物理化学知识点总结(热力学第一定律)

物理化学知识点总结(热力学第一定律).doc物理化学知识点总结（热力学第一定律）摘要：热力学第一定律是热力学的基础之一，它描述了能量守恒的原理。

本文将对热力学第一定律进行详细的阐述，包括其定义、数学表达式、应用以及在物理化学中的重要作用。

关键词：热力学第一定律；能量守恒；物理化学；系统；状态函数一、引言热力学是研究能量转换和能量传递规律的科学。

热力学第一定律，也称为能量守恒定律，是理解和分析热力学过程的关键。

二、热力学第一定律的定义热力学第一定律指出，能量既不能被创造也不能被消灭，只能从一种形式转换为另一种形式，或者从一个系统转移到另一个系统。

在封闭系统中，能量的总量保持不变。

三、热力学第一定律的数学表达式对于一个封闭系统，热力学第一定律可以用以下数学表达式表示：[ \Delta U = Q - W ]其中，( \Delta U ) 是系统内能的变化，( Q ) 是系统吸收的热量，( W ) 是系统对外做的功。

四、系统与状态函数在热力学中，系统是指我们研究的对象，它可以是封闭的或开放的。

状态函数是描述系统状态的物理量，如温度、压力、体积等，它们只与系统的状态有关，而与系统状态变化的过程无关。

五、热力学第一定律的应用理想气体的等体过程在等体过程中，体积保持不变，系统对外不做功，热力学第一定律简化为 ( \Delta U = Q )。

理想气体的等压过程在等压过程中，压力保持不变，系统对外做膨胀功，热力学第一定律可以表示为 ( \Delta U = Q + W )。

理想气体的等温过程在等温过程中，温度保持不变，理想气体的内能不发生变化，热力学第一定律简化为 ( 0 = Q - W )。

六、热力学第一定律与能量转换热力学第一定律不仅适用于热能和机械能之间的转换，还适用于其他形式的能量，如电能、化学能等。

七、热力学第一定律在物理化学中的应用化学反应在化学反应中，热力学第一定律用于计算反应热，即反应过程中系统吸收或释放的热量。

大学物理化学知识点归纳

大学物理化学知识点归纳一、物理化学的基本概念物理化学是研究物质的性质和变化规律的学科，它融合了物理学和化学的理论与方法，对于理解和探索物质世界具有重要意义。

二、物理化学的热力学1. 热力学基本概念：热力学研究物质在不同温度、压力和组成条件下的能量转化和热效应。

2. 热力学第一定律：能量守恒定律，描述了物质的内能和热交换之间的关系。

3. 热力学第二定律：能量的不可逆性原理，描述了自然界中能量转化的方向和过程的规律。

4. 熵的概念：熵是衡量系统混乱程度的物理量，与物质的排列和有序程度相关。

5. 自由能与平衡：自由能是描述系统稳定性和反应方向的指标，平衡状态下自由能取最小值。

三、物理化学的动力学1. 动力学基本概念：动力学研究物质内部结构与变化之间的关系，以及反应速率和反应机理等问题。

2. 反应速率与速率常数：反应速率描述了反应速度的快慢，速率常数与反应机理密切相关。

3. 反应平衡与化学平衡常数：反应平衡是指在一定条件下反应物与生成物浓度保持不变的状态，化学平衡常数决定了反应的平衡位置。

4. 反应机理与活化能：反应机理描述了反应的详细步骤和中间产物，活化能是指反应过程中所需的最小能量。

四、物理化学的量子化学1. 量子化学基本概念：量子化学研究微观粒子（如电子）在原子和分子尺度下的性质和行为。

2. 波粒二象性：微观粒子既具有波动性又具有粒子性，具体表现为波粒二象性。

3. 波函数与薛定谔方程：波函数是描述微观粒子状态的数学函数，薛定谔方程描述了波函数的演化和微观粒子的运动规律。

4. 量子力学的应用：量子力学提供了解释原子和分子结构、光谱学和化学键性质等的理论基础。

五、物理化学的电化学1. 电化学基本概念：电化学研究物质在电解质溶液中的电荷转移和电极反应等现象。

2. 电解与电解质：电解是指将化学物质转化为离子的过程，电解质是能够在溶液中导电的化合物。

3. 电流与电解质溶液：电流是指电荷流动的物理现象，电解质溶液中的电流与离子在电场中的迁移相关。

物理化学知识点总结

热力学第一定律一、基本概念1、体系和环境（1）、体系和环境体系：作为研究对象的物质及其所在的空间称为体系；环境：体系以外且与体系密切相关的物质及其所在空间称为环境；界面：体系和环境之间存在有界面，界面可以是容器的器壁，也可以是假想的界面，本质上，界面是认为设想的几何面，其中不包含物质，不具备物理和化学性质。

（2）、体系的分类体系和环境之间可以有物质和能量的交换，依据此，可将体系分为敞开体系、封闭体系、隔离体系。

①、敞开体系：体系与环境之间既有能量交换又有物质交换；②、封闭体系：体系与环境之间只有能量交换而无物质交换；③、隔离体系：体系与环境之间既无能量交换也无物质交换。

2、状态和状态函数（1）、状态和状态函数的定义状态：状态是指体系所有性质的总体表现；状态函数：体系的热力学性质称为状态函数。

（2）、状态函数的性质：①、体系的状态一定，状态函数就有定值。

②、状态函数的变化值只取决于始、末状态，与变化的经历无关。

③、状态函数的微分为全微分。

（3）、状态函数的分类。

①、广度性质：体系的广度量与物质的数量成正比，如V，U等，它具有加和性②、强度性质：体系的强度量与物质的数量无关，如T，p等，它不具有加和性。

（4）、热力学平衡态一定条件下，体系中各个相的宏观性质不随时间变化，将体系与环境隔离体系的性质仍不改变的状态。

热力学平衡态应满足如下条件：①、热平衡：体系中的各个部分温度相等，即体系内部处于热平衡，有单一的温度；②、力学平衡：体系内部处于力平衡，有单一的压力；③、相平衡：体系内部各相之间的分布达到平衡，宏观上没有任何一种物质从一个相转移到另一个相；④、化学平衡：体系内部处于化学平衡，宏观上表现为体系的组成不随时间变化。

（5）、状态函数的数学性质若状态函数①、单值性：环形积分等于零，，或可写作全微分性质：③、归一化关系④、复合函数的偏微分，则⑤、偏微商的分离⑥、完全微分3、过程与途径在一定环境条件下，体系发生由始态到终态的变化，则称体系发生了一个热力学过程，（1）、变化过程①、等温过程：体系始态与终态温度相同，且变化过程中温度始终等于环境温度、等于；②、等压过程：体系始态与终态压力相同，且变化过程中压力始终等于环境压力、等于；④、体系由变化到，程，计算其热力学函数，如热力学能、熵变等要设计过程。

物理化学知识点总结[物理化学知识点归纳]

物理化学知识点总结[物理化学知识点归纳]热力学第一定律...............................................................................（1）第二章热力学第二定律. (3)第三章化学势 (7)第四章化学平衡 (10)第五章多相平衡 (12)第六章统计热力学基础 (14)第七章电化学 (16)第八章表面现象与分散系统 (20)第九章化学动力学基本原理 (24)第十章复合反应动力学 (27)物理化学知识点归纳根据印永嘉物理化学简明教程第四版编写，红色的公式要求重点掌握，蓝色的公式掌握。

第一章热力学第一定律本章讨论能量的转换和守恒，其目的主要解决变化过程的热量，求功的目的也是为了求热。

1. 热力学第一定律热力学第一定律的本质是能量守恒定律，对于封闭系统，其数学表达式为∆U =Q +W 微小过程变化：d U =δQ +δW只作体积功：d U =δQ −p e d V 理想气体的内能只是温度的函数。

2. 体积功的计算：δW V =−p 外d VW V =−∫p 外d VV 1V 2外压为0（向真空膨胀，向真空蒸发）：W V =0；恒容过程：W V =0恒外压过程：W V =−p 外(V 2−V 1) 恒压过程：W V =−p (V 2−V 1) 可逆过程：W V =−∫V 2V 1p d V （主要计算理想气体等温可逆、绝热可逆过程的功）3. 焓和热容由于大多数化学反应是在等压下进行的，为了方便，定义一个新的函数焓：H =U +pV焓是状态函数，是广度性质，具有能量，本身没有物理意义，在等压下没有非体积功的热效应等于焓的改变量。

等容热容：C V = δQ V⎛∂U ⎛=⎛⎛ d T ⎛∂T ⎛V等压热容：C p =δQ p⎛∂H ⎛=⎛⎛ d T ⎛∂T ⎛p对于理想气体：C p −C V =nR4. 理想气体各基本过程中W 、Q 、∆U 、∆H 的计算5. 焦耳-汤姆逊系数µ=⎛⎛∂T ⎛1⎛∂H ⎛=−⎛⎛⎛，用于判断气体节流膨胀时的温度变化。

物理化学热力学第一定律总结

热一定律总结一、通用公式ΔU = Q + W绝热： Q = 0，ΔU = W 恒容(W ’=0)：W = 0，ΔU = Q V恒压(W ’=0)：W =-p ΔV =-Δ(pV )，ΔU = Q -Δ(pV ) → ΔH = Q p 恒容+绝热(W ’=0) ：ΔU = 0 恒压+绝热(W ’=0) ：ΔH = 0焓的定义式：H = U + pV → ΔH = ΔU + Δ(pV )典型例题：3.11思考题第3题，第4题。

二、理想气体的单纯pVT 变化恒温：ΔU = ΔH = 0变温：或或如恒容，ΔU = Q ，否则不一定相等。

如恒压，ΔH = Q ，否则不一定相等。

C p , m – C V , m = R双原子理想气体：C p , m = 7R /2, C V , m = 5R /2 单原子理想气体：C p , m = 5R /2, C V , m = 3R /2典型例题：3.18思考题第2,3,4题书2.18、2.19三、凝聚态物质的ΔU 和ΔH 只和温度有关或典型例题：书2.15ΔU = n C V , md T T 2T1∫ ΔH = n C p, md T T2 T1∫ ΔU = nC V , m (T 2-T 1) ΔH = nC p, m (T 2-T 1)ΔU ≈ ΔH = nC p, m d T T 2T 1∫ΔU ≈ ΔH = nC p, m (T 2-T 1)四、可逆相变（一定温度T 和对应的p 下的相变，是恒压过程）ΔU ≈ ΔH –ΔnRT(Δn ：气体摩尔数的变化量。

如凝聚态物质之间相变，如熔化、凝固、转晶等，则Δn = 0，ΔU ≈ ΔH 。

101.325 kPa 及其对应温度下的相变可以查表。

其它温度下的相变要设计状态函数不管是理想气体或凝聚态物质，ΔH 1和ΔH 3均仅为温度的函数，可以直接用C p,m计算。

或典型例题：3.18作业题第3题五、化学反应焓的计算其他温度：状态函数法Δ H m (T ) = ΔH 1 +Δ H m (T 0) + ΔH 3α ββ α Δ H m (T )α βΔH 1ΔH 3Δ H m (T 0)α β可逆相变298.15 K:ΔH = Q p = n Δ H m αβΔr H m ө =Δf H ө(生) – Δf H ө(反) = y Δf H m ө(Y) + z Δf H m ө(Z) – a Δf H m ө(A) – b Δf H m ө(B) Δr H m ө =Δc H ө(反) – Δc H ө(生) = a Δc H m ө(A) + b Δc H m ө(B) –y Δc H m ө(Y) – z Δc H m ө(Z)ΔH = nC p, m (T 2-T 1)ΔH = n C p, m d TT 2T1∫ΔU 和ΔH 的关系：ΔU = ΔH –ΔnRT （Δn ：气体摩尔数的变化量。

物化上热力学第一定律知识点总结

1 热力学第一定律1.1 重点与难点严格区分状态函数与非状态函数（Q 、W ），并熟练掌握状态函数的数学特征状态的定义，状态函数性质及数学特征。

体系始终态一旦确定，其状态函数改变量可通过设计途经而求算。

体系状态发生变化，其状态函数值可能发生变化，但并不一定全部状态函数都一定发生变化。

求算过程的热与功，不能随意设计途径。

唯有在特定条件下 Q,W 能与状态函数改变量相关联（如等压无其他功 Q p =ΔH ），才与途径无关。

体系状态函数具备五个数学特征。

1.1.1 热力学第一定律数学表达式及其在理想气体中的应用表达式()'V UQ W Q W W ∆=-=-+，只适用于封闭体系，随着条件变化，存在 ΔU 与 Q 、W 之间的转换关系。

一定量理想气体 U 和 H ，均决定于温度（但若有相变发生，或并非自始至终为理想气体，则不属此列）。

故它无论发生 p,V 怎样变化，只要有 T 变化，可直接引用2211T T vm pm T T U nC dTH nC dT∆=∆=⎰⎰或。

弄清节流过程与绝热过程的区别。

明确理想气体绝热可逆过程方程与状态方程的实质；前者指某过程进行中各参量间的关系，后者指体系达平衡状态时各参量间的关系。

在 p ～V 图上绝热线的陡度比等温线的大，两线只能相交一点。

自同一始态出发，经绝热可逆与绝热不可逆过程是不能达到相同的终态，但计算绝热体积功时可用同一式：,1122,(1p m a V mC p V p V W C γγγ-==-为热容商，即）1.1.2 掌握比较热力学可逆过程与不可逆过程的定义，特点。

热力学第一定律在热化学中的应用热总值不变定律，意味着固定始终且指定同一条件（全部恒压，或全部恒容，决非恒压恒容混相）下，ΔH 或 ΔU 可自设计各步途径热值之加和而求算。

基尔霍夫(Kirchhoff)定律：()()2121T r m r m Tr pm H T H T C dT θθ∆=∆+⎰∆ 有积分号"∫"意指可逆，故中间若有相变，则另添加焓变值。

《物理化学》热力学第一定律知识总结

第一章热力学第一定律和热化学理想气体:分子间无相互作用力，分子本身没有体积的气体PV=nRT 适用于理想气体，其中T 单位为K(开氏度=摄氏度+273.15），V 单位为m 3,R=8.314J.mol -1.k -1第二节热力学基本概念1.＊敞开系统：系统与环境之间没有物质的交换，只要能量的交换孤立系统（隔离系统）无物质，无能量交换2.状态函数：只与始终态有关，V 、P 、T 、热容、热力学能、焓、熵、吉布斯函数、亥姆兹函数等都属于状态函数过程函数：与途径有关3.＊热和功（状态函数）热（Q ）是无序的；功(W)是有序的，dv p 21v v e ⎰-=W （所采用的压力均外压力）系统吸热为正，Q>0; 系统对环境做功，W<0（dv>0）。

系统放热为负，Q<0; 系统从环境得到功，W>0(dv<0)。

功可表示为强度性质与广度性质改变量的乘积：机械工=F （力）*dl （位移）体积功=—p （外压）*dv （提及的改变） ——由于系统变化与环境交换的功。

除此为非体积功。

表面功（非体积功）=σ（表面张力）*da （表面积的改变）电功（非体积功）=E （电位）*dq （电量的改变）4.热力学第一定律的三种说法。

其数学式：W Q U +=∆5.＊热力学能又称内能（Q ）(状态函数）除掉宏观中的整体势能以及整体动能，在微观中其分子之间存在平动能和转动能等。

另一种说法：组成物体分子的无规则热运动动能和分子间相互作用势能的总功。

第四节功的过程与可逆过程定外压，）（12v v p --=W ；多次定外压，)'2()1'('v v Pe v v Pe W ----=准静态膨胀过程（可逆过程）)1/2ln(v v nRT W -=系统做功最大Ps ：自由膨胀和恒压定温膨胀（压缩）皆为不可逆过程压缩系放热；膨胀系吸热。

第五节焓（封闭，非体积功为零）定容热：U Q v ∆=; 焓（定压）)(12V V P U H Q e p -+∆=∆=第六节热容m p m v C C ,,-------2/'c ,T bT a C m p ++=（假若题目已经告知此经验公式，根据公式)(12,T T nC Q H m p p -==∆算出Qp ）如若未告知，则理想气体在常温下，单原子分子的R C R C m p m v 2/5,2/3,,==；刚性双原子分子（线性分子）的R C R C m p m v 2/7,2/5,,==非刚性双原子分子的R C R C m p m v 2/8,2/6,,==多原子分子的R C R C m p m v 4,3,,==绝热可逆过程：常数=-1r TV ；绝热过程功的计算公式标准摩尔生成热等于产物的标准摩尔生成焓乘以其系数的总和减去反应物的标准摩尔生成焓乘以其系数的总和。

物理化学第一章热力学第一定律

常用的热量单位是卡(cal)：
热力学所采用的热功当量为:
1
2
3
4
5
01
等压过程和焓
02
若体系经历一等压过程,且不作有用功,由热力学第一定律:
03
U＝Q＋W＝Q－∫p外dV
04
等压过程： p外＝p2=p1
05
U＝Q－p1or2(V2－V1)
06
对上式进行改写：
07
(U2－U1)＝Q－(p2V2－p1V1)
理想气体的微观模型: 满足以下两个条件的体系为理想气体.
. 分子之间没有作用力, 分子间不存在作用势能;
. 分子的体积可以忽略不计, 可视为数学上的点.
热力学定义: 满足理想气体状态方程的体系. 方程为:
pV = nRT
式中n为体系所含物质的量,R为气体常数: R=8.314 J/mol.K.
08
(U2+p2V2)－(U1+p1V1)＝Qp (1)
第二节焓 (enthalpy)
上式的左边全是状态函数，而右边为过程量Q，对于等压过程，式中括号中的量总是一起出现，故可定义： H≡U＋pV (2) H称为焓(enthalpy)。因为H是状态函数的组合，所以H必为状态函数。把H代入(1)式，可得： H＝Qp (3) 上式物理含义是：无有用功的等压过程热效应等于体系的焓变。
第一节热力学第一定律
1
热力学第一定律(first law of thermodynamics)
2
自然界的能量既不能创生,也不会消灭.
3
热力学第一定律即为：能量守恒原理.
4
更广泛地可定义为：物质不灭定律.
5
第一定律可表述为: 第一类永动机不可能

物理化学知识点总结(热力学第一定律)

物理化学上热力学第一定律知识框架图总结

物理化学知识点(全)

《物理化学》知识点汇总

物理化学知识点总结(热力学第一定律)

物理化学知识点归纳

物理化学热力学第一定律总结

物理化学 热力学一定律、二定律复习

物理化学知识点总结

物理化学基本知识点与公式总结

物理化学热力学第一定律精要

物理化学知识点归纳

物理化学知识点总结(热力学第一定律)

大学物理化学知识点归纳

物理化学知识点总结

物理化学知识点总结[物理化学知识点归纳]

物理化学热力学第一定律总结

物化上热力学第一定律知识点总结

《物理化学》热力学第一定律知识总结

物理化学第一章热力学第一定律

物理化学热力学一定律、二定律复习