计算机图形学-实验五 直线和多边形的裁剪
计算机图形学裁剪

学院:理学院专业:信息与计算科学班级:
姓名
学号
指导教师
实验时间
4.
实验地点
计算机实验室
成绩
实验项目名称
裁剪
实验环境
VC++ 6.0
实验内容
(1)理解直线裁剪的原理(Cohen-Surtherland算法、梁友栋算法)
(2)利用VC+OpenGL实现直线的编码裁剪算法,在屏幕上用一个封闭矩形裁剪任意一条直线。
};
Rectangle rect;
int x0,y0,x1,y1;
int CompCode(int x,int y,Rectangle rect)
{
int code=0x00;
if(y<rect.ymin)
code=code|4;
if(y>rect.ymax)
code=code|8;
if(x>rect.xmax)
x0=450,y0=0,x1=0,y1=450;
printf("Press key'c'to Clip!\nPress key'r'to Rrstore!\n");
}
void Reshape(int w,int h)
{
glViewport(0,0,(GLsizei)w,(GLsizei)h);
glMatrixMode(GL_PROJECTION);
accept=0;
done=0;
int code0,code1,codeout;
code0=CompCode(x0,y0,rect);
code1=CompCode(x1,y1,rect);
图形学实验报告直线段的裁剪算法

实验报告Experimentation Report of Taiyuan teachers College系部计算机系年级三年级课程图形学姓名同组者日期项目直线段的裁剪算法一、实验目的:1.熟悉图形裁剪的基本知识2.掌握Cohen-Sutherland 直线裁剪算法二、实验内容:在矩形窗口的裁剪算法中,考虑到构成图形的基本元素就是线段,曲线可看成是有很多小线段逼近而成的,因此,讨论线段的裁剪算法更为实用,即Cohen-Sutherland裁剪算法。
Cohen-Sutherland裁剪算法具体思路如下。
任意平面线段和矩形窗口的位置关系只会有如下3种:(1)完全落在窗口内。
(2)完全落在窗口外。
(3)部分落在窗口内,部分落在窗口外。
要想判断线段和窗口的位置关系,只要找到线段的两端点相对于矩形窗口的位置即可,线段的两端点相对于矩形窗口的位置可能会有如下几种情况:(1)线段的两个端点均在窗口内,这时线段全部落在窗口内,完全可见,应予以保留。
(2)线段的两个端点均在窗口边界线外同侧,这时线段全部落在窗口外,完全不可见,应予以舍弃。
(3)线段的一个端点在窗口内,另一个端点在窗口外,这时线段部分可见,应求出线段与窗口边界线的交点,从而得到线段在窗口内的可见部分。
(4)线段的两个端点均不在窗口内,但不处于窗口边界线外同侧,这时有可能线段是部分可见的,也可能是完全不可见的。
Cohen-Sutherland裁剪算法就是按照上述思路来对线段进行裁剪的,只是在线段的两端点相对于矩形窗口的位置上,巧妙地运用了编码的思想。
首先,延长窗口的四条边界线,将平面划分成9个区域,然后,用四位二进制数C3C2C1C0对这9个区域进行编码,编码规则如下:第0位C0:当线段的端点在窗口的左边界之左时,该位编码为1,否则,该位编码为0。
第1位C1:当线段的端点在窗口的右边界之右时,该位编码为1,否则,该位编码为0。
第2位C2:当线段的端点在窗口的下边界之下时,该位编码为1,否则,该位编码为0。
《计算机图形学》实验指导书

计算机图形学实验指导书袁科计算机技术实验中心目录实验一实现DDA、中点画线算法和Bresenham画线算法 (24)实验二实现Bezier曲线 (25)实验三实现B样条曲线 (26)实验四实现多边形填充的边界标志算法 (27)实验五实现裁剪多边形的Cohen-Sutherland算法 (28)实验六二维图形的基本几何变换 (30)实验七画图软件的编制 (31)实验一实现DDA、中点画线算法和Bresenham画线算法【实验目的】1、掌握直线的多种生成算法;2、掌握二维图形显示原理。
【实验环境】VC++6.0/ BC【实验性质及学时】验证性实验,2学时,必做实验【实验内容】利用任意的一个实验环境,编制源程序,分别实现直线的三种生成算法,即数字微分法(DDA)、中点画线法以及Bresenham画线算法。
【实验原理】1、数字微分法(Digital Differential Analyzer,DDA)算法思想:基于直线的微分方程来生成直线。
ε=1/max(|△x|,|△y|)max(|△x|,|△y|)=|△x|,即|k|≤1 的情况:max(|△x|,|△y|)=|△y|,此时|k|≥1:2、中点画线法算法思想:每次在最大位移方向上走一步,另一方向是否走步取决于误差项的判断。
3、Bresenham画线算法算法思想:其基本思想同中点算法一样,即每次在最大位移方向上走一步,而另一个方向是否走步取决于误差项的判断。
【实验要求】1.上交源程序;2.上交实验报告,实验报告内容如下:(1) 实验名称(2) 实验目的(3) 算法实现的设计方法及程序流程图(4) 程序结果分析【分析与思考】(1) 上述所阐述的三个算法,其基本算法只能适用于直线的斜率(|K|<=1) 的情形,如何将上述算法进行推广,使其能够处理任意斜率的直线?(2) 计算机显示屏幕的坐标圆心在哪里,与我们平时的习惯有什么差异,如何协调二者?实验二 实现Bezier 曲线【实验目的】1、掌握Bezier 曲线的定义;2、能编程实现N 次Bezier 曲线的绘制与显示。
图形剪裁算法

计算机图形学课程实验报告《直线、多边形剪裁图形软件设计》学生:班级:软件一班学号:200905070122目录一、任务描述 (1)二、算法原理 (2)1.1、线段剪裁 (2)1.2、多边形裁剪 (4)三、算法实现 (6)3.1、主窗体 (6)3.2、编辑菜单资源 (6)3.3、添加消息处理函数 (7)3.4、添加代码 (7)3.5、设计结果 (18)四、总结 (21)一、任务描述在使用计算机处理图形时,计算机内部存储的图形往往比较大,而屏幕显示的只是图的一部分。
因此需要确定图形中哪些部分落在显示区内,哪些落在显示区外,以便只显示落在显示区内的那部分图形。
这个选择过程称为裁剪。
最简单的方法就是把各图形扫描转换为点之后,再判断各点是否在窗内。
但那样太费时,一般不可取,这是因为当图形组成部分全部在窗口外,可以完全排除,不必进行扫描转换。
所以一般采用首先剪裁再扫描转换的方法。
图1 多边形剪裁二、算法原理1.1、线段剪裁(1)、直线和窗口的关系可以分为如下3类(图2):①整条直线在窗口内。
此时,不需剪裁,显示整条直。
②整条直线在窗口外,此时,不需剪裁,不显示整条直线。
③部分直线在窗口内,部分直线在窗口外。
此时,需要求出直线与窗框的交点,并将口外的直线部分剪裁掉,显示窗口内的直线部分。
直线剪裁算法有两个主要步骤。
首先将不需剪裁的直线挑出,即删去在窗外的直线。
然后,对其余直线,逐条直线与窗框求交点,并将窗口外的部分删去。
图2 直线与窗口的关系(2)、Cohen-Sutherland直线剪裁算法算法原理图3 窗口及其临域的5个区域及与直线的关系以区域编码为基础,将窗口及其周围的8个方向以4bit的二进制数进行编码。
如(图3)上图所示的编码方法将窗口及其邻域分为5个区域:①内域:区域(0000)。
②上域:区域(1001,1000,1010)。
③下域:区域(0101,0100,0110)。
④左域:区域(1001,0001,0101)。
计算机图形学课程设计 多边形的裁剪算法

河南理工大学万方科技学院课程设计报告2010 — 2011学年第二学期课程名称计算机图形学设计题目多边形裁剪算法学生姓名孙晓芳学号**********专业班级计算机科学与技术10升指导教师侯守明2011 年6 月29 日目录目录目录 (I)第1章程序运行环境................................................................................... 错误!未定义书签。
1.1 程序运行环境的简单介绍................................................................. 错误!未定义书签。
1.2 程序运行环境的安装......................................................................... 错误!未定义书签。
1.3 多边形裁剪算法设计的内容........................................................................... 第2章直线裁剪和多边形裁剪的简单比较 (4)2.1 直线裁剪的介绍 (4)2.1.1 直线裁剪的基本原理………………………………………......................................2.1.2 直线裁剪算法的分类以及和窗口交点参数值的计算……………………………..2.2 多边形裁剪介绍 (9)2.2.1 多边形裁剪的基本思想……………………………………………………………..2.2.2 多边形和窗口相交的判定方法…………………………………………..第3章多边形裁剪方法的详细介绍 (12)3.1 Sutherland-Hodgman算法………………………………………………………………….3.2 多边形裁剪算法的流程图 (12)3.3多边形裁剪算法的实现 (13)第4章代码的实现 (14)第5章总结 (21)参考文献 (22)第1章程序的运行环境1.1 程序运行环境的简单介绍本次设计主要是运用了程序设计语言主要以C/C++语言为主,开发平台为Visual C++。
计算机图形学 第5章 裁剪

3.直线裁剪实例 例5.1 用编码算法裁剪如图5-3(a)所示中的直线段 AB。
图5-3 AB线段的裁剪过程
例5.2 用编码算法裁剪如图5-4(a)所示中的直线段MN。
图5-4 MN线段的裁剪过程
5.1.2 中点分割算法 算法步骤:输入线段端点p1,p2;对于端点p2: (1) p2是否可见,若可见,则它为离p1最远的可见点, 处理结束。 (2) plp2是否全不可见,若是,没有输出,处理结束。 (3) 让pa = p1,pb = p2。
边 V1V2 V2V3 V3V4 V4V5 V5V1 n (1,1) (4,-3) (-1,-2) (-4,3) (0,1) f (2,0) (3,6) (3,6) (4,0) (2,0) w [-4,1] [-5,-5] [-5,-5] [-6,1] [-4,1] w· n -3 -5 15 27 1 D· n 11 30 -13 -30 2 -1/2 tL 3/11 1/6 15/13 9/10 tu
外裁剪有两个重要的应用。
(1) 应用于凹多边形裁剪窗口的线段裁剪。如图5-9 所示线段p1p2相对于凹多边形vlv2v3v4v5v1进行裁剪。 连接v2v4,v1v2v4v5v1为凸多边形,应用Cyrus-Beck算 法,先将p1p2对此凸多边形作内裁剪得到,再将对多 边形v2v3v4v2作外裁剪,最后得到窗口内部分为和。
(4) 沿vi+1p1将多边形一分为二,一个多边形由vi+1, vi+2,…, p1vi+1组成,另一个多边形由vip1及其余顶点组 成。 (5) 对分割的两个多边形递归地重复以上步骤,直到 所有新产生的多边形均为凸,算法结束。
5.1.7 Sutherland-Hodgman逐次多边形裁剪算法 多边形由顶点表p1, p2,…, pn所定义,于是边表为p1p2, p2p3,…, pn-1pn和pn p1。算法的基本思想是将原多边形和 每次裁剪所生成的多边形逐次对裁剪窗口的每一条边 界进行裁剪。考虑图5-12(a)原多边形被窗口左边界所 裁剪,如图5-12(b)所示;生成的多边形又被窗口顶边 所裁剪,如图5-12(c)所示;继续这一过程,生成的中 间多边形被窗口的右边界,如图5-12(d)所示,直至下 边界裁剪完,如图5-12(e)所示为止。
计算机图形学 图形裁剪

一 当p<0时,参数r用于更新u0: u0=max u0,rk 二 当p>0时,参数r用于更新u一: u一=min u一,rk 三 如果更新了u0或u一后,使u0>u一,则舍弃该线段 四 当p=0且q<0时,因为线段平行于边界并且位于边界之外,则舍
弃该线段.
四、p、q的四个值经判断后,如果该线段未被舍弃,则裁
16
Cohen-Sutherland裁剪算法
求交
将两个端点的编码CtCbCrCl进行逻辑或操作, 根据其结果中一的位置来确定可能相交的窗口边 求交按照固定的顺序来进行 左右下上或上下右左 一条线段与窗口最多求交四次
A 一0一0 FD
E C B 0一0一
17
Cohen-Sutherland裁剪算法
1001
1000
1010
0001
0000
0010
utherland裁剪算法
先排除简单情形:
若某线段两个端点的四位二进制编码全为0000 线段位于窗口内,显示之
若对两端点的四位二进制编码进行逻辑与运算 & 结果
不为0 线段位于窗口外,直接舍弃
1001
不仅在于求出新的顶点,删去界外顶点,还在于形成 正确的顶点序列
36
多边形的描述方式
多边形可以描述为一组顶点按一定顺序连接而成的 有向点列
一般可将多边形的顶点按逆时针方向顺序形成有向 线段,进而连接成一个环来描述多边形的组成
数据结构上,可用链表结构来描述
2
1
3 4
37
多边形裁剪的特点
多边形的各条边是顺次连接 直线裁剪
10
Cohen-Sutherland裁剪算法
计算机图形学裁剪算法

一、实验目标1.了解Cohen-SutherLand线段裁剪算法、Liang-Barsky线段裁剪算法、SutherLand-Hodgeman多边形裁剪算法的基本思想;2.掌握Cohen-SutherLand线段裁剪算法、Liang-Barsky线段裁剪算法、SutherLand-Hodgeman多边形裁剪算法的算法实现;二、实验内容本次实验主要是实现Cohen-SutherLand线段裁剪算法、Liang-Barsky线段裁剪算法、SutherLand-Hodgeman多边形裁剪算法。
Cohen-sutherland线段裁剪算法思想:该算法也称为编码算法,首先对线段的两个端点按所在的区域进行分区编码,根据编码可以迅速地判明全部在窗口内的线段和全部在某边界外侧的线段。
只有不属于这两种情况的线段,才需要求出线段与窗口边界的交点,求出交点后,舍去窗外部分。
对剩余部分,把它作为新的线段看待,又从头开始考虑。
两遍循环之后,就能确定该线段是部分截留下来,还是全部舍弃。
Cohen-sutherland线段裁剪算法步骤:1、分区编码延长裁剪边框将二维平面分成九个区域,每个区域各用一个四位二进制代码标识。
各区代码值如图中所示。
四位二进制代码的编码规则是:(1)第一位置1:区域在左边界外侧(2)第二位置1:区域在右边界外侧(3)第三位置1:区域在下边界外侧(4)第四位置1:区域在上边界外侧裁剪窗口内(包括边界上)的区域,四位二进制代码均为0。
设线段的两个端点为P1(x1,y1)和P2(x2,y2),根据上述规则,可以求出P1和P2所在区域的分区代码C1和C2。
2、判别根据C1和C2的具体值,可以有三种情况:(1)C1=C2=0,表明两端点全在窗口内,因而整个线段也在窗内,应予保留。
(2)C1&C2≠0(两端点代码按位作逻辑乘不为0),即C1和C2至少有某一位同时为1,表明两端点必定处于某一边界的同一外侧,因而整个线段全在窗外,应予舍弃。
直线段剪裁实验报告

《计算机图形学》实验报告《实验名称》直线段裁剪学号专业班级天津大学计算机科学与技术学院一、实验目的熟练掌握Cohen-Sutherland直线裁剪算法,并编程实现二、实验内容(1) 裁剪窗口为矩形窗口,且矩形边和坐标轴平行,长宽自己定。
(2) 待裁剪线段端点坐标自己定;裁剪线段涵盖完全可见、不完全可见、完全不可见类型。
(3) 要求显示待裁剪线段并用不同颜色标示出裁剪结果。
实现方法:一般情况下,需要判断一条直线是全部可见,全部不可见,部分裁剪(一段裁剪),全部裁剪(两端裁剪)。
通过把裁剪区域分成许多部分,然后给每一段被裁剪的线段的两端分配一位代码,通过少量if语句和一个case语句就可以判断出具体情况。
伪代码如下:#define CLIP_CODE_C 0x0000#define CLIP_CODE_N 0x0008#define CLIP_CODE_S 0x0004#define CLIP_CODE_E 0x0002#define CLIP_CODE_W 0x0001#define CLIP_CODE_NE 0x000a#define CLIP_CODE_SE 0x0006#define CLIP_CODE_NW 0x0009#define CLIP_CODE_SW 0x0005实验步骤:1)生成裁剪窗口,窗口由直线xl=250,xr=850,yb=250,yt=4502)绘制直线段3)编写Cohen-Sutherland直线裁剪算法,对直线段进行裁剪编码定义规则:第一位C1:若端点位于窗口之左侧,即X<xl,则C1=1,否则C1=0。
第二位C2:若端点位于窗口之右侧,即X>xr,则C2=1,否则C2=0。
第三位C3:若端点位于窗口之下侧,即Y<yb,则C3=1,否则C3=0。
第四位C4:若端点位于窗口之上侧,即Y>yt,则C4=1,否则C4=0。
裁剪步骤:对所有直线的端点都建立了区域码之后,就可按区域码判断直线在窗口之内或窗口之外。
计算机图形学实验五直线段裁剪

计算机图形学实验报告黔南民族师范学院信息与计算科学撰写人姓名: __ 撰写时间:2010年5月5日审查人姓名:实验过程记录一、实验目的:1、通过实验,进一步理解和掌握直线段的裁剪算法;2、通直线段的裁剪。
二、实验内容:要求:•1 、进一步理解并掌握线段的裁剪算法,并可以实践至少一种线段的裁剪算法;•2、注意:本次作业要求学生不能直接使用系统提供的线段裁剪函数,但是可以调用相关的画点、画线函数。
三、实验设备及软件软件需求:windows98以上操作系统、Turbo C 2.0 、Turbo C++3.0、Visual C++软件、Microsoft Word 97或2000。
硬件需求:建议Pentium IV CPU处理器、64MB以上内存、1GB以上硬盘空间的计算机、激光打印机四、实验方法及步骤1 实验准备上该实验课前将针对解决实验内容问题的C语言程序编制好,在实验课上,对编制完的程序进行调试、修改和分析,熟悉TurboC2.0的菜单,以及编译,运行程序和调试程序的方法,并编写程序。
2. 调试程序;程序一:#define LEFT 1#define RIGHT 2#define BOTTOM 4#define TOP 8#define XL 150#define XR 350#define YB 150#define YT 300#include <math.h>#include"graphics.h"main(){ int gdriver=DETECT,gmode;initgraph(&gdriver,&gmode,"c:\\tc");setcolor(12);line(XL,YT,XR,YT);line(XL,YB,XR,YB);line(XL,YT,XL,YB);line(XR,YT,XR,YB);setcolor(9);draw_ett();getch();closegraph();}encode (x,y,code)int x,y;int *code;{ int c;c=0;if (x<XL) c=c|LEFT;else if (x>XR) c=c|RIGHT;if (y<YB) c=c|BOTTOM;else if (y>YT) c=c|TOP;*code=c;return;}draw_ett(){ int x1,x2,y1,y2,x,y;int code1,code2,code;/* printf("XL=150,XR=350,YB=150,YT=300\n");scanf("%d,%d,%d,%d",&x1,&y1,&x2,&y2);*/x1=50;y1=210;x2=300;y2=100;setcolor(2);line(x1,y1,x2,y2);encode(x1,y1,&code1);encode(x2,y2,&code2);while ((code1!=0)||(code2!=0)) {if ((code1&code2)!=0) return;code=code1;if (code1==0) code=code2;if ((LEFT&code)!=0){x=XL;y=y1+(y2-y1)*(XL-x1)/(x2-x1);}else if ((RIGHT&code)!=0){x=XR;y=y1+(y2-y1)*(XR-x1)/(x2-x1);}else if ((BOTTOM&code)!=0) {y=YB;x=x1+(x2-x1)*(YB-y1)/(y2-y1); }else if ((TOP&code)!=0){y=YT;x=x1+(x2-x1)*(YT-y1)/(y2-y1);}if (code==code1){ x1=x;y1=y;encode(x,y,&code1);}else{ x2=x;y2=y;encode(x,y,&code2);}}setcolor(14);line(x1,y1,x2,y2);return;}运行结果:程序二:请按书上P109的Cohen-Sutherland算法写出完整的程序,并运行出效果图,可参考以上程序一#define XL 150#define XR 350#define YB 150#define YT 300#define FALSE 0#define TRUE 1#include <math.h>#include"graphics.h"typedef struct{int xmin,xmax,ymin,ymax;}Rectangle;typedef int boolean;typedef struct{unsigned all;unsigned left,right,top,bottom;}OutCode;void CompOutCode(float x,float y,Rectangle *rect,OutCode *outCode){outCode->all=0;outCode->top=outCode->bottom=0;if(y>(float)rect->ymax){outCode->top=1;outCode->all+=1;}else if(y<(float)rect->ymin){outCode->bottom=1;outCode->all+=1;}outCode->right=outCode->left=0 ; if(x>(float)rect->xmax){outCode->right=1;outCode->all+=1;}else if(x<(float)rect->xmin){outCode->left=1;outCode->all+=1;}}void CSLineClip(float x0,float y0,float x1,float y1,Rectangle *rect){boolean accept,done;OutCode outCode0,outCode1;OutCode *outCodeOut;float x,y;accept=FALSE;done=FALSE;CompOutCode(x0,y0,rect,&outCode0);CompOutCode(x1,y1,rect,&outCode1);do{if(outCode0.all==0&&outCode1.all==0){accept=TRUE;done=TRUE;}else if(outCode0.all&outCode1.all!=0)done=TRUE;else{if(outCode0.all!=0)outCodeOut=&outCode0;elseoutCodeOut=&outCode1;if(outCodeOut->left){y=y0+(y1-y0)*(rect->xmin-x0)/(x1-x0);x=(float)rect->xmin;}else if(outCodeOut->top){x=x0+(x1-x0)*(rect->ymax-y0)/(y1-y0);y=(float)rect->ymax;}else if(outCodeOut->right){y=y0+(y1-y0)*(rect->xmax-x0)/(x1-x0);x=(float)rect->xmax;}else if(outCodeOut->bottom){x=x0+(x1-x0)*(rect->ymin-y0)/(y1-y0);y=(float)rect->ymin;}if(outCodeOut->all==outCode0.all){x0=x;y0=y;CompOutCode(x0,y0,rect,&outCode0);}else{x1=x;y1=y;CompOutCode(x1,y1,rect,&outCode1);}}}while(!done);if(accept){line((int)x0,(int)y0,(int)x1,(int)y1);}}main(){ int gdriver=DETECT,gmode;Rectangle rect;rect.xmin=XL;rect.xmax=XR;rect.ymin=YB;rect.ymax=YT;initgraph(&gdriver,&gmode,"c:\\tc"); setcolor(12);line(XL,YT,XR,YT);line(XL,YB,XR,YB);line(XL,YT,XL,YB);line(XR,YT,XR,YB);setcolor(2);line(100,100,300,400);setcolor(WHITE);CSLineClip(100,100,300,400,&rect);getch();closegraph();}成绩评定:指导教师:。
mfc直线和多边形矩形窗口裁剪算法

mfc直线和多边形矩形窗口裁剪算法MFC直线和多边形矩形窗口裁剪算法是一种在MFC框架下用于裁剪直线和多边形的算法。
该算法可以确保在绘制图形时,图形的边界不会超出指定的矩形窗口范围。
这种裁剪算法是为了确保图形的可视性和美观性,以及提高程序的性能。
在MFC框架中,绘制图形一般是通过在窗口的OnPaint函数中完成的。
在OnPaint函数中,我们可以获取绘图设备上下文(device context,简称DC),并在DC上进行绘图操作。
为了实现裁剪效果,我们需要在绘图之前对要绘制的图形进行裁剪,确保图形不会超出指定的窗口范围。
对于直线的裁剪,我们可以使用Cohen-Sutherland裁剪算法。
该算法是一种基于线段的区域编码(region encoding)算法,用于裁剪位于矩形窗口外部的线段。
算法的基本思路是判断直线的两个端点是否在窗口的内部,如果都在内部,则直接绘制该直线;如果都在外部,则直接丢弃该直线;如果一个在内部,一个在外部,则通过计算交点并选择正确的端点来裁剪直线。
对于多边形的裁剪,我们可以使用Sutherland-Hodgman裁剪算法。
该算法是一种基于点的裁剪算法,用于裁剪位于矩形窗口外部的多边形。
算法的基本思路是将多边形分割为若干条边和端点,然后根据边与窗口的关系进行裁剪。
具体步骤包括:将多边形的各个顶点与窗口的边界进行比较,并根据顶点在内部和外部的情况确定裁剪结果;根据边界与窗口的关系确定新的裁剪结果,并将结果作为下一次裁剪的输入。
在MFC中实现直线和多边形的裁剪算法,可以按照以下步骤进行:1.获取绘图设备上下文(DC)。
2.设置裁剪区域为窗口矩形范围。
3.使用Cohen-Sutherland算法进行直线裁剪,对于每条需要绘制的直线,判断其裁剪结果并进行绘制。
4.使用Sutherland-Hodgman算法进行多边形裁剪,对于每个需要绘制的多边形,判断其裁剪结果并进行绘制。
5.释放绘图设备上下文。
计算机图形学-5

e旳交点I 否
(b)
输出I
退出
图(b)
用图(b)中旳算法对最终一条边PnP1作裁剪。裁 剪好一条边便输出一条边。
上述算法仅用一条裁剪边对多边形进行裁剪, 得到一种顶点序列,作为下一条裁剪边处理 过程旳输入。
裁剪成果旳顶点构成:裁剪边内侧旳原
顶点;多边形旳边与裁剪边旳交点。顺
e旳交点I 否
(a)
输出I SP
设封闭多边形旳顶点为 P1,P2,…Pn,框图中e是表达窗 口旳四条边中正在裁剪旳一条边,
每次裁剪时第一种点存储在F中, 以便对最终一条边裁剪时使用。
用图(a)中旳算法对边P1P2,
P2P3, …Pn-1Pn作裁剪。
是 输出S
S在e旳可见侧 否
退出
图(a)
取点F为P
怎样求窗口边界与线段P1P2旳交点?
怎样鉴定线段应该与窗口旳哪条边求交呢?
编码中相应位为1旳窗口边。
计算线段P1(x1,y1)P2(x2,y2)与窗口边界旳交点 Code代表线段某个端点旳编码。 if(LEFT&code !=0)
{ x=XL; y=y1+(y2-y1)*(XL-x1)/(x2-x1);} else if(RIGHT&code !=0) { x=XR; y=y1+(y2-y1)*(XR-x1)/(x2-x1);} else if(BOTTOM&code !=0) { y=YB; x=x1+(x2-x1)*(YB-y1)/(y2-y1);} else if(TOP & code !=0) { y=YT; x=x1+(x2-x1)*(YT-y1)/(y2-y1);}
计算机图形学裁剪算法详解
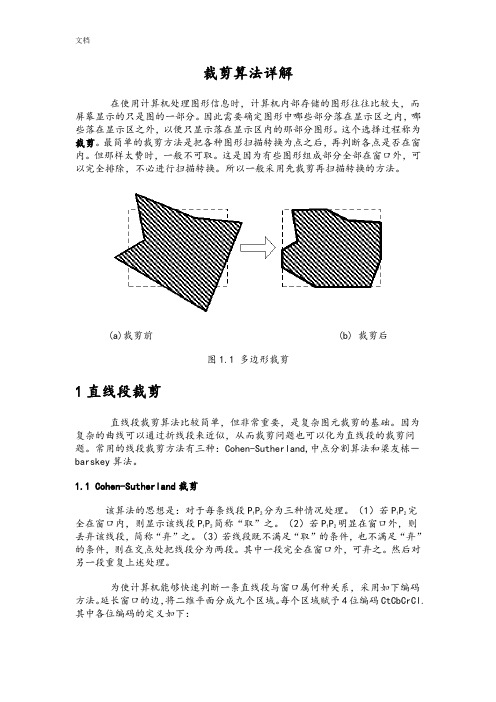
裁剪算法详解在使用计算机处理图形信息时,计算机内部存储的图形往往比较大,而屏幕显示的只是图的一部分。
因此需要确定图形中哪些部分落在显示区之内,哪些落在显示区之外,以便只显示落在显示区内的那部分图形。
这个选择过程称为裁剪。
最简单的裁剪方法是把各种图形扫描转换为点之后,再判断各点是否在窗内。
但那样太费时,一般不可取。
这是因为有些图形组成部分全部在窗口外,可以完全排除,不必进行扫描转换。
所以一般采用先裁剪再扫描转换的方法。
(a)裁剪前(b) 裁剪后图1.1 多边形裁剪1直线段裁剪直线段裁剪算法比较简单,但非常重要,是复杂图元裁剪的基础。
因为复杂的曲线可以通过折线段来近似,从而裁剪问题也可以化为直线段的裁剪问题。
常用的线段裁剪方法有三种:Cohen-Sutherland,中点分割算法和梁友栋-barskey算法。
1.1 Cohen-Sutherland裁剪该算法的思想是:对于每条线段P1P2分为三种情况处理。
(1)若P1P2完全在窗口内,则显示该线段P1P2简称“取”之。
(2)若P1P2明显在窗口外,则丢弃该线段,简称“弃”之。
(3)若线段既不满足“取”的条件,也不满足“弃”的条件,则在交点处把线段分为两段。
其中一段完全在窗口外,可弃之。
然后对另一段重复上述处理。
为使计算机能够快速判断一条直线段与窗口属何种关系,采用如下编码方法。
延长窗口的边,将二维平面分成九个区域。
每个区域赋予4位编码CtCbCrCl.其中各位编码的定义如下:图1.2 多边形裁剪区域编码图5.3线段裁剪裁剪一条线段时,先求出P1P2所在的区号code1,code2。
若code1=0,且code2=0,则线段P1P2在窗口内,应取之。
若按位与运算code1&code2≠0,则说明两个端点同在窗口的上方、下方、左方或右方。
可判断线段完全在窗口外,可弃之。
否则,按第三种情况处理。
求出线段与窗口某边的交点,在交点处把线段一分为二,其中必有一段在窗口外,可弃之。
计算机图形学-实验五直线和多边形的裁剪

大学实验报告学院:计算机科学与信息学院专业:软件工程班级:102班** 实验组实验时间指导教师成绩实验工程名称实验五直线和多边形的裁剪实验目的掌握直线段的裁剪算法以及多边形的裁剪算法实验要求熟练掌握直线段的裁剪算法以及多边形的裁剪算法的根本原理,并编写测试代码进展实验。
实验原理Cohen-Sutherland直线剪裁算法以区域编码为根底,将窗口及其周围的,8个方向以4 bit的二进制数进展编码。
右图所示的编码方法将窗口及其邻域分为5个区域:⑴域:区域(0000)。
⑵上域:区域(1001, 1000, 1010)。
⑶下域:区域(0101, 0100, 0110)。
⑷左域:区域(1001, 0001, 0101)。
⑸右域:区域(1010, 0010, 0110)。
当线段的两个端点的编码的逻辑"与〞非零时,线段为显然不可见的,对*线段的两个端点的区号进展位与运算,可知这两个端点是否同在视区的上、下、左、右;Cohen-Sutherland直线剪裁算法的算法思想是:对于每条线段P1P2分为三种情况处理。
〔1〕假设P1P2完全在窗口,则显示该线段P1P2简称"取〞之。
〔2〕假设P1P2明显在窗口外,则丢弃该线段,简称"弃〞之。
〔3〕假设线段既不满足"取〞的条件,也不满足"弃〞的条件,则在交点处把线段分为两段。
其while (code1 != 0 || code2 != 0) {if ((code1 & code2) != 0) {// 两端点的编码相与不为0,表示直线在窗口外return;}if (code1 != 0) {code = code1;} else {code = code2;}if ((LEFT & code) != 0) {// 直线的端点与矩形窗口的左边编码相与!=0* = *L;y = y1 + (y2 - y1) * (*L - *1) / (*2 - *1);// 求直线与矩形窗口的左边界的交点} elseif ((RIGHT & code) != 0) {// 直线的端点与矩形窗口的右边编码相与!=0* = *R;y = y1 + (y2 - y1) * (*R - *1) / (*2 - *1);// 求直线与矩形窗口的右边界的交点} elseif ((BOTTOM & code) != 0) {// 直线的端点与矩形窗口的下边编码相与!=0y = YB;* = *1 + (*2 - *1) * (YB - y1) / (y2 - y1);// 求直线与矩形窗口的下边界的交点} elseif ((TOP & code) != 0) {// 直线的端点与矩形窗口的上边编码相与!=0y = YT;* = *1 + (*2 - *1) * (YT - y1) / (y2 - y1);// 直线的端点与矩形窗口的上// 边编码相与!=0}if (code == code1) {*1 = *;y1 = y;code1 = encode(*, y);} else {*2 = *;y2 = y;code2 = encode(*, y);}}g.drawLine((int) (*1 + 0.5), (int) (y1 + 0.5), (int) (*2 + 0.5),(int) (y2 +0.5));}二、多边形裁剪的核心代码为:通过点集画直线或者多边形:privatevoid draw() {//通过点集画直线或者多边形for (int i = 1; i < points.size(); i++) {Point p1 = new Point();p1 = points.get(i);int *1 = (int) p1.get*();int y1 = (int) p1.getY();Point p2 = new Point();p2 = points.get(i - 1);int *2 = (int) p2.get*();int y2 = (int) p2.getY();g.drawLine(*1, y1, *2, y2);}}多边形的裁剪函数:private Point[] cutPicture(Point[] point, Point[] edge) {// 剪裁函数,参数为〔点集,边〕Point[] intersectPoint = new Point[20];//存放交点的集合for (int j = 0; j < 20; j++) {intersectPoint[j] = new Point();}Point s = new Point();Point p = new Point();Point t = new Point();int i = 0;int length = point.length;s = point[length - 1];for (int j = 0; j < length; j++) {p = point[j];if (inside(p, edge)) {// sp在窗口,情况1if (inside(s, edge)) {intersectPoint[i] = p;i += 1;} else {// s在窗口外,情况4t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;intersectPoint[i] = p;i += 1;}} elseif (inside(s, edge)) {// s在窗口,p在窗口外,情况3t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;}// 情况2没有输出s = p;}List<Point> tempList = new ArrayList<Point>();for (int k = 0; k < i; k++) {if (intersectPoint[k] != null) {Point pt = intersectPoint[k];tempList.add(pt);}}Point[] temp = new Point[tempList.size()];for (int j = 0; j < tempList.size(); j++) {temp[j] = new Point();temp[j] = tempList.get(j);}intersectPoint = temp;return intersectPoint;}判断点是否在裁剪边的可见侧:privateboolean inside(Point point, Point[] edge) {//判断点是否在裁剪边的可见侧// 裁剪边为窗口下边if ((edge[0].y == edge[1].y) && (edge[0].* < edge[1].*)) {if (point.y >= edge[0].y) {returntrue;}}// 裁剪边为窗口上边if ((edge[0].y == edge[1].y) && (edge[0].* > edge[1].*)) {if (point.y <= edge[0].y) {returntrue;}}// 裁剪边为窗口右边if ((edge[0].* == edge[1].*) && (edge[0].y < edge[1].y)) {if (point.* <= edge[0].*) {returntrue;}}// 裁剪边为窗口左边if ((edge[0].* == edge[1].*) && (edge[0].y > edge[1].y)) {if (point.* >= edge[0].*) {returntrue;}}returnfalse;}直线段与窗口边界求交:private Point intersect(Point s, Point p, Point[] edge) {//直线段与窗口边界求交,并返回交点Point t = new Point();if (edge[0].y == edge[1].y) {// 水平裁剪边t.y = edge[0].y;t.* = s.* + (edge[0].y - s.y) * (p.* - s.*) / (p.y - s.y);} elseif (edge[0].* == edge[1].*) {// 垂直裁剪边t.* = edge[0].*;t.y = s.y + (edge[0].* - s.*) * (p.y - s.y) / (p.* - s.*);}return t;}鼠标的监听类〔部类〕:class MouseMonitor e*tends MouseAdapter {//通过鼠标的单击获取点,并画出直线或者多边形publicvoid mouseClicked(MouseEvent e) {points.add(e.getPoint());if (points.size() > 1) {draw();}}}键盘的监听类〔部类〕:class KeyMonitor e*tends KeyAdapter {// 键盘控制publicvoid keyPressed(KeyEvent e) {switch (e.getKeyCode()) {case KeyEvent.VK_R:// 清空画布和点集panel.repaint();points.removeAll(points);break;case KeyEvent.VK_W://对裁剪窗口的处理g.setColor(Color.RED);g.drawRect(*L, YB, *R - *L, YT - YB);//存放裁剪窗口的边top = new Point[2];// 存放裁剪窗口的上边top[0] = new Point(*L, YB);top[1] = new Point(*R, YB);right = new Point[2];//存放裁剪窗口的右边right[0] = new Point(*R, YB);right[1] = new Point(*R, YT);bottom = new Point[2];//存放裁剪窗口的下边bottom[0] = new Point(*R, YT);bottom[1] = new Point(*L, YT);left = new Point[2];//存放裁剪窗口的左边left[0] = new Point(*L, YT);left[1] = new Point(*L, YB);break;case KeyEvent.VK_A://对直线段进展裁剪g.setColor(Color.GREEN);Point p1 = points.get(0);Point p2 = points.get(1);lineCut(p1.get*(), p1.getY(), p2.get*(), p2.getY()); break;case KeyEvent.VK_B://对多边形进展裁剪source = new Point[points.size()];//得到多边形的点for (int i = 0; i < points.size(); i++) {source[i] = points.get(i);}g.setColor(Color.GREEN);wT = cutPicture(source, top);//得到多边形与裁剪窗口上边的交点wR = cutPicture(wT, right);//得到多边形与裁剪窗口右边的交点wB = cutPicture(wR, bottom);//得到多边形与裁剪窗口下边的交点wL = cutPicture(wB, left);//得到多边形与裁剪窗口左边的交点第二种情况:线段在裁剪窗口的部,线段完全可见。
图形学实验报告--线段裁剪

计算机科学与技术学院2013-2014学年第一学期《计算机图形学》实验报告班级:110341B班学号:110341228姓名:王陈教师:惠康华成绩:实验项目: 二维裁剪一、实验目的与要求(1)掌握线段裁剪算法原理,并实现其算法。
(2)理解多边形裁剪、字符裁剪算法思想,能编程实现其算法。
二、实验内容(1)实现直线段的标号法、矩形窗口裁剪算法。
(2)参考教材中的算法,用矩形窗口实现多边形的裁剪算法。
三、重要算法分析(一)线段裁剪Cohen-Sutherland算法实验原理:1、线段裁剪生成算法:对于矩形的窗口,任何直线至多只有一段处于该窗口之内,即在此窗口范围内永远不会产生一条直线的两条或更多的可见部分线段。
该算法的基本思想为:对于每条待裁剪的线段分完全在窗口内(此时不需要裁剪,全部显示)、完全在窗口外(此时不需要裁剪,整条线段不显示)、部分在窗口内部分在窗口外三种情况讨论。
将窗口及其周围的八个方向以四位的二进制数进行编码,用来快速判断一条直线段与窗口属于何种关系。
其中全为0的区域为裁剪窗口。
(1) 判断线段两个端点的四位二进制编码,如果全为0,即两端点编码逻辑或运算为0,那么该线段完全位于窗口内,可直接保留;(2) 对两端点的四位二进制编码进行逻辑与运算,若结果不为0,那么整条线段必位于窗口外,可直接舍弃。
(3) 如果以上两种情况皆不是,则这条线段既不能直接保留,也不能直接舍弃,它可能与窗口相交。
此时,需要对线段进行再分割,即找到与窗口边线的一个交点,根据交点位置,赋予四位二进制编码,并对分割后的线段按照一定的顺序(左右下上)进行检查,决定保留、舍弃或再次进行分割。
(4) 重复第三步,直到出现正确的裁剪结果为止。
四、实验结果截图裁剪线段1、双击击鼠标左键,出现要裁剪的线段:如图3-1图3-1 生成裁剪窗口和待裁剪线段2、裁剪后的结果:如图3-2图3-2 裁剪后的结果五、总结与调试经验1、程序初期的结构搭建很重要:在VC中选择MFC APPWizard(exe),建立单文档应用程序,编辑菜单资源,重置ID,添加消息处理函数,建立类向导,最后添加程序代码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学实验报告学院:计算机科学与信息学院专业:软件工程班级:102班学号实验组实验时间指导教师成绩实验项目名称实验五直线和多边形的裁剪实验目的掌握直线段的裁剪算法以及多边形的裁剪算法实验要求熟练掌握直线段的裁剪算法以及多边形的裁剪算法的基本原理,并编写测试代码进行实验。
实验原理Cohen-Sutherland直线剪裁算法以区域编码为基础,将窗口及其周围的,8个方向以4 bit的二进制数进行编码。
右图所示的编码方法将窗口及其邻域分为5个区域:⑴域:区域(0000)。
⑵上域:区域(1001, 1000, 1010)。
⑶下域:区域(0101, 0100, 0110)。
⑷左域:区域(1001, 0001, 0101)。
⑸右域:区域(1010, 0010, 0110)。
当线段的两个端点的编码的逻辑“与”非零时,线段为显然不可见的,对某线段的两个端点的区号进行位与运算,可知这两个端点是否同在视区的上、下、左、右;Cohen-Sutherland直线剪裁算法的算法思想是:对于每条线段P1P2分为三种情况处理。
(1)若P1P2完全在窗口,则显示该线段P1P2简称“取”之。
(2)若P1P2明显在窗口外,则丢弃该线段,简称“弃”之。
(3)若线段既不满足“取”的条件,也不满足“弃”的条件,则在交点处把线段分为两段。
其中while (code1 != 0 || code2 != 0) {if ((code1 & code2) != 0) {// 两端点的编码相与不为0,表示直线在窗口外return;}if (code1 != 0) {code = code1;} else {code = code2;}if ((LEFT & code) != 0) {// 直线的端点与矩形窗口的左边编码相与!=0 x = XL;y = y1 + (y2 - y1) * (XL - x1) / (x2 - x1);// 求直线与矩形窗口的左边界的交点} else if ((RIGHT & code) != 0) {// 直线的端点与矩形窗口的右边编码相与!=0x = XR;y = y1 + (y2 - y1) * (XR - x1) / (x2 - x1);// 求直线与矩形窗口的右边界的交点} else if ((BOTTOM & code) != 0) {// 直线的端点与矩形窗口的下边编码相与!=0y = YB;x = x1 + (x2 - x1) * (YB - y1) / (y2 - y1);// 求直线与矩形窗口的下边界的交点} else if ((TOP & code) != 0) {// 直线的端点与矩形窗口的上边编码相与!=0y = YT;x = x1 + (x2 - x1) * (YT - y1) / (y2 - y1);// 直线的端点与矩形窗口的上// 边编码相与!=0}if (code == code1) {x1 = x;y1 = y;code1 = encode(x, y);} else {x2 = x;y2 = y;code2 = encode(x, y);}}g.drawLine((int) (x1 + 0.5), (int) (y1 + 0.5), (int) (x2 + 0.5),(int) (y2 + 0.5));}二、多边形裁剪的核心代码为:通过点集画直线或者多边形:private void draw() {//通过点集画直线或者多边形for (int i = 1; i < points.size(); i++) {Point p1 = new Point();p1 = points.get(i);int x1 = (int) p1.getX();int y1 = (int) p1.getY();Point p2 = new Point();p2 = points.get(i - 1);int x2 = (int) p2.getX();int y2 = (int) p2.getY();g.drawLine(x1, y1, x2, y2);}}多边形的裁剪函数:private Point[] cutPicture(Point[] point, Point[] edge) {// 剪裁函数,参数为(点集,边)Point[] intersectPoint = new Point[20];//存放交点的集合for (int j = 0; j < 20; j++) {intersectPoint[j] = new Point();}Point s = new Point();Point p = new Point();Point t = new Point();int i = 0;int length = point.length;s = point[length - 1];for (int j = 0; j < length; j++) {p = point[j];if (inside(p, edge)) {// sp在窗口,情况1if (inside(s, edge)) {intersectPoint[i] = p;i += 1;} else {// s在窗口外,情况4t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;intersectPoint[i] = p;i += 1;}} else if (inside(s, edge)) {// s在窗口,p在窗口外,情况3t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;}// 情况2没有输出s = p;}List<Point> tempList = new ArrayList<Point>();for (int k = 0; k < i; k++) {if (intersectPoint[k] != null) {Point pt = intersectPoint[k];tempList.add(pt);}}Point[] temp = new Point[tempList.size()];for (int j = 0; j < tempList.size(); j++) {temp[j] = new Point();temp[j] = tempList.get(j);}intersectPoint = temp;return intersectPoint;}判断点是否在裁剪边的可见侧:private boolean inside(Point point, Point[] edge) {//判断点是否在裁剪边的可见侧// 裁剪边为窗口下边if ((edge[0].y == edge[1].y) && (edge[0].x < edge[1].x)) {if (point.y >= edge[0].y) {return true;}}// 裁剪边为窗口上边if ((edge[0].y == edge[1].y) && (edge[0].x > edge[1].x)) {if (point.y <= edge[0].y) {return true;}}// 裁剪边为窗口右边if ((edge[0].x == edge[1].x) && (edge[0].y < edge[1].y)) {if (point.x <= edge[0].x) {return true;}}// 裁剪边为窗口左边if ((edge[0].x == edge[1].x) && (edge[0].y > edge[1].y)) {if (point.x >= edge[0].x) {return true;}}return false;}直线段与窗口边界求交:private Point intersect(Point s, Point p, Point[] edge) {//直线段与窗口边界求交,并返回交点Point t = new Point();if (edge[0].y == edge[1].y) {// 水平裁剪边t.y = edge[0].y;t.x = s.x + (edge[0].y - s.y) * (p.x - s.x) / (p.y - s.y);} else if (edge[0].x == edge[1].x) {// 垂直裁剪边t.x = edge[0].x;t.y = s.y + (edge[0].x - s.x) * (p.y - s.y) / (p.x - s.x);}return t;}鼠标的监听类(部类):class MouseMonitor extends MouseAdapter {//通过鼠标的单击获取点,并画出直线或者多边形public void mouseClicked(MouseEvent e) {points.add(e.getPoint());if (points.size() > 1) {draw();}}}键盘的监听类(部类):class KeyMonitor extends KeyAdapter {// 键盘控制public void keyPressed(KeyEvent e) {switch (e.getKeyCode()) {case KeyEvent.VK_R:// 清空画布和点集panel.repaint();points.removeAll(points);break;case KeyEvent.VK_W://对裁剪窗口的处理g.setColor(Color.RED);g.drawRect(XL, YB, XR - XL, YT - YB);//存放裁剪窗口的边top = new Point[2];// 存放裁剪窗口的上边top[0] = new Point(XL, YB);top[1] = new Point(XR, YB);right = new Point[2];//存放裁剪窗口的右边right[0] = new Point(XR, YB);right[1] = new Point(XR, YT);bottom = new Point[2];//存放裁剪窗口的下边bottom[0] = new Point(XR, YT);bottom[1] = new Point(XL, YT);left = new Point[2];//存放裁剪窗口的左边left[0] = new Point(XL, YT);left[1] = new Point(XL, YB);break;case KeyEvent.VK_A://对直线段进行裁剪g.setColor(Color.GREEN);Point p1 = points.get(0);Point p2 = points.get(1);lineCut(p1.getX(), p1.getY(), p2.getX(), p2.getY());break;case KeyEvent.VK_B://对多边形进行裁剪source = new Point[points.size()];//得到多边形的点for (int i = 0; i < points.size(); i++) {source[i] = points.get(i);}g.setColor(Color.GREEN);wT = cutPicture(source, top);//得到多边形与裁剪窗口上边的交点wR = cutPicture(wT, right);//得到多边形与裁剪窗口右边的交点wB = cutPicture(wR, bottom);//得到多边形与裁剪窗口下边的交点wL = cutPicture(wB, left);//得到多边形与裁剪窗口左边的交点第二种情况:线段在裁剪窗口的部,线段完全可见。
