数值计算课后答案
《数值计算方法》习题答案

《数值计算方法》课后题答案详解吉 林 大 学第一章 习 题 答 案1. 已知(1)2,(1)1,(2)1f f f −===,求()f x 的Lagrange 插值多项式。
解:由题意知:()01201212001020211012012202121,1,2;2,1,1()()(1)(2)()()6()()(1)(2)()()2()()(1)(1)()()3(1)(2)(1)(2)()2162nj j j x x x y y y x x x x x x l x x x x x x x x x x l x x x x x x x x x x l x x x x x x x x L x y l x ==−=====−−−−==−−−−+−==−−−−−+−==−−−−+−==×+×−∴∑()2(1)(1)131386x x x x +−+×=−+2. 取节点01210,1,,2x x x ===对x y e −=建立Lagrange 型二次插值函数,并估计差。
解11201201210,1,;1,,2x x x y y e y e −−======1)由题意知:则根据二次Lagrange插值公式得:02011201201021012202110.510.520.51()()()()()()()()()()()()()2(1)(0.5)2(0.5)4(1)(224)(43)1x x x x x x x x x x x x L x y y y x x x x x x x x x x x x x x x x e x x e e e x e e x −−−−−−−−−−−−=++−−−−−−=−−+−−−=+−+−−+22)Lagrange 根据余项定理,其误差为(3)2210122()1|()||()||(1)(0.5)|3!61max |(1)(0.5)|,(0,1)6()(1)(0.5),()330.5030.2113()61()0.2113(0.21131)(0.21130.5)0.008026x f R x x e x x x x x x t x x x x t x x x x t x R x ξξωξ−+≤≤==−−≤−−∈′=−−=−+=−==≤××−×−=∴取 并令 可知当时,有极大值3. 已知函数y =在4, 6.25,9x x x ===处的函数值,试通过一个二次插值函数求的近似值,并估计其误差。
(湖南大学-曾金平《数值计算方法》课后题答案)

1习题一1.设x>0相对误差为2%,4x的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x xf x f xδδ∆=≈得(1)()f x=11()()*2%1%22x xδδδ≈===;(2)4()f x x=时444()()'()4()4*2%8%xx x x xxδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P关于1212.m nx a a a bb b=±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算(1)31.97+2.456+0.1352;(2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352≈21((0.3197100.245610)0.1352)fl fl⨯+⨯+=2(0.3443100.1352)fl⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl≈⨯+⨯= 21(0.3197100.259110)fl⨯+⨯=0.3456210⨯易见31.97+2.456+0.1352=0.345612210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?2解:设该正方形的边长为x,面积为2()f x x=,由(())(())'()()()()f x xf x f x xf x f xδδ∆=≈解得(())()()'()f x f xxxf xδδ≈=2(())(())22f x x f xx xδδ==0.5%5.下面计算y的公式哪个算得准确些?为什么?(1)已知1x<<,(A)11121xyx x-=-++,(B)22(12)(1)xyx x=++;(2)已知1x>>,(A)y=,(B)y=;(3)已知1x<<,(A)22sin xyx=,(B)1cos2xyx-=;(4)(A)9y=(B)y=解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算方法课后习题答案

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算课后答案5

习 题 五 解 答1、用矩形公式、梯形公式、抛物线公式计算下列积分,并比较结果。
(1)120(8)4xdx n x =+⎰,(2)20sin (8)x xdx n π=⎰(3)1(4)n =⎰,(4)1(4)x e dxn -=⎰1*、用矩形公式、梯形公式、抛物线公式计算下列积分,并比较结果。
(1)120(4)4x dx n x =+⎰解:解:将区间[0,1]4等分,5个分点上的被积函数值列表如下(取2位小数)(1)矩形法。
用矩形法公式计算(取2位小数)或者 (2)梯形法用梯形法公式计算(取2位小数): (3)抛物线法用抛物线法公式计算(取2位小数):2、用复化梯形公式计算积分841dx x ⎰,由此计算ln2(注:841ln 2dx x=⎰),精度要求为410-。
解:8418ln8ln 4ln ln 24dx x =-==⎰,要求精度为410-,即误差不超过41102ε-=⨯。
将积分区间[4,8]n 等份,则步长844h n n -==在本题中,复化梯形公式的余项为2228484416()()()()12123r h f f f n nηηη--''''''=-=-=-注意到231(),(),()2f x f x x f x x x--'''==-=,所以在[4,8]区间上3()24f x -''≤⨯,则32232161621283346r n n n-⨯≤⨯⨯==⨯, 要使42111062n -≤⨯,需有42421110310577.36757862n n n n n -≤⨯⇒≥⇒≥⇒≥⇒=。
3、用复合梯形公式计算积分()baf x dx ⎰,问将积分区间[a,b]分成多少等份,才能保证误差不超过ε(不计舍入误差)?解:对于复合梯形公式来说,如果()f x ''在积分区间上连续,则其余项为2(),[,]12b a r h f a b ηη-''=-∈,设max ()a x bM f x ≤≤''=,则322()()()1212b a b a Mr h f nη--''=≤ 令32()12b a Mn ε-≤,得n ≥即当1n =+时,能保证计算的精度要求。
最新数值计算课后答案1

习 题 一 解 答1.取3.14,3.15,227,355113作为π的近似值,求各自的绝对误差,相对误差和有效数字的位数。
分析:求绝对误差的方法是按定义直接计算。
求相对误差的一般方法是先求出绝对误差再按定义式计算。
注意,不应先求相对误差再求绝对误差。
有效数字位数可以根据定义来求,即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位,再确定有效数的末位是哪一位,进一步确定有效数字和有效数位。
有了定理2后,可以根据定理2更规范地解答。
根据定理2,首先要将数值转化为科学记数形式,然后解答。
解:(1)绝对误差:e(x)=π-3.14=3.14159265…-3.14=0.00159…≈0.0016。
相对误差:3()0.0016()0.51103.14r e x e x x -==≈⨯ 有效数字:因为π=3.14159265…=0.314159265…×10,3.14=0.314×10,m=1。
而π-3.14=3.14159265…-3.14=0.00159…所以│π-3.14│=0.00159…≤0.005=0.5×10-2=21311101022--⨯=⨯ 所以,3.14作为π的近似值有3个有效数字。
(2)绝对误差:e(x)=π-3.15=3.14159265…-3.14=-0.008407…≈-0.0085。
相对误差:2()0.0085()0.27103.15r e x e x x --==≈-⨯ 有效数字:因为π=3.14159265…=0.314159265…×10,3.15=0.315×10,m=1。
而π-3.15=3.14159265…-3.15=-0.008407…所以│π-3.15│=0.008407……≤0.05=0.5×10-1=11211101022--⨯=⨯ 所以,3.15作为π的近似值有2个有效数字。
(3)绝对误差:22() 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈-L L 相对误差:3()0.0013()0.4110227r e x e x x--==≈-⨯ 有效数字:因为π=3.14159265...=0.314159265 (10)22 3.1428571430.3142857143107==⨯,m=1。
数值计算方法习题答案(第二版)(绪论)

数值分析(p11页)4 试证:对任给初值x 0,0)a >的牛顿迭代公式112(),0,1,2,......k ak k x x x k +=+= 恒成立下列关系式:2112(1)(,0,1,2,....(2)1,2,......kk k x k x x k x k +-=-=≥=证明:(1)(21122k k k k k kx a x x x x +-⎫⎛-=+==⎪ ⎝⎭(2) 取初值00>x ,显然有0>k x ,对任意0≥k ,a a x a x x a x x k k k k k ≥+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛+=+2121216 证明:若k x 有n 位有效数字,则n k x -⨯≤-110218, 而()k k k k k x x x x x 288821821-=-⎪⎪⎭⎫⎝⎛+=-+ nnk k x x 2122110215.22104185.28--+⨯=⨯⨯<-∴>≥ 1k x +∴必有2n 位有效数字。
8 解:此题的相对误差限通常有两种解法. ①根据本章中所给出的定理:(设x 的近似数*x 可表示为m n a a a x 10......021*⨯±=,如果*x 具有l 位有效数字,则其相对误差限为()11**1021--⨯≤-l a x x x ,其中1a 为*x 中第一个非零数)则7.21=x ,有两位有效数字,相对误差限为025.010221111=⨯⨯≤--x x e 71.22=x ,有两位有效数字,相对误差限为025.010221122=⨯⨯≤--x x e 3 2.718x =,有两位有效数字,其相对误差限为:00025.010221333=⨯⨯≤--x e x ②第二种方法直接根据相对误差限的定义式求解 对于7.21=x ,0183.01<-e x∴其相对误差限为00678.07.20183.011≈<-x e x 同理对于71.22=x ,有003063.071.20083.022≈<-x e x 对于718.23=x ,有00012.0718.20003.033≈<-x e x备注:(1)两种方法均可得出相对误差限,但第一种是对于所有具有n 位有效数字的近似数都成立的正确结论,故他对误差限的估计偏大,但计算略简单些;而第二种方法给出较好的误差限估计,但计算稍复杂。
《数值计算方法》课后题答案(湖南大学-曾金平)

习题一1.设x >0相对误差为2%,4x 的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x x f x f x δδ∆=≈得(1)()f x =11()()*2%1%22x x δδδ≈===;(2)4()f x x =时444()()'()4()4*2%8%x x x x x xδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P 关于1212.m nx a a a bb b =±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算 (1)31.97+2.456+0.1352; (2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352 ≈21((0.3197100.245610)0.1352)fl fl ⨯+⨯+ =2(0.3443100.1352)fl ⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl ≈⨯+⨯ = 21(0.3197100.259110)fl ⨯+⨯ =0.3456210⨯易见31.97+2.456+0.1352=0.210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?解:设该正方形的边长为x ,面积为2()f x x =,由(())(())'()()()()f x xf x f x x f x f x δδ∆=≈解得(())()()'()f x f x x xf x δδ≈=2(())(())22f x x f x x xδδ==0.5%5.下面计算y 的公式哪个算得准确些?为什么?(1)已知1x <<,(A )11121xy x x-=-++,(B )22(12)(1)x y x x =++; (2)已知1x >>,(A )y=,(B )y =; (3)已知1x <<,(A )22sin x y x =,(B )1cos 2xy x-=;(4)(A)9y =(B )y =解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算方法马东升等第 版习题解答

第1章 数值计算引论1.1 内容提要一、误差的来源数值计算主要研究以下两类误差。
1. 截断误差数学模型的准确解与用数值方法求得的解的差称为截断误差,又称为方法误差。
这种误差常常是由用有限过程代替无穷过程时产生的误差。
例如,要计算级数∑∞==+++++1!1!1!31!211k k n的值,当用计算机计算时,用前n 项(有限项)的和∑==+++++nk k n 1!1!1!31!211来代替无穷项之和,即舍弃了n 项后边的无穷多项,因而产生了截断误差∑∞+=1!1n k k2. 舍入误差由于计算机字长为有限位,原始数据和四则运算过程中进行舍入所产生的误差称为舍入误差。
例如,用3.141 59表示圆周率π时产生的误差0.000 002 6…,用0.333 33表示1÷3的运算结果时所产生的误差1÷3-0.333 33 = 0.000 003 3…都是舍入误差。
二.近似数的误差表示1. 绝对误差设x *是准值x 的一个近似值,称**)(x x x e -=为近似值x *的绝对误差,简称误差。
令|)(|*x e 的一个上界为*ε,即***|||)(|ε≤-=x x x e把*ε称为近似数*x 的绝对误差限,简称误差限。
2. 相对误差设*x 是精确值x 的一个近似值,称xx x xx e **)(-=为近似值x *的相对误差。
在实际应用中常取***)(xx x x e r -=为*x 的相对误差。
令相对误差绝对值 |)(|*x e r 的一个上界为ε*r,即 ****|||||)(|r r x x x x e ε≤-=把ε*r称为近似数*x 的相对误差限。
3. 有效数字对有多位数字的准确值四舍五入原则得到其前若干位的近似值时,该近似值的绝对误差不超过末位的半个单位。
设数x 的近似值m n x x x x 10.021*⨯±= ,其中,i x 是0~9之间的任一个数,但i x ≠0,n i ,2,1=是正整数,m 是整数,若nm x x -⨯≤-1021||*则称*x 为x 的具有n 位有效数字的近似值,*x 准确到第n 位,n x x x ,,,21 是*x 的有效数字。
数值计算课后规范标准答案2
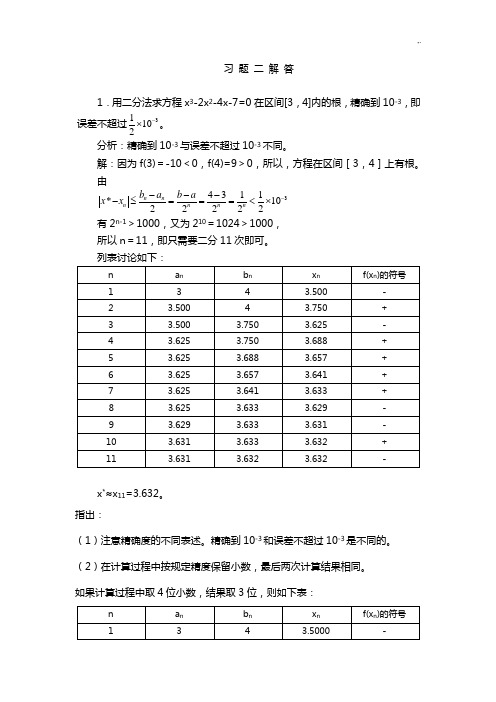
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
数值计算课后答案4

习题 四 解 答之勘阻及广创作1、设010,1x x ==,写出()x f x e -=的一次插值多项式1()L x ,并估计插值误差。
设插值函数为1()L x ax b =+解之得111a eb -⎧=-⎨=⎩则11()(1)1L x e x -=-+因为(),()x x y x e y x e --'''=-= 所以,插值余项为 所以010101()max max (1)2111248x r x e x x e ξξ-≤≤≤≤-≤-=⨯⨯=。
2解:设三次插值多项式为230123()f x a a x a x a x =+++,由插值条件,建立方程组为 即解之得则所求的三次多项式为23()0.41 6.29 3.489.98f x x x x =--+。
所以3、设(0,1,2,,)i x i n =是 n+1个互异节点,证明: (1)0()(0,1,2,,)nk k i i i x l x x k n ===∑;(2)0()()0(0,1,2,,)n k i i i x x l x k n =-==∑。
证明: (1)由拉格朗日插值定理,以x 0,x 1,x 2,…x n 为插值节点,对y=f(x)=x k作n 次插值,插值多项式为0()()nn i i i p x l x y ==∑,而y i =x i k,所以0()()()nnk n i i i i i i p x l x y l x x ====∑∑同时,插值余项 所以0()nk k i i i l x x x ==∑结论得证。
(2)取函数()(),0,1,2,,k f x x t k n =-=对此函数取节点(0,1,2,,)i x i n =,则对应的插值多项式为0()()()nk n i i i p x x t l x ==-∑,由余项公式,得(1)(1)011()()()()()()()()0(1)!(1)!nn kkn ki i i r x x t x t l x f x x t x n n ξξππ++==---==-=++∑所以令t=x ,4、给定数据(()f x =(1)试用线性插值计算f(2.3)的近似值,并估计误差;(2)试用二次Newton 插值多项式计算f(2.15)的近似值,并估计误差。
数值计算方法课后习题答案(李庆扬等) (修复的)

,。
第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++;[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
现代数值计算方法习题解答

现代数值计算方法习题答案习 题 一1、解:根据绝对误差限不超过末位数的半个单位,相对误差限为绝对误差限除以有效数字本身,有效数字的位数根据有效数字的定义来求.因此49×10-2:E = 0.005; r E= 0.0102; 2位有效数字. 0.0490 :E = 0.00005;r E = 0.00102; 3位有效数字. 490.00 :E = 0.005; r E = 0.0000102;5位有效数字. 2、解:722= 3.1428 …… , π = 3.1415 …… ,取它们的相同部分3.14,故有3位有效数字.E= 3.1428 - 3.1415 = 0.0013 ;r E = 14.3E = 14.30013.0 = 0.00041. 3、解:101的近似值的首位非0数字1α= 1,因此有 |)(*x E r |)1(10121−−××=n < = 21× 10-4, 解之得n > = 5,所以 n = 5 . 4、证:)()(1)()(1)(*11**11**x x x nx E x n x E n n n−=≈−−)(11)()(1)()(*****11****x E nx x x n x x x x nx x E x E r nnnn n r =−=−≈=− 5、解:(1)因为=204.4721…… , 又=)(*x E |*x x −| = |47.420−| = 0.0021 < 0.01, 所以 =*x4.47. (2)20的近似值的首位非0数字1α = 4,因此有|)(*x E r |)1(10421−−××=n < = 0.01 , 解之得n > = 3 .所以,=*x 4.47. 6、解:设正方形的边长为x ,则其面积为2x y =,由题设知x 的近似值为*x = 10 c m .记*y 为y 的近似值,则)(20)(20)(2)(*****x E x x x x x y E =−=−= < = 0.1,所以)(*x E< = 0.005 c m . 7、解:因为)()(*1x x nx x E n n −≈−,所以n x nE x x x n xx E x E r nn nr 01.0)()()(*==−≈=. 8、解:9、证:)()()(**t gtE t t gt S S S E =−≈−=t t E gt t t gt S S S S E r )(22/)()(2**=−≈−= 由上述两式易知,结论. 10、解:代入求解,经过计算可知第(3)个计算结果最好.11、解:基本原则为:因式分解,分母分子有理化、三角函数恒等变形…… (1)通分;(2)分子有理化;(3)三角函数恒等变形.12、解: 因为20=x ,41.1*0=x ,所以|*00x x −| < = δ=×−21021于是有|*11x x −| = |110110*00+−−x x | = 10|*00x x −| < =δ10|*22x x −| = |110110*11+−−x x | = 10|*11x x −| < =δ210类推有 |*1010x x −| < =810102110×=δ 即计算到10x ,其误差限为δ1010,亦即若在0x 处有误差限为δ,则10x 的误差将扩大1010倍,可见这个计算过程是不稳定的.习 题 二1、 解:只用一种方法. (1)方程组的增广矩阵为:−−−−11114423243112M M M → −−−−1010411101110112M M M →−−−11041001110112M M M → 31=x , 12=x , 13=x . (2)方程组的增广矩阵为:−−−−−−017232221413M M M → −−247210250413M M M → −−147200250413M M M → 21=x , 12=x, 2/13=x . (3)适用于计算机编程计算.2、 解:第一步:计算U 的第一行,L 的第一列,得611=u 212=u 113=u 114−=u3/1/112121==u a l 6/1/113131==u a l 6/1/114141−==u a l第二步:计算U 的第二行,L 的第二列,得3/1012212222=−=u l a u 3/213212323=−=u l a u 3/114212424=−=u l a u 5/1/)(2212313232=−=u u l a l 10/1/)(2212414242=−=u u l a l第三步:计算U 的第三行,L 的第三列,得10/37233213313333=−−=u l u l a u 10/9243214313434−=−−=u l u l a u 37/9/)(33234213414343−=−−=u u l u l a l第四步:计算U 的第四行,得370/9553443244214414444−=−−−=u l u l u l a u从而,−−−−3101141101421126 =−−137/910/16/1015/16/10013/10001−−−370/95500010/910/37003/13/23/1001126 由b LY =, 解得Y =(6,-3,23/5,-955/370)T . 由Y UX = , 解得X =(1,-1,1,-1)T . 3、(1)解:首先检验系数矩阵的对称正定性,这可以通过计算其各阶顺序主子式是否大于零来判断. 11a = 3 > 0,2223= 2 > 0, 301022123 = 4 > 0,所以系数矩阵是对称正定的.记系数矩阵为A ,则平方根法可按如下三步进行:第一步 分解:A = L L T . 由公式计算出矩阵的各元素:311=l 33221=l 3622=l 3331=l 3632−=l 233=l 因此, L =−23633036332003. 第二步 求解方程组LY = b . 解得Y = (335,36,2)T . 第三步 求解方程组L T X = Y . 解得X =(0,2,1)T .(2)解:首先检验系数矩阵的对称正定性,这可以通过计算其各阶顺序主子式是否大于零来判断.11a = 3 > 0,2223= 2 > 0, 1203022323 = 6 > 0,所以系数矩阵是对称正定的.记系数矩阵为A ,则平方根法可按如下三步进行:第一步 分解:A = L L T . 由公式计算出矩阵的各元素:311=l 33221=l 3622=l 331=l 632−=l 333=l因此, L =−363036332003 . 第二步 求解方程组LY = b . 解得Y = (335,66−,33)T. 第三步 求解方程组L T X = Y . 解得X = (1,21,31)T. 4、解: 对1=i , 2111==a d ;对2=i , 121−=t , 2121−=l ,252−=d ; 对3=i , 131=t , 2732=t ,2131=l , 5732−=l ,5273=d .所以数组A 的形式为:−−−=527572102521002A 求解方程组LY = b . 解得Y = (4,7,569)T .求解方程组DL T X = Y . 解得X = (910,97,923)T .5、解:(1)设A = LU =1010000000000010010015432l l l l5432106000000000600006006u u u u u 计算各元素得: 51=u ,512=l , 1952=u , 1953=l , 19653=u , 65194=l , 652114=u , 211655=l , 2116655=u .求解方程组LY = d . 解得Y = (1,51−,191,651−,211212)T.求解方程组UX = Y . 解得X = (6651509,6651145,665703,665395−,665212)T.(2)设A = LU =100100132l l3211001u u u 计算各元素得:51=u ,512=l ,5242=u ,2453=l ,241153=u . 求解方程组LY = d . 解得Y = (17,553,24115)T. 求解方程组UX = Y . 解得X = (3,2,1)T . 6、证:(1)(2)相同. 因为此方程组的系数矩阵为严格对角占优矩阵,所以雅可比迭代法和相应的高斯-赛德尔迭代法都收敛. (1)雅可比迭代公式:7107271)(3)(2)1(1+−−=+k k k x x x14141)(3)(1)1(2+−−=+k k k x x x329292)(2)(1)1(3+−−=+k k k x x x高斯-赛德尔迭代公式:7107271)(3)(2)1(1+−−=+k k k x x x14141)(3)1(1)1(2+−−=++k k k x x x329292)1(2)1(1)1(3+−−=+++k k k x x x(2)雅可比迭代公式:545152)(3)(2)1(1+−=+k k k x x x 525351)(3)(1)1(2++−=+k k k x x x 5115152)(2)(1)1(3++=+k k k x x x 高斯-赛德尔迭代公式:545152)(3)(2)1(1+−=+k k k x x x 525351)(3)1(1)1(2++−=++k k k x x x5115152)1(2)1(1)1(3++=+++k k k x x x7、(1)证:因为此方程组的系数矩阵为严格对角占优矩阵,所以雅可比迭代法和相应的高斯-赛德尔迭代法都收敛。
数值计算课后全部答案(整合)
目录第一章-----------------------------------------1 第二章-----------------------------------------4 第三章-----------------------------------------9 第四章-----------------------------------------15 第五章-----------------------------------------20 第六章-----------------------------------------27 第七章-----------------------------------------30第一章数值计算中的误差习题一1.1 下列各近似数的绝对误差限是最末位的半个单位,试指出它们各有几位有效数字。
1x =-3.105 , 2x =0.001, 3x =0.100, 4x =253.40, 5x =5000, 6x =5⨯310.答案:4,1,3,6,4,1.1.2 设100>*x >10,x 是*x 的有五位有效数字的的近似数,求x 的绝对误差限。
答案:当10<x<100时,因为有5位有效数字,所以绝对误差限为0.005. 1.3 求下列各近似数的相对误差限和有效数字位数: 1) 123x x x ++,2) 124x x x 3) 24x x 答案:()10.0005e x ≤()20.0005e x ≤()30.0005e x ≤ ()40.005e x ≤ ()50.5e x ≤ ()60.5e x ≤1)()()()()123123e x x x e x e x e x ++=++≤()()()123e x e x e x ++3221.5100.15100.510---≤⨯=⨯≤⨯2123()0.1510x x x ε-++=⨯123123123()()0.0004993...0.0004994r x x x e x x x x x x ε++++==≤++123x x x ++=-3.004 精确到小数点后两位,所以有三位有效数字。
数值计算方法课后习题答案吕同富

数值计算方法课后习题答案吕同富【篇一:《数值计算方法》(二)课程教学大纲】txt>课程编号: l124008课程类别:专业必修学分数: 3 学时数:48 适用专业:信息与计算科学应修(先修)课程:数学分析、高等代数一、本课程的地位和作用数值分析(二)为数值分析课程的第二部分,它是信息与计算科学专业的一门专业必修课。
主要内容包括函数最佳逼近、数值积分、数值微分、常微分方程数值解法。
通过本课程的学习,学生将初步具备用计算机去有效地解决实际问题的能力。
二、本课程的教学目标通过本课程的学习,使学生了解和掌握求解函数最佳逼近、数值积分、数值微分、常微分方程等问题所涉及的各种常用的数值计算方法、数值方法的构造原理及适用范围。
本课程坚持理论与实践教学并重的原则,理论上主要讲述求解函数最佳逼近、数值积分、数值微分、常微分方程等问题的基本理论和基本方法。
与此同时,通过上机实验加深学生对各种计算方法的理解,为今后用计算机去有效地解决实际问题打下基础。
三、课程内容和基本要求(“*”记号标记难点内容,“▽”记号标记重点内容,“▽*”记号标记既是重点又是难点的内容)第六章函数最佳逼近 1.教学基本要求(1)理解:几类常用的正交多项式。
(2)掌握:最佳一致逼近和最佳平方逼近。
(3)掌握:曲线拟合的最小二乘法。
2.教学内容(1)*正交多项式。
(2)▽*最佳一致逼近。
(3)▽最佳平方逼近。
(4)正交多项式的逼近性质。
(5)▽曲线拟合的最小二乘法。
第七章数值积分 1.教学基本要求(1)理解:机械求积公式的基本思想、插值型求积公式的特点。
(2)掌握:newton-cotes求积公式、复合求积公式。
(3)掌握:romberg求积公式、gauss求积公式。
2.教学内容(1)*机械求积公式。
(2)▽newton-cotes求积公式。
(3)▽复合求积公式。
(4)变步长求积公式。
(5)▽romberg求积公式。
(6)▽*gauss求积公式第八章数值微分 1.教学基本要求(1)了解:数值微分的中点法。
数值计算方法》习题答案

《数值计算方法》课后题答案详解吉 林 大 学第一章 习 题 答 案1. 已知(1)2,(1)1,(2)1f f f −===,求()f x 的Lagrange 插值多项式。
解:由题意知:()01201212001020211012012202121,1,2;2,1,1()()(1)(2)()()6()()(1)(2)()()2()()(1)(1)()()3(1)(2)(1)(2)()2162nj j j x x x y y y x x x x x x l x x x x x x x x x x l x x x x x x x x x x l x x x x x x x x L x y l x ==−=====−−−−==−−−−+−==−−−−−+−==−−−−+−==×+×−∴∑()2(1)(1)131386x x x x +−+×=−+2. 取节点01210,1,,2x x x ===对x y e −=建立Lagrange 型二次插值函数,并估计差。
解11201201210,1,;1,,2x x x y y e y e −−======1)由题意知:则根据二次Lagrange插值公式得:02011201201021012202110.510.520.51()()()()()()()()()()()()()2(1)(0.5)2(0.5)4(1)(224)(43)1x x x x x x x x x x x x L x y y y x x x x x x x x x x x x x x x x e x x e e e x e e x −−−−−−−−−−−−=++−−−−−−=−−+−−−=+−+−−+22)Lagrange 根据余项定理,其误差为(3)2210122()1|()||()||(1)(0.5)|3!61max |(1)(0.5)|,(0,1)6()(1)(0.5),()330.5030.2113()61()0.2113(0.21131)(0.21130.5)0.008026x f R x x e x x x x x x t x x x x t x x x x t x R x ξξωξ−+≤≤==−−≤−−∈′=−−=−+=−==≤××−×−=∴取 并令 可知当时,有极大值3. 已知函数y =在4, 6.25,9x x x ===处的函数值,试通过一个二次插值函数求的近似值,并估计其误差。
最新数值计算课后答案2
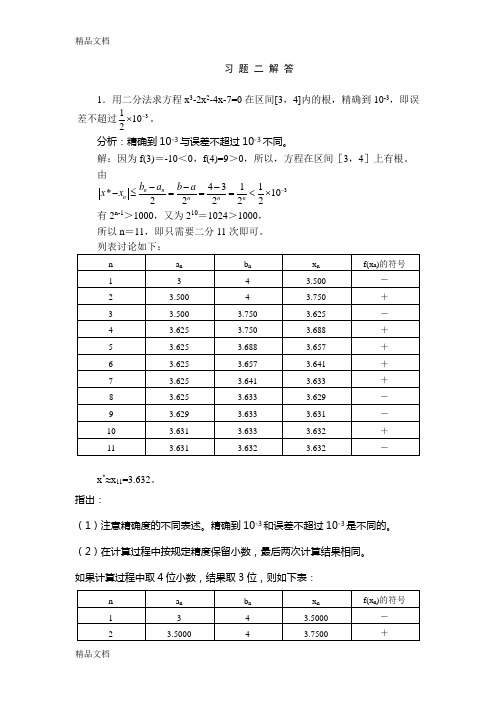
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根;因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
数值计算与MATLAB方法课后答案

第一章习题1. 序列满足递推关系,取及试分别计算,从而说明递推公式对于计算是不稳定的。
n1 1 0.01 0.00012 0.01 0.0001 0.0000013 0.0001 0.000001 0.000000014 0.000001 0.0000000110-105 0.00000001 10-10n1 1.000001 0.01 0.0000992 0.01 0.000099 -0.000099013 0.000099 -0.00009901-0.010000994 -0.00009901 -0.01000099-1.00015 -0.01000099-1.0001初始相差不大,而却相差那么远,计算是不稳定的。
2. 取y0=28,按递推公式,去计算y100,若取(五位有效数字),试问计算y100将有多大误差?y100中尚留有几位有效数字?解:每递推一次有误差因此,尚留有二位有效数字。
3.函数,求f(30)的值。
若开方用六位函数表,问求对数时误差有多大?若改用另一等价公式计算,求对数时误差有多大?设z=ln(30-y),,y*, |E(y)| 10-4z*=ln(30-y*)=ln(0.0167)=-4.09235若改用等价公式设z=-ln(30+y),,y*, |E(y)|⨯10-4z*=-ln(30+y*)=-ln(59.9833)=-4.094074.下列各数都按有效数字给出,试估计f的绝对误差限和相对误差限。
1)f=sin[(3.14)(2.685)]设f=sin xyx*=3.14, E(x)⨯10-2, y*=2.685, E(y)⨯10-3,sin(x*y*)=0.838147484, cos(x*y*)=-0.545443667⨯(-0.5454) ⨯⨯10-2+3.14(-0.5454) ⨯⨯10-3|⨯10-2⨯10-2|E r(f)| ⨯10-2⨯10-2<10-22)f=(1.56)设f = x y ,x*=1.56, E(x)⨯10-2, y*=3.414, E(y)⨯10-3,⨯⨯⨯10-2⨯⨯⨯10-3|⨯⨯⨯10-2⨯⨯⨯10-3|=0.051|E r(f)| =0.01125.计算,利用下列等式计算,哪一个得到的结果最好,为什么?6.下列各式怎样计算才能减少误差?7. 求方程x2-56x+1=0的二个根,问要使它们具有四位有效数字,至少要取几位有效数字?如果利用伟达定理, 又该取几位有效数字呢?解一:若要取到四位有效数字,如果利用伟达定理,解二:由定理二,欲使x1,x2有四位有效数字,必须使由定理一知,∆至少要取7位有效数字。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 四 解 答1、设010,1x x ==,写出()x f x e -=的一次插值多项式1()L x ,并估计插值误差。
解:根据已知条件,有设插值函数为1()L x ax b =+,由插值条件,建立线性方程组为1011a b a b e -⨯+=⎧⎨⨯+=⎩ 解之得111a e b -⎧=-⎨=⎩则11()(1)1L x e x -=-+ 因为(),()x x y x e y x e --'''=-= 所以,插值余项为(1)(2)(2)011()()()()()(1)!1()()2!1()()()2!1(0)(1)((0,1))2n r x f x p x f x n f x f x x x x e x x ξξπξπξξ+-=-=+==--=--∈所以010101()max max (1)2111248x r x e x x e ξξ-≤≤≤≤-≤-=⨯⨯=。
2、给定函数表i x()i f x选用合适的三次插值多项式来近似计算f 和f 。
解:设三次插值多项式为230123()f x a a x a x a x =+++,由插值条件,建立方程组为230123230123230123230123(0.1)(0.1)(0.1)0.9950.30.30.30.9950.70.70.70.7651.1 1.1 1.10.454a a a a a a a a a a a a a a a a ⎧+⨯-+⨯-+⨯-=⎪+⨯+⨯+⨯=⎪⎨+⨯+⨯+⨯=⎪⎪+⨯+⨯+⨯=⎩ 即012301230123123012312301230.10.010.0010.9950.10.010.0010.9950.30.090.0270.9950.40.080.02800.70.490.3430.7650.80.480.344 1.761.1 1.21 1.3310.454a a a a a a a a a a a a a a a a a a a a a a a a a a -+-=-+-=⎧⎪+++=++=⎪⇒⎨+++=++=⎪⎪+++=⎩12301231232330.40.720.9880.3110.10.010.0010.9950.40.080.02800.320.288 1.760.384 3.831a a a a a a a a a a a a a ⎧⎪⎪⎨⎪⎪++=-⎩-+-=⎧⎪++=⎪⇒⎨+=⎪⎪-=-⎩解之得 01230.416.293.489.98a a a a =⎧⎪=-⎪⎨=-⎪⎪=⎩ 则所求的三次多项式为23()0.41 6.29 3.489.98f x x x x =--+。
所以2323(0.2)0.41 6.290.2 3.480.29.980.20.91(0.8)0.41 6.290.8 3.480.89.980.8 1.74f f =-⨯-⨯+⨯=-=-⨯-⨯+⨯=-3、设(0,1,2,,)i x i n =是 n+1个互异节点,证明: (1)0()(0,1,2,,)nk k i i i x l x x k n ===∑;(2)0()()0(0,1,2,,)n k i i i x x l x k n =-==∑。
证明: (1)由拉格朗日插值定理,以x 0,x 1,x 2,…x n 为插值节点,对y=f(x)=x k 作n 次插值,插值多项式为 0()()nn i i i p x l x y ==∑,而y i =x i k ,所以0()()()nnk n i i i i i i p x l x y l x x ====∑∑同时,插值余项(1)(1)11()()()()()()0(1)!(1)!n k n k n r x x p x f x x x n n ξξππ++=-===++所以0()nk k i i i l x x x ==∑结论得证。
(2)取函数()(),0,1,2,,k f x x t k n =-=对此函数取节点(0,1,2,,)i x i n =,则对应的插值多项式为0()()()nk n i i i p x x t l x ==-∑,由余项公式,得(1)(1)011()()()()()()()()0(1)!(1)!nn kk n ki i i r x x t x t l x f x x t x n n ξξππ++==---==-=++∑所以()()()nkk i i i x t x t l x =-=-∑令t=x ,()()0nkiii x x l x =-=∑4、给定数据(()f x =xf(x)(1)试用线性插值计算f 的近似值,并估计误差;(2)试用二次Newton 插值多项式计算f 的近似值,并估计误差。
解:用线性插值计算f ,取插值节点为和,则相应的线性插值多项式是1.54919 1.48320() 1.48320( 2.2)2.4 2.21.483200.32995(2.2)p x x x -=+--=+- 用x=代入,得(2.3) 1.483200.32995(2.3 2.2) 1.450205f ≈+⨯-= (2)根据定理2,f(x)=f(x 0)+f[x 0,x 1](x-x 0)+f[x 0,x 1,x 2](x-x 0)(x-x 1)+…+f[x 0,x 1,…,x n ](x-x 0)(x-x 1)…(x-x n -1)+f[x 0,x 1,…,x n ,x]π(x) 。
以表中的上方一斜行中的数为系数,得 f =+ × × × = 指出: 误差未讨论。
5、给定函数表x 01245 y164688试求各阶差商,并写出牛顿插值多项式和插值余项。
57()0167(1)(1)(2)(1)(2)(4)26p x x x x x x x x x x x =++--------。
指出: 余项未讨论。
5*、给定函数表x 01234 y164688试求各阶差分,并求等距节点插值。
解:由已知条件,显然,x 0=0,h=1,x=t 。
0(1)(1)(2)(1)(2)(3)()()01614(2)(140)2!3!4!(1)(2)35167(1)(1)(2)(3)36n n t t t t t t t t t p x th p t t t t t t t t t t t t ------+==+⨯+⨯+⨯-+⨯---=+------指出:在本题这种情况下,实际上()()n n p t p x =,也就是说,在这样的条件下,t 的多项式就是x 的多项式,可以直接转换。
一般情况下,把t 的关系转换为x 的关系需要根据x=x 0+th ,将t 用x 表示,即将x x t h-=代入得到的多项式。
6解:所给节点是等距结点:000.125,0.125,,0,1,2,3,4,5i x h x x ih i ===+=。
令00()x x th t h=+=,根据等距结点插值公式,得 0(1)()()0.79618(0.02284)(0.00679)2!(1)(2)(1)(2)(3)(1)(2)(3)(4)(0.00316)0.00488(0.00460)3!4!5!n n t t p x th p t t t t t t t t t t t t t t -+==+⨯-+⨯----------+⨯-+⨯+⨯-则(0.1581)(0.1581)(0.1250.2648)0.790294822,(0.636)(0.6363)(0.125 4.088)0.651804826n n n n f p p h f p p h ≈=+=≈=+=。
7、设f(x)在[-4,4]有连续的4阶导数,且 (1)1,(0)2,(0)0,(3)1,(3)1f f f f f ''-=====(1)试构造一个次数最低的插值多项式p(x),使其满足(1)(1)1,(0)(0)2,(0)(0)0,(3)(3)1,(3)(3)1p f p f p f p f p f ''''-=-=-======== (2)给出并证明余项f(x)-p(x)的表达式。
解:(1)由7*可以求出满足(0)(0)2,(0)(0)0,(3)(3)1,(3)(3)1p f p f p f p f ''''======== 的三次埃尔米特插值多项式3252()2273H x x x =-+。
设22322252()()(3)2(3)273p x H x a x x x x a x x =+-=-++-,则p(x)满足 (0)(0)2,(0)(0)0,(3)(3)1,(3)(3)1p f p f p f p f ''''========, 由(1)1f -=得 3222521(1)(1)2(13)(1)1273108a a ⨯--⨯-++---=⇒=-, 所以223222432521()()(3)2(3)27310811332108544p x H x a x x x x x x x x x =+-=-+--=-++-+。
(2)余项具有如下结构22()()()()(1)(3)r x f x p x k x x x x =-=+- 作辅助函数22()()()()(1)(3)t f t p t k x t t t ϕ=--+-则显然()t ϕ在点,1,0,3x -处有6个零点(其中0,3是二重零点),即 ()0,(1)0,(0)0,(0)0,(3)0,(3)0x ϕϕϕϕϕϕ''=-=====, 不妨假设(1,0)x ∈-。
由罗尔定理,存在123(1,),(,0),(0,3)x x ξξξ∈-∈∈, 使得123()0,()0,()0ϕξϕξϕξ'''===,再注意到(0)0,(3)0ϕϕ''==,即()t ϕ'有5个互异的零点12303ξξξ<<<< 再次由罗尔定理得,存在111223343(,),(,0),(0,),(,3)ηξξηξηξηξ∈∈∈∈, 使得1234()0,()0,()0,()0ϕηϕηϕηϕη''''''''====第三次应用罗尔定理得,存在112223334(,),(,),(,)ξηηξηηξηη∈∈∈ 使得123()0,()0,()0ϕξϕξϕξ'''''''''===,第四次应用罗尔定理得,存在112223(,),(,)μξξμξξ∈∈ 使得(4)(4)12()0,()0ϕμϕμ==,第五次应用罗尔定理得,存在12(,)τμμ∈使得(5)()0ϕτ= 注意到(5)(5)(5)()()5!()()5!()t r t k x f t k x ϕ=-=-(()()()r t f t p t =-中p(t)是4次函数,其5次导数为0)。
