圆孔矩孔的菲涅尔衍射模拟(matlab实现)-工程光学

合集下载

圆盘衍射matlab

圆盘衍射matlab
在MATLAB中，我们可以使用以下步骤来模拟圆盘衍射：
1. 首先，我们需要定义一个圆形的光源。

这可以通过circle函数完成，例如：source circle = [0 0; 1 0];
2. 接下来，我们需要定义一个光栅，可以通过meshgrid 函数来实现。

例如：mesh grid = meshgrid(linspace(-1,1), linspace(-1,1), linspace(-1,1));
3. 然后，我们需要定义一个光源到光源的距离，例如：source to circle = 1;
4. 接着，我们需要定义一个光源到光栅的距离，例如：circle to grid = 1;
5. 最后，我们需要定义一个光源到光栅的距离，例如：circle to grid = 1;
6. 然后，我们可以通过以下公式来计算光栅的衍射图像：
diff image = (mesh grid.^2).*(source circle.^2).*(1 - (circle to grid.^2).*(source to circle.^2));
7. 最后，我们可以将这个公式放入MATLAB的代码中来实现圆孔衍射的模拟。

以上步骤只是一个基本的示例，具体的实现可能会根据你的具体需求有所不同。

基于matlab的衍射系统仿真(1)

《工程光学》综合性练习二题目：基于matlab的衍射系统仿真综合练习大作业二一、要求3-4人组成小组，对下面给出的各题目利用Matlab等工具进行仿真。

练习结束时每组提交一份报告及仿真程序。

在报告中应注明各仿真结果所对应的参数，如屏与衍射屏间距、孔径形状尺寸等。

二、仿真题目1.改变观察屏与衍射屏间距，观察观察屏上发生的衍射逐渐由菲涅耳衍射转为夫琅和费衍射1)原理图：S点光源发出的波长lam=500纳米S点发出光线经过单缝，缝宽a；单缝到衍射屏的距离L'2)Matlab代码clear;clcl=10; %l=input ('单缝到衍射屏的距离L=');a=0.2; %a=input('单缝的宽度(mm)a=');lam=500e-6; %lam=input('波长(nm)');x=-1:0.001:1; %接收屏边界y=x./sqrt(x.^2+l^2);z=a.*y/lam;I=1000*(sinc(z)).^2; %计算接受屏某点光强subplot(2,1,1) %绘制仿真图样及强度曲线image(2,x,I)colormap(gray(3))title('单缝衍射条纹')subplot(2,1,2)plot(x,I)title(光强分布)3)初始仿真图样（d=10）4)改变d之后的图样(d=1000)5)变化规律根据衍射屏以及接受屏的相对位置不同，由此产生菲涅尔衍射和夫琅禾费衍射的区别，根据我们模拟的情况得到菲涅尔衍射和夫琅禾费衍射的明显不同是夫琅禾费衍射条件下：中央有一条特别明亮的亮条纹，其宽度是其他亮条纹的两倍；其他亮条纹的宽度相等，亮度逐渐下降。

2.改变孔径形状、尺寸，观察图样变化1）原理图矩孔衍射：透镜焦距：1000mm;照射光波长：500nm;孔高：a（mm）；孔宽：b（mm）；圆孔衍射：圆孔直径：r（mm）；照射光波长：500nm;照射光波长：500nm;2）matlab代码矩孔衍射：focallength=1000;lambda=500;a=2.0;b=2.0;resolution=64;center=(resolution)/2;A=zeros(resolution,resolution);for i=1:1:resolutionfor j=1:1:resolutionif abs(i-center)<a*10/2 & abs(j-center)<b*10/2 A(j,i)=255;endendendE=ones(resolution,resolution);k=2*pi*10000/focallength/lambda;imag=sqrt(-1);for m=1:1:resolutionx=m-center;for n=1:1:resolutiony=n-center;C=ones(resolution,resolution);for i=1:1:resolutionp=i-center;for j=1:1:resolutionq=j-center;C(j,i)=A(j,i)*exp(-imag*k*(x*p+y*q)); endendE(n,m)=sum(C(:));endendE=abs(E);I=E.^2;I=I.^(1/3);I=I.*255/max(max(I));L=I;I=I+256;CM=[pink(255).^(2/3);gray(255)];Colormap(CM);edge=(resolution-1)/20;[X,Y]=meshgrid([-edge:0.1:edge]);x=linspace(-edge,edge,resolution);y=linspace(-edge,edge,resolution);subplot(1,2,1);surf(x,y,L);axis([-edge,edge,-edge,edge,0,255]);caxis([0,511]);subplot(1,2,2);image(x,y,I);axis([-edge,edge,-edge,edge,0,511]);view(2);axis square;圆孔衍射：clearlmda=500e-9; %波长r=1.2e-3; %f = 1; %焦距N = 19;K = linspace(-0.1,0.1,N) ;lmda1 = lmda* ( 1 + K) ;xm = 2000* lmda* f;xs = linspace(-xm,xm,2000) ;ys = xs;z0 = zeros( 2000) ;[x,y]= meshgrid( xs) ;for i = 1: 19s = 2*pi*r*sqrt(x.^2 + y.^2)./(lmda1( i) ) ;z = 4* ( besselj( 1,s)./( s + eps) ).^2; %光强公式z0 = z0 + z;endz1 = z0 /19;subplot( 1,2,1)imshow( z1* 255) ; %平面图xlabel( 'x')ylabel( 'y')subplot( 1,2,2)mesh( x,y,z1) %三维图colormap(gray)xlabel( 'x')ylabel( 'y')zlabel( '光强')3）仿真图样：矩孔衍射：a=1，b=2a=2，b=2可知：矩孔在一个维度上展宽一定倍数将导致衍射图样在相同维度上缩短相同倍数，同时能量会更向中心亮斑集中。

实验7 衍射的Matlab模拟

实验7衍射的Matlab模拟一、实验目的：掌握衍射的matlab模拟。

二、实验内容：1）单个圆孔夫朗和费衍射的matlab模拟2）双圆孔夫朗和费衍射的matlab模拟3）同一波长，狭缝数量分别为1、2、3、6、9、10时候的夫朗和费衍射的matlab模拟4）对4个不同波长的光照射时，狭缝数量分别为1、3时候的夫朗和费衍射的matlab 模拟5）单个圆孔菲涅尔衍射的matlab模拟6）模拟圆孔（或者单缝）衍射时，衍射屏到接收屏距离不同的时候衍射的图样1)clearclclam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;hh=(2*BESSELJ(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;B=b/max(b);endimage(xs,ys,b);colormap(gray(n));figure;plot(xs,B);colormap(green);-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-3-3-2-10123x 10-300.10.20.30.40.50.60.70.80.912)%双圆孔夫琅禾费衍射clear all close all clc %lam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:m r=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;h=(2*BESSELJ(1,x)).^2./x.^2;d=10*a;deltaphi=2*pi*d*xs(i)/lam;hh=4*h*(cos(deltaphi/2))^2;b(:,i)=(hh)'.*5000;end image(xs,ys,b);colormap(gray(n));-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-33)lamda=500e-9;%波长N=[1236910];for j=1:6a=2e-4;D=5;d=5*a;ym=2*lamda*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(j)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure(j);subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);plot(B1,ys,'k');end-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为2-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为3-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为9狭缝数为6-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.0254）lamda=400e-9:100e-9:700e-9;%波长N=[13];a=2e-4;D=5;d=5*a;for j=1:4ym=2*lamda(j)*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for k=1:2for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda(j);beta=pi*d*sinphi/lamda(j);B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(k)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);狭缝数为10plot(B1,ys,'k');end end-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02Lamda=400nm,N=1-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025Lamda=400nm,N=3Lamda=500nm,N=1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03Lamda=500nm,N=3Lamda=600nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04Lamda=600nm,N=3Lamda=700nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.045）clearclcN=300;r=15;a=1;b=1;I=zeros(N,N);[m,n]=meshgrid(linspace(-N/2,N/2-1,N));D=((m-a).^2+(n-b).^2).^(1/2);i=find(D<=r);I(i)=1;subplot(2,2,1);imagesc(I)colormap([000;111])axis imagetitle('衍射前的图样')L=300;M=300;[x,y]=meshgrid(linspace(-L/2,L/2,M));lamda=632.8e-6;k=2*pi/lamda;z=1000000;Lamda=700nm,N=3h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z); H=fftshift(fft2(h));%传递函数B=fftshift(fft2(I));%圆孔频谱G=H.*B;U=fftshift(ifft2(G));Br=(U/max(U));subplot(2,2,2);imshow(abs(U));axis image;colormap(hot)%figure,imshow(C);title('衍射后的图样');subplot(2,2,3);mesh(x,y,abs(U));subplot(2,2,4);plot(abs(Br))6)lamda=500e-9;%波长N=1;%缝数，可以随意更改变换a=2e-4;D=3:7;d=5*a;for j=1:5ym=2*lamda*D(j)/a;xs=ym;%屏幕上y的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:nsinphi=ys(i)/D(j);alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);endNC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1)image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2)plot(B1,ys,'k');end-0.4-0.200.20.4-0.015-0.01-0.00500.0050.010.01500.51-0.015-0.01-0.0050.0050.010.015D=3m-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025D=5m D=4m-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04D=7m D=6m。

菲涅耳衍射仿真

和观察屏之间时，观察
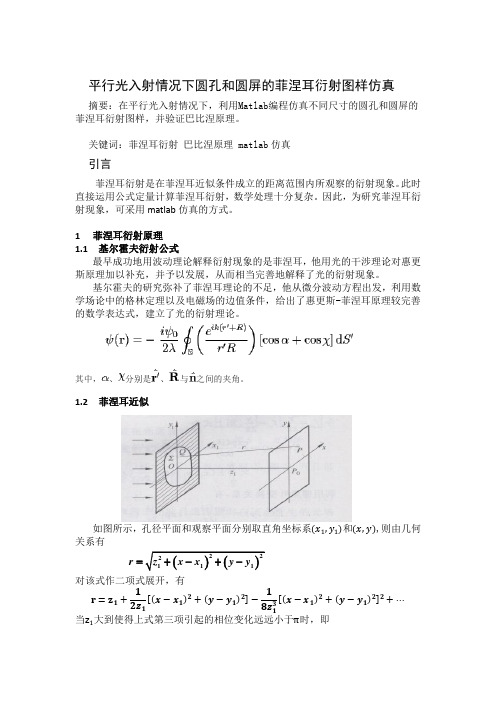
屏上 P 点的光场复振幅，��0 �� 表示无衍射屏时 P 点的光场复振幅，根据惠更斯菲涅耳原理，��1 �� 和��2 �� 可表示成对
1
和
2
开孔部分的积分，而两个屏
的开孔部分加起来就相当于屏不存在，因此 ��0 �� = ��1 �� + ��2 �� 该式说明，互补屏在衍射某点产生的复振幅之和等于光波自由传播时在该点产生的光场复振幅。 2 matlab 仿真程序设计 2.1 菲涅耳衍射的实现在菲涅耳近似下，P点的光场复振幅可表示为 �� , �� = �� 1 , ��1 ∗ ℎ(��, ��) 其中
总结与展望
利用所学知识基本完成了菲涅耳衍射的仿真。但在完成课程设计的过程中深深的感受到自身各方面的不足。还需更为努力。对于该仿真，因为使用了卷积，当采样数过大时，运算速度会变得很慢。该仿真还有更好的实现方式，是基于傅里叶变换的，可大大降低时间复杂度，无奈能力，精力有限，就不去实现了。
参考文献
【1】奥本海姆., Oppenheim A, 刘树棠. 信号与系统[M].西安: 西安交通大学出版社, 1998.
E3 (��)图样
E3 (��)分布图
E3 �� 与对应正方形衍射屏中央剖面光强分布对比图可见巴比涅定理成立。
3.4 夫琅禾费衍射
菲涅耳数F ≪ 1时，衍射图样为夫琅禾费衍射。选取F=0.1,n=400,p=2
F=0.1时圆孔衍射图样
F=0.1时圆孔衍射光强分布图

matlab实现夫朗和费矩形和圆孔衍射

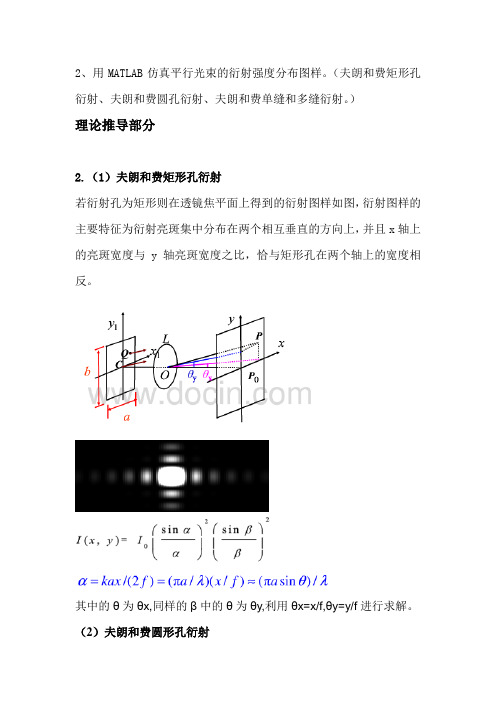
2、用MATLAB仿真平行光束的衍射强度分布图样。

（夫朗和费矩形孔衍射、夫朗和费圆孔衍射、夫朗和费单缝和多缝衍射。

）理论推导部分2.（1）夫朗和费矩形孔衍射若衍射孔为矩形则在透镜焦平面上得到的衍射图样如图，衍射图样的主要特征为衍射亮斑集中分布在两个相互垂直的方向上，并且x轴上的亮斑宽度与y轴亮斑宽度之比，恰与矩形孔在两个轴上的宽度相反。

其中的θ为θx,同样的β中的θ为θy,利用θx=x/f,θy=y/f进行求解。

（2）夫朗和费圆形孔衍射夫朗和费圆孔衍射的讨论方法和矩形孔衍射的讨论方法相同，只是由于圆孔的几何对称性，采用极坐标更为方便。

Ф=kaθ2.（1）夫朗和费矩形孔衍射clear all;lamda=500e-9;a=1e-3;b=1e-3;f=1;m=500;ym=8000*lamda*f;ys=linspace(-ym,ym,m)xs=ys;n=255;for i=1:msinth2=ys./sqrt(ys.^2+f^2);%相当于x/fsinth1=xs(i)/sqrt(xs(i).^2+f^2);%xs(i）作用每给一个ys值，要遍历到所有的x值angleA=pi*a*sinth1/lamda;%相当于书上的alfa=kax/2f k=2*pi/lamdaangleB=pi*b*sinth2./lamda;B(:,i)=(sin(angleA).^2.*sin(angleB).^2.*5000./(angleA.^2.*a ngleB.^2));%光强度公式endsubplot(1,2,1)image(xs,ys,B)colormap(gray(n))subplot(1,2,2)plot(B(m/2,:),ys)（2）夫朗和费圆孔衍射clearlam=500e-9a=1e-3f=1m=300;ym=5*0.61*lam*f/a;%取爱里光斑半径的5倍ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;%相当于r的平方sinth=sqrt(r./(r+f^2));%角度fai=2*pi*a*sinth./lam;%fai=k*a*sinthhh=(2*BESSELJ(1,fai)).^2./fai.^2;%贝塞尔函数 b(:,i)=hh.*5000;endsubplot(1,2,1)image(xs,ys,b)colormap(gray(n))subplot(1,2,2)b(:,m/2)plot(ys,b(:,m/2))。

写平行光束分别通过圆孔和矩形孔的菲涅尔衍射的matlab代码

写平行光束分别通过圆孔和矩形孔的菲涅尔衍射的matlab代码1. 引言1.1 概述在光学领域中，菲涅尔衍射是一种常见的现象，它描述了当平行光束通过孔洞或物体边缘时所产生的衍射效应。

这个现象在很多应用中都具有重要意义，例如光学仪器的设计、天文学以及激光技术等领域。

理解和研究菲涅尔衍射现象对于深入探究光的波动性质以及相干光的传播具有重要意义。

1.2 文章结构本文将从以下几个方面进行讨论：首先介绍菲涅尔衍射理论中与本文相关的基本概念和原理；其次详细阐述使用MATLAB代码实现菲涅尔衍射的方法和步骤；然后，通过对圆孔和矩形孔两种情况下的菲涅尔衍射结果进行分析和讨论；最后给出文章总结，并提出进一步研究方向。

1.3 目的本文旨在通过编写MATLAB代码来模拟实现平行光束通过圆孔和矩形孔时的菲涅尔衍射现象，并利用结果分析和比较两种情况下的衍射效应。

通过这样的研究，可以加深对菲涅尔衍射原理的理解，并为后续相关研究提供参考和借鉴。

同时，通过MATLAB代码实现，读者也可以根据自己的需求进行扩展和修改，从而进一步探索不同形状孔洞的菲涅尔衍射特性。

2. 菲涅尔衍射理论2.1 光的波动特性菲涅尔衍射是一种描述光波传播和衍射现象的理论。

根据光的波动特性，当光通过一个孔径较小的障碍物时，它会弯曲并发生衍射现象。

在菲涅尔衍射中，平行光束通过圆孔或矩形孔后，在进入屏幕上的观察点处产生干涉图样。

2.2 菲涅尔近似理论菲涅尔近似理论是在进一步简化计算过程中使用的近似方法。

它假设观察点距离光源和障碍物足够远，使得远场近似成立。

2.3 圆孔和矩形孔的描述圆孔和矩形孔是两种常见形状的障碍物，用于描述光线传播时发生的菲涅尔衍射效应。

- 圆孔: 圆孔通常由一个具有确定半径大小的圆形开口组成。

当平行光束通过圆孔时，它会扩散并形成一系列同心环状条纹。

- 矩形孔: 矩形孔是由一个具有确定边长的矩形开口组成。

当平行光束通过矩形孔时，它会扩散并在屏幕上生成一系列矩形衍射图样。

利用MatlabGUI模拟圆孔衍射

总第２７２期２０１２年第６期计算机与数字工程Ｃｏｍｐｕｔｅｒ　＆Ｄｉｇｉｔａｌ　ＥｎｇｉｎｅｅｒｉｎｇＶｏｌ．４０Ｎｏ．６１５１利用Ｍａｔｌａｂ　ＧＵＩ模拟圆孔衍射＊李芳菊　王菊霞（渭南师范学院物理与电气工程学院　渭南　７１４０００）摘　要　在惠更斯－菲涅尔原理的基础上，建立了衍射仿真实验的数学模型，分析了圆孔的夫琅禾费衍射图样及其强度分布，并实现了对圆孔衍射的仿真。

关键词　Ｍａｔｌａｂ　ＧＵＩ；夫琅禾费衍射；圆孔衍射中图分类号　Ｏ４３６．１Ｓｉｍｕｌａｔｉｏｎ　ｏｆ　Ａｐｅｒｔｕｒｅ　Ｄｉｆｆｒａｃｔｉｏｎ　Ｂａｓｅｄ　ｏｎ　ＭＡＴＬＡＢ　ＧＵＩＬＩ　Ｆａｎｇｊｕ　ＷＡＮＧ　Ｊｕｘｉａ（Ｓｃｈｏｏｌ　ｏｆ　Ｐｈｙｓｉｃｓ　ａｎｄ　Ｅｌｅｃｔｒｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，Ｗｅｉｎａｎ　Ｔｅａｃｈｅｒｓ　Ｕｎｉｖｅｒｓｉｔｙ，Ｗｅｉｎａｎ　７１４０００）Ａｂｓｔｒａｃｔ　Ｂａｓｅｄ　ｏｎ　ｔｈｅ　ｂａｓｉｃ　ｔｈｅｏｒｙ　ｏｆ　ｔｈｅ　Ｆｒａｕｎｈｏｆｅｒ　ｄｉｆｆｒａｃｔｉｏｎ，ｔｈｅ　ｍａｔｈｅｍａｔｉｃａｌ　ｍｏｄｅｌ　ｏｆ　ｄｉｆｆｒａｃｔｉｏｎ　ｅｘｐｅｒｉｍｅｎｔ　ｓｉｍｕｌａｔｉｏｎ　ｗａｓ　ｅｓ－ｔａｂｌｉｓｈｅｄ，ａｎｄ　ｔｈｅ　ａｐｅｒｔｕｒｅ　ｄｉｆｆｒａｃｔｉｏｎ　ｏｆ　Ｆｒａｕｎｈｏｆｅｒ　ｄｉｆｆｒａｃｔｉｏｎ　ｗｅｒｅ　ａｎａｌｙｚｅｄ．Ｆｉｎａｌｌｙ，ｔｈｅ　ｓｉｍｕｌａｔｉｏｎ　ｏｆ　ａｐｅｒｔｕｒｅ　ｄｉｆｆｒａｃｔｉｏｎ　ｗａｓ　ｓｕｃｃｅｓｓｆｕｌｌｙｃｏｍｐｌｅｔｅｄ．Ｋｅｙ　Ｗｏｒｄｓ　ＭＡＴＬＡＢ　ＧＵＩ，Ｆｒａｕｎｈｏｆｅｒ　ｄｉｆｆｒａｃｔｉｏｎ，ａｐｅｒｔｕｒｅ　ｄｉｆｆｒａｃｔｉｏｎＣｌａｓｓ　Ｎｕｍｂｅｒ　Ｏ４３６．１１　引言Ｍａｔｌａｂ语言是由墨西哥大学计算机系任主任的ＣｌｅｖｅＭｏｌｅｒ教授开发的一种专门作矩阵运算的数学软件［１～２］。

基于matlab gui设计的光学实验仿真

2007级计算机课程设计测控与光电技术学院电子科学与技术专业课程设计题目圆孔衍射现象计算机仿真设计学生姓名吴海班级070832指导教师钟可君日期2010 年6 月28 日南昌航空大学测试与光电工程学院计算机课程设计任务书电子科学与技术系070832 班学生：吴海课题名称：圆孔衍射现象计算机仿真设计课题内容：1、课题设计要求：(1)分析圆孔衍射的物理过程，建立数学模型；(2)设计算法流程图；(3)编写程序，并对仿真结果进行分析。

2、工作进度安排：查阅资料，设计算法流程图6月28日～7月4日第18周编写程序，撰写报告7月5日～7月9日第19周主要参考资料：[1]. 姚启钧.光学教程[M]. 北京：高等教育出版社[2]. 宋清，熊万杰.光学现象的计算机仿真[J].中山大学学报论丛，2005，25（3）：24-29.[3].圆孔衍射与像分辨本领的MATLABF仿真分析[J].湖北工学院学报，2004，19（5）：47-49.[4].MATLAB GUI在光学仿真中的应用[J].通化师范学院学报，2010,31（2）：52-54.系负责人：指导教师：钟可君时间：2010年6月21日单孔衍射上机试验上机试验程序（1）%圆孔衍射clcclearlam=500e-9a=1e-3f=1m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lamhh=(2*BESSELJ(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;endsubplot(1,2,1)image(xs,ys,b)colormap(gray(n))subplot(1,2,2)b(:,m/2)plot(ys,b(:,m/2))程序运行后的结果单孔衍射图光强分布图[摘要]运用MATLAB6的软件平台,编制演示程序,对圆孔衍射像分辨本领进行仿真分析.[关键词]圆孔衍射;分辨本领; Airy斑;仿真分析意义：圆孔作为光学仪器基本形状,其衍射现象在光学研究中占有重要地位.光学衍射现象的实验演示需要特定的实验仪器和实验所,给研究工作带来许多不便.另外,清晰的圆孔衍射图样,要求的圆孔半径很小,在一般实验中难以实现.基于MATLAB6软件强大的计算能力和可视化功能上的优势,利用计算机对圆孔衍射过程进行仿分析,可以使衍射现象直观地表现出来;通过调整实验参数,可以同步生成不同实验条件下的衍射图样,便于对衍射现象和像分辨本领进行比较分析;利用色图表现光强分布,使实验效果更为逼真,在实和研究中具有重要意义.1圆孔衍射的实验装置与数学模型的、建立圆孔夫琅禾费衍射装置如图1所示,S为点光源,位于透镜L1的焦平面的主光轴上,光屏E置于焦距为D的透镜L2的焦平面上.圆孔P的半径为R.入射光波长为λ.射圆孔时,沿衍射角θ方向传播的次波在光屏Q(x,y)处的光强分布为[1]Iθ= I0(J1(2m)m)2.其中:m=πRλsinθ,sinθ=x2+y2x2+y2+D2;I0为分常数.2主程序编写与衍射图样的生成运用MATLAB编制运算程序circle_aperturebase01.m,程序运行后,在坐标区可以生成圆孔琅禾费衍射图样.为了满足程序的普遍性和通用性,主程序中共设置5个输入参数,分别为λ,D,R,θ0(入射光垂直入射为θ0=0),最大坐标范围xmax.长度以毫米为单位.主程序circle_aperture_base01.m如下:function circle_aperture_base01(lambda,D,R,theta0,xmax) %对参量赋值lambda=6.328*1e-4;D=64;R=0.02;xmax=pi;theta0=0%设定图像的范围,并把x分成401个点(根据程序需要,设为奇数点).x=linspace(-xmax,xmax,401);[x,y]=meshgrid(x); %%建立x,y网格%建立强度分布矩阵x0=D*tan(theta0);sin_theta=sqrt(((x-x0).^2+y.^2)./((x-x0).^2+y.^2+D^2)); %%sin(theta)z=R*sin_theta/lambda; %%z=Rsin(theta)/lambdam=pi*z;I=(bessel(1,2*m)./m).^2;%生成强度分布图%绘制相对光强与x坐标的关系曲线(沿y=0方向) subplot('position',[0.15 0.6 0.7 0.35]),plot(x(1,:),I((end+1)/ 2,:))%绘制相对光强与坐标(R*sin(theta)/lambda)的关系曲线(沿y=0方向)subplot(2,2,3),plot(z((end+1)/2,:),I((end+1)/2,:));%绘制强度分布的灰度图NCLevers=255; %%确定用的灰度等级为255Imax=max(max(I));Ir=I/Imax*NCLevers;colormap(gray(NCLevers)); %%用灰度级颜色绘图subplot(2,2,4),image(x(1,:),y(:,1),Ir) %%绘制强度的灰度图axis squareaxis([-2 2 -2 2]);colorbar('vert')程序运行后,在坐标区,生成强度分布曲线和色图(如图2,图中的极值判断和文字标示命令在程序中未列出).图中,上图表示强度沿x坐标(y =0)分布,下图左侧表示强度随无量纲因子Rsinθ/λ的变化规律,右侧则表示光强在xoy平面的变化规律,中央的白色亮区为Airy斑.在光强曲线图中,用红点和绿点表示极大值点和极小值点,对应坐标也在图2(c)中央明区中给出.3衍射图样分析3.1Airy斑与极小值由图2可知,当Rsinθ/λ≈0.61时,出现第一级极小值.定义在光屏上由两个第一级极小值之间所围圆形区间为Airy斑.Airy斑的中心位于坐标原点,其角半径为0.61λ/R,如图所示.3.2第一级次极大由图2可知,当Rsinθ/λ≈0.82时,出现第一级次极大值,其相对光强为1.7%.其余次极大的光强将更小.3.3参数对衍射图样的影响进一步调整参数R、D及λ,其Airy斑及各级衍射环的相对位置发生变化.如图3所示,Airy斑的角半径与R成反比,与λ成正比,其线半径与D成正比.5结论从上面的一系列讨论可以发现,通过计算机编程,对圆孔夫琅禾费衍射进行仿真分析,无需复杂的实验仪器和苛刻的实验环境,可在短时间内完成多种实验条件衍射图样的演示.运用MATLAB强大的数值计算功能和优越的可视化特征,可以同步求出衍射图样的一些重要物理量的数值,满足仿真实验的需要,为教学和研究工作提供了强有力的演示工具.利用计算机编程,仿真演示复杂的物理现象, 作为计算物理学的一个发展方向,具有广阔的发展前景.[参考文献][1]姚启钧.光学教程[M].北京:高等教育出版社, 2002.[2]赵凯华,钟锡华.光学(上册)[M].北京:北京大学出版社, 1984.摘要:采用matlab7.0强大的函数作图功能对圆孔、矩孔和双矩孔的夫琅和费衍射进行模拟,建立直观形象并且精确完整的理论模型,并附上程序代码,将干涉理论联系起来,分析衍射和干涉的本质。

MATLAB编程用两种方法模拟光学实验

MATLAB编程用两种方法模拟光学实验03级物理一班李超PB03203017摘要：利用MATLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟；以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。

关键词：MATLAB；衍射积分；傅立叶变换；计算机模拟引言：美国Mathworks公司推出的MA TLAB，是一种集数值计算、符号预算、可视化建模、仿真和图形处理等多种功能于一体的优秀图形化软件。

本文介绍了通过MA TLAB软件编程实现用衍射积分和傅立叶变换实现夫琅和费衍射计算机模拟的方法。

计算机模拟为衍射实验的验证提供一条简捷、直观的途径。

从而加深了对物理原理、概念和图像的理解。

正文：大学教学课程中引入计算机模拟技术正日益受到重视，与Basic、C和Fortran相比，用MA TLAB软件做光学试验的模拟，只需要用数学方式表达和描述，省去了大量繁琐的编程过程。

下面来介绍利用MATLAB进行光学模拟的两种方法。

（一）衍射积分方法：该方法首先是由衍射积分算出接收屏上的光强分布，然后根据该分布调制色彩作图，从而得到衍射图案。

1．单缝衍射。

把单缝看作是np个分立的相干光源，屏幕上任意一点复振幅为np个光源照射结果的合成，对每个光源，光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2，其中α=2Δ/λ=πypys/λD编写程序如下，得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1) image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2．杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π（r 2-r 1）/λ,光强I=4I 0cos 2（Φ/2）编写程序如下，得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2); r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); end N=255;Br=(B/4.0)*Nsubplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3．光栅衍射公式：I=I 0（sin α/α）2（sin(λβ)/sin β）2α=(πa/λ)sin Φ β=(πd/λ)sin Φ编写程序如下：得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);图2 杨氏双缝干涉的光强分布图3 黑白光栅衍射光强分布end NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);（二）傅立叶变换方法：在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。

基于MATLAB的衍射场模拟计算

收稿日期:2003-09-09.基金项目:云南省教育厅基金资助项目(项目编号:03Y 225A ).第一作者简介:钱晓凡(1963～),男,副教授.主要研究方向:拉曼光谱和光信息处理.E -mail :qianciaofan1@hatmail.com基于MAT LAB 的衍射场模拟计算钱晓凡,胡涛,张晔(昆明理工大学理学院,云南昆明　650093)摘要:光的衍射现象研究,不仅具有重要的理论意义,而且在光学仪器研制和成象分析等均有重要价值.针对衍射计算困难的问题,选择合适的计算公式,并基于科学计算软件MAT LAB5.3编写计算程序,使计算得变得简洁,大大提高了实验的效率.用MAT LAB 编程得出的计算结果与用数码相机记录的衍射图样进行比较,两者吻合得很好.关键词:衍射计算;MAT LAB ;菲涅尔衍射;傅立叶变换;卷积中图分类号:O436.1文献标识码:A 文章编号:1007-855X (2004)03-0132-03On Simulated Calculation of Diffraction B ased on MATLABQIAN X ian 2fan ,HU Tao ,ZHAN G Ye(Faculty of Science ,K unming University of Science and Technology ,K unming 650093,China )Abstract :The calculation of diffraction was too complicated to be done until computer was invented.By choos 2ing proper formula and software ,not only can the result of calculation of diffraction be given ,but also figures can be worked out easily.It greatly improves the efficiency of experiments.At the same time ,since digital camera is more and more popularized ,it provides a new method for recording diffraction pattern.It turns out to be that the results gotten by using software MAT LAB 5.3are identical with photographs taken by digital camera.K ey words :calculation of diffraction ;MAT LAB ;Fresnel diffraction ;Fourier transform ;convolution0引言光的衍射是一重要的光学现象.对光的衍射现象的研究,不仅具有重要的理论意义,而且在光学仪器研制和成像分析等诸多实际应用方面均有重要价值.对光的衍射的研究,始于17世纪,但至19世纪才建立了一些定量分析理论及一些数学公式,由于这些数学公式的复杂性,使得实际的计算工作变得很繁杂.文章用MAT LAB5.3编写有关计算程序,使计算变得简洁,提高了实际应用的效率.因为计算是建立在基尔霍夫对衍射的解析分析理论上的,先简单介绍该理论.如图1,设Σ为衍射孔,d s 为Σ面的一个面积元,P 为前方一点,引起的振动振幅与面积元d s 成正比.根据惠更斯-菲涅尔原理,P 点的振动等于Σ面的所有面积元所引起的振动的叠加,所以P 点的合振动等于整个Σ面的积分: U (p )=κ6U 0(x ,y 1)k (φ)r cos (ωt -2πr λ)d s (1)式中,U 0(x 1,y 1)是Σ面上的光场分布,k (φ)为φ的一个函数,称为倾斜因子,ω为光波的圆频率,λ为波长.在菲涅尔的理论中倾斜因子k (φ)没有严格定义.1880年基尔霍夫从麦克斯韦理论出发,经过严格的数学处理建立了一个公式———基尔霍夫公式:第29卷第3期2004年6月昆明理工大学学报(理工版)Journal of K unming University of Science and Technology (Science and Technology )Vol.29　No 13　J un.2004 U (p )=A 2j λκ6U 0(x ,y 1)exp [jkr ]r [cos (n ,r )-cos (n ,l )]d s (2)其中(n ,r )和(n ,l )分别是孔径面的法线与l 和r 的夹角.在大多数衍射问题中,倾斜因子[cos (n ,r )-cos (n ,l )]2可看作常量.1菲涅尔近似和夫朗和费近似为了计算(2)式的积分,需要用坐标变换表示r 和d s.如图3,如果采用直角坐标系,可以将r 展开: r =z 1+(x -x 1)2+(y -y 1)22z 1+[(x -x 1)2+(y -y 1)2]28z 31+ (3)当z 1大到使z 31µ14λ[(x -x 1)2+(y -y 1)2]2成立时,为菲涅尔衍射,(2)式变为: U (p )=exp [jkz 1]jz 1λκ6U 0(x ,y 1)exp {jk 2z 1[(x -x 1)2+(y -y 1)2]}d x 1d y 1(4)或:U (p )=exp [jkz 1]jz 1λexp [jk 2z 1(x 2+y 2)]κ6U 0(x ,y 1)exp [jk 2z 1(x 21+y 21)]exp [-j 2π(x 1x λz 1+y 1y λz 1)d x 1d y 1(5)当继续增大z 1,使:πµk (x 21+y 21)2z 1成立时,为夫朗和费衍射,(4)式变为:U (p )=exp [jkz 1]jz 1λexp [jk 2z 1(x 2+y 2)]κ6U 0(x ,y 1)exp [-j 2π(x 1x λz 1+y 1y λz 1)]d x 1d y 1(6)2衍射计算公式2.1傅立叶变换与卷积2.1.1傅立叶变换非周期函数f (x ,y )在整个无限x ,y 平面上满足狄里赫利条件,且κ+∞-∞|f (x ,y )|d x d y 存在,则二元函数f (x ,y )的傅立叶变换定义为 F (ε,η)=κ+∞-∞f (x ,y )exp {-j 2π(εx +ηy )}d x d y (7)2.1.2卷积函数h (x ,y )和函数f (x ,y )为二维函数,它们的卷积定义为:331第3期钱晓凡,胡涛,张晔:基于MAT LAB 的衍射场模拟计算 g (x ,y )=κ+∞-∞f (α,β)·h (x -α,y -β)d αd β=f (f x ,y )3h (x ,y )(8)2.2衍射计算公式将(4),(5)和(6)式与(7)和(8)式比较,显见菲涅尔衍射可以用函数exp [jkz 1]jz 1λU 0(x 1,y 1)与函数exp [jk 2z 1(x 2+y 2)]的卷积来计算: U (p )=exp [jkz 1]jz 1λU 0(x 1,y 1)3exp [jk 2z 1(x 2+y 2)](9)菲涅尔衍射也可以用函数U 0(x 1,y 1)exp [jk 2z 1(x 21+y 21)]的傅立叶变换,再乘以函数exp [jkz 1]jz 1λexp [jk 2z 1(x 2+y 2)]来计算.而夫朗和费衍射则可以直接用函数U 0(x 1,y 1)的傅立叶变换,再乘以函数exp [jkz 1]jz 1λexp [jk 2z 1(x 2+y 2)]来计算.实际计算时,我们使用的就是上述三种计算方法.3用MAT LAB 进行计算机模拟计算的实验结果我们使用的软件是MAT LAB5.3,它是一个功能十分强大的应用软件,可以在很多学科中得到应用.与其它计算机语言相比它更加灵活,更加接近科技人员的思维方式,因而编程效率更高.我们用MAT LAB5.3编写程序分别计算了矩形孔、圆孔和三角形孔的菲涅尔和夫朗和费衍射,并与用数码相机记录的结果进行了比较,两者非常吻合.要特别指出的是,由于MAT LAB5.3已经内设了计算二维傅立叶变换的函数“fft2”和计算二维卷积的函数“conv ”,所以整个计算程序不到20行,非常容易编写和修改,而且每次运算时间不到10s.我们的实验器材有:He -Ne 激光器,光具座,凸透镜(焦距为77.1mm ),衍射屏,观察屏和数码相机.图4和图5分别是观察和记录菲涅尔衍射和夫朗和费衍射的光路图.我们计算了各种形状和尺寸的衍射孔在不同衍射距离上的菲涅尔衍射,下面给出一组典型结果:(下转第151页)431昆明理工大学学报(理工版) 第29卷大,手性的不同对膦铑络合物的少部分键长、键角数据有所影响;(3)在与(MAC )形成络合物前后,双膦配体上主要原子的电荷分布变化并不显著,但金属铑原子上的电荷则显著增加,可能是MAC 在与膦铑配体络合过程中有电荷向铑原子上进行了转移.参考文献:[1]林国强,陈耀全,陈新滋,李月明.手性合成-不对称反应及其应用[M ].北京:科学出版社,2000.250～253.[2]Steven Feldgus ,Clark rge -Scale C omputational M odeling of [Rh (DuPHOS )]+-Catalyzed Hydrogenation ofProchiarl Enamides :Reaction Pathways and the Origin of Enantioselection [J ].J.Am.Chem.S oc.,2000,122(51):12714～12727.[3]Achim K less ,Armin Borner ,Detlef Heller ,Rudiger Selke.Ab Initio Studies of Rhodium (I )-N -Alkenylamide Releyancefor the Mechanism of Catalytic Asymmetric Hydrogenation of Prochiral Dehydroamino Acids [J ].Organometallics.,1997,16(10):2096～2100.[4]Portmann S ,Luthi H P.M olekel :An Interractive M olecular G raphics T ool [J ].CHIMIA ,2000,(54):766～770.(上接第134页)以上图形是在衍射孔尺寸为1.5mm ,衍射距离为50mm 时的菲涅尔衍射结果,可以看出,计算的结果与数码相机记录结果很吻合,说明基于MAT LAB 模拟计算衍射场是可行的,这些结果我们已经用于教育厅基金项目研究中.MAT LAB 允许用不同格式输出图形,图7是用网格图的形式输出的矩形孔衍射图案,可以方便地观察衍射图案的细节.另外,夫朗和费衍射的计算结果吻合得也很好,这里不再给出.衍射是一个古老的问题,但直到19世纪科学家才把他弄清楚,而衍射的计算又很复杂,这使得很多问题很难解决,如今有了计算机和高级科学计算软件,使我们可以很方便地计算许多问题,这也使得光的传播问题可以用模拟的方式来解决.参考文献:[1]赵达尊,张怀玉.波动光学[M ].北京:北京理工大学出版社,1999.102～113.[2]苏显渝,李继陶.信息光学[M ].北京:科学出版社,2000.34～45.[3]G rant R.Fowles.Introduction to M odern Optics[M ].New Y ork :Dover Publications ,Inc.,1989.106～111.[4]王炳武,等.MAT LAB5.3实用教程[M ].北京:中国水利水电出版,2000.227～230.151第3期陈秀敏,李西平,刘有德:几种膦铑络合物及其MAC 络合物的量子化学计算。

圆孔矩孔的菲涅尔衍射模拟(matlab实现)-工程光学

圆孔矩孔的菲涅尔衍射模拟(m a t l a b实现)-工程光学-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII工程光学综合练习-----圆孔、矩孔的菲涅尔衍射模拟圆孔和矩孔的菲涅尔衍射模拟一、原理由惠更斯-菲涅尔原理可知接收屏上的P点的复振幅可以表示为其中为衍射屏上的复振幅分布，为倾斜因子。

根据基尔霍夫对此公式的完善，有设衍射屏上点的坐标为（x1, y1），接收屏上点的坐标为（x, y），衍射屏与接收屏间距离为z1，当满足菲涅尔近似条件时，即此时可得到菲涅尔衍射的计算公式把上式指数项中的二次项展开，并改写成傅里叶变换的形式，可以写成上式为菲涅尔衍射的傅里叶变换表达式，它表明除了积分号前面的一个与x1、y1无关的振幅和相位因子外，菲涅尔衍射的复振幅分布是孔径平面的复振幅分布和一个二次相位因子乘积的傅里叶变换。

相对于夫琅和费衍射而言，菲涅尔衍射的观察屏距衍射屏不太远。

在菲涅尔衍射中，输入变量和输出变量分别为衍射孔径平面的光场分布和观察平面的光场以及光强分布，考虑到这三个量都是二维分布,而且Matlab主要应用于矩阵数值运算,所以本程序选择用二维矩阵来存储衍射孔径平面和观察平面的场分布,并分别以矩阵的列数和行数来对应平面的直角坐标值(x, y)以及(x1, y1)。

二、圆孔菲涅尔衍射用MATLAB分别构造表示衍射屏和接收屏的二维矩阵。

注意使两矩阵阶次相同，考虑到运算量的要求，采样点数不能过多，所以每个屏的x和y方向各取200到300点进行运算。

根据式（4），选取合适的衍射屏和接收屏尺寸和相距的距离，模拟结果如下：取典型的He-Ne激光器波长λ=，固定衍射屏和接收屏尺寸和相距的距离，分别取不同的圆孔半径，得到以下三组衍射图样，其圆孔半径分别为12mm，20mm，50mm图 1（r=12mm）图 2（r=20mm）图 3(r=50mm)三、矩孔的菲涅尔衍射步骤与上述相同，仅需改变与衍射屏形状对应的矩阵。

基于Matlab GUI光的衍射实验仿真

基于Matlab GUI光的衍射实验仿真闫燕;丁益民;王喜艳【摘要】利用Matlab仿真软件的GUI图形用户界面可视化工具和FFT傅里叶变换工具,对圆孔、方形孔、多边形孔、圆盘四种不同的孔形进行菲涅尔光的衍射实验仿真.通过用户界面对光学参数进行数据交互,能形象直观地得到四种不同孔径光的衍射图纹、光强三维分布、光强二维分布图像.应用于物理课堂教学中能将抽象难于实现的衍射实验现象直观呈现,同时,有助于学生对衍射原理的理解,具有操作便捷、设计灵活等特点,从而达到较好的实验演示教学目的.【期刊名称】《大学物理实验》【年(卷),期】2019(032)004【总页数】4页(P88-91)【关键词】Matlab GUI;光的衍射;仿真实验【作者】闫燕;丁益民;王喜艳【作者单位】湖北大学物理与电子科学学院,湖北武汉 430062;湖北大学物理与电子科学学院,湖北武汉 430062;湖北大学物理与电子科学学院,湖北武汉430062【正文语种】中文【中图分类】O4-39菲涅尔衍射是大学物理重点学习内容，但光的衍射实验现象对实验设备及环境要求苛刻，通常不能达到较好的实验结果。

近年来，不断有人在光的衍射仿真方面上做了多种尝试，吕波、徐志军对远场的夫琅禾费衍射(光源和观察幕离障碍物的孔或屏均为无穷远的衍射现象)进行了研究，将菲涅尔衍射积分转化为含快速傅里叶变换的积分，求解出在任意形状衍射屏的夫琅禾费衍射图样和光强分布[1-4]。

惠更斯—菲涅尔提出的子波干涉原理与基尔霍夫求解波动方程所得的结果十分一致，都可以表示成类似的衍射公式。

本文研究的是在基于傅里叶变换的光学理论基础上，利用Matlab的FFT傅里叶变换工具和GUI图形用户界面工具[5]，通过控制观察屏距离和光的波长，将高性能的数据计算和GUI可视化结合在一起，实现多种衍射屏下菲涅尔衍射现象(光源与衍射屏距离z为有限远时，所观察到的衍射现象)的仿真模拟。

1 傅里叶光学理论基础假设一个有限孔径，设孔径屏的直角坐标系为(x0,y0)，并且观察平面与孔屏平行，两个平面间的间距为z，观察平面的坐标系为(x,y)，这时，观察平面上的场可以表示为：exp{j2π[fx(x-x0)+fy(y-y0)]}(1)根据近轴近似条件：(2)同时利用傅里叶变换关系先对fx，fy进行积分，得到如下的菲涅尔公式：(3)令则(3)式上式可以写为：(4)对(4)做傅里叶变换可以得到：A(fx,fy,z)=A0(fx,fy)H(fx,fy,z)(5)式中：A(fx,fy)=FFT{U0(x,y)}对于单位振幅入射平面波：A0(fx,fy)=FFT{t0(x,y)}H(fx,fy)=FFT{h(x,y)}根据以上原理，传递函数H(fx,fy)已知，只需要求得透射孔径的透过率函数t0(x,y)，然后对透过率函数进行傅里叶变换得，并与传递函数相乘得到A(fx,fy,z)，最后做一个逆傅里叶变换得到U(x,y,z)=IFFT{A(fx,fy,z)}，即可得到菲涅尔衍射图像。

用MATLAB语言模拟光衍射实验

第14卷第4期大　学　物　理　实　验　V ol.14N o.42001年12月出版PHY SIC A L EXPERI ME NT OF C O LLEGE Dec.2001收稿日期:2001-07-30文章编号:1007-2934(2001)04-0047-02用MAT LAB 语言模拟光衍射实验周　忆(安徽省科学技术培训中心,合肥,230031)　梁　齐(合肥工业大学,合肥,230009)摘　要:用M AT LAB 语言模拟编写了光衍射的模拟实验程度,给出了五种元件的夫琅和费衍射图。

关键词:衍射;模拟;M AT LAB 语言中图分类号:O4-39 文献标识码:A光的衍射现象是光具有波动性的重要特征,衍射无论在理论研究还是在大学物理教学中都占有较重要的地位。

笔者利用MAT LAB 较强的绘图和图像功能,针对多种衍射元件(单缝、双缝、光栅、矩孔、圆孔)编写了光衍射的模拟实验程序。

在计算机的模拟光的衍射,条件限制较少,对于衍射的实验教学是一种较好的补充。

程序首先根据衍射强度分布的理论公式及实验参数建立衍射相对强度的数据矩阵B (x ,y )然后利用image (B )和colormap (gray )命令绘出衍射图样。

同时,也绘制了衍射光强分布的二维或三维图。

单缝夫琅和费衍射的模拟结果见图1。

衍射光强公式为I =I 0(sin u/u )2,u =(πa sin θ/λ),a 是缝宽,λ是入射光的波长,θ是衍射角。

设观察屏位于单缝后正透镜的焦平面上,f 为透镜的焦距,x 为屏上横向坐标。

θ=arctan (x/f )。

模拟分成三组:第一组,λ=600nm ,f =600mm ,(a )a =0.20mm ;(b )a =0.10mm ;(c )a =0.05mm 第二组,a =0.10mm ,f =600mm ,(d )λ=500nm ;(e )a =600nm ;(f )λ=700nm第三组,a =0.10mm ,λ=600nm ,(g )f =300mm ;(h )f =600mm ;(i )f =900mm以下内容中,取λ=600nm ,f =600mm ,衍射图样横坐标x 和纵坐标y 的范围均为[-20,20]mm 。

Matlab仿真技术在大学物理光学实验教学中的应用

79
总第238期
分约20%，其余80%尽管是多数，却是次要的，因此称二八定律。以这条定律分析，我公司在每年年底都会对第二年的计划目标确定轻重缓急，使公司保证能超额完成上级交给我们的计划目标任务。
4.自我控制目标管理是以行为科学中的激励理论为基础产生的，它认为在目标明确的情况下，人们能够对自己负责，愿意承担责任，愿意做出贡献，愿意有所成就，所以能够实现自我管理。也就是说，目标管理能够从实现企业总目标出发，去协调企业各个组成部分乃至每个人的活动。目标管理是一种参与性、民主性、自我控制性比较强的管理制度，它把个人的需求和组织目标结合起来，用自我控制的管理来代替由别人统治的管理。电缆工程公司以目标管理为核心，在认真筹备、精心组织的基础上，对机构设置、岗位优化工作有计划地稳步推进，目前公司新的组织结构和人员配置已全面完成，原电缆管道公司全体及兴润公司的部分人员并入电缆工程公司，取消了原科室分公司三级管理模式，成立了八个新部室，包括党群工作部、办公室、人力资源部、工程管理部、市场部、安质部、物资部、财务部，实行部室制二级管理模式。在此基础上，落实了各岗位人员配置。 5.流程管理其基本思想是以企业的作业流程为核心，重新设计企业内部的组织结构、运作方式和行为准则。对企业流程进行最根本的重新思考和最彻底的重新设计，以达到诸如成本、品质、服务和速度等绩效的协同进步，而不再遵从分工论原则。企业内的一切流程都应以企业目标为根本依据，对外：面向客户，提高业务流程的效率；对内：面向企业目标，提高管理流程的效率，平衡企业各方资源（各项业务线平衡），控制总体效率的平衡，实现企业总体绩效。基于电力电缆工程有限公司具有工序清晰、重复性强、流水作业的生产特点，流程管理对于电力电缆工程有限公司尤为实用、有效。因此应该寻找一种符合目前从业人员素质现状的管理模式，来配合目标管理的实施。首先，企业的产品或服务要通过流程来实现，在精细管理中，只有每位员工和每个部门都尽职尽责，企业才会有较好的经济效益。因此，企业必须将着眼点放在流程管理上。流程是连接企业生产和客户需求的纽带，流程的输出来自于客户的需求和企业的目标，人、资金和材料等方面的输入通过某些步骤转化为输出。低成本输入，高质量输出，需要通过一系列的流程来实现，如果没有流程，材料永远无法成为产品。其次，流程的好坏直接影响着产品或服务的质量，产品或服务需要通过一系列的流程来实现，企业产品和服务的优劣差异体现在顾客的满意程度上。成功的企业，其赢得顾客好评的原因往往就是对细节问题的重视。细节问题一点也不能马虎，特别是电力企业，其产品的合格率或服务的满意度必须要达到双百分之一百。流程管理便是这样一种很好的模式，它能够在目标管理的过程中进行系统回馈修正以及风险评估，及时对出现的问题进行反应和纠正，尽量减少因人为因素造成的过程偏差。 6.坚持建立良好的运行监督机制首先，坚持定期研究制度。诸如每周的安全生产会、每旬的领

基于Matlab的光学衍射实验仿真

基于Matlab的光学衍射实验仿真（）摘要通过Matlab软件编程，实现对矩孔夫琅和费衍射的计算机仿真，结果表明：该方法直观正确的展示了衍射这一光学现象，操作性强，仿真度高，取得了较好的仿真效果。

关键词夫琅和费衍射；Matlab；仿真1引言物理光学是高校物理学专业的必修课，其中，光的衍射既是该门课程的重点内容，也是人们研究的热点。

然而由于光学衍射部分公式繁多，规律抽象，学生对相应的光学图像和物理过程的理解有一定的困难，大大影响了教学效果。

当然，在实际中可以通过加强实验教学来改善教学效果，但是光学实验对仪器设备和人员掌握的技术水平要求都较高，同时实验中物理现象容易受外界因素的影响，这给光学教学带来了较大的困难1【-5】。

随着计算机技术的迅速发展，现代化的教育模式走进了课堂，利用计算机对光学现象进行仿真也成为一种可能。

Matlab是一款集数值分析、符号运算、图形处理、系统仿真等功能于一体的科学与工程计算软件，它具有编程效率高、简单易学、人机交互好、可视化功能、拓展性强等优点[6-8]，利用Matlab编程仿真光学现象只需改变程序中的参数，就可以生成不同实验条件下的光学图像，使实验效果更为形象逼真。

在课堂教学中，能快速的验证实验理论，使学生更直观的理解理论知识，接受科学事实。

本文以矩孔夫琅和费衍射为例，介绍了Matlab在光学衍射实验仿真中的应用。

2 衍射基本原理衍射是光波在空间或物质中传播的基本方式。

实际上，光波在传播的过程中，只要光波波面受到某种限制，光波会绕过障碍物偏离直线传播而进入几何阴影，并在屏幕上出现光强分布不均匀的现象，称为光的衍射。

根据障碍物到光源和考察点的距离，把衍射现象分为两类：菲涅尔衍射和夫琅和费衍射。

研究不同孔径在不同实验条件下的光学衍射特性，对现代光学有重要的意义。

如图1所示，衍射规律可用菲涅尔衍射积分表示，其合振幅为[9]：(1)其中，K是孔径平面，E是观察平面，r是衍射孔径平面Q到观察平面P的距离，d是衍射孔径平面O到观察平面P0的距离，cosθ是倾斜因子，k=2π／λ是光波波数，λ是光波波长，x1，y1和x，y分别是孔径平面和观察平面的坐标。

基于Matlab GUI光的衍射实验仿真

１２２
λ ( ｆｘ＋ｆ２ｙ )
２
(１)
(２)
同时利用傅里叶变换关系先对ｆｘꎬｆｙ进行积
分ꎬ得到如下的菲涅尔公式:
Ｕ( ｘꎬｙꎬｚ) ＝
{ λｚπ [ ( ｘ－ｘ )
ｅｘｐｊ
令ｈ( ｘꎬｙ) ＝
∫
ｅｘｐ( ｊｋｚ)
ｄｘ０ｄｙ０Ｕ( ｘ０ ꎬｙ０ )
ｊλｚ
０
２
∑
＋ ( ｙ－ｙ０ ) ２ ]
操作便捷、设计灵活等特点ꎬ从而达到较好的实验演示教学目的ꎮ
关
键
词: ＭａｔｌａｂＧＵＩꎻ光的衍射ꎻ仿真实验Biblioteka 中图分类号: Ｏ４￣３９
文献标志码: Ａ
菲涅尔衍射是大学物理重点学习内容ꎬ但光
的衍射实验现象对实验设备及环境要求苛刻ꎬ通
常不能达到较好的实验结果ꎮ 近年来ꎬ不断有人
在光的衍射仿真方面上做了多种尝试ꎬ吕波、徐志
要: 利用Ｍａｔｌａｂ仿真软件的ＧＵＩ图形用户界面可视化工具和ＦＦＴ傅里叶变换工具ꎬ对圆孔、方
摘
形孔、多边形孔、圆盘四种不同的孔形进行菲涅尔光的衍射实验仿真ꎮ 通过用户界面对光学参数进行数
据交互ꎬ能形象直观地得到四种不同孔径光的衍射图纹、光强三维分布、光强二维分布图像ꎮ 应用于物
理课堂教学中能将抽象难于实现的衍射实验现象直观呈现ꎬ同时ꎬ有助于学生对衍射原理的理解ꎬ具有
内容为圆孔、方形、多边形、圆盘ꎬ则系统在ｐｏｐｕｐ￣
ｍｅｎｕ＿ＣｒｅａｔｅＦｃｎ函数中自动生成如下代码:
ｓｅｔ( ｈＯｂｊｅｃｔꎬ‘ Ｓｔｒｉｎｇ’ ꎬ{ ‘ 圆孔’ ꎬ‘ 方形’ ꎬ‘ 多
边形’ ‘ 圆盘’ ꎬ''} ) ꎻ在可编辑文本框中设置光学

菲涅耳衍射数字模拟仿真与实验

λz
L
时，传递函数算法（TF）准确；当抽样间
λz
L
时，脉冲响应函数算法（IR）准确。根据以上判据条件，选择
合适的算法，模拟光场分布大小为 5cm*5cm，波长为 0.532um，矩形孔半宽度 1cm 的情况下，在衍射距离 z=200mm，和 z=200m 时的菲涅耳光场分布，将所得结果保存在电脑中。 (4) 自己设计十字型窄缝物体（参考以前的实验一内容），如下图，物体大小 3cm*3cm，十字形窄缝的宽度为 1mm，长度为 1cm。
实验过程中要切记以上注意事项。如有违犯，将严重影响你的实验成绩！
1 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
菲涅耳衍射数字模拟仿真与实验
一、实验目的:
1. 2. 3. 掌握菲涅耳衍射的基本原理及其 Matlab 编程语言；利用 Matlab 数值模拟几种典型物体的菲涅耳衍射光场分布；利用现有激光实验系统自己动手搭建衍射光路，观察几种物体的菲涅耳衍射场的空间分布，加深对光的衍射现象和理论的理解。
二、实验原理
两种类型衍射现象：菲涅尔衍射（近场衍射）和夫琅和费衍射（远场衍射） (根据不同的衍射区域分的) 。不同的区域，衍射图样具有不同的性质，在数学上的近似程度也不同。光源和接受屏或二者之一距离衍射屏为有限远时，所观察到的衍射为菲涅尔衍射。在实验中我们使用能发射平行光的激光器+小孔扩束镜来模拟。
6 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
k=2*pi/lamda; %波数 w=0.005; %物体的半宽度 z=50000e-3;%衍射距离 %%%%----------矩形物体--------------[X1,Y1]=meshgrid(x1,y1); u1=rect(X1/(2*w)).*rect(Y1/(2*w)); %矩形物体光场分布 I1=abs(u1.^2); figure(1) imagesc(x1,y1,I1); axis square; axis xy; colormap('gray'); xlabel('x(m)'); ylabel('y(m)'); title('z= 0 m'); %%%-----------------衍射场的分布计算-----------% u2=profTF(u1,L1,lamda,z);% dx >= lamda*z/L 时准确 u2=profIR(u1,L1,lamda,z);% dx <= lamda*z/L 时准确 x2=x1; y2=y1; I2=abs(u2.^2); figure(2) imagesc(x2,y2,I2); axis square; axis xy; colormap('gray'); xlabel('x(m)'); ylabel('y(m)'); text_buffer = strcat( '传播距离为 z= ',num2str(z),'m'); title(text_buffer);