时间序列分析基于R_习题答案
时间序列分析——基于R(王燕)第四章

第四章:非平稳序列的确定性分析题目一:()()()()()()()12312123121231ˆ14111ˆˆ2144451.1616T T T T T T T T T T T T T T T T T T T T T xx x x x xx x x x x x x x x x x x x x x -------------=+++⎡⎤=+++=++++++⎢⎥⎣⎦=+++ 题目二:因为采用指数平滑法,所以1,t t x x +满足式子()11t t t x x x αα-=+-,下面式子()()11111t t t t t tx x x x x x αααα-++=+-⎧⎪⎨=+-⎪⎩ 成立,由上式可以推导出()()11111t t t t x x x x αααα++-=+-+-⎡⎤⎣⎦,代入数据得:2=5α. 题目三:()()()21221922212020192001ˆ1210101113=11.251ˆ 1010111311.2=11.04.5ˆˆˆ10.40.6.i i i xxxx x x x x αα-==++++=++++===+-=⋅∑(1)(2)根据程序计算可得:22ˆ11.79277.x= ()222019181716161ˆ2525xx x x x x =++++(3)可以推导出16,0.425a b ==,则425b a -=-. 题目四:因为,1,2,3,t x t t ==,根据指数平滑的关系式,我们可以得到以下公式:()()()()()()()()()()()()()()()221221 11121111 1111311. 2t t t t t tt x t t t x t t αααααααααααααααααααα----=+-------=-+---+--+++2+, ++2+用(1)式减去(2)式得:()()()()()221=11111.t t tt x t αααααααααααα-------------所以我们可以得到下面的等式:()()()()()()122111=11111=.t t t tt x t t αααααααα+-----------------()111lim lim 1.ttt ttxt tααα+→∞→∞----==题目五:1. 运行程序:最下方。
《金融计量学》题集

《金融计量学》题集一、选择题(每题10分,共100分)1.金融计量学主要应用于以下哪些领域?A. 金融市场预测B. 风险管理评估C. 文学作品分析D. 宏观经济政策制定2.在时间序列分析中,AR模型主要描述的是?A. 自回归过程B. 移动平均过程C. 季节性变动D. 长期趋势3.以下哪个统计量常用于衡量时间序列的平稳性?A. 均值B. 方差C. 自相关系数D. 偏度4.对金融数据进行对数变换的主要目的是?A. 简化计算B. 消除异方差性C. 提高数据的正态性D. 增加数据的波动性5.GARCH模型主要用于分析金融时间序列的哪种特性?A. 平稳性B. 季节性C. 波动性D. 趋势性6.VaR(Value at Risk)模型的核心思想是什么?A. 用历史数据来预测未来风险B. 用数学模型来量化潜在损失C. 用专家判断来评估风险D. 用模拟方法来估计风险7.在多元回归分析中,如果解释变量之间存在高度相关性,会导致什么问题?A. 模型拟合度提高B. 参数估计不稳定C. 残差增大D. 模型解释能力增强8.以下哪个不是金融计量模型的常见检验方法?A. 残差检验B. 稳定性检验C. 显著性检验D. 一致性检验9.在金融时间序列分析中,ADF检验主要用于检验什么?A. 序列的平稳性B. 序列的自相关性C. 序列的异方差性D. 序列的周期性10.以下哪个软件不是常用的金融计量学分析工具?A. EViewsB. R语言C. PythonD. Excel(基本功能)二、填空题(每题10分,共50分)1.金融计量学是研究__________________的学科,它运用统计和数学方法来分析和预测金融市场行为。
2.在进行时间序列分析时,如果序列不平稳,通常需要进行__________________处理,以使其满足建模要求。
3.GARCH模型中的“G”代表__________________,它用于描述时间序列的波动性聚集现象。
时间序列分析-基于R(第五章作业)

时间序列分析第五章作业T1(p164第1题):程序:rm(list=ls())# 清空工作环境P5T1data=read.table("C:\\Users\\DMXTC\\Documents\\SJXLZY_data\\E5_1.txt ",header=T)r5_1<-as.matrix(P5T1data$货运量)d5_1<-as.vector(t(r5_1))T5_1<-ts(d5_1,start=1949)# 绘制时序图par(mfrow=c(1,1))plot(T5_1,type = "o",col="blue",pch=13,main="表5-2时序图")diff_T5_1<-diff(T5_1)#1阶差分plot(diff_T5_1,type = "o",col="blue",pch=13,main="一阶差分后时序图")# ADF检验library(aTSA)adf.test(diff_T5_1)# 纯随机性检验for (k in 1:2)print(Box.test(diff_T5_1,lag=6*k))# 绘制自相关图和偏自相关图par(mfrow=c(1,2))acf(diff_T5_1)pacf(diff_T5_1)# x<-window(T5_1,start=1949,end = 1998)# test<-window(T5_1,start=1999)library(forecast)fit1<-Arima(T5_1,order=c(1,1,0),include.drift=T)fit1tsdiag(fit1)fore1<-forecast::forecast(fit1,h=5)fore1par(mfrow=c(1,1))plot(fore1,lty=2)lines(fore1$fitted,col=4)分析:首先我们绘制时序图如下:时序图显示该序列具有显著线性递增趋势,这是典型的非平稳序列特征,对该序列进行1阶差分,差分后时序图如下:差分后序列基本围绕在0值附近波动,已经没有明显的趋势特征,为进一步确定差分后序列的平稳性,对差分后的序列进行ADF检验,其检验结果显示如下:> adf.test(diff_T5_1)Augmented Dickey-Fuller Testalternative: stationaryType 1: no drift no trendlag ADF p.value[1,] 0 -3.24 0.0100[2,] 1 -2.78 0.0100[3,] 2 -1.95 0.0498Type 2: with drift no trendlag ADF p.value[1,] 0 -4.13 0.0100[2,] 1 -3.84 0.0100[3,] 2 -2.97 0.0462Type 3: with drift and trendlag ADF p.value[1,] 0 -4.69 0.0100[2,] 1 -4.46 0.0100[3,] 2 -3.63 0.0381----Note: in fact, p.value = 0.01 means p.value <= 0.01检验结果显示,该序列所有ADF检验统计量的P值均小于显著性水平(α=0.05),所以可以确定1阶差分后系列实现了平稳。
时间序列分析基于r

时间序列分析基于r时间序列分析是一种用于分析时间序列数据的统计方法,它可以帮助我们了解数据的趋势、季节性、周期性和随机性等特征。
R是一种流行的编程语言和环境,提供了丰富的时间序列分析工具和函数。
以下是一个基于R进行时间序列分析的详细步骤:1. 导入数据:首先,你需要将时间序列数据导入R环境中。
可以使用read.csv()或read.table()函数来读取CSV或文本文件,或使用其他适当的函数来读取其他类型的数据。
2. 转换为时间序列对象:将数据转换为R中的时间序列对象。
可以使用ts()函数来创建一个时间序列对象,指定数据和频率。
例如,如果数据是按月收集的,可以使用ts(data, start = c(year, month), frequency = 12)来创建一个月度频率的时间序列对象。
3. 可视化数据:使用plot()函数来绘制时间序列数据的图形。
这可以帮助你观察数据的趋势、季节性和周期性等特征。
4. 检查数据的平稳性:时间序列分析通常假设数据是平稳的,即数据的均值和方差在时间上保持不变。
可以使用adf.test()函数或kpss.test()函数来检验数据的平稳性。
5. 去除趋势和季节性:如果数据不是平稳的,你需要对其进行差分或转换来消除趋势和季节性。
可以使用diff()函数来进行一阶差分,或使用decompose()函数来分解数据为趋势、季节性和随机成分。
6. 拟合时间序列模型:根据数据的特征选择适当的时间序列模型。
常见的模型包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)和季节性自回归积分移动平均模型(SARIMA)。
可以使用arima()函数来拟合ARIMA模型。
7. 模型诊断:拟合模型后,需要对模型进行诊断,以评估其拟合优度和残差的性质。
可以使用tsdiag()函数来绘制模型的诊断图形,或使用Box.test()函数来进行残差的白噪声检验。
8. 预测未来值:根据拟合的时间序列模型,可以使用forecast()函数来预测未来的时间序列值。
《时间序列分析——基于R》王燕,读书笔记

《时间序列分析——基于R》王燕,读书笔记笔记:⼀、检验:1、平稳性检验:图检验⽅法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列⾃相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的⾃相关系数ρ会很快地衰减向0(指数级指数级衰减),反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验(Box.test(data,type,lag=n)——lag表⽰输出滞后n阶的⽩噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()⾃动定阶1.3建模arima()1.4模型显著性检验:残差的⽩噪声检验Box.test();参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合:直线、曲线(⼀般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差⾃回归模型:4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差⾃相关DW检验。
dwtest()——lmtest包,增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型:异⽅差检验:LM检验ArchTest()——FinTS包,⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法:1、频域分析⽅法2、时域分析⽅法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异⽅差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、⾮线性场合:门限⾃回归模型,马尔科夫转移模型第⼆章时间序列的预处理预处理内容:对它的平稳性和纯随机性进⾏检验,最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征,同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
时间序列分析课后习题答案1

时间序列分析课后习题答案(上机第二章 2、328330332334336338340342(1时序图如上:序列具有明显的趋势和周期性,该序列非平稳。
(2样本自相关系数:(3该样本自相关图上,自相关系数衰减为 0的速度缓慢,且有正弦波状,显示序列具有趋势和周期,非平稳。
3、 (1样本自相关系数:(2序列平稳。
(3因 Q 统计量对应的概率均大于 0.05,故接受该序列为白噪声的假设,即序列为村随机序列。
5、 (1时序图和样本自相关图:50100150200250300350(2序列具有明显的周期性,非平稳。
(3序列的 Q 统计量对应的概率均小于 0.05,该序列是非白噪声的。
6、 (1根据样本相关图可知:该序列是非平稳,非白噪声的。
(2对该序列进行差分运算:1--=t t t x x y {t y }的样本相关图:该序列平稳,非白噪声。
第三章:17、 (1结论:序列平稳,非白噪声。
(2 拟合 MA(2 model:VariableCoefficient Std. Error t-Statistic Prob. C 80.40568 4.630308 17.36508 0.0000 MA(1 0.336783 0.114610 2.938519 0.0047 R-squared0.171979 Mean dependent var 80.29524 Adjusted R-squared 0.144379 S.D. dependent var 23.71981 S.E. of regression 21.94078 Akaike info criterion 9.061019 Sum squared resid 28883.87 Schwarz criterion 9.163073 Log likelihood -282.4221 F-statistic 6.230976 Durbin-Watson stat 2.072640 Prob(F-statistic 0.003477Residual tests(3拟合 AR(2model:C 79.71956 5.442613 14.64729 0.0000 AR(10.2586240.1288102.0077940.0493R-squared0.154672 Mean dependent var 79.50492 Adjusted R-squared 0.125522 S.D. dependent var 23.35053 S.E. of regression 21.83590 Akaike info criterion 9.052918 Sum squared resid 27654.79 Schwarz criterion 9.156731 Log likelihood -273.1140 F-statistic 5.306195 Durbin-Watson stat 1.939572 Prob(F-statistic 0.007651Inverted AR Roots.62-.36Residual tests:(4 拟合 ARMA (2, 1 model :Variable Coefficient Std. Error t-Statistic Prob. C 79.17503 4.082908 19.39183 0.0000 AR(1 -0.586834 0.118000 -4.973170 0.0000 AR(2 0.376120 0.082091 4.581756 0.0000 MA(11.1139990.09712211.470120.0000R-squared0.338419 Mean dependent var 79.50492 Adjusted R-squared 0.303599 S.D. dependent var 23.35053 S.E. of regression 19.48617 Akaike info criterion 8.840611 Sum squared resid 21643.51 Schwarz criterion 8.979029 Log likelihood-265.6386 F-statistic9.719104Inverted AR Roots .39-.97 Inverted MA Roots-1.11Estimated MA process is noninvertible残差检验:(5拟合 ARMA (1, (2 model:Variable Coefficient Std. Error t-Statistic Prob. C 79.52100 4.621910 17.205230.0000 AR(1 0.270506 0.125606 2.153603 0.0354 R-squared0.157273 Mean dependent var 79.55161 Adjusted R-squared 0.128706 S.D. dependent var 23.16126 S.E. of regression 21.61946 Akaike info criterion 9.032242 Sum squared resid 27576.65 Schwarz criterion 9.135167 Log likelihood -276.9995 F-statistic 5.505386 Durbin-Watson stat 1.981887 Prob(F-statistic 0.006423Inverted AR Roots.27残差检验:(6优化根据 SC 准则,最优模型为 ARMA(2,1模型。
(完整word版)时间序列分析基于R__习题答案及解析
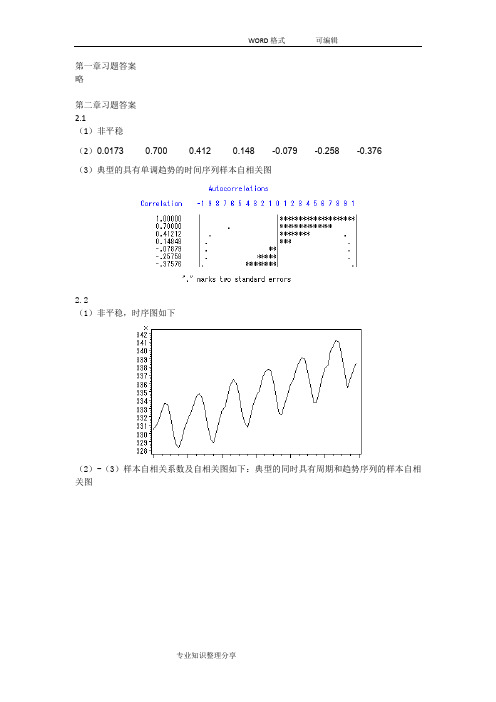
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
课后习题答案-时间序列分析及应用(R语言原书第2版)

stationary.
(b) Find the autocovariance function for {Yt}. Cov(Yt,Yt − k) = Cov(X,X) = σ2 for all t and k, free of t (and k). (c) Sketch a “typical” time plot of Yt. The plot will be a horizontal “line” (really a discrete-time horizontal line)
relation functions are the same for θ = 3 and θ = 1/3. For simplicity, suppose that the process mean is known
to be zero and the variance of Yt is known to be 1. You observe the series {Yt} for t = 1, 2,..., n and suppose that you can produce good estimates of the autocorrelations ρk. Do you think that you could determine which value of θ is correct (3 or 1/3) based on the estimate of ρk? Why or why not?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题答案第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图Au{oeorr&lal. i orsCorrelation M 7 6 5 4 3 2 1 0 I ; 3 4 5 6 7 9 9 11.00000■Hi ■ K. B H,J B ik L L1■* J.1 jA1-.IM L L*rn^rp ■ i>i™iTwin H'iTiii M[lrp i,*nfr 'TirjlvTilT'1 iBrpO.7QOO0■ill. Ii ill ■ _.ill«L■ ill iL si ill .la11 ■ fall■ 1 ■ rpTirp Tp和阳申■丽轉■晒?|•卉(ft0.41212■强:料榊<牌■0.14343'■讯榊*-.07078■-.25758, WWHOHHfi■-.375761marks two 总t and&rd errors2.2(1)非平稳,时序图如下(2)- (3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图raa rka two standard errors2.3(1) 自相关系数为: 0.20230.013 0.042-0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070-0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062-0.139 -0.034 0.206 -0.010 0.080 0.118(2 )平稳序列 (3) 白噪声序列 2.4LB=4.83 , LB 统计量对应的分位点为 0.9634 , P 值为0.0363。
显著性水平 =0.05,序列不能视为纯随机序列。
2.5(1) 时序图与样本自相关图如下-1 9 9 7 6 5 4^2101294567891Ctorrelat ionLOOOOO n.A'7F1 0.72171 0.51252 Q,34982 0.24600 0.20309 0.?1021 0.26429 0.36433 0.49472 0.58456 0.60198 0.51841 Q ・菲晡日0.20671 0.0013&-,03243 -.02710 Q.01124 0,08275 0.17011 0.24920Autocorrel at ions弗卅制iti 电卅栅冷卅樹 側樹 榊 惟1■ liihCidi iliihQriHi il>LljU_nll Hnlidiili Hialli iT ,,T^,,T^s •T*iTijTirr ,^T 1 IT * -i>■>- ■■*畑**・ ■■耶曲邯・■■■>|{和怦I {册卅KHi 笊出恸mrpmrp 山!rpEHi erp.卑*寧*a1*Autocorirelat i ons■"j,a *Jii ■»i 1 jjnl■'X*^X*iiL*\L a 'X*1丄"qiBE眾弗狀讯當划仲睢St*a■<■ TailiHiiiliiliiliiliali Hisjliiliila 爪营庐卷if口甲暉吓审■1rp 帀环■ill «l i iliilji : ill ■!■ all ill rli il ii li ill i !■ mvpUvi■payirFUfli ffia|iiTii^BB■■■Aai 11 ill il鼻鼻d 爪鼻心”-■■ B II I II I. nil il^i lnl r ill ill ■£nii X" 平暂牺中炉丁吓平举可i 曹平 at.Hiilijiidi Jbihijjiii ill vjiijjWiidi diili■ |iiTiirir]iI T I iTBfp nyiip(2) 非平稳 (3 )非纯随机 2.6 (1) 平稳,非纯随机序列(拟合模型参考:ARMA(1,2))(2) 差分序列平稳,非纯随机 第三章习题答案3.1E(x t ) °, Var(x t ) J 1.96 ,20.72 0.49, 22 01 0.723.27 115 1 2153.3E(x t ) ° , Var(x t )1 0.1511(1 °.15)(1 0.80.15)(1 0.8 0.15)1.980.8 1 0.150.7°,0.70 ,220.8 1 0.15,0.15 330.41,3 0.8 2 0.15 1 0.223.40,3.5 证明:该序列的特征方程为:2-cc 0,解该特征方程得三个特征根:无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
证毕。
3.6 (1) 错(2)错 (3)对 (4)错(5)13.7该模型有两种可能的表达式:x tt t 1和x tt 2 t 1。
23.8 将 x t 10 0.5x t 1 t 0.8 t 2 C t 3等价表达为12cc 1 0.8B 2 CB 3 20t1 0.5B1 0.8B2 CB3 (1 0.5B 0.52B 2 O.H B 3 L)t展开等号右边的多项式,整理为1 0.5B 0.52B2 0.53 B 34 40.5 BL0.8B 2 0.8 0.5B 3 0.8 0.52B 4LCB 30.5CB 4L合并同类项,原模型等价表达为2 23.9E(x t ) 0, Var(x t ) 1 0.70.4 1.65所以该差分序列为平稳序列。
3.11 ( 1 )非平稳,(2)平稳,(3)可逆,(4)不可逆,(5)平稳可逆,(6)不平稳不可逆3.131 1 0.252x t 20[1 0.5B 0.55B0.5k (0.53 0.4 C)B 3k ]tk 0当 0.53 0.4 C0时,该模型为 MA (2)模型,解出C 0.275。
0.7 0.7 0.41.650.59 0.4 1.650.24k0,k 32 23.10(1)证明:因为 V ar(x t ) k im(1 kC) ,所以该序列为非平稳序列。
(2) yt Xt Xt 1 t(C 1) t 1,该序列均值、方差为常数,E(y t ) 0, Var(y t )1 (C 1)2 2自相关系数只与时间间隔长度有关,与起始时间无关 1 (C 1)2k0,k 23.12G o 1, G1G 010.6 0.3 0.3 , G kk 1k 11G k 1 1 G 1 0.3 0.6 , k 2所以该模型可以等价表示为:X tt0.3 0.6 t k 1k 01丄,根据ARMA(1,1)模型Green函数的递推公式得: 43.14 证明:已知1G o 1 , G1 1G0 0.5 0.25 ,G k 1G k G i k 1 . 小1 ,k 22j1G2 j 0 2(j 1)151~41n27260.27G j G j j 0G j1 G j G j G jj 0,kG2 j 0G2j 0G23.15 (1) 成立(2)成立(3) 成立(4)不成立3.16 (1)(2) 95%置信区间为(3.83,16.15 )更新数据后95%置信区间为(3.91,16.18 )3.17 ( 1)平稳非白噪声序列(2) AR(1)(3) 5 年预测结果如下:Obs Forecas t Std Error853E Confidence Limits刷90.156322J29445.6075134.705093.800228. m3? J 698180.60868601.903323.944034.3769128.8376S791.2$2334 J 325128 •曲S1.0S5323.955834 J 3291?fi.O3?73.18 ( 1)平稳非白噪声序列(2) AR(1)(3) 5 年预测结果如下:Forecasts for vsiri&ble xObs Forec*si Sid Error Conf idence L i r 1 i L s750.70460.27710.1616 1.2476780.7S5G O.29E?0,21611,3751770-8295O.?3S10.245? 1.4139兀Q.S4210.29950.2571 1.427179O.a4G8O.29SE0.2617 1.4319 3.19 ( 1)平稳非白噪声序列(2) MA(1)(3) 下一年95%的置信区间为(80.41,90.96 )ForeGaats for var iabl e K第四章习题答案4.11X T 3的系数为一,X T1的系数为-516 164.2 解下面的方程组,得到0.4% 5.25 5(1 )5.26 5.5 (1 )%4.3 (1)11.04 ( 2)11.79277 (3) b a 0.4 0.24 0.16% t (t 1) (1 )(t 2) (1(1 )>% t (1 ) (t 1) (1(1)- -(2)得% t (1% t (1 )1t丄1则lim %lim t1。
t t t t (1)式等号•两边同乘(1 )有(2)式成立)2(t 2) (1 )3L (1))2(t 2) (1 )3L (2)) (1 )2L(1 )2L3.20 (1)平稳非白噪声序列(2)ARMA(1,3)序列(3)拟合及5年期预测图如下:4.4 根据指数平滑的定义有(1 )式成立,4.5该序列为显著的线性递增序列,利用本章的知识点,可以使用线性方程或者holt两参数指数平滑法进行趋势拟合和预测,答案不唯一,具体结果略。
4.6该序列为显著的非线性递增序列,可以拟合二次型曲线、指数型曲线或其他曲线,也能使用holt两参数指数平滑法进行趋势拟合和预测,答案不唯一,具体结果略。
4.7本例在混合模型结构,季节指数求法,趋势拟合方法等处均有多种可选方案,如下做法仅是可选方法之一,结果仅供参考(1 )该序列有显著趋势和周期效应,时序图如下(2)该序列周期振幅几乎不随着趋势递增而变化,所以尝试使用加法模型拟合该序列:X t T t S t I t。
(注:如果用乘法模型也可以)首先求季节指数(没有消除趋势,并不是最精确的季节指数)0.960722 0.912575 1.038169 1.064302 1.153627 1.1165661.04292 0.984162 0.930947 0.938549 0.902281 0.955179消除季节影响,得序列y t x t S t X,使用线性模型拟合该序列趋势影响(方法不唯一)T t 97.70 1.79268t,t 1,2,3丄(注:该趋势模型截距无意义,主要是斜率有意义,反映了长期递增速率)得到残差序列|t x t Sx y t T t,残差序列基本无显著趋势和周期残留。
