2018中考数学专题复习应用题经典例题
2018年中考数学真题滚动小(三)方程、不等式的实际应用(答案不全)

滚动小专题(三)方程、不等式的实际应用(2018玉林)(2018苏州)(2018赤峰)(2018资阳)(2018包头)(2018铜仁)(2018湘潭)23.(8分)湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.(1)求温馨提示牌和垃圾箱的单价各是多少元?(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?解:(1)设温情提示牌的单价为x元,则垃圾箱的单价为3x元,根据题意得,2x+3×3x=550,∴x=50,经检验,符合题意,∴3x=150元,即:温馨提示牌和垃圾箱的单价各是50元和150元;(2)设购买温情提示牌y个(y为正整数),则垃圾箱为(100﹣y)个,根据题意得,意,,∴≤y≤52,∵y为正整数,∴y为42,43,44,45,46,47,48,49,50,51,52,共11中方案;即:温馨提示牌42个,垃圾箱58个,温馨提示牌43个,垃圾箱57个,温馨提示牌44个,垃圾箱56个,温馨提示牌45个,垃圾箱55个,温馨提示牌46个,垃圾箱54个,温馨提示牌47个,垃圾箱53个,温馨提示牌48个,垃圾箱52个,温馨提示牌49个,垃圾箱51个,温馨提示牌50个,垃圾箱50个,温馨提示牌51个,垃圾箱49个,温馨提示牌52个,垃圾箱48个,根据题意,费用为30y+150(100﹣y)=﹣120y+15000,当y=52时,所需资金最少,最少是8760元.(2018烟台)(2018哈尔滨)(2018大庆)(2018贵阳)(2018安顺)23。
某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励。
2018全国中考数学分类汇编--3方程与不等式应用题

2018全国中考数学分类汇编--3方程与不等式应用题D【解析】分析:直接利用两周内共销售30台,销售收入5300元,分别得出等式进而得出答案.详解:设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组为:.故选C.点睛:本题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题的关键.10.(2018·山东淄博)(4分)“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是()A.B.C.D.【考点】B6:由实际问题抽象出分式方程.【分析】设实际工作时每天绿化的面积为x万平方米,根据工作时间=工作总量÷工作效率结合提前 30 天完成任务,即可得出关于x的分式方程.【解答】解:设实际工作时每天绿化的面积为x万平方米,则原来每天绿化的面积为万平方米,依题意得:﹣=30,即.故选:C.【点评】考查了由实际问题抽象出分式方程.找到关键描述语,找到合适的等量关系是解决问题的关键.10.(2018·四川眉山)我市某楼盘准备以每平方6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过连续两次下调后,决定以每平方4860元的均价开盘销售,则平均每次下调的百分率是A.8% B.9% C.10% D.11%答案:C8.(2018·四川绵阳)在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为()A.9人B.10人C.11人D.12人【答案】C【考点】一元二次方程的应用【解析】【解答】解:设参加酒会的人数为x人,依题可得:x(x-1)=55,化简得:x2-x-110=0,解得:x1=11,x2=-10(舍去),故答案为:C.【分析】设参加酒会的人数为x人,根据每两人都只碰一次杯,如果一共碰杯55次,列出一元二次方程,解之即可得出答案.6.(2018·四川宜宾)(3分)某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为()A.2% B.4.4% C.20% D.44%【考点】AD:一元二次方程的应用.【分析】设该市2018年、2019年“竹文化”旅游收入的年平均增长率为x,根据2017年及2019年“竹文化”旅游收入总额,即可得出关于x的一元二次方程,解之取其正值即可得出结论.【解答】解:设该市2018年、2019年“竹文化”旅游收入的年平均增长率为x,根据题意得:2(1+x)2=2.88,解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).答:该市2018年、2019年“竹文化”旅游收入的年平均增长率约为20%.故选:C.【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.6.(2018·浙江杭州)某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得-2分,不答的题得0分。
2018年中考数学阴影面积的经典题

数学专题:求阴影部分面积1.(2018重庆B )如图,在边长为4的正方形ABCD 中,以点B 为圆心,以AB 为半径画弧,交对角线BD 于点E .则图中阴影部分的面积是 (结果保留π)1 2 32.(2018重庆A )如图,在矩形ABCD 中,3AB =,2AD =,以点A 为圆心,AD 长为半径画弧,交AB 于点E ,图中阴影部分的面积是___________(结果保留π) 3.(2018眉山)如图,ABC ∆是等腰直角三角形,090ACB ∠=,2AC BC ==,把△ABC 绕点A 按顺时针方向旋转045后得到''AB C ∆,则线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积是4.(2018凉山州)将ABC ∆绕点B 逆时针旋转到''A BC ∆使A 、B 、'C 在同一直线上,若090BCA ∠=,030BAC ∠=,4AB cm =,则图中阴影部分面积为________2cm4 5 65.(2018青岛)如图,Rt ABC ∆,090B ∠=,030C ∠=,O 为AC 上一点,2OA =,以O 为圆心,以OA 为半径的圆与CB 相切于点E ,与AB 相交于点F ,连接OE OF 、,则图中阴影部分的面积是6.(2018十堰)如图,扇形OAB 中,100AOB ∠=︒,12OA =,C 是OB 的中点,CD OB ⊥ 交AB 于点D ,以OC 为半径的CE 交OA 于点E ,则图中阴影部分的面积是( ) A .12183π+ B .12363π+ C. 6183π+ D .6363π+7.(2018安顺)如图,C 为半圆内一点,O 为圆心,直径AB 长为2cm ,60BOC ∠=︒,90BCO ∠=︒,将BOC ∆绕圆心O 逆时针旋转至''B OC ∆,点'C 在OA 上,则边BC 扫过区域(图中阴影部分)的面积为 2cm .(结果保留π)7 8 98.(2018山西) 如图,正方形ABCD 内 接 于O ,O 的 半 径 为2,以点A 为 圆 心 ,以AC 为 半 径 画 弧 交AB 的延长线于点E ,交 AD 的延长线于点F ,则 图 中 阴 影 部 分 的 面 积 是 ( ) A.44π- B.48π- C.84π- D.88π-9.(2018南宁)如图,分别以等边三角形ABC 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若2AB =,则莱洛三角形的面积(即阴影部分面积)为( )A .3π+.3π-C .23π.223π-10.(2018•台湾)如图,ABC ∆中,D 为BC 的中点,以D 为圆心,BD 长为半径画一弧交AC 于E 点,若060A ∠=,0100B ∠=,4BC =,则扇形BDE 的面积(即阴影部分面积)为多少?( )A .13πB .23πC .49π D .59π10 11 1211.(2018•德州)如图,从一块直径为2m 的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积(即阴影部分面积)为( )A.22m π B.232m π C .2m π D .22m π12. (2018•成都)如图,在平行四边形ABCD 中,060B ∠=,C 的半径为3,则图中阴影部分的面积是( ) A .πB .2πC .3πD .6π6π13.(2018•荆门)如图,在平行四边形ABCD 中,AB AD <,030D ∠=,4CD =,以AB 为直径的O 交BC 于点E ,则阴影部分的面积为14.(2018•香坊区)如图,点A 、B 、C 是⊙O 上的点,且∠ACB=40°,阴影部分的面积为2π,则此扇形的半径为 3 .15.如图,△ABC 是⊙O 的内接正三角形,⊙O 的半径为3,则图中阴影部分的面积是 .16. 如图1,点C 、D 是以AB 为直径的半圆O 上的三等分点,AB=12,则图中由弦AC 、AD 和C D ⌒围成的阴影部分图形的面积为_________。
2018届中考数学第一轮复习考点强化12 统计类应用题(无答案 )

考点强化练十二 统计类应用题一、选择题1. (2016·六盘水)小颖随机抽样调查本班20名女同学所穿运动鞋尺码,并统计如表:学校附近的商店经理根据表中决定本月多进尺码为23.0cm 的女式运动鞋,商店经理的这一决定应用了哪个统计知识( ) A. 众数 B. 中位数 C. 平均数 D. 方差2. (2017·安徽)为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )A. 280B. 240C. 300D. 2603. (2016·广安)初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖,如下表:那么被遮盖的两个数据依次是( )A. 35,2B. 36,4C. 35,3D. 36,34. (2016·成都)学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数x -(单位:分)及方差s 2如下表所示:如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是()A. 甲B. 乙C. 丙D. 丁5. (2016·北京)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断正确的是()①年用水量不超过180m3的该市居民家庭按第一档水价交费;②年用水量超过240m3的该市居民家庭按第三档水价交费;③该市居民家庭年用水量的中位数在150~180之间;④该市居民家庭年用水量的平均数不超过180.A. ①③B. ①④C. ②③D. ②④二、填空题6. 某大学自主招生考试只考数学和物理.计算综合得分时,按数学占60%,物理占40%计算.已知孔明数学得分为95分,综合得分为93分,那么孔明物理得分是________分.7. (2017·江西)已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是________.8. 在某公益活动中,小明对本班同学的捐款情况进行了统计,绘制成如图不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是________元.三、解答题9. (2016·宁波)为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):根据统计图中的信息,解答下列问题:(1)求本次被调查的学生人数;(2)将条形统计图补充完整;(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.10. (2016·青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:根据以上信息,整理分析数据如下:(1)写出表格中a,b,c的值;(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?。
2018年中考数学专题复习折叠题含答案8
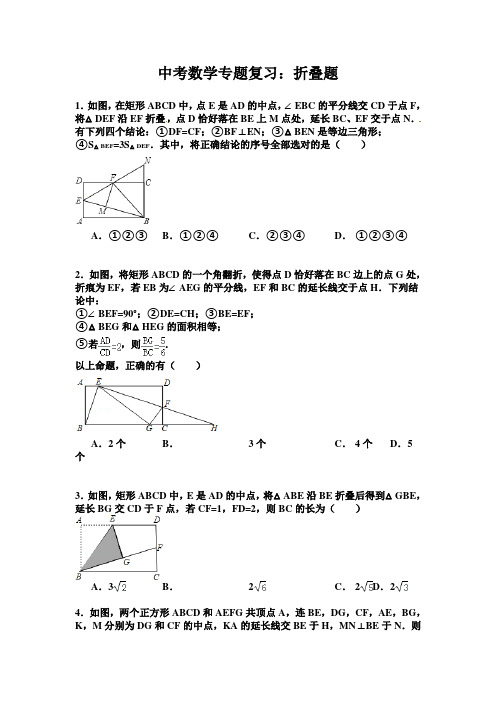
中考数学专题复习:折叠题1.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是()A.①②③B.①②④C.②③④D.①②③④2.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若,则.以上命题,正确的有()A.2个B.3个C. 4个D.5个3.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为()A.3B.2C. 2D.24.如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是()A.③④B.①②③C.①②④D.①②③④5.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN 的面积是()A.B.C.D.6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,则∠A′的大小是()A.40°B.36°C.32°D. 30°7.如图,已知△ABC中,∠CAB=∠B=30°,AB=2,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为()A.B.C.3﹣D.8.如图,已知△ABC中,∠CAB=∠B=30°,AB=,点D在BC边上,把△ABC沿AD翻折,使AB与AC重合,得△AED,则BD的长度为()A.B.C.D.9.如图,在Rt△ABC中,∠C=90°,AC=,BC=1,D在AC上,将△ADB 沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是()A.1 B. C.D.中考数学专题复习:折叠题解答1.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是()A.①②③B.①②④C.②③④D.①②③④解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC,∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN,∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN,故②正确;∵在△DEF和△CNF中,,∴△DEF≌△CNF(ASA),∴EF=FN,∴BE=BN,但无法求得△BEN各角的度数,∴△BEN不一定是等边三角形;故③错误;∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM,∴BE=3EM,∴S△BEF=3S△EMF=3S△DEF;故④正确.故选B.点评:此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.2.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若,则.以上命题,正确的有()A.2个B.3个C. 4个D.5个解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,则G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,则有y2+(2y﹣2x)2=(2y ﹣x)2,解得x1=y(不合题意舍去),x2=y.则,故正确.故正确的有3个.故选B.点评:本题考查了翻折变换,解答过程中涉及了矩形的性质、勾股定理,属于综合性题目,解答本题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.3.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为()A.3B.2C. 2D.2解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.故选B.点评:此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.4.如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是()A.③④B.①②③C.①②④D.①②③④解答:解:由两个正方形的性质易证△AED≌△AGB,∴BG=DE,∠ADE=∠ABG,∴可得BG与DE相交的角为90°,∴BG⊥DE.①正确;如图,延长AK,使AK=KQ,连接DQ、QG,∴四边形ADQG是平行四边形;作CW⊥BE于点W,FJ⊥BE于点J,∴四边形CWJF是直角梯形;∵AB=DA,AE=DQ,∠BAE=∠ADQ,∴△ABE≌△DAQ,∴∠ABE=∠DAQ,∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.∴△ABH是直角三角形.易证:△CWB≌△BHA,△EJF≌△AHE;∴WB=AH,AH=EJ,∴WB=EJ,又WN=NJ,∴WN﹣WB=NJ﹣EJ,∴BN=NE,③正确;∵MN是梯形WGFC的中位线,WB=BE=BH+HE,∴MN=(CW+FJ)=WC=(BH+HE)=BE;易证:△ABE≌△DAQ(SAS),∴AK=AQ=BE,∴MN∥AK且MN=AK;四边形AKMN为平行四边形,④正确.S△ABE=S△ADQ=S△ADG=S▱ADQG,②正确.所以,①②③④都正确;故选D.点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.5.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN 的面积是()A.B.C.D.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S△CMN=CM•CN=×6×2=6,∴S△CAB=4S△CMN=4×6=24,=S△CAB﹣S△CMN=24﹣6=18.∴S四边形MABN故选C.点评:此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质.此题难度适中,解此题的关键是注意折叠中的对应关系,注意数形结合思想的应用.6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,则∠A′的大小是()A.40°B.36° C.32° D.30°解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.故选B.点评:本题考查了折叠的性质,解答本题的关键是掌握翻折前后的对应角相等,注意本题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,根据四边形的内角和为360°求出每个角的度数.7.如图,已知△ABC中,∠CAB=∠B=30°,AB=2,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为()A.B.C. 3﹣D.解答:解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,∵△ABC中,∠CAB=∠B=30°,AB=2,∴AC=BC,∴AF=AB=,∴AC===2,由折叠的性质得:AB′=AB=2,∠B′=∠B=30°,∵∠B′CD=∠CAB+∠B=60°,∴∠CDB′=90°,∵B′C=AB′﹣AC=2﹣2,∴CD=B′C=﹣1,B′D=B′C•cos∠B′=(2﹣2)×=3﹣,∴DE===,∴S=AC•DE=×2×=.阴影故选A.点评:此题考查了折叠的性质,等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用,注意掌握折叠前后图形的对应关系.8.如图,已知△ABC中,∠CAB=∠B=30°,AB=,点D在BC边上,把△ABC沿AD翻折,使AB与AC重合,得△AED,则BD的长度为()A.B.C.D.解答:解:作CF⊥AB于点F.∵∠CAB=∠B∴AC=BC,∴BF=AB=,在直角△BCF中,BC==2,在△CDE中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,∴∠CDE=90°,设BD=x,则CD=DE=2﹣x,在直角△CDE中,tanE===tan30°=,解得:x=3﹣.故选B.点评:本题考查了图形的折叠,以及三线合一定理、三角函数,正确理解折叠的性质,找出图形中相等的线段、相等的角是关键.9.如图,在Rt△ABC中,∠C=90°,AC=,BC=1,D在AC上,将△ADB 沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是()A.1 B. C.D.解答:解:∵∠C=90°,AC=,BC=1,∴AB==2,∴∠BAC=30°∵△ADB沿直线BD翻折后,点A落在点E处,∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,∵AD⊥ED,∴BC∥DE,∴∠CBF=∠BED=30°,在Rt△BCF中,CF==,BF=2CF=,∴EF=2﹣,在Rt△DEF中,FD=EF=1﹣,ED=FD=﹣1,∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×BC•AD+AD•ED=2××1×(﹣1)+×(﹣1)(﹣1)=1.故选A.点评:本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了勾股定理和含30度的直角三角形三边的关系.。
2018年初中数学中考总复习:关于一棵树砸下来的问题(论勾股定理在生活中的应用)

20161214关于一棵树砸下来的问题-论勾股定理在生活中的应用江苏扬州祁荣圣 2016/12/14 12:58:17有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树______米之外才是安全的.江苏扬州祁荣圣 2016/12/14 12:58:25求教南京李玉荣 2016/12/14 13:01:09蹊跷江苏扬州祁荣圣 2016/12/14 13:01:22是3还是4青岛臧昌运 2016/12/14 13:03:014南京李玉荣 2016/12/14 13:03:14站树越近越安全啊!青岛臧昌运 2016/12/14 13:03:24至少南京李玉荣 2016/12/14 13:03:39爱数学爱教育爱孩子 2016-12-16 5:30:28青岛臧昌运 2016/12/14 13:03:014南京李玉荣 2016/12/14 13:03:14站树越近越安全啊!青岛臧昌运 2016/12/14 13:03:24至少南京李玉荣 2016/12/14 13:03:39徐州丁海科 2016/12/14 13:03:54相似处理?徐州丁海科 2016/12/14 13:04:16祁校好江苏朱冬青 2016/12/14 13:04:19安庆邓高清 2016/12/14 13:04:59安庆邓高清 2016/12/14 13:05:204显然南京李玉荣 2016/12/14 13:05:38靠近点更安全江苏扬州祁荣圣 2016/12/14 13:06:15 越远越安全安庆邓高清 2016/12/14 13:06:27没有树枝理想化徐州丁海科 2016/12/14 13:06:40此题有问题,感觉不常规南京李玉荣 2016/12/14 13:07:05不然就是4,安庆邓高清 2016/12/14 13:07:23游戏价值不大江苏扬州祁荣圣 2016/12/14 13:07:29生活与数学的区别南京李玉荣 2016/12/14 13:07:31所以蹊跷广州苏德杰 2016/12/14 13:07:36这种生活情景,硬套“数学来源于生活”。
2018年中考数学总复习经典(几何)试题(含答案)

中考数学总复习经典题(几何)(二)几何试题1、 如图,正方形ABCD 的边长为2,点E 在AB 边上.四边形EFGB 也为正方形,设△AFC 的面积为S ,则 ( )A .S=2B .S=2.4C .S=4D .S 与BE 长度有关2、正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图4所示,点G 在线段DK 上,正方形BEFG 的边长为4,则DEK △的面积为: (A)10 (B)12 (C)14 (D)163、如图,矩形ABCD 中,3AB =cm ,6AD =cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,2EF BE =,则AFC S =△ 2cm .4、 如图,在△ABC 中, ο70=∠CAB . 在同一平面内, 将△ABC 绕点A 旋转到△//C AB 的位置, 使得AB CC ///, 则=∠/BAB ( )A. ο30 B. ο35 C. ο40 D. ο50 5、如图,1P 是一块半径为1的半圆形纸板,在1P 的左下端剪去一个半径为12的半圆后得到图形2P ,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆1的半径)得图形34,,,,n P P P L L ,记纸板n P 的面积为n S , 试计算求出2S = ;3S = ;并猜想得到1n n S S --= ()2n ≥。
6、如图,在四边形ABCD 中,P 是对角线BD 的中点,E F ,分别是AB CD ,的中点,18AD BC PEF =∠=o ,,则PFE ∠的度数是 .(第16题)CFD BE A P (第6题)ADCEF GB 3题图 D ABRP F CGK图4E8题10题 12题7、如图,点G 是ABC △的重心,CG 的延长线交AB 于D ,5cm GA =,4cm GC =,3cm GB =,将ADG △绕点D 旋转180o得到BDE △,则DE = cm ,ABC △的面积= cm 2.8、如图,已知梯形ABCD ,AD BC ∥,4AD DC ==,8BC =,点N 在BC 上,2CN =,E 是AB 中点,在AC 上找一点M 使EM MN +的值最小,此时其最小值一定等于( ) A .6B .8C .4D .439、将一副直角三角板按图示方法放置(直角顶点重合),则AOB DOC ∠+∠= o.10、已知:如图,在正方形ABCD 外取一点E ,连接AE 、BE 、DE .过点A 作AE 的垂线交DE 于点P .若AE=AP =1,PB = 5 .下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为 2 ;③EB ⊥ED ;④S △APD +S △APB =1+ 6 ;⑤S 正方形ABCD =4+ 6 .其中正确结论的序号是()A .①③④B .①②⑤C .③④⑤D .①③⑤11、如图,直角梯形ABCD 中,∠BCD =90°,AD ∥BC ,BC =CD ,E 为梯形内一点,且∠BEC =90°,将△BEC 绕C 点旋转90°使BC 与DC 重合,得到△DCF ,连EF 交CD 于M .已知BC =5,CF =3,则DM:MC 的值为 ( ) A.5:3 B.3:5 C.4:3 D.3:412、如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD=2,将腰CD 以D 为中心逆时针旋转90°至ED ,AE 、DE ,△ADE 的面积为3,则BC 的长为 . 13、如图,四边形OABC 为菱形,点B 、C 在以点O 为为圆心的上,若OA = 3,∠1 = ∠2,则扇形OEF 的面积为_________.14、 如图,点P 是∠AOB 的角平分线上一点,过点P 作PC ∥OA 交OB 于点C.若∠AOB = 60o,OC = 4,则点P 到OA 的距离PD 等于__________. 15、如图,在Rt ABC △中,90ACB ∠=°,3BC =,4AC =,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( )A .32 B .76 C .256D .2B AC D O P (第14题) AD B EC (第15题) ABE G CD(第7题)C D AO B30°45°A D EM(第11题(第13题)O A B C F 1 2 E E D(第20题)16、如图,⊙P 内含于⊙O ,⊙O 的弦AB 切⊙P 于点C ,且OP AB //.若阴影部分的面积为π9,则弦AB 的长为( )A .3B .4C .6D .917、如图,等腰△ABC 中,底边a BC =,︒=∠36A ,ABC ∠的平分线交AC 于D ,BCD ∠的平分线交BD 于E ,设215-=k ,则=DE ( )A .a k 2B .a k 3C .2k aD .3ka18、如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,要使四边形EFGH 是菱形,四边形ABCD 还应满足的一个条件是19、如图,把矩形纸条ABCD 沿EF 、GH 同时折叠,B 、C 两点恰好落在AD 边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD 的边BC 长为 . 20、.梯形ABCD 中AB ∥CD ,∠ADC +∠BCD =90°,以AD 、AB 、BC 为斜边向形外作等腰直角三角形,其面积分别是S 1、S 2、S 3 ,且S 1 +S 3 =4S 2,则CD =( )A. 2.5ABB. 3ABC. 3.5ABD. 4AB21、如图,在□ABCD 中,AB =3,AD =4,∠ABC =60°,过BC 的中点E 作EF ⊥AB ,垂足为点F ,与DC 的延长线相交于点H ,则△DEF 的面积是 .22、如图,已知a ∥b ,∠1=70°,∠2=40°,则∠3= __________。
(通用版)2018年中考数学总复习 专题检测6 分式方程及其应用试题

专题检测6 分式方程及其应用(时间60分钟满分100分)一、选择题(每小题3分,共36分)1.在方程=7,-=2,+x=,=+4,=1中,分式方程有(B)A.1个B.2个C.3个D.4个2.已知方程=1的根为x=1,则k=(B)A.4B.-4C.1D.-13.解分式方程+=3时,去分母后变形正确的是(D)A.2+(x+2)=3(x-1)B.2-x+2=3(x-1)C.2-(x+2)=3D.2-(x+2)=3(x-1)4.解分式方程+=,下列四步中,错误的一步是(D)A.方程两边分式的最简公分母是x2-1B.方程两边都乘(x2-1),得整式方程2(x-1)+3(x+1)=6C.解B项中的整式方程得x=1D.原方程的解为x=15.分式方程=的解为(D)A.x=0B.x=3C.x=5D.x=96.关于x的分式方程=1,下列说法正确的是(C)A.方程的解是x=m+5B.m>-5时,方程的解是正数C.m<-5时,方程的解为负数D.无法确定7.若分式方程=有增根,则增根为(B)A.x=-1B.x=1C.x=±1D.x=08.已知关于x的方程=3的解是正数,则实数m的取值范围为(C)A.m>-6B.m<-6C.m>-6,且m≠-4D.m>-6,且m≠29.对于非零的两个实数a,b,规定a*b=-,若5*(3x-1)=2,则x的值为(B)A. B. C. D.-10.“五一”期间,东方中学“动感数学”活动小组的全体同学租一辆面包车前去某景点游览,面包车的车费为180元.出发时又增加了2名同学,结果每个同学比原来少摊了3元车费.若设“动感数学”活动小组有x人,则所列方程为(B)A.-=3B.-=3C.-=3D.-=311.某市为解决部分市民冬季集中取暖问题需铺设一条长3 000 m的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x m,则可得方程-=15,根据此情景,题中用“…”表示的缺失的条件应补为(C)A.每天比原计划多铺设10 m,结果延期15天才完成B.每天比原计划少铺设10 m,结果延期15天才完成C.每天比原计划多铺设10 m,结果提前15天完成D.每天比原计划少铺设10 m,结果提前15天完成12.如图所示的电路的总电阻为10 Ω,若R1=2R2,则R1,R2的值分别是(A)A.R1=30 Ω,R2=15 ΩB.R1=Ω,R2=ΩC.R1=15 Ω,R2=30 ΩD.R1=Ω,R2=Ω二、填空题(每小题3分,共24分)13.当x=1时,分式的值为-1.14.同学解分式方程=0,得出原方程的解为x=2或x=-2.你认为他的解答对吗?请你作出判断:不对,并说明理由:因为当x=2时,分母为零,无意义,所以x=2是原方程的增根.15.请选择一组a,b的值,写出一个关于x的形如=b的分式方程,使它的解是x=0,这样的分式方程可以是=1(答案不唯一).16.为改善生态环境,防止水土流失,某村准备在荒坡上植树960棵,由于青年志愿者的支持,每天比原计划多植20棵,结果提前4天完成任务,原计划每天植树多少棵?设原计划每天植树x棵,由题意得方程-=4.17.若分式无意义,当-=0时,m=.18.规定a·b=-,若x·(x+2)=,则x为-1.19.研究10,12,15这三个数的倒数发现:-=-,我们称15,12,10这三个数为一组调和数.现有一组调和数:3,5,x(x>5),则x的值是15.20.观察分析下列方程:①x+=3,②x+=5,③x+=7.请利用它们所蕴含的规律,求关于x的方程x+=2n+4(n为正整数)的根,你的答案是:x=n+3或x=n+4.三、解答题(共40分)21.(每小题5分,共10分)解方程:(1)=-3;(2)+=.=-3,两边同乘(x-2),得1=x-1-3(x-2),解得x=2,经检验x=2是增根,所以原方程无解.(2)+=,两边同乘x(x-1),得3(x-1)+6x=7,9x=10,x=,经检验x=是原方程的根,所以原方程的根是x=.解方程=去分母,得4(2x-1)去括号,得8x-=1-3x-x=-(1)小明的解答有错吗?如果有错,请指出错在第几步?(写出序号即可)解方程x-=.小明的解答有错,错在第①步;(2)去分母,得x2+x-2=2x,即(x-2)(x+1)=0,解得x=2或x=-1,经检验x=-1是增根,故分式方程的解为x=2.23.(7分)“”称为二阶行列式,已知它的运算法则为=ad-bc,请你根据上述规定求出下列等式中x的值.=1.=1整理,得2×-=1,即+=1,得x=4.经检验x=4是原方程的解.〚导学号92034152〛24.(8分)某文化用品商店用2 000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6 300元.(1)求第一批购进书包的单价是多少元?(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?设第一批购进书包的单价是x元,则第二批购进书包的单价是(x+4)元.由题意得×3=,解得x=80,经检验x=80是原方程的根.答:第一批购进书包的单价是80元.(2)×(120-80)+×(120-84)=3 700(元).答:商店共盈利3 700元.25.(9分)阅读下面的材料:例:用换元法解分式方程:已知+=7.解:设y=,则原方程可化为y+=7,即y2-7y+10=0,解这个方程得y1=5,y2=2,由y1==5,得方程x2-5x=0,解得x1=0,x2=5;由y2==2,得方程x2-2x-3=0,解得x3=-1,x4=3;经检验x1=0,x2=5,x3=-1,x4=3都是原方程的解.学习例题的方法,请你用换元法解下面的分式方程:-5-6=0.=y,则原方程化为y2-5y-6=0,解得y1=6,y2=-1.当y1=6时,=6,解得x1=;当y2=-1时,=-1,解得x2=;经检验x1=,x2=都是原方程的根,即原方程的根是x1=,x2=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018(上)NS数理推演拓展12
专题复习(三)应用题复习
姓名___________班级___________
1.已知A、B两地相距80km ,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑电动车,图中直线DE,OC分别表示甲、乙离开A地的路程s (km )与时间t (h )的函数关系的图象。
根据图象解答下列问题。
(1)甲比乙晚出发几个小时?乙的速度是多少?
(2)乙到达终点B地用了多长时间?
(3)在乙出发后几小时,两人相遇?
2.某果园有100棵橙子树,平均每棵树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。
根据经验估计,每多种一棵树,平均每棵果树就会少结5个橙子,假设果园多种x棵橙子树。
(1)直接写出平均每棵树结的橙子数y(个)与x之间的关系式。
(2)果园多种多少棵橙子树时,可以使橙子的总产量最大?最大为多少。
3.某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
4.把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子.
①要使折成的长方形盒子的底面积为484cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2,求此时长方形盒子的长、宽、高(只需求出符合要求的一种情况).
5.某商店经销某玩具每个进价60元,每个玩具不低于80元出售,玩具的销售单价m(元/个)与销售数量n(个)之间的函数关系如图.
(1)试求表示线段AB的函数的解析式,并求出当销售数量n=20时的单价m的值;
(2)写出该店当一次销售n(n>10)个时,所获利润w(元)与n(个)之间的函数关系式:(3)店长小明经过一段时间的销售发现:卖27个赚的钱反而比卖30个赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他条件不变的情况下,店长应把最低价每个80元至少提高到________ 元?
6.我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间 t (t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量 y
时间t (天) 0 5 10 15 20 25 30
日销售量y1 (百件) 0 25 40 45 40 25 0
,并求
1
出y1与t的函数关系式及自变量t的取值范围;
(2)求 y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
7.月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售。
已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分。
设公司销售这种电子产品的年利润为z (万元)。
(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本。
)
(1)请求出y(万件)与x(元/件)之间的函数关系式。
(2)求出第一年这种电子产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值。
(3)假设公司的这种电子产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x (元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围。
8.如图①是矩形包书纸的示意图,虚线是折痕,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.
(1)现有一本书长为25cm,宽为20cm,厚度是2cm,如果按照如图①的包书方式,并且折叠进去的宽度是3cm,则需要包书纸的长和宽分别为多少?(请直接写出答案).
(2)已知数学课本长为26cm,宽为18.5cm,厚为1cm,小明用一张面积为1260cm2的矩形包书纸按如图①包好了这本书,求折进去的宽度.
(3)如图②,矩形ABCD是一张一个角(△AEF)被污损的包书纸,已知AB=30,BC=50,AE=12,AF=16,要使用没有污损的部分包一本长为19,宽为16,厚为6的字典,小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典.设PM=x,矩形PGCH的面积为y,当x取何值时y最大?并由此判断小红的想法是否可行.。
