数学建模期末试卷A及答案教学文稿
广西大学数学建模考试试题A及参考答案

广西大学数学建模考试试题A及参考答案一.概念题(共3小题,每小题5分,本大题共15分)1、什么是数学模型?(5分)答:数学模型可以描述为,对于现实世界的一个特定对象,为了一个特定目的,根据特有的内在规律,做出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构。
2、数学建模有哪几个过程?(5分)答:数学建模有如下几个过程:模型准备,模型假设,模型构成,模型求解,模型分析,模型检验,模型应用。
3、试写出神经元的数学模型。
答:神经元的数学模型是其中某=(某1,…某m)输入向量,y为输出,wi是权系数;输入与输出具有如下关系:Tθ为阈值,f(某)是激发函数;它可以是线性函数,也可以是非线性函数.(5分)二、模型求证题(共2小题,每小题10分,本大题共20分)1、(l)以雇员一天的工作时间t和工资w分别为横坐标和纵坐标,画出雇员无差别曲线族的示意图。
解释曲线为什么是你画的那种形状。
(5分)(2)如果雇主付计时工资,对不同的工资率(单位时间的工资)画出计时工资线族。
根据雇员的无差别曲线族和雇主的计时工资线族,讨论双方将在怎样的一条曲线上达成协议。
(5分)答:(l)雇员的无差别曲线族f(w,t)=C是下凸的,如图1,因为工资低时,他愿以较多的工作时间换取较少的工资;而当工资高时,就要求以较多的工资来增加一点工作时间.(2)雇主的计时工资族是w=at,a是工资率.这族直线与f(w,t)=c的切点P1,P2,P3,…的连线PQ为雇员与雇主的协议线.通常PQ是上升的(至少有一段应该是上升的),见图1.2、试作一些合理的假设,证明在起伏不平的地面上可以将一张椅子放稳。
(7分)又问命题对长凳是否成立,为什么?(3分)答:(一)假设:电影场地面是一光滑曲面,方凳的四脚连线构成一正方形。
如图建立坐标系:其中A,B,C,D代表方凳的四个脚,以正方形ABCD的中心为坐标系原点。
图二记H为脚A,C与地面距离之和,G为脚B,D与地面距离之和,θ为AC连线与某轴的夹角,不妨设H(0)>0,G(0)=0,(为什么)令f(θ)=H(θ)-G(θ)则f是θ的连续函数,且f(0)=H(0)>0,将方凳旋转90°,则由对称性知H(π/2)=0,G(π/2)=H(0)从而f(π/2)=-H(0)<0由连续函数的介值定理知,存在θ∈(0,π/2),使f(θ)=0(二)命题对长凳也成立,只须记H为脚A,B与地面距离之和,G为脚C,D与地面距离之和,θ为AC连线与某轴的夹角,将θ旋转180同理可证。
数学建模试卷A参考答案
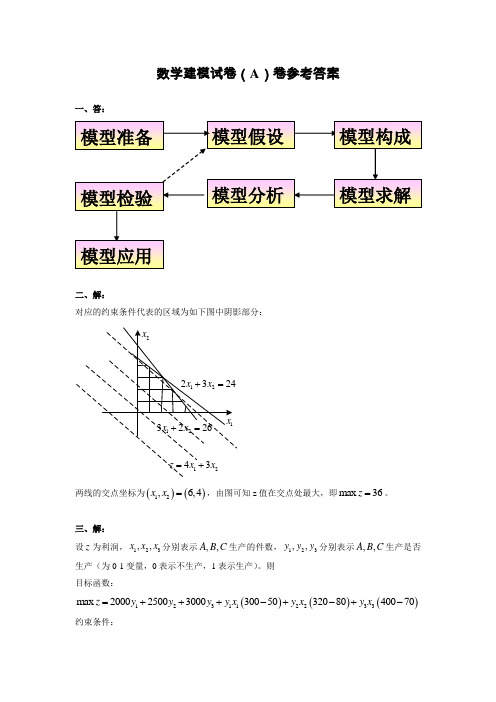
数学建模试卷(A )卷参考答案一、答:二、解:对应的约束条件代表的区域为如下图中阴影部分:两线的交点坐标为()()12,6,4x x =,由图可知z 值在交点处最大,即max 36z =。
三、解:设z 为利润,123,,x x x 分别表示,,A B C 生产的件数,123,,y y y 分别表示,,A B C 生产是否生产(为0-1变量,0表示不生产,1表示生产)。
则 目标函数:()()()123112233max 200025003000300503208040070z y y y y x y x y x =+++-+-+-约束条件:1231231231231232350024000350000,0,0;,0 1;x x x x x x x x x x x x y y or ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥≥≥=⎩四、解:(一)(二)目标层准则层方案层11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1(),0,ij n n ij ji ijA a a a a ⨯=>=层次分析法的基本步骤成对比较阵和权向量元素之间两两对比,对比采用相对尺度设要比较各准则C 1,C 2,… , C n 对目标O 的重要性:i j ijC C a ⇒A ~成对比较阵 A 是正互反阵要由A 确定C 1,… , C n 对O 的权向量选择旅游地(三)111122221212n n n n n n w w w w w w w w w w w w A w w w w w w ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎤⎥⎢⎥⎢⎥⎣⎦23a =一致比较允许不一致,但要确定不一致的允许范围考察完全一致的情况12(1),,nW w w w =⇒/ij i ja w w =令12(,,)~T n w w w w =权向量“选择旅游地”中准则层对目标的权向量及一致性检验11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦准则层对目标的成对比较阵最大特征根λ=5.073权向量(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T 5.07350.01851CI -==-一致性指标随机一致性指标 RI=1.12 (查表) 一致性比率CR =0.018/1.12=0.016<0.1通过一致性检验五、解:()221max ni i i a bx y =+-∑,对,a b 分别求偏导数,可以求解得0.9726,0.0500b a ==。
《数学建模》期末试卷A

《数学建模》期末试卷A一、填空题(每题2分,共20分)1、在数学建模中,我们将所要研究的问题________化。
2、在解决实际问题时,我们常常需要收集大量的数据,这些数据通常是不________的。
3、在建立数学模型时,我们通常需要对变量进行假设,这些假设通常是对________的描述。
4、在解决实际问题时,我们通常需要对多个因素进行________,以确定哪些因素对所要研究的问题有显著影响。
5、在建立数学模型时,我们通常需要对数据进行________,以发现数据之间的规律和关系。
6、在解决实际问题时,我们通常需要将复杂的问题________化,以方便我们更好地理解和解决它们。
7、在建立数学模型时,我们通常需要将实际问题________化,以将其转化为数学问题。
8、在解决实际问题时,我们通常需要考虑实际情况的________性,以避免我们的解决方案过于理想化。
9、在建立数学模型时,我们通常需要使用数学语言来________模型,以方便我们更好地描述和解决它。
10、在解决实际问题时,我们通常需要使用计算机来帮助我们进行________和计算。
二、选择题(每题3分,共30分)11、在下列选项中,不属于数学建模步骤的是()。
A.确定变量和参数B.建立模型C.进行实验D.验证模型12、在下列选项中,不属于数学建模方法的是()。
A.归纳法B.演绎法C.类比法D.反证法13、在下列选项中,不属于数学建模应用领域的是()。
A.物理学B.工程学C.经济学D.政治学14、在下列选项中,不属于数学建模语言的是()。
A.文字语言B.符号语言C.图形语言D.自然语言15、在下列选项中,不属于数学建模原则的是()。
A.简洁性原则B.一致性原则C.可行性原则D.可重复性原则16、在下列选项中,不属于数学建模步骤的是()。
A.对数据进行分析和处理B.对模型进行假设和定义C.对模型进行检验和修正D.对结果进行解释和应用17、在下列选项中,不属于数学建模应用领域的是()。
数学建模试卷A答案

第 1 页 共2页 第 1 页 共2页《数学建模》课程试卷A 答案适用专业: 考试日期:试卷类型:闭卷 考试时间:120分钟 试卷总分:100分一. 怎样解决下面的实际问题,包括需要哪些数据资料、观察、试验以及建立什么样的数学模型(10分) (1)确定火箭发射至最高点所需的时间 (2)为保险公司制定人寿保险金计划(1)依牛顿第二定理建立方程,并由试验及拟合方法确定阻力系数,再解方程。
5 (2)不同年龄死亡率,并估计未来一定时期的变化,还应考虑银行利率、物价指数。
10二.对于技术革新的推广,在下列几种情况下分别建立模型(10分)1.推广工作通过已经采用新技术的人进行,推广速度与已采用新技术的人数成正比,推广是无限的。
2.总人数有限,因而推广速度还会随着尚未采用新技术人数的减少而降低。
(1)x dt dxλ=………..5 (2))(x N ax dtdx-= (10)三. 已知甲乙两个种群在同一自然环境相互竞争而生存,试建立甲种群增长的方程和乙种群增长的方程(不要求解)(10分)设)(),(21t x t x 甲乙两个种群的数量,21,r r 是它们固有的增长率21,N N 是它们的最大容量)1(22111111N x N x x r dt dx σ--= 。
5 )1(11222222N xN x x r dt dx σ--=。
10四.试建立人口指数增长模型及阻滞增长模型(要求求出微分方程的解)(10分)人口指数增长模型: rt e x x rx dtdx0,==。
5 阻滞增长模型rtm m m ex x x x x xrx dt dx --+=-=)1(1),1(0。
10第 2 页 共2页 第 2 页 共2页60分)某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后售出,从钢管19cm ,现有一客户需要50根4m 、20根6m 和158m 的钢管,应如何下料最省?(程序计算结果可自由确定)摘要,关键词,符号假设,问题分析,模型建立及求解(要有程序),模型的 i x 表示按照第i 种模式切割的钢管的根数1124567333MinZ x x x x x x =+++++或21234567MinZ x x x x x x x =++++++ 1234543250x x x x x ++++≥24562320x x x x +++≥357215x x x ++≥编程 1234543250x x x x x *+*+*++>=; 24562320x x x x +*++*>=;357215x x x ++*>=;1234@();@();@();@();gin x gin x gin x gin x 567@();@();@();gin x gin x gin x第3 页共2页第3 页共2页。
数学建模期末答案

《数学建模》期末考试A卷姓名:专业:学号:学习中心:成绩:一、判断题(每题3分,共15分)1、模型具有可转移性。
------------------------------(√)2、一个原型,为了不同的目的可以有多种不同的模型。
------(√)3、一个理想的数学模型需满足模型的适用性和模型的可靠性。
---------------------------------------------(√)4、力学中把质量、长度、时间的量纲作为基本量纲。
-------(√)5、数学模型是原型的复制品。
-------------------- (×)二、不定项选择题(每题3分,共15分)1、下列说法正确的有AC 。
A、评价模型优劣的唯一标准是实践检验。
B、模型误差是可以避免的。
C、生态模型属于按模型的应用领域分的模型。
D、白箱模型意味着人们对原型的内在机理了解不清楚。
2、建模能力包括ABCD 。
A、理解实际问题的能力B、抽象分析问题的能力C、运用工具知识的能力D、试验调试的能力3、按照模型的应用领域分的模型有AE 。
A、传染病模型B、代数模型C、几何模型D、微分模型E、生态模型4、对黑箱系统一般采用的建模方法是 C 。
A、机理分析法B、几何法C、系统辩识法D、代数法5、一个理想的数学模型需满足AC 。
A、模型的适用性B、模型的可靠性C、模型的复杂性D、模型的美观性三、用框图说明数学建模的过程。
(10分)四、建模题(每题15分,共60分)1、四条腿长度相等的椅子放在起伏不平的地面上,4条腿能否同时着地?解:4条腿能同时着地(一)模型假设对椅子和地面都要作一些必要的假设:对于此题,如果不用任何假设很难证明,结果很可能是否定的。
因此对这个问题我们假设:(1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言,方桌的腿是足够长的(4)方桌的腿只要有一点接触地面就算着地。
那么,总可以让桌子的三条腿是同时接触到地面。
吉林师范成人教育《数学建模A》期末考试复习题及参考答案

《数学建模》A 卷
年级 专业 姓名 分数
一、解答题:(每题10分)
1. 设某产品的供给函数)(p ϕ与需求函数)(p f 皆为线性函数:
9)(,43)(+-=+=kp p f p p ϕ
其中p 为商品单价,试推导k 满足什么条件使市场稳定。
2.某植物园的植物基因型为AA 、Aa 、aa ,人们计划用AA 型植物与每种
基因型植物相结合的方案培育后代(遗传方式为常染色体遗传),经
过若干代后,这种植物后代的三种基因型分布将出现什么情形?总体
趋势如何?
3..试建立人口Logistic(逻辑)模型,并说明模型中何参数为自然增长率,为什么?
4、1968年,介壳虫偶然从澳大利亚传入美国,威胁着美国的柠檬生产。
随后,美国又从澳大利亚引入了介壳虫的天然捕食者——澳洲瓢虫。
后来,DDT被普通使用来消灭害虫,柠檬园主想利用DDT进一步杀死介壳虫。
谁料,DDT同样杀死澳洲瓢虫。
结果,介壳虫增加起来,澳洲瓢虫反倒减少了。
试建立数学模型解释这个现象。
福建师范大学2020年秋作业《数学建模》期末考试A卷答案

《数学建模》期末考试A卷姓名:专业:学号:学习中心:一、判断题(每题3分,共15分)1、模型具有可转移性。
------------------------------(对)2、一个原型,为了不同的目的可以有多种不同的模型。
----(对)3、一个理想的数学模型需满足模型的适用性和模型的可靠性。
-------------------------------------------(对)4、力学中把质量、长度、时间的量纲作为基本量纲。
------(对)5、数学模型是原型的复制品。
----------------- (错)二、不定项选择题(每题3分,共15分)1、下列说法正确的有AC 。
A、评价模型优劣的唯一标准是实践检验。
B、模型误差是可以避免的。
C、生态模型属于按模型的应用领域分的模型。
D、白箱模型意味着人们对原型的内在机理了解不清楚。
2、建模能力包括ABCD 。
A、理解实际问题的能力B、抽象分析问题的能力C、运用工具知识的能力D、试验调试的能力3、按照模型的应用领域分的模型有AE 。
A、传染病模型B、代数模型C、几何模型D、微分模型E、生态模型4、对黑箱系统一般采用的建模方法是 C 。
A、机理分析法B、几何法C、系统辩识法D、代数法5、一个理想的数学模型需满足AB 。
A、模型的适用性B、模型的可靠性C、模型的复杂性D、模型的美观性三、用框图说明数学建模的过程。
(10分)答:概括的说,数学模型就是一个迭代的过程,其一般建模步骤用框架图表示如下:四、建模题(每题15分,共60分)1、四条腿长度相等的椅子放在起伏不平的地面上,4条腿能否同时着地?解:4条腿能同时着地(一)模型假设对椅子和地面都要作一些必要的假设:对于此题,如果不用任何假设很难证明,结果很可能是否定的。
因此对这个问题我们假设:(1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言,方桌的腿是足够长的(4)方桌的腿只要有一点接触地面就算着地。
《数学建模》期末考试题(A卷)

云南财经大学 2006 至 2007 学年第 一 学期《数学建模》 课程期末考试试卷(A 卷)(全校性选修课)一、 题目:要求:以小组为单位(不超过3人)以论文形式提交答卷,要求包括摘要(10发分)、关键词(5分)、问题重述(10分)、模型假设(5分)、模型求解(50分)、模型评价(5分)、模型改进(5分)、模型推广(5分)、参考文献(5分)几个部分。
煤矿瓦斯和煤尘的监测与控制煤矿安全生产是我国目前亟待解决的问题之一,做好井下瓦斯和煤尘的监测与控制是实现安全生产的关键环节(见附件1)。
瓦斯是一种无毒、无色、无味的可燃气体,其主要成分是甲烷,在矿井中它通常从煤岩裂缝中涌出。
瓦斯爆炸需要三个条件:空气中瓦斯达到一定的浓度;足够的氧气;一定温度的引火源。
煤尘是在煤炭开采过程中产生的可燃性粉尘。
煤尘爆炸必须具备三个条件:煤尘本身具有爆炸性;煤尘悬浮于空气中并达到一定的浓度;存在引爆的高温热源。
试验表明,一般情况下煤尘的爆炸浓度是30~ 2000g/m 3,而当矿井空气中瓦斯浓度增加时,会使煤尘爆炸下限降低,结果如附表1所示。
国家《煤矿安全规程》给出了煤矿预防瓦斯爆炸的措施和操作规程,以及相应的专业标准 (见附件2)。
规程要求煤矿必须安装完善的通风系统和瓦斯自动监控系统,所有的采煤工作面、掘进面和回风巷都要安装甲烷传感器,每个传感器都与地面控制中心相连,当井下瓦斯浓度超标时,控制中心将自动切断电源,停止采煤作业,人员撤离采煤现场。
具体内容见附件2的第二章和第三章。
附图1是有两个采煤工作面和一个掘进工作面的矿井通风系统示意图,请你结合附表2的监测数据,按照煤矿开采的实际情况研究下列问题:(1)根据《煤矿安全规程》第一百三十三条的分类标准 (见附件2),鉴别该矿是属于“低瓦斯矿井”还是“高瓦斯矿井”。
(2)根据《煤矿安全规程》第一百六十八条的规定,并参照附表1,判断该煤矿不安全的程度(即发生爆炸事故的可能性)有多大?(3)为了保障安全生产,利用两个可控风门调节各采煤工作面的风量,通过一个局部通风机和风筒实现掘进巷的通风(见下面的注)。
最新数学模型(数学建模)期末考试试题及答案 详解(1)

)t的变化情2、在§6.1捕鱼业的持续收获的效益模型中,若单位捕捞强度的费用为捕捞强度E 的减函数, 即)0,0(,>>-=b a bE a c ,请问如何达到最大经济效益?三、简答题(本题满分16分,每小题8分)1、在§9.3 随机存储策略中,请用图解法说明为什么s 是方程)()(0S I c x I +=的最小正根。
2、请结合自身特点谈一下如何培养数学建模的能力?四、(本题满分20分)某中学有三个年级共1000名学生,一年级有219人,二年级有316人,三年级有465人。
现要选20名校级优秀学生,请用下列办(1)按比例加惯例的方法;(2)Q 值法。
另外如果校级优秀学21个,重新进行分配,并按照席位分配的理想化准则分析分配结果。
五、(本题满分16分)大学生毕业生小李为选择就业岗位建立了层次分析模型,影响就业的因素考虑了收入情况、发展空间、社会声誉三个方面,有三个业岗位可供选择。
层次结构图如图,已知准则层对目标层的成对比较矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=12/15/1213/1531,方案层对准则层的成对比较矩阵分别为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1272/1147/14/111B,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=13/17/1313/17312,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=12/16/1214/16413B。
选择就业岗位收入发展声誉岗位1 岗位2 岗位3六、(本题满分16分)某保险公司欲开发一种人寿保险,投保人需要每年缴纳一定数的额保险费,如果投保人某年未按时缴纳保费则视为保险合同终止(退保)。
保险公司需要对投保人的健康、疾病、死亡和退保的情况作出评估,从而制定合适的投保金额和理赔金额。
各种状态间相互转移的情况和概率如图。
试建立马氏链模型分析在投保人投保时分别为健康或疾病状态下,平均需要经过多少年投保人就会出现退保或死亡的情况,以及出现每种情况的概率各是多少?0.608/09学年 II 学期《数学模型》期末考试A 试卷解答16分,每小题8分) 1)得vt m m mr =++2)1(22πωπ, 。
《数学建模》期末考试试卷一与参考答案

《数学建模》期末考试试卷 班级 姓名 学号一、(15分)以色列的某社区联盟,其农业生产受农田面积和灌溉配水量的限制,其资料如表1所示,适合该地区种植的农作物有甜菜、棉花和栗子,其每英亩的期望净收益、用水量及可种植的最大面积如表2所示。
表1 农田面积和灌溉配水量 表2 农作物期望净收益、用水量试问,该社区联盟应如何安排这三种农作物的生产,方使总的收益最大?建立线性规划问题的数学模型并写出用LINGO 求解的程序。
二、(15分)用单纯形方法求解线性规划问题。
⎪⎩⎪⎨⎧≥≥≥≤++≤++++=000242126042..61314S max 321321321321x x x x x x x x x t s x x x ;;三、(15分)上海红星建筑构配件厂是红星集团属下之制造建材设备的专业厂家。
其主要产品有4种,分别用代号A 、B 、C 、D 表示,生产A 、B 、C 、D 四种产品主要经过冲压、成形、装配和喷漆四个阶段。
根据工艺要求及成本核算,单位产品所需要的加工时间、利润以及可供使用的总工时如下表所示:在现有资源的条件下如何安排生产,可获得利润最大?现设置上述问题的决策变量如下:1234,,,x x x x 分别表示A 、B 、C 、D 型产品的日产量,则可建立线性规划模型如下:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤+++≤+++≤+++≤++++++=0,,,300048462000552424005284480..81169max 432143214321432143214321x x x x x x x x x x x x x x x x x x x x t s x x x x z 利用LINGO10.0软件进行求解,得求解结果如下:Global optimal solution found at iteration: 4Objective value: 4450.000 Variable Value Reduced Cost X1 400.0000 0.000000 X2 0.000000 0.5000000 X3 70.00000 0.000000 X4 10.00000 0.000000 Row Slack or Surplus Dual Price 1 4450.000 1.000000 2 0.000000 2.500000 3 610.0000 0.000000 4 0.000000 0.5000000 5 0.000000 0.7500000(1)指出问题的最优解并给出原应用问题的答案;(2)写出线性规划问题的对偶线性规划问题,并指出对偶问题的最优解;(3)灵敏度分析结果如下:Ranges in which the basis is unchanged: Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient Increase Decrease X1 9.000000 0.5000000 0.1666667 X2 6.000000 0.5000000 INFINITY X3 11.00000 0.3333333 1.000000 X4 8.000000 1.000000 1.000000 Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 480.0000 20.00000 80.000003 2400.000 INFINITY 610.00004 2000.000 400.0000 20.000005 3000.000 40.00000 280.0000对灵敏度分析结果进行分析 四、(15分)(1)叙述层次分析法的步骤。
数学建模练习试题教学文稿

数学建模练习试题教学文稿一、前言数学建模是通过建立数学模型来解决实际问题的一种方法。
在数学建模的学习和实践中,练习试题是提高解题能力和理解数学建模思想的重要工具。
本文旨在通过教学文稿的形式,介绍数学建模练习试题的教学方法和要点,以帮助学生提高数学建模的能力。
二、理解题意和分析问题在解决数学建模练习试题时,首先要全面理解题目的要求和条件。
通过仔细阅读题目,分析问题的关键点和需要解决的具体内容。
同时,利用绘图、列式和符号等数学工具,抽象出问题的数学模型,将实际问题转化为数学问题。
三、模型的建立根据题目所给的条件和要求,选择合适的数学模型来描述问题。
常见的数学模型包括线性模型、非线性模型、优化模型等。
在建立模型的过程中,要注意模型的合理性和简洁性。
同时,要根据问题的具体特征,合理选择适当的方法和技巧。
四、模型的求解与分析在模型建立之后,需要通过数学方法来求解问题。
根据模型的特点和求解的要求,选择合适的数学工具和算法进行计算。
在求解过程中,要注重结果的分析和解释,理解结果背后的意义和实际应用。
五、结果的验证和评估在解决数学建模练习试题时,对于得到的结果要进行验证和评估。
通过比较实际情况和模型的预测结果,评估模型的有效性和可靠性。
如果结果符合实际要求,说明模型的建立和求解是正确的;如果结果与实际情况有较大偏差,需要重新检查建模和求解的过程,找出问题所在。
六、总结和拓展在解答数学建模练习试题的过程中,要及时总结和拓展所学的知识和技巧。
通过练习不同类型的试题,摸索出解题的规律和方法。
同时,要积极参与数学建模竞赛和实践活动,扩展自己的数学建模能力。
七、实例分析为了更好地理解和掌握数学建模练习试题的解法,在此给出一个实例进行分析。
题目描述:某城市A、B、C三个汽车租赁公司提供短途汽车租赁服务,分别拥有不同的汽车数量。
每辆汽车每天的租金不同。
三个公司的运营成本与租出的汽车数量成正比。
现假定A公司拥有10辆汽车,每辆汽车的租金为100元,运营成本为80元;B公司拥有20辆汽车,每辆汽车的租金为80元,运营成本为60元;C公司拥有30辆汽车,每辆汽车的租金为70元,运营成本为40元。
(完整版)数学建模期末试卷A及答案

用。
且阻滞作用随人口数量增加而变大,从而人口增长率 r(x) 是人口数量 x(t) 的的减函数。
假设 r(x) 为 x(t) 的线性函数:
The shortest way to do many things is
r(x) r sx (r 0, s 0)
,
其中, r 称为人口的固有增长率,表示人口很少时(理论上是 x 0 )的增长率。
在每个生产周期T 内,开始一段时间( 0 t T0 ) 边生产边销售,后一段时间(T0 t T )只销售不 生产,存贮量 q(t) 的变化如图所示。设每次生产开工
费为 c1 ,每件产品单位时间的存贮费为 c2 ,以总费用最小为准则确定最优周 期T ,并讨论 r k 和 r k 的情况。
c(T )
某家具厂生产桌子和椅子两种家具,桌子售价 50 元/个,椅子销售价格 30 元/个,生 产桌子和椅子要求需要木工和油漆工两种工种。生产一个桌子需要木工 4 小时,油漆工 2 小时。生产一个椅子需要木工 3 小时,油漆工 1 小时。该厂每个月可用木工工时为 120 小 时,油漆工工时为 50 小时。问该厂如何组织生产才能使每月的销售收入最大?(建立模型 不计算)(10’)
s r 当 x xm 时人口不再增长,即增长率 r(xm ) 0 ,代入有 xm ,从而有
根据 Malthus 人口模型,有
r(x)
r1
x xm
,
dx r(1 x )x
dt
xm
x(0) x0
4.(25 分)已知 8 个城市 v0,v1,…,v7 之间有一个公路网(如图所示), 每条公路为图中的边,边上的权数表示通过该公路所需的时间.
(1)设你处在城市 v0,那么从 v0 到其他各城市,应选择什么路径使所需 的时间最短? (1) v0 到其它各点的最短路如下图:
数学建模期末考试2018A试的题目与答案

华南农业大学期末考试试卷(A卷)2012-2013学年第二学期考试科目:数学建模考试类型:(闭卷)考试考试时间:120 分钟学号姓名年级专业题号一二三四五六七八总分得分评阅人得分一、(满分12分)一人摆渡希望用一条船将一只狼.一只羊.一篮白菜从河岸一边带到河岸对面.由于船的限制.一次只能带一样东西过河.绝不能在无人看守的情况下将狼和羊放在一起;羊和白菜放在一起.怎样才能将它们安全的带到河对岸去? 建立多步决策模型,将人、狼、羊、白菜分别记为i = 1.2.3.4.当i在此岸时记x i = 1.否则为0;此岸的状态下用s =(x1.x2.x3.x4)表示。
该问题中决策为乘船方案.记为d = (u1, u2, u3, u4).当i在船上时记u i = 1.否则记u i = 0。
(1) 写出该问题的所有允许状态集合;(3分)(2) 写出该问题的所有允许决策集合;(3分)(3) 写出该问题的状态转移率。
(3分)(4) 利用图解法给出渡河方案. (3分)解:(1)S={(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0)}及他们的5个反状(3分)(2) D = {(1,1,0,0), (1,0,1,0), (1,0,0,1), (1,0,0,0)} (6分)(3) s k+1 = s k + (-1) k d k (9分)(4)方法:人先带羊.然后回来.带狼过河.然后把羊带回来.放下羊.带白菜过去.然后再回来把羊带过去。
或: 人先带羊过河.然后自己回来.带白菜过去.放下白菜.带着羊回来.然后放下羊.把狼带过去.最后再回转来.带羊过去。
(12分)得分1、二、(满分12分)在举重比赛中.运动员在高度和体重方面差别很大.请就下面两种假设.建立一个举重能力和体重之间关系的模型:(1)假设肌肉的强度和其横截面的面积成比例。
6分(2)假定体重中有一部分是与成年人的尺寸无关.请给出一个改进模型。
数学建模期末试卷A及答案精编版

2009《数学建模》期末试卷A考试形式:开卷 考试时间:120分钟姓名: 学号: 成绩: ___ 1.(10分)叙述数学建模的基本步骤,并简要说明每一步的基本要求。
2.(10分)试建立不允许缺货的生产销售存贮模型。
设生产速率为常数k ,销售速率为常数r ,k r <。
在每个生产周期T 内,开始一段时间(00T t ≤≤) 边生产边销售,后一段时间(T t T ≤≤0)只销售不 生产,存贮量)(t q 的变化如图所示。
设每次生产开工费为1c ,每件产品单位时间的存贮费为2c ,以总费用最小为准则确定最优周期T ,并讨论k r <<和k r ≈的情况。
3.(10分)设)(t x 表示时刻t 的人口,试解释阻滞增长(Logistic )模型⎪⎩⎪⎨⎧=-=0)0()1(x x xx x r dtdxm中涉及的所有变量、参数,并用尽可能简洁的语言表述清楚该模型的建模思想。
4.(25分)已知8个城市v 0,v 1,…,v 7之间有一个公路网(如图所示), 每条公路为图中的边,边上的权数表示通过该公路所需的时间.(1)设你处在城市v 0,那么从v 0到其他各城市,应选择什么路径使所需的时间最短?(2)求出该图的一棵最小生成树。
5.(15分)求解如下非线性规划:20 s.t.2 1222121≤≤≤+-=x x x x x z Max 6.(20分)某种合金的主要成分使金属甲与金属乙.经试验与分析, 发现这两种金属成分所占的百分比之和x 与合金的膨胀系数y 之间有一定的相关关系.先测试了12次, 得数据如下表:的模型。
7.(10分)有12个苹果,其中有一个与其它的11个不同,或者比它们轻,或者比它们重,试用没有砝码的天平称量三次,找出这个苹果,并说明它的轻重情况。
《数学建模》模拟试卷(三)参考解答1.数学模型是对于现实世界的某一特定对象,为了某个特定目的,作出一些必要的简化和假设,运用适当的数学工具得到的一个数学结构。
数学建模期末考试2018A试的题目与答案

华南农业大学期末考试试卷(A 卷)2012-2013学年第 二 学期 考试科目:数学建模考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、(满分12分) 一人摆渡希望用一条船将一只狼.一只羊.一篮白菜从河岸一边带到河岸对面.由于船的限制.一次只能带一样东西过河.绝不能在无人看守的情况下将狼和羊放在一起;羊和白菜放在一起.怎样才能将它们安全的带到河对岸去 建立多步决策模型,将人、狼、羊、白菜分别记为i = 当i 在此岸时记x i = 1.否则为0;此岸的状态下用s =()表示。
该问题中决策为乘船方案.记为d = (u1, u 2, u 3, u 4).当i 在船上时记u i = 1.否则记u i= 0。
(1) 写出该问题的所有允许状态集合;(3分)(2) 写出该问题的所有允许决策集合;(3分)(3) 写出该问题的状态转移率。
(3分)(4) 利用图解法给出渡河方案. (3分)解:(1) S={(1,1,1,1), (1,1,1,0), (1,1,0,1), (1,0,1,1), (1,0,1,0)}及他们的5个反状(3分)(2) D = {(1,1,0,0), (1,0,1,0), (1,0,0,1), (1,0,0,0)} (6分)(3) s k+1 = s k + (-1) k d k (9分)(4)方法:人先带羊.然后回来.带狼过河.然后把羊带回来.放下羊.带白菜过去.然后再回来把羊带过去。
或: 人先带羊过河.然后自己回来.带白菜过去.放下白菜.带着羊回来.然后放下羊.把狼带过去.最后再回转来.带羊过去。
(12分)1、 二、(满分12分) 在举重比赛中.运动员在高度和体重方面差别很大.请就下面两种假设.建立一个举重能力和体重之间关系的模型:(1) 假设肌肉的强度和其横截面的面积成比例。
6分(2) 假定体重中有一部分是与成年人的尺寸无关.请给出一个改进模型。
6分解:设体重w (千克)与举重成绩y (千克)(1) 由于肌肉强度(I)与其横截面积(S)成比例.所以 y I S设h 为个人身高.又横截面积正比于身高的平方.则S h2 再体重正比于身高的三次方.则w h3故举重能力和体重之间关系的模型为: (6分)(2) 体重中与成年人尺寸无关的重量为a, 则一个最粗略的模型为( 12分)三、(满分14分) 某学校规定.运筹学专业的学生毕业时必须至少学习过两门数学课、三门运筹学课和两门计算机课。
最新数学建模(数学模型)期末考试题(试卷)及答案详解(附答案)

数学建模(数学模型)期末考试卷及答案详解第一部分 基本理论和应用1、计算题(满分10分)设电路供电网内有10000盏灯,夜间每一盏灯开着的概率为0.7,假设各灯的开关是相互独立的,利用中心极限定理计算同时开着的灯数在6900与7100之间的概率.2、计算题(满分10分)设某种电子元件的使用寿命服从正态分布) ,(2σμN ,现随机抽取了10个元件进行检测, 得到样本均值(h)1500=x ,样本标准差(h)14=S . 求总体均值μ的置信概率为99%的置信区间3、计算题(满分10分)从正态总体)6 ,4.3(~2N X 中抽取容量为n 的样本,如果要求样本均值位于区间 (1.4,5.4) 内的概率不小于0.95,问样本容量n 至少应取多大?4、计算题(满分10分) 设总体X 的概率密度为:⎩⎨⎧<<+=其他,,0,10,)1();(x x x f θθθ )1(->θn X X X ,,,21 是来自总体X 的简单随机样本,求参数θ的矩估计量和极大似然估计量.5.(15分)设总体X 服从区间[0,θ]上的均匀分布,θ>0未知,12,,,n X X X 是来自X的样本,(1)求θ的矩估计和极大似然估计;(2)上述两个估计量是否为无偏估计量,若不是请修正为无偏估计量;(3)试问(2)中的两个无偏估计量哪一个更有效?6. (15分)设),(~2σμN X ,n X X X ,,,21 是取自总体的简单随机样本,X 为样本均值,2nS 为样本二阶中心矩,2S 为样本方差,问下列统计量:(1)22σnnS ,(2)1/--n S X n μ,(3)212)(σμ∑=-ni iX各服从什么分布?7. (10分)一个小班有8位学生,其中有5人能正确回答老师的一个问题.老师随意地逐个请学生回答,直到得到正确的回答为止,求在得到正确的回答以前不能正确回答问题的学生个数的概率分布.8. (10分)设某人有100位朋友都会向他发送电子邮件,在一天中每位朋友向他发出电子邮件的概率都是0.04,问一天中他至少收到4位朋友的电子邮件的概率是多少?试用二项分布公式和泊松近似律分别计算.9. (10分)某商品的每包重量2~(200,)X N σ.若要求{195205}0.98P X <<≥,则需要把σ控制在什么范围内.10. (15分)设系统L 由两个相互独立的子系统12,L L 联接而成,联接的方式分别为串联,并联和备用(当系统1L 损坏时,系统2L 开始工作),如图7.1所示.1L 和2L 的寿命为X 和Y ,分别有密度(0,)()()x X p x e I x αα-+∞=和(0,)()()y Y p y e I y ββ-+∞=,其中0,0αβ>>且αβ≠.请就这三种联接方式分别写出系统L 的寿命Z 的密度.答案第一部分 基本理论和应用 1、计算题(满分10分)设电路供电网内有10000盏灯,夜间每一盏灯开着的概率为0.7,假设各灯的开关是相互独立的,利用中心极限定理计算同时开着的灯数在6900与7100之间的概率. 解:设同时开着的灯数为X ,(10000,0.7)Xb ……………2分(0,1)N (近似) ……………3分 {69007100}210.971P X ≤≤=Φ-= …………5分 2、计算题(满分10分)设某种电子元件的使用寿命服从正态分布) ,(2σμN ,现随机抽取了10个元件进行检测,得到样本均值(h)1500=x ,样本标准差(h)14=S . 求总体均值μ的置信概率为99%的置信区间. 解: T =(1)X t n - 0.005{(1)}0.99P T t n <-= ………4分0.0050.005{(1)(1)}0.99P X n X X n -<<+-= ………………4分 所求为(1485.61,1514.39) …………2分3、计算题(满分10分)从正态总体)6 ,4.3(~2N X 中抽取容量为n 的样本,如果要求样本均值位于区间 (1.4,5.4) 内的概率不小于0.95,问样本容量n 至少应取多大? 解:(0,1)X N ………………3分{1.4 5.4}21P X P <<=<=Φ- ……………4分解210.95Φ-≥ 得34.6n ≥ n 至少取35 ……………3分4、计算题(满分10分) 设总体X 的概率密度为:⎩⎨⎧<<+=其他,,0,10,)1();(x x x f θθθ )1(->θn X X X ,,,21 是来自总体X 的简单随机样本,求参数θ的矩估计量和极大似然估计量.解: 1101()(2E X dx θθθθ++==+⎰+1)x ……………3分 解12X θθ+=+,得θ的矩估计量为211X X -- ……………2分 1()1()ni i L x θθθ=+∏n=() 1ln ln 1ln nii L n x θθ==+∑()+ ……………2分令1ln ln 01ni i d L nx d θθ==+=+∑ 得θ的极大似然估计量为11ln nii nX=--∑ …………3分5.(15分)设总体X 服从区间[0,θ]上的均匀分布,θ>0未知,12,,,n X X X 是来自X的样本,(1)求θ的矩估计和极大似然估计;(2)上述两个估计量是否为无偏估计量,若不是请修正为无偏估计量;(3)试问(2)中的两个无偏估计量哪一个更有效? 解:(1)2EX θ=,令2X θ=,得θ的矩估计量1ˆ2X θ=; ……………5分 似然函数为:()12121,0,,,(,,,;)0n n n x x x L x x x θθθ⎧<<⎪=⎨⎪⎩,其它其为θ的单调递减函数,因此θ的极大似然估计为{}212()ˆmax ,,,n n X X X X θ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(10分)叙述数学建模的基本步骤,并简要说明每一步的基本要求。
(1)模型准备:首先要了解问题的实际背景,明确题目的要求,收集各种必要的信息。
(2)模型假设:为了利用数学方法,通常要对问题做出必要的、合理的假设,使问题的主要特征凸现出来,忽略问题的次要方面。
(3)模型构成:根据所做的假设以及事物之间的联系,构造各种量之间的关系,把问题化为数学问题,注意要尽量采用简单的数学工具。
4)模型求解:利用已知的数学方法来求解上一步所得到的数学问题,此时往往还要作出进一步的简化或假设。
(5)模型分析:对所得到的解答进行分析,特别要注意当数据变化时所得结果是否稳定。
(6)模型检验:分析所得结果的实际意义,与实际情况进行比较,看是否符合实际,如果不够理想,应该修改、补充假设,或重新建模,不断完善。
(7)模型应用:所建立的模型必须在实际应用中才能产生效益,在应用中不断改进和完善。
2.(10分)试建立不允许缺货的生产销售存贮模型。
设生产速率为常数k ,销售速率为常数r ,k r <。
在每个生产周期T 内,开始一段时间(00T t ≤≤)
边生产边销售,后一段时间(T t T ≤≤0)只销售不
生产,存贮量)(t q 的变化如图所示。
设每次生产开工
费为1c ,每件产品单位时间的存贮费为2c ,以总费用最小为准则确定最优周期T ,并讨论k r <<和k r ≈的情况。
单位时间总费用k T r k r c T c T c 2)()(21-+=,使)(T c 达到最小的最优周期
)(2T 21*r k r c k c -=。
当k r <<时,
r c c 21*2T =,相当于不考虑生产的情况;当k r ≈时,∞→*T ,因为产量
被售量抵消,无法形成贮存量。
3.(10分)设)(t x 表示时刻t 的人口,试解释阻滞增长(Logistic )模型
⎪⎩⎪⎨⎧=-=0)0()1(x x x x x r dt dx m
中涉及的所有变量、参数,并用尽可能简洁的语言表述清楚该模型的建模思想。
t ——时刻;
)(t x ——t 时刻的人口数量;
r ——人口的固有增长率;
m x ——自然资源和环境条件所能容纳的最大人口数量;
0x ——初始时刻的人口数量
人口增长到一定数量后,增长率下降的原因:资源、环境等因素对人口增长的阻滞作用。
且阻滞作用随人口数量增加而变大,从而人口增长率)(x r 是人口数量)(t x 的的减函数。
假设)(x r 为)(t x 的线性函数:
)0,0()(>>-=s r sx r x r ,
其中,r 称为人口的固有增长率,表示人口很少时(理论上是0=x )的增长率。
当m x x =时人口不再增长,即增长率0)(=m x r ,代入有
m x r s =
,从而有
⎪⎪⎭⎫ ⎝⎛-=m x x r x r 1)(, 根据Malthus 人口模型,有
⎪⎩⎪⎨⎧=-=0)0()1(x x x x x r dt dx m
4.(25分)已知8个城市v 0,v 1,…,v 7之间有一个公路网(如图所示), 每条公路为图中的边,边上的权数表示通过该公路所需的时间.
(1)设你处在城市v 0,那么从v 0到其他各城市,应选择什么路径使所需的时间最短?
(1)0v 到其它各点的最短路如下图:
各点的父点如下:
v0 v1 v2 v3 v4 v5 v6 v7
v0 v0 v0 v2 v3 v0 v5 v3
各点的最短路径及最短路长分别为:
v0: 0
v0→v1: 1
v0→v2: 2
v0→v2→v3: 3
v0→v2→v3→v4: 6
v0→v5: 4
v0→v5→v6: 6
v0→v2→→v3→v7: 9
(2)最小生成树如下图:
7.(10分)有12个苹果,其中有一个与其它的11个不同,或者比它们轻,或者比它们重,试用没有砝码的天平称量三次,找出这个苹果,并说明它的轻重情况。
先把苹果编号1~12,把1~4和5~8放在天平两边:
(1)两边持平:就在9~12中,再把9和10放在天平两边,再平就在11或12中,若9和10不平,则在9或10中;
(2)两边不平:假设1234重5678轻,则进行第二次称量125和349;若平了就在678中且是轻的,再称6与7即可;若125重349轻则在12中且是重的, 再称1与2即可;若125轻349重,则坏的是5。
某家具厂生产桌子和椅子两种家具,桌子售价50元/个,椅子销售价格30元/个,生产桌子和椅子要求需要木工和油漆工两种工种。
生产一个桌子需要木工4小时,油漆工2小时。
生产一个椅子需要木工3小时,油漆工1小时。
该厂每个月可用木工工时为120小时,油漆工工时为50小时。
问该厂如何组织生产才能使每月的销售收入最大?(建立模型不计算)(10’)
解:(1)确定决策变量:x1=生产桌子的数量 x2=生产椅子的数量
(2)确定目标函数:家具厂的目标是销售收入最大max z=50x1+30x2
(3)确定约束条件:
4x1+3x2<120(木工工时限制)2x1+x2>50(油漆工工时限制)
(4)建立的数学模型为:
max S=50x1+30x2
s.t.4x1+3x2<120
2x1+x2>50
x1,x2>0。
