高等数学同济第七版7版(下册)习题全解
同济大学数学系《高等数学》第7版笔记和课后习题含考研真题详解(函数与极限 下)【圣才出品】

x0
x0
1 cos x2
lim
x0
sin2 x
lim x0
1 2
x2
2
x2
0
所以当 x→0 时,(1-cosx)2 是比 sin2x 高阶的无穷小。
3.当 x→1 时,无穷小 1-x 和(1)1-x3,(2)(1-x2)/2 是否同阶,是否等价?
x0 x
x0 x
(3)
lim
x0
sin sin
2x 5x
;(4)
lim
x0
x
cot
x
;
(5) lim 1 cos 2x x0 x sin x
;(6) lim 2n n
sin
x 2n
(x
为不等于零的常数)。
解:(1)当ω≠0
时, lim x0
sin x x
lim
x0
sin x
x
lim
x0
sin x x
2 5
lim
x0
sin 2x 2x
lim
x0
5x sin 5x
2 5
(4)
lim
x0
x
cot
x
lim
x0
x sin
x
cos
x
lim
x0
x sin
x
lim x0
cos
x
1
(5) lim 1 cos 2x lim 2sin 2 x 2 lim sin x 2
x0 x sin x x0 x sin x
(4) lim n 1 x 1 x0
(5)
lim
x0
x
1 x
1
证:(1)因1
同济大学《高等数学》第七版上、下册答案(详解),DOC

解得 z 14
9
即所求点为 M(0,0,14 ).
9
7. 试证:以三点 A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形. 证明:因为|AB|=|AC|=7.且有 |AC|2+|AB|2=49+49=98=|BC|2. 故△ABC 为等腰直角三角形. 8. 验证: (a b) c a (b c) .
3 i 14
1 j 14
2 k.
14
14. 三个力 F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力 R 的大小和方向余弦.
解:R=(1-2+3,2+3-4,3-4+5)=(2,1,4)
| R | 22 12 42 21
cos 2 , cos 1 , cos 4 .
故 A 的坐标为 A(-2, 3, 0).
13. 一向量的起点是 P1(4,0,5),终点是 P2(7,1,3),试求:
(1) P1P2 在各坐标轴上的投影; (2) P1P2 的模;
(3) P1P2 的方向余弦;
(4) P1P2 方向的单位向量.
解:(1) ax Pr jx P1P2 3,
ay Pr jy P1P2 1,
练习 5-2
练习 5-3
练习 5-4
总习题五
练习 6-2
练习 6-3
(2) s 22 (3)2 (4)2 29
(3) s (1 2)2 (0 3)2 (3 4)2 67
(4) s (2 4)2 (1 2)2 (3 3)2 3 5 .
5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.
高等数学同济第七版7版下册习题 全解

第十章重积分95数,故/, = Jj( x2 + y1)3d(j = 2jj(x2+ y1) 3dcr.fh i)i又由于D3关于;t轴对称,被积函数(/+r2)3关于y是偶函数,故jj(x2+j2)3dcr=2j(x2+y2)3da=2/2.Dy1):从而得/, = 4/2.(2)利用对称性来计算二重积分还有以下两个结论值得注意:如果积分区域关于^轴对称,而被积函数/(x,y)关于y是奇函数,即fix, -y) = -f(x,y) ,PJjf/(x,y)da =0;D如果积分区域D关于:K轴对称,而被积函数/(x,y)关于:c是奇函数,即/(~x,y)=-/(太,y),则=0.D«3.利用二重积分定义证明:(1)jj da=(其中(7为的面积);IJ(2)JJ/c/( X ,y)drr =Aj|y’(A:,y)do■(其中A:为常数);o n(3 ) JJ/( x,y)clcr = JJ/( x,y)drr + jJ/( x ,y) dcr ,其中 /) = /)! U /)2,, A 为两个I)b\lh尤公共内点的WK域.96一、《高等数学》(第七版)下册习题全解jj'ltr = Hm y^/( ,rji) A<r, = lim ^ Ac,=l i m cr= a.A—0n(2)Ji/(x,j)(Ic7=lim^i)1n=A lim y/(^(,i7,)A(7-,=k\\f{x,y)Aa.A-°台•{!(3)因为函数/U,y)在闭区域/)上可积,故不论把£»怎样分割,积分和的极限总是不变的.因此在分割D时,可以使和/)2的公共边界永远是一条分割线.这样fix.y)在A U D2上的积分和就等于&上的积分和加D2上的积分和,记为^/(^, ,17,) A CT, = ^/( ^, , 17,) A CT, + ^/(^, ,17,) A CT,./)(U0,",l):令所有的直径的最大值A-0,上式两端同时取极限,即得Jf(x,y)i\a=jjf(x,y)da+JJ/(x f y)da.p,un}V,n;Sa4.试确定积分区域/),使二重积分][(1-2x2-y2)d«l y达到最大值.I)解由二重积分的性质可知,当积分区域/>包含了所有使被积函数1-2.v2-V2 大于等于零的点,而不包含使被积函数1-2/-y2小于零的点,即当£»是椭圆2/+y2= l所围的平面闭区域时,此二重积分的值达到最大.& 5.根据二重积分的性质,比较下列积分的大小:(1)Ju+y)2山7与J[U,其中积分区域D是由x轴、^轴与直线A+.、=D I)1所围成;(2)J(x+7)2如与■,其中积分区域0是由圆周(.r-2)2+(.v-l)2=t)n2所围成;(3)I'M A;+y)(lor与!"[In(X+y)]2(1(7,其中Z>是三角形闭K域,三顶点分别为l)"(1,0),(1,1),(2,0);(4)Jpn(:r+y)dcr与In(:t+y)]2fW,其中/)=|(.r,.v)|3,0彡、彡1 .i)i)解(1)在积分K域0上,故有(x + j) 3 ^ (x + y) 2.根据二重积分的性质4,可得J(.r + y) \lrx ^ J (.\ + v)0D(2)由于积分区域0位于半平面|(A:,V) | .V+ •、彡1第十章重积分97(3)由于积分区域D位于条形区域1U,y)|1彡1+7彡2丨内,故知区域/)上的点满足0彡InU+y)彡1,从而有[lnU+y)]2彡lnU+.y).因此jj[ln(A:+y)]2(Jo-^+y)d(4)由于积分区域/)位于半平面丨(x,y)| .v+y彡e|内,故在Z)上有ln(x+y)彡1,从而:In(-v+)')]2彡In(:c+)').因此Jj^ 1 n(.r + y) ] 2dcr ^ Jln( x + y) da.i)a36.利用二重积分的性质估计下列积分的值:(1) / = |^7(文+7)心,其中/)= \ (x ,y)1,01|;n(2)/=j^sin^sin^do■,其中/)=j(A:,y)|0^^^TT,0^y^TT1;i)(3)/= J*(A:+y + l)d(7,其中/>= { {x,y) |0^x^l,0^j^2[;it(4)/=J(x2 +4y2 +9)do•,其中D= \{x,y) \x2 +y2 ^ 4|.I)解(1)在积分区域D上,0矣;<:矣1,0英y矣1,从而0矣巧•(*+y)矣2•又£»的面积等于1,因此(2)在积分区域/)上,0矣sin J:矣1,0^sin1,从而0彡sin2A:sin2y彡1,又0的面积等于TT2,W此(3)在积分K域"上有\^x+y +\«4,/)的而积等于2,因此(4)W为在积分K域/>»上有0矣;t2+y2苳4,所以有9^+4r2+9^4( x2+y2)+9矣25.34I)的酣枳等于4TT,W此36TT^[[(x2+4/+9)(Ur^lOO-ir.二重积分的计算法.^1.计算下列二甩积分:98{高等数学> (第七叛)下册习题全第十) ;,其中"是由两坐标轴及直线-- + =听围成的闭区域;b ( 3 J jj( x J + 3x 2 \ + v 3 ) da ,其中 D =( x , v )0 ^ A : ^ 1 .0 ^ v ^ 1;u( 4 ) jjxcas( X + Y j do ■,其中Z >是顶点分别为( 0 .0 j < 77 ,0 )和( 77 , 77 )的三角形闭区域. 4- 2 2 ) dx fh 2) D 可用不等式表示为 2 r 3xy +y 2 ]l~x dx = | (4 + 2x - 2x 2 ) dx 203(+ + 3 > (文3+ 3.2 +、、).+ + "JC di (4l )可用不等式表示为0 ^ V ^ A : ,0 ^ .t ^ 7T .于是|A :COS JC + ) = + ) d I [ sin (.t + y ) ]Q ()^ = J V ( sin 2.v - sin .v ) <1 x x(\( cos .v —丄(.<,s 2.v )卜(1X (-TT r T X cos .v —rus TT.& 2. _出枳分ix:域,斤i 卜r): v 列m 分:第十章重积分99 x2^y^J^,0矣x矣1(图10-2).0«^^/4-y2,-2矣7矣2(图10-3),(1)J^^do■,其中/)是由两条抛物线7=v^,y=*2所围成的闭区域;D(2)jfxy2dcr,其中D是由圆周x2+J2=4及y轴所围成的右半闭区域;I)(3)JV+'dcr,其中/)=I(%,)•)||A;|+|J|^1!;D(4)|"U2+/-x)<lo•,其中D是由直线y:l、y二xh :2*所围成的闭区域.D解(1)0可用不等式表示为于是(2)D可用不等式表示为(3)如阁I()-4,W=/\U"2,其中/>1= \(x,y)\-x-\ ^y^Jc + 1,-1 ^a;^0|,I)2=\(x,y) |*-1+因此100一、《高等数学》(第七版)下册习题全解Ea 3.如果二重积分|/( .r ,y )心办的被积函数/( x ,v )是两个函数/] ( O 及)的乘n积,即/(X ,y) = f\(x) ./“y ),积分区域/) = { (.V , y ) I (1 ^ V ^ />, r ^,证叫这个二重积分等于两个单积分的乘枳,即|*/|U) -/2(r) flatly = [ J/, (.v)(l.v] - [ [/:( > )^v]-证Jj./1 ( x ) • .,2 ( / ) dvd V ~ J [ f J \ ( v ) ■ ./: t ^] l ^x *在上式右端的第一次单枳分f /,(.V )•/2(.V )dv 中,./,(A .)1Jfut 变招:、无关,nn 见为 常数提到积分5外,W 此上式“端笏T第十章重积分101fix/ = j [ dy ^/(*,y )tk.而在这个积分中,由于f/2 (y ) d y 为常数,故又可提到积分号外,从而得到• f 2<,y)^xAy= [| /2(y )dj ] - [ J n /, (x )dx ]证毕.^4.化二重积分/ = Jf(x ,y )daI)为二次积分(分别列出对两个变量先后次序不同的两个二次积分),其中积分区域£>是:(1)由直线及抛物线y 2 =4x 所围成的闭区域;(2)由x 轴及半圆周/ +y 2 =r 2(y 英0)所围成的闭区域;(3)由直线y =x ,;c = 2及双曲线:K = ^-(*>0)所围成的闭区域;X(4)环形闭区域 IU ,y ) | 1+y 2^4(.解(1)直线y =x 及抛物线y 2 =4;c 的交点为(0,0)和(4,4)(图10-6).于是f(x,y)dy,(2)将/)用不等式表示'fyO^y^r 2 -x 2,- r ^ W /•,于是可将/化为如下的先对y 、后对*的二次积分:r/ = J (1文Jf(x ,y)(\y ;如将0叫不等式表示为~Vr 2 -y 2^x^Vr 2 - y 2 ,0各/•,则可将/化为如卜的先对*、后对y 的二次枳分:102一、《高等数学》(第七版)下册习题全解dr x,y) dx.(3)如图 10-7.:条边界曲线两两相交,先求得3个交点为(1 ,1 ),2,y 和(2,2).于是dy (i_/(^,y)+ tlj /( x ,y)dx.dx • \/4J\x y y)dy + d.vl(1%/T /(A :,y)clr +d.vl■ yA -x 2/(.r ,v )d > -f/(.v V v ) dv ./(.v ,v )d.v -f.\/4-、/( \ , > ) d.v -f厂、/4 -、•'•I-v^ W"/( v , y) (l .\.| dxj[f(x,y)dy.注本题说明,将二重积分化为二次积分时,需注意根据积分区域的边界曲线的情况,选取恰当的积分次序.本题中的积分区域/)的上、下边界曲线均分别由—个方程给出,而左边界曲线却分为两段,由两个不同的方程给出,在这种情况下采取先对y 、后对^的积分次序比较有利,这样只需做一个二次积分,而如果采用相反的枳 分次序则需计算两个二次积分.需要指出,选择积分次序时,还需考虑被积函数/U , y )的特点.具体例子n ]'见教材下册第144页上的例2.(4)将D 按图10 - 8( a )和图10 - 8( 1>)的两种不同方式則分为4块,分別得o 第十章重积分103x ,r)d.t.(5) (lx\ f{x,y)Ay\广2 f yix -x2(4)|叫2f{x,y)dy-,fix /-sin x(6)I Ax\J(x,y)Ay.JO J - siny图10-8,5.设/U,Y)在D上连续,其中/)是由直线;==所围成的闭区域,证明dx| f(x,y)Ay证等式两端的二次积分均等于二重积分J/U,y)d o•,因而它们相等.I)^6.改换下列二次积分的积分次序:(2) J) dj|:f(x,y)dx;解(丨)所给二次积分等于二重积分J[/U,;K)(^,其中o=丨h,y)1°^^^r-"0 ^ j ^ I(. /> n|■改写为 | Uj) | * 矣y矣 1,0 ^^ I | (罔 10 - 9),于是原式=丄<ixj/(x,y)dy.(2)所给一.次枳分等于二'Ti积分|/U,y)山,.K:中/)=I|.y2^^<2y,0^21. M I) njm为{u’y) I 音矣 j ^ 7^,0 ^ x 在4)( 1冬1 1(> - I0),W此原式=J,i\xjy/(x,y)i\y.104一、《高等数学>(第七版)下册习题全解-y2^.V ^1$、飞V彡1(3)所给二次积分等于二重积分.其中D=:(.v.v)|-V 1UX^J1-y2,0彡>•彡1;•又D可表示为:(JC,)*)丨0彡y 彡V 1- .r2,-1=(图10-11),因此f 1 f V1 -X~原式=J^dxj/(x,v)dy.(4)所给二次积分等于二重积分其中D=:(.v.v)'2-hs/lx -x1%\彡.r彡2:.又D可表示为:(A:,V)|2-1彡.t•彡1+Y1—v2,0:(图10-12),故原式=丄d)j f(x %y)dx.(5)所给二次积分等于二重积分]|/(.10)(1^,)1:中/)=1(.v.v)|0^v^I)x彡e|•又/)可表示为|(A:,>•)|e、彡A•彡e,0彡、彡1i(|劄10-1,故原式=L(I.、|,./X .、,.、)(l.v.(6)m1()-14,将积分|><:域/)丧示为/),U/)2,其中A),=j U,、)|arcsin>^o 第十章重积分105/(x,y)dx.y广 1r ir - arcsin >原式=I dyf(x y y)c\xJO Jarcsin )T T - arcsin y ,0彡 y 彡 1 | 1 ,D 2 = |(.r, y)一 2arcsin, 一1彡)'彡0|.于是rt-x + xydrAy~d\2x c\)''i x E | o»•Y = s i n A 的反闲数足A = i i r r s »M y- -1 x足ih y - H in x = sin ( T T - x) "n!J T T - x ^ arcKiny,从ifii 得反闲数 ^(子•中,TTT T - iin-Hiny.^7.设平面薄片所占的闭区域D 由直线;t = 2,y = 和;r 轴所围成,它的面密度/x (.t ,v ) = x 2 +y 2,求该薄片的质量.解 D 如图10-15所示.所求薄片的质M = jJ/Lt( x 9y) dcr = ^ dyj ( x 2 + y 2 ) dxr[+(2”)3+2,12| 冬| 10 - 158. i |灯|l |四个平而A : = 0,y = 0,;t = I ,v = I 所闲成的柱休被平面z = 0及2.r +3y+z6藏得的立休的体积.V - (I 6 - ^ x 2 + y 2 ) dx(\y6 ( 1 - x ) - x 2 +——f 1\1_6"*10-17m 10 - 18解江力一 E J .它??芪是;c 0:. S 二苎泛7:省•。
高等数学(同济第七版下)课后习题及解答
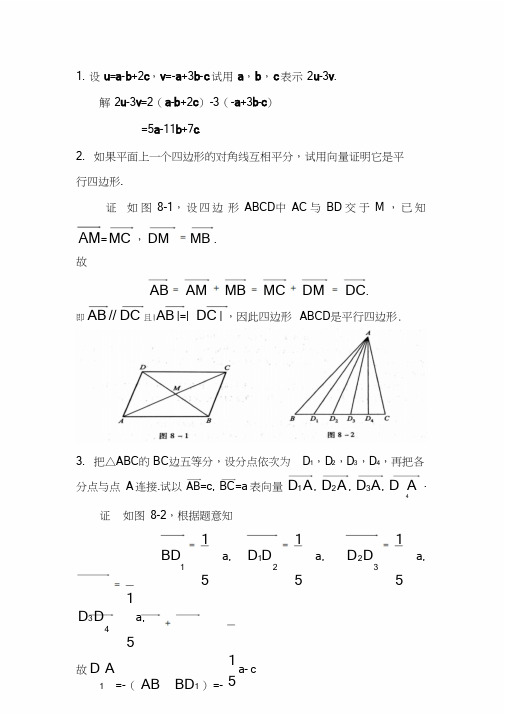
1.设u=a-b+2c,v=-a+3b-c.试用a,b,c表示2u-3v.解2u-3v=2(a-b+2c)-3(-a+3b-c)=5a-11b+7c.2.如果平面上一个四边形的对角线互相平分,试用向量证明它是平行四边形.证如图8-1,设四边形ABCD中AC与BD交于M,已知AM=MC,DM MB.故AB AM MB MC DM DC.即AB//DC且|A B|=|DC|,因此四边形ABCD是平行四边形.3.把△ABC的BC边五等分,设分点依次为D1,D2,D3,D4,再把各分点与点A连接.试以AB=c,BC=a表向量D1A,D2A,D3A,D A4.证如图8-2,根据题意知1 BD a,151D1D a,251D2D a,351 D3D a,45故D A1=-(AB BD1)=- 15a-cD2A=-(AB BD2)=- 25a-cD3A=-(AB BD3)=- 35a-cD4 A=-(AB BD)=-445a-c.4.已知两点M1(0,1,2)和M2(1,-1,0).试用坐标表示式表示向量M1M2及-2M1M2.解M1M2=(1-0,-1-1,0-2)=(1,-2,-2).-2M1M2=-2(1,-2,-2)=(-2,4,4).5.求平行于向量a=(6,7,-6)的单位向量.解向量a的单位向量为aa,故平行向量a的单位向量为a a =1(6,7,-6)=1167,,1111611 ,22 2其中a67(6)11.6.在空间直角坐标系中,指出下列各点在哪个卦限?A(1,-2,3),B(2,3,-4),C(2,-3,-4),D(-2,-3,1).解A点在第四卦限,B点在第五卦限,C点在第八卦限,D点在第三卦限.7.在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置:A(3,4,0),B(0,4,3),C(3,0,0),D(0,-1,0).解在坐标面上的点的坐标,其特征是表示坐标的三个有序数中至少有一个为零,比如xOy面上的点的坐标为(x0,y0,0),xOz面上的点的坐标为(x0,0,z0),yOz面上的点的坐标为(0,y0,z0).在坐标轴上的点的坐标,其特征是表示坐标的三个有序数中至少有两个为零,比如x轴上的点的坐标为(x0,0,0),y轴上的点的坐标为(0,y0,0),z轴上的点的坐标为(0,0,z0).A点在xOy面上,B点在yOz面上,C点在x轴上,D点在y轴上.8.求点(a,b,c)关于(1)各坐标面;(2)各坐标轴;(3)坐标原点的对称点的坐标.解(1)点(a,b,c)关于xOy面的对称点(a,b,-c),为关于yOz面的对称点为(-a,b,c),关于zOx面的对称点为(a,-b,c).(2)点(a,b,c)关于x轴的对称点为(a,-b,-c),关于y 轴的对称点为(-a,b,-c),关于z轴的对称点为(-a,-b,c).(3)点(a,b,c)关于坐标原点的对称点是(-a,-b,-c). 9.自点P(0x0,y0,z0)分别作各坐标面和各坐标轴的垂线,写出各垂足的坐标.解设空间直角坐标系如图8-3,根据题意,P0F为点P0关于xOz 面的垂线,垂足F坐标为(x0,0,z0);P0D为点P0关于xOy面的垂线,垂足D坐标为(,,0)x0y;P0E为点P0关于yOz面的垂线,垂足E坐标为(0),y0,z o.P0A为点P0关于x轴的垂线,垂足A坐标为(x o,0,0);P0B为点P0关于y轴的垂线,垂足B坐标为(0,y0,0);P0C为点P0关于z轴的垂线,垂足C坐标为(0,0,)z.10.过点P(0x0,y0,z0)分别作平行于z轴的直线和平行于xOy面的平面,问在它们上面的点的坐标各有什么特点?解如图8-4,过P0且平行于z轴的直线l上的点的坐标,其特点是,它们的横坐标均相同,纵坐标也均相同.而过点P0且平行于xOy面的平面上的点的坐标,其特点是,它们的竖坐标均相同.11.一边长为a的正方体放置在xOy面上,其底面的中心在坐标原点,底面的顶点在x轴和y轴上,求它各顶点的坐标.2 解 如图 8-5,已知 AB=a ,故 OA=OB=a2,于是各顶点的坐 22 2 标分别为 A0 0)(a ,, ,B ((0,a ,0)),C (-a222,0,0),D 2 (0,- a 2 2 ,0),E ( a 2 2 ,0,a ),F (0, a 2 2 ,a ),G (- a2, 2 0,a ),H (0,- a 2,a ). 12.求点 M (4,-3,5)到各坐标轴的距离 .2 2解 点 M 到 x 轴的距离为 d 1=( 3) 534,点 M 到 y 22轴 的 距 离 为 d 2=4541, 点 M 到 z 轴 的 距 离 为 22.d 3=4 ( 3) 25 513.在 yOz 面上,求与三点 A (3,1,2),B (4,-2,-2),C (0,5, 1)等距离的点 .解 所求点在 yOz 面上,不妨设为 P (0,y ,z ),点 P 与三点 A ,2y 2 z 2B ,C 等距离, PA 3( 1) ( 2) , PB2 y 2 z 4 ( 2)(2) 2,PC(y 2z1) 2 .5)(由 PAPBPC 知,2( 1)2 ( 2)2 42 (2)( 2)223yz yz2( 1)2( y 5)z ,即9 ( y 1) 9 ( y 1) 2 2 2 (z 2) 16 ( y 2) 22 2 (z 2) ( y 5)( z( z21) . 2 2), 解上述方程组,得 y=1,z=-2.故所求点坐标为( 0,1,-2). 14.试证明以三点 A (4,1,9),B (10,-1,6),C (2,4,3)为顶 点的三角形是等腰直角三角形 .证 由AB (10 24)( 1 1) 2( 6 29)7, AC (2 24)( 4 1)22(3 9)7,BC(2 210)(4 1) 2(3 26)98 7 2 222知.ABAC 及 BCABAC 故△ABC 为等腰直角三角形.15. 设已知两点为 M 1(4, 2 ,1),M 2(3,0,2),计算向量 M 1M 2的模、方向余弦和方向角 .解 向量M 1M=(3-4,0-2 ,2-1)=(-1,- 2 ,-1),2其模-1 2- 2 2 12 4 2M1M()().其方向余弦分2别为cos=- 12,cos=-22,cos=12.方向角分别为23,34,3.16.设向量的方向余弦分别满足(1)cos=0;(2)cos=1;(3)cos=cos=0,问这些向量与坐标轴或坐标面的关系如何?解(1)由cos=0得知,故向量与x轴垂直,平行于2yOz面.(2)由cos=1得知=0,故向量与y轴同向,垂直于xOz面.(3)由cos=cos=0知,故向量垂直于x轴和y轴,2即与z轴平行,垂直于xOy面.,求r在u轴上的投影.17.设向量r的模是4,它与u轴的夹角为3解已知|r|=4,则Prju r=|r|cos=4?cos 3 =4×12 =2.18.一向量的终点在点B(2,-1,7),它在x轴、y轴和z轴上的投影依次为4,-4和7,求这向量的起点A的坐标.解设A点坐标为(x,y,z),则AB=(2-x,-1-y,7-z),由题意知2-x=4,-1-y=-4,7-z=7,故x=-2,y=3,z=0,因此A点坐标为(-2,-3,0).19.设m=3i+4j+8k,n=2i-4j-7k和p=5i+j-4k.求向量a=4m+3n-p在x轴上的投影及在y轴上的分向量.解a=4m+3n-p=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k,a在x轴上的投影为13,在y轴上的分向量为7j.1.设a3i j2k,b i2j k,求(1)a b及a b;(2)(-2a)3b及a2b;(3)a,b的夹角的余弦.解(1)a b(3,-1,-2)(1,2,-1)31(-12-2-1 3)()(),i j ka b31 2=(5,1,7).12 1(2)(2a)3b6(a b)6318a2b2(a b)2(5,1,7)(10,2,14)(3 cos(a,b) aabb32(1)(2)12(1)222 232 3 31462212.设a,b,c为单位向量,满足a b c0,求a b b c c a.解已知a b c1,a b c0,故(a b c)(a b c)0.22 2即2220a b c a b b c c a.因此a b b c c a 122 2(a b c)2-323.已知M1(1,-1,2),M2(3,3,1)M3(3,1,3).求与M1M2,M2M3同时垂直的单位向量.解M1M2=(3-1,3-(-1),1-2)=(2,4,-1)M 2M=(3-3,1-3,3-1)=(0,-2,2)3由于 M 1M 2 M 2M 3 与M 1M 2,M 2M 3 同时垂直,故所求向量可取为a(M M1 2M M12M M23M M2)3,ij k 由M 1M 2 M 2M 3 =2 4 1 022=(6,-4,-4),M 1M M M2 232 6 ( 24) ( 24)68 2 17 132 2知). a(6, 4, 4)(, , 2 171717174. 设质量为 100kg 的物体从点 M1(3,1,8)沿直线移动到点 M2(1,4,2), 计算重力所作的功(坐标系长度单位为 m ,重力方向为 z 轴负方向).解M 1M 2 =(1-3,4-1,2-8)=(-2,3,-6)F=(0,0,-100×9.8)=(0,0,-980)W=F?M 1M 2 =(0,0,-980)?(-2,3 ,-6 )=588(0 J ).1处,有一与O P 1 5.在杠杆上支点 O 的一侧与点 O 的距离为 x 1 的点 P 成角 1 的力 F1作用着;在 O 的另一侧与点 O 的距离为 x 2 的点 P2处,有一与OP2成角2的力F2,F1,F2作用着(图8-6),问1,2,x1,x2符合怎样的条件才能使杠杆保持平衡?解如图8-6,已知有固定转轴的物体的平衡条件是力矩的代数和为零,又由对力矩正负符号的规定可得杠杆保持平衡的条件为F1x sin1F2x2sin20,1即F1x1sin1F2x2sin2.6.求向量a(4,-3,4)在向量b(2,2,1)上的投影.a b(4,3,4)(2,2,1) 6解 2Pr j b a.22 2b 322 17.设a(3,5,2),b(2,1,4),问与有怎样的关系,能使a b与z轴垂直?解a b=(3,5,-2)+(2,1,4)=(32,5,24).要a b与z轴垂直,即要(a b)(0,0,1),即(a b)?(0,0,1)=0,亦即(32,5,24)?(0,0,1)=0,故(24)=0,因此2时能使a b与z轴垂直.8.试用向量证明直径所对的圆周角是直角.证如图8-7,设AB是圆O的直径,C点在圆周上,要证∠ACB=,2 只要证明AC BC0即可.由AC BC=(AO OC)(BO OC)2AO BO AO OC OC BO OC =2 2=0AO AO OC AO OC OC.故AC BC,∠ACB为直角.9.已知向量a2i3j k,b i j3k和c i2j,计算:(1)(a b)c(a c)b(2)(a b)(b c)(3)(a b) c 解(1)a b(2,3,1)(1,1,3)8,a c(2,3,1)(1,2,0)8,(a b)c(a c)b8(1,2,0)8(1,1,3)(0,8,24)8i24k.(2)a b=(2,-3,1)+(1,-1,3)=(3,-4,4),b c=(1,-1,3)+(1,-2,0)=(2,-3,3),i j k(a b)(b c)344(0,1,1)j k.23323 1(3)(ab) c2. 1 1 3 12 010. 已知OA i 3k,OB j 3k ,求△OAB 的面积.解 由向量积的几何意义知1△OAB= OA OB S2,ij kOA OB 1 0 3 ( 3, 3,1) , 0 1 32 2OA OB( 3) ( 3) 119S△OAB19 211. 已知( , , ), ( , , ), ( , , )a a x a a bb b b cc c c ,试利用yzxyzxyz行列式的性质证明:(a b) c (b c) a (c a) baxa yazbxbybz证因为(), a b c bbbx y z (b c) acxcyczcxc yc zaxayazcx cy cz(c a) baxayaz,bxbybz而由行列式的性质知a x a y a zb x b y b zc x c y cz b x b y b z c x c y c z = a x a y a z ,故 c x c y c z a x a y a zb x b ybz(a b) c (b c) a (c a) b .12. 试用向量证明不等式:222222a 1aabbba ba b a b ,231231 12 23 3其中a 1,a 2 ,a 3,b 1,b 2,b 3 为任意实数 . 并指出等号成立的条件.证 设向量 a ( a 1,a ,a ),b (b 1,b 2,b 3).23由ab a b cos(a, b ) a b ,从而222222 a 1ba ba baaa bbb ,1 2 23 3121 233当a 1,a 2 ,a 3与b 1,b 2 ,b 3 成比例,即a1b1a 2b2a 3b3时,上述等式成立.1.求过点(3,0,-1)且与平面3x7y5z120平行的平面方程.解所求平面与已知平面3x7y5z120平行.因此所求平面的法向量可取为n=(3,-7,5),设所求平面为3x7y5z D0.将点(3,0,-1)代入上式得D=-4.故所求平面方程为3x7y5z40.2.求过点M0(2,9,-6)且与连接坐标原点及点M0的线段OM0垂直的平面方程.解OM(2,9,6.所求平面与0)O M垂直,可取n=OM0,0设所求平面方程为2x9y6z D0.将点M0(2,9,-6)代入上式得D=-121.故所求平面方程为2x9y6z1210.3.求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程.x1y1z 1解由021212 1,得x3y2z0,11112 1即为所求平面方程.注设M(x,y,z)为平面上任意一点,M(x,y,z)(i1,2,3)i为i i i平面上已知点.由()0,M1M M M M M即1213x x1 y y1z z1x 2 x1y2y1z2z10,x 3 x1y3y1z3z1它就表示过已知三点M i(i=1,2,3)的平面方程.4.指出下列各平面的特殊位置,并画出各平面:(1)x=0;(2)3y-1=0;(3)2x-3y-6=0;(4)x-3y=0;(5)y+z=1;(6)x-2z=0;(7)6x+5y-z=0.解(1)—(7)的平面分别如图8—8(a)—(g). (1)x=0表示yOz坐标面.1(2)3y-1=0表示过点(,00,)且与y轴垂直的平面.3(3)2x-3y-6=0表示与z轴平行的平面.(4)x-3y=0表示过z轴的平面.(5)y+z=1表示平行于x轴的平面.(6)x-2z=0表示过y轴的平面.(7)6x+5y-z=0表示过原点的平面.5.求平面2x2y z50与各坐标面的夹角的余弦.解平面的法向量为n=(2,-2,1),设平面与三个坐标面xOy,yOz,zOx的夹角分别为1,2,3.则根据平面的方向余弦知cosn kcos1n k(2,222,1)(0,0,1)21( 22)113,cos2cos nnii(2, 2,1)3(1,0,0)123,cos3 cos nnjj(2, 2,1)3(10,1,0)23.6.一平面过点(1,0,-1)且平行于向量a(2,1,1)和b(1,1,0),试求这个平面方程.解所求平面平行于向量a和b,可取平面的法向量i j kn a b211(1,1,3).110故所求平面为1(x1)1(y0)3(z1)0,即x y3z40.7.求三平面x3y z1,2x y z0,x2y2z3的交点.解联立三平面方程x3y z1,2x y z0,x2y2z 3.解此方程组得x1,y1,z 3.故所求交点为(1,-1,3). 8.分别按下列条件求平面方程:(1)平行于xOz面且经过点(2,-5,3);(2)通过z轴和点(-3,1,-2);(3)平行于x轴且经过两点(4,0,-2)和(5,1,7).解(1)所求平面平行于xOz面,故设所求平面方程为By D0.将点(2,-5,3)代入,得5B D0,即D5B.因此所求平面方程为By5B0,即y50.(2)所求平面过z轴,故设所求平面为Ax By0.将点(-3,1,-2)代入,得3A B0,即B3A.因此所求平面方程为Ax3Ay0,即x3y0.(3)所求平面平行于x轴,故设所求平面方程为By Cz D0. 将点(4,0,-2)及(5,1,7)分别代入方程得2C D0及B7C D0.C D2, B92D .因此,所求平面方程为9 2DDy z D0,2即9y z20.9.求点(1,2,1)到平面x2y2z100的距离.解利用点(,,)M0x y o z o到平面Ax By Cz D0的距离公式dA xABy2B2CzC2D1 2212 22212210 331.1.求过点(4,-1,3)且平行于直线x3y z21 51的直线方程.解所求直线与已知直线平行,故所求直线的方向向量s(2,1,5),直线方程即为x 4y1z 21 5 3 .2.求过两点M1(3,2,1)和M2(1,0,2)的直线方程.解取所求直线的方向向量s M1M(13,0(2),21)(4,2,1),2因此所求直线方程为x 3y2z4 2 1 1 .3.用对称式方程及参数方程表示直线x y z1,2x y z 4.解根据题意可知已知直线的方向向量i j ks111(2,1,3).21 1取x=0,代入直线方程得yzy z1,4.3 5解得.y,z这2 2样就得到直线经过的一点(3 50,,).因此直线的对称式方程为2 2x30y z22 1 352 .参数方程为x2t,y 32t ,z 523t.注由于所取的直线上的点可以不同,因此所得到的直线对称式方程或参数方程得表达式也可以是不同的.4.求过点(2,0,-3)且与直线x2y4z70,3x5y2z10垂直的平面方程.解根据题意,所求平面的法向量可取已知直线的方向向量,即i j kn s124(16,14,11),35 2故所求平面方程为16(x2)14(y0)11(z3)0.即16x14y11z650.5.求直线5x3x3y2y3zz91 00,与直线2x3x28yyzz23180,的夹角的余弦.解两已知直线的方向向量分别为i j k i j ks533(3,4,1),s221(10,5,10), 1 232138 1因此,两直线的夹角的余弦cos(cos s1,)s2 s1s1s2s22 332410(1)4252101(1025)2100.6.证明直线x 2yz2xyz7,7与直线3x2x6yy 3zz 08,平行.证已知直线的方向向量分别是i j k i j ks 1 121(3,1,5),s2363(9,3,15), 21121 1由s23s1知两直线互相平行.7.求过点(0,2,4)且与两平面x2z1和y3z2平行的直线方程.解所求直线与已知的两个平面平行,因此所求直线的方向向量可取i j ks n1 n102(201 32,3,1),故所求直线方程为x 2 0y2z3 14.注本题也可以这样解:由于所求直线与已知的两个平面平行,则可视所求直线是分别与已知平面平行的两平面的交线,不妨设所求直线为x2z a,y3z b.将点(0,2,4)代入上式,得a8,b10.故所求直线为x2z8,y3z10.8.求过点(3,1,-2)且通过直线x54y3z2 1的平面方程.解利用平面束方程,过直线x54y3z2 1的平面束方程为x4y3y 3(z)0,52 211将点(3,1,-2)代入上式得.因此所求平面方程为20x4y311y5220 23(z) 0,即8x9y22z590.9.求直线xxyy3zz0,与平面x y z10的夹角.i j k解已知直线的方向向量(2,4,2),s113平面11 1的法向量n(1,1,1).设直线与平面的夹角为,则sin cos(n, s) ssnn 2221244((1)22)21(2)((1) 21)( 21)0,即0.10.试确定下列各组中的直线和平面间的关系;(1)x3y4z27 3和4x2y2z3;(2)x3y2z7 和3x2y7z8;(3)x32y2z134和x y z 3.解设直线的方向向量为s,平面的法向量为n,直线与平面的夹角为,且s nsin cos(n,s).s n (1)s(2,7,3),n(4,2,2),sin ( 2) ( 2 2) ( 4 2 7) ( 7) 2 3 ( 2) 2 4 3 ( ( 2 2)2) ( 2) 20, 则0.故直线平行于平面或在平面上, 现将直线上的点 A (-3,-4,0)代入平面方程,方程不成立 .故点 A 不在平面上,因此直线不在平 面上,直线与平面平行 . (2)s(3, 2,7), n (3, 2,7),由于s n 或sin 2 3 3( 3 2) 2( 2) 2 7 ( 2)2 3 7 ( 7 2) 22 71,知,故直线与平面垂直 .2(3)s( 3,1, 4), n (1,1,1),由于s n 0或sin 2 3 3 2 1 1 ( 1 1 4) 2( 4) 2 1 1 2 1 21 0, 知0,将直线上的点 A (2,-2,3)代入平面方程,方程成立,即点 A 在平面上 .故直线在平面上 . 11.求过点(1,2,1)而与两直线x x2 yy z 1 0, 2x y z z 1 0xy z 00,和 平行的平面的方程.解 两直线的方向向量为i j k i j ks 1 121(1,2,3),s2211(0,1,1), 11111 1i j k取(1,1,1),n s s12 31 201 1则过点(1,2,1),以n为法向量的平面方程为1(x1)1(y2)1(z1)0,即x y z0.12.求点(-1,2,0)在平面x2y z10上的投影.解作过已知点且与已知平面垂直的直线.该直线与平面的交点即为所求.根据题意,过点(-1,2,0)与平面x2y z10垂直的直线为x 1 1y2z21,将它化为参数方程x1t,y22t,z t,代入平面方程得1t2(22t)(t)10,整理得2t.从而所求点(-1,2,0)在平面x2y z10上的3投影为(53,23,23).13.求点P(3,-1,2)到直线x2xy z 1y z 40,的距离.i j k解直线的方向向量(0,3,3).s11 121 1在直线上取点(1,-2,0),这样,直线的方程可表示成参数方程形式x 1, y 2 3t,z 3t.(1)又,过点 P (3,-1,2),以s (0, 3, 3)为法向量的平面方程为3(y 1) 3(z 2) 0,即y z 1 0.(2)将式(1)代入式(2)得11 3t,于是直线与平面的交点为 (1, , ),2 2 2故所求距离为 d (321) ( 1 1 2 ) 2 (2 3 2 ) 2322.14.设 M 0 是直线 L 外一点,M 是直线 L 上任意一点,且直线的方向向 量为s ,试证:点 M 0 到直线 L 的距离dM M ss.证 如图 8-9,点 M 0 到直线 L 的距离为 d.由向量积的几何意义知M 0 表示以 M 0M ,s 为邻边的平行四边形的面积 .而M s M 0Mss表示以 s为边长的该平面四边形的高, 即为点 M 0 到直线L 的距离.于是dM 0 Mss.15.求直线2x3x4yy z2z0,9 0在平面4x y z1上的投影直线的方程.解作过已知直线的平面束,在该平面束中找出与已知平面垂直的平面,该平面与已知平面的交线即为所求.设过直线2x3x4yy z2z0,9 0的平面束方程为2x4y z(3x y2z9)0,经整理得(23)x(4)y(12)z90. 由(23)4(4)(1)(12)10,得1311.代入平面束方程,得17x31y37z1170.因此所求投影直线的方程为17x31y37z1170,4x y z 1.16.画出下列各平面所围成的立体的图形.(1)x0,y0,z0,x2,y1,3x4y2z120;y(2).x0,z0,x1,y2,z4解(1)如图8-10(a);(2)如图8-10(b).1.一球面过原点及A(4,0,0),B(1,3,0)和C(0,0,-4)三点,求球面的方程及球心的坐标和半径.解设所求球面的方程为2()()2 22(x a)y b z c R,将已知点的坐标代入上式,得2b c R22 2a,(1)2b2c2R2(a4),(2)( 2b2c2R2a1)(3),(3)2b2(4c)2R2a,(4)联立(1)(2)得a2,联立(1)(4)得c2,将a2代入(2)(3)并联立得b=1,故R=3.因此所求球面方程为(x2y2z2)(1)(2) 2 9,其中球心坐标为(2,1,2),半径为3.2.建立以点(1,3,-2)为球心,且通过坐标原点的球面方程.解设以点(1,3,-2)为球心,R为半径的球面方程为(x1)2y z R22 2(3)(2),球面经过原点,故2R (021) ( 0 3)2 2(02) 14,从而所求球面方程为(x1)2(y3)2(z2)214.2y z x y z2 23.方程x2420表示什么曲面?解将已知方程整理成(x2y2z1)(2)( 1) 2 2(6) ,所以此方程表示以(1,-2,-1)为球心,以6为半径的球面.4.求与坐标原点O及点(2,3,4)的距离之比为1:2的点的全体所组成的曲面的方程,它表示怎样的曲面?解设动点坐标为(x,y,z),根据题意有2(x0) (y (x22) ( y220)3)((zz220)4)12,化简整理得(x 232y2z)(1)(43)2 (它表示以(23,1,43 2)为球心,以293为25.将xOz坐标面上的抛物线z5x 绕x轴旋转一周,求所生成的旋转曲面的方程.解以2z 22y代替抛物线方程z5x中的z,得22)2(y z5x,即y2z25x.注xOz面上的曲线F(x,z)0绕x轴旋转一周所生成的旋转2z2曲面方程为(,)0F x y.2z26.将xOz坐标面上的圆x9绕z轴旋转一周,求所生成的旋转曲面的方程.解以2y22z2x代替圆方程x9中的x,得9,( 2y22z2x)2y2z2即9.x2y27.将xOy坐标面上的双曲线4x936分别绕x轴及y轴旋转一周,求所生成的旋转曲面的方程.解以2z22y2y代替双曲线方程4936x中的y,得该双曲线绕x轴旋转一周而生成的旋转曲面方程为4 2y2z2 x9(2) 36,即4x29(y2z2)36.以2z22y2x代替双曲线方程4936x中的x,得该双曲线绕y轴旋转一周而生成的旋转曲面方程为4( 2z y22 2x)936,即4(x2z2)9y236.8.画出下列各方程所表示的曲面:2y2 a2a x2 2(1));(x)y((2)1;22492z2x(3)1;9 4(4)y2z0;(5)z2x2.解(1)如图8-11(a);(2)如图8-11(b);(3)如图8-11(c);(4)如图8-11(d);(5)如图8-11(e).9.指出下列方程在平面解析几何中和在空间解析几何中分别表示什么图形:(1)x2;(2)y x1;2y22y2(3)4;x(4)x 1.解(1)x2在平面解析几何中表示平行于y轴的一条直线,在空间解析几何中表示与yOz面平行的平面.(2)y x1在平面解析几何中表示斜率为1,y轴截距也为1的一条直线,在空间解析几何中表示平行于z轴的平面.2y2(3) 4x在平面解析几何中表示圆心在原点,半径为2的圆,在空间解析几何中表示母线平行于z轴,准线为2x2y4, z0的圆柱面.(4)x2y21在平面解析几何中表示以x轴为实轴,y轴为虚轴的双曲线,在空间解析几何中表示母线平行于z轴,准线为2 x2y1,的双曲柱面.z010.说明下列旋转曲面是怎样形成的:2y2z2x(1)1;49922y z2 (2)1;x4(3)x2y2z21;(4)(z a)2x2y2.2y2z22y2 xx解(1)1表示x Oy面上的椭圆 1绕x 499492z2 x轴旋转一周而生成的旋转曲面,或表示xOz面的椭圆 1绕49x轴旋转一周而生成的旋转曲面.2 22y z2y2(2) 1x表示xOy面上的双曲线x1绕y轴4 42y2旋转一周而生成的旋转曲面,或表示yOz面的双曲线 1z4绕y轴旋转一周而生成的旋转曲面.(3)x2y2z21表示xOy面上的双曲线x2y21绕x轴2z2旋转一周而生成的旋转曲面,或表示xOz面的双曲线 1x绕x轴旋转一周而生成的旋转曲面.(4)22 2(z a)x y表示x Oz面上的直线z x a或z x a绕z轴旋转一周而生成的旋转曲面,或表示yOz面的直线z y a或z y a绕z轴旋转一周而生成的旋转曲面.11.画出下列方程所表示的曲面:(1)4x2y2z24;(2)x2y24z24;2y2z x(3).349解(1)如图8-12(a);(2)如图8-12(b);(3)如图8-12(c);12.画出下列各曲面所围立体的图形:(1)z0,z3,x y0,x3y0,x2y21(在第一卦限内);222,22 2 x0,y0,z0,x y R y z R(在第一卦(2)限内).解(1)如图8-13所示;(2)如图8-14所示.1.画出下列曲线在第一卦限内的图形;(1)xy1,2;(2)zx y4 2 x0;y 2 ,(3)2x2x2y2z2a,2a.解(1)如图8-15(a);(2)如图8-15(b);(3)如图8-15(c).2.指出下列方程组在平面解析几何中与在空间解析几何中分别表示什么图形:(1)yy5x2x1,3;(2)2x4y2y3.91,解(1)yy5x2x1,3在平面解析几何中表示两直线的交点.在空间解析几何中表示两平面的交线,即空间直线.(2)2xy 32y91,2y2x在平面解析几何中表示椭圆 1与449 其切线y3的交点,即切点.在空间解析几何中表示椭圆柱面2y2 x49与其切平面y3的交线,即空间直线. 13.分别求母线平行于x轴及y轴而且通过曲线22x2x2y2z2z2y16,的柱面方程.解在22x2x2y2zy2z216,中消去x,得3 2z2y16,即为母线平行于x轴且通过已知曲线的柱面方程.在22x2xy2z2y2z216,中消去y,得2z23x 216,即为母线平行于y轴且通过已知曲线多的柱面方程.2y z2 2x与平面x z1的交线在xOy面上的投4.求球面9影的方程.解在2x2y2z 9, 中消去z,得x z 12y2x2x y2 2 x(1)9,即2x28,它表示母线平行于z轴的柱面,故2 22x2x yz08,表示已知交线在xOy面上的投影的方程.5.将下列曲线的一般方程化为参数方程:(1)2x(x1)y x;z0.2y2z 9, (2)2 2y ( z21) 4,。
高等数学同济第七版下册习题与答案完整版

高等数学同济第七版下册习题与答案完整版引言在学习高等数学课程中,习题是提高理解和掌握知识的重要方式。
然而,有时候我们在学习的过程中可能会遇到一些难题,不知道如何解答。
为了帮助同学们更好地学习和掌握高等数学知识,我们整理了高等数学同济第七版下册的习题与答案完整版,供大家参考。
第一章无穷级数习题1.11.讨论级数 $\\sum_{n=1}^{\\infty} \\frac{n^3 +2n}{(2n^2 + 3n - 4)^2}$ 的敛散性。
2.求级数 $\\sum_{n=1}^{\\infty} \\frac{(-1)^n}{n^2}$ 的和。
答案1.首先,我们将这个级数进行比较审敛法。
考虑到n3+2n的最高次项为n3,而(2n2+3n−4)2的最高次项为(2n2)2=4n4,因此我们可以得到 $\\frac{n^3 +2n}{(2n^2 + 3n - 4)^2} < \\frac{n^3 + 2n}{4n^4}$。
根据比较审敛法的基本原理,只需讨论 $\\sum_{n=1}^{\\infty} \\frac{n^3 + 2n}{4n^4}$ 的敛散性。
根据级数的性质,我们可以分别求前两项、前三项的和,并观察和的变化规律。
经过计算,可得前两项的和为 $\\frac{1}{16}$,前三项的和为 $\\frac{5}{96}$。
观察可以发现,当 n 的值逐渐增大时,和逐渐减小,并且趋于一个有限值。
因此,根据比较审敛法,原级数$\\sum_{n=1}^{\\infty} \\frac{n^3 + 2n}{(2n^2 + 3n - 4)^2}$ 也收敛。
2.我们可以使用交错级数的性质求解这个问题。
根据交错级数的性质,交错级数 $\\sum_{n=1}^{\\infty}\\frac{(-1)^n}{n^p}$ 的和为 $S = \\ln 2$,其中n=1。
对于这个问题,我们可以发现,级数$\\sum_{n=1}^{\\infty} \\frac{(-1)^n}{n^2}$ 的形式和交错级数一样,只是n=2。
高等数学同济第七版下课后习题及解答

高等数学同济第七版下课后习题及解答高等数学作为大学理工科专业的重要基础课程,对于培养学生的逻辑思维和解决问题的能力起着至关重要的作用。
而《高等数学》同济第七版更是被广泛使用的经典教材之一。
在学习过程中,课后习题是巩固知识、深化理解的重要环节。
下面,我们就来详细探讨一下这本教材下册的课后习题及解答。
首先,我们来了解一下这本教材下册所涵盖的主要内容。
下册主要包括多元函数微积分学、无穷级数、常微分方程等重要章节。
每个章节都配有丰富的习题,旨在帮助学生掌握相关的概念、定理和方法。
在多元函数微积分学部分,习题的类型多种多样。
有关于偏导数、全微分的计算,也有涉及多元函数极值和条件极值的问题。
例如,在计算偏导数时,学生需要熟练掌握对各个变量的求导法则,并且要注意函数的复合结构。
对于全微分的习题,需要理解全微分的定义以及其与偏导数的关系,通过练习能够准确地求出给定函数的全微分。
而在极值问题中,学生要学会运用拉格朗日乘数法,通过建立方程组来求解极值点。
无穷级数这一章节的习题则主要集中在级数的收敛性判别、函数展开成幂级数等方面。
对于级数的收敛性判别,需要掌握各种判别法,如比较判别法、比值判别法、根值判别法等。
在函数展开成幂级数的习题中,学生要熟悉常见函数的幂级数展开式,并能够运用相应的方法将给定的函数展开成幂级数。
常微分方程部分的习题包括一阶和二阶常微分方程的求解,以及线性微分方程解的结构等内容。
在求解一阶常微分方程时,要掌握分离变量法、一阶线性方程的求解公式等方法。
对于二阶常微分方程,要能够根据方程的特征根来确定通解的形式,并通过给定的初始条件求出特解。
接下来,我们谈谈如何有效地解答这些课后习题。
第一步,认真审题。
仔细阅读题目,理解题目所考查的知识点和要求。
明确题目中的已知条件和未知量,以及它们之间的关系。
第二步,回顾相关知识。
根据题目所涉及的知识点,迅速在脑海中回顾所学的概念、定理和方法。
如果对某些知识点感到模糊,应及时查阅教材进行复习。
同济大学高等数学第七版上下册答案详解

练习1-1
练习1-2
练习1-3
练习1-4
练习1-5
练习1-6
练习1-7
练习1-8
练习1-9
练习1-10
总习题一
练习2-1
练习2-2
练习2-3
练习2-4
练习2-5
总习题二
练习3-1
练习3-2
练习3-3
练习3-4
练习3-5
练习3-6
x
( 2)
2
(2 1)
1
(1 1)
1
(1 )
y
0
+
+
+
0
+
y
+
+
+
0
0
+
yf(x)
↘
17/5
极小值
↗
6/5
拐点
↗
2
拐点
↗
x
0
(0 1)
1
y
+
+
0
-
-
-
y
0
-
-
-
0
+
yf(x)
0
拐点
↗
极大值
↘
拐点
↘
x
1
y
+
+
+
0
-
-
-
y
+
0
-
-
-
0
+
yf(x)
↗
拐点
↗
1
极大值
↘
拐点
↘
x
( 1)
-1
高等数学(同济第七版)课后答案解析

当I V,w2时,s(!)=I - y(2-/)2=一£f2+ 2/-1 ,
当/>2HhS(f) =1.
放
/>2.
Q 16.求联系华氏温度(用F表示)和扱氏温度(用C表示)的转换公式.并求
(1)90叩的等价摄氏温度和-5 °C的等价华氏温度:
(2)是否存在一个温度值.使华氏温度汁和摄氏温度汁的读数是样的?如果存在,那么该温度值是多少?
xi
所以/(存)>/(%),即/(W在(0, + ao)内单调增加.
公5・设/U)为定义在(-/./)内的荷函数.若/(X)在(01)内单调増加,证明/(#)在(-L0)内也单凋増加.
证设-/<X, <X2<0,则0< “2 <-A,</,由/(、)是哉函数,從/g)V(X|)=-/(-知)+f(-旳)■因为/Xx)在(OJ)内单调増加.所以y(-X!)-/(-x2)>0.从而/(旳)>/(旳),即/(X〉在《・"0)内也単调增加.
解设尸.其中叽/,均为常数.
因为〃=32。相当于。=。。/ =212。相当于C= 100°.所以
7 "*=槌
故〃=1.80+32或C=扌(F-32).
(1)F=90°. C =刑90-32)52.2。.
C=-5。,F= 1.Xx(-5)+32= 23°.
(2)设温度値,符合题意.则有
/ = 1.8/ +32,I =-40.
尸銘EC
> =
y=•<>«< w
y=cotZ;
y=arcfiin lx I C1;
G2.卜列各题中,函数/(x)和g(x)是否相同?为什么”⑴/U) =lg/,g⑴=21gx;
同济大学数学系《高等数学》(第7版)(下册)复习笔记及课后习题和考研真题详解-第十章(圣才出品)

(1)若曲面 S 由方程 z=f(x,y)给出,D 为积分区域,且函数 f(x,y)在 D 上具
有连续偏导数 fx(x,y)和 fy(x,y),则曲面 S 的面积公式为
A
D
1
z x
2
z y
D
顶柱体的体积;
②当 f(x,y)<0 时, f x, y d 的绝对值等于以 D 为底,以曲面 z=f(x,y)
D
为顶的曲顶柱体的体积;
③当 f(x,y)在 D 上有正有负时, f x, y d 等于 xOy 面上方的柱体体积减去 xOy
D
面下方的柱体体积所得之差。
2.二重积分的性质
(1)设α与β为常数,则
sin
z z
其中ρ(0≤ρ<+∞),表示以 z 轴为轴的圆柱面;θ(0≤θ≤2π),表示为过 z 轴的半
平面;z(-∞<z<+∞),表示为与 xOy 面平行的平面,则柱面坐标形式的三重积分为
f x, y, z dxdydz F cos , sin , z dd dz
(3)利用球面坐标计算三频学习平台
第 10 章 重积分
10.1 复习笔记
一、二重积分的概念与性质
1.二重积分的概念
(1)定义
n
D
f x, y d
lim 0 i1
f i ,i i
(2)几何意义
①当 f(x,y)≥0 时, f x, y d 等于以 D 为底,以曲面 z=f(x,y)为顶的曲
Dxy={(x,y)|y1(x)≤y≤y2(x),a≤x≤b},则
f x, y, zdv
b
dx
y2 x dy
z2x,y f x, y, z dz
a
y1 x
同济大学数学系《高等数学》第7版笔记和课后习题含考研真题详解(无穷级数 下)【圣才出品】

k∈Z)
2.将下列函数 f(x)展开成傅里叶级数:
(1)f(x)=2sin(x/3)(-π≤x≤π) ;
(2)
f
(x)
ex ,
1,
x 0 0 x 。
解:(1)设φ(x)是 f(x)经周期延拓而得的函数,φ(x)在(-π,π)内连续,x
=±π是φ(x)的间断点。又φ(x)满足收敛定理的条件,故在(-π,π)内,它的傅里
cosnxdx
0
n
00
ab n
(1) n1
1 sin n
nx
0
a
n
b
(1) n1(
n 1, 2,
)
f(x)满足收敛定理的条件,而在 x=(2k+1)π(k∈z)处不连续,故
f
(x)
4
(a
b)
n1
1
(1)n n2
(b
a)
cos
nx
(1) n 1 (a n
b)
sin
nx
(x≠(2k+1)π,
an
n(1)n n2
e2 e2 4
(n 1, 2,)
f(x)满足收敛定理的条件,而在 x=(2k+1)π(k∈Z)处不连续,故
f
(x)
e2
e2
1
4
n1
(1)n n2 4
(2
cos
nx
n
sin
nx)
(x≠(2k+1)π,k∈Z)
(
3
)
a0
1
0 bxdx
axdx
(a b)
圣才电子书 十万种考研考证电子书、题库视频学习平台
同济大学数学系《高等数学》第 7 版笔记和课后习题含考研真题详解 第 12 章 无穷级数 下
高等数学(同济第七版下)课后习题及解答

高等数学(同济第七版下)课后习题及解答高等数学(同济第七版下)课后习题及解答一、函数与极限1. 已知函数 f(x) = x^2 + 3x - 2, 求以下极限:(1) lim(x→2) f(x)(2) lim(x→-1) f(x)解答:(1) 当x → 2 时,f(x) = x^2 + 3x - 2 = 2^2 + 3(2) - 2 = 12所以,lim(x→2) f(x) = 12(2) 当x → -1 时,f(x) = (-1)^2 + 3(-1) - 2 = -2所以,lim(x→-1) f(x) = -22. 求以下极限:(1) lim(x→0) (sin3x)/(sin4x)(2) lim(x→∞) (x^2 - 2x)/(x - 1)解答:(1) 利用极限的性质,lim(x→0) (sin3x)/(sin4x)= lim(x→0) (3x)/(4x) = 3/4(2) 利用极限的性质,lim(x→∞) (x^2 - 2x)/(x - 1)= lim(x→∞) x(x - 2)/(x - 1) = ∞二、导数与微分1. 求以下函数的导数:(1) y = x^3 + 2x^2 - 3x + 1(2) y = sin(2x) + cos(3x)(3) y = e^x/(1 + e^x)解答:(1) y' = 3x^2 + 4x - 3(2) y' = 2cos(2x) - 3sin(3x)(3) 利用商链规则和指数函数的导数性质,y' = e^x/(1 + e^x) - e^x*e^x/(1 + e^x)^2= e^x/(1 + e^x) - (e^x)^2/(1 + e^x)^2= e^x(1 - e^x)/(1 + e^x)^22. 求以下函数的微分:(1) y = 3x^2 + 4x - 2(2) y = sin(3x) + cos(2x)(3) y = ln(x) + e^x解答:(1) dy = (6x + 4)dx(2) dy = 3cos(3x)dx - 2sin(2x)dx(3) 利用对数函数和指数函数的微分性质,dy = (1/x)dx + e^xdx三、定积分与不定积分1. 求以下定积分:(1) ∫[0,1] (x^2 + 2x)dx(2) ∫[π/4,π/2] sinx dx解答:(1) ∫[0,1] (x^2 + 2x)dx = (1/3)x^3 + x^2 |[0,1]= (1/3)(1)^3 + (1)^2 - (1/3)(0)^3 - (0)^2= 4/3(2) 利用不定积分的基本公式,∫ sinx dx = -cosx∫[π/4,π/2] sinx dx = [-cosx] |[π/4,π/2] = -cos(π/2) - (-cos(π/4)) = -1 + √2/2 = √2/2 - 12. 求以下不定积分:(1) ∫(x^2 + 2x)dx(2) ∫sinx dx解答:(1) ∫(x^2 + 2x)dx = (1/3)x^3 + x^2 + C(2) ∫sinx dx = -cosx + C四、级数1. 判断以下级数的敛散性:(1) ∑(n=1,∞) (1/n)(2) ∑(n=1,∞) (1/2)^n解答:(1) 这是调和级数,已知调和级数∑(n=1,∞) (1/n) 发散。
(2021年整理)高等数学同济第七版7版下册习题全解

(完整版)高等数学同济第七版7版下册习题全解编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)高等数学同济第七版7版下册习题全解)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)高等数学同济第七版7版下册习题全解的全部内容。
(完整版)高等数学同济第七版7版下册习题全解编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望(完整版)高等数学同济第七版7版下册习题全解这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈(完整版)高等数学同济第七版7版下册习题全解> 这篇文档的全部内容。
数,故/, = Jj( x2 + y1)3d(j = 2jj(x2+ y1) 3dcr。
fh i)i又由于D3关于;t轴对称,被积函数(/ +r2)3关于y是偶函数,故jj(x2+j2)3dcr =2j(x2+y2)3da=2/2.Dy 1):从而得/, = 4/2。
(2)利用对称性来计算二重积分还有以下两个结论值得注意:如果积分区域关于^轴对称,而被积函数/(x,y)关于y是奇函数,即fix, —y)= -f(x,y),PJjf/(x,y)da =0;D如果积分区域D关于:K轴对称,而被积函数/(x,y)关于:c是奇函数,即/(~x,y) = -/(太,y),则=0.D«3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从而得
+ j2 ) 3dcr = 2j( x2 + y 2 ) 3 d a = 2/ 2 .
Dy
1 ):
/, = 4/2. (2) 利用对称性来计算二重积分还有以下两个结论值得注意:
如 果 积 分 区 域 关 于 ^ 轴 对 称 , 而 被 积 函 数 / ( x, y) 关 于 y 是 奇 函 数 , 即 fix , - y ) = -f(x,y) ,PJ
J(.r + y) \lrx ^ J (.\ + v)
..
.
0
D
( 2 ) 由 于 积 分 区 域 0 位 于 半 平 面 | (A:,V) | .V + • 、彡 1 1 内 , 故 在
/ ) | : & (.f + y) 2 彡(A + y) 3 • 从『("• J( v + > ):drr ^ jj ( x + y) \lfr.
f( x, y) i\a = jjf( x, y)da+ JJ/ ( xfy)
da.
p,un}
V,
n;
Sa4 . 试 确 定 积 分 区 域 / ) , 使 二 重 积 分 ][(1 - 2x2 - y2) d« ly 达 到 最 大 值 . I) 解 由 二 重 积 分 的 性 质 可 知 ,当 积 分 区 域 / > 包 含 了 所 有 使 被 积 函 数 1 - 2. v2 - V2 大
i)
a
3 6. 利 用 二 重 积 分 的 性 质 估 计 下 列 积 分 的 值 :
i)
1
n
= A lim y/ ( ^ ( , i7, ) A( 7- , = k \ \ f{ x, y) Aa.
A-° 台
• {!
( 3 ) 因 为 函 数 / U, y) 在 闭 区 域 / ) 上 可 积 , 故 不 论 把 £ » 怎 样 分 割 , 积 分 和 的 极
限总 是不变的.因此在分割 D时 , 可 以 使 和 / ) 2的公共边界永远是一条分割线.这样
b\
lh
..
.
尤 公 共 内 点 的 WK 域 .
证 ( 丨 ) 由 于 被 枳 函 数 . / U, y) = 1 , 故 山 二 t 积 分 定 义 得ltr = Hm y^/( ,rji) A<r, = lim ^ Ac, = l i m cr = a. A—0
n
( 2 ) Ji/ ( x, j) ( Ic7 = lim ^
..
.
( 3 ) 由 于 积 分 区 域 D 位 于 条 形 区 域 1 U, y) | 1 彡 1 + 7 彡 2 丨 内 , 故 知 区 域 / ) 上 的 点 满 足 0 彡 InU+ y) 彡 1, 从 而 有 [ lnU+ y) ] 2 彡 lnU+ . y ) . 因 此
jj[ ln( A: + y) ] 2( Jo- ^ + y)d
D
I)
1 所围成;
( 2 ) J(x + 7) 2 如 与 ■ , 其 中 积 分 区 域 0 是 由 圆 周 ( . r- 2)2 + ( . v- l)2 =
t)
n
2 所围成;
( 3 ) I'M A; + y) ( lor 与 ! " [ In( X + y) ] 2 ( 1 ( 7 , 其 中 Z> 是 三 角 形 闭
于 等 于 零 的 点 , 而 不 包 含 使 被 积 函 数 1 - 2/ - y2 小 于 零 的 点 , 即 当 £ » 是 椭 圆 2/ + y2
= l 所围的平面闭区域时,此二重积分的值达到最大.
& 5.根据二重积分的性质,比较下列积分的大小:
( 1 ) Ju+ y) 2 山 7 与 J[ U, 其 中 积 分 区 域 D 是 由 x 轴 、 ^ 轴 与 直 线 A + . 、 =
IJ
( 2) J J / c / ( X , y) drr = Aj| y’ ( A: , y) do■ ( 其 中 A: 为 常 数 ) ;
o
n
,
(3 ) JJ/( x,y)clcr = JJ/( x,y)drr + jJ/( x ,y) dcr
其中 /) = /)! U /)2, ,
A 为两个
I)
jf/ ( x, y)da = 0;
D
如 果 积 分 区 域 D 关 于 : K 轴 对 称 , 而 被 积 函 数 / ( x, y) 关 于 : c 是 奇 函 数 , 即
/ ( ~ x, y) = - / ( 太 , y) , 则
= 0. D « 3.利用二重积分定义证明:
(1 ) jj da = ( 其 中 ( 7 为 的 面 积 ) ;
y 2
D2
-1 O i T
-2 图 10 - 1
数,故
/ , = J j ( x 2 + y 1 ) 3d ( j = 2jj( x2 + y 1 ) 3 d c r .
fh
i)i
又 由 于 D3 关 于 ; t 轴 对 称 ,被 积 函 数 ( / + r2) 3 关 于 y 是 偶 函 数 ,故 jj( x 2
K 域,三顶点分别为
l)
"
(1,0),(1,1),(2,0);
( 4 ) Jpn(:r + y) dcr 与 In(:t + y) ] 2fW, 其 中 / ) = | (.r , . v) | 3 ,
0 彡、彡 1 .
i)
i)
解 ( 1) 在 积 分 K 域 0 上 , 故 有
(x + j) 3 ^ (x + y) 2. 根 据 二 重 积 分 的 性 质 4 ,可 得
( 4 ) 由 于 积 分 区 域 / ) 位 于 半 平 面 丨 ( x, y) | . v+ y 彡 e| 内 ,故 在 Z) 上 有 ln( x+ y) 彡 1, 从 而 :In (-v + ) ' ) ] 2 彡 In (:c + ) ' ) . 因 此
Jj^ 1 n(.r + y) ] 2dcr ^ Jln( x + y) da.
fix. y) 在 A U D 2 上 的 积 分 和 就 等 于 & 上 的 积 分 和 加 D2 上 的 积 分 和 , 记 为
^/(^, ,17,) ACT, = ^/( ^, , 17,) ACT, + ^/(^, ,17,) ACT,.
/)(U0,
",
l):
令 所 有 的 直 径 的 最 大 值 A- 0, 上 式 两 端 同 时 取 极 限 , 即 得 J
