专题52 巧用图形的旋转解决几何问题(解析版)

合集下载

巧“旋转”,妙解题

内一点，且 # + ) * - $ + ) # ，求证：
解析：虽然题目中相等的元素集中在 A + * ) 和
A + # ) 中，但无法证明 A + * ) 和 A + # ) 全等，所以需要
把条件转移之后再利用，
例3 如图5 ，菱形A # C& 中，' 、（分别为# C 、C& 上的
点，且 # # 'A (*60。，求证:A '*A (+
ALeabharlann A解析：如图 6 ，连接A C ，证明 A A # ' ! A A C ((A S A ) 即可!
事实上，A A C ( 可以看成是 A A # ' 绕点A 逆时针旋转60。而成的，其实旋转为我们认识全等提供了一个新的角度，即从动态的角度来重新认识全等.观察图2 、图 4,我们可以发现旋转必然会产生 “有公共顶点的等线段图形（线段和中点、等腰三角形、菱形、正方形等），反之，“有公共顶点的等线段图形（线段的中点、等腰三角形、菱形、正方形等）中必然隐藏着旋转型全等，我们只需找到它们，问题便随之解决.
2018年 2 月
巧 “旋转”，妙解题
! ! 东省烟台市教育科学研究院辛珍文
图形的旋转是《义务教育数学课程标准(2011年版 )》规定的学习内容，旋转变换在初中几何中占据非常重要的地位，它贯穿于三角形、四边形、圆等几乎所有重要的几何内容之中，在近几年的中考试题中所占的比重不断上升，是中考的热点，而且相关试题往往构思巧妙，令人耳目一新，学生在解决这类问题时倍感困难，经常没有头绪.本文试图从三个层次来帮助学生掌握旋转的特征，以期帮助学生抓住旋转的规律，从而轻松解决问题.

巧用旋转法解几何题资料讲解

巧用旋转法解几何题将一个图形绕着某一点旋转一个角度的图形变换叫做旋转，由旋转的性质可知旋转前后的图形全等，对应点到旋转中心的连线所组成的夹角等于旋转角。

旋转法是在图形具有公共端点的相等的线段特征时，可以把图形的某部分绕相等的线段的公共端点，旋转另一位置的引辅助线的方法，主要用途是把分散的元素通过旋转集中起来，从而为证题创造必要的条件。

旋转方法常用于等腰三角形、等边三角形及正方形等图形中。

现就旋转法在几何证题中的应用举例加以说明，供同学们参考。

例1．如图,在Rt△ABC中，∠C=90°，D是AB的中点，E，F分别AC和BC上，且DE⊥DF，求证：EF2=AE2+BF2分析：从所证的结论来看，令人联想到勾股定理，但注意到EF，AE，BF三条线段不在同一个三角形中，由于D是中点，我们可以考虑以D为旋转中心，将BF旋转到和AE相邻的位置，构造一个直角三角形，问题便迎刃而解。

证明：延长FD到G，使DG=DF，连接AG，EG∵AD=DB，∠ADG=∠BDF∴⊿ADG≌⊿BDF（SAS）∴∠DAG=∠DBF，BF=AG∴AG∥BC∵∠C=90°∴∠EAG=90°∴EG2=AE2+AG2=AE2+BF2∵DE⊥DF∴EG=EF∴EF2=AE2+BF2例2，如图2，在⊿ABC中，∠ACB=90°，AC=BC，P是⊿ABC内一点，且PA=3，PB=1，PC=2，求∠BPC的度数.分析：题目已知条件中给出了三条线段的长度和一个直角，但已知的三条线段不在同一三角形中，故可考虑通过旋转变换移至一个三角形中，由于⊿ACB是等腰直角三角形，宜以直角顶点C为旋转中心。

解：作MC⊥CP，使MC=CP，连接PM，BM∵∠ACB=90°，∠PCM=90°∴∠1=∠2∵AC=BC ， ∴⊿CAP ≌⊿CBM （SAS ）∴MB=AP=3∵PC=MC ，∠PCM=90°∴∠MPC=45°由勾股定理PM==22MC PC =22PC =22，在⊿MPB 中，PB 2+PM 2=（22）2+12=9=BM 2∴⊿MPB 是直角三角形∴∠BPC=∠CPM+∠MPB=45°+90°=135°例3，如图3，直角三角形ABC 中，AB=AC ，∠BAC=90°,∠EAF=45°，求证：EF 2=BE 2+CF 2分析：本题求证的结论和例1十分相似，无法直接用勾股定理，可通过旋转变换将BE ，CF 转移到同一个直角三角形中，由于⊿BAC 是等腰直角三角形，不妨以A 为旋转中心，将∠BAE 和∠CAF 合在一起，取零为整。

初中数学《几何旋转》重难点模型汇编(四大题型)含解析

专题旋转重难点模型汇编【题型1手拉手模型】【题型2“半角”模型】【题型3构造旋转模型解题】【题型4奔驰模型】【题型5费马点模型】【题型1手拉手模型】1如图1，在△ABC中，∠A=90°，AB=AC=2，点D、E分别在边AB、AC上，且AD=AE=2-2，连接DE．现将△ADE绕点A顺时针方向旋转，旋转角为α0°<α<360°，分别连接CE、BD．(1)如图2，当0°<α<90°时，求证：CE=BD；(2)如图3，当α=90°时，延长CE交BD于点F，求证：CF垂直平分BD；(3)连接CD，在旋转过程中，求△BCD的面积的最大值，并写出此时旋转角α的度数．【答案】(1)见解析(2)见解析(3)△BCD的面积的最大值为3-2，旋转角α=135°【详解】(1)证明：由题意得，AB=AC，AD=AE，∠CAB=∠EAD=90°，∵∠CAE+∠BAE=∠BAD+∠BAE=90°，∴∠CAE=∠BAD，在△ACE和△ABD中，AC =AB∠CAE =∠BAD AE =AD，∴△ACE ≌△ABD SAS ，∴CE =BD ；(2)证明：根据题意：AB =AC ，AD =AE ，∠CAB =∠EAD =90°，在△ACE 和△ABD 中，AC =AB∠CAE =∠BAD AE =AD∴△ACE ≌△ABD SAS ，∴∠ACE =∠ABD ，∵∠ACE +∠AEC =90°，且∠AEC =∠FEB ，∴∠ABD +∠FEB =90°，∴∠EFB =90°，∴CF ⊥BD ，∵AB =AC =2，AD =AE =2-2，∠CAB =∠EAD =90°，∴BC =AB 2+AC 2=2，CD =AC +AD =2，∴BC =CD ， ∵CF ⊥BD ，∴CF 是线段BD 的垂直平分线；(3)解：在△BCD 中，边BC 的长是定值，则BC 边上的高取最大值时，△BCD 的面积有最大值，∴当点D 在线段BC 的垂直平分线上时，△BCD 的面积取得最大值，如图，∵AB =AC =2，AD =AE =2-2，∠CAB =∠EAD =90°，DG ⊥BC ，∴AG =12BC =1，∠GAB =45°，∴DG =AG +AD =3-2，∠DAB =180°-45°=135°，∴△BCD 的面积的最大值为：12BC ⋅DG =12×2×3-2 =3-2，此时旋转角α=135°．【点睛】本题是几何变换综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质，垂直平分线的判定和性质等知识，寻找全等三角形，利用数形结合的思想解决问题是解题关键．2如图1，在Rt △ABC 中，∠C =90°，AC =BC =2，D ，E分别为AC ,BC 的中点，将△CDE 绕点C 逆时针方向旋转得到△CD E (如图2)，使直线D E 恰好过点B ，连接AD ．(1)判断AD 与BD 的位置关系，并说明理由；(2)求BE 的长；(3)若将△CDE绕点C逆时针方向旋转一周，当直线D E 过Rt△ABC的一个顶点时，请直接写出BE 长的其它所有值．【答案】(1)AD ⊥BD ，见详解(2)14-22(3)2+142或14-2 2【详解】(1)解：AD 与BD 的位置关系为AD ⊥BD ．∵AC=BC，D，E分别为AC,BC的中点，∴CD=CE，即CD =CE ，∵∠C=90°，即∠BCA=∠D CE =90°，∴∠ACD =∠BCE ,∴△CD A≌△CE B，∴∠CE B=∠CD A，∵∠C=90°，CD =CE ，AC=BC，∴∠CD E =∠CE D =∠CAB=∠CBA=45°，∴∠CE B=∠CD A=135°，∴∠AD B=135°-45°=90°，即：AD ⊥BD ．(2)解：Rt△ACB中，AC=BC=2，∴BA=AC2+BC2=22，同理可求D E =2，∵△CD A≌△CE B，∴AD =BE ，设AD =BE =x，在Rt△AD B中，由勾股定理得：x2+2+x2=222，解得：x=14-22(舍负)，∴BE =14-22．(3)解：①经过点B 时，题(2)已求BE =14-22；②经过点A 时，如图所示，同理可证：△CD A ≌△CE B ，∴∠D AC =∠E BC ，BE =AD∵∠1=∠2，∴∠AE B =∠BCA =90°，设BE =AD =x ，在Rt △AE B 中，由勾股定理得：x 2+x -2 2=22 2，解得：x =2+142(舍负)，即：BE =2+142；③再次经过点B 时，如下图：同理可证：△CD A ≌△CE B ，AD ⊥BE ，设BE =AD =x ，在Rt △AD B 中，由勾股定理得：x 2+x -2 2=22 2，解得：x =2+142(舍负)，即：BE =2+142；综上所述：BE =2+142或BE =14-22．【点睛】本题考查了旋转的性质，全等三角形的判定与性质，勾股定理等的应用，正确熟练掌握知识点是解题的关键．3如图，△ABC 和△DCE 都是等腰直角三角形，∠ACB =∠DCE =90°．(1)【猜想】如图1，点E 在BC 上，点D 在AC 上，线段BE 与AD 的数量关系是，位置关系是；(2)【探究】：把△DCE 绕点C 旋转到如图2的位置，连接AD ，BE ，(1)中的结论还成立吗？说明理由；(3)【拓展】：把△DCE 绕点C 在平面内自由旋转，若AC =6，CE =22，当A ，E ，D 三点在同一直线上时，直接写出BE的长．【答案】(1)BE=AD，BE⊥AD(2)(1)中的结论成立，理由见解析(3)42-2或42+2【详解】(1)解：∵△ABC和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，∴BC=AC，EC=DC，∠ACB=90°，∴BC-EC=AC-DC，∴BE=AD，∵∠ACB=90°，∴BE⊥AD，故答案为：BE=AD，BE⊥AD；(2)解：(1)中结论仍然成立，理由：由旋转知，∠BCE=∠ACD，∵BC=AC，EC=DC，∴△BCE≌△ACD，∴BE=AD，∠CBE=∠CAD，∵∠ACB=90°，∴∠CBE+∠BHC=90°，∴∠CAD+∠BHC=90°，∵∠BHC=∠AHG，∴∠CAD+∠AHG=90°，∴∠AGH=90°，∴BE⊥AD；(3)解：①当点E在线段AD上时，如图3，过点C作CM⊥AD于M，∵△DCE是等腰直角三角形，且CE=22，∴DE=CE2+CD2=4，∵CM⊥AD，DE=2，∴CM=EM=12在Rt△ACM中，AC=6，∴AM=AC2-CM2=42，∴AE=AM-EM=42-2，在Rt△ACB中，AC=6，AB=AC2+AB2=62，在Rt△ABE中，BE=AB2-AE2=42+2；②当点D在线段AE上时，如图4，过点C作CN⊥AE于N，∵△DCE是等腰直角三角形，且CE=22，∴DE=CE2+CD2=4，∵CN⊥AD，DE=2，∴CN=EN=12在Rt△ACN中，AC=6，∴AN=AC2-CN2=42，∴AE=AN+NE=42+2，在Rt△ACB中，AC=6，AB=AC2+AB2=62，在Rt△ABE中，BE=AB2-AE2=42-2；综上，BE的长为42-2或42+2．【点睛】此题是几何变换综合题，主要考查了等腰直角三角形的性质，旋转的性质，全等三角形的判定和性质，勾股定理，作出辅助线构造出直角三角形是解本题的关键．4已知：如图1，△ABC中，AB=AC∠BAC=60°，D、E分别是AB、AC上的点，AD=AE，不难发现BD、CE的关系．(1)将△ADE绕A点旋转到图2位置时，写出BD、CE的数量关系；(2)当∠BAC=90°时，将△ADE绕A点旋转到图3位置．①猜想BD与CE有什么数量关系和位置关系?请就图3的情形进行证明；②当点C、D、E在同一直线上时，直接写出∠ADB的度数．【答案】(1)BD=CE(2)①BD=CE，BD⊥CE，证明见解析，②45°或135°【详解】(1)∵∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，在△BAD和△CAE中，AB=AC，∠BAD=∠CAE，AD=AE，水不撩不知深浅∴△BAD≌△CAE SAS∴BD=CE；(2)①BD=CE，BD⊥CE，证明：如图，BD交AC于点F，交CE于点M，∵∠BAC=∠DAE=90°，∴∠BAC+∠DAC=∠DAE+∠DAC，即∠BAD=∠CAE，在△BAD和△CAE中，AB=AC，∠BAD=∠CAE，AD=AE，∴△BAD≌△CAE SAS∴BD=CE，∠ABD=∠ACE，在△BAF和△CMF中，∵∠ABD=∠ACE，∠AFB=∠MFC，∴∠FMC=∠FAB，∵∠BAC=90°，∴∠FMC=90°，∴BD⊥CE，因此BD=CE，BD⊥CE；②如图，当点 C、D、E 在同一直线上，且点D在线段CE上时，如图I所示，在等腰Rt△ADE中，∠ADE=45°，∵BD⊥CE，∴∠EDB=90°，∴∠ADB=∠EDB-∠ADE=45°；当点 C、D、E 在同一直线上，且点E在线段DE上时，如图II所示，在等腰Rt△ADE中，∠ADE=45°，∵BD⊥CE，∴∠EDB=90°，∴∠ADB =∠EDB +∠ADE =135°；故∠ADB 的度数为：45°或135°．5△ABC是等腰直角三角形，点D 是△ABC 外部的一点，连接AD ，AB =AC =2AD =6，将线段AD 绕点A 逆时针旋转90°得到线段AE ，连接ED ，CE ，BD ．(1)如图1，当点D 在线段EC 上时，线段EC 与线段BD 的数量关系是，位置关系是；(2)如图2，线段EC 交BD 于点P ，此时(1)中线段EC 与线段BD 的关系是否依然成立，请说明理由；(3)如图3，线段EC 交BD 于点P ，点Q 是AC 边的中点，连接DC ，PQ ，当DC =32时，求PQ 的长．【答案】(1)BD =CE ，BD ⊥CE(2)(1)中线段EC 与线段BD 的关系是否依然成立，理由见解析(3)PQ 的长为32【详解】(1)解：BD =CE ，BD ⊥CE ，理由如下：∵△ABC 是等腰直角三角形，∴∠BAC =90°，AB =AC ，∵将线段AD 绕点A 逆时针旋转90°得到线段AE ，∴∠DAE =90°，AE =AD ，∴∠BAD =∠CAE ，在△ABD 与△ACE 中，AB =AC∠BAD =∠CAE AD =AE，∴△ABD ≌△ACE ，∴BD =CE ，∠ABD =∠ACE ，∴∠ACE +∠DBC +∠ACB =∠ABD +∠DBC +∠ACB =∠ABC +∠ACB =90°，∴∠BDC =90°，∴BD ⊥CE ；故答案为：BD =CE ，BD ⊥CE ；(2)解：(1)中线段EC 与线段BD 的关系依然成立；理由：∵△ABC 是等腰直角三角形，∴∠BAC =90°，AB =AC ，∵将线段AD 绕点A 逆时针旋转 90° 得到线段AE ，∴∠DAE=90°，AE=AD，∴∠BAD=∠CAE，在△ABD与△ACE中，AB=AC∠BAD=∠CAE AD=AE，∴△ABD≌△ACE，∴BD=CE，∠ABD=∠ACE，∴∠ACE+∠DBC+∠ACB=∠ABD+∠DBC+∠ACB=∠ABC+∠ACB=90°，∴∠BPC=90°，∴BD⊥CE；(3)解：连接PQ，∵将线段AD绕点A逆时针旋转90°得到线段AE，∴∠DAE=90°，AE=AD=3，∴DE=2AD=32，∵DC=32，∴DE=CD，由(2)知BD⊥CE，∴EP=CP，∵点Q是AC边的中点，∴PQ=12AE=32．【点睛】本题考查了全等三角形的判定和性质，等腰直角三角形性质，旋转的性质，三角形中位线定理，熟练掌握全等三角形的判定和性质定理是解题的关键．【题型2“半角”模型】6如图①，四边形ABCD是正方形，M，N分别在边CD、BC上，且∠MAN=45°，我们称之为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法，如图①，将△ADM绕点A顺时针旋转90°，点D与点B重合，连接AM、AN、MN．(1)试判断DM，BN，MN之间的数量关系；(2)如图②，点M、N分别在正方形ABCD的边BC、CD的延长线上，∠MAN=45°，连接MN，请写出MN 、DM 、BN 之间的数量关系，并写出证明过程．(3)如图③，在四边形ABCD 中，AB =AD ，∠BAD =120°，∠B +∠D =180°，点N ，M 分别在边BC ，CD 上，∠MAN =60°，请直接写出BN ，DM ，MN 之间数量关系．【答案】(1)MN =DM +BN (2)MN =BN -DM ，证明见解析(3)MN =DM +BN【详解】(1)解：MN =DM +BN ，证明如下：如图：∵四边形ABCD 是正方形，∴∠ABC =∠BAD =∠D =90°，，由旋转的性质可得：AE =AM ，BE =DM ，∠ABE =∠D =90°，∠DAM =∠BAE ，∴∠ABE +∠ABC =180°，∴点E 、B 、C 共线，∵∠DAM +∠BAM =90°，∴∠BAE +∠BAM =90°=∠EAM ，∵∠MAN =45°，∴∠EAN =∠EAM -∠MAN =45°=∠MAN ，在△EAN 和△MAN 中，AE =AM∠EAN =∠MANAN =AN∴△EAN ≌△MAN SAS ，∴EN =MN ，∵EN =BE +BN ，∴MN =DM +BN ；(2)解：MN =BN -DM ，证明如下：如图，在BC 上取BE =MD ，连接AE ，，∵四边形ABCD 是正方形，∴∠ABC =∠ADC =∠BAD =90°，AB =AD ，∵∠ADC +∠ADM =180°，∴∠ADC =∠ADM =∠ABE =90°，在△ABE 和△ADM 中，AB =AD∠ABE =∠ADM BE =DM，∴△ABE≌△ADM SAS ，∴AE =AM ，∠BAE =∠MAD ，∵∠BAE +∠EAD =∠BAD =90°，∴∠DAM +∠EAD =∠EAM =90°，∵∠MAN =45°，∴∠EAN =∠EAM -∠MAN =45°=∠MAN ，在△EAN 和△MAN 中，AE =AM∠EAN =∠MAN AN =AN，∴△EAN ≌△MAN SAS ，∴EN =MN ，∵EN =BN -BE ，∴MN =BN -DM ；(3)解：如图，将△ABN 绕点A 逆时针旋转120°得△ADE ， ∴∠B =∠ADE ，AB =AD ，AE =AN ，∴∠B +∠ADC =180°，∴∠ADE +∠ADC =180°，∴点E 、D 、C 共线，∵∠BAN +∠NAD =∠BAD =120°，∴∠DAE +∠NAD =∠NAE =120°，∵∠MAN =60°，∴∠EAN =∠EAM -∠MAN =60°=∠MAN ，在△EAN 和△MAN 中，AE =AN∠EAM =∠NAM AM =AM，∴△EAM ≌△NAM SAS ，∴EM =MN ，∴MN =DM +BN ．【点睛】本题是四边形综合题，主要考查了正方形的性质，旋转的性质，全等三角形的判定与性质，利用旋转构造全等三角形是解题的关键．7如图，已知在△ABC 中，AB =AC ，D 、E 是BC 边上的点，将△ABD 绕点A 旋转，得到△ACD，连接D E ．(1)当∠BAC =120°，∠DAE =60°时，求证：DE =D E ；(2)当DE=D E时，∠DAE与∠BAC有怎样的数量关系？请写出，并说明理由．(3)在(2)的结论下，当∠BAC=90°，BD与DE满足怎样的数量关系时，△D EC是等腰直角三角形？(直接写出结论，不必证明)【答案】(1)见解析(2)∠DAE=12∠BAC，理由见解析(3)DE=2BD【详解】(1)证明：∵△ABD绕点A旋转得到△ACD ，∴AD=AD ，∠CAD =∠BAD，∵∠BAC=120°，∠DAE=60°，∴∠D AE=∠CAD +∠CAE=∠BAD+∠CAE=∠BAC-∠DAE=120°-60°=60°，∴∠DAE=∠D AE，在△ADE和△AD E中，∵AD=AD∠DAE=∠D AE AE=AE，∴△ADE≌△AD E(SAS)，∴DE=D E；(2)解：∠DAE=12∠BAC．理由如下：在△ADE和△AD E中，AD=AD AE=AE DE=D E，∴△ADE≌△AD′E(SSS)，∴∠DAE=∠D AE，∴∠BAD+∠CAE=∠CAD′+∠CAE=∠D′AE=∠DAE，∴∠DAE=12∠BAC；(3)解：∵∠BAC=90°，AB=AC，∴∠B=∠ACB=∠ACD =45°，∴∠D CE=45°+45°=90°，∵△D EC是等腰直角三角形，∴D E=2CD ，由(2)DE=D E，∵△ABD绕点A旋转得到△ACD ，∴BD=C D ，∴DE=2BD．【点睛】本题考查了几何变换的综合题，旋转的性质，全等三角形的判定与性质，等腰直角三角形的性质，熟记旋转变换只改变图形的位置不改变图形的形状与大小找出三角形全等的条件是解题的关键．8学完旋转这一章，老师给同学们出了这样一道题：“如图1，在正方形ABCD 中，∠EAF =45°，求证：EF =BE +DF ．”小明同学的思路：∵四边形ABCD 是正方形，∴AB =AD ，∠B =∠ADC =90°．把△ABE 绕点A 逆时针旋转到△ADE 的位置，然后证明△AFE ≌△AFE ，从而可得EF =E F ．E F =E D +DF =BE +DF ，从而使问题得证．(1)【探究】请你参考小明的解题思路解决下面问题：如图2，在四边形ABCD 中，AB =AD ，∠B =∠D =90°，∠EAF =12∠BAD ，直接写出EF ，BE ，DF 之间的数量关系．(2)【应用】如图3，在四边形ABCD 中，AB =AD ，∠B +∠D =180°，∠EAF =12∠BAD ，求证：EF =BE +DF ．(3)【知识迁移】如图4，四边形ABPC 是⊙O 的内接四边形，BC 是直径，AB =AC ，请直接写出PB +PC 与AP 的关系．【答案】(1)BE +DF =EF (2)证明见解析(3)PB +PC =2PA【详解】(1)解：结论：BE +DF =EF ，理由如下：证明：将△ABE 绕点A 逆时针旋转，旋转角等于∠BAD ，使得AB 与AD 重合，点E 转到点E 的位置，如图所示，可知△ABE≌△ADE ，∴BE=DE ．由∠ADC+∠ADE =180°知，C、D、E 共线，∠BAD，∵∠EAF=12∴∠BAF+∠DAF=∠EAF，∴∠DAE +∠DAF=∠EAF=∠E'AF，∴△AEF≌△AE F，∴EF=E F=BE+DF．(2)证明：将△ABE绕点A逆时针旋转，旋转角等于∠BAD，使得AB与AD重合，点E转到点E 的位置，如图所示，由旋转可知△ABE≌△ADE ，∴BE=DE ，∠B=∠ADE ，∠BAE=∠DAE ，AE=AE ．∴∠ADC+∠ADE =180°，∴点C，D，E 在同一条直线上．∠BAD，∵∠EAF=12∴∠BAE+∠DAF=1∠BAD，2BAD，∴∠DAE +∠DAF=12∠BAD，∴∠FAE =12∴∠EAF=∠FAE ．∵AF=AF，∴△FAE ≌△FAE，∴FE=FE ，即BE+DF=EF．(3)结论：PB+PC=2PA，理由如下：证明：将△ABP绕点A逆时针旋转90°得到△ACP ，使得AB与AC重合，如图所示，由圆内接四边形性质得：∠ACP +∠ACP=180°，即P，C，P 在同一直线上．∴BP=CP ，AP=AP ，∵BC为直径，∴∠BAC=90°=∠BAP+∠PAC=∠CAP +∠PAC=∠PAP ，∴△PAP 为等腰直角三角形，∴PP =2PA，即PB+PC=2PA．【点睛】本题考查了旋转与全等三角形的综合应用、直径所对的圆周角是直角、圆内接四边形的性质、等腰直角三角形的判定及性质等知识点．解题关键是利用旋转构造全等三角形．9阅读下面材料．小炎遇到这个一个问题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中，她先尝试了翻折、旋转、平移的方法，最后发现线段AB、AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE 绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决这个问题(如图2)．参考小炎同学思考问题的方法，解决下列问题：(1)写出小炎的推理过程；(2)如图3，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°，若∠B、∠D都不是直角，则当∠B与∠D满足于关系时，仍有EF=BE+DF；(3)如图4，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，若BD=1，EC =2，求DE的长．【答案】(1)见解析(2)∠B+∠ADC=180°(3)5【详解】(1)解：如图所示，将△ABE绕着点A逆时针旋转90°得到△ADG，∵四边形ABCD是正方形，∴AB=AD，∠B=∠ADC=∠BAD=90°，由旋转的性质可得AE=AG，BE=DG，∠BAE=∠DAG，∠ADG=∠B=90°，∴∠ADC+∠ADG=180°，即C、D、G三点共线，∵∠BAE+∠DAE=90°，∴∠DAG+∠DAE=90°，即∠EAG=90°，∵∠EAF=45°，∴∠GAF=45°=∠EAF，又∵AF=AF，∴△AEF≌△AGF SAS，∴EF=GF，又∵GF=DF+DG，DG=BE，∴EF=BE+DF；(2)解：当∠B+∠ADC=180°时，仍有EF=BE+DF，理由如下：如图所示，将△ABE绕点A逆时针旋转90°得到△ADG，∴BE=DG，AE=AG，∠BAE=∠DAG，∠B=∠ADG∵∠B+∠ADC=180°，∠B=∠ADG，∴∠ADC+∠ADG=180°，即C、D、G三点共线，∵∠BAD=90°∴∠BAE+∠DAE=90°，∴∠DAG+∠DAE=90°，即∠EAG=90°，∵∠EAF=45°，∴∠GAF=45°=∠EAF，又∵AF=AF，∴△AEF≌△AGF SAS，∴EF=GF，又∵GF=DF+DG，DG=BE，∴EF=BE+DF，故答案为：∠B+∠ADC=180°；(3)解：如图所示，将△ABD绕点A逆时针旋转90°得到△ACG，∴∠B=∠ACG，BD=CG=1，AD=AG，∵∠BAC=90°，∴∠B+∠ACB=90°，∠BAD+∠CAD=90°，∴∠CAG+∠CAD=90°，∠ACG+∠ACB=90°，即∠ECG=90°，∠DAG=90°，∵∠DAE=45°，∴∠GAE=45°=∠DAE，又∵AE=AE，∴△ADE≌△AGE SAS，∴GE=DE，在Rt△CEG中，由勾股定理得GE=CE2+CG2=5，∴DE=GE=5．【点睛】本题主要考查了正方形的性质，全等三角形的性质与判定，旋转的性质，勾股定理等等，正确作出辅助线构造全等三角形是解题的关键．10如图1，E，F分别是正方形ABCD的边CD，BC上的动点，且满足∠EAF=45°，试判断线段BF，EF，ED之间的数量关系，并说明理由．小聪同学的想法：将△DAE顺时针旋转90°，得到△BAH，然后通过证明三角形全等可得出结论．请你参考小聪同学的思路完成下面的问题．(1)线段BF，EF，ED之间的数量关系是．(2)如图2，在正方形ABCD中，∠EAF=45°，连接BD，分别交AF，AE于点M，N，试判断线段BM，MN，ND之间的数量关系，并说明理由．【答案】(1)EF=BE+DF(2)MN2=BM2+DN2【详解】(1)解：结论：EF=BE+DF理由：∵四边形ABCD是正方形，∴∠ABC=∠ADC=∠BAD=90°，由旋转的性质可知：AH=AE，∠ADE=∠ABH=90°，HB=DE，∠EAH=90°，∵∠EAF=45°，∴∠FAH=45°，∴∠FAH=∠EAF，∵∠ABF+∠ABH=90°+90°=180°，∴F、B、H三点共线，又∵AF=AF，∴△AFE≌△AFH SAS，∴EF=FH，∵FH=BF+BH=BF+DE，∴EF=BE+DF．(2)结论：MN2=BM2+DN2,证明如下：如图所示，将△ADN绕点A顺时针旋转90°得到△BAG．∵BA=AD，∠BAD=90°，∴∠ABD=∠ADB=45°，由旋转的性质可知：AN=AG，∠ABG=∠ADB=45°，∠GAE=90°，∴∠MBG=∠ABG+∠ABD=90°，∵∠EAF=45°，∴∠GAM=∠BAG+∠BAM=90°-∠EAF=45°，∴∠MAG=∠MAN，∵AM=AM，∴△AGM≌△ANM SAS，∴MN=GM，∵∠MBG=90°，∴BM2+BG2=GM2，∴MN2=BM2+DN2．【点睛】本题涉及了旋转变换，正方形的性质，等腰直角三角形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形，属于中考常考题型．【题型3构造旋转模型解题】11如图，正方形ABCD中，点E、F分别在线段BC、CD上运动，且满足∠EAF=45°，AE、AF分别与BD相交于点M、N，下列说法中：①BE+DF=EF；②点A到线段EF的距离一定等于正方形的边长；③BE=2，DF=3，则S△AEF=15；④若AB=62，BM=3，则MN=5．其中结论正确的个数是()A.4B.3C.2D.1【答案】A【分析】根据旋转的性质得到BH=DF，AH=AF，∠BAH=∠DAF，得到∠EAH=∠EAF=45°，根据全等三角形的性质得到EH=EF，∠AEB=∠AEF，于是得到BE+BH=BE+DF=EF，故①正确；过A作AG⊥EF于G，根据全等三角形的性质得到AB=AG，于是得到点A到线段EF的距离一定等于正方形的边长，故②正确；求出EF=BE+DF=5，设BC=CD=n，根据勾股定理即可得到S△AEF=15，故③正确；把△ADN绕点A顺时针旋转90°得到△ABQ，再证明△AMQ≌△AMN(SAS)，从而得MQ=MN，再证明∠QBM=∠ABQ+∠ABM=90°，设MN=x，再由勾股定理求出x即可．【详解】解：如图，把△ADF绕点A顺时针旋转90°得到△ABH，由旋转的性质得，BH=DF，AH=AF，∠BAH=∠DAF，∵∠EAF=45°，∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°-∠EAF=45°，∴∠EAH=∠EAF=45°，在△AEF和△AEH中，AH=AF∠EAH=∠EAF=45oAE=AE，∴△AEF≌△AEH(SAS)，∴EH=EF，∴∠AEB=∠AEF，∴BE+BH=BE+DF=EF，故①正确；过A作AG⊥EF于G，∴∠AGE=∠ABE=90°，在△ABE与△AGE中，∠ABE=∠AGE∠AEB=∠AEGAE=AE，∴△ABE≌△AGE(AAS)，∴AB=AG，∴点A到线段EF的距离一定等于正方形的边长；故②正确；∵BE=2，DF=3，∴EF=BE+DF=5，设BC=CD=n，∴CE=n-2，CF=n-3，∴EF2=CE2+CF2，∴25=(n-2)2+(n-3)2，∴n=6(负值舍去)，∴AG=6，∴S△AEF=12×6×5=15．故③正确；如图，把△ADN 绕点A 顺时针旋转90°得到△ABQ ，连接QM ，由旋转的性质得，BQ =DN ，AQ =AN ，∠BAQ =∠DAN ，∠ADN =∠ABQ =45°，∵∠EAF =45°，∴∠MAQ =∠BAQ +∠BAE =∠DAN +∠BAE =90°-∠EAF =45°，∴∠MAQ =∠MAN =45°，在△AMQ 和△AMN 中，AQ =AN∠MAQ =∠MAN AM =AM，∴△AMQ ≌△AMN (SAS )，∴MQ =MN ，∵∠QBM =∠ABQ +∠ABM =90°，∴BQ 2+MB 2=MQ 2，∴ND 2+MB 2=MN 2，∵AB =62，∴BD =2AB =12，设MN =x ，则ND =BD -BM -MN =9-x ，∴32+(9-x )2=x 2，解得：x =5，∴MN =5，故④正确，故选A ．【点睛】本题主要考查了旋转的性质，正方形的性质，全等三角形的性质与判定，勾股定理等等，解题的关键是旋转三角形ADF 和三角形AND ．12如图，已知点P 是正方形ABCD 内的一点，连接PA 、PB 、PC ．若PA =4，PB =2，∠APB =135°，则PC 的长为．【答案】26【分析】先根据正方形的性质得BA=BC，∠ABC=90°，则可把△BAP绕点B顺时针旋转90°得到△CBE，连接PE，如图，根据旋转的性质得BP=BE=2，CE=AP=4，∠PBE=90°，∠BEC=∠APB= 135°，于是可判断△PBE为等腰直角三角形，所以PE=2PB=22，∠PEB=45°，则∠PEC=90°，然后在Rt△PEC中利用勾股定理计算PC的长．【详解】解：∵四边形ABCD为正方形，∴BA=BC，∠ABC=90°，把△BAP绕点B顺时针旋转90°得到△CBE，连接PE，如图，∴BP=BE=2，CE=AP=4，∠PBE=90°，∠BEC=∠APB=135°，∴△PBE为等腰直角三角形，∴PE=2PB=22，∠PEB=45°，∴∠PEC=135°-45°=90°，在Rt△PEC中，∵PE=22，CE=4，∴PC=42+(22)2=26．故答案为：26．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．13(1)问题发现：如图1，△ABC和△DCE均为等边三角形，当△DCA应转至点A，D，E在同一直线上，连接BE，易证△BCE≌△ACD，则①∠BEC=；②线段AD，BE之间的数量关系；(2)拓展研究：如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A，D，E在同一直线上，若AE=12，DE=7，求AB的长度；(3)如图3，P为等边三角形ABC内一点，且∠APC=150°，∠APD=30°，AP=4，CP=3，DP=7，求BD的长．【答案】(1)①120°；②AD=BE；(2)13；(3)229【分析】本题主要考查了全等三角形的判定及性质和勾股定理的应用，(1)证明△ACD≌△BCE(SAS)．得到∠ADC=∠BEC．利用△DCE为等边三角形，得到∠CDE=∠CED=60°，再利用点A，D，E在同一直线上，可得∠ADC=120°，即可得∠BEC=120°；(2)证明△ACD≌△BCE(SAS)，可得AD=BE=AE-DE=15-7=8，∠ADC=∠BEC，再证明∠AEB=∠BEC-∠CED=90°，利用勾股定理求解即可；(3)把△APC绕点C逆时针旋转60°得△BEC，连接PE，可得△BEC≌△APC，证明△PCE是等边三角形，证明∠BED=90°，再证明D、P、E在同一条直线上，求出DE，利用勾股定理求解即可．【详解】解：(1)①∵△ACB和△DCE均为等边三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=60°．∴∠ACD=∠BCE．在△ACD和△BCE中，AC=BC∠ACD=∠BCE CD=CE，∴△ACD≌△BCE(SAS)．∴∠ADC=∠BEC．∵△DCE为等边三角形，∴∠CDE=∠CED=60°．∵点A，D，E在同一直线上，∴∠ADC=120°．∴∠BEC=120°．②由①得：△ACD≌△BCE，∴AD=BE；故答案为：①120°；②AD=BE．(2)∵△ACB和△DCE均为等腰直角三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=90°．∴∠ACD=∠BCE．在△ACD和△BCE中，AC=BC∠ACD=∠BCE CD=CE，∴△ACD≌△BCE(SAS)，∴AD=BE=AE-DE=12-7=5，∠ADC=∠BEC，∵△DCE为等腰直角三角形∴∠CDE=∠CED=45°．∵点A，D，E在同一直线上，∴∠ADC=135°．∴∠BEC=135°．∴∠AEB=∠BEC-∠CED=90°．∴AB=AE2+BE2=144+25=13；(3)把△APC绕点C逆时针旋转60°得△BEC，连接PE，如图所示：AP=4，CP=3，DP=7则△BEC≌△APC，∴CE=CP，∠PCE=60°，BE=AP=4，∠BEC=∠APC=150°，∴△PCE是等边三角形，∴∠EPC=∠PEC=60°，PE=CP=3，∴∠BED=∠BEC-∠PEC=90°，∵∠APD=30°，∴∠DPC=150°-30°=120°，又∵∠DPE=∠DPC+∠EPC=120°+60°=180°，即D、P、E在同一条直线上，∴DE=DP+PE=7+3=10，在Rt△BDE中，BD=BE2+DE2=229，即BD的长为229．【点睛】本题涉及全等三角形的判定及性质，等边三角形的性质，勾股定理，旋转的性质等知识点，解题的关键是利用旋转构造全等三角形，把分散的已知条件集中到同一个三角形中．【题型4奔驰模型】14如图，已知点D是等边△ABC内一点，且BD=3，AD=4，CD=5．(1)求∠ADB的度数；以下是甲，乙，丙三位同学的谈话：甲：我认为这道题的解决思路是借助旋转，我选择将△BCD绕点B顺时针旋转60°或绕点A逆时针旋转60°；乙：我也赞成旋转，不过我是将△ABD进行旋转；丙：我是将△ACD进行旋转．请你借助甲，乙，丙三位同学的提示，选择适当的方法求∠ADB的度数；(2)若改成BD=6，AD=8，CD=10，∠ADB的度数=°，点A到BD的距离为；类比迁移：(3)已知，∠ABC=90°，AB=BC，BE=1，CE=3，AE=5，求∠BEC的度数．【答案】(1)∠ADB=150°(2)150，4.(3)∠BEC=135°【详解】(1)解：(1)选择甲：如图1，作∠DBE=60°，且BE=BD，连接DE，AE，则△BDE是等边三角形，∴DE=BD=3，∠BDE=60°，∵△ABC是等边三角形，∴AB=BC，∠ABC=60°，∴∠ABE=∠CBD，∴△ABE≌△CBD，∴AE=CD=5，∵AD2+DE2=42+32=52=AE2，∴∠ADE=90°，∴∠ADB=∠ADE+∠BDE=90°+60°=150°；乙：如图2，同理可得，∠BFD=60°，∠DFC=90°，∴∠ADB=∠BFC=∠BFD+∠DFC=60°+90°=150；丙：如图3同理可得，∠AGD=60°，∠BDG=90°，∴∠ADB=∠ADG+∠BDG=60°+90°=150；(2)同理(1)可得：AD2+BD2=CD2，∴∠ADB=150°，如图4，过点A作BD的垂线AH，垂足为H，∴∠ADH=30°，AD=4，∴AH=12故答案为：150，4.(3)如图5，将△ABE绕着点B顺时针旋转90°，得到△CBF，连接EF，∴△ABE≌△CBF，∴BE=BF=1，AE=CF=5，∴∠FBE=∠BEF=45°，∴EF2=BE2+BF2=2∵EF2+EC2=2+3=5=AE2，∴∠FEC=90°，∴∠BEC=∠BEF+∠FEC=45°+90°=135°【点睛】本题属于四边形综合题，主要考查了旋转和平移的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用，解决问题的关键是作辅助线构造等边三角形和全等三角形，依据图形的性质进行计算求解．15(1)问题发现：如图1，等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A逆时针旋转60°到△ACP 处，这样就可以将三条线段PA,PB,PC转化到一个三角形中，从而求出∠APB的度数．请按此方法求∠APB的度数，写出求解过程；(2)拓展研究：请利用第(1)题解答的思想方法，解答下面的问题：①如图2，△ABC中，AB=AC,∠BAC=90°，点E，F为BC边上的点，且∠EAF=45°，判断BE,EF,CF 之间的数量关系并证明；②如图3，在△ABC中，∠ABC=30°，AB=4，BC=6，在△ABC内部有一点P，连接PA,PB,PC，直接写出PA+PB+PC的最小值．【答案】(1)150°，见解析；(2)①BE2+CF2=EF2，见解析；②213【分析】(1)连接PP ，根据题意得到AP=AP =3,∠PAP =60°，BP=CP =4，∠APB=∠AP C，进而得到△APP '为等边三角形，PP =AP=3,∠AP P=60°，根据勾股定理逆定理证明△PP C是直角三角形，且∠PP C=90°，即可求出∠APB=∠AP C=150°；(2)①证明∠B=∠ACB=45°，将△BAE绕点A逆时针旋转90°，得到△CAD，连接DF，得到∠BAE=∠DAC，∠ACD=∠B=45°，AD=AE，BE=CD，进而得到∠DCE=90°，根据勾股定理得到DF2=CF2 +CD2=CF2+BE2 ，证明△AEF≌△ADF，得到EF=DF，即可得到BE2+CF2=EF2；②将△ABP绕点B逆时针旋转60°，得到△A BP ，连接PP ，A C，即可得到∠ABA =∠PBP =60°，A B= AB=4，BP=BP ，A P =AP，从而得到△BPP 为等边三角形，∠A BC=90°，BP=PP ，根据两点之间线段最短得到PA+PB+PC=A P +PP +CP≥A C ，即可得到当且仅当A ，P ，P，C四点共线时，PA +PB+PC的值最小为 A C的长，根据勾股定理求出A C=213，即可得到PA+PB+PC的最小值为213 ．【详解】解：(1)连接PP ，∵将△APB绕顶点 A 逆时针PP 旋转60°到△ACP ，∴AP=AP =3,∠PAP =60°，BP=CP =4,∠APB=∠AP C，∴△APP '为等边三角形，∴PP =AP=3,∠AP P=60°，∵P P2+P C=32+42=25，PC2=52=25，∴P P2+P C=PC2，∴△PP C是直角三角形，且∠PP C=90°，∴∠AP C=∠AP P+∠CP P=150°，∴∠APB=∠AP C=150°；(2)①BE2+CF2=EF2．证明：∵AB=AC,∠BAC=90°，∴∠B=∠ACB=45°，如图，将△BAE绕点A逆时针旋转90°，得到△CAD，连接DF，则：∠BAE=∠DAC，∠ACD=∠B=45°，AD=AE，BE=CD，∴∠DCE=∠ACB+∠ACD=90°，∴DF2=CF2+CD2=CF2+BE2 ，∵∠EAF=45°，∠EAD=90°，∴∠DAF=∠EAF=45°，又∵AE=AD,AF=AF ，∴△AEF≌△ADF，∴EF=DF，∴BE2+CF2=EF2；②PA+PB+PC的最小值为 213如图，将△ABP绕点B逆时针旋转60°，得到△A BP ，连接PP ，A C，则：∠ABA =∠PBP =60°，A B=AB=4，BP=BP ，A P =AP，∴△BPP 为等边三角形，∠A BC=∠A BA+∠ABC=90°，∴BP=PP ，∴PA+PB+PC=A P +PP +CP≥A C ，∴当且仅当A ，P ，P，C四点共线时，PA+PB+PC的值最小为 A C的长，∵∠A BC=90°，∴A C=A B2+BC2=42+62=213，∴PA+PB+PC的最小值为213 ．【点睛】本题考查了旋转的性质，等边三角形的判定与性质，勾股定理及其逆定理，全等三角形的判定与性质等知识，综合性较强，熟知相关知识并根据题意灵活应用是解题关键．16(2023•崂山区模拟)阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数．小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．请你回答：图1中∠APB的度数等于150°．参考小伟同学思考问题的方法，解决下列问题：(1)如图3，在正方形ABCD内有一点P，且PA=，PB=1，PD=，则∠APB的度数等于135°，正方形的边长为；(2)如图4，在正六边形ABCDEF内有一点P，且PA=2，PB=1，PF=，则∠APB的度数等于120°，正六边形的边长为．【答案】见试题解答内容【解答】解：阅读材料：把△APB绕点A逆时针旋转60°得到△ACP′，由旋转的性质，P′A=PA=3，P′D=PB=4，∠PAP′=60°，水不撩不知深浅∴△APP′是等边三角形，∴PP′=PA=3，∠AP′P=60°，∵PP′2+P′C2=32+42=25，PC2=52=25，∴PP′2+P′C2=PC2，∴∠PP′C=90°，∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°；故∠APB=∠AP′C=150°；(1)如图3，把△APB绕点A逆时针旋转90°得到△ADP′，由旋转的性质，P′A=PA=22，P′D=PB=1，∠PAP′=90°，∴△APP′是等腰直角三角形，∴PP′=2PA=2×22=4，∠AP′P=45°，∵PP′2+P′D2=42+12=17，PD2=172=17，∴PP′2+P′D2=PD2，∴∠PP′D=90°，∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°，故，∠APB=∠AP′D=135°，∵∠APB+∠APP′=135°+45°=180°，∴点P′、P、B三点共线，过点A作AE⊥PP′于E，则AE=PE=12PP′=12×4=2，∴BE=PE+PB=2+1=3，在Rt△ABE中，AB===13；(2)如图4，∵正六边形的内角为16×(6-2)•180°=120°，∴把△APB绕点A逆时针旋转120°得到△AFP′，由旋转的性质，P′A=PA=2，P′F=PB=1，∠PAP′=120°，∴∠APP′=∠AP′P=12(180°-120°)=30°，过点A作AM⊥PP′于M，设PP′与AF相交于N，则AM=12PA=12×2=1，P′M=PM===3，∴PP′=2PM=23，∵PP′2+P′F2=(23)2+12=13，PF2=132=13，水不撩不知深浅∴PP′2+P′F2=PF2，∴∠PP′F=90°，∴∠AP′F=∠AP′P+∠PP′F=30°+90°=120°，故，∠APB=∠AP′F=120°，∵P′F=AM=1，∵△AMN和△FP′N中，，∴△AMN≌△FP′N(AAS)，∴AN=FN，P′N=MN=12P′M=32，在Rt△AMN中，AN===7 2，∴AF=2AN=2×72=7．故答案为：150°；(1)135°，13；(2)120°，7．【题型5费马点模型】17如图，四边形ABCD是菱形，AB=6，且∠ABC=60°，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM的最小值为．【答案】63【详解】以BM为边作等边△BMN，以BC为边作等边△BCE，则BM=BN=MN，BC=BE=CE，∠MBN=∠CBE=60°，∴∠MBC=∠NBE，∴△BCM≌△BEN，∴CM=NE，∴AM+MB+CM=AM+MN+NE．当A、M、N、E四点共线时取最小值AE．∵AB=BC=BE=6，∠ABH=∠EBH=60°，∴BH⊥AE，AH=EH，∠BAH=30°，AB=3，AH=3BH=33，∴BH=12∴AE=2AH=63．故答案为63．【点睛】本题考查了菱形的性质，全等三角形的判定与性质，等边三角形的性质．难度比较大．作出恰当的辅助线是解答本题的关键．18如图，在等边三角形ABC内有一点P．(1)若PA=2，PB=3，PC=1，求∠BPC的度数；(2)若等边三角形边长为4，求PA+PB+PC的最小值；(3)如图，在正方形ABCD内有一点P，且PA=5，PB=2，PC=1，求正方形ABCD的边长．【答案】(1)∠BPC=150°，(2)43(3)5【详解】(1)解：如图所示，将线段BP绕点B逆时针旋转60°得到线段B P ，连接A P 、P P ，∴△BPC≌△BP A，∴BP=B P ，A P =PC=1，∠PB P =60°，∠A P B=∠BPC，∴△B P P是等边三角形，∴∠B P P=∠PB P =60°，P P =BP=3，∵AP 2+PP 2=1+3=4=AP2，∴△A P P是直角三角形，∠A P P=90°，∴∠A P B=∠AP P +∠B P P=150°，∴∠BPC=150°，(2)解：如图所示，将△ABP绕点A顺时针旋转60°得到△ACD，则△ABP≌△ACD，PA=DA，∠PAD=60°，则△APD是等边三角形，∴AP=PD，再将△APC绕点A顺时针旋转60°得到△ADE，则△APC≌△ADE∴PC=DE，∠CAE=60°，CA=EA，∴PA+PB+PC=BP+PD+DE≥BE当B,P,D,E四点共线时，PA+PB+PC取得最小值，即BE的长，设BE，AC交于点F，∵AB=AC=AE,∠BAF=∠EAF，∠BAE=∠BAF+∠EAF=120°，BE ,∴BE⊥AF，BF=EF=12∴∠ABF=30°，AB=2 ,∴AF=12在Rt△ABF中，BF=AB2-AF2=23 ,∴BE=2BF=43，即PA+PB+PC的最小值为43；(3)如图，将△BPC绕点B逆时针旋转90°，得到△BEA，∴△BPC≌△BEA，∴BE=BP=2，AE=PC=1，∠PBE=90°，∠AEB=∠BPC，∴△BEP是等腰直角三角形，∴∠BEP=∠EPB=45°，PE=2PB=2，∵AE2+PE2=1+4=5=AP2，∴△AEP是直角三角形，∠AEP=90°，如图，延长AE，过点B作BF⊥AE于F，则∠F=90°，∵∠AEP=90°，∠BEP=45°，∴∠BEF=45°=∠EBF，∴BF=EF=1，∴AF=AE+EF=2，∴AB=AF2+BF2=22+1=5，即正方形的边长为5．【点睛】此题考查了等边三角形的性质，旋转的性质，全等三角形的判定与性质，正方形的性质，勾股定理及其逆定理，熟练掌握旋转的性质是解题的关键．19背景资料：在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小.这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．如图1，当△ABC三个内角均小于120°时，费马点P在△ABC内部，当∠APB=∠APC=∠CPB=120°时，则PA+PB+PC取得最小值．(1)如图2，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数，为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP 处，此时△ACP ≌△ABP这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB=；知识生成：怎样找三个内角均小于120°的三角形的费马点呢？为此我们只要以三角形一边在外侧作等边三角形并连接等边三角形的顶点与△ABC的另一顶点，则连线通过三角形内部的费马点．请同学们探索以下问题．(2)如图3，△ABC三个内角均小于120°，在△ABC外侧作等边三角形△ABB ，连接CB ，求证：CB 过△ABC的费马点．(3)如图4，在RT△ABC中，∠C=90°，AC=1，∠ABC=30°，点P为△ABC的费马点，连接AP、BP、CP，求PA+PB+PC的值．(4)如图5，在正方形ABCD中，点E为内部任意一点，连接AE、BE、CE，且边长AB=2；求AE+BE+ CE的最小值．【答案】(1)150°；(2)见详解；(3)7；(4)6+2．【详解】(1)解：连结PP′，∵△ABP≌△ACP ，∴∠BAP=∠CAP′，∠APB=∠AP′C，AP=AP′=3，BP=CP′=4，∵△ABC为等边三角形，。

九年级数学图形的旋转专题讲解+六大题型解析+专题训练,收藏学习

九年级数学图形的旋转专题讲解+六大题型解析+专题训练，收藏学习九年级数学图形的旋转专题讲解+六大题型解析+专题训练，收藏学习 -九年级数学图形的旋转专题讲解+六大题型解析+专题训练，收藏学习图形的旋转这一章节是初中几何内容中非常重要的一个章节，对于图形的运动的形式和规律以及旋转的性质都是我们在对几何的初步认识当中的一个过程，掌握其重要的性质之后，对于几何综合题型当中辅助线的运用起到了非常重要的作用。

并且图形的旋转加上已经学习过的平移和轴对称。

对几何图形的变化有充分地了解，建立几何空间思维的正确认识,对于几何空间能力的提升起到了非常重要的促进作用。

首先，在学习图形的旋转这一章节我们主要围绕以下两个重要的内容来展开:第一，掌握图形的旋转和中心对称的概念；第二，掌握旋转的本质。

这也是我们学习过程中的重点和难点内容。

因为在旋转前后的两个图形中，对应点与旋转中心之间的距离总是相同的，所以对应点必然分别在以旋转中心为圆心，以对应点到旋转中心的距离为半径的一组同心圆上，对应点与旋转中心连线所成的角等于且等于旋转角。

唐老师提醒大家，旋转过程中保持静止的点就是旋转的中心，不变的量就是对应的元素。

其次，旋转的三个要素：旋转中心、旋转的角度和旋转方向.第三，旋转的性质：（1）图形中的每一点都绕着旋转中心旋转了同样大小的连线所成的角度；—整体角度（2）对应点到旋转中心的距离相等；（3）对应线段相等，对应角相等；——局部角度（4）图形的形状和大小都没有发生变化，即旋转不改变图形的形状和大小.—变换结果.第四，简单图形的旋转作图：（1）确定旋转中心；（2）确定图形中的关键点；（3）将关键点沿指定的方向旋转指定的角度；(4)连接这些点，得到原始图形的旋转图形。

(以上四个步骤是我们在制作简单旋转图的过程中应该遵循的步骤。

按照以上步骤画图，可以提高大家的学习效率，保证其在画图过程中的正确率。

)第五，旋转对称图形：平面图形绕某点旋转一定角度(小于圆角)后，可以与自身重叠。

部编数学九年级下册专项16巧用旋转进行计算(解析版)含答案

专项16 巧用旋转进行计算将一个图形绕着某一点旋转一个角度的图形变换叫做旋转，由旋转的性质可知旋转前后的图形全等，对应点到旋转中心的连线所组成的夹角等于旋转角。

旋转方法常用于等腰三角形、等边三角形及正方形等图形中。

【考点1 利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】【典例1】（2021九上·番禺期末）如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到的△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′．若∠CC′B′＝20°，则∠B的大小是（）A．70°B．65°C．60°D．55°【答案】B【解答】解：∵将ΔABC绕点A顺时针旋转90°后得到的△A B′C′，∴AC=AC，∠CAC=90°，∠B=∠ABC，∴∠ACC=45°，∴∠ABC=∠ACC+∠CCB=45°+20°=65°，∴∠B=∠ABC=65°，故答案为：B．【变式1-1】（2021九上·上高月考）如图，将△AOB绕着点O顺时针旋转70°，得到△COD，若∠COD=40°，则∠BOC的度数为（）A．10°B．20°C．30°D．40°【答案】C【解答】解：∵将△AOB绕着点O顺时针旋转70°，得到△COD，∴∠BOD=70°，∵∠COD=40°，∴∠BOC=∠BOD－∠COD=70°－40°=30°．故答案为：C【变式1-2】（2021九上·南充期末）如图，在△ABC中，∠ACB=90°，∠A=30°，将△ABC绕点C逆时针旋转90°得到△DEC，则∠AED的度数为（）A．105°B．120°C．135°D．150°【答案】B【解答】解：由旋转的性质可得：∠A=∠D=30°，∠ACB=∠DCE=90°，∴∠AED=∠D+∠DCE=120°；故答案为：B.【变式1-3】（2021九上·澄海期末）如图，将△ABC绕点A按逆时针方向旋转得到△ABC．若点B刚好落在BC边上，且AB=C B′，若∠C=20°，则△ABC旋转的角度为（）A．60°B．80°C．100°D．120°【答案】C【解答】解：∵AB=C B′，∴∠B'AC=∠C，由旋转前后对应线段相等可知：AB’=AB，∴∠B=∠AB’B，由三角形外角定理可知：∠AB’B=∠B’AC+∠C=2∠C=40°，∴∠B=∠AB’B=40°，∴△ABC旋转的角度为∠BAB’=180°-∠B-∠AB’B=180°-40°-40°=100°，故答案为：C．【变式1-4】（2021九上·庐江期末）如图，在△ABC中，∠BAC＝65°，∠C＝20°，将△ABC 绕点A逆时针旋转n度（0＜n＜180）得到△ADE，若DE∥AB，则n的值为（）A．65B．75C．85D．130【答案】C【解答】∵DE∥AB，∴∠DAB＝180°－∠D，∵∠D=∠B=180°－20°－65°=95°，∴∠DAB=180°－95°=85°，∴n=85°，故答案为：C．【典例2】（2021九上·道里期末）如图，在Rt△ABC中，∠C＝90°，∠ABC=30°，AC＝Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，连接BB'，则BB'的长度是（）D．A．1B．3C【解答】解：∵在Rt△ABC中，∠C＝90°，∠ABC=30°，AC∴∠BAC=90°－∠ABC=60°，∵将Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，∴∠BAB'=∠BAC=60°，AB=AB'，∴△ABB'是等边三角形，∴故答案为：D．【变式2-1】（2021九上·香坊期末）如图，将RtΔABC绕点A按顺时针旋转一定角度得到RtΔADE，点B的对应点点D恰好落在边BC上，若AC=∠ABC=60°，则CD的长为（）A．3B．2CD．1【答案】B∠ABC=60°，∠BAC＝90°【解答】解：∵AC=∴∠C=90°-∠ABC=30°∵BC2=AC2+AB2∴AB＝2，BC＝2AB＝4，∵Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，∴AD＝AB，且∠B＝60°∴△ADB是等边三角形∴BD＝AB＝2，∴CD＝BC−BD＝4−2＝2故答案为：B．【变式2-2】（2021秋•韶关期末）如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB＝3cm，则BE等于（）A．2cm B．3cm C．4cm D．5cm【答案】B【解答】解：∵将△ABC绕点A顺时针旋转60°得到△AED，∴AB＝AE＝3cm，∠BAE＝60°，∴△ABE是等边三角形，∴AB＝AE＝BE＝3cm，故选：B【变式2-3】（2021秋•邓州市期末）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC ＝1，将△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在AB边上，连结BB'，则△A'BB'的周长为（）A．B．1+C．2+D．3+【解答】解：∵∠ACB＝90°，∠A＝60°，AC＝1，∴BC＝AC＝，AB＝2AC＝2，∵△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在AB边上，∴CA＝CA′，CB＝CB′，∠ACA′＝∠BAB′，∵CA＝CA′，∠A＝60°，∴△CAA′为等边三角形，∴∠ACA′＝60°，AA′＝AC＝1，∴A′B＝1，∴∠BCB′＝60°，∴△CBB′为等边三角形，∴BB′＝CB＝，∴△A'BB'的周长为A′B+AB′+BB′＝2+1+＝3+，故选：D．【典例3】（2021秋•岳池县期末）如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，连接OD，OA．（1）求∠ODC的度数；（2）试判断AD与OD的位置关系，并说明理由；（3）若OB＝2，OC＝3，求AO的长（直接写出结果）．【答案】（1）∠ODC＝60°（2）AD⊥OD （3）【解答】解：（1）由旋转的性质得，CD＝CO，∠ACD＝∠BCO，∴∠ACD+∠ACO＝∠BCO+∠ACO，即∠DCO＝∠ACB，∵三角形ABC是等边三角形，∴∠ACB＝60°，∴∠DCO＝60°，∴△OCD为等边三角形，∴∠ODC＝60°；（2）AD与OD的位置关系是：AD⊥OD，理由如下：由（1）知∠ODC＝60°，∵将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，∴∠ADC＝∠BOC＝150°，∴∠ADO＝∠ADC﹣∠ODC＝90°，∴AD⊥OD；（3）由旋转的性质得，AD＝OB＝2，∵△OCD为等边三角形，∴OD＝OC＝3，在Rt△AOD中，由勾股定理得：AO＝＝＝．【变式3-1】（2021九上·中山期末）如图，在Rt△ABC中，∠C＝90°，将△ABC绕着点B 逆时针旋转得到△FBE，点C，A的对应点分别为E，F．点E落在BA上，连接AF．（1）若∠BAC＝40°，求∠BAF的度数；（2）若AC＝8，BC＝6，求AF的长．【答案】（1）解：在Rt△ABC中，∠C=90°，∠BAC=40°，∴∠ABC=50°，∵将△ABC绕着点B逆时针旋转得到△FBE，∴∠EBF=∠ABC=50°，AB=BF，∴∠BAF=∠BFA=1（180°-50°）=65°2（2）解：∵∠C=90°，AC=8，BC=6，∴AB=10，∵将△ABC绕着点B逆时针旋转得到△FBE，∴BE=BC=6，EF=AC=8，∴AE=AB-BE=10-6=4，∴【变式3-2】（2021九上·谷城期中）如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．【答案】解：∵△ABC为等边三角形，∴AB=AC，∠BAC=60°，∵△PAC绕点A逆时针旋转后，得到△P′AB，∴AP′=AP，∠P′AP=∠BAC=60°，BP′=CP=10，∴△AP′P为等边三角形，∴P′P=AP=6，∠APP′=60°，在△PBP′中，PP′=6，BP′=10，PB=8，∵62+82=102，∴P′P2+PB2=P′B2，∴∠BPP′=90°，∴∠APB=∠APP′+∠BPP′=60°+90°=150°．故答案为6，150．【考点2 利用旋转计算面积】【典例4】（2021九上·鄞州月考）如图，在△ABC中，AB＝4，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分的面积为 .【答案】4【解答】解：∵在△ABC中，AB=4，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，∴△ABC≌△A1BC1，∴A1B=AB=4，∴△A1BA是等腰三角形，∠A1BA=30°，∴SΔA1BA= 12×4×2=4.又∵S阴影= SΔA1BA+ SΔA1BC1﹣S△ABC，SΔA1BC1=S△ABC，∴S阴影= SΔA1BA=4.故答案为：4.【变式4-1】（2022•瑞金市模拟）如图，将边长为的正方形绕点B逆时针旋转30°，那么图中阴影部分的面积为（）A．3B．C．D．【解答】解：设C'D'与AD交于M，连接BM，如图：∵边长为的正方形绕点B逆时针旋转30°，∴AB＝BC'，∠A＝∠C'＝90°，∠CBC'＝30°，∵BM＝BM，∴△ABM≌△C'BM（HL），∴∠ABM＝∠C'BM＝30°，在Rt△ABM中，AM ＝＝1，∴S △ABM ＝AB •AM ＝＝S △BC 'M ，∴S 阴影＝（）2﹣S △ABM ﹣S △BC 'M ＝3﹣，故选：C ．【变式4-2】（2021秋•丰泽区校级期末）如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，BC ＝2．将△ABC 绕点C 按顺时针方向旋转到点D 落在AB 边上，此时得到△EDC ，斜边DE 交AC 边于点F ，则图中阴影部分的面积为（）A ．3B ．1C ．D ．【解答】解：∵△ABC 是直角三角形，∠ACB ＝90°，∠A ＝30°，BC ＝2，∴∠B ＝60°，AC ＝BC ＝2×＝2，AB ＝2BC ＝4，∵△EDC 是△ABC 旋转而成，∴BC ＝CD ＝AB ＝2，∵∠B ＝60°，∴△BCD 是等边三角形，∴∠BCD ＝60°，∴∠DCF ＝30°，∠DFC ＝90°，即DE ⊥AC ，∴DE ∥BC ，∵BD ＝AB ＝2，∴DF 是△ABC 的中位线，∴DF ＝BC ＝×2＝1，CF ＝AC ＝×2＝，∴S 阴影＝DF ×CF ＝×1×＝，故选：D ．【变式4-3】（2021秋•南丹县期末）如图，边长相等的两个正方形ABCD和OEFG，若将正方形OEFG绕点O按逆时针方向旋转120°，两个正方形的重叠部分四边形OMCN的面积（）A．不变B．先增大再减小C．先减小再增大D．不断增大【解答】解：∵四边形ABCD和四边形OEFG是正方形，∴OB＝OC，∠BOC＝∠MON＝90°，∠OBC＝∠OCD＝45°，∴∠BOM＝∠CON，在△BOM和△CON中，，∴△BOM≌△CON（ASA），∴S△BOM ＝S△CON，∴两个正方形的重叠部分四边形OMCN的面积为S△BOC ＝S正方形ABCD，故选：A【考点3 坐标系中图形旋转的规律】【典例5】（2021秋•阳东区期末）如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2020次得到正方形OA2020B2020C2020，如果点A的坐标为（1，0），那么点B2020的坐标为（）A．（﹣1，1）B．C．（﹣1，﹣1）D．【答案】C【解答】解：∵四边形OABC是正方形，且OA＝1，∴B（1，1），连接OB，由勾股定理得：OB＝，由旋转得：OB＝OB1＝OB2＝OB3＝…＝，∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，相当于将线段OB绕点O逆时针旋转45°，依次得到∠AOB＝∠BOB1＝∠B1OB2＝…＝45°，∴B1（0，），B2（﹣1，1），B3（﹣，0），B4（﹣1，﹣1），…，发现是8次一循环，所以2020÷8＝252…4，∴点B2020的坐标为（﹣1，﹣1）故选：C．【变式5-1】（2021九上·惠来月考）如图，在正方形ABCD中，顶点A，B，C，D在坐标轴上，且B(2，0)，以AB为边构造菱形ABEF．将菱形ABEF与正方形ABCD组成的图形绕点O逆时针旋转，每次旋转45°，则第2020次旋转结束时，点F2020的坐标为（）A．(−2，B．(−2，C．−2)D．−2)【答案】D【解答】∵点B的坐标为(2，0)，∴OB=2，由正方形的性质，得OA=2，=∴AB=∵四边形ABEF为菱形，∴AF=AB=2)，∴由题，可知旋转为每8次一个循环，2020÷8=252⋯4，∴第2020次旋转结束时，点F2020与点F关于原点对称，−2)，∴F故答案为：D．【变式5-2】（2021•张家界）如图，在平面直角坐标系中，将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2019次得到正方形OA2019B2019C2019，那么点A2019的坐标是（）A．（，﹣）B．（1，0）C．（﹣，﹣）D．（0，﹣1）【答案】A【解答】解：∵四边形OABC是正方形，且OA＝1，∴A（0，1），∵将正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1，∴A1（，），A2（1，0），A3（，﹣），…，发现是8次一循环，所以2019÷8＝252 (3)∴点A2019的坐标为（，﹣）故选：A．【变式5-3】（2021秋•郧阳区期末）如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，若点A（3，0），B（0，4），则点B2021的横坐标为（）A．12120B．12128C．12123D．12125【答案】B【解答】解：∵点A（3，0），B（0，4），∴OA＝3，OB＝4，∴AB＝＝5，∴OA+AB1+B1C2＝3+5+4＝12，观察图象可知，点B2020的纵坐标为4，∵2020÷2＝1010，∴点B2020的横坐标为1010×12＝12120，12120+3+5＝12128∴点B2021的坐标为（12128，0）．故选：B．1．（2021九上·海曙期末）如图，在△ABC中，∠BAC=75∘，以点A为旋转中心，将△ABC绕点A逆时针旋转得到△ADE，点B、C的对应点分别为D、E，连接CE，若CE//AB，则∠CAE的值是( )A．25∘B．30∘C．35∘D．45∘【答案】B【解答】解：∵CE∥AB，∴∠BAC=∠ACE=75°；∵以点A为旋转中心，将△ABC绕点A逆时针旋转得到△ADE，∴AE=AC，∴∠AEC=∠ECA=75°；∴∠CAE=180°-2×75°=30°.故答案为：B.2．（2021九上·虎林期末）如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1cm，将Rt△ABC绕点A逆时针旋转得到Rt△ABC，使点C落在AB边上，连接BB，则BB的长度是（）A．1cm B．2cm CD．【解答】解：∵∠C=90°，∠ABC=30°，AC=1cm，由直角三角形中，30°角所对的直角边等于斜边的一半可知，∴AB=2AC=2cm，又∠CAB=90°-∠ABC=90°-30°=60°，由旋转的性质可知：∠CAB=∠BA B′=60∘，且AB=A B′，∴ΔBA B′为等边三角形，∴B B′=AB=2．故答案为：B．3．（2022春•泗县期中）如图所示，△ABC为直角三角形，BC为斜边，将△ABP绕点A逆时针旋转后，能与△ACP'重合．如果AP＝3，那么PP'的长等于（）A．B．C．3D．4【答案】A【解答】解：∵△ABC是直角三角形，∴∠BAC＝90°，∵△ABP绕点A逆时针旋转后，能与△ACP′重合，∴AP＝AP′，AB＝AC，∠PAP′＝∠BAC＝90°，∴△APP′为等腰直角三角形，∴PP′＝AP＝3，故选：A．4．（2021秋•甘井子区期末）如图，Rt△ABC中，∠ABC＝90°，∠BAC＝60°，AB＝1，将△ABC绕点B顺时针旋转得到△A'BC'，若直线A'C'经过点A，则CC'的长为（）A．1B．2C．D．4【答案】C【解答】解：∵将△ABC 绕点B 顺时针旋转得到△A 'BC '，∴BA ＝BA '，BC ＝BC '，∠BAC ＝∠BA 'C '，∵∠BAC ＝60°，∴∠A '＝60°，∴△ABA '是等边三角形，∴∠ABA '＝60°，∴∠CBC '＝∠ABA '＝60°，∴△BCC '是等边三角形，∴CC '＝BC ，∵∠ABC ＝90°，∠BAC ＝60°，∴∠ACB ＝30°，∴AC ＝2AB ＝2，∴BC ＝，∴CC '＝BC ＝，故选：C5（2022·呼和浩特）如图，△ABC 中，∠ACB =90°，将△ABC 绕点C 顺时针旋转得到△EDC ，使点B 的对应点D 恰好落在AB 边上，AC 、ED 交于点F ．若∠BCD =α，则∠EFC 的度数是（用含α的代数式表示）（）A ．90°+12αB ．90°−12αC ．180°−32αD ．32α【答案】C 【解答】解：∵将△ABC 绕点C 顺时针旋转得到△EDC ，且∠BCD =α∴BC=DC ，∠ACE=α，∠A=∠E ，∴∠B=∠BDC ，∴∠B=∠BDC=180°−α2=90°−α2，∴∠A=∠E=90°−∠B=90°−90°+α2=α2，∴∠A=∠E=α2，∴∠EFC=180°−∠ACE−∠E=180°−α−α2=180°−32α，故答案为：C．6．（2021九上·富裕期末）如图，点D是等边△ABC内一点，AD＝3，BD＝3，CD＝3△ACE是由△ABD绕点A逆时针旋转得到的，则∠ADC的度数是（）A．40°B．45°C．105°D．55°【答案】C【解答】解：连接DE，如图：∵ΔABC是等边三角形，∴AB=AC，∠BAC=60°∴∠BAD+∠CAD=60°由旋转可得，ΔBAD≅ΔCAE∴∠CAE=∠BAD，AD=AE=3，CE=BD=3∴∠CAE+∠CAD=60°，即∠DAE=60°∴ΔDAE是等边三角形，∴DE=AD=3，∠ADE=60°∵DE＝3，CE＝3，CD＝∴D E2=9，C E2=9，C D2=18∴D E2+C E2=C D2∴△CDE是等腰直角三角形，∴∠CDE=45°∴∠ADC=∠ADE+∠CDE=60°+45°=105°故答案为：C7．（2022·益阳）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（）A．①②③B．①②④C．①③④D．②③④【答案】B【解答】解：∵△ABC绕A点逆时针旋转50°得到△AB′C′，∴BC＝B′C′．故①正确；∵△ABC绕A点逆时针旋转50°，∴∠BAB′＝50°，∴∠B′AC＝∠BAB′−∠CAB＝50°-20°=30°，∵∠AB′C′＝∠ABC＝30°，∴∠AB′C′＝∠B′AC，∴AC∥C′B′．故②正确；在△BAB′中，∵AB＝AB′，∠BAB′＝50°，（180°−50°）＝65°，∴∠AB′B＝∠ABB′＝12∴∠BB′C′＝∠AB′B＋∠AB′C′＝65°＋30°＝95°，∴C′B′与BB′不垂直．故③错误；在△ACC′中，AC＝AC′，∠CAC′＝50°，∴∠ACC′＝1（180°−50°）＝65°，2∴∠ABB′＝∠ACC′，故④正确.∴正确结论的序号为：①②④.故答案为：B.8.（2021九上·集贤期末）如图，在△ABC中，∠C＝36°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB′＝CB′，则旋转角为度．【答案】36【解答】解：根据题意，可得∠BAB为旋转角，∵AB′＝CB′∴∠C=∠CAB=36°∴∠ABB=2∠C=72°由旋转的性质可得：AB=AB∴∠B=∠ABB=72°∴∠BAB=36°故答案为：369．（2022春•通道县期末）已知，正方形ABCD的边长是4，正方形OMNE（OM＞AC）绕着正方形ABCD的对称中心O旋转，那么两正方形重叠部分的面积是．【答案】4【解答】解：如图：∵四边形ABCD和四边形OENM都是正方形，∴OD＝OC，∠ODP＝∠OCF＝45°，∠DOC＝∠EOM＝90°，∴∠DOP＝∠COF．在△PDO和△FCO中，，∴△PDO≌△FCO（ASA），∴两正方形重叠部分的面积是等于△DOC的面积，即重叠部分面积不变，总是等于正方形面积的，∵正方形的边长为4，∴正方形的面积为16，∴重叠部分面积不变为．故答案为：4．10．（2022•新城区校级一模）如图，D是等边三角形ABC外一点，AD＝6，CD＝4，当BD 长最大时，△ABC的面积为　．【答案】19【解答】解：如图1，以CD为边作等边△DCE，连接AE．∵BC＝AC，CD＝CE，∠BCA＝∠DCE＝60°，∴∠BCD＝∠ACE，在△BCD和△ACE中，，∴△BCD≌△ACE（SAS），∴BD＝AE，∵AE≤AD+DE，当A、D、E三点共线时，AE＝AD+DE＝10，其值最大，∴AE的最大值为10，∴BD的最大值为10，过点A作AF⊥BD于F，如下图，∵△BCD≌△ACE，∴∠BDC＝∠E＝60°，∴∠ADF＝60°，∵AF⊥BD，∴∠DAF＝30°，∴DF＝AD＝3，AF＝DF＝3，∴BF＝10﹣3＝7，∴AB2＝AF2+BF2＝76，∴△ABC的面积＝AB2＝19，故答案为：1911.（2022春•高州市期末）如图，在△ABC中，AB＝8，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分面积为．【答案】16【解答】解：过A作AD⊥A1B于D，如图：在△ABC中，AB＝8，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，∴△ABC≌△A1BC1，∴A1B＝AB＝8，∴△A1BA是等腰三角形，∠A1BA＝30°，∵AD⊥A1B，∴AD＝AB＝4，∴S△A1BA＝×8×4＝16，又∵S阴影＝S△A1BA+S△A1BC1﹣S△ABC，且S△A1BC1＝S△ABC，∴S阴影＝S△A1BA＝16，故答案为：16．12．（2021九上·龙江期末）如图，在平面直角坐标系中，四边形ABOC是正方形，点A 的坐标为（1，1），AA1⌢是以点B为圆心，BA为半径的圆弧；A1A2⌢是以点O为圆心，OA1为半径的圆弧，A2A3⌢是以点C为圆心，CA2为半径的圆弧，A3A4⌢是以点A为圆心，AA3为半径的圆弧，继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”，那么点A2021的坐标是．【答案】（2021，0）【解答】解：∵A点坐标为（1，1），且A1为A点绕B点顺时针旋转90°所得∴A1点坐标为（2，0）又∵A2为A1点绕O点顺时针旋转90°所得∴A2点坐标为（0，-2）又∵A3为A2点绕C点顺时针旋转90°所得∴A3点坐标为（-3，1）又∵A4为A3点绕A点顺时针旋转90°所得∴A4点坐标为（1，5）由此可得出规律：A n为绕B、O、C、A四点作为圆心依次循环顺时针旋转90°，且半径为1、2、3、、n，每次增加1．∵2021÷4=505 (1)故A2021为以点B为圆心，半径为2021的A2020点顺时针旋转90°所得故A2021点坐标为（2021，0）．故答案为：（2021，0）．13.（2021九上·黔西南期末）如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A1BO1的位置，使点A的对应点A1落在直线y上，再将△A1BO1绕点A1顺时针旋转到△A1B1Q2的位置，使点O1的对应点O2落在直线y上，依次进行下去…，1），则点A12的横坐标是 .若点A的坐标是（0，1），点B的坐标是【答案】9）【解答】解：根据将△A 1BO 1绕点A 1顺时针旋转到△A 1B 1O 2的位置可知：∠BA 1O 1＝90°，∴∠OAB ＝90°，当y ＝1时，xAB ∴∠AOB ＝60°，如图，延长A 2O 2交x 轴于E ，则∠OEO 2＝90°，∴OO2＝＝∴O 2∴=32（），∴点A 2的横坐标为32（），同理可得：点A4的横坐标3），点A 6的横坐标92（），点A8的横坐标6），∴点A12的横坐标是32×6），即9）.故答案为：9）.14．（2021九上·新乡期末）如图，△ABC的顶点A，B分别在x轴，y轴上，∠ABC＝90°，OA＝OB＝1，BC＝△ABC绕点O顺时针旋转，每次旋转90°，则第2021次旋转结束时，点C的坐标为 .【答案】（3，-2）【解答】解：如图，过点C作CD⊥y轴于点D，∵OA＝OB＝1，∠AOB=90°，∴∠ABO=45°，∵∠ABC＝90°，∴∠CBD=45°，∴∠BCD=45°，∴BD=CD，∵BC＝2，∴B D2+C D2=B C2=∴BD=CD=2，∴OD=OB+BD=3，∴点C(2，3)，将△ABC绕点O顺时针旋转，第一次旋转90°后，点C（3，-2），将△ABC绕点O顺时针旋转，第二次旋转90°后，点C（-2，-3），将△ABC绕点O顺时针旋转，第三次旋转90°后，点C（-3，2），将△ABC绕点O顺时针旋转，第四次旋转90°后，点C（2，3），⋯⋯由此发现，△ABC绕点O顺时针旋转四次一个循环，∵2021÷4=55⋯⋯1，∴第2021次旋转结束时，点C的坐标为（3，-2）.故答案为：（3，-2）15.（2021九上·互助期中）如图将△ABC绕点A逆时针旋转得到△ADE，点C和点E是对应点，若∠CAE=90°，AB=1，求BD的长．【答案】解：由旋转的性质得：AB=AD=1，∠BAD=∠CAE=90°，=．∴BD=16．如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.（1）求证：△BDE≌△BCE；（2）试判断四边形ABED的形状，并说明理由．【答案】（1）证明：∵△BAD是由△BEC在平面内绕点B旋转60°而得，∴DB=CB，∠ABD=∠EBC，∠ABE=60°，∵AB⊥EC，∴∠ABC=90°，∴∠DBE=∠CBE=30°，在△BDE和△BCE中，∵DB=CB∠DBE=∠CBEBE=BE，∴△BDE≌△BCE；（2）解：四边形ABED为菱形；由（1）得△BDE≌△BCE，∵△BAD是由△BEC旋转而得，∴△BAD≌△BEC，∴BA=BE，AD=EC=ED，又∵BE=CE，∴四边形ABED为菱形17.（2016九上·涪陵期中）如图，P是正三角形ABC内的一点，且PA=5，PB=12，PC=13，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB 的度数．【答案】解：∵△ABC为等边三角形，∴AB=AC，∠BAC=60°，∵△PAC绕点A逆时针旋转后，得到△P′AB，∴∠P′AP=∠BAC=60°，AP′=AP，BP′=CP=13，∴△AP′P为等边三角形，∴PP′=AP=5，∠APP′=60°，在△BPP′中，∵PP′=5，BP=12，BP′=13，∴PP′2+BP2=BP′2，∴△BPP′为直角三角形，∠BPP′=90°，∴∠APB=∠APP′+∠BPP′=60°+90°=150°．答：点P与点P′之间的距离为5，∠APB的度数为150°．18．（2022春•渭滨区期末）如图，O是等边△ABC内一点，连接OA、OB、OC，且OA＝3，OB＝4，OC＝5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．（1）求线段OD的长；（2）求∠BDC的度数．【解答】解：（1）∵△BAO绕点B顺时针旋转后得到△BCD，∴BO＝BD，而∠OBD＝∠ABC＝60°，∴△OBD为等边三角形，∴OD＝BO＝4；（2）∵△BOD为等边三角形，∴∠BDO＝60°，OD＝4，∵△BAO绕点B顺时针旋转后得到△BCD，∴CD＝AO＝3，在△OCD中，CD＝3，OD＝4，OC＝5，∵CD2+OD2＝32+42＝52＝OC2，∴△OCD为直角三角形，∠ODC＝90°，∴∠BDC＝∠BDO+∠ODC＝60°+90°＝150°．19.（2022春•永丰县期中）如图，在△ABC中，BA＝BC，∠ABC＝40°，将△ABC绕点B按逆时针方向旋转110°，得到△DBE，连接AD，CE．（1）求证：△ABD≌△CBE．（2）求∠ACE的度数．【解答】（1）证明：∵△ABC绕点B按逆时针方向旋转110°，∴∠ABC＝∠DBE，∠ABD＝∠CBE，AB＝BC＝BD＝BE，在△ABD与△CBE中，，∴△ABD≌△CBE（SAS）；（2）解：∵∠ABD＝∠CBE＝110°，BA＝BC＝BD＝BE，∴∠BAD＝∠ADB＝∠BCE＝∠BEC＝35°．∵AB＝BC，∠ABC＝40°，∴∠ACB＝70°，∴∠ACE＝∠ACB+∠BCE＝105°．。

应用图形的旋转巧解“难题”

应用图形的旋转巧解 “难题图形旋转的实质是图形的全等，而图形的全等中有对应边相等、对应角相等的性质，通过旋转，可以得到一些新的特殊图形、特殊关系，利用这些图形和关系，能巧妙地解决一些 “难题 ”。

面通过例子说明利用旋转解题的一些思路方法，希望能为同学们学习、运用旋转更好地解决问题提供帮助。

一、正方形类型在正方形 ABCD 中，P 为正方形 ABCD 内一点，将 ΔAPD 绕 A 点按顺时针方向旋转 900，使得 AD 与 AB 重合，连接 PQ ，可得等腰直角 ΔAPQ ，且图 1 中与 PA 、 PB 、PD 三条线段相关的线段集中于图 2 中的 ?PBQ 中，对问题的解决起到重要的作用。

例 1、正方形 ABCD 内一点 P ，且 PA=2，PB=4，PD= 2 2 ，则∠ APD= _____ ；提示：正方形 ABCD 中， AB=AD ，∴ △APD 绕点 A 顺时针旋转 90°到△AQB ， ∴∠APD =∠AQB ，PA=QA 连结 PQ∵旋转角为 90°，∴∠ PAQ= 90°∴ △PAQ 是等腰直角三角形， ∴∠ AQP= 45°，又 AQ=PA= 2，Rt △PAQ 中，由勾股定理得： PQ=2 2又 BQ=PD= 2 2 ∴ PQ 2 BQ 2 (2 2)2 (2 2)2 16 PB 2 由勾股定理的逆定理得： ∠ PQB=90°图2∴ ∠APD= ∠AQB= ∠AQP+∠PQB=45°+90°=135°；变式：正方形ABCD中，E、F分别为BC、CD上的点，若BE=3，DF=2，且∠ EAF= 450，求EF 的长。

分析：本题看起来无从下手，只要将它与旋转联系起来问题就好解决了。

解：正方形ABCD中，AB=AD，将△ADF绕点A顺时针方向旋转900，使AD 与AB 重合，点 F 的对应点是G ，∴ △ ABG ≌△ADF ，则AG=AF ，∠BAG= ∠DAFBG=DF= 2，且∠ABG= ∠D =∠ABE=900∴ G、B、 E 三点在同一直线上。

巧用旋转解题例说

)))巧用旋转解题例说■ 韩敬摘要: 旋转是图形变换之一，它在解题中有着广泛的应用，本文是从等线段的视角下，利用旋转来思考，达到快速解题的目的．关键词: 等线段; 旋转; 速解题所谓旋转就是在平面内，把一个图形绕着一个定点沿顺时针或逆时针方向旋转一定的角度得到另一个图形的变换．旋转“前后的对应线段相等”这一特性在解题或分析问题中有着重要的作用．当条件中或结论中出现或隐含着共顶点等线段，且不能直接解决时，我们可用旋转法来解答，会有出奇制胜的效果．一、直接利用共顶点等线段旋转来解答例 1 ( 2015 年江苏常州市)如图 1，在 ⊙O 的内接四边形接四边形性质，解直角三角形，全等三角形的性质和判定的应用．速解本题的关键是将 △ACD 绕点 C 逆时针旋转120° 得 △C B E ．二、先寻找共顶点的等线段，再用旋转来解答例2 ( 2014 年湖北武汉) 如图2，在四边形 A B C D 中，A D = 4，C D = 3，∠A B C = ∠A C B = ∠A D C = 45°，则BD的长为．解析: 由 ∠A B C = ∠A C B = ∠A D C = 45°，得 A C = A B ，∠B A C = 90°，这里有共顶点等线段 A C = A B ，特殊角 ∠B A C = 90°，可考虑旋转，即把 △A B C 绕点 A 顺时针旋转90° 得△A C D '，由旋转性质得: C D ' = BD ， A D ' = A D ，∠D A D ' = ∠B A C = 90°，连接 DD '，从而得 ∠A DD ' = ∠A D 'D = 45°，所以 ∠C DD ' = ∠A DD ' + A B C D 中，A B = 3，A D = 5，∠B A D∠A D C = 90°，由勾股定理得 DD ' = 槡AD 2+ AD'2= = 60°，点 C 为BD 的中点，则 A C 4 槡2 ，C D ' = 槡CD 2+ DD'2= 槡41 ．的长是．解析: 因为 A 、B 、C 、D 四点共圆，所以 ∠ABC + ∠D = 180°， ∠BCD = 180° － ∠BAD = 120°，图 1因为B C = C D ，所以B C = C D ，∠C A D = ∠C A B = 30°，这里有共顶点等线段 BC = CD ，特殊角 ∠BCD = 120°，可考虑旋转，即将△A C D 绕点C 逆时针旋转120°得 △C B E ，则 ∠E = ∠C A D = 30°，∠D = ∠E B C ，B E = A D = 5，A C = C E ，从而得 ∠A B C + ∠E B C = 180°，即 A 、B 、E 三点共线，过 C 作 CM ⊥ A E 于 M ，因为A C = C E ，所以 A M = E M = 1 × A E = 1× ( 5 + 3) = 4，在点评: 本题考查了等腰三角形的判定，全等三角形的判定与性质，勾股定理，难度较大，利用旋转方法来解答，可很快得解．图2 图3 三、挖掘共顶点等线段，用以探索解题思路例 3 ( 2014 重庆市) 如图 3，正方形 A B C D 的边 2 2 长为6，点 O 是对角线 A C 、BD 的交点，点 E 在 C D 上，且Ｒt △A MC 中，A C = A M= 4 = 8 槡3 ．故填: 8 槡3．D E = 2C E ，连接 B E ．过点 C 作 C F ⊥ B E ，垂足是 F ，连 cos30° cos30° 3 3点评: 本题考查了圆心角、弧、弦之间的关系，圆内接 O F ，则O F 的长为．作者简介: 韩敬( 1977 － ) ，男，中学高级教师，主要从事中学数学教学研究·36·5解析: 在 B E 上截取 B G = C F ，连接 O G ，由 C F ⊥ B E ，可得 ∠E B C = ∠E C F ，因为 ∠OB C = ∠O C D = 45°，所以 ∠OB G = ∠O C F ，又 OB = O C ，可证 △OB G ≌ △O C F ，所以 O G = O F ，∠BO G = ∠C O F ，在Ｒt △B C E 中，B C = D C = 6，D E = 2E C ，可得 E C = 2， BE = 槡BC 2+ CE 2== 2 槡10 ，由 CF ⊥ 图 4 图5 ( 2) 在图6 中，D E 与 A C B E ，易证 △B C F ∽ △B E C ，所以 B C ∶ B E = B F ∶ B C ，即6 ∶ 2 槡10 = B F ∶ 6，解得 B F = 9槡10s ，所以E F = B E － BF = 槡10 ，类似地可得 CF = 3 槡10，所以 GF = BF延长线交于点P ，BD 与D P 是否相等? 请直接写出你的结论，无需证明．分析: ( 1) 要证5－ BG = BF － CF = 5，因为 ∠BOC = ∠BOG + 5 BD =D P ，直观观察 BD 所在的三角形只有 △ABD ，且它是钝图6∠G O C = ∠C O F + ∠G O C = ∠G O F = 90°，所以O G ⊥O F ，即在等腰直角 △O G F 中，O F 2= 1 G F 2 = 1 · 角的邻边，而 DP 所在的三角形只有△A D P ，且它是钝角的对边，因此这两个三角形 2 ( 6 槡10 ) 2，解得O F = 6 槡5 ．故填: 6 槡5． 5 5 52 不可能全等．于是利用所证结论 BD = DP 逆向思考，利用旋转方法，把 △A D P 绕点 D 顺时针旋转 90°，得 △F DB ，这样就找到解题思路，即可过点 D 作 D F ⊥ A D 点评: 本题考查了全等三角形的判定和性质，直角三角形的判定以及相似三角形的判定与性质、勾股定理．为什么要“在 B E 上截取 B G = C F ，连接 O G ”呢?理由: 由正方形 A B C D 得OB = O C ，∠BO C = 90°，因此可以考虑用旋转来找思路，即将把 △OCF 绕点 O 顺时针旋转90° 得△OB G ，此时△O G F 为等腰直角三角形，要求 O F 的长，只要求 G F 的长，而 G F = B F － B G ，于是只要求BF 与BG 的长，这可利用相似三角形求得，于是问题得解．四、根据结论中的共顶点等线段，逆向分析来探索解题思路例4 ( 2014 年黑龙江齐齐哈尔市) 在等腰直角三角形 A B C 中，∠B A C = 90°，A B = A C ，直线 M N 过点 A 且 M N ∥ B C ．以点 B 为一锐角顶点作Ｒt △BD E ，∠BD E = 90°，且点 D 在直线 M N 上( 不与点 A 重合) ．如图 4， D E 与 A C 交于点 P ，易证: BD = D P ． ( 无需写证明过程)( 1) 在图 5 中，D E 与 C A 延长线交于点 P ，BD = DP 是否成立? 如果成立，请给予证明，如果不成立，请说明理由;交A B 于点 F ．易证△A D P ≌ △F DB ，所以 BD = D P ; 可用同样的方法完成( 2) 、( 3) 问的解答．解: ( 1) BD = DP 成立．证明: 过点 D 作 D F ⊥ M N ，交 A B 的延长线于点 F ，则△A D F 为等腰直角三角形，所以 D A = D F ．因为∠1 + ∠A DB = 90°，∠A DB + ∠2 = 90°，所以 ∠1 = ∠2．因为∠D F B = ∠D A P = 45°，所以△BD F ≌ △P D A ，所以 BD = D P ．( 2) 答: BD = D P ．点评: 本题考查了全等三角形的判定与性质、等腰直角三角形的性质．本例是从结论入手，用旋转法逆向推理找到解题的思路，这就是作辅助线构造全等三角形的巧妙之处．通过上面的例子，可以看出: 共顶点的等线段有时在条件中直接给出( 如例 1) ，有时需要我们去寻找( 如例2、3) ，共顶点的等线段可以是条件中的( 如例2、3) ，也可以是结论中的( 如例 4) ，若在条件中，则可顺推; 若在结论中，则可逆推．［安徽省定远县第一初级中学 ( 233200) ］·37·槡62+ 226 槡10。

初中数学巧用旋转进行计算之三大题型及答案

解题技巧专题：巧用旋转进行计算之三大题型【考点导航】目录【典型例题】【题型一利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】【题型二利用旋转结合特殊三角形的判定、性质或勾股定理求长度】【题型三利用旋转计算面积】【典型例题】【题型一利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】1(2023春·内蒙古巴彦淖尔·九年级校考期中)如图，在△ABC中，BC<BA，将△BCA以点B为中心逆时针旋转得到△BED，点E在边CA上，ED交BA于点F，若∠FEA=40°，则∠DBF=()A.40°B.50°C.60°D.70°【变式训练】1(2023春·辽宁沈阳·八年级沈阳市第四十三中学校考期中)如图，在△ABC中，∠B=42°，将△ABC 绕点A逆时针旋转，得到△ADE，点D恰好落在BC的延长线上，则旋转角的度数()A.86°B.96°C.106°D.116°2(2023春·河南新乡·七年级统考期末)如图，在△ABC中，∠BAC=104°，将△ABC绕点A逆时针旋转94°得到△ADE，点B的对应点为点D，若点B，C，D恰好在同一条直线上，则∠E的度数为()A.25°B.30°C.33°D.40°3(2023·浙江温州·校联考三模)如图，在△ABC中，∠BAC=50°，将△ABC绕点A逆时针旋转得△ADE，使点D恰好落在AC边上，连结CE，则∠ACE的度数为()A.45°B.55°C.65°D.75°4(2023春·甘肃兰州·八年级兰州市第五十六中学校考期中)如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB C 的位置，使得CC ∥AB，划∠BAB 的度数是()A.35°B.40°C.50°D.70°5(2023春·江苏连云港·八年级校考阶段练习)如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为()A.60°B.70°C.75°D.85°6(2023春·江苏盐城·八年级校考阶段练习)如图，∠AOB=90°，∠B=20°，△A OB 可以看作是△AOB绕点O顺时针旋转α角度得到的．若点A 在AB上，则旋转角α的度数是.7(2023春·上海嘉定·七年级校考期末)已知△ABC中，AB=AC，将△ABC绕点C旋转得△CDE，使点B恰好落在边AB上点D处，边DE交边AC于点F(如图)，如果△CDF为等腰三角形，则∠A的度数为．【题型二利用旋转结合特殊三角形的判定、性质或勾股定理求长度】1(2023秋·福建莆田·九年级校考开学考试)如图，将△ABC绕点C逆时针旋转一定的角度得到△A B C ，此点A在边B C上，若BC=5,AC=3，则AB 的长为()A.5B.4C.3D.2【变式训练】1(2023春·四川达州·八年级校考期中)如图，把△ABC绕点C逆时针旋转90°得到△DCE，若∠ACB =90°，∠A=30°，AB=10，AC=8，则AD的长为()A.2B.3C.4D.52(2023春·陕西汉中·八年级统考期中)如图，在△ABC中，∠ACB=90°，将△ABC绕点A顺时针旋转90°，得到△ADE，连接BD，若AC=22,DE=1，则线段BD的长为．3(2023春·四川成都·八年级成都嘉祥外国语学校校考期中)如图．Rt△ABC中，∠C=90°，BC=3，AC=4，将△ABC绕点B逆时针旋转得△A BC ，若点C 在AB上，则AA 的长为．4(2023·山西运城·校联考模拟预测)如图，在Rt△ABC中，∠C=90°，AC=BC=6，点D为AC的中点，点E是AB边上的一点，连接DE，将线段DE绕点D顺时针旋转90°，得到DF，连接AF，EF，若BE= 22，则AF的长为．5(2023·河南周口·统考一模)如图1，在△ABC中，∠A=90°，AB=AC=2，D，E分别为边AB和AC的中点，现将△ADE绕点A自由旋转，如图2，设直线BD与CE相交于点P，当AE⊥EC时，线段PC 的长为．6(2023春·陕西渭南·八年级统考阶段练习)如图，在△ABC中，∠B=60°，AB=3，将△ABC绕点A 按逆时针方向旋转得到△ADE，若点B的对应点D恰好落在边BC上，求BD的长．【题型三利用旋转计算面积】1(2023秋·湖南永州·九年级校考开学考试)如图，正方形ABCD和正方形EFGO的边长都是1，正方形EFGO绕点O旋转时，两个正方形重叠部分的面积是()A.14B.12C.13D.不能确定【变式训练】1(2023春·山东青岛·八年级统考期中)将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后，得到△AB C ，则图中阴影部分的面积是( )cm2．A.12.5B.2536C.2533D.不能确定2(2023秋·四川德阳·九年级统考期末)如图，边长为定值的正方形ABCD的中心与正方形EFGH的顶点E重合，且与边AB、BC相交于M、N，图中阴影部分的面积记为S，两条线段MB、BN的长度之和记为l，将正方形EFGH绕点E逆时针旋转适当角度，则有()A.S变化，l不变B.S不变，l变化C.S变化，l变化D.S与l均不变3(2023春·广东清远·八年级校考期中)如图，在△ABC中，∠C=90°，AC=BC=2，将△ABC绕点A逆时针方向旋转60°到△ABC 的位置，则图中阴影部分的面积是．4(2023春·江苏宿迁·八年级校考阶段练习)马老师在带领学生学习《正方形的性质与判定》这一课时，给出如下问题：如图①，正方形ABCD的对角线AC、BD相交于点O，正方形A B C O与正方形ABCD的边长相等．在正方形A B C O绕点O旋转的过程中，OA 与AB相交于点M，OC 与BC相交于点N，探究两个正方形重叠部分的面积与正方形ABCD的面积有什么关系．(1)小亮第一个举手回答“两个正方形重叠部分的面积是正方形ABCD面积的”；请说明理由．(2)马老师鼓励同学们编道拓展题，小颖编了这样一道题：如图②，在四边形ABCD中，AB=AD，∠BAD =∠BCD=90°，连接AC．若AC=6，求四边形ABCD的面积．请你帮小颖解答这道题．5(2023春·广东深圳·八年级统考期末)【问题背景】如图1，在▱ABCD中，AB⊥DB．将△ABD绕点B逆时针旋转至△FBE，记旋转角∠ABF=α0°<α≤180°，当线段FB与DB不共线时，记△ABE的面积为S1，△FBD的面积为S2．【特例分析】如图2，当EF恰好过点A，且点F，B，C在同一条直线上时．(1)α=°；(2)若AD=43，则S1=，S2=；【推广探究】某数学兴趣小组经过交流讨论，猜想：在旋转过程中，S1与S2之间存在一定的等量关系．再经过独立思考，获得了如下一些解决思路：思路1：如图1，过点A，E分别作直线平行于BE，AB，两直线交于点M，连接BM，可证一组三角形全等，再根据平行四边形的相关性质解决问题；思路2：如图2，过点E作EH⊥AB于点H，过点D作DG⊥FB，交FB的延长线于点G，可证一组三角形全等，再根据旋转的相关性质解决问题；⋯⋯(3)如图3，请你根据以上思路，并结合你的想法，探究S1与S2之间的等量关系为，并说明理由．【拓展应用】在旋转过程中，当S1+S2为▱ABCD面积的12时，α的值为解题技巧专题：巧用旋转进行计算之三大题型【考点导航】目录【典型例题】【题型一利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】【题型二利用旋转结合特殊三角形的判定、性质或勾股定理求长度】【题型三利用旋转计算面积】【典型例题】【题型一利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】1(2023春·内蒙古巴彦淖尔·九年级校考期中)如图，在△ABC中，BC<BA，将△BCA以点B为中心逆时针旋转得到△BED，点E在边CA上，ED交BA于点F，若∠FEA=40°，则∠DBF=()A.40°B.50°C.60°D.70°【答案】A【分析】根据旋转的性质可得∠A=∠D，由对顶角相等可得∠BFD=∠EFA，根据三角形的外角性质可得∠DBF=∠AEF，即可求解．【详解】解：∵将△BCA以点B为中心逆时针旋转得到△BED，∴∠A=∠D，∵∠BFD=∠EFA，∴∠BFE=∠A+∠AEF=∠D+∠DBF∵∠FEA=40°，∴∠DBF=∠AEF=40°，故选：A．【点睛】本题考查了旋转的性质，三角形的外角的性质，熟练掌握旋转的性质是解题的关键．【变式训练】1(2023春·辽宁沈阳·八年级沈阳市第四十三中学校考期中)如图，在△ABC中，∠B=42°，将△ABC 绕点A逆时针旋转，得到△ADE，点D恰好落在BC的延长线上，则旋转角的度数()A.86°B.96°C.106°D.116°【答案】B【分析】由旋转的性质可知AB=AD，可算出∠ADB=42°，就可以算出旋转角．【详解】由旋转的性质可知：AB=AD，∠BAD是旋转角，∵AB=AD，∴∠ADB=∠B=42°，∴∠BAD=180°-∠ADB-∠B=96°，故选：B．【点睛】本题考查旋转的性质、等边对等角、三角形内角和定理，找到旋转的对应边、对应角是解决问题的关键．2(2023春·河南新乡·七年级统考期末)如图，在△ABC中，∠BAC=104°，将△ABC绕点A逆时针旋转94°得到△ADE，点B的对应点为点D，若点B，C，D恰好在同一条直线上，则∠E的度数为()A.25°B.30°C.33°D.40°【答案】C【分析】由旋转的性质可得∠BAD=94°，AB=AD，由等腰三角形的性质可得∠B=∠ADB=43°，即可求解．【详解】解：∵将△ABC绕点A逆时针旋转94°得到△ADE，∴∠BAD=94°，AB=AD，∴∠B=∠ADB=43°，∵∠BAC=104°，∴∠C=180°-104°-43°=33°，故选：C．【点睛】本题考查了旋转的性质，等腰三角形的性质，掌握旋转的性质是解题的关键．3(2023·浙江温州·校联考三模)如图，在△ABC中，∠BAC=50°，将△ABC绕点A逆时针旋转得△ADE，使点D恰好落在AC边上，连结CE，则∠ACE的度数为()A.45°B.55°C.65°D.75°【答案】C【分析】由旋转的性质可知，旋转前后对应边相等，对应角相等，得出等腰三角形，再根据等腰三角形的性质求解．【详解】解：由旋转的性质可知，∠CAE=∠BAC=50°，AC=AE，∴∠ACE=∠AEC，在△ACE中，∠CAE+∠ACE+∠AEC=180°，∴50°+2∠ACE=180°，解得：∠ACE=65°，故选：C．【点睛】本题主要考查了旋转的性质，找出旋转角和旋转前后的对应边得出等腰三角形是解答此题的关键．4(2023春·甘肃兰州·八年级兰州市第五十六中学校考期中)如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB C 的位置，使得CC ∥AB，划∠BAB 的度数是()A.35°B.40°C.50°D.70°【答案】B【分析】根据平行线的性质，结合旋转性质，由等腰三角形性质及三角形内角和定理求解即可得到答案．【详解】解：∵CC ∥AB，∠CAB=70°，∴∠C CA=∠CAB=70°，∵将△ABC绕点A逆时针旋转到△AB C 的位置，∴∠C AB =∠CAB=70°，AC =AC，∴∠AC C=∠C CA=70°，∴∠C AC=180°-70°-70°=40°，∵∠BAB =∠CAB-CAB ，∠CAC =∠C AB -CAB ，∴∠BAB =∠C AC=40°，即旋转角的度数是40°，故选：B．【点睛】本题考查旋转性质求角度，涉及平行线的性质、旋转性质、等腰三角形的判定与性质及三角形内角和定理，熟练掌握旋转性质，数形结合，是解决问题的关键．5(2023春·江苏连云港·八年级校考阶段练习)如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为()A.60°B.70°C.75°D.85°【答案】D【分析】根据旋转的性质得出∠C=∠E=70°，∠BAC=∠DAE，根据三角形内角和定理可得∠CAF=20°，进而即可求解．【详解】解：如图所示，设AD,BC交于点F，∵△ABC绕点A逆时针旋转得到△ADE，∴∠C=∠E=70°，∠BAC=∠DAE，∵AD⊥BC，∴∠AFC=90°，∴∠CAF=90°-∠C=90°-70°=20°，∴∠DAE=∠CAF+∠EAC=20°+65°=85°，∴∠BAC=∠DAE=85°．故选：D．【点睛】本题考查了旋转的性质，三角形的内角和定理，熟练掌握旋转的性质是解题的关键．6(2023春·江苏盐城·八年级校考阶段练习)如图，∠AOB=90°，∠B=20°，△A OB 可以看作是△AOB绕点O顺时针旋转α角度得到的．若点A 在AB上，则旋转角α的度数是.【答案】40°/40度【分析】根据旋转的性质得到AO=A O，根据等边对等角得到∠A=70°=∠OA A，再利用三角形内角和定理计算即可．【详解】解：△A OB 可以看作是△AOB绕点O顺时针旋转α角度得到的，点A 在AB上，∴AO=A O，∵∠B=20°，∠AOB=90°，∴∠A=70°=∠OA A，∴∠AOA =180°-2×70°=40°，即旋转角α的度数是40°，故答案为：40°．【点睛】本题考查了旋转的性质，等边对等角，三角形内角和定理，关键是得出∠A=70°=∠OA A，题目比较典型，难度不大．7(2023春·上海嘉定·七年级校考期末)已知△ABC中，AB=AC，将△ABC绕点C旋转得△CDE，使点B恰好落在边AB上点D处，边DE交边AC于点F(如图)，如果△CDF为等腰三角形，则∠A的度数为．【答案】36°或180°7【分析】如图，设∠B=x，利用等腰三角形的性质和三角形内角和定理得到∠A=180°-2x，再利用旋转的性质得CB=CD，∠2=∠B=x，则∠1=∠B=x，利用平角定理得∠5=180°-2x，利用三角形外角性质∠3=360°-4x得，讨论：当CD=CF时，∠2=∠3=x，则x=360°-4x；当CD=DF时，∠4=∠3，利用∠2+∠3+∠4=180°得到x+2360°-4x=180°；当CF=DF时，∠2=∠4=x，利用∠2+∠3+∠4= 180°得到x+x+360°-2x=180°，然后分别解关于x的方程，然后计算180°-2x即可得到∠A的度数．【详解】解：如图，设∠B=x，∵AB=AC，∴∠ACB=∠B=x∴∠A=180°-2x，∵△ABC绕点C旋转得△CDE，使点B恰好落在边AB上点D处，∴CB=CD，∠2=∠B=x，∴∠1=∠B=x，∴∠5=180°-2x，∠3=∠A+∠5=360°-4x，当CD=CF时，△CDF为等腰三角形，即∠2=∠3=x，则x=360°-4x，解得x=72°，此时∠A=180°-2x =36°；当CD=DF时，△CDF为等腰三角形，即∠4=∠3，而∠2+∠3+∠4=180°，则x+2360°-4x=180°，解得x=540°7，此时∠A=180°-2x=180°7，当CF=DF时，△CDF为等腰三角形，即∠2=∠4=x，而∠2+∠3+∠4=180°，则x+x+360°-2x=180°，无解，故舍去，综上所述，△CDF为等腰三角形时∠A的度数为36°或180°7，故答案为36°或180°7．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了三角形内角和、等腰三角形的性质和分类讨论思想．【题型二利用旋转结合特殊三角形的判定、性质或勾股定理求长度】1(2023秋·福建莆田·九年级校考开学考试)如图，将△ABC绕点C逆时针旋转一定的角度得到△A B C ，此点A在边B C上，若BC=5,AC=3，则AB 的长为()A.5B.4C.3D.2【答案】D【分析】根据图形旋转的性质可得CB =CB=5，即可求解．【详解】解：∵将△ABC绕点C逆时针旋转一定的角度得到△A B C ，此点A在边B C上，∴CB =CB=5，∴AB =CB -CA=5-3=2．故选：D．【点睛】本题主要考查了图形的旋转，熟练掌握图形旋转的性质是解题的关键．【变式训练】1(2023春·四川达州·八年级校考期中)如图，把△ABC绕点C逆时针旋转90°得到△DCE，若∠ACB =90°，∠A=30°，AB=10，AC=8，则AD的长为()A.2B.3C.4D.5【答案】A【分析】利用勾股定理求得BC=6，再根据旋转的性质可得CD=CB=6，即可求解．【详解】解；∵∠ACB=90°，AB=10，AC=8，∴BC=102-82=6，∵把△ABC绕点C逆时针旋转90°得到△DCE，∴CD=CB=6，∴AD=AC-CD=8-6=2，故选：A．【点睛】本题考查勾股定理和旋转的性质，熟练掌握旋转的性质是解题的关键．2(2023春·陕西汉中·八年级统考期中)如图，在△ABC中，∠ACB=90°，将△ABC绕点A顺时针旋转90°，得到△ADE，连接BD，若AC=22,DE=1，则线段BD的长为．【答案】32【分析】先由旋转的性质得到AD=AB，DE=BC=1，AE=AC=22，∠DAB=90°，然后由∠ACB= 90°计算出AB的长度，最后由勾股定理算出线段BD的长．【详解】解：由旋转得，AD=AB，DE=BC=1，AE=AC=22，∠DAB=90°，∵∠ACB=90°,∴AB=AC2+BC2=222+12=3，∴AD=AB=3，∵∠DAB=90°，∴BD=AB2+AD2=32+32=32，故答案为：32．【点睛】本题考查了旋转的性质和勾股定理，熟练应用“旋转过程中对应线段相等”是解题的关键．3(2023春·四川成都·八年级成都嘉祥外国语学校校考期中)如图．Rt△ABC中，∠C=90°，BC=3，AC=4，将△ABC绕点B逆时针旋转得△A BC ，若点C 在AB上，则AA 的长为．【答案】25【分析】先根据勾股定理求出AB的长，再利用旋转的性质可得AC=A C =4，BC=BC =3，∠C=∠BC A =90°，从而求出的长，然后在Rt△A C A中，利用勾股定理进行计算即可解答．【详解】解：∵∠C=90°，BC=3，AC=4，∴AB=AC2+BC2=42+32=5，由旋转得：AC=A C =4，BC=BC =3，∠C=∠BC A =90°，∴AC =AB-BC =5-3=2，∠AC A =180°-∠BC A =90°，∴AA =C A2+A C 2=22+42=25，故答案为：25．【点睛】本题考查了旋转的性质，勾股定理的应用，化为最简二次根式，熟练掌握旋转的性质是解题的关键．4(2023·山西运城·校联考模拟预测)如图，在Rt△ABC中，∠C=90°，AC=BC=6，点D为AC的中点，点E是AB边上的一点，连接DE，将线段DE绕点D顺时针旋转90°，得到DF，连接AF，EF，若BE= 22，则AF的长为．【答案】2【分析】由等腰直角三角形的性质可求AD=DH，由旋转的性质可得DE=DF，∠EDF=90°=∠ADH，由“SAS”可证△ADF≌△HDE，可得AF=HE=2．【详解】解：如图，取AB的中点H，连接CH，DH，∵∠C=90°，AC=BC=6，H是AB的中点，∴AB=62，AH=BH=32=CH，CH⊥AB，又∵点D是AC的中点，∴AD =CD =DH ，AD ⊥DH ，∵BE =22，∴EH =2，∵将线段DE 绕点D 顺时针旋转90°，∴DE =DF ，∠EDF =90°=∠ADH ，∴∠ADF =∠EDH ，∴△ADF ≌△HDE SAS ，∴AF =HE =2，故答案为：2．【点睛】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定和性质，添加恰当辅助线构造全等三角形是解题的关键．5(2023·河南周口·统考一模)如图1，在△ABC 中，∠A =90°，AB =AC =2，D ，E 分别为边AB 和AC 的中点，现将△ADE 绕点A 自由旋转，如图2，设直线BD 与CE 相交于点P ，当AE ⊥EC 时，线段PC 的长为．【答案】3-1或3+1【分析】由△ADE 绕点A 自由旋转可知有以下两种情况：①当点E 在AC 的右侧时，AE ⊥CE ，先证△ABD 和△ACE 全等，进而可证四边形AEPD 为正方形，然后求出PE =1，CE =3，进而可得PC 的长；②当点E 在AC 的右侧时，AE ⊥CE ，同理①证△ABD 和△ACE 全等，四边形AEPD 为正方形，进而得PE =1，CE =3，据此可求出PC 的长，综上所述即可得出答案．【详解】解：∵△ADE 绕点A 自由旋转，∴有以下两种情况：①当点E 在AC 的右侧时，AE ⊥CE ，如图：由旋转的性质得：∠DAE =∠BAC =90°，∴∠BAD +∠DAC =∠DAC +∠CAE =90°，∴∠BAD =∠CAE ，∵AB =AC =2，D ，E 分别为边AB 和AC 的中点，∴AD =AE =1，在△ABD 和△ACE 中，AB =AC∠BAD =∠CAE AD =AE，∴△ABD ≌△ACE (SAS )，∴∠ADB =∠AEC =90°，∴∠ADP =∠DAE =∠AEC =90°，∴四边形AEPD 为矩形，又AD =AE =1，∴矩形AEPD 为正方形，∴PE =AE =1，在Rt△AEC中，AE=1，AC=2，∠AEC=90°，由勾股定理得：CE=AC2-AE2=3，∴PC=CE-PE=3-1；②当点E在AC的右侧时，AE⊥CE，如图：同理可证：△ABD≌△ACE(SAS)，四边形AEPD为正方形，∴BD=CE，PE=AE=1，在Rt△ABD中，AD=1，AB=2，∠ADB=90°，由勾股定理的：BD=AB2-AD2=3，∴CE=BD=3，∴PC=CE+PE=3+1．综上所述：当AE⊥EC时，线段PC的长为3-1或3+1．答案为：3-1或3+1．【点睛】此题主要考查了图形的旋转变换及其性质，等腰直角三角形的性质，正方形的判定及性质，全等三角形的判定及性质，勾股定理等，解答此题的关键是熟练掌握图形的旋转变换，全等三角形的判定、正方形的判定方法，灵活运用勾股定理进行计算，难点是根据题意进行分类讨论并画出示意图，漏解是易错点之一．6(2023春·陕西渭南·八年级统考阶段练习)如图，在△ABC中，∠B=60°，AB=3，将△ABC绕点A 按逆时针方向旋转得到△ADE，若点B的对应点D恰好落在边BC上，求BD的长．【答案】3【分析】根据旋转的性质得出△ABD是等边三角形，根据等边三角形的性质即可求解．【详解】∵∠B=60°，AB=3，将△ABC绕点A按逆时针方向旋转得到△ADE，∴AB=AD，∠B=60°，AB=3，∴△ABD是等边三角形，∴BD=AB=3，【点睛】本题考查了旋转的性质，等边三角形的判定和性质，熟练掌握旋转的性质和等边三角形的判定是解题的关键．【题型三利用旋转计算面积】1(2023秋·湖南永州·九年级校考开学考试)如图，正方形ABCD和正方形EFGO的边长都是1，正方形EFGO绕点O旋转时，两个正方形重叠部分的面积是()A.14B.12C.13D.不能确定【答案】A【分析】根据正方形的性质得出OB=OC，∠OBA=∠OCB=45°，∠BOC=∠EOG=90°，推出∠BON=∠MOC，证出△OBN≌△OCM，即可求出两个正方形重叠部分的面积．【详解】解：∵四边形ABCD和四边形OEFG都是正方形，∴OB=OC，∠OBC=∠OCB=45°，∠BOC=∠EOG=90°，∴∠BON+∠BOM=∠MOC+∠BOM=90°∴∠BON=∠MOC．在△OBN与△OCM中，∠OBN=∠OCM OB=OC∠BON=∠COM，∴△OBN≌△OCM ASA，∴S△OBN=S△OCM，∴S四边形OMBN =S△OBC=14S正方形ABCD=14×1×1=14．故选：A．【点睛】本题考查了正方形的性质，旋转的性质，全等三角形的性质和判定等知识，能推出四边形OMBN 的面积等于三角形BOC的面积是解此题的关键．【变式训练】1(2023春·山东青岛·八年级统考期中)将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后，得到△AB C ，则图中阴影部分的面积是( )cm2．A.12.5B.2536C.2533D.不能确定【答案】B【分析】设AB 与B C 交于D 点，根据旋转角∠CAC =15°，等腰直角△ABC 的一锐角∠CAB =45°，可求∠C AD ，旋转前后对应边相等，对应角相等，AC =AC =5cm ，∠C =∠C =90°，解直角△AC D ，可求阴影部分面积．【详解】解：设AB 与B C 交于D 点，根据旋转性质得∠CAC =15°，而∠CAB =45°，∴∠C AD =∠CAB -∠CAC =30°，又∵AC =AC =5cm ，∠C =∠C =90°，∴设C D =x ，则AD =2x ，∴AD 2=AC 2+C D 2，即2x 2=52+x 2，∴解得x =533，∴C D =533cm ，∴阴影部分面积为：12×5×533=2536cm 2 .故选：B ．【点睛】本题考查了旋转的性质，等腰三角形的性质，勾股定理．关键是通过旋转的性质判断阴影部分三角形的特点，计算三角形的面积．2(2023秋·四川德阳·九年级统考期末)如图，边长为定值的正方形ABCD 的中心与正方形EFGH 的顶点E 重合，且与边AB 、BC 相交于M 、N ，图中阴影部分的面积记为S ，两条线段MB 、BN 的长度之和记为l ，将正方形EFGH 绕点E 逆时针旋转适当角度，则有()A.S 变化，l 不变B.S 不变，l 变化C.S 变化，l 变化D.S 与l 均不变【答案】D 【分析】如图，连接EB ，EC ．证明△EBM ≌△ECN ASA ，可得结论．【详解】解：如图，连接EB ，EC ．∵四边形ABCD 和四边形EFGH 均为正方形，∴EB =EC ，∠EBM =∠ECN =45°，∠MEN =∠BEC =90°，∴∠BEN +∠BEM =∠BEN +∠CEN =90°，∴∠BEM =∠CEN ，在△EBM 和△ECN 中，∠EBM =∠ECNEB =EC ∠BEM =∠CEN，∴△EBM ≌△ECN ASA ，∴BM =CN ，∴S 阴=S 四边形EMBN =S △EBC =14S 正方形ABCD=定值，l =MB +BN =CN +BN =BC =定值，故选：D ．【点睛】本题考查正方形的性质，旋转的性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．3(2023春·广东清远·八年级校考期中)如图，在△ABC 中，∠C =90°，AC =BC =2，将△ABC 绕点A 逆时针方向旋转60°到△ABC 的位置，则图中阴影部分的面积是．【答案】3【分析】过点B 作B D ⊥AB 于点D ，根据旋转的性质可得到△ABB 是等边三角形，S △ABC =S △AB C ，进而得到阴影部分的面积等于S △ABB ，再由勾股定理求出AB ，继而得到S △ABB，即可求解．【详解】解：如图，过点B 作B D ⊥AB 于点D ，∵将△ABC 绕点A 逆时针方向旋转60°到△ABC 的位置，∴AB =AB ,∠BAB =60°，△ABC ≌△AB C ，∴△ABB 是等边三角形，S △ABC =S △AB C，∴AB =BB ，阴影部分的面积等于S △ABB，∵AC =BC =2，∠C =90°，∴AB =AC 2+BC 2=2，∴BB =2,BD =1，∴B D =BB 2-BD 2=3，∴S △ABB=12AB ×B D =12×2×3=3，即阴影部分的面积是3．故答案为：3【点睛】本题主要考查了旋转的性质，等腰直角三角形的性质，等边三角形的判定和性质，熟练运用旋转的性质是本题的关键．4(2023春·江苏宿迁·八年级校考阶段练习)马老师在带领学生学习《正方形的性质与判定》这一课时，给出如下问题：如图①，正方形ABCD 的对角线AC 、BD 相交于点O ，正方形A B C O 与正方形ABCD 的边长相等．在正方形A B C O 绕点O 旋转的过程中，OA 与AB 相交于点M ，OC 与BC 相交于点N ，探究两个正方形重叠部分的面积与正方形ABCD 的面积有什么关系．(1)小亮第一个举手回答“两个正方形重叠部分的面积是正方形ABCD 面积的”；请说明理由．(2)马老师鼓励同学们编道拓展题，小颖编了这样一道题：如图②，在四边形ABCD 中，AB =AD ，∠BAD =∠BCD =90°，连接AC ．若AC =6，求四边形ABCD 的面积．请你帮小颖解答这道题．【答案】(1)14，见解析(2)18，见解析【分析】(1)只需要证明△MOB ≌△NOC 得到S △MOB =S △NOC ，即可求解．(2)过A 作AE ⊥AC ，交CD 的延长线于E ，证明△EAD ≌△CAB 得到S △ABC =S △ADE ，AE =AC =6，则S △AEC =12×6×6=18S 四边形ABCD =S △ACD +S △ABC =S △ACD +S △ADE =S △EAC =12AE ⋅AC =18．【详解】(1)解：∵四边形ABCD 是正方形，四边形OA B C 是正方形，∴AC ⊥BD ，OB =OC ，∠OBM =∠OCN =45°，∠A OC =90°，∴∠BOC =∠A OC =90°，∴∠BOM =∠CON ，∴△BOM ≌△CON ASA ，∴S △BOM =S △CON ，∴S 四边形OMBN =S △OBC =14S 正方形ABCD ．答案为：14；(2)过A 作AE ⊥AC ，交CD 的延长线于E ，∵AE ⊥AC ，∴∠EAC =90°，∵∠DAB =90°，∴∠DAE =∠BAC ，∵∠BAD =∠BCD =90°，∴∠ADC +∠B =180°，∵∠EDA+∠ADC =180°，∴∠EDA =∠B ，∵AD =AB ，在△ABC 与△ADE 中，∠EAD =∠CABAD =AB ∠EDA =∠B，∴△ABC ≌△ADE ASA ，∴AC =AE ，∵AC =6，∴AE =6，∴S △AEC =12×6×6=18，∴S 四边形ABCD =18．【点睛】本题主要考查了正方形的性质，全等三角形的性质与判定，四边形内角和，熟知全等三角形的性质与判定是解题的关键．5(2023春·广东深圳·八年级统考期末)【问题背景】如图1，在▱ABCD 中，AB ⊥DB ．将△ABD 绕点B 逆时针旋转至△FBE ，记旋转角∠ABF =α0°<α≤180° ，当线段FB 与DB 不共线时，记△ABE 的面积为S 1，△FBD 的面积为S 2．【特例分析】如图2，当EF 恰好过点A ，且点F ，B ，C 在同一条直线上时．(1)α=°；(2)若AD =43，则S 1=，S 2=；【推广探究】某数学兴趣小组经过交流讨论，猜想：在旋转过程中，S 1与S 2之间存在一定的等量关系．再经过独立思考，获得了如下一些解决思路：思路1：如图1，过点A ，E 分别作直线平行于BE ，AB ，两直线交于点M ，连接BM ，可证一组三角形全等，再根据平行四边形的相关性质解决问题；思路2：如图2，过点E 作EH ⊥AB 于点H ，过点D 作DG ⊥FB ，交FB 的延长线于点G ，可证一组三角形全等，再根据旋转的相关性质解决问题；⋯⋯(3)如图3，请你根据以上思路，并结合你的想法，探究S 1与S 2之间的等量关系为，并说明理由．【拓展应用】在旋转过程中，当S 1+S 2为▱ABCD 面积的12时，α的值为【答案】(1)60；(2)33；33；(3)S 1=S 2，理由见解析；拓展应用：60°或120°【分析】(1)由旋转的性质和平行四边形的性质，等角对等边，可得△ABF 是等边三角形，即可求解；(2)过点F 作FM ⊥BD 交DB 延长线于点M ，设AD ,BE 交于点N ，通过证明△ABN ≌△FBM AAS ，进而得出s 1=s 2，再证明AE =AF ，可得S △ABE =12S △EFB ，仅为求解即可；(3)分别根据思路1和2进行推理证明即可；拓展应用：先根据面积之间的关系得出BD=2DG，继而得出∠DBG=30°=∠ABE，分别在图3和图2中进行求解即可．【详解】(1)由旋转可得，∠F=∠BAD,BA=BF，∵四边形ABCD为平行四边形，∴AD∥BC，∴∠ABF=∠BAD，∴∠ABF=∠F，∴BA=AF，∴BA=AF=BF，∴△ABF是等边三角形，∴∠ABF=α=60°，故答案为：60；(2)如图，过点F作FM⊥BD交DB延长线于点M，设AD,BE交于点N，∵AD∥BC，∴∠ANE=∠ANB=∠EBF=90°=∠ABM，∠EAN=∠AFB，∴∠MBF=∠ABN，∵BF=BA，∴△ABN≌△FBM AAS，∴AN=FM，∵BD=BE，∴S1=S2，∵△ABF是等边三角形，∴∠AFB=60°=∠EAN,AB=AF，∴∠E=30°=∠ABE，∴AE=AB，∴AE=AF，S△EFB，∴S△ABE=12∵AD=43，∴AB=23=BF,BD=6=BE，×6×23=63，∴S△EFB=12∴S△ABE=33，∴s1=s2=33，故答案为：33,33；(3)解：S1=S2，理由如下：思路1：如图，过点A，E分别作直线平行于BE，AB，两直线交于点M，连接BM，∵AM∥BE,ME∥AB，∴四边形ABEM为平行四边形，∴AM=BE，∠MAB+∠ABE=180°，∵旋转，∴AB=BF，BD=BE，∠ABD=∠EBF=90°，∴BD =AM ，∵∠ABD +∠ABE +∠EBF +∠FBD =360°，∴∠ABE +∠DBF =180°，∴∠MAB =∠DBF ，在△MAB 和△DBF 中，AM =BD∠MAB =∠DBF AB =BF，∴△MAB ≌△DBF ，∴S △MAB =S 2，∵ME ∥AB ，∴S △MAB =S 1，∴S 1=S 2.思路2：如图，过点E 作EH ⊥AB 交AB 延长线于点H ，过点D 作DG ⊥BF 交BF 延长线于点G ，∵EH ⊥AB ，DG ⊥BF ，∴∠H =∠G =90°，∵旋转，∴BD =BE ，AB =BF ，∠DBA =∠EBF =90°，∴∠EBG =90°，∴∠EBG =∠ABD ，∴∠EBG -∠ABG =∠ABD -∠ABG ，即∠EBH =∠GBD ，在△EBH 和△DBG 中，∠H =∠G∠EBH =∠GBD BD =BE，∴△EBH ≌△DBG ，∴EH =DG ，∴S 1=12AB ⋅EH =12BF ⋅DG =S 2；拓展应用：∵S 1=S 2，∴当S 1+S 2为▱ABCD 面积的12时，S 1=S 2=14S 平行四边形ABCD ，由(3)思路2得，S 1=12⋅AB ⋅EH ,S 平行四边形ABCD =AB ⋅BD ,EH =DG ，∴12⋅AB ⋅EH =14AB ⋅BD ，∴BD =2EH ，即BD =2DG ，∴∠DBG =30°=∠ABE ，如图3，∠ABF =120°；如图2,∠DBE =∠ABF=90°-30°=60°，综上，α的值为60°或120°，故答案为：60°或120°．【点睛】本题考查了旋转的性质，等边三角形的判定和性质，等腰三角形的判定和性质，全等三角形的判定和性质，平行四边形的性质，直角三角形的性质，熟练掌握知识点是解题的关键．。

图形的旋转(6种题型)-2023年新九年级数学核心知识点与常见题型(浙教版)(解析版)

图形的旋转（6种题型）【知识梳理】一．生活中的旋转现象（1）旋转的定义：在平面内，把一个图形绕着某一个点O旋转一个角度的图形变换叫做旋转．点O叫做旋转中心，转动的角叫做旋转角，如果图形上的点P经过旋转变为点P′，那么这两个点叫做对应点．（2）注意：①旋转是围绕一点旋转一定的角度的图形变换，因而旋转一定有旋转中心和旋转角，且旋转前后图形能够重合，这时判断旋转的关键．②旋转中心是点而不是线，旋转必须指出旋转方向．二．旋转的性质（1）旋转的性质：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．（2）旋转三要素：①旋转中心；②旋转方向；③旋转角度．注意：三要素中只要任意改变一个，图形就会不一样．三．旋转对称图形（1）旋转对称图形如果某一个图形围绕某一点旋转一定的角度（小于360°）后能与原图形重合，那么这个图形就叫做旋转对称图形．（2）常见的旋转对称图形有：线段，正多边形，平行四边形，圆等．四．中心对称图形（1）定义把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．注意：中心对称图形和中心对称不同，中心对称是两个图形之间的关系，而中心对称图形是指一个图形自身的特点，这点应注意区分，它们性质相同，应用方法相同．（2）常见的中心对称图形平行四边形、圆形、正方形、长方形等等．五．坐标与图形变化-旋转（1）关于原点对称的点的坐标P（x，y）⇒P（﹣x，﹣y）（2）旋转图形的坐标图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．六．作图-旋转变换（1）旋转图形的作法：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．（2）旋转作图有自己独特的特点，决定图形位置的因素较多，旋转角度、旋转方向、旋转中心，任意不同，位置就不同，但得到的图形全等．七．利用旋转设计图案由一个基本图案可以通过平移、旋转和轴对称以及中心对称等方法变换出一些复合图案．利用旋转设计图案关键是利用旋转中的三个要素（①旋转中心；②旋转方向；③旋转角度）设计图案．通【考点剖析】一．生活中的旋转现象（共1小题）1．（2022秋•义乌市期中）商场卫生间旋转门锁的局部如图1所示，如图2锁芯O固定在距离门边（EF）3.5cm处（即ON＝3.5cm），在自然状态下，把手竖直向下（把手底端到达A）．旋转一定角度，把手底端B恰好卡住门边时，底端A、B的竖直高度差为0.5cm．当把手旋转90°到达水平位置时固定力最强，有效的固定长度（把手底端到门边的垂直距离）DN＝cm，当把手旋转到OC时，∠BOC＝∠BOD，此时有效的固定长度为cm．【分析】作BG⊥OA于G，设OA＝OB＝OC＝OD＝xcm，在Rt△OBG中利用勾股定理求出x，利用OD﹣ON 得到DN，连接OB，交OC于M，作CP⊥OD，MQ⊥OD，求出BD，OM，QM和OQ，证明△OPC∽△OQM，可得OP，可得PN，即可得到C到EF的距离．【解答】解：如图，作BG⊥OA于G，设OA＝OB＝OC＝OD＝xcm，则AG＝0.5cm，BG＝ON＝3.5cm，∴OG＝OA﹣AG＝x﹣0.5cm，∵在Rt△OBG中，OB2＝OG2+BG2，∴x2＝（x﹣0.5）2+3.52，解得：x＝12.5，∴OA＝OB＝OC＝OD＝12.5cm，∴DN＝OD﹣ON＝12.5﹣3.5＝9cm．连接OB，交OC于M，作CP⊥OD，MQ⊥OD，∵BN＝OG＝12.5﹣0.5＝12cm，DN＝9cm，∴DB＝DN2+BN2＝15cm，又∵∠BOC＝∠BOD，OD＝OB，∴OC⊥BD，DM＝BM＝DB＝7.5cm，∴OM＝＝＝10cm，∵△DNB中，QM∥NB，且M是DB中点，∴QM＝BN＝6cm，∴Rt△OQM中，OQ＝＝＝8cm，又∵CP∥MQ，∴△OPC∽△OQM，∴OC/OM＝OP/OQ，∴＝，∴OP＝10cm，∴PN＝OP﹣ON＝10﹣3.5＝6.5cm，∵CP⊥OD，EF⊥OD，∴C到EF的距离长等于PN 6.5cm．故答案为：9；6.5．【点评】本题考查了圆的基本性质，相似三角形的判定和性质，勾股定理，中位线定理，解题的关键是读懂题意，结合实际理解旋转门锁的运行原理．二．旋转的性质（共9小题）2．（2022秋•镇海区校级期中）如图，在正方形网格中，△ABC绕某点旋转一定的角度得到△A′B′C′，则旋转中心是点（）A．O B．P C．Q D．M【分析】根据旋转的性质，对应点到旋转中心的距离相等，可得对应点连线的垂直平分线的交点即为旋转中心．【解答】如图，连接BB′，AA′可得其垂直平分线相交于点P，故旋转中心是P点．故选：B．【点评】本题考查了旋转的性质，对应点连线的垂直平分线的交点即为旋转中心，熟练掌握旋转中心的确定方法是解题的关键．3．（2022秋•拱墅区校级期中）如图，将△ABC绕点A逆时针旋转70°，得到△ADE，若点D在线段BC 的延长线上，则∠B的大小是（）A．45°B．55°C．60°D．100°【分析】由旋转的性质可得AB＝AD，∠BAD＝70°，由等腰三角形的性质可求解．【解答】解：∵将△ABC绕点A逆时针旋转70°得到△ADE，∴AB＝AD，∠BAD＝70°，∴∠B＝∠ADB＝＝55°，故选：B．【点评】本题考查了旋转的性质，等腰三角形的性质，掌握旋转的性质是解题的关键．4．（2023•温州三模）如图，在△ABC中，∠BAC＝50°，将△ABC绕点A逆时针旋转得△ADE，使点D恰好落在AC边上，连结CE，则∠ACE的度数为（）A．45°B．55°C．65°D．75【分析】由旋转的性质可知，旋转前后对应边相等，对应角相等，得出等腰三角形，再根据等腰三角形的性质求解．【解答】解：由旋转的性质可知，∠CAE＝∠BAC＝50°，AC＝AE，∴∠ACE＝∠AEC，在△ACE中，∠CAE+∠ACE+∠AEC＝180°，∴50°+2∠ACE＝180°，解得：∠ACE＝65°，故选：C．【点评】本题主要考查了旋转的性质，找出旋转角和旋转前后的对应边得出等腰三角形是解答此题的关键．5．（2022秋•杭州期末）如图，将一个含30°角的直角三角板ABC绕点A逆时针旋转，点C的对应点为点C′，若点C′落在BA延长线上，则三角板ABC旋转的度数是（）A．60°B．90°C．120°D．150°【分析】根据旋转角的定义，两对应边的夹角就是旋转角，即可求解．【解答】解：旋转角是∠BAB′＝180°﹣30°＝150°．故选：D．【点评】本题考查的是旋转的性质，掌握对应点与旋转中心所连线段的夹角等于旋转角是解题的关键．6．（2023•天台县一模）如图，在矩形ABCD中，AB＝1，∠CBD＝18°，将矩形ABCD绕对角线中点O逆时针旋转α（0°＜α＜90°）得到矩形A′B′C′D′，当C′，D的距离等于1时，α的值为（）A．36°B．54°C．68°D．72°【分析】根据矩形的性质以及圆周角定理可得出∠COD＝∠DOC′＝∠C′OB′＝2∠CBD＝36°，进而得出∠COC′＝72°即可．【解答】解：如图，矩形ABCD的外接圆为⊙O，矩形A′B′C′D′的四个顶点也在⊙O上，∵AB＝CD＝B′C′＝DC′＝2，∴∠COD＝∠DOC′＝∠C′OB′＝2∠CBD＝36°，∴∠COC′＝72°，故选：D．【点评】本题考查旋转的性质，矩形的性质，掌握矩形的性质以及旋转的性质是正确解答的前提．7．（2023•长兴县一模）如图，矩形ABCD绕点B旋转得到矩形BEFG，在旋转过程中，FG恰好过点C，过点G作MN平行AD交AB，CD于M，N．若AB＝3，BC＝5，则图中阴影部分的面积的是（）A．3B．4C．5D．【分析】由旋转的性质可得BG＝BA＝3，由勾股定理可求CG，可求△BGC的面积，由平行四边形的性质可求解．【解答】解：∵矩形ABCD绕点B旋转得到矩形BEFG，∴BG＝BA＝3，∴CG＝＝＝4，∴S△BGC＝×BG•GC＝6，∵MN∥AD，CD∥AB，∴四边形AMND是平行四边形，MN∥BC，∴四边形BCNM是平行四边形，∴S平行四边形BCNM＝2S△BGC＝12，∴阴影部分的面积＝S矩形ABCD﹣S平行四边形BCNM＝15﹣12＝3，故选：A．【点评】本题考查了旋转的性质，矩形的性质，勾股定理等知识，灵活运用这些性质解决问题是解题的关键．8．（2023•仙居县二模）如图，在Rt△ABC中，∠C＝90°，AC＝10，BC＝6，点D是边AC的中点．点P 为边BC上的一个动点，将点P绕点D逆时针旋转90°得到点P′，则AP′的取值范围为．【分析】由“SAS”可证△ADP'，可得AP'＝PH，即可求解．【解答】解：如图，以AD为直角边，作等腰直角三角形ADH，连接PH，∴AD＝DH，∠ADH＝90°，∵将点P绕点D逆时针旋转90°得到点P′，∴DP＝DP'，∠PDP'＝90°＝∠ADH，∴∠ADP'＝∠PDH，∴△ADP'≌△HDP（SAS），∴AP'＝PH，∵AC＝10，点D是边AC的中点，∴CD＝AD＝DH＝5，∵点P为边BC上的一个动点，∴当PH⊥BC时，PH有最小值为5，当点P与点C重合时，PH有最大值为5，∴5≤HP≤5，∴，故答案为：．【点评】本题考查了旋转的性质，全等三角形的判定和性质，添加恰当辅助线构造全等三角形是解题的关键．9．（2023•萧山区二模）如图，在正方形ABCD中，，O是BC中点，点E是正方形内一动点，OE＝2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE，CF．则线段OF长的最小值为（）A．8B．C．D．【分析】连接DO，将DO绕点D逆时针旋转90°得到DM，连接FM，OM，证明△EDO≌△FDM，可得FM ＝OE＝2，由勾股定理可得，根据OF+MF≥OM，即可得出OF的最小值．【解答】解：如图，连接DO，将DO绕点D逆时针旋转90°得到DM，连接FM，OM，∵∠EDF＝∠ODM＝90°，∴∠EDO＝∠FDM，在△EDO与△FDM中，，∴△EDO≌△FDM（SAS），∴FM＝OE＝2，∵正方形ABCD中，，O是BC边上的中点，∴，∴，∴，∵OF+MF≥OM，∴OF≥10﹣2＝8，∴线段OF的最小值为8，故选：A．【点评】本题考查线段的最值问题，涉及三角形的三边关系、勾股定理、旋转的性质、正方形的性质、全等三角形的判定与性质等知识，添加辅助线构造全等三角形是解题关键．10．（2022秋•浦江县月考）阅读下面材料，并解决问题：（1）如图①等边△ABC P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段P A、PB、PC转化到一个三角形中，从而求出∠APB＝；（2）基本运用请你利用第（1）题的解答思想方法，解答下面问题已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF2＝BE2+FC2；（3）能力提升如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．【分析】（1）根据旋转变换前后的两个三角形全等，全等三角形对应边相等，全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答；（2）把△ABE绕点A逆时针旋转90°得到△ACE′，根据旋转的性质可得AE′＝AE，CE′＝CE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，再求出∠E′AF＝45°，从而得到∠EAF＝∠E′AF，然后利用“边角边”证明△EAF和△E′AF全等，根据全等三角形对应边相等可得E′F＝EF，再利用勾股定理列式即可得证．（3）将△AOB绕点B顺时针旋转60°至△A′O′B处，连接OO′，根据直角三角形30°角所对的直角边等于斜边的一半求出AB＝2AC，即A′B的长，再根据旋转的性质求出△BOO′是等边三角形，根据等边三角形的三条边都相等可得BO＝OO′，等边三角形三个角都是60°求出∠BOO′＝∠BO′O＝60°，然后求出C、O、A′、O′四点共线，再利用勾股定理列式求出A′C，从而得到OA+OB+OC＝A′C．【解答】解：（1）∵△ACP′≌△ABP，∴AP′＝AP＝3、CP′＝BP＝4、∠AP′C＝∠APB，由题意知旋转角∠PA P′＝60°，∴△AP P′为等边三角形，P P′＝AP＝3，∠A P′P＝60°，易证△P P′C为直角三角形，且∠P P′C＝90°，∴∠APB＝∠AP′C＝∠A P′P+∠P P′C＝60°+90°＝150°；故答案为：150°；（2）如图2，把△ABE绕点A逆时针旋转90°得到△ACE′，由旋转的性质得，AE′＝AE，CE′＝BE，∠CAE′＝∠BAE，∠ACE′＝∠B，∠EAE′＝90°，∵∠EAF＝45°，∴∠E′AF＝∠CAE′+∠CAF＝∠BAE+∠CAF＝∠BAC﹣∠EAF＝90°﹣45°＝45°，∴∠EAF＝∠E′AF，在△EAF和△E′AF中，∴△EAF≌△E′AF（SAS），∴E′F＝EF，∵∠CAB＝90°，AB＝AC，∴∠B＝∠ACB＝45°，∴∠E′CF＝45°+45°＝90°，由勾股定理得，E′F2＝CE′2+FC2，即EF2＝BE2+FC2．（3）如图3，将△AOB绕点B顺时针旋转60°至△A′O′B处，连接OO′，∵在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，∴AB＝2，∴BC＝，∵△AOB绕点B顺时针方向旋转60°，∴△A′O′B如图所示；∠A′BC＝∠ABC+60°＝30°+60°＝90°，∵∠C＝90°，AC＝1，∠ABC＝30°，∴AB＝2AC＝2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，∴△BOO′是等边三角形，∴BO＝OO′，∠BOO′＝∠BO′O＝60°，∵∠AOC＝∠COB＝∠BOA＝120°，∴∠COB+∠BOO′＝∠BO′A′+∠BOO′＝120°+60°＝180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C＝，∴OA+OB+OC＝A′O′+OO′+OC＝A′C＝．【点评】本题考查了旋转的性质，全等三角形的判定与性质，等腰直角三角形的性质，勾股定理，读懂题目信息，理解利用旋转构造出全等三角形和等边三角形以及直角三角形是解题的关键．三．旋转对称图形（共3小题）11．（2022秋•平阳县校级月考）把如图所示的五角星图案，绕着它的中心旋转，若旋转后的五角星能与自身重合．则旋转角至少为（）A．30°B．45°C．60°D．72°【分析】五角星图案，可以被平分成五部分，因而每部分被分成的圆心角是72°，并且圆具有旋转不变性，因而旋转72【解答】解：该图形被平分成五部分，旋转72度的整数倍，就可以与自身重合，因而A、B、C都错误，能与其自身重合的是D．故选：D．【点评】本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．12．（2022秋•张湾区期中）把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为（）A．30°B．90°C．120°D．180°【分析】根据图形的对称性，用360°除以3计算即可得解．【解答】解：∵360°÷3＝120°，∴旋转的角度是120°的整数倍，∴旋转的角度至少是120°．故选：C．【点评】本题考查了旋转对称图形，仔细观察图形求出旋转角是120°的整数倍是解题的关键．13．（2023•婺城区模拟）规定：在平面内，如果一个图形绕一个定点旋转一定的角度α（0°＜α≤180°）后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角度α称为这个图形的一个旋转角．例如：正方形绕着两条对角线的交点O旋转90°或180°后，能与自身重合（如图1），所以正方形是旋转对称图形，且有两个旋转角．根据以上规定，回答问题：（1）下列图形是旋转对称图形，但不是中心对称图形的是；A．矩形B．正五边形C．菱形D．正六边形（2）下列图形中，是旋转对称图形，且有一个旋转角是60度的有：（填序号）；（3）下列三个命题：①中心对称图形是旋转对称图形；②等腰三角形是旋转对称图形；③圆是旋转对称图形．其中真命题的个数有个；A．0B．1C．2D．3（4）如图2的旋转对称图形由等腰直角三角形和圆构成，旋转角有45°，90°，135°，180°，将图形补充完整．【分析】（1）根据旋转图形，中心对称图形的定义判断即可．（2）旋转对称图形，且有一个旋转角是60度判断即可．（3）根据旋转图形的定义判断即可．（4）根据要求画出图形即可．【解答】解：（1）是旋转图形，不是中心对称图形是正五边形，故选B．（2）是旋转对称图形，且有一个旋转角是60度的有（1）（3）（5）．故答案为（1）（3）（5）．（3）命题中①③正确，故选C．（4）图形如图所示：【点评】本题考查旋转对称图形，中心对称图形等知识，解题的关键是理解题意，灵活运用所学知识解决问题．四．坐标与图形变化-旋转（共8小题）14．（2022秋•莲都区期中）如图，在平面直角坐标系中，将点P（2，3）绕原点O顺时针旋转90°得到点P'，则P'的坐标为（）A．（3，﹣2）B．（3，﹣1）C．（2，﹣3）D．（3，2）【分析】作PQ⊥y轴于Q，如图，把点P（2，3）绕原点O顺时针旋转90°得到点P'看作把△OPQ绕原点O顺时针旋转90°得到△OP'Q′，利用旋转的性质得到∠P′Q′O＝90°，∠QOQ′＝90°，P′Q′＝PQ ＝2，OQ′＝OQ＝3，从而可确定P′点的坐标．【解答】解：作PQ⊥y轴于Q，如图，∵P（2，3），∴PQ＝2，OQ＝3，∵点P（2，3）绕原点O顺时针旋转90°得到点P'相当于把△OPQ绕原点O顺时针旋转90°得到△OP'Q′，∴∠P′Q′O＝90°，∠QOQ′＝90°，P′Q′＝PQ＝2，OQ′＝OQ＝3，∴点P′的坐标为（3，﹣2）．故选：A．【点评】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．15．（2022秋•吴兴区期中）如图，在平面直角坐标系中，线段AB的端点在方格线的格点上，将AB绕点P 顺时针方向旋转90°，得到线段A′B′，则点P的坐标为．【分析】依据旋转的性质可得，将AB绕点P顺时针方向旋转90°，得到线段A′B′，则点P到对应点的距离相等，因此作出两对对应点连线的垂直平分线，其交点即为所求．【解答】解：如图所示，作线段AA'和BB'的垂直平分线，交于点P，则点P即为旋转中心，由图可得，点P的坐标为（1，2），故答案为：（1，2）．【点评】本题主要考查了坐标与图形变换，解决问题的关键是掌握旋转的性质．一般情况，图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．16．（2022秋•苍南县期中）如图，点A的坐标为（0，3），点C的坐标为（1，0），B的坐标为（1，4），将△ABC沿y轴向下平移，使点A平移至坐标原点O，再将△ABC绕点O逆时针旋转90°，此时B的对应点为B′，点C的对应点为C′，则点C′的坐标为（）A．（4，1）B．（1，4）C．（3，1）D．（1，3）【分析】首先根据点A的平移规律得到C的平移后坐标，再根据旋转规律得到C′的坐标．【解答】解：∵点A平移至坐标原点O，点A的坐标为（0，3），∴向下平移三个单位长度，∴C平移后的坐标为（1，﹣3），∵平移后再将△ABC绕点O逆时针旋转90°，∴点C′的坐标为（3，1）．故选：C．【点评】此题主要考查了坐标与图形的变化中的旋转与平移，正确使用坐标与图形变化的规律是解题的关键．17．（2022秋•衢江区校级期末）如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣1，4）的对应点A′的坐标是（）A．（1，4）B．（4，1）C．（1，﹣4）D．（4，﹣1）【分析】由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出∠AOA′＝90°，AO＝A′O，作AC ⊥y轴于C，A′C′⊥x轴于C′，就可以得出△ACO≌△A′C′O，就可以得出AC＝A′C′，CO＝C′O，由A的坐标就可以求出结论．【解答】解：∵线段AB绕点O90°得到线段A′B′，∴∠AOA′＝90°，AO＝A′O．作AC⊥y轴于C，A′C′⊥x轴于C′，∴∠ACO＝∠A′C′O＝90°．∵∠COC′＝90°，∴∠AOA′﹣∠COA′＝∠COC′﹣∠COA′，∴∠AOC＝∠A′OC′．在△ACO和△A′C′O中，，∴△ACO≌△A′C′O（AAS），∴AC＝A′C′，CO＝C′O．∵A（﹣1，4），∴AC＝1，CO＝4，∴A′C′＝1，OC′＝4，∴A′（4，1）．故选：B．【点评】本题考查了旋转的性质的运用，全等三角形的判定及性质的运用，点的坐标的运用，正确作出辅助线并证得△ACO≌△A′C′O是解决问题的关键．18．（2022秋•西湖区校级期中）在平面直角坐标系中，把点P（1，﹣2）绕原点O顺时针旋转90°，所得到的对应点Q的坐标为．【分析】作PQ⊥y轴于Q，如图，把点P（1，﹣2）绕原点O顺时针旋转90°得到点P'看作把△OPQ绕原点O顺时针旋转90°得到△OP'Q′，利用旋转的性质得到∠P′Q′O＝90°，∠QOQ′＝90°，P′Q′＝PQ＝2，OQ′＝OQ＝3，从而可确定P′点的坐标．【解答】解：作PQ⊥y轴于Q，如图，∵P（1，﹣2），∴PQ＝1，OQ＝2，∵点P（1，﹣2）绕原点O顺时针旋转90°得到点P'相当于把△OPQ绕原点O顺时针旋转90°得到△OP'Q′，∴∠P′Q′O＝90°，∠QOQ′＝90°，P′Q′＝PQ＝1，OQ′＝OQ＝2，∴点P′的坐标为：（﹣2，﹣1）．故答案为：（﹣2，﹣1）．【点评】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．19．（2023•金华）在直角坐标系中，点（4，5）绕原点O逆时针方向旋转90°，得到的点的坐标．【分析】利用旋转变换的性质作出图形可得结论．【解答】解：如图，点A（4，5）绕原点O逆时针方向旋转90°，得到的点B的坐标（﹣5，4）．故答案为：（﹣5，4）．【点评】本题考查坐标与图形变化﹣旋转，解题的关键是正确作出图形，利用图象法解决问题．20．（2022秋•柯桥区期中）在平面直角坐标系中，O为坐标原点，已知点B（0，4），点A在x轴负半轴上，且∠BAO＝30°，将△AOB O顺时针旋转，得△COD，点A、B旋转后的对应点分别为C，D，记旋转角为α．（1）如图1，CD恰好经过点B时，①求此时旋转角α的度数；②求出此时点C的坐标；（2）如图2，若0°＜α＜90°，设直线AC和直线DB交于点P，猜测AC与DB的位置关系，并说明理由．【分析】（1）①根据旋转的性质得到OB＝OD，求得∠ABO＝60°＝∠D，得到△BOD是等边三角形根据等边三角形的性质得到∠BOD＝60°，于是得到结论；②过点C作CE⊥x轴于E，根据等腰三角形的性质得到CO＝AO＝4，求得∠AOC＝60°，求得OE＝2，CE＝6，于是得到C（﹣2，6）；（2）根据等腰三角形的性质得到∠OBD＝90°﹣，求得∠ABP＝180°﹣60°﹣（90°﹣）＝30°+，根据垂直的定义即可得到结论．【解答】解：（1）①由旋转可知，OB＝OD，∵∠BAO＝30°，∴∠ABO＝60°＝∠D，∴△BOD是等边三角形，∴∠BOD＝60°，∴旋转角α的度数为60°；②过点C作CE⊥x轴于E，∵∠AOB＝90°，B（0，4），∴CO＝AO＝4，∵α＝60°，∴∠AOC＝60°，∴OE＝2，CE＝6，∴C（﹣2，6）；（2）AC⊥BD，理由：∵∠AOC＝α，OB＝OD，∴∠OBD＝90°﹣，∴∠ABP＝180°﹣60°﹣（90°﹣）＝30°+，∴∠PBA+∠PAB＝60°﹣30°+＝90°，∴∠APB＝90°，∴AC⊥BD．【点评】本题考查了坐标与图形性质﹣旋转，等边三角形的性质，直角三角形的性质，旋转的性质，正确地作出辅助线是解题的关键．21．（2022秋•鄞州区校级期末）如图，在平面直角坐标系中，将边长为1的正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，继续旋转至2022次得到正方形OA2022B2022C2022，则点B2022的坐标是．【分析】根据图形可知：点B在以O为圆心，以OB为半径的圆上运动，再由旋转可知：将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，相当于将线段OB绕点O逆时针旋转45°，可得对应点B的坐标，然后发现规律是8次一循环，进而得出答案．【解答】解：∵点A的坐标为（1，0），∴OA＝1，∵四边形OABC是正方形，∴∠OAB＝90°，AB＝OA＝1，∴B（1，1），连接OB，如图：由勾股定理得：OB＝＝，由旋转的性质得：OB＝OB1＝OB2＝OB3＝…＝，∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，相当于将线段OB绕点O逆时针旋转45°，依次得到∠AOB＝∠BOB1＝∠B1OB2＝…＝45°，∴B1（0，），B2（﹣1，1），B3（﹣，0），B4（﹣1，﹣1），B5（0，﹣），B6（1，﹣1），…，发现是8次一循环，则2022÷8＝252…6，∴点B2022的坐标为（1，﹣1），故答案为：（1，﹣1）．【点评】本题考查了旋转的性质、正方形的性质、坐标与图形性质、勾股定理、规律型：点的坐标等知识，解题的关键是学会从特殊到一般的探究规律的方法，属于中考常考题型．五．作图-旋转变换（共5小题）22．（2023•龙游县一模）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．（1）把△ABC绕着原点O逆时针旋转90°得△A1B1C1，画出△A1B1C1，并写出C1的坐标．（2）若△ABC中的一点P（a，b），在①中变换下对应△A′B′C′中为P′点，请直接写出点P′的坐标（用含a、b的代数式表示）【分析】（1）根据图形旋转的性质画出△A1B1C1，并写出C1的坐标即可；（2）根据（1）中C点坐标找出规律即可得出结论．【解答】解：（1）如图所示，C1的坐标（1，4）．（2）∵C（4，﹣1），C1（1，4），∴P’（﹣b，a）．【点评】本题考查的是作图﹣旋转变换，熟知图形旋转不变性的性质是解答此题的关键．23．（2023•温州一模）如图，在6×4的方格纸中，已知线段AB（A，B均在格点上），请按要求画出格点四边形（顶点均在格点上）．（1）在图1中画一个以AB为边的四边形ABCD，使其为轴对称图形．（2）在图2中画一个以AB为对角线的四边形AEBF，使其为中心对称图形．【分析】（1）根据轴对称图形的定义画出图形即可；（2）根据中心对称图形的定义画出图形即可．【解答】解：（1）如图，四边形即为所求作：；（2）如图，四边形即为所求作：．【点评】本题考查了作图﹣旋转变换，轴对称变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题．24．（2023•乐清市模拟）如图是由边长为1的小正方形构成的6×6的网格，点A，B均在格点上，请按要求画出以AB为对角线的格点四边形（顶点均在格点上）．（1）在图1中画一个周长为整数的四边形ACBD；（2）在图2中画一个面积为8的四边形AEBF，且使其是中心对称图形但不是轴对称图形．【分析】（1）利用勾股定理作出，据此即可画出一个周长为整数的四边形ACBD；（2）根据三角形的面积公式以及平行四边形的性质即可画出一个面积为8的四边形AEBF，且使其是中心对称图形但不是轴对称图形．【解答】解：（1）如图，四边形ACBD即为所求作．（2）如图，四边形AEBF即为所求作．【点评】本题考查作图﹣旋转变换，勾股定理，平行四边形的性质等知识，解题的关键是理解题意，学会利用数形结合的思想解决问题．25．（2022•平阳县一模）如图，在10×8的方格纸巾，请按要求画图．（1）在图1中画一个格点C，使△ABC为等腰三角形．（2）在图2中两个格点F，G，使四边形DEFG为中心对称图形，且对角线互相垂直．【分析】（1）根据等腰三角形的概念作图即可（答案不唯一）；（2）根据中心对称图形的概念及菱形、正方形的性质作图即可（答案不唯一）．【解答】解：（1）如图所示，△ABC即为所求（答案不唯一）．（2）如图所示，四边形DEFG即为所求（答案不唯一）．【点评】本题主要考查作图—旋转变换，解题的关键是掌握旋转变换的定义与性质、等腰三角形的定义、菱形与正方形的性质．26．（2023•温州二模）如图在6×6的方格纸中，点A，B，C均在格点上，请按要求画出相应格点图形．（1）画出△ABC关于点C成中心对称的格点三角形△A1B1C（点A，B的对应点分别为A1，B1）．（2）画出△ABD，使得S△ABD＝3S△ABC．【分析】（1）根据中心对称的性质作图即可．（2）由图可得S△ABD＝3S△ABC＝6，结合三角形的面积找出点D的位置即可．【解答】解：（1）如图，三角形△A1B1C即为所求.（2）由图可得，S△ABC＝＝2，∴S△ABD＝3S△ABC＝6．如图，△ABD1，△ABD2，△ABD3均满足要求．【点评】本题考查中心对称、三角形的面积，熟练掌握中心对称的性质、三角形的面积是解答本题的关键．六．利用旋转设计图案（共3小题）27．（2022秋•宁波期末）如图，在4×4的网格纸中，△ABC的三个顶点都在格点上，现要在这张网格纸的四个格点M，N，P，Q中找一点作为旋转中心．将△ABC绕着这个中心进行旋转，旋转前后的两个三角形成中心对称，且旋转后的三角形的三个顶点都在这张4×4的网格纸的格点上，那么满足条件的旋转中心有（）A．点M，点N B．点M，点Q C．点N，点P D．点P，点Q【分析】画出中心对称图形即可判断【解答】解：观察图象可知，点P．点N满足条件．故选：C．【点评】本题考查利用旋转设计图案，中心对称等知识，解题的关键是理解题意，灵活运用所学知识解决问题．28．（2022秋•定海区校级月考）在冬奥会开幕式上，美丽的冬奥雪花呈现出浪漫空灵的气质．如图，雪花图案本身的设计呈现出充分的美感，它是一个中心对称图形．其实“雪花”图案也可以看成自身的一部分围绕图案的中心依次旋转一定角度得到的，这个角的度数可以是（）A．30°B．45°C．60°D．90°【分析】根据图形的对称性，用360°除以6计算即可得解．【解答】解：∵360°÷6＝60°，∴旋转角是60°的整数倍，∴这个角的度数可以是60°．故选：C．【点评】本题考查了旋转对称图形：如果某一个图形围绕某一点旋转一定的角度（小于360°）后能与原图形重合，那么这个图形就叫做旋转对称图形．常见的旋转对称图形有：线段，正多边形，平行四边形，圆等．29．（2022秋•慈溪市期末）美丽的冬奥雪花呈现出浪漫空灵的气质．如图，雪花图案是一个中心对称图形，也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的，这个角的度数可以是（）。

初三下数学课件(沪科版)- 素养专题运用旋转知识解决几何图形问题

解：(1)EG＝CG，且 EG⊥CG； (2)EG＝CG，且 EG⊥CG.
证明：如图，延长 FE 交 DC 延长线于 M，连 MG.∵∠AEM＝90°，∠EBC ＝90°，∠BCM＝90°，∴四边形 BEMC 是矩形．
∴BE＝CM，∠EMC＝90°.又∵BE＝EF，∴EF＝CM，∵∠EMC＝90°， FG＝DG，∴MG＝12FD＝FG.∵BC＝EM，BC＝CD，∴EM＝CD.∵EF＝ CM，∴FM＝DM.又∵∠F＝45°，FG＝DG，∠CMG＝12∠EMC＝45°.∴∠F ＝∠GMC. ∴△GFE≌△GMC(SAS)．∴EG＝CG，∠FGE＝∠MGC. 在等腰 Rt△DMF 中，FG＝DG, ∴MG⊥FD，∴∠FGM＝∠FGE＋∠EGM＝ 90°，∴∠MGC＋∠EGM＝90°，即∠EGC＝90°.∴EG⊥CG.
2．(随州中考)如图，在平面直角坐标系中，Rt△ABC 的直角顶点 C 的坐标为(1,0)，点 A 在 x 轴正半轴上，且 AC＝2.将△ABC 先绕点 C 逆时针旋转 90°，再向左平移 3 个单位，则变换后点 A 的对应点的坐标为 (－2,2) ．
3．(镇江中考)将边长为 1 的正方形 ABCD 绕点 C 按顺时针方向旋转到 FECG 的位置(如图)，使得点 D 落在对角线 CF 上，EF 与 AD 相交于点 H，则 HD ＝ 2－1 (结果保留根号)．
(1)如图②，当 BP＝BA 时，∠EBF＝
，猜想∠QFC＝
；
(2)如图①，当点 P 为射线 BC 上任意一点时，猜想∠QFC 的度数，并加以
证明．
解：(1)30° 60°； (2) 猜想 ∠QFC ＝ 60°. 证明： ∵∠BAP ＝ ∠BAE ＋ ∠EAP ＝ 60°＋ ∠EAP ， ∠EAQ＝∠QAP＋∠EAP＝60°＋∠EAP，∴∠BAP＝∠EAQ，在△ABP 和 △AEQ 中，∵AB＝AE，∠BAP＝∠EAQ，AP＝AQ，∴△ABP≌△AEQ(SAS)， ∴∠AEQ＝∠ABP＝90°，又∵∠BEF＝180°－∠AEQ－∠AEB＝180°－90° －60°＝30°，∴∠QFC＝∠EBF＋∠BEF＝30°＋30°＝60°.

几何中的旋转问题

熟练运用旋转解决平面几何中的问题平面几何的证题方法多种多样．利用旋转来解决平面几何问题，有时能收到事半功倍的效果．例图1中以△ABC的边AB、AC为一边向外作正方形ABDE及正方形ACFG，连结BG、CE．求证：(1)BG=CE；(2)BG⊥CE．分析：一般的证法是证明△ABG与△AEC全等，然后应用全等三角形的性质。

而如果采用旋转，则可以如下证明：由已知可知，点E绕点A逆时针旋转90°为点B，点C绕点A 逆时针旋转90°为点G，从而知线段EC绕点A逆时针旋转90°为线段BG，故有BG=CE，BG ⊥CE．本文将从最常见的两种旋转出发，谈谈旋转在平面几何中的应用。

一、按旋转的角度进行区分1、90°角旋转例1 如图2，E、F分别是边长为1的正方形ABCD的BC、CD—上的点，且△CEF的周长是2．求∠EAF的大小。

解：将△ABE绕点A作逆时针旋转90°，则AB边与AD边重合，设旋转后E→E′，由条件△CEF的周长为2，即CE+EF+CF=2，又BE+CE+CF+ DF=2，且显然有BE=DE′，故CE+ CF+FE′=2．从而必有EF=FE′，又AE= AE′，AF=AF，故△AEF≌△AE'F，∴∠EAF=E'AF，又从作图知∠EAE′=90°，故∠EAF=45°。

例2（北京东城2010年上学期期末）如图，P 为正方形ABCD 内一点，若PA =1，PB =2，PC =3 ，求:(1)∠APB 的度数;(2)正方形ABCD 的面积．分析:三条已知的线段PA 、PB 、PC 具有一个共公顶点，且它们不能构成三角形．但是当把△ABP 按顺时针方向旋转90°后，即会出现等腰直角三角形，于是PA 旋转后的线段与PC 构成了一个新的三角形．解:(1)将△ABP 绕点B 顺时针方向旋转90°得△CBQ ．则△ABP ≌ △CBQ 且PB ⊥QB ．于是PB =QB =2a ，PQ =22PB QB =22a ．在△PQC 中，∵PC 2=9a 2，PQ 2＋QC 2=9a 2． ∴PC 2=PQ 2＋QC 2． ∴∠PQC =90°． ∵△PBQ 是等腰直角三角形， ∴∠BPQ =∠BQP =45°．故∠APB =∠CQB =90°＋45°=135°．(2)∵∠APQ =∠APB ＋∠BPQ =135°＋45°=180°， ∴三点A 、P 、Q 在同一直线上．在Rt △AQC 中，AC 2=AQ 2＋QC 2=(a ＋22a )2＋a 2=(10＋42)a 2．故S 正方形ABCD =12AC 2=(5＋22)a 2．思考例2中，如果把△CBP 绕点B 逆时针方向旋转90°得△ABM ，怎样解以上问题?(答: (1)△PBM 是等腰直角三角形，且由勾股定理的逆定理得∠APM =90°;(2)过点B 作BN ⊥AP ，垂足为N ．则PN =BN =2a ，于是在△ABN 中可求出边长AB 的平方，即得正方形的面积．)2、60°角旋转．例1 如图3，分别以△ABC的边AB、AC为一边向外作等边三角形ABD及等边三角形ACE。

利用旋转解决几何问题

利用旋转解决几何问题在几何学中，旋转是一种常见的解决问题的方法。

通过将形状绕着某一点或某一轴旋转，可以得到新的形状，从而解决一些原本复杂的几何问题。

本文将通过几个例子，介绍如何利用旋转来解决几何问题。

一、旋转体的体积计算旋转体的体积计算是旋转解决几何问题的经典应用之一。

考虑一个曲线y=f(x)，如果将该曲线绕x轴旋转一周，就可以得到一个旋转体。

我们可以利用旋转体的性质来计算其体积。

例如，我们要计算曲线y=x^2在x=0到x=1之间的旋转体体积。

首先，我们将曲线绕x轴旋转，得到一个旋转体。

然后，我们将该旋转体切割成许多薄片，每个薄片的厚度为Δx。

每个薄片在x轴上的宽度为Δx，高度为f(x)。

因此，该薄片的体积可以用V=π(f(x))^2Δx来表示。

最后，将所有薄片的体积相加，即可得到旋转体的体积。

二、旋转体的表面积计算除了计算旋转体的体积，我们还可以计算旋转体的表面积。

同样，我们可以将旋转体切割成薄片，每个薄片在x轴上的宽度为Δx。

但是，不同于计算体积时使用薄片的高度f(x)，计算表面积时，我们使用薄片的周长。

例如，考虑一个曲线y=√x在x=1到x=4之间的旋转体。

我们可以将该旋转体切割成许多薄片，每个薄片的厚度为Δx。

每个薄片在x轴上的宽度为Δx，周长为2πf(x)。

因此，该薄片的表面积可以用S=2πf(x)Δx来表示。

最后，将所有薄片的表面积相加，即可得到旋转体的表面积。

三、旋转体的质心计算旋转体的质心是指旋转体的重心或质量中心，即旋转体的几何中心。

我们可以利用旋转解决几何问题的方法来计算旋转体的质心。

以曲线y=x为例，我们要计算其在x=0到x=1之间的旋转体的质心。

首先，我们将曲线绕x轴旋转，得到一个旋转体。

然后，根据物理学的原理，质心可以通过计算各个薄片的质心位置得到。

每个薄片的宽度为Δx，高度为f(x)。

根据几何学中的平均值定理，每个薄片的质心位置x可以用公式x=∫xf(x)Δx/∫f(x)Δx来表示。

巧用旋转解几何疑难问题

巧用旋转解几何疑难问题发布时间：2021-05-20T12:24:20.317Z 来源：《教学与研究》2021年4月上作者：王周民[导读] 图形的旋转是初中数学中一种重要的图形变换方法，利用它可以解决许多几何难题。

陕西省澄城县王庄镇初级中学王周民 715203摘要：图形的旋转是初中数学中一种重要的图形变换方法，利用它可以解决许多几何难题。

关键词：旋转例题体会作用图形的旋转是初中数学的重要内容，由于课本配套习题偏少，加之中考占分不多，所以，一些老师和初三学生对本节知识没有给予足够的重视，我这里想和大家共同探讨几道习题，深层体会旋转作为一种图形变换方法的重要作用。

例1、已知ΔABC中，AB=3，AC=7，AD是BC边的中线，试求AD的取值范围。

分析：一般的，求线段的取值范围，需要用到三边关系定理，但这道题不能直接用，原因是已知的AB、AC和所求的AD都是从点A出发的三条线段，它们没有围成三角形。

因此，要通过变换将它们集中在一个三角形中，从而，可以使用三边关系求解。

因为条件中有中线AD,如果将ΔACD绕点D旋转180，则AC、AB、和2AD可以组成一个三角形，从而得解。

解：延长AD到E,使DE=AD,连接BE.例2、正方形ABCD中，E是BC边上一点，AF平分交CD于F,求证：AE=BE+DF分析：一般的，要证明一条线段等于两条短线段之和，常用的办法是将两条较短的线段接续成一条线段，转变成证明两条线段相等。

此题关键是怎样将线段，BE和DF通过移动接续成一条线段？如果将绕点A旋转90,就可以将DF移动到CB的延长线上，从而将问题转化成证明线段AE=EG. 。

显然，这就要证明它们所对的角相等,仔细寻找你就可以找到需要的条件，从而使问题得解。

总之，旋转常常出现在等边三角形、正方形、正多边形中，因为正方形的四个角是直角，且四条边相等，这就为旋转创造了条件，而等边三角形三个角是60度，且三条边相等也是旋转的便利条件，故旋转常常能解决这些图形中的疑难问题。

2021年数学：人教版九年级上- -图形的旋转(典例解析)

感谢您使用本资源，本资源是由订阅号”初中英语资源库“制作并分享给广大用户，本资源制作于2020年底，是集实用性、可编辑性为一体。

本资源为成套文件，包含本年级本课的相关资源。

有教案、教学设计、学案、录音、微课等教师最需要的资源。

我们投入大量的人力、物力，聘请精英团队，从衡水中学、毛毯厂中学、昌乐中学等名校集合了一大批优秀的师资，精研中、高考，创新教学过程，将同学们喜闻乐见的内容整体教给学生。

本资源适用于教师下载后作为教学的辅助工具使用、适合于学生家长下载后打印出来作为同步练习使用、也适用于同学们自己将所学知识进行整合，整体把握进度和难度，是一个非常好的资源。

如果需要更多成套资料，请微信搜索订阅号“初中英语资源库”，在页面下方找到“资源库”，就能得到您需要的每一份资源（包括小初高12000份主题班会课课件免费赠送！）23.1图形的旋转典型例题例1 如图，将△ABC 绕点A 旋转得到△AEF ，指出图中的旋转中心、旋转角度及对应线段、对应角。

分析旋转角是连结对应点与旋转中心所形成的角，而对应线段是对应点所在的线段，对应角则由对应点所形成的角，因此关键是要分清楚是谁的对应点。

解旋转中心是点A ；旋转角是∠BA E 或∠CAF ；对应线段是：AB 与AE 、B C 与EF 、AC 与AF ；对应角是：∠BAC 与∠EAF 、∠B 与∠E 、∠C 与∠F 。

点评要记清旋转（对称）的如下特征：旋转后的图形的对应点到旋转中心的距离相等，对应线段相等，对应相等，图形的形状与大小都没有发生变化。

例2 如图，已知R ｔ△ABC 的周长为12，∠B ＝90°，∠CAB ＝30°，△ABC 的边AC 在直线l 上，按顺时针方向在直线l 上转动两次，使它转到△ 222C B A 位置，则=2AA ,∠=B C A 11分析由旋转后对应角相等，∠=111B C A ∠AC B=60°可知第一次旋转的角度∠2ACA ＝ 120°，第二次旋转了90°后至△222C B A 的位置，所以∠=B C A 11180°－120°＝60°，又由旋转后对应线段相等，11C B BC =，AB B A =22，故1222112=++=++=AB BC AC A B C B AC AA 。

专题52 巧用图形的旋转解决几何问题(解析版)

7
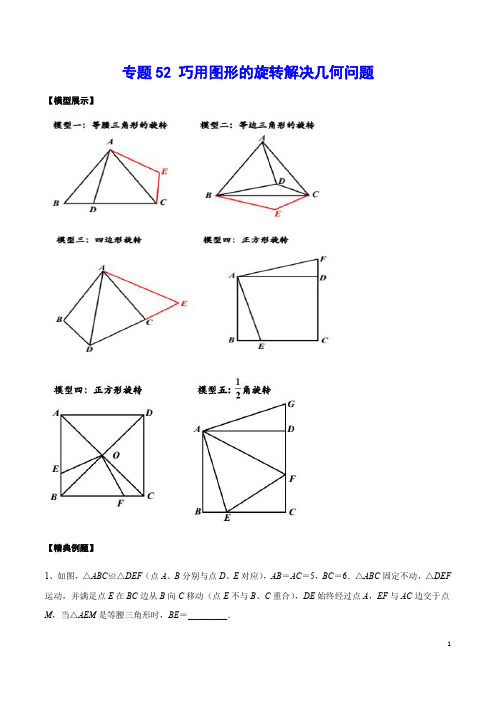
∴BF＝
＝3，
∴EF＝ BF＝3 ， ∴AF＝6 +3， ∴AE2＝AF2+EF2＝（6 +3）2+（3 ）2＝144+36 ． ∵AE＝2 BH， ∴AE2＝12BH2， ∴BH2＝12+3
如图 3﹣2 中，当 DE 在 BC 的上方时，同法可得 AF＝6 ﹣3，EF＝3 ，
∴BH2＝＝（
＝12﹣3 ．
9
6．如图，点 P 是∠MON 内的一点，过点 P 作 PA⊥OM 于点 A，PB⊥ON 于点 B，且 OA＝OB．（1）求证：PA＝PB；（2）如图②，点 C 是射线 AM 上一点，点 D 是线段 OB 上一点，且∠CPD+∠MON＝180°，若 OC＝8， OD＝5．求线段 OA 的长．（3）如图③，若∠MON＝60°，将 PB 绕点 P 以每秒 2°的速度顺时针旋转，12 秒后，PA 开始绕点 P 以每秒 10°的速度顺时针旋转，PA 旋转 270°后停止，此时 PB 也随之停止旋转．旋转过程中，PA 所在直线与 OM 所在直线的交点记为 G，PB 所在直线与 ON 所在直线的交点记为 H．问 PB 旋转几秒时，PG＝PH？
（2）△PMN 是等腰直角三角形．由旋转知，∠BAD＝∠CAE， ∵AB＝AC，AD＝AE， ∴△ABD≌△ACE（SAS）， ∴∠ABD＝∠ACE，BD＝CE，利用三角形的中位线得，PN＝ BD，PM＝ CE， ∴PM＝PN， ∴△PMN 是等腰三角形，同（1）的方法得，PM∥CE，
15
∴∠DPM＝∠DCE，同（1）的方法得，PN∥BD， ∴∠PNC＝∠DBC， ∵∠DPN＝∠DCB+∠PNC＝∠DCB+∠DBC， ∴∠MPN＝∠DPM+∠DPN＝∠DCE+∠DCB+∠DBC ＝∠BCE+∠DBC＝∠ACB+∠ACE+∠DBC ＝∠ACB+∠ABD+∠DBC＝∠ACB+∠ABC， ∵∠BAC＝90°， ∴∠ACB+∠ABC＝90°， ∴∠MPN＝90°， ∴△PMN 是等腰直角三角形；

专题巧用旋转解决几何问题

小专题:巧用旋转解决几何问题广州市东圃中学樊继珍教学过程：科目：数学年级：初三级教学时间：教学目标：1．能根据题目条件灵活使用旋转变换2．利用旋转性质解题重点、难点：发现旋转三角形教学资源：导学案、网络画板、希沃授课助手教学内容师生活动设计意图一、以题点知作图题：作出△ABC 绕点A 顺时针旋转900后的图形。

你能发现哪些结论？二、典例分析1、引例：如图，在正方形ABCD 中，E 、F 分别是AB 、BC 边上的点，且∠EDF ＝45°。

求证：AE+FC=EF . 2、例题：如图，△ABC 中，AB=AC ，∠BAC=900，点P 是△ABC 内一点，满足P A =2，PB =1，PC =3，求∠APB 的度数.3、变式：在四边形ABCD 中，∠BAD =∠BCD =90°，BC =CD ，AC=2，求四边形ABCD 的面积.三、能力训练1、如图，△ABC 中，AB=AC ，∠BAC=60度，学生画图，根据作图过程回忆旋转性质。

教师投影学生学卷，复习旋转的三要素和旋转的性质。

1、教师分析审题，注重分析结论是解决此题的突破口。

2、学生独立思考3、学生组内讨论探究不同方法4、学生代表展示分享5、教师总结思路1、学生独立思考2、组内讨论解题方法3、教师用画板演示不符合的旋转，带领学生归纳旋转的特征及解题步骤学生独立完成教师简单归纳学生独立完成教师简单归纳学生独立完成教师简单归纳通过动手操作，进一步加深对图形旋转的回忆，为后续作图打下基础。

本题在学习三角形全等时“利用取长补短”已经证明，今天用旋转思想证明，意在强调旋转也是一种作辅助线的方法。

由正方形开始探究，是由特殊到一般，由学生熟悉的问题入手，便于学生发现解题规律。

本题等线段，共顶点，可考虑利用旋转化“散”为“聚”，一题多解。

重点讲解，重在归纳方法。

该题背景图形是普通图形，具备旋转所需要的共端点的等线段。

由特殊图形到一般图形，进一步强调旋转方法适应的条件。

巧用“旋转”解几何问题

巧用“旋转”解几何问题临城镇中学郭粉霞【摘要】“旋转”作为图形的三大运动之一，在初中数学第十一章图形的运动中和平移、对称两种运动一起出现，学生在学那个章节包括老师在教那个章节时可能侧重点在如何按照要求画出相应的图形上，或许会忽略对于三种运动的性质及其特点的学习或教学，所以会造成学生在后期学习过程中，尤其是在几何证明时不太会巧用图形运动的性质及特点，特别是“旋转”运动的性质及特点来巧解相应的几何问题。

我发现，利用“旋转”运动，能够把条件集中化，使图形中的各种关系明朗化，达到促进思维方法和解题能力的提高的目的。

我总结了一下这类题目，发现这些题目和图形的“旋转”运动有些关联，所以我对图形的求解进行了一些研究。

下面我主要通过几道例题的求解，对两类问题“角的求解和边的求解”进行讨论，这仅是我的心得体会，供大家参考。

【关键词】“旋转”运动性质及特点巧解几何问题一、巧用“旋转”的性质求角根据旋转的性质，我们知道对应点到旋转中心的距离相等，对应线段的长度相等，对应角的大小相等，旋转前后图形的大小和形状没有改变，在性质中“对应线段的长度相等，对应角的大小相等”，我们可以利用这个性质将要求的角转换成求旋转图形的对应角，然而图形在“旋转”运动中，往往会产生特殊的图形，我们再通过这些特殊的图形来求对应角，进而求未知角，这样问题就迎刃而解了。

通过“旋转”运动，可以将毫无思路的问题明朗化，有助于他们找到准确的解题思路或方向，达到事半功倍的作用。

我们一起来看这样的一个例子：如图1，P为正方形ABCD内一点，且PA=1，PB=2，PC=3.求∠APB的度数。

分析：我们分析题目，发现题目所给的条件是边长，而所要求的是角度，显然，只有将这些边长组合成特殊三角形（直角三角形或等腰三角形），通过特殊三角形的已知角来求未知角。

要想构造特殊三角形，我们知道，通过“旋转”运动可以得到，从而化未知角为已知角来解决问题。

又因为所给的图形是正方形，我们发现，正方形的边长是相等的，旋转时有一条对应边正好与正方形的另一边重合，形成了对应的图形△CMB，从而可将求∠APB转化成求对应角∠CMB。

八年级数学下册利用旋转妙解正方形问题(人教版)

利用旋转妙解正方形问题正方形是最特殊的四边形，具有高度的对称性.因此，在正方形中的线段证明和计算等问题上，利用旋转变换可巧妙地拼接图形，使条件发生转化并相对集中，可达到化难为易的目的. 现举例如下.例1如图正方形ABCD中，E、F分别是AD、CD边上两点，BF平分∠EBC.求证：BE=AE+CF.分析：四边形ABCD是正方形，AB=BC，∠A=∠C=90°，把△BCF绕点B 逆时针旋转90°到△BAG的位置，如图，此时AG=CF，只需再证BE=GE即可，由于∠CBF=∠FBE=∠GBA，所以∠GBE=∠ABF=∠BFC=∠G.因而BE=GE.证明略.评注：本题将△BCF绕点B进行旋转变换，使线段CF与AE巧妙拼接，并与BE组成三角形，从而利用等腰三角形的知识解题.例2如图P为正方形ABCD内一点，PA=1，PB=2，∠APB=135°，求PC的长.分析：由AB=BC，∠ABC=90°，可将△BAP绕点B按顺时针方向旋转90°，得△BCP′，如图连结PP′，则△BPP′是等腰直角三角形.因为PB=P′B=2，根据勾股定理，得PP′=2 2 .又因为∠CP′B=∠APB=135°，∠PP′B=45°，所以∠CP′P=90°，即△CP′P是直角三角形，从而PC=3.评注：本题通过旋转变换，将线段PC、C P′与PP′巧妙构成直角三角形，且使已知条件相对集中，并与结论沟通起来，达到了化难为易的目的.以下两题供同学们练习：1、如图，在正方形ABCD中，E、F是BC、CD边上的两点，∠EAF=45°.求证：EF=BE=DF.2、如图，正方形ABCD的边长为1，BC、CD边上各有一点E、F，若△CEF的周长为2，求∠EAF的度数.。

专题52 巧用图形的旋转解决几何问题(解析版)

巧“旋转”,妙解题

巧用旋转法解几何题资料讲解

初中数学《几何旋转》重难点模型汇编(四大题型)含解析

九年级数学图形的旋转专题讲解+六大题型解析+专题训练,收藏学习

部编数学九年级下册专项16巧用旋转进行计算(解析版)含答案

应用图形的旋转巧解“难题”

巧用旋转解题例说

初中数学巧用旋转进行计算之三大题型及答案

图形的旋转(6种题型)-2023年新九年级数学核心知识点与常见题型(浙教版)(解析版)

初三下数学课件(沪科版)- 素养专题 运用旋转知识解决几何图形问题

几何中的旋转问题

利用旋转解决几何问题

巧用旋转解几何疑难问题

2021年数学：人教版九年级上- -图形的旋转(典例解析)

专题52 巧用图形的旋转解决几何问题(解析版)

专题巧用旋转解决几何问题

巧用“旋转”解几何问题

八年级数学下册利用旋转妙解正方形问题(人教版)

初三下数学课件(沪科版)- 素养专题运用旋转知识解决几何图形问题