第三节生物聚合物的压电特性10级
合集下载
第三节生物聚合物的压电特性11级
第一章
第一节 第二节 第三节 第四节
生物电学
概述 生物聚合物的介电特性 生物聚合物的压电特性 人体组织和器官的电阻抗和电活动图
引入
生物组织普遍存在压电效应
1941年Martin首次观察到木材和毛发的压电效应。 70 年代以来发现多种生物大分子和生物组织都具 有压电效应，一些合成多肽和光学活性聚合物也 表现出压电效应。 在对取向的固态生物聚合物进行定量研究时发现： 生物聚合物和合成多肽的液晶态和大分子溶液也 具有压电效应。
c c d14 FC (d14 d 25 )/2
压电常数的测量
通常用动力学方法测定复合压电常数，把正 弦状的力加到样品上，测量得到的电压或电 荷。
压电常数的测量
待测样品
应变计Βιβλιοθήκη 激荡器恒温槽压力测量计
运算电路 e’ e”
电荷放大器
运算电路 d’ d”
压电常数e和d的测量原理图
二、一些生物物质的压电特性
骨和韧带 把干燥的骨一端固定，另一端弯 曲时，附在骨上各部位的电极之间就会出现 电位差。因为骨的形状复杂，故与应力相对 应的极化分布也很复杂。
大腿骨压缩时的压电电位分布（电压单位mV)
液晶和溶液
液晶的弯曲压电性
液晶有三种形变：倾斜、弯曲和扭转。 液晶中的压电效应是由弯曲形变产生的，而不 是象固体晶体那样由切应变或张应变产生压电 性。因此，有对称中心的晶体结构无压电性， 而有对称中心的液晶却有压电性。
机械和电刺激与骨骼的生长
已有不少用外加电刺激促进骨生长的实验。 例如
在兔的大腿骨上装上螺旋正电极和线状负电极，连续三 周通以1μA直流电，可看到从负极到正极方向的软组织 长出假骨。 用Teflon驻极体薄膜或PMLG薄膜把折断的兔股骨包裹 起来，四周后，在薄膜上生长出桥样的刚性骨。 近年，出现直流、交流、脉冲和电磁场等方法治疗骨折 的技术。
第一节 第二节 第三节 第四节
生物电学
概述 生物聚合物的介电特性 生物聚合物的压电特性 人体组织和器官的电阻抗和电活动图
引入
生物组织普遍存在压电效应
1941年Martin首次观察到木材和毛发的压电效应。 70 年代以来发现多种生物大分子和生物组织都具 有压电效应，一些合成多肽和光学活性聚合物也 表现出压电效应。 在对取向的固态生物聚合物进行定量研究时发现： 生物聚合物和合成多肽的液晶态和大分子溶液也 具有压电效应。
c c d14 FC (d14 d 25 )/2
压电常数的测量
通常用动力学方法测定复合压电常数，把正 弦状的力加到样品上，测量得到的电压或电 荷。
压电常数的测量
待测样品
应变计Βιβλιοθήκη 激荡器恒温槽压力测量计
运算电路 e’ e”
电荷放大器
运算电路 d’ d”
压电常数e和d的测量原理图
二、一些生物物质的压电特性
骨和韧带 把干燥的骨一端固定，另一端弯 曲时，附在骨上各部位的电极之间就会出现 电位差。因为骨的形状复杂，故与应力相对 应的极化分布也很复杂。
大腿骨压缩时的压电电位分布（电压单位mV)
液晶和溶液
液晶的弯曲压电性
液晶有三种形变：倾斜、弯曲和扭转。 液晶中的压电效应是由弯曲形变产生的，而不 是象固体晶体那样由切应变或张应变产生压电 性。因此，有对称中心的晶体结构无压电性， 而有对称中心的液晶却有压电性。
机械和电刺激与骨骼的生长
已有不少用外加电刺激促进骨生长的实验。 例如
在兔的大腿骨上装上螺旋正电极和线状负电极，连续三 周通以1μA直流电，可看到从负极到正极方向的软组织 长出假骨。 用Teflon驻极体薄膜或PMLG薄膜把折断的兔股骨包裹 起来，四周后，在薄膜上生长出桥样的刚性骨。 近年，出现直流、交流、脉冲和电磁场等方法治疗骨折 的技术。
聚合物电学性能
影响聚合物介电性能的因素
高聚物的分子结构
交变电场的频率
影响高聚物介电性的因素 温度 湿度 增塑剂
• 1. 结构因素是决定高聚物介电性的内在原因，包括是高聚物 分子极性大小和极性基团的密度，以及极性基团的可动性。 a. 分子极性 • 根据单体单元偶极矩的大小，可将高聚物大致归为四类
• 单体单元偶极矩增加，高分子极性增加，介电系数和介电损 耗增加。
• 高聚物的压电极化与热电极化力场可以是应变恒定或应力 恒定的，由此导致的电极化（P）改变可分别用压电系数 d和e表示
• 式中，d是压电应变系数，e是压电应力系数，A是电极面 积，P为电极化强度，X代表外应力，S代表应变，E是电 场强度，T是温度 • 由温度改变导致的焦电性可由焦电系数p表示
• 高聚物的压电极化与热电极化
位置发生了变化。极化所需时间约为10-13s，并伴有微量能量损耗；适用
对象：所有高聚物
电子极化和原子极化是由于分子中正负电荷中心发生位移或分子变形引起
的，所以统称为变形极化或诱导极化，其极化率不随温度变化而变化。
iii. 取向极化（又称偶极极化）: 是指在外电场的作用下，极性分子沿电 场方向排列而发生取向。 由于极性分子沿外电场方向的转动需要克服本身的惯性和旋转阻力， 所以极化所需时间长，而且由于高分子运动单元可从小的侧基到整个大分 子链，所以完成取向极化所需的时间范围很宽，一般为10-9s，发生在低频 区域，适用对象：极性高聚物
第 7 章
聚合物的电学性能
第一节：聚合物的介电极化和介电松弛行为
第二节：聚合物的压电极化与焦电极化
莫芳
电学性质： 在外加电压或电场作用下的行为及其所表现出来的
各种物理现象，包括在交变电场中的介电性质、在
聚合物的结构与介电性能
结构
频率与温度
添加剂
1.分子结构 （1）极性：偶极取向极化对介电性质影响最大。极性 越大，tanδ越大。
聚偏氟乙烯（PVDF）具有较高的介电常数。由于分子链中H原子与 F 原 子的电负性不同，会在 PVDF 分子链中产生偶极矩。在外加电场的作用 下，PVDF分子中正、负电荷中心发生分离，产生电偶极矩，发生取向 极化。
tan在交变电场中介电常数可以写成复数形式介质损耗角正切能量交换能量交换取向极化时存在克服偶极子转向的粘滞阻力消耗电能转化为热能变形极化时当电场频率与原子或电子的固有频率相同时发生共振吸收介电损耗产生的原因电导损耗导电载流子产生导电电流消耗电能转化为热能偶极的取向极化偶极的取向极化聚合物名称tan104聚合物名称tan104聚四氟乙烯2环氧树脂20100聚乙烯2硅橡胶40100聚丙烯23氯化聚醚100四氟乙烯六氟乙烯共聚3聚酰亚胺40150聚苯乙烯13聚氯乙烯70200交联苯乙烯5聚氨酯150200聚砜68abs树脂40300聚碳酸酯9氯丁橡胶300天然橡胶230尼龙6100400丁苯橡胶20尼龙66140600丁基橡胶30pmma400600聚甲醛40酚醛树脂6001000聚邻苯二甲酸二丙烯酯80硝化纤维素9001200常见聚合物tan2050hz聚合物及多组分聚合物的结构与介电性能聚合物的介电性能的影响因素结构频率与温度添加剂聚偏氟乙烯pvdf具有较高的介电常数
聚合物名称 聚四氟乙烯 聚乙烯 聚丙烯 四氟乙烯-六氟乙烯共聚 tanδ*104 <2 2 2-3 <3 聚合物名称 环氧树脂 硅橡胶 氯化聚醚 聚酰亚胺 tanδ*104 20-100 40-100 100 40-150
聚苯乙烯
交联苯乙烯 聚砜 聚碳酸酯 天然橡胶
1-3
5 6-8 9 2-30
频率与温度
添加剂
1.分子结构 （1）极性：偶极取向极化对介电性质影响最大。极性 越大，tanδ越大。
聚偏氟乙烯（PVDF）具有较高的介电常数。由于分子链中H原子与 F 原 子的电负性不同，会在 PVDF 分子链中产生偶极矩。在外加电场的作用 下，PVDF分子中正、负电荷中心发生分离，产生电偶极矩，发生取向 极化。
tan在交变电场中介电常数可以写成复数形式介质损耗角正切能量交换能量交换取向极化时存在克服偶极子转向的粘滞阻力消耗电能转化为热能变形极化时当电场频率与原子或电子的固有频率相同时发生共振吸收介电损耗产生的原因电导损耗导电载流子产生导电电流消耗电能转化为热能偶极的取向极化偶极的取向极化聚合物名称tan104聚合物名称tan104聚四氟乙烯2环氧树脂20100聚乙烯2硅橡胶40100聚丙烯23氯化聚醚100四氟乙烯六氟乙烯共聚3聚酰亚胺40150聚苯乙烯13聚氯乙烯70200交联苯乙烯5聚氨酯150200聚砜68abs树脂40300聚碳酸酯9氯丁橡胶300天然橡胶230尼龙6100400丁苯橡胶20尼龙66140600丁基橡胶30pmma400600聚甲醛40酚醛树脂6001000聚邻苯二甲酸二丙烯酯80硝化纤维素9001200常见聚合物tan2050hz聚合物及多组分聚合物的结构与介电性能聚合物的介电性能的影响因素结构频率与温度添加剂聚偏氟乙烯pvdf具有较高的介电常数
聚合物名称 聚四氟乙烯 聚乙烯 聚丙烯 四氟乙烯-六氟乙烯共聚 tanδ*104 <2 2 2-3 <3 聚合物名称 环氧树脂 硅橡胶 氯化聚醚 聚酰亚胺 tanδ*104 20-100 40-100 100 40-150
聚苯乙烯
交联苯乙烯 聚砜 聚碳酸酯 天然橡胶
1-3
5 6-8 9 2-30
第一章生物电学第一节及第二节生物大分子的介电特性10级
生物电研究和微电测量技术
1922年，Erlanger 和Gasser 开始把电子学技术引 入生物电测量。玻璃微电极及相应的电技术的应用， 大大的促进了生物电的研究。 20世纪50年代，Hodgkin 等应用微电极技术定量的 研究了乌贼巨神经轴突的膜离子电流，建立了揭示 动作电位的发生、传播的机制和规律的“H-H 模 型”。 60年代，Katz证实了电兴奋突触传递的量子化现象。 Hodgkin， Katz两人获得诺贝尔奖。
多肽链的偶极矩
任意伸长的多肽链偶极矩
α－螺旋和蛋白质的偶极矩
α－螺旋是蛋白质的DNA的一种典型的二级结 构,最简单情况是一种伸展的、刚性的α－螺 旋 α－螺旋的稳定性主要靠氢键维持
α－螺旋和蛋白质的偶极矩
在每一圈主链骨架上，每个肽单位的N-H基 的氢原子与相邻圈的肽单位的C=O基的氧原 子之间形成氢键，这样每个氢键形成封闭的 环
生物电的研究和应用
1.在组织和器官的宏观水平上研究电现象及 其活动规律。
如中枢神经系统，感觉器官，心脏，肌肉，骨， 各种腺体，消化系统，泌尿系统，生殖系统等。包 括低等动物，高等动物，人和某些植物的生物电现 象。
生物电的研究和应用
2.在微观水平上，对生物电现象发生机制研 究从细胞水平上，已发展到分子和亚分子水 平。
• 除了对传统的以离子通透为基础的生物电研究 外，还对生物大分子的介电、压电和电荷分布 及其相互作用的研究。它与生命活动中DNA、 RNA、各种蛋白质的生物功能和酶的催化作用 等生化、遗传过程密切相关，将从本质上揭示 各种生命活动的原初过程和机制。
生物电的研究和应用
3.生物电学研究在各个领域的应用正在发 挥越来越大的作用。
第二节 生物聚合物的介电特性
聚合物电学性能
Chapter10 聚合物的电性能
• 热合PVC等极性材料是适宜的。而PE薄膜等非极 性材料就很难用高频热合。
• 轮胎经高频热处理消除内应力，可大幅度延长使 用寿命。
• 塑料注射成型时常因含水而产生气泡，经高频干 燥能很好解决这个问题。
Chapter10 聚合物的电性能
(3)高聚物的介电松弛谱
□ 高分子分子运动的时间与温度依赖性可在其介电性质上得 到反映。借助于介电参数的变化可研究聚合物的松弛行为。
以上两种极化统称为变形极化或诱导极化 其极化率不随温度变化而变化，聚合物在高频区均能发生变 形极化或诱导极化
Chapter10 聚合物的电性能
• 偶极极化（取向极化）：
是具有永久偶极矩的极性分子沿外场方向排列的现象。极 化所需要的时间长，一般为10-9s，发生于低频区域。
(a)无电场
（b）有电场
图1 偶极子在电场中取向
Chapter10 聚合物的电性能
三、影响聚合物介电性能的因素
• 高分子材料的介电性能首先与材料的极性有关。 这是因为在几种介质极化形式中，偶极子的取向 极化偶极矩最大，影响最显著。
• 决定聚合物介电损耗大小的内在因素： ①分子极性大小和极性基团的密度 ② 极性基团的可动性
Chapter10 聚合物的电性能
Chapter10 聚合物的电性能
• 介电损耗温度谱示意图
在这些图谱上，高聚物的介电损耗一 般都出现一个以上的极大值，分别对 应于不同尺寸运动单元的偶极子在电 场中的介电损耗(因偶极子的取向极化 过程伴随着分子运动过程，运动模式 各异，其松弛时间也不一致,其受阻程 度不同)按照这些损耗峰在图谱上出现 的先后，在温度谱上从高温到低温， 在频率谱上从低频到高频，依次用、 、命名。
压电性能及其应用PPT课件
可编辑
2019/
43
9/22
在相界附近的PZT瓷压电性能比BaTiO3瓷高得多 。 由于相界处PZT瓷的Tc高(360℃)，因而在200℃以内,KP 和 ε都很稳定，是理想的压电材料。
PZT陶瓷的掺杂改性
为了满足不同的使用目的，我们需要具有各种性能的 PZT压电陶瓷，为此我们可以添加不同的离子来取代A位的 Pb2+离子或B位的Zr4+, T i 4+离子，从而改进材料的性能。
可编辑
2019/
26
9/22
机电耦合系数的定义是：
K 2 通过逆压电效应转换所得的机械能
转换时输入的总电能
或
K 2 通过正压电效应转换所得的电能
转换时输入的总机械能
可编辑
2019/
27
9/22
机械能与压电振子形状和振动ቤተ መጻሕፍቲ ባይዱ式有关
： 压电陶瓷振子（具有一定形状、大小和被覆工作电 极的压电陶瓷体）的机械能与其形状和振动模式有 关，不同的振动模式将有相应的机电耦合系数。
dij33的简化矩阵表示8548548522p351转换时输入的总电能通过逆压电效应转换所得的机械能转换时输入的总机械能通过正压电效应转换所得的电能压电陶瓷振子具有一定形状大小和被覆工作电极的压电陶瓷体的机械能与其形状和振动模式有关不同的振动模式将有相应的机电耦合系数
（书上8.5 压电性
）8.3 介电材料的 压
常见的压电常数有四种：dij、gij、 eij、 hij。
可编辑
2019/
22
9/22
电极化的一个分量将由压电常数的九个分 量来表述（二阶张量）
可编辑
2019/
23
9/22
高分子物理第十章
10.5 聚合物的表面和界面性能 10.5.2 表征仪器,方法 聚合物表面与界面的表征方法:仪器表征和接触角表征 (1)用于化学分析的电子光谱,也称X射线光电子能谱. 该法基于在X射线辐照下,观察电子的发射信息. 被发射的电子的能量是产生于电子对特定原子的 结合能. (2)衰减全反射红外光谱 这是一种以内反射为基础的方法.
10.2 聚合物的导电性能 10.2.3 导电性复合材料 导电复合材料是在聚合物原料中加入各种导电性物质, 通过分散复合,层积复合,形成表面导电膜等方式构成 的材料
10.3 聚合物的热性能 10.3.1 耐热性 表征聚合物耐热的温度参数为玻璃华温度和熔点.欲提高 聚合物的耐热性,主要有以下3个结构因素: (1)增加高分子链的刚性 (2)提高聚合物的结晶性 (3)进行交联
10.2 聚合物的导电性能 10.2.2 导电聚合物的结构与导电性 (2)电荷转移型聚合物 电荷转移复合物是一种分子复合物,它是在电子给体 分子D和电子受体分子A之间由于分子D部分或完全地 转移到分子A上而形成的复合物,这种分子聚合物可用 [ D δ + Aδ ]表示,这里δ代表了相互作用的强度.这类 电荷转移相互作用是电性质的,它比范德华力强些,但 是通常比离子或共价键弱些.这样形成的电荷转移复合 物的偶极矩和电导性都已不同于起始分子. 另一类电荷转移型聚合物是离子自由基盐聚合物.
10.1 聚合物的介电性能 10.1.3 聚合物驻极体及热释电介 驻极体:具有被冻结的长寿命(相对于观察时间而言)非平 衡电矩的电介质的统称 应用:聚偏氟乙烯,聚四氟乙烯,聚丙烯等聚合物超薄薄膜 驻极体已广泛用作能量转换器件;并在空气净化,骨伤治疗, 抗血栓等技术以及医疗领域显示了很大的潜力.
10.1 聚合物的介电性能 10.1.4 聚合物的电击穿 聚合物击穿时的破坏机理有多种形式: 如:电击穿,电机械击穿,热击穿,化学击穿,放电击等. 电击穿:当电场的强度达到某些临界数值(这对不同材 料是不同的)时,载流子从外部电场所获得的能量大大 超过它们与周围碰撞所损失的部分能量,将使被撞击的 高分子链发生电离,产生新的载流子,如此继续,就会 发生所谓的"雪崩"现象,以致电流急剧上升,聚合物发 生击穿.这类击穿叫做电击穿.
生物骨的压电常数-概述说明以及解释
生物骨的压电常数-概述说明以及解释1.引言1.1 概述概述部分应该对文章主题进行简要介绍，并指出为什么人们对生物骨的压电常数感兴趣。
以下是概述部分的一种可能写法：文章提供了对生物骨压电常数的深入探究。
生物骨作为人体最基本的结构之一，其压电效应成为近年来研究的热点之一。
通过对生物骨的压电常数的研究，可以更好地理解生物骨的力学性质，也为医学诊断和治疗等领域提供了新的途径。
在本文中，我们将首先介绍生物骨的压电现象，探讨生物骨是如何表现出压电效应的。
然后，我们将深入了解生物骨的压电常数，这是一个重要的物理参数，可以定量描述生物骨的压电性质。
在该部分中，我们将探讨传统测量方法和现代测量方法以获得准确的压电常数。
最后，我们将总结目前对生物骨压电常数的研究，并提出未来的研究方向。
生物骨的压电常数研究具有重要的理论和实践价值，对于理解骨骼生物力学、骨骼疾病的诊断和治疗等领域具有重要意义。
通过本文的研究，我们希望能够增加人们对生物骨压电常数的了解，促进相关研究的发展，为人体骨骼研究和医学领域的科学进展做出贡献。
1.2 文章结构文章结构部分的内容应包括对整篇文章的组织和内容进行介绍。
可以按照以下内容来撰写：文章结构部分旨在向读者介绍本篇文章的整体组织和内容安排。
本文将按照以下顺序展开内容。
首先，在引言部分，我们将概述生物骨的压电常数的研究背景和意义。
通过概述生物骨的压电效应及其相关现象，引起读者对本文主题的兴趣。
接下来介绍文章的结构，明确本文的目的和主要研究内容。
其次，在正文部分，我们将分为两个小节来讨论生物骨的压电常数。
首先，在2.1小节中，我们将详细介绍生物骨的压电效应，包括其基本原理和压电现象的表现形式。
然后，在2.1.2小节中，我们将重点探讨生物骨的压电常数，包括其定义、计算方法以及已有研究成果。
通过对生物骨的压电常数的深入了解，我们可以更好地理解生物骨的压电效应的特性和应用潜力。
接着，在2.2小节中，我们将介绍压电常数的测量方法。
功能转换材料
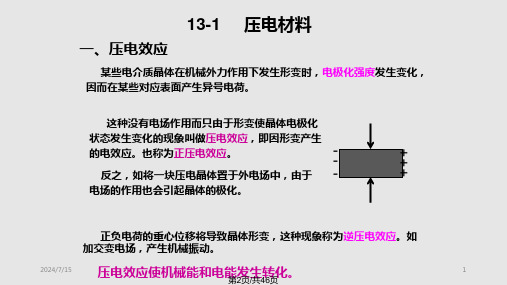
压电效应反映晶体电量与机械应力间的关系，机械应力有方向，引起正 负电荷相对位移。
热释电效应中晶体电荷变化来自于温度变化。热膨胀各向同性。只有晶 体存在着与其他极轴不同的唯一极化轴，才有可能发生热释电。
2、热释电晶体一定存在压电效应，但压电晶体不一定存在热释 电效应。
2024/7/15
11
第12页/共46页
h 1 mv2 A h A时产生光电发射效应
2
2024/7/15
16
第17页/共46页
二、光电子材料及其应用
1、光电导材料及应用
CdS,CdSe,CdTe,ZnSe,HgSe,HgTe,PbS,PbSe,InP,
InAs,InSb,GaAs,GaSb,Ge,Si. 光电探测器（光敏器件），光电导摄像管，固体图像传感器。
1969年，日本河合平司发现聚偏四氟乙烯（极化处 理后）有强压电性，使压电聚合物逐步进入实用化。
与压电陶瓷相比：柔性、耐冲击、能制成大面积薄 膜传感材料。
2024/7/15
6
第7页/共46页
两类：
（1）固有压电性聚合物
一些结晶聚合物化学结构不对称，有极性基团。未拉伸时， 微晶取向随机，总极化强度为0。
热电偶：通过测电动势来测温。把热 学量变为电学量测量。
非电量电测法
2、用做温差电源
T
BC
电位 差计
A
C
2024/7/15
T0
恒温装置
25
第26页/共46页
3、用于制冷
利用半导体帕尔贴效应（比金属强得多），实现热、电能 转换，制成半导体制冷机（电流流过时，低温端吸热，高温端 放热）
发生火花）
引燃引爆、压电开关、小型电源、压电变压器等 3、电声设备
第八章 聚合物的电学性能
第八章 聚合物电学、热、光学性能
第一节 高聚物极化及介电性质
8.1.1 极化现象
聚合物材料在外电场作用下其内部分子或某些基团电荷分布发生变化， 这种现象称为极化。 ①电子极化是外电场作用下分子中原子或离子的价电子云相对原子核的位移。极 化时间约为10-13～10-15s。除去电场，位移立即恢复，无能量损耗。 ②原子极化是分子骨架在外电场作用下发生变形造成的。极化时间约为10-13s， 并伴随有微量能量损耗。
8.1.2 介电系数
1.介电系数 如果在真空平行板电容器中加上直 流电压V，两极板上将产生电荷 Q0 ，则 电容器电容为 Q0
C0 V
(8-1)
当电容器两极板间充满电介质时，由于电介质分子的极化，两极板上 将产生感应电荷 Q’，这时，电源需给平板上补充和极化电量Q’相等的电量 来抵消极化反电场，以维持原平板电容器的电场强度，从而使电容器的电荷 量从Q0 增加到Q0 +Q’，电容器的电容也相应增加到 Q (8-2) C V 含电介质的电容器的电容与该真空电容器电容之比称该电介质的介电系数，
后两种情况下，由于极性基团 浓度随组成变化而减小，介电损耗 峰的强度将单调地逐渐减小。各种 情况下，介电损耗都随增塑剂含量 增加而移向低温。
(5) 杂质
导电杂质和极性杂质（特别是水）会大大增加高聚物的电导电 流和极化度，因而使介电性能严重恶化。
对于非极性高聚物来说，杂质是引起介电损耗的主要原因。 用金属有机催化剂合成的高聚物，须经过特别的纯化，否则影响 介电损耗。如聚乙烯，当其灰份含量从1.9%降到0.03%时，tanσ 从0.0014降到0.0003 。 极性高聚物由于吸水从而对介电性能产生重大影响。 水在低频下会产生离子电导引起介电损耗；在微波频率范围 内，它发生偶极松弛，出现损耗峰。在水—高聚物界面，还会发 生界面极化，结果在低频下出现损耗峰。
第一节 高聚物极化及介电性质
8.1.1 极化现象
聚合物材料在外电场作用下其内部分子或某些基团电荷分布发生变化， 这种现象称为极化。 ①电子极化是外电场作用下分子中原子或离子的价电子云相对原子核的位移。极 化时间约为10-13～10-15s。除去电场，位移立即恢复，无能量损耗。 ②原子极化是分子骨架在外电场作用下发生变形造成的。极化时间约为10-13s， 并伴随有微量能量损耗。
8.1.2 介电系数
1.介电系数 如果在真空平行板电容器中加上直 流电压V，两极板上将产生电荷 Q0 ，则 电容器电容为 Q0
C0 V
(8-1)
当电容器两极板间充满电介质时，由于电介质分子的极化，两极板上 将产生感应电荷 Q’，这时，电源需给平板上补充和极化电量Q’相等的电量 来抵消极化反电场，以维持原平板电容器的电场强度，从而使电容器的电荷 量从Q0 增加到Q0 +Q’，电容器的电容也相应增加到 Q (8-2) C V 含电介质的电容器的电容与该真空电容器电容之比称该电介质的介电系数，
后两种情况下，由于极性基团 浓度随组成变化而减小，介电损耗 峰的强度将单调地逐渐减小。各种 情况下，介电损耗都随增塑剂含量 增加而移向低温。
(5) 杂质
导电杂质和极性杂质（特别是水）会大大增加高聚物的电导电 流和极化度，因而使介电性能严重恶化。
对于非极性高聚物来说，杂质是引起介电损耗的主要原因。 用金属有机催化剂合成的高聚物，须经过特别的纯化，否则影响 介电损耗。如聚乙烯，当其灰份含量从1.9%降到0.03%时，tanσ 从0.0014降到0.0003 。 极性高聚物由于吸水从而对介电性能产生重大影响。 水在低频下会产生离子电导引起介电损耗；在微波频率范围 内，它发生偶极松弛，出现损耗峰。在水—高聚物界面，还会发 生界面极化，结果在低频下出现损耗峰。
生物骨的压电常数
生物骨的压电常数全文共四篇示例，供读者参考第一篇示例：生物骨的压电常数是指生物骨组织所具有的压电效应的特性参数。
压电效应是指某些材料受到外力作用时会产生电荷分布不对称而产生电位差的现象。
生物骨组织是一种复杂的生物材料，其具有一定的压电性质，因此在医学和生物工程领域具有重要意义。
压电效应在生物领域中已被广泛应用。
生物骨的压电常数是描述材料在受到压力作用时产生电荷的能力，其数值越大表示材料对外部压力的敏感性越高。
生物骨的压电常数受到动物种类、个体差异、骨骼部位以及生长环境等因素的影响，因此具有一定的差异性。
生物骨的压电常数与生物髓内的细胞和纤维结构有关。
生物骨组织中含有大量的矿物质和胶原蛋白，这些成分对压电效应起到重要的作用。
矿物质在受到压力时会产生电荷，而胶原蛋白则有助于增强材料的压电性质。
生物骨组织的压电常数可以通过调控其矿物质和胶原蛋白的含量来改变。
生物骨的压电常数在医学领域中有着广泛的应用。
通过测量生物骨组织的压电常数，可以对骨骼的健康状态进行评估，为骨科医生提供诊断和治疗的参考依据。
在生物工程领域中，生物骨的压电特性还可以用于制造人工骨骼和关节等器官，为患者提供更好的治疗选择。
生物骨的压电常数是生物骨组织独特的物理性质，对于研究生物骨的力学性能、生物医学应用以及生物工程技术具有重要的意义。
随着生物材料科学的不断发展，生物骨的压电常数将会成为一个重要的研究领域，为人类健康和生命质量的提升带来更多的可能性。
第二篇示例：生物骨的压电常数是指生物体内骨骼组织所具有的压电效应的特性参数。
压电效应是指在受到外部压力或变形时，材料会产生电荷的分离和电势的变化，这种效应被称为压电效应。
生物骨具有类似于压电材料的特性，当受到外部力/变形时会产生微小的电荷分离。
生物骨是具有一定弹性的硬组织，主要由钙磷复合物组成。
在生物体内，骨骼组织承受着人体的重量，并提供支撑和保护身体器官的功能。
生物骨还起到了一种微弱的压电效应，这种效应十分微弱，但足以引发电信号传递的过程。
聚合物的电性能光学性能热性能PPT
tgδ=ε″/ε′
13
式中δ称介电损耗角， tg称介电损耗正切。 tg 的物理意义是在每个交变电压周期中，介质
损耗的能量与储存能量之比。
tg 越小，表示能量损耗越小。 理想电容器（即真空电容器）tg =0，无能量损失。
正'' 比于 tg，故也常用 表示材料介电损耗的大小。
14
✓ 影响聚合物介电性能的因素
相反，支化结构会使大分子间相互作用力减弱，分子链活 动性增强，使介电系数增大。
18
（2） 温度和交变电场频率的影响
温度的影响 温度升高一方面使材料粘度下降，有利于极性基团取向， 另一方面又使分子布朗运动加剧，反而不利于取向。
聚氯乙烯的ε′和ε″的温度依赖性（曲线上的数字为增塑剂含量）19
电场频率的影响 与材料的动态力学性能相似，高分子材料的介电性能也随 交变电场频率而变。
提高聚合物的结晶性
进行交联
49
50
（2）热稳定性
提高聚合物热稳定性的途径： 在高分子链中避免弱键 在高分子链中避免一长串连接的亚甲基
－CH2－，并尽量引入较大比例的环状结构 合成“梯形”、“螺形”和“片状”结构的
聚合物
常用热重分析研究聚合物的热稳定性
51
52
53
绝缘料的热稳定性能
➢ 聚合物电介质在外电场中的极化
在外电场作用下，电介质分子中电荷分布发生变化，使材 料出现宏观偶极矩，这种现象称电介质的极化。 （电子极 化、原子极化、取向极化、界面极化）
极化方式
感应极化
取向极化
3
✓ 电子极化
• 电子极化是外电场作用下分子中各个原子或离 子的价电子云相对原子核的位移。
• 极化过程所需的时间极短，约为10-13~10-15s。 • 当除去电场时，位移立即恢复，无能量损耗，
高分子物理_电性能
注意：表中偶极矩大小是以高聚物重复单元计。
一、高分子的极化
2、高分子的极化(polarization) 极化是指电解质在电场作用下，分子内束缚的电荷产生弹 性位移或偶极子转向排列，从而对外呈现出极性的现象。 极化的类型 电子极化(electron polarization) 原子极化(atom polarization) 偶极极化(dipole polarization)
对极性高聚物，温度较低时，随温度升高，介电常数增大；而温度 较高时，则随温度升高，介电常数减小。
不管是何种高聚物，温度升高时，介电损耗均会增大。
4、湿度(moisture)
因为水是极性分子，所以当高聚物吸湿后，使电导和极化均增大， 从而使介电常数和介电损耗增大。 影响程度的大小取决于材料的吸湿程度，这种吸湿性一是与高聚物 的结构有关，如极性高聚物容易吸湿，所以影响大；二是与环境的 湿度大小有关。
另，聚丙烯腈纤维不导电，但如经高温焦化处理后，则能导电，这 就是碳纤维(carbon fiber)。
值得指出的是，一般来说，所有用作半导体和导体的高聚物都具有 共轭结构，并且具有共轭结构的高聚物也是耐高温材料，但并不是 所有（形式上的）共轭结构的高聚物都是导电高聚物。
第三节
高聚物的电击穿性能
1、电击穿现象
非极性高聚物的介电常数较小，通常在2~3左右。极性高聚物则较 大，且极性越强，介电常数越大。 交联能阻碍极化，因而使介电常数降低。 应用： 通信电缆材料的介电常数越小越好。通常采用PE、PP和PS等。 电容器则宜采用介电常数较大的材料以提高电容量；
高压电机、开关等宜选用介电常数相近的材料做组合介质。
在弱电场作用下，高聚物是绝缘体。但随着电压的不断升高，流过 材料的电流不断增大，当电压超过某一极限值后（强电场下），材 料的绝缘性能完全丧失而导电。这种现象称为电击穿。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
毛细胞
传感和换能作用
皮肤中起压力感觉器作用的是帕西尼小体的末 端，被由胶原层组成的鳞茎样结构所包围，这 种结构起压电换能器作用。
一种物质的压电性与其晶体的对称性有关，采用Z轴 为取向轴的正交坐标系表达正向压电效应时，应力 用6个张量分量表示，则d系数要用dij的18个分量表 示为矩阵形式。 根据不同材料的对称性，可以简化矩阵。
如拉伸制备的合成多肽薄膜可用 D∞（∞2）表示为：
0 0 0
0 0 0
0 0 0
d14 0 0 0 -d14 0 0 0 0
生物大分子
纤维蛋白 环网络。 由纤维蛋白组成的凝胶可形成交联
例如，牛的血浆或牛的纤维蛋白水溶液中加入凝血酶 即可形成凝胶，用水充分清洗后压缩成薄膜，然后在 水合状态下延伸成各种尺寸。 试验表明，纤维蛋白薄膜的d常数与延伸度之间有线 性关系。
若薄膜充分干燥，则随温度增加d常数升高； 若膜含水，温度增加到0℃以上d常数下降，这可能是冰融化 后导致水泄漏所致。
生物大分子
多糖
木材中的正向和逆向压电效应可用纤维素的微晶压电性说明。
木材用液氨、氢氧化钠等处理后压电常数显著增加。 二醋酸纤维素由晶相和取向的非晶相组成，二者都有压电性。
1976年测定了晶相 压电常数和非晶相压 电常数与温度的关系 dc为结晶相的参数 da为非结晶相的参数 温度单位℃
生物组织
h (
E T ) D 0 4 ( ) S 0 S D
压电特性和压电常数
压电常数通常可表示成复合量：
d d 'id "; e e'ie"; g g 'ig"; h h'ih";
常用的压电常数是e（压变应变常数）和d（压变应力常数）。
压电特性和压电常数
机械和电刺激与骨骼的生长
研究表明，在电场作用下成骨细胞与破骨细胞有不同的趋 电性。
适宜宜的电刺激可以促进未分化的间充质细胞活化为成骨 细胞，促进成骨细胞的增殖和分化，并可以通过成骨细胞 调控破骨细胞对骨的吸收，进一步调控骨的改建。 适宜的电刺激可以明显促进体外培养的成骨细胞的生物矿 化，形成钙结节，碱性磷酸酶的活性增加，胶原和骨钙蛋 白的分泌增加。 电磁可以诱导骨生长因子的表达上调，如胰岛素样生长因 子Ⅱ、形成蛋白2、转化生长因子β1、细胞内游离的钙离 子浓度。
大分子溶液的压电性 生物体中的大分子多数 处于溶液态。 实验：1982年，在PMLG溶液中，相
距2cm的电极上加直流电压，在与 PMLG取向成45°方向上加上100Hz 的超声振荡，则在垂直于切应力平面的 两个电极间观测到100Hz的电振荡。
结果：加上直流电压后由PMLG分子逐 渐取向而发生的压电电压随时间变化， 结果提示，生物体内溶液态的蛋白质 分子也具有压电性。
机械和电刺激与骨骼的生长
实验证明，电刺激对处理困难的骨矫形和持 久性骨不愈合征有实用价值。 根据骨胶原压电效应的可逆性，在骨折治疗 中，可以综合施加各种方式的应力和电刺激， 施加的应力包括恒张力、压力或不同频率的 振动。
传感和换能作用
生物聚合物压电效应的换能作用和传感作用 引起人们极大兴趣。
第一章
第一节 第二节 第三节 第四节
生物电学
概述 生物聚合物的介电特性 生物聚合物的压电特性 人体组织和器官的电阻抗和电活动图
引入
生物组织普遍存在压电效应
1941年Martin首次观察到木材和毛发的压电效应。 70 年代以来发现多种生物大分子和生物组织都具 有压电效应，一些合成多肽和光学活性聚合物也 表现出压电效应。 在对取向的固态生物聚合物进行定量研究时发现： 生物聚合物和合成多肽的液晶态和大分子溶液也 具有压电效应。
一些生物聚合物的压电特性
名称 木材 二醋酸纤维薄膜 二醋酸纤维薄膜 骨 壳质 甲壳 腱 韧带 主动脉 d25 (10-9cgs· esu) 3 16 8 6 2 21 70 8 0.6 肌肉 筋 肌球蛋白薄膜 肌球蛋白薄膜 纤维蛋白薄膜 角 鲑精子DNA 小牛胸腺DNA 纤维素薄膜 名称 d25 (10-9cgs· esu) 12 2 0.3 1.5 6 55 0.3 0.05 100
引入
对生物聚合物的压电特性及其应用的研究， 有助于深入认识一些生命活动的本质和规律， 在医学诊断和治疗，生物医学工程等方面有 着广阔的应用前景。
第三节 生物聚合物的压电特性
生物聚合物的压电特性 一些生物物质的压电特性 压电的生理意义和医学应用
一、生物聚合物的压电特性
1. 压电特性和压电常数 2. 压电常数的测量
d14称为剪切压电常数。由于生物聚合物通常是不均匀的，不 能严格符合压电常数的矩阵表达式。
压电特性和压电常数
实验研究表明，骨和腱等已测到d13和d33分量 的压电性，它相当于具有C∞（∞）对称： 0 0 0 d14 d15 0 0 0 0 d15 -d14 0 d31 d32 d33 0 0 0 对极性高分子、压电陶瓷粉末与高分子的复 合物等，可预期符合C∞v对称，即简化为只有 d15、d31、d33分量。
机械和电刺激与骨骼的生长
已有不少用外加电刺激促进骨生长的实验。 例如
在兔的大腿骨上装上螺旋正电极和线状负电极，连续三 周通以1μA直流电，可看到从负极到正极方向的软组织 长出假骨。 用Teflon驻极体薄膜或PMLG薄膜把折断的兔股骨包裹 起来，四周后，在薄膜上生长出桥样的刚性骨。 近年，出现直流、交流、脉冲和电磁场等方法治疗骨折 的技术。
骨和韧带 把干燥的骨一端固定，另一端弯 曲时，附在骨上各部位的电极之间就会出现 电位差。因为骨的形状复杂，故与应力相对 应的极化分布也很复杂。
大腿骨压缩时的压电电位分布（电压单位mV)
液晶和溶液
液晶的弯曲压电性
液晶有三种形变：倾斜、弯曲和扭转。 液晶中的压电效应是由弯曲形变产生的，而不 是象固体晶体那样由切应变或张应变产生压电 性。因此，有对称中心的晶体结构无压电性， 而有对称中心的液晶却有压电性。
三、压电的生理意义和医学应用
机械和电刺激与骨骼的生长 传感和换能作用
机械和电刺激与骨骼的生长
Friedenberg等观测到，在兔的有干骺端生长的骨 中，直流电位与干骨比较显负电性，当骨折时，骨 折部位可看到最大的负电位。 研究发现，成骨细胞在负极化区被激活，破骨细胞 在正极化区被激活。 运动对保持骨中成骨细胞的活性至关重要，因为运 动可使骨上的应力产生压电和流动电位，从而保持 骨细胞的新陈代谢活性。 另报道，长时间失去重力作用情况下骨的重量会减 轻。
合成多肽
1975年， Takashita首次 研究了不同分 子构象的聚γ －甲基－D－ 谷氨酸盐 （PMDG）压 电性与温度的 关系。 温度单位℃ 。
生物大分子
胶原 胶原是骨压电性的来源。在长骨中，胶 原纤维沿骨轴方向取向，其切变极化最明显。
酶溶解的骨胶原空气 干燥薄膜的e和d常数 与温度的关系
机械应力
g (
E S ) D 0 4 ( )T 0 T D
压电常数 S d和g分别表示在短路时 ( ) T 0 （E=0）和开路（D=0） E 电场强度 条件下由单位应力引起 的电极化和电场； e和h表示由单位应变引 起的电极化和电场。
机械应变
1 D P T e ( ) E 0 ( ) E 0 ( ) S 0 4 S S E
传感和换能作用
例如，1977年，提出生物材料的压电性可 把机械能转化成生物电流
如针刺治疗的针刺
传感物聚合物的压电性和热电性能相关。
传感和换能作用
听觉感受器位于耳蜗基膜中的毛细胞中，毛细胞的弯曲运动产 生与声振幅成正比的电位，该现象称微音电位。其机制是毛细 胞的纤维状蛋白通过其压电效应起了机械－电换能作用。
液晶和溶液
生物体中有多种形式的液晶结构，最显著的 是细胞膜的类脂结构，由磷脂和胆固醇组成 的细胞膜框架，可以成平行双层或六角形排 列。 有人提出，细胞膜类脂有近似于晶体液晶结 构，具有由机械波传送信息的奇特功能。 对生物体液晶的结构和物理的及生理的功能 研究，引起研究者浓厚的兴趣。
液晶和溶液
c c d14 FC (d14 d 25 )/2
压电常数的测量
通常用动力学方法测定复合压电常数，把正 弦状的力加到样品上，测量得到的电压或电 荷。
压电常数的测量
待测样品
应变计
激荡器
恒温槽
压力测量计
运算电路 e’ e”
电荷放大器
运算电路 d’ d”
压电常数e和d的测量原理图
二、一些生物物质的压电特性
压电特性和压电常数
一种物质由应力和应变而诱发出电场的现象，称正 向压电效应； 由外加电场而产生应变和应力的现象称逆压电效应。
压电特性和压电常数
压电常数是反应不同物质的应力或应变与电场相互关系特征 的一种物理量 有四种压电常数分别表示正效应和逆效应：
电位移 极化强度
1 D P d ( ) E 0 ( ) E 0 4 T T
合成多肽 生物大分子 生物组织 液晶和溶液
合成多肽
合成多肽仅由一种氨基酸构成，多肽分子有 结晶态和非结晶态两种构型。 结晶态又有α－螺旋和β－折叠两种立体构象。 只有高结晶度和高取向度的合成多肽才有明 显的压电效应。 利用在磁场中取向和压延的方法制备测试样 品，得到一些合成多肽的压电参数。
压电特性和压电常数
压电常数数值与物质结构的诸因素相关。
例如，木材的压电性来源于纤维素晶体的压电 特性，木材的压电常数d14与其密度ρ、分子团 取向度FC 和结晶度Φ有关。 一般而言，当大量晶体在样品的Z轴方向取向时， d14与取向度FC 、结晶度Φ和剪切压电常数dC14 与dC25的平均值成正比：
传感和换能作用
皮肤中起压力感觉器作用的是帕西尼小体的末 端，被由胶原层组成的鳞茎样结构所包围，这 种结构起压电换能器作用。
一种物质的压电性与其晶体的对称性有关，采用Z轴 为取向轴的正交坐标系表达正向压电效应时，应力 用6个张量分量表示，则d系数要用dij的18个分量表 示为矩阵形式。 根据不同材料的对称性，可以简化矩阵。
如拉伸制备的合成多肽薄膜可用 D∞（∞2）表示为：
0 0 0
0 0 0
0 0 0
d14 0 0 0 -d14 0 0 0 0
生物大分子
纤维蛋白 环网络。 由纤维蛋白组成的凝胶可形成交联
例如，牛的血浆或牛的纤维蛋白水溶液中加入凝血酶 即可形成凝胶，用水充分清洗后压缩成薄膜，然后在 水合状态下延伸成各种尺寸。 试验表明，纤维蛋白薄膜的d常数与延伸度之间有线 性关系。
若薄膜充分干燥，则随温度增加d常数升高； 若膜含水，温度增加到0℃以上d常数下降，这可能是冰融化 后导致水泄漏所致。
生物大分子
多糖
木材中的正向和逆向压电效应可用纤维素的微晶压电性说明。
木材用液氨、氢氧化钠等处理后压电常数显著增加。 二醋酸纤维素由晶相和取向的非晶相组成，二者都有压电性。
1976年测定了晶相 压电常数和非晶相压 电常数与温度的关系 dc为结晶相的参数 da为非结晶相的参数 温度单位℃
生物组织
h (
E T ) D 0 4 ( ) S 0 S D
压电特性和压电常数
压电常数通常可表示成复合量：
d d 'id "; e e'ie"; g g 'ig"; h h'ih";
常用的压电常数是e（压变应变常数）和d（压变应力常数）。
压电特性和压电常数
机械和电刺激与骨骼的生长
研究表明，在电场作用下成骨细胞与破骨细胞有不同的趋 电性。
适宜宜的电刺激可以促进未分化的间充质细胞活化为成骨 细胞，促进成骨细胞的增殖和分化，并可以通过成骨细胞 调控破骨细胞对骨的吸收，进一步调控骨的改建。 适宜的电刺激可以明显促进体外培养的成骨细胞的生物矿 化，形成钙结节，碱性磷酸酶的活性增加，胶原和骨钙蛋 白的分泌增加。 电磁可以诱导骨生长因子的表达上调，如胰岛素样生长因 子Ⅱ、形成蛋白2、转化生长因子β1、细胞内游离的钙离 子浓度。
大分子溶液的压电性 生物体中的大分子多数 处于溶液态。 实验：1982年，在PMLG溶液中，相
距2cm的电极上加直流电压，在与 PMLG取向成45°方向上加上100Hz 的超声振荡，则在垂直于切应力平面的 两个电极间观测到100Hz的电振荡。
结果：加上直流电压后由PMLG分子逐 渐取向而发生的压电电压随时间变化， 结果提示，生物体内溶液态的蛋白质 分子也具有压电性。
机械和电刺激与骨骼的生长
实验证明，电刺激对处理困难的骨矫形和持 久性骨不愈合征有实用价值。 根据骨胶原压电效应的可逆性，在骨折治疗 中，可以综合施加各种方式的应力和电刺激， 施加的应力包括恒张力、压力或不同频率的 振动。
传感和换能作用
生物聚合物压电效应的换能作用和传感作用 引起人们极大兴趣。
第一章
第一节 第二节 第三节 第四节
生物电学
概述 生物聚合物的介电特性 生物聚合物的压电特性 人体组织和器官的电阻抗和电活动图
引入
生物组织普遍存在压电效应
1941年Martin首次观察到木材和毛发的压电效应。 70 年代以来发现多种生物大分子和生物组织都具 有压电效应，一些合成多肽和光学活性聚合物也 表现出压电效应。 在对取向的固态生物聚合物进行定量研究时发现： 生物聚合物和合成多肽的液晶态和大分子溶液也 具有压电效应。
一些生物聚合物的压电特性
名称 木材 二醋酸纤维薄膜 二醋酸纤维薄膜 骨 壳质 甲壳 腱 韧带 主动脉 d25 (10-9cgs· esu) 3 16 8 6 2 21 70 8 0.6 肌肉 筋 肌球蛋白薄膜 肌球蛋白薄膜 纤维蛋白薄膜 角 鲑精子DNA 小牛胸腺DNA 纤维素薄膜 名称 d25 (10-9cgs· esu) 12 2 0.3 1.5 6 55 0.3 0.05 100
引入
对生物聚合物的压电特性及其应用的研究， 有助于深入认识一些生命活动的本质和规律， 在医学诊断和治疗，生物医学工程等方面有 着广阔的应用前景。
第三节 生物聚合物的压电特性
生物聚合物的压电特性 一些生物物质的压电特性 压电的生理意义和医学应用
一、生物聚合物的压电特性
1. 压电特性和压电常数 2. 压电常数的测量
d14称为剪切压电常数。由于生物聚合物通常是不均匀的，不 能严格符合压电常数的矩阵表达式。
压电特性和压电常数
实验研究表明，骨和腱等已测到d13和d33分量 的压电性，它相当于具有C∞（∞）对称： 0 0 0 d14 d15 0 0 0 0 d15 -d14 0 d31 d32 d33 0 0 0 对极性高分子、压电陶瓷粉末与高分子的复 合物等，可预期符合C∞v对称，即简化为只有 d15、d31、d33分量。
机械和电刺激与骨骼的生长
已有不少用外加电刺激促进骨生长的实验。 例如
在兔的大腿骨上装上螺旋正电极和线状负电极，连续三 周通以1μA直流电，可看到从负极到正极方向的软组织 长出假骨。 用Teflon驻极体薄膜或PMLG薄膜把折断的兔股骨包裹 起来，四周后，在薄膜上生长出桥样的刚性骨。 近年，出现直流、交流、脉冲和电磁场等方法治疗骨折 的技术。
骨和韧带 把干燥的骨一端固定，另一端弯 曲时，附在骨上各部位的电极之间就会出现 电位差。因为骨的形状复杂，故与应力相对 应的极化分布也很复杂。
大腿骨压缩时的压电电位分布（电压单位mV)
液晶和溶液
液晶的弯曲压电性
液晶有三种形变：倾斜、弯曲和扭转。 液晶中的压电效应是由弯曲形变产生的，而不 是象固体晶体那样由切应变或张应变产生压电 性。因此，有对称中心的晶体结构无压电性， 而有对称中心的液晶却有压电性。
三、压电的生理意义和医学应用
机械和电刺激与骨骼的生长 传感和换能作用
机械和电刺激与骨骼的生长
Friedenberg等观测到，在兔的有干骺端生长的骨 中，直流电位与干骨比较显负电性，当骨折时，骨 折部位可看到最大的负电位。 研究发现，成骨细胞在负极化区被激活，破骨细胞 在正极化区被激活。 运动对保持骨中成骨细胞的活性至关重要，因为运 动可使骨上的应力产生压电和流动电位，从而保持 骨细胞的新陈代谢活性。 另报道，长时间失去重力作用情况下骨的重量会减 轻。
合成多肽
1975年， Takashita首次 研究了不同分 子构象的聚γ －甲基－D－ 谷氨酸盐 （PMDG）压 电性与温度的 关系。 温度单位℃ 。
生物大分子
胶原 胶原是骨压电性的来源。在长骨中，胶 原纤维沿骨轴方向取向，其切变极化最明显。
酶溶解的骨胶原空气 干燥薄膜的e和d常数 与温度的关系
机械应力
g (
E S ) D 0 4 ( )T 0 T D
压电常数 S d和g分别表示在短路时 ( ) T 0 （E=0）和开路（D=0） E 电场强度 条件下由单位应力引起 的电极化和电场； e和h表示由单位应变引 起的电极化和电场。
机械应变
1 D P T e ( ) E 0 ( ) E 0 ( ) S 0 4 S S E
传感和换能作用
例如，1977年，提出生物材料的压电性可 把机械能转化成生物电流
如针刺治疗的针刺
传感物聚合物的压电性和热电性能相关。
传感和换能作用
听觉感受器位于耳蜗基膜中的毛细胞中，毛细胞的弯曲运动产 生与声振幅成正比的电位，该现象称微音电位。其机制是毛细 胞的纤维状蛋白通过其压电效应起了机械－电换能作用。
液晶和溶液
生物体中有多种形式的液晶结构，最显著的 是细胞膜的类脂结构，由磷脂和胆固醇组成 的细胞膜框架，可以成平行双层或六角形排 列。 有人提出，细胞膜类脂有近似于晶体液晶结 构，具有由机械波传送信息的奇特功能。 对生物体液晶的结构和物理的及生理的功能 研究，引起研究者浓厚的兴趣。
液晶和溶液
c c d14 FC (d14 d 25 )/2
压电常数的测量
通常用动力学方法测定复合压电常数，把正 弦状的力加到样品上，测量得到的电压或电 荷。
压电常数的测量
待测样品
应变计
激荡器
恒温槽
压力测量计
运算电路 e’ e”
电荷放大器
运算电路 d’ d”
压电常数e和d的测量原理图
二、一些生物物质的压电特性
压电特性和压电常数
一种物质由应力和应变而诱发出电场的现象，称正 向压电效应； 由外加电场而产生应变和应力的现象称逆压电效应。
压电特性和压电常数
压电常数是反应不同物质的应力或应变与电场相互关系特征 的一种物理量 有四种压电常数分别表示正效应和逆效应：
电位移 极化强度
1 D P d ( ) E 0 ( ) E 0 4 T T
合成多肽 生物大分子 生物组织 液晶和溶液
合成多肽
合成多肽仅由一种氨基酸构成，多肽分子有 结晶态和非结晶态两种构型。 结晶态又有α－螺旋和β－折叠两种立体构象。 只有高结晶度和高取向度的合成多肽才有明 显的压电效应。 利用在磁场中取向和压延的方法制备测试样 品，得到一些合成多肽的压电参数。
压电特性和压电常数
压电常数数值与物质结构的诸因素相关。
例如，木材的压电性来源于纤维素晶体的压电 特性，木材的压电常数d14与其密度ρ、分子团 取向度FC 和结晶度Φ有关。 一般而言，当大量晶体在样品的Z轴方向取向时， d14与取向度FC 、结晶度Φ和剪切压电常数dC14 与dC25的平均值成正比：