青海师范大学附属中学数学三角形填空选择达标检测(Word版 含解析)
青海省青海师范大学附属第二中学高中数学 第一章 解三角形练习题 新人教A版选修5

青海省青海师范大学附属第二中学2014高中数学 第一章 解三角形练习题 新人教A 版选修5一、选择题1.已知锐角△ABC 的面积为33,BC =4,CA =3,则角C 的大小为( )A .75°B .60°C .45°D .30° 2.在△ABC 中,AB =3,AC =2,BC =10,则BA →·AC →等于( )A .-32B .-23C.23D.32 3.根据下列情况,判断三角形解的情况,其中正确的是( ) A .a =8,b =16,A =30°,有两解 B .b =18,c =20,B =60°,有一解 C .a =5,c =2,A =90°,无解D .a =30,b =25,A =150°,有一解4.在△ABC 中,已知a =5,b =15,A =30°,则c 等于( )A . 2 5B. 5C .25或 5D .以上都不对5.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a cos A =b sin B ,则sin A cos A +cos 2B 等于( )A .-12B.12C .-1D .16.已知a ,b ,c 分别是△ABC 的三个内角A ,B ,C 所对的边.若a =1,b =3,A +C =2B ,则sin C 等于( ) A.12B.32C.66D .17.已知△ABC 中,A 、B 、C 的对边分别为a 、b 、c .若a =c =6+2,且A =75°,则b 等于( ) A .2B.6-2C .4-2 3D .4+2 38.在△ABC 中,三个角A ,B ,C 的对边边长分别为a =3,b =4,c =6,则bc cos A +ca cos B +ab cos C 的值为( ) A .61B.612C.614D .1229.在△ABC 中,cos 2 A 2=b +c2c (a 、b 、c 分别为角A 、B 、C 的对边),则△ABC 的形状为( )A .直角三角形B .等腰三角形或直角三角形C .等腰直角三角形D .正三角形10.在△ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,若C =120°,c =2a ,则( ) A .a >b B .a <bC .a =bD .a 与b 的大小关系不能确定11.一船向正北方向航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半个小时后,看见一灯塔在船的南偏西60°方向,另一灯塔在船的南偏西75°方向,则这只船的速度是( )A .15海里/时B .5海里/时C .10海里/时D .20海里/时12.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若 (a 2+c 2-b 2)tan B =3ac ,则角B 的值为( )A.π6B.π3C.π6或5π6D.π3或2π3二、填空题13.在△ABC 中,2a sin A -b sin B -csin C=________.14.如图,在山腰测得山顶仰角∠CAB =45°,沿倾斜角为30°的斜坡走1 000米至S 点,又测得山顶仰角∠DSB =75°,则山高BC 为________米. 15.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若其面积S =14(b 2+c 2-a 2),则A =______. 16.在锐角三角形ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若b a +a b =6cos C ,则tan C tan A +tan Ctan B=______. 三、解答题17.设锐角三角形ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,a =2b sin A .(1)求角B 的大小; (2)若a =33,c =5,求b .18.如图所示,我艇在A 处发现一走私船在方位角45°且距离为12海里的B 处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的时间.19.已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ,设向量m =(a ,b ),n =(sin B ,sin A ),p =(b -2,a -2).(1)若m ∥n ,求证:△ABC 为等腰三角形;(2)若m ⊥p ,边长c =2,角C =π3,求△ABC 的面积.20.在△ABC 中,内角A ,B , C 的对边分别为a ,b ,c .已知cos A -2cos C cos B =2c -ab.(1)求sin Csin A的值;(2)若cos B =14,△ABC 的周长为5,求b 的长.21.如图所示,甲船以每小时302海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距102海里.问乙船每小时航行多少海里?22.在△ABC中,a、b、c分别是角A、B、C的对边,且cos Bcos C=-b2a+c.(1)求角B的大小;(2)若b=13,a+c=4,求△ABC的面积.。
青海师范大学附属中学数学几何图形初步达标检测(Word版 含解析)

一、初一数学几何模型部分解答题压轴题精选(难)1.将一副三角板中的两个直角顶点叠放在一起(如图①),其中,, .(1)猜想与的数量关系,并说明理由;(2)若,求的度数;(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.【答案】(1)解:,理由如下:,(2)解:如图①,设,则,由(1)可得,,,(3)解:分两种情况:①如图1所示,当时,,又,;②如图2所示,当时,,又,.综上所述,等于或时, .【解析】【分析】(1)由∠BCD=∠ACB+∠ACD=90°+∠ACD,即可求出∠BCD+∠ACE的度数.(2)如图①,设∠ACE=a,可得∠BCD=3a,结合(1)可得3a+a=180°,求出a的度数,即得∠BCD的度数.(3)分两种情况讨论,①如图1所示,当AB∥CE时,∠BCE=180°-∠B=120°,②如图2所示,当AB∥CE时,∠BCE=∠B=60°,分别求出∠BCD的度数即可.2.如图1,∠AOB=120°,∠COE=60°,OF平分∠AOE(1)若∠COF=20°,则∠BOE=________°(2)将∠COE绕点O旋转至如图2位置,求∠BOE和∠COF的数量关系(3)在(2)的条件下,在∠BOE内部是否存在射线OD,使∠DOF=3∠DOE,且∠BOD=70°?若存在,求的值,若不存在,请说明理由.【答案】(1)40(2)解:∵∴∴(3)解:存在.理由如下:∵设∴∵∴∴∴∴【解析】【解答】⑴∴∵OF平分∠AOE,∴∴∴故答案为:40。
【分析】(1)根据,∠EOF=∠COE-∠COF=40°,再由角平分线的定义得出∠AOF=∠EOF=40°,最后∠BOE=∠AOB−∠AOE=120°−80°=40°.(2)由角平分线的定义得出∠AOE=2∠EOF,再利用等量代换得∠AOE=120°−∠BOE=2(60°−∠COF) , 整理得∠BOE=2∠COF;(3)∠DOF=3∠DOE,设∠DOE=α,∠DOF=3α ,∠AOF=∠EOF=2α ,根据∠AOD+∠BOD=120°,构建一个含α的方程,5α+70°=120°求出α,进而求出∠DOF和∠COF.3.如图(1),在△ABC和△EDC中,D为△ABC边AC上一点,CA平分∠BCE,BC=CD,AC=CE.(1)求证:△ABC≌△EDC;(2)如图(2),若∠ACB=60°,连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.①求∠DHF的度数;②若EB平分∠DEC,试说明:BE平分∠ABC.【答案】(1)证明:∵CA平分∠BCE,∴∠ACB=∠ACE.在△ABC和△EDC中.∵BC=CD,∠ACB=∠ACE,AC=CE.∴△ABC≌△EDC(SAS).(2)解:①在△BCF和△DCG中∵BC=DC, ∠BCD=∠DCE,CF=CG,∴△BCF≌△DCG(SAS),∴∠CBF=∠CDG.∵∠CBF+∠BCF=∠CDG+∠DHF∴∠BCF=∠DHF=60°.②∵EB平分∠DEC,∴∠DEH=∠BEC.∵∠DHF=60°,∴∠HDE=60°-∠DEH.∵∠BCE=60°+60°=120°,∴∠CBE=180°-120°-∠BEC=60°-∠BEC.∴∠HDE=∠CBE. ∠A=∠DEG.∵△ABC≌△EDC, △BCF≌△DCG(已证)∴∠BFC=∠DGC,∵∠ABF=∠BFC-∠A, ∠HDE=∠DGC-∠DEG,∴∠ABF=∠HDE,∴∠ABF=∠CBE,∴BE平分∠ABC.【解析】【分析】(1)由角平分线定义得出∠ACB=∠ACE,由ASA证明△ABC≌△EDC即可.(2)①由ASA证明△BCF≌△DCG,得出∠CBF=∠CDG;在△BCF,△DHF中,由三角形内角和定理得出∠BCF=∠DHF=60°.②由全等三角形的性质得出∠A=∠DEG,∠ABF=∠BFC-∠A, ∠HDE=∠DGC-∠DEG,从而得出∠ABF=∠HDE,∠ABF=∠CBE,即BE平分∠ABC.4.已知BM、CN分别是△的两个外角的角平分线,、分别是和的角平分线,如图①;、分别是和的三等分线(即,),如图②;依此画图,、分别是和的n等分线(即,),,且为整数.图①图②(1)若,求的度数;(2)设,请用和n的代数式表示的大小,并写出表示的过程;(3)当时,请直接写出 + 与的数量关系.【答案】(1)解:,∵、分别是和的角平分线,∴∴(2)解:在△中, + ,,(3)解:【解析】【分析】(1)先根据三角形内角和定理求出,根据角平分线求出,再根据三角形内角和定理求出即可;(2)先根据三角形内角和定理求出 + ,根据n等分线求出,再根据三角形内角和定理得出,代入求出即可.(3)本题以三角形为载体,主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质、角平分线的性质、三角形的内角和是的性质,熟记性质然灵活运用有关性质来分析、推理、解答是解题的关键.5.探究题学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题。
2020-2021青海师范大学附属中学初三数学下期中试题(带答案)

2020-2021青海师范大学附属中学初三数学下期中试题(带答案)一、选择题1.如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的()A.23DEBC=B.25DEBC=C.23AEAC=D.25AEEC=2.如图所示,在△ABC中, cos B=22,sin C=35,BC=7,则△ABC的面积是()A.212B.12C.14D.213.如图,河坝横断面迎水坡AB的坡比是1:3(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高3mBC=,则坡面AB的长度是().A.9m B.6m C.63m D.33m4.如图,在同一平面直角坐标系中,反比例函数y=kx与一次函数y=kx﹣1(k为常数,且k>0)的图象可能是()A.B.C.D.5.观察下列每组图形,相似图形是()A.B.C.D.6.如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞()A.8米B.9米C.10米D.11米7.如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是()A.△PAB∽△PCA B.△ABC∽△DBA C.△PAB∽△PDA D.△ABC∽△DCA 8.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是()A.252-B.25-C.251-D.52-9.若反比例函数2yx=-的图象上有两个不同的点关于y轴的对称点都在一次函数y=-x+m的图象上,则m的取值范围是()A.22m>B.-22m<C.22-22m m>或<D.-2222m<<10.如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8cm(如箭头所示),则木桩上升了()A.8tan20°B.C.8sin20°D.8cos20°11.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的12,得到△COD,则CD的长度是()A.2 B.1 C.4 D.512.如图所示,在△ABC 中,AB =6,AC =4,P 是AC 的中点,过 P 点的直线交AB 于点Q ,若以 A 、P 、Q 为顶点的三角形和以A 、B 、C 为顶点的三角形相似,则AQ 的长为 ( )A .3B .3或43C .3或34D .43二、填空题13.若△ABC ∽△A’B’C’,且△ABC 与△A’B’C’的面积之比为1:4,则相似比为____.14.如图,已知点A ,C 在反比例函数(0)a y a x=>的图象上,点B ,D 在反比例函(0)b y b x=<的图象上,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB=5,CD=4,AB 与CD 的距离为6,则a −b 的值是_______.15.已知一个反比例函数的图象经过点(2,3)--,则这个反比例函数的表达式为________.16.如图,在平面直角坐标系中,已知点A 、B 的坐标分别为(8,0)、(0,23),C 是AB 的中点,过点C 作y 轴的垂线,垂足为D ,动点P 从点D 出发,沿DC 向点C 匀速运动,过点P 作x 轴的垂线,垂足为E ,连接BP 、EC .当BP 所在直线与EC 所在直线垂直时,点P 的坐标为____17.在ABC ∆中,若45B ∠=o ,102AB =,55AC =ABC ∆的面积是______.18.如图,l 1∥l 2∥l 3,AB=25AC ,DF=10,那么DE=_________________.19.一个几何体是由一些大小相同的小正方块摆成的,其俯视图与主视图如图所示,则组成这个几何体的小正方块最多有________.20.近视眼镜的度数(y 度)与镜片焦距(x 米)呈反比例,其函数关系式为120.y x =如果近似眼镜镜片的焦距0.3x =米,那么近视眼镜的度数y 为______.三、解答题21.如图1,为放置在水平桌面l 上的台灯,底座的高AB 为5cm .长度均为20cm 的连杆BC ,CD 与AB 始终在同一水平面上.(1)旋转连杆BC ,CD ,使BCD ∠成平角,150ABC ∠=︒,如图2,求连杆端点D 离桌面l 的高度DE .(2)将(1)中的连杆CD 绕点C 逆时针旋转,使165BCD ∠=︒,如图3,问此时连杆端点D 离桌面l 的高度是增加了还是减少?增加或减少了多少?(精确到0.1cm ,参考数据:2 1.41≈,3 1.73≈)22.如图,在△ABC 和△ADE 中,∠BAD =∠CAE ,∠ABC =∠ADE .(1)求证:△ABC ∽△ADE ;(2)判断△ABD 与△ACE 是否相似?并证明.23.如图,在△ABC 中,AB=AC ,点P ,D 分别是BC ,AC 边上的点,且∠APD=∠B.(1)求证:△ABP∽△PCD;(2)若AB=10,BC=12,当PD∥AB时,求BP的长.24.已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.(1)如图1,求证:AD=CD;(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.25.如图,点C、D在线段AB上,△PCD是等边三角形,且CD2=AD•BC.(1)求证:△APD∽△PBC;(2)求∠APB的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】运用平行线分线段成比例定理对各个选项进行判断即可.【详解】∵AD:DB=2:3,∴ADAB=25.∵DE ∥BC ,∴DE BC =AD AB =25,A 错误,B 正确; AE AC=AD AB =25,C 错误; AE EC =AD DB =23,D 错误. 故选B .【点睛】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键. 2.A解析:A【解析】【分析】【详解】试题分析:过点A 作AD ⊥BC ,∵△ABC 中,cosB=22,sinC=35,AC=5,∴cosB=22=BD AB ,∴∠B=45°,∵sinC=35=AD AC =5AD ,∴AD=3,∴CD=4,∴BD=3,则△ABC 的面积是:12×AD×BC=12×3×(3+4)=212.故选A .考点:1.解直角三角形;2.压轴题.3.B解析:B【解析】由图可知,:3BC AC =tan 3BAC ∠=, ∴30BAC ∠=︒, ∴36m 1sin 302BC AB ===︒. 故选B . 4.B解析:B【解析】当k>0时,直线从左往右上升,双曲线分别在第一、三象限,故A、C选项错误;∵一次函数y=kx-1与y轴交于负半轴,∴D选项错误,B选项正确,故选B.5.D解析:D【解析】【分析】根据相似图形的定义,形状相同,可得出答案.【详解】解:A、两图形形状不同,故不是相似图形;B、两图形形状不同,故不是相似图形;C、两图形形状不同,故不是相似图形;D、两图形形状相同,故是相似图形;故选:D.【点睛】本题主要考查相似图形的定义,掌握相似图形形状相同是解题的关键.6.C解析:C【解析】如图所示,AB,CD为树,且AB=13,CD=8,BD为两树距离12米,过C作CE⊥AB于E,则CE=BD=8,AE=AB-CD=6,在直角三角形AEC中,AC=10米,答:小鸟至少要飞10米.故选C.7.B解析:B【解析】【分析】根据相似三角形的判定,采用排除法,逐条分析判断.【详解】∵∠APD =90°,而∠P AB ≠∠PCA ,∠PBA ≠∠P AC ,∴无法判定△P AB 与△PCA 相似,故A 错误;同理,无法判定△P AB 与△PDA ,△ABC 与△DCA 相似,故C 、D 错误;∵∠APD =90°,AP =PB =BC =CD ,∴AB =P A ,AC =P A ,AD =P A ,BD =2P A ,∴=,∴,∴△ABC ∽△DBA ,故B 正确.故选B .【点睛】本题考查了相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法. 8.A解析:A【解析】 根据黄金比的定义得:512AP AB = ,得5142522AP =⨯= .故选A. 9.C解析:C【解析】【分析】 根据题意可知反比例函数2y x =-的图象上的点关于y 轴的对称的点在函数2y x =上,由此可知反比例函数2y x=的图象与一次函数y=-x+m 的图象有两个不同的交点,继而可得关于x 的一元二次方程,再根据根的判别式即可求得答案.【详解】 ∵反比例函数2y x =-上有两个不同的点关于y 轴对称的点在一次函数y =-x +m 图象上, ∴反比例函数2y x=与一次函数y =-x +m 有两个不同的交点, 联立得2y x y x m ⎧=⎪⎨⎪=-+⎩,消去y 得:2x m x =-+, 整理得:220x mx -+=,∵有两个不同的交点∴220x mx -+=有两个不相等的实数根,∴△=m 2-8>0,∴m >m <故选C.【点睛】本题考查了反比例函数图象上点的坐标特征,关于x 轴、y 轴对称的点的坐标,熟练掌握相关内容、正确理解题意是解题的关键.10.A解析:A【解析】【分析】根据已知,运用直角三角形和三角函数得到上升的高度为:8tan20°.【详解】设木桩上升了h 米,∴由已知图形可得:tan20°=8h , ∴木桩上升的高度h =8tan20°故选B. 11.A解析:A【解析】【分析】直接利用位似图形的性质结合A 点坐标可直接得出点C 的坐标,即可得出答案.【详解】∵点A (2,4),过点A 作AB ⊥x 轴于点B ,将△AOB 以坐标原点O 为位似中心缩小为原图形的12,得到△COD , ∴C (1,2),则CD 的长度是2,故选A . 【点睛】本题主要考查了位似变换以及坐标与图形的性质,正确把握位似图形的性质是解题关键.12.B解析:B【解析】AP AQ AB AC =,264AQ =,AQ=43,AP AQ AC AB =,246AQ =,AQ =3.故选B.点睛:相似常见图形(1)称为“平行线型”的相似三角形(如图,有“A 型”与“X 型”图)(2)如图:其中∠1=∠2,则△ADE ∽△ABC 称为“斜交型”的相似三角形,有“反A 共角型”、“反A 共角共边型”、 “蝶型”,如下图:二、填空题13.1:2【解析】【分析】由△ABC 相似△A′B′C′面积比为1:4根据相似三角形的面积比等于相似比的平方即可求解【详解】解:∵△ABC 相似△A′B′C′面积比为1:4∴△ABC 与△A′B′C′的相似比解析:1:2【解析】【分析】由△ABC 相似△A ′B ′C ′,面积比为1:4,根据相似三角形的面积比等于相似比的平方,即可求解.【详解】解:∵△ABC 相似△A ′B ′C ′,面积比为1:4,∴△ABC 与△A ′B ′C ′的相似比为:1:2,故答案为: 1:2.【点睛】本题主要考查的是相似三角形的性质,解决本题的关键是要熟知相似三角形面积的比等于相似比的平方.14.【解析】【分析】利用反比例函数k 的几何意义得出a-b=4•OEa -b=5•OF 求出=6即可求出答案【详解】如图∵由题意知:a-b=4•OEa -b=5•OF ∴OE=OF=又∵OE+OF=6∴=6∴a- 解析:403 【解析】【分析】利用反比例函数k 的几何意义得出a-b=4•OE ,a-b=5•OF ,求出45a b a b --+=6,即可求出答案.【详解】 如图,∵由题意知:a-b=4•OE ,a-b=5•OF ,∴OE=4a b -,OF=5a b -, 又∵OE+OF=6,∴45a b a b --+=6, ∴a-b=403, 故答案为:403. 【点睛】本题考查了反比例函数图象上点的坐标特征,能求出方程45a b a b --+=6是解此题的关键. 15.【解析】【分析】把已知点的坐标代入可求出k 值即得到反比例函数的解析式【详解】设这个反比例函数的表达式为了则所以这个反比例函数的表达式为故答案是:【点睛】考查的是用待定系数法求反比例函数的解析式解题关 解析:6y x =【解析】【分析】把已知点的坐标代入可求出k 值,即得到反比例函数的解析式.【详解】设这个反比例函数的表达式为了(0)k y k x=≠,则 (2)(3)6k =-⨯-=, 所以这个反比例函数的表达式为6y x =. 故答案是:6y x=. 【点睛】考查的是用待定系数法求反比例函数的解析式,解题关键是设关系式、再将已知点坐标代入,从而求解即可. 16.(1)【解析】【分析】先根据题意求得CD 和PE 的长再判定△EPC∽△PDB 列出相关的比例式求得DP 的长最后根据PEDP 的长得到点P 的坐标【详解】由题意可知OB=2AO=8∵CD⊥BOC 是AB 的中点∴解析:(1,3)【解析】【分析】先根据题意求得CD 和PE 的长,再判定△EPC ∽△PDB ,列出相关的比例式,求得DP 的长,最后根据PE 、DP 的长得到点P 的坐标.【详解】由题意可知,OB=23,AO=8,∵CD ⊥BO ,C 是AB 的中点,∴BD=DO=12BO==PE ,CD=12AO=4. 设DP=a ,则CP=4﹣a ,当BP 所在直线与EC 所在直线第一次垂直时,∠FCP=∠DBP , 又∵EP ⊥CP ,PD ⊥BD ,∴∠EPC=∠PDB=90°,∴△EPC ∽△PDB. DP DB PE PC ∴= ∴343a=-, ∴a 1=1,a 2=3(舍去).∴DP=1,∵PE=3,∴P (1,3).考点:1相似三角形性质与判定;2平面直角坐标系.17.75或25【解析】【分析】过点作于点通过解直角三角形及勾股定理可求出的长进而可得出的长再利用三角形的面积公式即可求出的面积【详解】解:过点作垂足为如图所示在中;在中∴∴或∴或25故答案为:75或25解析:75或25【解析】【分析】过点A 作AD BC ⊥于点D ,通过解直角三角形及勾股定理可求出AD ,BD ,CD 的长,进而可得出BC 的长,再利用三角形的面积公式即可求出ABC ∆的面积.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ABD ∆中,sin 10AD AB B =⋅=,cos 10BD AB B =⋅=;在Rt ACD ∆中,10AD =,55AC =∴225CD AC AD =-=,∴15BC BD CD =+=或5BC BD CD =-=, ∴1752ABC S BC AD ∆=⋅=或25. 故答案为:75或25.【点睛】本题考查了解直角三角形、勾股定理以及三角形的面积,通过解直角三角形及勾股定理,求出AD ,BC 的长度是解题的关键.18.【解析】试题解析::∵l1∥l2∥l3∴∵AB=AC∴∴∵DF=10∴∴DE=4 解析:【解析】试题解析::∵l 1∥l 2∥l 3, ∴AB DE AC DF =. ∵AB=25AC , ∴25AB AC =, ∴25DE DF =. ∵DF=10,∴2105DE =, ∴DE=4. 19.6【解析】符合条件的最多情况为:即最多为2+2+2=6解析:6【解析】符合条件的最多情况为:即最多为2+2+2=620.400【解析】分析:把代入即可算出y 的值详解:把代入故答案为400点睛:此题主要考查了反比例函数的定义本题实际上是已知自变量的值求函数值的问题比较简单解析:400【解析】分析:把0.3x =代入120y x=,即可算出y 的值.详解:把0.3x =代入120x , 400y =,故答案为400.点睛:此题主要考查了反比例函数的定义,本题实际上是已知自变量的值求函数值的问题,比较简单.三、解答题21.(1)39.6DE cm ≈;(2)下降了,约3.2cm .【解析】【分析】(1)如图2中,作BO ⊥DE 于O .解直角三角形求出OD 即可解决问题.(2)作DF ⊥l 于F ,CP ⊥DF 于P ,BG ⊥DF 于G ,CH ⊥BG 于H .则四边形PCHG 是矩形,求出DF ,再求出DF-DE 即可解决问题.【详解】(1)过点B 作BO DE ⊥,垂足为O ,如图2,则四边形ABOE 是矩形,1509060OBD =-=o o o ∠,∴sin 6040sin 60203DO BO =⋅=⨯=o o ,∴203539.6DE DO OE DO AB cm =+=+=+≈.(2)下降了.如图3,过点D 作DF l ⊥于点F ,过点C 作CP DF ⊥于点P ,过点B 作BG DF ⊥于点G ,过点C 作CH BG ⊥于点H ,则四边形PCHG 为矩形,∵60CBH ︒∠=,∴30BCH ︒∠=,又∵165BCD ︒∠=,∴45DCP ︒∠=,∴sin 60CH BC ︒==*sin 45DP CD ==,∴DF DP PG GF DP CH AB =++=++5=.∴下降高度:55DE DF -=-=3.2cm ≈.【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.22.(1)见解析 (2) △ABD ∽△ACE【解析】分析:(1)由∠BAD=∠CAE 易得∠BAC=∠DAE ,这样结合∠ABC=∠ADE ,即可得到△ABC ∽△ADE .(2)由(1)中结论易得AB AC AD AE =,从而可得: AB AD AC AE =,这样结合∠BAD=∠CAE 即可得到△ABD ∽△ACE 了.详解;(1)∵∠BAD=∠CAE ,∴∠BAC=∠DAE ,∵∠ABC=∠ADE ,∴△ABC ∽△ADE .(2)△ABD ∽△ACE ,理由如下:由(1)可知△ABC ∽△ADE , ∴AB AC AD AE =, ∴AB AD AC AE=, 又∵∠BAD=∠CAE ,∴△ABD ∽△ACE .点睛:这是一道考查“相似三角形的判定与性质的题目”,熟悉“相似三角形的判定定理和性质”是解答本题的关键.23.(1)证明见解析;(2)BP=253. 【解析】【分析】(1)由题意可得∠ABC=∠ACB,∠DPC=∠BAP,可证△ABP∽△PCD;(2))由△ABP∽△PCD,可得PC ABCD BP=,由PD∥AB,可得PC BCCD AC=,即AB BCBP AC=,可求BP的长.【详解】(1)∵AB=AC,∴∠ABC=∠ACB.∵∠APC=∠ABC+∠BAP,∴∠APD+∠DPC=∠ABC+∠BAP,且∠APD=∠B,∴∠DPC =∠BAP且∠ABC=∠ACB,∴△BAP∽△CPD.(2)∵△ABP∽△PCD,∴PC CDAB BP=即PC ABCD BP=.∵PD∥AB,∴PC CDBC AC=即PC BCCD AC=,∴AB BCBP AC=,∴101210BP=,∴BP253=.【点睛】本题考查了相似三角形的判定与性质,等腰三角形的性质,熟练掌握相似三角形的性质是本题的关键.24.(1)证明见解析;(2)△ACD、△ABE、△BCE、△BHG.【解析】分析:(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;(2)设DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,据此知S△ADC=2a2=2S△ADE,证△ADE≌△BGE得BE=AE=2a,再分别求出S△ABE、S△ACE、S△BHG,从而得出答案.详解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD、BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD;(2)设DE=a,则AE=2DE=2a,EG=DE=a,∴S△ADE=12AE×DE=12×2a×a=a2,∵BH是△ABE的中线,∴AH=HE=a,∵AD=CD、AC⊥BD,∴CE=AE=2a,则S△ADC=12AC•DE=12•(2a+2a)•a=2a2=2S△ADE;在△ADE和△BGE中,∵AED BEG DE GEADE BGE ∠∠⎧⎪⎨⎪∠∠⎩===,∴△ADE≌△BGE(ASA),∴BE=AE=2a,∴S△ABE=12AE•BE=12•(2a)•2a=2a2,S△ACE=12CE•BE=12•(2a)•2a=2a2,S△BHG=12HG•BE=12•(a+a)•2a=2a2,综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.点睛:本题主要考查全等三角形的判定与性质,解题的关键是掌握等腰三角形的判定与性质及全等三角形的判定与性质.25.(1)见解析;(2)120°【解析】【分析】(1)CD2=AD•BC可得AD:PC=PD:BC,又由△PCD是等边三角形,所以可求出∠ADP=∠BCP=120°,进而证明△ACP∽△PDB;(2)由△APD∽△PBC,可得∠APD=∠B,则可求得∠APB的大小.【详解】(1)证明:∵△PCD是等边三角形,∴PD=PC=DC,∠PDC=∠PCD=60°,∴∠ADP=∠BCP=120°,∵CD2=AD•BC,∴AD:PC=PD:BC,∴△APD∽△PBC;(2)∵△APD∽△PBC,∴∠APD=∠B,∵∠B+∠BPC=60°,∴∠APD+∠BPC=60°,∴∠APB=60°+∠DPC=120°.【点睛】本题考查了相似三角形的判定和性质,等边三角形的性质,熟练掌握相似三角形的性质是解题的关键.。
青海省西宁市青海师范大学附属实验中学2022-2023学年高二上学期12月月考数学试题(含答案)

青海师范大学附属实验中学2022-2023学年度第一学期教学质量检测高二数学一、单选题:本题12小题,共60分。
1.函数()221f x x =+在区间[]1,1x +∆上的平均变化率是( )A .42x +∆B .2x ∆C .4D .22.向一个半球形的水池注水时,向池子注水速度不变(即单位时间内注入水量相同),若池子中水的高度h 是关于时间t 的函数()h t ,则函数()h t 的图象可能是( )A .B .C .D .3.已知函数()sin f x a x =-,且0()()lim 2x f x f xππ∆→+∆-=∆,则实数a 的值为( )A .2πB .2π-C .2D .2-4.下列函数求导运算正确的个数为( )①()333log e x x '=;②()e e x x '=;③1ln x x '⎛⎫= ⎪⎝⎭;④()e e 1x xx '⋅=+.A .1B .2C .3D .45.已知函数()2xf x e =,则A .()()'2f x f x =+B .()()'f x f x =C .()()'3f x f x =D .()()'2f x f x =6.已知()tan f x x =,则()f x '=( )A .21sin xB .21cos xC .21sin x-D .21cos x-7.曲线2()1f x x x =++ 在点(0,1) 处的切线方程为( )A .x +y +1=0B .x +y ﹣1=0C .x ﹣y +1=0D .x ﹣y ﹣1=08.已知函数3()f x x x =+,则0a b +>是()()0f a f b +>的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件9.在抛物线212x y =第一象限内一点(),n n a y 处的切线与x 轴交点横坐标记为1n a +,其中*n ∈N ,已知232a =,n S 为{}n a 的前n 项和,若n m S ≥恒成立,则m 的最小值为( )A .16B .32C .64D .12810.已知函数()1f x ax =-,且(1)2f '=,则=a ( )A .0B .1C .2D .411.函数()()lg 1f x x =-的定义域为( )A .(]1,3B .()3,+∞C .(],3-∞D .()1,+∞12.若函数2(62)711,1,()42ln 4,1a x a x f x x x ax x -+-<⎧=⎨+-≥⎩在(,)∞∞-+上单调递增,则实数a 的取值范围是( )A .15,32⎛⎤⎥⎝⎦B .1,23⎛⎤ ⎥⎝⎦C .51,2⎡⎤⎢⎥⎣⎦D .[]1,2二、填空题:本题5小题,共20分。
青海师范大学附属中学七年级下册数学期末试卷达标检测(Word版 含解析) (2)

青海师范大学附属中学七年级下册数学期末试卷达标检测(Word 版 含解析) 一、解答题1.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结FA 、FB ,E 是射线FA 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.2.已知点C 在射线OA 上.(1)如图①,CD //OE ,若∠AOB =90°,∠OCD =120°,求∠BOE 的度数;(2)在①中,将射线OE 沿射线OB 平移得O ′E '(如图②),若∠AOB =α,探究∠OCD 与∠BO ′E ′的关系(用含α的代数式表示)(3)在②中,过点O ′作OB 的垂线,与∠OCD 的平分线交于点P (如图③),若∠CPO ′=90°,探究∠AOB 与∠BO ′E ′的关系.3.如图,∠EBF =50°,点C 是∠EBF 的边BF 上一点.动点A 从点B 出发在∠EBF 的边BE 上,沿BE 方向运动,在动点A 运动的过程中,始终有过点A 的射线AD ∥BC .(1)在动点A 运动的过程中, (填“是”或“否”)存在某一时刻,使得AD 平分∠EAC ? (2)假设存在AD 平分∠EAC ,在此情形下,你能猜想∠B 和∠ACB 之间有何数量关系?并请说明理由;(3)当AC ⊥BC 时,直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系.4.已知,AB∥CD.点M在AB上,点N在CD上.(1)如图1中,∠BME、∠E、∠END的数量关系为:;(不需要证明)如图2中,∠BMF、∠F、∠FND的数量关系为:;(不需要证明)(2)如图3中,NE平分∠FND,MB平分∠FME,且2∠E+∠F=180°,求∠FME的度数;(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,且EQ∥NP,则∠FEQ的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ的度数.5.已知:AB∥CD,截线MN分别交AB、CD于点M、N.(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足30a+(β﹣60)2=0,求∠BEM的度数;(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为(直接写出答案).二、解答题6.已知,如图①,∠BAD =50°,点C 为射线AD 上一点(不与A 重合),连接BC . (1)[问题提出]如图②,AB ∥CE ,∠BCD =73 °,则:∠B = .(2)[类比探究]在图①中,探究∠BAD 、∠B 和∠BCD 之间有怎样的数量关系?并用平行....线的性质....说明理由. (3)[拓展延伸]如图③,在射线BC 上取一点O ,过O 点作直线MN 使MN ∥AD ,BE 平分∠ABC 交AD 于E 点,OF 平分∠BON 交AD 于F 点,//OG BE 交AD 于G 点,当C 点沿着射线AD 方向运动时,∠FOG 的度数是否会变化?若变化,请说明理由;若不变,请求出这个不变的值.7.已知ABC ,//DE AB 交AC 于点E ,//DF AC 交AB 于点F .(1)如图1,若点D 在边BC 上, ①补全图形; ②求证:A EDF ∠=∠.(2)点G 是线段AC 上的一点,连接FG ,DG .①若点G 是线段AE 的中点,请你在图2中补全图形,判断AFG ∠,EDG ∠,DGF ∠之间的数量关系,并证明;②若点G 是线段EC 上的一点,请你直接写出AFG ∠,EDG ∠,DGF ∠之间的数量关系. 8.已知两条直线l 1,l 2,l 1∥l 2,点A ,B 在直线l 1上,点A 在点B 的左边,点C ,D 在直线l 2上,且满足115ADC ABC ∠=∠=o .(1)如图①,求证:AD ∥BC ;(2)点M ,N 在线段CD 上,点M 在点N 的左边且满足MAC BAC ∠=∠,且AN 平分∠CAD ;(Ⅰ)如图②,当30ACD ∠=o 时,求∠DAM 的度数;(Ⅱ)如图③,当8CAD MAN ∠=∠时,求∠ACD 的度数. 9.已知:ABC 和同一平面内的点D .(1)如图1,点D 在BC 边上,过D 作//DE BA 交AC 于E ,//DF CA 交AB 于F .根据题意,在图1中补全图形,请写出EDF ∠与BAC ∠的数量关系,并说明理由;(2)如图2,点D 在BC 的延长线上,//DF CA ,EDF BAC ∠=∠.请判断DE 与BA 的位置关系,并说明理由.(3)如图3,点D 是ABC 外部的一个动点.过D 作//DE BA 交直线AC 于E ,//DF CA 交直线AB 于F ,直接写出EDF ∠与BAC ∠的数量关系,并在图3中补全图形.10.问题情境(1)如图1,已知//AB CD ,125PBA ︒∠=,155PCD ︒∠=,求BPC ∠的度数.佩佩同学的思路:过点P 作PG//AB ,进而//PG CD ,由平行线的性质来求BPC ∠,求得BPC ∠=________. 问题迁移(2)图2.图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合,90ACB ︒∠=,//DF CG ,AB 与FD 相交于点E ,有一动点P 在边BC 上运动,连接PE ,PA ,记PED α∠=∠,PAC β∠=∠.①如图2,当点P 在C ,D 两点之间运动时,请直接写出AOE ∠与α∠,β∠之间的数量关系;②如图3,当点P 在B ,D 两点之间运动时,APE ∠与α∠,β∠之间有何数量关系?请判断并说明理由;拓展延伸(3)当点P 在C ,D 两点之间运动时,若PED ∠,PAC ∠的角平分线EN ,AN 相交于点N ,请直接写出ANE ∠与α∠,β∠之间的数量关系.三、解答题11.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交BC 于点F .(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角:;所有与∠C相等的角:.(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .① 求∠B的度数;②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.12.如图,直线m与直线n互相垂直,垂足为O、A、B两点同时从点O出发,点A沿直线m向左运动,点B沿直线n向上运动.(1)若∠BAO和∠ABO的平分线相交于点Q,在点A,B的运动过程中,∠AQB的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.(2)若AP是∠BAO的邻补角的平分线,BP是∠ABO的邻补角的平分线,AP、BP相交于点P,AQ的延长线交PB的延长线于点C,在点A,B的运动过程中,∠P和∠C的大小是否会发生变化?若不发生变化,请求出∠P和∠C的度数;若发生变化,请说明理由.13.如图,已知直线a∥b,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧,线段EF沿射线AD的方向平移,在平移的过程中BD所在的直线与EF所在的直线交于点P.问∠1的度数与∠EPB的度数又怎样的关系?(特殊化)(1)当∠1=40°,交点P在直线a、直线b之间,求∠EPB的度数;(2)当∠1=70°,求∠EPB 的度数;(一般化)(3)当∠1=n°,求∠EPB 的度数(直接用含n 的代数式表示).14.己知:如图①,直线MN ⊥直线PQ ,垂足为O ,点A 在射线OP 上,点B 在射线OQ 上(A 、B 不与O 点重合),点C 在射线ON 上且2OC =,过点C 作直线//l PQ .点D 在点C 的左边且3CD =(1)直接写出的BCD ∆面积 ;(2)如图②,若AC BC ⊥,作CBA ∠的平分线交OC 于E ,交AC 于F ,试说明CEF CFE ∠=∠;(3)如图③,若ADC DAC ∠=∠,点B 在射线OQ 上运动,ACB ∠的平分线交DA 的延长线于点H ,在点B 运动过程中HABC∠∠的值是否变化?若不变,求出其值;若变化,求出变化范围.15.如图1,已知线段AB 、CD 相交于点O ,连接AC 、BD ,我们把形如图1的图形称之为“8字形”.如图2,∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,并且与CD 、AB 分别相交于M 、N .试解答下列问题:(1)仔细观察,在图2中有 个以线段AC 为边的“8字形”; (2)在图2中,若∠B=96°,∠C=100°,求∠P 的度数;(3)在图2中,若设∠C=α,∠B=β,∠CAP=13∠CAB ,∠CDP=13∠CDB ,试问∠P 与∠C 、∠B 之间存在着怎样的数量关系(用α、β表示∠P ),并说明理由; (4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F 的度数为 .【参考答案】一、解答题1.(1)100;(2)75°;(3)n=3. 【分析】(1)如图:过O 作OP//MN ,由MN//OP//GH 得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OB 解析:(1)100;(2)75°;(3)n =3. 【分析】(1)如图:过O 作OP //MN ,由MN //OP //GH 得∠NAO +∠POA =180°,∠POB +∠OBH =180°,即∠NAO +∠AOB +∠OBH =360°,即可求出∠AOB ;(2)如图:分别延长AC 、CD 交GH 于点E 、F ,先根据角平分线求得58NAC ∠=︒,再根据平行线的性质得到58CEF ∠=︒;进一步求得18DBF ∠=︒,17DFB ∠=︒,然后根据三角形外角的性质解答即可;(3)设BF 交MN 于K ,由∠NAO =116°,得∠MAO =64°,故∠MAE =641nn ︒⨯+,同理∠OBH =144°,∠HBF =n ∠OBF ,得∠FBH =1441n n ︒⨯+,从而=n BKA FBH n ∠∠=⨯︒+1441,又∠FKN =∠F +∠FAK ,得144606411n nn n ︒︒︒⨯=+⨯++,即可求n . 【详解】解:(1)如图:过O 作OP //MN , ∵MN //GHl ∴MN //OP //GH∴∠NAO +∠POA =180°,∠POB +∠OBH =180° ∴∠NAO +∠AOB +∠OBH =360° ∵∠NAO =116°,∠OBH =144°∴∠AOB =360°-116°-144°=100°;(2)分别延长AC 、CD 交GH 于点E 、F ,∵AC 平分NAO ∠且116NAO ∠=︒, ∴58NAC ∠=︒, 又∵MN //GH , ∴58CEF ∠=︒;∵144OBH ∠=︒,36OBG ∠=︒ ∵BD 平分OBG ∠, ∴18DBF ∠=︒, 又∵,CDB ∠=︒35∴351817DFB CDB DBF ∠=∠-∠=-=︒; ∴175875ACD DFB AEF ∠=∠+∠=︒+︒=︒; (3)设FB 交MN 于K ,∵116NAO ∠=︒,则MAO ∠=︒64; ∴641nMAE n ∠=⨯︒+ ∵144OBH ∠=︒, ∴+1n FBH n ∠=⨯︒144,=n BKA FBH n ∠∠=⨯︒+1441, 在△FAK 中,64601nBKA FKA F n ∠=∠+∠=⨯︒+︒+, ∴144646011n n n n ⨯︒=⨯︒+︒++, ∴3n =.经检验:3n =是原方程的根,且符合题意. 【点睛】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.2.(1)150°;(2)∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′【分析】(1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;(2)解析:(1)150°;(2)∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′【分析】(1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;(2)如图②,过O点作OF∥CD,根据平行线的判定和性质可得∠OCD、∠BO′E′的数量关系;(3)由已知推出CP∥OB,得到∠AOB+∠PCO=180°,结合角平分线的定义可推出∠OCD=2∠PCO=360°-2∠AOB,根据(2)∠OCD+∠BO′E′=360°-∠AOB,进而推出∠AOB=∠BO′E′.【详解】解:(1)∵CD∥OE,∴∠AOE=∠OCD=120°,∴∠BOE=360°-∠AOE-∠AOB=360°-90°-120°=150°;(2)∠OCD+∠BO′E′=360°-α.证明:如图②,过O点作OF∥CD,∵CD∥O′E′,∴OF∥O′E′,∴∠AOF=180°-∠OCD,∠BOF=∠E′O′O=180°-∠BO′E′,∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E′=360°-(∠OCD+∠BO′E′)=α,∴∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′.证明:∵∠CPO′=90°,∴PO′⊥CP,∵PO′⊥OB,∴CP∥OB,∴∠PCO+∠AOB=180°,∴2∠PCO=360°-2∠AOB,∵CP是∠OCD的平分线,∴∠OCD=2∠PCO=360°-2∠AOB,∵由(2)知,∠OCD+∠BO′E′=360°-α=360°-∠AOB,∴360°-2∠AOB+∠BO′E′=360°-∠AOB,∴∠AOB=∠BO′E′.【点睛】此题考查了平行线的判定和性质,平移的性质,直角的定义,角平分线的定义,正确作出辅助线是解决问题的关键.3.(1)是;(2)∠B=∠ACB,证明见解析;(3)∠BAC=40°,AC⊥AD.【分析】(1)要使AD平分∠EAC,则要求∠EAD=∠CAD,由平行线的性质可得∠B=∠EAD,∠ACB=∠CAD解析:(1)是;(2)∠B=∠ACB,证明见解析;(3)∠BAC=40°,AC⊥AD.【分析】(1)要使AD平分∠EAC,则要求∠EAD=∠CAD,由平行线的性质可得∠B=∠EAD,∠ACB=∠CAD,则当∠ACB=∠B时,有AD平分∠EAC;(2)根据角平分线可得∠EAD=∠CAD,由平行线的性质可得∠B=∠EAD,∠ACB=∠CAD,则有∠ACB=∠B;(3)由AC⊥BC,有∠ACB=90°,则可求∠BAC=40°,由平行线的性质可得AC⊥AD.【详解】解:(1)是,理由如下:要使AD平分∠EAC,则要求∠EAD=∠CAD,由平行线的性质可得∠B=∠EAD,∠ACB=∠CAD,则当∠ACB=∠B时,有AD平分∠EAC;故答案为:是;(2)∠B=∠ACB,理由如下:∵AD平分∠EAC,∴∠EAD=∠CAD,∵AD∥BC,∴∠B=∠EAD,∠ACB=∠CAD,∴∠B=∠ACB.(3)∵AC⊥BC,∴∠ACB=90°,∵∠EBF=50°,∴∠BAC=40°,∵AD∥BC,∴AD⊥AC.【点睛】此题考查了角平分线和平行线的性质,熟练掌握角平分线和平行线的有关性质是解题的关键.4.(1)∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND;(2)120°;(3)不变,30°【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB解析:(1)∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND;(2)120°;(3)不变,30°【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB,易得FH∥AB∥CD,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME+∠END)+∠BMF-∠FND=180°,可求解∠BMF=60°,进而可求解;∠BME,进而可求解.(3)根据平行线的性质及角平分线的定义可推知∠FEQ=12【详解】解:(1)过E作EH∥AB,如图1,∴∠BME=∠MEH,∵AB∥CD,∴HE∥CD,∴∠END=∠HEN,∴∠MEN=∠MEH+∠HEN=∠BME+∠END,即∠BME=∠MEN﹣∠END.如图2,过F作FH∥AB,∴∠BMF=∠MFK,∵AB∥CD,∴FH∥CD,∴∠FND=∠KFN,∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN+∠MFN=180°,∴2(∠BME+∠END)+∠BMF﹣∠FND=180°,∴2∠BME+2∠END+∠BMF﹣∠FND=180°,即2∠BMF+∠FND+∠BMF﹣∠FND=180°,解得∠BMF=60°,∴∠FME=2∠BMF=120°;(3)∠FEQ的大小没发生变化,∠FEQ=30°.由(1)知:∠MEN=∠BME+∠END,∵EF平分∠MEN,NP平分∠END,∴∠FEN=12∠MEN=12(∠BME+∠END),∠ENP=12∠END,∵EQ∥NP,∴∠NEQ=∠ENP,∴∠FEQ=∠FEN﹣∠NEQ=12(∠BME+∠END)﹣12∠END=12∠BME,∵∠BME=60°,∴∠FEQ=12×60°=30°.【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键.5.(1)30°;(2)∠DEF+2∠CDF=150°,理由见解析;(3)【分析】(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;(2)过点E作直线EH∥AB,由角平分线的性质和平行解析:(1)30°;(2)∠DEF+2∠CDF=150°,理由见解析;(3)12【分析】(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;(2)过点E作直线EH∥AB,由角平分线的性质和平行线的性质可求∠DEF=180°﹣30°﹣2x°=150°﹣2x°,由角的数量可求解;(3)由平行线的性质和外角性质可求∠PMB=2∠Q+∠PCD,∠CPM=2∠Q,即可求解.【详解】解:(1)∵30α-+(β﹣60)2=0,∴α=30,β=60,∵AB∥CD,∴∠AMN=∠MND=60°,∵∠AMN=∠B+∠BEM=60°,∴∠BEM=60°﹣30°=30°;(2)∠DEF+2∠CDF=150°.理由如下:过点E作直线EH∥AB,∵DF平分∠CDE,∴设∠CDF=∠EDF=x°;∵EH∥AB,∴∠DEH=∠EDC=2x°,∴∠DEF=180°﹣30°﹣2x°=150°﹣2x°;∴∠DEF=150°﹣2∠CDF,即∠DEF+2∠CDF=150°;(3)如图3,设MQ与CD交于点E,∵MQ平分∠BMT,QC平分∠DCP,∴∠BMT=2∠PMQ,∠DCP=2∠DCQ,∵AB∥CD,∴∠BME=∠MEC,∠BMP=∠PND,∵∠MEC=∠Q+∠DCQ,∴2∠MEC=2∠Q+2∠DCQ,∴∠PMB=2∠Q+∠PCD,∵∠PND=∠PCD+∠CPM=∠PMB,∴∠CPM=2∠Q,∴∠Q与∠CPM的比值为1,2故答案为:12.【点睛】本题主要考查了平行线的性质、角平分线的性质,准确计算是解题的关键. 二、解答题6.(1);(2),见解析;(3)不变,【分析】(1)根据平行线的性质求出,再求出的度数,利用内错角相等可求出角的度数;(2)过点作∥,类似(1)利用平行线的性质,得出三个角的关系; (3)运用解析:(1)23︒;(2)BCD A B ∠=∠+∠,见解析;(3)不变, 25FOG ∠=︒【分析】(1)根据平行线的性质求出50A DCE ∠=∠=︒,再求出BCE ∠的度数,利用内错角相等可求出角的度数;(2)过点C 作CE ∥AB ,类似(1)利用平行线的性质,得出三个角的关系;(3)运用(2)的结论和平行线的性质、角平分线的性质,可求出FOG ∠的度数,可得结论.【详解】(1)因为CE ∥AB ,所以50A DCE ∠=∠=︒,B BCE ∠=∠因为∠BCD =73 °,所以23BCE BCD DCE ∠=∠-∠=︒,故答案为:23︒(2)BCD A B ∠=∠+∠,如图②,过点C 作CE ∥AB ,则A DCE ∠=∠,B BCE ∠=∠.因为BCD DCE BCE ∠=∠+∠,所以BCD BAD B ∠=∠+∠,(3)不变,设ABE x ∠=,因为BE 平分ABC ∠,所以CBE ABE x ∠=∠=.由(2)的结论可知BCD BAD ABC ∠=∠+∠,且50BAD ︒∠=,则:502BCD x ∠=︒+.因为MN ∥AD ,所以502BON BCD x ∠=∠=︒+,因为OF 平分BON ∠,所以1252COF NOF BON x ∠=∠=∠=︒+. 因为OG ∥BE ,所以COG CBE x ∠=∠=,所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒.【点睛】本题考查了平行线的性质和角平分线的定义,解题关键是熟练运用平行线的性质证明角相等,通过等量代换等方法得出角之间的关系.7.(1)①见解析;②;见解析(2)①∠AFG+∠EDG=∠DGF ;②∠AFG-∠EDG=∠DGF【分析】(1)①根据题意画出图形;②依据DE ∥AB ,DF ∥AC ,可得∠EDF+∠AFD=180°,∠解析:(1)①见解析;②;见解析(2)①∠AFG +∠EDG =∠DGF ;②∠AFG -∠EDG =∠DGF【分析】(1)①根据题意画出图形;②依据DE ∥AB ,DF ∥AC ,可得∠EDF +∠AFD =180°,∠A +∠AFD =180°,进而得出∠EDF =∠A ;(2)①过G 作GH ∥AB ,依据平行线的性质,即可得到∠AFG +∠EDG =∠FGH +∠DGH =∠DGF ;②过G 作GH ∥AB ,依据平行线的性质,即可得到∠AFG -∠EDG =∠FGH -∠DGH =∠DGF .【详解】解:(1)①如图,②∵DE ∥AB ,DF ∥AC ,∴∠EDF +∠AFD =180°,∠A +∠AFD =180°,∴∠EDF =∠A ;(2)①∠AFG +∠EDG =∠DGF .如图2所示,过G 作GH ∥AB ,∵AB ∥DE ,∴GH ∥DE ,∴∠AFG =∠FGH ,∠EDG =∠DGH ,∴∠AFG +∠EDG =∠FGH +∠DGH =∠DGF ;②∠AFG -∠EDG =∠DGF .如图所示,过G 作GH ∥AB ,∵AB ∥DE ,∴GH ∥DE ,∴∠AFG =∠FGH ,∠EDG =∠DGH ,∴∠AFG -∠EDG =∠FGH -∠DGH =∠DGF .【点睛】本题考查了平行线的判定和性质:两直线平行,内错角相等.正确的作出辅助线是解题的关键.8.(1)证明见解析;(2)(Ⅰ);(Ⅱ).【分析】(1)先根据平行线的性质可得,再根据角的和差可得,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得,从而可得,再根据角的和差可得 解析:(1)证明见解析;(2)(Ⅰ)5DAM ∠=︒;(Ⅱ)25ACD ∠=︒.【分析】(1)先根据平行线的性质可得65BAD ∠=︒,再根据角的和差可得180BAD ABC ∠+∠=︒,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得30BAC ACD ∠=∠=︒,从而可得30MAC ∠=︒,再根据角的和差可得35DAC ∠=︒,然后根据DAM DAC MAC ∠=∠-∠即可得;(Ⅱ)设MAN x ∠=,从而可得8CAD x ∠=,先根据角平分线的定义可得142CAN CAD x ∠=∠=,再根据角的和差可得5BAC MAC x ∠=∠=,然后根据65CAD BAC BAD ∠+∠=∠=︒建立方程可求出x 的值,从而可得BAC ∠的度数,最后根据平行线的性质即可得.【详解】(1)12//,115l l ADC ∠=︒,18065BAD ADC ∴∠=︒-∠=︒,又115ABC ∠=︒,180BAD ABC ∴∠+∠=︒,//AD BC ∴;(2)(Ⅰ)12//,30l l ACD ∠=︒,30BAC ACD ∴∠=∠=︒,MAC BAC ∠=∠,30MAC ∴∠=︒,由(1)已得:65BAD ∠=︒,35DAC BAD BAC ∴∠=∠-∠=︒,35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒;(Ⅱ)设MAN x ∠=,则8CAD x ∠=, AN 平分CAD ∠,142CAN CAD x ∴∠=∠=, 5MAC CAN MAN x ∴∠=∠+∠=,MAC BAC ∠=∠,5BAC x ∴∠=,由(1)已得:65BAD ∠=︒,65CAD BAC BAD ∴∠+∠=∠=︒,即8565x x +=︒,解得5x =︒,525BAC x ∴∠==︒,又12//l l ,25ACD BAC ∴∠=∠=︒.【点睛】本题考查了平行线的判定与性质、角的和差、角平分线的定义、一元一次方程的几何应用等知识点,熟练掌握平行线的判定与性质是解题关键.9.(1)图见解析,,理由见解析;(2),理由见解析;(3)图见解析,或.【分析】(1)根据平行线的画法补全图形即可得,根据平行线的性质可得,由此即可得;(2)如图(见解析),先根据平行线的性质可解析:(1)图见解析,EDF BAC ∠=∠,理由见解析;(2)//DE BA ,理由见解析;(3)图见解析,EDF BAC ∠=∠或180EDF BAC ∠+∠=︒.【分析】(1)根据平行线的画法补全图形即可得,根据平行线的性质可得,EDF BFD B B D AC F ∠=∠∠∠=,由此即可得;(2)如图(见解析),先根据平行线的性质可得BAC BOD ∠=∠,再根据等量代换可得EDF BOD∠=∠,然后根据平行线的判定即可得;(3)先根据点D的位置画出如图(见解析)的两种情况,再分别利用平行线的性质、对顶角相等即可得.【详解】(1)由题意,补全图形如下:∠=∠,理由如下:EDF BACDE BA,//∴∠=∠,EDF BFDDF CA,//∴∠=∠,BABFD C∴∠=∠;EDF BACDE BA,理由如下:(2)//如图,延长BA交DF于点O,DF CA,//∴∠=∠,BAC BOD∠=∠,EDF BAC∴∠=∠,EDF BOD∴;DE BA//(3)由题意,有以下两种情况:∠=∠,理由如下:①如图3-1,EDF BACDE BA,//∴∠+∠=︒,180E EAFDF CA,//E EDF∴∠+∠=︒,180∴∠=∠,EAF EDF由对顶角相等得:BAC EAF∠=∠,∴∠=∠;EDF BAC②如图3-2,180EDF BAC ∠+∠=︒,理由如下://DE BA ,180EDF F ∴∠+∠=︒,//DF CA ,BAC F ∴∠=∠,180EDF BAC ∴∠+∠=︒.【点睛】本题考查了平行线的判定与性质等知识点,较难的是题(3),正确分两种情况讨论是解题关键.10.(1);(2)①,②,理由见解析;(3)【分析】(1)过点作,则,由平行线的性质可得的度数;(2)①过点作的平行线,依据平行线的性质可得与,之间的数量关系; ②过作,依据平行线的性质可得,,即解析:(1)80︒;(2)①APE αβ∠=∠+∠,②APE βα∠=∠-∠,理由见解析;(3)1()2ANE αβ∠=∠+∠ 【分析】(1)过点P 作//PG AB ,则//PG CD ,由平行线的性质可得BPC ∠的度数; (2)①过点P 作FD 的平行线,依据平行线的性质可得APE ∠与α∠,β∠之间的数量关系;②过P 作//PQ DF ,依据平行线的性质可得QPA β∠=∠,QPE α∠=∠,即可得到APE APQ EPQ βα∠=∠-∠=∠-∠;(3)过P 和N 分别作FD 的平行线,依据平行线的性质以及角平分线的定义,即可得到ANE ∠与α∠,β∠之间的数量关系为1()2ANE αβ∠=∠+∠. 【详解】解:(1)如图1,过点P 作//PG AB ,则//PG CD ,由平行线的性质可得180B BPG ︒∠+∠=,180C CPG ︒∠+∠=,又∵125PBA ︒∠=,155PCD ︒∠=,∴36012515580BPC ︒︒︒︒∠=--=,故答案为:80︒;(2)①如图2,APE ∠与α∠,β∠之间的数量关系为APE αβ∠=∠+∠; 过点P 作PM ∥FD ,则PM ∥FD ∥CG ,∵PM ∥FD ,∴∠1=∠α,∵PM ∥CG ,∴∠2=∠β,∴∠1+∠2=∠α+∠β,即:APE αβ∠=∠+∠,②如图,APE ∠与α∠,β∠之间的数量关系为APE βα∠=∠-∠;理由: 过P 作//PQ DF ,∵//DF CG ,∴//PQ CG ,∴QPA β∠=∠,QPE α∠=∠,∴APE APQ EPQ βα∠=∠-∠=∠-∠;(3)如图,由①可知,∠N=∠3+∠4,∵EN 平分∠DEP ,AN 平分∠PAC ,∴∠3=12∠α,∠4=12∠β, ∴1()2ANE αβ∠=∠+∠,∴ANE ∠与α∠,β∠之间的数量关系为1()2ANE αβ∠=∠+∠. 【点睛】本题主要考查了平行线的性质,解决问题的关键是过拐点作平行线,利用平行线的性质得出结论.三、解答题11.(1)∠E 、∠CAF ;∠CDE 、∠BAF ; (2)①20°;②30【分析】(1)由翻折的性质和平行线的性质即可得与∠B 相等的角;由等角代换即可得与∠C 相等的角;(2)①由三角形内角和定理可得,解析:(1)∠E 、∠CAF ;∠CDE 、∠BAF ; (2)①20°;②30【分析】(1)由翻折的性质和平行线的性质即可得与∠B 相等的角;由等角代换即可得与∠C 相等的角;(2)①由三角形内角和定理可得90B C ∠+∠=︒,再由50C B ∠∠︒-=根据角的和差计算即可得∠C 的度数,进而得∠B 的度数.②根据翻折的性质和三角形外角及三角形内角和定理,用含x 的代数式表示出∠FDE 、∠DFE 的度数,分三种情况讨论求出符合题意的x 值即可.【详解】(1)由翻折的性质可得:∠E =∠B ,∵∠BAC =90°,AE ⊥BC ,∴∠DFE =90°,∴180°-∠BAC =180°-∠DFE =90°,即:∠B +∠C =∠E +∠FDE =90°,∴∠C =∠FDE ,∴AC ∥DE ,∴∠CAF =∠E ,∴∠CAF =∠E =∠B故与∠B 相等的角有∠CAF 和∠E ;∵∠BAC =90°,AE ⊥BC ,∴∠BAF +∠CAF =90°, ∠CFA =180°-(∠CAF +∠C )=90°∴∠BAF +∠CAF =∠CAF +∠C =90°∴∠BAF =∠C又AC ∥DE ,∴∠C =∠CDE ,∴故与∠C 相等的角有∠CDE 、∠BAF ;(2)①∵90BAC ∠=︒∴90B C ∠+∠=︒又∵50C B ∠∠︒-=,∴∠C =70°,∠B =20°;②∵∠BAD =x °, ∠B =20°则160ADB x ∠︒︒=-,20ADF x ∠︒︒=+,由翻折可知:∵160ADE ADB x ∠∠︒︒==-, 20E B ∠∠︒==,∴1402FDE x ∠︒︒=-, 202DFE x ∠︒︒=+,当∠FDE =∠DFE 时,1402202x x ︒︒︒︒-=+, 解得:30x ︒︒=;当∠FDE =∠E 时,140220x ︒︒︒-=,解得:60x ︒︒=(因为0<x ≤45,故舍去); 当∠DFE =∠E 时,20220x ︒︒︒+=,解得:0x ︒=(因为0<x ≤45,故舍去);综上所述,存在这样的x 的值,使得△DEF 中有两个角相等.且30x =.【点睛】本题考查图形的翻折、三角形内角和定理、平行线的判定及其性质、三角形外角的性质、等角代换,解题的关键是熟知图形翻折的性质及综合运用所学知识.12.(1)∠AQB 的大小不发生变化,∠AQB =135°;(2)∠P 和∠C 的大小不变,∠P=45°,∠C=45°.【分析】第(1)题因垂直可求出∠ABO 与∠BAO 的和,由角平分线和角的和差可求出∠BA 解析:(1)∠AQB 的大小不发生变化,∠AQB =135°;(2)∠P 和∠C 的大小不变,∠P=45°,∠C=45°.【分析】第(1)题因垂直可求出∠ABO 与∠BAO 的和,由角平分线和角的和差可求出∠BAQ 与∠ABQ 的和,最后在△ABQ 中,根据三角形的内角各定理可求∠AQB 的大小.第(2)题求∠P 的大小,用邻补角、角平分线、平角、直角和三角形内角和定理等知识求解.【详解】解:(1)∠AQB 的大小不发生变化,如图1所示,其原因如下:∵m⊥n,∴∠AOB=90°,∵在△ABO中,∠AOB+∠ABO+∠BAO=180°,∴∠ABO+∠BAO=90°,又∵AQ、BQ分别是∠BAO和∠ABO的角平分线,∴∠BAQ=12∠BAC,∠ABQ=12∠ABO,∴∠BAQ+∠ABQ=12 (∠ABO+∠BAO)=190452⨯=又∵在△ABQ中,∠BAQ+∠ABQ+∠AQB=180°,∴∠AQB=180°﹣45°=135°.(2)如图2所示:①∠P的大小不发生变化,其原因如下:∵∠ABF+∠ABO=180°,∠EAB+∠BAO=180°∠BAQ+∠ABQ=90°,∴∠ABF+∠EAB=360°﹣90°=270°,又∵AP、BP分别是∠BAE和∠ABP的角平分线,∴∠PAB=12∠EAB,∠PBA=12∠ABF,∴∠PAB+∠PBA=12 (∠EAB+∠ABF)=12×270°=135°,又∵在△PAB中,∠P+∠PAB+∠PBA=180°,∴∠P=180°﹣135°=45°.②∠C的大小不变,其原因如下:∵∠AQB=135°,∠AQB+∠BQC=180°,∴∠BQC=180°﹣135°,又∵∠FBO=∠OBQ+∠QBA+∠ABP+∠PBF=180°∠ABQ=∠QBO=1∠ABO,∠PBA=∠PBF=∠ABF,2∴∠PBQ=∠ABQ+∠PBA=90°,又∵∠PBC=∠PBQ+∠CBQ=180°,∴∠QBC=180°﹣90°=90°.又∵∠QBC+∠C+∠BQC=180°,∴∠C=180°﹣90°﹣45°=45°【点睛】本题考查三角形内角和定理,垂直,角平分线,平角,直角和角的和差等知识点,同时,也是一个以静求动的一个点型题目,有益于培养学生的思维几何综合题.13.(1)∠EPB=170°;(2)①当交点P在直线b的下方时:∠EPB=20°,②当交点P在直线a,b之间时:∠EPB=160°,③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当解析:(1)∠EPB=170°;(2)①当交点P在直线b的下方时:∠EPB=20°,②当交点P在直线a,b之间时:∠EPB=160°,③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|.【分析】(1)利用外角和角平分线的性质直接可求解;(2)分三种情况讨论:①当交点P在直线b的下方时;②当交点P在直线a,b之间时;③当交点P在直线a的上方时;分别画出图形求解;(3)结合(2)的探究,分两种情况得到结论:①当交点P在直线a,b之间时;②当交点P在直线a上方或直线b下方时;【详解】解:(1)∵BD平分∠ABC,∴∠ABD=∠DBC=1∠ABC=50°,2∵∠EPB是△PFB的外角,∴∠EPB=∠PFB+∠PBF=∠1+(180°﹣50°)=170°;(2)①当交点P在直线b的下方时:∠EPB=∠1﹣50°=20°;②当交点P在直线a,b之间时:∠EPB =50°+(180°﹣∠1)=160°;③当交点P 在直线a 的上方时:∠EPB =∠1﹣50°=20°;(3)①当交点P 在直线a ,b 之间时:∠EPB =180°﹣|n°﹣50°|;②当交点P 在直线a 上方或直线b 下方时:∠EPB =|n°﹣50°|;【点睛】考查知识点:平行线的性质;三角形外角性质.根据动点P 的位置,分类画图,结合图形求解是解决本题的关键.数形结合思想的运用是解题的突破口.14.(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD 的高为OC ,所以S △BCD=CD•OC ,(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠解析:(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD 的高为OC ,所以S △BCD =12CD •OC ,(2)利用∠CFE +∠CBF =90°,∠OBE +∠OEB =90°,求出∠CEF =∠CFE .(3)由∠ABC +∠ACB =2∠DAC ,∠H +∠HCA =∠DAC ,∠ACB =2∠HCA ,求出∠ABC =2∠H ,即可得答案.详解:(1)S △BCD =12CD •OC =12×3×2=3. (2)如图②,∵AC ⊥BC ,∴∠BCF =90°,∴∠CFE +∠CBF =90°.∵直线MN ⊥直线PQ ,∴∠BOC =∠OBE +∠OEB =90°.∵BF 是∠CBA 的平分线,∴∠CBF =∠OBE .∵∠CEF =∠OBE ,∴∠CFE +∠CBF =∠CEF +∠OBE ,∴∠CEF =∠CFE .(3)如图③,∵直线l ∥PQ ,∴∠ADC =∠PAD .∵∠ADC =∠DAC∴∠CAP =2∠DAC .∵∠ABC +∠ACB =∠CAP ,∴∠ABC +∠ACB =2∠DAC .∵∠H +∠HCA =∠DAC ,∴∠ABC +∠ACB =2∠H +2∠HCA ∵CH 是,∠ACB 的平分线,∴∠ACB =2∠HCA ,∴∠ABC =2∠H ,∴H ABC ∠∠=12.点睛:本题主要考查垂线,角平分线和三角形面积,解题的关键是找准相等的角求解.15.(1)3;(2)98°;(3)∠P=(β+2α),理由见解析;(4)360°.【分析】(1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;(2)根据角平分线的定义得到∠CAP=∠解析:(1)3;(2)98°;(3)∠P=(β+2α),理由见解析;(4)360°.【分析】(1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;(2)根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P=(∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;(3)与(2)的证明方法一样得到∠P=(2∠C+∠B).(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.【详解】解:(1)在图2中有3个以线段AC为边的“8字形”,故答案为3;(2)∵∠CAB和∠BDC的平分线AP和DP相交于点P,∴∠CAP=∠BAP,∠BDP=∠CDP,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=∠P﹣∠B,即∠P=(∠C+∠B),∵∠C=100°,∠B=96°∴∠P=(100°+96°)=98°;(3)∠P=(β+2α);理由:∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠BAC,∠BDP=∠BDC,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=∠BDC﹣∠BAC,∠P﹣∠B=∠BDC﹣∠BAC,∴2(∠C﹣∠P)=∠P﹣∠B,∴∠P=(∠B+2∠C),∵∠C=α,∠B=β,∴∠P=(β+2α);(4)∵∠B+∠A=∠1,∠C+∠D=∠2,∴∠A+∠B+∠C+∠D=∠1+∠2,∵∠1+∠2+∠F+∠E=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为360°.。
青海师范大学附属中学八年级数学上册第一单元《三角形》测试(包含答案解析)

一、选择题1.如果一个三角形的三边长分别为5,8,a .那么a 的值可能是( ) A .2 B .9C .13D .152.如图,ABC 中,55,B D ∠=︒是BC 延长线上一点,且130ACD ∠=︒,则A ∠的度数是( )A .50︒B .65︒C .75︒D .85︒3.下列命题是真命题的个数为( ) ①两条直线被第三条直线所截,内错角相等. ②三角形的内角和是180°.③在同一平面内平行于同一条直线的两条直线平行. ④相等的角是对顶角. ⑤两点之间,线段最短. A .2 B .3C .4D .54.如图,ABC 中,将A ∠沿DE 翻折,若30A ∠=︒,25BDA '∠=︒,则CEA '∠多少度( )A .60°B .75°C .85°D .90° 5.在下列长度的四根木棒中,能与2m 、5m 长的两根木棒钉成一个三角形的是( ) A .2m B .3m C .5m D .7m 6.在ABC 中,若B 与C ∠互余,则ABC 是( )三角形 A .锐角三角形 B .直角三角形 C .钝角三角形 D .等边三角形 7.下列长度的三条线段能组成三角形的是( )A .3,3,4B .7,4,2C .3,4,8D .2,3,5 8.在△ABC 中,∠A =x °,∠B =(2x +10)°,∠C 的外角大小(x +40)°,则x 的值等于( ) A .15B .20C .30D .409.如果一个三角形的两边长分别为4和7,则第三边的长可能是( )A .3B .4C .11D .1210.如图,在五边形ABCDE 中,AB ∥CD ,∠A =135°,∠C =60°,∠D =150°,则∠E 的大小为( )A .60°B .65°C .70°D .75° 11.下列长度的三条线段,能组成三角形的是( ) A .3,5,6 B .3,2,1 C .2,2,4 D .3,6,10 12.以下列各组线段为边,能组成三角形的是( )A .1,2,3B .2,3,4C .2,5,8D .6,3,3二、填空题13.如图是一块正多边形的碎瓷片,经测得30ACB ∠=︒,则这个正多边形的边数是_________.14.如图,点D ,E ,F 分别是边BC ,AD ,AC 上的中点,若图中阴影部分的面积为3,则ABC 的面积是________.15.已知三角形三边长分别为m ,n ,k ,且m 、n 满足2|9|(5)0n m -+-=,则这个三角形最长边k 的取值范围是________.16.如图,则A B C D E ∠+∠+∠+∠+∠的度数为________.17.如图,飞机P 在目标A 的正上方,飞行员测得目标B 的俯角为30°,那么APB ∠的度数为______°.18.如图,在ABC 中,点,,D E F 分别在三边上,点E 是AC 的中点,,,AD BE CF 交于一点,283BGDAGEG BD DC S S===,,,则ABC 的面积是________.19.如图,已知AE 是ABC 的边BC 上的中线,若8AB cm =,ACE △的周长比AEB △的周长多2cm ,则AC =______cm .20.如图中,36B ∠=︒,76C ∠=︒,AD 、AF 分别是ABC 的角平分线和高,DAF ∠=________.三、解答题21.如图,△ABC 中,∠ABC 的角平分线与外角∠ACD 的平分线交于A 1.(1)∵BA 1、CA 1是∠ABC 与∠ACD 的平分线, ∴∠A 1BD =12∠ABD ,∠A 1CD =12∠ACD , ∴∠A 1CD ﹣∠A 1BD =12(∠ACD ﹣∠ABD ), ∵∠A 1CD ﹣∠A 1BD = ,∠ACD ﹣∠ABD =∠ , ∴∠A 1= .(2)如图2,四边形ABCD 中,∠F 为∠ABC 的角平分线及外角∠DCE 的平分线所在的直线构成的角,若∠A +∠D =230°,求∠F 的度数.(3)如图3,△ABC 中,∠ABC 的角平分线与外角∠ACD 的平分线交于A 1,若E 为BA 延长线上一动点,连接EC ,∠AEC 与∠ACE 的角平分线交于Q ,当E 滑动时有下面两个结论:①∠Q +∠A 1的值为定值; ②∠Q ﹣∠A 1的值为定值,其中有且只有一个是正确的,请写出正确的结论,并求出其值. 22.△ABC 中,AD 是∠BAC 的角平分线,AE 是△ABC 的高. (1)如图1,若∠B =40°,∠C=60°,求∠DAE 的度数;(2)如图2,∠B <∠C ,则DAE 、∠B ,∠C 之间的数量关系为___________; (3)如图3,延长AC 到点F ,∠CAE 和∠BCF 的角平分线交于点G ,求∠G 的度数.23.如图,四边形ABCD 中,ABC ∠和BCD ∠的平分线交于点O . (1)如果130A ∠=︒,110D ∠=︒,求BOC ∠的度数; (2)请直接写出BOC ∠与A D ∠+∠的数量关系.24.如图所示,已知AD ,AE 分别是△ABC 的高和中线,AB =3cm ,AC =4 cm ,BC=5 cm ,∠CAB =90°.(1)求AD 的长. (2)求△ABE 的面积.25.如图,在ABC 中,D 是AB 上一点,E 是AC 上一点,BE 、CD 相交于点F ,62A ∠=︒,35ACD ∠=︒,20ABE ∠=︒.求:(1)BDC ∠的度数;(2)BFD ∠的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学公式)解:(1)∵BDC A ACD ∠=∠+∠( ) ∴623597BDC ∠=︒+︒=︒(等量代换) (2)∵BFD BDC ABE ∠+∠+∠=______( ) ∴180BFD BDC ABE ∠=︒-∠-∠(等式的性质)1809720=︒-︒-︒(等量代换) 63=︒26.如图,AB ∥CD ,点E 是CD 上一点,连结AE .EB 平分∠AED ,且DB ⊥BE ,AF ⊥AC ,AF 与BE 交于点M .(1)若∠AEC =100°,求∠1的度数;(2)若∠2=∠D ,则∠CAE =∠C 吗?请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】根据三角形三边关系得出a的取值范围,即可得出答案.【详解】解:8-5<a<8+53<a<13,故a的值可能是9,故选:B.【点睛】本题考查了三角形三边关系,掌握知识点是解题关键.2.C解析:C【分析】根据三角形的外角性质求解.【详解】解:由三角形的外角性质可得:∠ACD=∠B+∠A,∴∠A=∠ACD-∠B=130°-55°=75°,故选C.【点睛】本题考查三角形的外角性质,熟练掌握三角形的外角性质定理并能灵活运用是解题关键.3.B解析:B【分析】首先判断所给命题的真假,再选出正确的选项.【详解】解:∵两条直线被第三条直线所截,两直线平行,内错角相等,∴①错误;∵三角形的内角和是180°,∴②正确;∵在同一平面内平行于同一条直线的两条直线平行,∴③正确;∵相等的角可以是对顶角,也可以是内错角、同位角等等,∴④错误;∵连接两点的所有连线中,线段最短,∴⑤正确;∴真命题为②③⑤,故选B .【点睛】本题考查命题的真假判断,根据所学知识判断一个命题条件成立的情况下,结论是否一定成立来判断命题是真命题还是假命题是解题关键.4.C解析:C 【分析】根据折叠前后对应角相等可得ADE A DE '∠=∠,AED A ED '∠=∠,再运用平角的定义和三角形内角和定理依次求得ADE ∠、AED ∠,再次运用平角的定义即可求得CEA '∠. 【详解】解:∵将A ∠沿DE 翻折,∴ADE A DE '∠=∠,AED A ED '∠=∠, ∵D 是线段AB 上的点,25BDA '∠=︒,∴180ADE A D B E DA '∠+∠-'∠=︒,即251280ADE ︒=∠-︒, 解得102.5ADE ∠=︒,∵30A ∠=︒,180A AED ADE ∠+∠+∠=︒,∴180180102.53047.5AED ADE A ∠=︒-∠-∠=︒-︒-︒=︒, ∴18018047.547.585CEA AED A ED ''∠=︒-∠-∠=︒-︒-︒=︒. 故选:C . 【点睛】本题考查折叠的性质,三角形内角和定理,平角的定义.理解折叠前后对应角相等是解题关键.5.C解析:C 【分析】判定三条线段能否构成三角形,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形. 【详解】解:设三角形的第三边为x m ,则 5-2<x <5+2 即3<x <7,∴当x=5时,能与2m 、5m 长的两根木棒钉成一个三角形, 故选:C . 【点睛】本题考查了三角形的三边关系的运用,解题时注意:三角形两边之和大于第三边,三角形的两边差小于第三边.6.B解析:B 【分析】由B 与C ∠互余,结合180A B C ∠+∠+∠=︒,求解A ∠,从而可得答案. 【详解】解:B 与C ∠互余,90B C ∴∠+∠=︒, 180A B C ∠+∠+∠=︒, 90A ∴∠=︒,ABC ∴是直角三角形,故A 、C 、D 不符合题意,B 符合题意, 故选:B . 【点睛】本题考查的是两个角互余的概念,三角形的内角和定理的应用,二元一次方程组的解法,掌握以上知识是解题的关键.7.A解析:A 【分析】看哪个选项中两条较小的边的和大于最大的边即可. 【详解】解:A 、3+3>4,能构成三角形,故此选项正确; B 、4+2<7,不能构成三角形,故此选项错误; C 、3+4<8,不能构成三角形,故此选项错误; D 、2+3=5,不能构成三角形,故此选项错误. 故选:A . 【点睛】此题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.8.A解析:A 【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,列出方程求解即可. 【详解】解:∵∠C 的外角=∠A+∠B , ∴x+40=2x+10+x , 解得x=15. 故选:A . 【点睛】本题考查了三角形的外角性质,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.9.B解析:B根据三角形的三边关系定理可得7-4<x<7+4,计算出不等式的解集,再确定x的值即可.【详解】设第三边长为x,则7-4<x<7+4,3<x<11,∴A、C、D选项不符合题意.故选:B.【点睛】考查了三角形的三边关系,解题关键是掌握第三边的范围:大于已知的两边的差,而小于两边的和.10.D解析:D【分析】先根据多边形的内角和公式求出五边形的内角和,根据AB∥CD得到∠B+∠C=180°,即可求出∠E的大小.【详解】解:由五边形的内角和公式得(5-2)×180°=540°,∵AB∥CD,∴∠B+∠C=180°,∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-180°-150°=75°.故选:D【点睛】本题考查了多边形的内角和公式,平行线的性质,熟练掌握多边形的内角和公式是解题关键.11.A解析:A【分析】根据三角形三边长关系,逐一判断选项,即可得到答案.【详解】A. ∵3+5>6,∴长度为3,5,6的三条线段能组成三角形,故该选项符合题意,B. ∵1+2=3,∴长度为3,2,1的三条线段不能组成三角形,故该选项不符合题意,C. ∵2+2=4,∴长度为2,2,4的三条线段不能组成三角形,故该选项不符合题意,D. ∵3+6<10,∴长度为3,6,10的三条线段不能组成三角形,故该选项不符合题意,故选A【点睛】本题主要考查三角形三边长的关系,掌握三角形任意两边之和大于第三边,是解题的关键.12.B解析:B根据三角形的三边关系定理:两边之和大于第三边,即两条较短的边的长大于最长的边即可. 【详解】A 、1+2=3,不能构成三角形, A 错误;B 、2+3=5>4可以构成三角形,B 正确;C 、2+5=7<8,不能构成三角形, C 错误;D 、3+3=6,不能构成三角形,D 错误. 故答案选:B . 【点睛】本题主要考查三角形的三边关系,比较简单,熟记三边关系定理是解决本题的关键.二、填空题13.12【分析】根据瓷片为正多边形及可知正多边形的外角为进而可求得正多边形的边数【详解】如图延长BC 可知∠1为正多边形的外角∵瓷片为正多边形∴AD=DB=BC ∠ADB=∠DBC ∴四边形ACBD 为等腰梯形解析:12 【分析】根据瓷片为正多边形及=30ACB ∠︒,可知正多边形的外角为30︒,进而可求得正多边形的边数. 【详解】如图,延长BC ,可知∠1为正多边形的外角,∵瓷片为正多边形, ∴AD=DB=BC ,∠ADB=∠DBC , ∴四边形ACBD 为等腰梯形, ∴BD ∥AC , ∴∠1==30ACB ∠︒, ∴正多边形的边数为:360=1230︒︒, 故答案为:12. 【点睛】本题考查正多边形的外角和,掌握相关知识点是解题的关键.14.8【分析】利用三角形的中线将三角形分成面积相等的两部分S △ABD=S △ACD=S △ABCS △BDE=S △ABDS △ADF=S △ADC 再得到S △BDE=S △ABCS △DEF=S △ABC 所以S △ABC=解析:8【分析】利用三角形的中线将三角形分成面积相等的两部分,S △ABD =S △ACD =12S △ABC ,S △BDE =12S △ABD ,S △ADF =12S △ADC ,再得到S △BDE =14S △ABC ,S △DEF =18S △ABC ,所以S △ABC =83S 阴影部分.【详解】解:∵D 为BC 的中点,∴12ABD ACD ABC S S S ==△△△, ∵E ,F 分别是边,AD AC 上的中点, ∴111,,222BDE ABD ADF ADC DEF ADF SS S S S S ===, ∴111,448BDE ABC DEF ADC ABC S S S S S ===, ∵113488BDE DEF ABC ABC ABC S SS S S S =+=+=阴影部分, ∴888333ABC S S ⨯===阴影部分, 故答案为:8.【点睛】本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S △=12×底×高.三角形的中线将三角形分成面积相等的两部分. 15.【分析】根据求出mn 的长根据三角形三边关系求出k 的取值范围再根据k 为最长边进一步即可确定k 的取值【详解】解:由题意得n-9=0m-5=0解得m=5n=9∵mnk 为三角形的三边长∴∵k 为三角形的最长边解析:914k ≤<【分析】根据2|9|(5)0n m -+-=求出m 、n 的长,根据三角形三边关系求出k 的取值范围,再根据k 为最长边进一步即可确定k 的取值.【详解】解:由题意得n-9=0,m-5=0,解得 m=5,n=9,∵m ,n ,k ,为三角形的三边长,∴414k ≤<,∵k 为三角形的最长边,∴914k ≤<.故答案为:914k ≤<【点睛】本题考查了绝对值、偶次方的非负性,三角形的三边关系,根据题意求出m 、n 的长是解题关键,确定k 的取值范围时要注意k 为最长边这一条件.16.180°【分析】两次运用三角形的外角定理求出∠B+∠C+∠D=∠2再通过三角形的内角和定理即可求解【详解】解:如图∵∠1是△CDF 外角∴∠C+∠D=∠1∵∠2是三角形BFG 外角∴∠B+∠1=∠2∴∠解析:180°【分析】两次运用三角形的外角定理求出∠B+∠C+∠D=∠2,再通过三角形的内角和定理即可求解【详解】解:如图,∵∠1是△CDF 外角,∴∠C+∠D=∠1,∵∠2是三角形BFG 外角,∴∠B+∠1=∠2,∴∠B+∠C+∠D=∠2,∴=2180A B C D E A E ∠+∠+∠+∠+∠∠+∠+∠=︒.故答案为:180°【点睛】本题考查了三角形的外角定理、内角和定理,通过三角形的外角定理将∠B+∠C+∠D 转化为∠2是解题关键.17.60【分析】先由题意得到∠A=∠B=根据直角三角形两锐角互余求得结果【详解】∵飞机P 在目标A 的正上方飞行员测得目标B 的俯角为30°∴∠A=∠CPB=∵CP ∥AB ∴∠B=∠CPB=∴=-∠B=故答案为解析:60【分析】先由题意得到∠A=90︒,∠B=30,根据直角三角形两锐角互余求得结果.【详解】∵飞机P 在目标A 的正上方,飞行员测得目标B 的俯角为30°,∴∠A=90︒,∠CPB=30,∵CP ∥AB ,∴∠B=∠CPB=30,∴APB ∠=90︒-∠B=60︒,故答案为:60.【点睛】此题考查直角三角形两锐角互余的性质,理解飞行员测得目标B 的俯角为30°得到∠B=30是解题的关键.18.30【分析】根据部分三角形的高相等由这些三角形面积与底边的比例关系可求三角形ABC 的面积【详解】解:在和中∵∴∴∵点是的中点∴∴∴故答案为:【点睛】本题中由于部分三角形的高相等可根据这些三角形面积的 解析:30【分析】根据部分三角形的高相等,由这些三角形面积与底边的比例关系可求三角形ABC 的面积.【详解】解:在BDG 和GDC 中,∵2BD DC =,∴2BDG GDC SS =,8BGD S =△,∴4GDC S =, ∵点E 是AC 的中点,3AGE S = ∴ 3.GEC AGE SS == ∴84315BEC BDG GDC GEC SS S S =++=++=, ∴230.ABC BEC S S ==故答案为:30.【点睛】本题中由于部分三角形的高相等,可根据这些三角形面积的比等于底边的比例关系来求三角形ABC 的面积是解题关键.19.10【分析】依据AE 是△ABC 的边BC 上的中线可得CE=BE 再根据AE=AE △ACE 的周长比△AEB 的周长多2cm 即可得到AC 的长【详解】解:∵AE 是△ABC 的边BC 上的中线∴CE=BE 又∵AE=A解析:10【分析】依据AE 是△ABC 的边BC 上的中线,可得CE=BE ,再根据AE=AE ,△ACE 的周长比△AEB 的周长多2cm ,即可得到AC 的长.【详解】解:∵AE 是△ABC 的边BC 上的中线,∴CE=BE ,又∵AE=AE ,△ACE 的周长比△AEB 的周长多2cm ,∴AC-AB=2cm ,即AC-8=2cm ,∴AC=10cm ,故答案为:10;【点睛】本题考查了三角形的角平分线、中线和高,求出两个三角形的周长的差等于两边的差是解题的关键.20.【分析】根据三角形内角和定理及角平分线的性质求出∠BAD 度数再由三角形内角与外角的性质可求出∠ADF 的度数由AF ⊥BC 可求出∠AFD=90°再由三角形的内角和定理即可解答【详解】∵AF 是的高∴在中∴解析:20︒【分析】根据三角形内角和定理及角平分线的性质求出∠BAD 度数,再由三角形内角与外角的性质可求出∠ADF 的度数,由AF ⊥BC 可求出∠AFD=90°,再由三角形的内角和定理即可解答.【详解】∵AF 是ABC 的高,∴90AFB ∠=︒,在Rt ABF 中,36B ∠=︒,∴90BAF B ∠=︒-∠9036=︒-︒54=︒.又∵在ABC 中,36B ∠=︒,76C ∠=︒,∴18068BAC B C ∠=︒-∠-∠=︒,又∵AD 平分BAC ∠, ∴11683422BAD CAD BAC ∠=∠=∠=⨯=︒, ∴DAF BAF BAD ∠=∠-∠5434=︒-︒ 20=︒.故答案为:20︒.【点睛】本题考查了三角形内角和定理、三角形的高线、及三角形的角平分线等知识,难度中等.三、解答题21.(1)∠A1,A,12∠A;(2)25°;(3)①的结论是正确的,且这个定值为180°.【分析】(1)根据角平分线的定义可得∠A1BD=12∠ABC,∠A1CD=12∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,则可得出答案;(2)先根据四边形内角和等于360°,得出∠ABC+∠DCB=360°﹣(∠A+∠D),根据内角与外角的关系和角平分线的定义得出∠ABC+(180°﹣∠DCE)=2∠FBC+(180°﹣2∠DCF)=180°﹣2(∠DCF﹣∠FBC)=180°﹣2∠F,从而得出结论;(3)依然要用三角形的外角性质求解,易知2∠A1=∠AEC+∠ACE=2(∠QEC+∠QCE),利用三角形内角和定理表示出∠QEC+∠QCE,即可得到∠A1和∠Q的关系.【详解】解:(1)∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,∴∠A1BD=12∠ABD,∠A1CD=12∠ACD,∴∠A1CD﹣∠A1BD=12(∠ACD﹣∠ABD),∵∠A1CD﹣∠A1BD=∠A1,∠ACD﹣∠ABD=∠A,∴∠A1=12∠A.故答案为:∠A1,A,12∠A;(2)∵∠ABC+∠DCB=360°﹣(∠A+∠D),∵∠ABC+(180°﹣∠DCE)=2∠FBC+(180°﹣2∠DCF)=180°﹣2(∠DCF﹣∠FBC)=180°﹣2∠F,∴360°﹣(∠A+∠D)=180°﹣2∠F,2∠F=∠A+∠D﹣180°,∴∠F=12(∠A+∠D)﹣90°,∵∠A+∠D=230°,∴∠F=25°;(3)△ABC中,由三角形的外角性质知:∠BAC=∠AEC+∠ACE=2(∠QEC+∠QCE);即:2∠A1=2(180°﹣∠Q),化简得:∠A1+∠Q=180°,因此①的结论是正确的,且这个定值为180°.【点睛】此题考查三角形的角平分线的性质,三角形内角和定理,三角形外角定理,熟练掌握三角形的外角等于与它不相邻的两个内角的和是解题的关键.22.(1)10°;(2)∠DAE=12(∠C−∠B);(3)45°.【分析】(1)根据三角形的内角和定理可求得∠BAC=80°,由角平分线的定义可得∠CAD的度数,利用三角形的高线可求∠CAE得度数,进而求解即可得出结论;(2)根据(1)的推理方法可求解∠DAE、∠B、∠C的数量关系;(3)设∠ACB=α,根据角平分线的定义得∠CAG=12∠EAC=12(90°−α)=45°−12α,∠FCG=12∠BCF=12(180°−α)=90°−12α,再利用三角形外角的性质即可求得结果.【详解】解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,∴∠BAC=80°,∵AD平分∠BAC,∴∠CAD=∠BAD=12∠BAC=40°,∵AE是△ABC的高,∴∠AEC=90°,∵∠C=60°,∴∠CAE=90°−60°=30°,∴∠DAE=∠CAD−∠CAE=10°;(2)∵∠BAC+∠B+∠C=180°,∴∠BAC=180°−∠B−∠C,∵AD平分∠BAC,∴∠CAD=∠BAD=12∠BAC,∵AE是△ABC的高,∴∠AEC=90°,∴∠CAE=90°−∠C,∴∠DAE=∠CAD−∠CAE=12∠BAC−(90°−∠C)=12(180°−∠B−∠C)−90°+∠C=1 2∠C−12∠B,即∠DAE=12(∠C−∠B).故答案为:∠DAE=12(∠C−∠B).(3)设∠ACB=α,∵AE ⊥BC ,∴∠EAC =90°−α,∠BCF =180°−α,∵∠CAE 和∠BCF 的角平分线交于点G ,∴∠CAG =12∠EAC =12(90°−α)=45°−12α, ∠FCG =12∠BCF =12(180°−α)=90°−12α, ∵∠FCG =∠G +∠CAG , ∴∠G =∠FCG −∠CAG =90°−12α−(45°−12α)=45°. 【点睛】本题考查了三角形的内角和定理、三角形的高及角平分线等知识,熟练掌握三角形内角和定理并能灵活运用三角形的高、角平分线这些知识解决问题是关键.23.(1)120°;(2)1()2BOC A D ∠=∠+∠ 【分析】(1)先由四边形内角和定理求出∠ABC+∠DCB=120°,再由角平分线定义得出∠OBC+∠OCB=60°,最后根据三角形内角和定理求出∠O=120°即可;(2)方法同(1)【详解】解:(1)∵∠A+∠ABC+∠BCD+∠D=360°,且∠A+∠D=130°+110°=240°,∴∠ABC+∠BCD=360°-(∠A+∠D )=360°-240°=120°,∵OB ,OC 分别是∠ABC 和∠BCD 的平分线, ∴∠OBC+∠OCB=111(221)1206220AB ABC DC C BCD B ∠+∠=⨯+∠︒=∠=︒ , ∴∠O=180°-(∠OBC+∠OCB )=180°-60°=120°; (2)1()2BOC A D ∠=∠+∠ 证明:在四边形ABCD 中,360A B C D ∠+∠+∠+∠=︒∴360()ABC DCB A D ∠+∠=︒-∠+∠∵OB ,OC 分别是∠ABC 和∠BCD 的平分线,∴∠OBC+∠OCB=1111((222)180)2ABC BCD AB D A C D CB ∠+∠=︒-∠∠=+∠∠+ ∴180(1)()2O BOC BC OCB A D ∠+∠=︒-∠=∠+∠ 【点睛】 此题主要考查了四边形内角和定理,三角形的内角和定理以及角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°;一个角的角平分线把这个角分成两个大小相等的角.24.(1)125cm ;(2)3cm 2 【分析】 (1)利用“面积法”来求线段AD 的长度;(2)△AEC 与△ABE 是等底同高的两个三角形,它们的面积相等【详解】解:∵∠BAC=90°,AD 是边BC 上的高, ∴12AB•AC=12BC•AD , ∴341255AB AC AD BC ⋅⨯===(cm ),即AD 的长度为125cm ; (2)如图,∵△ABC 是直角三角形,∠BAC=90°,AB=3cm ,AC=4cm , ∴S △ABC =12AB•AC=12×3×4=6(cm 2). 又∵AE 是边BC 的中线,∴BE=EC , ∴12BE•AD=12EC•AD ,即S △ABE =S △AEC , ∴S △ABE=12S △ABC =3(cm 2). ∴△ABE 的面积是3cm 2.【点睛】本题考查了中线的性质.解题的关键是利用三角形面积的两个表达式相等,求出AD . 25.(1)三角形的外角性质;(2)180,三角形内角和定理【分析】(1)在△ACD 中,利用三角形的外角性质,三角形的一个外角等于与它不相邻的两个内角的和计算即可;(2)在△BFD 中,利用三角形的内角和定理计算即可.【详解】(1)∵∠BDC=∠A+∠ACD (三角形的外角性质),∴∠BDC=62°+35°=97°(等量代换),故答案为:三角形的外角性质;(2)∵∠BFD+∠BDC+∠ABE=180°(三角形内角和定理),∴∠BFD=180°-∠BDC-∠ABE (等式的性质),=180°-97°-20°(等量代换)=63°;故答案为:180°,三角形内角和定理.【点睛】本题主要考查了三角形的外角性质与三角形的内角和定理,熟记性质与定理是解题的关键.26.(1)40°;(2)∠CAE=∠C,理由见解析.【分析】(1)根据邻补角的定义可求∠AED,再根据角平分线的定义和平行线的性质可求∠1的度数;(2)根据三角形内角和定理可求∠BED=∠C,根据平行线的判定可知AC∥BE,根据平行线的性质可得∠CAE=∠AEB,根据角平分线的定义和等量关系即可求解.【详解】(1)∵∠AEC=100°,∴∠AED=80°,∵EB平分∠AED,∴∠BED=40°,∵AB∥CD,∴∠1=∠BED=40°;(2)∵DB⊥BE,AF⊥AC,∴∠EBD=∠CAF=90°,∵∠2=∠D,∴∠BED=∠C,∴AC∥BE,∴∠CAE=∠AEB,∵EB平分∠AED,∴∠AEB=∠BED,∴∠CAE=∠C.【点睛】本题考查平行线的判定和性质,邻补角的定义,角平分线的定义,三角形内角和定理.熟悉相应的性质和定义是解答本题的关键.。
青海师范大学附属中学九年级数学下册第三单元《锐角三角函数》测试(包含答案解析)

一、选择题1.如图,这是某市政道路的交通指示牌,BD 的距离为5m ,从D 点测得指示牌顶端A 点和底端C 点的仰角分别是60°和45°,则指示牌的高度,即AC 的长度是( )A .53mB .52mC .()5352m -D .()535m - 2.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在 改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD 的平台BC 上(如图),测得52.5,5AED BC ︒∠==米,35CD =米,19DE =米,则铁塔AB的高度约为( )(参考数据:52.50.79,52.50.61,52.5 1.30sin cos tan ︒︒︒≈≈≈)A .7.6 米B .27.5 米C .30.5 米D .58.5 米 3.如图,在网格中,小正方形的边长均为1,点A ,B ,C 都在格点上,则∠ABC 的正切值是( )A .2B 25C 5D .124.如图,在矩形ABCD 中,AB =6,BC =2,点E 是边BC 上一动点,B 关于AE 的对称点为B ′,过B ′作B ′F ⊥DC 于F ,连接DB ′,若△DB ′F 为等腰直角三角形,则BE 的长是( )A .6B .3C .32D .62﹣6 5.三角形在正方形网格纸中的位置如图所示,则cos α的值是( )A .34B .43C .35D .456.如图,在Rt ABC ∆中,90ACB ∠=︒,22AC BC ==,CD AB ⊥于点D .点P 从点A 出发,沿A D C →→的路径运动,运动到点C 停止,过点P 作PE AC ⊥于点E ,作PF BC ⊥于点F .设点P 运动的路程为x ,四边形CEPF 的面积为y ,则能反映y 与x 之间函数关系的图象是( )A .B .C .D .7.如图,点A ,B ,C 在正方形网格的格点上,则sin ∠BAC=( )A .26B .2626C .2613D .13138.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt △ACB 中,∠C =90°,∠ABC =30°,延长CB 使BD =AB ,连接AD ,得∠D =15°,所以tan15°()()12323232323AC CD -====-++-.类比这种方法,计算tan22.5°的值为( )A .21+B .2﹣1C .2D .129.如图,反比例函数k y x=(0)k ≠第一象限内的图象经过ABC ∆的顶点A ,C ,AB AC =,且BC y ⊥轴,点A ,C ,的横坐标分别为1,3,若120BAC ∠=︒,则k 的值为( )A .1B 2C 3D .210.如图,Rt △ABC 中,AB =4,BC =2,正方形ADEF 的边长为2,F 、A 、B 在同一直线上,正方形ADEF 向右平移到点F 与B 重合,点F 的平移距离为x ,平移过程中两图重叠部分的面积为y ,则y 与x 的关系的函数图象表示正确的是( )A .B .C .D .11.如图,在扇形OAB 中,120AOB ∠=︒,点P 是弧AB 上的一个动点(不与点A 、B 重合),C 、D 分别是弦AP ,BP 的中点.若33CD =,则扇形AOB 的面积为( )A .12πB .2πC .4πD .24π 12.在Rt △ABC 中,∠C =90°,AB =13,AC =5,则sin A 的值为( )A .513B .1213C .512D .125二、填空题13.点A 、B 、C 都在半径为6的O 上,且120AOC ∠=︒,点M 是弦AB 的中点,则CM 的长度的最大值为______.14.已知在Rt △ABC 中,∠C =90°,∠A =α,AB =m ,那么边AB 上的高为___. 15.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,OH ⊥AB 于H .若菱形ABCD 的周长为16,∠BAD =60°,则OH =_____.16.如图,在四边形ABCD 中,AD =CD ,∠D=60°,∠A =105°,∠B =120°,则AD BC 的值为__________.17.计算:112tan 6032()2-+---____. 18.如图,已知∠AOB =60°,点P 在边OA 上,OP =12,点M ,N 在边OB 上,PM =PN ,若MN =2,则OM =____.19.如图,在△BDE 中,∠BDE =90°,BD =4,点D 的坐标是(6,0),∠BDO =15°,将△BDE 旋转到△ABC 的位置,点C 在BD 上,则旋转中心的坐标为__________.20.锐角α和锐角β互余,记f =sinα+sinβ,则f 的取值范围为_____.参考答案三、解答题21.如图,在ABC 中,AD BC ⊥,BE AC ⊥,垂足分别为D ,E ,AD 与BE 相交于点F .(1)求证:ACD △∽BFD △;(2)当tan 1ABD ∠=,3AC =时,求BF 的长.22.计算:()2tan 451tan 602cos30︒--︒+︒ . 23.计算:(1)|-2|-2cos60°+(π-2020)0;(2)(13)-1+18+|-2|-4sin45° 24.如图,四边形ABCD 内接于⊙O ,对角线AC 为⊙O 的直径,过点C 作AC 的垂线交AD 的延长线于点E ,点F 为CE 的中点,连接DB ,DC ,DF .(1)求∠CDE 的度数;(2)求证:DF 是⊙O 的切线;(3)若AC =25DE ,求tan ∠ABD 的值.参考答案25.门环,在中国绵延了数千多年的,集实用、装饰和门第等級为一体的一种古建筑构件,也成为中国古建“门文化”中的一部分,现有一个门环的示意图如图所示,点O 为正六边形 ABCDEF 的中心.(1)请用无刻度直尺与圆规,过点O 作一个⊙P ,使⊙P 与直线AF 和直线AB 同时相切.(请保留作图痕迹)(2)若正六边形 ABCDEF E 的边长为18cm ,试求(1)中⊙P 的半径.(结果保留根号) 26.已知:直线3y kx k =+,交x 轴于B ,交y 轴于A ,且3OA OB =.(1)如图1,求直线AB 的解析式;(2)如图2,点D 在AO 上且AD t =连接BD ,过BD 作DE BD ⊥于D ,过A 作AE y ⊥轴于A ,E 点的横坐标为m ,求m 与t 的函数关系式;(3)如图3,在(2)的条件下,点P 在BD 的延长线上,P 的横坐标为t ,点F 在EA 的延长线上,点N 在AD 上,连接FN ,连接PF 并延长交直线AB 于点M ,若E BPM ∠=,2ANF ADE ∠=∠,2AN DN =,求点M 的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】由题意可得到BD=BC=5,根据锐角三角函数关系得出方程,然后解方程即可.【详解】解:由题意可得:∠CDB=∠DCB=45°,∴BD=BC=5,设AC=x m ,则AB=(x +5)m ,在Rt △ABD 中,tan60°=AB BD , 则535x += 解得:535x =,即AC 的长度是()535m ;故选:D .【点睛】此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键. 2.C解析:C【分析】延长AB 交ED 于G ,过C 作CF ⊥DE 于F ,得到GF=BC=5,设DF=3k ,CF=4k ,解直角三角形得到结论.【详解】解:延长AB 交ED 于G ,过C 作CF ⊥DE 于F ,则四边形BGFC 是矩形∴GF=BC=5,∵山坡CD 的坡度为1:0.75,∴设DF=3k ,CF=4k ,∴CD=5k=35,∴k=7,∴DF=21,BG=CF=28,∴EG=GF+DF+DE=5+21+19=45,∵∠AED=52.5°,∴AG=EG•tan52.5°=45×1.30=58.5,∴AB=AG-BG=30.5米,答:铁塔AB 的高度约为30.5米.故选:C .【点睛】本题考查了解直角三角形的应用-坡度坡角问题和解直角三角形的应用-坡度坡角问题,难度适中,通过作辅助线,构造直角三角形,利用三角函数求解是解题的关键. 3.D解析:D【分析】连接AC ,根据网格图不难得出=90CAB ∠︒,求出AC 、BC 的长度即可求出ABC ∠的正切值.【详解】连接AC ,由网格图可得:=90CAB ∠︒,由勾股定理可得:AC 2AB =2∴tan ABC ∠=21222AC AB ==. 故选:D .【点睛】本题主要考查网格图中锐角三角函数值的求解,根据网格图构造直角三角形是解题关键. 4.D解析:D【分析】根据 B 关于 AE 的对称点为 B′,可得2AB AD '=1AB D ∴等腰直角三角形,可得D B E '、、三点共线,可求出BE 的长.【详解】 解:26,62,AB AB AB AD AD ==='∴=', 又△DB′F 为等腰直角三角形,045FDB ∴∠=,又在矩形 ABCD ,090ADF ∠=,045ADB ∴='∠, 又22AB AD '= AB D ∴'等腰直角三角形, 090AB D ∴='∠,090AB E ∠=',D BE ∴'、、三点共线,在等腰直角△RCE ,CE=CD=6,∴BE=BC-CE=626,故选D..【点睛】本题考查三角形的性质及解直角三角形,找出D B E '、、三点共线是解题关键. 5.D解析:D【分析】根据锐角三角函数的定义得出cosα=BC AB进而求出即可.【详解】解:如图所示:∵AC=3,BC=4,∴AB=5,∴cosα=45BC AB =. 故选:D .【点睛】此题主要考查了锐角三角函数的定义以及勾股定理,正确构造直角三角形是解题关键. 6.A解析:A【分析】 分两段来分析:①点P 从点A 出发运动到点D 时,写出此段的函数解析式,则可排除C 和D ;②P 点过了D 点向C 点运动,作出图形,写出此阶段的函数解析式,根据图象的开口方向可得答案.【详解】解:∵90ACB ∠=︒,22AC BC ==,∴45A ∠=︒,4AB =,又∵CD AB ⊥,∴2AD BD CD ===,45ACD BCD ∠=∠=︒,∵PE AC ⊥,PF BC ⊥,∴四边形CEPF 是矩形,I .当P 在线段AD 上时,即02x <≤时,如解图1∴2sin AE PE AP A x ===, ∴222CE x =,∴四边形CEPF 的面积为2221222222y x x x x ⎛⎫=-=-+ ⎪ ⎪⎝⎭,此阶段函数图象是抛物线,开口方向向下,故选项CD 错误;II .当P 在线段CD 上时,即24x <≤时,如解图2:依题意得:4CP x =-,∵45ACD BCD ∠=∠=︒,PE AC ⊥,∴sin CE PE CP ECP ==⨯∠,∴()()24sin 4542CE PE x x ==-︒=-, ∴四边形CEPF 的面积为()22214482x x x y ⎡⎤-=-+⎢⎥⎣⎦=,此阶段函数图象是抛物线,开口方向向上,故选项B 错误;故选:A .【点睛】本题考查了动点问题的函数图象,分段写出函数的解析式并数形结合进行分析是解题的关键.7.B解析:B【分析】作BD ⊥AC 于D ,根据勾股定理求出AB 、AC ,利用三角形的面积求出BD ,最后在直角△ABD 中根据三角函数的意义求解.【详解】解:如图,作BD ⊥AC 于D ,由勾股定理得,22223213,3332AB AC =+==+=∵1113213222ABC S AC BD BD =⋅=⨯=⨯⨯,∴22BD =, ∴2262sin 2613BD BAC AB ∠===. 故选:B .【点睛】本题考查了勾股定理,解直角三角形,三角形的面积,三角函数的意义等知识,根据网格构造直角三角形和利用三角形的面积求出BD 是解决问题的关键.8.B解析:B【分析】作Rt △ABC ,使∠C =90°,∠ABC =45°,延长CB 到D ,使BD =AB ,连接AD ,根据构造的直角三角形,设AC =x ,再用x 表示出CD ,即可求出tan22.5°的值.【详解】解:作Rt △ABC ,使∠C =90°,∠ABC =90°,∠ABC =45°,延长CB 到D ,使BD =AB ,连接AD ,设AC =x ,则:BC =x ,AB =2x ,CD =()1+2x , ()22.5==211+2AC C tan ta D x n D =∠=-︒故选:B.【点睛】本题考查解直角三角形,解题的关键是根据阅读构造含45°的直角三角形,再作辅助线得到22.5°的直角三角形.9.C解析:C【分析】先表示出CD ,AD 的长,然后在Rt △ACD 中利用∠ACD 的正切列方程求解即可.【详解】过点A 作AD BC ⊥,∵点A 、点C 的横坐标分别为1,3,且A ,C 均在反比例函数k y x=第一象限内的图象上,∴(1,)A k ,3,3k C ⎛⎫ ⎪⎝⎭, ∴CD=2,AD=k-3k , ∵AB AC =,120BAC ∠=︒,AD BC ⊥,∴30ACD ∠=︒,90ADC ∠=︒,∵tan ∠ACD=AD DC, ∴3DC AD =,即233k k ⎛⎫=- ⎪⎝⎭,∴3k =. 故选:C .【点睛】本题考查了等腰三角形的性质,解直角三角形,以及反比例函数图像上点的坐标特征,熟练掌握各知识点是解答本题的关键.10.B解析:B【分析】分三种情况分析:当0<x≤2时,平移过程中两图重叠部分为Rt △AA'M ;当2<x≤4时,平移过程中两图重叠部分为梯形F'A'MN ;当4<x≤6时,平移过程中两图重叠部分为梯形F'BCN .分别写出每一部分的函数解析式,结合排除法,问题可解.【详解】设AD 交AC 于N ,A D ''交AC 于M ,当0<x ≤2时,平移过程中两图重叠部分为Rt △AA 'M ,∵Rt △ABC 中,AB =4,BC =2,正方形ADEF 的边长为2,AA x '=,∴tan ∠CAB =A M BC AA AB ='', ∴A 'M =12x ,其面积y=12AA A M ''=12x •12x =14x 2, 故此时y 为x 的二次函数,排除选项D ; 当2<x ≤4时,平移过程中两图重叠部分为梯形F 'A 'MN ,AA x '=,2AF x '=-,同理:A 'M =12x ,()122F M x ='-, 其面积y=12AA A M ''-12AF F M ''=12x •12x ﹣12(x ﹣2)•12(x ﹣2)=x ﹣1, 故此时y 为x 的一次函数,故排除选项C .当4<x ≤6时,平移过程中两图重叠部分为梯形F 'BCN ,AF '=x ﹣2,F 'N =12(x ﹣2),F 'B =4﹣(x ﹣2)=6﹣x ,BC =2, 其面积y =12 [12(x ﹣2)+2]×(6﹣x )=﹣14x 2+x +3, 故此时y 为x 的二次函数,其开口方向向下,故排除A ;综上,只有B 符合题意.故选:B .【点睛】本题考查了动点问题的函数图象以及三角函数的知识,数形结合并运用排除法,是解答本题的关键.11.A解析:A【分析】如图,作OH ⊥AB 于H .利用三角形中位线定理求出AB 的长,解直角三角形求出OB 即可解决问题.【详解】解:如图作OH ⊥AB 于H .∵C 、D 分别是弦AP 、BP 的中点.∴CD 是△APB 的中位线,∴AB =2CD =63∵OH ⊥AB ,∴BH =AH =33∵OA =OB ,∠AOB =120°,∴∠AOH =∠BOH =60°,在Rt △AOH 中,sin ∠AOH =AH AO, ∴AO =336sin 3AH AOH ==∠, ∴扇形AOB 的面积为:2120612360ππ=, 故选:A .【点睛】本题考查扇形面积公式,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.12.B解析:B【分析】先根据勾股定理求出BC=12,再利用余弦函数的定义即可求解.【详解】解:在Rt △ABC 中,由勾股定理得,BC 22AB AC -12,∴sin A =1213BC AB =, 故选:B .【点睛】 此题考查勾股定理以及锐角三角函数的定义,解题关键在于计算出BC 的长度.二、填空题13.【分析】如图取AO 的中点J 连接JMJC 过点J 作JH ⊥OC 交CO 的延长线于H 求出MJCJ 根据CM≤MJ+CJ 即可解决问题【详解】解:如图取的中点连接过点作交的延长线于的最大值为故答案为:【点睛】本题考 解析:337+【分析】如图,取AO 的中点J ,连接JM ,JC ,过点J 作JH ⊥OC ,交CO 的延长线于H .求出MJ ,CJ ,根据CM≤MJ+CJ 即可解决问题.【详解】解:如图,取AO 的中点J ,连接JM ,JC ,过点J 作JH OC ⊥,交CO 的延长线于H .120AOC ∠=︒,60JOH ∴∠=︒, JH OH ⊥,90JHO ∴∠=︒,132AJ JO OA ===, 3cos602OH OJ ∴=︒=,33sin 60JH OJ =︒=, 315622CH OH OC ∴=+=+=, 22223315()()3722CJ JH CH ∴=+=+=, AM MB =,AJ JO =,132MJ OB ∴==, CM MJ JC +,337CM ∴+,CM ∴的最大值为337+故答案为:337+【点睛】本题考查轨迹,三角形中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.14.msinαcosα【分析】利用直角三角形中的余弦三角函数的定义求得AC的长度然后利用三角形的面积公式求得AB边上的高的长度【详解】如图所示:根据题意可得:AC=mcosαBC=msinα∴AC•BC解析:m sinαcosα【分析】利用直角三角形中的余弦三角函数的定义求得AC的长度,然后利用三角形的面积公式求得AB边上的高的长度.【详解】如图所示:根据题意可得:AC=m cosα,BC=m sinα,∴12AC•BC=12mh,即h=m sinαcosα,故答案是:m sinαcosα.【点睛】考查了解直角三角形.解题关键利用了三角函数的定义求得直角三角形两条直角边的长.15.【分析】由菱形的性质可得AB=BC=CD=ADBO=DO可证△ABD是等边三角形可得BD=4BO=2解直角三角形即可求解【详解】∵四边形ABCD是菱形∴AB=BC=CD=ADBO=DO∵菱形ABCD3【分析】由菱形的性质可得AB=BC=CD=AD,BO=DO,可证△ABD是等边三角形,可得BD=4,BO=2,解直角三角形即可求解.【详解】∵四边形ABCD是菱形,∴AB=BC=CD=AD, BO=DO,∵菱形ABCD的周长为16,∴AB=AD=4,∵∠BAD=60°,∴△ABD是等边三角形,∴BD=4,∠ABD=60°,∴BO=DO=2,在Rt△OBH中,∠ABD=60°,BO =2,∴sin60OHOB︒=,∴OH=2332⨯=.故答案为:3.【点睛】本题考查了菱形的性质,等边三角形的判定和性质,解直角三角形等知识,求出BO的长是解题的关键.16.【分析】沿AB作垂线与C的延长线相交于M点可得到等边直角三角形和锐角为30°的直角三角形根据三角函数求解即可【详解】解:如图连接AC并过B点作BM⊥CM设BM=k∵AD=CD∠D=60°∴△ACD是解析:6【分析】沿AB作垂线与C的延长线相交于M点,可得到等边直角三角形和锐角为30°的直角三角形,根据三角函数求解即可.【详解】解:如图连接AC并过B点作BM⊥CM,设BM=k,∵AD=CD,∠D=60°,∴△ACD是等边三角形,AD=AC,∵∠A=105°,∠B=120°,∠DAC=60°,∴∠MBC=60°,∠BCM=30°,∠BAC=45°,∵BM=k,∴BC=2k,MC=BMtan30=3,∵∠BAC=45°,∠MCA=45°,∴AD=AC=MC3ksin452=6k,∴2k 2==AD BC . 【点睛】 本题考查了特殊角的三角函数值和公式的应用,正确应用公式和作出辅助线是解题的关键.3tan 30=,sin45=2. 17.【分析】先利用特殊的三角函数值计算再利用绝对值和负指数得出结论【详解】解:原式=故答案为:【点睛】本题涉及特殊角的三角函数值绝对值负整数指数幂3个考点在计算时需要针对每个考点分别进行计算然后根据实数解析:4【分析】先利用特殊的三角函数值计算,再利用绝对值和负指数得出结论.【详解】解:原式=22224=+=+故答案为:4.【点睛】本题涉及特殊角的三角函数值、绝对值、负整数指数幂3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.18.5【分析】过P 作PD ⊥OB 交OB 于点D 在直角三角形POD 中利用锐角三角函数定义求出OD 的长再由PM=PN 利用三线合一得到D 为MN 中点根据MN 求出MD 的长由OD-MD 即可求出OM 的长【详解】过P 作PD解析:5.【分析】过P 作PD ⊥OB ,交OB 于点D ,在直角三角形POD 中,利用锐角三角函数定义求出OD 的长,再由PM=PN ,利用三线合一得到D 为MN 中点,根据MN 求出MD 的长,由OD-MD 即可求出OM 的长.【详解】过P 作PD ⊥OB ,交OB 于点D ,在Rt △OPD 中,cos60°12OD OP ==,OP =12, ∴OD =6.∵PM =PN ,PD ⊥MN ,MN =2,∴MD =ND 12=MN =1, ∴OM =OD ﹣MD =6﹣1=5.故答案为:5.【点晴】本题考查的是勾股定理,含30度直角三角形的性质,等腰三角形的性质等知识,熟练掌握直角三角形的性质是解本题的关键.19.【分析】根据旋转的性质AB与BD的垂直平分线的交点即为旋转中心P连接PD过P作PF⊥x轴于F再根据点C在BD上确定出∠PDB=45°并求出PD的长然后求出∠PDO=60°根据直角三角形两锐角互余求出解析:(62,6)【分析】根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x 轴于F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,然后解直角三角形求出点P的坐标.【详解】如图,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F,∵点C在BD上,∴点P到AB、BD的距离相等,都是12BD,即1422⨯=,∴∠PDB=45°,22PD=∵∠BDO=15°,∴∠PDO=45°+15°=60°,∴∠DPF=30°,∴DF=12PD=12222⨯=,3cos302262PF PD︒=⋅==∵点D的坐标是(6,0),∴OF=OD﹣DF=62-∴旋转中心的坐标为(62,6),故答案为:(62,6).【点睛】本题考查坐标与图形变化-旋转,解直角三角形,熟练掌握旋转的性质确定出旋转中心的位置是解题的关键.20.1<f≤【分析】根据锐角三角函数的定义即可求出答案【详解】∵α+β=90°∴sinβ=sin (90°−α)=cosα∴f =sinα+cosα=sin (α+45°)∵α是锐角∴<sin (α+45°)≤解析:1<2【分析】根据锐角三角函数的定义即可求出答案.【详解】∵α+β=90°,∴sinβ=sin (90°−α)=cosα,∴f =sinα+cosα2sin (α+45°)∵α是锐角, ∴22<sin (α+45°)≤1, ∴1<2,故答案为:1<2.【点睛】本题考查锐角三角函数,解题的关键是正确理解锐角三角函数的定义,本题属于中等题型.三、解答题21.(1)见解析;(2)3【分析】(1)由90C DBF ∠+∠=︒,90C DAC ∠+∠=︒,推出DBF DAC ∠=∠,由此即可证明;(2)先证明AD BD =,由ACD △∽BFD △,得1AC AD BF BD==,即可解决问题. 【详解】(1)证明:∵AD BC ⊥,BE AC ⊥,∴90BDF ADC BEC ∠=∠=∠=︒,∴90C DBF ∠+∠=︒,90C DAC ∠+∠=︒,∴DBF DAC ∠=∠,∴ACD △∽BFD △.(2)∵tan 1ABD ∠=,90ADB ∠=︒, ∴1AD BD=, ∴AD BD =,∵ACD △∽BFD △, ∴1AC AD BF BD==, ∴3BF AC ==.【点睛】 本题考查相似三角形的判定和性质、三角函数等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.22.2.【分析】由特殊角的三角函数值,二次根式的性质,二次根式的加减乘除混合运算进行化简,即可得到答案.【详解】解:()2tan 451tan 602cos30︒-︒︒ =3131)2-+ =1313+=2.【点睛】本题考查了特殊角的三角函数值,二次根式的性质,二次根式的加减乘除混合运算,解题的关键是掌握运算法则进行化简.23.(1)2;(2)5【分析】本题涉及零指数幂、负指数幂、绝对值、二次根式、特殊角的三角函数5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【详解】解:(1)原式12212=-⨯+,211=-+,2=.解:原式3242=+-⨯32=+-5=【点睛】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.24.(1)90°;(2)证明见解析;(3)2.【分析】(1)根据圆周角定理即可得∠CDE的度数;(2)连接DO,根据直角三角形的性质和等腰三角形的性质易证∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,即可判定DF是⊙O的切线;(3)根据已知条件易证△CDE∽△ADC,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可.【详解】解:(1)解:∵对角线AC为⊙O的直径,∴∠ADC=90°,∴∠EDC=90°;(2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)解:如图所示:可得∠ABD=∠ACD,∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,∴∠DCA=∠E,又∵∠ADC=∠CDE=90°,∴△CDE∽△ADC,∴DC DEAD DC=,∴DC2=AD•DE∵AC=25DE,∴设DE=x,则AC=25x,则AC2﹣AD2=AD•DE,期(25x)2﹣AD2=AD•x,整理得:AD2+AD•x﹣20x2=0,解得:AD=4x或﹣4.5x(负数舍去),则DC=22(25)(4)2x x x-=,故tan∠ABD=tan∠ACD=422AD xDC x==.25.(1)作图见解析;(2)⊙P的半径为36354.【分析】(1)先过点O作OM⊥AF交AF于点M(或延长EF、BA交于点H,作直线HO),然后作∠HOA 的角平分线OI交AF于点I,再过点I作IP//MO交OA于点P(或在KC上截取KL=MI),最后以点P为圆心,PO长为半径作圆,⊙P即为所求;(2)设OP=PI=r,由题意可得PA=33r,在Rt△API中,PA+PO=18,代入求解即可.【详解】解:(1)第一步过点O作OM⊥AF交AF于点M(或延长EF、BA交于点H,作直线HO)第二步作∠HOA的角平分线OI交AF于点I第三步过点I作IP//MO交OA于点P(或在KC上截取KL=MI)第四步以点P为圆心,PO长为半径作圆,⊙P即为所求.(2)∵AF=18,∴AO=18,∠AOM=∠API=30°(△OAF 为等边三角形),设OP=PI=r ,PA=PI÷cos30°=233r , 在Rt △API 中,23r +=18 , 解得r=354.【点睛】本题考查解直角三角形和正多边形与圆的关系,掌握等边三角形的性质是解题的关键. 26.(1)y=3x+9;(2)m=2133t t -;(3)M(1,10).【分析】(1)先设OB b =,表示出A 、B 的坐标,代入求解即可;(2)根据lBD lDE k k ⋅= -1,得出93t -·t m=-1,变形求解即可; (3)首先得出直线BD 的解析式,再得出直线NF 为:y=222mt m t -,设F(n ,9),得出直线FD ,再根据直线AB 求解即可.【详解】解:(1)设OB b =,∴B(-b,0),∵OA=3OB ,∴A(0,3b),∵A 、B 在直线y=kx+k 上,代入得3033bk k k b -+=⎧⎨=-⎩, 解得:33k b =⎧⎨=⎩,∴y=3x+9; (2)由(1)知A(0,9),B(-3,0),∵AE ⊥y 轴,∴E(m ,9),∵AD=t ,∴D(0,9-t),∵BD ⊥DE ,∴lBD lDE k k ⋅= -1,而lBD k =93t -,lDE k =t m, ∴93t -·t m=-1, ∴-t²+9t+3m=0, ∴m=2133t t -;(3)由(2)和(1)知:直线BD 为:y=993t x t -+- , ∵P 在直线BD 上且横坐标为t , ∴P(t ,26273t t -++), ∵AN=2DN ,∴N(0,9-t),∵∠ANF=2∠ADE 且lDE k =t m,则直线NF 为:y=222mt m t - , 设F(n ,9),则22223t mt n m t =-,解得n=223m t m-, ∴F(223m t m-,9), 由F 、P 得FP l :y=222222()933m t m t x m t mt m---+--①, 由(1)得:AB l :y=3x+9②,∵∠E=∠BPM ,∴tan ∠E=tan ∠BPM③,由M 为AB 和PF 的交点,联立①②③得:M(1,10).【点睛】本题考查了一次函数的性质、待定系数法等知识,解题的关键是学会利用参数、构建方程解决问题.。
青海师范大学第二附属中学2018-2019学年八年级(上)期中数学试卷

2018-2019学年青海师大二附中八年级(上)期中数学试卷一、选择题(每小题3分,共30分)1.以下各组线段为边,能组成三角形的是( )A.2cm ,4cm ,6cmB.8cm ,6cm ,4cmC.14cm ,6cm ,7cmD.2cm ,3cm ,6cm2.下列说法错误的是( )A.锐角三角形的三条高线、三条中线、三条角平分线分别交于一点B.钝角三角形有两条高线在三角形外部C.直角三角形只有一条高线D.任意三角形都有三条高线、三条中线、三条角平分线3.从n 边形的一个顶点作对角线,把这个n 边形分成三角形的个数是( )A.nB.(n −1)C.(n −2)D.(n −3)4.若等腰三角形的顶角为80∘,则它的底角度数为( )A.80∘B.50∘C.40∘D.20∘5.已知x m =6,x n =3,则的x 2m−n 值为( )A.9B.34C.12D.436.下列各式中,分式的个数有( )x−13、b 2a+1、2x+y π、−1m−2、12+a 、(x−y)2(x+y)2、−511.A.2个B.3个C.4个D.5个7.若(x−2)(x+3)=x2+ax+b,则a、b的值分别为()A.a=5,b=6B.a=1,b=−6C.a=1,b=6D.a=5,b=−68.如图,∠CBD、∠ADE为△ABD的两个外角,∠CBD=70∘,∠ADE=149∘,则∠A的度数是()A.28∘B.31∘C.39∘D.42∘9.下列计算正确的是()A.( ab4)4= a4b8B.( a2)3÷(a3)2=0C.(−x)6÷(−x3)=−x3D.x0=110.下列各式由左边到右边的变形中,是分解因式的为()A.a(x+y)=ax+ayB.x2−4x+4=x(x−4)+4C.10x2−5x=5x(2x−1)D.x2−16+3x=(x−4)(x+4)+3x二、填空题(每小题2分,共16分)11.当x________时,分式−4x 2−1有意义.12.若等腰三角形的顶角为100∘,则它腰上的高与底边的夹角是________度.13.2x x−5与3x x+5的最简公分母是________.14.如图,在△ABC 中,∠A =80∘,点D 是BC 延长线上一点,∠ACD =150∘,则∠B =________.15.若分式|x|−1x+1的值为零,则x 的值为________.16.多项式4a 2+1加上一个单项式后,使它能成为一个整式的完全平方,那么加上的单项式可以是________.(填上一个你认为正确的即可)17.计算:(a 3)2=________.18.若x 2−kxy +4y 2是一个完全平方式,则k 的值是________.三、解答题(共7小题,满分54分)19.计算.(1)−3ab x ⋅2x 29a 2b(2)x2−9.x2−6x+920.因式分解.(1)x2+2xy+y2(2)m2(a−b)+n2(b−a)21.一个多边形的内角和比它的外角的和的2倍还大180∘,求这个多边形的边数.22.先化简,再求值:(2x−1)2−(x+2)(x−2)−4x(x−1),其中x=2.23.如图,∠B=45∘,∠A+15∘=∠1,∠ACD=60∘.求证:AB // CD.24.如图,在△ABC中,AD,AE分别是边BC上的中线和高,AE=3cm,S△ABC= 12cm2.求BC和DC的长.25.已知m+n=8,mn=15,求m2−mn+n2的值.答案1.【答案】B【解析】根据三角形任意两边的和大于第三边,进行分析判断.【解答】解:A、2+4=6,不能组成三角形;B、4+6=10>8,能组成三角形;C、6+7=13<14,不能够组成三角形;D、2+3=5<6,不能组成三角形.故选B.2.【答案】C【解析】根据三角形的高线、中线、角平分线的性质分析各个选项.【解答】解:A、解:A、锐角三角形的三条高线、三条角平分线分别交于一点,故本选项说法正确;B、钝角三角形有两条高线在三角形的外部,故本选项说法正确;C、直角三角形也有三条高线,故本选项说法错误;D、任意三角形都有三条高线、中线、角平分线,故本选项说法正确;故选:C.3.【答案】C【解析】可根据n边形从一个顶点引出的对角线与边的关系:n−3,可分成(n−2)个三角形直接判断.【解答】解:从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是(n−2).故选C.4.【答案】B【解析】根据等腰三角形两底角相等列式进行计算即可得解.【解答】解:∵等腰三角形的顶角为80∘,(180∘−80∘)=50∘.∴它的底角度数为12故选B.5.【答案】C【解析】根据同底数幂的除法的性质的逆用和幂的乘方的性质计算即可.【解答】解:∵x m=6,x n=3,∴x2m−n=(x m)2÷x n=62÷3=12.故选C.6.【答案】B【解析】根据分式的定义:如果A ,B 表示两个整式,并且B 中含有字母,那么式子A B 叫做分式进行分析即可.【解答】解:b 2a+1、−1m−2、(x−y)2(x+y)2是分式,共3个, 故选:B .7. 【答案】B【解析】已知等式左边利用多项式乘多项式法则计算,利用多项式相等的条件求出a 与b 的值即可.【解答】解:∵(x −2)(x +3)=x 2+x −6=x 2+ax +b ,∴a =1,b =−6.故选B .8. 【答案】C【解析】根据平角的定义求出∠ABD ,根据三角形的外角性质得出∠ADE =∠ABD +∠A ,代入即可求出答案.【解答】解:∵∠ABD +∠CBD =180∘,∠CBD =70∘,∴∠ABD =110∘,∵∠ADE =∠ABD +∠A ,∠ADE =149∘,∴∠A =39∘.故选C .9. 【答案】C【解析】利用积的乘方法则、单项式的除法法则、0指数幂的意义,分别计算各个选项,确定出正确答案.【解答】解:( ab 4)4=a 4b 16≠a 4b 8;( a 2)3÷(a 3)2=a 6÷a 6=1≠0;(−x)6÷(−x 3)=x 6÷(−x 3)=−x 3;当x ≠0时,x 0=1.综上正确的是C .故选C .10. 【答案】C【解析】根据分解因式就是把一个多项式化为几个整式的积的形式,利用排除法求解.【解答】解:A 、是多项式乘法,故A 选项错误;B 、右边不是积的形式,x 2−4x +4=(x −2)2,故B 选项错误;C 、提公因式法,故C 选项正确;D 、右边不是积的形式,故D 选项错误;故选:C .11. 【答案】≠±1【解析】根据分式有意义的条件可得x 2−1≠0,再解即可.【解答】解:由题意得:x 2−1≠0,解得:x ≠±1,故答案为:≠±1.12. 【答案】50【解析】已知给出了等腰三角形的顶角为100∘,要求腰上的高与底边的夹角可以根据等腰三角形的性质:等腰三角形的一腰上的高与底边的夹角等于顶角的一半求解.【解答】解:∵等腰三角形的顶角为100∘∴根据等腰三角形的性质:等腰三角形的一腰上的高与底边的夹角等于顶角的一半; ∴高与底边的夹角为50∘.故填50.13. 【答案】(x −5)(x +5)【解析】确定最简公分母的方法是:(1)取各分母系数的最小公倍数;(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.【解答】解:2x x−5与3x x+5的最简公分母是(x −5)(x +5);故答案为:(x −5)(x +5)14. 【答案】70∘【解析】根据三角形的外角等于与它不相邻的两个内角和,即可得出∠B 的度数.【解答】解:∵∠ACD =∠A +∠B ,∠A =80∘,∠ACD =150∘,∴∠B =70∘.故答案为:70∘.15. 【答案】1【解析】分式的值为0的条件是:(1)分子=0;(2)分母≠0.两个条件需同时具备,缺一不可.据此可以解答本题.【解答】解:|x|−1x+1=0,则|x|−1=0,即x=±1,且x+1≠0,即x≠−1.故x=1.故若分式|x|−1x+1的值为零,则x的值为1.16.【答案】4a或−4a或4a4【解析】分①4a2是平方项,②4a2是乘积二倍项,然后根据完全平方公式的结构解答.【解答】解:①4a2是平方项时,4a2±4a+1=(2a±1)2,可加上的单项式可以是4a或−4a,②当4a2是乘积二倍项时,4a4+4a2+1=(2a2+1)2,可加上的单项式可以是4a4,综上所述,可以加上的单项式可以是4a或−4a或4a4.17.【答案】a6【解析】按照幂的乘方法则:底数不变,指数相乘计算.即(a m)n=a mn(m,n是正整数)【解答】解:(a3)2=a6.故答案为:a6.18.【答案】±4【解析】利用完全平方公式的定义求解即可.【解答】解:∵x2−kxy+4y2是一个完全平方式,∴k=±4.故答案为:±4.19.【答案】解:(1)−3abx ⋅2x2 9a2b=−2x3a .; (2)x2−9x2−6x+9=(x+3)(x−3) (x−3)2=x+3x−3.【解析】结合分式乘除法的运算法则进行求解即可.;【解答】解:(1)−3abx ⋅2x2 9a2b=−2x3a .; (2)x2−9x2−6x+9=(x+3)(x−3) (x−3)2=x+3x−3.20.【答案】解:(1)原式=(x+y)2;; (2)原式=(a−b)(m2−n2)=(a−b)(m−n)(m+ n)【解析】根据提取公因式以及公式法即可判断.;【解答】解:(1)原式=(x+y)2;; (2)原式=(a−b)(m2−n2)=(a−b)(m−n)(m+n) 21.【答案】解:设这个多边形的边数为n,根据题意,得(n−2)×180∘=2×360∘+180∘,解得n=7.故这个多边形的边数是7.【解析】设这个多边形的边数为n,根据多边形的内角和公式(n−2)⋅180∘与外角和定理列出方程,求解即可.【解答】解:设这个多边形的边数为n,根据题意,得(n−2)×180∘=2×360∘+180∘,解得n=7.故这个多边形的边数是7.22.【答案】解:(2x−1)2−(x+2)(x−2)−4x(x−1)=4x2−4x+1−x2+4−4x2+4x=−x2+5,当x=2时,原式=1.【解析】先算乘法,再合并同类项,最后代入求出即可.【解答】解:(2x−1)2−(x+2)(x−2)−4x(x−1)=4x2−4x+1−x2+4−4x2+4x=−x2+5,当x=2时,原式=1.23.【答案】证明:∵∠A+∠B+∠1=180∘,∠A+15∘=∠1,∴∠A+45∘+∠A+15∘=180∘,解得:∠A=60∘,∵∠ACD=60∘,∴∠ACD=∠A,∴AB // CD.【解析】由三角形内角和定理和已知条件求出∠A=60∘,得出∠ACD=∠A,即可得出AB // CD.【解答】证明:∵∠A+∠B+∠1=180∘,∠A+15∘=∠1,∴∠A+45∘+∠A+15∘=180∘,解得:∠A=60∘,∵∠ACD=60∘,∴∠ACD=∠A,∴AB // CD.24.【答案】解:∵AD,AE分别是边BC上的中线和高,AE=3cm,S△ABC=12cm2,∴S△ADC=6cm2,×AE×CD=6,∴12×3×CD=6,∴12解得:CD=4(cm),∴BC=2×4=8(cm).【解析】利用三角形的中线平分三角形面积得出S△ADC=6cm2,进而利用三角形面积得出CD的长,即可得出BC的长.【解答】解:∵AD,AE分别是边BC上的中线和高,AE=3cm,S△ABC=12cm2,∴S△ADC=6cm2,×AE×CD=6,∴12×3×CD=6,∴12解得:CD=4(cm),∴BC=2×4=8(cm).25.【答案】解:∵m+n=8,mn=15,∴m2−mn+n2=(m+n)2−3mn=82−3×15=19.即m2−mn+n2的值是19.【解析】首先将m2−mn+n2配方,进而结合已知代入求出即可.【解答】解:∵m+n=8,mn=15,∴m2−mn+n2=(m+n)2−3mn=82−3×15=19.即m2−mn+n2的值是19.。
青海师范大学附属中学八年级数学下册第二单元《勾股定理》测试(包含答案解析)

一、选择题1.如图,在单位正方形组成的网格图中标有AB 、CD 、EF 、GH 四条线段,其中能构成一个直角三角形三边的线段是()A .CD 、EF 、GHB .AB 、EF 、GHC .AB 、CD 、GH D .AB 、CD 、EF 2.下列各组线段能构成直角三角形的一组是( ) A .30,40,50 B .8,12,13 C .5,9,13 D .3,4,6 3.下列条件中不能确定ABC 为直角三角形的是( ).A .ABC 中,三边长的平方之比为1:2:3B .ABC 中,222AB BC AC +=C .ABC 中,::3:4:5A B C ∠∠∠=D .ABC 中,1,2,3AB BC AC === 4.如图,2×2的方格中,小正方形的边长是1,点A 、B 、C 都在格点上,则ABC 中AB边上的高长为( )A .35B .25C .35D .32 5.下列各组数中,以a ,b ,c 为边的三角形不是直角三角形的是( )A .a =7,b =25,c =24B .a =11,b =41,c =40C .a =12,b =13,c =5D .a =8,b =17,c =15 6.如图,长方形的长为3,宽为2,对角线为OB ,且OA OB =,则下列各数中与点A表示的数最接近的是( )A .-3.5B .-3.6C .-3.7D .-3.87.《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多6尺,门的对角线长10尺,那么门的高和宽各是多少?如果设门的宽为x 尺,根据题意可列方程( )A .222(6)10x x ++=B .222(6)10x x -+=C .222(6)10x x +-=D .222610x +=8.如图,在ABC 中,13,17,AB AC AD BC ==⊥,垂足为D ,M 为AD 上任一点,则22MC MB -等于( )A .93B .30C .120D .无法确定 9.如图,90ABC ︒∠=,//AD BC ,以B 为圆心,BC 长为半径画弧,与射线AD 相交于点E ,连接BE ,过点C 作CF BE ⊥,垂足为F .若6AB =,10BC =,则EF 的长为( )A .1B .2C .3D .410.如图,将一根长为20cm 的筷子置于底面直径为5cm ,高为12cm 的圆柱形水杯中,筷子露在杯子外面的长度为( )A .13cmB .8cmC .7cmD .15cm11.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE ,EB 在一条直线上,证明中用到的面积相等关系是( )A .EDA CEB S S =△△B .EDA CDE CEB ABCD S S S S ++=△△△四边形C .EDA CEB CDE S S S +=△△△D .AECD DEBC S S =四边形四边形12.给出下列说法:①在直角三角形ABC 中,已知两边长为3和4,则第三边长为5;②三角形的三边a b c 、、满足222+=a b c ,则90︒∠=C ;③ABC ∆中,若::1:5:6A B C ∠∠∠=,则ABC ∆是直角三角形;④ABC ∆中,若::1:2:3a b c =,则这个三角形是直角三角形.其中,错误的说法的个数为( )A .1B .2C .3D .4 二、填空题13.如图,已知OA OB =,若点A 对应的数是a ,则a 与52-的大小关系是a ____52-.14.如图,在Rt ABC ∆中,90A ∠=︒,ABC ∠的平分线BD 交AC 于点D ,DE 是BC 的垂直平分线,点E 是垂足.若2DC =,1AD =,则BE 的长为__________.15.长方形零件图ABCD 中,2BC AB =,两孔中心M ,N 到边AD 上点P 的距离相等,且MP NP ⊥,相关尺寸如图所示,则两孔中心M ,N 之间的距离为__________mm .16.如图,在正方形网格中,A ,B ,C ,D ,E 都是格点,则BAC CDE ∠+∠=_______.17.“东方之门”座落于美丽的金鸡湖畔,高度约为301.8米,是苏州的地标建筑,被评为“中国最高的空中苏式园林”.现以现代大道所在的直线为x 轴,星海街所在的直线为y 轴,建立如图所示的平面直角坐标系(1个单位长度表示的实际距离为100米),东方之门的坐标为4(6,)A -,小明所在位置的坐标为(2,2)B -,则小明与东方之门的实际距离为___________米.18.如图所示的正方形网格中,A ,B ,C ,D ,P 是网格线交点.若∠APB =α,则∠BPC 的度数为 ____(用含α的式子表示).19.已知O 为平面直角坐标系的坐标原点,等腰三角形AOB 中,A(2,4),点B 是x 轴上的点,则AOB 的面积为_____.20.如图,教室的墙面ADEF 与地面ABCD 垂直,点P 在墙面上.若5PA AB ==米,点P 到AD 的距离是3米,有一只蚂蚁要从点P 爬到点B ,它的最短行程是______米.三、解答题21.如图,已知AB=CD ,∠B=∠C ,AC 和BD 交于点O ,OE ⊥AD 于点E .(1)△AOB 与△DOC 全等吗?请说明理由;(2)若OA=3,AD=4,求△AOD 的面积.22.如图,已知Rt △ABC 中,∠C =90°,点D 是AC 上一点,点E 、点F 是BC 上的点,且∠CDF =∠CEA ,CF =CA .(1)如图1,若AE 平分∠BAC ,∠DFC =25°,求∠B 的度数;(2)如图2,若过点F 作FG ⊥AB 于点G ,连结GC ,求证:AG +GF =2GC . 23.如图①,在ABC 中,90,ACB AC BC ∠=︒=,以C 为顶点作45DCE ∠=︒,且CD CE 、分别与AB 相交于D E 、两点,将ACD △绕点C 逆时针旋转90︒得到BCF △.(1)若64AD EB ==,,求DE 的长;(2)若将DCA ∠绕点C 逆时针旋转使CD 与AB 相交于点D ,边CE 与AB 的延长线相交于点E ,而其他条件不变,如图②所示,猜想DE 与AD EB 、之间有何数量关系?证明你的猜想.24.如图,已知长方形ABCD 中,AB =8cm ,BC =10cm ,在边CD 上取一点E ,将△ADE 折叠使点D 恰好落在BC 边上的点F ,求EF 的长.25.细心观察图形,认真分析各式,然后回答问题:OA 12=1;222(1)OA =+1=2;223(2)OA =+1=3224(3)OA =+1=4;… S 1=12;S 2=22;S 3=32;… 1010(2)直接用含n (n 为正整数)的式子表示OA n 的长和S n 的值;(3)求S 12+S 22+S 32+…+S 102的值.26.如图,在锐角△ABC 中,AD ⊥BC 于点D ,点E 在AD 上,DE =DC ,BE =AC ,点F 为BC 的中点,连结EF 并延长至点M ,使FM =EF ,连结CM .(1)求证:△BDE ≌△ADC ;(2)求证:AC ⊥MC ;(3)若AC =m ,则点A 、点M 之间的距离为 (用含m 的代数式表示).【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】设出正方形的边长,利用勾股定理,解出AB、CD、EF、GH各自的长度,再由勾股定理的逆定理分别验算,看哪三条边能够成直角三角形.【详解】解:设小正方形的边长为1,则AB2=22+22=8,CD2=22+42=20,EF2=12+22=5,GH2=22+32=13.因为AB2+EF2=GH2,所以能构成一个直角三角形三边的线段是AB、EF、GH.故选:B.【点睛】本题考查了勾股定理逆定理的应用;解题的关键是解出AB、CD、EF、GH各自的长度. 2.A解析:A【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.【详解】解:A、∵302+402=502,∴该三角形符合勾股定理的逆定理,故是直角三角形,故正确;B、∵82+122≠132,∴该三角形不符合勾股定理的逆定理,故不是直角三角形,故错误;C、∵52+92≠122,∴该三角形不符合勾股定理的逆定理,故不是直角三角形,故错误;D、∵32+42≠62,∴该三角形不符合勾股定理的逆定理,故不是直角三角形,故错误;故选:A.【点睛】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.3.C解析:C【分析】根据三角形内角和定理和勾股定理进行判断即可.【详解】解:A选项:ABC中,三边长的平方之比为1:2:3,ABC ∴是直角三角形.B 选项:∵在ABC 中,222AB BC AC +=,ABC ∴是直角三角形.C 选项:ABC 中,::3:4:5A B C ∠∠∠=,∴设3,4,5A x B x C x ∠=∠=∠=,又180A B C ︒∠+∠+∠=,12180x ︒∴=,345x ︒=,460x ︒=,575x ︒=,ABC ∴不是直角三角形.D 选项:在ABC 中,1,2,3AB BC AC ===,222AB BC AC ∴+=,ABC ∴是直角三角形.故选C .【点睛】本题考查了三角形内角和定理以及勾股定理,熟练掌握三角形内角和定理和勾股定理是本题的关键.4.A解析:A【分析】首先利用大正方形的面积减去周围三个三角形的面积计算出△ABC 的面积和AB 的长,利用三角形面积公式可得答案.【详解】过C 作CD ⊥AB 于D ,如图:∵2111321211122222ABC S =-⨯⨯-⨯⨯-⨯⨯=△, 且12ABC S AB CD =⋅△, ∵22125AB =+=∴1322AB CD ⋅=,则5CD ==, 故选:A .【点睛】本题主要考查了勾股定理与网格问题,关键是正确求出三角形面积.5.B解析:B【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,就是直角三角形,没有这种关系,就不是直角三角形.【详解】解:A 、72+242=52,能构成直角三角形,不符合题意;B 、112+402≠412,不能构成直角三角形,符合题意;C 、52+122=132,能构成直角三角形,不符合题意;D 、82+152=172,能构成直角三角形,不符合题意.故选:B .【点睛】本题主要考查了勾股定理的逆定理,准确分析计算是解题的关键.6.B解析:B【分析】先根据勾股定理求得A 点坐标,再利用二分法估算即可得出比较接近-3.6.【详解】解:∵长方形的长为3,宽为2,∴OA OB ==∴A 所表示的数为∵23.612.9613=<,23.713.6913=>, ∴-3.6和-3.7之间,∵23.6513.322513=>, ∴-3.6,故选:B .【点睛】本题考查勾股定理,算术平方根的估算.掌握二分法估算是解题关键.7.A解析:A【分析】设门的宽为x 尺,则高为(x+6)尺,根据勾股定理解答.【详解】设门的宽为x 尺,则高为(x+6)尺,根据题意可列方程222(6)10x x ++=,故选:A .【点睛】此题考查勾股定理计算,正确理解题意掌握勾股定理计算公式是解题的关键. 8.C解析:C【分析】由,AD BC ⊥结合勾股定理可得:2222,AC AB DC BD -=-2222MC MB DC BD -=-,再把已知线段的长度代入计算即可得到答案.【详解】解:,AD BC ⊥222222,,AB AD BD AC AD DC ∴=+=+22222222,AC AB AD DC AD BD DC BD ∴-=+--=-1713AC AB ==,,22221713304120DC BD ∴-=-=⨯=,,AD BC ⊥222222,,MC MD DC BM BD DM ∴=+=+22222222120.MC MB MD DC DM BD DC BD ∴-=+--=-=故选:.C【点睛】本题考查的是勾股定理的应用,掌握利用勾股定理解决问题是解题的关键.9.B解析:B【分析】根据题意结合勾股定理可求出AE 长,再根据//AD BC ,可证明AEB CBF ∠=∠,即可证明()ABE FCB AAS ≅,得出结论BF=AE ,即可求出EF .【详解】根据题意可知BC=BE=10,90BAE BFC ∠=∠=︒.在Rt ABE △中,22221068AEBE AB . ∵//AD BC ,∴AEB CBF ∠=∠,∴()ABE FCB AAS ≅,∴BF=AE=8,∴EF=BE-BF=10-8=2.故选:B .【点睛】本题考查三角形全等的判定和性质,平行线的性质以及勾股定理.利用“角角边”证明ABE FCB ≅是解答本题的关键.10.C解析:C【分析】根据勾股定理求出杯子内的筷子长度,即可得到答案.【详解】解:由题意可得:,则筷子露在杯子外面的筷子长度为:20﹣13=7(cm ).故选:C .【点睛】此题考查勾股定理的实际应用,熟记勾股定理的计算公式是解题的关键.11.B解析:B【分析】直接根据梯形ABCD 的面积的两种算法进行解答即可.【详解】解:由图形可得:EDA CDE CEB ABCD S S S S ++=△△△四边形故答案为B .【点睛】本题主要考查了勾股定理的证明方法,将图形的面积用两种方式表示出来成为解答本题的关键.12.A解析:A【分析】分4为直角三角形的直角边和斜边两种情况,根据勾股定理即可判断①;根据勾股定理的逆定理即可判断②④;根据三角形的内角和定理即可求出三角形的三个内角,进而可判断③;从而可得答案.【详解】解:若4为直角三角形ABC 5=,若4为直角三角形ABC=,故①错误;三角形的三边a b c 、、满足222+=a b c ,则90C ∠=︒,故②正确;△ABC 中,若::1:5:6A B C ∠∠∠=,所以11801512A ∠=︒⨯=︒,51807512B ∠=︒⨯=︒,61809012C ∠=︒⨯=︒,所以ABC 是直角三角形,故③正确;△ABC 中,若::1:2a b c =,2,a k b k c ===,因为)()222222242a c k k k b +=+===,所以这个三角形是直角三角形,故④正确.综上,错误的说法是①,有1个.故选:A .【点睛】 本题考查了三角形的内角和、勾股定理及其逆定理等知识,属于基础题型,熟练掌握上述知识是解题的关键.二、填空题13.>【分析】根据勾股定理求出OB 长确定点A 表示的数再用估算法比较大小即可【详解】解:由图可知∴则点A 表示的数为∵∴∴故答案为:>【点睛】本题考查了勾股定理实数在数轴上的表示和实数大小的比较熟练的运用勾 解析:>【分析】根据勾股定理求出OB 长,确定点A 表示的数,再用估算法比较大小即可.【详解】解:由图可知,OB = ∴OA OB ==A 表示的数为∵225()2<,∴52<,∴52>-, 故答案为:>.【点睛】 本题考查了勾股定理、实数在数轴上的表示和实数大小的比较,熟练的运用勾股定理求出OB 长,确定A 点表示的数,能够利用算术平方根与被开方数大小之间的关系是解题关键.14.【分析】根据是的垂直平分线得到BD=CDBE=CE 推出∠DBC=∠C 根据BD 平分推出∠ABD=∠CBD=∠C 求出∠C=得到DE=1利用勾股定理求出CE 即可得到BE 【详解】∵是的垂直平分线∴BD=CD【分析】根据DE 是BC 的垂直平分线,得到BD=CD ,BE=CE ,推出∠DBC=∠C ,根据BD 平分ABC ∠,推出∠ABD=∠CBD=∠C ,求出∠C=30,得到DE=1,利用勾股定理求出CE 即可得到BE .【详解】∵DE 是BC 的垂直平分线,∴BD=CD,BE=CE ,∴∠DBC=∠C ,∵BD 平分ABC ∠,∴∠ABD=∠CBD ,∴∠ABD=∠CBD=∠C ,∵∠ABD+∠CBD+∠C=90︒,∴∠C=30,∵2DC =,∴DE=1,∴=,【点睛】此题考查线段垂直平分线的性质,角平分线的性质,直角三角形30度角的性质,勾股定理,熟记线段垂直平分线的性质及角平分线的性质是解题的关键.15.【分析】作MQ ⊥BCNF ⊥AB 交于点O 作根据AAS 证明△得到由得出从而得出OMON 的长最后由勾股定理可求出MN 【详解】解:作MQ ⊥BCNF ⊥AB 交于点O 作MK ⊥AB 于点K 作∵四边形ABCD 是矩形∴M解析:【分析】作MQ ⊥BC ,NF ⊥AB 交于点O ,作MM AD '⊥,NN AD '⊥,根据AAS 证明△M PM N NP ''≅∆得到PN MM ''=,NN M P ''=,由2BC AB =得出24NN '=,从而得出OM ,ON 的长,最后由勾股定理可求出MN .【详解】解:作MQ ⊥BC ,NF ⊥AB 交于点O ,作MK ⊥AB 于点K ,作MM AD '⊥,NN AD '⊥,∵四边形ABCD 是矩形,∴MK//AD//BC∴∠90KMM KMQ '=∠=︒∴M '、M 、Q 三点共线,∵∠90MPN =︒,∴∠90M PM N PN ''+∠=︒,∠90N PN PNN ''+∠=︒∴∠M PM PNN ''=∠又∠90PM M PN N ''=∠=︒,MP PN =∴△M PM N NP ''≅∆∴10PN MM ''==,NN M P ''=又∵10ON M P N P N M N M N N ''''+='=+=+则11AB NN '=+,5054104(10)BC ON NN '=+-=-+又∵2BC AB =,即104(10)2(11)NN NN ''-+=+∴24NN '=∴1014OM NN '=-=,1034ON NN '=+=在Rt OMN ∆中,222214341352262()MN ON OM mm =+=+== 故答案为:2【点睛】此题主要考查了运用勾股定理示线段的长,作辅助线构造直角三角形是解答此题的关键. 16.;【分析】首先根据三角形内角与外角的关系计算出∠1+∠BAC=45°∠2+∠CDE=45°再利用勾股定理逆定理∠BCE=90°再证明∠ADC=90°进而得到∠ACD=45°从而得到∠1+∠2=45°解析:45︒;【分析】首先根据三角形内角与外角的关系计算出∠1+∠BAC=45°,∠2+∠CDE=45°,再利用勾股定理逆定理∠BCE=90°,再证明∠ADC=90°,进而得到∠ACD=45°,从而得到∠1+∠2=45°,继而得到∠BAC+∠CDE=45°.【详解】解:∵BF=CF,CK=EK ,∴∠FBC=CEK=45°,∴∠1+∠BAC=45°,∠2+∠CDE=45°,连接AD、BE,∵BC²=2²+2²=8,CE²=1²+1²=2,BE²=3²+1²=10,∴BC²+CE²=BE²,∴∠BCE=90°,∵AD²=3²+1²=10,CD²=3²+1²=10,AC²=4²+2²=20,∴AD²+CD²=AC²,∴∠ADC=90°,∴∠ACD=45°,∴∠1+∠2=45°,∴∠BAC+∠CDE=45°,故答案为:45°.【点睛】本题考查了勾股定理逆定理,以及三角形内角与外角的关系,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a²+b²=c²,那么这个三角形就是直角三角形.17.【分析】运用勾股定理可求出平面直角坐标系中AB的长度再根据个单位长度表示的实际距离为米求出结果即可【详解】解:如图AC=6-(-2)=8BC=2-(-4)=6∴∴小明与东方之门的实际距离为10×10解析:1000【分析】运用勾股定理可求出平面直角坐标系中AB的长度,再根据1个单位长度表示的实际距离为100米求出结果即可.【详解】解:如图,AC=6-(-2)=8,BC=2-(-4)=6∴2222+AB BC AC=6+8=10∴小明与东方之门的实际距离为10×100=1000(米)故答案为:1000.【点睛】此题主要考查了勾股定理的应用,构造直角三角形运用勾股定理是解答此题的关键.18.【分析】由图可知AC的长根据勾股定理可以求得PAPC的长再利用勾股定理的逆定理可以判断△PAC的形状从而可以得到∠CPA的度数然后即可得到∠BPC=∠CPA−∠APB的度数【详解】设网格的长度为1则︒解析:90-α【分析】由图可知AC的长,根据勾股定理可以求得PA、PC的长,再利用勾股定理的逆定理可以判断△PAC的形状,从而可以得到∠CPA的度数,然后即可得到∠BPC=∠CPA−∠APB的度数.【详解】设网格的长度为1,则223332+=,AC=63332+=22222AP PC AC+=∴△PAC为等腰直角三角形∴∠CPA=90︒∴∠BPC=∠CPA−∠APB=90-α︒︒故答案为:90-α【点睛】本题考查勾股定理的逆定理、勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.19.8或4或10【分析】根据已知画出坐标系进而得出AE的长以及BO的长即可得出△AOB 的面积【详解】解:如图所示:过点A 作AE ⊥x 轴于点E ∵点O (00)A (24)∴AE =4OE =2OA =当OA =AB 时∴解析:8或45或10【分析】根据已知画出坐标系,进而得出AE 的长以及BO 的长,即可得出△AOB 的面积.【详解】解:如图所示:过点A 作AE ⊥x 轴于点E ,∵点O (0,0),A (2,4),∴AE =4,OE =2,OA 222425+=当OA =AB 时,∴AE 是△AOB 边OB 的垂直平分线, ∴BE=OE=2,∴OB=4,∴B 的坐标为(4,0),此时S △AOB =12OB AE •=1442⨯⨯=8; 当OA =OB 时, ∴25OB OA ==,∴B 的坐标为(5±0),此时S △AOB =12OB AE •=12542⨯=45 当OB =AB 时, 设AB OB x ==,则2BE x =-,∴2224(2)x x =+-,解得:5x =,∴5OB =,∴B 的坐标为(5,0),此时S△AOB=12OB AE•=1542⨯⨯=10;∴△AOB的面积为:8或45或10.故答案为:8或45或10.【点睛】此题主要考查了三角形面积以及坐标与图形的性质,利用等腰三角形的性质求得OB的长是解题关键.20.【分析】可将教室的墙面ADEF与地面ABCD展开连接PB根据两点之间线段最短利用勾股定理求解即可【详解】解:如图过P作PG⊥BF于G连接PB∵AG=3AP=AB=5∴∴BG=8∴故这只蚂蚁的最短行程解析:45【分析】可将教室的墙面ADEF与地面ABCD展开,连接PB,根据两点之间线段最短,利用勾股定理求解即可.【详解】解:如图,过P作PG⊥BF于G,连接PB,∵AG=3,AP=AB=5,∴224PG AP AG==-,∴BG=8,∴2245P GB GPB+=故这只蚂蚁的最短行程应该是5故答案为:5【点睛】本题考查了平面展开-最短路径问题,立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.三、解答题21.(1)△AOB≌△DOC,理由见解析;(2)△AOD的面积为5【分析】(1)根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到AO=DO ,根据等腰三角形的性质得到AE=12AD=2,由勾股定理得到OE ==【详解】(1)证明:在△AOB 和△DOC 中, AOB COD B CAB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, 所以△AOB ≌△DOC (AAS );(2)因为△AOB ≌△DOC ,所以AO =DO ,因为OE ⊥AD 于点E .所以AE 12=AD =2, 所以OE ==所以S △AOD 142=⨯=【点睛】本题考查了全等三角形的判定和性质,勾股定理,三角形的面积的计算,熟练掌握全等三角形的判定和性质是解题的关键.22.(1)∠B=40°;(2)见解析.【分析】(1)先利用SAS 证明△AEC ≌△FDC ,得出∠EAC=∠DFC=25°,从而得出∠BAC=50°,再根据直角三角形的两个锐角互余即可得出结论(2)过点C 作GC 的垂线交GF 的延长线于点P ,根据同角的余角得出∠PCF =∠GCA ,再根据ASA 得出△AGC ≌△FPC ,从而得出△GCP 是等腰直角三角形,即可得出答案【详解】(1)在△AEC 和△FDC 中,∵∠CDF=∠CEA CE=CD ∠C=∠C ,∴△AEC ≌△FDC ,∴∠EAC=∠DFC=25°∵AE 平分∠BAC ,∴∠BAC=2∠EAC=50°∵∠C=90°,∴在Rt △ABC 中,∠B=90°-∠BAC=40°.(2)如答图,过点C 作GC 的垂线交GF 的延长线于点P∴∠GCP = 90°∴∠GCF+∠PCF = 90°,∵∠ACB = 90°∴∠GCF+∠GCA = 90°,∴∠PCF =∠GCA.∵∠ACB=90°,GF⊥AB∴∠B+∠BAC=∠B+∠BFG= 90°,∴∠BAC=∠BFG.又∵∠PFC=∠BFG∴∠GAC=∠PFC.由(1)知,△AEC≌△FDC,∴CA=CF,∴△AGC≌△FPC,∴GC=PC,AG=FP.又∵PC⊥GC,∴△GCP是等腰直角三角形,∴GF+2GC,∴AG+2GC【点睛】本题考查了全等三角形的判定和性质、等腰直角三角形的性质、勾股定理等知识,正确作出辅助线构造全等三角形是解题的关键.23.(1)213DE=2)222DE AD BE=+,证明见解析.【分析】(1)证明△ECD≌△ECF(SAS),然后证明∠EBF=90°,利用全等三角形的性质以及勾股定理解决问题即可.(2)利用全等三角形的性质以及勾股定理解决问题即可.【详解】解:如图①中,∵ACD △绕点C 逆时针旋转90︒得到BCF △∴90ACD BCF ACB DCF ∠=∠=︒≌, ∴6ACD BCF A CBF CD CF AD BF ∠=∠∠=∠===,,, ∵45DCE ∠=︒ ∴45DCE ECF ∠=∠=︒ ∵CE CE = ∴ECD ECF ≌ ∴DE EF = ∵90AC BC ACB =∠=︒, ∴45A ABC CBF ∠=∠=∠=︒ ∴90EBF ∠=︒ ∴222246213DE EF BE BF ==+=+= (2)解:222DE AD BE =+理由:如图②中,连接EF∵CBF 是由CAD ∠旋转得到∴45ACD BCF CD CF AD BF A CBF ∠=∠==∠=∠=︒,,,∴90ACB DCF ∠=∠=︒∵45DCE ∠=︒∴45ECF ECD ∠=∠=︒∵CE CE =∴ECD ECF ≌∴DE EF =∵4545ABC CBF ∠=︒∠=︒,∴90ABF EBF ∠=∠=︒∴222BF BE EF +=∵BF AD EF DE ==,∴222DE AD BE =+【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题. 24.5cm【分析】先根据折叠求出AF =10,进而用勾股定理求出BF ,即可求出CF ,最后用勾股定理即可得出结论.【详解】解:∵四边形ABCD 是矩形,∴AD =BC =10cm ,CD =AB =8cm ,由折叠可知:Rt △ADE ≌Rt △AFE ,∴∠AFE =90°,AF =10cm ,EF =DE ,设EF =xcm ,则DE =EF =xcm ,CE =CD ﹣CE =(8﹣x )cm ,在Rt △ABF 中,由勾股定理得:AB 2+BF 2=AF 2,即82+BF 2=102,∴BF =6cm ,∴CF =BC ﹣BF =10﹣6=4(cm ),在Rt △ECF 中,由勾股定理可得:EF 2=CE 2+CF 2,即x 2=(8﹣x )2+42, ∴x =5即:EF 的长为5cm .【点睛】本题考查勾股定理、图形的翻折变换、全等三角形,方程思想等知识点,关键是熟练掌握勾股定理,运用方程求解.25.(1)OA 101010102S =;(2)n OA n =2n n S =;(3)554 【分析】(1)根据前面几个线段的值平方得出规律2211n OA n n =-+=,即可求出10OA 的长,根据前面几个三角形的面积得到规律2n n S =10S 的值; (2)根据规律发现2211n OA n n =-+=,n n S =(3)根据(2)中的规律得原式的值为()1123104⨯++++,即可求出结果. 【详解】(1)∵22212OA =+=,22313OA =+=,22414OA =+=…, ∴2210110OA =+=,∴10OA =∵12S =,22S =,32S =…,∴2n S =10S =;(2)由(1)可知,221n OA n =+=,即n OA =2n S = (3)222212310123104444S S S S ++++=++++()1551231044=⨯++++=. 【点睛】 本题考查找规律,解题的关键是总结出题目中式子之间的规律进行计算求解.26.(1)证明见解析;(2)证明见解析;(3.【分析】(1)先根据垂直的定义可得BDE 和ADC 都是直角三角形,再利用HL 定理证明三角形全等即可;(2)先根据(1)中的全等三角形可得DBE DAC ∠=∠,再根据三角形全等的判定定理与性质可得DBE FCM ∠=∠,从而可得DAC FCM ∠=∠,然后根据角的和差、等量代换即可得证;(3)先根据(2)中的全等三角形可得BE CM =,从而可得CM AC m ==,再在Rt ACM △中,利用勾股定理即可得.【详解】 (1)AD BC ⊥,90BDE ADC ∠∴∠==︒,∴BDE 和ADC 都是直角三角形,在BDE 和ADC 中,DE DC BE AC =⎧⎨=⎩, ()BDE ADC HL ∴≅;(2)BDE ADC ≅,DBE DAC ∠=∠∴,点F 为BC 的中点,BF CF ∴=,由对顶角相等得:BFE CFM ∠=∠,在BEF 和CMF 中,BF CF BFE CFM EF MF =⎧⎪∠=∠⎨⎪=⎩,()BEF CMF SAS ∴≅,FBE FCM ∴∠=∠,即DBE FCM ∠=∠,DAC FCM ∠=∠∴, 又在Rt ACD △中,90DAC ACD ∠+∠=︒,90FCM ACD ∴∠+∠=︒,即90ACM ∠=︒,AC MC ∴⊥;(3)如图,连接AM ,BEF CMF ≅,BE CM ∴=,,BE AC AC m ==,CM AC m ∴==,AC MC ⊥,ACM ∴是直角三角形,222AM AC CM m ∴+,即点A 、点M 2m .【点睛】本题考查了直角三角形全等的判定定理与性质、直角三角形的性质、勾股定理等知识点,熟练掌握三角形全等的判定方法是解题关键.。
青海师范大学附属中学九年级数学下册第二十八章《锐角三角函数》经典练习卷(培优练)

一、选择题1.如图,在等边△ABC 中,点O 在边AB 上,⊙O 过点B 且分别与边AB 、BC 相交于点D 、E ,F 是AC 上的点,判断下列说法错误的是( )A .若EF ⊥AC ,则EF 是⊙O 的切线B .若EF 是⊙O 的切线,则EF ⊥ACC .若BE =EC ,则AC 是⊙O 的切线D .若32BE EC =,则AC 是⊙O 的切线 2.在ABC 中,若21cos |1tan |02A B ⎛⎫-+-= ⎪⎝⎭,则C ∠的度数是( ) A .45︒ B .60︒ C .75︒ D .105︒3.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在 改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD 的平台BC 上(如图),测得52.5,5AED BC ︒∠==米,35CD =米,19DE =米,则铁塔AB的高度约为( )(参考数据:52.50.79,52.50.61,52.5 1.30sin cos tan ︒︒︒≈≈≈)A .7.6 米B .27.5 米C .30.5 米D .58.5 米 4.如图,O 是ABC 的外接圆,60BAC ∠=︒,若O 的半径OC 为1,则弦BC 的长为( )A .12B .32C .1D .35.如图,在矩形ABCD 中,E 是AD 边的中点,BE ⊥AC ,垂足为点F ,连接DF ,下面四个结论:①CF=2AF ;②tan ∠CAD=22 ;③DF=DC ;④△AEF ∽△CAB ;⑤S 四边形CDEF =52S △ABF ,其中正确的结论有( )A .2个B .3个C .4个D .5个6.在Rt △ABC 中,∠ACB =90°,AB =5,tan ∠B =2,则AC 的长为 ( ) A .1B .2C .5D .25 7.如图,半径为5的O 中, OA BC ⊥,30ADC ∠=︒,则BC 的长为( )A .52B .53C 522D 5328.某兴趣小组想测量一座大楼 AB 的高度.如图,大楼前有一段斜坡BC ,已知 BC 的长为 12 米它的坡度1:3i =.在离 C 点 40 米的 D 处,用测量仪测得大楼顶端 A 的仰角为 37度,测角仪DE 的高度为 1.5米,求大楼AB 的高度约为( )米(sin 370.60,cos370.80,tan 373 1.73︒=︒=︒==)A .39.3B .37.8C .33.3D .25.79.如图,在△ABC 中,sinB=13, tanC=2,AB=3,则AC 的长为( )A .2B .52C .5D .210.如图,在Rt ABC ∆中,90ACB ∠=︒,22AC BC ==,CD AB ⊥于点D .点P 从点A 出发,沿A D C →→的路径运动,运动到点C 停止,过点P 作PE AC ⊥于点E ,作PF BC ⊥于点F .设点P 运动的路程为x ,四边形CEPF 的面积为y ,则能反映y 与x 之间函数关系的图象是( )A .B .C .D .11.如图,小明想要测量学校操场上旗杆AB 的高度,他作了如下操作:(1)在点C 处放置测角仪,测得旗杆顶的仰角ACE α∠=;(2)量得测角仪的高度CD a =;(3)量得测角仪到旗杆的水平距离DB b =.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )A .tan a b α+B .sin a b α+C .tan b a α+D .sin b a α+ 12.如图,反比例函数k y x=(0)k ≠第一象限内的图象经过ABC ∆的顶点A ,C ,AB AC =,且BC y ⊥轴,点A ,C ,的横坐标分别为1,3,若120BAC ∠=︒,则k 的值为( )A .1B .2C .3D .213.如图,平行四边形ABCD 中,AB ⊥AC ,AB =3,BC =7,对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交B C ,AD 于点E ,F ,下列说法:①在旋转过程中,AF =CE . ②OB =AC ,③在旋转过程中,四边形ABEF 的面积为212,④当直线AC 绕点O 顺时针旋转30°时,连接BF ,DE 则四边形BEDF 是菱形,其中正确的是( )A .①②④B .① ②C .①②③④D .② ③ ④ 14.如图,分别以直角三角形三边为边向外作等边三角形,面积分别为1S 、2S 、3S ;如图2,分别以直角三角形的三边为直径向外半圆,面积分别为4S 、5S 、6S .其中116S =,245S =,511S =,614S =,则34S S +=( )A .86B .64C .54D .4815.如图所示,矩形ABCD 的边长AB =2,BC =23,△ADE 为正三角形.若半径为R 的圆能够覆盖五边形ABCDE (即五边形ABCDE 的每个顶点都在圆内或圆上),则R 的最小值是( )A .23B .4C .2.8D .2.5二、填空题16.如图,矩形ABCD 中,1AB =,3BC =,以B 为圆心,BD 为半径画弧,交BC 延长线于M 点,以D 为圆心,CD 为半径画弧,交AD 于点N ,则图中阴影部分的面积是________.17.将一副三角板如图摆放,使得一块三角板的直角边AC 和另一块三角板的斜边ME 重叠,点A 与点M 重合,已知AB=AC=8,则重叠的面积是__________.18.如图,长方形ABCD 中,BC=6,CD=3,将△BCD 沿对角线BD 翻折,点C 落在点C’处,BC’交AD 于点E ,则线段DE 的长为____.19.如图,正方形ABCD 的边长为22,过点A 作AE ⊥AC,AE=1,连接BE ,则tanE= .20.在ABCD 中,若30B ∠=︒,BC 10cm =,6AB cm =,则ABCD 的面积是__________.21.如图所示,AOB ∠是放置在正方形网格中的一个角,则sin AOB ∠的值是________.22.已知在矩形ABCD 中,AC =12,∠ACB =15°,那么顶点D 到AC 的距离为_____. 23.计算:112tan 6032()2-+---____. 24.如图,已知∠AOB =60°,点P 在边OA 上,OP =12,点M ,N 在边OB 上,PM =PN ,若MN =2,则OM =____.25.如图,ABCD 是一张边长为4cm 的正方形纸片,E ,F 分别为AB ,CD 的中点,沿过点D 的折痕将A 角翻折,使得点A 落在EF 上的点A′处折痕交AE 于点G ,则∠ADG=____°EG=___cm .26.如图,在矩形ABCD 中,连接AC ,以点B 为圆心,BA 为半径画弧,交BC 于点E ,已知3BE =,33BC =,则图中阴影部分的面积为_______.(结果保留π)三、解答题27.如图,以ABC ∆的一边BC 为直径的O ,交AB 于点D ,连结CD ,OD ,已知1902A DOC ∠+∠=︒.(1)判断AC 是否为O 的切线?请说明理由.(2)①若60A ∠=︒,1AD =,求O 的半径.②若DOC α∠=︒,AC m =,OB r =,请用含r 、α的代数式表示m . 28.如图,有一个半径为3cm 球形的零件不能直接放在地面上,于是我们找了两个三角形的垫块把这个零件架起来,两个三角形与球的接触点分别是点P 和Q ,已知70α=,40β=,一侧接触点离地面距离PM 是4cm(sin 700.94,cos700.34,tan 70 2.75;sin 400.64,cos 400.77,tan 400.84≈≈≈≈≈≈)(1)求圆心O 距离地面的高度;(2)直接写出QOP ∠与α、β的关系;(3)另一侧接触点离地面距离QN 又是什么?29.有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长50cm AB =,拉杆BC 的伸长距离最大时可达35cm ,点A 、B 、C 在同一条直线上,在箱体底端装有圆形的滚筒A ,A 与水平地面切于点D ,在拉杆伸长至最大的情况下,当点B 距离水平地面38cm 时,点C 到水平面的距离CE 为59cm ,设AF ∥MN .(1)求A 的半径长;(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C 端拉旅行箱时,CE 为80cm ,64CAF ∠=︒,求此时拉杆BC 的伸长距离.(精确到1cm ,参考数据:sin 640.90︒≈,cos640.39︒≈,tan64 2.1︒≈)30.计算或解方程:(111754640.583⎛ ⎝︒+︒-︒(26045cos60(3)2430-+=x x。
青海师范大学附属中学八年级数学上册第十一章《三角形》经典题

一、选择题1.已知实数x 、y 满足|x -4|+ 8y -=0,则以x 、y 的值为两边长的等腰三角形周长是( )A .20或16B .20C .16D .182.下列四组线段中,不可以构成三角形的是( )A .4,5,6B .1.5,2,2.5C .13,14,15D .1,2,3 3.若一个正多边形的内角和等于其外角和的3倍,则这个正多边形是( ) A .5边形 B .6边形 C .7边形 D .8边形 4.如图,ABC 中,BC 边上的高是( )A .AEB .ADC .CD D .CF 5.已知三角形的两边长分别为1和4,则第三边长可能是( ) A .3B .4C .5D .6 6.若一个多边形的每个内角都等于160°,则这个多边形的边数是( ) A .18B .19C .20D .21 7.下列长度(单位:cm )的三条线段能组成三角形的是( ) A .13,11,12B .3,2,1C .5,12,7D .5,13,5 8.一副透明的三角板,如图叠放,直角三角板的斜边AB 、CE 相交于点D ,则BDC∠的度数是( )A .65︒B .75︒C .85︒D .105︒ 9.下列每组数分别三根小木棒的长度,用它们能摆成三角形的是( )A .3,4,8cm cm cmB .7,8,15cm cm cmC .12,13,22cm cm cmD .10,10,20cm cm cm10.如图,直线//BC AE ,CD AB ⊥于点D ,若150∠=︒,则BCD ∠的度数是( )A .60°B .50°C .40°D .30°11.现有两根木棒,长度分别为5cm 和13cm ,若不改变木棒的长度,要钉成一个三角形木架,则应在下列四根木棒中选取( )A .20cm 的木棒B .18cm 的木棒C .12cm 的木棒D .8cm 的木棒 12.小红有两根长度分别为4cm 和8cm 的木棒,他想摆一个三角形,现有长度分别为3cm ,4cm ,8cm ,15cm 四根木棒,则他应选择的木棒长度为( ).A .3cmB .4cmC .8cmD .15cm 13.如图,已知AE 交CD 于点O ,AB ∥CD ,∠A =50°,∠E =15°,则∠C 的度数为( )A .50°B .65°C .35°D .15°14.如图,在ABC ∆中,80,BAC ∠=︒点D 在BC 边上,将ABD △沿AD 折叠,点B 恰好落在AC 边上的点'B 处,若'20B DC ∠=.则C ∠的度数为( )A .20B .25C .35D .4015.具备下列条件的三角形中,不是..直角三角形的是( ) A .A B C ∠+∠=∠B .12A BC ∠=∠=∠ C .3A B C ∠=∠=∠D .1123A B C ∠=∠=∠ 二、填空题16.如图是一块正多边形的碎瓷片,经测得30ACB ∠=︒,则这个正多边形的边数是_________.17.如图,BD 是ABC 的中线,点E 、F 分别为BD 、CE 的中点,若AEF 的面积为23cm ,则ABC 的面积是______2cm .18.如图1,△ABC 中,有一块直角三角板PMN 放置在△ABC 上(P 点在△ABC 内),使三角板PMN 的两条直角边PM 、PN 恰好分别经过点B 和点C .若∠A =52°,则∠1+∠2=__________;19.如图,C 为∠AOB 的边OA 上一点,过点C 作CD ∥OB 交∠AOB 的平分线OE 于点F ,作CH ⊥OB 交BO 的延长线于点H ,若∠EFD =α,现有以下结论:①∠COF =α;②∠AOH =180°﹣2α;③CH ⊥CD ;④∠OCH =2α﹣90°.其中正确的是__(填序号).20.如图,六边形ABCDEF 中,AB ∥DC ,∠1、∠2、∠3、∠4分别是∠BAF 、∠AFE 、∠FED 、∠EDC 的外角,则∠1+∠2+∠3+∠4=_____.21.已知//AB CD ,点P 是平面内一点,若30,20BPD PBA ∠=︒∠=︒,则CDP ∠=___________度.22.如图,△ABC 中,D 为BC 边上的一点,BD :DC=2:3,△ABC 的面积为10,则△ABD 的面积是_________________23.如图所示,∠A+∠B+∠C+∠D+∠E+∠F=____.(填写度数).24.如图,若//AB CD ,BF 平分ABE ∠,DF 平分CDE ∠,90BED ∠=,则BFD ∠=______.25.如图,在ABC ∆中,BD 平分ABC ∠,AE BD ⊥.若30ABC ∠=︒,50C ∠=︒,则CAE ∠的度数为_______︒.26.如图,在ABC 中,E 、D 、F 分别是AD 、BF 、CE 的中点,若DEF 的面积是1,则ABC S =______.三、解答题27.如图,已知△ABC 中,∠B =60°,AD 是BC 边上的高,AE 是∠BAC 的平分线,且∠DAE=10°,求∠C 的度数.28.如图1,已知ACD ∠是ABC 的一个外角,我们容易证明ACD A B ∠=∠+∠,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?尝试探究:(1)如图2,DBC ∠与ECB ∠分别为ABC 的两个外角,则DBC ECB ∠+∠_______180A ∠+︒(横线上填“>”、“<”或“=”).初步应用:(2)如图3,在ABC 纸片中剪去CED ,得到四边形ABDE ,1135∠=︒,则2C ∠-∠=_______.(3)解决问题:如图4,在ABC 中,BP 、CP 分别平分外角DBC ∠、ECB ∠,P ∠与A ∠有何数量关系?请尝试证明.(4)如图5,在四边形ABCD 中,BP 、CP 分别平分外角EBC ∠、FCB ∠,请利用上面的结论直接写出P ∠与A ∠、D ∠的数量关系.29.已知在四边形ABCD 中,90A C ∠=∠=︒.(1)如图1,若BE 平分ABC ∠,DF 平分ADC ∠的邻补角,请写出BE 与DF 的位置关系并证明;(2)如图2,若BF 、DE 分别平分ABC ∠、ADC ∠的邻补角,判断DE 与BF 位置关系并证明;(3)如图3,若BE 、DE 分别五等分ABC ∠、ADC ∠的邻补角(即11,55CDE CDN CBE CBM ∠=∠∠=∠),求E ∠度数.30.如图,AD、AE分别是ABC的高和角平分线.(1)已知∠B=40°,∠C=60°,求∠DAE的度数;(2)设∠B=α,∠C=β(α<β),请用含α,β的代数式表示∠DAE,并证明.。
青海师范大学附属中学必修第一册第五单元《三角函数》测试(包含答案解析)
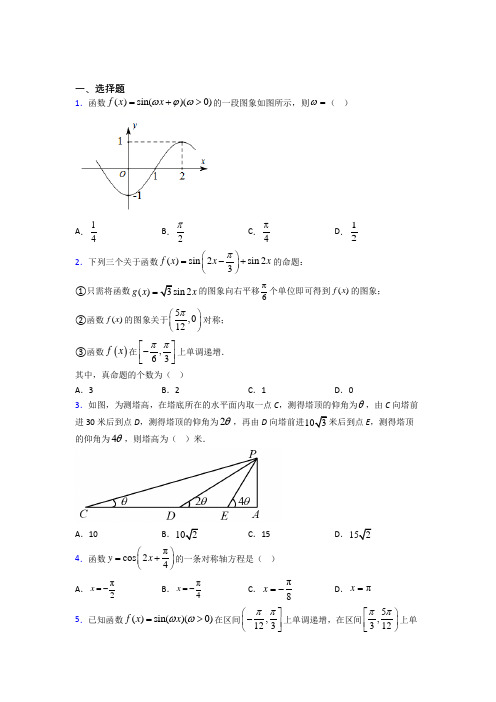
一、选择题1.函数()sin()(0)f x x ωϕω=+>的一段图象如图所示,则ω=( )A .14B .2π C .4π D .122.下列三个关于函数()sin 2sin 23f x x x π⎛⎫=-+ ⎪⎝⎭的命题: ①只需将函数()3sin 2g x x =的图象向右平移6π个单位即可得到()f x 的图象;②函数()f x 的图象关于5,012π⎛⎫⎪⎝⎭对称; ③函数()f x 在,63ππ⎡⎤-⎢⎥⎣⎦上单调递增. 其中,真命题的个数为( ) A .3B .2C .1D .03.如图,为测塔高,在塔底所在的水平面内取一点C ,测得塔顶的仰角为θ,由C 向塔前进30米后到点D ,测得塔顶的仰角为2θ,再由D 向塔前进103米后到点E ,测得塔顶的仰角为4θ,则塔高为( )米.A .10B .2C .15D .1524.函数πcos 24y x ⎛⎫=+ ⎪⎝⎭的一条对称轴方程是( ) A .π2x =-B .π4x =-C .π8x =-D .πx =5.已知函数()sin()(0)f x x ωω=>在区间,123ππ⎛⎤-⎥⎝⎦上单调递增,在区间5,312ππ⎡⎫⎪⎢⎣⎭上单调递减,则ω=( ) A .362k -,k ∈N B .362k +,k ∈N C .32D .36.已知()3sin 5πα+=,则sin()cos()sin 2απαπα--=⎛⎫- ⎪⎝⎭( ) A .45-B .45 C .35D .357.已知函数()cos 2cos sin(2)sin f x x x ϕπϕ=⋅-+⋅在3x π=处取得最小值,则函数()f x 的一个单调递减区间为( )A .4,33ππ⎛⎫⎪⎝⎭B .2,33ππ⎛⎫-⎪⎝⎭ C .5,36ππ⎛⎫⎪⎝⎭D .,63ππ⎛⎫-⎪⎝⎭ 8.若函数sin 3y x πω⎛⎫=+ ⎪⎝⎭的图象向右平移6π个单位后与函数cos y x ω=的图象重合,则ω的值可能为( ) A .1-B .2-C .1D .29.sin 20cos10cos160sin10-=( ) A. B .12C .12-D.210.已知sin()cos(2)()cos()tan x x f x x xπππ--=--,则313f π⎛⎫- ⎪⎝⎭的值为( ) A .12B .13 C .12-D .13-11.已知,2παπ⎛⎫∈ ⎪⎝⎭且1sin 23πα⎛⎫+=- ⎪⎝⎭,则()tan απ+=( )A.-B.C.4-D.412.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n 很大时,用圆内接正n 边形的周长近似等于圆周长,并计算出精确度很高的圆周率 3.1416π≈.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想,可以说他是中国古代极限思想的杰出代表.运用此思想,当π取3.1416时可得cos89︒的近似值为( ) A .0.00873B .0.01745C .0.02618D .0.03491二、填空题13.将函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移4π单位,所得到的函数解析式是_________. 14.求值tan 2010︒=_______.15.设()sin 2cos2f x a x b x =+,0ab ≠,若()6f x f π⎛⎫≤ ⎪⎝⎭对任意x ∈R 成立,则下列命题中正确的命题是______.(填序号) ①11012f π⎛⎫=⎪⎝⎭;②7105f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭;③()f x 不具有奇偶性;④()f x 的单调增区间是()2,63k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z ;⑤可能存在经过点(),a b 的直线与函数的图象不相交. 16.化简cos()sin()2sin()cos()πααπααπ+-=--___________.17.下列函数中,以π2为周期且在区间ππ,42⎛⎫⎪⎝⎭单调递增的是______.①()cos2f x x =;②()sin 2f x x =;③()cos f x x =;④()sin f x x = 18.已知7sin cos 17αα+=,()0,απ∈,则tan α= ________. 19.若函数()πsin 26g x x ⎛⎫=+ ⎪⎝⎭在区间0,3a ⎡⎤⎢⎥⎣⎦和7π4,6a ⎡⎤⎢⎥⎣⎦上均递增,则实数a 的取值范围是______.20.已知0sin 245ππαα⎛⎫⎛⎫∈-= ⎪ ⎪⎝⎭⎝⎭,,,则tan α=__________. 三、解答题21.已知0,2πα⎛⎫∈ ⎪⎝⎭,3cos 5α=. (1)求sin 6απ⎛⎫+ ⎪⎝⎭的值; (2)求cos 23πα⎛⎫+⎪⎝⎭的值. 22.已知函数()sin 1f x x x =++. (Ⅰ)设[0,2π]α∈,且()1f α=,求α的值; (Ⅱ)将函数(2)y f x =的图像向左平移π6个单位长度,得到函数()y g x =的图像. 当ππ[,]22x ∈-时,求满足()2g x ≤的实数x 的集合.23.如图为一个观览车示意图,该观览车圆半径为4.8m ,圆上最低点与地面距离为0.8m ,60秒转动一圈.图中OA 与地面垂直,以OA 为始边,逆时针转动θ到OB .设B 点与地面的距离为h .(1)求h 与θ的函数关系式;(2)设从OA 开始转动,经过10秒到达OB ,求h . 24.已知()()3sin f x x a ωϕ=++0,2πωϕ⎛⎫>< ⎪⎝⎭的图象过点,12a π⎛⎫⎪⎝⎭,且图象的相邻两条对称轴的距离为2π. (1)求函数()f x 的单调区间; (2)若()f x 在区间,122ππ⎡⎤-⎢⎥⎣⎦上的最大值与最小值之和为3,求实数a 的值. 25.如图为函数()sin()(0,0,||)2f x A x A πωφωφ=+>><的一个周期内的图象.(1)求函数()f x 的解析式及单调递减区间; (2)当1,43x ⎛⎫∈ ⎪⎝⎭时,求()f x 的值域.26.如图,以Ox 为始边作角α与β(0)βαπ<<<),它们的终边分别与单位圆相交于点P 、Q ,已知点P 的标为34,55⎛⎫- ⎪⎝⎭(1)求sin 2cos 211tan ααα+++的值;(2)若0OP OQ ⋅=,求sin()αβ+的值【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据函数的图象,求得函数的最小正周期,结合三角函数周期的公式,即可求解. 【详解】由题意,函数()sin()(0)f x x ωϕω=+>的一段图象, 可得2114T=-=,所以4T =,又由24w π=,解得2w π=. 故选:B. 2.C解析:C 【分析】先对函数()f x 进行化简,得到()3sin 26f x x π⎛⎫- ⎪⎝⎭,对于①运用三角函数图像平移进行判断;对于②计算出函数()f x 的对称中心进行判断;对于③计算出函数()f x 的单调增区间进行判断. 【详解】因为1()sin 2sin 2sin 22sin 232f x x x x x x π⎛⎫=-+=+ ⎪⎝⎭3sin 2222x x =-26x π⎛⎫=- ⎪⎝⎭对于①,将函数()2g x x =的图像向右平移6π个单位可得函数23y x π⎛⎫=- ⎪⎝⎭的图像,得不到()26f x x π⎛⎫=- ⎪⎝⎭,故①错误; 对于②,令()26x k k Z ππ-=∈,解得()122k x k Z ππ=+∈,故无论k 取何整数,函数()f x 的图像不会关于点5,012π⎛⎫⎪⎝⎭对称,故②错误; 对于③,当()222262k x k k Z πππππ-+≤-≤+∈,即()63k x k k Z ππππ-+≤≤+∈时函数()f x 递增,当0k =时,()f x 的一个递增区间为,63ππ⎡⎤-⎢⎥⎣⎦,故③正确.只有1个命题正确. 故选:C 【点睛】思路点睛:解答此类题目需要熟练掌握正弦型函数的单调性、对称性,以及三角函数的图像平移,在计算单调区间和对称中心时要能够通过整体代入计算求出结果,如()222262k x k k Z πππππ-+≤-≤+∈等.3.C解析:C 【分析】由,2,4PCA PDA PEA θθθ∠=∠=∠=,得PDE △是等腰三角形,且可求得230θ=︒,在直角PEA 中易得塔高PA . 【详解】由题知,2CPD PCD DPE PDE θθ∠=∠=∠=∠= ∴30PE DE PD CD ====∴等腰EPD △的230θ︒=,∴460θ︒= ∴Rt PAE 中,AE =15PA =.故选:C .4.C解析:C 【分析】根据余弦函数的对称轴可得π22π4x k +=,解方程即可求解. 【详解】π22π4x k +=,k Z ∈,则有ππ8x k =-+,k Z ∈ 当0k =时,πcos 24y x ⎛⎫=+ ⎪⎝⎭的一条对称轴方程为π8x =-. 故选:C5.C解析:C 【分析】 由题意知,当3x π=时,函数()f x 取得最大值,可求得362k ω=+,k ∈N .再由函数的单调区间得出不等式组,解之可得选项. 【详解】 由题意知,当3x π=时,函数()f x 取得最大值,所以232k ππωπ⋅=+,k Z ∈.得362k ω=+,k ∈N .因为()f x 在区间,123ππ⎛⎤-⎥⎝⎦上递增,在5,312ππ⎡⎫⎪⎢⎣⎭上递减,所以312πππω≥+且5123πππω≥-, 解得1205ω<≤.因此32ω=.故选:C.6.C解析:C 【分析】由条件利用诱导公式进行化简所给的式子,可得结果. 【详解】 ∵3sin()sin 5παα+==-,∴3sin 5α=-, 则sin()cos()sin (cos )3sin cos 5sin 2απααααπαα---⋅-===-⎛⎫- ⎪⎝⎭, 故选:C7.D解析:D 【分析】先化简()f x 并根据已知条件确定出ϕ的一个可取值,然后根据余弦函数的单调递减区间求解出()f x 的一个单调递减区间. 【详解】 因为()()()cos2cos sin 2sin cos2cos sin 2sin cos 2f x x x x x x ϕπϕϕϕϕ=⋅-+⋅=⋅+⋅=-,且()f x 在3x π=处有最小值,所以2cos 133f ππϕ⎛⎫⎛⎫=-=- ⎪⎪⎝⎭⎝⎭,所以22,3k k Z πϕππ-=+∈, 所以2,3k k Z πϕπ=--∈,取ϕ的一个值为3π-, 所以()cos 23f x x π⎛⎫=+ ⎪⎝⎭,令222,3k x k k Z ππππ≤+≤+∈,所以,63k x k k Z ππππ-≤≤+∈,令0k =,所以此时单调递减区间为,63ππ⎡⎤-⎢⎥⎣⎦, 故选:D. 【点睛】思路点睛:求解形如()()cos f x A x ωϕ=+的函数的单调递减区间的步骤如下: (1)先令[]2,2+,k k k x Z ωϕπππ+∈∈;(2)解上述不等式求解出x 的取值范围即为()f x 的单调递减区间.8.A解析:A 【分析】先求解出sin 3y x πω⎛⎫=+ ⎪⎝⎭右移6π个单位后的函数解析式,然后根据诱导公式求解出ω的可取值. 【详解】 因为sin 3y x πω⎛⎫=+⎪⎝⎭右移6π个单位后得到sin 63y x ωππω⎛⎫=-+ ⎪⎝⎭, 又因为sin 63y x ωππω⎛⎫=-+ ⎪⎝⎭与cos sin 2y x x πωω⎛⎫==+ ⎪⎝⎭的图象重合,所以令2,632k k Z ωππππ-+=+∈,所以121,k k Z ω=--∈,所以ω可取1-,此时0k =, 故选:A. 【点睛】思路点睛:根据三角函数的图象重合求解参数ω或ϕ的思路: (1)先根据诱导公式将函数名统一; (2)然后分析三角函数初相之间的关系;(3)对k 进行取值(有时注意结合所给范围),确定出满足条件的ω或ϕ的值.9.B解析:B 【分析】利用诱导公式cos160cos 20=-,再利用两角和的正弦公式即可求解. 【详解】sin 20cos10cos160sin10-()sin 20cos10cos 18020sin10=-- sin 20cos10cos 20sin10=+()sin 2010=+sin30=12=故选:B10.C解析:C 【分析】利用诱导公式先化简整理函数()f x ,再利用诱导公式求值即可. 【详解】 由sin()cos(2)()cos()tan x x f x x xπππ--=--,利用诱导公式得:sin cos ()cos cos tan x xf x x x x==--,所以31311cos cos 103332f ππππ⎛⎫⎛⎫⎛⎫-=--=---=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; 故选:C.11.A解析:A 【分析】由条件可得1cos 3α=-,然后可得sin α=,然后()sin tan tan cos ααπαα+==,即可算出答案.【详解】因为1sin cos 23παα⎛⎫+==- ⎪⎝⎭,,2παπ⎛⎫∈ ⎪⎝⎭,所以sin α=所以()sin tan tan cos ααπαα+===-故选:A12.B解析:B 【分析】根据cos89sin1︒=,将一个单位圆分成360个扇形,由这360个扇形的面积之和近似为单位圆的面积求解. 【详解】因为()cos89cos 901sin1︒=-=,所以将一个单位圆分成360个扇形,则每一个扇形的圆心角为1︒, 所以这360个扇形的面积之和近似为单位圆的面积,即2136011sin112π⨯⨯⨯⨯≈,所以 3.1416sin10.01745180180π≈≈≈, 故选:B二、填空题13.【分析】利用三角函数图象的平移和伸缩变换即可得正确答案【详解】函数的图象上各点的纵坐标不变横坐标伸长到原来的倍得到再向右平移个单位得到故最终所得到的函数解析式为:故答案为: 解析:()sin f x x =【分析】利用三角函数图象的平移和伸缩变换即可得正确答案. 【详解】 函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象上各点的纵坐标不变,横坐标伸长到原来的2倍, 得到sin 4y x π⎛⎫=+ ⎪⎝⎭, 再向右平移4π个单位,得到sin sin 44y x x ππ⎛⎫=-+= ⎪⎝⎭,故最终所得到的函数解析式为:()sin f x x =. 故答案为:()sin f x x =.14.【分析】根据诱导公式化为锐角后可求得结果【详解】故答案为:【分析】根据诱导公式化为锐角后可求得结果. 【详解】tan 2010tan(5360210)=⨯+tan 210=3tan(18030)tan 30=+==。
青海师范大学附属中学八年级数学上册第十二章《全等三角形》经典题

一、选择题1.如图,△ABC ≌△ADE ,AB =AD ,AC =AE ,∠B =28︒,∠E =95︒,∠EAB =20︒,则∠BAD 等于( )A .75︒B .57︒C .55︒D .77︒ 2.如图,OM 、ON 、OP 分别是AOB ∠,BOC ∠,AOC ∠的角平分线,则下列选项成立的( )A .AOP MON ∠>∠B .AOP MON ∠=∠C .AOP MON ∠<∠D .以上情况都有可能3.MAB ∠为锐角,AB a ,点C 在射线AM 上,点B 到射线AM 的距离为d ,BC x =,若△ABC 的形状、大小是唯一确定的,则x 的取值范围是( )A .x d =或x a ≥B .x a ≥C .x d =D .x d =或x a > 4.如图,在ABC 中,AD BC ⊥于D ,CE AB ⊥于E ,AD 与CE 交于点F .请你添加一个适当的条件,使AEF ≌CEB △.下列添加的条件不正确的是( )A .EF EB = B .EA EC = C .AF CB =D .AFE B ∠=∠ 5.如图,AB ⊥CD ,且AB =CD .E 、F 是AD 上两点,CE ⊥AD ,BF ⊥AD .若CE =a ,BF =b ,EF =c ,则AD 的长为( )A .a +cB .b +cC .a +b -cD .a -b +c6.如图,点O 在ABC 内,且到三边的距离相等.若110BOC ∠=°,则A ∠的度数为( )A .40︒B .45︒C .50︒D .55︒7.如图,123,,l l l 是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.A .1B .2C .3D .48.下列判断正确的个数是( )①三角形的三条高都在三角形的内部,并且相交于一点;②两边及一角对应相等的两个三角形全等;③两角及一边对应相等的两个三角形全等;④到三角形的三边所在的直线距离相等的点有三个;⑤两边及第三边上的高对应相等的两个三角形全等.A .4B .3C .2D .19.已知:如图,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA ,过E 作EF ⊥AB ,F 为垂足,下列结论:①△ABD ≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF 其中正确的是( )A .①②③B .①③④C .①②④D .①②③④ 10.如图,在Rt ABC 中,C 90∠=,AD 是BAC ∠的平分线,若AC 3=,BC 4=,则ABD ACD S :S 为( )A .5:4B .5:3C .4:3D .3:4 11.如图,AD 是△ABC 中∠BAC 的角平分线,DE ⊥AB 于点E ,S △ABC =7,DE =2,AB =4,则AC 长是( )A .2.5B .3C .3.5D .412.如图,在△ABC 中,点E 和F 分别是AC ,BC 上一点,EF ∥AB ,∠BCA 的平分线交AB 于点D ,∠MAC 是△ABC 的外角,若∠MAC =α,∠EFC =β,∠ADC =γ,则α、β、γ三者间的数量关系是( )A .β=α+γB .β=2γ﹣αC .β=α+2γD .β=2α﹣2γ 13.如图,AD 是ABC 的高,AD BD 8==,E 是AD 上的一点,BE AC 10==,AE 2=,BE 的延长线交AC 于点F ,则EF 的长为( )A .1.2B .1.5C .2.5D .314.如图,△ACB ≌△A 'CB ',∠BCB '=25°,则∠ACA '的度数为( )A .35°B .30°C .25°D .20°15.下列说法正确的是 ( )A .一直角边对应相等的两个直角三角形全等B .斜边相等的两个直角三角形全等C .斜边相等的两个等腰直角三角形全等D .一边长相等的两个等腰直角三角形全等二、填空题16.如图,D ,E 分别是AB ,AC 上的点,AD=AE ,请添加一个条件,使得ABE ≌ACD .这个条件可以为_____(只填一个条件即可).17.如图,点D 、E 分别在线段AB 、AC 上,BE 与CD 相交于点O .若AB AC =,AD AE =,60A ∠=︒,80ADC ∠=︒,则B 的度数为______.18.如图,ABC 中,D 是AB 上的一点,DF 交AC 于点E ,AE CE =,//CF AB ,若四边形DBCF 的面积是26cm ,则ABC 的面积为______2cm .19.如图,AB =4cm ,AC =BD =3cm ,∠CAB =∠DBA ,点P 在线段AB 上以1cm/s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动.设运动时间为t (s ),则当△ACP 与△BPQ 全等时,点Q 的运动速度为__cm/s .20.如图,在△ABC 中,∠C =90°,AD 是∠BAC 的角平分线,若BC =8cm ,BD =5cm ,AB=10cm,则S △ABD =______.21.如图,在Rt ABC △中,90C ∠=︒,10AC =,5BC =,线段PQ AB =,P ,Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AD 上运动,当AQ =______时,ABC 和PQA △全等.22.如图所示,ABC ≅△AB C '',20CAC ∠'=︒,BAB ∠'=___度.23.如图,ABC ADE ≅,延长BC ,分别交AD ,ED 于点F ,G ,若120EAB ∠=︒,30B ∠=︒,10CAD ∠=︒,则CFD ∠=________︒.24.在ABC 中,48ABC ︒∠=,点D 在BC 边上,且满足18,BAD DC AB ︒∠==,则CAD ∠=________度. 25.如图,在Rt △ABC 中,∠C =90°,D 、E 分别为边BC 、AB 上的点,且AE =AC ,DE ⊥AB .若∠ADC =61°,则∠B 的度数为_____.26.如图,已知AB AC =,D 为BAC ∠的角平分线上面一点,连接BD ,CD ;如图,已知AB AC =,D 、E 为BAC ∠的角平分线上面两点,连接BD ,CD ,BE ,CE ;如图,已知AB AC =,D 、E 、F 为BAC ∠的角平分线上面三点,连接BD ,CD ,BE ,CE ,BF ,CF ;…,依此规律,第n 个图形中有全等三角形的对数是______.三、解答题27.如图,在ABC 和BCD △中,90BAC BCD ︒∠=∠=,AB AC =,CB CD =;延长CA 至点E ,使AE AC =;延长CB 至点F ,使BF BC =.连接AD ,AF ,DF ,EF .延长DB 交EF 于点N .(1)求证:AD AF =;(2)求证:BD EF =.28.如图,点E ,F 在BC 上,A D ∠=∠,AF DE =,AFC DEB ∠=∠.求证:BE CF =.29.已知4,BC BA BC =⊥,射线CM BC ⊥,动点P 在BC 上,PD PA ⊥交CM 于D .(1)如图1,当3,1BP AB ==时,求DC 的长;(2)如图2,连接AD ,当DP 平分ADC ∠时,求BP 的长.30.沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由C 走到D 的过程中,通过隔离带的空隙P ,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图,AB//PM //CD ,相邻两平行线间的距离相等AC ,BD 相交于P ,PD CD ⊥垂足为D .已知16CD =米.请根据上述信息求标语AB 的长度.。
青海师范大学附属中学二年级数学上册第三单元《角的初步认识》单元测试(包含答案解析)

青海师范大学附属中学二年级数学上册第三单元《角的初步认识》单元测试(包含答案解析)一、选择题1.左图中有()个直角。
A. 1B. 2C. 32.钟面上9时30分,时针与分针所夹较小的角是()。
A. 锐角B. 直角C. 钝角D. 平角3.钟面上5时整,时针与分针形成的角是()A. 钝角B. 直角C. 平角4.钟面上9时整,时针和分针组成的角是()A. 锐角B. 钝角C. 直角5.把平角分成两个角,其中一个是锐角,另一个角是()。
A. 锐角B. 直角C. 钝角6.下图中有( )个锐角。
A. 3B. 4C. 67.两张相同的长方形纸组成下图,已知∠1=60°,则∠2=()A. 30°B. 60°C. 无法确定8.下边的图形有()个角。
A. 1B. 2C. 39.两条直线相交,如果其中一个是直角,那么其他三个是()角。
A. 锐角B. 直角C. 钝角10.三角尺中没有()。
A. 锐角B. 直角C. 钝角11.一张长方形纸片,剪掉一个角,还剩()个角。
A. 3个B. 5个C. 3个,4个或5个12.下面的角中,()比直角大。
A. B. C.二、填空题13.三角板上最大的角是________角,其余的2个角都是________角。
14.3时整,时针与分针所成的角是________角;10时整,时针和分针所成的锐角是________度.15.直角的一半是________度,至少再增加________度就是一个钝角。
(填整数)16.下图中,________是锐角,________是钝角。
A. B. C.17.4时整,钟面上时针与分针所成的角是________角,是________度。
18.在45°、130°、90°、15°、140°这些角中,是锐角的有________,是直角的有________,是钝角的有________。
19.下图中是锐角的是________,是钝角的是________。
青海师范大学附属中学八年级数学上册第十一章【三角形】测试(培优提高)

一、选择题1.随着人们物质生活的提高,玩手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的哪一个性质( )A .三角形两边之和大于第三边B .三角形具有稳定性C .三角形的内角和是180D .直角三角形两个锐角互余2.如图,下列结论中正确的是( )A .12A ∠>∠>∠B .12A ∠>∠>∠C .21A ∠>∠>∠D .21A ∠>∠>∠ 3.如图,在△ABC 中,∠ACB=90°,D 在AB 上,将△ABC 沿CD 折叠,点B 落在AC 边上的点B′处,若'20ADB ∠=︒,则∠A 的度数为( )A .25°B .30°C .35°D .40°4.下列命题中,是假命题的是( )A .直角三角形的两个锐角互余B .在同一个平面内,垂直于同一条直线的两条直线平行C .同旁内角互补,两直线平行D .三角形的一个外角大于任何一个内角 5.下列四组线段中,不可以构成三角形的是( )A .4,5,6B .1.5,2,2.5C .13,14,15D .12,36.已知长度分别为3cm ,4cm ,xcm 的三根小棒可以摆成一个三角形,则x 的值不可能是( )A .2.4B .3C .5D .8.57.已知,D 是ABC ∠的边BC 上一点,//DE BA ,CBE ∠和CDE ∠的平分线交于点F ,若F α∠=,则ABE ∠的大小为( )A .αB .52αC .2αD .32α 8.在ABC 中,若一个内角等于另两个内角的差,则( )A .必有一个内角等于30°B .必有一个内角等于45°C .必有一个内角等于60°D .必有一个内角等于90°9.如图,为估计池塘岸边A 、B 的距离,小方在池塘的一侧选取一点O ,测得OA =15米,OB=10米,A 、B 间的距离不可能是( )A .20米B .15米C .10米D .5米10.下列说法正确的有( )个①把一个角分成两个角的射线叫做这个角的角平分线;②连接C 、D 两点的线段叫两点之间的距离;③两点之间直线最短;④射线上点的个数是直线上点的个数的一半;⑤n 边形从其中一个顶点出发连接其余各顶点,可以画出()3n -条对角线,这些对角线把这个n 边形分成了()2n -个三角形.A .3B .2C .1D .011.设四边形的内角和等于a ,五边形的外角和等于b ,则a 与b 的关系是( ). A .a b = B .180a b =+° C .180b a =+︒ D .360b a =+︒二、填空题12.从n 边形的一个顶点出发,连接其余各顶点,可以将这个n 边形分割成17个三角形,则n =______.13.2016年2月6日凌晨,宝岛高雄发生6.7级地震,得知消息后,中国派出武警部队探测队,探测队探测出某建筑物下面有生命迹象,他们在生命迹象上方建筑物的一侧地面上的,A B 两处,用仪器探测生命迹象C ,已知探测线与地面的夹角分别是30︒和60︒(如图),则C ∠的度数是_________.14.若等腰三角形两边的长分别为3cm 和6cm ,则此三角形的周长是______________cm . 15.如图所示,在ABC 中,80A ∠=︒,延长BC 到D ,ABC ∠与ACD ∠的平分线相交于1A 点,1A BC ∠与1A CD ∠的平分线相交于A 点,依此类推,4A BC ∠与4A CD ∠的平分线相交于5A 点,则5A ∠的度数是_________.16.如图,在ABC 中,点,,D E F 分别在三边上,点E 是AC 的中点,,,AD BE CF 交于一点,283BGD AGE G BD DC S S ===,,,则ABC 的面积是________.17.已知等腰三角形的一边长等于11cm ,一边长等于5cm ,它的周长为______. 18.如图中,36B ∠=︒,76C ∠=︒,AD 、AF 分别是ABC 的角平分线和高,DAF ∠=________.19.一副分别含有30°和45°的直角三角板,拼成如图,则BFD ∠的度数是______.20.如图,AB BE ,分别是ABC 中,BC AC 边上的高,6cm BC ,4cm AC =,若3cm =AD ,则BE 的长为__________cm .21.如图,ABC 的角平分线OB 、OC 相交于点O ,40A ∠︒=,则BOC ∠=______.三、解答题22.△ABC 中,AD 是∠BAC 的角平分线,AE 是△ABC 的高.(1)如图1,若∠B =40°,∠C=60°,求∠DAE 的度数;(2)如图2,∠B <∠C ,则DAE 、∠B ,∠C 之间的数量关系为___________;(3)如图3,延长AC 到点F ,∠CAE 和∠BCF 的角平分线交于点G ,求∠G 的度数.23.如图,是A 、B 、C 三个村庄的平面图,已知B 村在A 村的南偏西65°方向,C 村在A 村的南偏东15°方向,C 村在B 村的北偏东85°方向,求从C 村观测A 、B 两村的视角ACB ∠的度数.24.已知在四边形ABCD 中,90A C ∠=∠=︒.(1)如图1,若BE 平分ABC ∠,DF 平分ADC ∠的邻补角,请写出BE 与DF 的位置关系并证明;(2)如图2,若BF 、DE 分别平分ABC ∠、ADC ∠的邻补角,判断DE 与BF 位置关系并证明;(3)如图3,若BE 、DE 分别五等分ABC ∠、ADC ∠的邻补角(即11,55CDE CDN CBE CBM ∠=∠∠=∠),求E ∠度数.25.观察探究及应用.(1)如图,观察图形并填空:一个四边形有_______条对角线;一个五边形有_______条对角线;一个六边形有_______条对角线;(2)分析探究:由凸n 边形的一个顶点出发,可作_______条对角线,多边形有n 个顶点,若允许重复计数,共可作_______条对角线;(3)结论:一个凸n边形有_______条对角线;(4)应用:一个凸十二边形有多少条对角线?一、选择题1.小李同学将10,12,16,22cm cm cm cm 的四根木棒首尾相接,组成一个凸四边形,若凸四边形对角线长为整数,则对角线最长为( )A .25cmB .27cmC .28cmD .31cm2.如图,AD 是ABC 的外角CAE ∠的平分线,35B ∠=︒,60=︒∠DAC ,则ACD ∠的度数为( )A .25︒B .85︒C .60︒D .95︒3.三角形的两条边长为3和7,那么第三边长可能是( )A .1B .4C .7D .104.如图,在ABC 中,AD 是角平分线,AE 是高,已知2BAC B ∠=∠,2B DAE ∠=∠,那么C ∠的度数为( )A .72°B .75°C .70°D .60°5.将一个直角三角板和一把直尺如图放置,如果∠α=47°,则∠β的度数是( )A .43°B .47°C .30°D .60°6.正十边形每个外角等于( )A .36°B .72°C .108°D .150°7.如图,已知,,90,//AD BC FG BC BAC DE AC ⊥⊥∠=︒.则结论①//FG AD ;②DE 平分ADB ;③B ADE ∠=∠;④CFG BDE ∠+∠90=︒.正确的是( )A .①②③B .①②④C .①③④D .②③④ 8.如图,在五边形ABCDE 中,AB ∥CD ,∠A =135°,∠C =60°,∠D =150°,则∠E 的大小为( )A .60°B .65°C .70°D .75°9.如图,已知AE 交CD 于点O ,AB ∥CD ,∠A =50°,∠E =15°,则∠C 的度数为( )A .50°B .65°C .35°D .15°10.以下列各组线段为边,能组成三角形的是( )A .1,2,3B .2,3,4C .2,5,8D .6,3,3 11.如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是( )A .两点之间线段最短B .长方形的对称性C .长方形四个角都是直角D .三角形的稳定性二、填空题12.如图,已知//,AB CD E 是直线AB 上方一点,G 为直线AB 下方一点,F 为直线CD 上一点,148EAF ︒∠=,3BAF BAG ∠=∠,3DCE DCG ∠=∠,则E ∠和G ∠的数量关系为___________.13.一个三角形的三条高的长都是整数,若其中两条高的长分别为4和12,则第三条高的长为_____.14.如图,∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H 的度数为___________.15.一个三角形的两边长分别是3和7,且第三边长为奇数,这样的三角形的周长最大值是___________,最小值是___________.16.一副直角,三角板有一个角的顶点如图所示重合,则下列说法中正确的有_________.①如图 1,若 AB ⊥AE ,则∠BFC=75°;②图 2 中 BD 过点C ,则有∠DAE+∠DCE=45°;③图 3中∠DAE+∠DFC 等于 135°;④保持重合的顶点不变,改变三角板BAD 的摆放位置,使得D 在边AC 上,则∠BAE=105°. 17.如图,已知AE 是ABC 的边BC 上的中线,若8AB cm =,ACE △的周长比AEB △的周长多2cm ,则AC =______cm .18.如图,已知∠A =47°,∠B =38°,∠C =25°,则∠BDC 的度数是______.19.如图,∠BAK +∠B +∠C +∠CDE +∠E +∠F +∠MGN +∠H +∠K =________.20.如图,把正三角形、正四边形、正五边形按如图所示的位置摆放,若150,222∠=︒∠=︒,则3∠=_______.21.如图,线段AD ,BE ,CF 两两相交于点H ,I ,G ,分别连接AB ,CD ,EF .则A B C D E F ∠+∠+∠+∠+∠+∠=____.三、解答题22.在锐角三角形ABC 中,∠C=2∠B ,求∠B 的取值范围23.在ABC ∆中, ,AB AC CG BA =⊥交BA 的延长线于点G ,点D 是线段BC 上的一个动点.特例研究:()1当点D 与点B 重合时,过B 作BF AC ⊥交AC 的延长线于点F ,如图①所示,通过观察﹑测量BF 与CG 的长度,得到BF CC =.请给予证明.猜想证明:()2当点D 由点B 向点C 移动到如图②所示的位置时,过D 作DF AC ⊥交CA 的延长线于点F ,过D 作DE BA ⊥交BA 于点E ,此时请你通过观察,测量DE DF 、与CG 的长度,猜想并写出DE DF 、与CG 之间存在的数量关系,并证明你的猜想.拓展延伸:()3当点D由点B向点C继续移动时(不与C重合),过D作DF AC⊥交AC于点F,⊥交BA(或BA的延长线)于点E,如图③,图④所示,请你判断(2)过D作DF BA中的猜想是否仍然成立?(不用证明)24.如果正多边形的每个内角都比它相邻的外角的4倍多30°.(1)它是几边形?(2)这个正多边形的内角和是多少度?(3)求这个正多边形对角线的条数.25.(1)一个多边形的内角和等于1800度,求这个多边形的边数.(2)一个多边形的每一个内角都是108°,求这个多边形的边数.一、选择题1.如图,//,40,50,AB CD B C ∠=︒∠=︒则E ∠的度数为( )A .70︒B .80︒C .90︒D .100︒2.若一个三角形的三边长分别为3,7,x ,则x 的值可能是( )A .6B .3C .2D .113.若一个正多边形的内角和等于其外角和的3倍,则这个正多边形是( )A .5边形B .6边形C .7边形D .8边形4.如图,ABC 中,BC 边上的高是( )A .AEB .ADC .CD D .CF5.如图,在ABC 中,55A ∠=︒,65C =︒∠,BD 平分ABC ∠,//DE BC ,则BDE ∠的度数是( )A .50°B .25°C .30°D .35°6.如果一个三角形的三边长分别为5,8,a .那么a 的值可能是( )A .2B .9C .13D .157.以下列各组线段为边,能组成三角形的是( )A .1,2,3B .1,3,5C .2,3,4D .2,6,10 8.如图,△ABC 中AC 边上的高是哪条垂线段.( )A .AEB .CDC .BFD .AF9.如图,直线//BC AE ,CD AB ⊥于点D ,若150∠=︒,则BCD ∠的度数是( )A .60°B .50°C .40°D .30°10.现有两根木棒,长度分别为5cm 和13cm ,若不改变木棒的长度,要钉成一个三角形木架,则应在下列四根木棒中选取( )A .20cm 的木棒B .18cm 的木棒C .12cm 的木棒D .8cm 的木棒 11.如图,已知AE 交CD 于点O ,AB ∥CD ,∠A =50°,∠E =15°,则∠C 的度数为( )A .50°B .65°C .35°D .15°二、填空题12.如图1,△ABC 中,有一块直角三角板PMN 放置在△ABC 上(P 点在△ABC 内),使三角板PMN 的两条直角边PM 、PN 恰好分别经过点B 和点C .若∠A =52°,则∠1+∠2=__________;13.若等腰三角形两边的长分别为3cm 和6cm ,则此三角形的周长是______________cm .14.多边形每一个内角都等于108°,多边形一个顶点可引的对角线的条数是________条. 15.如图,ACD ∠是ABC 的外角,ABC ∠的平分线与ACD ∠的平分线交于点1A ,1A BC ∠的平分线与1A CD ∠的平分线交于点2A ,…,1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A ,设=A θ∠,则2=A ∠___________,=n A ∠___________.16.如图,将长方形纸片的一角折叠,使顶点A 落在F 处,折痕为BC ,FBD ∠的角平分线为BE ,将FBD ∠沿BF 折叠使BE ,BD 均落在FBC ∠的内部,且BE 交CF 于点M ,BD 交CF 于点N ,若BN 平分CBM ∠,则ABC ∠的度数为_________.17.如图,AD 、AE 分别是ABC 的高和角平分线,且76B ∠=︒,36C ∠=︒,则DAE ∠的度数为_________.18.如图,∠BAK +∠B +∠C +∠CDE +∠E +∠F +∠MGN +∠H +∠K =________.19.如图,ABC 面积为1,第一次操作:分别延长,,AB BC CA 至点111,,A B C 使111,,A B AB B C BC C A CA ===顺次结111,,A B C ,得到111A B C △,第二次操作:分别延长111111,,A B B C C A 至点222A B C ,使211121112111,,A B A B B C B C C A C A ===,顺次连结222,,A B C ,得到222A B C △…,按此规律,则333A B C △的面积为_______.20.如图,若//AB CD ,BF 平分ABE ∠,DF 平分CDE ∠,90BED ∠=,则BFD ∠=______.21.如图,在ABC 中,E 、D 、F 分别是AD 、BF 、CE 的中点,若DEF 的面积是1,则ABC S =______.三、解答题22.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若∠1与∠2都是锐角,请写出∠C 与∠1,∠2之间的数量关系并说明理由. (2)把Rt △ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有∠BDF =∠GDF ,求AEN CDG∠∠的值.(3)如图3,若点D 是MN 下方一点,BC 平分∠PBD ,AM 平分∠CAD ,已知∠PBC =25°,求∠ACB +∠ADB 的度数.23.如图,△ABC 中,∠ABC 的角平分线与外角∠ACD 的平分线交于A 1.(1)∵BA 1、CA 1是∠ABC 与∠ACD 的平分线,∴∠A 1BD =12∠ABD ,∠A 1CD =12∠ACD , ∴∠A 1CD ﹣∠A 1BD =12(∠ACD ﹣∠ABD ), ∵∠A 1CD ﹣∠A 1BD = ,∠ACD ﹣∠ABD =∠ ,∴∠A 1= .(2)如图2,四边形ABCD 中,∠F 为∠ABC 的角平分线及外角∠DCE 的平分线所在的直线构成的角,若∠A +∠D =230°,求∠F 的度数.(3)如图3,△ABC 中,∠ABC 的角平分线与外角∠ACD 的平分线交于A 1,若E 为BA 延长线上一动点,连接EC ,∠AEC 与∠ACE 的角平分线交于Q ,当E 滑动时有下面两个结论: ①∠Q +∠A 1的值为定值;②∠Q ﹣∠A 1的值为定值,其中有且只有一个是正确的,请写出正确的结论,并求出其值.24.如图1,已知ACD ∠是ABC 的一个外角,我们容易证明ACD A B ∠=∠+∠,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?尝试探究:(1)如图2,DBC ∠与ECB ∠分别为ABC 的两个外角,则DBC ECB ∠+∠_______180A ∠+︒(横线上填“>”、“<”或“=”). 初步应用:(2)如图3,在ABC 纸片中剪去CED ,得到四边形ABDE ,1135∠=︒,则2C ∠-∠=_______.(3)解决问题:如图4,在ABC 中,BP 、CP 分别平分外角DBC ∠、ECB ∠,P ∠与A ∠有何数量关系?请尝试证明.(4)如图5,在四边形ABCD 中,BP 、CP 分别平分外角EBC ∠、FCB ∠,请利用上面的结论直接写出P ∠与A ∠、D ∠的数量关系.25.一个多边形的每个外角都等于40°,求这个多边形的内角和.。
青海师范大学附属中学小学数学六年级上册第四单元经典题

一、选择题1.一个三角形的三个内角度数的比是1:1:2,这是一个( )三角形。
A. 直角 B. 钝角 C. 锐角 D. 等边三角形A 解析: A【解析】【解答】解:180°×21+1+2=90°,这是一个直角三角形。
故答案为:A 。
【分析】三角形最大角的度数占三角形内角和的21+1+2, 根据分数乘法的意义先计算出最大角的度数,然后确定三角形的类型即可。
2.苹果和雪梨的质量比是3:2,如果苹果有180kg ,那么雪梨有( )kg . A. 72 B. 108 C. 120 D. 270C 解析: C【解析】【解答】解:180÷3×2=120(千克),所以雪梨有120千克。
故答案为:C 。
【分析】雪梨的质量=苹果的质量÷苹果占的份数×雪梨占的份数,据此代入数据作答即可。
3.一项工程,甲独做12小时完成,乙独做8小时完成.甲乙的工作效率最简整数比是( )。
A. 12:8B. 112: 18 C. 3:2 D. 2:3D解析: D【解析】【解答】解:112:18=2:3,所以甲乙的工作效率最简整数比是2:3。
故答案为:D 。
【分析】甲的工作效率=1÷甲单独做需要的时间,乙的工作效率=1÷乙单独做需要的时间,然后作比即可。
4.某工厂甲车间人数是乙车间人数的5倍,甲车间男工人数是女工人数的 32 倍,乙车间男工人数是女工人数的 34,全长工人中男工人数和女工人数的比是( )。
A. 3:4B. 7:9C. 4:3C 解析: C【解析】【解答】设乙车间的人数为x ,则甲车间的人数为5x , 甲车间男工人数=5x×33+2=3x ,甲车间女工人数=5x×23+2=2x ;乙车间男工人数=x×33+4=37x ,乙车间女工人数=x×43+4=47x ;(3x+37x ):(2x+47x )=247:187=4:3。
青海师范大学附属中学八年级数学上册第十二章【全等三角形】测试(培优提高)

一、选择题1.如图,△ABC ≌△ADE ,AB =AD ,AC =AE ,∠B =28︒,∠E =95︒,∠EAB =20︒,则∠BAD 等于( )A .75︒B .57︒C .55︒D .77︒2.如图,在ABC 中,8AB AC ==厘米,6BC =厘米,点D 为AB 的中点.如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上,由C 点向A 点运动,为了使BPD CPQ △≌△,点Q 的运动速度应为( )A .1厘米/秒B .2厘米/秒C .3厘米/秒D .4厘米/秒 3.如图,已知ABC DCB ∠=∠,添加一个条件使ABC DCB △△≌,下列添加的条件不能使ABC DCB △△≌的是( )A .A D ∠=∠B .AB DC = C .AC DB =D .ACB DBC ∠=∠ 4.如图,在ABC 中,AD BC ⊥于D ,CE AB ⊥于E ,AD 与CE 交于点F .请你添加一个适当的条件,使AEF ≌CEB △.下列添加的条件不正确的是( )A .EF EB = B .EA EC = C .AF CB =D .AFE B ∠=∠ 5.如图,AD 平分BAC ∠交BC 于点D ,DE AB ⊥于点E ,DF AC ⊥于点F ,若ABC S 12=,DF 2=,AC 3=,则AB 的长是 ( )A .2B .4C .7D .96.下列说法不正确的是( )A .三边分别相等的两个三角形全等B .有两边及一角对应相等的两个三角形全等C .有两角及一边对应相等的两个三角形全等D .斜边和一条直角边分别相等的两个直角三角形全等7.如图,在Rt ABC △中,90C ∠=︒,CAB ∠的平分线交BC 于点D ,且DE 所在直线是AB 的垂直平分线,垂足为E .若3DE =,则BC 的长为( ).A .6B .7C .8D .98.如图,OB 平分∠MON ,A 为OB 的中点,AE ⊥ON ,EA=3,D 为OM 上的一个动点,C 是DA 延长线与BC 的交点,BC //OM ,则CD 的最小值是( )A .6B .8C .10D .129.如图,AC 与DB 相交于E ,且BE CE =,如果添加一个条件还不能判定ABE △≌DCE ,则添加的这个条件是( ).A .AC DB = B .A D ∠=∠C .B C ∠=∠D .AB DC = 10.如图,AD 是ABC 的高,AD BD 8==,E 是AD 上的一点,BE AC 10==,AE 2=,BE 的延长线交AC 于点F ,则EF 的长为( )A .1.2B .1.5C .2.5D .311.如图,要判定△ABD ≌△ACD ,已知AB =AC ,若再增加下列条件中的一个,仍不能说明全等,则这个条件是( )A .CD ⊥AD ,BD ⊥ADB .CD =BDC .∠1=∠2D .∠CAD =∠B AD二、填空题12.如图,已知在ABC ∆和ADC ∆中,,ACB ACD ∠=∠请你添加一个条件:_________,使ABC ADC ∆≅∆(只添一个即可).13.如图,在Rt ABC △中,90B ∠=︒,12AB =,5BC =,射线AP AB ⊥于点A ,点E 、D 分别在线段AB 和射线AP 上运动,并始终保持DE AC =,要使ABC 和DAE △全等,则AE 的长为______.14.如图所示,在ABC 中,D 是BC 的中点,点A 、F 、D 、E 在同一直线上.请添加一个条件,使BDE CDF ≌(不再添其他线段,不再标注或使用其他字母),并给出证明.你添加的条件是______15.如图,△ABC ≌△DEF ,由图中提供的信息,可得∠D =__________°.16.如图,AC AE =,AD AB =,90ACB DAB ∠=∠=︒,33BAE ∠=︒,//CB AE ,AC 与DE 相交于点F .(1)DAC ∠=______.(2)当1AF =时,BC 的长为______.17.如图,BD 平分ABC ∠交AC 于点D ,DE BC ⊥于点E ,若2DE =,7BC =,12ABC S =△,则AB 的长为______.18.如图,在Rt ABC △中,90C ∠=︒,以顶点A 为圆心,任意长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交BC 于点D .若3CD =,10AB =,则ABD △的面积是______.19.如图,四边形ABDC 中,对角线AD 平分BAC ∠,136ACD ∠=︒,44BCD ∠=︒,则ADB ∠的度数为_____20.如图,点D ,E 分别在线段AB ,AC 上,CD 与BE 相交于点P ,已知AD =AE .若△ABE ≌△ACD ,则可添加的条件为_____.21.如图,ABC 中,90C ∠=,AD 平分BAC ∠,若2DC =,则点D 到线段AB 的距离等于________.三、解答题22.在ABC 中,AD 是ABC 的高,30B,52C ︒∠=(1)尺规作图:作ABC 的角平分线AE(2)求DAE ∠的大小.23.如图,在△ABD 中,∠ABD =90°,AB=BD ,点E 在线段BD 上,延长AB 使BC=BE ,连接AE 、CE 、CD ,点M 在线段AE 上,点N 在线段CD 上,BM ⊥BN ,易证△ABE ≌△DBC ;仔细观察,请逐一找出图中其他的全等三角形,并说明理由.24.如图,点D ,E 分别在AB 和AC 上,DE//BC ,点F 是AD 上一点,FE 的延长线交BC 延长线BH 于点G .(1)若∠DBE =40°,∠EBC =35°,求∠BDE 的度数;(2)求证:∠EGH >∠ADE ;(3)若点E 是AC 和FG 的中点,△AFE 与△CEG 全等吗?请说明理由.25.如图,在平面直角坐标系中,已知点()1,A a a b -+,(),0B a ,且()2320a b a b +-+-=,C 为x 轴上点B 右侧的动点,以AC 为腰作等腰三角形ACD ,使AD AC =,CAD OAB ∠=∠,直线DB 交y 轴于点P .(1)求证:AO AB =;(2)求证:AOC ABD ∆∆≌;(3)当点C 运动时,点P 在y 轴上的位置是否发生改变,为什么?一、选择题1.如图,AB ∥CD ,BE 和CE 分别平分∠ABC 和∠BCD ,AD 过点E ,且AD ⊥AB ,点P 为线段BC 上一动点,连接PE .若AD =14,则PE 的最小值为( )A .7B .10C .6D .52.MAB ∠为锐角,AB a ,点C 在射线AM 上,点B 到射线AM 的距离为d ,BC x =,若△ABC 的形状、大小是唯一确定的,则x 的取值范围是( )A .x d =或x a ≥B .x a ≥C .x d =D .x d =或x a > 3.如图,在△ABC 中,∠B =∠C =50°,BD =CF ,BE =CD ,则∠EDF 的度数是( )A .40°B .50°C .60°D .30°4.如图,BD 是四边形ABCD 的对角线, AD//BC ,AB AD <,分别过点A ,C 作AE BD ⊥,CF BD ⊥,垂足分别为点E ,F ,若BE DF =,则图中全等的三角形有( )A .1对B .2对C .3对D .4对5.下列说法正确的是( )①近似数232.610⨯精确到十分位;②在2,()2--,38-,2--中,最小的是38-;③如图所示,在数轴上点P 所表示的数为15-+;④用反证法证明命题“一个三角形最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”;⑤如图,在ABC 内一点P 到这三条边的距离相等,则点P 是三个角平分线的交点.A .1B .2C .3D .46.如图所示的正方形ABCD 中,点E 在边CD 上,把ADE 绕点A 顺时针旋转得到ABF ,20FAB ∠=︒.旋转角的度数是( )A .110°B .90°C .70°D .20°7.如图,∠ACB=90°,AC=BC ,AD ⊥CE ,BE ⊥CE ,垂足分别是点D 、E ,AD=3,BE=1,则DE 的长是( )A .1.5B .2C .22D 10 8.下列命题中,假命题是( )A .在同一平面内,垂直于同一条直线的两直线平行B .到线段两端点距离相等的点在这条线段的垂直平分线上C .一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等D .一边长相等的两个等腰直角三角形全等9.如图,已知△ABC 的周长是20,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于,且OD=2,△ABC 的面积是( )A .20B .24C .32D .4010.已知:如图,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA ,过E 作EF ⊥AB ,F 为垂足,下列结论:①△ABD ≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF 其中正确的是( )A .①②③B .①③④C .①②④D .①②③④ 11.已知,如图,OC 是∠AOB 内部的一条射线,P 是射线OC 上任意点,PD ⊥OA ,PE ⊥OB ,下列条件中:①∠AOC =∠BOC ,②PD =PE ,③OD =OE ,④∠DPO =∠EPO ,能判定OC 是∠AOB 的角平分线的有( )A .1个B .2个C .3个D .4个二、填空题12.如图,ABC 中,D 是AB 上的一点,DF 交AC 于点E ,AE CE ,//CF AB ,若四边形DBCF 的面积是26cm ,则ABC 的面积为______2cm .13.如图,已知//AD BC ,点E 为CD 上一点,AE ,BE 分别平分DAB ∠,CBA ∠.若3cm AE =,4cm BE =,则四边形ABCD 的面积是________.14.如图(1),已知AB AC =,D 为BAC ∠的角平分线上一点,连接BD ,CD ;如图(2),已知AB AC =,D ,E 为BAC ∠的角平分线上两点,连接BD ,CD ,BE ,CE ;如图(3),已知AB AC =,D ,E ,F 为BAC ∠的角平分线上三点,连接BD ,CD ,BE ,CE ,BF ,CF ;……,依此规律,第7个图形中有全等三角形的对数是________.15.如图,在ABC 中,C 90∠=,A ∠、B ∠的平分线交于O ,OD AB ⊥于D .若AC 3=,BC 4=,AB 5=,则AD =________.16.小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第____块去,这利用了三角形全等中的____原理.17.如图,在Rt ABC 中,90C ∠=︒,AD AC =,DE AB ⊥,交BC 于点E .若26B ∠=︒,则AEC ∠=______︒.18.已知△ABC ≌△DEF ,△ABC 的三边分别为3,m ,n ,△DEF 的三边分别为5,p ,q .若△ABC 的三边均为整数,则m+n+p+q 的最大值为________.19.如图,△ABC 的外角∠MBC 和∠NCB 的平分线BP 、CP 相交于点P ,PE ⊥BC 于E 且PE =3cm ,若△ABC 的周长为14cm ,S △BPC =7.5,则△ABC 的面积为______cm 2.20.如图,在ABC 中,60BAC ∠=︒,BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ,DE AB ⊥交AB 的延长线于点E ,DF AC ⊥于点F ,现有下列结论:①120EDF ∠=︒;②DM 平分EDF ∠;③DE DF AD +=;④2AB AC AE +>;其中正确的有________(请将正确结论的序号填写在横线上).21.如图,在△ABC 中,∠C =90°,∠A 的平分线交BC 于D ,若20ABD S ∆=cm 2,AB =10cm ,则CD 为__________cm .三、解答题22.作图题:已知∠α,线段m 、n ,请按下列步骤完成作图(不需要写作法,保留作图痕迹)(1)作∠MON =∠α(2)在边OM 上截取OA =m ,在边ON 上截取OB =n .(3)作直线AB .23.如图,已知点D ,E 分别在等边三角形ABC 的边BC ,CA 上,且BD CE =,连接AD ,BE 相交于点F ,AH BE ⊥于点H ,求FAH ∠的度数.24.已知ABC 是等腰直角三角形,90ACB ∠=︒,BC AC =.直角顶点C 在x 轴上,锐角顶点B 在y 轴上,过点A 作AD x ⊥轴,垂足为点D .当点B 不动,点C 在x 轴上滑动的过程中.(1)如图1,当点C 的坐标是()1,0-,点A 的坐标是()3,1-时,请求出点B 的坐标; (2)如图2,当点C 的坐标是()1,0时,请写出点A 的坐标;(3)如图3,过点A 作直线AE y ⊥轴,交y 轴于点E ,交BC 延长线于点F .AC 与y 轴交于点G .当y 轴恰好平分ABC ∠时,请写出AE 与BG 的数量关系.25.如图,在△ABC 中,90ACB ∠=︒,AC =BC ,BE ⊥CE 于E ,AD ⊥CE 于D .(1)求证:AD =CE(2)AD =6cm ,DE =4cm ,求BE 的长度一、选择题1.如图,在ABC 中,8AB AC ==厘米,6BC =厘米,点D 为AB 的中点.如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上,由C 点向A 点运动,为了使BPD CPQ △≌△,点Q 的运动速度应为( )A .1厘米/秒B .2厘米/秒C .3厘米/秒D .4厘米/秒 2.芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁,2020年9月29日公路段投入运营,其侧面示意图如图所示,其中AB CD ⊥,现添加以下条件,不能判定ABC ABD △≌△的是( )A .ACB ADB ∠=∠B .AB BD =C .AC AD = D .CAB DAB ∠=∠3.如图,在ABC 和DEF 中,,B DEF AB DE ∠=∠=,添加下列一个条件后,仍然不能证明ABC DEF ≌,这个条件是( )A .A D ∠=∠B .BC EF = C .ACB F ∠=∠D .AC DF = 4.如图,ABC 和DEF 中,∠A=∠D ,∠C=∠F ,要使ABC DEF ≅,还需增加的条件是( )A .AB=EFB .AC=DFC .∠B=∠ED .CB=DE5.如图,∠ACB=90°,AC=BC ,AD ⊥CE ,BE ⊥CE ,垂足分别是点D 、E ,AD=3,BE=1,则DE 的长是( )A .1.5B .2C .22D 10 6.点Р在AOB ∠的角平分线上,点Р到OA 边的距离等于5,点Q 是OB 边上的任意一点,则下列选项正确的是( )A .5PQ >B .5PO ≥C . 5PQ <D .5PO ≤ 7.对于ABC 与DEF ,已知∠A=∠D ,∠B=∠E ,则下列条件:①AB=DE ;②AC=DF ;③BC=DF ;④AB=EF 中,能判定它们全等的有( )A .①②B .①③C .②③D .③④8.如图所示,已知∠A =∠C ,∠AFD =∠CEB ,那么给出的条件不能得到ADF CBE △≌△是( )A .∠B =∠D B .EB=DFC .AD=BCD .AE=CF9.如图,OB 平分∠MON ,A 为OB 的中点,AE ⊥ON ,EA=3,D 为OM 上的一个动点,C 是DA 延长线与BC 的交点,BC //OM ,则CD 的最小值是( )A .6B .8C .10D .1210.下列命题,真命题是( )A .全等三角形的面积相等B .面积相等的两个三角形全等C .两个角对应相等的两个三角形全等D .两边和其中一边的对角对应相等的两个三角形全等11.如图,已知AE 平分∠BAC ,BE ⊥AE 于E ,ED ∥AC ,∠BAE =34°,那么∠BED =( )A .134°B .124°C .114°D .104°二、填空题12.如图,已知//AD BC ,点E 为CD 上一点,AE ,BE 分别平分DAB ∠,CBA ∠.若3cm AE =,4cm BE =,则四边形ABCD 的面积是________.13.如图,AB =4cm ,AC =BD =3cm ,∠CAB =∠DBA ,点P 在线段AB 上以1cm/s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动.设运动时间为t (s ),则当△ACP 与△BPQ 全等时,点Q 的运动速度为__cm/s .14.如图,在Rt ABC △中,90C ∠=︒,10AC =,5BC =,线段PQ AB =,P ,Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AD 上运动,当AQ =______时,ABC 和PQA △全等.15.在ABC 中,48ABC ︒∠=,点D 在BC 边上,且满足18,BAD DC AB ︒∠==,则CAD ∠=________度. 16.如图,在ABC 中,90C ∠=︒,AD 平分BAC ∠,交BC 边于点D ,若12AB =,4CD =,则ABD △ 的面积为__________.17.如图,四边形ABDC 中,对角线AD 平分BAC ∠,136ACD ∠=︒,44BCD ∠=︒,则ADB ∠的度数为_____18.如图,在Rt ABC 中,90C ∠=︒,AD AC =,DE AB ⊥,交BC 于点E .若26B ∠=︒,则AEC ∠=______︒.19.如图,在ABC 中,AB CB =,90ABC ∠=︒,AD BD ⊥于点D ,CE BD ⊥于点E ,若7CE =,5AD =,则DE 的长是______.20.如图,已知△ABC 的面积为18,BP 平分∠ABC ,且AP ⊥BP 于点P ,则△BPC 的面积是_____.21.如图,已知ABC DCB ∠=∠,则需添加的一个条件是______可使ACB DBC ≌.(只写一个即可,不添加辅助线).三、解答题22.如图,点D 在边AC 上,BC 与DE 交于点P ,AB DB =,C E ∠=∠,CDE ABD ∠=∠.(1)求证:ABC DBE ≌;(2)已知162ABE ∠=︒,30DBC ∠=︒,求CDE ∠的度数.23.沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由C 走到D 的过程中,通过隔离带的空隙P ,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图,AB//PM //CD ,相邻两平行线间的距离相等AC ,BD 相交于P ,PD CD ⊥垂足为D .已知16CD =米.请根据上述信息求标语AB 的长度.24.如图1,在平面内取一个定点O ,自O 引一条射线O x ,设M 是平面内一点,点O 与点M 的距离为m (m >0), 以射线O x 为始边,射线OM 为终边的∠x OM 的度数为x °(x≥0).那么我们规定用有序数对(m ,x °)表示点M 在平面内的位置,并记为M (m ,x °).例如,在如图2中,如果OG=4,∠x OG=120°,那么点G 在平面内的位置记为G (4,120°).(1)如图3,如果点N 在平面内的位置记为N (6,35°),那么ON= ;xON ∠= °; (2)如图4,点A ,点B 在射线O x 上,点A ,B 在平面内的位置分别记为(a ,0°), (2a ,0°)点A ,E ,C 在同一条直线上. 且OE=BC .用等式表示∠OEA 与∠ACB 之间的数量关系,并证明.25.已知:如图,AOB ∠.求作: A O B '''∠,使A O B AOB '''∠=∠.作法:①以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ; ②画一条射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C '; ③以点C '为圆心,CD 长为半径画弧,与②中所画的弧相交于点D ; ④过点D 画射线O B '',则A O B AOB '''∠=∠;A OB '''∠就是所求作的角.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明证明:连接C D ''.由作法可知OC O C ''=,,, ∴COD C O D '''≅.( )(填推理依据). ∴A O B AOB '''∠=∠. ∴A O B '''∠就是所求作的角.。
青海师范大学附属中学必修四第一章《三角函数》测试(包含答案解析)

一、选择题1.已知函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,则下列结论正确的个数是( ) ①()f x 的最小值为2-; ②点,012π⎛⎫⎪⎝⎭是()f x 的图象的一个对称中心; ③()f x 的最小正周期为π; ④()f x 在,06π⎛⎫- ⎪⎝⎭上单调递增. A .1B .2C .3D .42.函数()2cos 3⎛⎫=+ ⎪⎝⎭πf x x 在[]0,π的单调递增区间是( ) A .20,3π⎡⎤⎢⎥⎣⎦B .2,33ππ⎡⎤⎢⎥⎣⎦C .,3ππ⎡⎤⎢⎥⎣⎦D .2π,π33.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称 C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 4.如果一个函数在给定的区间上的零点个数恰好为8,则称该函数为“比心8中函数”.若函数()2sin()1f x x ωπ=-,(0)>ω是区间[0,1]上的“比心8中函数”,则ω的取值范围是( ) A .4149,66⎡⎫⎪⎢⎣⎭B .4953,66⎡⎫⎪⎢⎣⎭C .3741,66⎡⎫⎪⎢⎣⎭D .[8,9)5.使函数())cos(2)f x x x θθ+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π6.已知()f x 是定义在R 上的奇函数,()1f x +也是奇函数,当(]0,1x ∈时,()11f x x=-.若函数()()sin F x f x x π=+,则()F x 在区间[]1949,2021上的零点个数是( ) A .108B .109C .144D .1457.设函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减,则下述结论: ①()f x 关于,012π⎛⎫⎪⎝⎭中心对称;②()f x 关于直线23x π=轴对称; ③()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦;④方程()1f x =在[]0,2π有4个不相同的根. 其中正确结论的编号是( ) A .①②B .②③C .②④D .③④8.函数2()cos sin (R)f x x x x =+∈的最小值为( ) A .54B .1C .1-D .2-9.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,0ϕπ≤≤)的部分图象如图所示,则()f x 的解析式是( )A .()2sin 6f x x π⎛⎫=+⎪⎝⎭B .()2sin 3f x x π⎛⎫=+⎪⎝⎭C .()2sin 26f x x π⎛⎫=+⎪⎝⎭D .2n 2)3(si f x x π⎛⎫=+⎪⎝⎭10.将函数()2sin (04)6f x x πωω⎛⎫=-<< ⎪⎝⎭的周期为π,则以下说法正确的是( ) A .1ω=B .函数()y f x =图象的一条对称轴为12x π=C .()3f f x π⎛⎫⎪⎝⎭D .函数()y f x =在区间0,2π⎛⎫⎪⎝⎭,上单调递增11.已知函数()()()()2sin 0,0,f x x ωϕωϕπ=+>∈的部分图像如图所示,将()y f x =图像上所有点的横坐标缩小到原来的12(纵坐标不变),所得图像对应的函数()g x 解析式为( )A .()2sin 46g x x π⎛⎫=+ ⎪⎝⎭B .()2sin 43g x x π⎛⎫=+ ⎪⎝⎭C .()2sin 23g x x π⎛⎫=+⎪⎝⎭D .()2sin 3g x x π⎛⎫=+⎪⎝⎭12.函数22y cos x sinx =- 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1D .2,-2二、填空题13.若函数()sin (0)4f x x πωωω⎛⎫=-> ⎪⎝⎭取得最值的点到y 轴的最近距离小于6π,且()f x 在711,2020ππ⎛⎫⎪⎝⎭单调递增,则ω的取值范围为_________. 14.已知函数cos ,[],y a x x ωππ=+∈-(其中,a ω为常数,且0>ω)有且仅有3个零点,则ω的最小值是_________. 15.关于1()sin sin f x x x=-,有如下四个结论: ①()f x 是奇函数. ②()f x 图像关于y 轴对称. ③2x π=是()f x 的一条对称轴.④()f x 有最大值和最小值. 其中说法正确的序号是________.16.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,||2ϕπ<)的部分图象如图所示.则函数()y f x =的解析式为________.17.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60和30,第一排和最后一排的距离为106米(如图所示),旗杆底部与第一排在一个水平面上,若国歌长度约为50秒,升旗手应以__________(米 /秒)的速度匀速升旗.18.已知M 是函数()()238sin f x x x x R π=--∈的所有零点之和.则M 的值为_____. 19.函数()sin 2cos 1sin x xf x x=-的值域为________.20.已知函数()()()sin 0,0,f x A x A ωϕωπϕπ=+>>-<<的部分图象如下图所示,则ϕ=________.三、解答题21.已知()2sin 216f x x a π⎛⎫=-++⎪⎝⎭(a 为常数). (1)求()f x 的最小正周期和单调递增区间; (2)若当0,2x π⎡⎤∈⎢⎥⎣⎦时,()f x 的最大值为4,求a 的值. 22.函数()()()sin 0,0,0πf x A x A ωϕωϕ=+>><<的部分图象如图所示.(1)求函数()f x 的解析式;(2)求函数()f x 的单调递增区间,并求()f x 取最小值时的自变量x 的集合. 23.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象如图所示.(1)求()f x 的解析式;(2)将()f x 图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到()g x 的图象.又()14g θ=求2114sin sin 63ππθθ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭的值. 24.已知函数()3π2sin 24⎛⎫=+ ⎪⎝⎭f x x ,R x ∈.(1)求函数()f x 的最小正周期T 及()f x 的图象的对称轴;(2)完成表格,并在给定的坐标系中,用五点法作出函数()f x 在一个周期内的图象.x3π24u x =+()f x25.如图,有一矩形空地ABCD ,240AB BC ==米,现计划种植甲、乙两种蔬菜,已知单位面积种植甲蔬菜的经济价值是种植乙蔬菜经济价值的3倍,但种植甲蔬菜需要有辅助光照.AB 边中点O 处处恰有一可旋转光源满足甲蔬菜生长的需要,该光源照射范围是60EOF ∠=︒,其中E 、F 分别在边BC ,CD 上.(1)若30BOE ∠=︒,求四边形OECF 的面积; (2)求该空地产生最大经济价值时种植甲种蔬菜的面积.26.已知函数()3,4f x x x R π⎛⎫=+∈ ⎪⎝⎭.(1)求f (x )的最小正周期;(2)求f (x )的单调递增区间和单调递减区间; (3)当0,2x π⎡⎤∈⎢⎥⎣⎦,求f (x )值域.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】求出()min f x 可判断①的正误;利用正弦型函数的对称性可判断②的正误;求出()f x 的最小正周期可判断③的正误;利用正弦型函数的单调性可判断④的正误. 【详解】 对于①,()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,()()min 212f x ∴=⨯-=-,①正确;对于②,2sin 22sin 20121232f ππππ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭,所以,点,012π⎛⎫⎪⎝⎭不是()f x 的图象的一个对称中心,②错误;对于③,函数()f x 的最小正周期为22T ππ==,③正确; 对于④,当,06x π⎛⎫∈- ⎪⎝⎭时,2666x πππ-<+<,所以,函数()f x 在,06π⎛⎫- ⎪⎝⎭上单调递增. ④正确.因此,正确命题的序号为①③④. 故选:C. 【点睛】关键点点睛:对于正弦型函数基本性质的判断问题,一般将函数解析式化为()sin y A x b ωϕ=++或()cos y A x b ωϕ=++,将x ωϕ+视为一个整体,利用正弦函数或余弦函数的基本性质来求解.2.C解析:C 【分析】先求出函数的单调增区间,再给k 取值即得解. 【详解】 令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z ), 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z ), 当1k =-时,5233ππx -<<- 当0k =时,433x ππ<<又∵[]0,x π∈, 故选:C 【点睛】方法点睛:求三角函数()cos()f x A wx ϕ=+的单调区间,一般利用复合函数的单调性原理解答:首先是对复合函数进行分解,接着是根据复合函数的单调性原理分析出分解出的函数的单调性,最后根据分解函数的单调性求出复合函数的单调区间.3.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论. 【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫⎪⎝⎭对称,选项A 错误;当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.4.A解析:A 【分析】根据题意问题转化为方程1sin()2x ωπ=在区间[0,1]上有8个解,根据正弦函数的图像与性质可求得1sin()2x ωπ=在区间[0,1]上取第8个解为416x ω=、第9个解为496x ω=,则4149166ωω≤<,解不等式即可. 【详解】根据题意,函数()2sin()1f x x ωπ=-,(0)>ω是区间[0,1]上零点个数为8,即方程1sin()2x ωπ=在区间[0,1]上有8个解, ∴26x k πωππ=+或52,6x k k Z πωππ=+∈,当0k =时,1sin()2x ωπ=在区间[0,1]上取第1个解16x ω=,取第2个解56x ω=; 当1k =时,1sin()2x ωπ=在区间[0,1]上取第3个解136x ω=,取第4个解176x ω=; 当3k =时,1sin()2x ωπ=在区间[0,1]上取第7个解376x ω=,取第8个解416x ω=; 当4k =时,1sin()2x ωπ=在区间[0,1]上取第9个解496x ω=. 则4149166ωω≤<,解得414966ω≤<. 故选:A5.B解析:B 【解析】1())cos(2))cos(2))2sin(2)26f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos 2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos 2f x x =为减函数,符合题意,所以选B.6.D解析:D 【分析】由题可得()f x 是周期为2的函数,进而判断()F x 是周期为2的函数,可求得()0=0F ,102F ⎛⎫= ⎪⎝⎭,()10F =,利用周期性即可求出零点个数.【详解】()f x 是定义在R 上的奇函数,()1f x +也是奇函数,()00f ∴=,()()()111f x f x f x +=--+=-,()f x ∴是周期为2的函数,sin y x π=的周期为2,∴()()sin F x f x x π=+是周期为2的函数,()()00sin00=F f ∴+=,11sin 0222F f π⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,()()11sin 0F f π=+=,则在区间[]1949,2021上,()()()111949194919501950202122F F F F F ⎛⎫⎛⎫=+==+== ⎪ ⎪⎝⎭⎝⎭,则()F x 在区间[]1949,2021上的零点个数是()2021194921145-⨯+=个.故选:D. 【点睛】本题考查函数奇偶性和周期性的应用,解题的关键是判断出()F x 是周期为2的函数,根据函数的周期性即可判断出零点的个数.7.D解析:D 【分析】利用题干中的已知条件求得2ω=,可得出()sin 216f x x π⎛⎫=-+ ⎪⎝⎭,利用正弦型函数的对称性可判断①②的正误,利用正弦型函数的值域可判断③的正误,求出方程()1f x =在[]0,2π上的解,可判断④的正误. 【详解】N ω*∈,由55,126x ππ⎡⎤∈⎢⎥⎣⎦可得55126666x πωπππωπω-≤-≤-,由于函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以,()553,2,21266622k k k Z πωππωπππππ⎡⎤⎡⎤--⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,所以,521262532662k k ωππππωππππ⎧-≥+⎪⎪⎨⎪-≤+⎪⎩,解得()248121055k k k Z ω++≤≤∈,由248121055k k ++≤,解得16k ≤,N ω*∈且k Z ∈,0k ∴=,可得825ω≤≤,2ω∴=,则()sin 216f x x π⎛⎫=-+ ⎪⎝⎭.对于①,sin 2sin 00126ππ⎛⎫⨯-== ⎪⎝⎭,所以,112f π⎛⎫= ⎪⎝⎭, 所以,函数()f x 的图象关于点,112π⎛⎫⎪⎝⎭成中心对称,①错误; 对于②,271sin 2sin 13662πππ⎛⎫⨯-==-≠± ⎪⎝⎭,②错误;对于③,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,5112,666x πππ⎡⎤-∈⎢⎥⎣⎦,则11sin 262x π⎛⎫-≤-≤ ⎪⎝⎭, 所以,()302f x ≤≤,即()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦,③正确; 对于④,当[]0,2x π∈时,232,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 令()1f x =,可得sin 206x π⎛⎫-= ⎪⎝⎭,206x π∴-=或26x ππ-=或226x ππ-=或236x ππ-=.所以,方程()1f x =在[]0,2π有4个不相同的根,④正确. 故选:D. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).8.C解析:C 【分析】由平方关系化为sin x 的函数,换元后利用二次函数性质得最小值. 【详解】由已知2()1sin sin f x x x =-+,令sin t x =,则[1,1]t ∈-,2()()1f x g t t t ==-++215()24t =--+,∵[1,1]t ∈-,∴1t =-时,min ()1g t =-. 故选:C . 【点睛】本题考查与三角函数有关的复合函数的最值.求三角函数的最值有两种类型:(1)利用三角恒等变换公式化函数为()sin()f x A x k ωϕ=++形式,然后由正弦函数性质得最值或值域.(2)转化为关于sin x (或cos x )的函数,用换元法,设sin t x =(或cos t x =)变成关于t 的二次函数,利用二次函数的性质求得最值或值域.9.D【分析】结合图象,依次求得,,A ωϕ的值. 【详解】 由图象可知2A =,2,,22362T T πππππωω⎛⎫=--==== ⎪⎝⎭,所以()()2sin 2f x x ϕ=+,依题意0ϕπ≤≤,则2333πππϕ-≤-≤, 2sin 0,0,6333f ππππϕϕϕ⎛⎫⎛⎫-=-+=-+== ⎪ ⎪⎝⎭⎝⎭,所以2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭.故选:D. 【点睛】方法点睛:根据三角函数()()sin f x A x b ωϕ=++或的部分图象求函数解析式的方法: (1)求A 、()()max min:2f x f x b A -=,()()max min2f x f x b +=;(2)求出函数的最小正周期T ,进而得出2Tπω=; (3)取特殊点代入函数可求得ϕ的值.10.C解析:C 【分析】由周期求出ω,然后由正弦函数的性质判断. 【详解】函数()2sin (04)6f x x πωω⎛⎫=-<< ⎪⎝⎭的周期为π,所以22πωπ==,A 错; 12x π=时,206x π-=,12x π=不是对称轴,B 错;3x π=时,226x ππ-=,即23f π⎛⎫= ⎪⎝⎭为最大值,因此()3f f x π⎛⎫⎪⎝⎭正确,C 正确; 0,2x π⎛⎫∈ ⎪⎝⎭时,52,666x πππ⎛⎫-∈- ⎪⎝⎭,而sin y x =在5,66ππ⎛⎫- ⎪⎝⎭上不单调,D 错; 故选:C . 【点睛】方法点睛:本题考查三角函数的性质,对函数()sin()f x A x ωϕ=+,掌握五点法是解题关键.解题时可由x 的值或范围求得x ωϕ+的值或范围,然后结合正弦函数性质判断.11.B【分析】由32341234T πππ⎛⎫=--= ⎪⎝⎭可求出T π=,进而可得2ω=,令 ()22122k k Z ππϕπ⨯+=+∈结合()0,ϕπ∈即可求得ϕ的值,再根据三角函数图象的伸缩变换即可求()g x 的解析式. 【详解】 由图知32934123124T ππππ⎛⎫=--== ⎪⎝⎭, 所以T π=,可得2ππω=,解得2ω=,所以()()2sin 2f x x ϕ=+, 令()22122k k Z ππϕπ⨯+=+∈,所以()23k k Z πϕπ=+∈,因为()0,ϕπ∈,所以令0k =,可得3πϕ=,所以()2sin 23f x x π⎛⎫=+⎪⎝⎭, 将()y f x =图像上所有点的横坐标缩小到原来的12(纵坐标不变), 可得()2sin 43g x x π⎛⎫=+ ⎪⎝⎭, 故选:B12.D解析:D 【解析】分析:将2cos x 化为21sin x -,令()sin 11x t t =-≤≤,可得关于t 的二次函数,根据t 的取值范围,求二次函数的最值即可.详解:利用同角三角函数关系化简,22cos 2sin sin 2sin 1y x x x x =-=--+设()sin 11x t t =-≤≤,则()()22211211y t t t t =--+=-++-≤≤,根据二次函数性质当1t =-时,y 取最大值2,当1t =时,y 取最小值2-. 故选D.点睛:本题考查三角函数有关的最值问题,此类问题一般分为两类,一种是解析式化为2sin sin y A x B x C =++的形式,用换元法求解;另一种是将解析式化为()sin y A x k ωϕ=++的形式,根据角的范围求解.二、填空题13.【分析】根据题意可得为的一个零点且且上有且只有一个最值点从而可得再由在单调递增可得解不等式组即可求解【详解】依题意为的一个零点且所以在上有且只有一个最值点可得化简得又则所以解得当时可得又所以故答案为解析:65,53⎛⎤⎥⎝⎦【分析】 根据题意可得,04π⎛⎫⎪⎝⎭为()f x 的一个零点,且45T π≥,且,66ππ⎛⎫- ⎪⎝⎭上有且只有一个最值点,从而可得665ω<<,再由()f x 在711,2020ππ⎛⎫ ⎪⎝⎭单调递增,可得221032210k k ππωπππωπ⎧-+≤⎪⎪⎨⎪+≥⎪⎩,解不等式组即可求解. 【详解】 依题意,04π⎛⎫⎪⎝⎭为()f x 的一个零点且117420205T πππ≥-=, 所以在,66ππ⎛⎫- ⎪⎝⎭上有且只有一个最值点, 可得46446T ππππ-<<+,化简得665ω<<, 又711,2020x ππ⎛⎫∈⎪⎝⎭,则3,41010x πωπωπω⎛⎫⎛⎫-∈ ⎪⎪⎝⎭⎝⎭所以221032210k k ππωπππωπ⎧-+≤⎪⎪⎨⎪+≥⎪⎩,解得5520203k k ω-+≤≤+,k Z ∈,当0k =时,可得553ω-≤≤,又665ω<<,所以6553ω<≤. 故答案为:65,53⎛⎤⎥⎝⎦【点睛】关键点点睛:本题考查了三角函数的性质,解题的关键是根据三角函数的最值得665ω<<,以及函数的单调递增区间可得5520203k k ω-+≤≤+,k Z ∈,考查了分析、计算能力.14.2【分析】根据函数为偶函数可知函数必有一个零点为可得根据函数的图象可知解得即可得解【详解】因为函数为偶函数且有且仅有3个零点所以必有一个零点为所以得所以函数的图象与直线在上有且仅有3个交点因为函数的解析:2 【分析】根据函数为偶函数可知函数必有一个零点为0x =,可得1a =-,根据函数cos y x ω=(0)>ω的图象可知222πππωω≤<⨯,解得24ω≤<即可得解.【详解】因为函数cos ,[],y a x x ωππ=+∈-为偶函数,且有且仅有3个零点, 所以必有一个零点为0x =, 所以cos 00a +=,得1a =-,所以函数cos y x ω=(0)>ω的图象与直线1y =在[,]-ππ上有且仅有3个交点, 因为函数cos y x ω=(0)>ω的最小正周期2T πω=,所以2T T π≤<,即222πππωω≤<⨯,得24ω≤<,所以ω的最小值是2. 故答案为:2 【点睛】关键点点睛:根据偶函数图象的对称性求出a 是解题关键.15.①③【分析】借助于的性质对照四个选项一一验证【详解】的定义域对于①:定义域关于原点对称即是奇函数故①正确;是奇函数图像关于原点对称故②错误;对于③:而所以故③正确;对于④:令则无最小值无最大值故④错解析:①③ 【分析】借助于sin y x =的性质,对照四个选项,一一验证. 【详解】1()sin sin f x x x=-的定义域{}|,x x k k Z π≠∈ 对于①:定义域关于原点对称,()()11()sin sin ()sin sin f x x x f x x x ⎛⎫-=--=-+=- ⎪-⎝⎭,即()f x 是奇函数,故①正确;()f x 是奇函数,图像关于原点对称,故②错误;对于③:11()sin cos 22cos sin 2f x x x x x πππ⎛⎫-=--=-⎪⎛⎫⎝⎭- ⎪⎝⎭而11()sin cos 22cos sin 2f x x x x x πππ⎛⎫+=+-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭,所以()()22f x f x ππ-=+,故③正确; 对于④:令[)(]sin ,1,00,1t x t =∈-,则1y t t=-(),∈-∞+∞, 无最小值,无最大值,故④错误. 故答案为:①③ 【点睛】这是另一种形式的多项选择,多项选择题是2020年高考新题型,需要要对选项一一验证.16.【分析】由最值求得由周期求得由最高点的坐标求得【详解】由题意所以又所以所以故答案为:【点睛】方法点睛:由函数图象确定三角函数的解析式主要参考正弦函数图象中五点法由最大值和最小值确定由周期确定利用点的解析:2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭. 【分析】由最值求得A ,由周期求得ω,由最高点的坐标求得ϕ. 【详解】由题意2A =,4312T πππ⎛⎫=⨯-=⎪⎝⎭,所以22πωπ==,2sin 2212πϕ⎛⎫⨯+= ⎪⎝⎭,2,62k k Z ππϕπ+=+∈,又2πϕ<,所以3πϕ=.所以2n 2)3(si f x x π⎛⎫=+⎪⎝⎭. 故答案为:2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭. 【点睛】方法点睛:由函数图象确定三角函数的解析式,主要参考正弦函数图象中“五点法”,由最大值和最小值确定A ,由周期确定ω,利用点的坐标确定ϕ,这样可得出表达式()sin()f x A x ωϕ=+.17.6【分析】根据题意可求得然后利用正弦定理求得最后在中利用求得答案【详解】在中由正弦定理得;在中(米)所以升旗速度(米/秒)故答案为06【点睛】本题主要考查了解三角形的实际应用此类问题的解决关键是建立解析:6 【分析】根据题意可求得,45BDC ∠=︒,30CBD ∠=︒,CD =BC ,最后在Rt ABC 中利用sin 60AB BC =︒求得答案.【详解】在BCD 中,45BDC ∠=︒,30CBD ∠=︒,106CD =, 由正弦定理,得sin 45203sin 30CD BC ︒==︒;在Rt ABC 中,3sin?6020330AB BC =︒=⨯=(米). 所以升旗速度300.650t AB v ===(米/秒). 故答案为0.6. 【点睛】本题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用所学知识解决,属于中档题.18.【分析】根据和的函数图像的对称点和交点个数得出答案【详解】令可得作出和的函数图像如图所示:由图像可知两函数图像有个交点又两函数图像均关于直线对称的个零点之和为故答案为:【点睛】本题考查了函数零点之和 解析:12【分析】根据8sin y x π=和23y x =-的函数图像的对称点和交点个数得出答案. 【详解】令()0f x =可得8sin 23x x π=-,作出8sin y x π=和23y x =-的函数图像如图所示:由图像可知两函数图像有8个交点, 又两函数图像均关于直线32x =对称, ∴()f x 的8个零点之和为324122⨯⨯=.故答案为:12 【点睛】本题考查了函数零点之和,考查了转化与化归、数形结合的思想,属于基础题.19.【分析】由二倍角的正弦公式以及同角三角函数的基本关系化简函数的解析式为且有利用二次函数的基本性质可求得函数的值域【详解】由题意可得所以因此函数的值域为故答案为:【点睛】本题考查含正弦的二次函数值域的解析:1,42⎡⎫-⎪⎢⎣⎭【分析】由二倍角的正弦公式以及同角三角函数的基本关系化简函数()y f x =的解析式为()()2sin 1sin f x x x =+,且有1sin 1x -≤<,利用二次函数的基本性质可求得函数()y f x =的值域.【详解】()()()2222sin 1sin sin 2cos 2sin cos 112sin 1sin 2sin 1sin 1sin 1sin 22x x x x x x f x x x x x x x -⎛⎫====+=+-⎪---⎝⎭,由题意可得1sin 1x -≤<,所以,()2131214222f x ⎛⎫-≤<⨯+-= ⎪⎝⎭,因此,函数()sin 2cos 1sin x x f x x =-的值域为1,42⎡⎫-⎪⎢⎣⎭.故答案为:1,42⎡⎫-⎪⎢⎣⎭. 【点睛】本题考查含正弦的二次函数值域的求解,同时也考查了二倍角的正弦公式以及同角的三角函数基本关系的应用,考查计算能力,属于中等题.20.【分析】根据图象得出函数的最小正周期可得出的值再将点代入函数解析式结合的取值范围可求出的值【详解】由图象可知函数的最小正周期则将点代入函数解析式得即因为函数在附近单调递减则得故答案为:【点睛】本题考 解析:6π【分析】根据图象得出函数()y f x =的最小正周期T ,可得出ω的值,再将点5,012π⎛⎫⎪⎝⎭代入函数解析式,结合ϕ的取值范围,可求出ϕ的值. 【详解】由图象可知,函数()y f x =的最小正周期11521212T πππ⎛⎫=⨯-=⎪⎝⎭,222T ππωπ∴===, 则()()sin 2f x A x ϕ=+, 将点5,012π⎛⎫⎪⎝⎭代入函数解析式得55sin 201212f A ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,即5sin 06πϕ⎛⎫+= ⎪⎝⎭, 因为函数()y f x =在512x π=附近单调递减,则()526k k Z πϕππ+=+∈, 得()26k k Z πϕπ=+∈,πϕπ-<<,0k ∴=,6π=ϕ. 故答案为:6π. 【点睛】本题考查利用图象求三角函数解析式中的参数,考查分析问题和解决问题的能力,属于中等题.三、解答题21.(1)π,5,,36k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z ;(2)2a =. 【分析】(1)利用诱导公式化简函数的解析式,再根据正弦函数的周期性和单调性求解.(2)根据0,2x π⎡⎤∈⎢⎥⎣⎦得到52,666x πππ⎡⎤-∈-⎢⎥⎣⎦,然后利用正弦函数的性质求解. 【详解】 (1)()2sin 212sin 2166f x x a x a ππ⎛⎫⎛⎫=-++=--++ ⎪ ⎪⎝⎭⎝⎭,它的最小正周期为22ππ=. 令3222262k x k πππππ+≤-≤+, 解得536k x k ππππ+≤≤+, 所以函数的单调递增区间为5,,36k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z .(2)因为0,2x π⎡⎤∈⎢⎥⎣⎦时, 所以52,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 所以()f x 的最大值为42sin 16a π⎡⎤⎛⎫=-⨯-++ ⎪⎢⎥⎝⎭⎣⎦, 解得2a =. 【点睛】方法点睛:1.讨论三角函数性质,应先把函数式化成y =A sin(ωx +φ)(ω>0)的形式; 2.函数y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2πω,y =tan(ωx +φ)的最小正周期为πω;3.对于函数的性质(定义域、值域、单调性、对称性、最值等)可以通过换元的方法令t =ωx +φ,将其转化为研究y =sin t 的性质. 22.(1)()22sin 23f x x π⎛⎫=+⎪⎝⎭;(2)递增区间为7,,1212ππππ⎡⎤-+-+∈⎢⎥⎣⎦k k k Z ,x 的集合为5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭【分析】(1)先求出2A =,根据图形得出周期,可求出2ω=,再代入,06π⎛⎫⎪⎝⎭可求出ϕ;(2)令2222,232k x k k Z πππππ-+≤+≤+∈可求出增区间,当2322,32x k k Z πππ+=+∈时可得最小值. 【详解】(1)由图可知,2A =,46124T πππ⎛⎫=--= ⎪⎝⎭,即T π=,22πωπ∴==, 则()()2sin 2f x x ϕ=+,2sin 2066f ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,即,3k k Z πϕπ+=∈,则,3k k Z πϕπ=-∈,0πϕ<<,23πϕ∴=, ()22sin 23f x x π⎛⎫∴=+⎪⎝⎭;(2)令2222,232k x k k Z πππππ-+≤+≤+∈,解得27,121ππππ-+≤≤-+∈k x k k Z , 故()f x 的单调递增区间为7,,1212ππππ⎡⎤-+-+∈⎢⎥⎣⎦k k k Z , 当2322,32x k k Z πππ+=+∈,即25,1ππ=+∈x k k Z 时,()f x 取得最小值为2-, 此时x 的集合为5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 【点睛】方法点睛:根据三角函数()()sin f x A x =+ωϕ部分图象求解析式的方法: (1)根据图象的最值可求出A ; (2)求出函数的周期,利用2T πω=求出ω;(3)取点代入函数可求得ϕ. 23.(1)()sin 26f x x π⎛⎫+ ⎝=⎪⎭;(2)1116. 【分析】(1)由顶点及周期可得1A =,2ω=,再由sin 163f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,可得6π=ϕ,从而得解;(2)根据条件得1sin 64πθ⎛⎫+= ⎪⎝⎭,再结合诱导公式和同角三角函数关系可得解. 【详解】(1)由图可知1A =, 由311341264T πππ=-=,得2T ππω==,所以2ω=, 所以()()sin 2f x x ϕ=+, 因为sin 163f ππϕ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭,所以2,32k k Z ππϕπ+=+∈,则2,6k k Z πϕπ=+∈, 因为2πϕ<,所以6π=ϕ, ()sin 26f x x π⎛⎫+ ⎝=⎪⎭,(2)由题意,()sin 6g x x π⎛⎫=+⎪⎝⎭,由()14g θ=,得1sin 64πθ⎛⎫+= ⎪⎝⎭,221143sin sin sin[2()]sin [()]63662πππππθθπθθ⎛⎫⎛⎫-+-=-+++- ⎪ ⎪⎝⎭⎝⎭221111sin()cos ()sin()1sin ()1666641616ππππθθθθ=-+++=-++-+=-+-=.【点睛】方法点睛:确定()sin()(0,0)f x A x B A ωϕω=++>>的解析式的步骤:(1)求A ,B ,确定函数的最大值M 和最小值m ,则2M mA ,2M mB +=; (2)求ω,确定函数的周期T ,则2Tπω=; (3)求ϕ,常用方法有以下2种方法:①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入;②五点法:确定ϕ值时,往往以寻找“五点法”中的特殊点作为突破口. 24.(1)最小正周期为π,对称性ππ28k x =-,Z k ∈;(2)答案见解析. 【分析】(1)利用函数sin y A =()x ωϕ+的周期性和对称性,求得()f x 的最小正周期和对称轴. (2)利用五点法作图,结合题意即可列表,进而作出函数的一个周期内的图象. 【详解】解:(1)∵()3π2sin 24⎛⎫=+ ⎪⎝⎭f x x ,故它的最小正周期为2ππ2=, 令3ππ2π42x k +=+,Z k ∈, ππ28k x =-,Z k ∈ (2)由题意可得表格如下:【点睛】本题考查求正弦型函数的周期与对称性,考查“五点法”画图,掌握正弦函数的性质是解题关键. 25.(1)2003400平方米;(2)200平方米. 【分析】(1)四边形OECF 的面积OBCF BOE S S S =-△;(2)设[0BOE α∠=∈︒,45]︒,过点F 作FM AB ⊥于点M ,利用三角函数的知识可得EOF S △;设单位面积种植乙蔬菜的经济价值为m ,该空地产生的经济价值为y ,可用含α的式子表示出y ;令()cos sin(120)f ααα=⋅︒-,结合三角恒等变换公式和余弦函数的图象与性质求出()f α取得最小值时,α的值,再将其代入EOF S △的表达式中即可得解. 【详解】解:(1)由60EOF ∠=︒,30BOE ∠=︒,可知⊥OF OB ,O 为AB 中点,2AB BC =,OB BC ∴=,∴四边形FOBC 为正方形.在Rt BOE △中,30BOE ∠=︒,20OB =米,203BE ∴=, ∴四边形OECF 的面积为12032003202020400233OBCF BOE S S -=⨯-⨯⨯=-△平方米.(2)设[0BOE α∠=∈︒,45]︒,则120AOF α∠=︒-,过点F 作FM AB ⊥于点M ,在Rt OBE △中,cos OB BOE OE ∠=,20cos cos OB OE BOE α∴==∠,在Rt OMF △中,sin FMAOF OF∠=,20sin sin(120)FM OF AOF α∴==∠︒-.1120201003·sin sin 6022cos sin(120)cos sin(120)EOF S OE OF EOF αααα∴=∠=⨯⨯⨯︒=︒-⋅︒-△,设单位面积种植乙蔬菜的经济价值为m ,该空地产生的经济价值为y , 则()3EOF EOF ABCD y mS m S S =+-△△矩形3(2040m m =+⨯[800m =.令21()cos sin(120)cos sin cos 22f αααααα=⋅︒-=-cos 2111sin 2cos(230)242ααα+=-⨯=+︒.[0α∈︒,45]︒,230[30α∴+︒∈︒,120]︒,1cos(230)[2α∴+︒∈-.若该空地产生的经济价值y 最大,则()f α应取得最小值,为12-,此时0α=︒,200cos sin(120)cos0sin120EOF S αα∴====⋅︒-︒⋅︒△平方米. 故该空地产生最大经济价值时种植甲种蔬菜的面积为200平方米. 【点睛】本题考查函数的实际应用,还涉及三角恒等变换与三角函数的图象与性质,选择适当的函数模型是解题的关键,考查学生的逻辑推理能力和运算能力,属于中档题. 26.(1)23π;(2)单调递增区间为22,,34312k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦;单调递减区间为225,,312312k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(3)⎡⎣. 【分析】 (1)由公式2T πω=求周期;(2)利用正弦函数的单调性求单调区间; (3)求出34x π+的范围,然后结合正弦函数的性质得值域.【详解】解:(1)由解析式得ω=3, 则函数的最小周期223T ππω==. (2)由232242k x k πππππ-≤+≤+,k ∈Z ,所以2234312k k x ππππ-≤≤+,k ∈Z , 即函数的单调递增区间为22,34312k k ππππ⎡⎤-+⎢⎥⎣⎦,k ∈Z , 由3232242k x k πππππ+≤+≤+k ∈Z , 得225312312k k x ππππ+≤≤+,k ∈Z , 即函数的单调递减区间为225,312312k k ππππ⎡⎤++⎢⎥⎣⎦ ,k ∈Z . (3)当x ∈[0,2π]时,73,444x πππ⎡⎤+∈⎢⎥⎣⎦,则当3x +4π=2π时,函数f (x )取得最大值,此时f (x 2π=,当3x +342ππ=时,函数f (x )取得最小值,此时f (x 32π=即f (x )值域为[. 【点睛】关键点点睛:本题考查正弦型三角函数的性质.对于()sin()f x A x ωϕ=+(0,0)A ω>>,最小正周期为2T πω=,利用正弦函数sin y x =的性质,把x ωϕ+作为一个整体替换sin x 中的x ,可得()f x 的性质.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青海师范大学附属中学数学三角形填空选择达标检测(Word 版 含解析)一、八年级数学三角形填空题(难)1.如图,在ABC ∆中,A α∠=.ABC ∠与ACD ∠的平分线交于点1A ,得1A ∠: 1A BC ∠与1A CD ∠的平分线相交于点2A ,得2A ∠;;2019A BC ∠与2019A CD ∠的平分线相交于点2020A ,得2020A ∠,则2020A ∠=________________.【答案】20202α【解析】【分析】 根据角平分线的定义,三角形的外角性质及三角形的内角和定理可知21211112222a A A A A a ∠=∠=∠=∠=,,…,依此类推可知2020A ∠的度数. 【详解】解:∵∠ABC 与∠ACD 的平分线交于点A 1,∴11118022A ACD ACB ABC ∠=︒-∠-∠-∠ 1118018022ABC A A ABC ABC =︒-∠+∠-︒-∠-∠-∠()() 1122a A =∠=, 同理可得221122a A A ∠=∠=, …∴2020A ∠=20202α. 故答案为:20202α. 【点睛】 本题是找规律的题目,主要考查三角形的外角性质及三角形的内角和定理,同时也考查了角平分线的定义.2.将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=40°,∠2=50°,那么∠ 3的度数等于______________.【答案】12°【解析】等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是108°,则∠3=360°-60°-90°-108°-∠1-∠2=12°.点睛:本题考查的是多边形的内角,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.3.小明在用计算器计算一个多边形的内角和时,得出的结果为2005°,小芳立即判断他的结构是错误的,小明仔细地复算了一遍,果然发现自己把一个角的度数输入了两遍.你认为正确的内角和应该是________.【答案】1980【解析】【详解】解:设多边形的边数为n,多加的角度为α,则(n-2)×180°=2005°-α,当n=13时,α=25°,此时(13-2)×180°=1980°,α=25°故答案为1980.4.某多边形内角和与外角和共1080°,则这个多边形的边数是__________.【答案】6【解析】∵多边形内角和与外角和共1080°,∴多边形内角和=1080°−360°=720°,设多边形的边数是n,∴(n−2)×180°=720°,解得n=6.故答案为6.点睛:先根据多边形的外角和为360°求出其内角和,再根据多边形内角和定理即可求出多边形的边数.5.一机器人以0.3m/s的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为__s.【答案】160.【解析】试题分析:该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数,即可求得周长,利用周长除以速度即可求得所需时间.试题解析:360÷45=8,则所走的路程是:6×8=48m,则所用时间是:48÷0.3=160s.考点:多边形内角与外角.6.一个多边形内角和是一个四边形内角和的4倍,则这个多边形的边数是_________【答案】10【解析】【分析】【详解】解:本题根据题意可得:(n-2)×180°=4×360°,解得:n=10.故答案为:10 .考点:多边形的内角和定理.7.有公共顶点A,B的正五边形和正六边形按如图所示位置摆放,连接AC交正六边形于点D,则∠ADE的度数为()A.144°B.84°C.74°D.54°【答案】B【解析】正五边形的内角是∠ABC=()521805-⨯=108°,∵AB=BC,∴∠CAB=36°,正六边形的内角是∠ABE=∠E=()621806-⨯=120°,∵∠ADE+∠E+∠ABE+∠CAB=360°,∴∠ADE=360°–120°–120°–36°=84°,故选B.8.若正多边形的一个外角是45°,则该正多边形的边数是_________.【答案】8;【解析】【分析】根据多边形外角和是360度,正多边形的各个内角相等,各个外角也相等,直接用360°÷45°可求得边数.【详解】∵多边形外角和是360度,正多边形的一个外角是45°,∴360°÷45°=8即该正多边形的边数是8.【点睛】本题主要考查了多边形外角和是360度和正多边形的性质(正多边形的各个内角相等,各个外角也相等).9.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC=______°.【答案】110【解析】已知∠A =50°,∠ABO =28°,∠ACO =32°,根据三角形外角的性质可得∠BDC =∠A +∠ABO =78°,∠BOC =∠BDC +∠ACO =110°.10.如图所示,请将12A ∠∠∠、、用“>”排列__________________.【答案】21A ∠∠∠>>【解析】【分析】根据三角形的外角的性质判断即可.【详解】解:根据三角形的外角的性质得,∠2>∠1,∠1>∠A∴∠2>∠1>∠A ,故答案为:∠2>∠1>∠A .【点睛】本题考查了三角形的外角的性质,掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键.二、八年级数学三角形选择题(难)11.已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+12∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-12∠A.上述说法正确的个数是()A.0个B.1个C.2个D.3个【答案】C【解析】【分析】根据三角形的内角和外角之间的关系计算.【详解】解:(1)∵若P点是∠ABC和∠ACB的角平分线的交点,∴∠ABP=∠PBC,∠ACP=∠PCB∵∠A=180°-∠ABC-∠ACB=180°-2(∠PBC+∠PCB)∠P=180°-(∠PBC+∠PCB)∴∠P=90°+12∠A;故(1)的结论正确;(2)∵∠A=∠ACB-∠ABC=2∠PCE-2∠PBC=2(∠PCE-∠PBC)∠P=∠PCE-∠PBC∴2∠P=∠A故(2)的结论是错误.(3)∠P=180°-(∠PBC+∠PCB)=180°-12(∠FBC+∠ECB)=180°-12(∠A+∠ACB+∠A+∠ABC)=180°-12(∠A+180°)=90°-12∠A.故(3)的结论正确.正确的为:(1)(3).故选:C【点睛】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和;(2)三角形的内角和是180度.求角的度数常常要用到三角形的内角和是180°这一隐含的条件.12.如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为()A.13B.710C.35D.1320【答案】B【解析】【分析】连接CP.设△CPE的面积是x,△CDP的面积是y.根据BD:DC=2:1,E为AC的中点,得△BDP的面积是2y,△APE的面积是x,进而得到△ABP的面积是4x.再根据△ABE的面积是△BCE的面积相等,得4x+x=2y+x+y,解得y=43x,再根据△ABC的面积是3即可求得x、y的值,从而求解.【详解】连接CP,设△CPE的面积是x,△CDP的面积是y.∵BD:DC=2:1,E为AC的中点,∴△BDP的面积是2y,△APE的面积是x,∵BD:DC=2:1∴△ABD的面积是4x+2y ∴△ABP的面积是4x.∴4x+x=2y+x+y,解得y=43x.又∵△ABC的面积为3∴4x+x=32,x=310.则四边形PDCE的面积为x+y=710.故选B.【点睛】此题能够根据三角形的面积公式求得三角形的面积之间的关系.等高的两个三角形的面积比等于它们的底的比;等底的两个三角形的面积比等于它们的高的比.13.能够铺满地面的正多边形组合是()A.正三角形和正五边形B.正方形和正六边形C.正方形和正五边形D.正五边形和正十边形【答案】D【解析】【分析】正多边形的组合能否铺满地面,关键是要看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.【详解】解:A、正五边形和正三边形内角分别为108°、60°,由于60m+108n=360,得m=6-95 n,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;B、正方形、正六边形内角分别为90°、120°,不能构成360°的周角,故不能铺满,故此选项错误;C、正方形、正五边形内角分别为90°、108°,当90n+108m=360,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;D、正五边形和正十边形内角分别为108、144,两个正五边形与一个正十边形能铺满地面,故此选项正确.故选:D.【点睛】此题主要考查了平面镶嵌,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°-360°÷边数.14.如图P 为ABC ∆内一点,070,BAC ∠=0120,BPC ∠=BD 是ABP ∠的平分线,CE 是ACP ∠的平分线,BD 与CE 交于F ,则BFC ∠=( )A .085B .090C .095D .0100【答案】C【解析】 ∵070,BAC ∠= 0120,BPC ∠=∴∠ABC+∠ACB=110°,∠PBC+∠PCB=60°,∴∠ABP+∠ACP=(∠ABC+∠ACB)-(∠PBC+∠PCB)=110°-60°=50°,∵BD 是ABP ∠的平分线,CE 是ACP ∠的平分线,∴∠FBP+∠FCP=12 (∠ABP+∠ACP)=00150252⨯=; ∴∠FBC+∠FCB=∠FBP+∠FCP+∠PBC+∠PCB=25°+60°=85°,∴BFC ∠=180°-(∠FBC+∠FCB )=180°-85°=95°.故选C.点睛:本题主要考查了三角形的内角和定理和角平分线的定义,根据图形正确找出角与角之间的数量关系是解题的关键.15.已知一个正多边形的内角是140°,则这个正多边形的边数是( )A .9B .8C .7D .6 【答案】A【解析】分析:根据多边形的内角和公式计算即可.详解:.答:这个正多边形的边数是9.故选A.点睛:本题考查了多边形,熟练掌握多边形的内角和公式是解答本题的关键.16.如图,△ABC 的角平分线CD 、BE 相交于F ,∠A=90°,EG∥BC,且CG⊥EG 于G ,下列结论:①∠CEG=2∠DCB;②∠DFB= ∠CGE;③∠ADC=∠GCD;④CA 平分∠BCG;其中正确的个数是()A.1B.2C.3D.4【答案】C【解析】【分析】根据平行线、角平分线、垂直的性质及三角形内角和定理依次判断即可得出答案.【详解】①∵EG∥BC,∴∠CEG=∠ACB.又∵CD是△ABC的角平分线,∴∠CEG=∠ACB=2∠DCB,故正确;④无法证明CA平分∠BCG,故错误;③∵∠A=90°,∴∠ADC+∠ACD=90°.∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC+∠BCD=90°.∵EG∥BC,且CG⊥EG,∴∠GCB=90°,即∠GCD+∠BCD=90°,∴∠ADC=∠GCD,故正确;②∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,∴∠DFE=360°﹣135°﹣90°=135°,∴∠DFB=45°=∠CGE,∴∠CGE=2∠DFB,∴∠DFB=∠CGE,故正确.故选C.点睛:本题主要考查的是三角形内角和定理,熟知直角三角形的两锐角互余是解答此题的关键.17.如图,将一张含有30角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠的大小为()244∠=,则1α-A.14B.16C.90α-D.44【答案】A【解析】分析:依据平行线的性质,即可得到∠2=∠3=44°,再根据三角形外角性质,可得∠3=∠1+30°,进而得出结论.详解:如图,∵矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得:∠3=∠1+30°,∴∠1=44°﹣30°=14°.故选A.点睛:本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.18.如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数()A.24°B.25°C.30°D.35°【答案】D【解析】【分析】首先根据三角形内角和定理可得∠AEF+∠AFE=120°,再根据邻补角的性质可得∠FEB+∠EFC=360°-120°=240°,再根据由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,然后计算出∠1+∠2的度数,进而得到答案.【详解】解:∵∠A=60°,∴∠AEF+∠AFE=180°-60°=120°,∴∠FEB+∠EFC=360°-120°=240°,∵由折叠可得:∠B ′EF+∠EFC ′=∠FEB+∠EFC=240°,∴∠1+∠2=240°-120°=120°,∵∠1=85°,∴∠2=120°-85°=35°.故选:D .【点睛】此题主要考查了翻折变换,关键是根据题意得到翻折以后,哪些角是对应相等的.19.如图,三角形ABC 中,D 为BC 上的一点,且S △ABD =S △ADC ,则AD 为( )A .高B .角平分线C .中线D .不能确定 【答案】C【解析】 试题分析:三角形ABD 和三角形ACD 共用一条高,再根据S △ABD =S △ADC ,列出面积公式,可得出BD=CD .解:设BC 边上的高为h ,∵S △ABD =S △ADC ,∴,故BD=CD ,即AD 是中线.故选C .考点:三角形的面积;三角形的角平分线、中线和高.20.在ΔABC 中,AB 3=,AC 5=,第三边BC 的取值范围是( )A .10BC 13<<B .4BC 12<< C .3BC 8<<D .2BC 8<< 【答案】D【解析】【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边的边长的取值范围.【详解】∵AB=3,AC=5,∴5-3<BC<5+3,即2<BC<8,故选D.【点睛】考查了三角形三边关系,一个三角形任意两边之和大于第三边,任意两边之差小于第三边.熟练掌握三角形的三边关系是解题关键.。
