发酵动力学
发酵动力学

发酵动力学第一篇:发酵动力学第八章发酵动力学发酵动力学是研究各种环境因素与微生物代谢活动之间的相互作用随时间变化的规律的科学。
fermentation kinetics 生化反应工程的基础内容之一,以研究发酵过程的反应速率和环境因素对速率的影响为主要内容。
通过发酵动力学的研究,可进一步了解微生物的生理特征,菌体生长和产物形成的合适条件,以及各种发酵参数之间的关系,为发酵过程的工艺控制、发酵罐的设计放大和用计算机对发酵过程的控发酵动力学制创造条件。
研究发酵过程中菌的生长速率、培养基的消耗速率和产品形成速率的相互作用和随时间变化的规律。
发酵动力学包括化学热力学(研究反应的方向)和化学动力学(研究反应的速度)并涉及酶反应动力学和细胞生长动力学。
它为发酵过程的控制、小罐试验数据的放大以及从分批发酵过渡到半连续发酵和连续发酵提供了理论基础。
发酵动力学也是计算机模拟发酵过程研究及发酵过程计算机在线控制的基础。
在发酵中同时存在着菌体生长和产物形成两个过程,它们都需要消耗培养基中的基质,发酵动力学因此有各自的动力学表达式,但它们之间是有相互联系的,都是以菌体生长动力学为基础的。
所谓菌体生长动力学是以研究菌体浓度、限制性基质(培养基中含量最少的基质,其他组分都是过量的)浓度、抑制剂浓度、温度和pH等对菌体生长速率的影响为内容的。
在分批发酵中,菌体浓度X,产物浓度P和限制性基质浓度S均随时间t变化菌体生长可分迟滞、对数、减速、静止、衰退等五个时期。
其中菌体的主要生长期是对数期,它的特点是:随着基质浓度继续下降,菌体的衰老死亡逐步与生长平衡以至超过生长,也即进入静止和衰退期。
发酵动力学J.莫诺于1949年提出了一个μ与S间的经验关联式,此式被称莫诺方程式:μm为最大比生长速率, 即不因基质浓度变化而改变的最大μ值;Ks为饱和常数,即在数量上相当于μ=0.5μm时的S值。
Ks值愈小,说明在低基质浓度范围中,S对μ愈为敏感,而保持μm的临界S 值愈低。
第6章 发酵动力学

发酵过程反应速度的描述
X S(底物) ─→ X(菌体) + P(产物)
基质的消耗速度:
ds r dt
X
(g.L-1.s-1)
ds 基质的消耗比速: dt
(h-1.s-1)
单位时间内单位菌体消耗基质或形成产物(菌体)的量称为 比速,是生物反应中用于描述反应速度的常用概念
发酵过程反应速度的描述
的比生长速率µ 保持一定。
连续发酵动力学-发酵装置-细胞回流式
F Se
(1 ) F X
F Xe
F, cX
细胞回流的单级连续发酵示意图
a: 再循环比率(回流比) c: 浓缩因子
连续发酵动力学-发酵装置-塞流式
无菌培养 基流入
发酵罐 d 供给连续接 种再循环
培养物 流出
物料衡算(连续培养的反应器特性)
催化剂
改变条件
温度 酸碱度
破坏平衡
浓度
如何确定高产高效 的最佳条件?
采用反应动力学方法 进行定量研究
发酵动力学研究的几个层次(尺度)
分子层次(酶催化与生物转化) 基于关键生化反应(限速步)及其关键酶的动力学特征 及其影响因素 采用一系列分子水平的方法 细胞层次(代谢网络与细胞工厂) 基于细胞信号传导、代谢网络、细胞物质运输的系列关 键生化反应的综合表现 采用一系列细胞水平的方法,包括细胞群体行为分析 反应器层次(过程工程) 基于细胞群体生长及产物合成对外部环境综合响应 采用一系列优化反应器发酵条件的方法
二、微生物的生长动力学、Monod方程
微生物的生长速度:
μ=f(s,p,T,pH,……,)
在一定条件下(基质限制):
发酵动力学实验
特定的基质及在特定环境条件下培养的特定微生物,它是
一个常数,又称最大生长得率或生长得率常数。
12
4.产物得率:产物的合成相对于基质消耗量的 收得率。
YP/S
P (S )
YP/s: 相对于基质消耗的实际产物得率系数
Yps
P (S )P
Yps: 相对于基质消耗的产物理论得率系数
理论产物得率取决于产物的生物合成途径,对于由特定基质
设计合理的发酵过程,也必须以发酵动力学模型作为依据, 利用计算机进行程序设计、模拟最合适的工艺流程和发酵工 艺参数,从而使生产控制达到最优化。
发酵动力学的研究还在为试验工厂比拟放大、为分批发酵过 渡到连续发酵提供理论依据。
五、发酵动力学模型
1、几个基本概念
发酵过程中,基质主要消耗在:①满足菌体生长消
的适用范围
5
微生物发酵动力学的研究与发酵的种类、 方式密切相关
氧需求
液体表面发酵
好氧发酵
液体深层发酵
兼性好氧发酵
厌氧发酵 深层发酵
操作方法
分批发酵 分批补料发酵
连续发酵
6
四、发酵动力学研究的意义
通过对发酵反应动力学的研究,进行最佳发酵生产工艺条件的 控制。发酵过程中,菌体的浓度、基质浓度、温度、pH值、溶解 氧等工艺参数的控制方案,可以在这研究的基础上进行优化。
ms
dS dtMFra bibliotek1 Xms:以基质消耗为基准
的维持因数, X:菌体干重; S:基质量 t:发酵时间; M:表示维持。
9
2.比速(率):单位时间内,单位干菌体消耗基质或形 成产物(菌体)的量 (消耗的基质用于维持代谢,菌体 生长和产物合成)。比速率是生物反应中用于描述反应 速度的常用概念
第六章发酵动力学

发酵装置-细胞回流式
F Se
(1 ) F X
F Xe
F , cX
细胞回流的单级连续发酵示意图
a: 再循环比率(回流比) c: 浓缩因子
2.2连续发酵动力学-理论
2.2.1单级恒化器连续发酵
定义: ① 稀释率 将单位时间内连续流入发酵罐中的新鲜培养基体积与 发酵罐内的培养液总体积的比值 D=F/V (h-1) F—流量(m3/h) V—培养液体积(m3) ② 理论停留时间
μ
残留的限制性底物浓度对微生物
比生长率的影响
Ks—底物亲和常数,速度 等于处于1/2μm时的底物浓 度,表征微生物对底物的亲 和力,两者成反比。
酶促反应动力学-米氏方程:
Vm [ s ] v K m [ s]
受单一底物酶促反应限制的微生物 生长动力学方程-Monod方程:
m s
Ks s
克P和每个有效电子所生成的细胞克数; ③ Yx/ATP:消耗每克分子的三磷酸腺苷生成的细胞克数。
基质消耗动力学 产物得率系数:
Yp/s , YP / O2 , YATP / s , YCO2 / s
:
消耗每克营养物(s)或每克分 子 氧 (O2) 生 成 的 产 物 (P) 、 ATP 或
CO2的克数。
细胞生长动力学
Decline(开始出现一种底物不足的限制):
若不存在抑制物时
Monod 模型:
m s
Ks s
m s
Ks s
t
ln x ln x0
t
x x0e
细胞生长动力学
式中: S—限制性基质浓度,mol/m3 Ks—底物亲和常数(也称半饱和速度常数),表示微生 物对底物的亲和力 , mol/m3 ; Ks越大,亲和力越 小, µ 越小。
发酵动力学名词解释

发酵动力学名词解释
发酵动力学是研究微生物在发酵过程中的生长、代谢和动力学行为的学科。
以下是一些常见的发酵动力学名词解释:
1. 比生长速率 (μ):每小时单位质量的菌体所增加的菌体量,是表征微生物生长速率的一个参数,也是发酵动力学中的一个重要参数。
2. 基质消耗动力学:指消耗单位营养物所生产的产物或细胞数量,可以通过确定菌体和基质之间的动力学关系来研究。
3. 最大比生长速率 (μmax):微生物在最优生长条件下的最大比生长速率。
4. 饱和常数 (Ks):表示微生物细胞浓度达到最大值时的营养物浓度。
5. 动力学参数 (kinetic parameters):用于描述微生物生长和代谢过程的一些参数,如比生长速率、饱和常数等。
6. 发酵热 (fermentative heat):在发酵过程中产生的热能,可以用于加热发酵液或产生蒸汽。
7. 非竞争性抑制剂 (non-competitive inhibitor):一种能够
与酶结合并抑制其活性的抑制剂,但其结合常数小于竞争性抑制剂。
8. 群体动力学 (population dynamics):研究微生物种群数量
的动态变化,包括菌落形成和灭绝、种群增长和衰退等。
这些名词解释可以帮助读者更好地理解发酵动力学的基本概念
和应用。
发酵动力学
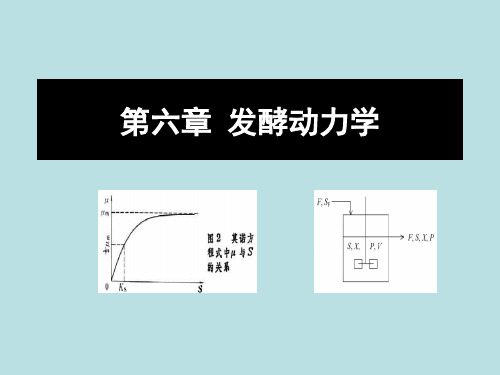
减速期: d 0
dt
静止期: dx 0
dt
; X Xmax
衰亡期: dx 0
dt
二、微生物的生长动力学、Monod方程
微生物的生长速度:
μ=f(s,p,T,pH,……,)
在一定条件下(基质限制):
μ=f(S)
Monod研究了基质浓度与生长速度的关系 ———Monod方程(1949)
1.2 V1m
td=ln2/ μmax=0.64 h
基质消耗动力学的基本概念
S1 菌体
维持消耗(m) :
S
S2 产物
指维持细胞最低活性所 需消耗的能量,一般来
讲,单位重量的细胞在
S3 维持
单位时间内用于维持消 耗所需的基质的量是一
个常数。
X S(底物) ─→ X(菌体) + P(产物)+维持
X S(底物) ─→ X(菌体) + P(产物)+维持
p x
〖二类发酵〗 产物的形成和菌体的生长部分偶联
p x
〖三类发酵〗 产物的形成和菌体的生长非偶联偶联
〖Pirt方程〗
π=a + bμ
a=0、b≠0: 可表示一类发酵 a≠0、b=0: 可表示二类发酵 a≠0、b≠0:可表示三类发酵
产物的生成动力学
发酵类型Ⅰ: 发酵类型Ⅱ 发酵类型Ⅲ=
dP
dX
YP / X
dt
dt
dP dX X
dt dt
dP X
dt
Ⅱ
Ⅰ
Ⅲ
分批发酵的优缺点
➢ 优点:
操作简单、周期短、染菌机会减少、生产过程及产品 容易控制。
➢ 缺点:
不利于测定生长动力学。
第二节 连续发酵动力学
发酵动力学

• 把它们随时间变化的过程绘制成图,就
成为所说的代谢曲线。
• 比生长速率μ
每小时(单位时间)单位质量的菌体所
增加的菌体量称为菌体比生长速率。
它是表征微生物生长速率的一个参数 ,也是发酵动力学中的一个重要参数。
发酵过程
• 微生物生长
• 底物消耗
• 代谢产物合成
• Gaden's fermentation classification(按照菌体生长,
产物直接来源于产能的初级
第 一 类 型 ( 生 长 关 联 型 )
代谢(自身繁殖所必需的代 谢),菌体生长与产物形成
■
不分开。
例如单细胞蛋白和葡萄糖酸
的发酵
dP dt
x 或
P
Q
dP Xdt
:生长关联型产物的形 成比例(g产物 / g菌体)
Q :产物合成的比速率
P
■
第 二 类 型 ( 部 分 生 长 关 联 型 )
产物合成动力学
• Gaden根据产物生成速率和细胞生长速率之间的 关系,将产物形成区分为三种类型 • 类型Ⅰ∶也称为偶联模型(醇类、葡萄糖酸、乳 酸)
rP YP / X rX YP / X X
• 类型Ⅱ∶也称部分偶联模型(柠檬酸、氨基酸)
rP rX X
• 类型Ⅲ∶也称为非偶联模型(抗生素、酶、维生
补料分批发酵(Fed-batch fermentation) 连续发酵(Continuous fermentation)
分批发酵
分批发酵:指在一封闭系统内含有初
始限量基质的发酵方式。在这一过程
中,除了氧气、消泡剂及控制pH的酸 或碱外,不再加入任何其它物质。发 酵过程中培养基成分减少,微生物得 到繁殖。
第一章 发酵动力学

求在该培养条件下,求大肠杆菌的μmax,Ks?
解:将数据整理:
s
S
100 137.5 192.5 231.8 311.3
6
33
64
153
221
S
S
m
m
Ks
s
400
S
300
S
m
m
Ks
/s
200
1
100
m 0.9
ks
0 0
m 108.4
100 200
μmax=1.11 (h-1); Ks=97.6 mg/L
⑴ YG的计算
例:以碳水化合物为碳源,通风培养饲料酵母,建立以下平衡: 6.67 CH2O+ 2.10 O2 → C3.92H6.5O1.94 + 2.75 CO2 + 3.42 H2O
200
67.2
84.6≈100(加上N、S和无机盐等)
(2)产物的比形成速率(μp )
单位时间单位菌体产生的产物的量。 1 dp p x dt
式中,μp ——产物的比形成速率[(h-1)或者mol/(g菌体· h)] ;
2 分批发酵动力学
2.1 微生物生长动力学 2.2 产物形成的动力学
2.1 微生物生长动力学
延滞期 = 0 加速期 0< <max 对数期 = max 减速期 0< <max 图1 单细胞生物分批培养生长曲线
= max
式中,s ——限制性基质浓度;
s Ks s
Ks —— 饱和常数,数值上等于当 = 1μmax 时的基 质浓度,是生物对某种基质的亲和力大小的量 度。Ks越大,表示生物对该基质的亲和力越小;
发酵工程_6发酵动力学

首先研究微生物生长和产物合成限制因子;
建立细胞生长、基质消耗、产物生成模型;
确定模型参数;
实验验证模型的可行性与适用范围;
根据模型实施最优控制。
本章主要内容
分批发酵动力学 连续发酵动力学 补料分批发酵动力学
什么是分批发酵?
分批发酵:准封闭培养,指一次性投料、接种 直到发酵结束,属典型的非稳态过程。 分批发酵过程中,微生物生长通常要经历延滞 期、对数生长期、衰减期、稳定期(静止期) 和衰亡期五个时期。
菌体浓度X t1
dx 0, 0, x xmax dt
(浓度最大)
t5
t2
t3 时间 t
t4
图6-1 分批发酵时典型的微生物生长动力学曲线
此阶段次级代谢活跃,次级代谢物大量合成。
dying:
a
(比死亡速率 ,s-1)
假定整个生长阶段无抑制物作用存在,则微生物生长动 力学可用阶段函数表示如下:
反应器层次(过程工程)
基于细胞群体生长及产物合成对外部环境综合响应
采用一系列优化反应器发酵条件的方法
针对微生物发酵的表观动力学,通过研究微生物群 体的生长、代谢,定量反映细胞群体酶促反应体 系的宏观变化速率,主要包括:
细胞生长动力学 底物消耗动力学 产物合成动力学
发酵动力学研究的基本过程
Y*X/S表示底物的细胞绝对得率,也称理论细胞得率; m为细胞维持系数
扣除细胞量的影响,
qS
将qS用µ表示,可得
1 Y
* X /S
m
YX / S
1 Y
* X /S
m
1 YX / S
发酵动力学的概念和研究内容

发酵动力学的概念和研究内容
发酵动力学是研究发酵过程中微生物生长和代谢的速率和规律
的科学,是微生物发酵工程的重要组成部分。
发酵动力学的研究内容包括发酵过程中的微生物生长动力学、底物代谢动力学和产物生成动力学。
微生物生长动力学是研究微生物在发酵过程中生长的速率和规律。
在发酵过程中,微生物对培养基中的营养物质进行吸收和利用,生长并繁殖。
微生物的生长速率受到多种因素的影响,如温度、pH值、氧
气浓度、营养物质浓度等。
通过实验和数学模型,可以了解微生物的生长速率与这些因素之间的关系,为优化发酵过程提供理论依据。
底物代谢动力学是研究微生物在发酵过程中对底物的利用速率和规律。
微生物通过代谢途径将底物转化为产物,同时产生能量和细胞所需的物质。
底物的利用速率受到微生物的生长速率和代谢途径的调控。
通过研究底物代谢动力学,可以了解微生物对底物的利用效率,为优化底物供应策略和产物生成提供指导。
产物生成动力学是研究发酵过程中产物的生成速率和规律。
在发酵过程中,微生物通过代谢途径将底物转化为产物。
产物的生成速率受到微生物的生长速率和底物的利用速率的影响,同时也受到产物对微生物生长的抑制效应。
通过研究产物生成动力学,可以了解产物的积累
速率和抑制效应,为优化发酵过程和产物纯化提供理论指导。
综上所述,发酵动力学的研究内容涵盖微生物生长动力学、底物代谢动力学和产物生成动力学三个方面,通过研究这些内容,可以深入了解发酵过程中微生物的生长和代谢规律,为优化发酵工艺和提高产物产量提供理论支持。
发酵动力学

主流产物(与初生代谢紧密关联)。
分批发酵动力学-产物形成动力学
与生长不相关→无关联:抗生素发酵
dP x dt
qp
若考虑到产物可能存在分解时,则
dP x kd P q p x kd P dt
产物生成与能量代谢不直接相关,通过细胞
① 当S较高时,(对数期满足S>>10Ks),此时,µ µ = m
② 当S较低时,(减速期, S<<10Ks),此时S↓,µ ↓ ∴ 减速期, µ ↓
m s
Ks s
Monod方程:
比 生 长 素 率
mSt Ks St
表征μ 与培养基中残留的 生长限制性底物St的关系
限制性底物残留浓度St
单级连续发酵示意图
连续发酵动力学-发酵装置-多级串联
两个及以上的发酵罐串联起来,前一级发酵罐的出 料作为下一级发酵罐的进料。
两级连续发酵示意图
连续发酵动力学-发酵装置-多级串联
培养基输入 培养基进入 下一级发酵罐
培养基进入 后处理或到 下一级发酵罐
多级罐式连续发酵装置示意图
罐式连续发酵实现方法
认识发酵过程的规律
优化发酵工艺条件,确定最优发 酵过程参数,如:基质浓度、温 度、pH、溶氧,等等
提高发酵产量、效率和转化率等
本章的重要性
• 一条主线:
发酵工艺过程 • 两个重点: 发酵过程的优化与放大 • 三个层次: 分子、细胞、反应器 • 四个目标: 高产、高效、高转化率、低成本 主要方法:基于发酵动力学研究来实现
进行的独特的生物合成反应而生成。
分批发酵动力学
发酵动力学

dP dt
YP / X
dX dt
YP / X X
或
QP YP / X
根据细胞生长与产物形成的关系
非相关型
细胞生长时无产物;细胞停止生长后,则有大量
产物积累。产物的形成速率只与细胞积累量有关, 产物的合成发生在细胞停止生长之后,习惯上把这 类与细胞生长无关联的产物称为次级代谢产物。如 大多数抗生素和微生物毒素的发酵。
Contois方程式 前面的方程中都没有出现X,即菌体浓度。 当菌浓很高,发酵液黏度很大时,采用如下 方程 :
u um s KX X s
其中KX是考虑了菌浓的饱和常数
多种底物现象
同时使用型 优先使用型
其它
K1s K2s
K1s s K2s s
K1
maxs1 s2
s1K2
s2
dX X
dt
营养物质限制生长微生物的典型生长形式 符合Monod方程
u um s Ks s
Monod方程
u um s Ks s
μ 为比生长速率(s-1); μmax为最大比生长速率(s-1), s为限制性底物浓度(g/L)。 Ks为饱和常数(g/L),其值等于比生长速率恰为最大比生长
max
s1 Ka1
s1Biblioteka s2 Ka2 s2
分批发酵-底物消耗动力学
实际产物得率与菌体生长得率的关系
-ΔS = (-ΔS)M + (-ΔS)G + (-ΔS)P
生长得率
YX / S
X S
理论生长得率
Ygs
X (S )G
同样,对于产物得率
实际产物得率
P YP / S S
理论产物得率 (产物最大得率)
第9章 发酵动力学

根据实验数据,以[P-B(t)]~A(t)作图,其斜率为。
对产物生成动力学,采用Luedeking-Piret方程。在 平衡期,即dX/dt = 0,则可用下式求得:
dP dX X 则Luedeking-Piret方程两边乘以dt得: dt dt
( dp / dt) st Xm
dP dX Xdt
将Logistic方程的积分式代入上式,并以t=0, P=0, X=X0为边界条件,积分后得:
X 0 X me X max t X m X 0 X 0e
利用Origin的非线性回归功能,首先编辑其积分 式函数,然后根据Xm和实验数据,进行非线性回 归,便可方便地求取动力学参数,并将模型计算 值与实验值进行比较,以评价模型的正确性。
max t
因此, X0=P1=0.42 g/L Xm=P2=2.40 g/L
产物生成速率rP
dP rP dt
氧的消耗速率rO 、CO2生成速率rCO2
4.
比速率
1 dX X dt
比生长速率 比消耗速率qS
1 dS qS X dt
1 dP qP X dt
比生成速率qP
维持系数m S
1 S mS ( )M X t
9.2 细胞生长动力学模型
无抑制的细胞生 长动力学模型 细胞生 长动力 学模型 有抑制的细胞生 长动力学模型
两边除于X,则
qS mS
1 YX / S
*
微生物发酵动力学

微生物比生长速率与底物之间有一定的关系
�
a表示一样物质浓 线段 线段a 度很低时。 b为符合 Monod 方程 线段 线段b 为符合Monod Monod方程 段。 c表示营养物质浓 线段 线段c 度很高时。
�
�
Monod方程的参数求解(双倒数法):
µ = µ max S Ks + S
将Monod方程取倒数可得:
或 Q P=αµ+β
式中:α —与生长偶联的产物形成系数,g / g细胞;
β —非生长偶联的比生产速率,g /( g细胞 • h )。
说明:代谢产物收率
�
定义:生成的代谢产物量ΔP对底物的消耗量 ΔS(g)之比定义为代谢产物收率(YP/S)。
YP / S
∆P =− ( g / g或mol / mol ) ∆S
− υS =
υX YX / S
=-
YX / S —菌体得率系数,g / g
υ υ= S X
µ YX/S
当基质既是能源又是碳源时:
碳源总消耗速率=用于生长的消耗速率+用于维持代谢的消耗速率
基质的消耗速率
1 − υS = υX + m • X YG
m —基质维持代谢系数,mol /( g, 菌体 • h) -υS —碳源总消耗速率,mol /( L • h)
�
其动力学方程可表示为:
d [P] = β X 或 Q P = β dt
式中:β —非生长偶联的比生产速率,g /( g 细胞 • h)。
�
(3)类型Ⅱ(混合型)
产物的形成与细胞生长部分相关或具有间接关 系,例如柠檬酸、谷氨酸发酵等。 其动力学方程可表示为:
d [ P] dX =α + β X = αµ X + β X dt dt
发酵动力学

非结构模型
最理想情况
结构模型
均衡 生长 细胞之间无差异, 是均一的,细胞内 有多个组分存在。
确定论模型 不考虑细胞内部结构
各种细胞均一 细胞群体做为一种溶质
A
不考虑细胞内部结构 均衡 生长
B 实际情况:
概率论模型 各种细胞不均一
C 对细胞群体的描述模型
细胞内多组分;
细胞之间不均一 D
(2) 宏观处理法
(3) 发酵周期
实验周期是指接种开始至培养结束放罐这段时 间。 工业生产周期,计算劳动生产率时则应把发酵 罐的清洗、投料、灭菌,冷却等辅助时间计算 在内,以反映发酵设备的利用效率。即从第一 罐接种经发酵结束至第二次接种为止这段时间 为一个发酵周期。
2. 有机化合物中的化合能 ① 完全燃烧需氧量
6. 发酵动力学与过程优化控制 发酵动力学通过对微生物生长率、基质 和氧消耗率、产物合成率的动态研究, 实现发酵条件参数的在线检测,确定发 酵动力学模型,实现动态过程优化控制, 取得发酵产物最大量。
第 2节
发酵动力学分类
1. 根据细胞生长与产物形成有否偶联进行分类
细胞浓度 (x) 或产物浓度对时间作图时, 两者密切平行,其最大的比生长速率和 最大的产物合成比速率出现在同一时刻。 一般来说在这种类型的发酵生产中,控 制好最佳生长条件就可获得产物合成的 最适条件。
〖Ⅰ型发酵〗 产物的形成和菌体的生长相偶联
p x
(2)生长产物合成半偶联类型:亦称Ⅱ型
它是介于生长产物合成偶联型与生长产物合成非偶联 之间的中间类型,产物的合成存在着与生长相联和不 相联两个部分。
该类型的动力学产物合成比速率的最高时刻要迟于比 生长速率最高时刻的到来。 如柠檬酸、谷氨酸、赖氨酸、依康酸、丙酮、丁醇发 酵
发酵动力学

• 如柠檬酸、谷氨酸、赖氨酸、依康酸、丙酮、丁醇发酵
(3)生产与产物合成非偶联类型:Ⅲ型
特点
• 多数次生代谢产物的发酵属这种类型,如各种抗生素和
微生物毒素等物质的生产速率很难与生长相联系。产物
• 产物的形成与生长是平行的。
• 产物合成速度与微生物生长速度呈线性关系,而且生长与
营养物的消耗成准定量关系。
• 这种类型的产物主要是葡萄糖代谢的初级中间产物, • 如酒精、葡萄糖酸、乳酸发酵就属于此类型。
(2)生长产物合成半偶联类型:亦称Ⅱ型
特点
• 它是介于生长产物合成偶联型与生长产物合成非偶联之间
dying:
a
x xme
(比死亡速率 ,s-1)
ln x ln xm at
at
分批发酵动力学-细胞生长动力学
假定整个生长阶段无抑制物作用存在,则微生物生长 动力学可用阶段函数表示如下:
0 µm µ=
m s
K0 s s
x0 (0<t<t1) x0e µm t (t1<t<t2) x= x0e µ (t -t ) e µt
(3) 类型Ⅲ • 产物的形成显然与基质 (糖类)的消耗无关,例如青霉
素、链霉素等抗生素发酵。
• 即产物是微生物的次级代谢产物,其特征是产物合成
与利用碳源无定量关系。产物合成在菌体生长停止及
底物被消耗完以后才开始。此种培养类型也叫做无生 长联系的培养。
3.
根据反应形式分类
(1) 简单反应型
• 营养成分以固定的化学量转化为产物,没有中间物积聚。
发酵工程第6章 发酵动力学

则表明通风不足,有部分电子没有传递给
氧,氧化不彻底。
第三节 细胞反应本征动力学
➢反应动力学:研究反应速度变化规律
(反应速度影响因素)的学科。包括:
➢本征动力学(反映生物催化剂内在性
能):又称微观动力学,指没有传递等
工程因素影响时,生化固有的速率。
➢宏观动力学(反映反应器特性):又称
反应器动力学,指在一定反应器内所测
葡萄糖
微生物细胞
(1)试确定计量系数a、b、c、d、e;
(2)试计算其细胞对底物的得率YX / S ;
(3)试计算呼吸商RQ。
解:(1)细胞反应的方程式系数的计算
1mol葡萄糖所含有的C元素为72g,根据题
意1mol葡萄糖转化为微生物细胞的C元素为:
g
72 2 / 3 48
则有:
48
c
(2)细胞反应的比速率:单位时间内单位
菌体消耗基质或形成产物(菌体)的量称为比速
率,是生物反应中用于描述反应速度的常用概念
(不同反应间的对比,消除细胞量的效应)在细
胞反应中主要的反应的比速率有:
① 细胞的比生长速率
1 dC X
CX
dt
(1/h)
② 底物的比消耗速率
1 dC S
qS
0.909
4.4 12
转化为CO2的C元素为:
72 48 24 g
则:
24 12e
e2
,
对N元素平衡,有:
a 0.86c 0.782
对H元素平衡,有:
,
12 3a 7.3c 2d
12 3a 7.3c
d
2
12 3 0.782 7.3 0.909
11.发酵动力学

发酵动力学:研究发酵过程中菌体生长、基质消 耗、产物生成的动态平衡及其内在规律。 内容:微生物生长过程中的质量和能量平衡,发 酵工程中菌体生长速率、基质消耗速率产物生成 速率的相互关系,环境因素对三者的影响及反应 速度的条件。 目的:通过发酵动力学的研究,进行最佳工艺条 件的控制。如菌体浓度、基质浓度、温度、pH、 溶解氧以及各种发酵参数之间的关系,为发酵过 程的工艺控制、发酵罐的设计放大和用计算机对 发酵过程的控制提供依据。
(4) 衰亡期(decline phase)
细胞生活力衰退,死亡率增加,细菌总数急剧 下降。 细胞出现多形态,有的微生物出现自溶现象;
有的会进一步合成或释放对人类有益的抗生素 等次生代谢物;
11.1.2 分批培养的生长动力学方程
比生长速率和限制性营养物浓度的关系的模型表 3-1 1942年Monod提出的Monod方程(莫诺方程)。 比生长速率作为常数条件:特定温度、pH、营养 物的种类、营养物质的浓度条件下
生产实践中缩短迟缓期的常用手段
①通过遗传学方法改变种的遗传特性使迟
缓期缩短;
②利用对数生长期的细胞作为种子;
③尽量使接种前后所使用的培养基组成不
要相差太大;
④适当扩大接种量
(2) 指数期(对数生长期,exponential phase)
①菌数以几何级数增加;生长速率常 数最大,代时最短而且稳定;
产物,产物合成与利用碳源无准量关系,产物合
成在菌体生长停止才开始。
微生物细胞生长和产物生成关系
生长相关型:合成的产物通常是分解代谢的直接 产物,这类初级代谢产物的生产速率与生长直接 相关; 生长部分相关型:生长与产物形成部分相关。 生长非相关型:细胞生长时无产物形成,但细胞 停止生长后,有大量产物积累,产物的形成量只 与细胞的积累量有关;
发酵动力学的应用

发酵动力学的应用发酵动力学是研究发酵过程中菌体生长、基质消耗和产物生成的动力学过程的科学,它在发酵工程的生产实践与科学研究中具有非常重要的指导意义。
通过发酵动力学的研究,人们可以更深入地理解发酵过程的本质,优化发酵工艺,提高产品的产量和质量,降低生产成本,从而为发酵工业的持续发展提供有力的支持。
一、发酵动力学在发酵过程优化中的应用发酵过程优化是发酵工程的核心任务之一,而发酵动力学在这一过程中发挥着重要的作用。
通过构建菌体生长、基质消耗和产物生成的动力学模型,可以对发酵过程进行定量描述和预测,从而为发酵过程的优化提供理论依据。
例如,在抗生素发酵过程中,通过建立菌体生长和抗生素合成的动力学模型,可以研究不同发酵条件下菌体生长速率和抗生素合成速率的变化规律,进而确定最佳的发酵温度、pH值、溶氧量等工艺参数,以提高抗生素的产量和纯度。
二、发酵动力学在发酵产物质量控制中的应用发酵产物的质量是评价发酵工程成功与否的重要指标之一,而发酵动力学对于发酵产物质量的控制具有重要意义。
通过研究发酵过程中产物生成的动力学规律,可以实现对发酵产物质量的实时监控和调控。
例如,在啤酒发酵过程中,通过建立啤酒风味物质生成的动力学模型,可以研究不同发酵阶段啤酒风味物质的变化规律,进而确定适宜的发酵时间和发酵温度,以保证啤酒风味的稳定性和一致性。
三、发酵动力学在发酵新工艺开发中的应用随着生物技术的不断发展,新型发酵工艺不断涌现,而发酵动力学在新工艺开发中具有重要的指导作用。
通过构建新型发酵工艺的动力学模型,可以预测新工艺的可行性和优化方向,从而缩短新工艺的开发周期,降低开发成本。
例如,在开发高密度发酵工艺过程中,通过建立高密度发酵的动力学模型,可以研究高密度条件下菌体生长和产物生成的特殊规律,进而确定适宜的高密度发酵策略和工艺条件,以实现高产、高效的发酵目标。
四、发酵动力学在发酵废弃物处理中的应用发酵工程在生产过程中会产生大量的废弃物,如废水、废气等,这些废弃物的处理对于环境保护和资源利用具有重要意义。
发酵动力学

在连续培养系统中,微生物细胞的浓度、比生 长速率和环境条件(如营养物质浓度和产物浓 度),均处于不随时间而变化的稳定状态之下
在连续培养技术中被称为稀释速率,用符号“D”表示
(等于培养液在罐中平均停留时间的倒数)
在稳定状态下,细胞的比生长速率等于稀释速率。
连续培养过程中的主要问题
杂菌污染问题 生产菌株突变问题
程中,需要长时间连续不断地向 发酵系统供给无菌的新鲜空气和培养基,这就 不可避免地发生杂菌污染问题。 杂菌污染问题是连续培养中难以解决的问题。
要了解污染的杂菌在什么样的条件下会在系统 中发展成为主要的微生物群体。
2. 生产菌株突变问题
微生物在复制过程中难免会出现差错引起突变, 一旦在连续培养系统中的生产菌细胞群体中某 一个细胞发生了突变,而且突变的结果使这一 细胞获得在给定条件下高速生长的能力,那么 它就有可能像杂菌Z一样,取代系统中原来的 生产菌株,而使连续发酵过程失败。
3、产物的形成
K
产物形成的速率 = 产物合成速率-产物移去速率-产物被 破坏速率
二、代谢产物形成的动力学模型
Gaden根据产物生成速率与细胞生长速率之间 的关系,将其分为三种类型:
类型Ⅰ称为相关模型,或称伴随生长的产物形 成模型; 类型Ⅱ称为部分相关模型,或称不完全伴随生 长的产物形成模型; 类型Ⅲ称为非相关模型或称不伴随生长的产物 形成模型。
类型Ⅰ是指产物的生成与细胞的生长相关的过程, 此时产物通常是基质的分解代谢产物,代谢产物的 生成与细胞的生长是同步的。
动力学方程为:
或
类型Ⅱ反应产物的生成与细胞生长仅有间接关系。 在细胞生长期内,基本无产物生成。 动力学方程为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章发酵动力学
发酵动力学是研究各种环境因素与微生物代谢活动之间的相互作用随时间变化的规律的科学。
fermentation kinetics
生化反应工程的基础内容之一,以研究发酵过程的反应速率和环境因素对速率的影响为主要内容。
通过发酵动力学的研究,可进一步了解微生物的生理特征,菌体生长和产物形成的合适条件,以及各种发酵参数之间的关系,为发酵过程的工艺控制、发酵罐的设计放大和用计算机对发酵过程的控
发酵动力学
制创造条件。
研究发酵过程中菌的生长速率、培养基的消耗速率和产品形成速率的相互作用和随时间变化的规律。
发酵动力学包括化学热力学(研究反应的方向)和化学动力学(研究反应的速度)并涉及酶反应动力学和细胞生长动力学。
它为发酵过程的控制、小罐试验数据的放大以及从分批发酵过渡到半连续发酵和连续发酵提供了理论基础。
发酵动力学也是计算机模拟发酵过程研究及发酵过程计算机在线控制的基础。
在发酵中同时存在着菌体生长和产物形成两个过程,它们都需要消耗培养基中的基质,
发酵动力学
因此有各自的动力学表达式,但它们之间是有相互联系的,都是以菌体生长动力学为基础的。
所谓菌体生长动力学是以研究菌体浓度、限制性基质(培养基中含量最少的基质,其他组分都是过量的)浓度、抑制剂浓度、温度和pH等对菌体生长速率的影响为内容的。
在分批发酵中,菌体浓度X,产物浓度P和限制性基质浓度S均随时间t变化
菌体生长可分迟滞、对数、减速、静止、衰退等五个时期。
其中菌体的主要生长期是对数期,它的特点是:
随着基质浓度继续下降,菌体的衰老死亡逐步与生长平衡以至超过生长,也即进入静止和衰退期。
发酵动力学
J.莫诺于1949年提出了一个μ与S间的经验关联式,此式被称莫诺方程式:
μm为最大比生长速率, 即不因基质浓度变化而改变的最大μ值;Ks为饱和常数,即在数量上相当于μ=0.5μm时的S值。
Ks值愈小,说明在低基质浓度范围中,S对μ愈为敏感,而保持μm的临界S值愈低。
在一般情况下,当S>10Ks时,μ=μm 当时,μ=(μm/Ks)S。
产物的形成常与菌体的生长或浓度有关.α、β为常数
;qP为比产物形成速率。
在限制性基质的消耗和菌体生长间常用下式表示:
公式1
式中YG为菌体得率常数;1/YG则为单纯用于合成单位菌体所耗用的基质量;m为维持系数,即单位菌体、单位时间内耗用于菌体维持生命活动的基质量;qS为比限制性基质消耗速率。
若在菌体生长时还伴有产物形成,则
式中YP为产物得率系数;1/YP则为单纯用于合成单位产物所耗用的基质量。
公式2。
